A Collaborative Planning Method for Distributed Energy Storage Based on Differentiated Demands

Abstract

With the continuous increase in the proportion of wind and solar power, the strong randomness and volatility of distributed new energy output have brought great challenges to the planning, regulation, and operation of the new distribution system. Distributed energy storage, with its characteristics such as scattered location distribution, flexible installation, small capacity, and diverse forms and application scenarios, is increasingly becoming an important resource and technical means to enhance the consumption capacity of new energy and ensure the safe and reliable operation of the power system. This paper proposes a collaborative planning method for distributed energy storage based on differentiated demands. First, the typical application scenarios of distributed energy storage are analyzed; secondly, the source–load matching degree and modularity are proposed as cluster division indicators. Voltage fluctuation, load fluctuation, and the net income of distributed energy storage are combined into multiple optimization objectives. Based on differentiated demands, a two-layer optimal configuration model of distributed energy storage is proposed and solved by using the improved particle swarm optimization algorithm. Finally, the feasibility and effectiveness of the proposed method were verified through a modified IEEE33 node simulation example.

1. Introduction

The construction of a new type of power system is an inevitable requirement for the transformation of energy and power, and also an important way to achieve the goals of “carbon peak and carbon neutrality”. However, the high proportion of new energy access has brought profound changes to the power system in many aspects such as planning and configuration, dispatching, and operation. With the continuous increase in the proportion of wind and solar power, the strong randomness and volatility of distributed new energy output have brought great challenges to the planning, regulation, and operation of the new distribution system [1,2,3]. Meanwhile, under the large-scale development trend in new energy such as wind power and photovoltaic power, there will be serious consumption bottlenecks, which will lead to the phenomenon of wind and solar power being abandoned.

Energy storage systems are increasingly becoming an important resource and technical means for enhancing the capacity to accommodate new energy and ensuring the safe and reliable operation of the power system [4,5]. The issue of its planning and configuration has gradually become a research hotspot both at home and abroad [6,7]. At present, there have been many studies on the optimal configuration of energy storage. Reference [8] conducts research on centralized and distributed energy storage and proposes a collaborative planning method. Reference [9] considers enhancing the efficiency and economy of transmission-storage coordinated planning and proposes a transmission-storage planning model for new energy consumption that includes risk measurement. Reference [10] ensures the power quality of the distribution network through the optimal configuration of energy storage. In Reference [11], to achieve economic and reliable operation of energy storage and distribution networks, the energy storage system is modeled considering the average daily comprehensive cost, voltage, and load fluctuations. Reference [12] proposes an energy storage planning method that takes into account the schedulable potential of 5G base stations and the division of distribution network clusters, thereby enhancing the system voltage level and low-carbon benefits. Reference [13] comprehensively considers both the economic performance of the active distribution network under normal conditions and the power supply reliability under fault conditions. A coordinated optimization method for distributed energy storage and dynamic reconstruction is proposed, which is aimed at improving the economic efficiency and reliability of the distribution network.

This paper focuses on the collaborative planning research of distributed energy storage systems (DESSs), aiming to explore their differentiated planning requirements in different scenarios. Compared with centralized energy storage, distributed energy storage has higher flexibility, faster response speed, and shorter construction period, which enables it to better demonstrate its application value in distribution networks. Distributed energy storage can increase the consumption rate of new energy and reduce the phenomenon of wind and solar power curtailment by being built in conjunction with new energy sources. On the power grid side, it can participate in application scenarios such as auxiliary power peak shaving, reserve capacity, grid congestion relief, reactive power support, and auxiliary dynamic operation, enhancing the grid’s regulation capacity and power supply reliability. On the user side, distributed energy storage is used in the form of “low storage and high discharge” for peak–valley difference arbitrage and capacity cost management, improving power quality and power supply reliability. These typical application scenarios of distributed energy storage make it one of the key technologies for the modernization and intelligence of distribution networks, which is of great significance for achieving efficient and reliable operation of the power grid.

According to the installation location and configuration mode of distributed energy storage in the power system, its typical application scenarios are divided into the power generation side, the grid side, and the user side. Reference [14] takes the construction of energy storage in conjunction with new energy as the background and proposes a two-layer optimal configuration model for energy storage. The outer layer considers economic factors, while the inner layer takes into account the operational characteristics of distributed energy storage, effectively reducing the amount of wind and solar power curtailment in new energy. Reference [15] proposed a method for configuring the capacity of distributed energy storage applied in peak shaving scenarios, effectively reducing the difficulty of addressing capacity allocation. Reference [16] proposed a distributed energy storage capacity configuration method to reduce the network loss of the distribution network. Based on the analysis of the difference in electricity consumption on the user side, Reference [17] established a double-layer energy storage sharing model. Reference [18] optimized the capacity configuration of distributed energy storage by considering both economy and voltage quality. However, the above-mentioned literature only conducts research on a single application scenario of distributed energy storage and cannot make configuration plans based on actual differentiated demands.

This paper, through a literature review, finds that the existing research on distributed energy storage planning mostly focuses on a single application scenario and fails to make corresponding configuration planning based on actual differentiated demands. Therefore, it is still necessary to comprehensively consider the source–load characteristics of different regions and the cost/benefit models of energy storage with different configuration methods, and conduct scientific, reasonable, and differentiated planning for large-scale distributed energy storage.

Compared with the existing research results, the novelty and main contributions of this paper are as follows:

• A distributed energy storage planning framework based on differentiated thinking has been established. Cluster division is carried out based on the differentiated source–load characteristics, and the source–load feature matching degree index is proposed to meet the functional principle as the division index. Different configuration methods are selected for energy storage based on the current problem situation in different regions. A major strength of the work is that it does not treat energy storage as a single, uniform asset. Instead, it considers that generation-side storage, grid-side storage, and user-side storage each operate under different physical and economic conditions. This perspective addresses a real gap in the existing literature, where many studies evaluate storage under only one scenario or one revenue model.
• A two-tier planning model for distributed energy storage that coordinates the planning and operation phases was proposed. The outer optimization model takes investment cost, construction cost, and retirement recovery value into account in the energy storage planning. The inner optimization model further introduces differentiated operation cost and revenue models for energy storage, achieving scientific, reasonable, and differentiated planning for large-scale distributed energy storage.
• The improved particle swarm optimization algorithm was adopted to solve the model. Based on the IEEE33 node system, the feasibility and effectiveness of the strategy proposed in this paper were verified by comparing the voltage fluctuation, load fluctuation, and net benefit of three different examples.

The main work of this article includes analyzing the typical application scenarios of distributed energy storage. On this basis, modularity and source–load feature matching degree are used as the basis for cluster division. Voltage fluctuation, load fluctuation, and the net income of distributed energy storage are combined into multiple optimization objectives. A two-layer optimal configuration model of distributed energy storage based on differentiated demands is proposed, and it is solved using the improved particle swarm optimization algorithm. The comprehensive benefits of distributed energy storage systems are maximized.

2. Typical Application Scenarios of Distributed Energy Storage

Distributed energy storage, with its characteristics of flexible access, rapid response, and local regulation, has become a key link in supporting the new power system and plays a crucial role in energy transition and power system optimization.

(1)

Consumption of new energy power generation (photovoltaic/wind power matching)

Renewable energy sources such as distributed photovoltaic and decentralized wind power are affected by weather conditions, and their output power is intermittent (such as when there is no photovoltaic power at night or wind power shuts down when there is no wind) and fluctuating (sudden changes in power within a short period of time), which can easily lead to “wind and solar power curtailment” or fluctuations in grid voltage/frequency. Distributed energy storage systems can smooth out the active power fluctuations of distributed wind and solar power generation, improve power quality, and enhance the ability to track planned output, thereby reducing the impact of distributed wind and solar power generation on the power grid and increasing the consumption rate of distributed new energy.

(2)

Grid peak shaving/frequency regulation/inertia support

With the large-scale integration of new energy into the grid, the peak shaving capacity of traditional thermal power units has declined, and the power grid is facing problems such as “difficulty in peak shaving” (the need to consume excess electricity when wind and solar power are at their peak at night) and “difficulty in frequency regulation” (frequency deviation caused by fluctuations in wind and solar power output). Meanwhile, the high proportion of power electronic devices connected reduces the system inertia, which is prone to cause frequency instability.

The peak shaving and frequency regulation function of distributed energy storage on the grid side is the core value manifestation of it as the “flexible regulation core unit of the new power system”. It directly addresses the two major pain points brought about by the high proportion of renewable energy access and load fluctuations—the peak shaving pressure caused by the expansion of peak–valley difference and the frequency fluctuations caused by the intermittency of new energy. Dynamic support is provided for the power grid through “rapid response + precise control”.

(3)

User-side peak–valley arbitrage/enhancing power supply reliability

The value of user-side energy storage in peak–valley arbitrage and power supply reliability is the key support for it to become a core tool for user-side energy transformation under the “dual carbon” goals. At the peak–valley arbitrage level, user-side energy storage, through a flexible model of “low storage and high discharge”, converts low-priced off-peak electricity into high-priced peak electricity for use, directly reducing the overall electricity cost.

To prevent economic losses to key users in the power system during grid failures or power outages, the reliability of power supply can be effectively enhanced by configuring a certain capacity of energy storage systems as emergency power sources or uninterruptible power supplies. In addition, by configuring energy storage systems with appropriate capacity, efficient and rapid active and reactive power control can be achieved, smoothing out fluctuations in new energy and loads, realizing dynamic voltage adjustment, and providing power support to important users in the event of grid failures, thereby enhancing the reliability of power supply and power quality of the system.

3. Cluster Division

There are too many system nodes in the distribution network. Distributed power sources have the characteristics of small scale and scattered locations. Clustering the nodes within the system is conducive to the regulation and control of the distribution network. All nodes in the same cluster share the same characteristics, which enables unified management of nodes within the cluster, enhancing work efficiency and reducing resource waste. In order to ensure that each group is independent after cluster division while guaranteeing the integrity of the distribution network system, the principles of logic, structure, and functionality must be met.

This paper selects the modularity based on spatial electrical distance to meet the structural principle and simultaneously proposes the source–load feature matching degree index to meet the functional principle as the division index. The source–load characteristic matching degree index is $\xi$, which refers to the matching degree between the distributed energy output curve and the load curves of each node. The expression is as follows:

$$\xi ={\displaystyle \sum _{h=1}^m\frac{{\displaystyle \sum _{i=1}^{24}{x}_{i,h}}{y}_{i,h}}{{\left({\displaystyle \sum _{i=1}^{24}{x}_{i,h}^2}{\displaystyle \sum _{i=1}^{24}{y}_{i,h}^2}\right)}^{\frac{1}{2}}}}$$

(1)

In the formula, $m$ represents the number of clusters, and $x_{i,h}$ and $y_{i,h}$, respectively, denote the sum of the output values of distributed power sources and the sum of the load electricity consumption within cluster $h$ at the $i$-th moment.

Among them, $\left|\xi \right|\le 1$. The closer $\left|\xi \right|$ is to 1, the closer curve $x$ is to curve $y$. The closer $\left|\xi \right|$ is to 0, the greater the difference between curve $x$ and curve $y$.

The theory of modularity $\rho$ proposed by Girvan and Newman is adopted to reflect the dynamic interactivity among nodes within the cluster, and based on this, an improved modularity metric function suitable for weighted networks is constructed to achieve the quantitative evaluation of cluster division. The following formula is given:

$$\rho ={\displaystyle \frac{1}{2m}}{\displaystyle \sum _i{\displaystyle \sum _j\left(B_{ij}-\frac{k_i{k}_j}{2m}\right)}}\delta (i,j)$$

(2)

$$m={\displaystyle \frac{{\displaystyle \sum _i{\displaystyle \sum _j{B}_{ij}}}}{2}}$$

(3)

$$k_i={\displaystyle \sum _j{B}_{ij}}, k_j={\displaystyle \sum _i{B}_{ij}}$$

(4)

$$\delta (i,j)=\left\{\begin{array}{l}1, \mathrm{Node} i \mathrm{and} \mathrm{node} j \mathrm{are} \mathrm{in} \mathrm{the} \mathrm{same} \mathrm{cluster}\\ 0,\mathrm{otherwise}\end{array}\right.$$

(5)

In the formula, $B_{ij}$ represents the edge weight between nodes $i$ and $j$ in the distribution network, determined by the electrical distance between the nodes; $m$ is the sum of the weights of all edges in the distribution network; $k_i$ and $k_j$ are the sums of the weights of all edges connected to nodes $i$ and $j$, respectively; and $\delta (i,j)$ indicates whether nodes $i$ and $j$ belong to the same community.

The electrical distance is calculated by the sensitivity method, and the coupling degree between nodes is characterized by constructing a voltage sensitivity matrix:

$$\Delta V=S_{VP}\Delta P$$

(6)

In the formula, $\Delta V$ represents the change in the voltage magnitude of a node, $S_{VP}$ represents the active voltage sensitivity matrix, and $\Delta P$ represents the change in active power of the node.

The voltage sensitivity $a_{ij}$ is expressed as follows:

$$a_{ij}=\lg {\displaystyle \frac{S_{VP,jj}}{S_{VP,ij}}}$$

(7)

In the formula, $S_{VP,ij}$ is the element in the $i$-th row and $j$-th column of $S_{VP}$, representing the change in voltage at node $i$ corresponding to a unit change in active power at node $j$. The larger the value of $a_{ij}$, the greater the electrical distance between the two nodes, indicating a lower degree of coupling.

The electrical distance between node $i$ and node $j$ is defined as $d_{ij}$ and can be expressed as follows:

$$d_{ij}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{z=1}^n\left(\left|{\alpha }_{iz}-{\alpha }_{jz}\right|\right)}$$

(8)

The expression $B_{ij}$ is given as follows:

$$B_{ij}=1-{\displaystyle \frac{d_{ij}}{\max (d)}}$$

(9)

This paper, based on the modularity and source–sink matching indicators, uses the particle swarm optimization algorithm to perform community division on distribution networks with high penetration of photovoltaic power through distributed energy storage. The specific planning process is as follows:

(1)

Initialize the particle swarm size, dimensions, and number of iterations.

(2)

Initialize the position and velocity of each particle.

(3)

Calculate the fitness value of each particle based on the comprehensive performance indicator calculation formula proposed in this paper.

(4)

Determine whether there are isolated points within the swarm; if there are, update the fitness value through penalty items, but if not, proceed to the next step.

(5)

Update the individual and global optimal swarm position of the particles based on the fitness value, and if the termination condition is met, end the operation; if not, return to step 3.

4. Distributed Energy Storage Planning Model

4.1. Multi-Objective Optimization

The site selection and capacity determination of distributed energy storage are influenced by many factors and are a multi-objective optimization problem. In this paper, three indicators, namely voltage fluctuation, load fluctuation, and net income of energy storage, are selected as the objective functions.

(1)

Voltage fluctuation at nodes. With access to distributed power sources, although the node voltage in the system has increased to a certain extent, the fluctuation has intensified. The objective function of voltage fluctuation is

$$F_1={\displaystyle \sum _{i=1}^{N_{bus}}{\displaystyle \sum _{j=1}^T\left|V_{ij}-{\overline{V}}_i\right|}}$$

(10)

In the formula, $N_{bus}$ represents the number of nodes in the system, $V_{ij}$ represents the voltage value of node $i$ at time $j$, and $\overline{V}$ is the average voltage value of node $i$.

(2)

Load fluctuation. The randomness and uncertainty of distributed power sources can also intensify the load fluctuations in the system. The calculation formula is

$$F_2={\displaystyle \sum _{i=1}^T{\left[P_s(i)-\overline{P}\right]}^2}$$

(11)

In the formula, $P_s(i)$ represents the power input to the grid at time $i$, and $\overline{P}$ represents the average power input to the grid.

(3)

Net income from distributed energy storage. The difference between the total cost and total revenue of distributed energy storage is taken as the objective function, and its calculation formula is

$$F_3=f_{31}+f_{32}$$

(12)

In the formula, $f_{31}$ represents the outer optimization objective of the distributed energy storage planning, and $f_{32}$ represents the inner optimization objective of the distributed energy storage planning. The double-layer optimization framework is shown in Figure 1.

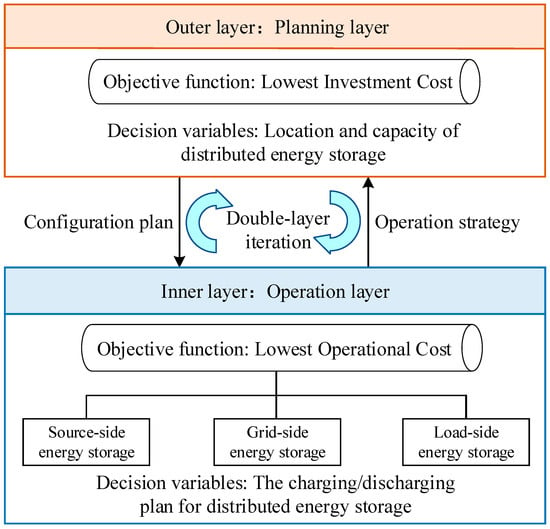
Figure 1. Double-layer programming framework.

After comprehensively taking into account the voltage fluctuations of system nodes, load fluctuations, and the net income of energy storage, the multi-objective optimization function for the location and capacity determination of distributed energy storage is as follows:

$$\min F=[F_1,F_2,F_3]$$

(13)

4.2. Outer-Layer Optimization Model

This paper selects the currently operating distribution network as the research object. A two-layer optimization model for distributed energy storage is established. The annual total cost of a distributed energy storage system mainly includes the initial investment cost of distributed energy storage, construction cost, battery scrapping cost, and retirement and recycling cost. The objective function of the inner planning stage is

$$\min f_{31}=C_{in}+C_{\mathrm{IC},\mathrm{D}}+C_{\mathrm{ess}\_\mathrm{scrap}}-S^{ess\_recycle}$$

(14)

$$C_{in}=\left[{\displaystyle \sum _{i=1}^{N_{\mathrm{DESS}}}\left(a{E}_{\mathrm{DESS},i}+b{P}_{\mathrm{DESS},i}\right)}\right]\times \mu$$

(15)

$$\mu ={\displaystyle \frac{\rho {(1+\rho )}^{\gamma }}{{(1+\rho )}^{\gamma }-1}}$$

(16)

In the formula, $C_{in}$ represents the initial investment cost of distributed energy storage, $N_{DESS}$ represents the number of energy storage devices, $E_{\mathrm{DESS},i}$ represents the rated capacity of the $i$-th energy storage device, $P_{\mathrm{DESS},i}$ represents the rated power of the $i$-th energy storage device; $a$ and $b$ represent the unit capacity investment cost and unit power investment cost of energy storage, respectively; $\mu$ is the annual capital recovery rate; $\gamma$ is the service life of the distributed energy storage system; and $\rho$ is the discount rate.

$$C_{\mathrm{IC},\mathrm{D}}=\mu {\displaystyle \sum _{i\in \phi }{c}_{\mathrm{CON}.\mathrm{D}}{E}_i^{\mathrm{DES}}}$$

(17)

In the formula, $C_{\mathrm{IC},\mathrm{D}}$ represents the construction cost of distributed energy storage, $\phi$ represents the set of installation nodes for DESS, $c_{\mathrm{CON}.\mathrm{D}}$ represents the civil construction cost per unit capacity of DESS, and $E_i^{\mathrm{DES}}$ represents the capacity of DESS configured at node $i$.

$$C_{\mathrm{ess}\_\mathrm{scrap}}=c_{\mathrm{scrap}\_\mathrm{e}}^{\mathrm{ess}}{E}_{\mathrm{rated}}^{\mathrm{ess}}{(1+\rho )}^{-\gamma }$$

(18)

In the formula, $C_{\mathrm{ess}\_\mathrm{scrap}}$ represents the scrapping cost of energy storage, $c_{\mathrm{scrap}\_\mathrm{e}}^{\mathrm{ess}}$ represents the scrapping cost per unit battery, and $E_{\mathrm{rated}}^{\mathrm{ess}}$ represents the total planned capacity of the energy storage station.

$$S^{\mathrm{ess}\_\mathrm{recycle}}=\left(\delta (C_{in}+C_{om}){(1+\rho )}^{-\gamma }\right)$$

(19)

In the formula, $S^{\mathrm{ess}\_\mathrm{recycle}}$ represents the scrapping and recycling value of the energy storage station, $\delta$ is the scrapping and recycling value coefficient, taken as 5%, and $C_{om}$ represents the operation and maintenance cost of energy storage.

Constraint conditions:

Optional ensemble constraints for distributed energy storage planning are represented as follows:

$$\left\{\begin{array}{l}i\in {\phi }_I\\ j\in {\phi }_J\\ k\in {\phi }_K\end{array}\right.$$

(20)

In the formula, $i$, $j$, $k$ represent the nodes that can be equipped with distributed energy storage, ${\phi }_I$ represents the area where new energy sources are connected with energy storage, ${\phi }_J$ represents the area where independent energy storage stations are connected, and ${\phi }_K$ represents the area where user-side energy storage is connected.

Constraints on the number and capacity of distributed energy storage configurations are represented as follows:

$$\begin{array}{l}{E}_{i,\min }^{\mathrm{DES}} \le E_i^{\mathrm{DES}}\le E_{i,\max }^{\mathrm{DES}}\\ N_{es}^{\min } \le N_{es} \le N_{es}^{\max }\end{array}$$

(21)

In the formula, $E_{i,\max }^{\mathrm{DES}}$ and $E_{i,\min }^{\mathrm{DES}}$ represent the upper and lower limits of the distributed energy storage capacity at node i, respectively; $N_{es}^{\max }$ and $N_{es}^{\min }$ represent the upper and lower limits of the energy storage site selection positions.

4.3. Inner-Layer Optimization Model

The inner operation stage includes operating costs and operating income. The objective function of the inner optimization model is

$$\min f_{32}=C_{om}-S$$

(22)

$$C_{om}={\lambda }_{\mathrm{OM}.\mathrm{D}}{\displaystyle \sum _{y\in Y}{\theta }_y{D}_y}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i,j,k\in {\phi }_{I,J,K}}{c}_{\mathrm{IN}.\mathrm{D}}^{\mathrm{P}}}}\left|P_{t,y,i}^{\mathrm{DES}}\right|$$

(23)

In the formula, $C_{om}$ represents the operation and maintenance cost of distributed energy storage; $D_y$ is the total number of days in a year; ${\theta }_y$ is the proportion of typical season $y$ days in the whole year; $Y$ is the set of typical seasons; $T$ is the total number of time periods in a dispatch cycle, $T$ = 24 h; ${\lambda }_{\mathrm{OM}.\mathrm{D}}$ is the operation and maintenance cost coefficient per unit power of distributed energy storage; $c_{\mathrm{IN}.\mathrm{D}}^{\mathrm{P}}$ is the production cost per unit power of DESS; and $P_{i,t,y}^{\mathrm{DES}}$ is the active power output of the distributed energy storage at node $i$ during time period $t$ in typical season $y$.

Based on the differentiated demand at the terminal, distributed energy storage is divided into three typical configuration scenarios: new energy storage co-located with new energy, grid-side independent storage, and user-side storage.

(1)

Scenarios for energy storage in conjunction with new energy

In the scenario of new energy being equipped with energy storage, the revenue is divided into peak–valley price difference revenue, new energy consumption revenue, and capacity leasing revenue:

$$S=S_{in1}+S_{re}+S_{zl}$$

(24)

$$S_{in1}={\displaystyle \sum _{y\in Y}{\theta }_y{D}_y}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i\in {\phi }_I}\left(p_{\mathrm{pur},\mathrm{t}}{P}_{\mathrm{cha},t,y,i}-p_{\mathrm{sell},\mathrm{t}}{P}_{\mathrm{dis},t,y,i}\right)}}$$

(25)

In the formula, $S_{\mathrm{in}1}$ represents the peak–valley price difference revenue, in yuan; $p_{\mathrm{pur},t}$ and $p_{\mathrm{sell},t}$ represent the purchase and sale electricity prices of energy storage at time $t$, respectively; $P_{\mathrm{cha},t,y,i}$ and $P_{\mathrm{dis},t,y,i}$ represent the charging and discharging power of energy storage $i$ at time $t$ during typical season $y$, respectively; and $T$ is the operating duration of a day, $T$ = 24 h.

$$S_{re}={\displaystyle \sum _{y\in Y}{\theta }_y{D}_y}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i\in {\phi }_I}{p}_{\mathrm{re},t,y}{E}_{\mathrm{out},t,y,i}}}$$

(26)

In the formula, $S_{re}$ represents the revenue from the consumption of new energy, $p_{\mathrm{re},t,y}$ represents the electricity price of renewable energy at time $t$ during typical season $y$, and $E_{\mathrm{out},t,y,i}$ represents the amount of renewable energy curtailed by energy storage $i$ at time $t$ during typical season $y$.

$$S_{zl}={\displaystyle \sum _{y\in Y}{\theta }_y{D}_y}{\displaystyle \sum _{i\in {\phi }_I}{E}_{\mathrm{DESS},i}{Y}_{zl,y}T}$$

(27)

In the formula, $S_{zl}$ represents the total revenue from capacity and rental; $Y_{zl,y}$ represents the rental price during typical season $y$; and $T$ represents the rental period.

(2)

Independent energy storage scenarios on the grid side

$$S=S_{in1}+S_{zl}+S_{2,s}$$

(28)

$$S_{2,s}={\displaystyle \sum _{y\in Y}{\theta }_y{D}_y}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{j\in {\phi }_J}\left[P_{\mathrm{com},t,y,i}\left({\eta }_{\mathrm{C}}{P}_{c,t,y,i}+{\eta }_{\mathrm{D}}{P}_{d,t,y,i}\right)\right]}}$$

(29)

In the formula, $S_{2,s}$ represents the peak shaving compensation revenue, $P_{\mathrm{com},t,y,i}$ represents the peak compensation price for the $i$-th energy storage unit at time $t$ during typical season $y$, in yuan; ${\eta }_{\mathrm{C}}$ and ${\eta }_{\mathrm{D}}$ are the charging and discharging efficiencies of the energy storage, respectively, expressed as percentages; $P_{c,t,y,i}$ and $P_{d,t,y,i}$ are the charging and discharging powers of energy storage unit $i$ at time $t$ during typical season $y$, respectively; and $\Delta t$ represents the sampling time step, which is taken as 1 h in this paper.

(3)

User-side energy storage

$$S=S_{in1}+S_{bas}$$

(30)

$$S_{bas}={\displaystyle \sum _{t=1}^{\gamma }M}\theta (P_{\mathrm{peak},\mathrm{m}}-{P^{\prime }}_{\mathrm{peak},\mathrm{m}}){\left({\displaystyle \frac{1+i_r}{1+\rho }}\right)}^{\gamma }$$

(31)

In the formula, $S_{bas}$ represents the demand reduction revenue, $B_2$ represents the demand reduction revenue (demand response revenue) for energy storage in a month, $M$ represents the number of months of operation per year, $\theta$ represents the basic electricity price, $P_{\mathrm{peak},\mathrm{m}}$ represents the original monthly peak load peak value, ${P^{\prime }}_{\mathrm{peak},\mathrm{m}}$ represents the monthly peak load value after installing energy storage, and $i_r$ represents the inflation rate.

Constraints: Energy balance constraints of the energy storage system are represented as follows:

$${\mathrm{SOC}}_{i,1}^{DESS}={\mathrm{SOC}}_{i,T+1}^{DESS}$$

(32)

$$\begin{array}{ll}{\mathrm{SOC}}_{i,t+1}^{DESS}=& {\mathrm{SOC}}_{i,t}^{DESS}+{\displaystyle \frac{{\eta }_{cha}{P}_{i,t,cha}^{DESS}{K}_{i,t,cha}^{DESS}}{E_i^{DESS}}}\\ & +{\displaystyle \frac{P_{i,t,dis}^{DESS}{K}_{i,t,dis}^{DESS}}{{\eta }_{dis}{E}_i^{DESS}}}\end{array}$$

(33)

In the formula, ${\eta }_{cha}$ and ${\eta }_{dis}$ represent the charging and discharging efficiency of the DESS, respectively; $T$ is the total number of time periods in a dispatch cycle, $T$ = 24 h; ${\mathrm{SOC}}_{i,t}^{DESS}$ represents the state of charge of the DESS at node $i$ at time period $t$; $K_{i,t,cha}^{DESS}$ and $K_{i,t,dis}^{DESS}$ are the charging and discharging state indicators of the DESS at node $i$, where 0 indicates discharging and 1 indicates charging; $P_{i,t,cha}^{DESS}$ and $P_{i,t,dis}^{DESS}$ are the charging and discharging powers of the DESS at node $i$ at time period $t$, respectively; and $E_i^{DESS}$ represents the capacity of the DESS at node $i$.

Constraints on the charging and discharging state of the energy storage are represented as follows:

$$\left\{\begin{array}{l}0\le P_{i,t,cha}^{DESS}\le K_{i,t,cha}^{DESS}{P}_{i,cha,\max }^{DESS}\\ 0\le P_{i,t,dis}^{DESS}\le K_{i,t,dis}^{DESS}{P}_{i,dis,\max }^{DESS}\\ K_{i,t,cha}^{DESS}{K}_{i,t,dis}^{DESS}=0\\ {\mathrm{SOC}}_{\min }^{DESS}\le {\mathrm{SOC}}_{i,t}^{DESS}\le {\mathrm{SOC}}_{\max }^{DESS}\end{array}\right.$$

(34)

In the formula, $P_{i,cha,\max }^{DESS}$ and $P_{i,dis,\max }^{DESS}$ represent the maximum charging and discharging power of the DESS at node $i$ during time period $t$, respectively, and ${\mathrm{SOC}}_{\max }^{DESS}$ and ${\mathrm{SOC}}_{\min }^{DESS}$ represent the upper and lower limits of the state of charge of the DESS, respectively.

Constraints on node voltage are represented as follows:

$$U_i^{\min }\le U_i\le U_i^{\max }$$

(35)

In the formula, $U_i^{\min }$ and $U_i^{\max }$ represent the minimum and maximum voltage values at node $i$, respectively.

Branch power constraints are represented as follows:

$$\left\{\begin{array}{l}{P}_{ij,\min }\le P_{ij}\le P_{ij,\max }\hfill \\ Q_{ij,\min }\le Q_{ij}\le Q_{ij,\max }\hfill \end{array}\right.$$

(36)

In the formula, $P_{ij}$ and $Q_{ij}$ represent the active and reactive power transmitted through branch $ij$, respectively; $P_{ij,\max }$ and $P_{ij,\min }$ represent the upper and lower limits of active power, respectively; and $Q_{ij,\max }$ and $Q_{ij,\min }$ represent the upper and lower limits of reactive power, respectively.

Peak shaving and valley filling constraints: To ensure the effectiveness of demand reduction revenue, the total load on the user’s side of the main line must not exceed the monthly load peak value, and the monthly load peak value must not exceed the annual peak value. The constraints are as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{load},t}-P_{\mathrm{dis},t}+P_{\mathrm{ch},t}\le {P^{\prime }}_{\mathrm{peak}.\mathrm{m}}\\ {P^{\prime }}_{\mathrm{peak}.\mathrm{m}}\le {P^{\prime }}_{\mathrm{peak}.\mathrm{y}}\end{array}\right.$$

(37)

In the formula, $P_{\mathrm{load},t}$ represents the user load power at time period $t$; $P_{\mathrm{ch},t}$ and $P_{\mathrm{dis},t}$ represent the charging and discharging powers of the energy storage at time period $t$, respectively; and ${P^{\prime }}_{\mathrm{peak}.\mathrm{y}}$ represents the annual peak load value after installing energy storage.

Power balance constraints are represented as follows:

$${\displaystyle \sum _{k=1}^{N_{bus}}{P}_{k,t}}+{\displaystyle \sum _{l=1}^{N_l}{P}_{l,t}^{\mathrm{loss}}}={\displaystyle \sum _{i=1}^{N_{DESS}}{P}_{i,t}}+{\displaystyle \sum _{w=1}^{N_{\mathrm{w}}}{P}_{w,t}^W}+{\displaystyle \sum _{v=1}^{N_{\mathrm{v}}}{P}_{v,t}^V}$$

(38)

In the formula, $P_{k,t}$ represents the active power at node $k$ at time period $t$; $P_{l,t}^{\mathrm{loss}}$ represents the grid power loss on line $l$ during period $t$; $P_{i,t}$ represents the power of the $i$-th energy storage unit at time period $t$; $P_{w,t}^W$ represents the power generation of the $w$-th distributed wind farm at period $t$; $P_{v,t}^V$ represents the power generation of the $v$-th distributed photovoltaic power station at period $t$; $N_{bus}$ represents the number of nodes; $N_l$ represents the number of lines; $N_w$ represents the number of distributed wind farms; and $N_v$ represents the number of distributed photovoltaic power stations.

This paper uses the improved multi-objective particle swarm optimization algorithm to solve the above model. The initial parameters of the improved particle swarm algorithm are set as follows: initial population size is 50, dimension is 260, number of iterations is 50, maximum inertia weight is 0.9, minimum inertia is 0.4, and self-learning factor and swarm learning factor are both set to 1.4962. By initializing the position and velocity of the swarm, calculating the objective function value of each particle, and determining the historical best and global best solutions of each particle, the inertia weight and velocity of each particle are updated through the calculation formula, and the position distribution of each particle is updated to ultimately obtain the global optimal solution.

5. Simulation Verification

To verify the effectiveness of the comprehensive performance indicators proposed in this paper and the particle swarm optimization algorithm in the division of distribution network clusters, the algorithm guides the selection of inertia weight according to the distance between each particle and the global best particle of the population, enabling the adaptive adjustment of inertia weight for each particle. When the distance between them is small, a crossover and mutation operation is introduced to avoid falling into local optimal solutions. Meanwhile, dynamic crowding distance sorting is adopted to update the non-dominated solution set and guide the selection of the global optimal solution of the population, ensuring the scale of the solution set while achieving a more uniform distribution of solutions. To avoid the impact of decision-makers’ preferences on the final results, an ordinal preference method based on information entropy is used to select the optimal energy storage access scheme from the optimal Pareto solution set. An improved IEEE33 node system is adopted as an example for simulation analysis. Among them, a total of 13 distributed photovoltaic systems were connected at nodes 4, 7, 8, 9, 14, 15, 19, 20, 24, 25, 29, 30, and 32. The installed capacity at each photovoltaic location is shown in Table 1. In the same system, the positions of each photovoltaic are close, so the same photovoltaic output curve is adopted. The corresponding photovoltaic output curve is shown in Figure 2. The load curve adopts the typical daily load curve given in reference [19].

Table 1. The installation location and capacity of photovoltaic systems.

Node Location	Installation Capacity/kw
4	250
7	350
8	350
11	350
14	350
15	450
19	350
20	450
24	350
25	350
29	550
30	350
32	450

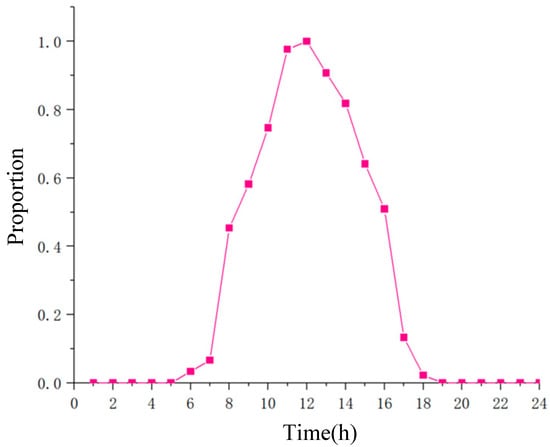
Figure 2. Photovoltaic output curve graph.

5.1. Comparison of Optimization Results Based on Cluster Division

The clusters were divided based on modularity and source–load feature matching degree and were divided into a total of six regions. The results are shown in Figure 3.

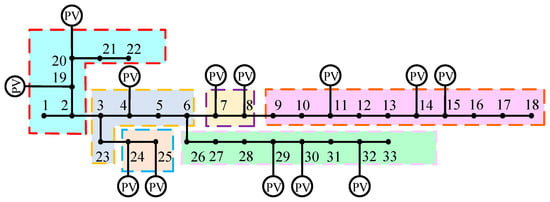
Figure 3. The division results of distributed energy storage clusters.

To verify the optimization results of the cluster division model proposed in this paper, the distributed energy storage planning scheme considering differentiated demands is compared with the traditional distributed energy storage optimization scheme and the non-energy storage scheme. The improved particle swarm optimization algorithm is adopted to optimize the energy storage of the scheme. Among them, scheme 1 considers the benefit results under different configuration methods of distributed energy storage. Scheme 2 adopts an independent energy storage configuration method, while scheme 3 does not consider energy storage. The optimization results of the energy storage installation location, total installation capacity, net income of energy storage, node voltage fluctuation, and network loss under the three schemes are shown in Table 2. The location diagrams of distributed energy storage for two different schemes are shown in Figure 4 and Figure 5.

Table 2. Comparison of energy storage optimization results under different schemes.

Plan	Install the Node		Installation Capacity (MWh)
1	4, 6, 12, 13, 14, 22, 27, 28, 30, 31		1.069/0.24/1.235/1.103/1.124/1.085/0.819/1.103/1.103/1.124
2	4, 7, 13, 14, 10, 26, 30, 26, 20, 28		1.318/0.504/0.257/1.235/0.257/1.390/1.282/1.282/1.282/1.201
Plan	Net income (CNY)	Voltage fluctuation/pu	Load fluctuation/pu	Total capacity (MWh)
1	4,130,022.4108	0.3834	1.0478	10
2	1,713,622.8747	0.3956	0.9142	10
3	0	0.3846	0.9273	0

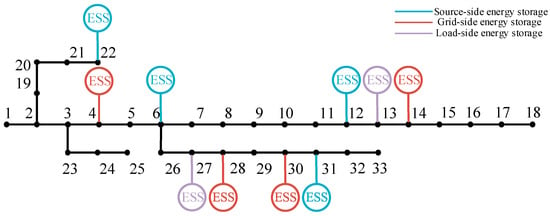
Figure 4. Plan one: site selection map.

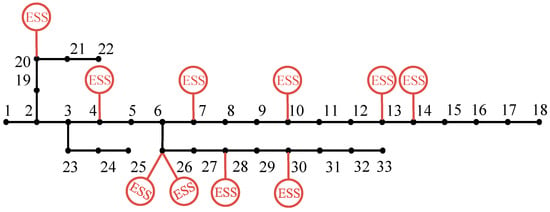
Figure 5. Plan two: site selection map.

5.2. Analysis of Distributed Energy Storage Planning Results Under Cluster Division

The revenue results of distributed energy storage based on different configuration methods are shown in Table 3 [20]. The Pareto solution set corresponding to scheme 1 is shown in Figure 6.

Table 3. The revenue results of distributed energy storage.

Peak–Valley Price Difference Gain (CNY)	Lease Income (CNY)	Peak Shaving Compensation Income (CNY)	Revenue From the Consumption of New Energy (CNY)	Demand Reduction Revenue (CNY)	Government Subsidy Income (CNY)
181,537.1265	2,001,000	832,679.6034	47,982.024	3,836,817.9389	462,627.372

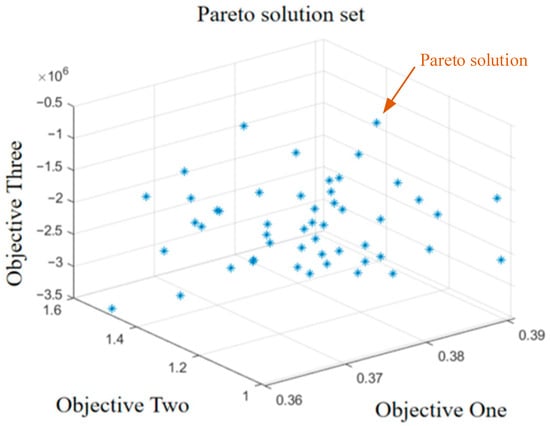
Figure 6. The distribution of Pareto solutions.

The improved particle swarm optimization algorithm has excellent search accuracy. As observed from the Pareto solution set plot, the number of solution points is abundant and their distribution is relatively uniform, covering different trade-off regions in the multi-objective space. This indicates that the solving algorithm exhibits good breadth and balance in exploring the Pareto front, thus providing decision-makers with a rich set of “optimal trade-off solutions” to choose from.

The 24 h output of the distributed energy storage optimized by taking node 6 as an example under the proposed scheme in this paper is shown in Figure 7. Combining the photovoltaic output curve and load changes in Figure 1, it can be seen that in the zeroth to the fifth time period, the night load is relatively low, and the energy storage maintains the load demand after a brief discharge. At this time, the electricity price is relatively low, so the energy storage stores electricity again in this period. In the 7th to the 10th time period, the morning load is relatively high, but the new energy power generation has not yet reached its peak, and it is difficult to meet the load demand. At this time, the energy storage is discharging. From the 10th to the 15th period, the power generation of new energy gradually reaches its peak and can meet the load demand. The discharge of distributed energy storage gradually decreases. Overall, energy storage charges at night when electricity prices are low and discharges during peak hours to achieve the purpose of peak shaving and valley filling. Figure 8 and Figure 9, respectively, show the output of load-side energy storage and independent energy storage configuration modes, corresponding to nodes 4 and 5.

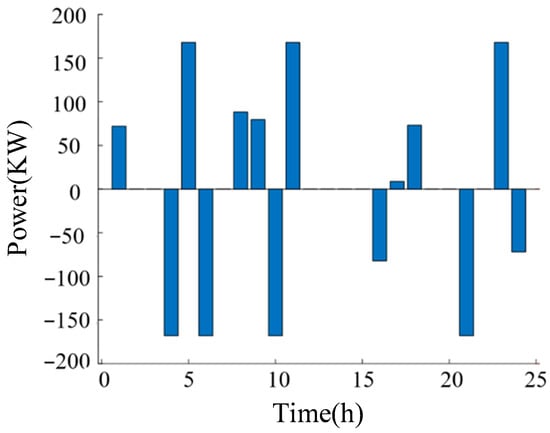
Figure 7. Power generation for 24 h under source-side energy storage mode.

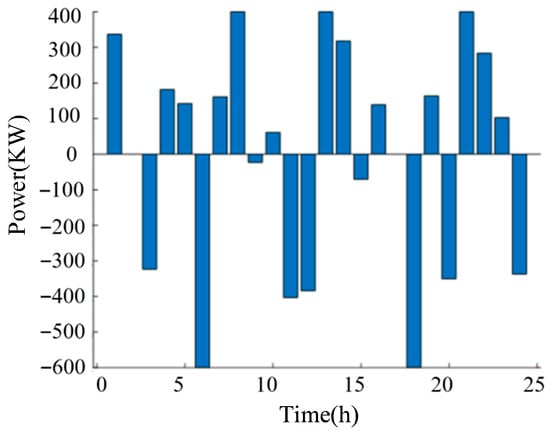
Figure 8. Power generation for 24 h under load-side energy storage mode.

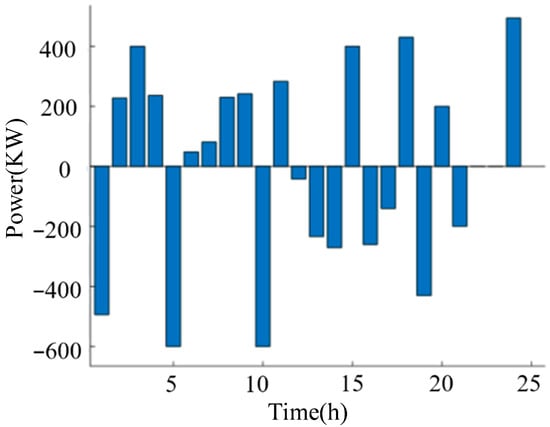
Figure 9. Power generation for 24 h under independent energy storage mode.

6. Conclusions

The main work of this article includes analyzing the typical application scenarios of distributed energy storage. On this basis, modularity and source–load feature matching degree are used as the basis for cluster division. Voltage fluctuation, load fluctuation, and the net income of distributed energy storage are combined into multiple optimization objectives. A two-layer optimal configuration model of distributed energy storage based on differentiated demands is proposed and is solved using the improved particle swarm optimization algorithm. The comprehensive benefits of distributed energy storage systems are maximized. The economic assumptions (pricing structures, incentives, rental income models, etc.) are scenario-based and may vary in real deployments. This research is based on typical daily scenarios. More refined research will be further carried out in the future (e.g., 15 or 5 min intervals).