Mechanisms of Proppant Pack Instability and Flowback During the Entire Production Process of Deep Coalbed Methane

Abstract

Deep coalbed methane (DCBM) reservoirs often experience severe proppant flowback during large-scale hydraulic fracturing, which undermines fracture conductivity and limits long-term recovery. The critical flowback velocity (CFVP) is the key parameter controlling proppant pack instability and flowback. In this study, the instability and flowback behavior of proppant packs throughout the entire production process, from early water flowback to late gas-dominated stages, were systematically investigated. Proppant flowback under closure stress was simulated using a CFD–DEM approach to clarify the flowback process and mechanical mechanisms. Laboratory experiments on coal fracture surfaces under gas-liquid two-phase and gas-liquid-solid three-phase conditions were then conducted to quantify CFVP and its variation across different production stages. Finally, a semi-empirical CFVP predictive model was developed through dimensional analysis. Results show that proppant flowback proceeds through three distinct stages—no flowback, gradual flowback, and rapid flowback. Increasing fracture width reduces proppant pack stability and lowers CFVP but allows higher flow capacity, and within the typical gas and water production ranges of deep coalbed methane reservoirs, flowback is significantly reduced when the width exceeds about 8 mm. Closure stress enhances CFVP below 15 MPa but has little effect above this threshold, while higher stresses progressively stabilize the proppant pack and minimize flowback. Larger average proppant size raises CFVP and preserves conductivity, whereas higher gas–liquid ratios elevate CFVP and reduce flowback, with ratios above 40 sustaining consistently low flowback levels. These findings clarify the mechanisms and threshold conditions of proppant flowback, establish quantitative CFVP benchmarks, and deliver theoretical as well as experimental guidance for optimizing DCBM production.

1. Introduction

China possesses an estimated 45.81 × 10¹² m³ of deep coalbed methane (DCBM) resources buried at depths greater than 1500 m [1]. Since 2019, significant breakthroughs have been achieved in the development of DCBM. In 2024, the daily gas production of the Daning–Jixian block exceeded 7.0 × 10⁶ m³, establishing the world’s first million-ton oil-equivalent DCBM field [2,3]. Reservoir stimulation has been conducted using large-scale volume fracturing, with proppant injection per horizontal well stage reaching 400–600 m³ [4,5]. However, severe proppant flowback has been observed during production, with sand-producing wells accounting for 57% of all workovers. The flowback period ranges from 1 to 11 months, covering all production stages of DCBM wells [6]. Proppant entering the wellbore can damage downhole equipment and disrupt production continuity [7,8]. More critically, proppant flowback near the wellbore leads to fracture closure and failure, thereby reducing the estimated ultimate recovery (EUR) of wells [9,10,11]. Therefore, proppant flowback remains a critical challenge in the development of DCBM.

Stim-Lab experimentally divided the fracture during the flowback process into three zones: the near-well angle stability zone, the channelized flow zone, and the matrix flow zone [12]. Numerical simulations are often applied to investigate the underlying microscopic mechanisms. Roman employed the discrete element method (DEM) to simulate proppant flowback during fracture closure, where drag forces were directly calculated using empirical formulas without coupling the fluid field [13]. Federico simulated rough fracture surfaces using a quadrangular pyramid model and conducted proppant flowback studies based on coupled computational fluid dynamics and discrete element method (CFD–DEM) [14]. Similarly, Sun [15] and Liu [16] constructed a rough fracture model and applied CFD–DEM to simulate proppant placement and flowback behavior in supercritical CO₂-fractured systems, classifying the pre-closure flowback into three stages: translation-controlled, rolling-controlled, and stable. However, the mechanisms and processes of proppant flowback after fracture closure remain insufficiently understood. It is generally accepted that the stability of the proppant pack is closely related to the formation of sand bridges within fractures [17]. The bridging limit of proppants depends on the ratio of fracture width to particle width (w/d), yet its critical value remains debated [18]. Naval [19] identified a critical w/d value of 3–6 through experiments, whereas Dimitry [20] argued that proppant packs become unstable when w/d exceeds 3. When the width-to-diameter ratio surpasses the critical threshold and the combined tangential and drag forces overcome interparticle friction, proppants lose stability and initiate flowback. Daneshy further highlighted three prerequisites for proppant flowback: initiation of particle motion, maintenance of particle transport, and the presence of an unrestricted flow path [21]. Among these, the critical flowback velocity (CFVP)—defined as the fluid velocity within the fracture at which proppant motion begins—represents the key controlling factor. In field operations, CFVP can serve as a reference for adjusting production rates to effectively suppress proppant flowback [22,23].

In early studies, Mark measured CFVP under zero confining stress using a Pipe-Perforation apparatus [24]. However, the cylindrical geometry was not representative of natural fracture morphology. Romero [25], Diederik [26], Chen [27] employed parallel-plate devices, similar to those used for proppant placement, to simulate flowback. The advantage of such devices lies in the direct observation of proppant migration within fractures, though they cannot realistically apply closure stress to fracture walls. Unlike the placement stage, the rapid pressure decline following pump shutdown subjects the proppant pack to fracture closure stress, making its mechanical response more complex. Naval utilized a parallel-plate device capable of applying low closure stress and observed that higher stress led to increased proppant flowback, though real rock surfaces were not considered [19]. The embedding of proppants into fracture walls can enhance stability by anchoring particles, which led to the widespread use of modified API linear cells in flowback experiments. Guo [28] applied API cells to investigate flowback in fractures within steel plates, sandstones, and shale blocks. Dimitry [29] and ElSebaee [30] modified the API cell into a square configuration and obtained the quantitative relationship of CFVP with w/d and closure stress. Liu also used improved square API cells to test CFVP under varying closure stresses, proppant types, and other conditions [31]. Additionally, Zhang employed a Hassler-type core holder to systematically study CFVP in shale fractures [32]. The key difference lies in the loading method: API cells apply stress by moving plates hydraulically in the vertical fracture direction, whereas Hassler core holders load confining pressure radially on cylindrical cores, realistically simulating local closure after proppant flowback. Notably, existing studies on proppant flowback have mainly focused on liquid–solid or gas–solid conditions, without addressing the more realistic gas–liquid–solid transport that develops shortly after drainage in deep coal seams [33,34]. In addition, coal is mechanically weak and prone to proppant embedment, particle breakage, and fines generation, all of which complicate particle stability and alter flowback pathways [35]. While recent international studies have primarily targeted shale and tight-gas reservoirs, the earlier multiphase evolution and stronger coal–proppant interactions in DCBM make its flowback behavior fundamentally different from global shale cases. These factors introduce large uncertainties into the determination of CFVP and lead to inconsistent flowback criteria reported in the literature. Therefore, a clearer understanding of multiphase flowback behavior is still required to support the production characteristics of DCBM reservoirs.

Previous studies on proppant flowback did not incorporate closure stress into numerical simulations, leaving the post-closure flowback mechanisms unclear. In addition, the lack of proppant flowback experiments under gas–liquid–solid three-phase conditions and on realistic coal fracture surfaces has limited the understanding of the critical flowback conditions during the water-drainage and gas–water co-production stages in DCBM reservoirs. In this work, a CFD–DEM approach was used to simulate proppant flowback under closure stress, to clarify the full flowback process and the underlying mechanical interactions. Building on these insights, the principal controlling factors were identified, and the CFVP was systematically examined for different production stages in coal fractures. Finally, a semi-empirical CFVP model for the water production and gas–water co-production stages was developed through dimensional analysis. These integrated investigations clarify the mechanisms of proppant migration and provide practical guidance for field operations, enabling production rate adjustment based on the critical flowback velocity to effectively control proppant flowback in deep coalbed methane wells.

2. Numerical and Experimental Methods

2.1. Numerical Simulation

Under closure stress loading and real core-wall conditions, the proppant flowback process cannot be directly visualized in experiments, and it is difficult to reveal the underlying microscopic mechanisms. The CFD–DEM method treats the fluid as a continuous phase and the particles as discrete elements, incorporating fluid–solid interactions to achieve two-way coupling, thereby enabling accurate simulation of particle transport within the flow field. Therefore, CFD–DEM was employed to simulate proppant flowback under closure stress loading, with the aim of elucidating the flowback process and its mechanical mechanisms.

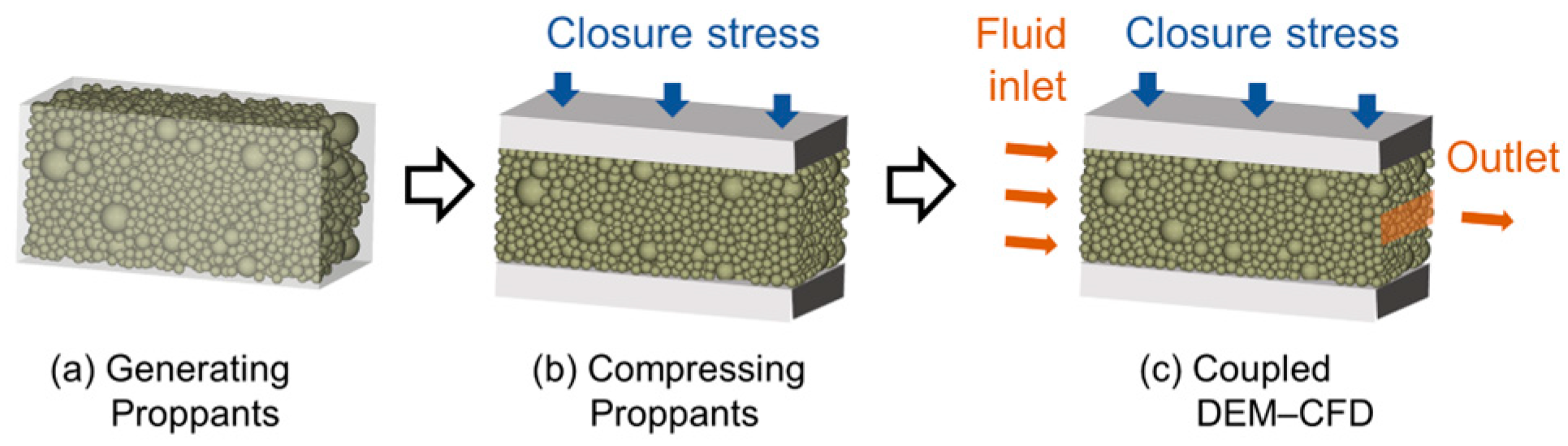
2.1.1. Numerical Model

In DEM, the Lagrangian approach is employed to solve Newton’s second law, calculating the translational and rotational motions of each particle. In the model, the fracture walls were represented by particles with an infinite radius, equivalent to smooth planar boundaries. Therefore, the closure stress was treated as a uniformly applied normal load on the wall surfaces to simulate the overall compressive effect of fracture closure.

$$m_p{\displaystyle \frac{d{v}_p}{dt}}=F_{pp}+F_{pw}+F_{fp}+m_{p}g$$

(1)

$$I_p{\displaystyle \frac{d{\omega }_p}{dt}}=T_{pp}+T_{pw}+T_{fp}$$

(2)

In the equation:

m_p—particle mass, kg;

I_p—particle moment of inertia, kg·m²;

v_p—particle velocity, m/s;

ω_p—particle angular velocity, rad/s;

F_pp—interparticle force, N;

T_pp—interparticle torque, N·m;

F_pw—particle–wall interaction force, N;

T_pw—particle–wall interaction torque, N·m;

F_fp—fluid–particle interaction force, N;

T_fp—fluid–particle interaction torque, N·m.

The contact forces between particles and the wall were calculated using the Hertz–Mindlin contact model:

$$F_{cn}={\displaystyle \frac{4}{3}}{E}^{*}\sqrt{R^{*}}{\delta }_n^{3/2}-{\gamma }_n{v}_n$$

(3)

$$F_{ct}=-8G^{*}\sqrt{R^{*}{\delta }_n}{\delta }_t+{\gamma }_t{v}_t$$

(4)

In the equation:

F_cn, F_ct—normal force and tangential force, N;

$E^{*}$, $G^{*}$—equivalent elastic modulus and shear modulus, Pa;

$R^{*}$—equivalent radius, m;

δ_n, δ_t—normal overlap and tangential displacement increment, m;

γ_n, γ_t—normal and tangential damping coefficients, s⁻¹;

v_n, v_t—relative normal and tangential velocities, m/s.

The fluid forces acting on particles mainly include drag force (F_D), pressure gradient force (F_∇p), virtual mass force (F_vm), and lift force (F_L). The drag force is expressed by Equation (5):

$$F_D={\displaystyle \frac{1}{2}}{C}_D{\rho }_f{A}_p\left|u_f-v_p\right|\left(u_f-v_p\right)$$

(5)

In the equation:

C_D—drag coefficient, determined by the Huilin & Gidaspow [36] model, which was adopted because it provides a smooth transition between the Wen–Yu and Ergun regimes, enabling accurate description of drag behavior for solid volume fractions up to approximately 0.8. This range covers the dense-to-dilute flow transitions observed during proppant flowback;

A_p—particle projected area in the flow direction, m²;

u_f—fluid velocity, m/s;

v_p—particle velocity, m/s.

In CFD, the fluid phase is governed by the mass conservation equation and the Navier–Stokes (N–S) equations, as shown in Equation (6). To accurately characterize the turbulence features under high Reynolds number conditions, the standard k–ε turbulence model was adopted. By solving the turbulent kinetic energy (k) and its dissipation rate (ε), the equations were closed to describe the processes of energy transfer and dissipation within the turbulent flow field.

$${\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_f{\rho }_f\right)+\nabla ·\left({\alpha }_f{\rho }_f{u}_f\right)=0$$

(6)

$${\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_f{\rho }_f{u}_f\right)+\nabla ·\left({\alpha }_f{\rho }_f{u}_f{u}_f\right)=-{\alpha }_f\nabla p+\nabla ·\left({\alpha }_f{{\rm T}}_f\right)+{\alpha }_f{\rho }_{f}B+F_{pf}$$

(7)

In the equation, α_f represents the fluid volume fraction. F_pf denotes the source term arising from fluid–particle interactions, which is defined as the sum of all fluid forces acting on the particles within a computational cell, divided by the cell volume.

$$F_{pf}={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n{F}_{fp,i}}}{V_c}}$$

(8)

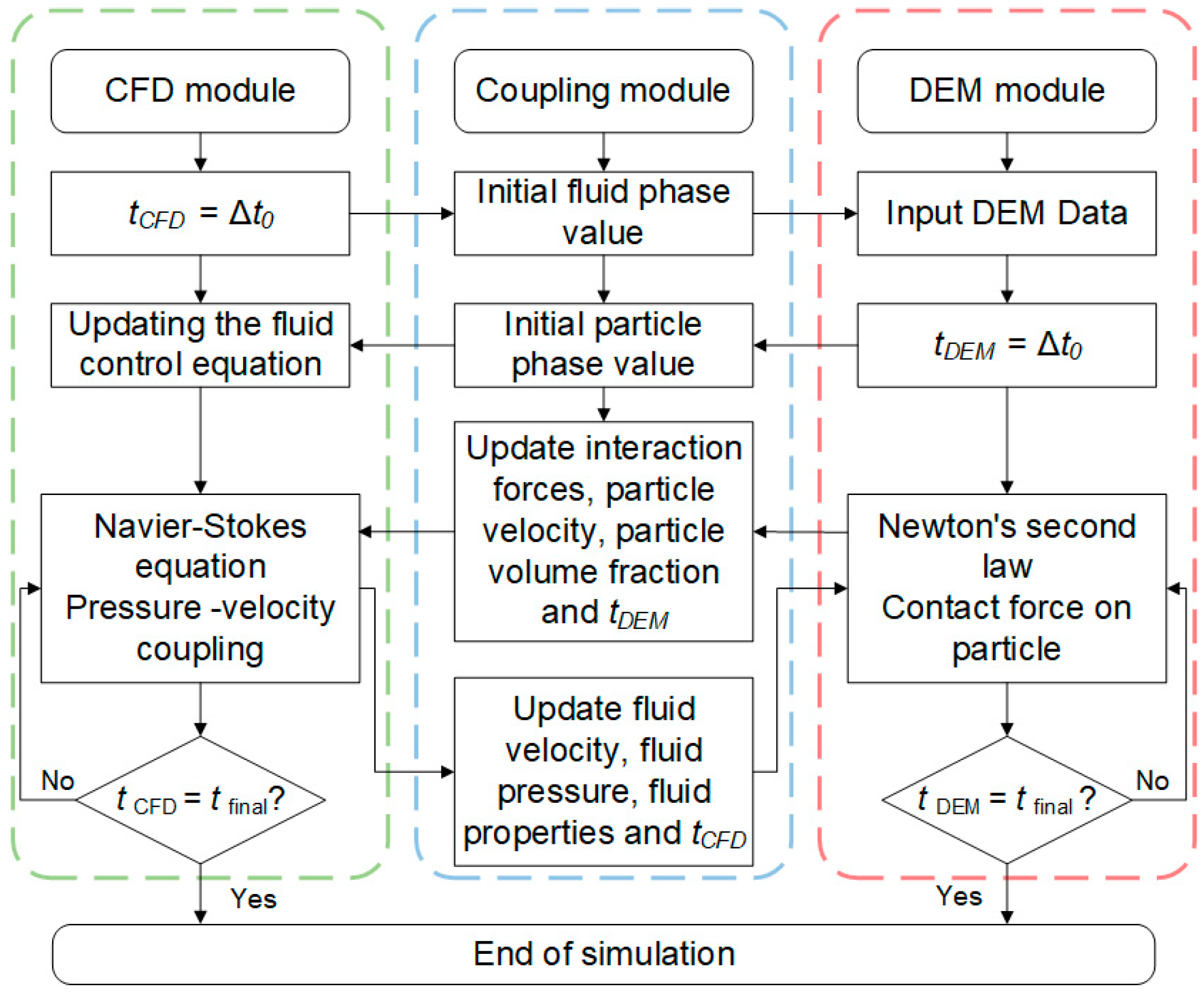
2.1.2. Numerical Process

The coupling workflow of CFD–DEM is illustrated in Figure 1. The CFD–DEM coupling method achieves high-accuracy analysis of fluid–solid interaction mechanisms by enabling two-way exchange of mechanical quantities between the continuous fluid field and the discrete particle system.

The numerical simulation workflow of proppant flowback is illustrated in Figure 2. (a) Proppant particles are first generated in the fracture model according to the prescribed particle-size distribution. (b) Closure stress is then gradually applied until the target value is reached, and after the proppant pack attains mechanical stability, the wall geometry and particle arrangement are exported. (c) Finally, the fluid field is coupled with the particles, and flowback boundary conditions are imposed to simulate the proppant flowback process.

2.2. Laboratory Experiments

The mechanistic understanding derived from CFD–DEM simulations can guide the identification of key controlling parameters. Nevertheless, because numerical models inevitably simplify fracture morphology and fluid–particle interactions, laboratory experiments are indispensable for accurately determining the CFVP and confirming the validity of the model.

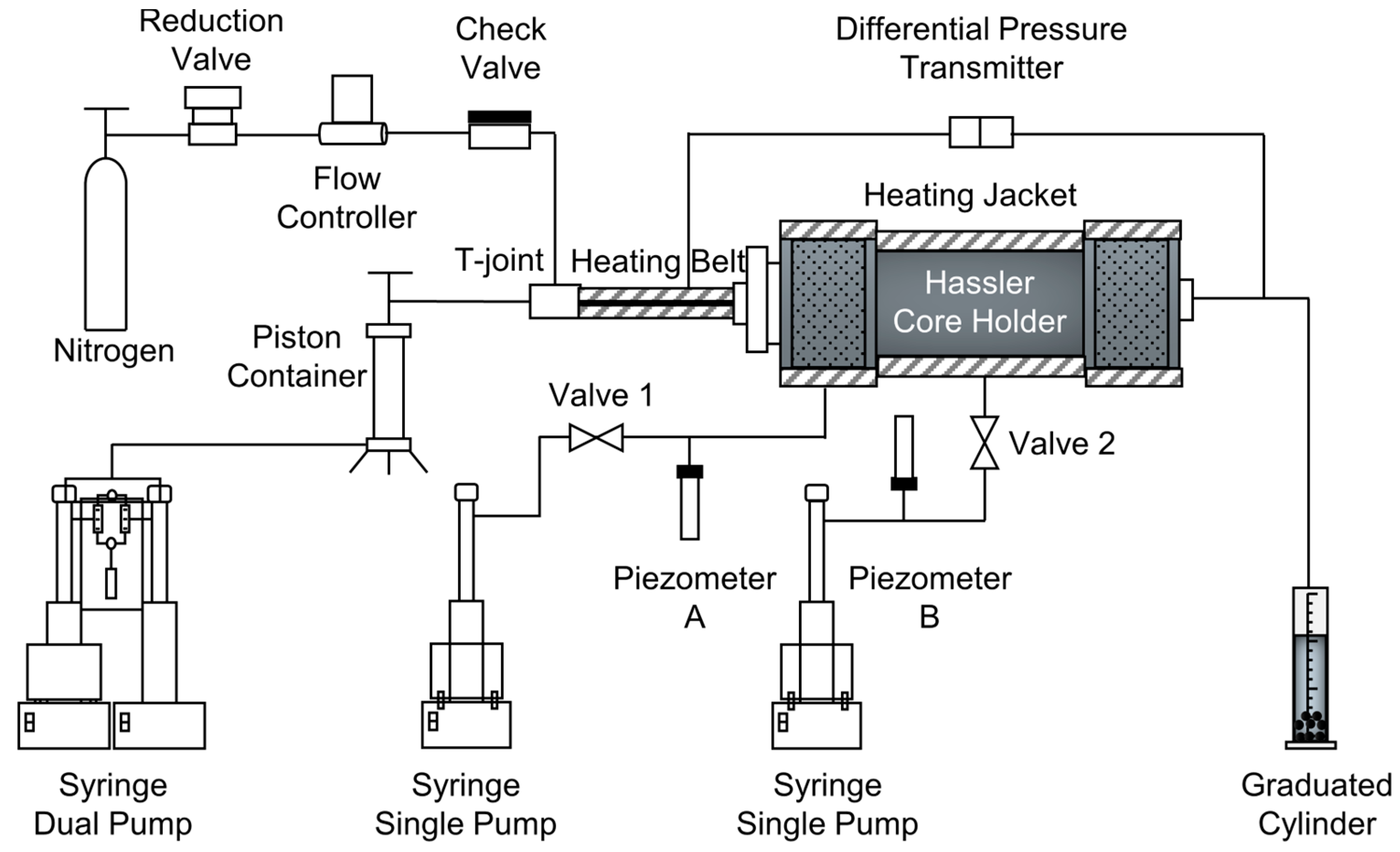
2.2.1. Experimental Setup

The proppant flowback apparatus is illustrated in Figure 3. A core pre-packed with proppants was mounted in a Hassler core holder. Axial and confining pressures up to 65 MPa were applied using two syringe single pumps. A heating sleeve covering the core holder and heating tapes wrapped around the pipelines maintained a constant temperature of up to 100 °C. At the fluid inlet cross-section, grooves were machined along the fracture direction to ensure uniform injection of fluids from one end of the fracture. Liquid supply was driven by a syringe dual pump, which delivered fluid from a piston container into the core holder at flow rates ranging from 0.001 to 132 mL/min. Gas supply was provided by a cylinder, with flow rate controlled between 0 and 200 mL/min by a flow controller downstream of a pressure regulator. A check valve was installed to prevent gas flowback. Differential pressure across the core holder was measured by a differential pressure transmitter with a measurement range of 0–200 kPa.

2.2.2. Experimental Materials

The coal samples used in this study were obtained from the No. 4 + 5 coal seam of the Daning–Jixian block in China. The proppants were identical to those applied in hydraulic fracturing operations of deep CBM wells in the same block, where fracturing fluids typically consist of weakly alkaline, low-salinity “active water,” and the formation water is of similar ionic composition and salinity. The characterization results of the proppants are summarized in

Table 1. Proppant characteristic parameter.

Type	Average Diameter (μm)	Sphericity	Roundness	Turbidity (FTU)	Bulk Density (g/cm3)	Apparent Density (g/cm3)	Crush Resistance (28 MPa) (%)
30/50 mesh	459.3	0.7	0.7	70	1.49	2.63	7.8
40/70 mesh	341.1	0.7	0.7	83	1.47	2.67	8.8
70/140 mesh	138.6	0.7	0.7	142	1.42	2.67	8.5

. The experimental gas was high-purity nitrogen (99.99%), and the liquid phase was a 2 wt% KCl solution. Nitrogen was used instead of methane for safety and experimental controllability. Under the present pressure–temperature ranges, CH₄–water and N₂–water systems exhibit comparable interfacial behavior and gas viscosities; thus, the substitution does not alter the governing gas–liquid–solid flow regimes. The density and viscosity of nitrogen are 0.98 kg/m³ and 0.019 mPa·s, respectively, while those of methane are 0.56 kg/m³ and 0.012 mPa·s. The relative differences lead to less than 5% variation in the calculated Reynolds number under the tested flow velocities, indicating that this substitution introduces a negligible effect on the determination of CFVP [37,38].

2.2.3. Experimental Procedure

Based on different simulated production stages, the experiments were conducted under liquid-solid two-phase and gas-liquid-solid three-phase conditions to determine the CFVP of proppants. The experimental procedure is summarized as follows:

(a)

Cylindrical cores (ϕ50 × 100 mm) were obtained by wire cutting and then split longitudinally into two halves. Proppants of predetermined quantities were filled between the halves to simulate fractures with varying widths. Figure 4 shows the setup, where the white circular areas indicate the openings formed on the coal block during wire cutting.

(b)

The proppant-packed cores were mounted in a core holder with the fracture oriented vertically. Axial and confining pressures were gradually increased to the preset values to establish the designed stress state.

(c)

A total of 2000 mL of 2 wt% KCl solution was prepared and loaded into the piston container.

(d)

The temperature was adjusted to the target value and maintained for 4 h. Outlet temperature was continuously monitored to ensure equilibrium with the set conditions.

(e)

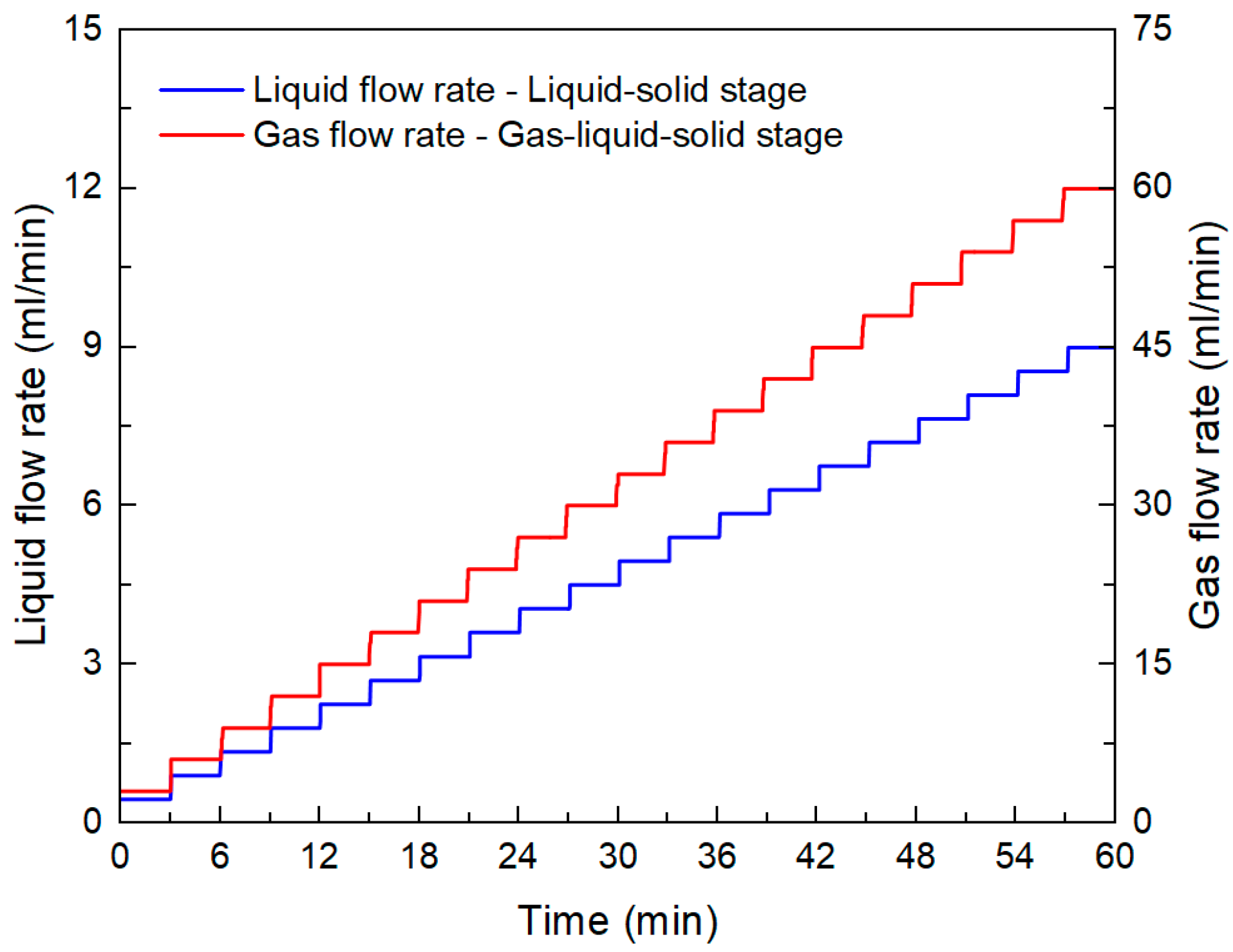
For liquid-solid two-phase tests, liquid flow rate was adjusted to 0.45 mL/min and maintained for more than 5 min until no bubbles appeared at the outlet. For gas-liquid-solid three-phase tests, gas flow rate was adjusted to 2 mL/min and maintained for more than 5 min until no liquid was discharged at the outlet.

(f)

The data acquisition system was activated to monitor flow rate, pressure, and temperature. Flow rate was then increased stepwise at fixed gradients every 3 min, while graduated cylinders at the outlet were replaced to collect flowback proppants.

(g)

After 60 min, the experiment was terminated. The core was removed, and photographs were taken to record the morphology of the proppant pack after flowback. The returned proppants were subsequently dried and weighed.

(h)

After the experiments, some proppants were found to be embedded in or attached to both fracture surfaces. To quantify their post-flowback distribution, the acquired images were converted into the HSV color space, and a fixed threshold range for the yellow hue was applied to extract the proppant pixels. The threshold range was calibrated by extracting the HSV distribution of proppants from several reference images taken under identical illumination and camera settings, so that the selected hue interval could be statistically determined and consistently applied to all images. This procedure ensured reproducibility and minimized subjective bias in image segmentation. After thresholding, coal regions were removed by transparency processing, and the proppant masks from both sides were merged to obtain the final spatial distribution. The complete image-processing workflow is illustrated in Figure 5.

2.2.4. Flow Rate Settings

Due to the scale differences between the laboratory setup and field conditions, as well as the requirement for real-time measurement of proppant flowback at atmospheric outlet pressure, the flow rates needed to be converted by considering the differences in geometry and fluid density. The conversion formula is given in Equation (9).

$$q_{ie}=694.44{\displaystyle \frac{q_i·h_{fe}}{n_f{h}_f}}·{\displaystyle \frac{{\rho }_{i0}}{{\rho }_i}}$$

(9)

In the equation:

q_ie—experimental gas/liquid flow rate, cm³/min;

q_i—field gas/liquid production rate, m³/day;

n_f—number of fractures in the field, calculated as the product of average fracturing stages and clusters per stage;

h_f—fracture height in the field, m;

h_fₑ—fracture height in the experiment, m;

ρ_i0—density of gas or water at 1 atm and 25 °C, kg/m³;

ρ_i—density of gas or water under reservoir fracture conditions, kg/m³.

According to Equation (1), in liquid-solid two-phase tests, the liquid flow rate was increased from 0.45 mL/min to 9 mL/min in increments of 0.45 mL/min. In gas-liquid-solid three-phase tests, the gas flow rate was increased from 3 mL/min to 60 mL/min in increments of 3 mL/min, while the liquid flow rate was set according to the prescribed gas–liquid ratio, as shown in Figure 6.

3. Results and Discussion

3.1. Proppant Flowback Mechanism

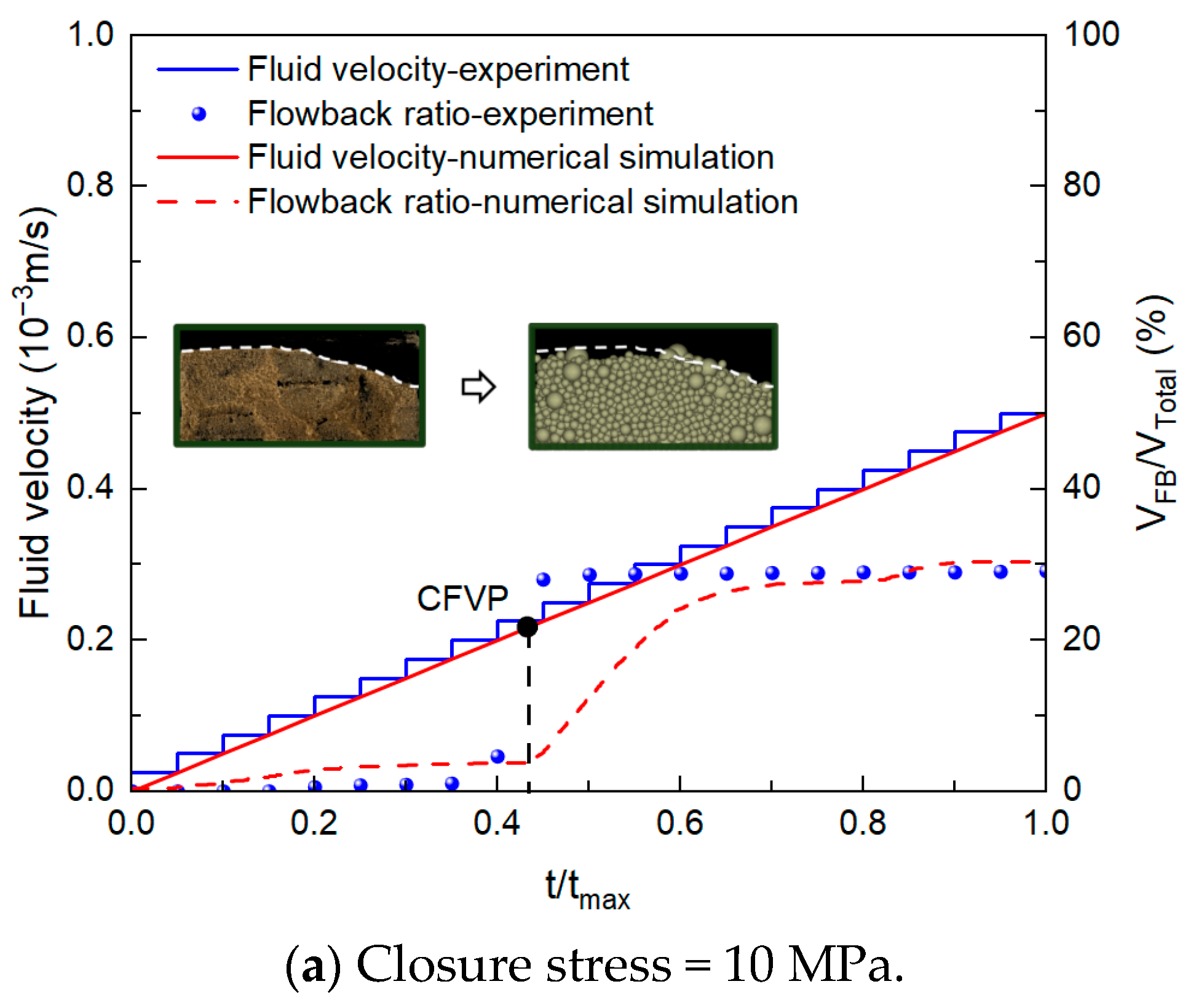
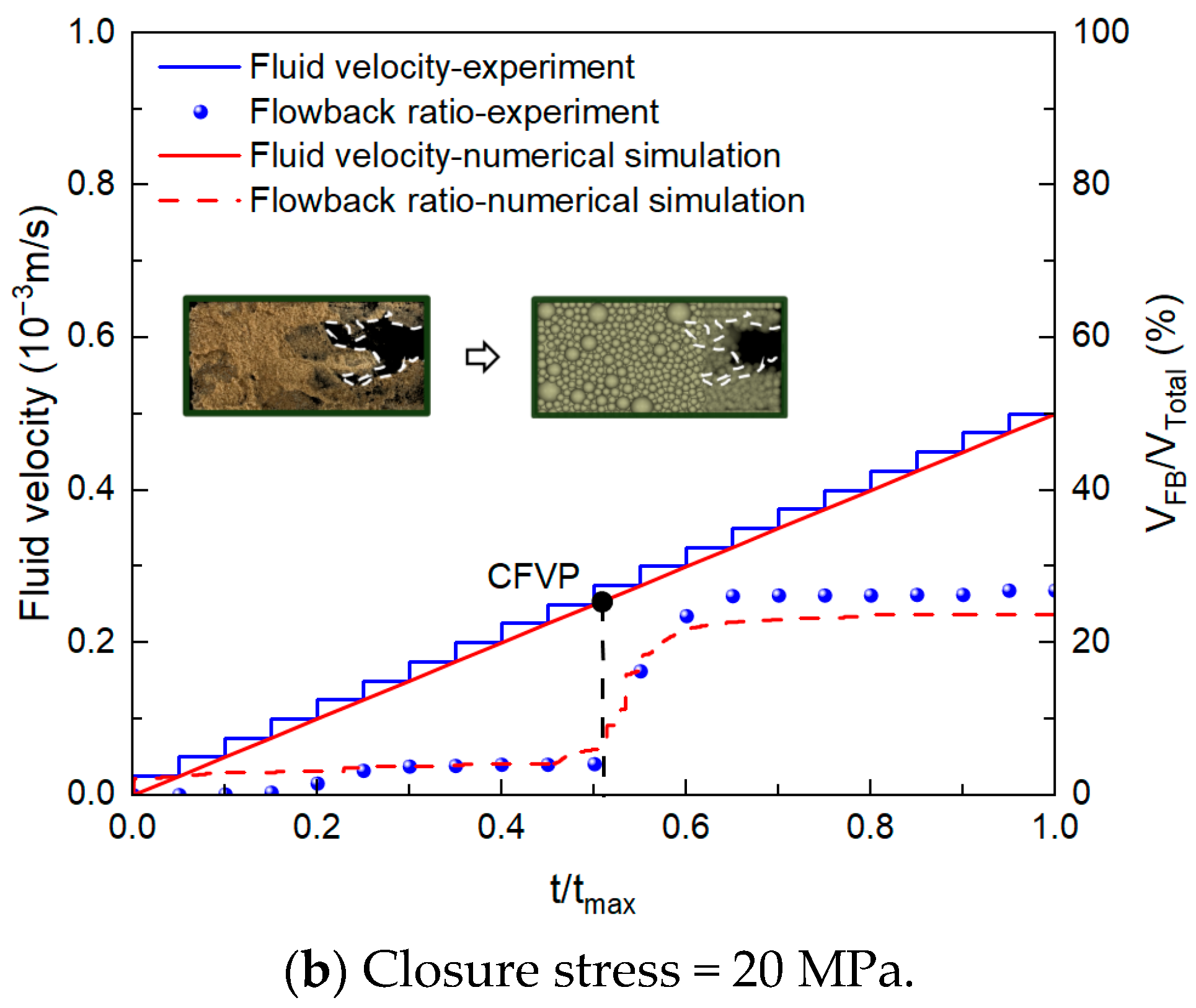
3.1.1. Model Validation

The domain size and physical parameters used in the simulations are listed in

Table 2. Simulation parameters.

Parameters	Value	Parameters	Value
Particle density	2630 kg/m3	Static Friction between particles	0.6
Particle Young’s modulus	10 GPa	Dynamic Friction between particles	0.2
Particle Poisson’s ratio	0.25	Static Friction between particle and wall	0.5
Particle size distribution	1:3:6	Dynamic Friction between particle and wall	0.15
Wall density	1650 kg/m3	Fracture size	4 × 2 × 2 mm
Wall Young’s modulus	5 GPa	DEM time step	3 × 10−8 s
Wall Poisson’s ratio	0.3	CFD time step	3 × 10−4 s
Fluid viscosity	1 mPa·s	Simulation time	3 s

. A constant-gradient velocity inlet corresponding to the experimental conditions was applied at the fracture entrance, as shown in Figure 7. Wall roughness effects were represented through the particle–wall friction coefficients, and the entire fracture geometry was modeled without applying symmetry simplifications. Mesh independence and time-step sensitivity tests were conducted before the main simulations. The CFD mesh and DEM time steps were refined until variations in average velocity and pressure drop were below 2%, ensuring numerical stability and accuracy. Proppant flowback was simulated under closure stresses of 10 MPa and 20 MPa, and the simulated flowback rates and proppant pack morphologies were compared with the experimental results, as shown in Figure 7. The white dashed lines indicate the contours of the proppant flowback channels observed in the experiments.

In the numerical simulations, the dimensionless times corresponding to the CFVP under closure stresses of 10 MPa and 20 MPa were 0.43 and 0.51, respectively, both of which fell within the time range observed in the experiments. This indicates good agreement between the experimental and simulated CFVP values. The errors between experimental and simulated final flowback ratios were 4.2% and 11.5%, respectively. The morphologies of the proppant packs were also generally consistent. Under the 10 MPa condition, the increase in flowback ratio was delayed in the numerical simulations. This delay occurred because the applied closure stress significantly enhanced particle–particle and particle–wall contact forces. To maintain numerical stability under such conditions and accurately capture transient contact behavior, a small DEM time step of 3 × 10⁻⁸ s was required. Due to computational cost constraints, the total simulation time was limited to 3 s, which contributed to the slower evolution of the flowback ratio. In addition, a continuous channel formed near the top of the fracture at 10 MPa, reducing local fluid velocity and further slowing proppant transport. Although the transient response exhibited a time lag, this does not affect the determination of the critical flowback behavior, as both the numerical and experimental results converge to similar instability conditions and final flowback ratios.

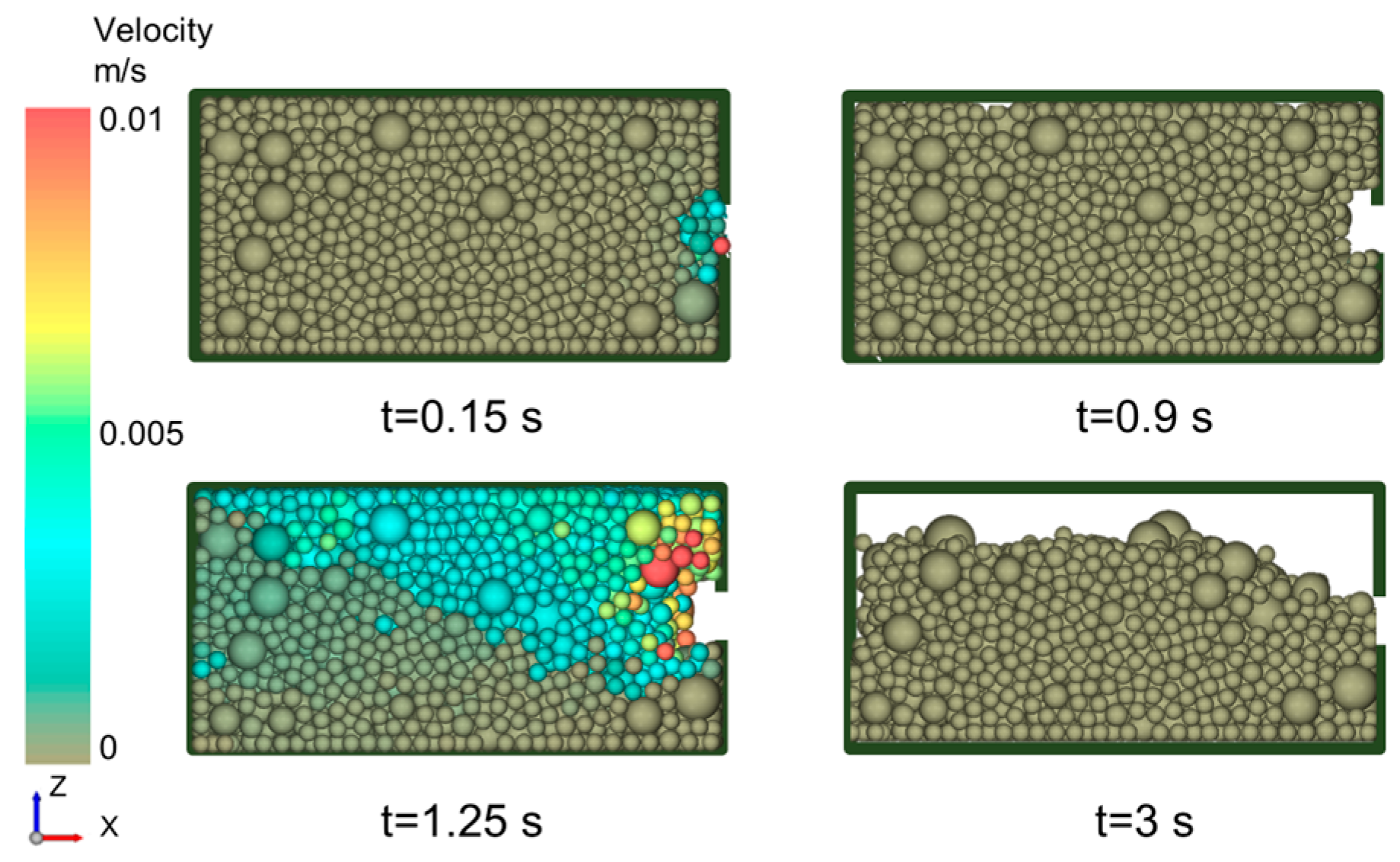
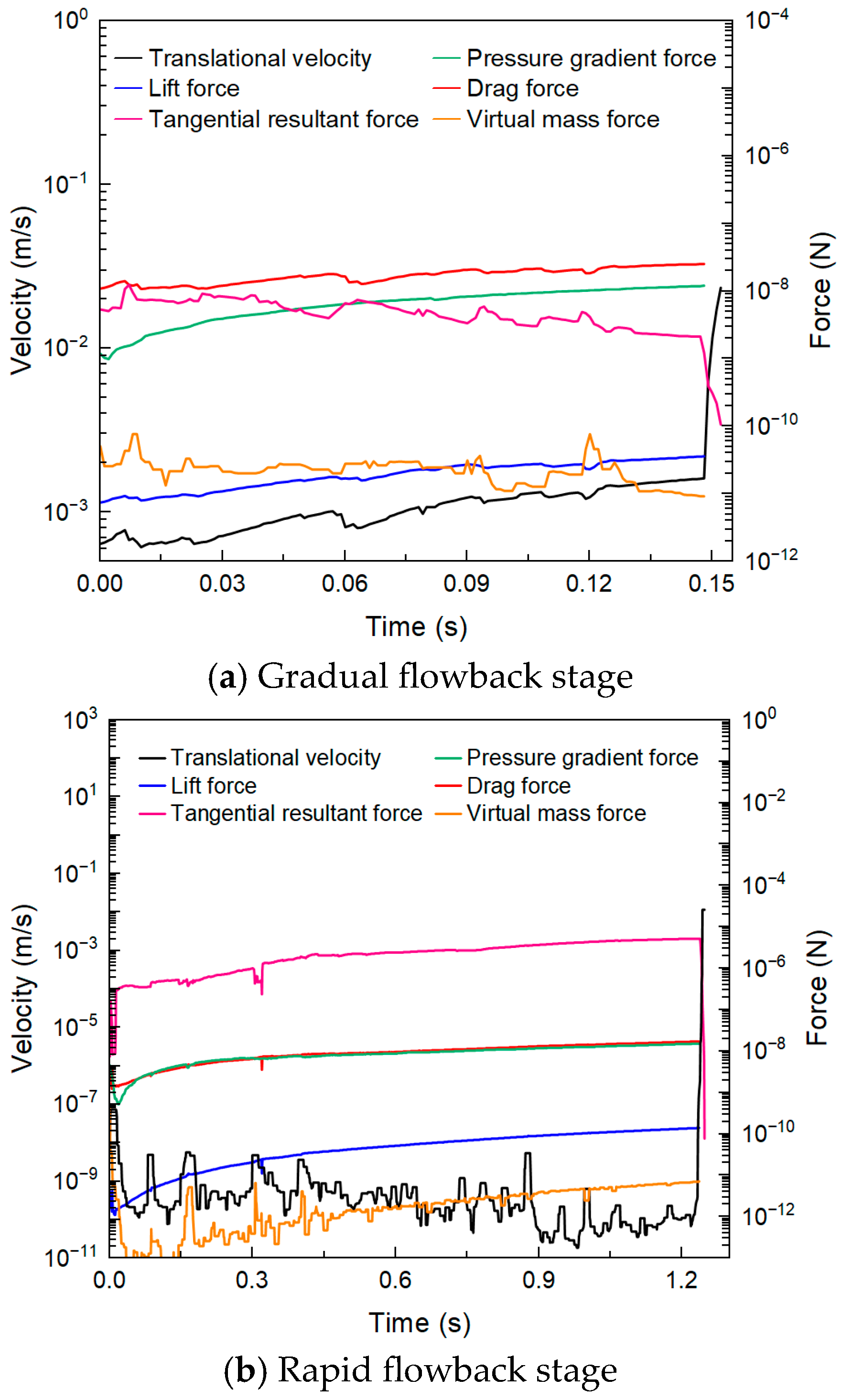
3.1.2. Process and Mechanisms of Proppant Flowback

As shown in Figure 7, similar to the experimental results, the numerical simulations demonstrated a staged flowback behavior of proppants as the flow velocity increased. Taking the proppant flowback at a closure stress of 10 MPa as an example, the flowback mechanism can be analyzed as follows. The evolution of the proppant pack morphology during the flowback process is shown in Figure 8.

At the initial stage, the forces acting on a particle near the outlet are shown in Figure 9a. With increasing flow velocity, the drag force and pressure gradient force increased simultaneously, while the lift force and virtual mass force were three orders of magnitude smaller than the drag force and could thus be neglected. The particle was subjected to a gravitational force of approximately 3.6 × 10⁻⁸ N, which was gradually overcome by the fluid forces. Consequently, the tangential resultant force gradually decreased, and the particle velocity remained below 10⁻¹¹ m/s without significant displacement. Therefore, this stage is defined as the no-flowback stage.

At 0.15 s, the fluid forces completely offset the gravitational influence, and the particle velocity increased rapidly, as shown in Figure 9a. The tangential resultant force dropped sharply, and the particle began to flow back slowly. Once the loosely arranged particles near the outlet had fully flowed back, particle movement ceased, as illustrated in Figure 8. This stage is thus defined as the gradual flowback stage.

At 0.9 s, the forces acting on a particle at the interface of the flowback channel are shown in Figure 9b. Similarly to the gradual flowback stage, the drag force and pressure gradient force remained the dominant fluid forces and increased with flow velocity. However, the tangential resultant force to rise progressively. At 1.25 s, the tangential resultant force reached the static friction limit, and the particle velocity increased sharply, initiating particle transport. The breakdown of the stable bridge structure triggered cooperative motion among particles, causing large-scale proppant instability and the formation of a flowback channel at the fracture top. This stage is defined as the rapid flowback stage.

3.2. Regularities of Critical Flowback Velocity of Proppants

3.2.1. Experimental Scheme

Numerical simulations revealed that the onset of proppant flowback is governed by the competition between fluid driving forces—primarily drag and pressure gradient forces—and frictional resistance arising from interparticle tangential contact forces and normal stresses. This mechanistic understanding suggests that any macroscopic parameter directly affecting the fluid velocity field, particle frictional state, or interfacial interactions can exert a critical influence on the critical flowback velocity. Accordingly, fracture width, closure stress, proppant size, and gas–liquid ratio were identified as the key controlling factors. Specifically, fracture width alters the fluid velocity distribution and local pressure gradients, thereby determining the magnitude and range of drag forces; closure stress regulates normal loading and interparticle friction while controlling the effective fracture aperture; proppant size dictates packing density, contact area, and bridging capacity; and the gas–liquid ratio influences mixture density, viscosity, and interfacial tension, thereby modifying the fluid driving forces. Previous studies on surface morphology and roughness have shown that these factors may influence proppant–wall interactions and flowback behavior [39,40]. However, to maintain consistent wall conditions and quantitatively evaluate the effects of closure stress and fracture width, this study did not consider surface roughness, wettability, or surface energy.

To evaluate the influence of individual variables on CFVP, a single-factor experimental design was adopted. The experimental parameter ranges were determined from actual field data of deep CBM reservoirs, and the corresponding ranges of fracture width, closure stress, proppant size, and gas/liquid ratio are listed in

Table 3. Field parameter ranges of DCBM reservoirs.

Parameter	Maximum Daily Liquid Production (m3)	Maximum Daily Gas Production (×104 m3)	Minimum Principal Stress (MPa)	Fracturing Stages	Clusters Per Stage	Fracture Width (mm)	Average Fracture Height (m)	Temperature (°C)
Value	300	10	31.8–45.0	10–13	4–5	2–10	25	61.3–73.4

. Considering the relatively narrow temperature range in DCBM reservoirs, all experiments were conducted at 70 °C. The experimental program is summarized in

Table 4. Experimental program.

Core No.	Fracture Width (mm)	Effective Closure Stress (MPa)	Proppant Size Distribution	Gas–Liquid Ratio
FB-L-1~5	2, 4, 6, 8, 10	25	1:3:6	-
FB-L-6~10	6	5, 15, 25, 35, 45	1:3:6	-
FB-L-11~15	6	25	1:0:0, 0:1:0, 0:0:1, 1:5:4, 1:3:6	-
FB-G-1~5	2, 4, 6, 8, 10	25	1:3:6	20
FB-G-6~10	6	5, 15, 25, 35, 45	1:3:6	20
FB-G-11~15	6	25	1:0:0, 0:1:0, 0:0:1, 1:5:4, 1:3:6	20
FB-G-16~20	6	25	1:3:6	10, 20, 30, 40, 50

, where FB-L-1 to FB-L-15 represent liquid-solid two-phase tests, and FB-G-1 to FB-G-20 represent gas-liquid-solid three-phase tests. The proppant size distribution refers to a mixture of 30/50, 40/70, and 70/140 mesh proppants placed together. To verify the scaling validity, the Reynolds number (Re) and Stokes number (St) were compared under laboratory and field conditions. The results show that Re ranges from 1.09 to 21.8, and St from 2.6 × 10⁻⁴ to 5.2 × 10⁻³ for both cases. Since Re ≪ 2000 and St ≪ 1, the flow remains laminar and viscous-dominated, and particles closely follow the fluid motion. These comparable dimensionless ranges confirm dynamic similarity between the experiments and field conditions. Three repeated tests were conducted under typical experimental conditions, and the obtained CFVP values showed no significant difference; for other cases, each condition was tested once under strictly controlled boundary and flow conditions.

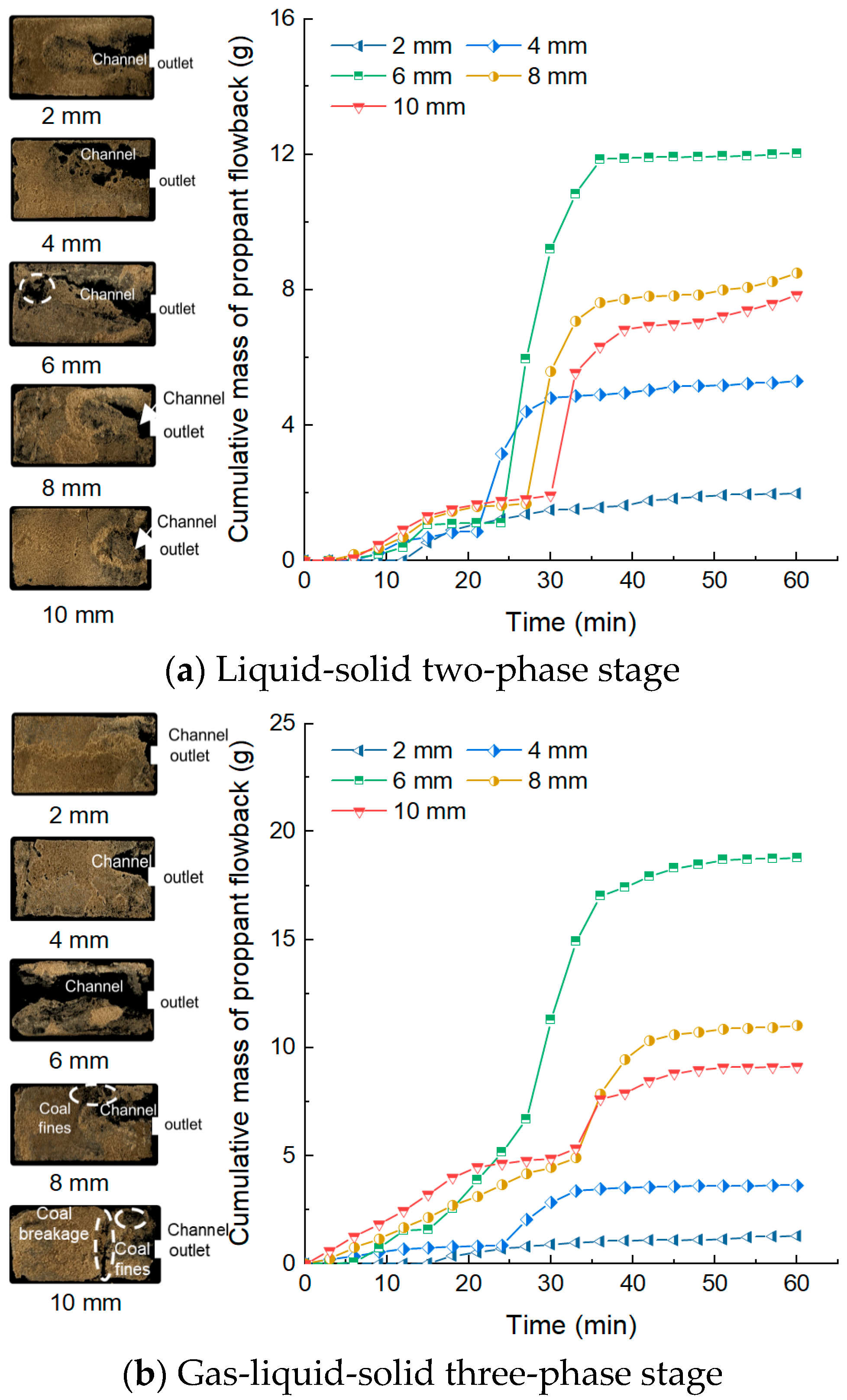
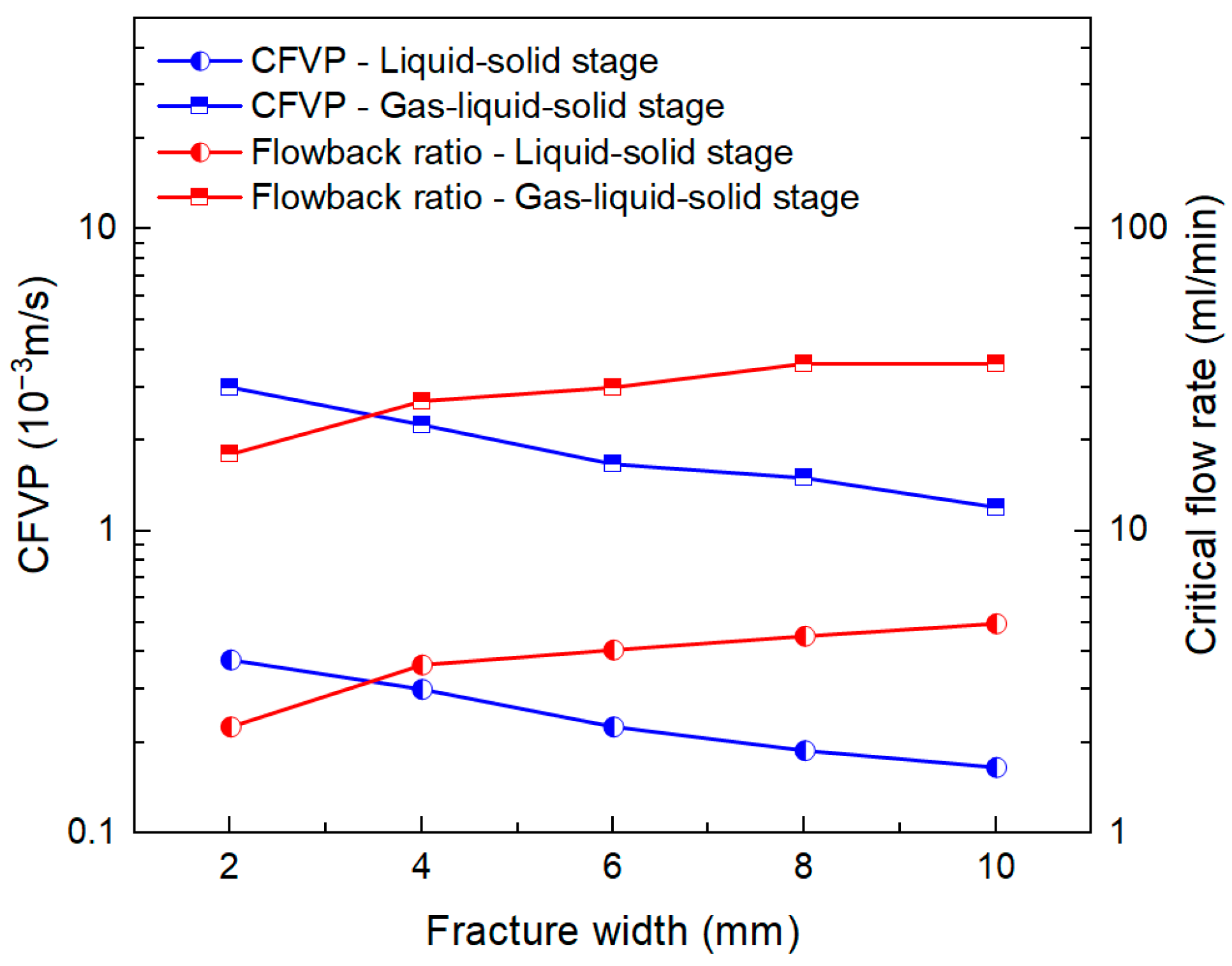
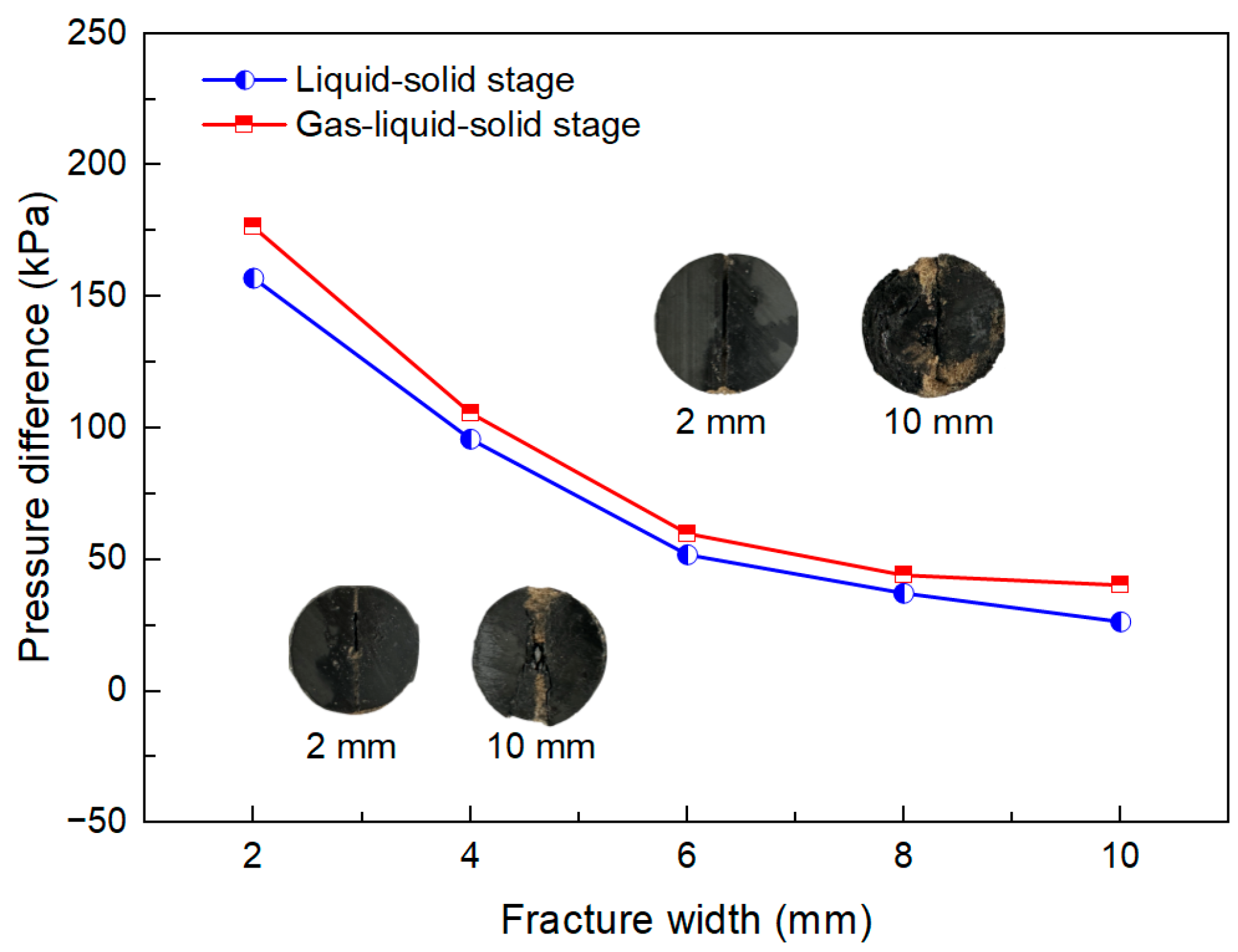
3.2.2. Effect of Fracture Width Stress on CFVP

As shown in Figure 10, because the gradual flowback stage involves only a small amount of loosely packed proppants near the outlet and exhibits minimal variation, the flow velocity at the onset of the rapid flowback stage is taken as the CFVP. The final proppant flowback mass in both the liquid-solid two-phase stage and the gas-liquid-solid three-phase stage follows the same overall trend. When the fracture width increased from 2 mm to 6 mm, the final flowback mass rose sharply, with the flowback ratio in liquid-solid two-phase stage increasing from 14.7% to 29.7% and that in gas-liquid-solid three-phase increasing from 9.5% to 46.3%. However, when the fracture width exceeded 6 mm, the final flowback mass gradually decreased. At a width of 8 mm, the flowback ratio was significantly reduced, dropping to 15.7% in liquid-solid two-phase stage and 20.4% in gas-liquid-solid three-phase stage. Mechanically, two competing effects govern this behavior. On the one hand, increasing fracture width enlarges the w/d, which weakens bridging capacity of the proppant pack, thereby reducing its structural stability. On the other hand, at a constant injection rate, a larger fracture width lowers the average fluid velocity and thus diminishes the fluid drag force acting on the proppants. It is noted that the 8 mm threshold is derived under controlled laboratory conditions, and its exact value may vary in heterogeneous natural fractures and under different flow-rate conditions. These opposing mechanisms are reflected in the evolution of the internal flowback channel. After proppants begin to move, a preferential flowback pathway gradually forms within the packed layer. With increasing fracture width, the cross-sectional area of this flowback channel first expands and then shrinks. It is worth noting, however, that the size of the flowback channel does not strictly correspond to the total flowback ratio, because proppants adjacent to the channel may also partially migrate. As local fracture closure proceeds, these surrounding particles can be re-compacted, which slows further flowback and reduces the local proppant concentration. In addition, when the fracture width is 2 mm, the w/d is only 8.4, and the proppant bridging structure remains relatively stable. Consequently, during closure stress loading, the proppant pack near the outlet stays compacted, so no gradual flowback stage occurs. In gas-liquid-solid three-phase stage, however, the presence of gas–liquid interfacial tension can still induce localized proppant movement at the lowest set flow rate, and therefore in some cases the no-flowback stage does not appear.

Figure 11 shows the curves of CFVP and critical flow rate, where in gas-liquid-solid three-phase stage both flow rate and velocity refer to gas. As the fracture width increased from 2 mm to 10 mm, the CFVP in liquid-solid two-phase stage decreased from 0.38 × 10⁻³ m/s to 0.17 × 10⁻³ m/s, while in gas-liquid-solid three-phase stage it decreased from 3 × 10⁻³ m/s to 1.2 × 10⁻³ m/s. This indicates that narrower fractures provide better stability of the proppant pack. However, for field production, the critical flow rate is a more practical parameter under a given production rate. As shown in Figure 11, the larger the fracture width, the higher the critical flow rate. At a fracture width of 10 mm, the critical flow rate was 2.2 times that of 2 mm in liquid-solid two-phase stage, and twice that of 2 mm in gas-liquid-solid three-phase stage. From the perspective of controlling proppant flowback, production should be maintained below the critical flow rate. This implies that wider fractures allow for higher production rates while mitigating proppant flowback.

Figure 12 shows the fracture closure at the outlet surface after proppant flowback. Although all fractures experienced varying degrees of closure, wider fractures still retained a considerable portion of effective fracture space. As fracture width increased, the pressure difference between the inlet and outlet gradually decreased, indicating that wider fractures maintained higher conductivity after proppant flowback.

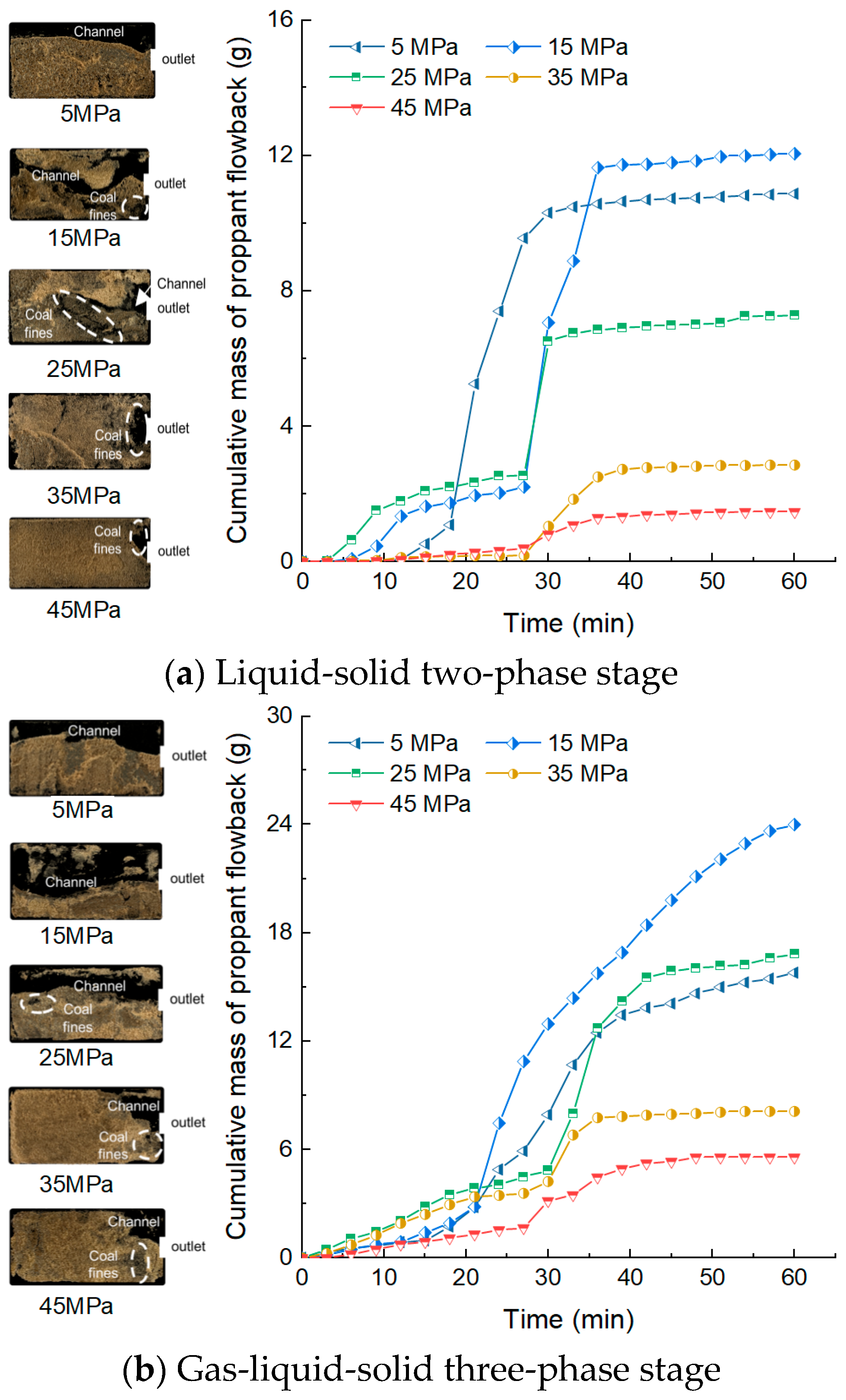
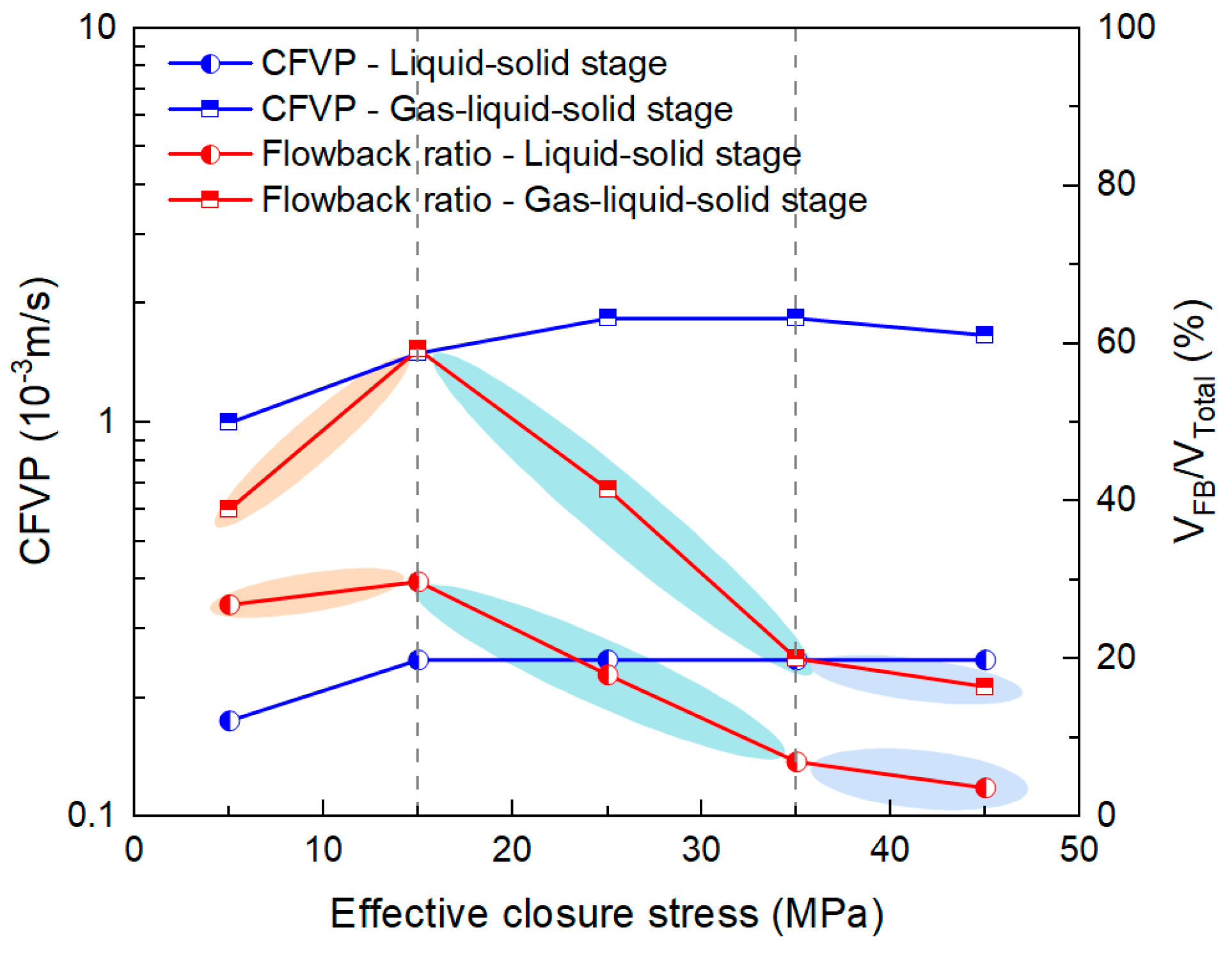
3.2.3. Effect of Effective Closure Stress on CFVP

From the proppant flowback mass curves in Figure 13a and the flowback-ratio curves in Figure 14, it can be observed that with increasing closure stress, the proppant flowback in liquid-solid two-phase stage first rises and then decreases. When the closing stress is 5 MPa, a regular flowback channel forms at the top of the proppant pack, indicating that the pack has not yet reached full mechanical stability and that the static friction limit between particles remains relatively low. Driven by gravity, proppants gradually settle, and under fluid scouring a regular channel develops along the fracture top. Meanwhile, the increase in closure stress narrows the fracture aperture and elevates the average fluid velocity, thereby enhancing the fluid drag force.

When the closure stress reaches around 15 MPa, the flowback ratio peaks at 29.8%, and irregular flowback channels appear within the fracture. At this stage, the proppant pack becomes relatively stable, and the channel geometry is jointly influenced by the flow field and the internal packing structure. Nevertheless, the velocity increase caused by the reduced fracture width continues to dominate the flowback process. As the closure stress further rises from 15 MPa to 35 MPa, the flowback ratio gradually declines to 6.9%. The increasing normal stress raises the static friction limit between particles, so that fewer particles can reach this threshold with their tangential resultant force, and overall flowback is significantly suppressed. When the closure stress exceeds 35 MPa, the flowback ratio stabilizes at a low level of 3.6%~6.9%, and the proppant pack can be regarded as mechanically stable. Moreover, during the flowback process, unsupported segments of the flowback channel may undergo local collapse as the coal-rock fracture walls close, further contributing to the continuous decrease in flowback ratio under high closure stress.

Figure 13b shows that gas-liquid-solid three-phase stage exhibits the same overall trend, but with generally higher flowback ratios. This is mainly due to the larger gas flow rate and the additional influence of gas–liquid interfacial tension, which increase fluid mobility and enhance the detachment of proppant particles.

As shown in Figure 14, when the closure stress was below 15 MPa, the CFVP increased with increasing stress. This was because higher closure stress enhanced the friction between proppants and the fracture wall, as well as the tangential forces between particles. When the closure stress exceeded 15 MPa, the CFVP in liquid-solid two-phase stage ranged from 0.25 to 0.28 × 10⁻³ m/s, while in gas-liquid-solid three-phase stage it remained between 1.6 and 1.8 × 10⁻³ m/s, with only minor differences. This indicates that although the overall stability of the proppant pack continued to improve, fracture compression simultaneously increased fluid velocity. Beyond 15 MPa, these two opposing effects offset each other. Although local fracture closure after flowback led to variations in flowback ratio, the CFVP at the onset of flowback showed little difference.

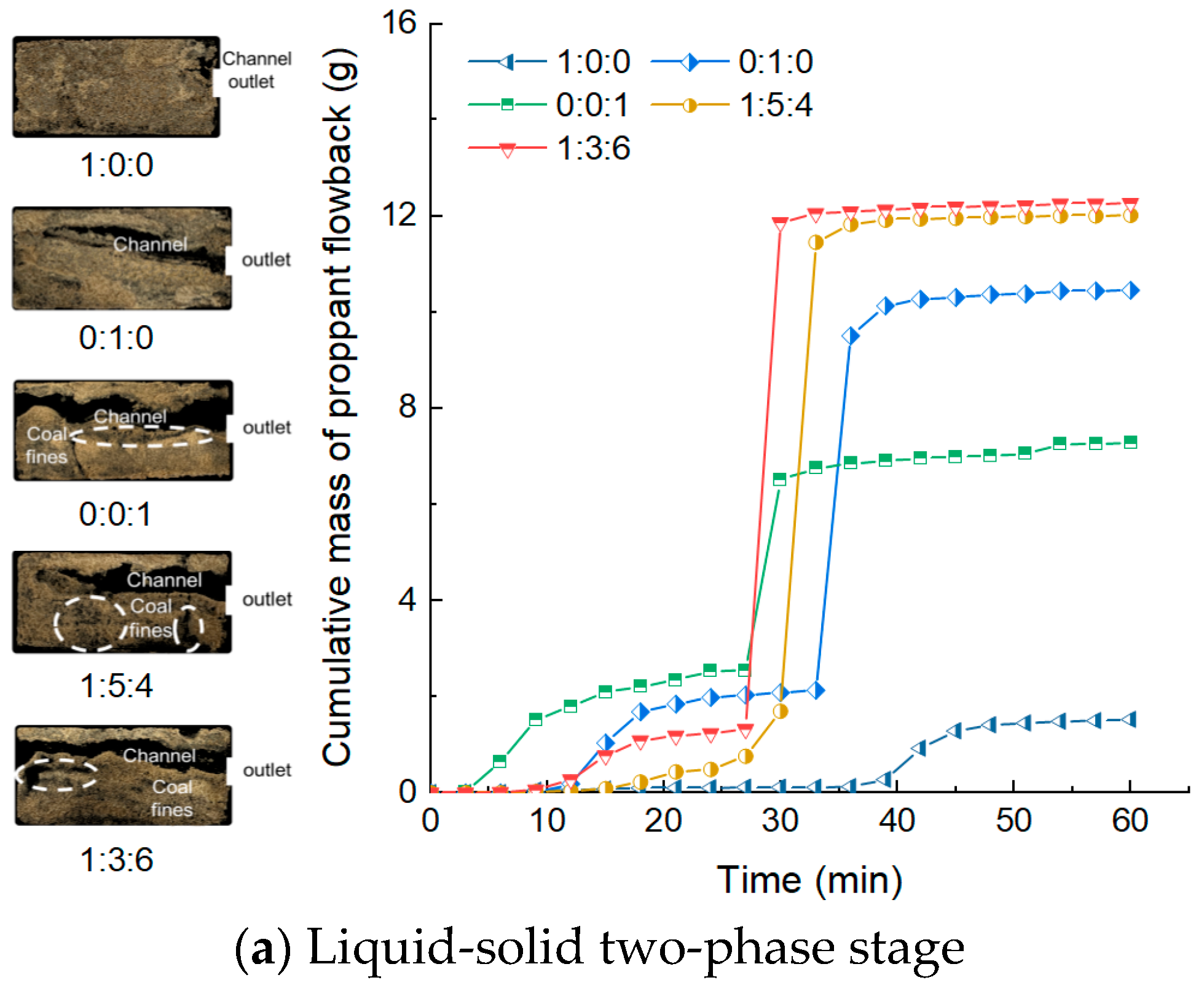
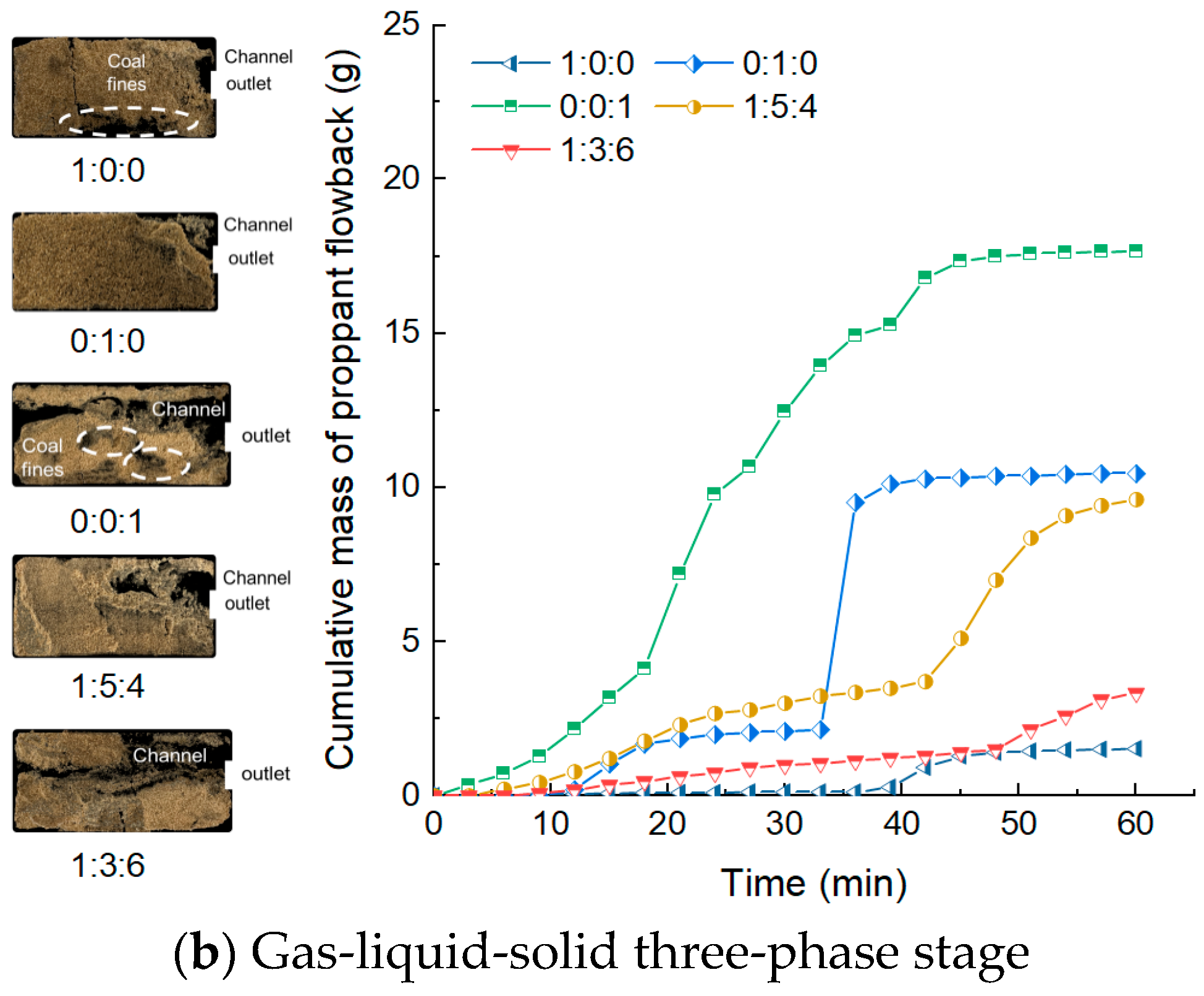
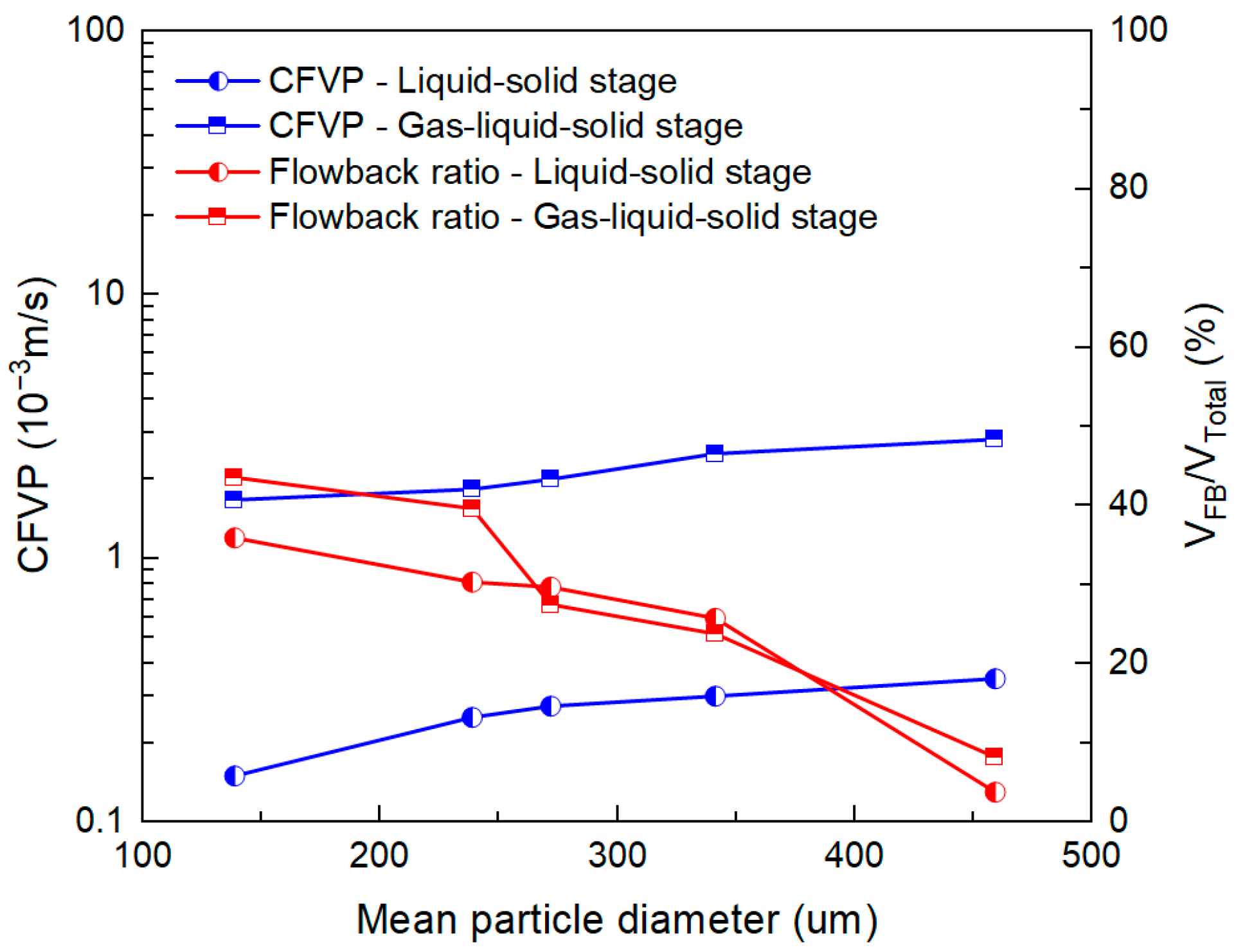
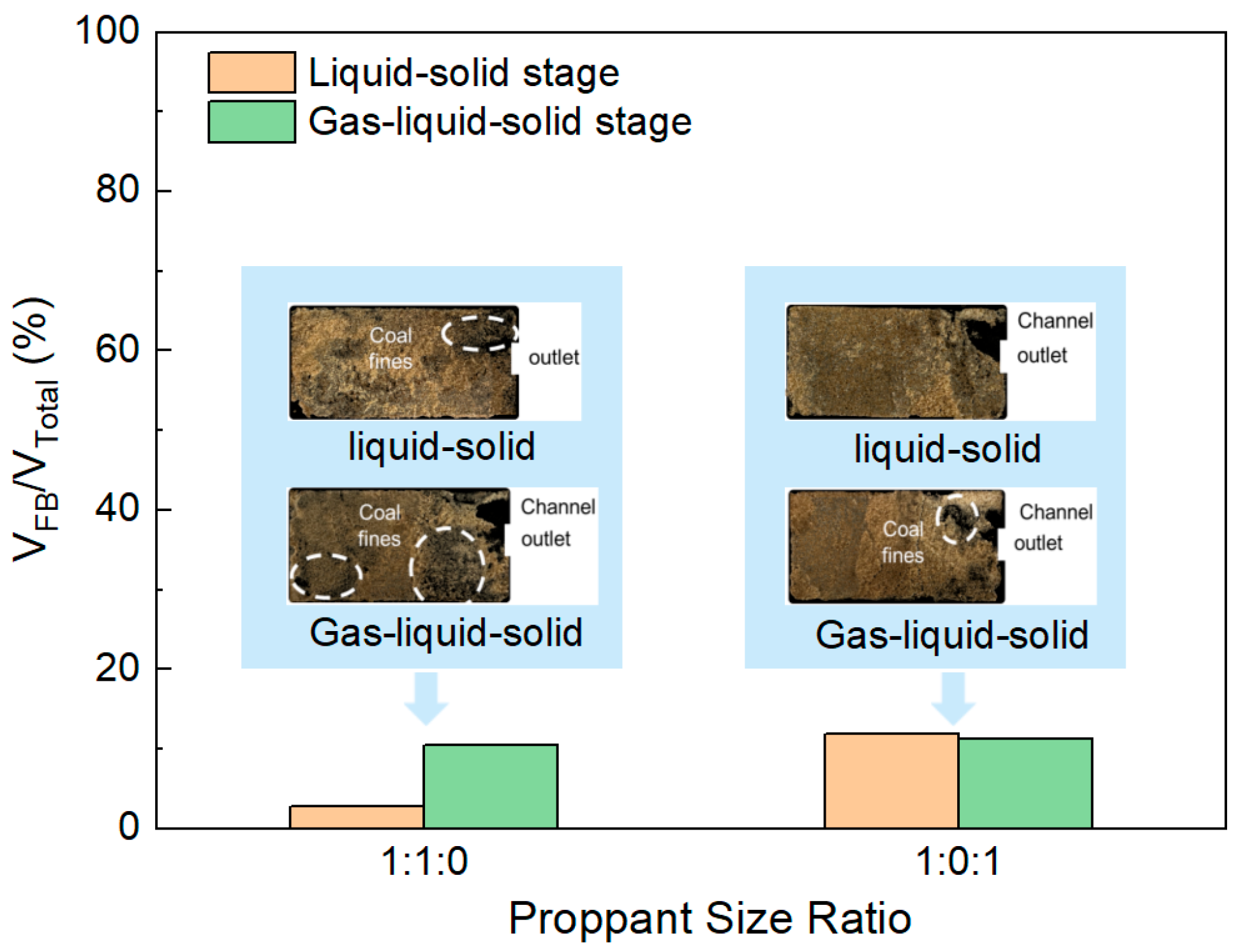
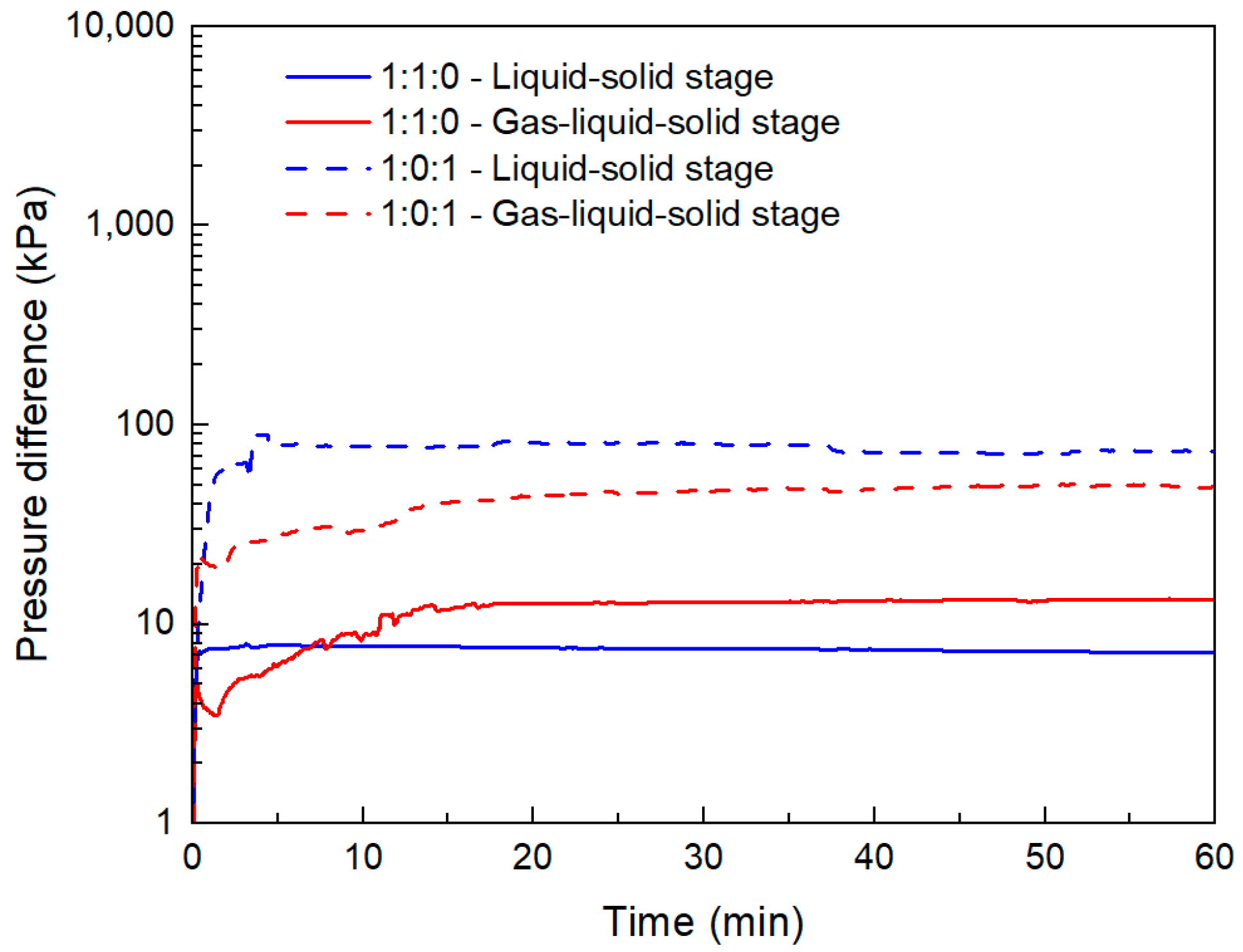
3.2.4. Effect of Proppant Size on CFVP

Figure 15 present the proppant flowback mass curves and proppant packs under different proportions of 30/50, 40/70, and 70/140 mesh proppants. As shown in Figure 16, when the average particle size increased from 138.3 μm to 459.3 μm, the flowback ratio in liquid-solid two-phase stage decreased from 35.9% to 3.7%, while the CFVP gradually increased from 0.15 × 10⁻³ m/s to 0.35 × 10⁻³ m/s. In gas-liquid-solid three-phase stage, the flowback ratio decreased from 43.6% to 8.2%, and the CFVP increased from 1.2 × 10⁻³ m/s to 2.8 × 10⁻³ m/s. These results indicate that a smaller w/d effectively enhances the stability of the proppant pack and suppresses flowback. In particular, when only 30/50 mesh proppants were placed, the flowback ratio was significantly lower than for other particle-size combinations, with flowback occurring only in a small area near the fracture outlet.

To evaluate the blocking effect of 30/50 mesh proppants on 40/70 and 70/140 mesh proppants, flowback experiments were conducted with two particle-size combinations: 1:1:0 and 1:0:1. Proppants were placed in layers, with smaller particles at the inlet side and larger particles at the outlet side. The fluid flow rate was set above the CFVP of the 30/50 mesh proppants and maintained constant, with 9 mL/min in liquid-solid two-phase stage and 60 mL/min of gas flow in gas-liquid-solid three-phase stage. As shown in Figure 17, under both combinations, the flowback ratios in liquid-solid two-phase stage and gas-liquid-solid three-phase stage were below 12%, with flowback occurring only near the outlet and not extending to the inlet side where smaller proppants were placed. The pressure-difference curves in Figure 18 show that fracture closure caused by rapid early-stage flowback led to a sharp increase in pressure. In the later stage, the flowback rate slowed and the pressure stabilized. At 60 min, the pressure difference for the 1:0:1 combination was 10.2 times that of the 1:1:0 combination in liquid-solid two-phase stage and 3.5 times higher in gas-liquid-solid three-phase stage. These results indicate that direct contact between 30/50 and 70/140 mesh proppants significantly reduces conductivity, likely due to pore blockage in the 30/50 mesh layer caused by the smaller 70/140 mesh proppants.

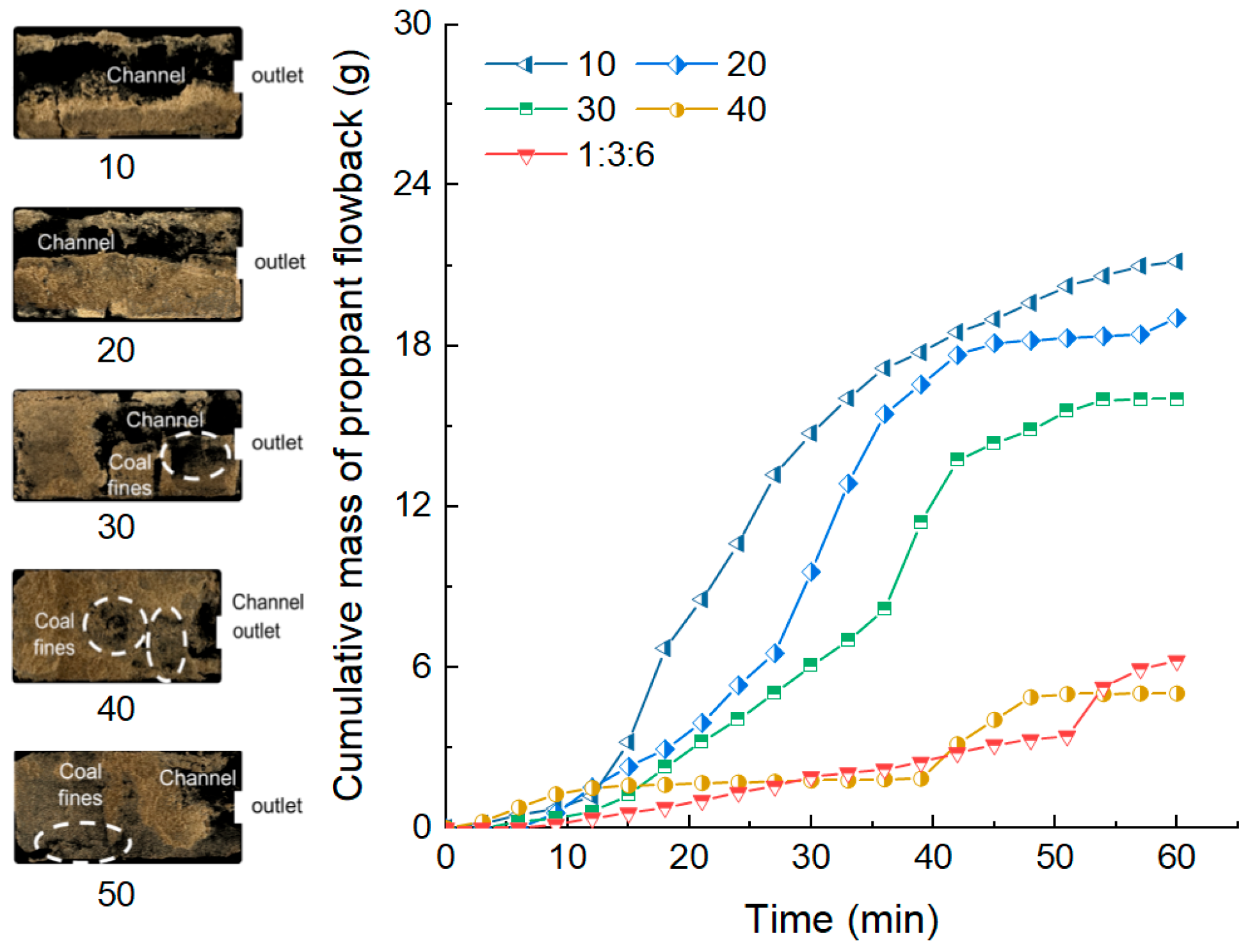
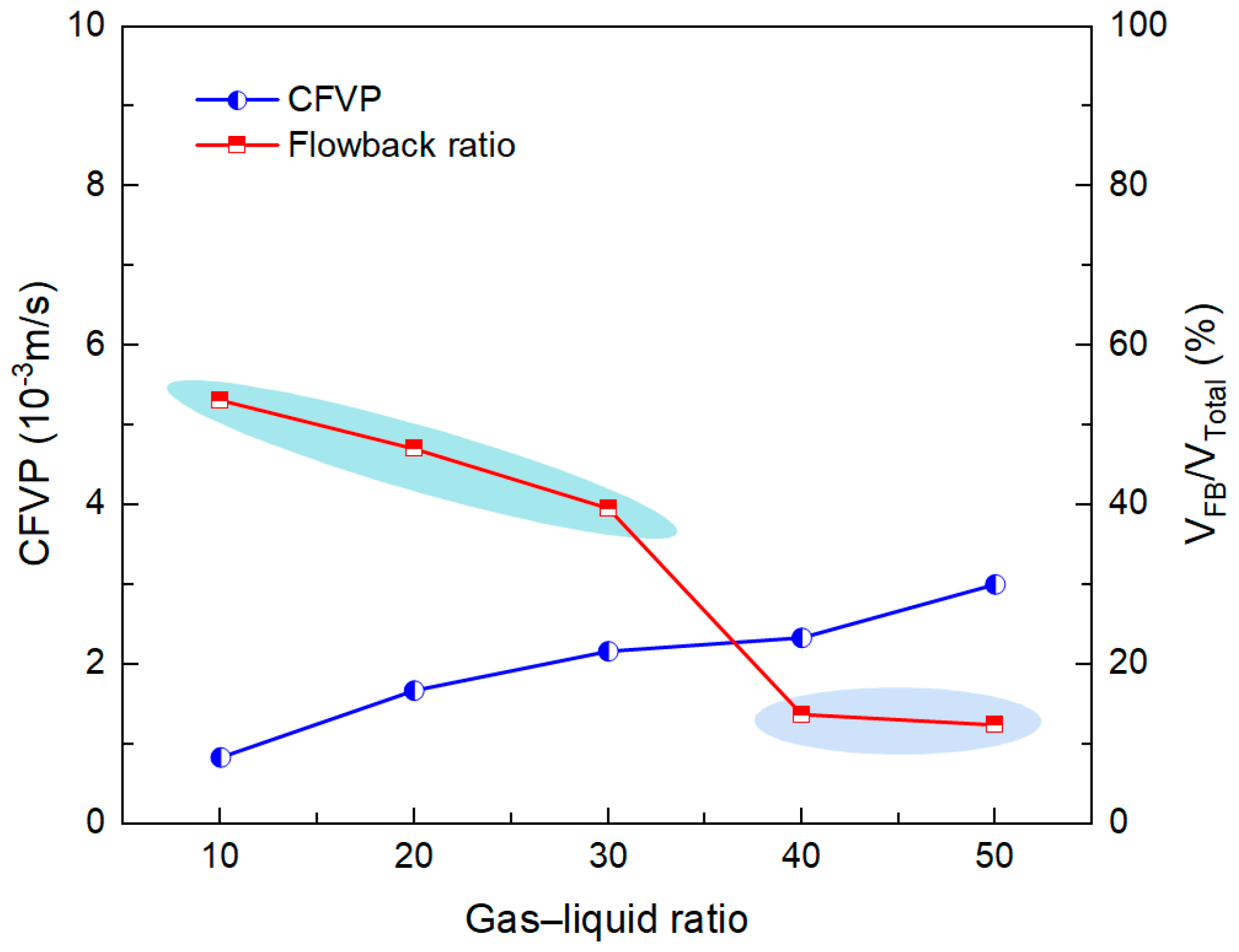
3.2.5. Effect of Gas–Liquid Ratio on CFVP

As the gas–liquid ratio in the fracture increased from 10 to 50, both the proppant flowback mass and the flowback area gradually decreased, while the CFVP rose from 0.8 × 10⁻³ m/s to 3 × 10⁻³ m/s (Figure 19 and Figure 20). This indicates that the gas–liquid ratio exerts a pronounced influence on proppant flowback. The progressive replacement of liquid by gas lowers the overall mixture viscosity, thereby reducing viscous resistance and pressure-gradient forces acting on particles and promoting the formation of a more stable proppant pack. At the same time, the much larger gas volume diminishes the number of particles located at the gas–liquid interface, which weakens capillary action and interparticle cohesion. Consequently, as the gas–liquid ratio increased from 10 to 30, the proppant flowback ratio decreased from 53.1% to 39.5%. Once the ratio exceeded 40, the flowback ratio stabilized at a low level of about 12–14%. Therefore, when the gas–liquid ratio in reservoir fractures exceeds 40, proppant flowback becomes negligible, and production-rate constraints can be gradually relaxed.

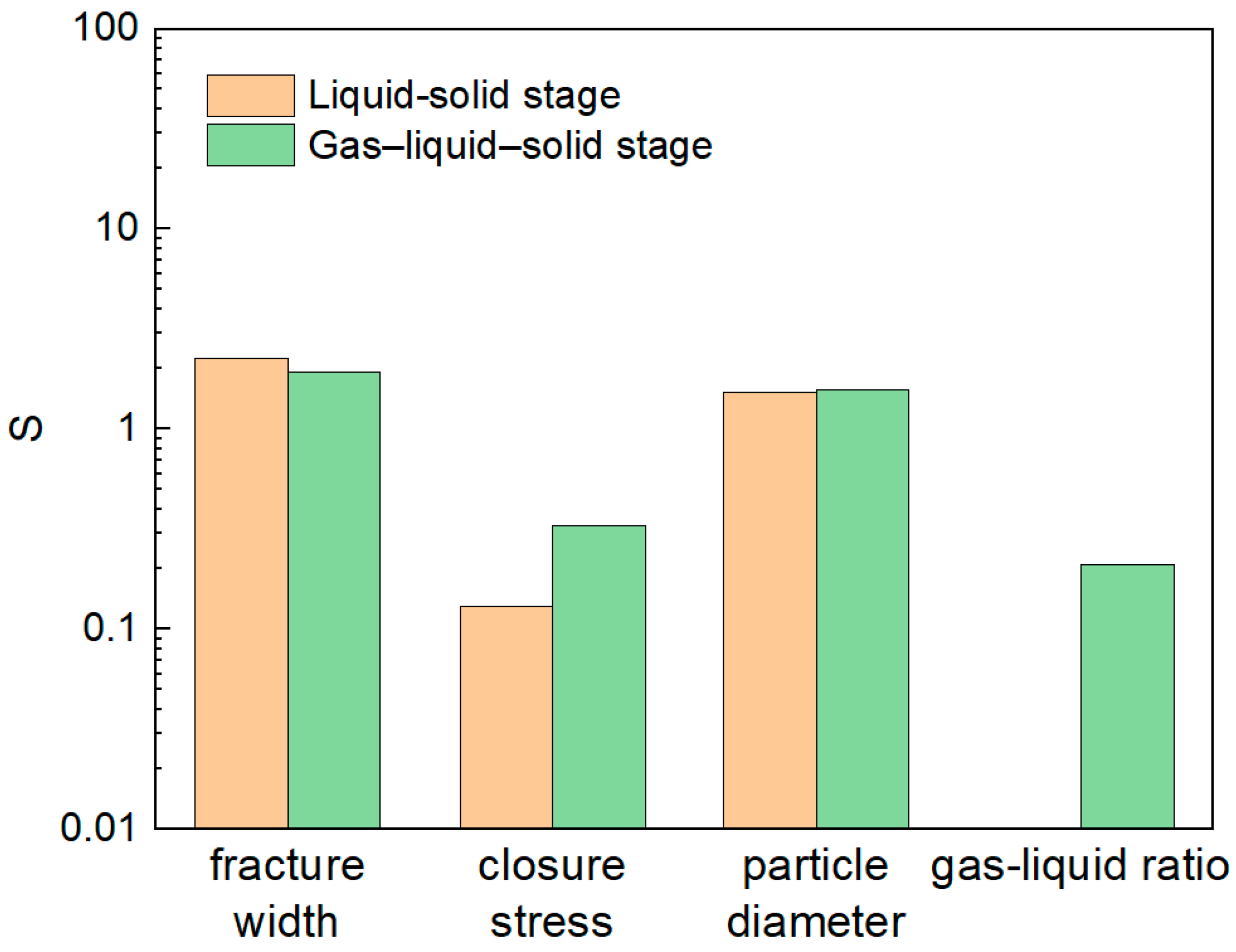
3.3. Predictive Model for CFVP

The experimental investigation clarified the key regularities governing the CFVP of proppants, revealing the dominant effects of fracture width, closure stress, proppant size, and gas–liquid ratio. To translate these empirical findings into a practical forecasting tool, it is necessary to establish a predictive model capable of estimating CFVP under various reservoir and production conditions. Dimensional analysis provides a rigorous framework for this purpose, as it systematically incorporates the physical relationships among controlling variables and ensures the resulting model is dimensionally homogeneous and scalable. By expressing CFVP as a function of dimensionless groups, the dimensional analysis-based model captures the underlying physics while allowing reliable extrapolation to field-scale operations.

Because the mechanical mechanisms of proppant flowback differ between the liquid-solid two-phase stage and the gas-liquid-solid three-phase stage, separate models were established for the two production regimes. Under low closure stress, a local flowback channel may form at the top of the proppant pack, whereas higher closure stresses significantly enhance particle confinement. In field conditions, the rapid pressure drop after fracturing leads to a sharp increase in closure stress, making the relative influence of gravity negligible. As the studied system represents deep CBM reservoirs with small fluid-density variations, gravity and fluid density were therefore neglected in the dimensional analysis. Seven governing variables were selected as listed in Equation (10):

$$v_c=f\left(w_f,{\sigma }_e,d,\gamma ,{\rho }_p,{\mu }_f\right)$$

(10)

where

v_c—critical flowback velocity, 10⁻³ m/s (LT⁻¹);

w_f—fracture width, mm (L);

σ_e—effective closure stress, MPa (M L⁻¹ T⁻²);

d—mean proppant diameter, μm (L);

γ—gas–liquid ratio (dimensionless);

ρ_p—proppant density, kg/m³ (M L⁻³);

μ_f—fluid viscosity, mPa·s (M L⁻¹ T⁻¹).

Taking w_f, σ_e and μ_f as the fundamental variables and applying the Buckingham π theorem yields four independent dimensionless groups (Equation (11)).

$${\pi }_1={\displaystyle \frac{v_c{\mu }_f}{{\sigma }_e{w}_f}},{\pi }_2={\displaystyle \frac{d}{w_f}},{\pi }_3={\displaystyle \frac{{\rho }_p{\sigma }_e{w}_f^2}{{\mu }_f^2}},{\pi }_4=\gamma$$

(11)

Among them, π₁ characterizes the ratio of characteristic viscous shear stress to effective closure stress; π₂ is the inverse of the width–diameter ratio and governs proppant bridging and structural stability; π₃ represents the relative magnitude of particle inertia to viscous and normal constraints; and π₄ is the gas–liquid ratio.

Accordingly, power-law models were developed to describe the relationships for the liquid-solid two-phase stage and the gas-liquid-solid three-phase stage (Equations (12) and (13)).

$${\pi }_1=A{\pi }_2^B{\pi }_3^C$$

(12)

$${\pi }_1=a{\pi }_2^b{\pi }_3^c{\pi }_4^d$$

(13)

Based on experimental data, the nonlinear least-squares method was used to fit the power functions. The liquid-solid two-phase stage yielded A = 3.11 (95% CI:2.55~3.67), B = 1.53 (95% CI:1.16~1.90), C = −0.87 (95% CI:−0.92~−0.83) For the gas-liquid-solid three-phase stage, a = 1.18 (95% CI:1.03~1.33), b = 1.58 (95% CI:1.25~1.93), c = −0.67 (95% CI:−0.79~−0.56), and d = 0.21 (95% CI:0.0139~0.4) were obtained. By substituting these coefficients into Equations (12) and (13) and combining with the dimensionless groups in Equation (11), predictive models for CFVP in the liquid-solid two-phase stage (v_cl) and the gas-liquid-solid three-phase stage (v_cg) were established, as given in Equations (14) and (15). The overall fits achieved coefficients of determination R² of 0.91 and 0.96, with root-mean-square errors of 2.9× 10⁻⁵ m/s and 6.7 × 10⁻⁴ m/s, respectively, demonstrating strong predictive capability. Using the RMSE together with the mean experimental CFVP, the prediction uncertainty is approximately ±12% for the liquid–solid stage and ±36% for the gas–liquid–solid stage within the tested parameter space.

$$v_{cl}=3.11{\displaystyle \frac{w_f{\sigma }_e}{{\mu }_f}}{\left({\displaystyle \frac{d}{w_f}}\right)}^{1.53}{\left({\displaystyle \frac{{\rho }_p{\sigma }_e{w}_f^2}{{\mu }_f^2}}\right)}^{-0.87}$$

(14)

$$v_{cg}=1.18{\displaystyle \frac{w_f{\sigma }_e}{{\mu }_f}}{\left({\displaystyle \frac{d}{w_f}}\right)}^{1.58}{\left({\displaystyle \frac{{\rho }_p{\sigma }_e{w}_f^2}{{\mu }_f^2}}\right)}^{-0.67}{\gamma }^{0.21}$$

(15)

Since proppant instability within reservoir fractures cannot be directly observed, field data related to CFVP are unavailable, and experimental studies on proppant flowback under gas–liquid–solid three-phase conditions are still lacking. Therefore, independent experimental data that were not used for model fitting were employed for model validation. As shown in

Table 5. Comparison between experimental and predicted results.

Stage	Fracture Width (mm)	Closure Stress (MPa)	Proppant Size (μm)	Gas–Liquid Ratio	Experimental Value (10−3 m/s)	Model Value (10−3 m/s)	Relative Error (%)
liquid–solid	6	5	238.68	-	0.175	0.171	2.5
	6	25	271.8	-	0.275	0.257	6.7
	6	45	238.68	-	0.250	0.227	9.2
gas–liquid–solid	6	5	238.68	20	1.000	0.887	11.3
	6	25	271.8	20	2.000	1.852	7.4
	6	45	238.68	20	1.667	1.831	9.8

, the model exhibits good predictive performance in reproducing the measured CFVP values.

A sensitivity analysis was conducted to evaluate the influence of key parameters on the CFVP model. Given the power-law form of Equations (14) and (15), the normalized sensitivity of CFVP to each variable was obtained from the logarithmic elasticities, as expressed in Equation (16), which are equal to the exponents of the corresponding variables. In this equation, x_i denotes the independent variable. As shown in Figure 21, the sensitivity analysis indicates that fracture width and proppant diameter are the dominant parameters affecting the CFVP in both liquid–solid and gas–liquid–solid stages, implying that geometric constraints and particle size exert the strongest control on proppant instability. Closure stress shows a moderate influence, which becomes slightly more significant under gas–liquid–solid conditions due to the enhanced normal loading on the proppant pack.

$$S_i=\left|{\displaystyle \frac{\partial \ln v_c}{\partial \ln x_i}}\right|$$

(16)

4. Conclusions

This study simulated proppant flowback under closure stress using the CFD–DEM method, revealing the flowback process and underlying mechanical mechanisms. On the basis of the controlling-factor analysis, the CFVP in coal fractures was further investigated experimentally for different production stages. Finally, a semi-empirical CFVP model for the water-production stage and the gas–water co-production stage was established through dimensional analysis. The findings provide mechanistic understanding and practical thresholds that can guide production optimization in DCBM wells.

The following conclusions were drawn:

(1)

Proppant flowback proceeds in three stages—no flowback, gradual flowback, and rapid flowback—driven by the balance between fluid forces and interparticle contact forces. Gradual flowback occurs when fluid forces overcome gravity to mobilize loosely packed proppants near the outlet, whereas rapid flowback is triggered once the tangential resultant force exceeds the static friction threshold, causing the stable bridging structure to collapse.

(2)

Fracture width strongly controls flowback behavior. Wider fractures reduce pack stability and lower CFVP but allow higher critical flow rates. A threshold of 8 mm was identified, beyond which flowback ratios drop sharply while post-flowback conductivity remains high, enabling higher production rates without compromising fracture performance.

(3)

Closure stress exerts a dual influence on proppant flowback. At stresses below 15 MPa, enhanced tangential contact forces promote the breakdown of bridge structures, whereby increasing closure stress elevates CFVP but simultaneously accelerates proppant transport. Once the stress exceeds 15 MPa, however, the rise in normal forces increases the static friction threshold and strengthens the overall stability of the proppant pack. Although higher pore-scale flow velocities within the pack cause CFVP to remain nearly constant, the overall flowback rate gradually decreases. Beyond 35 MPa, the proppant pack becomes highly stable, and flowback is largely suppressed.

(4)

Increasing the average proppant size raises CFVP and lowers flowback, because larger particles possess greater self-weight and contact stiffness, which increase normal loading and the static-friction threshold, thereby enhancing the mechanical stability of the packed bed. Stepwise placement is recommended, since direct contact between 30/50-mesh and 70/140-mesh particles allows fine particles to infill interstices and weaken the force-chain framework, markedly reducing fracture conductivity.

(5)

Higher gas–liquid ratios suppress proppant flowback and raise CFVP by lowering the mixture’s effective density and viscosity and by enhancing gas–liquid interfacial tension effects. These changes diminish drag and pressure-gradient forces on particles while strengthening capillary and interparticle cohesion. Once the gas–liquid ratio in reservoir fractures exceeds about 40, the flowback ratio remains consistently low, permitting a gradual relaxation of production-rate constraints.