Designs of Bayesian EWMA Variability Control Charts in the Presence of Measurement Error

Abstract

Statistical process control may lead to false detection results in the presence of measurement error, so it is necessary to deal with the effect of measurement error. The Bayesian exponentially weighted moving average (EWMA) variability control chart, first proposed by Lin et al., is a distribution-free control chart, and it can effectively monitor process variance even if the process skewness varies with time. This paper investigates the influence of measurement error on the Bayesian EWMA variability control chart, and it proposes two designs for the Bayesian EWMA variability control chart in the presence of measurement error. One is to modify the control limits based on the biased error-prone monitoring statistics, called the error-embedded control chart. The other is to design the control limits based on the error-corrected monitoring statistics, called the error-corrected control chart. Simulation results prove that both of the proposed control charts are reliable and have good detection performance in the presence of measurement error. Moreover, the average run lengths of the proposed control charts are exactly the same, indicating that both of them are equivalent control charts. Comparison results show that the existing control chart in Lin et al. is not in-control robust and fails to detect a downward shift in process variance when measurement error is present. Thus, using the error-embedded control chart or the error-corrected control chart to monitor processes with measurement errors is reliable and effective. Moreover, the proposed control charts, where π₁₁ = 1 and π₁₀ = 0, can be applied to monitor processes without measurement errors since their detection performance is equal to that of the existing control chart in Lin et al. Finally, we demonstrate the application of the error-embedded control chart and the error-corrected control chart to analyze the data from the service time system of a bank branch and the data from a semiconductor manufacturing process, showing that the proposed control charts can indeed be applied to data with measurement errors.

1. Introduction

Control charts are a very effective tool for maintaining a process or processes at a stable level. The main method is to find a sampling distribution of the monitoring statistic related to an in-control process and collect data period by period to monitor changes in this in-control process. When the observed statistics appear abnormal and fall outside the control limits, it indicates that the process is out of control. The assignable causes must be immediately identified and eliminated to adjust the process to a state under control. The determination of control limits of a control chart is based on the in-control sampling distribution of this monitoring statistic, satisfying a preset in-control average run length (ARL₀). Usually, it is necessary to first figure out what the process distribution is. In the beginning, the control chart proposed by Shewhart [1] was applied to the process of a normal distribution.

In recent years, statistical process control, which has been widely used in the manufacturing industry, has also been gradually used in the service industry to improve service quality. However, the variability of service processes has more complex factors, and the process control of service quality is more difficult than the process control of product quality [2,3,4]. The main reason is that the service process is usually either not normally distributed or the distribution is unknown, and the skewness of the distribution may change over time, even under the in-control process [5].

There are a lot of studies on monitoring process location with non-normal or unknown distributions, such as Ferrell [6], Bakir and Reynolds [7], Amin et al. [8], Chakraborti et al. [9], Altukife [10,11], Bakir [12,13], Chakraborti and Eryilmaz [14], Chakraborti and Graham [15], Li et al. [16], and Graham et al. [17,18]. On the other hand, fewer studies focus on monitoring process variability with non-normal or unknown distributions. Zou and Tsung [19] developed a distribution-free exponentially weighted moving average (EWMA) control chart based on a nonparametric goodness-of-fit test to detect changes in process variability. Jones-Farmer and Champ [20] proposed a phase I scale control chart that is distribution-free to define the in-control state of process variability. Zombade and Ghute [21] developed a nonparametric control chart based on run rules to monitor changes in process variability. Yang and Arnold [22] a proposed new distribution-free control chart to monitor process variability. Lin et al. [5] considered the Bayesian method to modify a distribution-free variability control chart, which can be applied to situations where the process skewness varies with time. When the normal distribution assumption is violated, the non-parametric or distribution-free control charts mentioned above provide evidence that they are always superior to Shewhart control charts, whatever in monitoring process location or variability.

The data collected from manufacturing or service processes may have measurement errors; that is, the observed data is different from the underlying true but unobservable data. Obviously, data containing measurement errors may lead to misinterpretation about the process state due to wrong detection in control charts, resulting in the failure of the statistical process control. Some studies construct control charts for continuous data containing measurement error. Maravelakis et al. [23] proposed an EWMA control chart in the presence of measurement error. Tran et al. [24] proposed a variable sampling interval EWMA median control chart in the presence of measurement error. Noor-ul-Amin et al. [25] examined the effect of measurement error on an auxiliary variable based on EWMA-Z control charts by using a covariable model, multiple measurements, and a linearly increasing variance model. Chen and Yang [26] constructed a p-control chart for attribute data containing measurement errors and proposed an efficient measurement error correction method. Yang et al. [27] constructed a distribution-free EWMA dispersion control chart with measurement error correction based on the error-corrected sign statistic with transition probabilities. The use of this distribution-free control chart is limited to when the population skewness is constant or under in-control conditions [5].

The Bayesian exponentially weighted moving average (EWMA) variability control chart, first proposed by Lin et al. [5], is also a distribution-free control chart, and it can effectively monitor process variability even if the process skewness is unstable. This study aims to develop two appropriate Bayesian EWMA variability control charts in the presence of measurement error. Two designs of the control charts will be developed to deal with the problem of measurement error. One is to modify the control limits based on the distribution of the error-prone monitoring statistic. The other is to correct the error-prone monitoring statistic and construct the control charts for a distribution of the error-corrected statistic. According to the results of simulation work, the proposed control charts both have exactly the same performance for each setting of the parameters, showing that they are equivalent control charts. Our contribution is to propose Bayesian distribution-free variability control charts in the presence of measurement error that provide reliable control limits and effectively detect out-of-control processes.

This article is organized as follows. In Section 2, following Lin et al. [5], we introduce the general framework of the Bayesian EWMA variability control chart and complete the preliminary setting of our control scheme. In Section 3, we revise the control limits for a biased EWMA statistic due to measurement errors, and we propose a new Bayesian EWMA variability control chart in which measurement errors are embedded since both the statistic and control limits contain errors. The out-of-control average run lengths show that the proposed chart has excellent detection performance. In Section 4, we first correct the biased EWMA statistic and then calculate the corresponding control limits based on the error-corrected EWMA statistic. Accordingly, we propose a new error-corrected Bayesian EWMA variability control chart. Results from Monte Carlo simulations show that, for each parameter setting, the two newly proposed control charts yield identical detection performance, confirming that they are equivalent. In Section 5, we compare the detection performance of the two proposed control charts with that of the existing control chart in Lin et al. [5] for the error-prone data, showing that the former performs better. In Section 6, we apply the proposed control charts to analyze the data from the service time system of a bank branch [22] and the SECOM dataset from the UCI Machine Learning Repository [28]. Finally, we summarize the findings and provide recommendations in Section 7.

2. Preliminary Settings

We first review the Bayesian variability control chart proposed by Lin et al. [5] as the basis for the subsequent development in this study. Assume that the process variability of the critical quality characteristic, X, is ${\sigma }^2$. A random sample of size 2n, denoted by X₁, …, X_2n, is collected from such a process. A transformed variable is defined as

$$Y_j={\displaystyle \frac{{(X_{2j}-X_{2j-1})}^2}{2}},j=1,2,\dots ,n.$$

(1)

Obviously, $E\left(Y_j\right)={\sigma }^2,j=1,2,\dots ,n.$

Define a process proportion, $p=P\left(Y>{\sigma }_0^2\right)$, where ${\sigma }_0^2$ is the in-control process variance. If the process is under in-control conditions, then $p=p_0$. The process proportion, p, will differ from $p_0$, while the process variance, ${\sigma }^2$, shifts away from ${\sigma }_0^2$. Hence, the control of p achieves the purpose of controlling ${\sigma }^2$.

A monitoring statistic is defined as

$$M_t|p={\sum }_{j=1}^{n}I(Y_j>{\sigma }_0^2)~Binomial(n,p)$$

(2)

This is used to control the process proportion, p. However, in addition to changes in process variance, changes in process skewness will also cause changes in the process proportion, p. In other words, the process variance is still under control, but the process proportion, p, is not fixed. Hence, the process proportion, p, is assumed to be random, and its prior distribution under in-control conditions is a Beta distribution:

$$p~Beta\left({\alpha }_0,{\beta }_0\right),{\alpha }_0>0,{\beta }_0>0.$$

(3)

Then, the monitoring statistic, $M_t$, is used to control $E_0\left(p\right)={\alpha }_0/({\alpha }_0+{\beta }_0)$, and the prediction distribution of $M_t$ under in-control conditions is a Beta-Binomial distribution:

$$M_t~Beta-Binomial\left(n,{\alpha }_0,{\beta }_0\right).$$

(4)

The mean and variance of $M_t$ are

$$E\left(M_t\right)={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}$$

(5)

and

$$Var\left(M_t\right)={\displaystyle \frac{n{\alpha }_0{\beta }_0({\alpha }_0+{\beta }_0+n)}{{\left({\alpha }_0+{\beta }_0\right)}^2({\alpha }_0+{\beta }_0+1)}},$$

(6)

respectively.

To detect small changes in $E_0\left(p\right)$, we construct a Bayesian EWMA variability control chart based on the $M_t$ statistic. Let the monitoring statistic, ${EWMA}_t$, be defined as

$${EWMA}_t=\lambda M_t+\left(1-\lambda \right){EWMA}_{t-1},0<\lambda \le 1,$$

(7)

where $\lambda$ is a smoothing parameter.

Because $E\left(M_t\right)=n{\alpha }_0/({\alpha }_0+{\beta }_0)$ and EWMA₀ is set to be the mean of $M_t$, the mean and variance of EWMA_t are specified as

$$E\left({EWMA}_t\right)={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}$$

(8)

and

$$Var\left({EWMA}_t\right)={\displaystyle \frac{n{\alpha }_0{\beta }_0({\alpha }_0+{\beta }_0+n)}{{\left({\alpha }_0+{\beta }_0\right)}^2({\alpha }_0+{\beta }_0+1)}}\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right),$$

(9)

respectively.

Hence, the Bayesian EWMA variability control chart can be constructed, and the control limits, upper control limit (UCL), center line (CL), and lower control limit (LCL) are specified as follows.

$${UCL}_{{EWMA}_t}={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}+k_1\sqrt{{\displaystyle \frac{n{\alpha }_0{\beta }_0({\alpha }_0+{\beta }_0+n)}{{\left({\alpha }_0+{\beta }_0\right)}^2({\alpha }_0+{\beta }_0+1)}}\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right)},$$

(10)

$${CL}_{{EWMA}_t}={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}},$$

(11)

$${LCL}_{{EWMA}_t}={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}-k_2\sqrt{{\displaystyle \frac{n{\alpha }_0{\beta }_0({\alpha }_0+{\beta }_0+n)}{{\left({\alpha }_0+{\beta }_0\right)}^2({\alpha }_0+{\beta }_0+1)}}\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right)},$$

(12)

where the control coefficients, k₁ and k₂, can be obtained given the preset in-control average run length.

3. Error-Embedded Bayesian EWMA Variability Control Charts

3.1. Construction

Assume that the process variance in the critical quality characteristic, X, is ${\sigma }^2$. In the processes with measurement errors, we usually do not collect correct samples, X₁, …, X_2n, of size 2n, but we do observe error-prone samples, X₁*, …, X_2n*, which are defined as follows.

$$X_i^{\mathrm{*}}=X_i+{\epsilon }_i,i=1,2,\dots ,2n,$$

(13)

where $E\left(X_i\right)=\mu$, $Var\left(X_i\right)={\sigma }^2$, $E\left({\epsilon }_i\right)={\mu }_{\epsilon }$, and $Var\left({\epsilon }_i\right)={\sigma }_{\epsilon }^2$. Suppose that $X_i$ and ${\epsilon }_i$ are independent; then, $E\left(X_i^{\mathrm{*}}\right)={\mu }^{*}=\mu +{\mu }_{\epsilon }$ and $Var\left(X_i^{\mathrm{*}}\right)={\sigma }^{2*}={\sigma }^2+{\sigma }_{\epsilon }^2$. Instead of the unbiased statistic, $Y_j={(X_{2j}-X_{2j-1})}^2/2$, the observable statistic is

$$Y_j^{\mathrm{*}}={\displaystyle \frac{{(X_{2j}^{\mathrm{*}}-X_{2j-1}^{\mathrm{*}})}^2}{2}}.$$

(14)

However, $Y_j^{\mathrm{*}}$ is biased since

$$E\left(Y_j^{\mathrm{*}}\right)=E\left(Y_j\pm \sqrt{2Y_j}\left({\epsilon }_{2j}-{\epsilon }_{2j-1}\right)+{\displaystyle \frac{{\left({\epsilon }_{2j}-{\epsilon }_{2j-1}\right)}^2}{2}}\right)=E\left(Y_j\right)+{\displaystyle \frac{Var\left({\epsilon }_{2j}-{\epsilon }_{2j-1}\right)}{2}}={\sigma }^2+{\sigma }_{\epsilon }^2.$$

(15)

Assume that the in-control process variance, ${\sigma }_0^2$, is known, meaning that the true value of the process variance is obtained during the experimental phase or that the target value is set during the design phase. Originally, the process variance, ${\sigma }^2$, is controlled through indirect control, $p=P\left(Y>{\sigma }_0^2\right)$, but the actual control is

$$p^{*}=P\left(Y^{*}>{\sigma }_0^2\right).$$

(16)

The relationship between $p^{*}$ and $p$ can be expressed as follows.

$$\begin{array}{cc}& p^{*}=P\left(\left(Y^{*}>{\sigma }_0^2\right)\cap \left(Y>{\sigma }_0^2\right)\right)+P\left(\left(Y^{*}>{\sigma }_0^2\right)\cap \left(Y<{\sigma }_0^2\right)\right)\\ =& P\left(Y>{\sigma }_0^2\right)P\left(Y^{*}>{\sigma }_0^2|Y>{\sigma }_0^2\right)+P\left(Y<{\sigma }_0^2\right)P\left(Y^{*}>{\sigma }_0^2|Y<{\sigma }_0^2\right)\\ & =p{\pi }_{11}+\left(1-p\right){\pi }_{10}={\pi }_{10}+\left({\pi }_{11}-{\pi }_{10}\right)p,\end{array}$$

(17)

where

$${\pi }_{11}=P\left(Y^{*}>{\sigma }_0^2|Y>{\sigma }_0^2\right),$$

(18)

and

$${\pi }_{10}=P\left(Y^{*}>{\sigma }_0^2|Y<{\sigma }_0^2\right).$$

(19)

Figure 1 depicts the relationships of ${\pi }_{11}$ vs. ${\sigma }_{\epsilon }/\sigma$ and ${\pi }_{10}$ vs. ${\sigma }_{\epsilon }/\sigma$ under a normal process and an exponential process. The plots strongly suggest that the larger the value of ${\sigma }_{\epsilon }^2$ relative to ${\sigma }^2$, the smaller ${\pi }_{11}$ and the larger ${\pi }_{10}$.

On the other hand, the observed monitoring statistic with measurement errors is defined as

$$M_t^{*}|p^{*}={\sum }_{j=1}^{n}I(Y_j^{*}>{\sigma }_0^2)~Binomial(n,p^{\mathrm{*}}).$$

(20)

From (17), we can obtain

$$E\left(M_t^{*}\right)=E\left(E\left(M_t^{*}|p^{*}\right)\right)=E\left(n{p}^{*}\right)=n\left(E\left(p\right){\pi }_{11}+\left(1-E\left(p\right)\right){\pi }_{10}\right)=n{\displaystyle \frac{{\alpha }_0{\pi }_{11}+{\beta }_0{\pi }_{10}}{{\alpha }_0+{\beta }_0}},$$

(21)

and

$$\begin{array}{c}Var\left(M_t^{*}\right)=E\left(Var\left(M_t^{*}|p^{*}\right)\right)+Var\left(E\left(M_t^{*}|p^{*}\right)\right)=E\left(n{p}^{*}\left(1-p^{*}\right)\right)+Var\left(n{p}^{*}\right)\\ =n{\pi }_{10}\left(1-{\pi }_{10}\right)+{\displaystyle \frac{n\left({\pi }_{11}-{\pi }_{10}\right)\left(1-2{\pi }_{10}\right){\alpha }_0}{{\alpha }_0+{\beta }_0}}-{\displaystyle \frac{{n\left({\pi }_{11}-{\pi }_{10}\right)}^2{\alpha }_0\left({\alpha }_0+1\right)}{\left({\alpha }_0+{\beta }_0\right)\left({\alpha }_0+{\beta }_0+1\right)}}+{\displaystyle \frac{n^2{\left({\pi }_{11}-{\pi }_{10}\right)}^2{\alpha }_0{\beta }_0}{{\left({\alpha }_0+{\beta }_0\right)}^2({\alpha }_0+{\beta }_0+1)}},\end{array}$$

(22)

since $p~Beta\left({\alpha }_0,{\beta }_0\right)$ under an in-control process.

Similarly, we further denote the monitoring statistic, ${EWMA}_t^{*}$, as follows.

$${EWMA}_t^{*}=\lambda M_t^{*}+(1-\lambda ){EWMA}_{t-1}^{*},0<\lambda \le 1.$$

(23)

Because $E\left(M_t^{*}\right)=n{\displaystyle \frac{{\alpha }_0{\pi }_{11}+{\beta }_0{\pi }_{10}}{{\alpha }_0+{\beta }_0}}$ and ${EWMA}_0^{*}$ is set to be the mean of $M_t^{*}$, the mean and variance of ${EWMA}_t^{*}$ are specified as

$$E\left({EWMA}_t^{*}\right)=n{\displaystyle \frac{{\alpha }_0{\pi }_{11}+{\beta }_0{\pi }_{10}}{{\alpha }_0+{\beta }_0}},$$

(24)

and

$$Var({EWMA}_t^{*})=Var\left(M_t^{*}\right)\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right),$$

(25)

where $Var\left(M_t^{*}\right)$ can be obtained from (22).

Assuming that ${\sigma }_0^2$, ${\pi }_{11}$, ${\pi }_{10}$, and $({\alpha }_0,{\beta }_0)$ are known, the error-embedded Bayesian EWMA variability control chart can thus be constructed, and the control limits are specified as

$${UCL}_{{EWMA}_t^{*}}=n{\displaystyle \frac{{\alpha }_0{\pi }_{11}+{\beta }_0{\pi }_{10}}{{\alpha }_0+{\beta }_0}}+k_3\sqrt{Var\left(M_t^{*}|{\alpha }_0,{\beta }_0\right)\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right)},$$

(26)

$${CL}_{{EWMA}_t^{*}}=n{\displaystyle \frac{{\alpha }_0{\pi }_{11}+{\beta }_0{\pi }_{10}}{{\alpha }_0+{\beta }_0}},$$

(27)

$${LCL}_{{EWMA}_t^{*}}=n{\displaystyle \frac{{\alpha }_0{\pi }_{11}+{\beta }_0{\pi }_{10}}{{\alpha }_0+{\beta }_0}}-k_4\sqrt{Var\left(M_t^{*}|{\alpha }_0,{\beta }_0\right)\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right)},$$

(28)

where k₃ and k₄ denote the coefficients of the control limits. The Monte Carlo simulations are applied to calculate k₃ and k₄, satisfying a preset, ARL₀, for various combinations of λ, n, (${\alpha }_0$,${\beta }_0$), and (${\pi }_{11}$,${\pi }_{10}$). The procedure of calculation is presented as follows.

1.

Given n, ${\alpha }_0$,${\beta }_0$, ${\pi }_{11}$,${\pi }_{10}$, λ, and ARL₀, ${UCL}_{{EWMA}_t^{*}}$ can be expressed as the function of k₃ by Equation (26), and ${LCL}_{{EWMA}_t^{*}}$ can be expressed as the function of k₄ by Equation (28).

2.

Let ${EWMA}_0^{*}={CL}_{{EWMA}_t^{*}}$ as in Equation (27).

3.

Simulate random numbers, $p_t$, from $Beta\left({\alpha }_0,{\beta }_0\right)$; compute $p_t^{*}$ with Equation (17); simulate random numbers, $M_t^{*}$, from $Binomial\left(n,p_t^{*}\right)$; and compute ${EWMA}_t^{*}$ with Equation (23) until ${EWMA}_t^{*}>{UCL}_{{EWMA}_t^{*}}$; then, record the run length, t.

4.

Repeat step 3 10,000 times, and obtain the average run length, ARL(k₃).

5.

Determine the k₃ value to make sure ARL(k₃) is within 2 × ARL₀ ± 2.

6.

After k₃ is obtained, simulate random numbers, $p_t$, from $Beta\left({\alpha }_0,{\beta }_0\right)$; compute $p_t^{*}$ with Equation (17); simulate random numbers, $M_t^{*}$, from $Binomial\left(n,p_t^{*}\right)$; and compute ${EWMA}_t^{*}$ with Equation (23) until ${EWMA}_t^{*}>{UCL}_{{EWMA}_t^{*}}$ or ${EWMA}_t^{*}<{LCL}_{{EWMA}_t^{*}}$; then, record the run length, t.

7.

Repeat step 6 10,000 times, and obtain the average run length, ARL(k₄).

8.

Determine the k₄ value to make sure ARL(k₄) is within ARL₀ ± 1.

Table 1. The coefficients of the control limits (k₃, k₄) of the error-embedded Bayesian EWMA variability control chart with parameters (λ = 0.1, ARL₀ = 370.4, π₁₁ = 0.94, π₁₀ = 0.04).

(α0, β0)	E0(p)	E0(p*)	n = 2	n = 5	n = 15	n = 25
(1, 1)	0.5000	0.4900	(2.6409, 2.6347)	(2.6452, 2.6544)	(2.6378, 2.6519)	(2.6327, 2.6633)
(1, 2)	0.3333	0.3400	(2.8344, 2.4322)	(2.8389, 2.4727)	(2.8441, 2.4716)	(2.8467, 2.4712)
(1, 3)	0.2500	0.2650	(2.9211, 2.3265)	(2.9274, 2.3981)	(2.9371, 2.4091)	(2.9481, 2.3925)
(1, 4)	0.2000	0.2200	(3.0066, 2.2305)	(2.9964, 2.3466)	(2.9985, 2.3632)	(3.0096, 2.3516)
(1, 5)	0.1667	0.1900	(3.0730, 2.1540)	(3.0345, 2.3173)	(3.0383, 2.3391)	(3.0493, 2.3301)
(1, 6)	0.1429	0.1686	(3.1232, 2.0949)	(3.0715, 2.2929)	(3.0630, 2.3224)	(3.0736, 2.3211)
(1, 7)	0.1250	0.1525	(3.1722, 2.0531)	(3.0904, 2.2673)	(3.0783, 2.3170)	(3.0978, 2.3047)
(1, 8)	0.1111	0.1400	(3.2013, 2.0041)	(3.1117, 2.2476)	(3.0961, 2.2987)	(3.1092, 2.2997)
(1, 9)	0.1000	0.1300	(3.2305, 1.9608)	(3.1202, 2.2306)	(3.1034, 2.2993)	(3.1148, 2.3010)

and

Table 2. The coefficients of the control limits (k₃, k₄) of the error-embedded Bayesian EWMA variability control chart with parameters (λ = 0.1, ARL₀ = 370.4, π₁₁ = 0.81, π₁₀ = 0.14).

(α0, β0)	E0(p)	E0(p*)	n = 2	n = 5	n = 15	n = 25
(1, 1)	0.5000	0.4750	(2.6725, 2.6295)	(2.6776, 2.6542)	(2.6637, 2.6557)	(2.6581, 2.6630)
(1, 2)	0.3333	0.3633	(2.8017, 2.4913)	(2.8013, 2.5323)	(2.8188, 2.5356)	(2.8277, 2.5129)
(1, 3)	0.2500	0.3075	(2.8355, 2.4257)	(2.8611, 2.4983)	(2.8825, 2.4956)	(2.9026, 2.4670)
(1, 4)	0.2000	0.2740	(2.8868, 2.3664)	(2.8818, 2.4784)	(2.9103, 2.4855)	(2.9365, 2.4583)
(1, 5)	0.1667	0.2517	(2.9229, 2.3364)	(2.8960, 2.4711)	(2.9218, 2.4845)	(2.9482, 2.4607)
(1, 6)	0.1429	0.2357	(2.9495, 2.3062)	(2.9126, 2.4600)	(2.9241, 2.4904)	(2.9522, 2.4664)
(1, 7)	0.1250	0.2238	(2.9712, 2.2825)	(2.9193, 2.4520)	(2.9252, 2.4908)	(2.9490, 2.4772)
(1, 8)	0.1111	0.2144	(2.9867, 2.2617)	(2.9310, 2.4551)	(2.9162, 2.4917)	(2.9431, 2.4796)
(1, 9)	0.1000	0.2070	(2.9992, 2.2460)	(2.9348, 2.4401)	(2.9164, 2.4994)	(2.9315, 2.5042)

show the coefficients of the control limits (k₃, k₄) of the error-embedded Bayesian EWMA variability control chart for λ = 0.1 and ARL₀ = 370.4. $E_0\left(p\right)={\alpha }_0/({\alpha }_0+{\beta }_0)$ is the original target to be controlled, but the target actually controlled is $E_0\left(p^{*}\right)=({\pi }_{11}{\alpha }_0+{\pi }_{10}{\beta }_0)/({\alpha }_0+{\beta }_0)$ due to measurement error. Since ${\sigma }_{\epsilon }/\sigma$ is negatively correlated with π₁₁ and positively correlated with π₁₀, we set π₁₁ = 0.94 and π₁₀ = 0.04 in Table 1 to represent a smaller level of ${\sigma }_{\epsilon }/\sigma$. The results in Table 1 reveal that k₃ and k₄ are very close when E₀(p) = 0.5 (or E₀(p*) = 0.49), but the difference between the two values increases as E₀(p) (or E₀(p*)) decreases. Obviously, the smaller E₀(p) (or E₀(p*)) is, the greater the asymmetry of the control limits. However, the asymmetry of the control limits is alleviated as the sample size increases.

Since ${\sigma }_{\epsilon }/\sigma$ is negatively correlated with π₁₁ and positively correlated with π₁₀, we set π₁₁ = 0.81 and π₁₀ = 0.14 in Table 2 to represent a larger level of ${\sigma }_{\epsilon }/\sigma$. The results in Table 2 are similar to those of Table 1, but k₃ is smaller, and k₄ is larger. This means that the larger the ratio, ${\sigma }_{\epsilon }/\sigma$, the smaller the asymmetry of the control limits.

3.2. Detection Performance

In this section, we will adopt out-of-control average run lengths (ARL₁) to evaluate the detection performance of the error-embedded Bayesian EWMA variability control chart. Thus, the Monte Carlo simulation approach is used to calculate the value of ARL₁ when the in-control process parameters (${\alpha }_0$,${\beta }_0$) are changed to (${\alpha }_1$,${\beta }_1$). The procedure of calculation is presented as follows.

1.

Given n, ${\alpha }_0$,${\beta }_0$, ${\pi }_{11}$,${\pi }_{10}$, λ, and ARL₀, (k₃, k₄) can be obtained, and ${UCL}_{{EWMA}_t^{*}}$ and ${LCL}_{{EWMA}_t^{*}}$ can be calculated by Equations (26) and (28).

2.

Let ${EWMA}_0^{*}={CL}_{{EWMA}_t^{*}}$ as in Equation (27).

3.

Given ${\alpha }_1$ and ${\beta }_1$.

4.

Simulate random numbers, $p_t$, from $Beta\left({\alpha }_1,{\beta }_1\right)$, compute $p_t^{*}$ with Equation (17); simulate random numbers, $M_t^{*}$, from $Binomial\left(n,p_t^{*}\right)$; and compute ${EWMA}_t^{*}$ with Equation (23) until ${EWMA}_t^{*}>{UCL}_{{EWMA}_t^{*}}$ or ${EWMA}_t^{*}<{LCL}_{{EWMA}_t^{*}}$; then, record the run length, t.

5.

Repeat step 4 10,000 times, and obtain the out-of-control average run length, ARL₁.

Without loss of generality, we specify the in-control process parameter, (${\alpha }_0$,${\beta }_0$) = (1, 2); smoothing parameter, λ = 0.1; and the preset, ARL₀ = 370.4.

Table 3. The ARL₁s of the error-embedded Bayesian EWMA variability control chart with parameters (λ = 0.1, π₁₁ = 0.94, π₁₀ = 0.04) and (α₀, β₀) = (1, 2).

(α1, β1)	E1(p)	E1(p*)	n = 2	n = 5	n = 15	n = 25
(9, 1)	0.9000	0.8500	4.57	3.27	2.37	2.21
(4, 1)	0.8000	0.7600	6.40	4.44	3.24	3.00
(3, 1)	0.7500	0.7150	7.73	5.24	3.85	3.57
(2, 1)	0.6666	0.6399	11.21	7.56	5.56	5.16
(4, 3)	0.5714	0.5543	20.94	13.99	10.38	9.65
(1, 1)	0.5000	0.4900	35.91	23.13	16.78	15.39
(3, 4)	0.4286	0.4257	111.21	90.28	80.03	77.55
(1, 2) IC	0.3333 IC	0.3400 IC	373.60	372.26	371.85	371.61
(1, 3)	0.2500	0.2650	121.47	84.86	62.27	57.34
(1, 4)	0.2000	0.2200	55.38	35.53	24.93	23.03
(1, 5)	0.1667	0.1900	35.68	22.79	16.33	15.02
(1, 6)	0.1429	0.1686	28.08	17.80	12.70	11.70
(1, 9)	0.1000	0.1300	19.07	12.07	8.66	7.95

^IC denotes that in-control and ARL₀s are presented in this row.

and

Table 4. The ARL₁s of the error-embedded Bayesian EWMA variability control chart with parameters (λ = 0.1, π₁₁ = 0.81, π₁₀ = 0.14) and (α₀, β₀) = (1, 2).

(α1, β1)	E1(p)	E1(p*)	n = 2	n = 5	n = 15	n = 25
(9, 1)	0.9000	0.7430	7.14	4.14	2.67	2.37
(4, 1)	0.8000	0.6760	9.96	5.80	3.71	3.30
(3, 1)	0.7500	0.6425	12.14	7.01	4.42	3.95
(2, 1)	0.6666	0.5866	17.69	10.03	6.45	5.67
(4, 3)	0.5714	0.5228	33.50	19.21	12.31	10.83
(1, 1)	0.5000	0.4750	57.69	31.62	19.53	17.13
(3, 4)	0.4286	0.4272	152.04	112.50	87.94	83.05
(1, 2) IC	0.3333 IC	0.3633 IC	371.38	371.23	370.99	373.48
(1, 3)	0.2500	0.3075	171.99	117.98	78.29	68.91
(1, 4)	0.2000	0.2740	89.69	54.11	32.20	27.60
(1, 5)	0.1667	0.2517	61.27	34.81	20.83	17.80
(1, 6)	0.1429	0.2357	47.73	27.13	16.18	13.79
(1, 9)	0.1000	0.2070	32.81	18.29	10.97	9.44

^IC denotes that in-control and ARL₀s are presented in this row.

show the ARL₁s of the error-embedded Bayesian EWMA variability control chart for (${\alpha }_1$,${\beta }_1$) = (9, 1), (4, 1), (3, 1), (2, 1), (4, 3), (1, 1), (3, 4), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 9), and n = 2, 5, 15, 25, where the presented values in the row of (${\alpha }_1$,${\beta }_1$) = (1, 2) are ARL₀s. While π₁₁ = 0.94, and π₁₀ = 0.04 (see Table 3), the original target to be controlled is $E_0\left(p\right)$ = 0.3333, but the target actually controlled is $E_0\left(p^{*}\right)$ = 0.3400 due to measurement error. Thus, the error-embedded statistic, ${EWMA}_t^{*}$, has a positive bias.

Table 3 reveals that the ARL₀s are all close to 370.4, and the ARL₁s all continue to decrease as E₁(p) deviates from 0.3333 (or E₁(p*) deviates from 0.3400) for different n values, where $E_1\left(p\right)={\alpha }_1/({\alpha }_1+{\beta }_1)$ and $E_1\left(p^{*}\right)=({\pi }_{11}{\alpha }_1+{\pi }_{10}{\beta }_1)/({\alpha }_1+{\beta }_1)$. Naturally, the decreasing speed increases with n, showing better detection performance due to the larger sample size.

While π₁₁ = 0.81 and π₁₀ = 0.14 (see Table 4), the original target to be controlled is $E_0\left(p\right)$=0.3333, but the target actually controlled is $E_0\left(p^{*}\right)$ = 0.3633 due to measurement error. Thus, the error-embedded statistic, ${EWMA}_t^{*}$, has a positive bias. Table 4 reveals that the ARL₀s are all slightly larger than 370.4, and the ARL₁ is larger than that in Table 3 for each combination of (${\alpha }_1$,${\beta }_1$) and n. It means that the chart for the larger ${\sigma }_{\epsilon }/\sigma$ possesses lower detection performance.

Figure 2 complements Table 3 and Table 4 with visualizations to make the detection performance of the proposed error-embedded control chart more accessible and intuitive. The plots depict each ARL₁ curve quickly decreasing as $E_1\left(p\right)$ departs from $E_0\left(p\right)$ = 0.3333, indicating that the proposed error-embedded control chart is sensitive to shifts in process variance even in the presence of measurement error. Furthermore, the comparison shows that the larger the sample size, the more quickly the ARL₁ curve decreases, indicating higher detection performance. In contrast, when the variance of the measurement error is large relative to the process variance (i.e., when the ${\sigma }_{\epsilon }/\sigma$ ratio is larger), the ARL₁ curves decrease more slowly, indicating lower detection performance.

4. Error-Corrected Bayesian EWMA Variability Control Charts

4.1. Construction

Equation (17) shows that the process proportion with measurement errors is a function of the original process proportion. The original process proportion can also be expressed as a function of the process proportion with measurement errors by using an inverse function, as follows:

$$p={\displaystyle \frac{p^{*}-{\pi }_{10}}{{\pi }_{11}-{\pi }_{10}}}.$$

(29)

The above formula provides a way to correct the process proportion with measurement errors back to the original process proportion without measurement errors. Consequently, the error-corrected in-control process proportion, denoted as $p^{**}$, is defined as the right-hand side of Equation (29). That is,

$$p^{**}\triangleq {\displaystyle \frac{p^{*}-{\pi }_{10}}{{\pi }_{11}-{\pi }_{10}}}.$$

(30)

Thus, this suggests that the error-corrected statistic is given by

$$M_t^{**}\triangleq {\sum }_{j=1}^n{\displaystyle \frac{I\left(Y_j^{*}>{\sigma }_0^2\right)-{\pi }_{10}}{{\pi }_{11}-{\pi }_{10}}}={\displaystyle \frac{M_t^{*}-n{\pi }_{10}}{{\pi }_{11}-{\pi }_{10}}}.$$

(31)

Under the prior distribution of p, $Beta({\alpha }_0,{\beta }_0)$, the mean and variance of $M_t^{**}$ are

$$E\left(M_t^{**}\right)={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}$$

(32)

and

$$\begin{array}{c}Var\left(M_t^{**}\right)={\displaystyle \frac{1}{{\left({\pi }_{11}-{\pi }_{10}\right)}^2}}Var\left(M_t^{*}\right)\\ ={\displaystyle \frac{n{\pi }_{10}\left(1-{\pi }_{10}\right)}{{\left({\pi }_{11}-{\pi }_{10}\right)}^2}}+{\displaystyle \frac{n\left(1-2{\pi }_{10}\right){\alpha }_0}{\left({\pi }_{11}-{\pi }_{10}\right)({\alpha }_0+{\beta }_0)}}-{\displaystyle \frac{n{\alpha }_0\left({\alpha }_0+1\right)}{\left({\alpha }_0+{\beta }_0\right)\left({\alpha }_0+{\beta }_0+1\right)}}+{\displaystyle \frac{n^2{\alpha }_0{\beta }_0}{{\left({\alpha }_0+{\beta }_0\right)}^2\left({\alpha }_0+{\beta }_0+1\right)}},\end{array}$$

(33)

respectively.

Similarly, we further denote the monitoring statistic, ${EWMA}_t^{**}$, of the error-corrected Bayesian EWMA variability control chart as follows.

$${EWMA}_t^{**}=\lambda M_t^{**}+(1-\lambda ){EWMA}_{t-1}^{**},0<\lambda \le 1.$$

(34)

Because $E\left(M_t^{**}\right)=n{\alpha }_0/({\alpha }_0+{\beta }_0)$ and ${EWMA}_0^{**}$ is set to be the mean of $M_t^{**}$, the mean and variance of ${EWMA}_t^{**}$ are specified as

$$E\left({EWMA}_t^{**}\right)={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}$$

(35)

and

$$Var({EWMA}_t^{**})=Var\left(M_t^{**}\right)\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right),$$

(36)

respectively.

Thus, the error-corrected Bayesian EWMA variability control chart can be constructed, and the control limits are specified as

$${UCL}_{{EWMA}_t^{**}}={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}+k_5\sqrt{Var\left(M_t^{**}\right)\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right)}$$

(37)

$${CL}_{{EWMA}_t^{**}}={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}},$$

(38)

$${LCL}_{{EWMA}_t^{**}}={\displaystyle \frac{n{\alpha }_0}{{\alpha }_0+{\beta }_0}}-k_6\sqrt{Var\left(M_t^{**}\right)\times {\displaystyle \frac{\lambda }{2-\lambda }}\times (1-\left(1-\lambda {)}^{2t}\right)}$$

(39)

where k₅ and k₆ denote the coefficients of the control limits. Monte Carlo simulations are applied to calculate k₅ and k₆, satisfying a preset ARL₀ for various combinations of λ, n, (${\alpha }_0$,${\beta }_0$), and (${\pi }_{11}$,${\pi }_{10}$). The procedure of calculation is presented as follows:

1.

Given n, ${\alpha }_0$,${\beta }_0$, ${\pi }_{11}$,${\pi }_{10}$, λ, and ARL₀, ${UCL}_{{EWMA}_t^{**}}$ can be expressed as the function of k₅ by Equation (37), and ${LCL}_{{EWMA}_t^{**}}$ can be expressed as the function of k₆ by Equation (39).

2.

Let ${EWMA}_0^{**}={CL}_{{EWMA}_t^{**}}$ as in Equation (38).

3.

Simulate random numbers, $p_t$, from $Beta\left({\alpha }_0,{\beta }_0\right)$; compute $p_t^{*}$ with Equation (17); simulate random numbers, $M_t^{*}$, from $Binomial\left(n,p_t^{*}\right)$; compute $M_t^{**}$ with Equation (31); and compute ${EWMA}_t^{**}$ with Equation (34) until ${EWMA}_t^{**}>{UCL}_{{EWMA}_t^{**}}$; then, record the run length, t.

4.

Repeat step 3 10,000 times, and obtain the average run length, ARL(k₅).

5.

Determine the k₅ value to make sure ARL(k₅) is within 2 × ARL₀ ± 2.

6.

After k₅ is obtained, simulate random numbers, $p_t$, from $Beta\left({\alpha }_0,{\beta }_0\right)$; compute $p_t^{*}$ with Equation (17); simulate random numbers, $M_t^{*}$, from $Binomial\left(n,p_t^{*}\right)$; compute $M_t^{**}$ with Equation (31); and compute ${EWMA}_t^{**}$ with Equation (34) until ${EWMA}_t^{**}>{UCL}_{{EWMA}_t^{**}}$ or ${EWMA}_t^{**}<{LCL}_{{EWMA}_t^{**}}$; then, record the run length, t.

7.

Repeat step 6 10,000 times, and obtain the average run length, ARL(k₆).

8.

Determine k₆ value to make sure the ARL(k₆) is within ARL₀ ± 1.

Table 5. The coefficients of the control limits (k₅, k₆) of the error-corrected Bayesian EWMA variability control chart with parameters (λ = 0.1, ARL₀ = 370.4, π₁₁ = 0.94, π₁₀ = 0.04).

(α0, β0)	E0(p)/E0(p**)	E0(p*)	n = 2	n = 5	n = 15	n = 25
(1, 1)	0.5000	0.4900	(2.6409, 2.6347)	(2.6452, 2.6544)	(2.6378, 2.6519)	(2.6327, 2.6633)
(1, 2)	0.3333	0.3400	(2.8344, 2.4322)	(2.8389, 2.4727)	(2.8441, 2.4716)	(2.8467, 2.4712)
(1, 3)	0.2500	0.2650	(2.9211, 2.3265)	(2.9274, 2.3981)	(2.9371, 2.4091)	(2.9481, 2.3925)
(1, 4)	0.2000	0.2200	(3.0066, 2.2305)	(2.9964, 2.3466)	(2.9985, 2.3632)	(3.0096, 2.3516)
(1, 5)	0.1667	0.1900	(3.0730, 2.1540)	(3.0345, 2.3173)	(3.0383, 2.3391)	(3.0493, 2.3301)
(1, 6)	0.1429	0.1686	(3.1232, 2.0949)	(3.0715, 2.2929)	(3.0630, 2.3224)	(3.0736, 2.3211)
(1, 7)	0.1250	0.1525	(3.1722, 2.0531)	(3.0904, 2.2673)	(3.0783, 2.3170)	(3.0978, 2.3047)
(1, 8)	0.1111	0.1400	(3.2013, 2.0041)	(3.1117, 2.2476)	(3.0961, 2.2987)	(3.1092, 2.2997)
(1, 9)	0.1000	0.1300	(3.2305, 1.9608)	(3.1202, 2.2306)	(3.1034, 2.2993)	(3.1148, 2.3010)

and

Table 6. The coefficients of the control limits (k₅, k₆) of the error-corrected Bayesian EWMA variability control chart with parameters (λ = 0.1, ARL₀ = 370.4, π₁₁ = 0.81, π₁₀ = 0.14).

(α0, β0)	E0(p)/E0(p**)	E0(p*)	n = 2	n = 5	n = 15	n = 25
(1, 1)	0.5000	0.4750	(2.6725, 2.6295)	(2.6776, 2.6542)	(2.6637, 2.6557)	(2.6581, 2.6630)
(1, 2)	0.3333	0.3633	(2.8017, 2.4913)	(2.8013, 2.5323)	(2.8188, 2.5356)	(2.8277, 2.5129)
(1, 3)	0.2500	0.3075	(2.8355, 2.4257)	(2.8611, 2.4983)	(2.8825, 2.4956)	(2.9026, 2.4670)
(1, 4)	0.2000	0.2740	(2.8868, 2.3664)	(2.8818, 2.4784)	(2.9103, 2.4855)	(2.9365, 2.4583)
(1, 5)	0.1667	0.2517	(2.9229, 2.3364)	(2.8960, 2.4711)	(2.9218, 2.4845)	(2.9482, 2.4607)
(1, 6)	0.1429	0.2357	(2.9495, 2.3062)	(2.9126, 2.4600)	(2.9241, 2.4904)	(2.9522, 2.4664)
(1, 7)	0.1250	0.2238	(2.9712, 2.2825)	(2.9193, 2.4520)	(2.9252, 2.4908)	(2.9490, 2.4772)
(1, 8)	0.1111	0.2144	(2.9867, 2.2617)	(2.9310, 2.4551)	(2.9162, 2.4917)	(2.9431, 2.4796)
(1, 9)	0.1000	0.2070	(2.9992, 2.2460)	(2.9348, 2.4401)	(2.9164, 2.4994)	(2.9315, 2.5042)

show the coefficients of the control limits (k₅, k₆) of the error-corrected Bayesian EWMA variability control chart for λ = 0.1 and ARL₀ = 370.4. Since ${\sigma }_{\epsilon }/\sigma$ is negatively correlated with π₁₁ and positively correlated with π₁₀, we set π₁₁ = 0.94 and π₁₀ = 0.04 in Table 5 to represent a smaller level of ${\sigma }_{\epsilon }/\sigma$. The results in Table 5 reveal that k₅ and k₆ are very close when E₀(p**) = 0.5 (or E₀(p*) = 0.49), but the difference between the two values increases as E₀(p**) (or E₀(p*)) decreases. Obviously, the smaller E₀(p**) (or E₀(p*)) is, the greater the asymmetry of the control limits. However, the asymmetry of the control limits is alleviated as the sample size increases. Moreover, the results in Table 5 are the same as the results in Table 1, indicating that the linear transformation of a monitoring statistic (refer to Equation (31)) does not change the asymmetric magnitude of the control limits.

Since ${\sigma }_{\epsilon }/\sigma$ is negatively correlated with π₁₁ and positively correlated with π₁₀, we set π₁₁ = 0.81 and π₁₀ = 0.14 in Table 6 to represent a larger level of ${\sigma }_{\epsilon }/\sigma$. The results in Table 6 are similar to those of Table 5, but k₅ is smaller, and k₆ is larger. This means that the larger the ratio, ${\sigma }_{\epsilon }/\sigma$, the smaller the asymmetry of the control limits. On the other hand, the results in Table 6 are the same as the results in Table 2 since the linear transformation of a monitoring statistic does not change the asymmetric magnitude of the control limits.

4.2. Detection Performance

In this subsection, we will adopt ARL₁ to evaluate the detection performance of the error-corrected Bayesian EWMA variability control chart. Thus, the Monte Carlo simulation approach is used to calculate the value of ARL₁ when the in-control process parameters (${\alpha }_0$,${\beta }_0$) are changed to (${\alpha }_1$,${\beta }_1$). The procedure of calculation is presented as follows:

1.

Given n, ${\alpha }_0$,${\beta }_0$, ${\pi }_{11}$,${\pi }_{10}$, λ, and ARL₀, (k₅, k₆) can be obtained, and ${UCL}_{{EWMA}_t^{**}}$ and ${LCL}_{{EWMA}_t^{**}}$ can be calculated by Equations (37) and (39).

2.

Let ${EWMA}_0^{**}={CL}_{{EWMA}_t^{**}}$ as in Equation (38).

3.

Given ${\alpha }_1$ and ${\beta }_1$.

4.

Simulate random numbers, $p_t$, from $Beta\left({\alpha }_1,{\beta }_1\right)$; compute $p_t^{*}$ with Equation (17); simulate random numbers, $M_t^{*}$, from $Binomial\left(n,p_t^{*}\right)$; compute $M_t^{**}$ with Equation (31); and compute ${EWMA}_t^{**}$ with Equation (34) until ${EWMA}_t^{**}>{UCL}_{{EWMA}_t^{**}}$ or ${EWMA}_t^{**}<{LCL}_{{EWMA}_t^{**}}$; then, record the run length, t.

5.

Repeat step 4 10,000 times, and obtain ARL₁.

Without loss of generality, we specify the in-control process parameter, (${\alpha }_0$,${\beta }_0$) = (1, 2); the smoothing parameter, λ = 0.1; and the preset, ARL₀ = 370.4.

Table 7. The ARL₁s of the error-corrected Bayesian EWMA variability control chart with parameters (λ = 0.1, π₁₁ = 0.94, π₁₀ = 0.04) and (α₀, β₀) = (1, 2).

(α1, β1)	E1(p)/E1(p**)	E1(p*)	n = 2	n = 5	n = 15	n = 25
(9, 1)	0.9000	0.8500	4.57	3.27	2.37	2.21
(4, 1)	0.8000	0.7600	6.40	4.44	3.24	3.00
(3, 1)	0.7500	0.7150	7.73	5.24	3.85	3.57
(2, 1)	0.6666	0.6399	11.21	7.56	5.56	5.16
(4, 3)	0.5714	0.5543	20.94	13.99	10.38	9.65
(1, 1)	0.5000	0.4900	35.91	23.13	16.78	15.39
(3, 4)	0.4286	0.4257	111.21	90.28	80.03	77.55
(1, 2) IC	0.3333 IC	0.3400 IC	373.60	372.26	371.85	371.61
(1, 3)	0.2500	0.2650	121.47	84.86	62.27	57.34
(1, 4)	0.2000	0.2200	55.38	35.53	24.93	23.03
(1, 5)	0.1667	0.1900	35.68	22.79	16.33	15.02
(1, 6)	0.1429	0.1686	28.08	17.80	12.70	11.70
(1, 9)	0.1000	0.1300	19.07	12.07	8.66	7.95

^IC denotes that in-control and ARL₀s are presented in this row.

and

Table 8. The ARL₁s of the error-corrected Bayesian EWMA variability control chart with parameters (λ = 0.1, π₁₁ = 0.81, π₁₀ = 0.14) and (α₀, β₀) = (1, 2).

(α1, β1)	E1(p)/E1(p**)	E1(p*)	n = 2	n = 5	n = 15	n = 25
(9, 1)	0.9000	0.7430	7.14	4.14	2.67	2.37
(4, 1)	0.8000	0.6760	9.96	5.80	3.71	3.30
(3, 1)	0.7500	0.6425	12.14	7.01	4.42	3.95
(2, 1)	0.6666	0.5866	17.69	10.03	6.45	5.67
(4, 3)	0.5714	0.5228	33.50	19.21	12.31	10.83
(1, 1)	0.5000	0.4750	57.69	31.62	19.53	17.13
(3, 4)	0.4286	0.4272	152.04	112.50	87.94	83.05
(1, 2) IC	0.3333 IC	0.3633 IC	371.38	371.23	370.99	373.48
(1, 3)	0.2500	0.3075	171.99	117.98	78.29	68.91
(1, 4)	0.2000	0.2740	89.69	54.11	32.20	27.60
(1, 5)	0.1667	0.2517	61.27	34.81	20.83	17.80
(1, 6)	0.1429	0.2357	47.73	27.13	16.18	13.79
(1, 9)	0.1000	0.2070	32.81	18.29	10.97	9.44

^IC denotes that in-control and ARL₀s are presented in this row.

show the ARL₁s of the error-corrected Bayesian EWMA variability control chart for (${\alpha }_1$,${\beta }_1$) = (9, 1), (4, 1), (3, 1), (2, 1), (4, 3), (1, 1), (3, 4), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 9), and n = 2, 5, 15, 25, where the presented values in the row of (${\alpha }_1$,${\beta }_1$) = (1, 2) are ARL₀s. While π₁₁ = 0.94 and π₁₀ = 0.04 (see Table 7), the original target to be controlled is $E_0\left(p\right)$ = 0.3333, and the target actually controlled is also $E_0\left(p^{**}\right)$ = 0.3333 through the error correction. Thus, the error-corrected statistic, ${EWMA}_t^{**}$, is unbiased.

Table 7 reveals that the ARL₀s are all close to 370.4, and the ARL₁s all continue to decrease as E₁(p) deviates from 0.3333. Naturally, the decreasing speed increases with n, showing better detection performance due to the larger sample size. Moreover, the results in Table 7 are the same as the results in Table 3, indicating that the performance of the error-corrected Bayesian EWMA variability control chart is equal to that of the error-embedded Bayesian EWMA variability control chart for π₁₁ = 0.94 and π₁₀ = 0.04.

While π₁₁ = 0.81 and π₁₀ = 0.14 (see Table 8), the original target to be controlled is $E_0\left(p\right)$ = 0.3333, and the target actually controlled is also $E_0\left(p^{**}\right)$ = 0.3333 through the error correction. Thus, the error-corrected statistic, ${EWMA}_t^{**}$, is unbiased. Table 8 reveals that the ARL₀s are all slightly larger than 370.4, and the ARL₁ is larger than that in Table 7 for each combination of (${\alpha }_1$,${\beta }_1$) and n. This means that the chart for the larger ${\sigma }_{\epsilon }/\sigma$ possesses lower detection performance. On the other hand, the results in Table 8 are the same as the results in Table 4, indicating that the performance of the error-corrected Bayesian EWMA variability control chart is equal to that of the error-embedded Bayesian EWMA variability control chart for π₁₁ = 0.81 and π₁₀ = 0.14. It can be implied that both proposed control charts have the same detection performance for any level of ${\sigma }_{\epsilon }/\sigma$ due to the linear transformation relationship between the two monitoring statistics. That is, both charts are equivalent. In summary, both the error-embedded design and the error-corrected design equivalently achieve effective controls in the presence of measurement error.

5. Comparisons

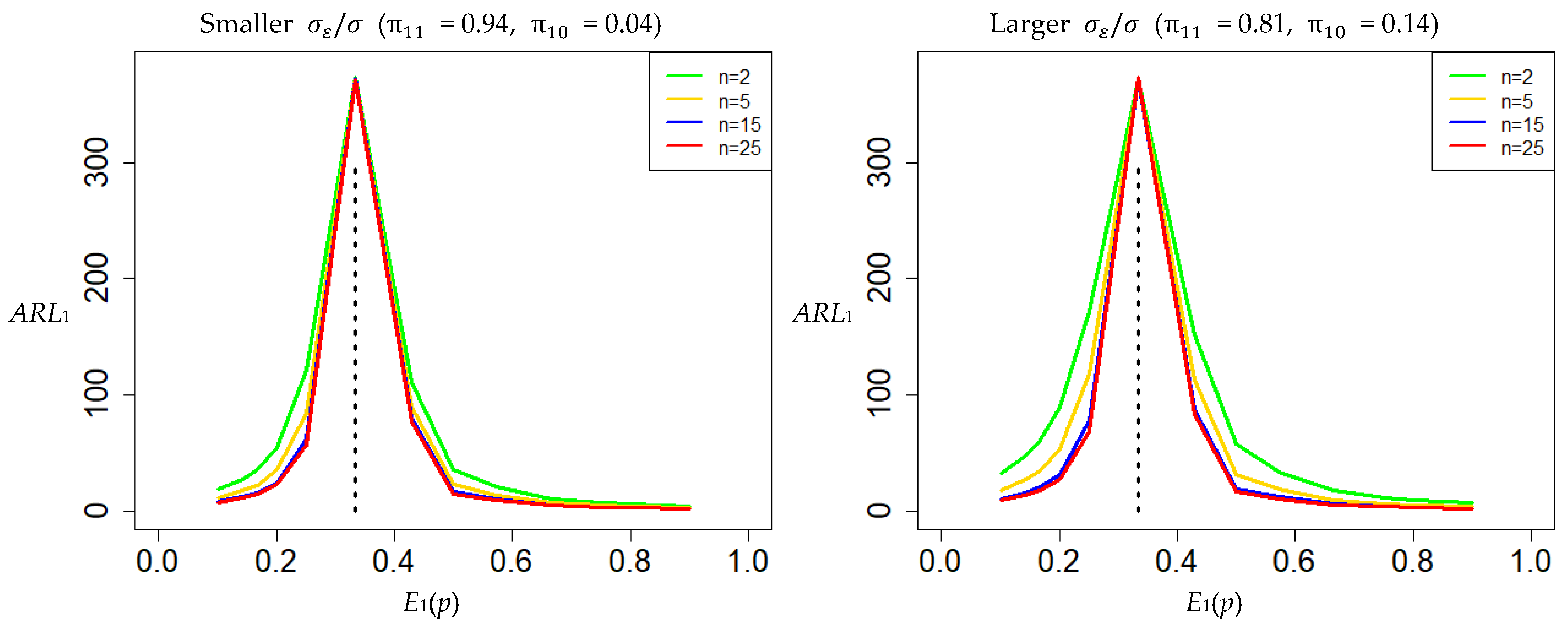
In this section, we will provide evidence to show that measurement errors should be accounted for in distribution-free control charts. Thus, the Bayesian EWMA variability control chart proposed by Lin et al. [5], which assumes no measurement errors, will be applied to error-prone data for comparisons.

5.1. The Impact of Misusing Control Charts

One of the misuses of control charts is using the control charts without measurement errors to monitor processes with measurement errors. The impact of such a misuse will be presented in this subsection.

Again, we specify the in-control process parameters, (${\alpha }_0$,${\beta }_0$) = (1, 3) and (1, 4); the smoothing parameter, λ = 0.1; and the preset, ARL₀ = 370.4, without loss of generality. As a result, the coefficients of the control limits (k₁, k₂) of the existing control chart in Lin et al. [5] are (2.9600, 2.2719) for (${\alpha }_0$,${\beta }_0$, n) = (1, 3, 2), (2.9578, 2.3599) for (${\alpha }_0$,${\beta }_0$, n) = (1, 3, 15), (3.0644, 2.1528) for (${\alpha }_0$,${\beta }_0$, n) = (1, 4, 2), and (3.0292, 2.3125) for (${\alpha }_0$,${\beta }_0$, n) = (1, 4, 15). Compared to control limits (k₃, k₄) and (k₅, k₆) in Table 2 and Table 5, respectively, we find the UCL-LCL ranges of the existing control chart are larger than those of the proposed error-embedded and error-corrected charts.

Table 9. ARLs of two proposed control charts compared with the existing control chart in Lin et al. [5] in the presence of measurement error with parameters (λ = 0.1, π₁₁ = 0.94, π₁₀ = 0.04). (A) (α₀, β₀) = (1, 3); (B) (α₀, β₀) = (1, 4).

Panel A.	(α0, β0) = (1, 3), E0(p) = 0.2500, and E0(p*) = 0.2650
			n = 2		n = 15
(α1, β1)	E1(p)	E1(p*)	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts
(9, 1)	0.9000	0.8500	2.84	2.92	1.67	1.41
(3, 1)	0.7500	0.7150	4.52	4.64	2.52	2.24
(1, 1)	0.5000	0.4900	14.26	15.45	7.03	6.66
(1, 2)	0.3333	0.3400	78.04	96.36	39.42	40.82
(1, 3) IC	0.2500 IC	0.2650 IC	376.48	370.81	536.30	370.69
(1, 4)	0.2000	0.2200	313.92	211.46	407.28	116.32
(1, 5)	0.1666	0.1899	155.05	106.38	111.64	45.82
(1, 9)	0.1000	0.1300	45.91	35.98	21.61	14.40
Panel B.	(α0, β0) = (1, 4), E0(p) = 0.2000, and E0(p*) = 0.2200
			n = 2		n = 15
(α1, β1)	E1(p)	E1(p*)	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts
(3, 1)	0.7500	0.7150	4.13	4.27	1.79	1.77
(1, 1)	0.5000	0.4900	9.94	10.99	4.33	4.27
(1, 2)	0.3333	0.3400	33.03	41.77	14.01	15.42
(1, 3)	0.2500	0.2650	113.86	164.84	58.49	77.21
(1, 4) IC	0.2000 IC	0.2200 IC	335.12	370.88	407.68	370.45
(1, 5)	0.1666	0.1899	426.53	269.61	1040.31	170.40
(1, 9)	0.1000	0.1300	99.15	66.11	54.79	23.80
(1, 19)	0.0500	0.0850	38.45	30.01	16.68	10.63

^IC denotes that in-control and ARL₀s are presented in this row.

and

Table 10. ARLs of two proposed control charts compared with the existing control chart in Lin et al. [5] in the presence of measurement error with parameters (λ = 0.1, π₁₁ = 0.81, π₁₀ = 0.14). (A) (α₀, β₀) = (1, 3); (B) (α₀, β₀) = (1, 4).

Panel A.	(α0, β0) = (1, 3), E0(p) = 0.2500, and E0(p*) = 0.3075
			n = 2		n = 15
(α1, β1)	E1(p)	E1(p*)	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts
(9, 1)	0.9000	0.7430	4.03	5.36	2.32	1.93
(3, 1)	0.7500	0.6425	6.22	8.27	3.34	2.84
(1, 1)	0.5000	0.4750	16.47	26.39	8.39	8.30
(1, 2)	0.3333	0.3633	59.37	143.42	32.87	50.85
(1, 3) IC	0.2500 IC	0.3075 IC	184.84	370.61	223.60	370.67
(1, 4)	0.2000	0.2740	449.28	269.21	2862.30	146.99
(1, 5)	0.1666	0.2516	615.74	162.35	14995.95	63.28
(1, 9)	0.1000	0.2070	273.29	67.23	1769.88	19.84
Panel B.	(α0, β0) = (1, 4), E0(p) = 0.2000, and E0(p*) = 0.2740
			n = 2		n = 15
(α1, β1)	E1(p)	E1(p*)	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts	The Existing Chart in Lin et al. [5]	The Error-Embedded/ Error-Corrected Charts
(3, 1)	0.7500	0.6425	5.30	6.19	2.26	2.02
(1, 1)	0.5000	0.4750	10.98	17.73	4.84	5.12
(1, 2)	0.3333	0.3633	26.68	69.44	12.02	19.33
(1, 3)	0.2500	0.3075	56.31	222.62	29.07	94.84
(1, 4) IC	0.2000 IC	0.2740 IC	111.09	370.35	81.91	370.67
(1, 5)	0.1666	0.2516	193.40	309.54	267.60	216.23
(1, 9)	0.1000	0.2070	581.26	117.85	16623.06	35.94
(1, 19)	0.0500	0.1735	388.81	58.65	6526.48	15.87

^IC denotes that in-control and ARL₀s are presented in this row.

show the ARLs of the Bayesian EWMA variability control charts, including the existing chart in Lin et al. [5] and the error-embedded/error-corrected charts for n = 2, 15, and several settings of (${\alpha }_1$,${\beta }_1$). Since ${\sigma }_{\epsilon }/\sigma$ is negatively correlated with π₁₁ and positively correlated with π₁₀, we set π₁₁ = 0.94 and π₁₀ = 0.04 in Table 9 to represent a smaller level of ${\sigma }_{\epsilon }/\sigma$. The results in Table 9 reveal that the ARL₀s of the existing chart in Lin et al. [5] are far from the preset, 370.4. This means that the in-control ARL fails to achieve 370.4 while using the control chart without measurement errors to monitor the process with measurement errors. On the other hand, the ARL₁s of the existing chart in Lin et al. [5] are obviously larger than those of the error-embedded/error-corrected control charts when E₁(p) has a downward shift. Table 9 shows that the error-embedded/error-corrected control charts are more reliable and have better detection performance.

Since ${\sigma }_{\epsilon }/\sigma$ is negatively correlated with π₁₁ and positively correlated with π₁₀, we then set π₁₁ = 0.81 and π₁₀ = 0.14 in Table 10 to represent a larger level of ${\sigma }_{\epsilon }/\sigma$. The results in Table 10 reveal that the ARL₀s of the existing chart in Lin et al. [5] are far less than the preset, 370.4, meaning that the chart is not in-control robust while using the control chart without measurement errors to monitor the process with measurement errors. On the other hand, the ARL₁s of the existing chart in Lin et al. [5] are abnormally large when E₁(p) has a downward shift, so the chart fails to detect a downward shift in process variance. Table 10 documents, again, that the error-embedded/error-corrected control charts are more reliable and have better detection performance, especially when the variance in measurement error is large relative to the in-control process variance.

5.2. Widely Applicable Control Charts

In this subsection, we will show that the proposed control chart can be used not only to monitor processes with measurement errors but also to monitor processes without measurement errors. For comparison, four control cases are presented below.

Case 1:

Using the existing control chart in Lin et al. [5] to monitor a process without measurement errors;

Case 2:

Using the proposed control charts to monitor a process without measurement errors;

Case 3:

Using the proposed control charts to monitor a process with measurement errors, where the variance of measurement error is small relative to the in-control process variance;

Case 4:

Using the proposed control charts to monitor a process with measurement errors, where the variance of measurement error is large relative to the in-control process variance.

Without loss of generality, we specify the in-control process parameters, (${\alpha }_0$,${\beta }_0$) = (1, 3); the smoothing parameter, λ = 0.1; and the preset, ARL₀ = 370.4, in four control cases. It is reasonable to set π₁₁ = 1 and π₁₀ = 0 in the error-embedded control chart or the error-corrected control chart while monitoring processes without measurement errors. In Case 3, we set π₁₁ = 0.94 and π₁₀ = 0.04 to represent a situation where the variance in measurement error is small relative to the in-control process variance. On the other hand, we set π₁₁ = 0.81 and π₁₀ = 0.14 in Case 4 to represent a situation where the variance in measurement error is large relative to the in-control process variance. The ARLs of the four control cases are presented in

Table 11. ARLs of four control cases with parameters (λ = 0.1 and (α₀, β₀) = (1, 3)). (A) n = 2; (B) n = 15.

Panel A.	n = 2
		Case 1	Case 2	Case 3	Case 4
(α1, β1)	E1(p)	Data Without ME: Using Existing Chart in Lin et al. [5]	Data Without ME: Using Error-Corrected Chart π11 = 1, π10 = 0	Data with ME: Using Error-Corrected Chart π11 = 0.94, π10 = 0.04	Data with ME: Using Error-Corrected Chart π11 = 0.81, π10 = 0.14
(9, 1)	0.9000	2.50	2.50	2.92	5.36
(3, 1)	0.7500	3.92	3.92	4.64	8.27
(1, 1)	0.5000	13.01	13.00	15.45	26.39
(1, 2)	0.3333	81.76	81.65	96.36	143.42
(1, 3) IC	0.2500 IC	370.24	370.90	370.81	370.61
(1, 4)	0.2000	177.71	178.22	211.46	269.21
(1, 5)	0.1666	86.05	86.23	106.38	162.35
(1, 9)	0.1000	28.69	28.73	35.98	67.23
Panel B.	n = 15
		Case 1	Case 2	Case 3	Case 4
(α1, β1)	E1(p)	Data Without ME: Using Existing Chart in Lin et al. [5]	Data Without ME: Using Error-Corrected Chart π11 = 1, π10 = 0	Data with ME: Using Error-Corrected Chart π11 = 0.94, π10 = 0.04	Data with ME: Using Error-Corrected Chart π11 = 0.81, π10 = 0.14
(9, 1)	0.9000	1.42	1.40	1.41	1.93
(3, 1)	0.7500	2.20	2.21	2.24	2.84
(1, 1)	0.5000	6.43	6.45	6.66	8.30
(1, 2)	0.3333	39.48	38.57	40.82	50.85
(1, 3) IC	0.2500 IC	370.81	370.47	370.69	370.67
(1, 4)	0.2000	102.12	104.61	116.32	146.99
(1, 5)	0.1666	40.95	40.90	45.82	63.28
(1, 9)	0.1000	12.69	12.82	14.40	19.84

^IC denotes that in-control and ARL₀s are presented in this row.

for n = 2 and n = 15. The results in Table 11 reveal that the ARL₀s of the four control cases are all close to 370.4, demonstrating that the four control cases are in-control robust. The ARL₁s of the four control cases all continue to decrease as E₁(p) deviates from 0.2500. It is noted that Case 1 and Case 2 dominate Case 3, and Case 3 dominates Case 4 in the decreasing speed of ARL₁s, demonstrating that the detection performance is negatively related to the variance in measurement error divided by the in-control process variance. Finally, the ARLs of Case 2 are all close to those of Case 1, meaning that the detection performance of Case 2 is the same as that of Case 1. That is, the error-embedded and error-corrected control charts can perfectly monitor processes without measurement errors as long as specifying π₁₁ = 1 and π₁₀ = 0.

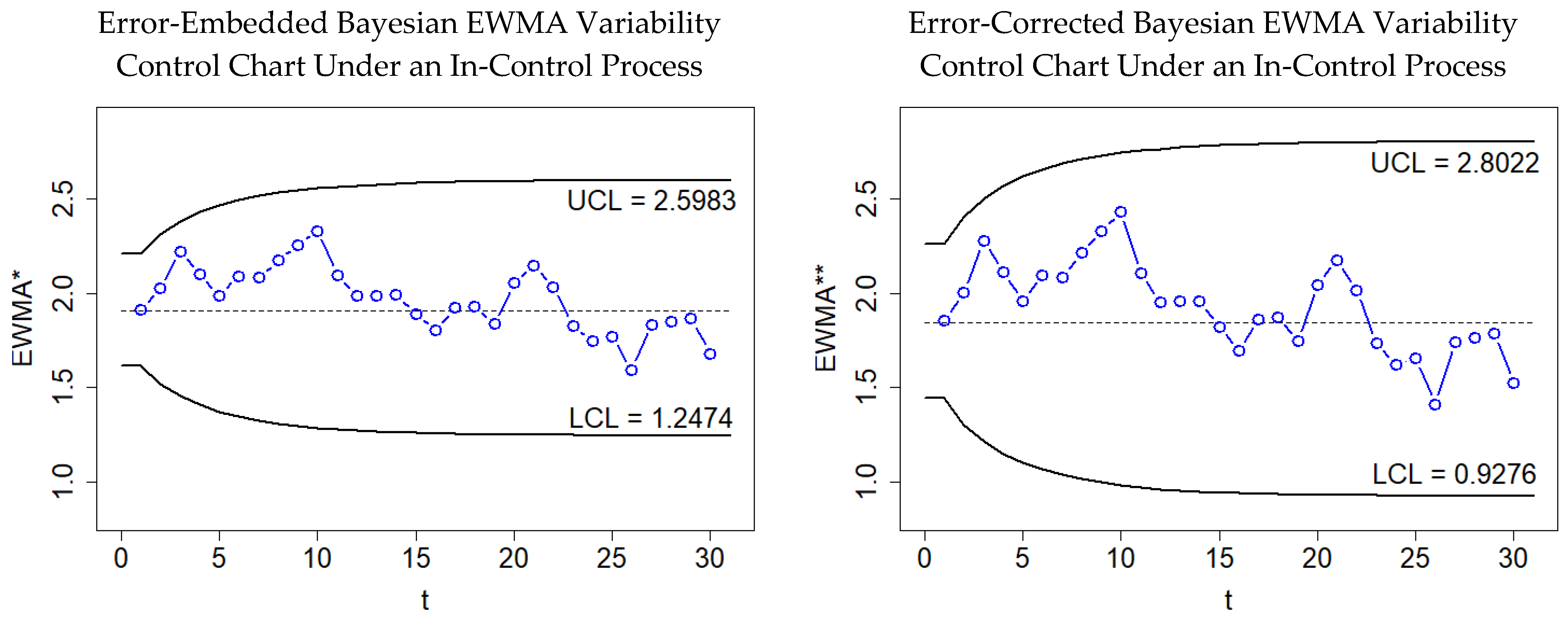
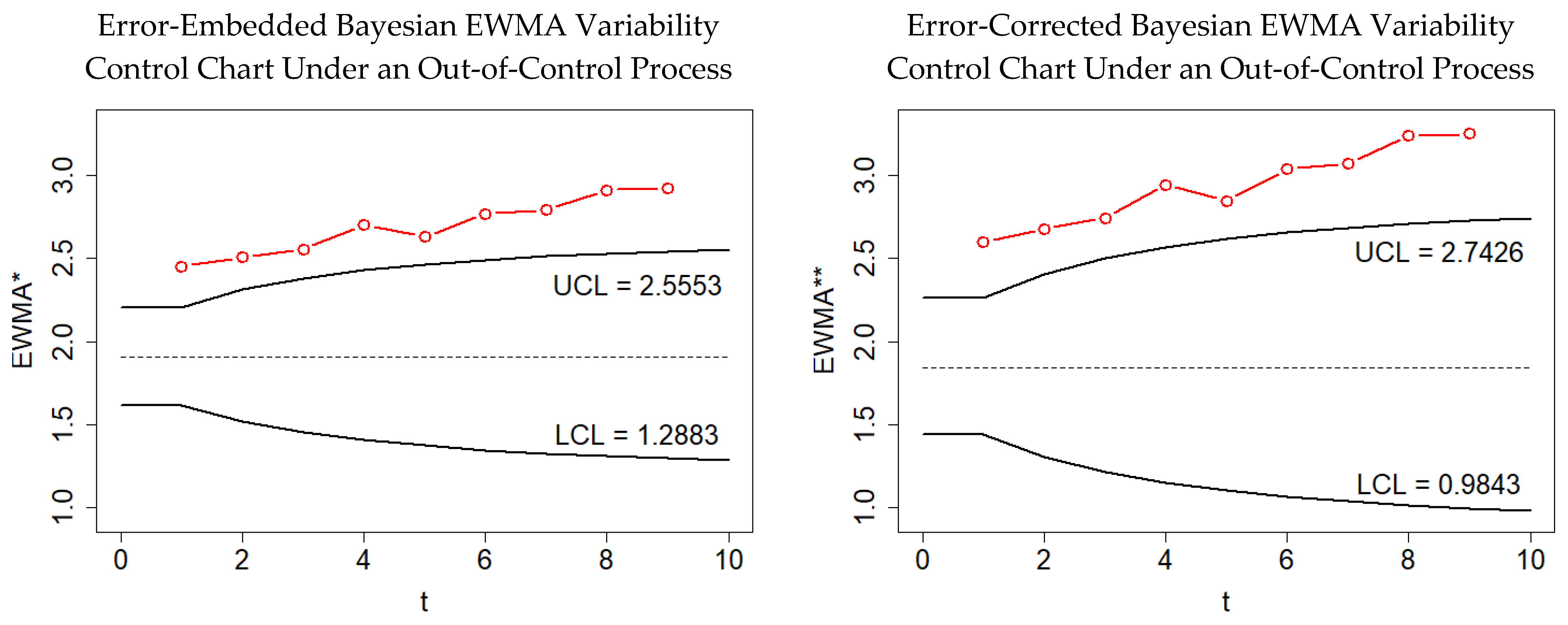
6. Examples for Demonstration

6.1. A Banking Example

A banking example from Yang and Arnold [22] is further applied to illustrate the proposed error-embedded Bayesian EWMA variability control chart and error-corrected Bayesian EWMA variability control chart. Service time is an important quality variable in the banking industry. However, measurement error is unavoidable in the collection of service time data. In order to avoid false detection in statistical process control, the designs of control charts should consider or correct the effect of measurement errors.

For the in-control service system of a banking branch, the service times are measured from 10 counters every day for 15 days. We assume that 15 samples of size 2n = 10 were precisely collected, that is, with no measurement errors. We do not know the population distribution from which the data comes. The true process variance, ${\sigma }_0^2$, is then estimated with ${\widehat{\sigma }}_0^2$ = 30.0969 based on the in-control samples without measurement errors. The prior distribution of p is Beta(${\alpha }_0$,${\beta }_0$). We initially specify ${\alpha }_0$ = 1 and ${\beta }_0$ = 1. After incorporating the information of 15 in-control true samples, we obtain the estimates ${\widehat{\alpha }}_0=1+\sum _{t=1}^{15}{M}_t=23$ and ${\widehat{\beta }}_0=1+5\times 15-\sum _{t=1}^{15}{M}_t=54$ (see Lin et al. [5]).

In order to show the application and effect of the proposed control charts in the presence of measurement error, we simulate a random error from N(0, 0.03) for each observation and add it to the original observation. Thus, the in-control error-prone samples are listed in

Table 12. Service times with measurement errors from 10 counters in a bank branch.

t	${\mathit{X}}_1^{\mathit{*}}$	${\mathit{X}}_2^{\mathit{*}}$	${\mathit{X}}_3^{\mathit{*}}$	${\mathit{X}}_4^{\mathit{*}}$	${\mathit{X}}_5^{\mathit{*}}$	${\mathit{X}}_6^{\mathit{*}}$	${\mathit{X}}_7^{\mathit{*}}$	${\mathit{X}}_8^{\mathit{*}}$	${\mathit{X}}_9^{\mathit{*}}$	${\mathit{X}}_{10}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}\mathit{*}}$
1	0.36	0.81	4.91	5.60	2.97	6.10	11.52	1.42	1.05	3.32	1.5020	1.4327
2	3.66	13.59	5.26	3.21	32.18	3.30	2.91	1.52	2.54	7.54	1.5518	1.4870
3	1.79	3.87	10.68	30.40	0.13	8.35	5.11	2.66	9.21	3.99	1.5966	1.5359
4	16.63	8.84	8.34	3.48	7.49	1.86	1.25	6.06	8.27	7.10	1.5369	1.4708
5	0.44	9.67	0.96	1.40	2.36	0.38	8.92	5.42	11.88	6.44	1.4832	1.4122
6	4.34	8.90	11.91	3.48	19.54	1.15	7.90	6.10	7.77	0.01	1.6349	1.5777
7	15.03	7.20	4.39	5.87	9.96	2.57	1.87	0.98	4.31	14.17	1.6714	1.6175
8	14.06	0.40	3.20	11.18	10.01	4.38	10.48	1.98	10.85	1.25	1.9043	1.8715
9	0.07	12.71	2.52	7.46	1.70	3.64	4.13	2.32	3.54	3.48	1.8139	1.7729
10	12.90	18.36	2.90	3.14	0.95	12.68	4.23	5.92	2.42	6.92	1.7325	1.6841
11	7.53	1.33	0.92	0.45	3.62	0.72	0.38	3.47	0.40	2.63	1.5592	1.4951
12	5.63	6.49	3.62	2.70	3.87	10.79	1.75	5.57	0.37	4.10	1.4033	1.3250
13	3.00	1.57	1.20	2.61	18.73	10.89	18.33	3.12	3.18	6.28	1.4630	1.3901
14	1.53	1.61	0.13	11.15	8.82	3.77	4.60	1.95	1.79	1.87	1.4167	1.3396
15	21.51	0.57	8.72	3.29	6.92	3.33	3.74	6.28	1.39	12.86	1.4750	1.4033

. The classification probabilities (${\pi }_{11}$, ${\pi }_{10}$) are estimated with (0.9545, 0.0377) from 15 in-control true samples and 15 in-control error-prone samples. Thus, the control coefficients of the error-embedded Bayesian EWMA variability control chart or the error-corrected Bayesian EWMA variability control chart can be obtained from the procedures described in Section 3.1 and Section 4.1. That is, (k₃, k₄) = (k₅, k₆) = (2.8123, 2.5521) for n = 5, (${\alpha }_0$,${\beta }_0$) = (23, 54), λ = 0.1, and ARL₀=370.4. The control limits are calculated as (${UCL}_{{EWMA}_t^{*}}$, ${LCL}_{{EWMA}_t^{*}}$) using the statistic ${EWMA}_t^{*}$ through Equations (26) and (28) and (${UCL}_{{EWMA}_t^{**}}$, ${LCL}_{{EWMA}_t^{**}}$) using the statistic ${EWMA}_t^{**}$ through Equations (37) and (39). Then, plotted statistics ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ from in-control error-prone samples are computed in order by Equation (23) and Equation (34), respectively, which are presented in Table 12.

Figure 3 shows the proposed Bayesian EWMA variability control charts with the error-prone data under an in-control service time system. The observed monitoring statistics, ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$, are plotted in order. Since all ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ values fall into the regions between the control limits, the two charts both reveal that the process is in control.

In order to illustrate the detection performance for the changed variance, ten new samples of size 10 were collected from a new automatic service system of the bank branch (see Yang and Arnold [22]). Installing an automatic service system makes for a more consistent service time. The process variance will be reduced significantly. However, the measurement errors in service time may occur even using a new automatic service system. Similarly, we assume that 10 samples of size 2n = 10 were precisely collected from the new service system. Then, a random error is simulated from N(0, 0.03) for each observation and added to the original observation. Thus, the error-prone data from the new service system are listed in

Table 13. New service times with measurement errors from 10 counters in a bank branch.

t	${\mathit{X}}_1^{\mathit{*}}$	${\mathit{X}}_2^{\mathit{*}}$	${\mathit{X}}_3^{\mathit{*}}$	${\mathit{X}}_4^{\mathit{*}}$	${\mathit{X}}_5^{\mathit{*}}$	${\mathit{X}}_6^{\mathit{*}}$	${\mathit{X}}_7^{\mathit{*}}$	${\mathit{X}}_8^{\mathit{*}}$	${\mathit{X}}_9^{\mathit{*}}$	${\mathit{X}}_{10}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}\mathit{*}}$
1	3.74	0.10	1.15	6.89	5.47	0.31	1.66	1.01	2.63	0.70	0.9168	0.7944
2	0.73	1.56	1.22	0.82	0.46	3.24	4.14	0.13	2.43	0.13	0.8251	0.6944
3	1.32	0.21	3.92	0.22	0.05	0.88	0.67	0.88	3.62	2.93	0.7426	0.6044
4	1.12	0.16	1.55	1.31	0.65	6.01	4.70	1.57	3.84	4.75	0.6684	0.5234
5	2.68	2.46	0.06	1.92	3.16	2.00	2.27	1.45	2.14	0.23	0.6015	0.4505
6	1.24	3.80	0.39	0.60	1.69	2.05	0.58	0.99	6.93	0.72	0.5414	0.3849
7	4.93	2.04	2.94	0.85	0.01	0.91	2.61	2.90	1.48	2.30	0.4872	0.3258
8	4.98	0.59	1.51	4.14	4.16	1.56	1.41	0.76	0.67	0.25	0.4385	0.2727
9	1.12	0.76	0.79	0.92	2.17	2.74	1.75	2.98	1.76	0.46	0.3947	0.2249
10	4.62	0.10	5.46	2.79	1.91	2.35	0.44	1.87	7.06	2.22	0.3552	0.1818

. The corresponding ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ are then computed in order by Equations (23) and (34), respectively, which are presented in Table 13.

We then plot the ten out-of-control new observed statistics, ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$, in order on the proposed control charts; see Figure 4. The two proposed control charts both detect the out-of-control signals since the values of ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ are below the lower control limits from the first sample onward (samples 1–10). That is, our proposed charts can quickly notify us of an out-of-control signal in the presence of measurement error when the variance in the new service time system becomes smaller.

6.2. A Semiconductor Example

The semiconductor manufacturing process is very complex, involving multiple steps and sophisticated equipment to produce high-quality chips. The equipment and materials used in the process require extremely high precision, and any slight deviation may affect the yield of the final product. Each step requires precise control to ensure the performance and reliability of the final product. Hence, the semiconductor process is under consistent surveillance via the monitoring of quality variables collected from sensors or process measurement points. However, measurement errors exist in the collection of quality variable data, and the error variation is not negligible relative to the quality variation of the intelligent manufacturing.

In this section, we implement the proposed error-embedded Bayesian EWMA variability control chart and the error-corrected Bayesian EWMA variability control chart to analyze the SECOM data that are available in the UC Irvine Machine Learning Repository [28]. The dataset consists of 591 quality variables and 1567 observations, including 104 out-of-control observations. We choose the variable in the second column as the quality variable of concern and assume that the collected values contain measurement errors.

We take 300 in-control observations to constitute 30 in-control samples of size 10 and 90 out-of-control observations to constitute 9 out-of-control samples of size 10. The observed error-prone samples are listed in

Table A1. The in-control samples with measurement errors from the SECOM dataset.

t	${\mathit{X}}_1^{\mathit{*}}$	${\mathit{X}}_2^{\mathit{*}}$	${\mathit{X}}_3^{\mathit{*}}$	${\mathit{X}}_4^{\mathit{*}}$	${\mathit{X}}_5^{\mathit{*}}$	${\mathit{X}}_6^{\mathit{*}}$	${\mathit{X}}_7^{\mathit{*}}$	${\mathit{X}}_8^{\mathit{*}}$	${\mathit{X}}_9^{\mathit{*}}$	${\mathit{X}}_{10}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}\mathit{*}}$
1	2564.00	2465.14	2479.90	2502.87	2432.84	2529.27	2489.70	2524.18	2475.53	2484.31	1.9157	1.8551
2	2565.80	2492.29	2500.81	2459.87	2547.43	2447.89	2545.34	2560.99	2436.17	2512.49	2.0241	2.0056
3	2416.73	2531.34	2432.85	2576.84	2406.22	2546.75	2493.32	2486.59	2501.93	2436.12	2.2217	2.2798
4	2496.56	2538.75	2540.95	2506.27	2526.22	2491.55	2480.54	2491.60	2549.73	2460.94	2.0995	2.1102
5	2554.29	2488.50	2513.05	2533.49	2467.11	2505.03	2486.48	2477.46	2540.19	2512.51	1.9896	1.9577
6	2413.92	2393.78	2405.53	2484.62	2412.41	2531.63	2517.54	2460.91	2456.65	2475.50	2.0906	2.0979
7	2570.93	2533.52	2441.22	2501.88	2467.94	2434.32	2436.69	2541.21	2526.73	2516.11	2.0816	2.0853
8	2556.22	2485.50	2550.52	2484.78	2506.32	2526.16	2598.02	2523.36	2492.81	2516.33	2.1734	2.2128
9	2502.25	2511.92	2568.35	2413.65	2545.77	2458.12	2576.19	2560.92	2573.36	2497.49	2.2561	2.3275
10	2440.82	2527.77	2484.78	2568.93	2573.09	2564.29	2498.91	2468.65	2473.55	2565.47	2.3305	2.4307
11	2497.13	2541.12	2467.40	2482.88	2515.32	2545.48	2505.70	2491.13	2464.33	2502.48	2.0974	2.1073
12	2516.95	2512.65	2510.76	2539.59	2448.07	2540.35	2557.58	2590.45	2542.64	2560.61	1.9877	1.9550
13	2415.75	2452.28	2435.47	2508.80	2453.53	2472.23	2595.82	2461.82	2502.89	2504.01	1.9889	1.9567
14	2435.34	2460.05	2445.20	2440.93	2420.32	2474.88	2499.75	2515.91	2464.40	2535.14	1.9900	1.9583
15	2473.10	2507.22	2454.80	2483.71	2494.75	2572.62	2572.78	2526.44	2461.58	2484.90	1.8910	1.8209
16	2440.94	2475.50	2461.17	2438.56	2447.43	2456.68	2462.75	2469.59	2403.24	2473.67	1.8019	1.6972
17	2467.40	2498.67	2569.45	2453.25	2435.14	2495.16	2434.60	2449.84	2494.57	2553.90	1.9217	1.8635
18	2548.91	2554.21	2488.15	2561.21	2497.58	2570.46	2481.64	2522.35	2515.83	2481.32	1.9295	1.8743
19	2501.13	2490.26	2493.13	2483.29	2463.23	2524.62	2438.58	2448.68	2458.09	2493.20	1.8366	1.7453
20	2533.39	2475.59	2496.49	2512.10	2577.58	2517.21	2476.10	2532.40	2427.20	2552.96	2.0529	2.0456
21	2552.65	2456.06	2522.77	2512.14	2528.73	2412.64	2508.94	2585.92	2464.45	2503.52	2.1476	2.1770
22	2496.32	2479.17	2472.60	2490.63	2514.52	2491.01	2501.26	2462.85	2454.38	2548.76	2.0329	2.0177
23	2565.73	2521.93	2574.34	2572.48	2544.85	2563.75	2489.86	2523.78	2522.40	2506.21	1.8296	1.7356
24	2514.38	2405.19	2510.19	2485.82	2548.79	2500.38	2484.43	2517.11	2524.88	2488.94	1.7466	1.6205
25	2464.86	2497.33	2538.76	2504.01	2520.88	2414.63	2503.48	2414.43	2474.55	2512.63	1.7720	1.6557
26	2516.34	2555.88	2474.97	2442.51	2449.85	2446.55	2529.90	2525.74	2499.15	2538.38	1.5948	1.4097
27	2504.20	2403.89	2516.06	2419.25	2493.21	2448.34	2458.90	2585.72	2458.88	2521.87	1.8353	1.7435
28	2534.66	2574.43	2507.66	2504.81	2536.87	2451.53	2547.65	2548.46	2507.01	2444.67	1.8518	1.7664
29	2549.85	2498.02	2543.10	2451.31	2506.00	2512.02	2447.26	2575.41	2481.99	2437.76	1.8666	1.7870
30	2558.56	2532.71	2499.79	2487.91	2488.18	2489.06	2521.98	2528.55	2503.30	2466.84	1.6799	1.5279

and

Table A2. The out-of-control samples with measurement errors from the SECOM dataset.

t	${\mathit{X}}_1^{\mathit{*}}$	${\mathit{X}}_2^{\mathit{*}}$	${\mathit{X}}_3^{\mathit{*}}$	${\mathit{X}}_4^{\mathit{*}}$	${\mathit{X}}_5^{\mathit{*}}$	${\mathit{X}}_6^{\mathit{*}}$	${\mathit{X}}_7^{\mathit{*}}$	${\mathit{X}}_8^{\mathit{*}}$	${\mathit{X}}_9^{\mathit{*}}$	${\mathit{X}}_{10}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}}$	${\mathit{E}\mathit{W}\mathit{M}\mathit{A}}_{\mathit{t}}^{\mathit{*}\mathit{*}}$
1	2548.21	2479.40	2629.48	2514.54	2542.24	2446.25	2345.95	2533.91	2446.74	2586.05	2.4531	2.6009
2	2388.74	2483.66	2628.76	2502.62	2502.05	2359.01	2491.19	2524.44	2529.16	2508.56	2.5078	2.6768
3	2504.38	2497.03	2509.65	2391.71	2521.84	2463.11	2458.15	2483.06	2467.49	2593.63	2.5570	2.7451
4	2470.81	2575.68	2408.46	2522.90	2509.24	2526.22	2499.72	2559.27	2551.17	2439.82	2.7013	2.9453
5	2517.34	2574.32	2478.88	2488.76	2518.96	2514.95	2523.71	2536.48	2527.25	2384.19	2.6312	2.8480
6	2425.46	2497.56	2369.95	2436.65	2449.25	2485.81	2448.37	2512.61	2443.10	2506.43	2.7680	3.0380
7	2522.41	2471.50	2391.56	2477.01	2465.11	2584.79	2422.00	2518.89	2539.50	2500.85	2.7912	3.0702
8	2534.16	2524.13	2457.42	2571.41	2512.77	2598.77	2473.14	2588.74	2410.53	2587.86	2.9121	3.2379
9	2565.93	2425.30	2467.73	2559.42	2470.60	2493.72	2515.51	2477.13	2428.64	2585.48	2.9209	3.2501

of Appendix A. The empirical in-control estimate of variance (${\sigma }_0^{2*}$) is given by ${\widehat{\sigma }}_0^{2*}=1709.08$. However, the empirical out-of-control estimate of variance (${\sigma }_1^{2*}$) is given by ${\widehat{\sigma }}_1^{2*}=3611.62$, indicating that there may be an upward shift in process variance.

In order to demonstrate the application of the proposed control charts in the presence of measurement error, we let each observation be $X_i^{*}$ with measurement error, ${\epsilon }_i$. ${\epsilon }_i$ is calculated by the following equation.

$${\epsilon }_i={\displaystyle \frac{16}{116}}{X}_i^{*}-{\displaystyle \frac{16}{116}}E\left(X^{*}\right)+{\displaystyle \frac{40}{116}}\sqrt{Var\left(X^{*}\right)}·Z_i,$$

(40)

where $Z_i$ is simulated from N(0, 1), $E\left(X^{*}\right)$ is estimated with 2427.19, and $Var\left(X^{*}\right)$ is estimated with 1709.08 by using in-control error-prone samples. Then, we can obtain the true value without measurement errors as follows:

$$X_i=X_i^{*}-{\epsilon }_i={\displaystyle \frac{100}{116}}{X}_i^{*}+{\displaystyle \frac{16}{116}}E\left(X^{*}\right)-{\displaystyle \frac{40}{116}}\sqrt{Var\left(X^{*}\right)}·Z_i.$$

(41)

It is easy to show that $E\left({\epsilon }_i\right)=0$, $Var\left({\epsilon }_i\right)={\sigma }_{\epsilon }^2$, $E\left(X_i\right)=E\left(X^{*}\right)$, $Var\left(X_i\right)={\sigma }^2$, $Cov\left(X_i,{\epsilon }_i\right)=0$, and ${\sigma }_{\epsilon }/\sigma =0.4$.

The in-control true process variance, ${\sigma }_0^2$, is then estimated with ${\widehat{\sigma }}_0^2=1487.03$ based on the in-control samples without measurement errors. As a result, the classification probabilities (${\pi }_{11}$, ${\pi }_{10}$) can be estimated with (0.8364, 0.1158) from 30 in-control true samples, X₁, …, X₁₀, and 30 in-control error-prone samples, X₁*, …, X₁₀*. The prior distribution of p is Beta(${\alpha }_0$,${\beta }_0$). We initially specify ${\alpha }_0$ = 1 and ${\beta }_0$ = 1. After incorporating the information of 30 in-control true samples, we obtain the estimates ${\widehat{\alpha }}_0=1+\sum _{t=1}^{30}{M}_t=56$ and ${\widehat{\beta }}_0=1+5\times 30-\sum _{t=1}^{30}{M}_t=96$ [5].

Thus, the control coefficients of the error-embedded Bayesian EWMA variability control chart and the error-corrected Bayesian EWMA variability control chart can be obtained from the procedures described in Section 3.1 and Section 4.1. That is, (k₃, k₄) = (k₅, k₆) = (2.7603, 2.6293) for n = 5, (${\alpha }_0$,${\beta }_0$) = (56, 96), λ = 0.1, and ARL₀ = 370.4. The control limits are calculated as (${UCL}_{{EWMA}_t^{*}}$, ${LCL}_{{EWMA}_t^{*}}$) using ${EWMA}_t^{*}$ through Equations (26) and (28) and (${UCL}_{{EWMA}_t^{**}}$, ${LCL}_{{EWMA}_t^{**}}$) using ${EWMA}_t^{**}$ through Equations (37) and (39). Then, monitoring statistics ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ from in-control samples are computed in order by Equation (23) and Equation (34), respectively, which are presented in Table A1 of Appendix A.

Figure 5 shows the proposed Bayesian EWMA variability control charts with the error-prone data under an in-control semiconductor manufacturing process. The observed monitoring statistics ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ are plotted in order. Since all ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ values fall into the regions between the control limits, the two charts both reveal that the process is in control.

In order to illustrate the detection performance for the changed variance, the ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ values from the out-of-control samples are further computed in order by Equation (23) and Equation (34), respectively, which are presented in Table A2 of Appendix A.

We then plotted nine new out-of-control observed statistics, ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$, in order on the proposed control charts; see Figure 6. The two proposed control charts both detect the out-of-control signals since the values of ${EWMA}_t^{*}$ and ${EWMA}_t^{**}$ are above the upper control limits from the first sample onward (samples 1–9). That is, our proposed charts can quickly notify us of an out-of-control signal in the presence of measurement error when the variance in the semiconductor manufacturing process becomes bigger.

7. Conclusions

The Bayesian EWMA variability control chart, first proposed by Lin et al. [5], is a distribution-free control chart, and it can effectively monitor process variance even if the process skewness varies with time. In this paper, we propose two designs for a Bayesian EWMA variability control chart in the presence of measurement error. One is used to determine control limits based on biased error-prone monitoring statistics, called the error-embedded control chart. The other is used to determine the control limits based on error-corrected monitoring statistics, called the error-corrected control chart. The simulation results prove that both proposed control charts are reliable and have good detection performance in the presence of measurement error. Moreover, the ARLs of the proposed control charts are exactly the same, indicating that both of them are equivalent control charts. Comparison results show that the existing control chart in Lin et al. [5] is not in-control robust and fails to detect a downward shift in process variance when measurement error is present. Thus, using the error-embedded control chart or the error-corrected control chart to monitor processes with measurement errors is reliable and effective. Moreover, the proposed control charts with π₁₁ = 1 and π₁₀ = 0 can be applied to monitor processes without measurement errors since their detection performance is equal to that of the existing control chart in Lin et al. [5]. Finally, we successfully demonstrate the application of the error-embedded control chart and the error-corrected control chart to analyze the data from a semiconductor manufacturing process, showing that the proposed control charts can indeed be applied to data with measurement errors.

This study assumes that the in-control true process variance is known. However, in some practical cases, it may be unknown since measurement tools cannot achieve absolute precision, even in the experimental stage. Subsequent researchers may consider such practical scenarios to develop the Bayesian EWMA variability control charts.