Ultimate Bearing Simulation of an 80 MN Compression–Shear–Torsion Multifunctional Bridge Bearing Testing Machine with a Plate-Column Composite Frame
Abstract
1. Introduction
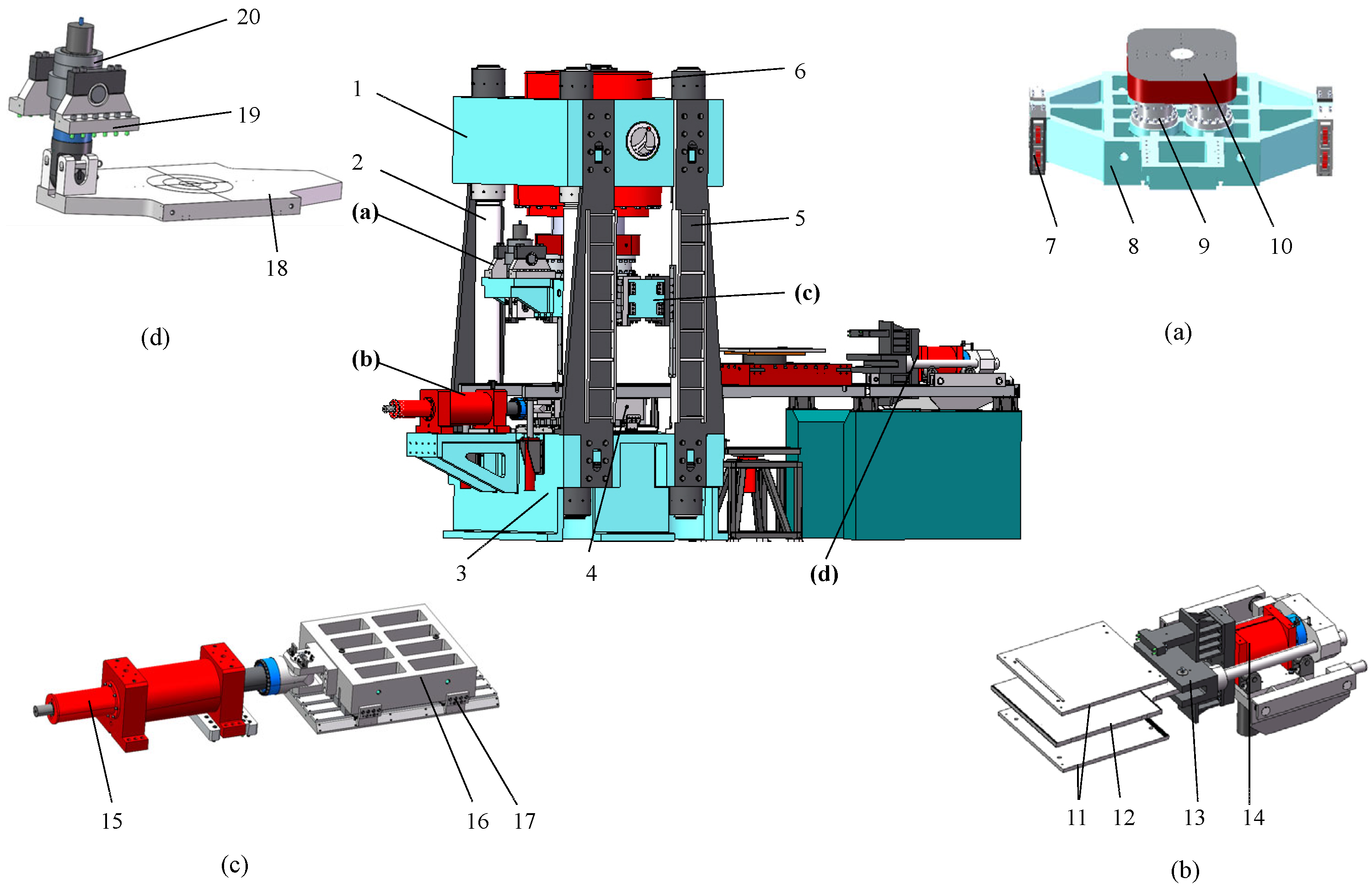
2. Mechanical Structure Design
3. Analysis of Loading States
3.1. Loading State of Vertical Compression
3.2. Loading State of Double Compression-Shear

3.3. Loading State of Single Compression-Shear
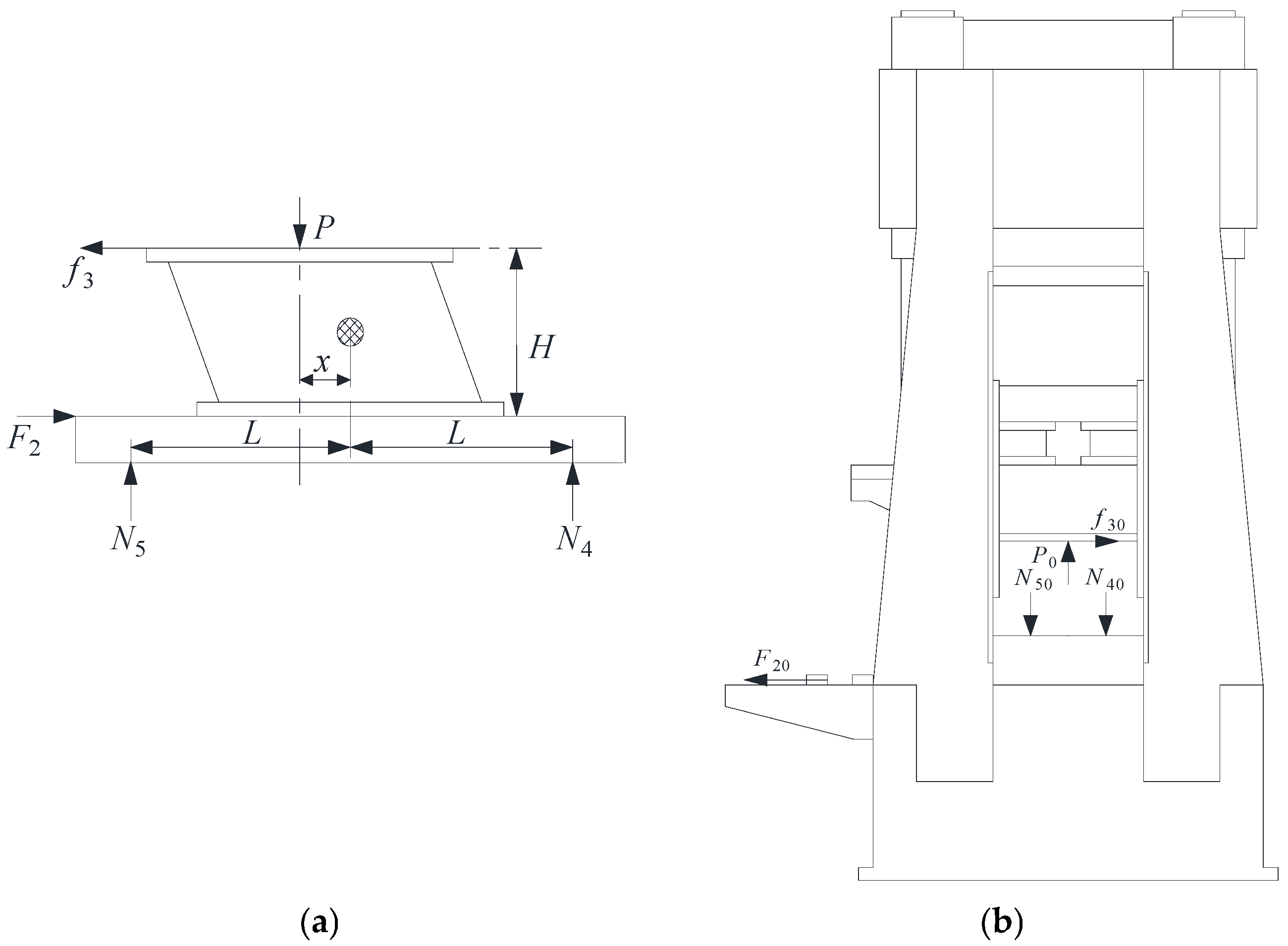
3.4. Loading State of Compression-Torsion
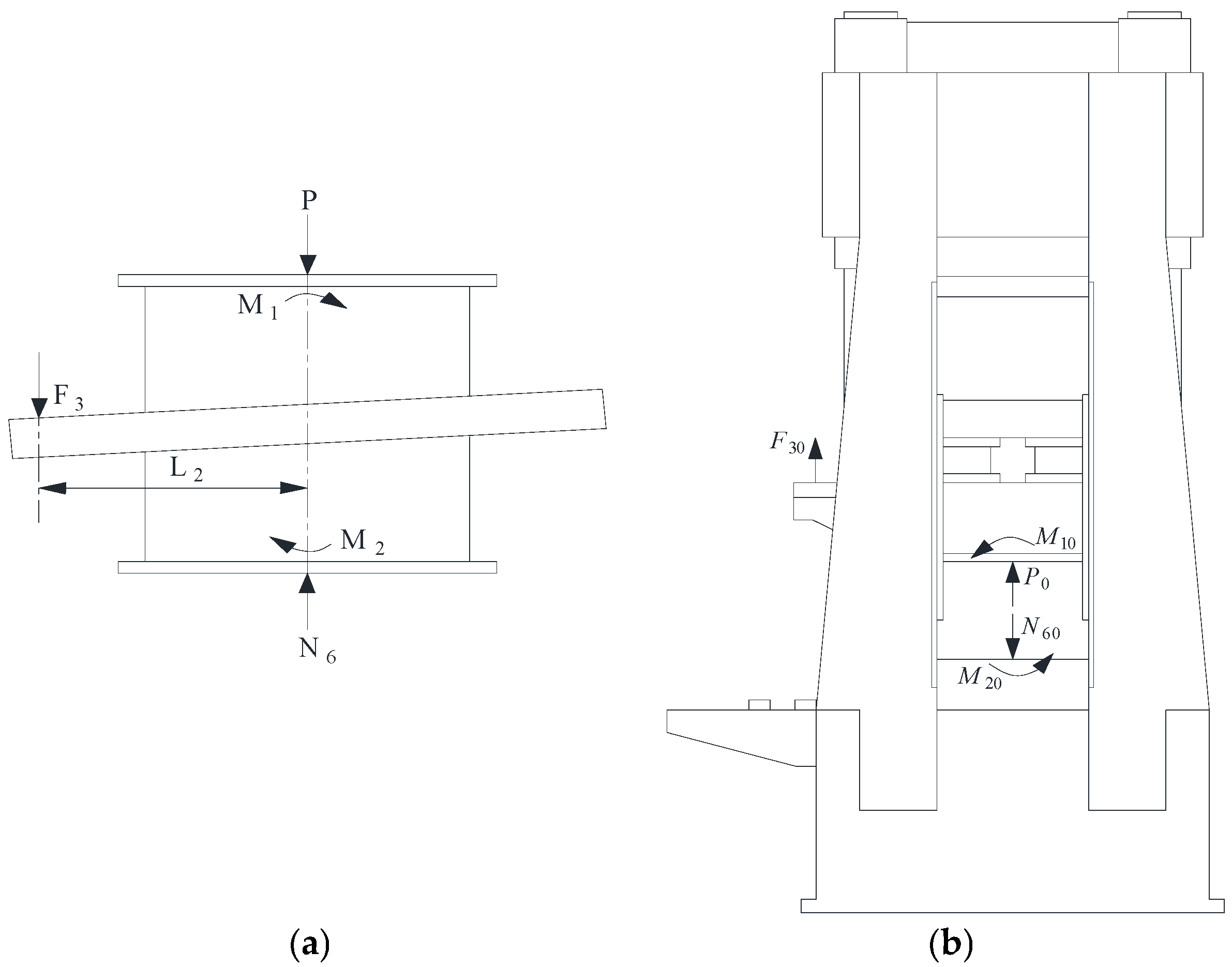
4. Simulation Settings
4.1. Model Establishment
4.2. Boundary Conditions
4.3. Mesh Division and Independence Verification
5. Results and Discussion
5.1. Simulation on Ultimate Static Vertical Compression
5.2. Simulation on Ultimate Static Double Compression-Shear
5.3. Simulation on Ultimate Static Single Compression-Shear
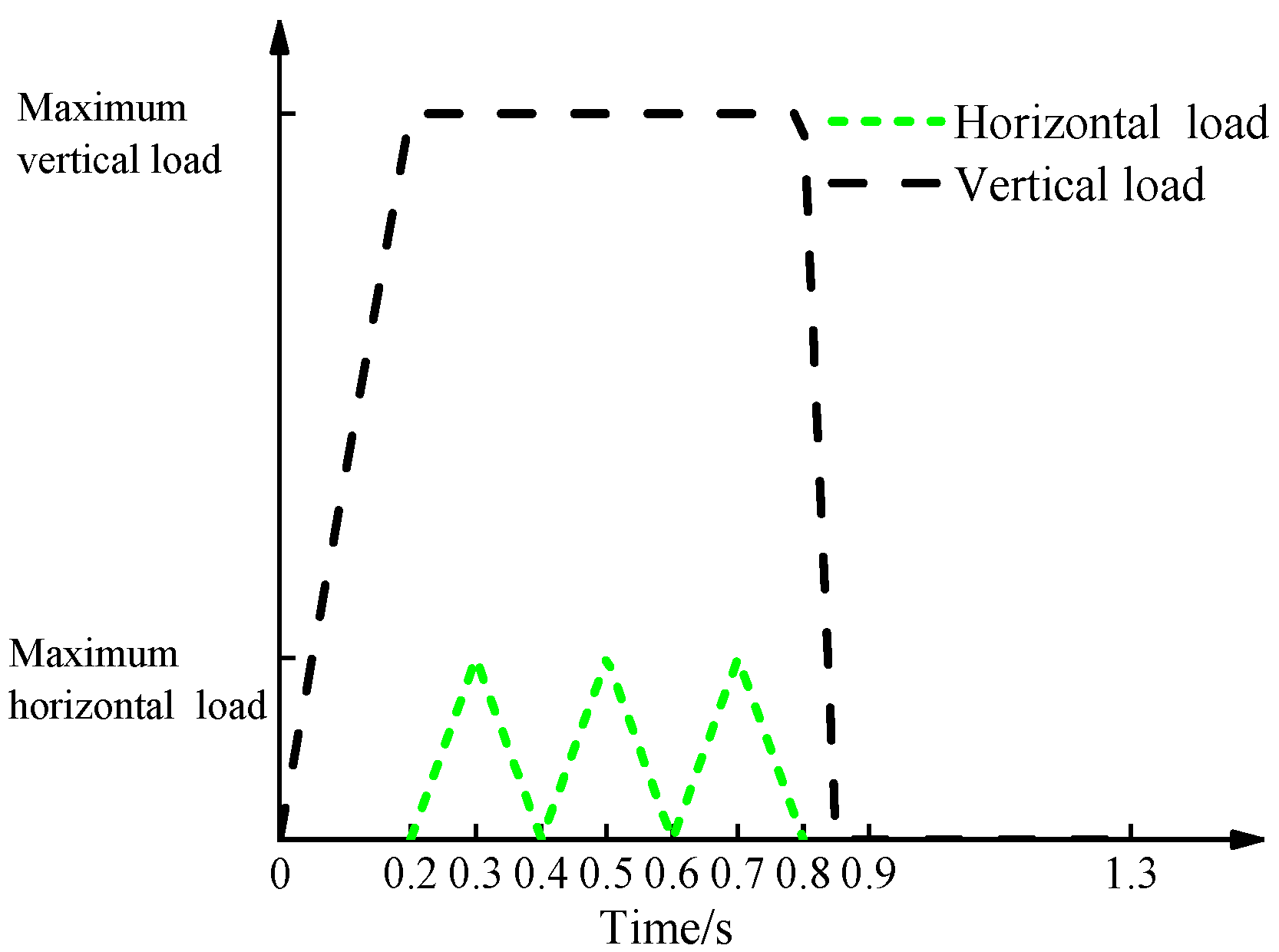
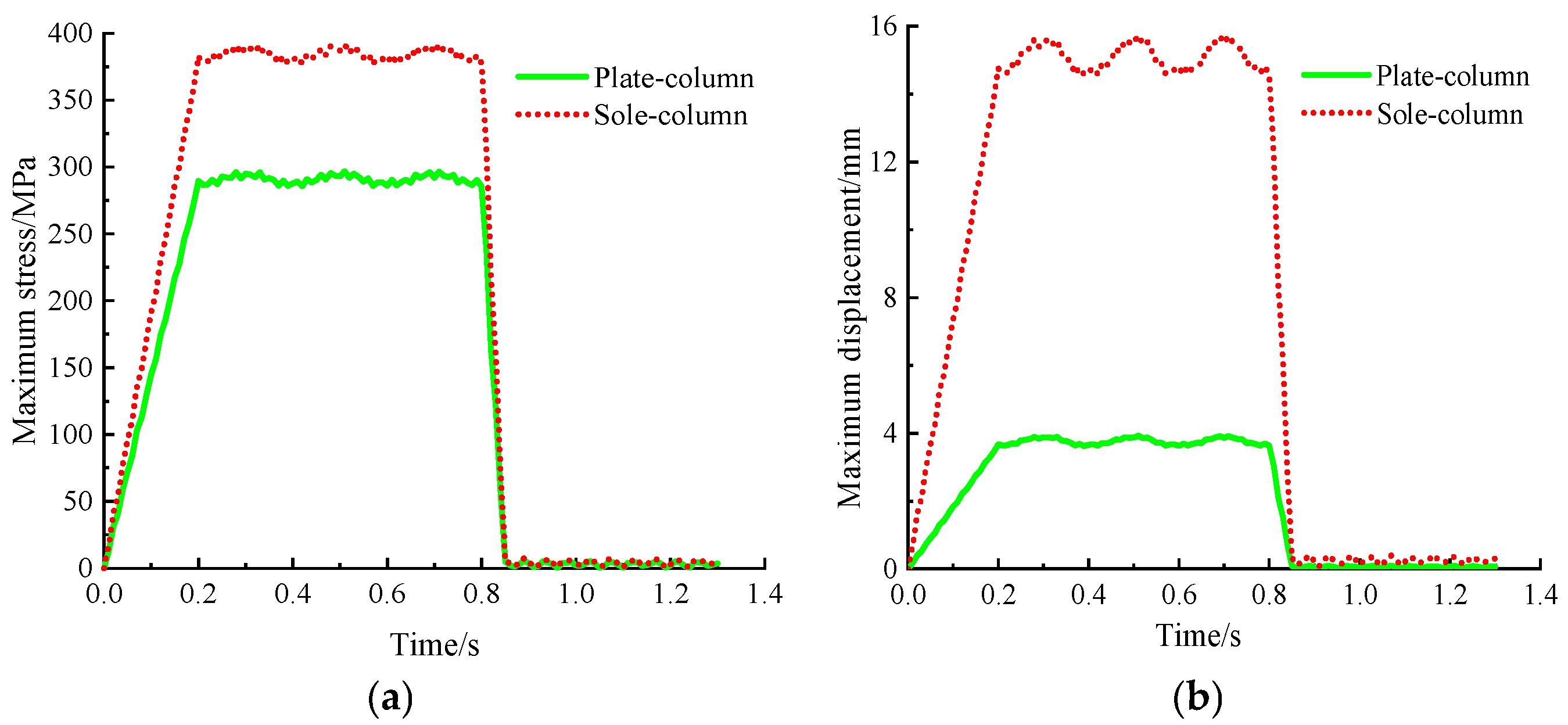
5.4. Simulation on Ultimate Dynamic Single Compression-Shear
5.5. Simulation on Ultimate Static Compression-Torsion
6. Simulation Comparison and Experimental Observation
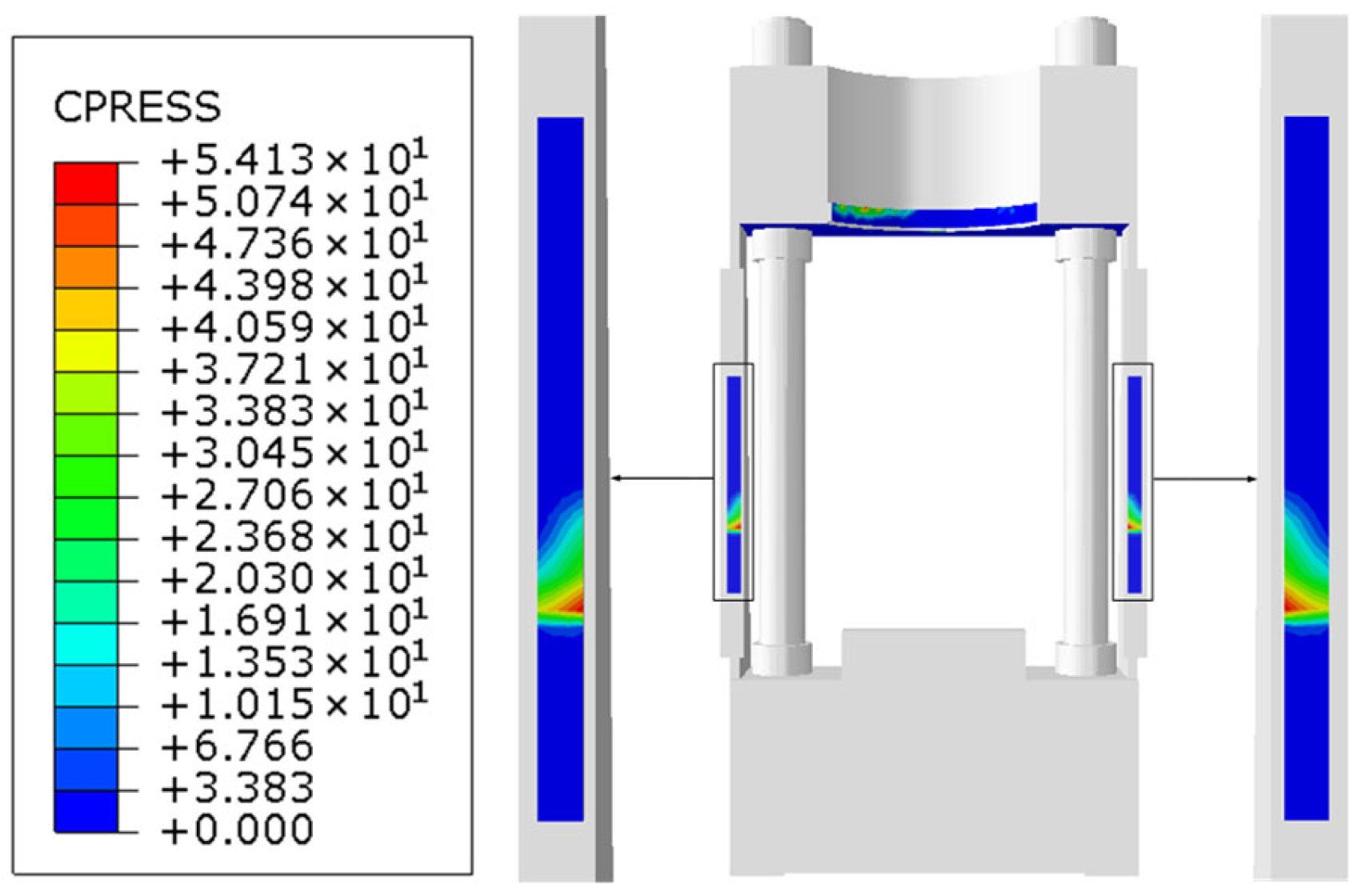
6.1. Simulation Comparison
6.2. Experimental Observation
6.3. Simulation Guidance
7. Conclusions
- (1)
- This compression–shear–torsion multifunctional bridge bearing testing machine consists of a vertical compression device, a single shear device, a double shear device, a torsion device, enabling five loading tests: static vertical compression, static double compression-shear, static single compression-shear, dynamic single compression-shear, and static compression-torsion.
- (2)
- Because the lateral reaction plates increase the bearing area in the vertical direction and bear the load in the shear direction, the maximum stress position is successfully transferred from the high-cost columns to the low-cost lateral reaction plates, and both the maximum stress and the maximum displacement under the five ultimate loading conditions are decreased after introducing the lateral reaction plates.
- (3)
- The lateral reaction plates have a great promoting effect on single compression-shear. During ultimate static single compression-shear and dynamic single compression-shear, the maximum total stress of the whole machine is reduced by 18.8% and 24.4%, respectively, and the maximum displacement of the whole machine is reduced by up to 72.5% and 75.0%, respectively.
- (4)
- Under the five ultimate loading conditions, the maximum stress is less than the yield strength, and the maximum displacement is less than the maximum allowable displacement, indicating that this testing machine meets the strength and stiffness requirements and can bear the five ultimate loading tests and withstand an ultimate vertical load of 80 MN.
- (5)
- As a result of the plate-column composite frame, the maximum stress and maximum displacement become smaller than the yield strength and the maximum allowable displacement. Thus, the testing machine can be continuously extended to a larger tonnage or three combined loading actions. Moreover, this ultimate bearing simulation method can also be applied to other testing machines to replace experiments for determining the values and positions of the maximum stress and maximum displacement.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Lu, G.; Yang, C.; Xu, M.; Wang, K. Seismic damage assessment of bonded versus unbonded laminated rubber bearings: A deep learning perspective. Eng. Struct. 2024, 321, 118996. [Google Scholar] [CrossRef]
- Shi, Q.; Bu, Z. Numerical Simulation of Quasi-Static Tests on Prefabricated Composite Rubber-Concrete Bridge Piers. J. Phys. Conf. Ser. 2025, 3027, 012067. [Google Scholar] [CrossRef]
- Zhou, J.; Tang, T.; Wang, X.; Huang, C.; Su, J.; Yi, J.; Guo, J. Influence of Bridge Bearings on Mitigating Nonlinear Seismic Responses of Straddle-Type Monorail Trains. Struct. Control Health Monit. 2025, 6724029. [Google Scholar] [CrossRef]
- Wang, J.; Liang, C.; Miao, F.; Xu, J.; Qi, W. Research on Seismic Mitigation Performance of Zinc-Aluminum-Core GFRP High-Damping Rubber Bearings for Long-Span Continuous Girder Bridge. Bridge Constr. 2025, 55, 25–33. [Google Scholar]
- Shen, J.; Igarashi, A.; Dang, J.; Hamada, Y.; Himeno, T. Low-temperature effect on seismic performance of isolated highway bridges with high damping rubber bearings. Eng. Struct. 2025, 343, 121008. [Google Scholar] [CrossRef]
- Yang, J.; Pan, W.; Zhang, Y.; Cai, Z. A study on mechanical properties of variable stiffness rubber bearings based on the stiffness matrix analysis method. J. Vib. Shock 2024, 43, 106–118. [Google Scholar]
- Sebaq, S.M.; Zhou, Y.; Zhang, Z. Hysteretic and seismic behavior of thick rubber bearings under bidirectional shear loading. Soil Dyn. Earthq. Eng. 2025, 191, 109279. [Google Scholar] [CrossRef]
- Simsek, A.; Ozdemir, G.; Yazgan, U. Effect of lead core heating on residual displacements of lead rubber bearings under bi-directional earthquake excitations. J. Earthq. Eng. 2024, 28, 4621–4643. [Google Scholar] [CrossRef]
- Zhong, H.; Yuan, W.; Dang, X.; Deng, X. Seismic Performance of Composite Rubber Bearings for Highway Bridges, Bearing Test and Numerical Parametric Study. Eng. Struct. 2022, 253, 113680. [Google Scholar] [CrossRef]
- Xue, B.; Lu, W.; Ren, X.; Wen, W. Coupled Thermal and Mechanical Behavior of Lead–Rubber Bearings: Full-Scale Testing and Numerical Modeling Methodology. Struct. Control Health Monit. 2025, 8186890. [Google Scholar] [CrossRef]
- Wang, B.; Niu, Q.; Chen, P.; Zhang, Z.; Karavasilis, T.L. Experimental and numerical investigations on mechanical properties of high-damping rubber bearings under large strain loading. Constr. Build. Mater. 2025, 467, 140390. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Sun, R.; Zhang, W. Electro-hydraulic servo testing machine of analysis and optimization based on FEM. J. Changchun Univ. Technol. 2018, 39, 243–247. [Google Scholar]
- Wu, T. Direct Drive Electro-Hydraulic Servo Control System and Its Application in 20MN Pressure-Shear Testing Machine. Master’s Thesis, Jilin University, Jilin, China, 2018. [Google Scholar]
- Yan, X.; Chen, B. Analysis of a novel energy-efficient system with 3-D vertical structure for hydraulic press. Energy 2021, 218, 119518. [Google Scholar] [CrossRef]
- Xu, M. Development of 50MN bridge bearing compression-shear-rotation multi-functional testing machine. Eng. Constr. 2016, 30, 499–501. [Google Scholar]
- Wu, C.; Shi, W. Structural design of large compression and shear testing machine. Struct. Eng. 2023, 39, 30–37. [Google Scholar]
- Zahalka, M. Modal analysis of hydraulic press frames for open die forging. Procedia Eng. 2014, 69, 1070–1075. [Google Scholar] [CrossRef]
- Wand, J. Main Structure Design and Performance Analysis of 60MN Compression Shear Testing Machine. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2022. [Google Scholar]
- Wu, G.; Cui, B.; Li, Y.; Shao, J.; He, Z.; Zhao, S.; Li, C.; Yu, J. Static topology optimization and dynamic characteristics analysis of 6000T compression-shear test machine frame. Adv. Civ. Eng. 2021, 6954576. [Google Scholar] [CrossRef]
- Li, Y.; Li, C. Topology optimization and simulation of compression-shear test machine frame. Mech. Tool Hydraul. 2023, 51, 189–195. [Google Scholar]
- Zhang, J.; Liu, K.; Wu, G. Research on Fuzzy PID Control System of 60MN Pressure Shear Tester in Variable Theory Domain. Mech. Design Manuf. 2025, 408, 198–202. [Google Scholar]
- Amar, J.; Priam, V.P.; Salim, J. Development of bench top biaxial tensile testing machine. Mater. Sci. Eng. 2020, 810, 012028. [Google Scholar]
- Oance, I.S.; Gelmambet, S.; Popa, A.R. Tension and compression testing machine for friction dampers. Ovid. Univ. Ann. Constanta-Ser. Civil Eng. 2019, 21, 105–108. [Google Scholar] [CrossRef]
- Aydın, M.; Yasin, K. Hydraulic press design under different loading conditions using finite element analysis. Eng. Sci. Technol. Int. J. 2013, 16, 129–138. [Google Scholar]
- Han, B.; Wang, D.; Liu, L. Structural analysis of plate-type hydroforming hydraulic press. Ferroelectrics 2024, 618, 2101–2111. [Google Scholar] [CrossRef]
- Shan, G.; Guo, J. Structure and Hydraulic System Design of Large-Scale Compression-Shear Testing Machine for Shock-Absorbing Rubber Bearings. Mech. Tool Hydraul. 2022, 50, 101–106. [Google Scholar]
- Cai, J.; Li, Z.; Wang, C.; Shi, Y.; Su, B. A High-Sensitivity 3-D Displacement Sensor for Deformation Monitoring of Rubber Bearing. IEEE Sens. J. 2024, 24, 31114–31130. [Google Scholar] [CrossRef]
- Wang, S.; Wu, Q.; Li, Y.; Zi, D.; Wei, L.; Liang, Y. Experimental investigation on mechanical and aging properties of novel high durability NR/EPDM blended rubber bearings. Constr. Build. Mater. 2025, 492, 142832. [Google Scholar] [CrossRef]
- Wu, D.; Li, C.; Yang, Z.; Liu, Y.; Xiong, Y.; Jiang, G. Probability Distribution Characteristics of Horizontal and Vertical Mechanical Properties of Rubber Bearings. Materials 2022, 15, 8031. [Google Scholar] [CrossRef]
- Kuang, C.; Tan, P.; Chen, M.; Li, Z.; Luo, H. Experimental research on mechanical properties of high damping thick rubber bearings. J. Vib. Eng. 2024, 37, 1584–1592. [Google Scholar]
- GB/T 20688.4-2023; Rubber Bearings—Part 4: Normal Rubber Bearings. State Administration for Market Regulation: Beijing, China, 2023.













| Device | Maximum Load | Maximum Displacement | Function |
|---|---|---|---|
| Vertical compression device | 80 MN | 1200 mm | Static vertical compression |
| Double shear device | 3 MN | 250 mm | Static double compression-shear |
| Single shear device | 3 MN | 250 mm | Static single compression-shear dynamic single compression-shear |
| Torsion device | 1.8 MN | 100 mm | Static compression-torsion |
| Elastic Modulus (GPa) | Density (kg/m3) | Poisson Ratio | Yield Strength (MPa) | Tensile Strength (MPa) | |
|---|---|---|---|---|---|
| 20Mn | 210 | 7810 | 0.28 | 275 | 450 |
| Q345B | 206 | 7820 | 0.3 | 345 | 480 |
| 45 Steel | 209 | 7890 | 0.269 | 355 | 600 |
| 40Cr | 211 | 7850 | 0.277 | 785 | 890 |
| 42Cr | 212 | 7850 | 0.286 | 930 | 1080 |
| Mesh | Maximum Stress | Maximum Displacement | |||
|---|---|---|---|---|---|
| Type | Size (mm) | Value (MPa) | Relative Error | Value (mm) | Relative Error |
| Coarse | 100 | 208.29 | 12.3% | 4.24 | 6.4% |
| Medium | 75 | 223.54 | 6.1% | 4.38 | 3.3% |
| Fine | 50 | 234.97 | 1.3% | 4.49 | 0.9% |
| Ultrafine | 25 | 238.15 | 0 | 4.53 | 0 |
| Order | 1st | 2nd | 3rd | 4th |
|---|---|---|---|---|
| Natural frequency | 7.1699 Hz | 11.585 Hz | 13.958 Hz | 40.618 Hz |
| Maximum displacement | 0.12217 mm | 0.13282 mm | 0.1554 mm | 0.58928 mm |
 |  |  |  |
| Static Vertical Compression | Static Double Compression-Shear | Static Single Compression-Shear | Dynamic Single Compression-Shear | Static Compression Torsion | |||||
|---|---|---|---|---|---|---|---|---|---|
| Whole Machine | Frame | Whole Machine | Frame | Whole Machine | Frame | Whole Machine | Whole Machine | Frame | |
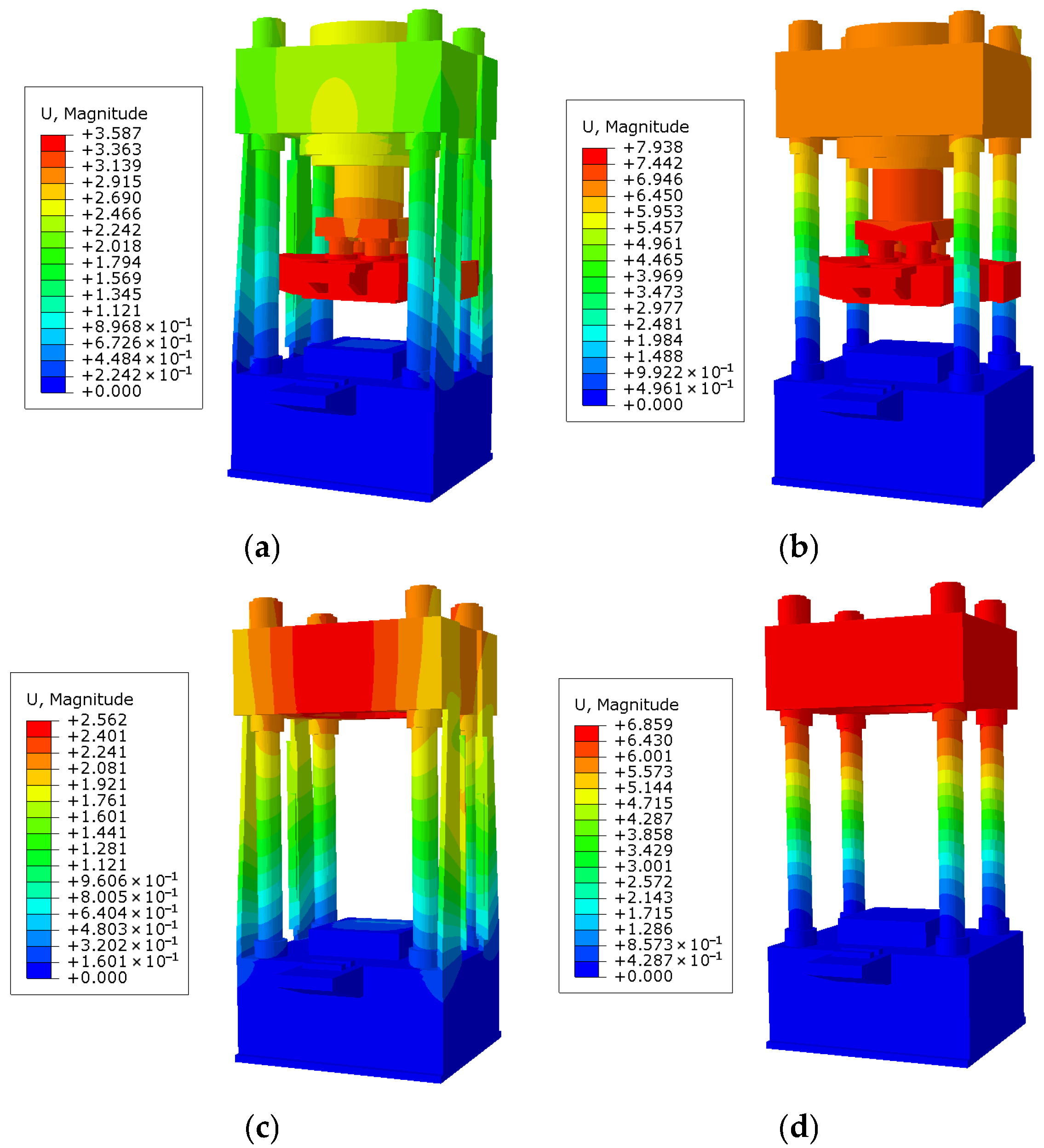
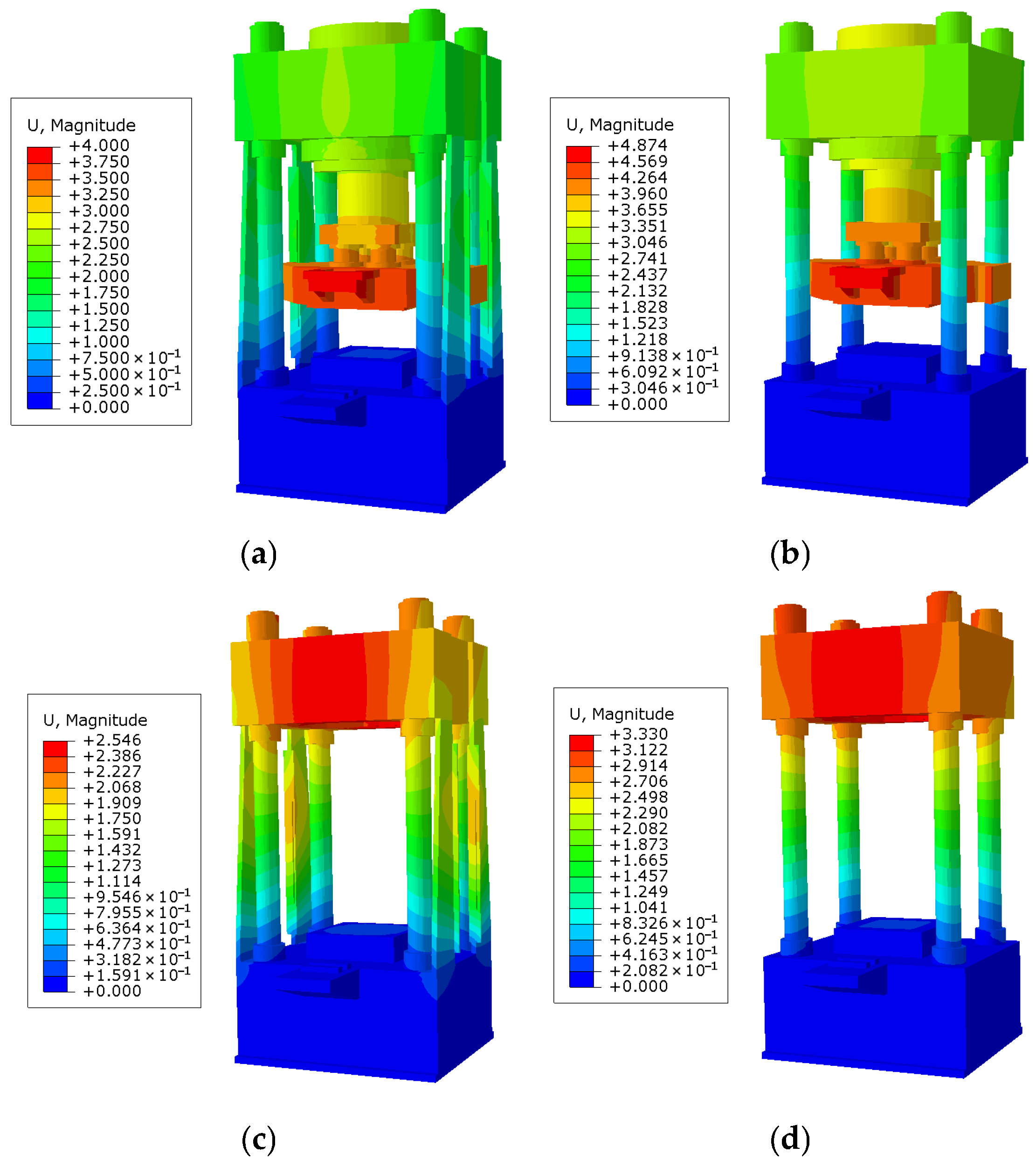
| Sole-column (MPa) | 233.5 | 161.6 | 232.1 | 232.1 | 335.8 | 335.8 | 391.5 | 228.3 | 164.2 |
| Plate-column (MPa) | 205 | 133 | 204.5 | 188.9 | 272.6 | 272.6 | 296.1 | 215.4 | 141.9 |
| Reduction amplitude | 12.2% | 17.7% | 11.9% | 18.6% | 18.8% | 18.8% | 24.4% | 5.6% | 13.5% |
| Static Vertical Compression | Static Double Compression-Shear | Static single Compression-Shear | Dynamic Single Compression-Shear | Static Compression Torsion | |||||
|---|---|---|---|---|---|---|---|---|---|
| Whole machine | Frame | Whole machine | Frame | Whole Machine | Frame | Whole Machine | Whole Machine | Frame | |
| Sole-column (mm) | 4.387 | 3.198 | 7.938 | 6.859 | 13.9 | 12.44 | 15.7 | 4.874 | 3.33 |
| Plate-column (mm) | 3.503 | 2.421 | 3.587 | 2.562 | 3.819 | 2.851 | 3.92 | 4.000 | 2.546 |
| Reduction amplitude | 20.15% | 24.3% | 54.8% | 62.6% | 72.5% | 77.1% | 75.0% | 17% | 23.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, S.; Chen, M.; Li, T.; Shao, J. Ultimate Bearing Simulation of an 80 MN Compression–Shear–Torsion Multifunctional Bridge Bearing Testing Machine with a Plate-Column Composite Frame. Processes 2025, 13, 3331. https://doi.org/10.3390/pr13103331
Mi S, Chen M, Li T, Shao J. Ultimate Bearing Simulation of an 80 MN Compression–Shear–Torsion Multifunctional Bridge Bearing Testing Machine with a Plate-Column Composite Frame. Processes. 2025; 13(10):3331. https://doi.org/10.3390/pr13103331
Chicago/Turabian StyleMi, Shuzhen, Mengting Chen, Tianyu Li, and Jinggan Shao. 2025. "Ultimate Bearing Simulation of an 80 MN Compression–Shear–Torsion Multifunctional Bridge Bearing Testing Machine with a Plate-Column Composite Frame" Processes 13, no. 10: 3331. https://doi.org/10.3390/pr13103331
APA StyleMi, S., Chen, M., Li, T., & Shao, J. (2025). Ultimate Bearing Simulation of an 80 MN Compression–Shear–Torsion Multifunctional Bridge Bearing Testing Machine with a Plate-Column Composite Frame. Processes, 13(10), 3331. https://doi.org/10.3390/pr13103331





