Abstract
Fault prediction and diagnosis are critical for enhancing the maintenance and reliability of power system equipment, reducing operational costs, and preventing potential failures. In power transformers, periodic oil sampling and gas ratio analysis provide valuable insights for predictive maintenance and life-cycle assessment. Machine learning methods, such as XGBoost, have proven to deliver more accurate results, especially when historical data is limited. However, the performance of XGBoost is highly dependent on the optimization of its hyperparameters. To address this, this paper proposes an improved Particle Swarm Optimization (IPSO) method to optimize the hyperparameters of XGBoost for transformer fault diagnosis. The PSO algorithm is enhanced by introducing topology optimization, adaptively adjusting the acceleration factor, dividing the swarm into master–slave particle groups to strengthen search capability, and dynamically adjusting inertia weights using a linear adaptive strategy. IPSO is applied to optimize key hyperparameters of the XGBoost model, improving both its diagnostic accuracy and generalization ability. Experimental results confirm the effectiveness of the proposed model in enhancing fault prediction and diagnosis in power systems.
1. Introduction
Power transformers play a vital role in the transmission and distribution of electrical power. The reliable functioning of these transformers is crucial for maintaining the overall stability and safety of the power grid. Timely detection and accurate diagnosis of early transformer faults are of great significance for preventing serious accidents, avoiding system failures, and reducing maintenance costs [1,2]. As the power demand grows, transformers are required to operate under increasingly stressful conditions, which makes them more susceptible to faults. With the development of condition-based maintenance technology, the prediction and diagnosis of transformer faults have become essential research areas. However, transformers exhibit multiple fault symptoms, and the relationship between fault causes and gas generation patterns is complex [3]. Different fault types lead to different characteristic gases, and the ratios of these gases provide valuable information for diagnosing transformer conditions. Traditional diagnostic methods, which rely on periodic oil sampling and gas ratio coding, often struggle to provide timely alerts of potential faults, especially in complex situations where multiple fault types coexist or evolve slowly. Furthermore, the ability to interpret these gas ratios accurately and consistently is limited by the complexity of fault behaviors and environmental factors. As a result, there is an urgent need for more advanced and efficient diagnostic models that can analyze real-time monitoring data and address the complex fault characteristics of transformers. The rapid development of data-driven machine learning methods provides a promising avenue for tackling this challenge. These methods can learn fault patterns from large datasets, recognize subtle correlations in data, and predict transformer faults with higher accuracy and reliability compared to traditional methods.
When a transformer fails, characteristic gases are generated in the oil, and their composition and relative ratios provide crucial indicators of the fault type [4,5]. These gases, such as hydrogen, methane, and ethylene, can reveal valuable insights into the nature of the fault, such as overheating, partial discharge, or arcing. Traditional dissolved gas analysis (DGA) criteria have limitations in diagnostic accuracy, especially when handling multiple simultaneous faults. While DGA remains a common practice, it often struggles to diagnose complex fault scenarios or cases involving mixed fault types. In recent years, data-driven machine learning models have emerged as a promising approach to overcome these limitations. These models learn fault patterns from large datasets, offering the ability to detect subtle correlations that traditional methods may miss. Early studies in transformer fault diagnosis employed shallow models like Support Vector Machine (SVM) and decision trees for fault type classification. SVM, for instance, demonstrated good classification performance on small-sample datasets, and its performance was enhanced by combining it with rough sets for feature dimensionality reduction or using chemical reaction optimization-based binary SVM to improve diagnostic accuracy [6,7]. However, the classification performance of SVM is highly susceptible to issues like sample imbalance and parameter selection, which can result in suboptimal performance when fault data is limited or unbalanced.
Recently, ensemble learning and deep learning technologies have shown significant promise in transformer fault diagnosis, offering more robust solutions than traditional methods. Ensemble methods, including Random Forest and boosting techniques, have been widely used to improve diagnostic accuracy and stability by aggregating multiple weak learners to form a stronger predictive model [8,9,10]. Among these, XGBoost stands out as an efficient gradient boosting implementation, excelling at handling large datasets and preventing overfitting through regularization. XGBoost’s ability to effectively manage complex, high-dimensional data while maintaining strong performance even in noisy environments has made it a popular choice for fault diagnosis. On the other hand, deep neural networks (DNNs) have been applied to capture the intricate nonlinear relationships within transformer status data. For example, Reference [11] utilizes a combination of DNN and Principal Component Analysis (PCA) to perform early diagnosis of subtle, gradual faults and predict the remaining useful life of transformers. While deep learning methods can significantly improve diagnostic accuracy, they often require large amounts of training data to perform optimally. In cases where fault samples are limited, deep learning models are susceptible to overfitting, which can degrade their generalization ability. Long Short-Term Memory (LSTM) networks, however, demonstrate strong generalization capability even in small-sample scenarios, making them competitive with boosting models in certain cases. Despite the strengths of deep learning, recent literature generally agrees that boosting algorithms like XGBoost offer a better balance of accuracy, stability, and training efficiency, making them particularly well-suited for transformer fault diagnosis [12,13,14].
Another critical challenge in developing data-driven diagnostic models is the selection of model hyperparameters and the optimization of the training process. The performance of models like XGBoost is highly sensitive to the tuning of multiple hyperparameters, and traditional methods such as grid search or cross-validation are often time-consuming and inefficient, especially when dealing with high-dimensional parameter spaces. These methods may struggle to find the global optimum, particularly in complex models with many parameters [15,16,17,18]. To address this challenge, evolutionary algorithms and swarm intelligence-based optimization techniques have been increasingly used for automatic model parameter optimization. Genetic Algorithm (GA) has been applied to optimize the hyperparameters of XGBoost for transformer fault diagnosis, leading to improvements in diagnostic accuracy and model stability when compared to using default parameters. For instance, Reference [19] combines GA with XGBoost and reports a significant increase in diagnostic accuracy, demonstrating GA’s capability to effectively find optimal hyperparameter combinations. However, standard GA suffers from slow convergence and the risk of getting stuck in local optima, limiting its overall efficiency. Further advancements have been made by using Principal Component Analysis (PCA) for feature extraction and optimizing key parameters of Support Vector Machines (SVM) using improved Artificial Bee Colony (ABC) algorithms, as discussed in Reference [20]. This approach aims to mitigate the limitation of limited fault information. The authors of Reference [21] proposed preserving diversity within the population to accelerate convergence, thereby achieving faster convergence and better generalization than traditional GA or random search methods. PSO has also been employed to optimize the hyperparameters of SVM models in transformer diagnosis, significantly improving the generalization performance of the model. The authors of Reference [22] extended PSO to optimize XGBoost and showed that the resulting PSO-optimized XGBoost model outperforms other machine-learning models in fault-classification accuracy. However, traditional PSO suffers from premature convergence, where particles may get trapped in local optima, and slow fine-tuning in the later stages of optimization. Without modifications, the fixed inertia weights and acceleration coefficients in PSO restrict the balance between exploration and exploitation, which can negatively impact optimization performance.
To enhance the fault diagnosis accuracy and overcome the challenges mentioned earlier, the core idea of this study is to integrate an improved Particle Swarm Optimization (IPSO) algorithm for optimizing the hyperparameters of the XGBoost model. This integration aims to construct a high-precision diagnostic model that is less susceptible to local optima. The standard PSO algorithm is improved in two key ways: (1) by modifying the particle swarm topology, dividing particles into master–slave groups, which allows for a more effective local search while maintaining strong global search capabilities; (2) by adaptively adjusting inertia weights and acceleration factors during each iteration to optimize the balance between exploration and exploitation. These improvements enable the IPSO algorithm to more effectively explore the hyperparameter space and converge to better solutions more rapidly compared to standard PSO, thereby improving both the speed and accuracy of the optimization process. The main contributions are as follows:
- (a)
- Designing the IPSO-XGBoost diagnostic framework and providing a detailed theoretical analysis of the algorithm improvements and optimization mechanisms implemented.
- (b)
- Developing an enhanced PSO scheme with master–slave multi-populations and adaptive learning factors, which significantly boosts both the optimization speed and accuracy of hyperparameter tuning.
- (c)
- Conducting comprehensive experiments that demonstrate the significant advantages of the IPSO-XGBoost model in terms of diagnostic accuracy, faster convergence, and greater stability, as compared to existing diagnostic methods.
2. XGBoost Fault Diagnosis Model
Extreme Gradient Boosting (XGBoost) is a popular machine learning algorithm based on gradient boosting, which combines the predictions of multiple weak models to create a strong predictive model. It is particularly known for its efficiency, scalability, and ability to handle large datasets with missing values. XGBoost has become widely used in classification and regression tasks due to its strong performance in a variety of domains, including predictive maintenance and fault diagnosis. In the context of transformer fault diagnosis, we treat this problem as a classification task, where the goal is to categorize the transformer’s condition into predefined fault types, such as overheating, partial discharge, and others. This approach allows us to predict the transformer’s fault condition based on the analysis of gas ratio features from oil samples.
The objective function of XGBoost can be expressed as:
where represents the loss function; is the actual label value of sample i in the t-th iteration; is the predicted value; is the model complexity regularization term; and denotes the k-th decision tree.
The loss function is defined as follows:
where represents the indicator variable for the true class j of the i -th sample; denotes the predicted probability j, which is obtained by transforming the model output scores through the softmax function.
The expression of the regularization term is as follows:
where denotes the number; represents the weight; is the tree complexity penalty factor; and serves as the weight regularization penalty factor, preventing overfitting caused by excessively large weights.
XGBoost employs an additive model during training, where a new decision tree is added in each iteration. This newly added tree is used to minimize the residual errors generated by the previous prediction. The mathematical representation of this process is as follows:
To facilitate the solution, the objective function can be expressed as:
The node splitting criterion for XGBoost decision trees is to maximize the decrease in the objective function, and the gain can be expressed as:
where is a regularization parameter to prevent overfitting.
The update formula for determining the node weight is given by:
where denotes the optimal weight for leaf node j.
In multi-class classification problems, XGBoost employs the softmax function to convert the raw scores output by the model into probability values:
where denotes the predicted probability; represents the raw prediction value of class j; is the sum of exponents of prediction values for all classes, which is used to normalize the probability values.
XGBoost efficiently optimizes its objective function to prevent overfitting by constraining the number of leaf nodes and their weights. Key hyperparameters of XGBoost include: Number of decision trees (N): Determines the scale of model ensemble. Learning rate (): Controls the contribution of each tree to the model. Maximum tree depth (): Determines the complexity of the model. Split loss penalty (): Prevents over-complex trees by penalizing splits. L2 regularization term (): Constrains leaf weights to avoid overfitting. Regularization parameter (): A general regularization factor to prevent overfitting. These hyperparameters play crucial roles in balancing model accuracy and generalization ability, with proper tuning essential for optimal performance.
3. Algorithm Design
XGBoost’s predictive performance is highly sensitive to a set of interdependent hyperparameters spanning a mixed search space of continuous and integer variables (e.g., learning rate, maximum depth, subsampling ratio, min_child_weight, gamma, and regularization terms). The resulting objective landscape is non-convex and noisy because validation accuracy depends on data splits and limited samples. Gradient information is unavailable, and exhaustive or grid search is computationally expensive yet coarse. PSO is a derivative-free, population-based global optimizer that is well suited to this setting: it handles mixed and non-convex spaces, is robust to noisy objectives, converges quickly with few control parameters, and parallelizes naturally by evaluating particles concurrently. Compared with random/grid search, PSO attains higher-quality solutions under comparable budgets; compared with GA, PSO typically requires fewer design choices (no crossover/mutation) and exhibits stable early convergence; compared with Bayesian optimization, PSO avoids kernel/prior modeling, offering robustness when the objective is noisy and moderately high-dimensional. Building on these advantages, we further introduce an IPSO with a master–slave particle topology and adaptive inertia/learning factors to strengthen the exploration–exploitation trade-off and mitigate premature convergence. IPSO therefore provides an efficient and practical mechanism to tune XGBoost hyperparameters using cross-validation accuracy as the fitness function.
3.1. Standard PSO
The velocity and position update formulas of the standard PSO are as follows:
where represents the current position; denotes the velocity; is the personal best position; is the current global best position of the particle swarm; is the inertia weight, controlling the continuity of velocity; and are learning factors corresponding to the influence degrees of the individual and the swarm, respectively; and are random numbers in the interval [0, 1], enhancing the randomness of the algorithm. The value of the inertia weight determines the exploration ability of particles: a larger value helps the particles escape from local optima, while a smaller value is conducive to fine-grained local search.
3.2. PSO Algorithm Improvement Strategies
In the transformer fault diagnosis setting considered in this paper, XGBoost involves numerous interdependent hyperparameters. While traditional PSO remains applicable, its solutions tend to be sub-optimal or converge more slowly compared with the proposed improved PSO, particularly under non-convex and noisy objectives. The IPSO therefore enhances exploration–exploitation balance and mitigates premature convergence, yielding higher-quality hyperparameter configurations. To enhance the convergence speed and global optimization capability of standard PSO in tuning XGBoost hyperparameters, this paper proposes two improvement strategies. The particle swarm is organized into a two-tier hierarchy consisting of Master Particles and Slave Particles. Master particles serve as global search guides, exploring unexplored regions of the parameter space, while slave particles conduct localized searches around their respective master particles. The velocity and position update formulas for master and slave particles are as follows:
where K is the contraction factor, which is used to stabilize the velocity update; and are variable acceleration coefficient.
The inertia weight determines the magnitude of a particle’s motion inertia during the current iteration. A larger inertia weight maintains the particle’s high-speed movement trend, which facilitates extensive global exploration by the PSO algorithm in the early stages of the search and effectively prevents premature convergence to local optima. Conversely, a smaller inertia weight reduces the particle’s motion inertia, which aids the algorithm in conducting fine-grained local searches in later stages to gradually approach the optimal solution. To this end, this paper devises an inertia weight variation formula that dynamically adjusts with the number of iterations:
where k denotes the current iteration index; denotes the inertia weight used in the k-th iteration; denotes the maximum number of IPSO iterations; and denote the initial and final inertia weights, respectively.
The inertia weight in the PSO algorithm gradually decreases as the iteration number increases, following a quadratic nonlinear decline. This carefully designed nonlinear schedule is critical for optimizing the search process. In the early stages of the optimization, the relatively larger inertia weight enables more extensive global exploration, helping the algorithm avoid prematurely converging to suboptimal solutions. As the number of iterations increases, the inertia weight decreases, promoting more refined and focused local searches. This gradual reduction allows the algorithm to strike a balance between exploring new areas of the solution space and exploiting the best-known solutions. The adaptive nature of this design contributes to the algorithm’s ability to avoid getting stuck in local optima. By maintaining a larger inertia weight during the initial stages, the algorithm has a broader search radius, allowing it to escape local minima and explore better solutions in unexplored regions. As the algorithm converges, the decreasing inertia weight gradually shifts the focus to exploiting the promising regions identified earlier in the search process. This dynamic balance between exploration and exploitation helps prevent premature convergence and ensures that the solution quality improves over time. Consequently, the optimization process becomes more efficient, converging faster while reducing the risk of local optima. The adaptive nature of this approach significantly improves the overall performance of the PSO algorithm, leading to better solutions in fewer iterations. In practice, this method results in faster convergence and higher solution quality, making the algorithm particularly suitable for complex optimization tasks. The flowchart of the improved PSO algorithm is shown in Figure 1.
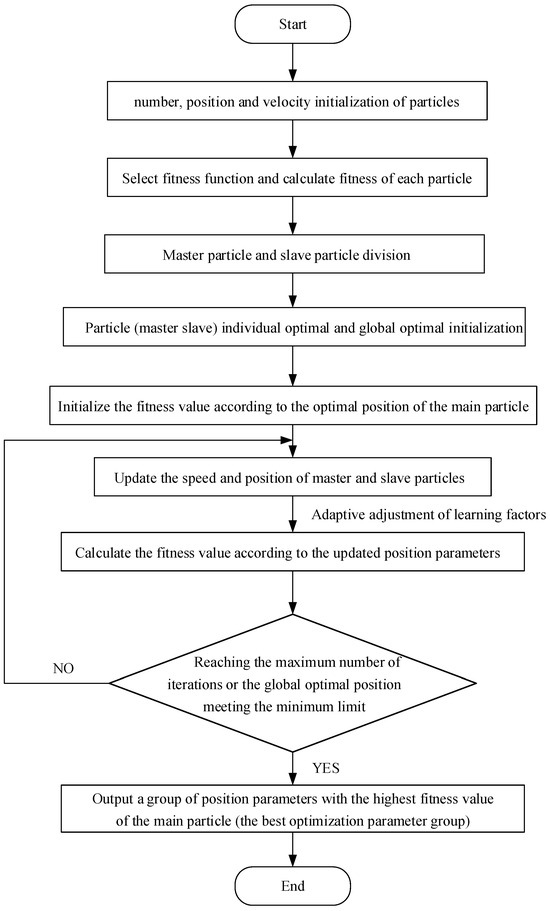
Figure 1.
IPSO flowchart.
By implementing the dynamic inertia weight adjustment strategy described earlier, significant improvements are achieved in both the exploration efficiency of the search space and the convergence performance of the PSO algorithm. This strategy allows for more effective global exploration, ensuring that a broader range of possible solutions is considered. As the optimization progresses, the adaptive adjustment of inertia weights enables a more refined local search, which accelerates the fine-tuning process. As a result, the PSO algorithm is better able to identify the optimal hyperparameter combination with greater accuracy. This approach ensures that the model converges faster and with higher precision, ultimately improving both the efficiency and effectiveness of fault diagnosis.
3.3. Improved Particle Swarm Optimization (IPSO) and XGBoost Fusion Mechanism
To avoid the drawbacks of speculative parameter tuning and high computational costs during the parameter optimization process, this study integrates the Improved Particle Swarm Optimization (IPSO) algorithm. By leveraging the IPSO algorithm to optimize the hyperparameter values, the predictive performance of the model is enhanced. During the training phase of the IPSO-XGBoost model, the accuracy is selected as the fitness function for the particles. Firstly, randomly initialize the particle swarm, setting the initial values and feasible ranges for each parameter of the XGBoost model. The IPSO algorithm is then employed to iteratively refine these parameter values. Then, after each iteration, the model’s performance is evaluated using a validation dataset. The fitness function, based on prediction accuracy, determines whether the current parameter configuration is optimal. If improved, the parameters are updated; otherwise, the existing values are retained. Upon termination, the best-performing hyperparameters identified during the iterative process are output. If the convergence criterion is not met, the IPSO algorithm continues to refine the parameters. The flowchart for constructing the IPSO-XGBoost transformer fault prediction model is presented in Figure 2.
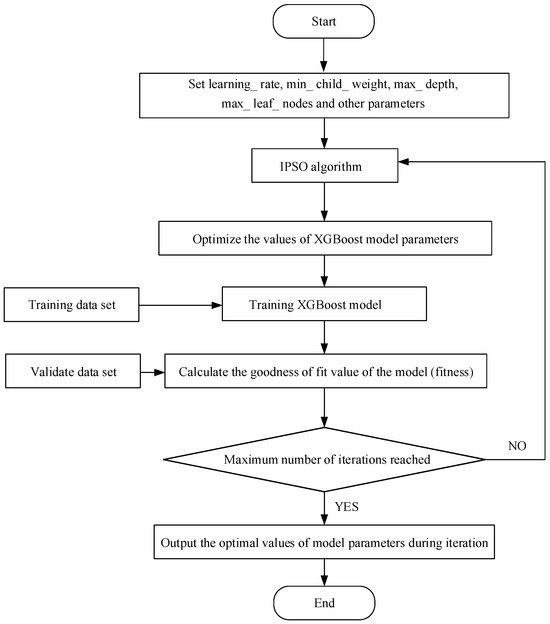
Figure 2.
IPSO XGBoost model construction flowchart.
4. Simulation
The dataset used in this paper is derived from the fault data of transformers in actual operation, which includes transformer oil chromatographic samples collected under different operating conditions. After preprocessing, six gas ratio features were extracted from the actual operating transformer oil chromatographic samples: H2/CH4, C2H6/C2H4, C2H4/CH4, C2H6/CH4, C3H8/C2H4, and C3H6/C2H6. These features are key indicators for diagnosing various transformer fault types. The data preprocessing steps include handling missing values through mean imputation, applying the SMOTE data augmentation technique to balance the dataset, and normalizing the feature values to ensure consistency across samples. After augmentation, the dataset consists of 1449 samples, achieving a balanced class distribution, with each fault type equally represented. Based on the gas ratios observed in the oil samples, these six gas ratio features classify the transformer fault status into six categories: normal, overheating, partial discharge, low energy discharge, high energy discharge, and mixed faults. To ensure fairness in the experiments, the dataset was divided into training and testing sets. The training set contains 1047 samples generated through data augmentation, and the test set contains 402 original samples. The dataset partitioning ensures that all comparative methods maintain consistency in data splitting and model training parameters, with hyperparameters optimized through grid search within the same parameter space. The number of samples for each fault category and their corresponding fault codes are detailed in Table 1. The coefficients and parameters for the IPSO method is shown in Table 2.

Table 1.
Sample distribution.

Table 2.
Coefficients and Parameters for the IPSO Method.
We used the grid search method to exhaustively evaluate the combinations of these hyperparameters and selected the best-performing set based on cross-validation accuracy. This approach ensures that the XGBoost model is optimized for transformer fault diagnosis, balancing bias and variance to improve prediction accuracy and generalization. The hyperparameter settings for the XGBoost grid search are shown in Table 3.

Table 3.
Hyperparameter Settings for XGBoost Model in the Grid Search.
When using IPSO to optimize the hyperparameters of the XGBoost model, the curve representing the fitness value based on the test set, as a function of the IPSO and PSO generations, is shown in Figure 3.
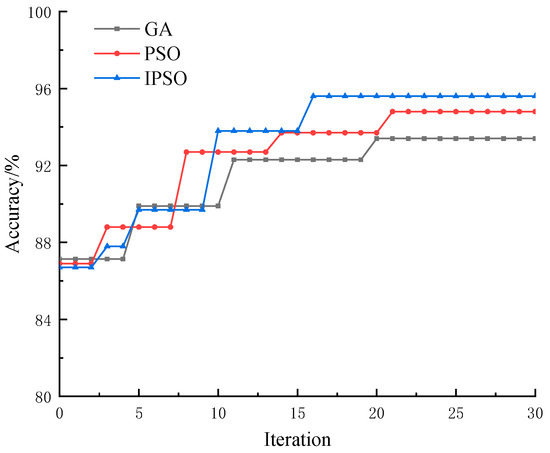
Figure 3.
Parameter iteration curves of XGBoost optimized by IPSO and PSO.
In Figure 3, the IPSO-XGBoost model exhibits a faster convergence speed compared to the PSO-XGBoost model. The fault diagnosis accuracy of the IPSO-XGBoost model is also significantly improved over the base XGBoost model, thanks to the optimized hyperparameters. However, the performance of the Genetic Algorithm (GA) is influenced by factors such as crossover and variance probability, while the performance of PSO depends on parameters such as weights and learning factors. As a result, both GA and PSO tend to converge more frequently. The improved PSO algorithm, through its dynamic adjustment strategies, allows for more comprehensive exploration in the early stages of the optimization process, while facilitating a more refined local search during the later stages. These improvements contribute to better overall convergence efficiency and enhanced optimization performance.
In the transformer fault diagnosis task, we compared different models (XGBoost, GA-XGBoost, PSO-XGBoost, and IPSO-XGBoost). To provide a more intuitive view of how these models perform across different fault types, we present the confusion matrices for the four models. Each confusion matrix shows the model’s performance on the test set, including the correct classification rates and misclassification cases for each fault category. The confusion matrices for the four models are shown in Figure 4.
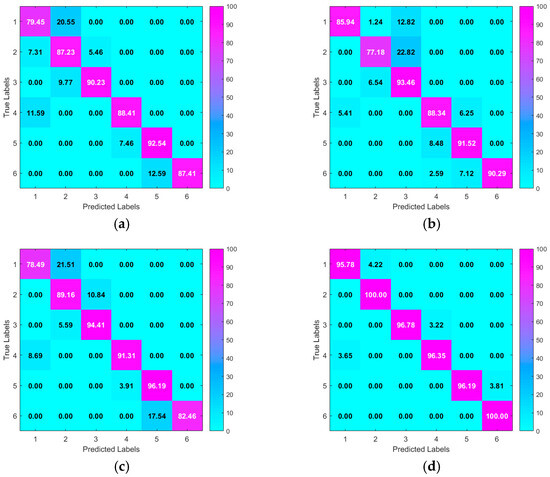
Figure 4.
Confusion Matrices for Fault Diagnosis Using Different Models: (a) XGBoost, (b) GA-XGBoost, (c) PSO-XGBoost, and (d) IPSO-XGBoost.
As seen in Figure 4, the XGBoost model performs well on basic fault categories (such as normal and overheating), but it has some limitations when dealing with more complex fault types (such as mixed faults and partial discharge), especially in cases of lower classification accuracy. GA-XGBoost, by optimizing hyperparameters through a genetic algorithm, improves the overall performance of the model, particularly in the classification of low-energy and high-energy discharge faults. However, there are still some misclassifications in the normal state and mixed fault categories. PSO-XGBoost performs excellently in most fault types, especially in the classification of low-energy and high-energy discharge faults, demonstrating the effectiveness of particle swarm optimization in hyperparameter tuning. Yet, some misclassifications still occur, particularly in the normal state and mixed fault categories. IPSO-XGBoost, with its improved particle swarm optimization, further enhances the model’s performance, showing significantly higher accuracy across all categories, especially in handling complex fault types. Compared to other methods, IPSO-XGBoost achieves higher accuracy, proving its effectiveness and superiority in transformer fault diagnosis.
To thoroughly evaluate the performance of the proposed model, a comprehensive comparison is conducted between different models using the same dataset, as illustrated in Figure 5, Figure 6, Figure 7 and Figure 8. The diagnostic effectiveness of each model is assessed by analyzing their ability to classify faults across multiple categories. Notably, the proposed model demonstrates significant improvements in handling the distribution of samples, especially for those classes with fewer samples. For instance, the diagnostic accuracy for the fault classes with fault codes 2 and 5, which represent less frequent fault types, shows a remarkable enhancement. This improvement indicates that the model is not only effective for diagnosing more prevalent fault types but also capable of accurately identifying faults in less represented categories, thus improving overall diagnostic robustness.
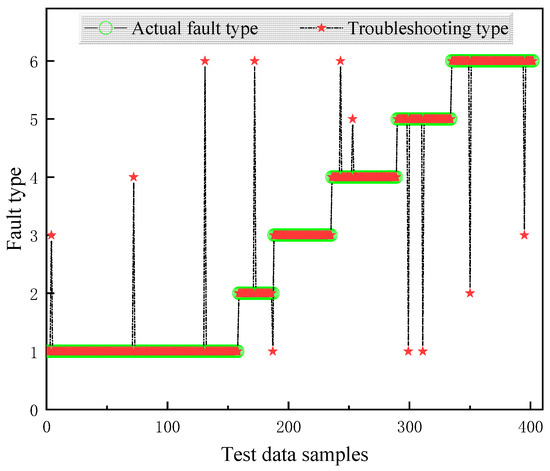
Figure 5.
Fault diagnosis results based on XGBoost.
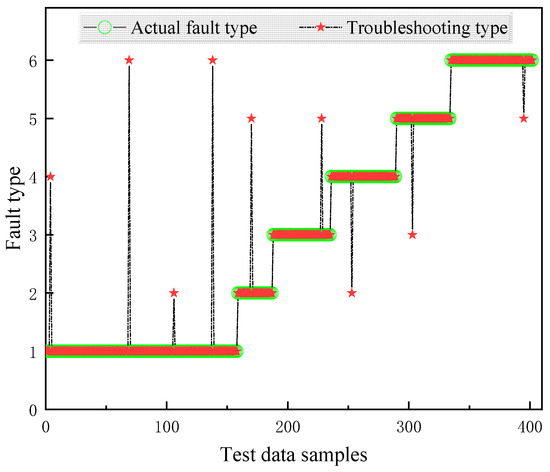
Figure 6.
Fault diagnosis results based on GA-XGBoost.
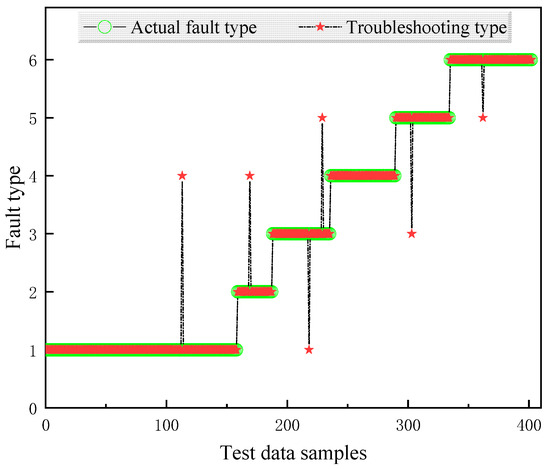
Figure 7.
Fault diagnosis results based on PSO-XGBoost.
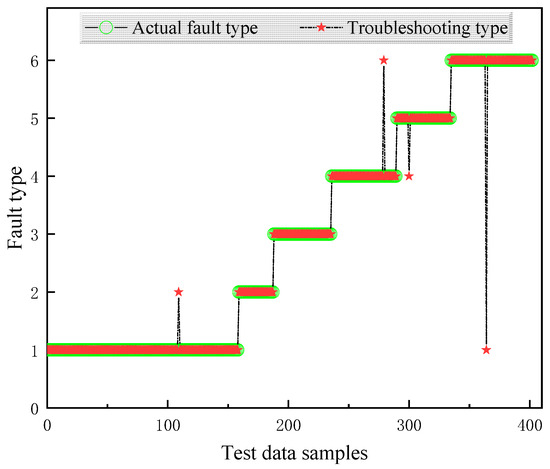
Figure 8.
Fault diagnosis results based on IPSO-XGBoost.
With the current and historical data of gas volume fraction in transformer oil, the membership degree of operating conditions, maintenance records, and operating time as input, the transformer status for one week is predicted. To comprehensively evaluate the effectiveness of the proposed IPSO-XGBoost model, it is compared with several other optimization-based models, including traditional XGBoost, GA-XGBoost, PSO-XGBoost, GWO-XGBoost, GSA-XGBoost, and CNN-XGBoost. The accuracy of each model in both the training and test sets is shown in Table 4.

Table 4.
Prediction accuracy of transformer status (prediction scale: one week).
In Table 4, the performance of the IPSO-XGBoost model is compared with several other optimization-based models, including traditional XGBoost, GA-XGBoost, PSO-XGBoost, as well as GWO-XGBoost, GSA-XGBoost, and CNN-XGBoost. The accuracy of the IPSO-XGBoost model in the training set shows significant improvements, with increases of 11.3%, 6.8%, 6.2%, 3.0%, 3.7%, and 2.7% over the traditional XGBoost, GA-XGBoost, PSO-XGBoost, GWO-XGBoost, GSA-XGBoost, and CNN-XGBoost models, respectively. Similarly, in the test set, the IPSO-XGBoost model outperforms the other models, achieving accuracy improvements of 11.4%, 6.9%, 4.8%, 3.3%, 4.7%, and 3.9%, respectively. These results demonstrate the effectiveness of the IPSO-XGBoost model in enhancing fault diagnosis accuracy, both in terms of generalization to new data (test set) and performance on the training set. The IPSO-XGBoost model consistently shows superior performance, confirming its robustness and reliability for transformer fault diagnosis.
With the current and historical data of gas volume fraction in transformer oil, the membership degree of operating conditions, maintenance records, and operating time as input, the transformer status for one month is predicted. The prediction accuracy of various models, including XGBoost, GA-XGBoost, PSO-XGBoost, GWO-XGBoost, GSA-XGBoost, CNN-XGBoost, and IPSO-XGBoost, is shown in Table 5.

Table 5.
Prediction accuracy of transformer status (prediction scale: one month).
In Table 5, the prediction time scale is set to one month, and the prediction accuracy has been significantly improved across all models. The IPSO-XGBoost model outperforms the XGBoost, GA-XGBoost, PSO-XGBoost, GWO-XGBoost, GSA-XGBoost, and CNN-XGBoost models in both training and testing phases, achieving 27.6%, 17.2%, and 7.2% higher accuracy on the training set, and 28.5%, 18.7%, and 7.4% higher accuracy on the test set compared to XGBoost, GA-XGBoost, and PSO-XGBoost, respectively. Specifically, GWO-XGBoost achieves 85.4% on the training set and 84.2% on the test set, showing improvement over XGBoost and other optimization methods but still falling short of IPSO-XGBoost by 3.3% and 3.7%, respectively. GSA-XGBoost shows similar results with 84.9% on the training set and 83.7% on the test set. The CNN-XGBoost model, incorporating convolutional neural networks for feature extraction, achieves 85.7% on the training set and 85.2% on the test set, exhibiting strong performance in capturing complex patterns but still not surpassing IPSO-XGBoost. As the number of available samples decreases, performance generally declines, particularly for XGBoost, due to limited exposure to data variation. While XGBoost still performs reasonably well in small-sample scenarios, models like PSO-XGBoost, GWO-XGBoost, and GSA-XGBoost exhibit a smaller performance drop due to their better generalization capabilities. However, as the sample size increases, the XGBoost model benefits from more data, leading to improved accuracy through better feature extraction and parameter optimization. Despite CNN-XGBoost’s ability to capture intricate features, it is outperformed by IPSO-XGBoost, which demonstrates superior accuracy, generalization, and convergence speed across both small and large datasets, establishing it as the most effective solution for transformer fault diagnosis.
To comprehensively evaluate the computational efficiency and resource consumption of different models, we compared XGBoost, GA-XGBoost, PSO-XGBoost, GWO-XGBoost, GSA-XGBoost, CNN-XGBoost, and IPSO-XGBoost. Table 6 presents the performance differences in these models in terms of training time, prediction latency, CPU usage, computation time, and memory requirements.

Table 6.
Computational Performance Comparison for XGBoost, GA-XGBoost, PSO-XGBoost, GWO-XGBoost, GSA-XGBoost, and CNN-XGBoost, IPSO-XGBoost.
In Table 6, the introduction of optimization methods leads to a gradual increase in the computational resource requirements and training time of the models. XGBoost is the most efficient, with a training time of 120 s and a computation time of 130 s, while its CPU and memory usage are relatively low. GA-XGBoost and PSO-XGBoost show an increase in both training and computation times, with times of 180 s and 200 s, respectively, and also higher CPU usage and memory consumption. IPSO-XGBoost has the highest training and computation times, with 250 s and 270 s, respectively, and memory usage reaching 2GB. Meanwhile, GWO-XGBoost and GSA-XGBoost also demonstrate relatively good efficiency, with training times of 220 s and 230 s, respectively. Their memory consumption and computation time are slightly higher than those of XGBoost but lower than IPSO-XGBoost. Although IPSO-XGBoost consumes more computational resources, its optimization performance and accuracy advantages make it highly valuable for complex fault diagnosis, especially in accurately diagnosing and resolving multi-class fault problems.
5. Conclusions
In this paper, the method combines the powerful modeling capability of XGBoost with the efficient hyperparameter optimization capability of IPSO. The IPSO algorithm is improved by adopting a master–slave particle swarm structure and a dynamic adaptive strategy, which results in enhanced optimization efficiency and prevents the occurrence of local optima. It has been demonstrated through experiments that the IPSO-XGBoost model outperforms the traditional XGBoost, GA-XGBoost, and PSO-XGBoost models in terms of both prediction accuracy and efficiency. The accuracy of the IPSO-XGBoost model in the training set has been increased by 11.8%, 7.1%, and 6.5%, respectively, compared to XGBoost, GA-XGBoost, and PSO-XGBoost models. In the test set, the accuracy has been increased by 11.9%, 7.4%, and 5.1%, respectively. These results highlight the effectiveness of IPSO in optimizing the hyperparameters of XGBoost, leading to better convergence and higher fault diagnosis accuracy.
As the prediction time scale increases, a decline in accuracy is observed across all models. However, even with this decrease, the IPSO-XGBoost model consistently maintains superior accuracy compared to the other models. While the XGBoost model provides more comprehensive features and more accurate prediction parameters, it is still outperformed by IPSO-XGBoost in overall prediction performance. This suggests that, although the XGBoost model excels in feature representation and parameter prediction, the role of IPSO in fine-tuning hyperparameters is crucial for improving fault diagnosis performance.
Overall, the IPSO-XGBoost method provides significant advantages in transformer fault diagnosis and offers a powerful tool for real-time monitoring and predictive maintenance of transformers. Future research could focus on further enhancing the IPSO algorithm to address more complex fault scenarios or on extending the model to other industrial applications, thereby contributing to the development of more reliable and efficient fault diagnosis systems.
Author Contributions
Conceptualization, Y.Z., C.R., F.W. and H.Z.; software, Y.Z., C.R., F.W. and H.Z.; writing—original draft preparation, Y.Z., C.R., F.W. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, L.; Song, J.; Wang, X.; Lu, J.; Lu, S. High-Resistance Connection Fault Diagnosis of SRM Based on Multisensor Calibrated Transformer with Shifted Windows. IEEE Sens. J. 2023, 23, 30971–30983. [Google Scholar] [CrossRef]
- Wang, H.; Yu, T.; Jiang, L.; Chen, X.; Zhang, G.; Su, M. Open-Circuit Fault Diagnosis and Tolerant Control of Matrix-Type Solid-State Transformer. IEEE Trans. Ind. Electron. 2024, 71, 16706–16716. [Google Scholar] [CrossRef]
- Rastogi, S.K.; Shah, S.S.; Singh, B.N.; Bhattacharya, S. Mode Analysis, Transformer Saturation, and Fault Diagnosis Technique for an Open-Circuit Fault in a Three-Phase DAB Converter. IEEE Trans. Power Electron. 2023, 38, 7644–7660. [Google Scholar] [CrossRef]
- Sun, W.; Wang, H.; Xu, J.; Yang, Y.; Yan, R. Effective Convolutional Transformer for Highly Accurate Planetary Gearbox Fault Diagnosis. IEEE Open J. Instrum. Meas. 2022, 1, 3500209. [Google Scholar] [CrossRef]
- Gong, Y.; Jiang, Y.; Cheng, C.; Wang, S. A Difference-Sensitive Mechanism Transformer Model for Incipient Fault Diagnosis in Electrical Drive Systems. IEEE Trans. Instrum. Meas. 2025, 74, 3543112. [Google Scholar] [CrossRef]
- Lin, J.; Yeo, L.Y.; Afrouzi, H.N.; Ektesabi, M.M.; Tavalaei, J. From limited data to reliable diagnosis: An interpretable deep learning framework for transformer fault analysis. Int. J. Electr. Power Energy Syst. 2025, 172, 111227. [Google Scholar] [CrossRef]
- Zhang, X.; Song, X.; Han, Y.; Dai, Q. Analysis of the feasibility of CF3I/CO2 used in C-GIS by partial discharge inception voltages in positive half cycle and breakdown voltages. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3234–3243. [Google Scholar] [CrossRef]
- An, Y.; Zhang, K.; Chai, Y.; Zhu, Z.; Liu, Q. Gaussian Mixture Variational-Based Transformer Domain Adaptation Fault Diagnosis Method and Its Application in Bearing Fault Diagnosis. IEEE Trans. Ind. Inform. 2024, 20, 615–625. [Google Scholar] [CrossRef]
- Yan, J.; Wang, Y.; Yang, Z.; Ding, Y.; Wang, J.; Geng, Y. Few-Shot Mechanical Fault Diagnosis for a High-Voltage Circuit Breaker via a Transformer–Convolutional Neural Network and Metric Meta-Learning. IEEE Trans. Instrum. Meas. 2023, 72, 3528011. [Google Scholar] [CrossRef]
- Wen, T.; Zhang, Q.; Ma, J.; Wu, Z.; Shimomura, N.; Chen, W. A new method to evaluate the effectiveness of impulse voltage for detecting insulation defects in GIS equipment. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1301–1307. [Google Scholar] [CrossRef]
- Luo, X.; Wang, H.; Han, T.; Zhang, Y. FFT-Trans: Enhancing Robustness in Mechanical Fault Diagnosis with Fourier Transform-Based Transformer Under Noisy Conditions. IEEE Trans. Instrum. Meas. 2024, 73, 2515112. [Google Scholar] [CrossRef]
- Weng, C.; Lu, B.; Gu, Q.; Zhao, X. A Novel Multisensor Fusion Transformer and Its Application into Rotating Machinery Fault Diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 3507512. [Google Scholar] [CrossRef]
- Rastogi, S.K.; Shah, S.S.; Singh, B.N.; Bhattacharya, S. Vector-Based Open-Circuit Fault Diagnosis Technique for a Three-Phase DAB Converter. IEEE Trans. Ind. Electron. 2024, 71, 8207–8211. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Hai, C.; Guo, M. Transformer Fault Diagnosis Based on Multi-Class AdaBoost Algorithm. IEEE Access 2022, 10, 1522–1532. [Google Scholar] [CrossRef]
- Sosa, J.E.O.; Núñez, R.O.; Oggier, G.E.; Aguilera, F.; Oggier, G.G.; Aldosari, O. Transistor Open-Circuit Fault Diagnosis for Three-Phase DAB Converters Using a Reduced Number of Sensors. IEEE Open J. Power Electron. 2025, 6, 1547–1558. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, D. An Auxiliary Classifier Generative Adversarial Network Based Fault Diagnosis for Analog Circuit. IEEE Access 2023, 11, 86824–86833. [Google Scholar] [CrossRef]
- Arismar, M.G.; Boaventura, W.C.; Boaventura, W.C.; Lopes, S.M.A.; Flauzino, R.A.; Altafim, R.A.C. Localisation of inter-layer partial discharges in transformer windings by logistic regression and different features extracted from current signals. IET Sci. Meas. Technol. 2021, 14, 55–67. [Google Scholar]
- Zhang, J.; Zhang, M.; Wang, D.; Yang, M.; Liang, C. Multi-scale convolutional sparse attention transformer: A lightweight fault diagnosis model for rotating machinery. Neurocomputing 2025, 650, 130934. [Google Scholar] [CrossRef]
- Kim, S.; Park, J.; Kim, W.; Jo, S.-H.; Youn, B.D. Learning from even a weak teacher: Bridging rule-based Duval method and a deep neural network for power transformer fault diagnosis. Int. J. Electr. Power Energy Syst. 2022, 136, 107–119. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, J.; Zeng, J. MDTCNet: A Novel Multiscale Denoising Transformer Convolutional Network for Fault Diagnosis of Partial Discharge. IEEE Trans. Dielectr. Electr. Insul. 2025, 32, 2938–2947. [Google Scholar] [CrossRef]
- Sun, W.; Yan, R.; Jin, R.; Xu, J.; Yang, Y.; Chen, Z. LiteFormer: A Lightweight and Efficient Transformer for Rotating Machine Fault Diagnosis. IEEE Trans. Reliab. 2024, 73, 1258–1269. [Google Scholar] [CrossRef]
- Ji, H.X.; Ma, G.M.; Li, C.; Pang, Z.-K.; Zheng, S.-S. Influence of voltage waveforms on partial discharge characteristics of pro-trusion defect in GIS. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1058–1067. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).