Modeling Anisotropic Permeability of Coal and Shale with Gas Rarefaction Effects, Matrix–Fracture Interaction, and Adsorption Hysteresis
Abstract
1. Introduction
2. Conceptual Models
2.1. Matrix Blocks and Fractures
2.2. Matrix–Fracture Interactions
3. Formulation of the Conceptual Model
3.1. Pressure of Matrix and Fracture Systems
3.2. Rock Swelling Models
3.3. Permeability Models
4. Model Verification
4.1. Constant Average Pore Pressure Conditions
4.2. Constant Confining Pressure Conditions
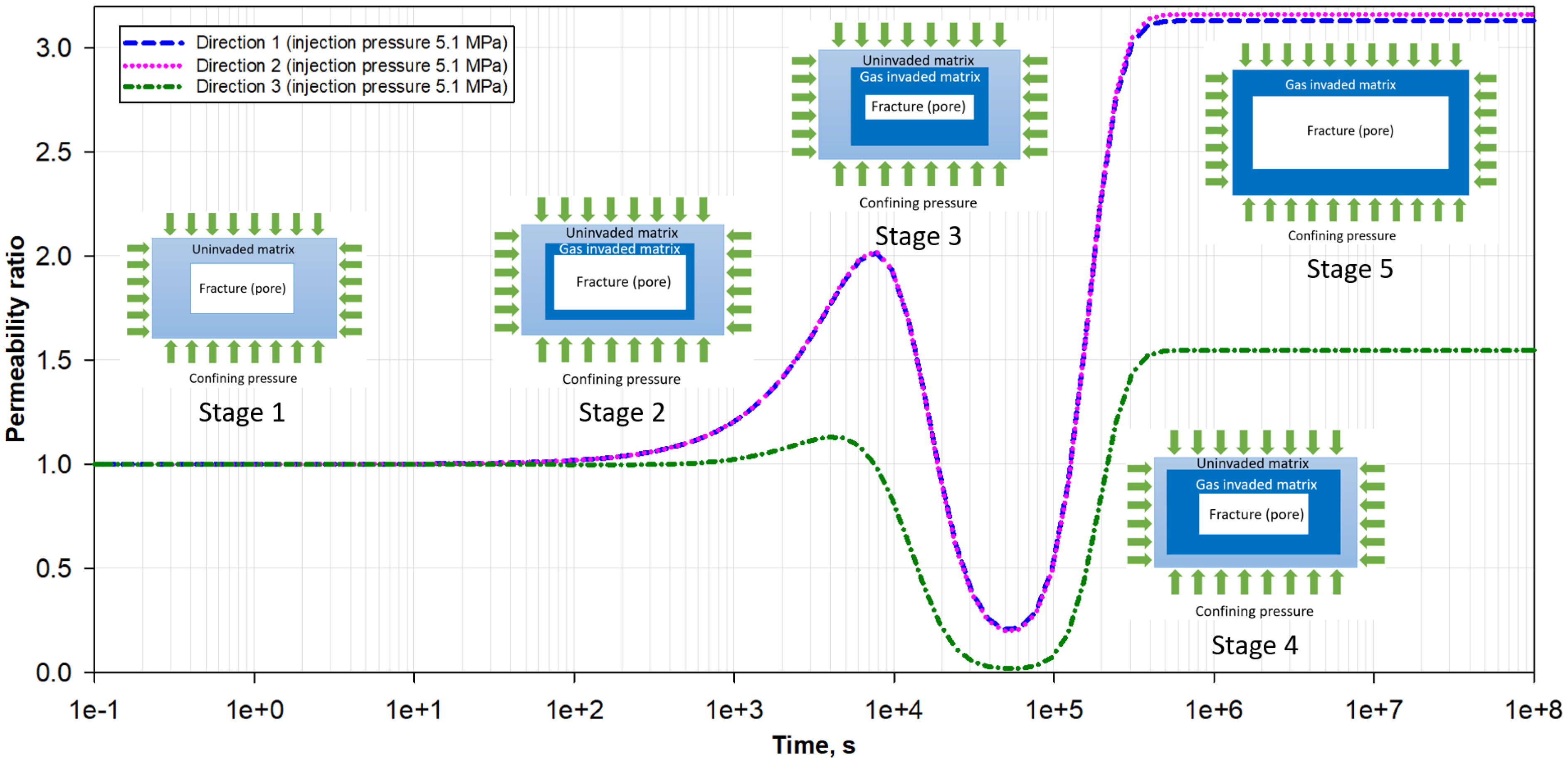
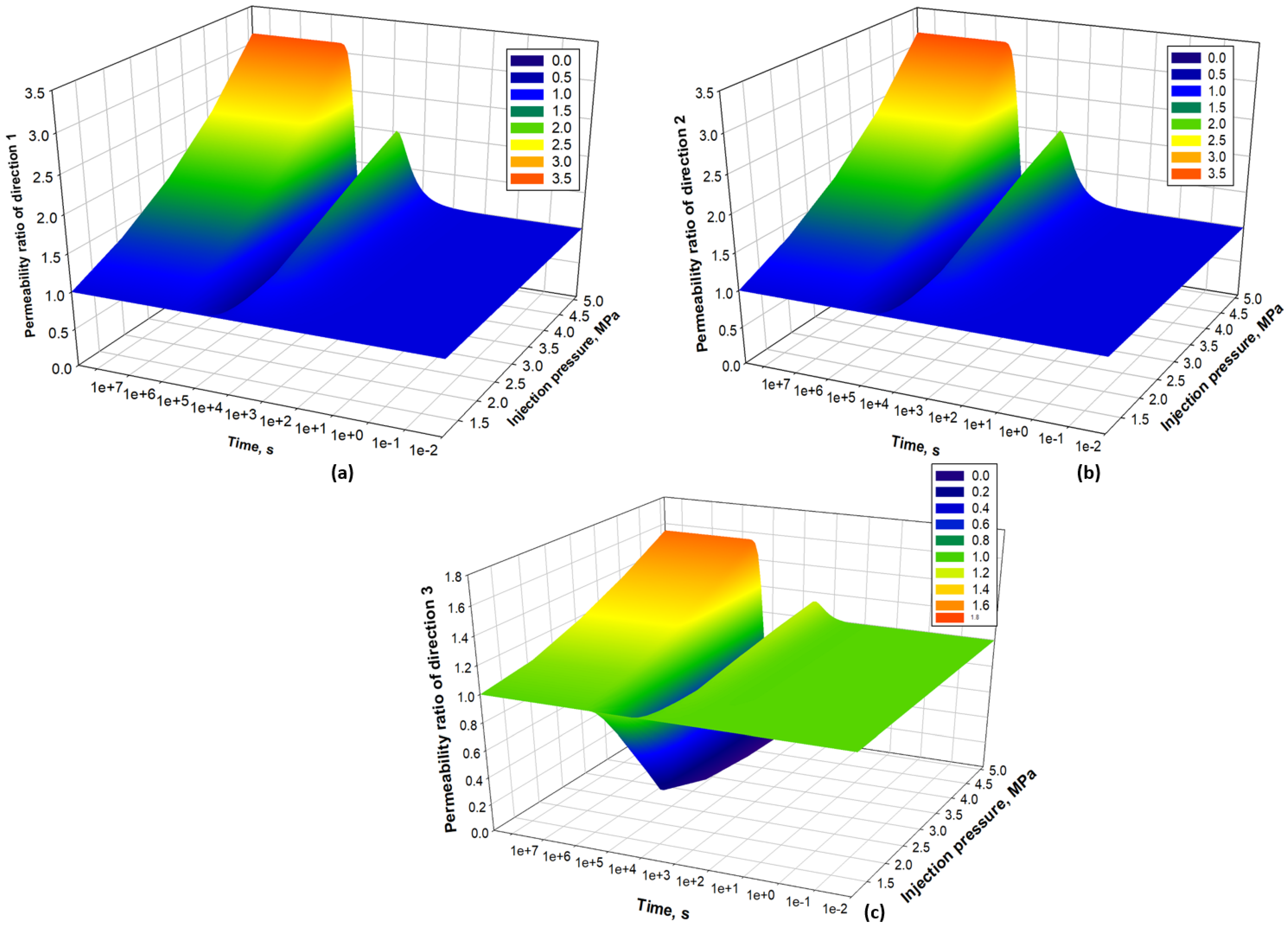
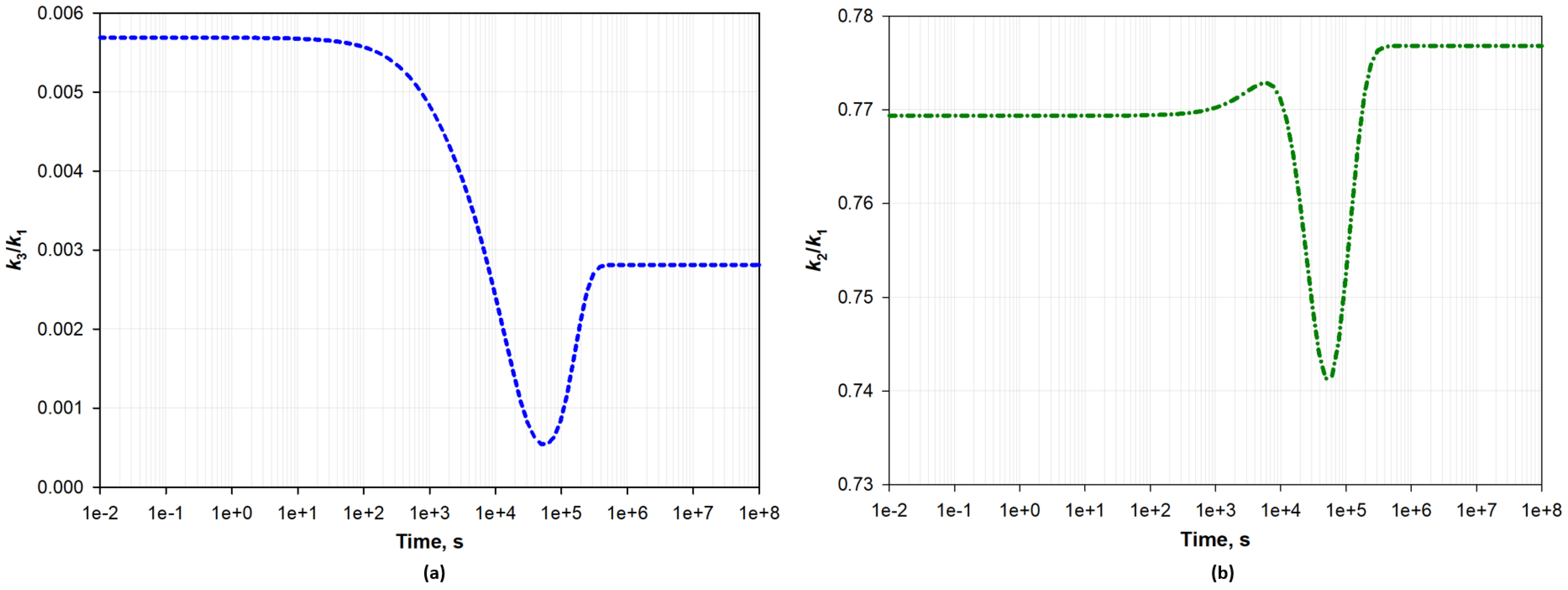
5. Results and Discussion
5.1. Anisotropic Permeability Ratios
5.2. Effects of Adsorption Hysteresis on Permeability Evolution
5.3. Effects of Tortuosity on Permeability Evolution
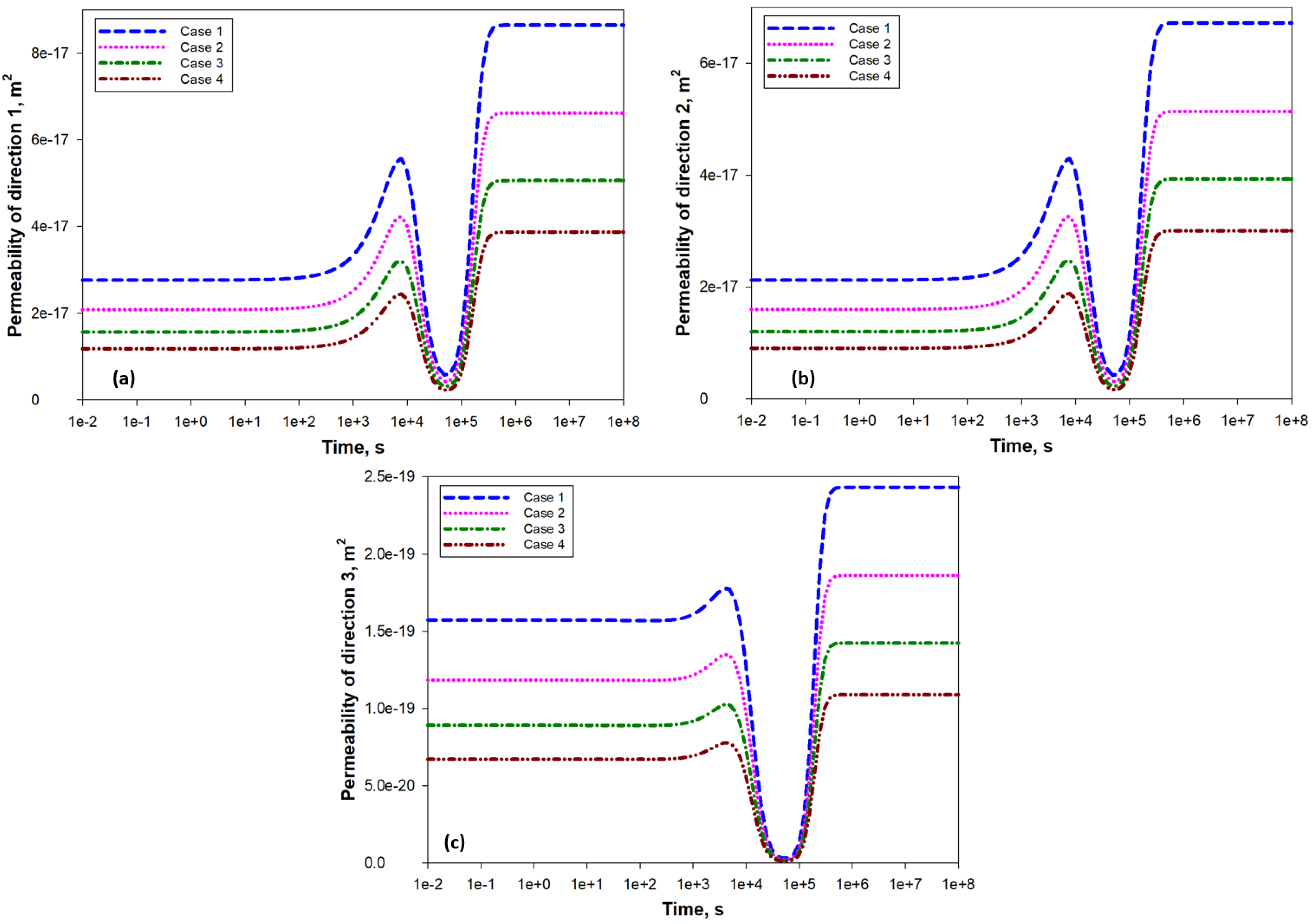
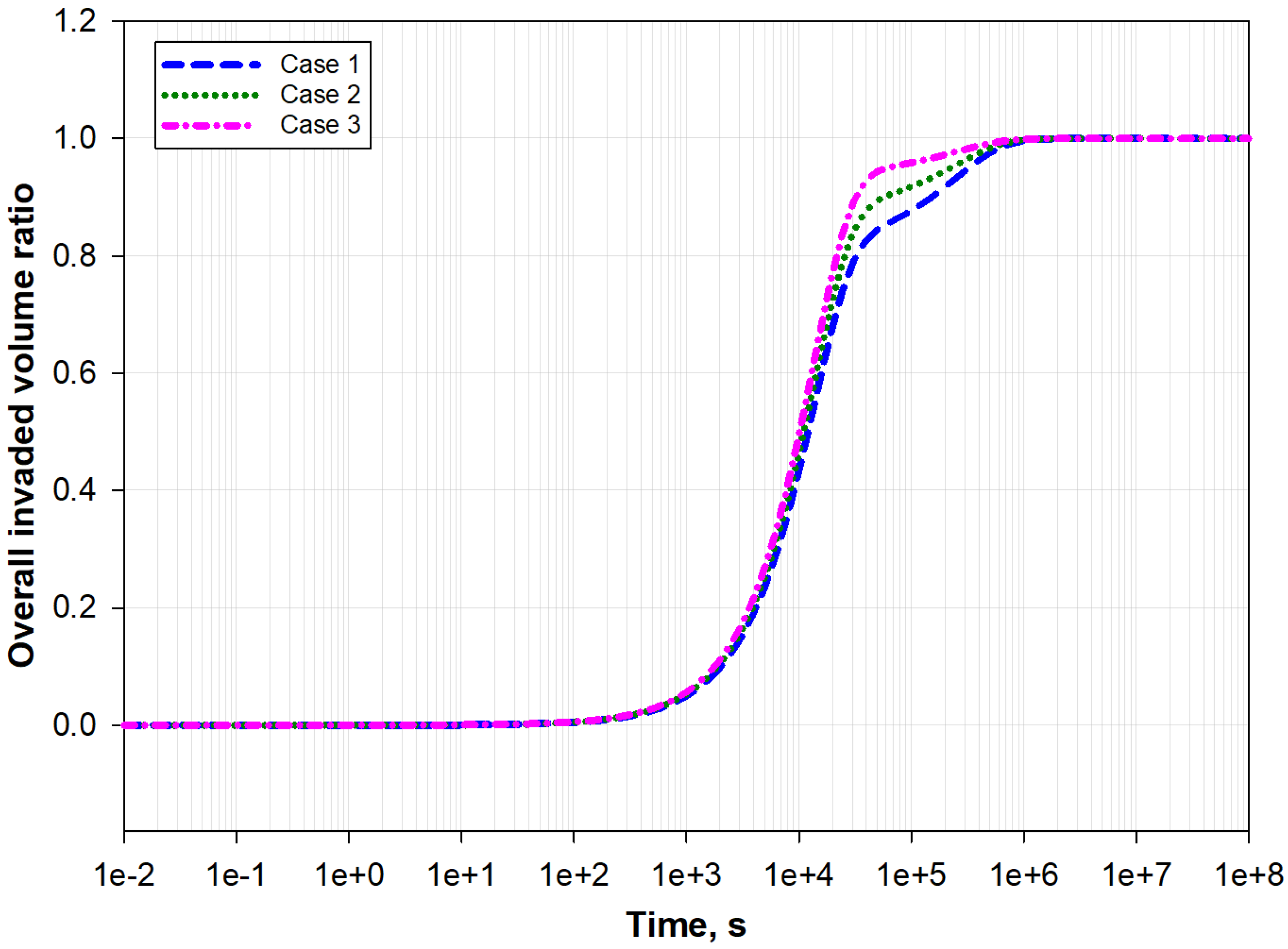
5.4. Effects of Different Matrix Blocks on Permeability Evolution
6. Conclusions
- (1)
- Permeability evolution in each direction shows unique features depending on the rock anisotropic structure, directional swelling, and anisotropic mechanical properties. Conventional isotropic permeability models may only accurately explain the permeability evolution in one direction.
- (2)
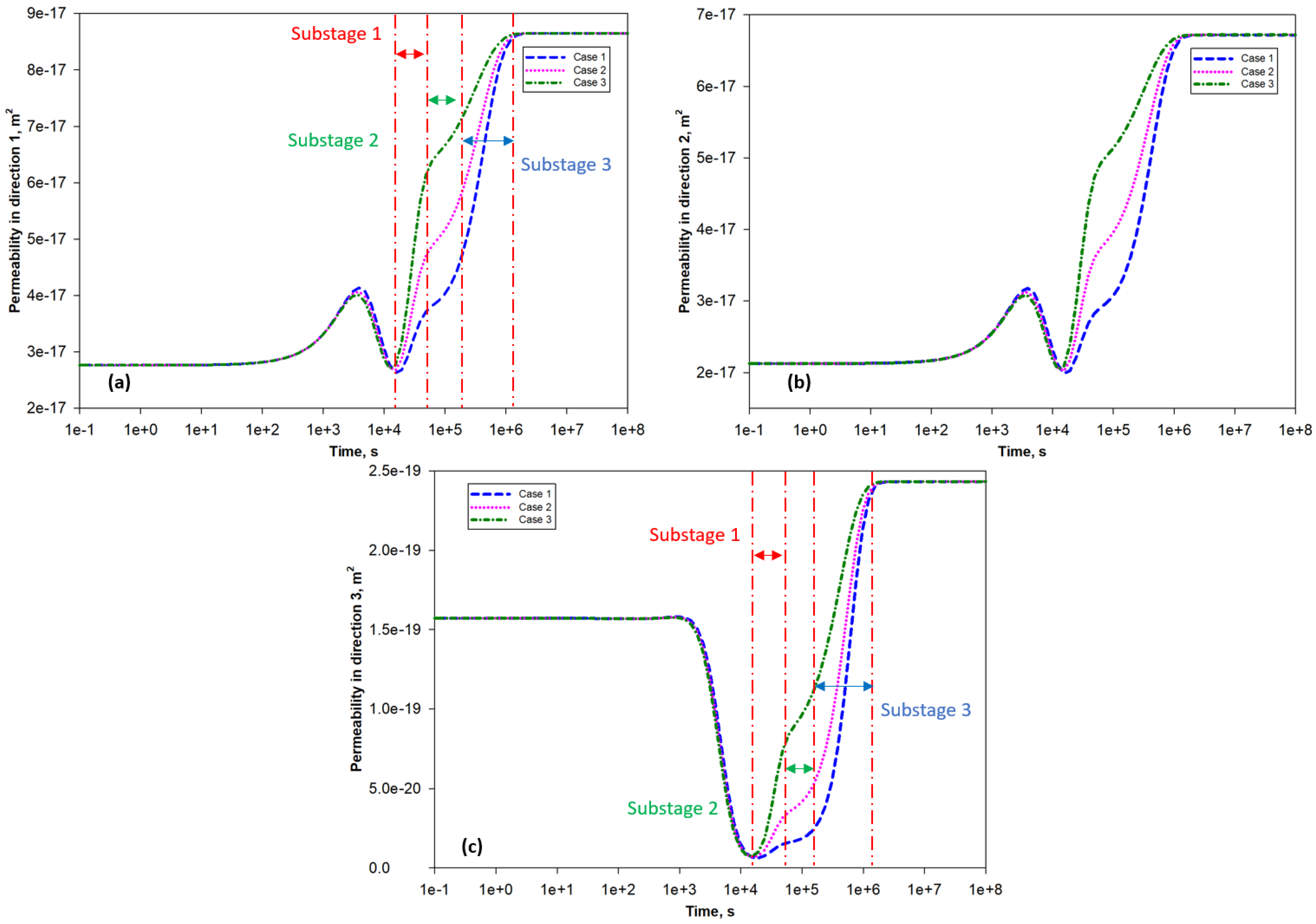
- Matrix–fracture mechanical interaction generates four-stage permeability evolution behavior under the constant confining pressure condition, including permeability increase, decline, rebound, and pressure equilibrium stages.
- (3)
- For each stress condition, an upper and a lower permeability can be used to demonstrate the range of permeability values during the pressure nonequilibrium period. By combining the upper and lower permeability values, the upper and lower permeability limit curves can be drawn, which envelopes all possible permeability values at different time and stress conditions. Three-dimensional permeability diagrams are proposed for different directions.
- (4)
- The magnitude of adsorption hysteresis mainly influences the local shrinkage period during gas extraction. The variation of this coefficient has a marginal influence on permeability when the hysteresis coefficient is larger than 0.75.
- (5)
- Tortuosity variation significantly affects permeability but has the smallest influence on the localized swelling period. Increments in flow channel tortuosity reduces permeability with almost the same magnitude in different regions.
- (6)
- Different matrix blocks achieve matrix-–fracture equilibrium asynchronously, which complicates the overall permeability evolution of certain regions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jaeger, J.C.; Cook, N.G.; Zimmerman, R. Fundamentals of Rock Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Amadei, B. Rock Anisotropy and the Theory of Stress Measurements; Springer Science & Business Media: New York, NY, USA, 2012; Volume 2. [Google Scholar]
- Hudson, J.A.; Harrison, J.P. Engineering Rock Mechanics: An Introduction to the Principles; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Wong, T.F. Anisotropic Poroelasticity in a Rock with Cracks: Anisotropic Poroelasticity. J. Geophys. Res. Solid Earth. 2017, 122, 7739–7753. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Liu, J.; Zhou, F.; Connell, L.D.; Sun, W.; Haque, A. Experimental study of impact of anisotropy and heterogeneity on gas flow in coal. Part II: Permeability. Fuel 2018, 230, 397–409. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, R.; Xie, H.; Gao, M.; Zha, E.; Jia, Z. An anisotropic coal permeability model that considers mining-induced stress evolution, microfracture propagation and gas sorption-desorption effects. J. Nat. Gas Sci. Eng. 2017, 46, 664–679. [Google Scholar] [CrossRef]
- Moore, R.; Palmer, I.; Higgs, N. Anisotropic Model for Permeability Change in Coalbed-Methane Wells. SPE Reserv. Eval. Eng. 2015, 18, 456–462. [Google Scholar] [CrossRef]
- Yue, G.; Li, M.; Wang, L.; Liang, W. Optimal layout of blasting holes in structural anisotropic coal seam. PloS ONE 2019, 14, e0218105. [Google Scholar] [CrossRef]
- Qi, C.; Wang, X.; Wang, W.; Liu, J.; Tuo, J.; Liu, K. Three-dimensional characterization of micro-fractures in shale reservoir rocks. Pet. Res. 2018, 3, 259–268. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; He, J. Numerical Study on the Permeability of the Hydraulic-Stimulated Fracture Network in Naturally-Fractured Shale Gas Reservoirs. Water 2016, 8, 393. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Yin, G.; Zhang, D.; Deng, B. Permeability evolution of anthracite coal considering true triaxial stress conditions and structural anisotropy. J. Nat. Gas Sci. Eng. 2018, 52, 492–506. [Google Scholar] [CrossRef]
- Raza, S.S.; Ge, L.; Rufford, T.E.; Chen, Z.; Rudolph, V. Anisotropic coal permeability estimation by determining cleat compressibility using mercury intrusion porosimetry and stress–strain measurements. Int. J. Coal Geol. 2019, 205, 75–86. [Google Scholar] [CrossRef]
- Smith, D.H.; Bromhal, G.; Sams, W.N.; Jikich, S.; Ertekin, T. Simulating Carbon Dioxide Sequestration/ECBM Production in Coal Seams: Effects of Permeability Anisotropies and the Diffusion-Time Constant. SPE Reserv. Eval. Eng. 2005, 8, 156–163. [Google Scholar] [CrossRef]
- Chalmers, G.R.L.; Ross, D.J.K.; Bustin, R.M. Geological controls on matrix permeability of Devonian Gas Shales in the Horn River and Liard basins, northeastern British Columbia, Canada. Int. J. Coal Geol. 2012, 103, 120–131. [Google Scholar] [CrossRef]
- Bhandari, A.R.; Flemings, P.B.; Polito, P.J.; Cronin, M.B.; Bryant, S.L. Anisotropy and Stress Dependence of Permeability in the Barnett Shale. Transp Porous Med. 2015, 108, 393–411. [Google Scholar] [CrossRef]
- Pan, Z.; Ma, Y.; Connell, L.D.; Down, D.I.; Camilleri, M. Measuring anisotropic permeability using a cubic shale sample in a triaxial cell. J. Nat. Gas Sci. Eng. 2015, 26, 336–344. [Google Scholar] [CrossRef]
- Ma, Y.; Pan, Z.; Zhong, N.; Connell, L.D.; Down, D.I.; Lin, W.; Zhang, Y. Experimental study of anisotropic gas permeability and its relationship with fracture structure of Longmaxi Shales, Sichuan Basin, China. Fuel 2016, 180, 106–115. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Elsworth, D.; Miao, X.; Mao, X. Development of anisotropic permeability during coalbed methane production. J. Nat. Gas Sci. Eng. 2010, 2, 197–210. [Google Scholar] [CrossRef]
- Pan, Z.; Connell, L.D. Modelling of anisotropic coal swelling and its impact on permeability behaviour for primary and enhanced coalbed methane recovery. Int. J. Coal Geol. 2011, 85, 257–267. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. Drawdown Induced Changes in Permeability of Coalbeds: A New Interpretation of the Reservoir Response to Primary Recovery. Transp. Porous Media 2004, 56, 1–16. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Elsworth, D.; Miao, X.; Mao, X. Linking gas-sorption induced changes in coal permeability to directional strains through a modulus reduction ratio. Int. J. Coal Geol. 2010, 83, 21–30. [Google Scholar] [CrossRef]
- Chen, D.; Pan, Z.; Liu, J.; Connell, L.D. Characteristic of anisotropic coal permeability and its impact on optimal design of multi-lateral well for coalbed methane production. J. Pet. Sci. Eng. 2012, 88–89, 13–28. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, J.; Kabir, A. Combined effects of directional compaction, non-Darcy flow and anisotropic swelling on coal seam gas extraction. Int. J. Coal Geol. 2013, 109–110, 1–14. [Google Scholar] [CrossRef]
- Wang, K.; Zang, J.; Wang, G.; Zhou, A. Anisotropic permeability evolution of coal with effective stress variation and gas sorption: Model development and analysis. Int. J. Coal Geol. 2014, 130, 53–65. [Google Scholar] [CrossRef]
- An, H.; Wei, X.R.; Wang, G.X.; Massarotto, P.; Wang, F.; Rudolph, V.; Golding, S. Modeling anisotropic permeability of coal and its effects on CO2 sequestration and enhanced coalbed methane recovery. Int. J. Coal Geol. 2015, 152, 15–24. [Google Scholar] [CrossRef]
- Li, J.; Li, B.; Cheng, Q.; Gao, Z. Evolution of Anisotropic Coal Permeability Under the Effect of Heterogeneous Deformation of Fractures. Nat. Resour. Res. 2021, 30, 3623–3642. [Google Scholar] [CrossRef]
- Qi, X.; Fu, P.; Wang, S. Numerical Investigation of an Anisotropic Permeability Model for Bedded Coal Based on the Equivalent Fracture Aperture Coefficient. Shock. Vib. 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Zeng, J.; Guo, J.; Liu, J.; Li, W.; Zhou, Y.; Tian, J. Anisotropic Permeability Model for Coal Considering Stress Sensitivity, Matrix Anisotropic Internal Swelling/Shrinkage, and Gas Rarefaction Effects. Energy Fuels 2023, 37, 2811–2832. [Google Scholar] [CrossRef]
- Zeng, J.; Guo, J.; Liu, J.; Zhang, T.; Zhao, Z.; Liu, J.; Chen, Z. A Strain-Driven Model for Anisotropic Permeability Evolution of Shale and Coal Incorporating Creep Deformation, Anisotropic Internal Swelling/Shrinkage, and Gas Rarefaction Effects. In Proceedings of the SPE Conference at Oman Petroleum & Energy Show, Muscat, Oman, 22–24 April 2024; p. D021S026R002. [Google Scholar] [CrossRef]
- He, L.; Mei, H.; Hu, X.; Dejam, M.; Kou, Z.; Zhang, M. Advanced Flowing Material Balance to Determine Original Gas in Place of Shale Gas Considering Adsorption Hysteresis. SPE Reserv. Eval. Eng. 2019, 22, 1282–1292. [Google Scholar] [CrossRef]
- Wei, M.; Liu, J.; Shi, R.; Elsworth, D.; Liu, Z. Long-Term Evolution of Coal Permeability Under Effective Stresses Gap Between Matrix and Fracture During CO2 Injection. Transp. Porous Med. 2019, 130, 969–983. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Li, W.; Leong, Y.K.; Elsworth, D.; Guo, J. Evolution of Shale Permeability under the Influence of Gas Diffusion from the Fracture Wall into the Matrix. Energy Fuels 2020, 34, 4393–4406. [Google Scholar] [CrossRef]
- Reiss, L.H. The Reservoir Engineering Aspects of Fractured Formations; Editions Technip: Paris, France, 1980; Volume 3. [Google Scholar]
- Peng, Y.; Liu, J.; Pan, Z.; Connell, L.D.; Chen, Z.; Qu, H. Impact of coal matrix strains on the evolution of permeability. Fuel 2017, 189, 270–283. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.; Chen, Z.; Wang, S.; Elsworth, D.; Jiang, Y. Impact of transition from local swelling to macro swelling on the evolution of coal permeability. Int. J. Coal Geol. 2011, 88, 31–40. [Google Scholar] [CrossRef]
- Civan, F.; Rai, C.S.; Sondergeld, C.H. Determining Shale Permeability to Gas by Simultaneous Analysis of Various Pressure Tests. SPE J. 2012, 17, 717–726. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; Pan, Z.; Connell, L.D. A sequential model of shale gas transport under the influence of fully coupled multiple processes. J. Nat. Gas Sci. Eng. 2015, 27, 808–821. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Chen, G.; Bodvarsson, G.S. A Dual-Porosity Reservoir Model with an Improved Coupling Term. In Proceedings of the Seventeenth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 29–31 January 1992; p. 11. [Google Scholar]
- Zeng, J.; Li, W.; Liu, J.; Leong, Y.-K.; Elsworth, D.; Tian, J.; Guo, J.; Zeng, F. Analytical solutions for multi-stage fractured shale gas reservoirs with damaged fractures and stimulated reservoir volumes. J. Pet. Sci. Eng. 2020, 187, 106686. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, X.; Guo, J.; Zeng, F. Composite linear flow model for multi-fractured horizontal wells in heterogeneous shale reservoir. J. Nat. Gas Sci. Eng. 2017, 38, 527–548. [Google Scholar] [CrossRef]
- Ren, W.; Lau, H.C. Analytical modeling and probabilistic evaluation of gas production from a hydraulically fractured shale reservoir using a quad-linear flow model. J. Pet. Sci. Eng. 2020, 184, 106516. [Google Scholar] [CrossRef]
- Heidari Sureshjani, M.; Behmanesh, H.; Soroush, M.; Clarkson, C.R. A direct method for property estimation from analysis of infinite acting production in shale/tight gas reservoirs. J. Pet. Sci. Eng. 2016, 143, 26–34. [Google Scholar] [CrossRef]
- Fuentes-Cruz, G.; Valko, P.P. Revisiting the Dual-Porosity/Dual-Permeability Modeling of Unconventional Reservoirs: The Induced-Interporosity Flow Field. SPE J. 2015, 20, 124–141. [Google Scholar] [CrossRef]
- Lim, K.T.; Aziz, K. Matrix-fracture transfer shape factors for dual-porosity simulators. J. Pet. Sci. Eng. 1995, 3, 169–178. [Google Scholar] [CrossRef]
- Donohue, M.D.; Aranovich, G.L. Adsorption Hysteresis in Porous Solids. J. Colloid Interface Sci. 1998, 205, 121–130. [Google Scholar] [CrossRef]
- Ren, W. Modeling Hysteretic Adsorption and Desorption of Methane on Shale. Energy Fuels 2025, 39, 16214–16222. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, S. Experimental and theoretical characterization of methane and CO2 sorption hysteresis in coals based on Langmuir desorption. Int. J. Coal Geol. 2017, 171, 49–60. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, L.; Kang, Q.; Viswanathan, H.S.; Yao, J.; Tao, W. Nanoscale simulation of shale transport properties using the lattice Boltzmann method: Permeability and diffusivity. Sci. Rep. 2015, 5, 8089. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in porous media: A critical review. Soil Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Cui, X.; Bustin, R.M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams. Bulletin 2005, 89, 1181–1202. [Google Scholar] [CrossRef]
- Berryman, J.G. Poroelastic Response of Orthotropic Fractured Porous Media. Transp. Porous Media 2012, 93, 293–307. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, Y.; Wang, H.; Zhou, H.; Wang, L.; Li, W.; Liu, H. Numerical assessment of the effect of equilibration time on coal permeability evolution characteristics. Fuel 2015, 140, 81–89. [Google Scholar] [CrossRef]
- Mian, C.; Zhida, C. Effective stress laws for multi-porosity media. Appl. Math. Mech. 1999, 20, 1207–1213. [Google Scholar] [CrossRef]
- Mehrabian, A.; Abousleiman, Y.N. Generalized Biot’s theory and Mandel’s problem of multiple-porosity and multiple-permeability poroelasticity: Multiple-porosity poroelasticity. J. Geophys. Res. Solid Earth 2014, 119, 2745–2763. [Google Scholar] [CrossRef]
- Wang, H.F. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Mehrabian, A.; Abousleiman, Y.N. Gassmann equations and the constitutive relations for multiple-porosity and multiple-permeability poroelasticity with applications to oil and gas shale: Multiple-porosity and Multiple-permeability Poroelasticity. Int. J. Numer. Anal. Meth. Geomech. 2015, 39, 1547–1569. [Google Scholar] [CrossRef]
- Carroll, M.M. An effective stress law for anisotropic elastic deformation. J. Geophys. Res. 1979, 84, 7510–7512. [Google Scholar] [CrossRef]
- Blioumi, A. On Linear-Elastic, Cross-Anisotropic Rock; Logos Verlag Berlin GmbH: Berlin, Germany, 2014; Volume 19. [Google Scholar]
- Beskok, A.; Karniadakis, G.E. Report: A Model for Flows in Channels, Pipes, and Ducts at Micro and Nano Scales. Microscale Thermophys. Eng. 1999, 3, 43–77. [Google Scholar] [CrossRef]
- Karniadakis, G.; Beskok, A.; Aluru, N. Microflows and Nanoflows: Fundamentals and Simulation; Springer Science & Business Media: New York, NY, USA, 2006; Volume 29. [Google Scholar]
- Peng, Y.; Liu, J.; Pan, Z.; Qu, H.; Connell, L. Evolution of shale apparent permeability under variable boundary conditions. Fuel 2018, 215, 46–56. [Google Scholar] [CrossRef]
- Jing, Y.; Armstrong, R.T.; Ramandi, H.L.; Mostaghimi, P. Coal cleat reconstruction using micro-computed tomography imaging. Fuel 2016, 181, 286–299. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Cai, Y.; Yao, Y. Fracture permeability evaluation of a coal reservoir using geophysical logging: A case study in the Zhengzhuang area, southern Qinshui Basin. Energy Explor. Exploit. 2016, 34, 378–399. [Google Scholar] [CrossRef]
- Chi, A.; Yuwei, L. The Model for Calculating Elastic Modulus and Poisson’s Ratio of Coal Body. Open Fuels Energy Sci. J. 2013, 6, 36–43. [Google Scholar] [CrossRef]
- Zheng, G.; Pan, Z.; Chen, Z.; Tang, S.; Connell, L.D.; Zhang, S.; Wang, B. Laboratory Study of Gas Permeability and Cleat Compressibility for CBM/ECBM in Chinese Coals. Energy Explor. Exploit. 2012, 30, 451–476. [Google Scholar] [CrossRef]
- Ghanizadeh, A.; Amann-Hildenbrand, A.; Gasparik, M.; Gensterblum, Y.; Krooss, B.M.; Littke, R. Experimental study of fluid transport processes in the matrix system of the European organic-rich shales: II. Posidonia Shale (Lower Toarcian, northern Germany). Int. J. Coal Geol. 2014, 123, 20–33. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.; Wei, M.; Elsworth, D. Coal permeability maps under the influence of multiple coupled processes. Int. J. Coal Geol. 2018, 187, 71–82. [Google Scholar] [CrossRef]
- Sone, H.; Zoback, M.D. Mechanical properties of shale-gas reservoir rocks—Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 2013, 78, D381–D392. [Google Scholar] [CrossRef]
- Tan, Y.; Pan, Z.; Feng, X.T.; Zhang, D.; Connell, L.D.; Li, S. Laboratory characterisation of fracture compressibility for coal and shale gas reservoir rocks: A review. Int. J. Coal Geol. 2019, 204, 1–17. [Google Scholar] [CrossRef]
- Zhang, Y.; Mostaghimi, P.; Fogden, A.; Middleton, J.; Sheppard, A.; Armstrong, R.T. Local diffusion coefficient measurements in shale using dynamic micro-computed tomography. Fuel 2017, 207, 312–322. [Google Scholar] [CrossRef]
- Liu, H.H.; Rutqvist, J. A New Coal-Permeability Model: Internal Swelling Stress and Fracture–Matrix Interaction. Transp. Porous Med. 2010, 82, 157–171. [Google Scholar] [CrossRef]
- Shi, R.; Liu, J.; Wei, M.; Elsworth, D.; Wang, X. Mechanistic analysis of coal permeability evolution data under stress-controlled conditions. Int. J. Rock Mech. Min. Sci. 2018, 110, 36–47. [Google Scholar] [CrossRef]
- Kumar, H.; Elsworth, D.; Mathews, J.P.; Marone, C. Permeability evolution in sorbing media: Analogies between organic-rich shale and coal. Geofluids 2016, 16, 43–55. [Google Scholar] [CrossRef]
- Wu, Y.; Tahmasebi, P.; Yu, H.; Lin, C.; Wu, H.; Dong, C. Pore-Scale 3D Dynamic Modeling and Characterization of Shale Samples: Considering the Effects of Thermal Maturation. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018309. [Google Scholar] [CrossRef]
- Huang, L.; Ning, Z.; Wang, Q.; Qi, R.; Li, J.; Zeng, Y.; Ye, H.; Qin, H. Thermodynamic and Structural Characterization of Bulk Organic Matter in Chinese Silurian Shale: Experimental and Molecular Modeling Studies. Energy Fuels 2017, 31, 4851–4865. [Google Scholar] [CrossRef]
- Wang, S.; Feng, Q.; Zha, M.; Javadpour, F.; Hu, Q. Supercritical Methane Diffusion in Shale Nanopores: Effects of Pressure, Mineral Types, and Moisture Content. Energy Fuels 2018, 32, 169–180. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Elsworth, D.; Leong, Y.K.; Li, W. An effective stress-dependent dual-fractal permeability model for coal considering multiple flow mechanisms. Fuel 2023, 334, 126800. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Li, W.; Guo, J. A process-based coal swelling model: Bridging the gaps between localized swelling and bulk swelling. Fuel 2021, 293, 120360. [Google Scholar] [CrossRef]
- Qu, H.; Liu, J.; Chen, Z.; Wang, J.; Pan, Z.; Connell, L.; Elsworth, D. Complex evolution of coal permeability during CO2 injection under variable temperatures. Int. J. Greenh. Gas Control. 2012, 9, 281–293. [Google Scholar] [CrossRef]
- Yin, B.; Zhai, X.; Lou, Y.; Liu, S.; Wei, K.; Cheng, W. Transport mechanism of coal particles in multiphase flow during early coalbed methane production. Phys. Fluids 2025, 37, 053327. [Google Scholar] [CrossRef]
- Li, Q. Reservoir Science: A Multi-Coupling Communication Platform to Promote Energy Transformation, Climate Change and Environmental Protection. Reserv. Sci. 2025, 1, 1–2. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Li, W.; Tian, J.; Leong, Y.K.; Elsworth, D.; Guo, J. Effects of heterogeneous local swelling and multiple pore types on coal and shale permeability evolution. In Proceedings of the SPE Europec Featured at EAGE Conference and Exhibition, Virtual, 7 December 2020. [Google Scholar]
- Zeng, J.; Liu, J.; Li, W.; Leong, Y.K.; Elsworth, D.; Guo, J. Combined effects of laminae characteristics and matrix-fracture equilibrium hysteresis on permeability evolution of fractured sorbing rocks. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Virtual, 17–19 November 2020. [Google Scholar]
- Zou, C.; Dong, D.; Wang, S.; Li, J.; Li, X.; Wang, Y.; Li, D.; Cheng, K. Geological characteristics and resource potential of shale gas in China. Pet. Explor. Dev. 2010, 37, 641–653. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wang, F.; Wu, J.; Wang, Y.; Jin, J. Effects of Geological and Fluid Characteristics on the Injection Filtration of Hydraulic Fracturing Fluid in the Wellbores of Shale Reservoirs: Numerical Analysis and Mechanism Determination. Processes 2025, 13, 1747. [Google Scholar] [CrossRef]

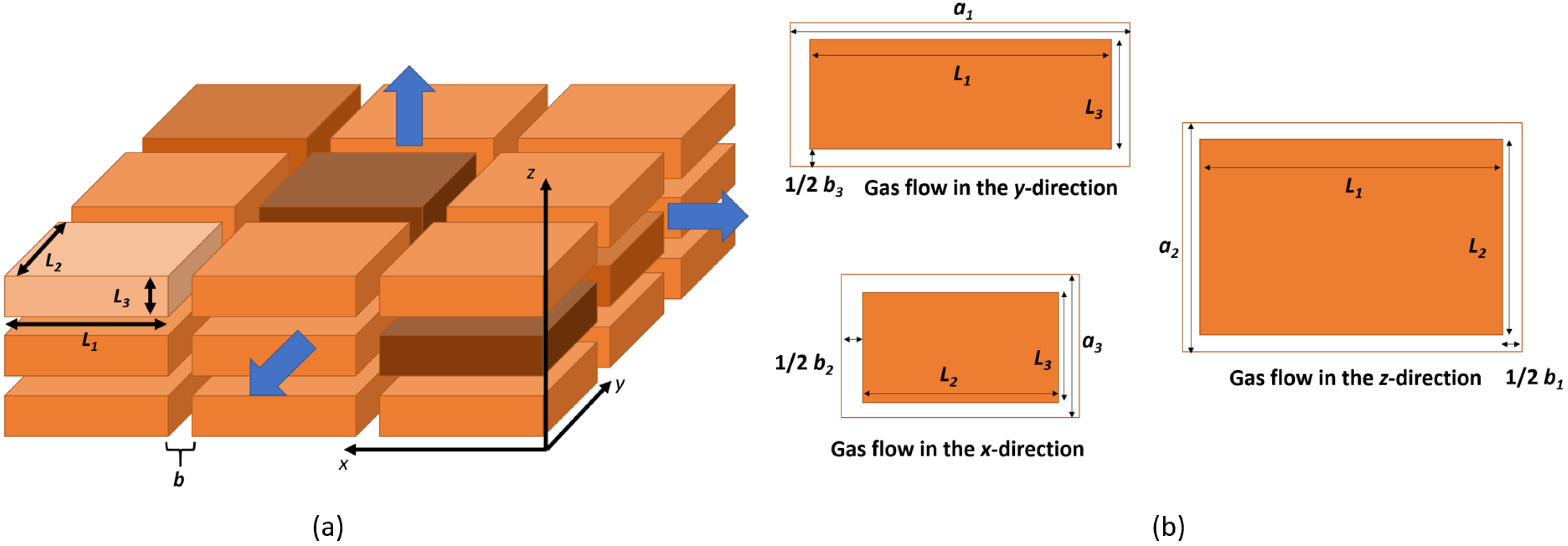
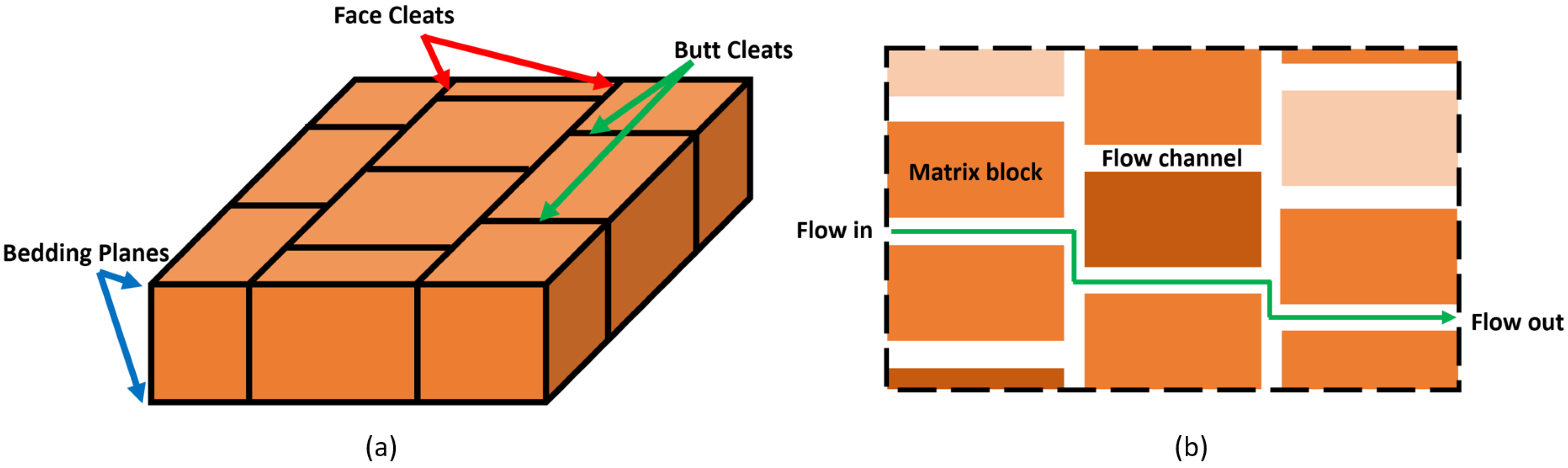
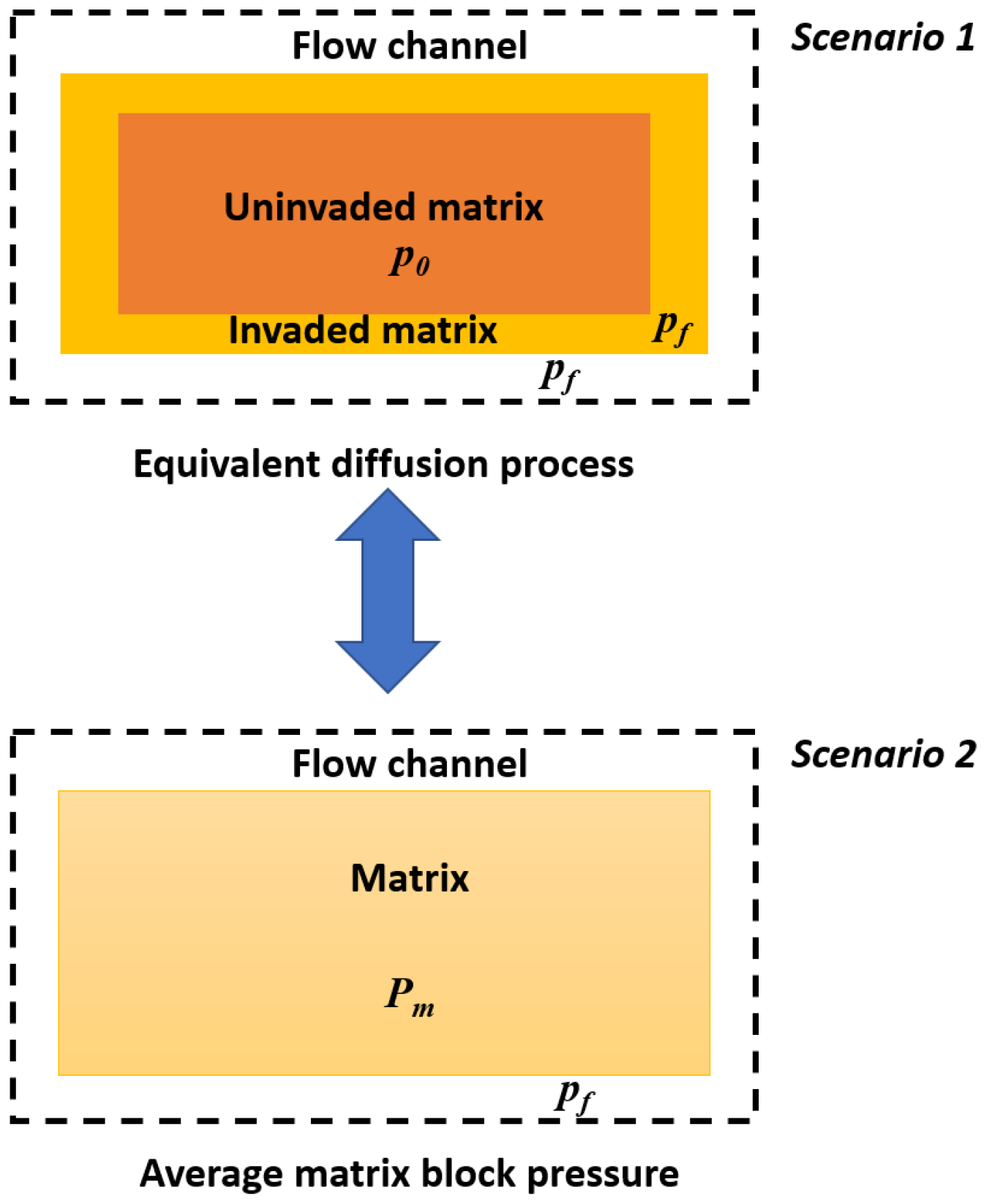
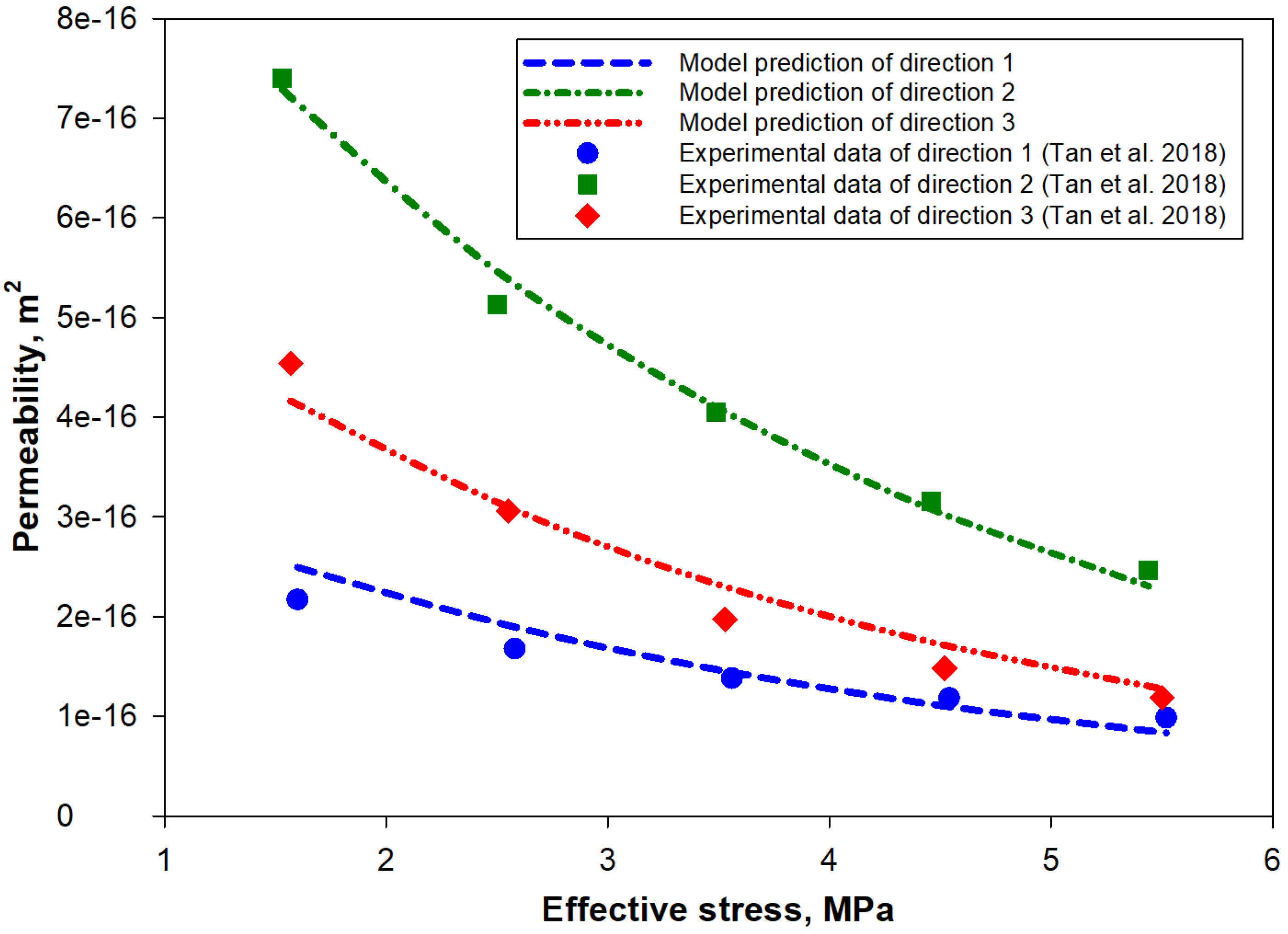
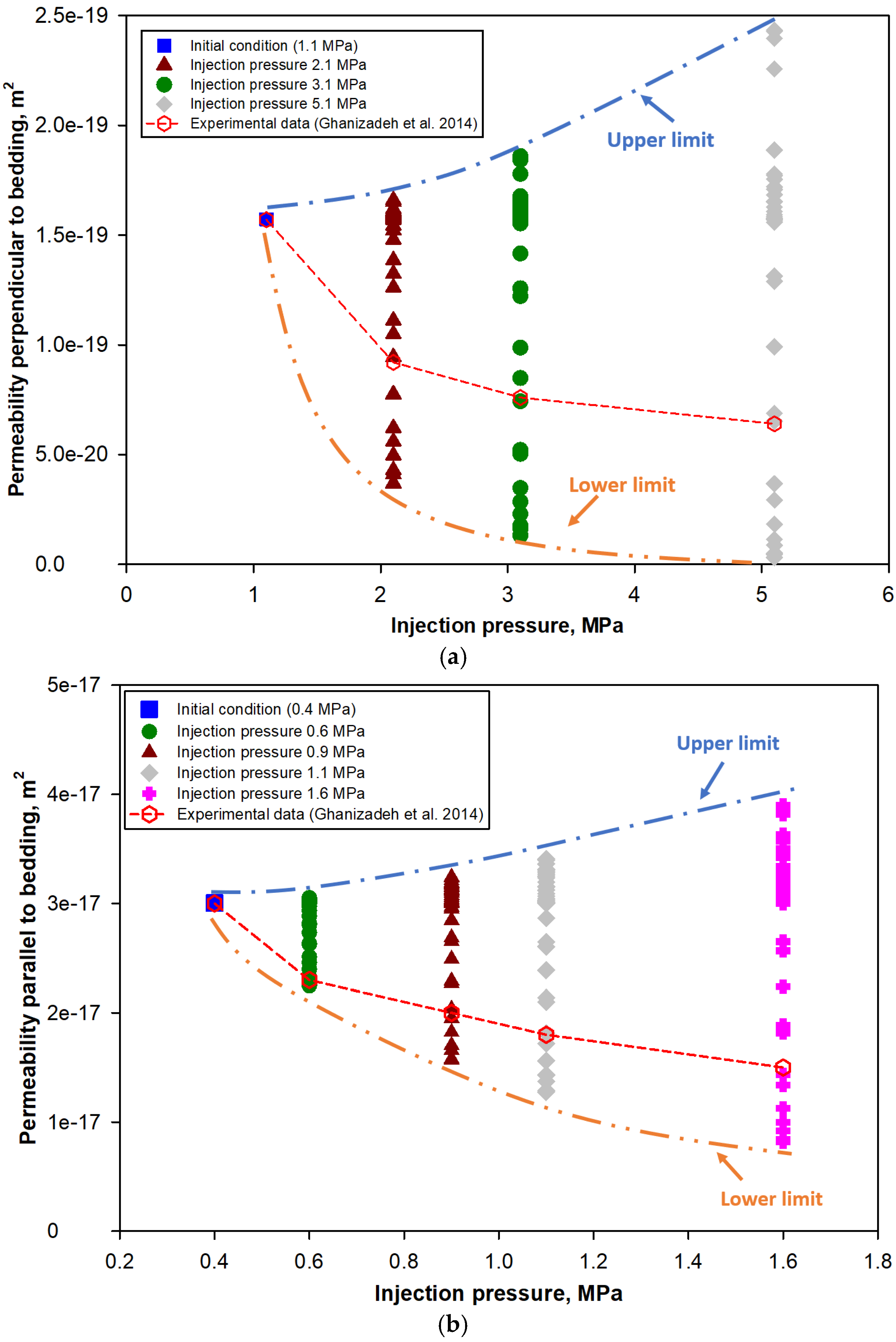


| Parameters | Values | Data Sources |
|---|---|---|
| Initial flow channel spacing | m | Jing et al. [62] and experimental data matching |
| Initial flow channel spacing | m | Jing et al. [62] and experimental data matching |
| Initial flow channel spacing | m | Jing et al. [62] and experimental data matching |
| Initial flow channel aperture | m | Li et al. [63] and experimental data matching |
| Initial flow channel aperture | m | Li et al. [63] and experimental data matching |
| Initial flow channel aperture | m | Li et al. [63] and experimental data matching |
| Tortuosity exponential coefficient | 0.314 | Ghanbarian et al. [49], Chen et al. [48], and experimental data matching |
| Tortuosity exponential coefficient | 0.42 | Ghanbarian et al. [49], Chen et al. [48], and experimental data matching |
| Tortuosity exponential coefficient | 0.51 | Ghanbarian et al. [49], Chen et al. [48], and experimental data matching |
| Coal bulk Young’s modulus | Pa | Chi and Yuwei [64] and experimental data matching |
| Coal bulk Young’s modulus | Pa | Chi and Yuwei [64] and experimental data matching |
| Coal bulk Young’s modulus | Pa | Chi and Yuwei [64] and experimental data matching |
| Coal bulk Poisson’s ratio | 0.33 | Cui and Bustin [50] and experimental data matching |
| Coal bulk Poisson’s ratio | 0.28 | Cui and Bustin [50] and experimental data matching |
| Coal bulk Poisson’s ratio | 0.30 | Cui and Bustin [50] and experimental data matching |
| Flow channel Young’s modulus | Pa | Converted from the cleat compressibility of Zheng et al. [65] and experimental data matching |
| Flow channel Young’s modulus | Pa | Converted from the cleat compressibility of Zheng et al. [65] and experimental data matching |
| Flow channel Young’s modulus | Pa | Converted from the cleat compressibility of Zheng et al. [65] and experimental data matching |
| Flow channel Poisson’s ratio | 0.33 | Cui and Bustin [50] and experimental data matching |
| Flow channel Poisson’s ratio | 0.28 | Cui and Bustin [50] and experimental data matching |
| Flow channel Poisson’s ratio | 0.30 | Cui and Bustin [50] and experimental data matching |
| Temperature | K | Room temperature |
| Sample 1: HAD, 2, Dry (Perpendicular to Bedding) | ||
| Confining pressure, MPa | Pore (fracture) pressure, MPa | Permeability, m2 |
| 30.0 | 1.1 | |
| 30.0 | 2.1 | |
| 30.0 | 3.1 | |
| 30.0 | 5.1 | |
| Sample 2: HAD, 2, dry (parallel to bedding) | ||
| Confining pressure, MPa | Pore (fracture) pressure, MPa | Permeability, m2 |
| 30.1 | 0.4 | |
| 30.2 | 0.6 | |
| 29.8 | 0.9 | |
| 29.9 | 1.1 | |
| 30.0 | 1.6 | |
| Parameters | Values | Data Sources |
|---|---|---|
| Initial flow channel spacing | m | Zeng et al. [32] and experimental data matching |
| Initial flow channel spacing | m | Zeng et al. [32] and experimental data matching |
| Initial flow channel spacing | m | Zeng et al. [32] and experimental data matching |
| Initial flow channel aperture | m | Zeng et al. [32] and experimental data matching |
| Initial flow channel aperture | m | Zeng et al. [32] and experimental data matching |
| Initial flow channel aperture | m | Zeng et al. [32] and experimental data matching |
| Tortuosity exponential coefficient | 0.302 | Ghanbarian et al. [49], Chen et al. [48], and experimental data matching |
| Tortuosity exponential coefficient | 0.35 | Ghanbarian et al. [49], Chen et al. [48], and experimental data matching |
| Tortuosity exponential coefficient | 0.45 | Ghanbarian et al. [49], Chen et al. [48], and experimental data matching |
| Shale bulk Young’s modulus | Pa | Sone and Zoback [68] and experimental data matching |
| Shale bulk Young’s modulus | Pa | Sone and Zoback [68] and experimental data matching |
| Shale bulk Young’s modulus | Pa | Sone and Zoback [68] and experimental data matching |
| Shale bulk Poisson’s ratio | 0.35 | Sone and Zoback [68] and experimental data matching |
| Shale bulk Poisson’s ratio | 0.3 | Sone and Zoback [68] and experimental data matching |
| Shale bulk Poisson’s ratio | 0.32 | Sone and Zoback [68] and experimental data matching |
| Flow channel Young’s modulus | Pa | Converted from the shale fracture compressibility of Tan et al. [69] and experimental data matching |
| Flow channel Young’s modulus | Pa | Converted from the shale fracture compressibility of Tan et al. [69] and experimental data matching |
| Flow channel Young’s modulus | Pa | Converted from the shale fracture compressibility of Tan et al. [69] and experimental data matching |
| Flow channel Poisson’s ratio | 0.35 | Sone and Zoback [68] and experimental data matching |
| Flow channel Poisson’s ratio | 0.3 | Sone and Zoback [68] and experimental data matching |
| Flow channel Poisson’s ratio | 0.32 | Sone and Zoback [68] and experimental data matching |
| Shale matrix bulk modulus | Pa | Converted from the Young’s modulus of Sone and Zoback [68] and experimental data matching |
| Matrix grain bulk modulus | Pa | Converted from the Young’s modulus of Sone and Zoback [68] and experimental data matching |
| Characteristic time coefficient | Pa/s | Zeng et al. [32] and experimental data matching |
| Equivalent matrix diffusivity | m2/s | Zhang et al. [70] and experimental data matching |
| Bulk swelling strain constant | 0.025 | Peng et al. [61] and experimental data matching |
| Bulk swelling strain constant | 0.028 | Peng et al. [61] and experimental data matching |
| Bulk swelling strain constant | 0.038 | Peng et al. [61] and experimental data matching |
| Bulk Langmuir pressure | Pa | Wang et al. [23] and experimental data matching |
| Bulk Langmuir pressure | Pa | Wang et al. [23] and experimental data matching |
| Bulk Langmuir pressure | Pa | Wang et al. [23] and experimental data matching |
| Matrix swelling strain constant | 0.01 | Liu and Rutqvist [71] and experimental data matching |
| Matrix swelling strain constant | 0.015 | Liu and Rutqvist [71] and experimental data matching |
| Matrix swelling strain constant | 0.035 | Liu and Rutqvist [71] and experimental data matching |
| Matrix Langmuir pressure | Pa | Peng et al. [34] and experimental data matching |
| Matrix Langmuir pressure | Pa | Peng et al. [34] and experimental data matching |
| Matrix Langmuir pressure | Pa | Peng et al. [34] and experimental data matching |
| Temperature | K | Ghanizadeh [66] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Li, Z.; Zeng, J.; Chen, B.; Li, J.; Jia, H.; Wang, W.; Zhang, J.; Wang, Y.; Zhao, Z. Modeling Anisotropic Permeability of Coal and Shale with Gas Rarefaction Effects, Matrix–Fracture Interaction, and Adsorption Hysteresis. Processes 2025, 13, 3304. https://doi.org/10.3390/pr13103304
Wang L, Li Z, Zeng J, Chen B, Li J, Jia H, Wang W, Zhang J, Wang Y, Zhao Z. Modeling Anisotropic Permeability of Coal and Shale with Gas Rarefaction Effects, Matrix–Fracture Interaction, and Adsorption Hysteresis. Processes. 2025; 13(10):3304. https://doi.org/10.3390/pr13103304
Chicago/Turabian StyleWang, Lilong, Zongyuan Li, Jie Zeng, Biwu Chen, Jiafeng Li, Huimin Jia, Wenhou Wang, Jinwen Zhang, Yiqun Wang, and Zhihong Zhao. 2025. "Modeling Anisotropic Permeability of Coal and Shale with Gas Rarefaction Effects, Matrix–Fracture Interaction, and Adsorption Hysteresis" Processes 13, no. 10: 3304. https://doi.org/10.3390/pr13103304
APA StyleWang, L., Li, Z., Zeng, J., Chen, B., Li, J., Jia, H., Wang, W., Zhang, J., Wang, Y., & Zhao, Z. (2025). Modeling Anisotropic Permeability of Coal and Shale with Gas Rarefaction Effects, Matrix–Fracture Interaction, and Adsorption Hysteresis. Processes, 13(10), 3304. https://doi.org/10.3390/pr13103304







