Hybrid Supervised–Unsupervised Fusion Clustering for Intelligent Classification of Horizontal Gas Wells Leveraging Integrated Dynamic–Static Parameters
Abstract
1. Introduction
| Authors | Classification Methods | Static Parameters | Dynamic Parameters | Identification Method |
|---|---|---|---|---|
| Jia et al. [5] | Static | Energy storage coefficient, formation coefficient | - | Arthogonal matrix-based approach |
| Li et al. [6] | Dynamic | - | Gas production per unit casing pressure drop, casing pressure drop rate, open flow rate | Cluster analysis |
| Dong et al. [7] | Dynamic | - | Average daily gas and liquid production, cumulative water–gas ratio | Threshold-based method |
| Zhu et al. [8] | Dynamic | - | Remaining pressure, gas production, supplementary gas volume after well shut-in, water production, standard deviation of the water–gas ratio | Linear Discriminant Analysis |
| Yuan et al. [13] | Static and dynamic | Dynamic reserves, water saturation | Current gas production, cumulative gas production, cumulative water production, gas production per unit casing pressure drop | Gray relational analysis |
| Chi et al. [9] | Static and dynamic | Energy storage coefficient, skin factor, permeability, dynamic reserves, formation pressure | Water–gas ratio, open flow rate | Gray relational analysis |
| Shang et al. [1] | Static and dynamic | Effective thickness, porosity, matrix permeability, gas saturation, original formation pressure | Open flow rate, production allocation, tubing pressure before production, casing pressure before production | XGBoost algorithm |
| Zhao et al. [10] | Static and dynamic | Effective porosity, gas relative density, casing depth, original formation temperature, initial gas saturation, skin factor, formation water salinity, permeability, perforation thickness, initial formation pressure | Effective fracture half-length, total fracturing sand volume, fracturing fluid flowback rate, open flow rate | CNN algorithm |
| Dong et al. [14] | Static and dynamic | Number of combined sand bodies, effective sand body thickness, porosity, permeability, gas saturation | Cumulative production contribution rate | Entropy weight—ideal point method |
2. Materials and Methods
2.1. Description of the Study Area
2.2. Static Parameter Classification Methods
2.3. Dynamic Parameter Classification Methods
2.3.1. Liquid Production Intensity
2.3.2. Liquid Drainage Capacity
2.3.3. Liquid Carrying Efficiency
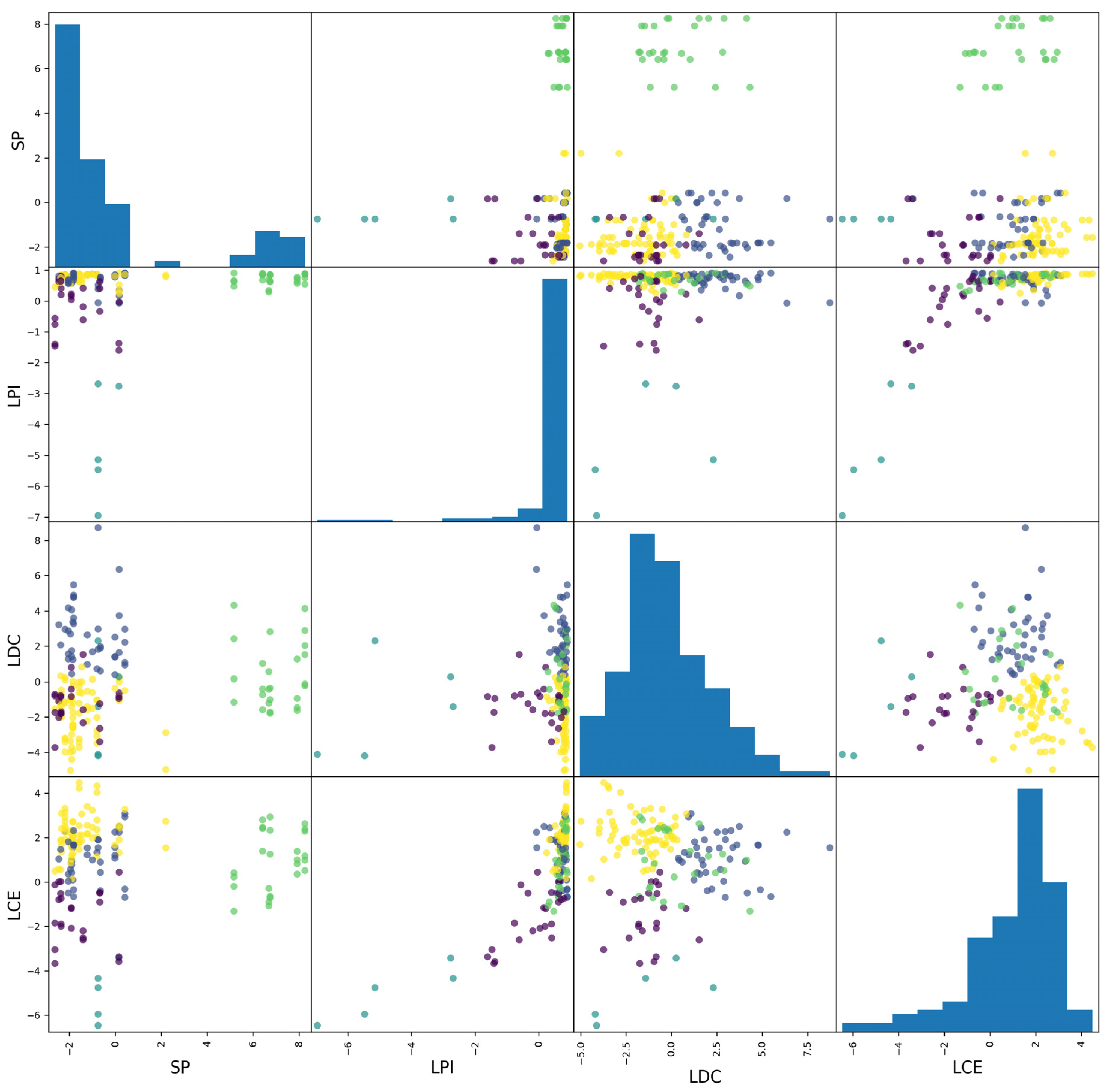
2.4. Comparative Analysis of Static and Dynamic Classification Approaches Based on LDA
2.4.1. LDA-Based Dimensionality Reduction in Indicators
2.4.2. Comparison of Static and Dynamic Classification
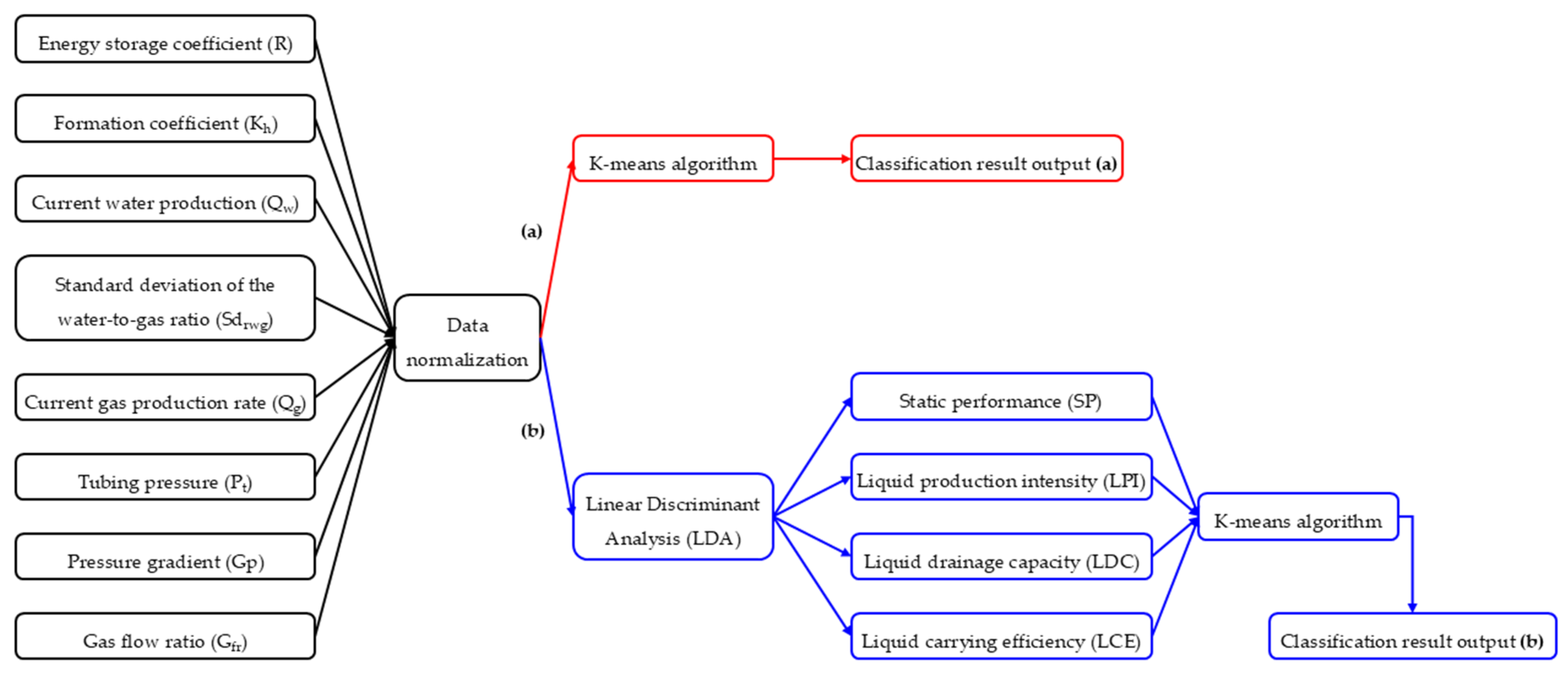
3. Hybrid Supervised–Unsupervised Fusion Clustering Method Based on Integrated Dynamic and Static Parameters
3.1. K-Means Algorithm
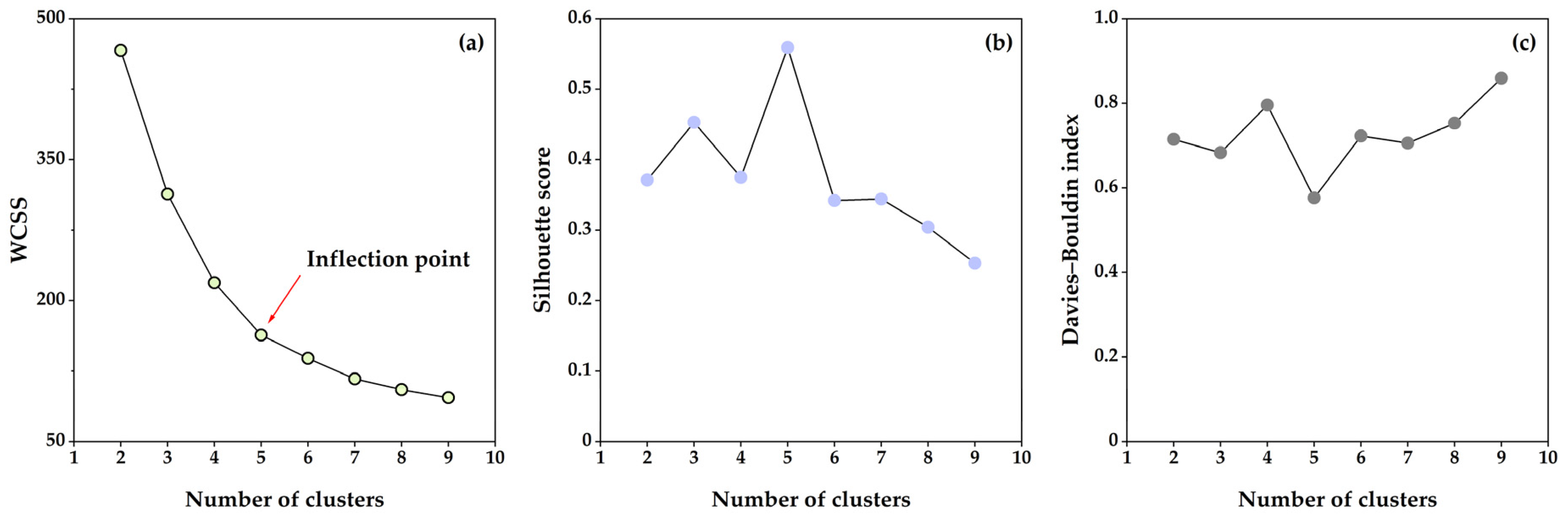
3.2. Fusion Clustering Method Integrating LDA and K-Means Algorithm
4. Results and Discussions
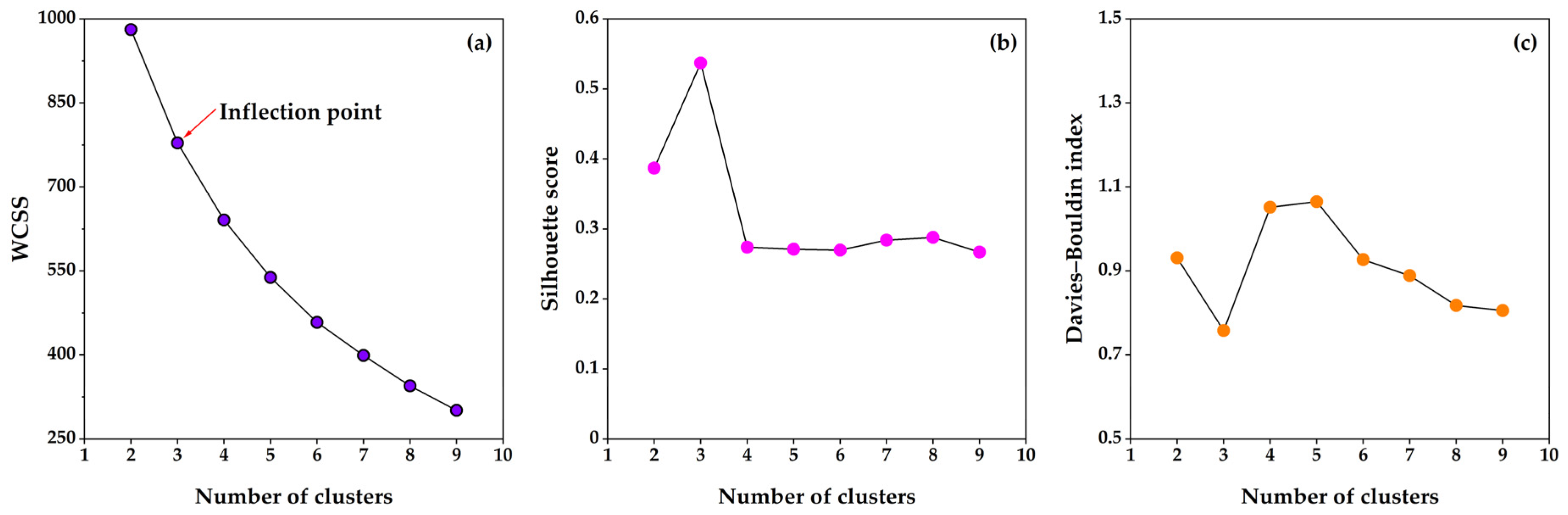
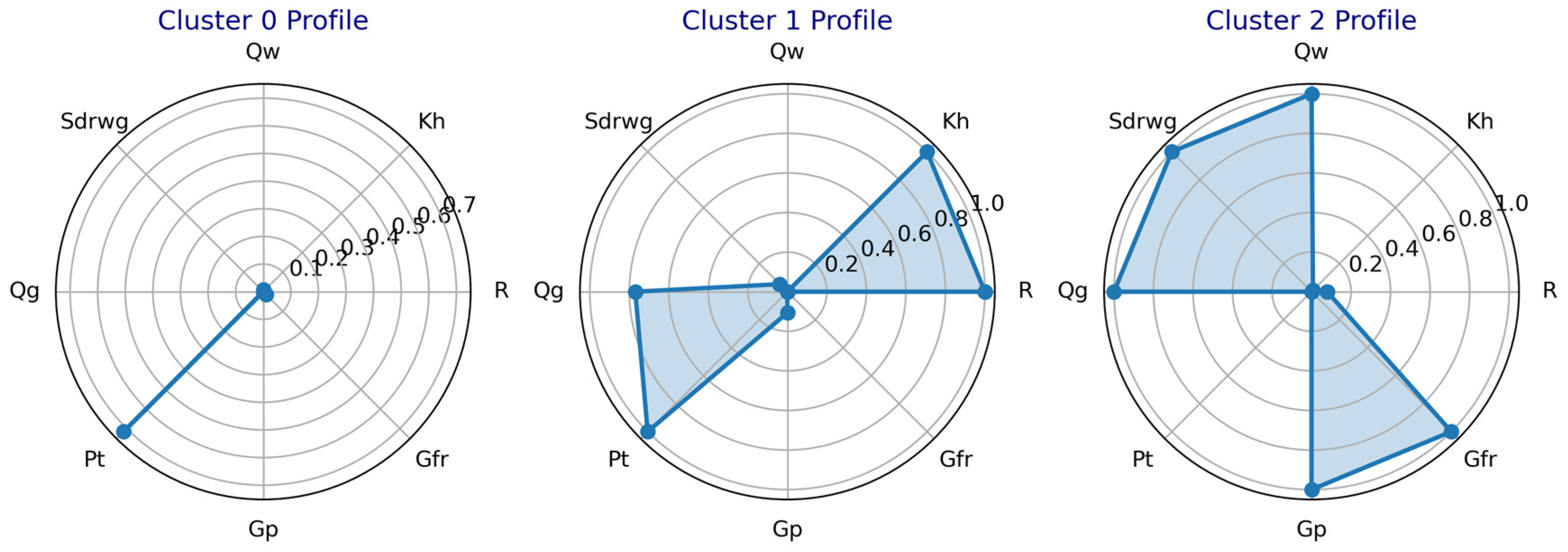
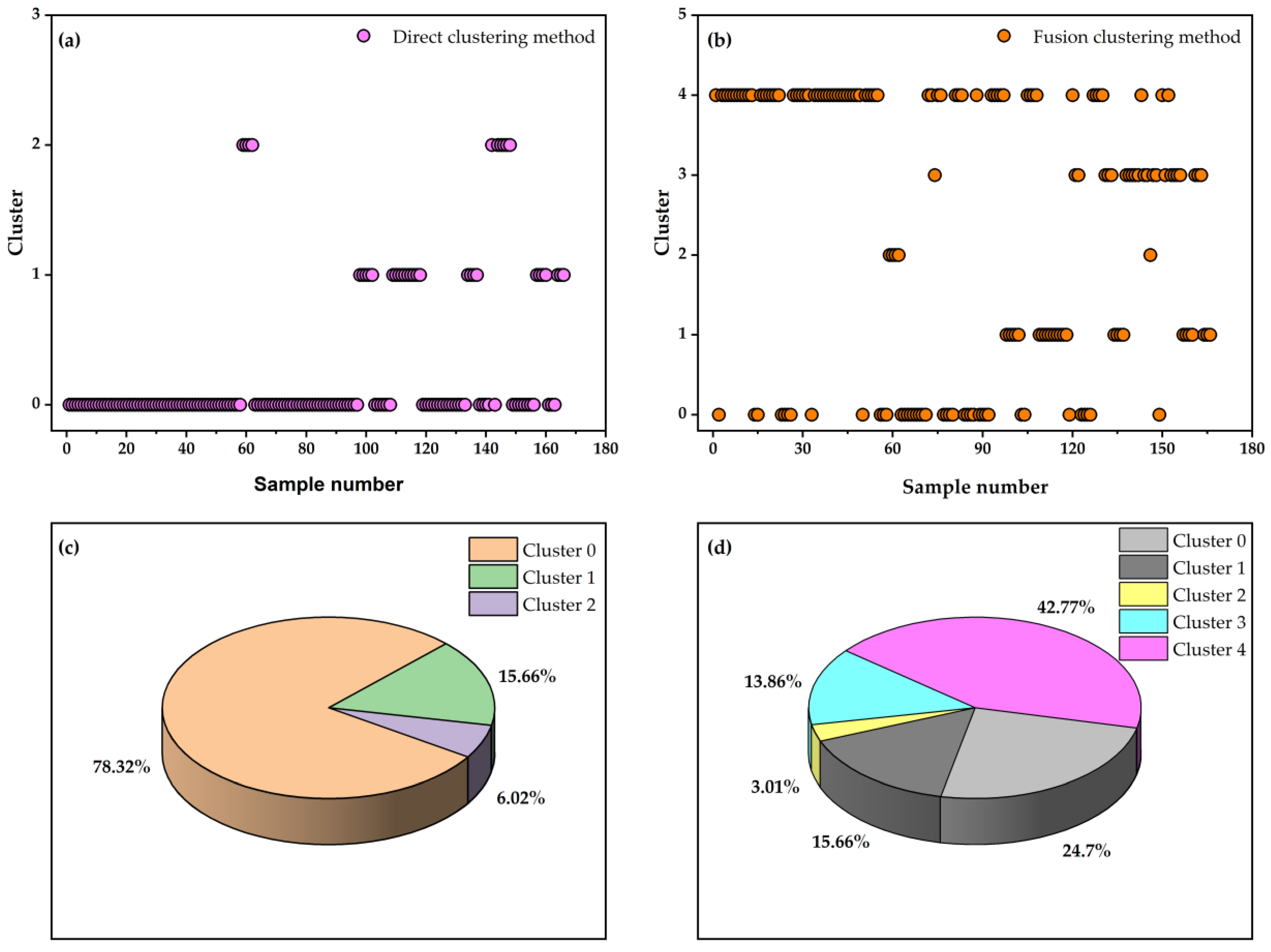
4.1. Classification of Horizontal Gas Wells via Direct K-Means Clustering
- (1)
- Cluster 0: The Pt index value is moderately high (approximately 0.7), whereas the values of other indicators are relatively low (close to 0). This suggests that the current tubing pressure of this gas well type is acceptable, but the overall production capacity is relatively low.
- (2)
- Cluster 1: The R, Kh, Pt, and Qg indices exhibit high values (approaching 1), while other indicators remain low. This type of gas well demonstrates favorable static reservoir performance, characterized by high tubing pressure and gas production capacity. Additionally, it possesses the ability to continuously carry liquid naturally, indicating no requirement for additional drainage or production enhancement measures.
- (3)
- Cluster 2: The Qg, Qw, Sdrwg, Gp, and Gfr indices are significantly elevated (approaching 1), with other indicators at low levels. This gas well type exhibits high liquid production intensity and presents a substantial demand for effective liquid drainage strategies.
4.2. LDA and K-Means Fusion Clustering
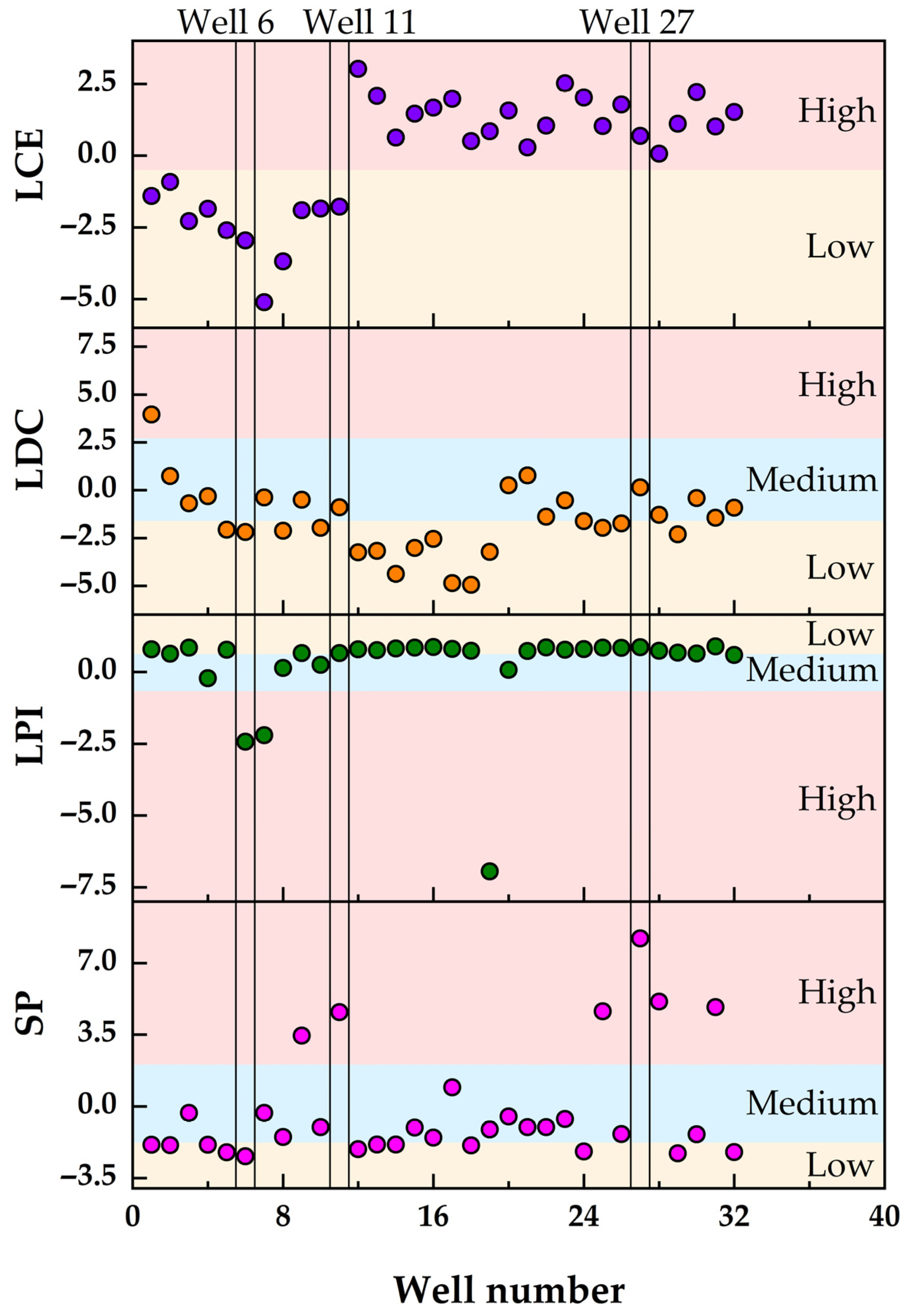
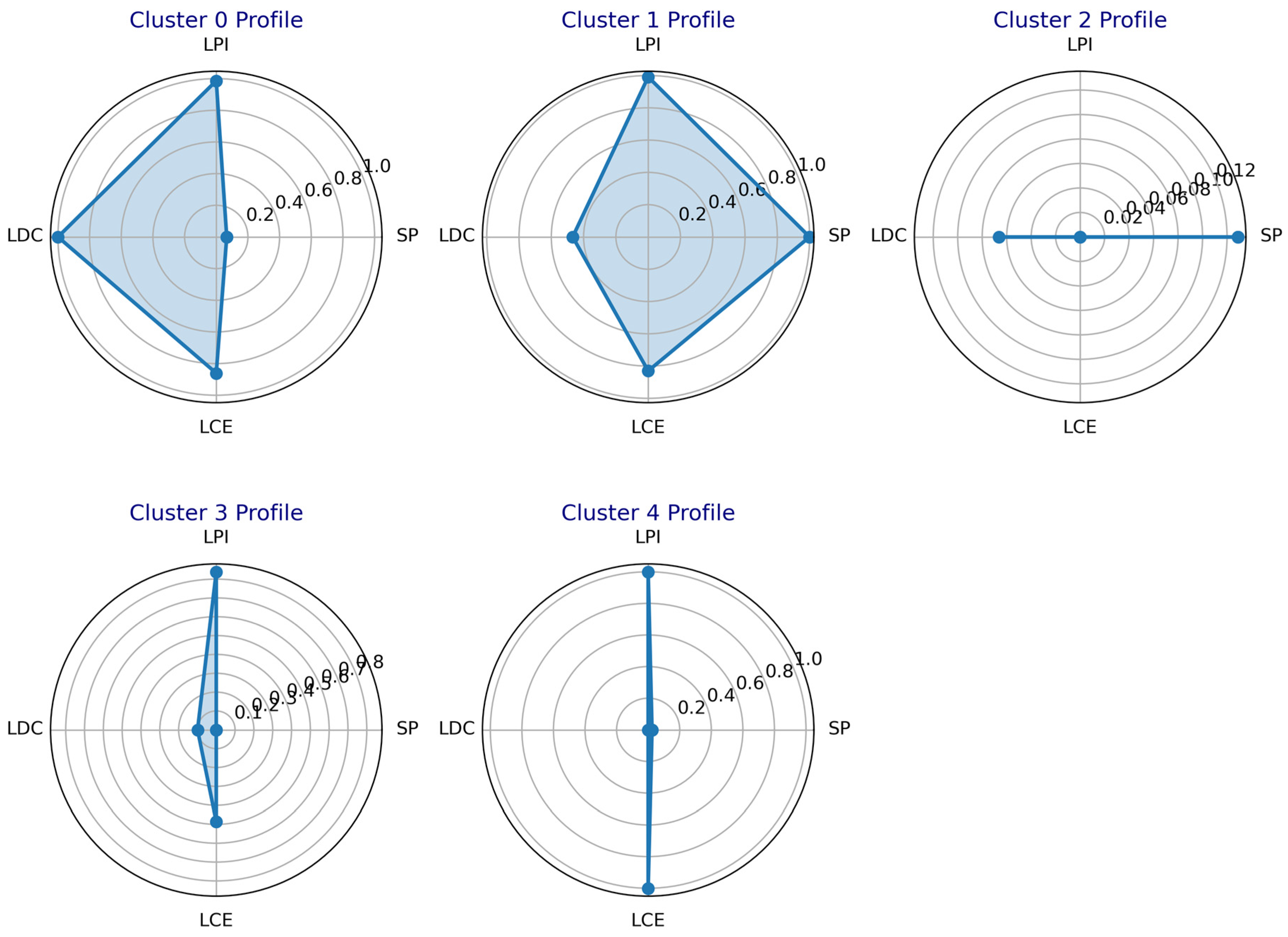
- (1)
- Cluster 0: This cluster exhibits high values for LPI, LDC, and LCE indices (close to 1), while the SP index remains low (close to 0). These characteristics indicate poor static reservoir performance and low liquid production intensity. However, both liquid drainage capacity and liquid carrying efficiency are relatively high. The well demonstrates a moderate capacity for production allocation adjustment, suggesting that optimization of the production allocation strategy is recommended.
- (2)
- Cluster 1: The SP, LPI, and LCE indices are high (close to 1), while the LDC index is at a moderate level. This cluster represents gas wells with favorable static reservoir performance, low liquid production intensity, and high liquid carrying efficiency. The wells exhibit medium liquid drainage capacity, strong stable production capability, and the ability to continuously carry liquid without requiring additional drainage or production enhancement measures.
- (3)
- Cluster 2: All indicator values are relatively low. These wells are characterized by high liquid production intensity, poor static reservoir performance, and limited liquid drainage capacity. They exhibit low gas production rates and face challenges in maintaining continuous liquid carrying, resulting in intermittent production behavior. Therefore, the implementation of effective artificial drainage gas recovery measures is strongly recommended.
- (4)
- Cluster 3: The LPI index is high, the LCE index is moderate, and the remaining indices are low. These wells exhibit low liquid production intensity and moderate liquid carrying efficiency, but poor static reservoir performance and limited liquid drainage capacity. The gas production rate is low, and it is recommended to apply the foam drainage gas recovery technique to enhance performance.
- (5)
- Cluster 4: This cluster is characterized by high LPI and LCE indices, with all other indices at low levels. The wells exhibit low liquid production intensity and high liquid carrying efficiency, but extremely poor static reservoir performance and inadequate liquid drainage capacity. Given the low gas production rate, it is recommended to implement optimized tubing string or plunger gas lift drainage gas recovery technologies to improve the liquid carrying efficiency of these wells.
4.3. Comparative Analysis of Two Clustering Approaches
5. Conclusions
- (1)
- Horizontal gas wells were classified based on four dimensions: static performance, liquid production intensity, liquid drainage capacity, and liquid carrying efficiency. The results indicate a low degree of alignment between dynamic and static classification outcomes, suggesting that single-dimensional classification methods—whether dynamic or static—are insufficient to comprehensively characterize the actual production conditions of gas wells.
- (2)
- By integrating dynamic and static parameters and applying a strategy combining LDA-based dimensionality reduction with K-means clustering, horizontal gas wells were categorized into five distinct types. In comparison to direct clustering, the proposed method yields more refined classification results with enhanced practical relevance for production guidance.
- (3)
- Significant differences in production characteristics were observed among the five well types. Accordingly, targeted production optimization strategies were proposed, including production allocation optimization, continuous production (without the need for drainage), intensified drainage measures, foam-assisted drainage, and selection of optimal tubing or plunger lift systems.
- (4)
- The methodologies and conclusions presented in this study offer theoretical support and technical insights that can be applied to the classification of horizontal gas wells in other unconventional reservoirs, such as shale gas formations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shang, Y.; Zhai, S.; Lin, X.; Li, X.; Li, H.; Feng, Q. Dynamic and static integrated classification model for low permeability tight gas wells based on XGBoost algorithm. Spec. Oil Gas Reserv. 2023, 30, 135–143. [Google Scholar] [CrossRef]
- Wei, Y.; Jia, A.; He, D.; Liu, Y.; Ji, G.; Cui, B.; Ren, L. Classification and evaluation of horizontal well performance in Sulige tight gas reservoirs, Ordos Basin. Nat. Gas Ind. 2013, 33, 47–51. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Kou, S.; Zhang, X.; Liu, R.; Wang, J. Study on main controlling factors of water production in tight gas wells. Xinjiang Oil Gas 2022, 18, 20–25. [Google Scholar] [CrossRef]
- Chen, R. Well selection conditions of velocity string fluid drainage and gas production technology. Xinjiang Oil Gas 2022, 18, 67–73. [Google Scholar] [CrossRef]
- Jia, Y.; Shi, J.; Li, X.; Chen, H.; Fang, J.; Jiao, T.; Zhang, H.; Wang, Y. Classification and evaluation methods for low-permeability tight gas wells in the Zizhou gas field of Changqing. Geol. Explor. 2021, 57, 647–655. [Google Scholar] [CrossRef]
- Li, T.; Huang, X. Classification of horizontal wells based on dynamic data and its application in ultra-low permeability gas reservoirs. Chem. Technol. Fuels Oils 2017, 53, 123–134. [Google Scholar] [CrossRef]
- Dong, J.; Yue, X.; Ding, J. Evaluation model of liquid production and its application in tight water-bearing gas reservoir. Spec. Oil Gas Reserv. 2018, 25, 90–94. [Google Scholar] [CrossRef]
- Zhu, Z.; Han, G.; Liang, X.; Chang, S.; Yang, B.; Yang, D. Rapid Classification and Diagnosis of Gas Wells Driven by Production Data. Processes 2024, 12, 1254. [Google Scholar] [CrossRef]
- Chi, M.; Ma, W.; Guo, L.; Xin, X.; Liao, R.; Gao, H.; Du, J.; Wang, X. An effective classification method for low-pressure and low production gas wells in XJ oilfield. J. Kunming Univ. Sci. Technol. (Nat. Sci.) 2023, 48, 55–63. [Google Scholar] [CrossRef]
- Zhao, C.; Jia, Y.; Qu, Y.; Zheng, W.; Hou, S.; Wang, B. Forecasting Gas Well Classification Based on a Two-Dimensional Convolutional Neural Network Deep Learning Model. Processes 2024, 12, 878. [Google Scholar] [CrossRef]
- Tian, L.; Zhu, Z.; Wang, L.; Yu, J.; Wang, Y. A rock drillability characterization method based on big data and unsupervised clustering algorithm. Xinjiang Oil Gas 2024, 20, 29–36. [Google Scholar] [CrossRef]
- Song, X.; Wang, Y.; Yang, Y.; Liu, M.; Zhu, Z. Intelligent diagnosis and analysis of stuck pipe based on supervised and unsupervised algorithms. Xinjiang Oil Gas 2025, 21, 24–34. [Google Scholar] [CrossRef]
- Yuan, J.; Xia, Y.; Li, J.; Ai, Q.; Xie, S.; Wu, Y. Classification of low pressure water producing gas wells by grey relational analysis. Petrochem. Ind. Appl. 2018, 37, 73–75. [Google Scholar] [CrossRef]
- Dong, F.; Sun, Z.; Gao, Z.; Sun, Z.; Huang, H.; Chen, Y.; Lu, X. Optimization of low-production and low-efficiency gas wells based on multi-method fusion. Geol. Explor. 2023, 59, 657–663. [Google Scholar] [CrossRef]
- Cai, J.; Peng, X.; Yang, C.; Li, L.; Liu, W.; Liu, X.; Xu, R.; Wang, B.; Li, Y.; Jiang, J. Research status and prospect of methods for determining the lower limit of reservoir physical properties in carbonate gas reservoirs. Nat. Gas Geosci. 2024, 35, 104–118. [Google Scholar]
- Sun, W.; Lou, Y.; Kamgue Lenwoue, A.R.; Li, Z.; Zhu, L.; Wu, H. Classification and Evaluation of Volcanic Rock Reservoirs Based on the Constraints of Energy Storage Coefficient. Front. Earth Sci. 2022, 10, 914383. [Google Scholar] [CrossRef]
- Zhang, H.; Pu, J.; Zhang, L.; Deng, H.; Yu, J.; Xie, Y.; Tong, X.; Man, X.; Liu, Z. Gas Production Prediction Model of Volcanic Reservoir Based on Data-Driven Method. Energies 2024, 17, 5461. [Google Scholar] [CrossRef]
- Albiter, A.; Vargas, J.A.; Contreras, A.; Cruz-Castro, L. A case study on the application of a mechanical system in a Mexican gas well with liquid loading issues. Flow Meas. Instrum. 2025, 104, 102887. [Google Scholar] [CrossRef]
- Mukherjee, H.; Brill, J.P. Liquid holdup correlations for inclined two-phase flow. J. Pet. Technol. 1983, 35, 1003–1008. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, C.; Zhou, Z.; He, Z.; Chen, M. Comprehensive optimal selection method of drainage gas recovery technology for shale gas horizontal wells. Drill. Prod. Technol. 2022, 45, 154–159. [Google Scholar] [CrossRef]
- Beggs, D.H.; Brill, J.P. A study of two-phase flow in inclined pipes. J. Pet. Technol. 1973, 25, 607–617. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, B.; Yang, J.; Zhou, J.; Xu, Y. Linear discriminant analysis. Nat. Rev. Methods Primers 2024, 4, 70. [Google Scholar] [CrossRef]
- Sinaga, K.P.; Yang, M. Unsupervised K-means clustering algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Mollajan, A.; Akbarzadeh, S.; Kadkhodaie, A. Rock type based-estimation of pore throat size distribution in carbonate reservoirs using integrated analysis of well logs and seismic attributes. Carbonates Evaporites 2024, 39, 46. [Google Scholar] [CrossRef]
- Abbas, M.A.; Al-Mudhafar, W.J.; Anees, A.; Wood, D.A. Integrating petrophysical data into efficient iterative cluster analysis for electrofacies identification in clastic reservoirs. Energy Geosci. 2024, 5, 100341. [Google Scholar] [CrossRef]
- Kazemi, H.; Yazdjerdi, K.; Asadi, A.; Mozafari, M.R. Comparison of clustering methods and conventional approaches for geological fracture analysis: A case study in northern Shiraz, Iran. An. Acad. Bras. Ciências 2025, 97, e20250043. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, P.; Wang, Y.; Feng, G.; Yang, C.; Wang, Q. From clustering to federated learning: A collaborative approach to optimizing data-driven models for the production monitoring of unconventional natural gas wells. Gas Sci. Eng. 2025, 137, 205580. [Google Scholar] [CrossRef]
- Wang, W.; Lei, Y.; Liao, R.; Shi, H.; Zhang, Z. Mechanism-Data Coupling Driven Prediction Models of Liquid Leakage for Plunger Lift in Inclined Tube. Energy Sci. Eng. 2025, 13, 4825–4838. [Google Scholar] [CrossRef]
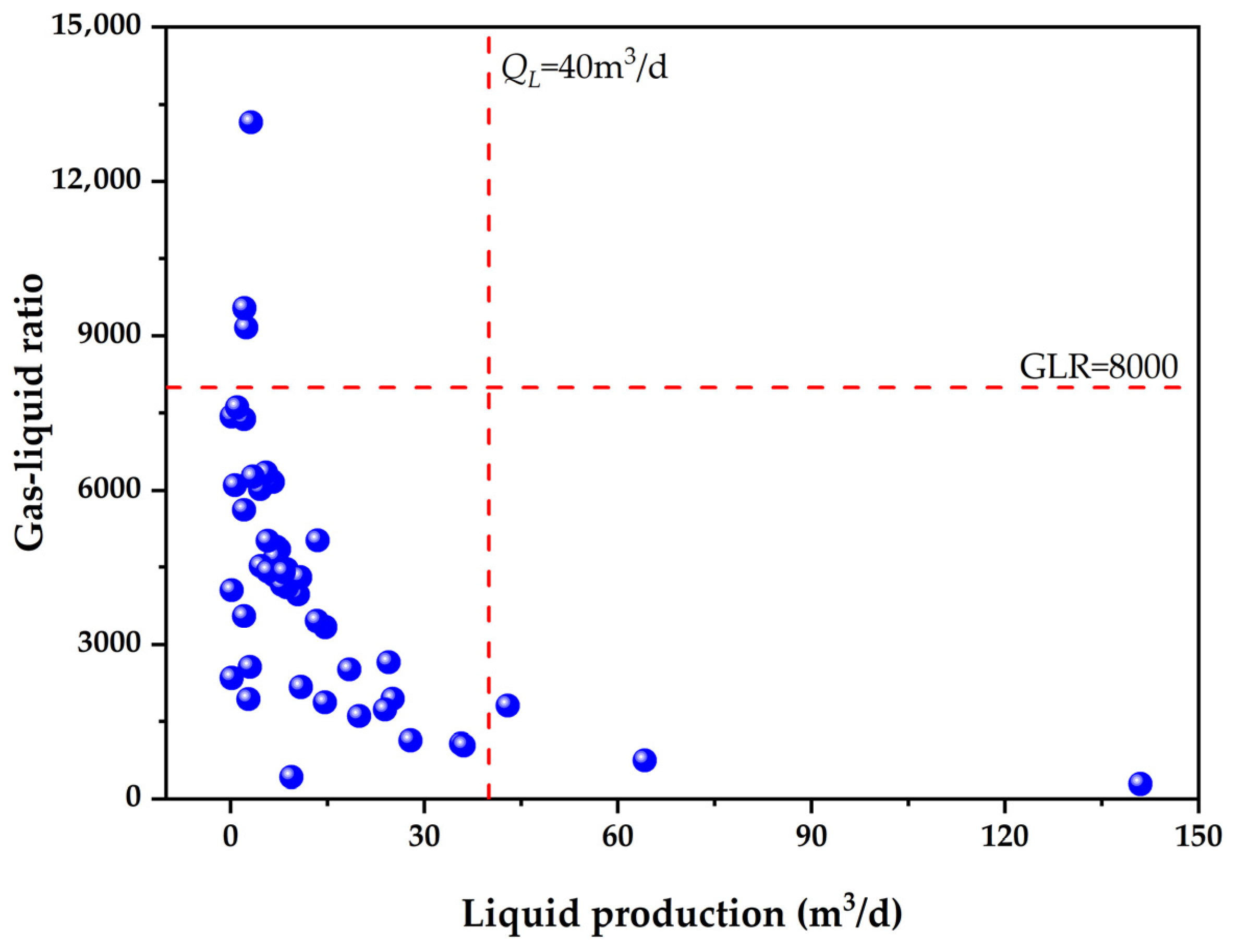

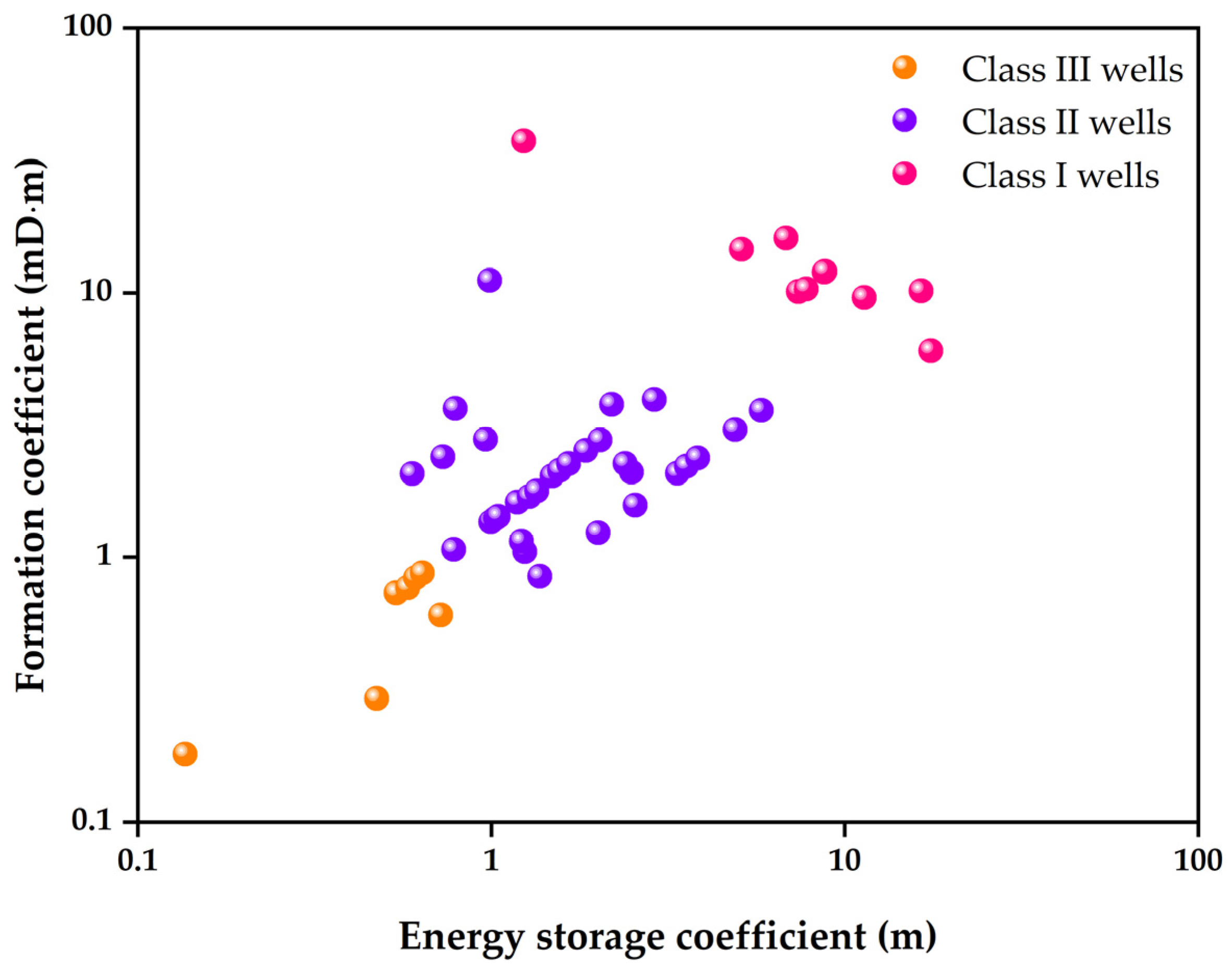
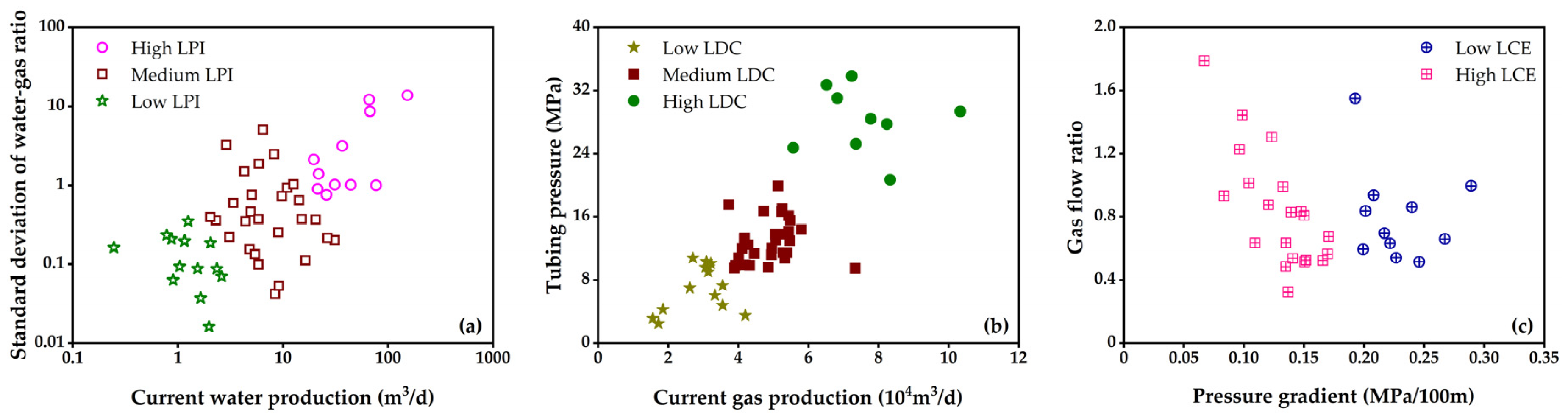

| Variables | Unit | Range | Mean | Variance |
|---|---|---|---|---|
| R | m | 0.473~11.345 | 2.464 | 6.523 |
| Kh | mD∙m | 0.293~37.484 | 4.275 | 53.603 |
| Qw | m3/d | 0.080~196.533 | 11.079 | 661.050 |
| Sdrwg | Dimensionless | 0.001~17.559 | 1.080 | 6.516 |
| Qg | 104 m3/d | 1.341~21.297 | 5.571 | 7.847 |
| Pt | MPa | 1.673~27.067 | 12.464 | 31.067 |
| Gp | MPa/100 m | 0034~0.316 | 0.144 | 0.003 |
| Gfr | Dimensionless | 0.323~6.230 | 1.114 | 0.925 |
| Methods | Optimal Number of Clusters | WCSS | Silhouette Score | Davies–Bouldin Index |
|---|---|---|---|---|
| Direct K-means | 3 | 778.376 | 0.537 | 0.758 |
| Hybrid clustering | 5 | 163.382 | 0.559 | 0.576 |
| Models | Excluded Feature | Optimal Number of Clusters | WCSS | Silhouette Score | Davies–Bouldin Index |
|---|---|---|---|---|---|
| Full model | None | 5 | 163.382 | 0.559 | 0.576 |
| Variant model 1 | LPI | 4 | 147.283 | 0.433 | 0.765 |
| Variant model 2 | LDC | 4 | 151.843 | 0.481 | 0.597 |
| Variant model 3 | LCE | 3 | 219.991 | 0.519 | 0.581 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Wang, J.; Liu, T.; Lai, S.; Wang, B.; Guo, L.; Zhang, Z.; Wang, G.; Liao, R. Hybrid Supervised–Unsupervised Fusion Clustering for Intelligent Classification of Horizontal Gas Wells Leveraging Integrated Dynamic–Static Parameters. Processes 2025, 13, 3278. https://doi.org/10.3390/pr13103278
Gao H, Wang J, Liu T, Lai S, Wang B, Guo L, Zhang Z, Wang G, Liao R. Hybrid Supervised–Unsupervised Fusion Clustering for Intelligent Classification of Horizontal Gas Wells Leveraging Integrated Dynamic–Static Parameters. Processes. 2025; 13(10):3278. https://doi.org/10.3390/pr13103278
Chicago/Turabian StyleGao, Han, Jia Wang, Tao Liu, Siyu Lai, Bo Wang, Ling Guo, Zhao Zhang, Guowei Wang, and Ruiquan Liao. 2025. "Hybrid Supervised–Unsupervised Fusion Clustering for Intelligent Classification of Horizontal Gas Wells Leveraging Integrated Dynamic–Static Parameters" Processes 13, no. 10: 3278. https://doi.org/10.3390/pr13103278
APA StyleGao, H., Wang, J., Liu, T., Lai, S., Wang, B., Guo, L., Zhang, Z., Wang, G., & Liao, R. (2025). Hybrid Supervised–Unsupervised Fusion Clustering for Intelligent Classification of Horizontal Gas Wells Leveraging Integrated Dynamic–Static Parameters. Processes, 13(10), 3278. https://doi.org/10.3390/pr13103278






