Interfacial Electrostatics of Low Salinity-Enhanced Oil Recovery: A Review of Theoretical Foundations, Applications and Correlation to Experimental Observations

Abstract

Low salinity-enhanced oil recovery has gained universal recognition regarding its ability to provide an environmentally friendly and low-cost method of improved oil recovery. Research findings so far based on experimentation and simulation suggest that the success of the scheme stems considerably from double layer expansion and wettability enhancement, among others. However, while the double layer expansion and wettability effects have robust theoretical foundations that can be sought within the Mean Field Poisson–Boltzmann theory, there is hardly any published research work that has tackled this task. In this paper, we fill the knowledge gap by using the MFPB theory to calculate electric double layer (EDL) parameters as functions of salinity and to successfully correlate theoretical findings to literature-based experimental observations. Additionally, we have, for the first time integrated the concept of free energy of formation of the EDL in LSWFOR research, given its intimate relationship to EDL parameters. The theoretical findings are, therefore, indicators that theoretical foundations also provide reliable and alternative means of understanding and predicting the success of LSWFOR.

1. Introduction

Petroleum reservoir rocks are defined as systems composed of an aggregate of minerals, in the geological domain [1,2], with some minerals having ionizable groups. Such ionizable groups on rock surfaces are functional groups with the capacity to gain or lose protons, impacting the surface acidity or alkalinity, which influences the rock’s ability to demonstrate acidic or basic properties [3,4]. Crude oil systems also possess heteroatomic molecules, notably fused aromatic rings, such as asphaltenes [5], which contain basic and acidic ionizable groups [4,6]. Therefore, in a typical hydrocarbon system defined by aqueous fluid–crude oil and rock–aqueous fluid interfaces, the evolution of the electric double layer (EDL) [4,7] and its associated physicochemical processes is eminent [8,9].

Experience from hydrocarbon field development shows that out of the oil or gas originally in place, only about one-third is producible, using in situ natural primary energy drive associated with rock and fluid expansion [10]. To augment production, additional energy drive is required in field development schemes, which can be in the form of water flooding (Dyah et al.) [11] and enhance oil recovery [12,13]. At the fluid–fluid and fluid–solid interfaces, the existence of separate EDLs implies imminent EDL interactions. In the literature, the role the EDL interactions’ contribution to water flood oil recovery through wettability enhancement has been extensively discussed [14,15,16,17,18]. The universal consensus in the literature is that EDL contribution to disjoining pressure forces [19,20] is strongest where the salinity of injected water is lower.

In recent times, Low Salinity Enhanced Oil Recovery (LSWF) schemes have gained global recognition due to several advantages, famous among them being multicomponent Ionic Exchange, pH effect, fines migration, and electric double layer expansion [21]. In this regard, the thicknesses of the double layers depend on the ion concentration in the surrounding water such that for high-salinity water containing more ions, the EDL is more compact, expanding under low-salinity water injection. Several authors have demonstrated experimentally the benefits of LSWF by comparing additional oil recoveries to those of high-salinity water injection recoveries [21,22,23,24,25,26,27]. For instance, core flooding experiments were conducted using Berea sandstone cores with salinity-dependent densities varying from 0.5 to 55 kg/L [28]. The efficiency of oil recovery by seawater and its diluted samples was also evaluated through core-flooding experiments performed using silica sand packs [29]. An experimental and numerical study of LSWF was conducted to verify efficiency. An improved Amott wettability Index approach was used to verify the efficiency of LSWF [30,31]. In all cases, EDL repulsion was a significant contributor to oil recovery. For instance, Xie et al. [32] have integrated atomic force microscopy and disjoining pressure force calculations together with surface complexation modeling to demonstrate that EDL repulsion is at least one of the mechanisms for the LSWF effect, which can be interpreted using disjoining pressure isotherm. In all experiments conducted so far, the universal consensus is that as salinity falls, cumulative oil recovery increases. In the crude oil–water rock system, electrostatic phenomena are among fundamental physiochemical processes that govern oil recovery [33]. In the thermodynamic literature, the electrostatics of interface is well understood [34,35,36,37]. However, there is no literature that has attempted to theoretically and electrostatically reveal the universally acknowledged experimental trend in LSWF.

In the opinion of the present authors, a quantitative electrostatic assessment of the role of EDL repulsion in the LSWF process is imperative, given its immense effect. The zeta potential is a measure of the electrical potential at the shear plane of the EDL [38], and it correlates with those at mineral–brine and oil–brine interfaces [33]. It controls the electrostatic forces acting between these interfaces, which have direct bearing on the EDL repulsion effect in LSWF. Several scholars have measured the zeta potential at the oil–brine and brine–oil interfaces to assess the contribution of EDL repulsion [39,40,41,42]. In this regard, Nasralla et al. (2014) [28] demonstrated experimentally that the expansion of the double layer is a dominant mechanism of oil recovery improvement by LSWF. On the other hand, electrostatic surface charge density existence in the relationship to the EDL structure is paramount to its repulsion contribution to LSWF success. Additionally, within the Mean Field Poisson–Boltzmann (MFPB) theory, there exists a direct relationship between zeta potential and surface charge density (Delgado et al.) [43]. Therefore, we contend that a theoretical assessment of the EDL contribution to LSWF can be carried out, using the theoretical foundations of MFPB theory, and this is the focus of the present paper.

In the literature, the accuracy of the MFPB theory in light of the LSWF success has universal recognition [44,45,46]. Fundamental to this success are the favorable EDL repulsion and thermodynamic free energy of formation of this double layer [47,48]. Thus, the effect of salinity on recovery trends as revealed experimentally must correlate with the effect of salinity on EDL repulsion and free energy. This paper will focus on revealing the electrostatic aspects of the salinity effect on EDL repulsion and its free energy of formation through a quantitative assessment, utilizing the analytical solution to the nonlinear Poisson–Boltzmann theory, which is applicable under low-salinity conditions. Accordingly, based on the constant potential approximation [49], it is possible to quantify the double layer interaction between two surfaces with different surface potentials. We use the theoretical relationship between potential and distance to calculate the zeta potential, assuming the distance to the shear [50], and to also calculate surface potential for zero distance [50] using the appropriate analytical solution to the MFPB equation. Considering the intimate relationship between the EDL repulsion and the free energy of its formation, which is thermodynamically significant [51], the electrostatic assessment of the success of LSWF was advanced by calculating this energy as a function of salinity. The novelty of this paper stems from three standpoints. First, we use the nonlinear MFPB theory, which best describes low-salinity conditions under which it is most accurate (Ruiz-Cabello et al.) [52], limiting ourselves to cylindrical geometry, which best describes the geometry of a petroleum reservoir pore throat, where reservoir fluids are found. Second, we reveal theoretically and electrostatically that experimentally established trends for crude oil recovery versus salinity in LSWF have direct correlations to those of salinity versus EDL repulsion and the thermodynamic free energy of formation. Third, experimental work on LSWF has extensively focused on the wettability/contact angle, and EDL expansion investigations, although the free energy of formation of the EDL is equally important. In this regard, the present theoretical research work fills the gap by integrating the concept of free energy of formation of the EDL in addition to its salinity-dependent calculations, correlating it to literature-based experimental observations.

2. Backgrounds

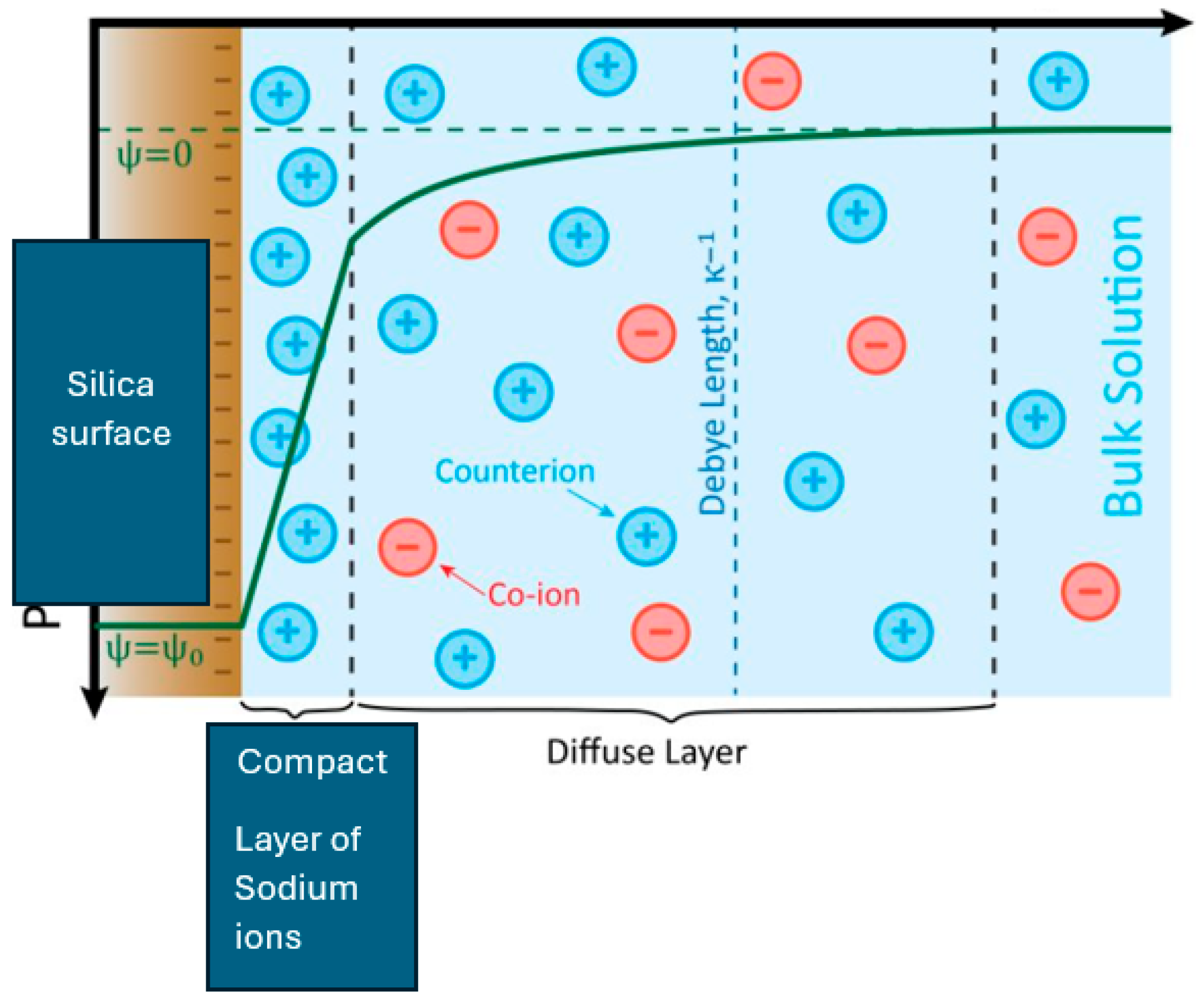
2.1. Ionizable Group and Surface Complexation Models at the Pore Wall–Low-Salinity Brine Interface

Above the point of zero charge pH, the surface of a pH-dependent ionizable surface group will develop a negative charge (Ezeuko et al.) [53]. We assume that the surface of reservoir pore throats is related to a sandstone with a surface chemistry that can be approximated by that of silica material [54] with a point of zero charge pH equal to 3 of [55]. Therefore, the principal ionizable surface group is silanol. Thus, at the pH of low-salinity brine (LSB), which is generally closer to neutral (Isfehani et al.) [56], the silanols will deprotonate in accordance with the following reaction, which is similar to that reported elsewhere [57]:

$$>SiOH\leftrightarrow >Si{O}^{-}+H^{+}$$

(1)

$$>SiOH+H^{+}\leftrightarrow >SiO{H}_2^{+}$$

The dissociation constants are given as in (Onizhuk et al., 2018) [58].

The equilibrium constant for the reaction is

$$K_b={\displaystyle \frac{\left[>SiOH\right]}{\left[>Si{O}^{-}\right]\left[H^{+}\right]}}$$

(2)

$$K_a={\displaystyle \frac{\left[>SiO{H}_2^{+}\right]}{\left[>SiOH\right]\left[H^{+}\right]}}$$

(3)

in which $K_b$ is the basic dissociation constant [M⁻¹], $\left[>SiOH\right]$ is the silanol surface concentration [molm⁻²], $\left[Si{O}^{-}\right]$ is the surface concentration of deprotonated silanol [molm⁻²], $\left[H^{+}\right]$ is hydrogen ion concentration [M], and $\left[>SiO{H}_2^{+}\right]$ is the surface concentration of protonated surface silanols [molm⁻²].

Assuming a predominantly sodium chloride brine, the dissociation reaction of sodium chloride is given as

$$NaCl\leftrightarrow >{Na}^{+}+{Cl}^{-}$$

(4)

Consequently, from Equation (1), a surface complexation of deprotonated negative surface sites of silanols will occur in accordance with the following reaction:

$$>Si{O}^{-}{+Na}^{+}\to >Si{O}^{-}{Na}^{+}$$

(5)

In Equation (4), the right-hand side corresponds to adsorbed sodium ions on the surface of pore walls, which will attract counter ions, leading to the formation of the diffuse layer, and hence the EDL and the bulk layer with the characteristic Debye length scale (see Figure 1).

In the following section, we will discuss the evolution of the EDL at the oil–low-salinity brine interface.

2.2. Ionizable Group and Surface Complexation Models at the Crude Oil–Low-Salinity Brine Interface

At the oil–water interface, the presence of acidic OH and basic NH groups (see Figure 2) of oil will cause deprotonation and protonation reactions, respectively, at a given pH of aqueous fluids. The reactions are given as follows:

Acidic group dissociation:

$$>OH\leftrightarrow >O^{-}+H^{+}$$

(6)

Basic group dissociation:

$$>NH+H^{+}\leftrightarrow >{NH}^{2+}$$

(7)

The equilibrium constants for the reactions described by Equations (5) and (6) read:

$$K_a={\displaystyle \frac{\left[>O^{-}\right]\left[H^{+}\right]}{\left[>OH\right]}}$$

(8)

$$K_b={\displaystyle \frac{\left[>{NH}^{2+}\right]}{\left[>NH\right]\left[H^{+}\right]}}$$

(9)

Equation (9) is possible because at lower pH values, the basic nitrogen groups are protonated [60].

Based on Equations (8) and (9), complexation of the oil–water interface will occur in accordance with the following reactions:

$$>O^{-}+{Na}^{+}\to >O^{-}{Na}^{+}$$

(10)

$$>{NH}^{2+}+{Cl}^{-}\to >{NH}^{2+}{Cl}^{-}$$

(11)

Following Equations (7) and (8), an EDL will evolve at the oil–water interface that can be represented by Figure 3.

Based on Figure 1 and Figure 3, the MFPB theory can be used to theoretically describe the electrostatics of the interfaces, which permits the calculation of the double layer repulsion for two surfaces with distinct surface or zeta potentials interacting across a low-salinity brine medium (LSB) with a definite thickness [62]. The following section will be devoted to the theoretical aspects of the problem.

3. Theory

3.1. Electrostatics at the Rock–Low-Salinity Brine Interface

Referring to Figure 1, we assume that the EDL is formed at the low-salinity water-pore surface and that the reservoir rock is a siliceous sandstone composed predominantly of silica [63]. We assume further that the reservoir rock is characterized by cylindrical pore throats (Yang et al.) [64] and that the ionizable surface group on the pore walls is predominantly silanol. Accordingly, under low-salinity conditions, where the pH is closer to neutral (Isfehani et al.) [56], the pore surface will be negatively charged, given that the point of zero charge pH of silica is 3 [55]. Consequently, considering the surface complexation model, [61], an EDL will evolve, where the distribution of ions in the diffuse layer will be governed by Boltzmann statistics, and the Poisson equation, which relates the mass redistribution potential to the displacement [65]. Thus, the Poisson–Boltzmann equation (PBE), which describes the potential distribution in the electric double layer for a cylindrical geometry can be given [66]:

$${\displaystyle \frac{d^2\psi }{{dr}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\psi }{dr}}=sinh\left(\psi \right)$$

(12)

The analytical solution to Equation (12) is given as (Shkel et al., 2002) [67]

$$y_0=2K_0\left(x{ϵ}^{-1}\right)+2\gamma -2ln\left({\beta }^{-1}S\left(\beta K_0\left(x{ϵ}^{-1}\right)\right)+\beta C\right)$$

(13)

Here, $y_0$ is the reduced potential defined as ${\displaystyle \frac{ez{\psi }_0}{k_{B}T}},$ $x={\displaystyle \frac{r}{a}}$, $ϵ$ is the ratio of the radius a, to Debye length $\lambda ={\left({\displaystyle \frac{\epsilon k_{B}T}{2e^2{n}_b}}\right)}^{0.5}$, and r is the radial distance.

Moreover, $n_b$ is the bulk number density of ions [m⁻³], $\beta$ and $C$ are integration constants.

The solution is subject to the following boundary (ref) conditions

$${\displaystyle \frac{1}{r}}{\displaystyle \frac{d\psi }{dr}}@r=a={\sigma }^{*}{a}^{-1}$$

(14)

$$r{\displaystyle \frac{d\psi }{dr}}@r=\infty =0$$

(15)

In Equation (12) through Equation (15), $r$ [m] is the radial distance from the center of the cylinder, $\psi$ is the electrostatic potential [V], $a$ is the radius of the cylinder, and ${\sigma }^{*}$ is the dimensionless surface charge density defined as

$${\sigma }^{*}={\displaystyle \frac{\sigma eza}{\epsilon k_{B}T}}$$

(16)

in which $\sigma$ is surface charge density [Cm⁻²], $e$ is the electronic charge [C], $z$ is the ion valence [-], $\epsilon$ is the permittivity [Fm⁻¹], $k_B$ is Boltzmann’s constant [KK⁻¹], and $T$ is absolute temperature.

Another parameter of interest is the reduced axial charge density of the cylinder $\xi ,$ defined as

$${\sigma }^{*}=2\xi z$$

(17)

The relevance of these equations to the principal objective of the paper will be discussed in the methodology section.

3.2. Electrostatics at the Oil–Low-Salinity Brine Interface

Following Hirasaki [68], we assume the existence of an oil–water interface and a thickness of water between this interface and that of reservoir rock pore throat over which electrostatic interaction occurs. Considering that basic and acidic ionizable groups at the crude oil–low-salinity brine interface will warrant the evolution of EDL, the distribution of charge in the EDL at the oil–water interface has been discussed [61]. Moreover, the research of Buckley has highlighted the role of interfacial zeta potential of such systems in reservoir rock wettability evolution, and crude oil adhesion to pore wall mechanism in addition to providing the solution for the potential of the EDL system related to the oil–water interface (Buckley et al.) [69]. In this regard, the analytical solution to the MFPB equation reads (Buckley et al.) [69]

$$\psi \left(x\right)={\displaystyle \frac{2k_{B}T}{e}}ln{\displaystyle \frac{1+Y_{0}exp\left(-\mathrm{K}x\right)}{1-Y_{0}exp\left(-\mathrm{K}x\right)}}$$

(18a)

Here, $\psi \left(x\right)$ is the electrostatic potential at a distance x from the interface [V], $\mathrm{K}$ is the reciprocal of the Debye length [m], and

$$Y_0={\displaystyle \frac{exp\left(y_{0ow}/2\right)-1}{exp\left({yo}_{0w}/2\right)+1}}$$

(18b)

where $y_{0ow}$ is the reduced potential of the oil–water interface [-] defined as

$$y_{0ow}={\displaystyle \frac{e{\psi }_{0,O-W}}{k_{B}T}}$$

(19)

in which ${\psi }_{0,O-W}$ is the surface potential at the oil–water interface [V].

Given the experimental data on zeta potential versus salinity, which reflects the reciprocal of Debye length ($\mathrm{K}$) and the distance to the plane of shear in the EDL, the surface potential at the oil–brine interface can be calculated for the case of LSWF using Equation (18) through Equation (19). This objective will be pursued in the appropriate section.

Surface potential and surface charge density related to the EDL have direct correlations to the thermodynamic free energy of its formation, and the following section will be devoted to the energetic aspects of this paper.

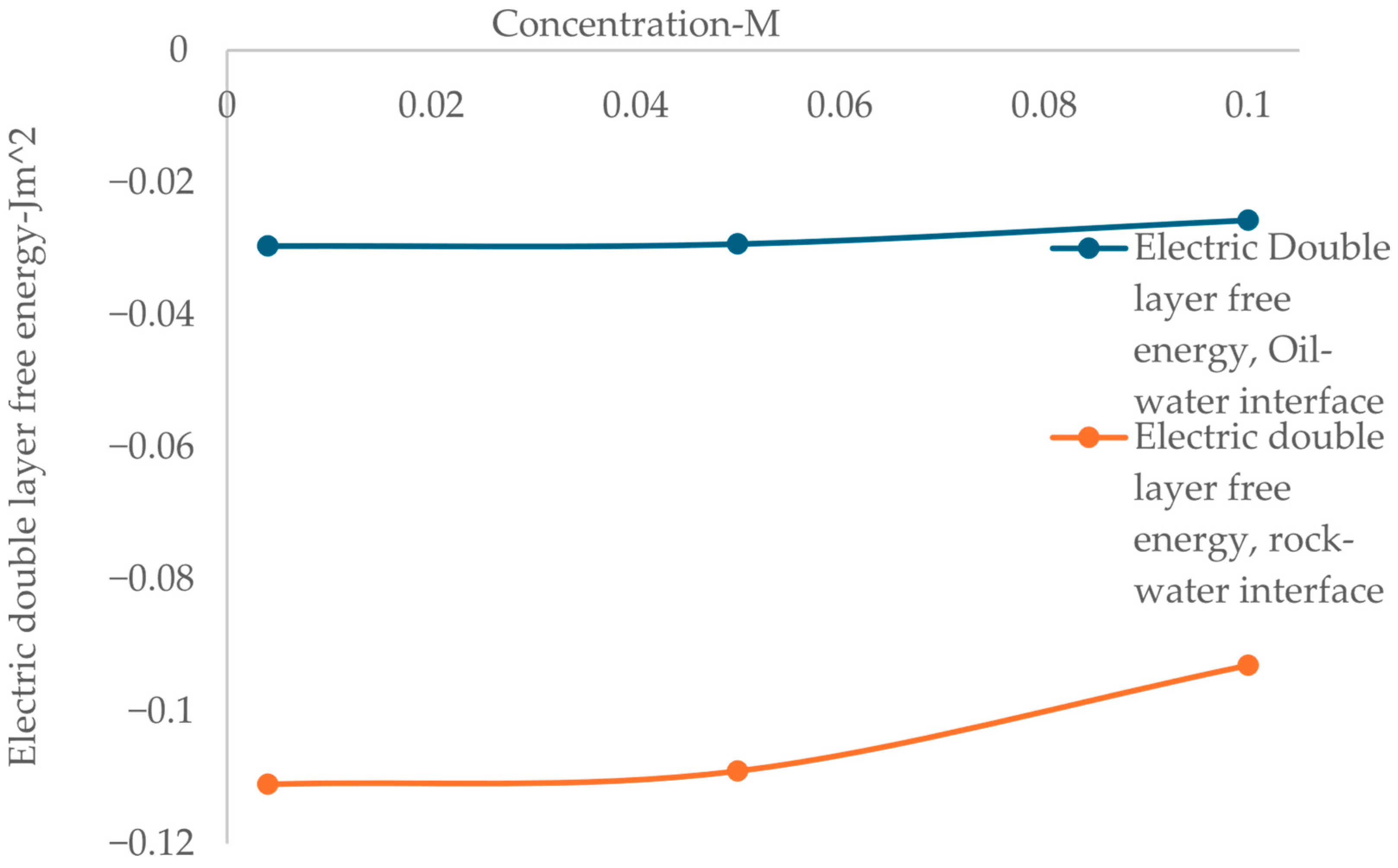
3.3. Total Free Energy Model

In an EDL, the total free energy consists of three contributions: electrostatic energy, entropic energy and chemical energy (Overbeek et al.) [70]. The electrostatic energy arises from the interaction between charges on the electrode surface and the ions in the electrolytic solution, creating an electrical field, and it quantifies the electrostatic work required to create an EDL [71]. The chemical energy, on the other hand, stems from chemical reactions or processes occurring at the interface, such as the adsorption or desorption of molecules or ions, and it captures the impact of chemical reactions or processes on the overall thermodynamic state of the interface [72]. The product of the entropy difference is $\Delta S$, between the distribution of ions in the EDL and the same ions and solvent molecules in the bulk solution, where the electrostatic potential is zero and temperature accounts for the entropic component of the free energy of the EDL. The summation of the three components gives the free energy of the EDL as [71]

$$F_{EDL}=-{\int }_0^{{\psi }_0}{\sigma }_0\left(\psi \right)d\psi$$

(20)

The successful application of Equation (20) to the derivation of the thermodynamic free energy for an interface relies on substitution of the appropriate model for the surface charge density, ${\sigma }_0$, which is thermodynamically accessible (Buckley et al.) [69].

3.3.1. Oil–Water Interface

The surface charge density, ${\sigma }_{O-W}$, at the oil–water interface reads [69]

$${\sigma }_{O-W}=e{N}_{a1}\left[\left({\displaystyle \frac{f}{1+\left(K_{a2}/\left[H_b^{+}\right]\right)exp\left(y_0\right)}}\right)-\left({\displaystyle \frac{1}{1+\left(\left[H_b^{+}\right]/K_{a1}\right)exp\left(-y_0\right)}}\right)\right]$$

(21)

where fractional coverage, $f$, of the surface by acidic and basic groups of crude oil is defined as

$f=N_{a2}/N_{a1}$, where $N_{a1}$ and $N_{a2}$ are the total number of acidic and basic groups of crude oil, respectively.

Substituting Equation (21) into Equation (20) and noting the definition of dimensionless potential given as the ratio of the product of electronic charge and potential to Boltzmann’s energy leads to the following equation:

$$F_{EDLo-w}=-{\int }_0^{{\displaystyle \frac{{e\psi }_0}{k_{B}T}}}{N}_{a1}{k}_{B}T\left[\left({\displaystyle \frac{f}{1+\left(K_{a2}/\left[H_b^{+}\right]\right)exp\left(y_0\right)}}\right)-\left({\displaystyle \frac{1}{1+\left(\left[H_b^{+}\right]/K_{a1}\right)exp\left(-y_0\right)}}\right)\right]d{y}_0$$

(22)

Equation (22) was integrated, using Maple version 2021 to give the following equation:

$$F_{EDL-O-W}=0.0257Aln\left(1+D{e}^{-38.91y_0}\right)-0.0257Aln\left(e^{-38.91y_0}\right)-0.0257ABln\left(e^{-38.91y_0}\right)+0.0257ABln\left(1+C{e}^{-38.91y_0}\right)$$

(23)

In Equation (23)

$$A=N_{a1}{k}_{B}T$$

$$C=\left(K_{a2}/\left[H_b^{+}\right]\right)$$

$$D=\left(\left[H_b^{+}\right]/K_{a1}\right)$$

$K_{a2}$ is the equilibrium constant for basic site dissociation [M], $K_{a1}$ is the equilibrium constant for acidic site dissociation [M], and $\left[H_b^{+}\right]$ is the bulk concentration of hydrogen ion in solution [M].

3.3.2. Rock–Water Interface

The surface charge density, ${\sigma }_{R-W}$, at the rock–water interface is given as (Buckley et al.) [69]

$${F_{EDLr-w}=N}_{a1}{k}_{B}T\left[\left({\displaystyle \frac{\left(\left[H_b^{+}\right]/K_{+}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-y_0\right)-\left(K_{-}/\left[\left[H_b^{+}\right]\right]\right)exp\left(y_0\right)}{1+\left(\left[H_b^{+}\right]/K_{+}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-y_0\right)+\left(K_{-}/\left[\left[H_b^{+}\right]\right]\right)exp\left(y_0\right)}}\right)\right]$$

(24)

Substituting Equation (24) into Equation (20) and following the same integration procedure as before leads to the following equation for the free energy of the rock–water interface.

$$F_{EDLr-w}=N_{a1}{k}_{B}T{y}_0+0.0257Qln\left(J{\left(e^{-38.91y_0}\right)}^2+M+e^{-38.91y_0}\right)$$

(25)

In Equation (25), we made the following substitutions to render the equation more simplified for calculation:

$$Q=N_{a1}{k}_{B}T$$

$$M=\left(\left[H_b^{+}\right]/K_{+}\right)$$

$$J=K_{-}/\left[\left[H_b^{+}\right]\right]$$

In which $K_{+}$ is the acidic dissociation constant for surface silanols, $K_{-}$ is the basic dissociation constant for surface silanols, and $N_{a1}$ is the number density of acidic functional groups on silica (silanol).

3.3.3. Double Layer Repulsion Model

Double layer forces between charged objects exist across liquids, typically in aqueous media, acting over distances that are comparable to the Debye screening length, with their magnitude increasing with surface charge density [73]. The double layer interaction between the oil–water interface and the rock–water interface with reduced potentials $y_1$ and $y_2$, respectively, can be approximated under the constant potential approximation theory, which gives [74]

$$F_D\left(D\right)=n_b{k}_{B}T\left[2y_1{y}_{1}cosh\left(\mathrm{K}h\right)-y_1^2-y_2^2\right]/sinh\left(\mathrm{K}h\right)$$

(26)

In Equation (26), $y_1$ and $y_1$ are reduced potentials defined as

$$y_1={\displaystyle \frac{e{\psi }_{O-W}}{k_{B}T}}$$

(27)

$$y_2={\displaystyle \frac{e{\psi }_{R-W}}{k_{B}T}}$$

(28)

where ${\psi }_{O-W}$ and ${\psi }_{R-W}$ are the surface potentials of the oil–water and water–rock interfaces, respectively.

Equations (13), (18a), (18b), (22) and (26)–(28) form the fundamental theoretical foundations of the present paper and in the following section, we will discuss their uses regarding the principal goal of the paper.

4. Methodology

4.1. Petroleum Reservoir Model

Calculation of potential from Equation (13) requires knowledge of the mean pore radius of the cylindrical conduit of the reservoir rock. We assume a predominantly silica rich sandstone petroleum reservoir rock. Therefore, the properties of such a rock are approximate to those of Fontainebleau sandstone with 99% silica content. Fontainebleau sandstone has a mean grain diameter around 250 micrometers (µm), with grain sizes normally ranging from 150 to 300 µm. Pore diameters within the sandstone generally vary but are in the range of 16 to 30 µm. (Saadi et al.) [75]. In this paper, we assume a pore diameter of 20 × 10⁻⁵ m. The assumption of 99% silica content of the reservoir rock justifies the assumption of silica surface chemistry.

4.2. Dielectric Permittivity of Low Salinity Brine

The dielectric constant of a fluid is salinity dependent as [76]:

$${\epsilon }_0\left(T,T\right)={\epsilon }_0\left(T,0\right)a\left(N\right)$$

(29)

$$a\left(N\right)=1.000-0.255N+5.15 \ast {10}^{-2}{N}^2-6.889 \ast {10}^{-3}{N}^3$$

where N is the normality.

$$N=S\left(1.707 \ast {10}^{-10}+1.205 \ast {10}^{-5}S+4.058 \ast {10}^{-9}{S}^2\right)$$

(30)

where $S$ is the salinity in parts per thousand for $0\le S\le 260$

$${\epsilon }_0\left(T,0\right)=87.74-0.40008T+9.398 \ast {10}^{-4}{T}^2+1.410 \ast {10}^{-6}{T}^3$$

(31)

where $T$ is the temperature in Celsius.

To calculate the salinity-dependent static dielectric constant, typical salinity ranges reported in the literature in connection with LSWF experiments [77] were used. The values are 0.004 M, 0.05 M, and 0.1 M.

4.3. Reduced Surface Potential Calculation

In their recent research in connection with exploring the electrical potential inside cylinders beyond the Debye–Huckel approximation using a computer code, Leroy & Maineult [78] demonstrated, using the triple layer surface complexation model, that the surface charge density of amorphous silica measured using potentiometric titrations agrees with the model. Therefore, experimentally assessable electrostatic parameters, such as zeta potential and surface charge density will be used in the present paper, together with mathematical models for calculating electrostatic interactions at the interface. In this regard, Collini and Jackson [79] have published experimental data on the zeta potential of crude oil in an aqueous solution, using electrophoretic mobility (see Appendix A) as have Duffy et al. [80] on the surface charge density of silica in different concentrations of sodium chloride brine (see Appendix B), as well as Takeya et al. [81]. In the cited research papers, concentrations within LSWF were used. Therefore, following Takeya et al. (2020) [81], LSWF electrostatics is studied using 0.001 M, 0.004 M, 0.05 M, and 0.1 M.

4.4. Debye Length

The square of the reciprocal of the Debye length ($\lambda$) is a fundamental length scale that is salinity dependent as [74]

$$K^2=2e^2{n}_b/{\epsilon }_0{\epsilon }_r{k}_{B}T$$

(32)

where $\mathrm{K}={\displaystyle \frac{1}{\lambda }}$, and $\lambda$ is the Debye length [m], $n_b$ is the number density of ions, $\epsilon$ is the permittivity of the electrolyte solution [Fm⁻¹], $k_B$ is the Boltzmann constant, and $T$ is the absolute temperature.

To calculate the Debye length, the ionic strength of the electrolyte is required, which is then calculated to the number density, using Avogadro’s number. The ionic strength is calculated as [82]

$$I=0.5\sum _1^{n}c{z}^2$$

(33)

where I is the ionic strength, c is the concentration [M] of ion, and z is the ionic valence.

4.5. Reduced Surface Potential Calculation for Oil–Water Interface

From Equation (18a), the zeta potential can be calculated, knowing the distance to the hydrodynamic shear plane, the inverse of the Debye length, and $Y_0$. However, if zeta potential and the first two parameters are known, the value of $Y_0$ can be calculated. In this paper, experimental zeta potentials corresponding to 0.004 M, 0.05 M, and 0.2 M were substituted into Equation (18a) together with the assumed value of the inverse of the distance to the shear plane, which correlates to the inverse of the Debye length. Calculated values of $Y_0$ were substituted into Equation (18b) to calculate the reduced oil–water surface potential, $y_{0ow}$.Values of reduced potential were then calculated to dimensional potentials ${\psi }_{0,O-W}$ using Equation (19). In all calculations, a value 0.6 nm was used for the distance to the hydrodynamic shear plane [83,84] for the oil–water interface.

4.6. Reduced Surface Potential Calculation for Rock–Water Interface

From Equation (13), the reduced surface potential is obtained by equating radial distance to the radius of a pore throat, rendering x equal to unity, leading to the following expression:

$$y_{0a}=y_0@x=a=ln\left[4{ϵ}^2\left({\left(\xi -1\right)}^2\pm {\beta }^2\right)\right]$$

(34)

Consequently, surface charge densities corresponding to 0.004 M, 0.05 M, and 0.1 M were extracted from Appendix B to calculate the dimensionless surface charge density parameter (${\sigma }^{*}$) defined by Equation (16), following which the parameter ($\xi$) defined by Equation (17) was calculated.

The application of Equation (34) for the calculation of the reduced surface potential requires knowing the integration constant $\beta$, the calculation of which requires knowledge of the parameter $ϵ$, the ratio of the radius, a, to Debye length. The value of this parameter together with $\xi$ enables selection of the appropriate equation for calculating $\beta$ Shkel et al. [67]. In this paper, Equation (7b), found in the cited literature was used for the calculation of reduced rock–water surface potential.

4.7. Calculation of Electric Double Layer Free Energy

4.7.1. Free Energy of the Oil–Water Interface Electric Double Layer

Equation (23) for calculating the free energy of the ELD for the oil–water system requires data on the number density of basic and acidic groups. In the work of Plassard et al. [79], the total acid number of the oil used is 2.04 mgKOHg⁻¹. Kolltveit [85] has provided experimental data on the chemistry of a typical black oil sample (B), found in Bonto et al. [86], where they reported a total acid number of 2, number density of acidic site ($N_{-COOH})$ equal to 1.8 per nm², and number density of basic sites ($N_{-NH})$ equal to 0.6 per nm². Considering the insignificant difference between the values of total acid number reported by Kolltveit (2016) [85] and Plassard et al. [79] (2024), the data for Kolltveit (2016) [85] are used to represent those of the crude oil studied by the latter research group. Equation (23) also requires data on equilibrium constants for the acidic and basic groups’ dissociation. Accordingly, the values used in this paper are log (K_a) = −4.65 and log (K_b) = 6.7 for acidic and basic groups’ dissociation constants, respectively.

4.7.2. Free Energy of the Rock–Water Interface Electric Double Layer

Equation (25) for calculating the free energy of the ELD for the rock–water system requires data on the number density of silanol groups. In this paper, we use 4.9 per [87]. Equations (23) and (25) also require data on the equilibrium constants for the acidic and basic dissociation of silica. The values used in this paper are log (K_a) = 7.5 [88] and log (K_B) = 4.5 [89], respectively.

4.8. Experimental Conditions

In this study, temperature-dependent parameters are encountered in several equations. Literature-based experimental data used for achieving the principal objectives were measured at room temperature, 25 °C (298 K). Therefore, 298 K was used for calculations. Given that the pH of petroleum reservoir is closer to neutral [90], the concentration of bulk hydrogen ion $\left[H_b^{+}\right]$ used in this paper is 10⁷ M. Values of the fundamental physical constants used in this paper are found in Appendix C.

5. Results and Discussion

In the literature on LSWOR, improvement on mechanisms originally encountered in conventional high-salinity-enhanced oil recovery (HSEOR) schemes have been highlighted, notable of which are the wettability and double layer expansion effects (Katende and Sagala) [21]. Moreover, considering the intimate relationship between zeta potential and surface charge density [91], which reflects the extent of electrostatic interactions at interfaces, Alias [92] demonstrated the relationship between the electrical double layer and the zeta potential, showing it to be the phenomenon where oppositely charged ions (counterions) are preferentially attracted toward the surface, and where ions of the same charge (co-ions) tend to be repelled. Yet, in the concept of LSWOR, a critical thermodynamic aspect remains to be theoretically/experimentally researched, which is the interfacial energetics pertaining to the thermodynamic free energy required for the creation of the EDL, which is critical for achieving all the desired goals. Therefore, considering the theoretical findings of the present paper, the electrostatics of LSWOR will be discussed, considering the effect of salinity on the ease of evolution of the EDL, its enhancement/expansion and interactions.

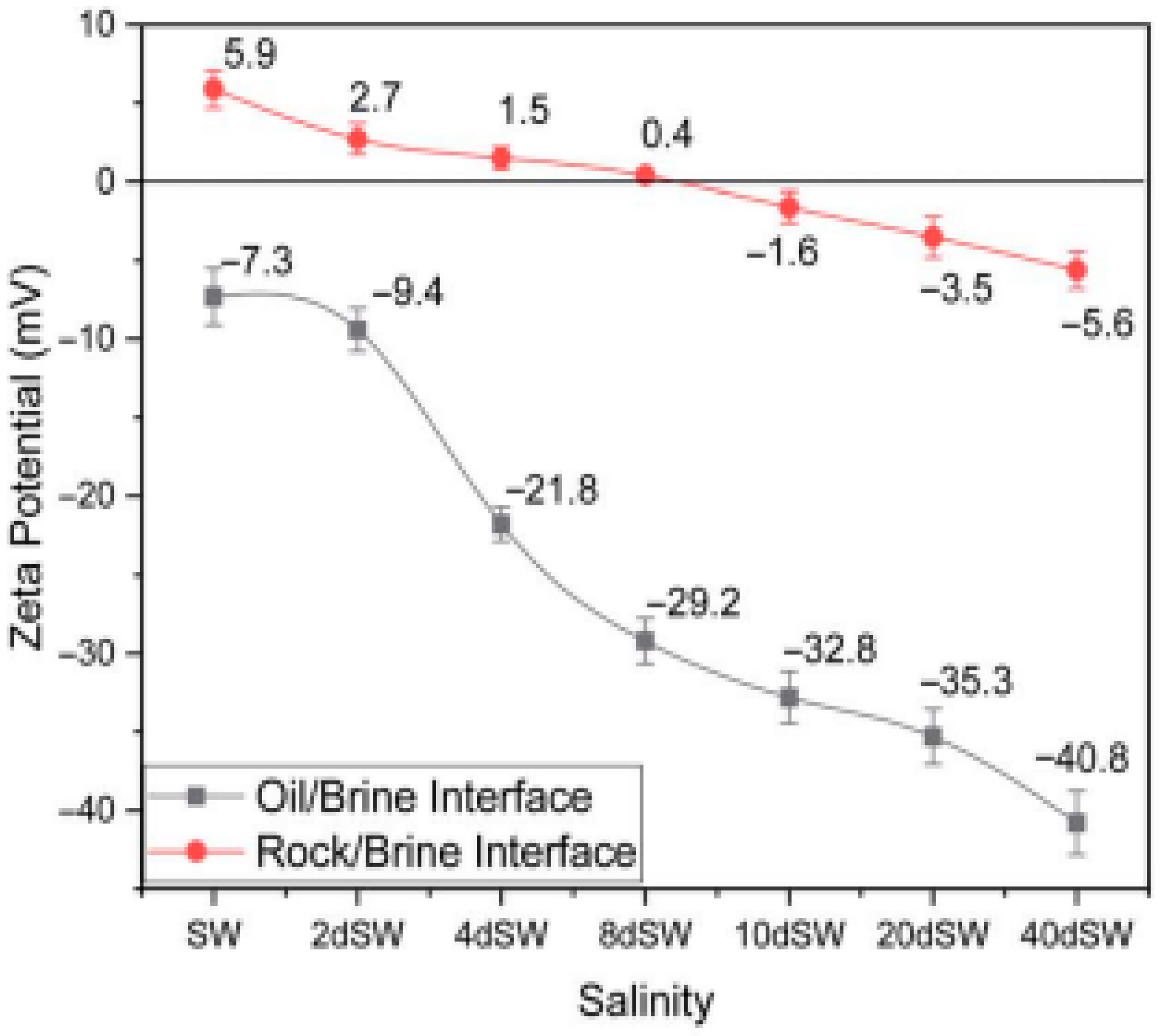
5.1. Electrostatics

Consequently, Figure 4 and Figure 5 show plots of surface and zeta potential at the rock–water and oil–water interfaces, respectively, using Equation (34) and the theoretical definition for reduced potential (See Section 4.6) for the rock–water interface and Equation (18a) through Equation (19), respectively, all versus salinity. Accordingly, the figures show that increasing salinity causes both zeta and surface potential at all interfaces to become less negative. For both figures, at low salinity, both surface and zeta potentials appear to be the same, becoming dissimilar with salinity increase. In the case of the oil–water interface, both zeta and surface potential appear to achieve plateau values for salinities above 0.06 M. In the colloid literature, electrostatic stabilization between colloidal particles has been shown to be more effective for increasing values of negative/positive surface potentials [93,94]. Consequently, the figures testify to the enhanced stability of interaction between oil–water and rock–water interfaces with the decreasing salinity of water flooding. Moreover, in all figures, surface potential is more negative than zeta potential, which is consistent with the Debye–Huckel equation that links surface potential to the potential at a given distance from the surface in an exponential manner [95].

Trends in zeta and surface potentials obtained as seen in Figure 4 and Figure 5 are equally revealed in the literature using experimental measurements as seen in Appendix D.

Figure 6 shows the plots of disjoining pressure interactions for the oil–water and rock–water interfaces versus interfacial separation for different anticipated injection water salinities, calculated using Equations (26)–(28), decreasing with salinity. In all plots, the reduction in disjoining pressure with the distance of separation is imminent. Moreover, the figure clearly demonstrates that at a given separation, disjoining pressure is higher the lower the salinity, which demonstrates the wettability enhancement phenomenon widely reported in the literature [21].

Generally, the EDL evolves in response to the ionization of ionizable surface groups (Lin et al.) [96], which causes disequilibrium in the distribution of interfacial ions in adjacent electrolyte solutions [97]. Therefore, the EDL concept is an interfacial phenomenon. In thermodynamics, the concept of free energy underpins the physics of several processes, defining the feasibility of their occurrences, which is applicable to interfacial science [48,98]. In this regard, processes involved in the deprotonation and protonation of surface functional groups (Lowe et al.) [99] have definite free energy requirements which must reflect not only the chemistry of substrates, but also those of aqueous electrolyte solutions. Accordingly, Figure 7 shows plots of the free energy of formation of the EDL per unit area at the oil–water and rock–water interfaces versus anticipated salinity of injected water, based on Equation (22) and Equation (24), respectively. In all cases, the free energy is negative, consistent with the thermodynamic requirement, given that the EDL forms spontaneously [100]. Additionally, the change in free energy with concentration is less pronounced for the case of the oil–water interface compared to that of the rock–water interface. Theoretically, the concept of free energy here is analogous to those associated with interfaces in thermodynamics. Accordingly, values given by Figure 7, correspond to those required to form the unit surface area of the oil–water/rock–water interface at a given salinity of injection water. Therefore, the figure shows that as salinity increases, the free energy of formation of an interface becomes less negative or increases, testifying to the decreasing feasibility of formation. Another distinct feature of the figure is that the free energy of formation of an EDL for the rock–water interface is smaller, compared to that of the oil–water interface.

The observation highlights the theoretical foundations for the derivation of the free energy equation (see Equations (20)–(25)), where the density of surface ionizable $N_{a1}$ is the most relevant parameter. In this regard, the bigger this parameter, the lower the value of the free energy of formation. Protonation and deprotonation of silanol functional groups at the water–rock interface are causes of electric double layer formation as are the ionization of basic and acidic groups of oil at the oil–water interface. Therefore, the number densities of these groups reflect the magnitude of free energy of formation at interfaces. In this regard, the recent research paper of Bonto et al. (Bonto et al., 2019) [86] has demonstrated that, on the average, the sum of the number densities of acidic and basic sites of crude oils is less than that of the number density of silanols on a silica surface, averagely 4.5 per square nanometer (Onizhuk et al.) [101]. Therefore, theoretically, the free energy of formation of the electric double layer at the water–silica interface must be less than that of the oil–water interface at a given salinity and pH of aqueous solution, consistent with Figure 7.

5.2. Correlation to Literature-Based Observations in Low-Salinity-Enhanced Oil Recovery

5.2.1. Correlation to Atomic Force Microscopy Observations

The concept of disjoining pressure is not new, and it has attracted a lot of attention with the growing popularity of LSEOR, where the three intermolecular forces are explained by the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory. Considering the ubiquity of intermolecular interactions, these forces can be accurately measured in an oil/brine/rock system using atomic force microscopy (AFM). Accordingly, information obtained from force vs. distance curves has been used to evaluate the theoretical model. The two theories have been integrated to explain the wettability alteration induced by DLE because of an alteration from high salinity to low salinity [102]. Hassenkam et al. [103] have reported an atomic force microscope (AFM) study of the nature and magnitude of the interaction between hydrocarbon molecules with carboxylic acid end groups and the pore surfaces of oil reservoir sandstones. In this regard, using functionalization of the AFM tip with polar molecules, they were able to quantitatively measure the adhesion forces between these molecules and the mineral surfaces under 36,500 and 1500 ppm TDS artificial seawater (ASW) solutions. A combination of these measurements into a force map revealed that adhesion was highest on the quartz grain surfaces during exposure to high-salinity solutions and it decreased when salinity decreased in nearly all cases. In the cited literature, the principal goal of the functionalization of the tip of AFM with ionizable functional groups was to facilitate the formation of a pair of EDLs like the oil–water and rock–water interfacial systems studied in the present paper. Moreover, in the context of the present paper, increasing salinity corresponds to decreasing disjoining pressure forces, which corresponds to increasing adhesion forces like that observed by Hassenkam et al. (2012) [103], implying that the theoretical findings of the present paper have direct correlations to literature-based experimental observations.

5.2.2. Correlation to Wettability Enhancement

Mechanistically, water flooding oil recovery improvement is only possible where injected water imbibes spontaneously into the matrix of reservoir rocks, thereby causing a counter current oil flow, which can be swept into producing wells [104]. Therefore, wettability is a fundamental requirement for enhanced oil recovery by water flooding in general [105,106,107]. Consequently, dewetting, which is characterized by high values of the thermodynamic contact angle, is detrimental to enhance/improved oil recovery schemes. In this regard, it is important to know that the mechanism of dewetting in water flood oil recovery has been known to be associated with the adsorption of the hydrophobic crude oil component on reservoir rock surfaces, a phenomenon that has been reported in connection with carbonate reservoirs [108,109]. The adsorption-induced dewetting of reservoir rock surfaces is possible where there is a direct interaction of the oil–water interface with pore walls [110]. The disjoining pressure at the oil–water and rock–water interface is the total pressure that tends to separate the interfaces. Therefore, the greater the pressure, the less the chances of oil–water interface interacting directly with the rock surface and the lesser the chances of adsorption induced dewetting (Yuan et al.) [111]. Generally, the total disjoining pressure is the sum of three distinct contributions, notably electrostatic, van der Waal, and hydration forces (Kuchins et al.) [112]. The structural contribution results from the structuring of water molecules in confined geometries [113], while van der Wall contribution stems from van der Waal forces. In this paper, Figure 6 shows the electrostatic contribution to total disjoining pressure at a given salinity and pH of aqueous solution.

In the literature, several authors have highlighted the role of low-salinity water flooding in wettability enhancement. For instance, Berg et al. [114] have given experimental evidence of wettability enhancement, using LSEORS at a microscopic scale. In the cited literature, the authors observed the release of crude oil from a substrate covered with solidly attached clay particles when changing the brine from high salinity to low salinity. Macroscopically, Khishvand et al. [115] have provided core flooding evidence of experimental wettability alteration during low-salinity water flooding, integrating X-Ray computer Tomography techniques. Al-Bayati et al. [116] conducted experiments for unsteady-state and steady-state flow for both imbibition and drainage processes, where a shift to the right was observed for the relative permeability curve of 0.2 M NaCl along with a drop in irreducible water saturation and in residual oil saturation compared to 0.6 M. In the context of the present paper, Figure 6 gives a robust explanation of the cited wettability enhancements as follows below.

As salinity reduces, the electrostatic component of the total disjoining pressure increases. Therefore, for a given pH and low salinity, total disjoining pressure increases, which hinders the direct interaction of the oil surface with the pore surface, implying less chances of crude oil adsorption induced dewetting. Consequently, wettability enhancement by increased double layer repulsion as salinity decreases is the principal cause of enhanced spontaneous water imbibition with corresponding water flooding efficiency as reported by Al-Bayati et al. [116].

5.2.3. Correlation to Observation in Colloidal Systems

The evolution of the EDL is critical to the stability of a colloidal system. Therefore, its ease of formation, measured by the free energy (see Figure 7) is equally fundamentally important. In this regard, experimental evidence testifies to destabilization/coagulation resulting from increased salinity, which has a negative effect on zeta potential for a given pH [117]. In the context of the present paper, increasing salinity corresponds to increasing the free energy of formation of the electric double layer, implying a higher interfacial energy budget required to form the unit surface area of the electric double layer. In this regard, high salinities correspond to higher free energy requirement due to decreased electrostatic contribution to total disjoining pressure. Thus, with increasing salinity at a given pH, the formation of the electric double layer and its associated repulsion are gradually compromised, leading to instability in colloidal systems.

5.2.4. Relationship of Study Findings to Practical Field Scale Recovery Problems

In the context of improved oil recovery in petroleum reservoir engineering, LSEOR is classified as tertiary, given that the injected fluid is the kind not normally encountered in the reservoir domain [118]. The universally acknowledged success of LSEOR derives from improved wettability and double layer repulsive forces as proven by the present paper, which can only be possible through stronger electrostatic repulsion at low salinities of injection water.

The literature shows that the most predominant minerals of petroleum reservoirs are sandstones and carbonates, with the latter hosting a greater proportion of hydrocarbon reserves [119]. Under prevailing reservoir conditions, sandstones and carbonates develop distinct surface charges due to the acid base properties of predominant rock mineralogy. In this regard, sandstones develop negative charges due to abundant silica, while carbonates develop opposite charges due to abundant calcite [120]. Therefore, trends in double layer repulsion as revealed by Figure 6 provide a practical guide to designing LSEOR in a manner that will enhance electrostatic repulsion beyond that encountered under ordinary low-salinity brine injection. The following section sums up the details of the design.

Enhanced Interfacial Electrostatic Repulsion Using Cationic Surfactants

The application of surfactants in enhanced oil recovery schemes in the petroleum industry has been mostly associated with reducing capillary forces to assist in mobilizing discontinuous oil blobs into continuous streams that can be effectively swept to producing wells. Current research concerning surfactant science and technology involves a variety of requirements relating to the design of surfactant structures with widely varying architectures to achieve physicochemical properties and dedicated functionality [121]. Generally, multicharged surfactants have unique properties, including good solubilization, low Krafft temperatures, low critical micelle concentration (cmc), great rheological behavior, as well as high efficacy in lowering the surface tension [122]. Therefore, the absorption of such surfactants with cationic ability onto sandstones could provide two distinct advantages, notably increase surface charge density on sandstones [123] and decrease interfacial tension, which reduces capillary pressure to enhance the capillary number [124]. In this regard, Gemini Surfactants with multi-charge can be used in low-salinity water injections to enhance wettability, double layer repulsion and for capillary number improvement [125].

Nearly 60% of hydrocarbon reserves are hosted by carbonate hydrocarbon reservoirs [126]. Considering the predominantly positive charge of carbonates under normal geologic conditions of oil production, task-specific anionic surfactants with multi-headed charge groups [127] can be used to enhance both interfacial electrostatic repulsion and wettability enhancement, similar to those encountered in sandstones. Here, anionic sulfonate Gemini Surfactants [128] fulfill the role in exploiting the findings of the present paper to improve the design of LSEOR schemes.

Recently, there has been an increased emphasis on the prospective applications of nanotechnology in enhanced oil recovery, where interaction between nanofluid and reservoir fluids leads to enhanced wettability and reduced interfacial tension, improving the oil recovery [129]. In the field of nano drug delivery, functionalization of nanoparticles has led to the design of task-specific nano delivery technology, following surface functionalization with desired functional groups [130]. Functional groups that can introduce multiple surface charges on nanoparticles include amines (positively charged at physiological pH), carboxylates (negatively charged) and sulfonates (negatively charged) [131]. Therefore, to enhance electrostatic interaction and wettability in line with the findings of the present paper, the approach encountered in nano drug delivery technology can be employed to develop more robust and multi-charge surfaces on nano particles.

5.2.5. Limitation of This Study

In petroleum geology, the assumption of a cylindrical pore network of sediments has been universally adopted, particularly when calculating capillary pressure. For instance, In the case of mercury intrusion porosimetry, the Washburn equation provided a simplified and convenient interpretation of the pressure to pore size of porous solids based on the cylindrical pore geometry, generally known as pore and throat geometry [132]. However, depending on the depositional environment of the sediment, the assumption of a cylindrical pore model may fail to hold, particularly for clastic sediments. In this regard, Li et al. [133] have given a classification of the heterogeneous conglomerate reservoirs of the North Slope of the Mahu Depression for the purpose of effective hydraulic fracturing. They agree that the fan delta front conglomerates generally exhibit superior reservoir quality compared to fan delta plain conglomerates. These lithofacies stand out with the best physical properties, such as higher porosity and permeability, due to their fine-to-medium gravel size, high cement content, and low matrix content. These characteristics support effective fracture propagation and complex fracture networks, which are essential for enhancing hydrocarbon production. Therefore, the assumption of a cylindrical pore network employed in the present paper can be applied to the conglomerate of the fan delta front due to their petrophysical properties being similar to those of conventional sandstones.

6. Conclusions

The potential of low-salinity water flooding to enhance oil recovery has been demonstrated experimentally, using both microscopic and macroscopic approaches. In addition, the potential has been demonstrated using Molecular dynamic simulation approaches [134,135,136]. In all approaches, consistent observations pertaining to the effect of salinity on wettability and disjoining pressure have been reported. However, while experimental and simulation approaches have been reported in the literature, a purposeful theoretical approach to verifying the experimental trends/results is lacking, albeit the mean field Poisson–Boltzmann theory provides a robust approach for calculating the electrostatics of LSEOR. In this paper, we have studied theoretically LSEOR, using the analytical solution to the Mean Field theory of Poisson–Boltzmann and models of the free energy of formation of the EDL. In this paper, we limited our approaches solely to the classical interfacial cases of fluid–fluid and rock–fluid for LWSF, where asphaltenes are the only ionizable groups at the oil–water interface for simplicity, neglecting the case of nanofluid injection. The following points sum up the conclusion of the paper:

• Theoretical surface and zeta potential become less negative with increasing salinity, like those reported in the literature-based experimental approaches, testifying to decrease electrostatic interaction, which correlates with dominant van der Waals forces at field scale and decreased oil recovery.
• Double layer disjoining pressure decreases with increasing salinity like that reported in the literature based on atomic force microscopy measurements, which correlate with decrease disjoining pressure forces and dewetting at the rock–water interface at field scale.
• As salinity increases, the thermodynamic free energy required to create unit interfacial area increases for oil–water and rock–water interfaces, limiting double layer repulsion and wettability enhancement from the practical viewpoint in water flood oil recovery.
• Theoretical findings based on the analytical solution to the Poisson–Boltzmann equation correlate with experimental observations on low-salinity oil recovery reported in the literature, which highlights the role of the interfacial electrostatic theory in guiding the future design of LSWF oil recovery schemes.
• This paper adds an incremental advancement in LSWF by considering the theoretical calculation of the free energy of formation of an interfacial electrical double layer as a function of salinity.