Study on Lower Limb Motion Intention Recognition Based on PO-SVMD-ResNet-GRU
Abstract
1. Introduction
- (1)
- An sEMG signal denoising method is proposed, which optimizes Sequential Variational Mode Decomposition (SVMD) based on the Parrot Optimization (PO) algorithm and integrates it with wavelet thresholding. This method improves the signal-to-noise ratio (SNR) through adaptive parameter optimization;
- (2)
- A prediction model for lower limb joint movement angles is constructed, which combines Residual Network (ResNet) and Gated Recurrent Unit (GRU). Compared with a variety of commonly used models, this model achieves higher prediction accuracy.
2. sEMG Signal Denoising Method Based on PO-SVMD
2.1. Sequential Variational Mode Decomposition
2.2. Determination of SVMD Parameters by PO Algorithm
- (1)
- Population initialization
- (2)
- Foraging behavior
- (3)
- Perching behavior
- (4)
- Communication behavior
- (5)
- Fear of strangers
2.3. Combining with Wavelet Threshold
3. Prediction Method of ResNet-GRU Combined Model
3.1. Convolutional Neural Network
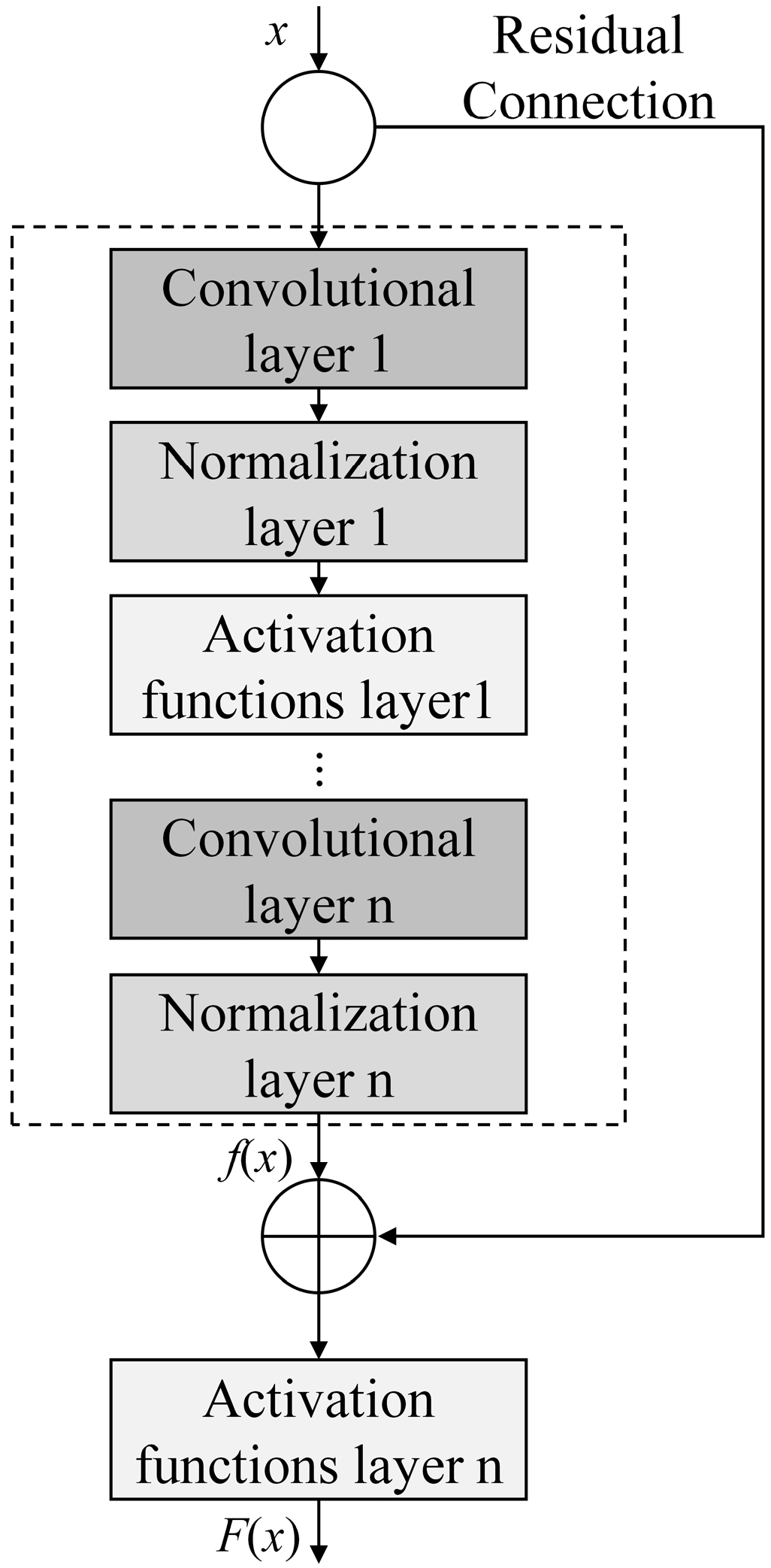
3.2. Residual Network
3.3. Gated Recurrent Unit
3.4. ResNet-GRU Combined Prediction Model
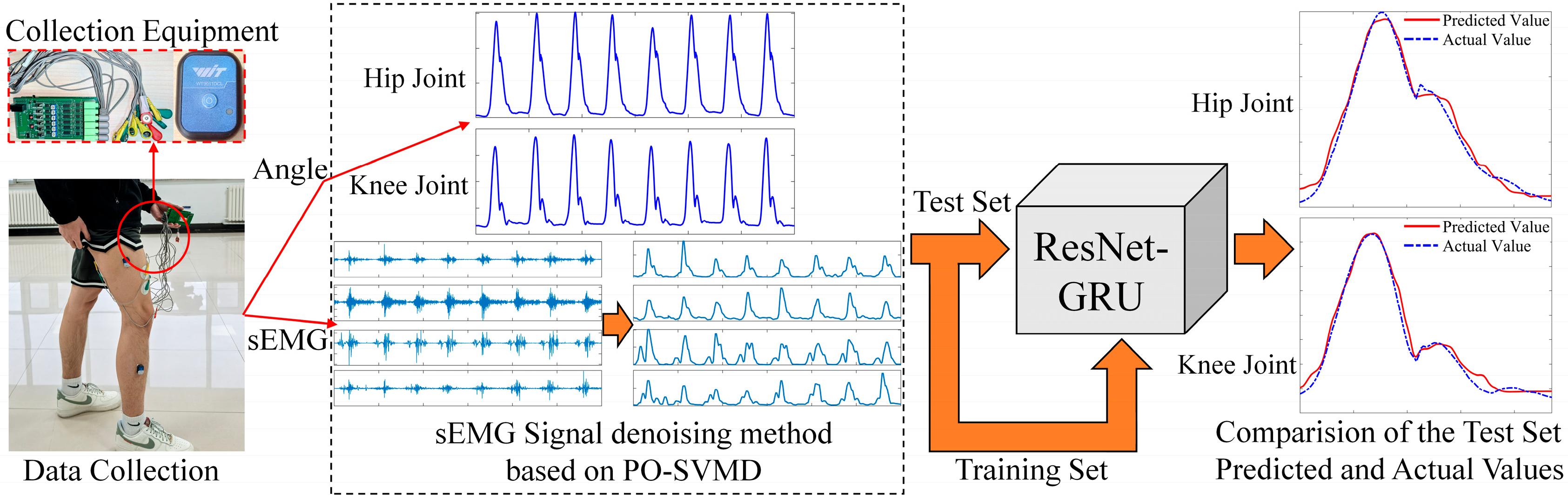
4. Data Collection and Processing
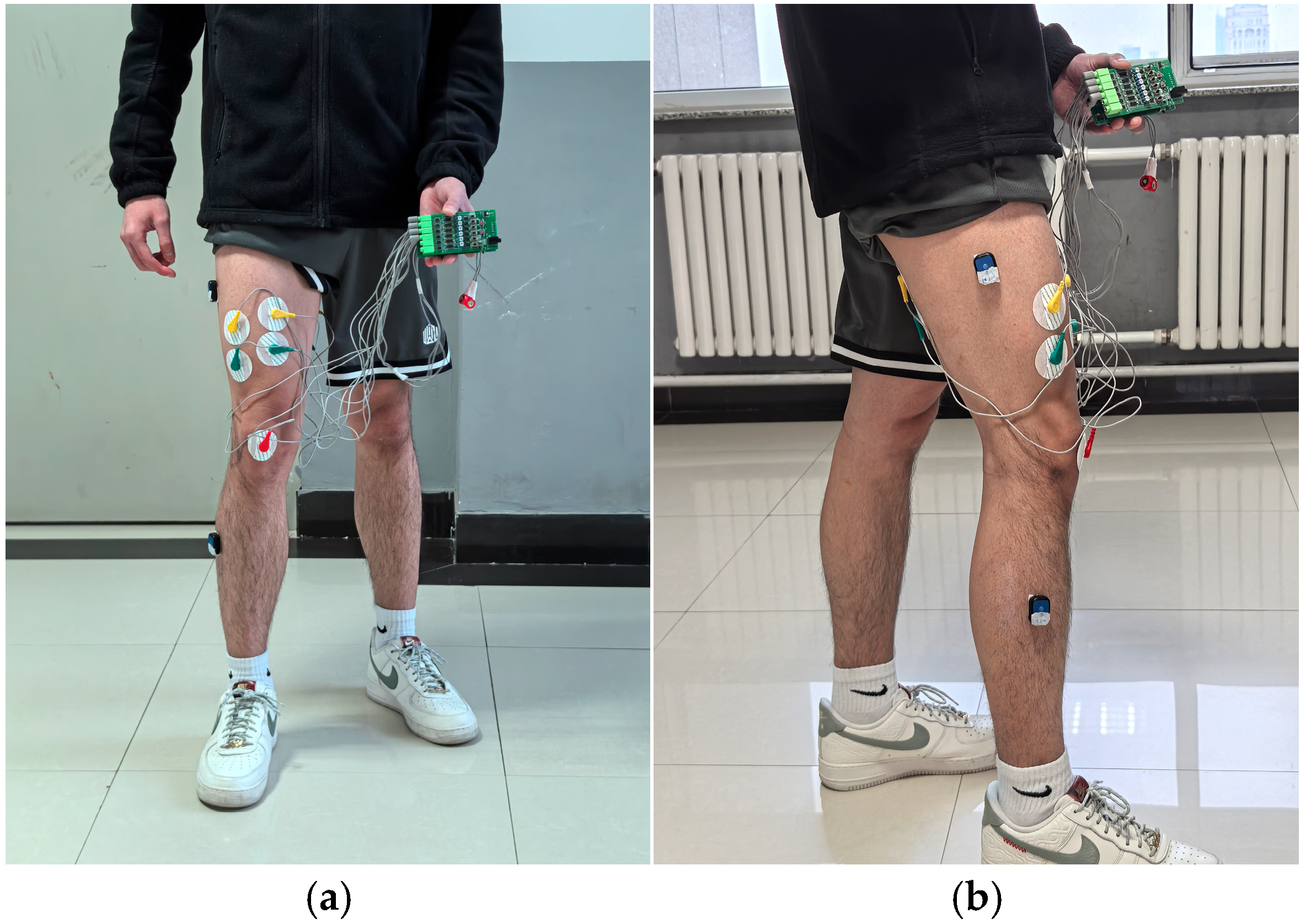
4.1. Signal Collection Equipment
4.2. Muscle Selection
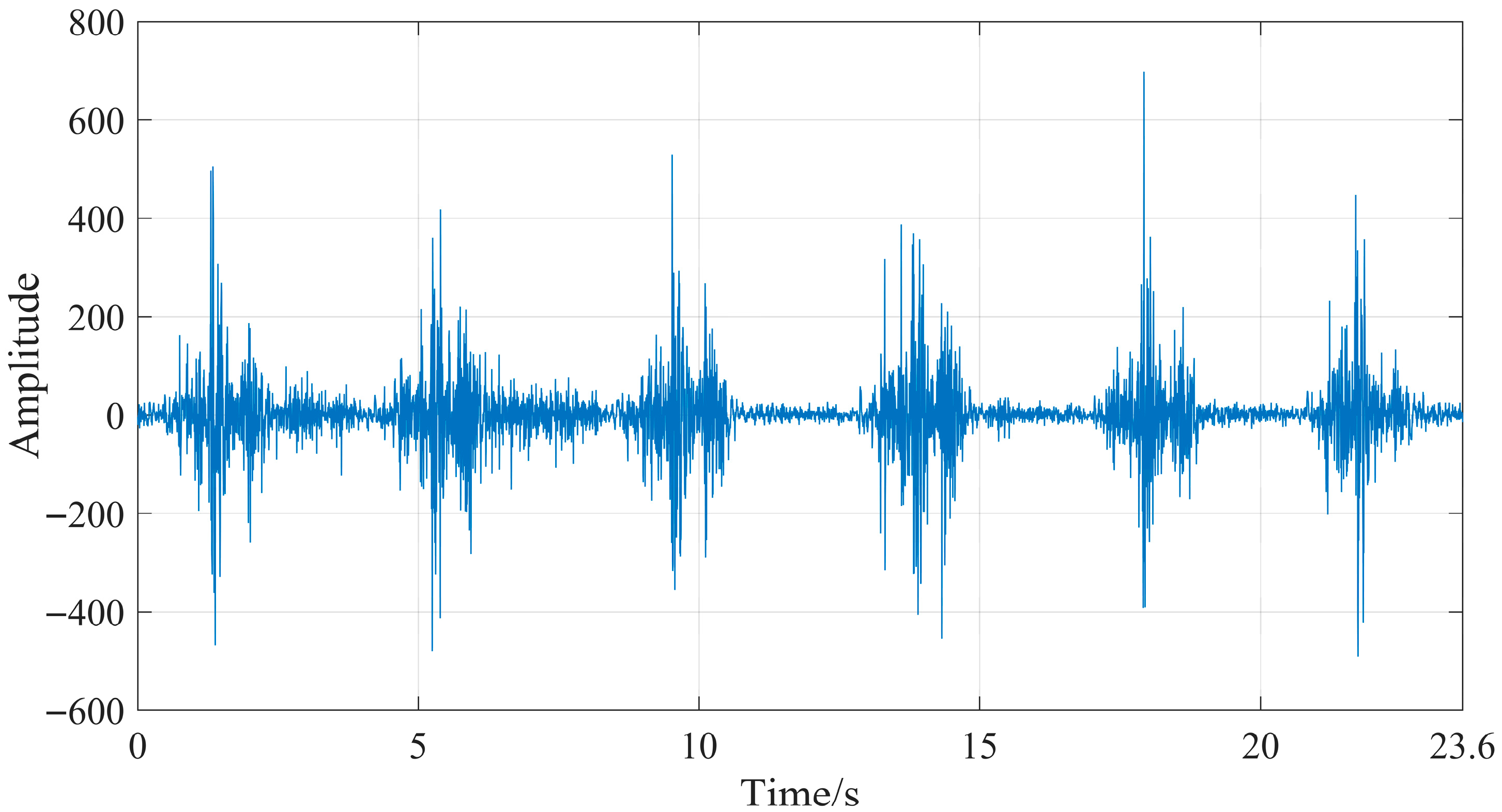
4.3. Signal Collection
4.4. Processing of sEMG Signals Based on PO-SVMD
4.4.1. Denoising Processing
4.4.2. Extraction of Absolute Peak Envelope
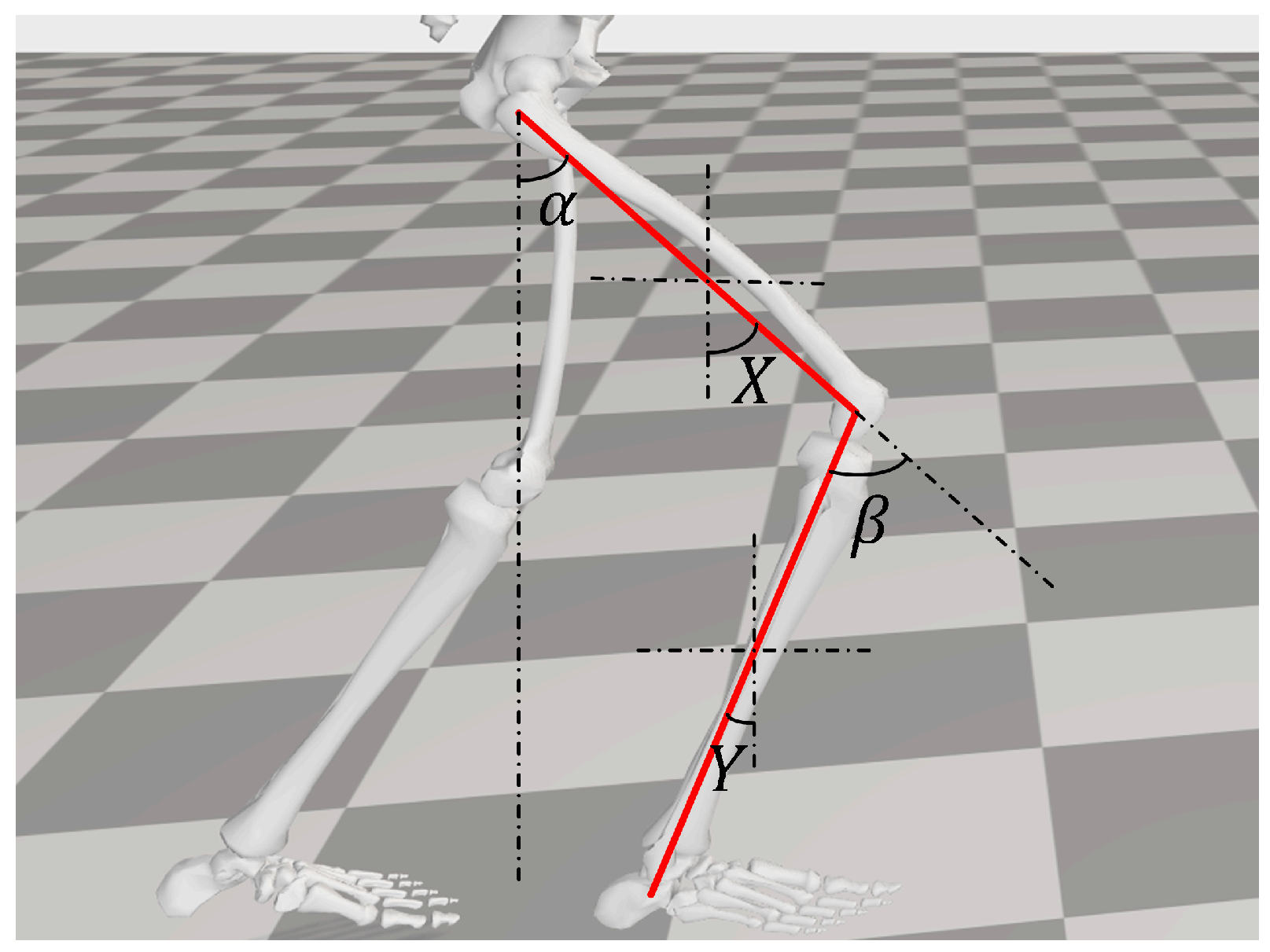
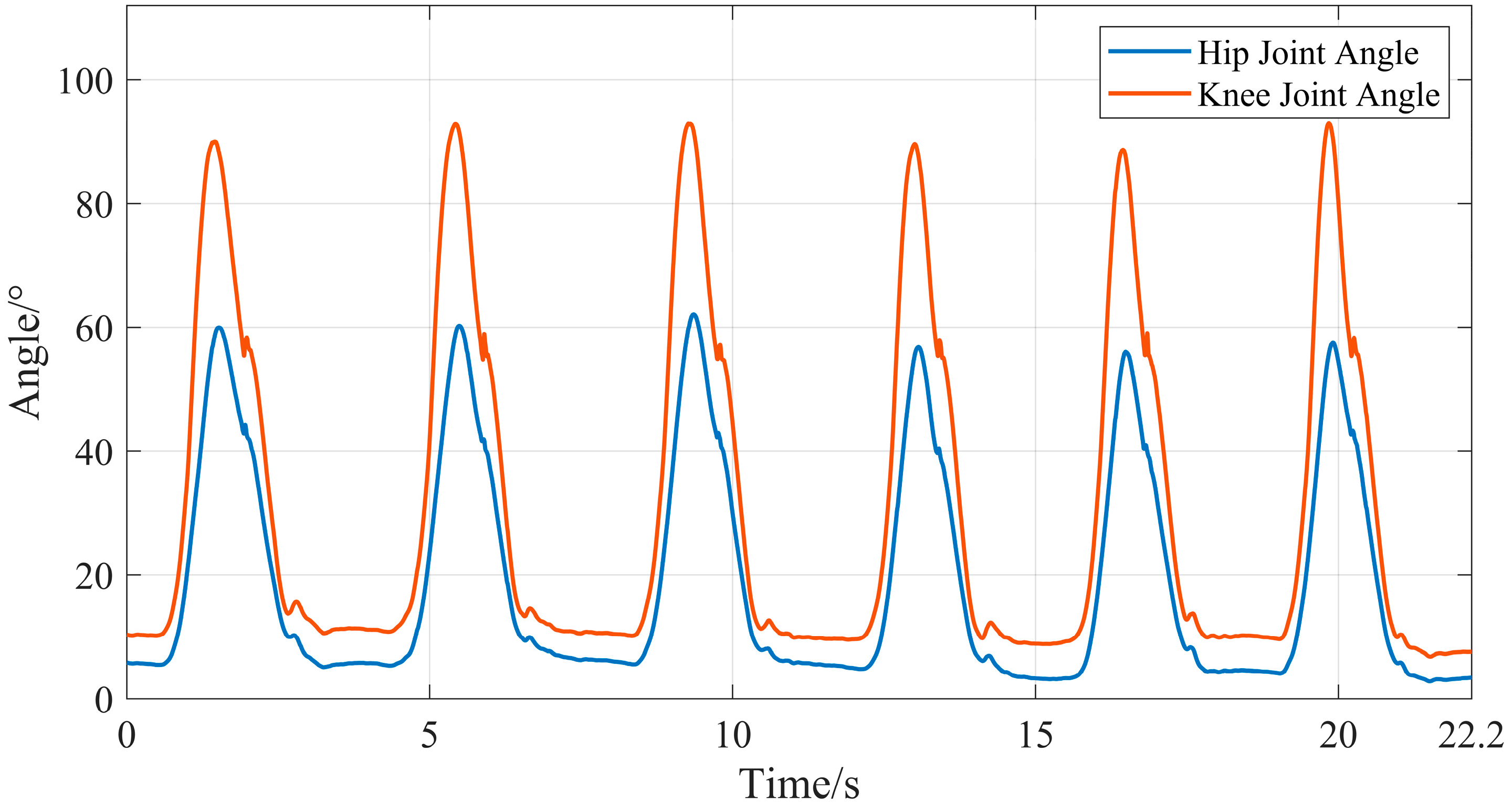
4.5. Processing of Joint Motion Angles
5. Prediction of Lower Limb Hip and Knee Joint Motion Angles Based on ResNet-GRU
5.1. Data Partitioning
5.2. Model Training
5.2.1. Model Parameter Settings
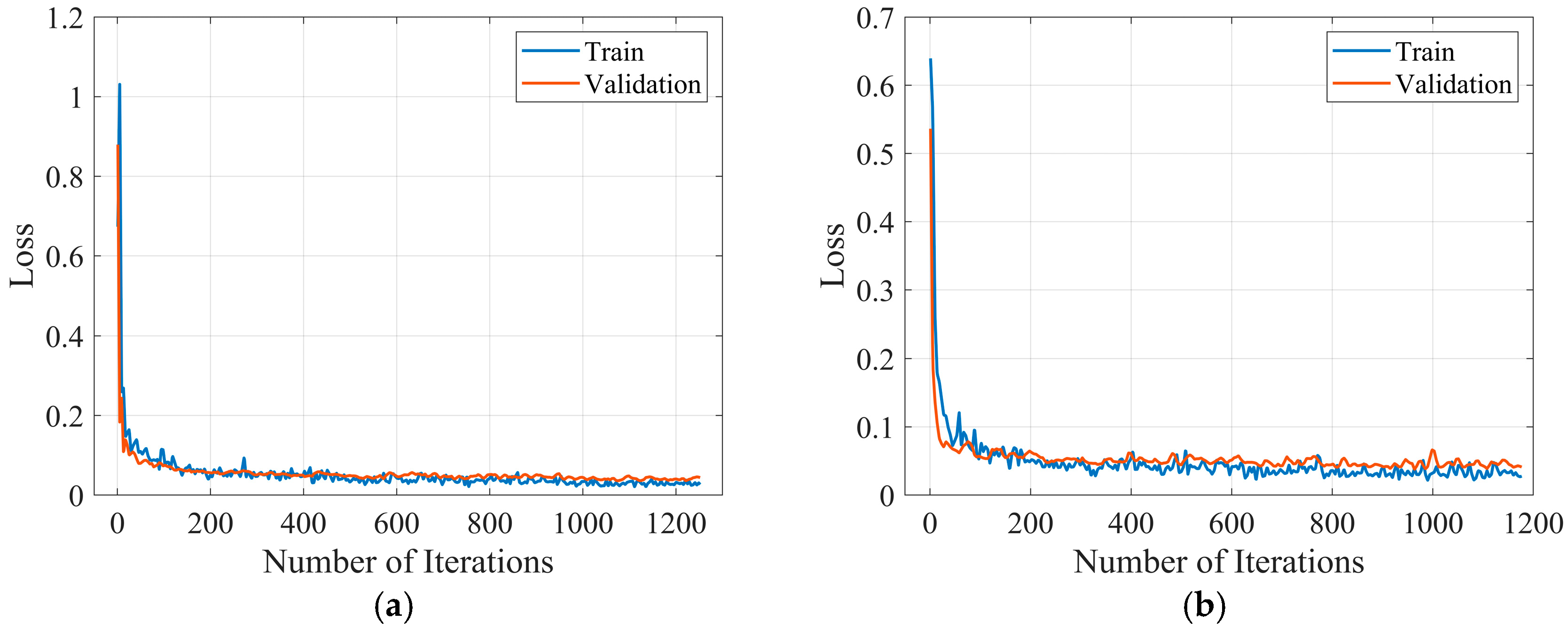
5.2.2. Training Strategy
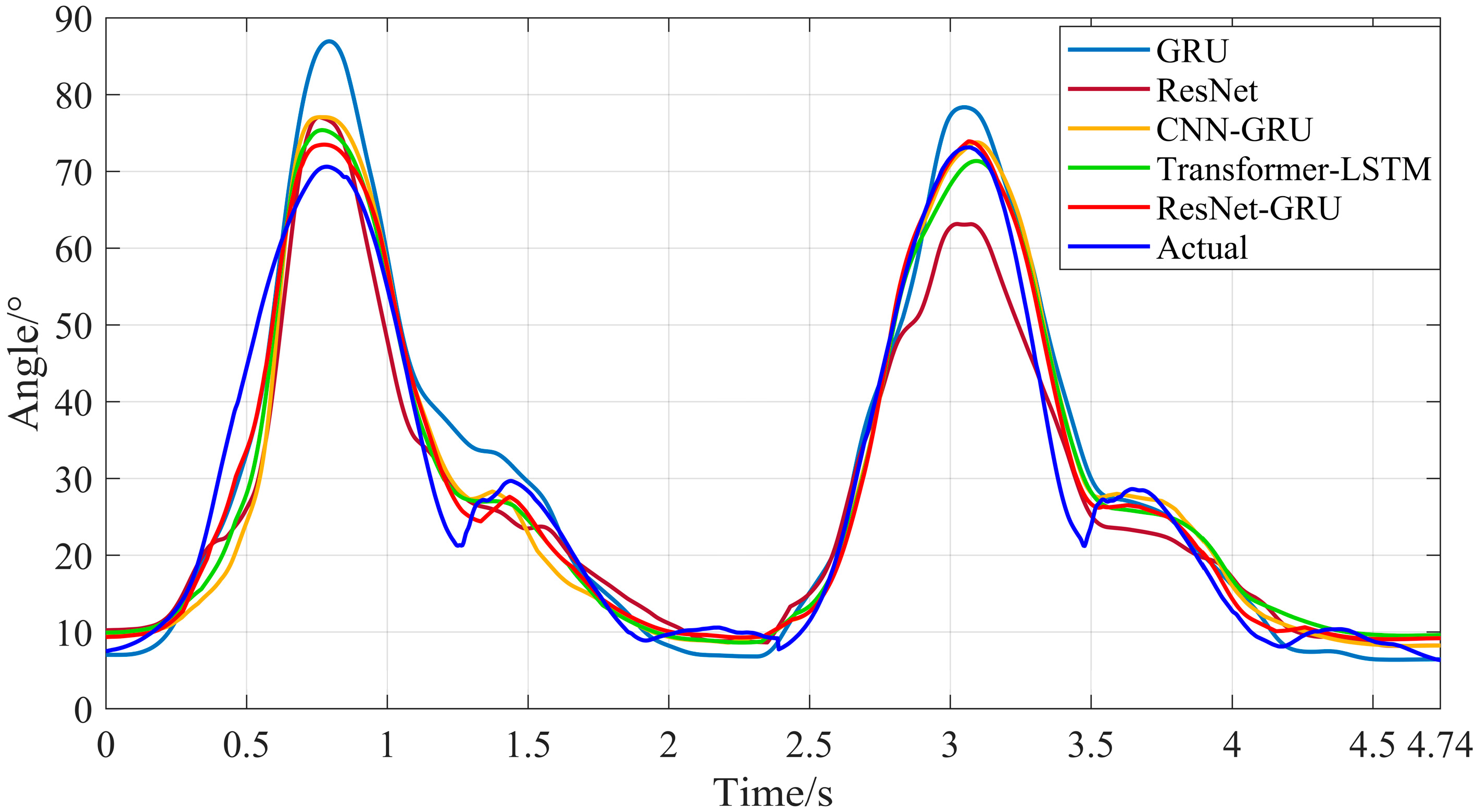
5.3. Model Test Results and Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| sEMG | surface electromyography |
| PO | Parrot Optimization |
| SVMD | Sequential Variational Mode Decomposition |
| ResNet | Residual Network |
| CNN | convolutional neural network |
| GRU | Gated Recurrent Unit |
| MAE | mean absolute error |
| R2 | C4oefficient of determination |
References
- Nanbancha, A.; Mawhinney, C.; Sinsurin, K. The effect of motor imagery and action observation in the rehabilitation of lower limb injuries: A scoping review. Clin. Rehabil. 2023, 37, 145–161. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.; Shi, P.; Yu, H. A review on human intent understanding and compliance control strategies for lower limb ex-oskeletons. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 1067–1086. [Google Scholar]
- Peng, Y.; Sakai, Y.; Nakagawa, K.; Funabora, Y.; Aoyama, T.; Yokoe, E.; Doki, S. Funabot-Suit: A bio-inspired and McKibben muscle-actuated suit for natural kinesthetic perception. Biomim. Intell. Robot. 2023, 3, 100127. [Google Scholar] [CrossRef]
- Wu, J.; Li, X.; Liu, W.; Wang, Z.J. sEMG signal processing methods: A review. J. Phys. Conf. Ser. 2019, 1237, 032008. [Google Scholar] [CrossRef]
- Laport, F.; Iglesia, D.; Dapena, A.; Castro, P.M.; Vazquez-Araujo, F.J. Proposals and comparisons from one-sensor EEG and EOG human-machine interfaces. Sensors 2021, 21, 2220. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, C.; Cai, L.; Liu, B.; Zhang, T. An improved wavelet threshold denoising approach for surface electromyography signal. EURASIP J. Adv. Signal Process. 2023, 2023, 108. [Google Scholar] [CrossRef]
- Sun, Z.; Xi, X.; Yuan, C.; Yang, Y.; Hua, X. Surface electromyography signal denoising via EEMD and improved wavelet thresholds. Math. Biosci. Eng. 2020, 17, 6945–6962. [Google Scholar] [CrossRef]
- Ashraf, H.; Shafiq, U.; Sajjad, Q.; Waris, A.; Gilani, O.; Boutaayamou, M.; Khan, S. Variational mode decomposition for surface and intramuscular EMG signal denoising. Biomed. Signal Process. Control 2023, 82, 104560. [Google Scholar] [CrossRef]
- Rani, G.J.; Hashmi, M.F.; Muhammad, G. Variational Mode Decomposition and Empirical Wavelet Transform-Based Feature Extraction and Ensemble Classifier for Lower Limb Movement Prediction with Surface Electromyography Signal. IEEE Access 2024, 12, 55201–55217. [Google Scholar] [CrossRef]
- Zhao, H.; Qiu, Z.; Peng, D.; Wang, F.; Wang, Z.; Qiu, S.; Shi, X.; Chu, Q. Prediction of Joint Angles Based on Human Lower Limb Surface Electromyography. Sensors 2023, 23, 5404. [Google Scholar] [CrossRef]
- Li, C.X.; Li, M.T.; Huang, Z.Q.; Liu, M.; Mao, Y. Application of optimized variational mode decomposition for masseter surface electromyography classification. In Proceedings of the 2025 International Conference on Artificial Intelligence and Computational Intelligence (AICI 2025), Kuala, Malaysia, 14–16 February 2025. [Google Scholar]
- Li, C.; Deng, H.; Yin, S.; Wang, C.; Zhu, Y. sEMG signal filtering study using synchrosqueezing wavelet transform with differential evolution optimized threshold. Results Eng. 2023, 18, 101150. [Google Scholar] [CrossRef]
- Yang, R.; Deng, H.; Xu, W.; Wang, X.; Li, C. Multi-stream CNN-SVM hybrid model for gesture recognition based on sEMG signals. In Proceedings of the 2023 6th International Conference on Electronics Technology (ICET 2023), Guangzhou, China, 12–15 May 2023; pp. 1435–1440. [Google Scholar]
- Li, S.; Zhang, Y.; Tang, Y.; Li, W.; Sun, W.; Yu, H. Real-time sEMG pattern recognition of multiple-mode motions for artificial limbs based on CNN-RNN algorithm. Electronics 2023, 12, 2444. [Google Scholar] [CrossRef]
- Zhu, M.; Guan, X.; Li, Z. sEMG-based lower limb motion prediction using CNN-LSTM with improved PCA optimization algo-rithm. J. Bionic Eng. 2023, 20, 612–627. [Google Scholar] [CrossRef]
- Zaim, T.; Abdel-Hadi, S.; Mahmoud, R.; Khandakar, A.; Rakhtala, S.M.; Chowdhury, M.E.H. Machine Learning- and Deep Learning-Based Myoelectric Control System for Upper Limb Rehabilitation Utilizing EEG and EMG Signals: A Systematic Review. Bioengineering 2025, 12, 144. [Google Scholar] [CrossRef]
- Nazari, M.; Sakhaei, S.M. Successive variational mode decomposition. Signal Process. 2020, 174, 107610. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, L.; Wang, K.; Jiang, T.; Luo, S.; Xu, S. Research on off-axis integrated cavity output spectrum signal denoising based on CSGWO-SVMD-SVD method. Opt. Express 2024, 32, 33698–33715. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G.; Ma, L.; Zhu, T.; Wu, X.; Heidari, A.A.; Chen, Y.; Chen, H. Parrot optimizer: Algorithm and applications to medical problems. Comput. Biol. Med. 2024, 172, 108064. [Google Scholar] [CrossRef]
- Koppolu, P.K.; Chemmangat, K. A Comparison of Different Signal Processing Techniques for Upper Limb Muscle Activity Onset Detection using Surface Electromyography. In Proceedings of the 2023 3rd International conference on Artificial Intelligence and Signal Processing (AISP), Vijayawada, India, 18–20 March 2023. [Google Scholar]
- Zhao, H.; Wang, Z.; Yang, Y.; Zhang, Z. FastICA-based noise reduction algorithm for surface electromyographic signals. In Proceedings of the 2024 4th International Conference on Neural Networks, Information and Communication Engineering (NNICE), Guangzhou, China, 19–21 January 2024. [Google Scholar]
- Vijayvargiya, A.; Khimraj; Kumar, R.; Dey, N. Voting-based 1D CNN model for human lower limb activity recognition using sEMG signal. Phys. Eng. Sci. Med. 2021, 44, 1297–1309. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Hou, J.; Li, G.; Sun, B.; Lu, P. Deep Learning for Electromyographic Lower-Limb Motion Signal Classification Using Residual Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 2078–2086. [Google Scholar] [CrossRef] [PubMed]
- Zarzycki, K.; Ławryńczuk, M. Advanced predictive control for GRU and LSTM networks. Inf. Sci. 2022, 616, 229–254. [Google Scholar] [CrossRef]
- Latash, M.L. Human Movements: Synergies, Stability, and Agility. In Biomechanics of Anthropomorphic Systems; Springer: Cham, Switzerland, 2018; Volume 124, pp. 135–154. [Google Scholar]
- Lv, S.; Tao, C.; Zhai, Y.; Shi, W.; Hou, Z.; Ni, H.; Tan, L. Research on noise reduction of pressure pulsation signal of axial flow pump based on global optimization parrot algorithm improved variational mode decomposition. Phys. Fluids 2025, 37, 077185. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, Y.; Wen, Y.; Luo, X. Whale sound signal denoising based on SVMD and improved wavelet thresholding. Meas. Sci. Technol. 2024, 35, 095008. [Google Scholar] [CrossRef]
- Koppolu, P.K.; Chemmangat, K. Automatic selection of IMFs to denoise the sEMG signals using EMD. J. Electromyogr. Kinesiol. 2023, 73, 102834. [Google Scholar] [CrossRef]
- Zhu, M.; Guan, X.; Li, Z.; Gao, Y.; Zou, K.; Gao, X.; Wang, Z.; Li, H.; Cai, K. Prediction of knee trajectory based on surface electromyogram with independent component analysis combined with support vector regression. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221119668. [Google Scholar] [CrossRef]
- Sharma, T.; Sharma, K.P.; Veer, K. Decomposition and evaluation of SEMG for hand prostheses control. Measurement 2021, 186, 110102. [Google Scholar] [CrossRef]
- De la Fuente, C.; Martinez-Valdes, E.; Priego-Quesada, J.I.; Weinstein, A.; Valencia, O.; Kunzler, M.R.; Alvarez-Ruf, J.; Carpes, F.P. Understanding the effect of window length and overlap for assessing sEMG in dynamic fatiguing contractions: A non-linear dimensionality reduction and clustering. J. Biomech. 2021, 125, 110598. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Liang, S. sEMG-based recognition of wrist-hand movements using a composite transformer-LSTM model. Rev. Sci. Instrum. 2025, 96, 085208. [Google Scholar] [CrossRef] [PubMed]














| Subject | Gender | Height/cm | Weight/kg | Health Status |
|---|---|---|---|---|
| 1 | Male | 175 | 65 | Health |
| 2 | Female | 169 | 58 | Health |
| 3 | Male | 178 | 70 | Health |
| 4 | Female | 165 | 55 | Health |
| 5 | Male | 172 | 62 | Health |
| IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | |
| G | 0.0434 | 0.0270 | 0.0237 | 0.0465 | 0.0605 |
| IMF6 | IMF7 | IMF8 | IMF9 | IMF10 | |
| G | 0.0649 | 0.0727 | 0.0738 | 0.0560 | 0.0427 |
| Muscle | PO-SVMD Combine with WT | PEEMD | EMD | ICA | WT |
|---|---|---|---|---|---|
| Rectus Femoris | 19.56 | 13.02 | 12.31 | 15.69 | 13.36 |
| Vastus Lateralis | 16.75 | 14.31 | 13.92 | 11.35 | 12.03 |
| Semitendinosus | 18.26 | 14.78 | 12.11 | 17.65 | 15.62 |
| Biceps Femoris | 19.48 | 18.13 | 16.48 | 16.29 | 13.58 |
| Muscle | PO-SVMD Combine with WT | PEEMD | EMD | ICA | WT |
|---|---|---|---|---|---|
| Rectus Femoris | 23.42 | 20.36 | 18.69 | 16.28 | 20.68 |
| Vastus Lateralis | 20.25 | 16.09 | 16.94 | 17.26 | 9.63 |
| Semitendinosus | 21.69 | 17.56 | 16.28 | 11.62 | 18.55 |
| Biceps Femoris | 20.76 | 18.23 | 15.74 | 14.09 | 10.81 |
| Number of Residual Modules | Number of GRU Modules | Hip Joint | Knee Joint |
|---|---|---|---|
| 1 | 1 | 2.8342 | 3.3294 |
| 1 | 2 | 2.3156 | 2.5305 |
| 2 | 2 | 1.6642 | 1.9204 |
| 2 | 3 | 1.9865 | 2.1688 |
| 3 | 2 | 2.3245 | 2.3647 |
| 3 | 3 | 2.3689 | 2.4651 |
| Number of Residual Modules | Number of GRU Modules | Hip Joint | Knee Joint |
|---|---|---|---|
| 1 | 1 | 2.642 | 3.234 |
| 1 | 2 | 2.2612 | 2.8622 |
| 2 | 2 | 1.9487 | 2.6324 |
| 2 | 3 | 1.9243 | 2.2624 |
| 3 | 2 | 2.0289 | 2.3351 |
| 3 | 3 | 2.164 | 2.6135 |
| Structure | Parameters | Output |
|---|---|---|
| Residual block 1 | (convolutional kernel size 10 × 1, number 128, BN, ReLU) × 1 (convolutional kernel size 10 × 1, number 64, BN, ReLU) × 1 | 4 × 1 × 64 |
| Residual block 2 | (convolutional kernel size 10 × 1, number 128, BN, ReLU) × 1 (convolutional kernel size 10 × 1, number 64, BN, ReLU) × 1 | 4 × 1 × 64 |
| GRU block 1 | 128 hidden layer nodes, dropout rate 0.25 | 128 |
| GRU block 2 | 64 hidden layer nodes, dropout rate 0.25 | 64 |
| GRU block 3 | 32 hidden layer nodes, dropout rate 0.25 | 32 |
| Structure | Parameters | Output |
|---|---|---|
| Residual block 1 | (convolutional kernel size 10 × 1, number 128, BN, ReLU) × 1 (convolutional kernel size 10 × 1, number 64, BN, ReLU) × 1 | 4 × 1 × 64 |
| Residual block 2 | (convolutional kernel size 10 × 1, number 128, BN, ReLU) × 1 (convolutional kernel size 10 × 1, number 64, BN, ReLU) × 1 | 4 × 1 × 64 |
| GRU block 1 | 128 hidden layer nodes, dropout rate 0.25 | 128 |
| GRU block 2 | 64 hidden layer nodes, dropout rate 0.25 | 64 |
| Structure | Parameters | Output |
|---|---|---|
| Input layer | sEMG signal | 4 × 1 × 1 |
| Initial convolutional layer | convolutional kernel size 10 × 1, number 64 | 4 × 1 × 64 |
| Normalization layer | BN | 4 × 1 × 64 |
| Activation function layer | ReLU | 4 × 1 × 64 |
| Pooling layer | average pooling, pooling window stride 4, number 64 | 1 × 1 × 64 |
| Unfolding layer | sequence unfolding | 1 × 1 × 64 |
| Flattening layer | flattening | 64 |
| Fully connected layer | 64 weights, 2 biases | 2 |
| Output layer | hip and knee joint motion angle | 2 |
| Model | Hip Joint | Knee Joint | ||||
|---|---|---|---|---|---|---|
| RMSE/° | MAE/° | R2 | RMSE/° | MAE/° | R2 | |
| ResNet-GRU | 2.512 ± 0.415 | 1.863 ± 0.265 | 0.979 ± 0.007 | 3.785 ± 0.386 | 2.487 ± 0.325 | 0.973 ± 0.006 |
| Transformer-LSTM | 3.642 ± 0.468 | 2.785 ± 0.324 | 0.96 ± 0.008 | 4.658 ± 0.445 | 3.215 ± 0.346 | 0.952 ± 0.007 |
| CNN-GRU | 3.956 ± 0.428 | 3.112 ± 0.293 | 0.949 ± 0.01 | 5.587 ± 0.506 | 3.612 ± 0.325 | 0.931 ± 0.01 |
| ResNet | 4.925 ± 0.516 | 4.238 ± 0.372 | 0.93 ± 0.011 | 5.798 ± 0.603 | 4.189 ± 0.443 | 0.923 ± 0.013 |
| GRU | 4.568 ± 0.574 | 3.512 ± 0.426 | 0.94 ± 0.01 | 5.987 ± 0.562 | 4.295 ± 0.395 | 0.92 ± 0.012 |
| Model | Hip Joint | Knee Joint | ||||
|---|---|---|---|---|---|---|
| RMSE/° | MAE/° | R2 | RMSE/° | MAE/° | R2 | |
| ResNet-GRU | 2.475 ± 0.442 | 2.012 ± 0.336 | 0.98 ± 0.009 | 4.086 ± 0.453 | 3.485 ± 0.412 | 0.976 ± 0.008 |
| Transformer-LSTM | 3.485 ± 0.526 | 3.087 ± 0.352 | 0.958 ± 0.009 | 5.062 ± 0.532 | 4.398 ± 0.435 | 0.961 ± 0.008 |
| CNN-GRU | 4.315 ± 0.469 | 3.572 ± 0.334 | 0.936 ± 0.011 | 6.612 ± 0.615 | 5.638 ± 0.487 | 0.927 ± 0.011 |
| ResNet | 5.126 ± 0.574 | 4.258 ± 0.398 | 0.911 ± 0.012 | 7.852 ± 0.674 | 6.598 ± 0.543 | 0.908 ± 0.013 |
| GRU | 5.098 ± 0.623 | 4.412 ± 0.465 | 0.914 ± 0.011 | 7.615 ± 0.652 | 6.398 ± 0.574 | 0.911 ± 0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Wang, M.; Sun, D.; Jia, Z.; Yue, Z. Study on Lower Limb Motion Intention Recognition Based on PO-SVMD-ResNet-GRU. Processes 2025, 13, 3252. https://doi.org/10.3390/pr13103252
Li W, Wang M, Sun D, Jia Z, Yue Z. Study on Lower Limb Motion Intention Recognition Based on PO-SVMD-ResNet-GRU. Processes. 2025; 13(10):3252. https://doi.org/10.3390/pr13103252
Chicago/Turabian StyleLi, Wei, Mingsen Wang, Daxue Sun, Zhuoda Jia, and Zhengwei Yue. 2025. "Study on Lower Limb Motion Intention Recognition Based on PO-SVMD-ResNet-GRU" Processes 13, no. 10: 3252. https://doi.org/10.3390/pr13103252
APA StyleLi, W., Wang, M., Sun, D., Jia, Z., & Yue, Z. (2025). Study on Lower Limb Motion Intention Recognition Based on PO-SVMD-ResNet-GRU. Processes, 13(10), 3252. https://doi.org/10.3390/pr13103252





