Numerical Study of 3D Heat Transfer in Heat Sinks with Circular Profile Fins Using CFD
Abstract
1. Introduction
2. Materials and Methods
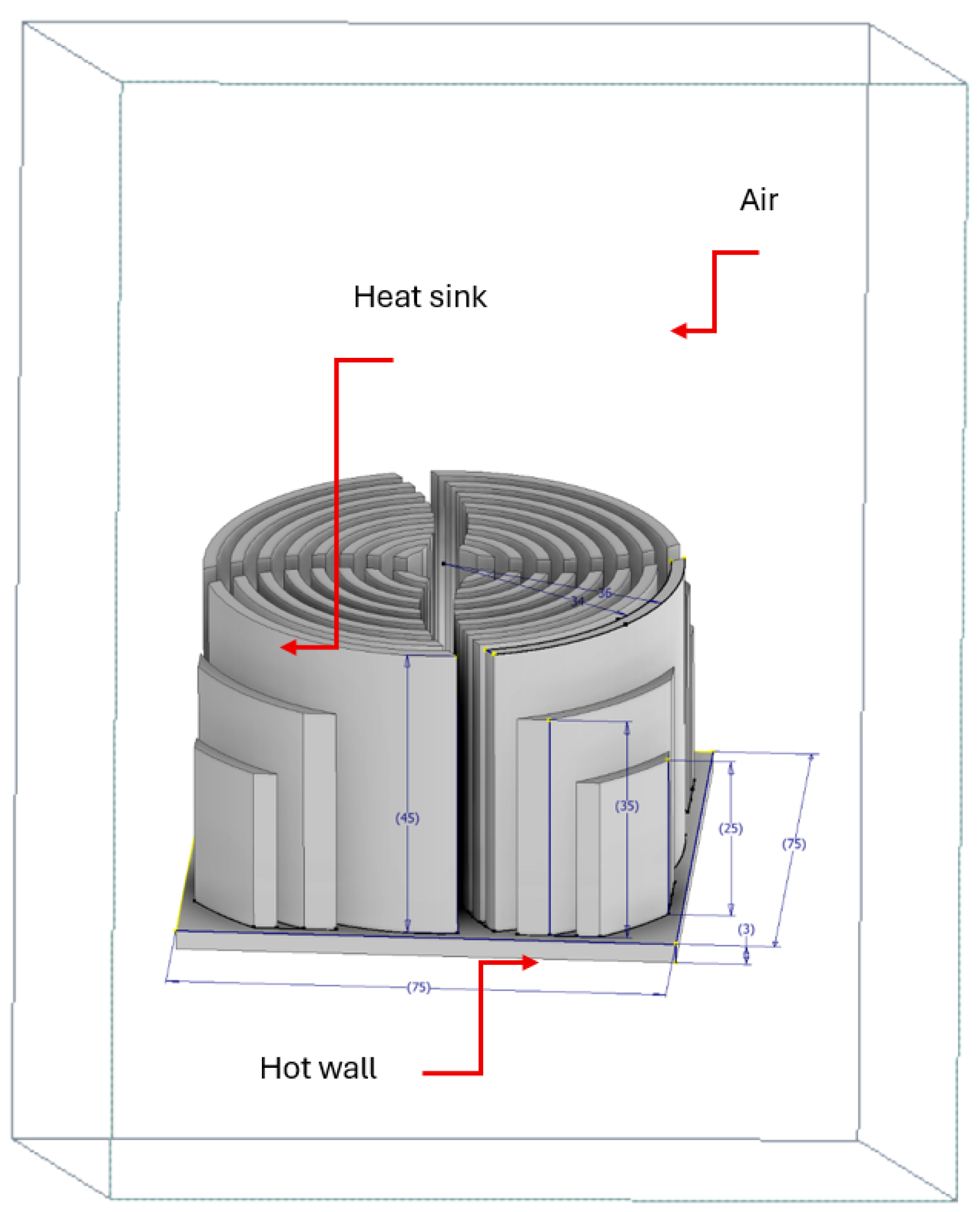
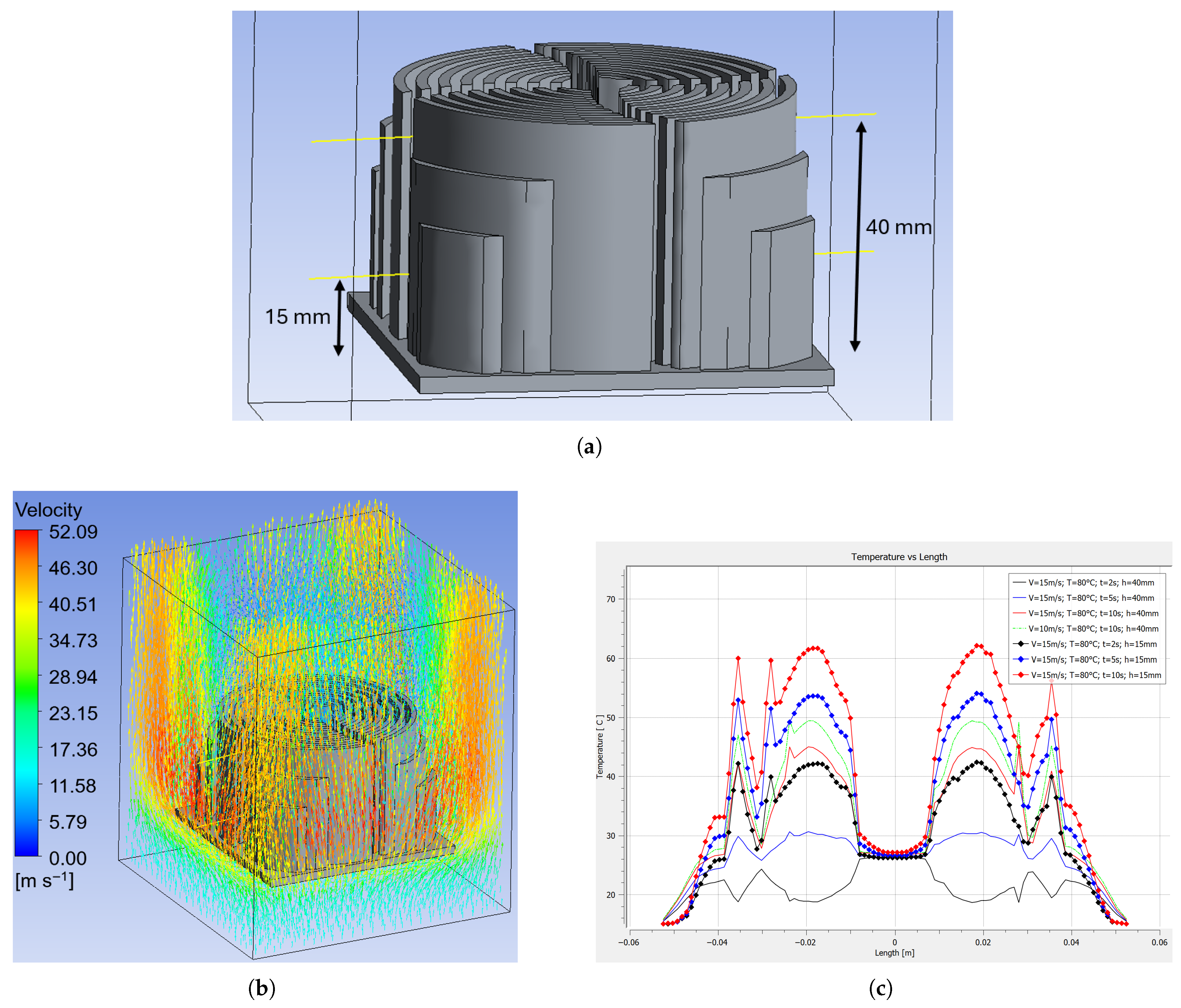
2.1. Geometry and Meshing
2.2. Governing Equations
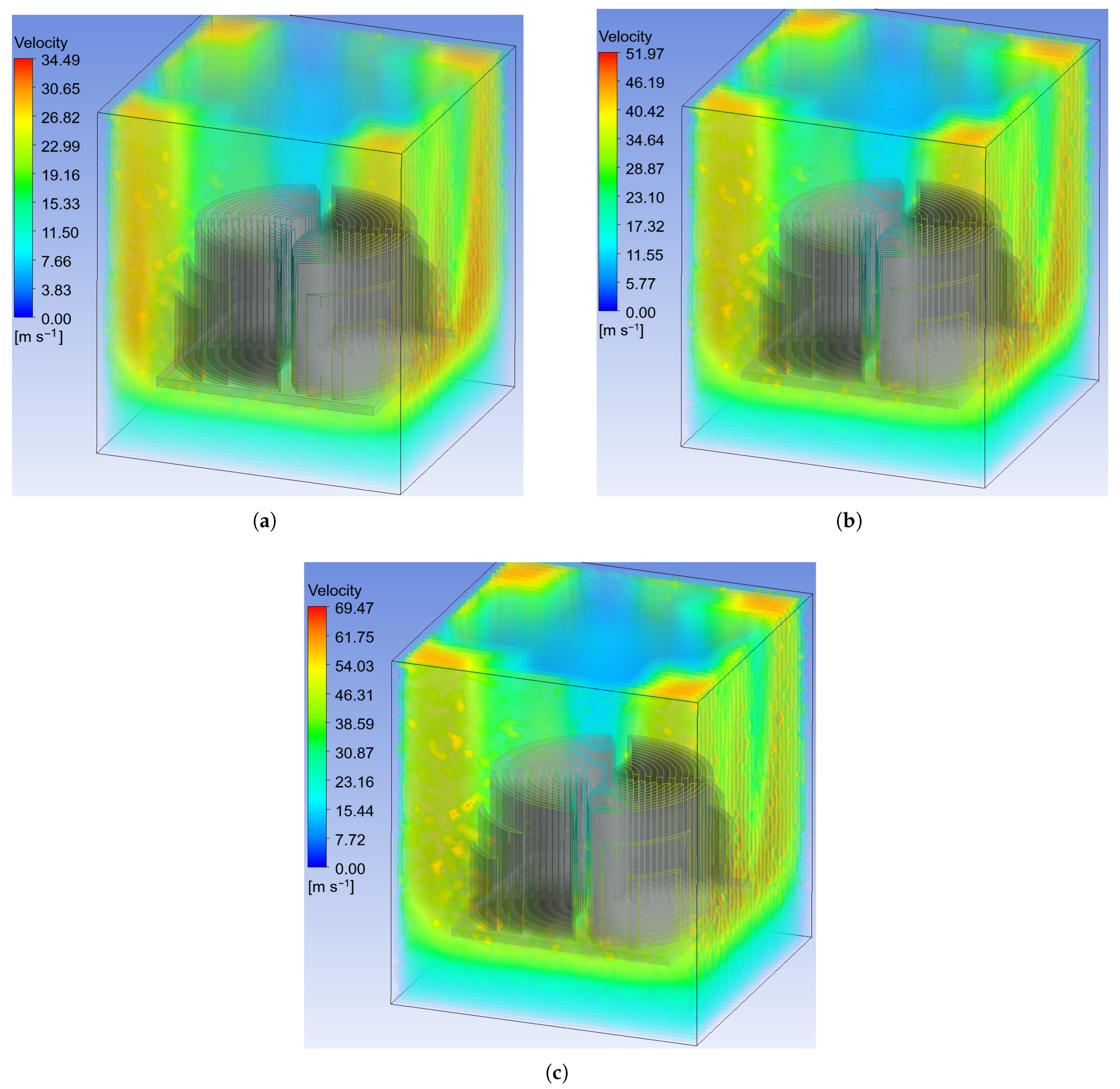
3. Results and Discussion
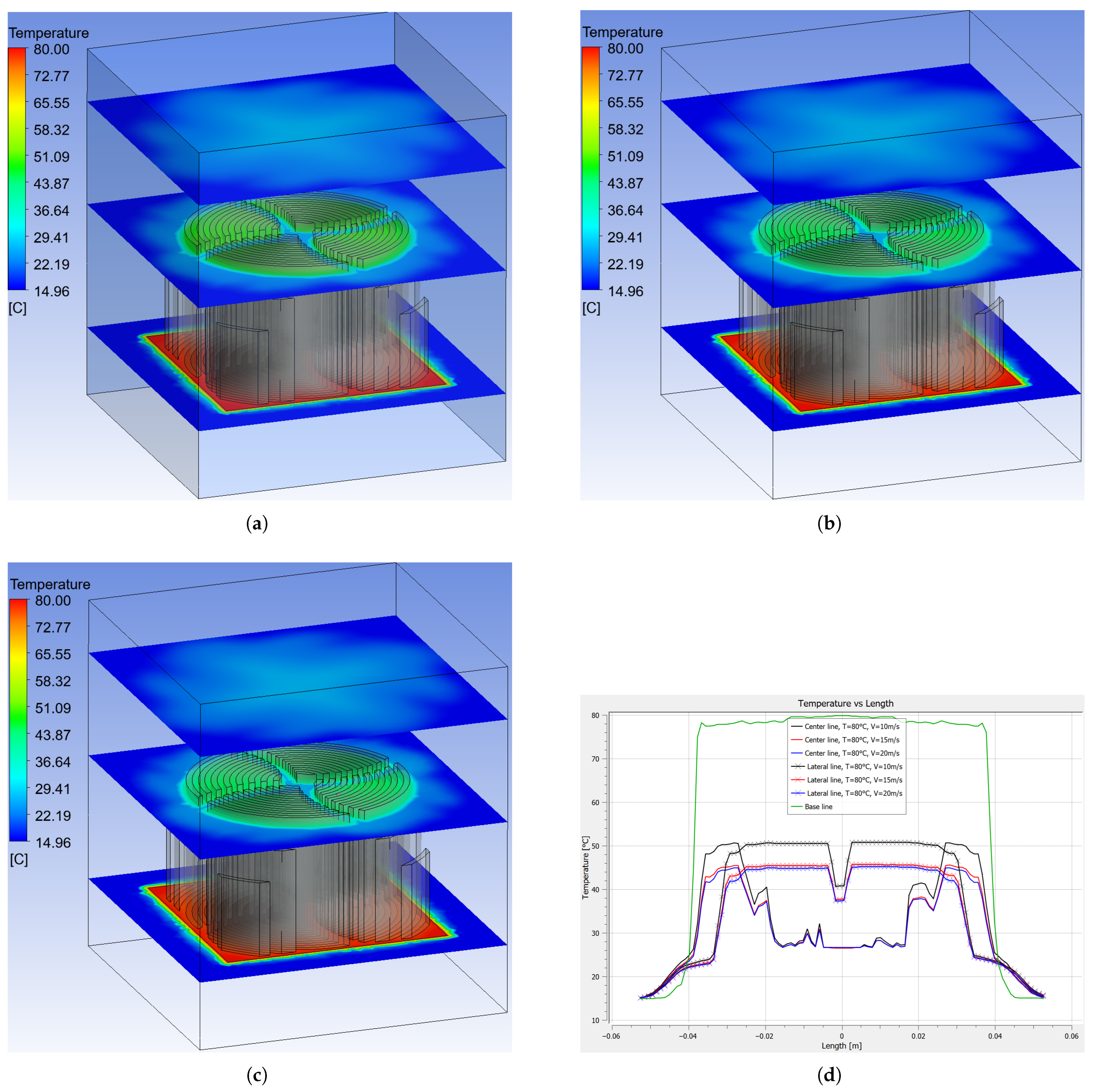
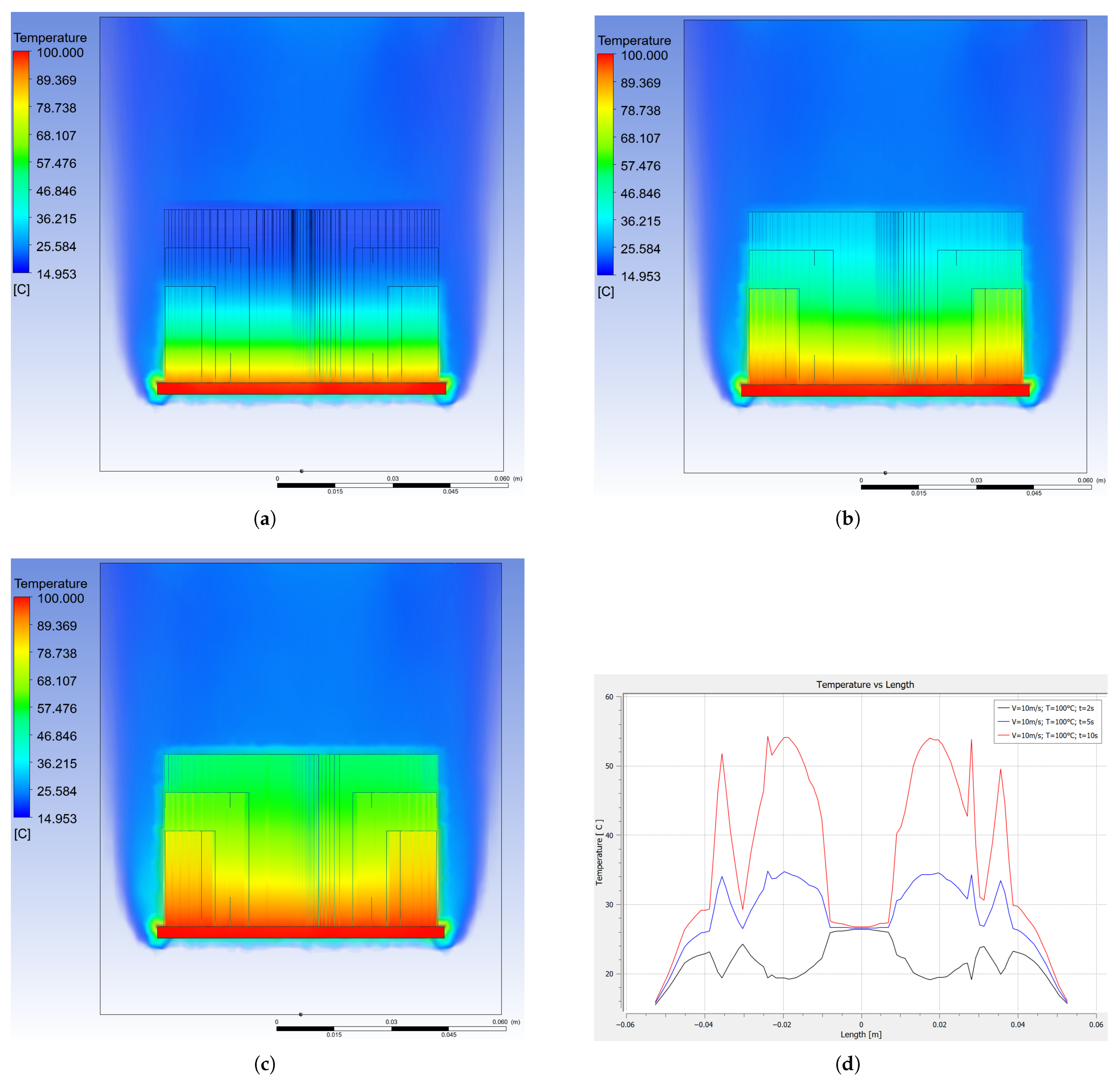
3.1. Temperature at the Heat Sink for Time 2 s
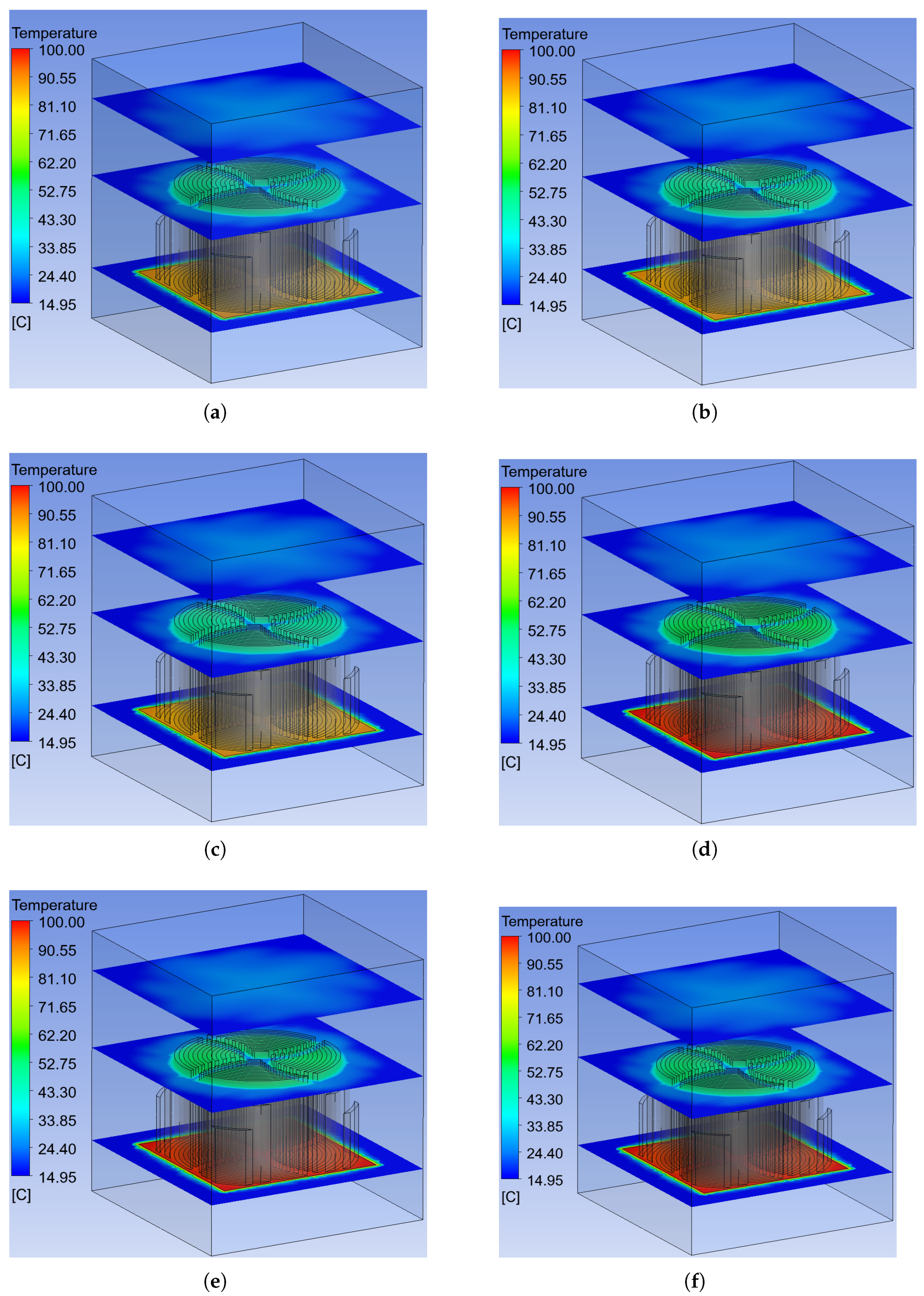
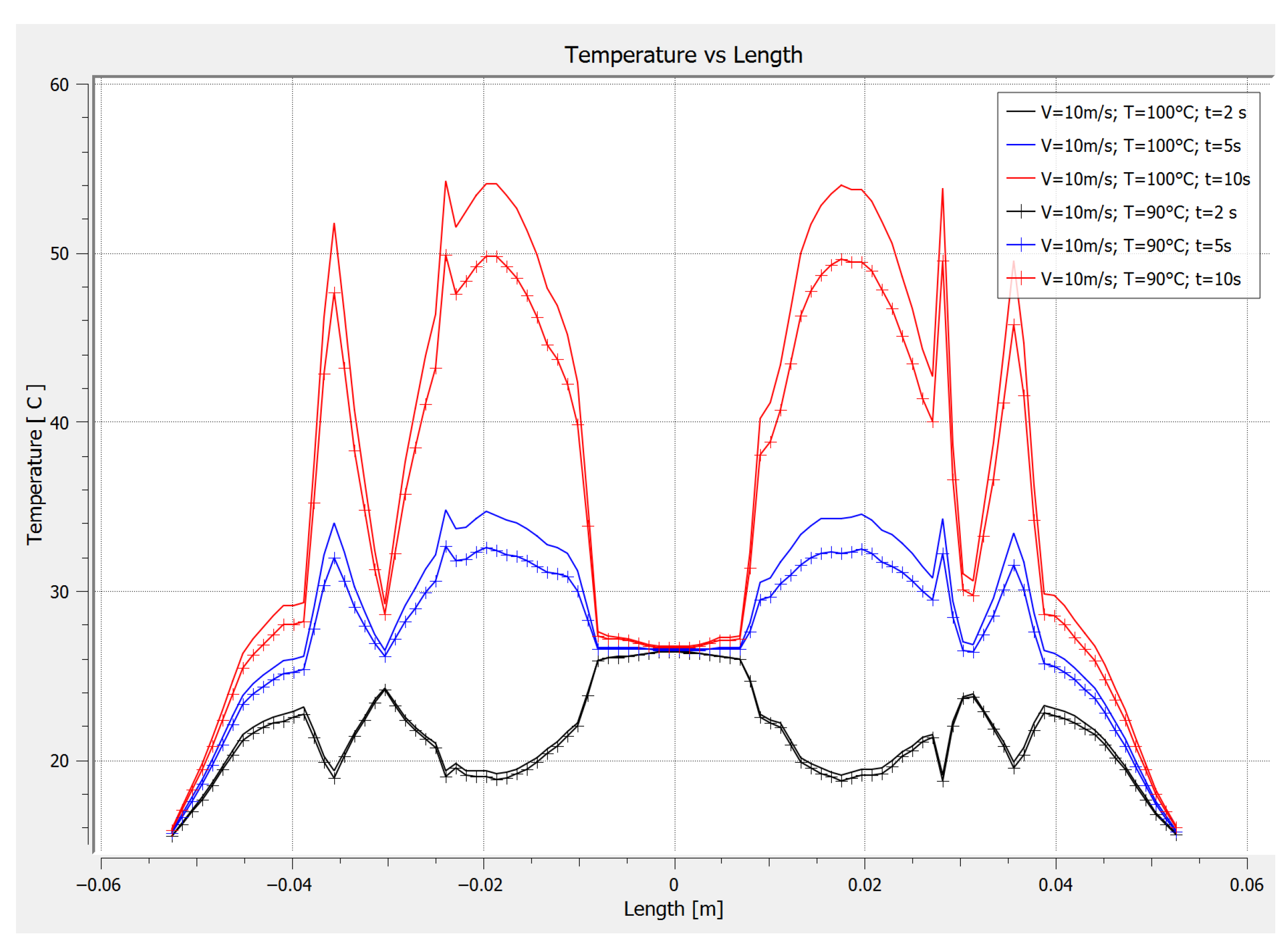
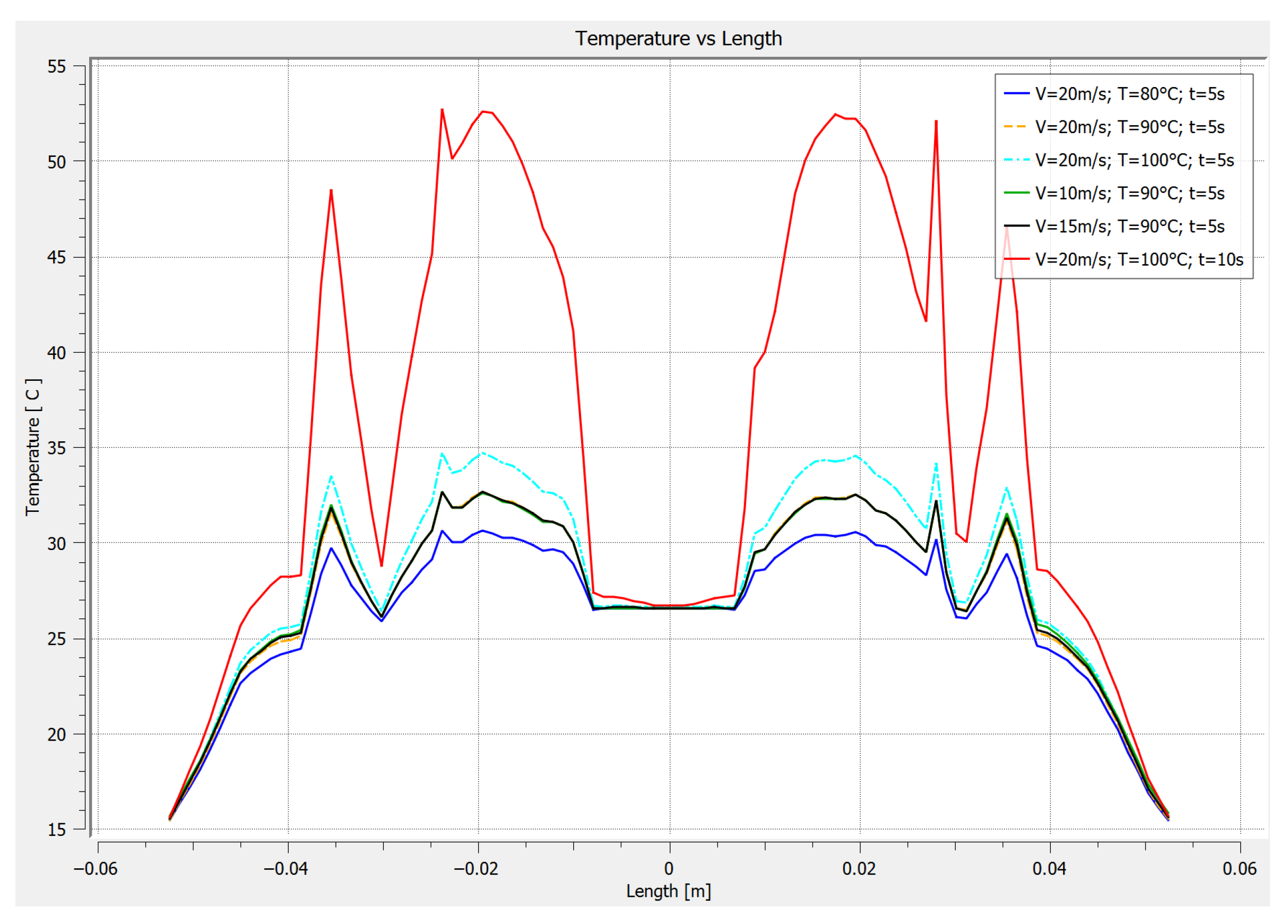
3.2. Temperature for Analysis Times
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haghighi, S.S.; Goshayeshi, H.R.; Safaei, M.R. Natural convection heat transfer enhancement in new designs of plate-fin based heat sinks. Int. J. Heat Mass Transf. 2018, 125, 640–647. [Google Scholar] [CrossRef]
- Khalaf-Allah, R.A.; Eid, E.I.; Ellithy, A.E.H.A.; Easa, A.S. Experimental investigation of the influence of modifying the inner tube outer surface on free convection in a concentrated double pipe. Exp. Heat Transf. 2024, 37, 335–355. [Google Scholar] [CrossRef]
- Shakeri, H.; Moghadasi, H.; Saffari, H. Experimental parametric study of hierarchical micro/nano electrodeposited (six-step) pattern with respect to volcano-shape morphology in pool boiling performance augmentation. Exp. Heat Transf. 2023, 36, 210–233. [Google Scholar] [CrossRef]
- Fuse, H.; Oe, S.; Haga, T. Effects of Fin Height, Base Thickness, Blackening, Emissivity and Thermal Conductivity on Heat Dissipation of Die-Cast Aluminum Alloy Heat Sink. Metals 2025, 15, 696. [Google Scholar] [CrossRef]
- Şevik, S.; Özdilli, Ö.; Akbulut, F. Numerical investigation of the effect of different heat sink fin structures on the thermal performance of automotive LED headlights. Int. J. Automot. Sci. Technol. 2022, 6, 17–26. [Google Scholar] [CrossRef]
- Mallikarjuna, V.; Rajesh, K.; Ramesh, K.; Reddy, B.R.B. Modeling and Optimization of shape of a Heat Sink Fins on Motherboard. J. Comput. Math. Sci. 2015, 65, 228–251. [Google Scholar]
- Zhong, L.; Shi, J.; Li, Y.; Wang, Z. Thermo-Hydrodynamic Features of Grooved Heat Sink with Droplet-Shaped Fins Based on Taguchi Optimization and Field Synergy Analysis. Energies 2025, 18, 3396. [Google Scholar] [CrossRef]
- Moustafa, S.; Wei, G.; Hamid, H.; Abd El-Hamid, M. Thermal management of cascaded finned heat sink incorporating phase change material using optimization with multiple objectives approach. Appl. Therm. Eng. 2025, 279, 127735. [Google Scholar] [CrossRef]
- Xiong, M.; Wang, N.; Li, W.; Garg, A.; Gao, L. Study on the Heat Dissipation Performance of a Liquid Cooling Battery Pack with Different Pin-Fins. Batteries 2023, 9, 44. [Google Scholar] [CrossRef]
- Nilpueng, K.; Ahn, H.S.; Jerng, D.W.; Wongwises, S. Heat transfer and flow characteristics of sinusoidal wavy plate fin heat sink with and without crosscut flow control. Int. J. Heat Mass Transf. 2019, 137, 565–572. [Google Scholar] [CrossRef]
- Ebere, I.E.; Khan, A.A.; Ogundahunsi, S.; Ugwuemeaju, E.; Khan, U.A.; Ahmed, S. Design and Optimization of the Heatsink of a Level 1 Electric Vehicle Charger. Energies 2025, 18, 180. [Google Scholar] [CrossRef]
- Li, M.; Gao, X.; Li, H.; Ma, Y.; Sang, J.; Xu, T. Effect of curvature ratio on curved microchannel heat sinks. Int. J. Thermofluids 2024, 22, 100635. [Google Scholar] [CrossRef]
- Kahbandeh, F.; Azarifar, M.; Arik, M.; Harris, D.K. Numerical simulation of thermal performance of radial manifold microchannel heat sink for electronics thermal management. Therm. Sci. Eng. Prog. 2025, 65, 103930. [Google Scholar] [CrossRef]
- Chatterjee, R.; Duryodhan, V.S.; Agrawal, A. Impact of aspect ratio and thermophysical properties on heat transfer behavior in spiral microchannel. Int. J. Therm. Sci. 2022, 172, 107335. [Google Scholar] [CrossRef]
- Narendran, G.; Mallikarjuna, B.; Nagesha, B.K.; Gnanasekaran, N. Experimental investigation on additive manufactured single and curved double layered microchannel heat sink with nanofluids. Heat Mass Transf. 2023, 59, 1311–1332. [Google Scholar] [CrossRef]
- Singh, A.; Singh, V.; Trivedi, V. Optimization and numerical simulation of heat sink for cooling electronic chip. Int. J. Energy Water Resour. 2025, 9, 1317–1338. [Google Scholar] [CrossRef]
- Fattahi, R.; Saidi, M. Numerical investigation of curved shape fins height effect on heat transfer and flow characteristics in open microchannel heat sink. Int. J. Therm. Sci. 2023, 185, 108060. [Google Scholar] [CrossRef]
- Ashrafi, M.M.A.; Hosseini, S.M.J.; Ranjbar, A.A.; Pahamli, Y.; Bahrampoury, R. Innovative Disk and Helical Fin Designs for Thermohydrodynamic Enhancement of Minichannel Heat Sinks. Case Stud. Therm. Eng. 2025, 73, 106613. [Google Scholar] [CrossRef]
- Mohsen, H.K.; Hamza, N. Investigation of laminar forced convection using a different shape of a heat sink. Al-Qadisiyah J. Eng. Sci. 2022, 15, 73–80. [Google Scholar] [CrossRef]
- Yildirim, O.G.; Ozkan, G.M. Enhancement of heat transfer by inclined holes through perforated heat sinks. Int. J. Therm. Sci. 2025, 213, 109810. [Google Scholar] [CrossRef]
- Gupta, D.; Saha, P.; Roy, S. Computational analysis of perforation effect on the thermo-hydraulic performance of micro pin-fin heat sink. Int. J. Therm. Sci. 2021, 163, 106857. [Google Scholar] [CrossRef]
- Jasim, A.A.; Fazlizan, A.; Azeez, H.L.; Ibrahim, A.; Almaawi, R.; Sopian, K. Enhancing PV Module Performance Through a Novel Fin Heat Sink Design: A Numerical and Experimental Study. Case Stud. Therm. Eng. 2025, 74, 106842. [Google Scholar] [CrossRef]
- Djebara, A.; Bessanane, N.; Si-Ameur, M.; Ibrahim, A.; Al-Tarabsheh, A.; Noui, Z.; Azeez, H.L.; Imad ud din, S.; Ishak, A.A. Performance evaluation of a Folded heat sink designs for solar cell Cooling: Numerical study. Therm. Sci. Eng. Prog. 2025, 63, 103724. [Google Scholar] [CrossRef]
- Nazzal, I.T.; Salem, T.K.; Al Doury, R.R.J. Theoretical investigation of a pin fin heat sink performance for electronic cooling using different alloys materials. Iop Conf. Ser. Mater. Sci. Eng. 2021, 1094, 012087. [Google Scholar] [CrossRef]
- ANSYS. Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2011; Volume 15317, pp. 724–746. [Google Scholar]
- Kosdere, O.; Sert, Z.; Altun, O. Investigation of thermal performance at forced convection in plate-fin heat sink. Energy 2024, 307, 132621. [Google Scholar] [CrossRef]

| Properties | Aluminum | Air (15 °C) | Unit |
|---|---|---|---|
| Density | 2719 | 1.225 | kg/m3 |
| Specific heat Cp | 871 | 1006 | J/kg·K |
| Thermal conductivity | 202.4 | 0.0247 | W/m·k |
| Viscosity | - | 1.082 × 10−5 | Pa·s |
| Mesh No. | Max. Element Size (mm) | Node Elements | Average (Skewness) |
|---|---|---|---|
| 1 | 8 | 65,624 | 0.35245 |
| 2 | 5 | 128,415 | 0.28346 |
| 3 | 4 | 209,823 | 0.25009 |
| 4 | 3 | 441,003 | 0.21811 |
| Temperature (°C) | Velocity (m/s) | Time (s) |
|---|---|---|
| 80 | 10 | 2 |
| 90 | 15 | 5 |
| 100 | 20 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toapanta-Ramos, F.; Guashco Rubio, M.; Ortega-Loza, F.; Diaz, W. Numerical Study of 3D Heat Transfer in Heat Sinks with Circular Profile Fins Using CFD. Processes 2025, 13, 3199. https://doi.org/10.3390/pr13103199
Toapanta-Ramos F, Guashco Rubio M, Ortega-Loza F, Diaz W. Numerical Study of 3D Heat Transfer in Heat Sinks with Circular Profile Fins Using CFD. Processes. 2025; 13(10):3199. https://doi.org/10.3390/pr13103199
Chicago/Turabian StyleToapanta-Ramos, Fernando, Mayra Guashco Rubio, Fernando Ortega-Loza, and William Diaz. 2025. "Numerical Study of 3D Heat Transfer in Heat Sinks with Circular Profile Fins Using CFD" Processes 13, no. 10: 3199. https://doi.org/10.3390/pr13103199
APA StyleToapanta-Ramos, F., Guashco Rubio, M., Ortega-Loza, F., & Diaz, W. (2025). Numerical Study of 3D Heat Transfer in Heat Sinks with Circular Profile Fins Using CFD. Processes, 13(10), 3199. https://doi.org/10.3390/pr13103199






