Research on Optimization Method of Operating Parameters for Electric Submersible Pumps Based on Multiphase Flow Fitting
Abstract
1. Introduction
- (1)
- Liquid Level Monitoring through Sensors:
- (2)
- Regulation through Electrical Parameter Alarm Mechanisms:
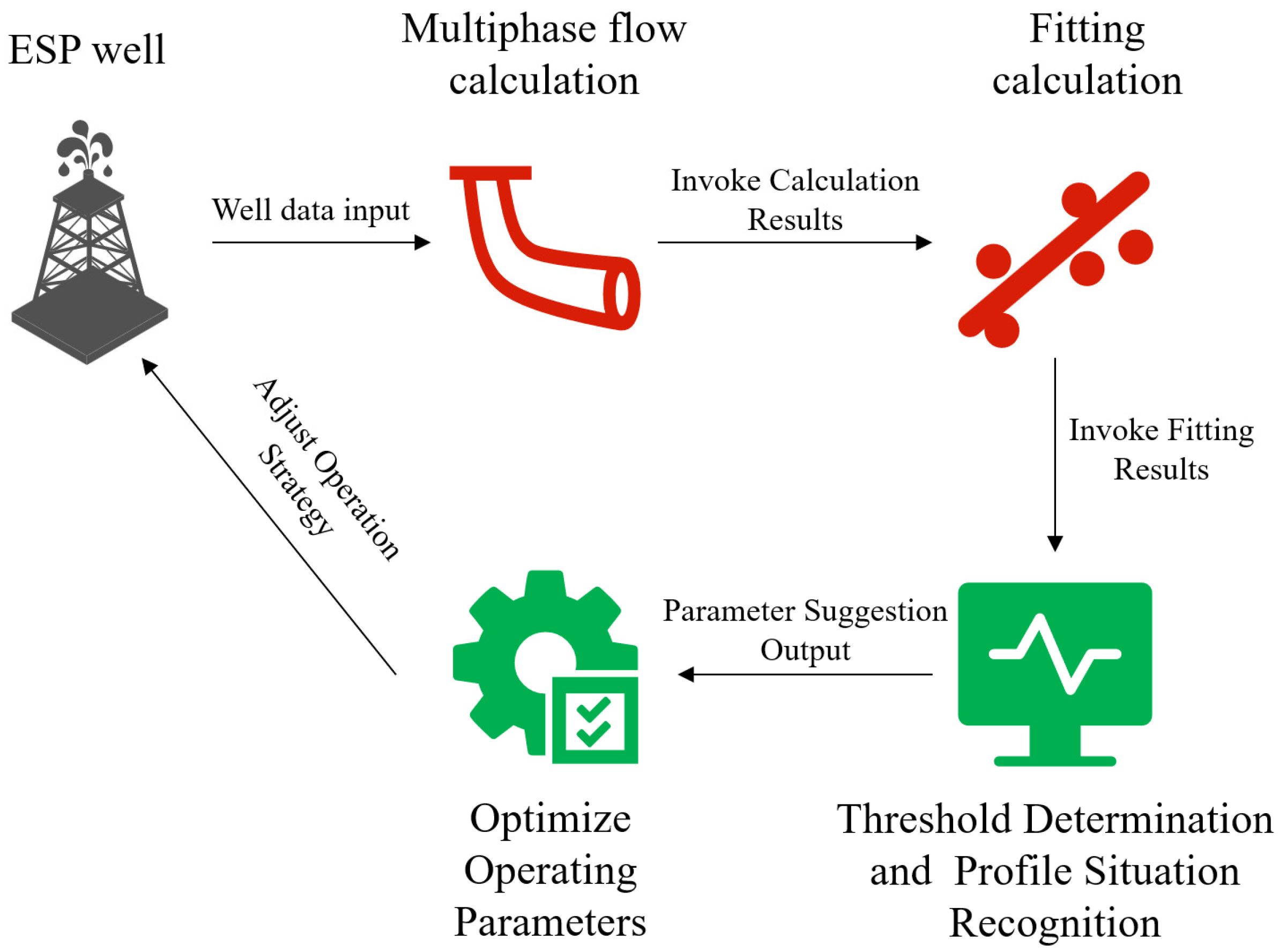
2. Fitting Model and Parameter Optimization Method
2.1. Multiphase Flow Calculation Model
- (1)
- Pressure Gradient Calculation:
- ①
- Frictional Pressure Gradient
- ②
- Hydrostatic Pressure Gradient
- ③
- Acceleration Pressure Gradient
- (2)
- Liquid hold-up calculation:
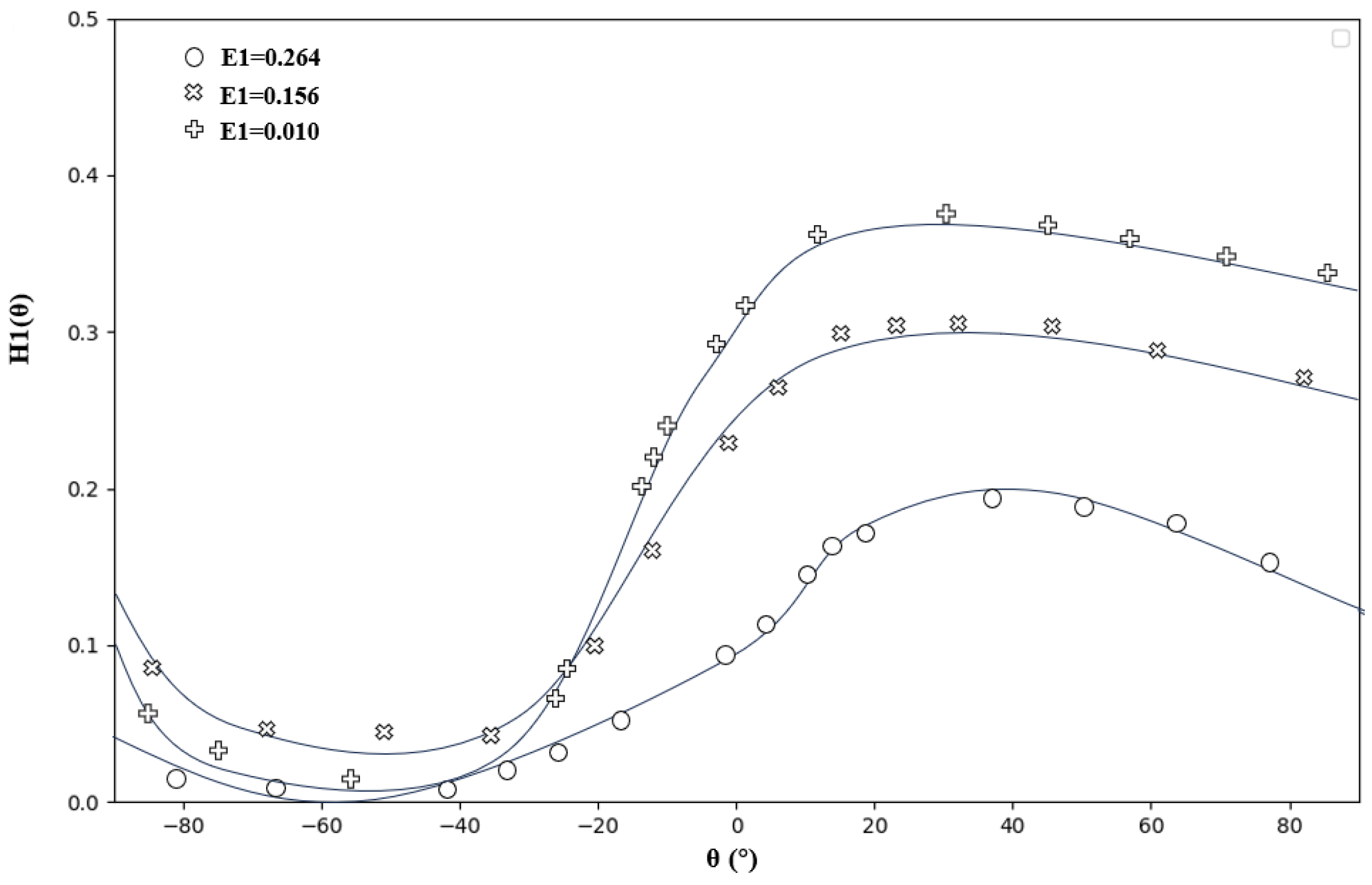
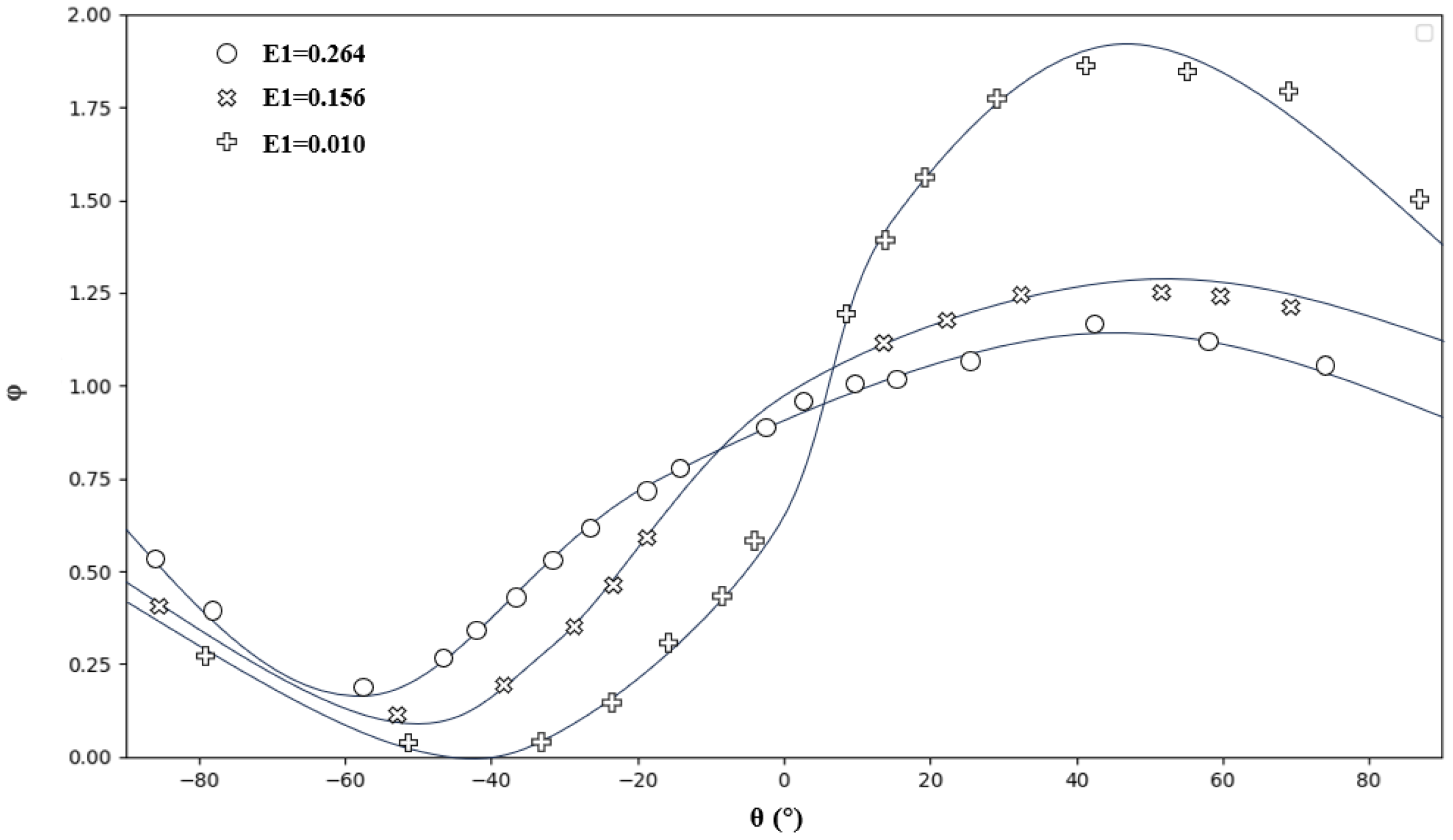
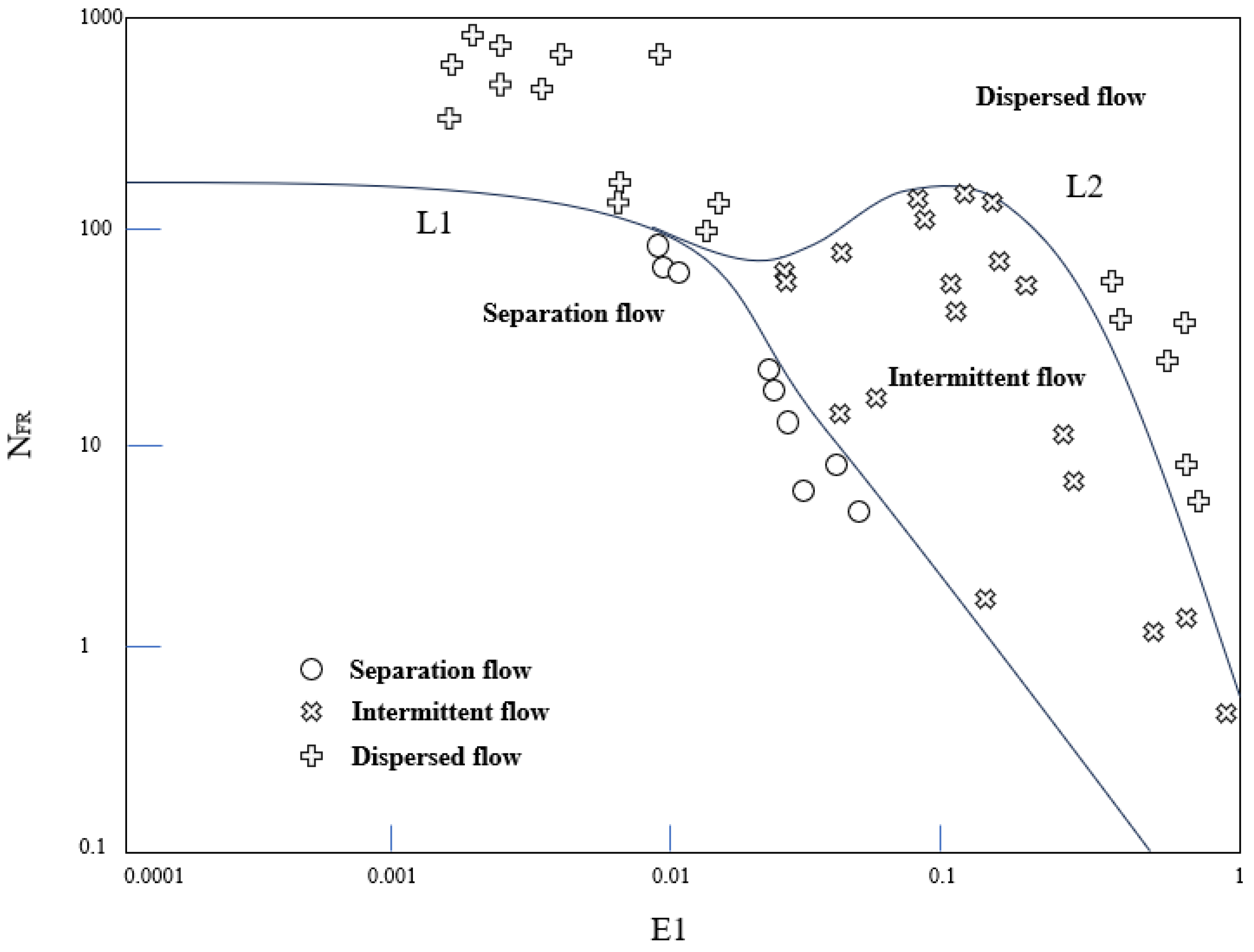
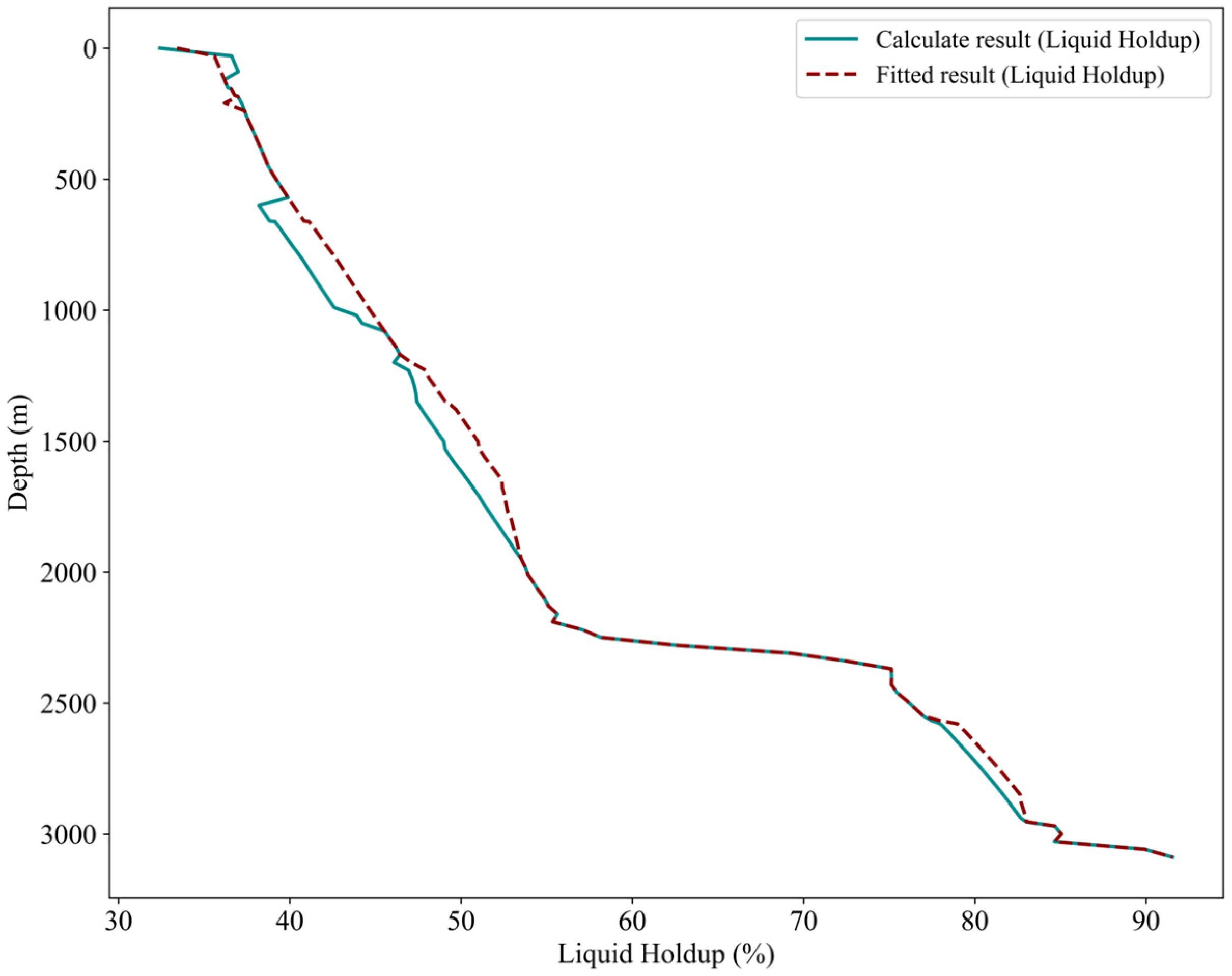
2.2. Multiphase Flow Fitting Model
2.3. Design of Rule-Based Parameter Optimization Logic Based on Fitted Flow Profile
- The principle of frequency optimization is as follows:
- (1)
- Low Liquid Proportion at the Inlet:
- ①
- Reducing Gas Entrainment: By lowering the pump operating speed, gas entrainment can be minimized, restoring gas–liquid separation and optimizing the flow state at the inlet section.
- ②
- Mitigating Pressure Fluctuations: Moderately reducing the pump frequency helps alleviate pressure fluctuations caused by increased gas, thus maintaining pressure balance within the wellbore.
- ③
- Reducing Equipment Wear: Frequency adjustments can also reduce mechanical wear on equipment, prolonging the pump’s lifespan and decreasing maintenance frequency.
- (2)
- Low Inlet Pressure
- 2.
- The basic principle of optimizing the nozzle opening is as follows:
- (1)
- Insufficient Liquid Column Height
- (2)
- High Back Pressure
- 3
- Optimization of Pump Shutdown Time
- (1)
- Periodic Gas Lock
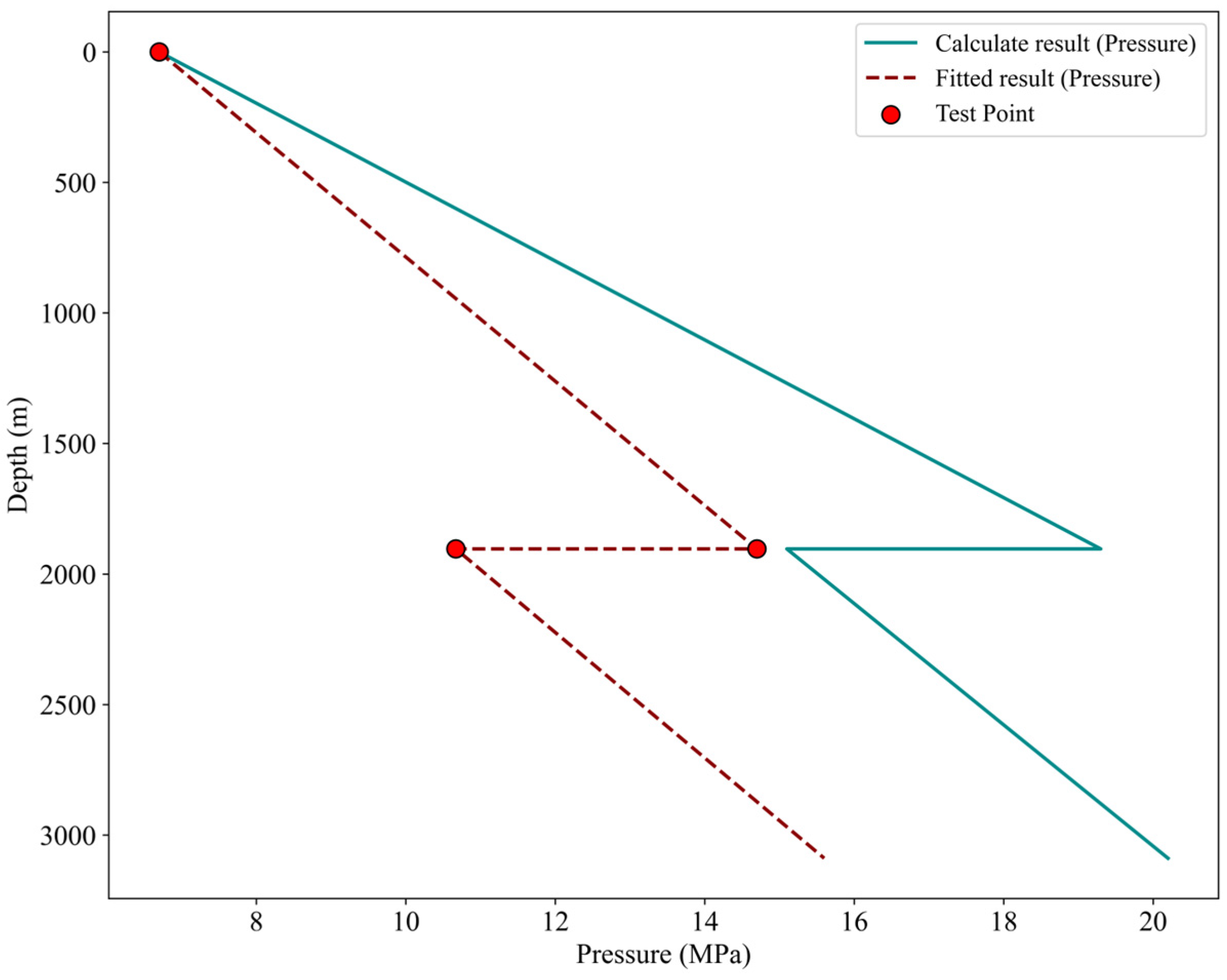
3. Experiments and Result Verification
- (1)
- Well A1:
- (2)
- Well A2:
- (3)
- Well A3:
- (1)
- The average daily liquid production increased from 107 m3/d to 140 m3/d, indicating a certain improvement in yield.
- (2)
- The stable operating duration of the pump increased from 10.6 h to 22.3 h.
- (3)
- The coefficient of fluctuation in pump current decreased from 0.21 to 0.08, indicating a more stable operating state.
- (4)
- The energy consumption per unit of liquid produced decreased from 2.7 kWh/m3 to 2.2 kWh/m3, indicating a significant gain in energy efficiency and implying tangible economic benefits through reduced power expenditures.
4. Conclusions
- (1)
- The method proposed in this paper, based on the multi-phase flow fitting in the wellbore, can effectively reconstruct the gas–liquid profile, thereby identifying flow anomalies during operation. This innovative approach provides real-time monitoring of flow status for the ESP system, contributing to enhanced operational stability.
- (2)
- By analyzing the identified anomalies in the flow profile, this paper developed optimization control recommendations, including adjustments to frequency, choke valve opening, and start-stop durations. These recommendations not only improve the operational efficiency of the ESP but also provide scientific decision-making support for operators.
- (3)
- Compared with traditional alarm methods, the proposed profile-matching approach reduced the false alarm rate from ~25% to <10% and shortened the average response time from more than 10 min to less than 2 min. Relative to MCSA-based approaches, which report typical detection accuracies of around 80%, the proposed method achieved over 90% accuracy in identifying gas interference events. In contrast to sensor-based methods, which require additional hardware investment of 15–20% CAPEX, our approach relies solely on existing well data, thus significantly reducing implementation costs.
- (4)
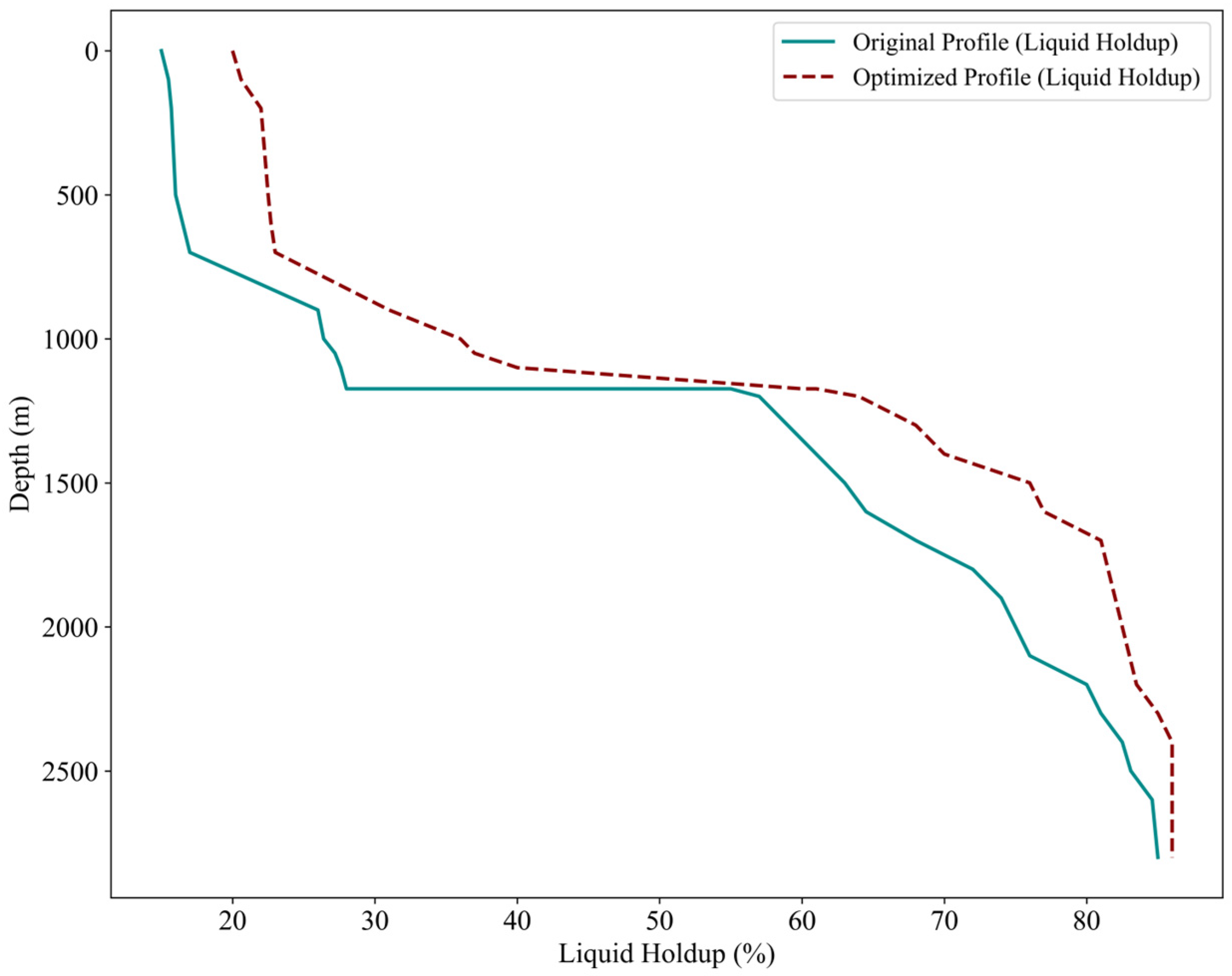
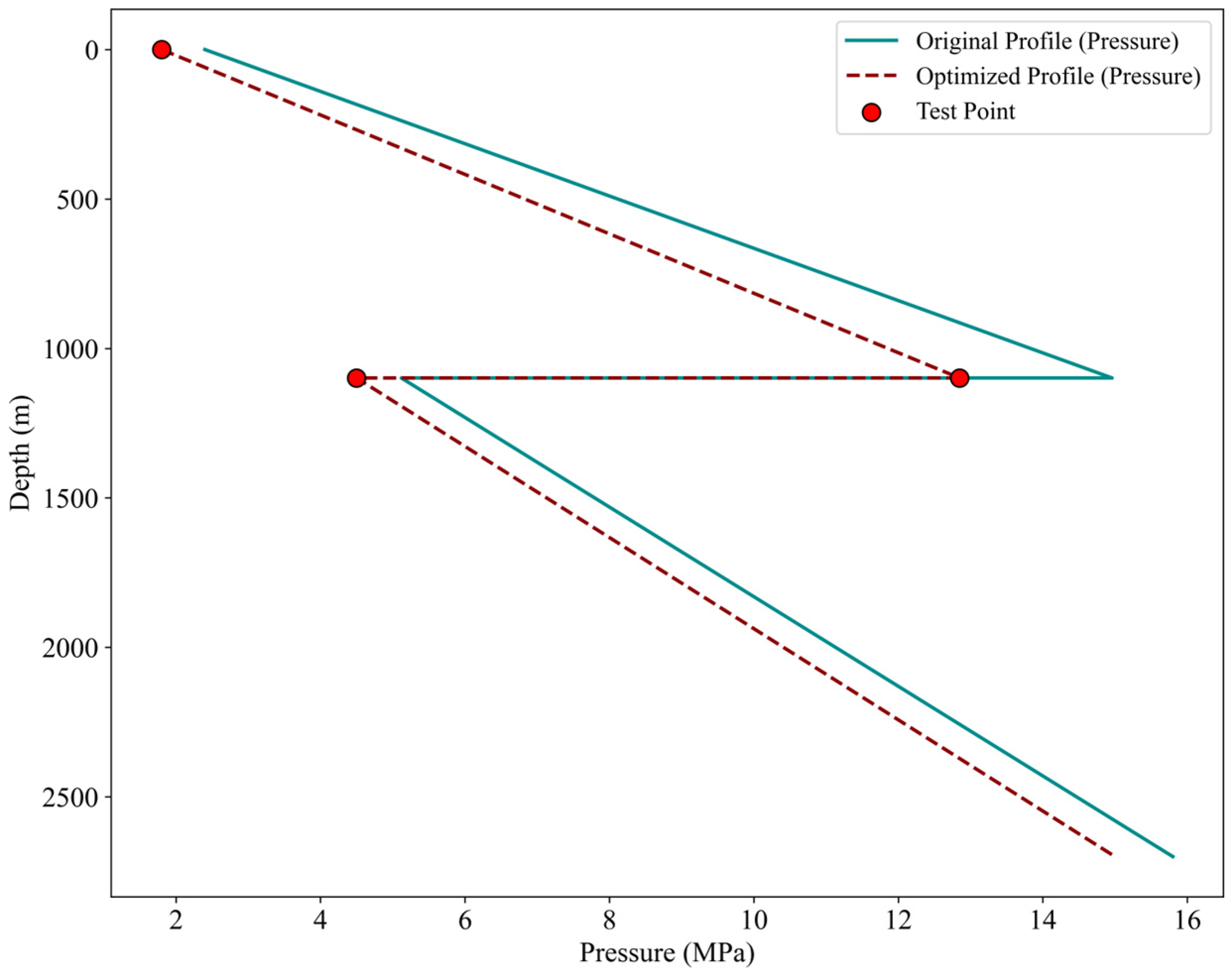
- After applying the optimization methods, the continuity and stability of the ESP system have significantly improved. For wells experiencing insufficient pressure and suboptimal liquid holdup, post-optimization results show an average increase of 2 MPa in pump suction pressure and an average 10% improvement in liquid holdup. This enhancement effectively reduces the number of pump starts and stops, thereby minimizing equipment wear and failures caused by frequent switching.
- (5)
- Following the optimization of operating parameters, energy consumption can be significantly reduced average of 0.5 kWh/m3 while prolonging the lifespan of submersible pump equipment. This advantage not only presents considerable economic benefits but also aligns with the sustainability requirements advocated in the current industrial sector, providing new insights and references for future ESP system optimizations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Janadeleh, M.; Ghamarpoor, R.; Abbood, N.K.; Seyednooroldin, H.; Hasan, N.; Ali, Z.H. Evaluation and selection of the best artificial lift method for optimal production using pipesim software. Heliyon 2024, 10, e36934. [Google Scholar] [CrossRef] [PubMed]
- Leon, F.I.; Alvear, J.L.; Naranjo, R.R.; Vela, N.A.; Amores, D.A.; Perez, M.A.; Pancho, J.G.; Aguirre, L.X.; Sierra, O.G.; Villalobos, J.L.; et al. Comparative Study of the World’s First Deployment of a Compact Wide-Range ESP System with Induction Motor at MDC Field, Ecuador; ADIPEC: Abu Dhabi, United Arab Emirates, 2024. [Google Scholar]
- Pant, H. Best Pumping Practices to Optimize Dewatering in CBM wells: Lessons Learned Developing Raniganj East Field, India. In Proceedings of the SPE Unconventional Resources Conference and Exhibition-Asia Pacific, Brisbane, Australia, 11 November 2013. [Google Scholar]
- Wang, H. Electrical Submersible Pump Theory and Application; Petroleum Industry Press: Beijing, China, 1994. [Google Scholar]
- Han, G.; Chen, M.; Zhang, H.; Ling, K. Real-Time Monitoring and Diagnosis of Electrical Submersible Pump. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar]
- Hoefel, A.; Kelly, D.; Jin, R.; Meier, D.; Chu, T.; Anderson, J.; Chong, J. ESP System Monitoring and Diagnosis from Surface Power Acquisition. In Proceedings of the SPE Gulf Coast Section—Electric Submersible Pumps Symposium, The Woodlands, TX, USA, 2–6 October 2023. [Google Scholar]
- Lu, X.; Han, G.; Wang, L.; Zhang, Z.; Liang, X. Fault Diagnosis of Electric Submersible Pump System Based on Motor Current Signal Analysis and Deep Learning Method. SPE J. 2025, 30, 2238–2255. [Google Scholar] [CrossRef]
- Jiang, L.; Jiang, L.; Guo, S.; Xue, H.; Yang, L.; Tang, X. Intelligent ESPs Diagnostic Model Based on Big Data and Machine Learning; ADIPEC: Abu Dhabi, United Arab Emirates, 2024. [Google Scholar]
- Ulyanov, S.; Sagyndykov, R.; Davydov, D.; Dolinyuk, V.; Gilaev, G.; Totanov, A.; Nosov, S.; Ilyin, A. The Individual Certified Flowmeter of Liquid in the Well. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 15–17 October 2018. [Google Scholar]
- Cohen, D.J. Captain Field Electric Submersible Pump, Condition Monitoring And Completion Systems. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 1997. [Google Scholar]
- Nolen, K.B.; Glbbs, S.G. Analysis of Electric Submersible Pumping Systems, SPE16196. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, OK, USA, 8–10 March 1987; Volume 2, pp. 114–115. [Google Scholar]
- Badkoubeh, A.; Waldner, L.B.; Imanfard, M. Field Validation: ESP Reliability Monitoring and Production Optimization by Trending Condition and Performance Data Extracted from ESP Surface Electrical Signals. In Proceedings of the SPE Gulf Coast Section—Electric Submersible Pumps Symposium, The Woodlands, TX, USA, 2–6 October 2023. [Google Scholar]
- El Mahbes, R.; Manfoumbi, W.; Kadio-Morokro, B. Real-Time Remote Monitoring to Enhance Electrical Submersible Pump System Run Life and Maximize Production. In Proceedings of the SPE Middle East Artificial Lift Conference and Exhibition, Manama, Bahrain, 28–30 November 2018. [Google Scholar]
- Beggs, D.H.; Brill, J.P. A study of two-phase flow in inclined pipes. J. Pet. Technol. 1973, 25, 607–617. [Google Scholar] [CrossRef]
- Rammay, M.H.; Alnuaim, S. Flow Regime Prediction Using Fuzzy Logic and Modification in Beggs and Brill Multiphase Correlation. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 6–9 December 2015. [Google Scholar]
- Velez-Langs, O. Genetic algorithms in oil industry: An overview. J. Pet. Sci. Eng. 2005, 47, 15–22. [Google Scholar] [CrossRef]
- Costa, E.A.; Rebello, C.M.; Santana, V.V.; Reges, G.; Silva, T.O.; Abreu, O.S.L.; Ribeiro, M.P.; Foresti, B.P.; Fontana, M.; Nogueira, I.B.R.; et al. An uncertainty approach for Electric Submersible Pump modeling through Deep Neural Network. Heliyon 2024, 10, e24047. [Google Scholar] [CrossRef] [PubMed]
- Albori, M.; Alsadah, H. Comparative Simulation Studies of ESP Permanent Magnet and Induction Current Motors in ESP Selective Applications. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2023. [Google Scholar]

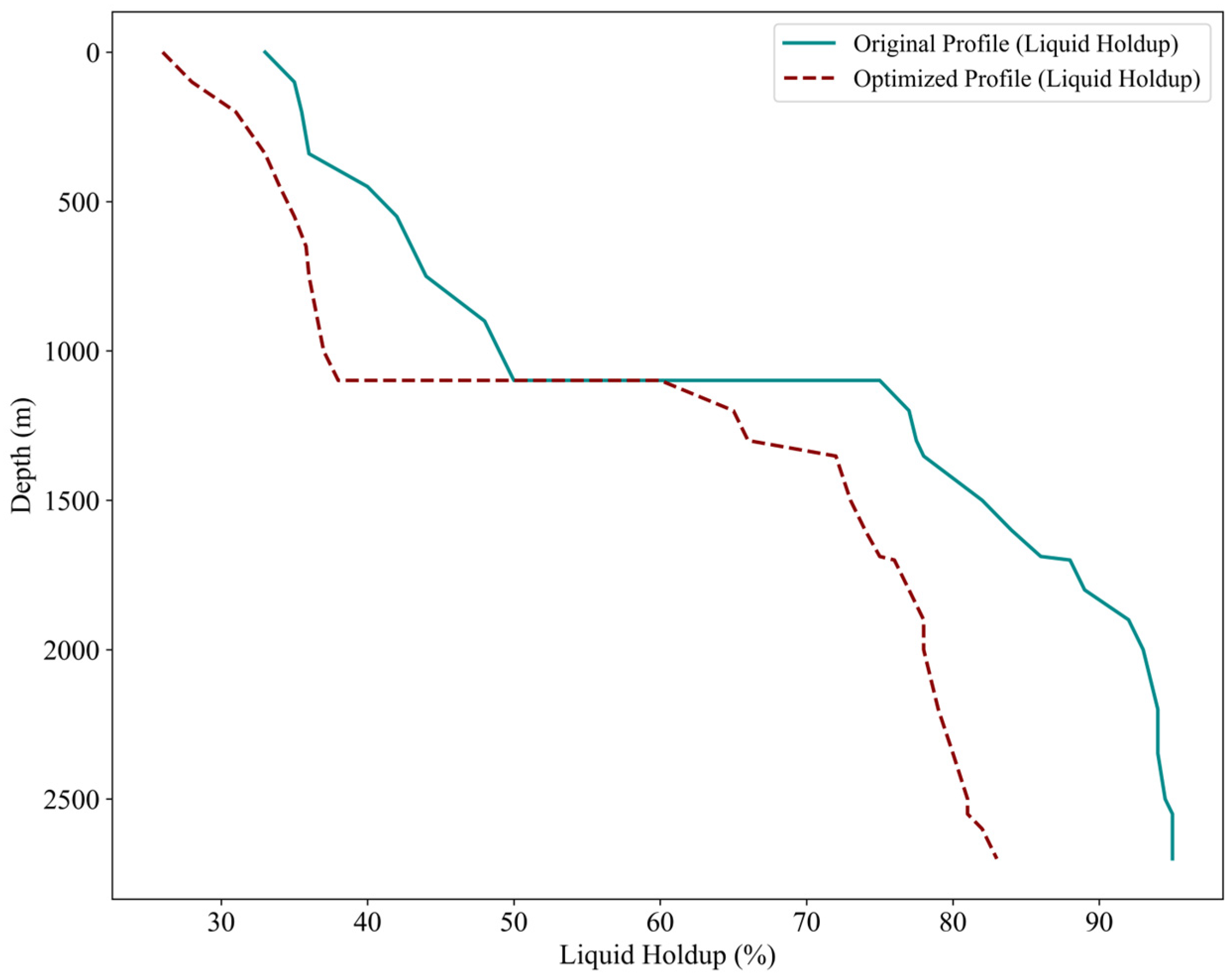
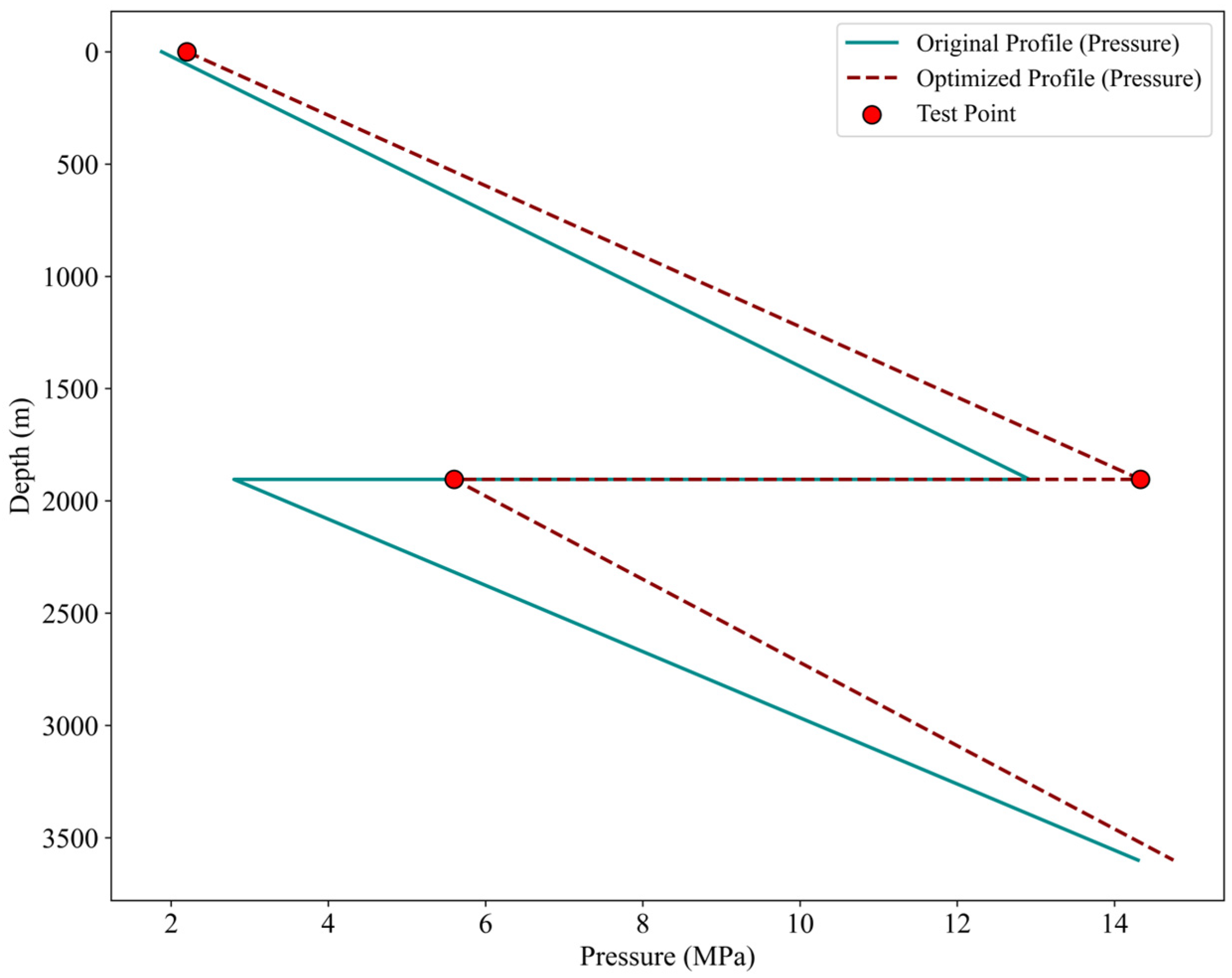
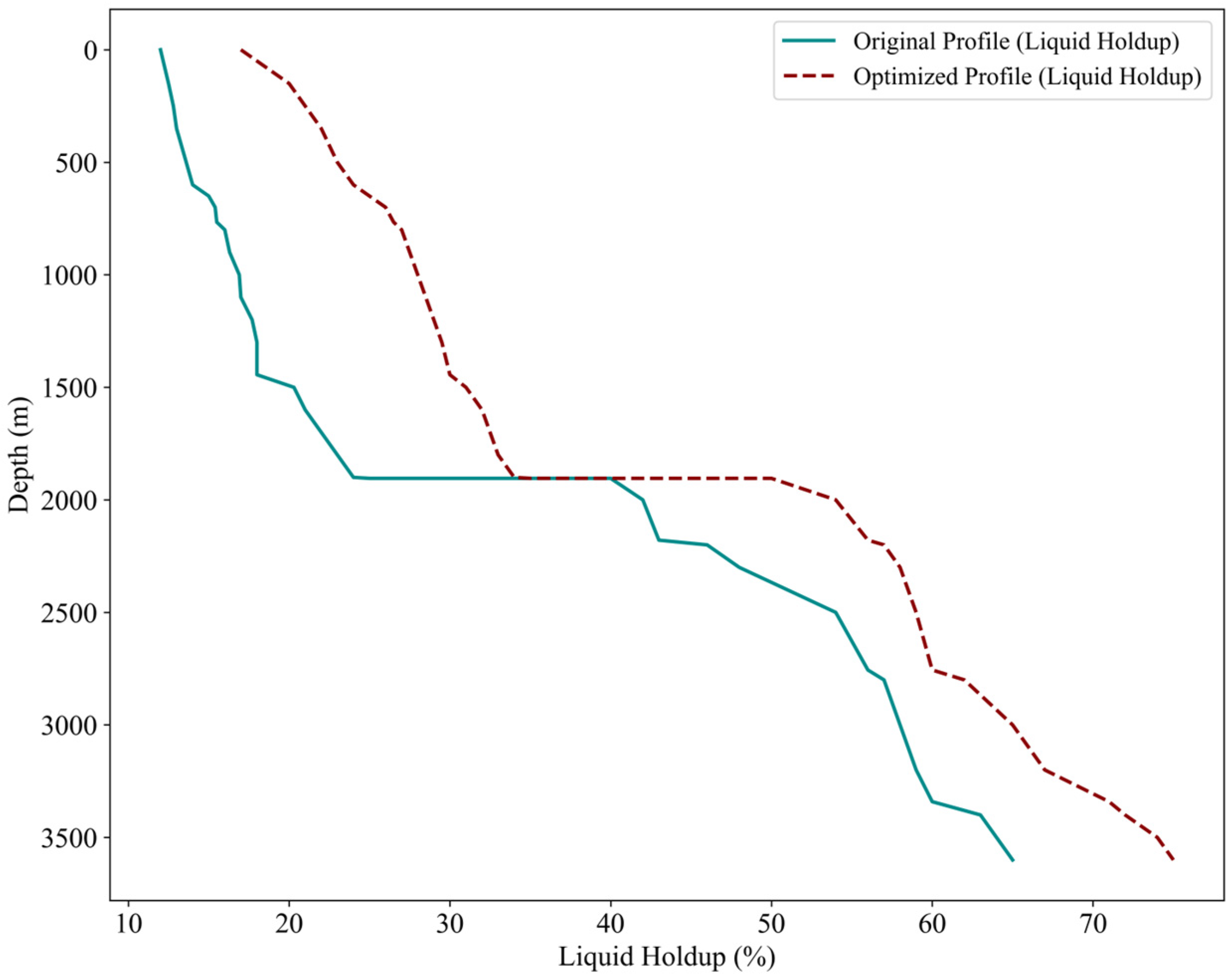
| Fitted Profile Condition | Determination Basis | Recommended Action |
|---|---|---|
| Liquid proportion at the inlet is low | The liquid hold-up rate at the inlet segment is less than 30%, and the gravitational pressure drop in that segment is significantly reduced | Reduce pump frequency by 3 to 5 Hz |
| Inlet pressure is too low | The pressure at the inlet segment is significantly lower than the minimum pressure required for stable liquid suction | Reduce pump frequency by 2 Hz |
| Fitted Profile Condition | Determination Basis | Recommended Action |
|---|---|---|
| Liquid column height is insufficient | The hold-up rate in the middle section is less than 30%, and the gravitational pressure drop is small | Close the nozzle by 5% to 10% to increase pump inlet pressure |
| Back pressure is too high | Overall frictional pressure drop is large, hold-up rate is high, but there is no significant increase in current or shaft power | Open the nozzle by 5% to reduce system back pressure and increase flow rate |
| Fitted Profile Condition | Determination Basis | Recommended Action |
|---|---|---|
| Periodic gas locking occurs | Intermittent abnormal pressure drop at the pump inlet | Extend the pump shutdown time to avoid frequent starts and stops that can damage the pump body |
| Well | Pump Intake Pressure (MPa) | Liquid Production (m3/d) | Liquid Holdup (%) | Energy Consumption (kWh/m3) |
|---|---|---|---|---|
| A1 | 3.5 → 5.5 | 168.68 → 177.8 | 30 → 40 | 2.7 → 2.2 |
| A2 | 5.2 → 4.2 | 82.3 → 93.4 | 50 → 40 | 2.6 → 2.1 |
| A3 | 2.8 → 5.6 | 71.5 → 82 | 30 → 20 | 2.5 → 2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, X.; Ji, Y.; Liu, Y.; Wang, T.; Xing, Z.; Han, G.; Sun, Y. Research on Optimization Method of Operating Parameters for Electric Submersible Pumps Based on Multiphase Flow Fitting. Processes 2025, 13, 3156. https://doi.org/10.3390/pr13103156
Wang M, Zhang X, Ji Y, Liu Y, Wang T, Xing Z, Han G, Sun Y. Research on Optimization Method of Operating Parameters for Electric Submersible Pumps Based on Multiphase Flow Fitting. Processes. 2025; 13(10):3156. https://doi.org/10.3390/pr13103156
Chicago/Turabian StyleWang, Mingchun, Xinrui Zhang, Yuchen Ji, Yupei Liu, Tianhao Wang, Zixiao Xing, Guoqing Han, and Yinmingze Sun. 2025. "Research on Optimization Method of Operating Parameters for Electric Submersible Pumps Based on Multiphase Flow Fitting" Processes 13, no. 10: 3156. https://doi.org/10.3390/pr13103156
APA StyleWang, M., Zhang, X., Ji, Y., Liu, Y., Wang, T., Xing, Z., Han, G., & Sun, Y. (2025). Research on Optimization Method of Operating Parameters for Electric Submersible Pumps Based on Multiphase Flow Fitting. Processes, 13(10), 3156. https://doi.org/10.3390/pr13103156







