Experimental Optimization, Scaling Up, and Characterization for Continuous Aragonite Synthesis from Lime Feedstock Using Magnesium Chloride as Chemical Inducer
Abstract
1. Introduction
2. Literature Review
Ca(Cl)2(aq) + H2CO3(aq) + Mg(OH)2(s) → CaCO3(s) + MgCl2(aq) + 2H2O
Ca(OH)2(s) + Mg2+ + 2Cl−(aq) → Mg(OH)2(s) + Ca2+(aq) + 2Cl−(aq)
3. Method
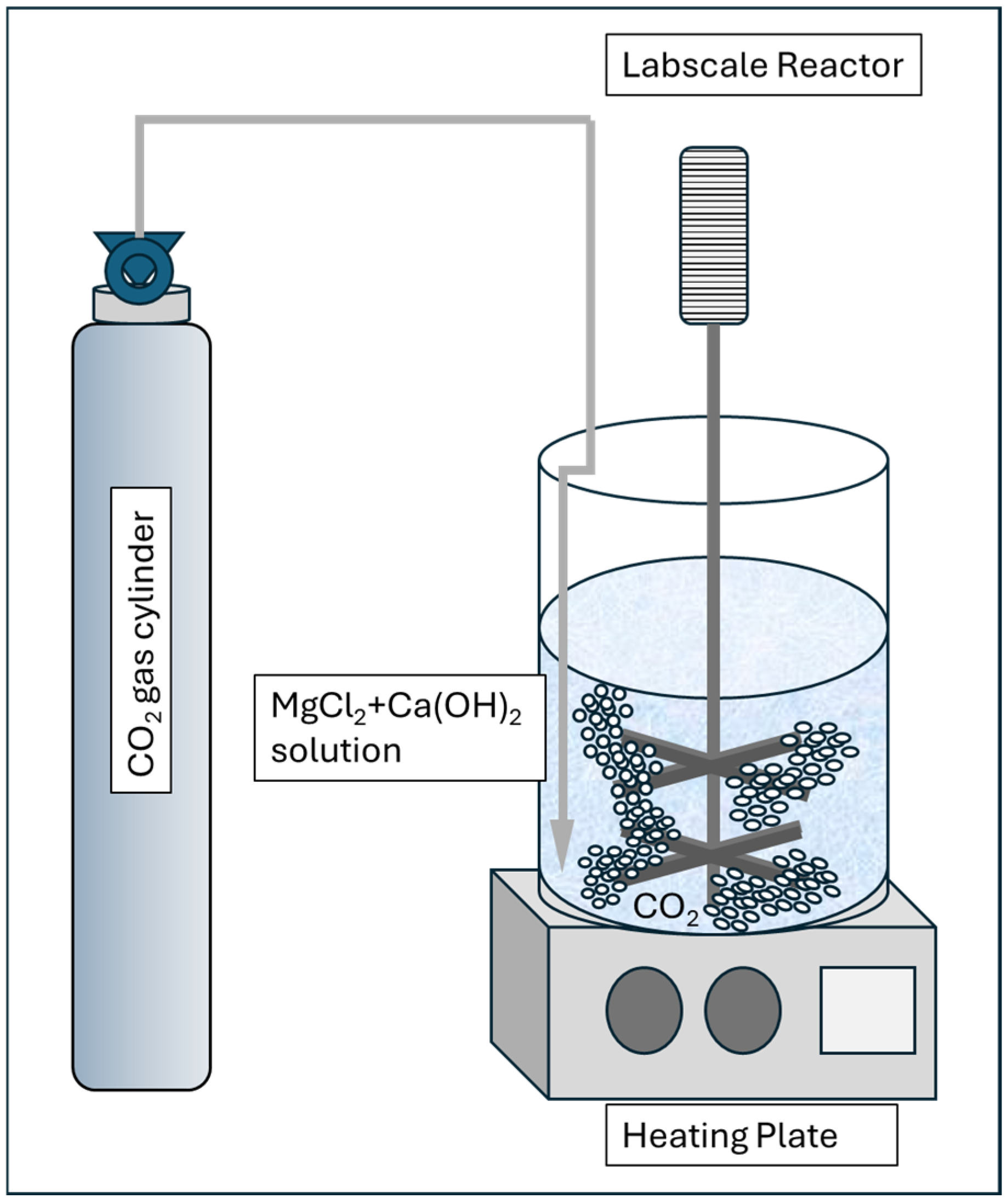
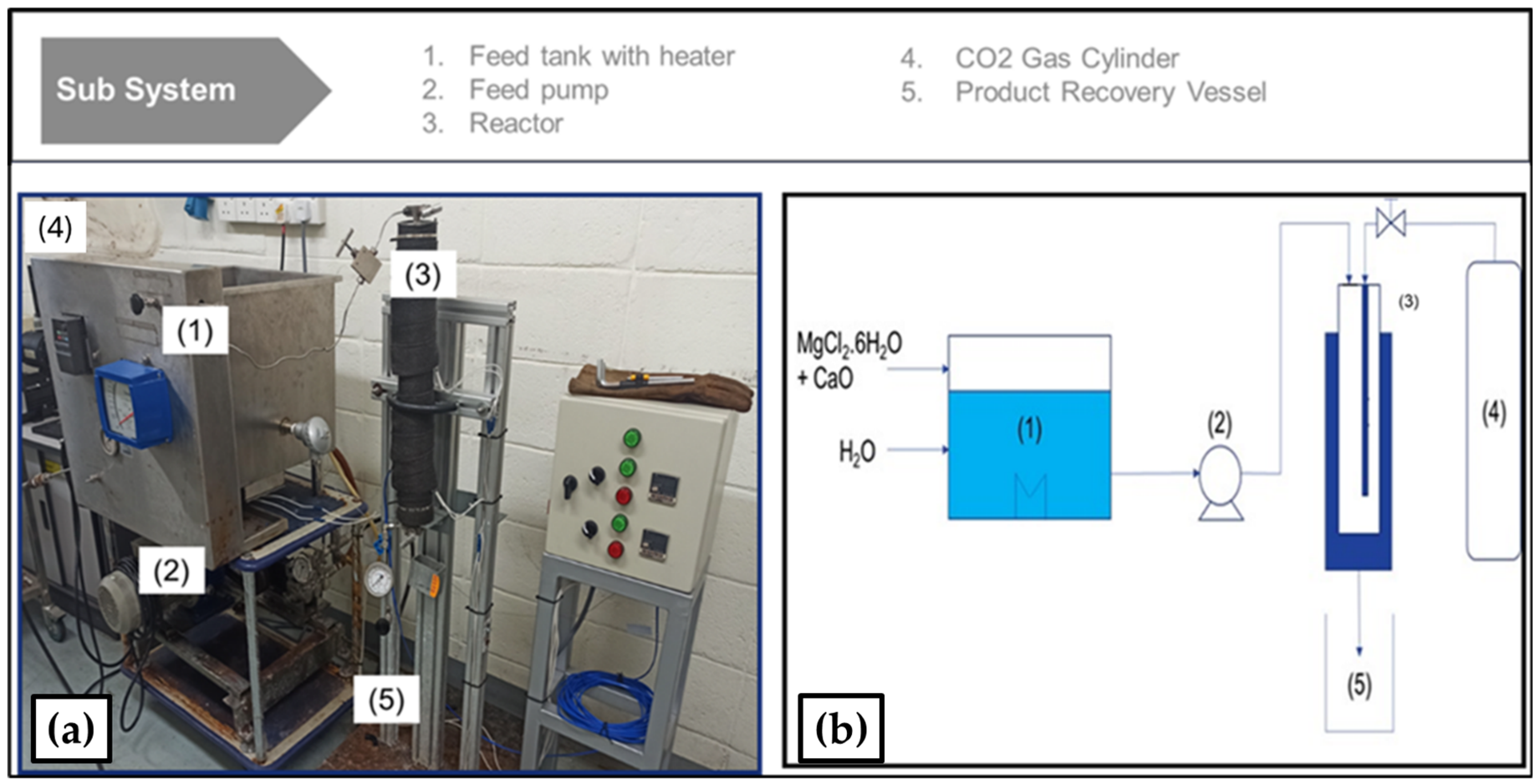
3.1. Experimental Setup and Procedure Using Lab Scale Glass Reactor
3.2. Synthesis of Aragonite
3.2.1. Laboratory Procedure
- Solution of MgCl2 and Ca(OH)2 mixture with specific concentrations as demonstrated by Park et al. (2008) [12] and Shen et al. (2022) [50] was heated until reaching the target temperature between 40 and 90 °C and stirred at 250 rpm [43,44,45].
- A total of 1 g of Calcium Hydroxide powder Ca(OH)2 laboratory grade is stirred into 1 L of double distilled water until a stable milk of lime solution is formed.
- Add 2.33 g of anhydrous magnesium chloride into the milk of lime solution slowly until evenly mixed and no further solid clumping observed.
- The mixture is continuously stirred for another 1 min.
- Allow the solution to react in accordance with the reaction time requirement (1–10 min) until solution becomes clear and mineral precipitates are formed.
- Stop the stirring and let the precipitation settle down. Siphon out the clear liquid until a third of the solution volume is left. Vacuum filter the liquid and solid precipitate mixture.
- The solid sample is analyzed using X-Ray Diffraction, XRD, particle size analyzer, PSA, and the spent reactant is analyzed using Induction Coupled Plasma, ICP, method.
3.2.2. Analytical Equipment Settings
3.3. Design of Experiment
- Reaction time, t: 1–10 min [52].
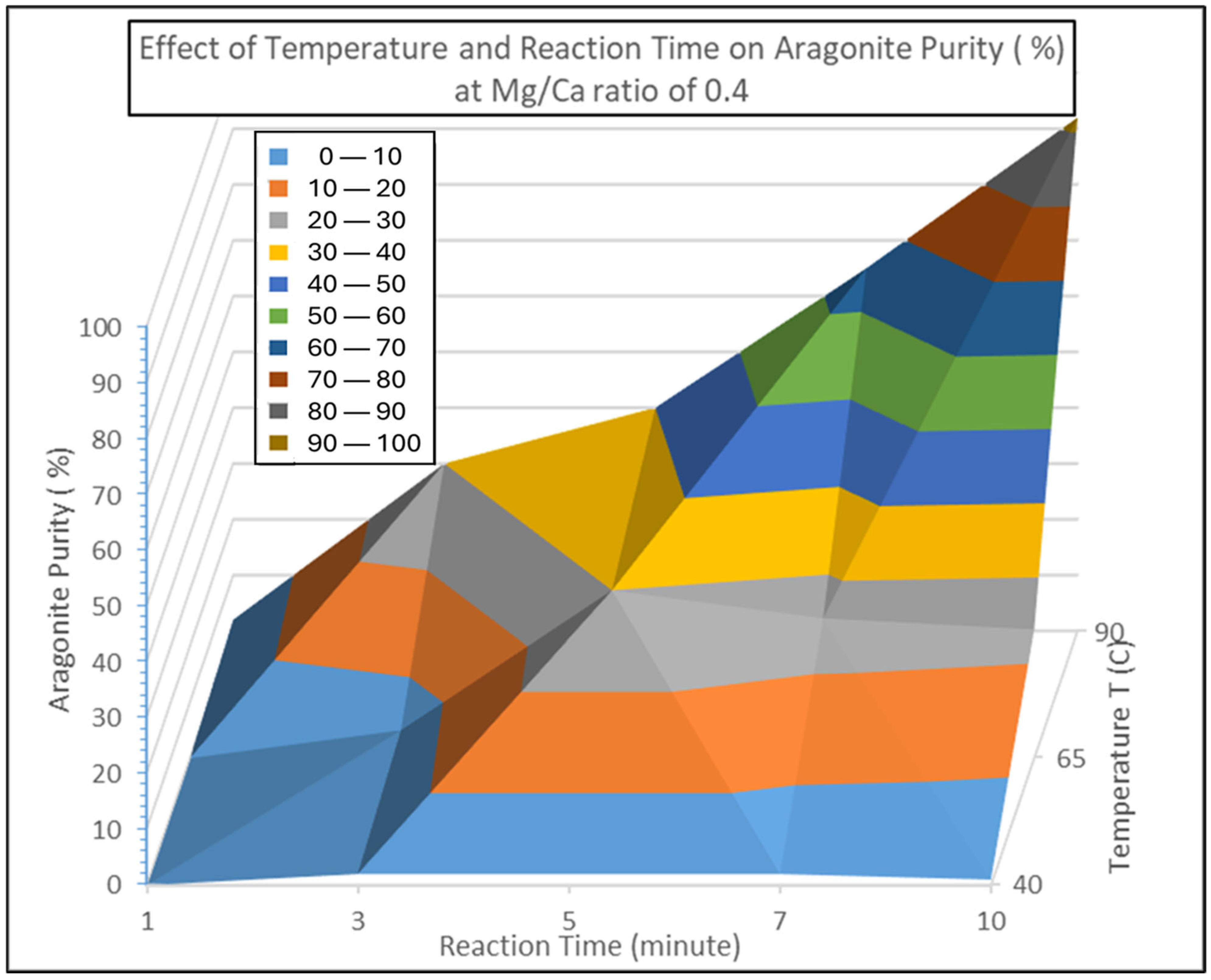
3.4. Results
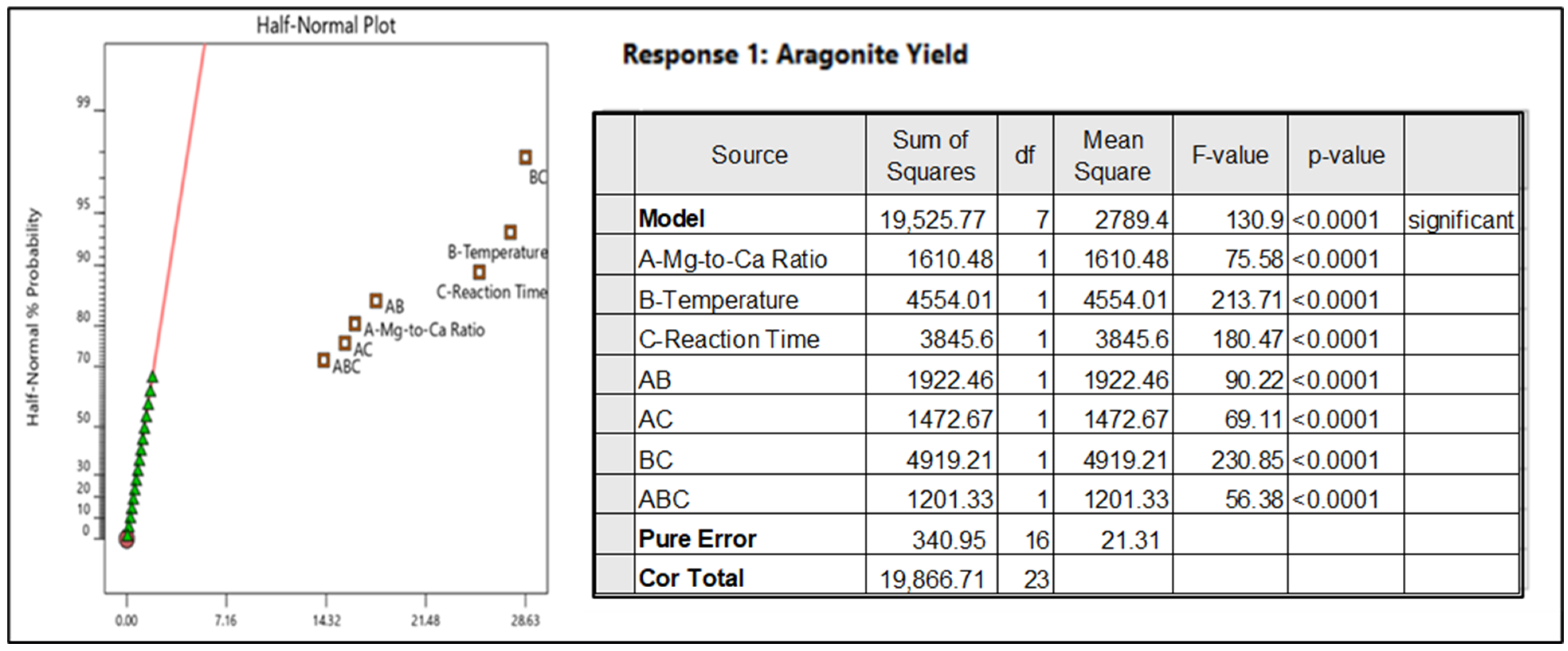
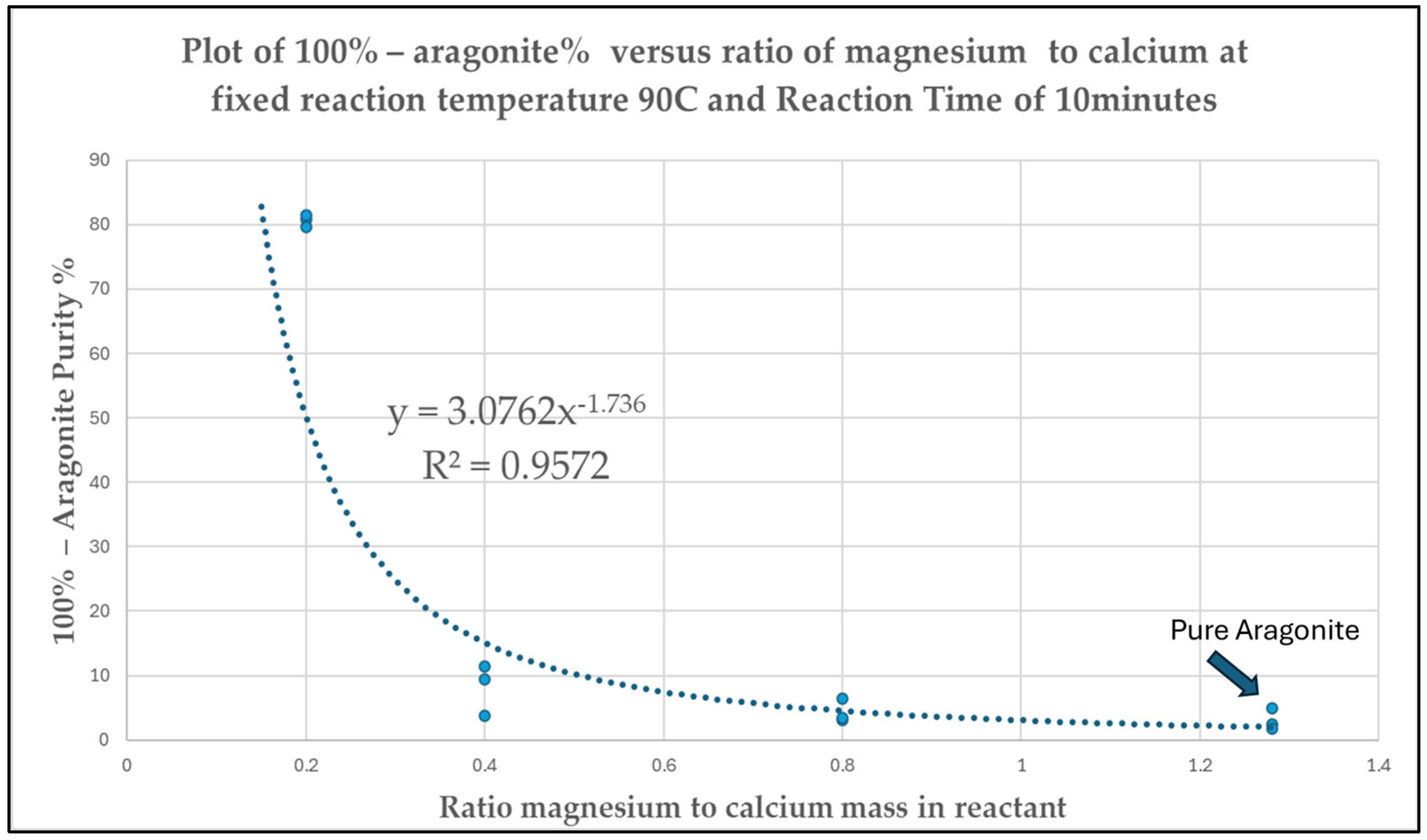
3.5. Optimization
= 3.0762 × (Ratio of magnesium-to-calcium)−1.736
= 3.0762 × ([Mg2+]/[Ca2+])−1.736
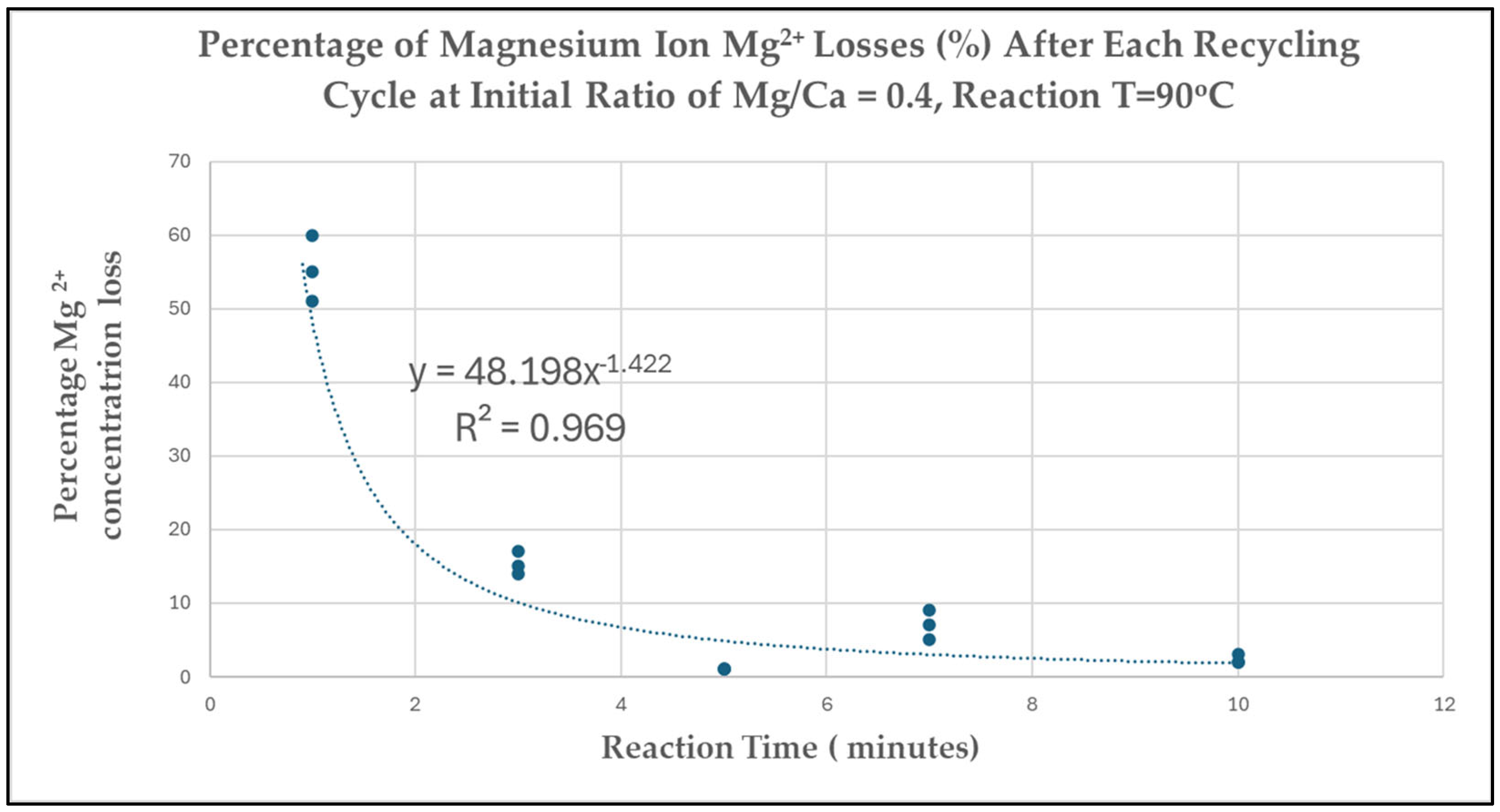
3.6. Losses of Chemical Inducer MgCl2 During Recycling
3.6.1. Method
3.6.2. Losses
3.6.3. Optimized Reaction Parameters
3.7. Performance Run Using Continuous Reactor System
- Plunger type pump, motor driver, and speed controller.
- Inlet to reactor liquid flow meter and pressure gauge.
- Feedstock tank.
- An 800 mL high pressure tubular reactor with inlet flow valve, and an outflow backpressure regulator with pressure indicator.
4. Physico-Chemical Characterization
- Induction coupled plasma ICP for metal ion presence and concentrations.
- X-Ray diffraction, XRD, to identify the crystalline morphology of the calcium carbonate precipitates.
- Particle Size Distribution, PSD, to precipitate particle size distribution.
- FESEM–imaging of crystalline structure.
- Thermal Gravimetric Analysis, TGA, to characterize thermal decomposition of the crystalline precipitate.
4.1. Induction Couple Plasma ICP Analysis
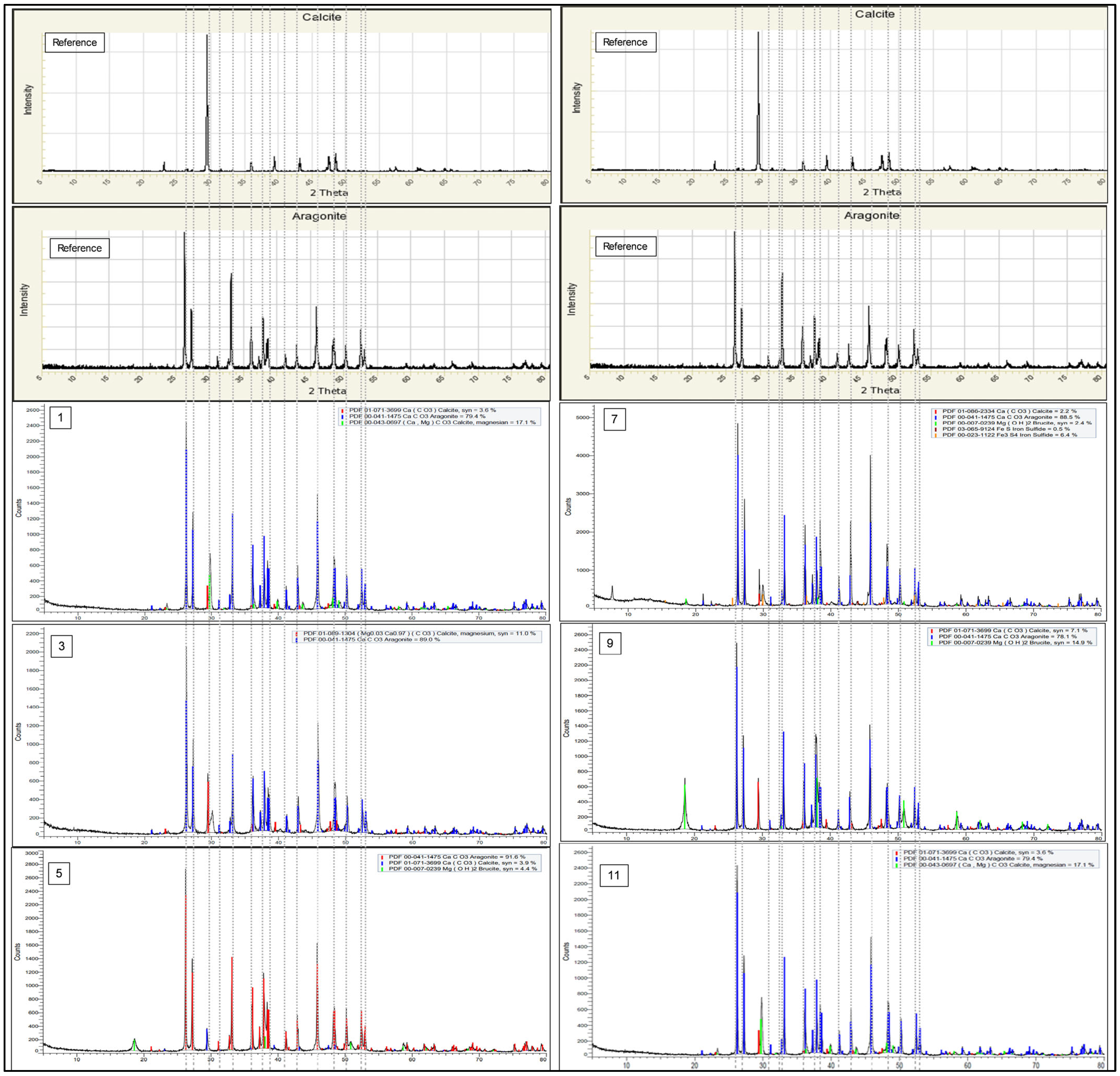
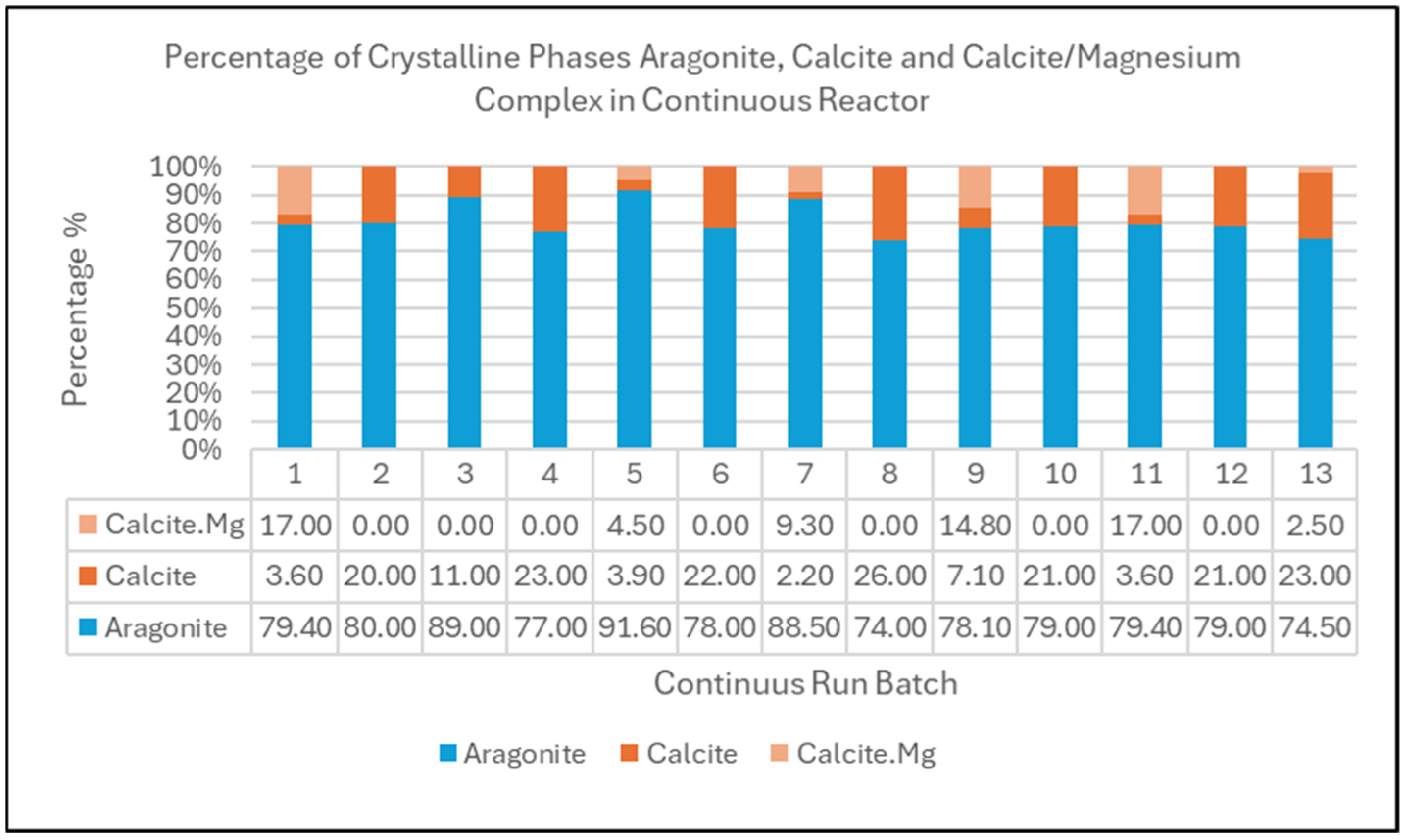
4.2. X-Ray Diffractogram XRD
- Insufficient contact time between the CO2 gas and the reactant injected into the reactor resulting in net reduction in reaction time to be shorter than 10 min.
- Insufficient heating lines which produced uneven temperature gradient throughout the different sections of the continuous reactor, thus resulting in the effective average real time temperature to be lower than the 90 °C setting.
- Incoming reactant flow rate and product outflow rate affected by the inaccuracies of the manual liquid level controller settings resulting in constant variation in exposure time of the reactant to the pressurized CO2 gas.
- Product recovered has been contaminated by the residue precipitation during the initial phase of reactor start up where temperature ramp up was still in progress or remnants of precipitation from the previous run interacted with the current reaction cycle.
4.3. Particle Size Distribution PSD
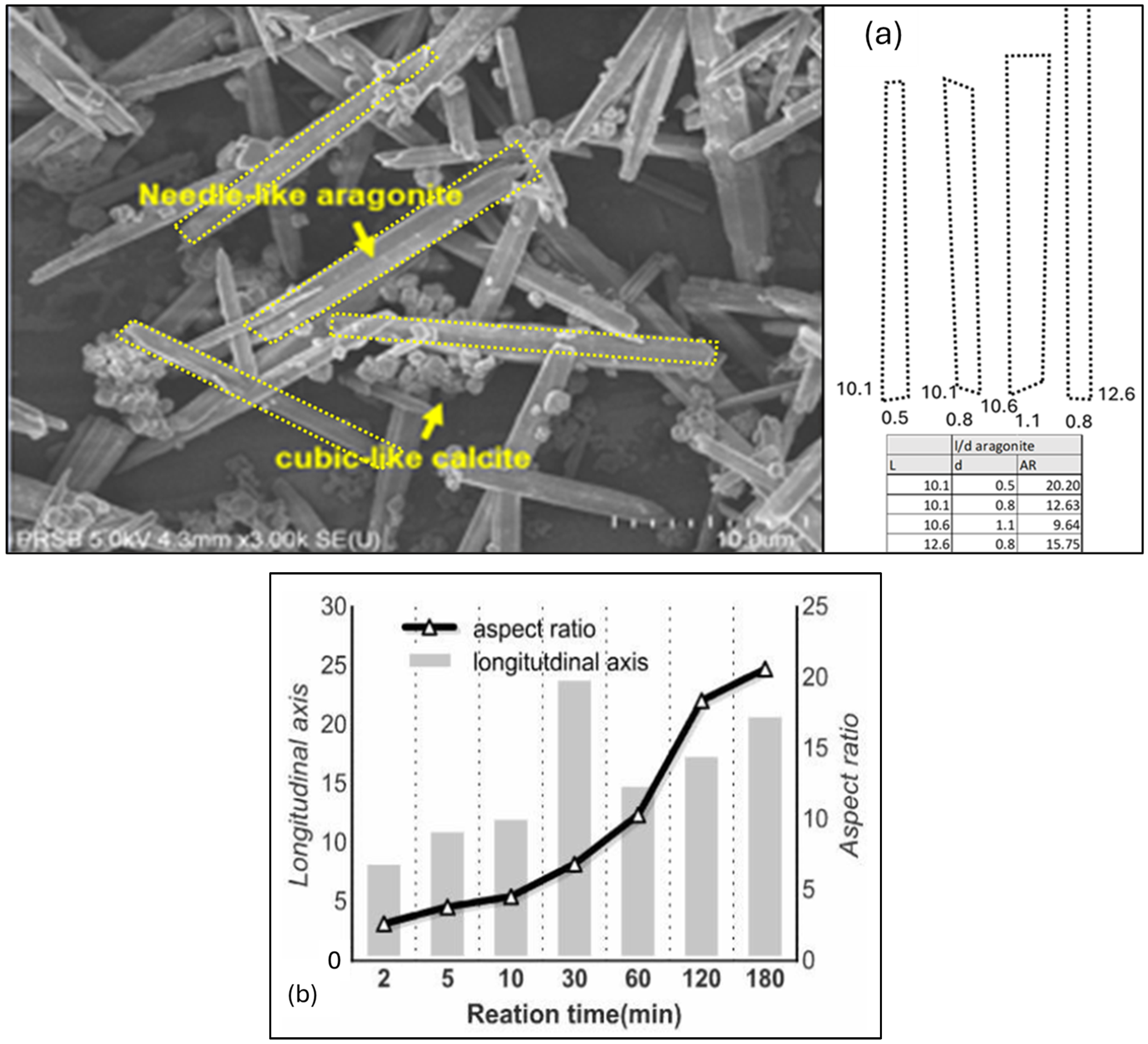
4.4. FESEM Imaging
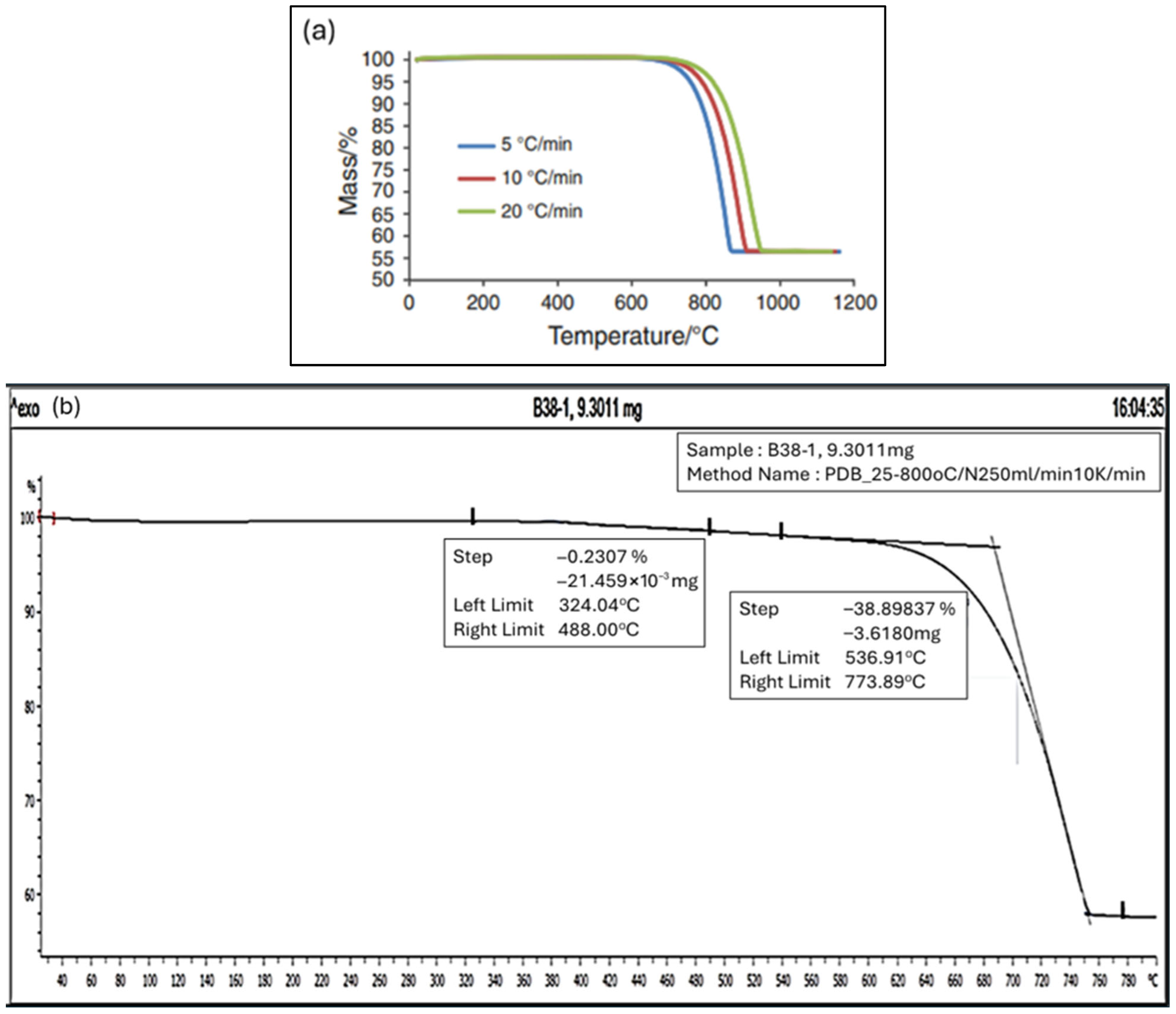
4.5. Thermal Gravimetric Analysis TGA
- (a)
- Minor decomposition starts taking place between 400 °C and 550 °C, possibly from the decomposition of traces of magnesium oxides or brucite, which originate from the traces of magnesium metal ion complex as detected during the ICP analysis earlier. TGA decomposition analysis conducted by Wong et al. [66] reported that TGA weight loss of magnesium oxide MgO was approximately at 70% at 550 °C also supportsd this observation.
- (b)
- (c)
- The decomposition, or weight loss, stopped after 800 °C, leaving 56% of the original weight. This finding is similar to the studies conducted by [64], where the corresponding weight loss for 10 °C/min and 15 °C/min was between 58% and 55% of the initial weight.
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shokrollahi, M.; Teymouri, N.; Navarri, P. Identification and evaluation of most promising CO2 utilization technologies: Multi criteria decision analysis and techno-economic assessment. J. Clean. Prod. 2024, 434, 139620. [Google Scholar] [CrossRef]
- Aresta, M.; Quaranta, E.; Tommasi, I.; Giannoccaro, P.; Ciccarese, G. Carbon dioxide utilization in the chemical industry. Chim. Ital. 1995, 125, 509–538. [Google Scholar]
- Sakakura, T.; Choi, J.-C.; Yasuda, H. Transformation of Carbon Dioxide. Chem. Rev. 2007, 107, 2365–2387. [Google Scholar] [CrossRef] [PubMed]
- Aresta, M.; Dibenedetto, A.; Angelini, A. The changing paradigm in CO2 utilization. J. CO2 Util. 2013, 3–4, 65–73. [Google Scholar] [CrossRef]
- Metz, B.; Davidson, O.; de Coninck, H.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2005. [Google Scholar]
- Huijgen, W.J.J. Carbon Dioxide Sequestration by Mineral Carbonation. Ph.D. Thesis, Energy Research Centre of the Netherlands, Petten, The Netherlands, 2007. [Google Scholar]
- Carbon Upcycling Technologies 2023. Available online: https://carbonupcycling.com/ (accessed on 28 January 2023).
- Sinha, A. A Mechanochemical Process to Produce Exfoliated Nanoparticles. U.S. Patent Application No. WO/2019/012474, 12 July 2018. [Google Scholar]
- Sinha, A. A Mechanically Carboxylated Fly Ash, Methods of Its Production and Uses Thereof. U.S. Patent Application No. WO/2021/087605, 2 October 2020. [Google Scholar]
- Sinha, A. Compositions Comprising a Mechanochemically Carboxylated Mineral Filler and a Cement and/or Asphalt Binder. U.S. Patent Application No. WO/2021/087606, 2021. [Google Scholar]
- Choudens-Sánchez, D.; González, L.A. Calcite and aragonite precipitation under controlled instantaneous supersaturation: Elucidating the role of CaCO3 saturation state and Mg/Ca ratio on calcium carbonate polymorphism. J. Sediment. Res. 2009, 79, 363–376. [Google Scholar]
- Park, W.K.; Ko, S.-J.; Lee, S.W.; Cho, K.-H.; Ahn, J.-W.; Han, C. Effects of magnesium chloride and organic additives on the synthesis of aragonite precipitated calcium carbonate. J. Cryst. Growth 2008, 310, 2593–2601. [Google Scholar] [CrossRef]
- Jung, W.M.; Kang, S.H.; Kim, W.-S.; Choi, C.K. Particle morphology of calcium carbonate precipitated by gas–liquid reaction in a Couette–Taylor reactor. Chem. Eng. Sci. 2000, 55, 733–747. [Google Scholar] [CrossRef]
- Liendo, F.; Arduino, M.; Deorsola, A.F.; Bensaid, S. Factors controlling and influencing polymorphism, morphology and size of calcium carbonate synthesized through the carbonation route: A review. Powder Technol. 2022, 398, 117050. [Google Scholar] [CrossRef]
- Meldrum, F.C.; Hyde, S.T. Morphological influence of magnesium and organic additives on the precipitation of calcite. J. Cryst. Growth 2001, 231, 544–558. [Google Scholar] [CrossRef]
- Hashim, M.S.; Kaczmarek, S.E. The transformation of aragonite to calcite in the presence of magnesium: Implications for marine diagenesis. Earth Planet. Sci. Lett. 2021, 574, 117166. [Google Scholar] [CrossRef]
- Nancollas, G.H.; Sawada, K. Formation of Scales of Calcium Carbonate Polymorphs: The Influence of Magnesium Ion and Inhibitors. J. Pet. Technol. 2012, 34, 645–652. [Google Scholar] [CrossRef]
- Bischoff, J.L. Kinetics of calcite nucleation: Magnesium ion inhibition and ionic strength catalysis. J. Geophys. Res. 1968, 73, 3315–3322. [Google Scholar] [CrossRef]
- Bischoff, J.L.; Fyfe, W.S. Catalysis, inhibition, and the calcite-aragonite transformation. Am. J. Sci. 1968, 266, 65–79. [Google Scholar] [CrossRef]
- Berner, R.A. The Role of Magnesium in the Crystal Growth of Calcite and Aragonite from Sea Water. Geochim. Et. Cosmochim. Acta 1975, 39, 489–494. [Google Scholar] [CrossRef]
- Astilleros, J.M.; Fernández-Díaz, L.; Putnis, A. The role of magnesium in the growth of calcite: An AFM study. Chem. Geol. 2010, 271, 52–58. [Google Scholar] [CrossRef]
- Nielsen, L.C.; De Yoreo, J.J.; DePaolo, D.J. General model for calcite growth kinetics in the presence of impurity ions. Geochim. Cosmochim. Acta 2013, 115, 100–114. [Google Scholar] [CrossRef]
- Mucci, A.; Morse, J.W. The incorporation of Mg2+ and Sr2+ into calcite overgrowths: Influences of growth rate and solution composition. Geochim. Cosmochim. Acta 1983, 47, 217–233. [Google Scholar] [CrossRef]
- Chen, P.-C.; Clifford, T.Y.; Lee, K.C. Morphology and growth rate of calcium carbonate crystals in a gas-liquid-solid reactive crystallizer. Chem. Eng. Sci. 1997, 52, 4171–4177. [Google Scholar] [CrossRef]
- Christoffersen, J.; Christoffersen, M.R. Kinetics of spiral growth of calcite crystals and determination of the absolute rate constant. J. Cryst. Growth 1990, 100, 203–211. [Google Scholar] [CrossRef]
- Hu, Z.; Deng, Y. Synthesis of needle-like aragonite from calcium chloride and sparingly soluble magnesium carbonate. Powder Technol. 2004, 140, 10–16. [Google Scholar] [CrossRef]
- Wang, L.; Sondi, I.; Matijević, E. Preparation of Uniform Needle-Like Aragonite Particles by Homogeneous Precipitation. J. Colloid Interface Sci. 1999, 218, 545–553. [Google Scholar] [CrossRef]
- Sun, W.; Jayaraman, S.; Chen, W.; Persson, K.A.; Ceder, G. Nucleation of metastable aragonite CaCO3 in seawater. Proc. Natl. Acad. Sci. USA 2015, 112, 3199–3204. [Google Scholar] [CrossRef] [PubMed]
- Kajiyama, S.; Nishimura, T.; Sakamoto, T.; Kato, T. Aragonite Nanorods in Calcium Carbonate/Polymer Hybrids Formed through Self-Organization Processes from Amorphous Calcium Carbonate Solution. Small 2014, 10, 1634–1641. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishna, C.; Thenepalli, T.; Huh, J.-H.; Ahn, J.W. Preparation of Needle like Aragonite Precipitated Calcium Carbonate (PCC) from Dolomite by Carbonation Method. J. Korean Ceram. Soc. 2016, 53, 7–12. [Google Scholar] [CrossRef]
- Meigen, W. A simple reaction for distinguishing between aragonite and calcite. Fresenius. Z. Für Anal. Chem. 1902, 41, 119–120. [Google Scholar] [CrossRef]
- Linck, G. Die Bildung der Oolithe und Rogensteine. Nues Jahebuch Beil 1903, 16, 495–513. [Google Scholar]
- Johnston, J.; Merwin, H.E.; Williamson, E.D. The several forms of calcium carbonate. Am. J. Sci. 1916, 41, 473–512. [Google Scholar] [CrossRef]
- Kohlschütter, V.; Egg, C. Über somatoide Bildungsformen. Helv. Chim. Acta 1925, 8, 457–469. [Google Scholar] [CrossRef]
- Saylor, C.H. Calcite and aragonite. J. Phys. Chem. 1927, 32, 1441–1460. [Google Scholar] [CrossRef]
- Faivre, M.R. Reserche des conditions physiochimiques de précipitation des trois formes cristallines du carbonate de calcium prépare par double décompositon due chlorure de calcium et du carbonate de sodium. Comptes Rendus 1946, 222, 140. [Google Scholar]
- Togari, K.; Togari, S. Conditions controlling the crystal form of calcium carbonate minerals (I) (on influence of the temperature and the presence of magnesium ion). J. Fac. Sci. Hokkaido Univ. Ser. 4 Geol. Miner. 1955, 9, 55–65. [Google Scholar]
- Zeller, E.; Wray, J. Factors influencing precipitation of calcium carbonate. Bull. Am. Assoc. Pet. Geol. 1956, 40, 140–152. [Google Scholar]
- Jones, B. Review of calcium carbonate polymorph precipitation in spring systems. Sediment. Geol. 2017, 353, 64–75. [Google Scholar] [CrossRef]
- Suganuma, I. On the Constituents and Genesis of a Few Minerals Produced from Hot Springs and Their Vicinities in Japan. III. Calcium Carbonate Minerals Deposited from Effervescent Springs. Bull. Chem. Soc. Jpn. 1928, 3, 87–89. [Google Scholar] [CrossRef]
- Goto, M. Some mineralo-chemical problems concerning calcite and aragonite, with special reference to the genesis of aragonite. J. Fac. Sci. Hokkaido Univ. Ser. 4 Geol. Miner. 1961, 10, 571–640. [Google Scholar]
- Roques, H.; Girou, A. Kinetics of the formation conditions of carbonate tartars. Water Res. 1974, 8, 907–920. [Google Scholar] [CrossRef]
- Chakrabarty, D.; Mahapatra, S. Aragonite crystals with unconventional morphologies. J. Mater. Chem. 1999, 9, 2953–2957. [Google Scholar] [CrossRef]
- Nebel, H.M. Epple Continuous preparation of calcite, aragonite and vaterite, and of magnesium-substituted amorphous calcium carbonate (Mg-ACC). J. Inorg. Gen. Chem. 2008, 634, 1439–1443. [Google Scholar]
- Chen, J.L. Xiang Controllable synthesis of calcium carbonate polymorphs at different temperatures. Powder Technol. 2009, 189, 64–69. [Google Scholar] [CrossRef]
- Tai, C.Y.; Chen, F. Polymorphism of CaCO3 precipitated in a constant-composition environment. AICHE J. 1998, 44, 1790–1798. [Google Scholar] [CrossRef]
- Hu, Z.; Shao, M.; Cai, Q.; Ding, S.; Zhong, C.; Wei, X.; Deng, Y. Synthesis of needle-like aragonite from limestone in the presence of magnesium chloride. J. Mater. Process. Technol. 2009, 209, 1607–1611. [Google Scholar] [CrossRef]
- Matsumoto, M.; Fukunaga, T.; Onoe, K. Polymorph control of calcium carbonate by reactive crystallization using microbubble technique. Chem. Eng. Res. Des. 2010, 88, 1624–1630. [Google Scholar] [CrossRef]
- Gomez-Villalba, L.S.; Lo´pez-Arce, P.; Alvarez de Buergo, M.; Fort, R. Atomic defects and their relationship to aragonite-calcite transformation in portlandite nanocrystal carbonation. Cryst. Growth Des. 2012, 12, 4844–4852. [Google Scholar] [CrossRef]
- Shen, P.; Lu, J.; Zhang, Y.; Jiang, Y.; Zhang, S.; Poon, C.S. Preparation aragonite whisker-rich materials by wet carbonation of cement: Towards yielding micro-fiber reinforced cement and sequestrating CO2. Cem. Concr. Res. 2022, 159, 106891. [Google Scholar] [CrossRef]
- Ding, X.; Li, W.; Chang, J. Preparation of aragonite from calcium carbonate via wet carbonation to improve properties of steel slag building materials. Constr. Build. Mater. 2024, 451, 138763. [Google Scholar] [CrossRef]
- Altiner, M.; Yildirim, M. Production and characterization of synthetic aragonite prepared from dolomite by eco-friendly leaching–carbonation process. Adv. Powder Technol. 2017, 28, 553–564. [Google Scholar] [CrossRef]
- Habte, L.; Khan, M.D.; Shiferaw, N.; Farooq, A.; Lee, M.-H.; Jung, S.-H.; Ahn, J.W. Synthesis, Characterization and Mechanism Study of Green Aragonite Crystals from Waste Biomaterials as Calcium Supplement. Sustainability 2020, 12, 5062. [Google Scholar] [CrossRef]
- Morse, J.W.; Arvidson, R.S.; Lüttge, A. Calcium carbonate formation and dissolution. Chem. Rev. 2007, 107, 342–381. [Google Scholar] [CrossRef]
- Onn, M.S.; Noh, M.G.M.; Shukor, M.S.M.; Isa, M.A. Experimental Proof of Concept for Continuous Mineral Carbonation System using High Pressure Calcium Hydroxide Spray into Supercritical CO2. J. Phys. Conf. Ser. 2019, 1349, 01207981. [Google Scholar]
- D’aMora, M.; Liendo, F.; Deorsola, F.A.; Bensaid, S.; Giordani, S. Toxicological profile of calcium carbonate nanoparticles for industrial applications. Colloids Surf. B Biointerfaces 2020, 190, 110947. [Google Scholar] [CrossRef]
- Memar, M.Y.; Adibkia, K.; Farajnia, S.; Kafil, H.S.; Dizaj, S.M.; Ghotaslou, R. Biocompatibility, cytotoxicity and antimicrobial effects of gentamicin-loaded CaCO3 as a drug delivery to osteomyelitis. J. Drug Deliv. Sci. Technol. 2019, 54, 101307. [Google Scholar] [CrossRef]
- Sturcal, F. Available online: https://polymer-additives.specialchem.com/product/a-specialty-minerals-sturcal-f (accessed on 19 August 2025).
- Ko, S.-J.; Park, W.-K.; Lee, S.-W.; Han, C.; Ahn, J.-W. Control of Particle Size and Aspect Ratio of Aragonite Precipitated Calcium Carbonate on Adding Seed. J. Korean Earth Sci. Soc. 2007, 44, 153–158. [Google Scholar]
- Hu, Z.; Shao, M.; Li, H.; Cai, Q. Synthesis of Needle-Like Aragonite Crystals in the Presence of Magnesium Chloride and Their Application in Papermaking. Adv. Compos. Mater. 2009, 18, 315–326. [Google Scholar] [CrossRef]
- Gill, T.; Scott, W. The relative effects of different calcium carbonate filler pigments on optical properties. Tappi J. 1987, 70, 93–99. [Google Scholar]
- Shang, W.; Liu, Q.; He, E.; Chen, S. Study on properties of polymers packed by aragonite whisker. Proc. IEEE Intl Conf. Prop. Appl. Dielectr. Mater. 2000, 1, 431–434. [Google Scholar]
- Karunadasa, K.S.; Manoratne, C.; Pitawala, H.; Rajapakse, R. Thermal decomposition of calcium carbonate (calcite polymorph) as examined by in-situ high-temperature X-ray powder diffraction. J. Phys. Chem. Solids 2019, 134, 21–28. [Google Scholar] [CrossRef]
- Zhuang, D.; Chen, Z.; Sun, B. Thermal Decomposition of Calcium Carbonate at Multiple Heating Rates in Different Atmospheres Using the Techniques of TG, DTG, and DSC. Crystals 2025, 15, 108. [Google Scholar] [CrossRef]
- Galan, I.; Glasser, F.; Andrade, C. Calcium carbonate decomposition. CEEC-TAC1 Conference Special Issue. J. Therm. Anal. Calorim. 2013, 111, 1197–1202. [Google Scholar] [CrossRef]
- Wong, C.W.; Chan, Y.S.; Jeevanandam, J.; Pal, K.; Bechelany, M.; Elkodous, M.A.; El-Sayyad, G.S. Response Surface Methodology Optimization of Mono-dispersed MgO Nanoparticles Fabricated by Ultrasonic-Assisted Sol–Gel Method for Outstanding Antimicrobial and Antibiofilm Activities. J. Clust. Sci. 2020, 31, 367–389. [Google Scholar] [CrossRef]

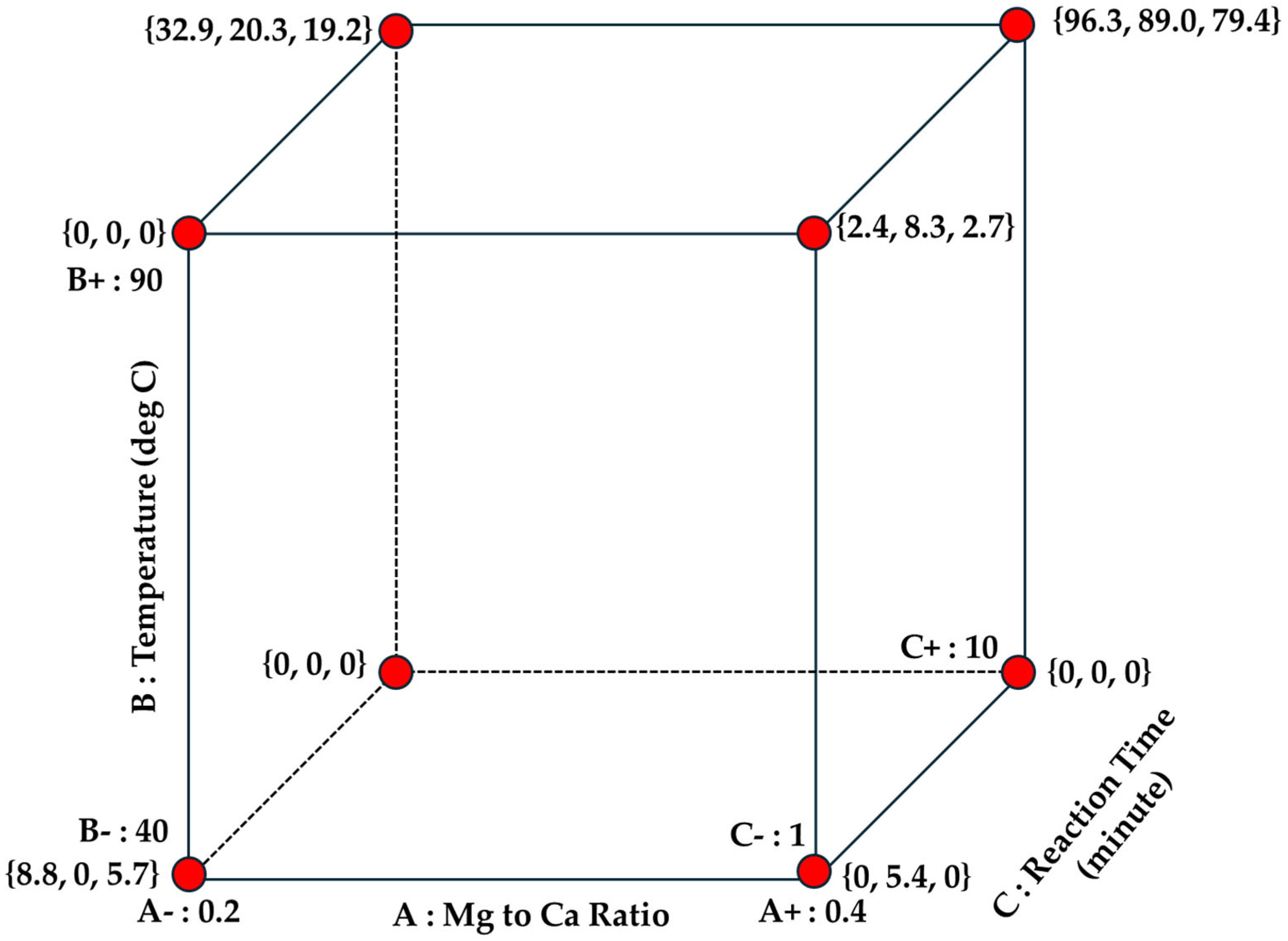

| Randomized Run | Randomized Run | Factor A: Mg-to-Ca Ratio (A) | Factor B: Temperature (B) | Factor C: Reaction Time (C) | Response Y Aragonite Yield |
|---|---|---|---|---|---|
| - | °C | Minutes | % | ||
| 13 | 1 | 0.2 | 40 | 10 | 1.7 |
| 1 | 2 | 0.2 | 40 | 1 | 8.8 |
| 9 | 3 | 0.2 | 90 | 1 | <1.0 |
| 24 | 4 | 0.4 | 90 | 10 | 96.3 |
| 22 | 5 | 0.4 | 90 | 10 | 89.0 |
| 2 | 6 | 0.2 | 40 | 1 | <1.0 |
| 19 | 7 | 0.2 | 90 | 10 | 32.9 |
| 15 | 8 | 0.2 | 40 | 10 | <1.0 |
| 6 | 9 | 0.4 | 40 | 1 | <1.0 |
| 21 | 10 | 0.2 | 90 | 10 | 20.3 |
| 8 | 11 | 0.2 | 90 | 1 | <1.0 |
| 18 | 12 | 0.4 | 40 | 10 | <1.0 |
| 4 | 13 | 0.4 | 40 | 1 | 5.4 |
| 12 | 14 | 0.4 | 90 | 1 | 2.4 |
| 7 | 15 | 0.2 | 90 | 1 | <1.0 |
| 3 | 16 | 0.2 | 40 | 1 | 5.7 |
| 14 | 17 | 0.2 | 40 | 10 | <1.0 |
| 11 | 18 | 0.4 | 90 | 1 | 8.3 |
| 23 | 19 | 0.4 | 90 | 10 | 79.4 |
| 10 | 20 | 0.4 | 90 | 1 | 2.7 |
| 5 | 21 | 0.4 | 40 | 1 | <1.0 |
| 20 | 22 | 0.2 | 90 | 10 | 19.2 |
| 16 | 23 | 0.4 | 40 | 10 | <1.0 |
| 17 | 24 | 0.4 | 40 | 10 | <1.0 |
| Runs | Metal Ions (ppm) in Reactant | Metal Ions (%) in Solids | |||
|---|---|---|---|---|---|
| Mg | Ca | Total | Mg | Ca | |
| 1 | 230 | 11,200 | 11,430 | 2.01 | 97.99 |
| 2 | 475 | 10,811 | 11,286 | 4.21 | 95.79 |
| 3 | 548 | 10,960 | 11,508 | 4.76 | 95.24 |
| 4 | 440 | 9988 | 10,428 | 4.22 | 95.78 |
| 5 | 550 | 11,008 | 11,558 | 4.76 | 95.24 |
| 6 | 580 | 10,705 | 11,285 | 5.14 | 94.86 |
| 7 | 529 | 10,588 | 11,117 | 4.76 | 95.24 |
| 8 | 539 | 10,790 | 11,329 | 4.76 | 95.25 |
| 9 | 390 | 11,201 | 11,591 | 3.36 | 96.64 |
| 10 | 590 | 11,005 | 11,595 | 5.09 | 94.91 |
| 11 | 549 | 10,998 | 11,547 | 4.75 | 95.25 |
| 12 | 290 | 9899 | 10,189 | 2.85 | 97.15 |
| 13 | 539 | 10,789 | 11,328 | 4.76 | 95.24 |
| Average | 481 | 10,765 | 4.26 | 95.74 | |
| Standard Deviation | 113 | 406 | 0.95 | 0.95 | |
| Runs | Particle Size Distribution PSD Analysis (Micron) | ||
|---|---|---|---|
| 10% | 50% | 90% | |
| 1 | 3.49 | 9.47 | 18.37 |
| 2 | 3.22 | 11.35 | 23.89 |
| 3 | 4.11 | 10.78 | 21.78 |
| 4 | 4.34 | 9.01 | 15.21 |
| 5 | 5.11 | 9.12 | 18.32 |
| 6 | 3.67 | 9.45 | 18.98 |
| 7 | 4.21 | 9.01 | 17.34 |
| 8 | 5.01 | 10.12 | 19.23 |
| 9 | 4.12 | 9.45 | 18.33 |
| 10 | 5.55 | 9.34 | 18.46 |
| 11 | 6.12 | 8.67 | 16.78 |
| 12 | 3.02 | 9.35 | 18.67 |
| 13 | 6.23 | 9.75 | 19.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
M. Noh, M.G.; Yuhana, N.Y.; Jumali, M.H.H.; Onn, M.S.; Sanum, R. Experimental Optimization, Scaling Up, and Characterization for Continuous Aragonite Synthesis from Lime Feedstock Using Magnesium Chloride as Chemical Inducer. Processes 2025, 13, 3142. https://doi.org/10.3390/pr13103142
M. Noh MG, Yuhana NY, Jumali MHH, Onn MS, Sanum R. Experimental Optimization, Scaling Up, and Characterization for Continuous Aragonite Synthesis from Lime Feedstock Using Magnesium Chloride as Chemical Inducer. Processes. 2025; 13(10):3142. https://doi.org/10.3390/pr13103142
Chicago/Turabian StyleM. Noh, Mohammad Ghaddaffi, Nor Yuliana Yuhana, Mohammad Hafizuddin Hj Jumali, Mohammad Syazwan Onn, and Ruzilah Sanum. 2025. "Experimental Optimization, Scaling Up, and Characterization for Continuous Aragonite Synthesis from Lime Feedstock Using Magnesium Chloride as Chemical Inducer" Processes 13, no. 10: 3142. https://doi.org/10.3390/pr13103142
APA StyleM. Noh, M. G., Yuhana, N. Y., Jumali, M. H. H., Onn, M. S., & Sanum, R. (2025). Experimental Optimization, Scaling Up, and Characterization for Continuous Aragonite Synthesis from Lime Feedstock Using Magnesium Chloride as Chemical Inducer. Processes, 13(10), 3142. https://doi.org/10.3390/pr13103142







