Phenomenological Comparison of Vacuum Membrane Distillation for VOC Removal and Desalination

Abstract

Vacuum Membrane Distillation (VMD) is a separation process applied to liquid solutions; however, there are phenomenological and operational differences depending on whether the component to be separated is the solute or the solvent. The objective of this article is to develop a mathematical and phenomenological model of the VMD process applied to the separation of volatile organic compound (VOCs) from aqueous solutions and the desalination of saline aqueous solutions. This approach enabled the evaluation of the influence of variables and operating conditions on both separation efficiency and system productivity. Under the analyzed conditions, increasing the temperature, flow rate, and vacuum pressure led to approximate increases in permeate flux of 400%, 10%, and 50%, respectively. In the case of concentration increase, the permeate flux increases linearly for VOC separation and decreases asymptotically for saline solution desalination. Therefore, adjusting the feed temperature is recommended to achieve significant changes in permeate flux.

1. Introduction

Vacuum membrane distillation (VMD) is a separation process applied for liquid solutions, which utilizes a negative pressure gradient (vacuum) across both sides of a membrane. This configuration enables the generation of a product or distillate flux at a significantly higher rate compared to other membrane distillation methods. Due to the higher driving force, a greater permeate flux through the membrane is achieved [1,2]. In the VMD process, the main resistance to mass transfer is located at the feed liquid–membrane interface, adjacent to the membrane surface [3,4,5]. VMD has been extensively researched from both theoretical and experimental perspectives [6,7,8,9]. These studies identify various flow streams within a membrane system that result in the separation of compounds (see Figure 1). It is important to note that stream (4) typically has a higher concentration of the undesired compound than stream (1). Additionally, non-condensable gases are usually present in the feed stream, which necessitates an additional outlet for the removal of these non-volatile gas phases.

VMD employs a hydrophobic porous membrane that enables efficient component separation without the need for high temperatures, making it particularly suitable for heat-sensitive substances. As a result, VMD has a wide range of applications, including treatment of industrial wastewater, particularly effluents with high salinity or the presence of volatile organic compounds (VOCs) [10,11], the chemical and pharmaceutical industries [12] and food and beverage production (concentration of juices, dairy products, and other liquid foodstuffs) [13]. In all these studies, VMD has been shown to be a technological alternative for desalination and the extraction of VOCs.

Desalination involves the removal of dissolved saline solutes from brackish water, seawater, and brines to produce low-salinity water suitable for human consumption, industrial use, and agriculture. Currently, reverse osmosis (RO) is the preferred membrane-based separation technology for desalination, due to its high adaptability and scalability to industrial levels [14]. In 2023, the total global contracted desalination capacity is at least 109.2 million m³/day [15], where 65 to 70% are RO plants [16]. The implementation of RO has led to an environmental issue related to the high salt concentration in the reject brine. This waste stream has become a challenge for industries, as its discharge into the sea causes significant environmental impacts, preventing its direct disposal into marine bodies [16,17,18]. For this reason, there is a need to implement processes capable of addressing this issue, with VMD presenting a promising alternative for the treatment of reject streams or brines.

VOCs are defined as organic substances with a saturated vapor pressure above 133.32 Pa at ambient temperature or boiling points in the range of 50–260 °C at atmospheric pressure [19]. VOCs are primarily found in industrial wastewater. Hydrosoluble VOCs can disperse through the natural hydrological cycle, contaminating potential water sources and posing ecological and human health risks, even at low concentrations [19]. Current methods for the removal of volatile compounds from aqueous matrices include adsorption [20], aeration [21], oxidation processes [22], and biological treatment [23]. However, these methods have demonstrated lower extraction efficiency compared to membrane techniques, which offer advantages such as simpler operation and the absence of secondary contamination [19]. Therefore, similar to desalination, VMD emerges as a technological solution for the removal of VOCs.

1.1. Transport Phenomena in VMD

The VMD process combines principles of thermal distillation and membrane separation. Separation occurs by heating the feed solution while applying a vacuum on the permeate side of the membrane. This causes partial evaporation of the solution, generating vapor that passes through a hydrophobic and macroporous membrane, which acts as a physical barrier. The membrane’s hydrophobicity allows the formation of a liquid–vapor interface within each pore, controlled by the feed liquid pressure. The driving force of the process is the vapor pressure difference across the membrane, induced by the temperature gradient between both sides. 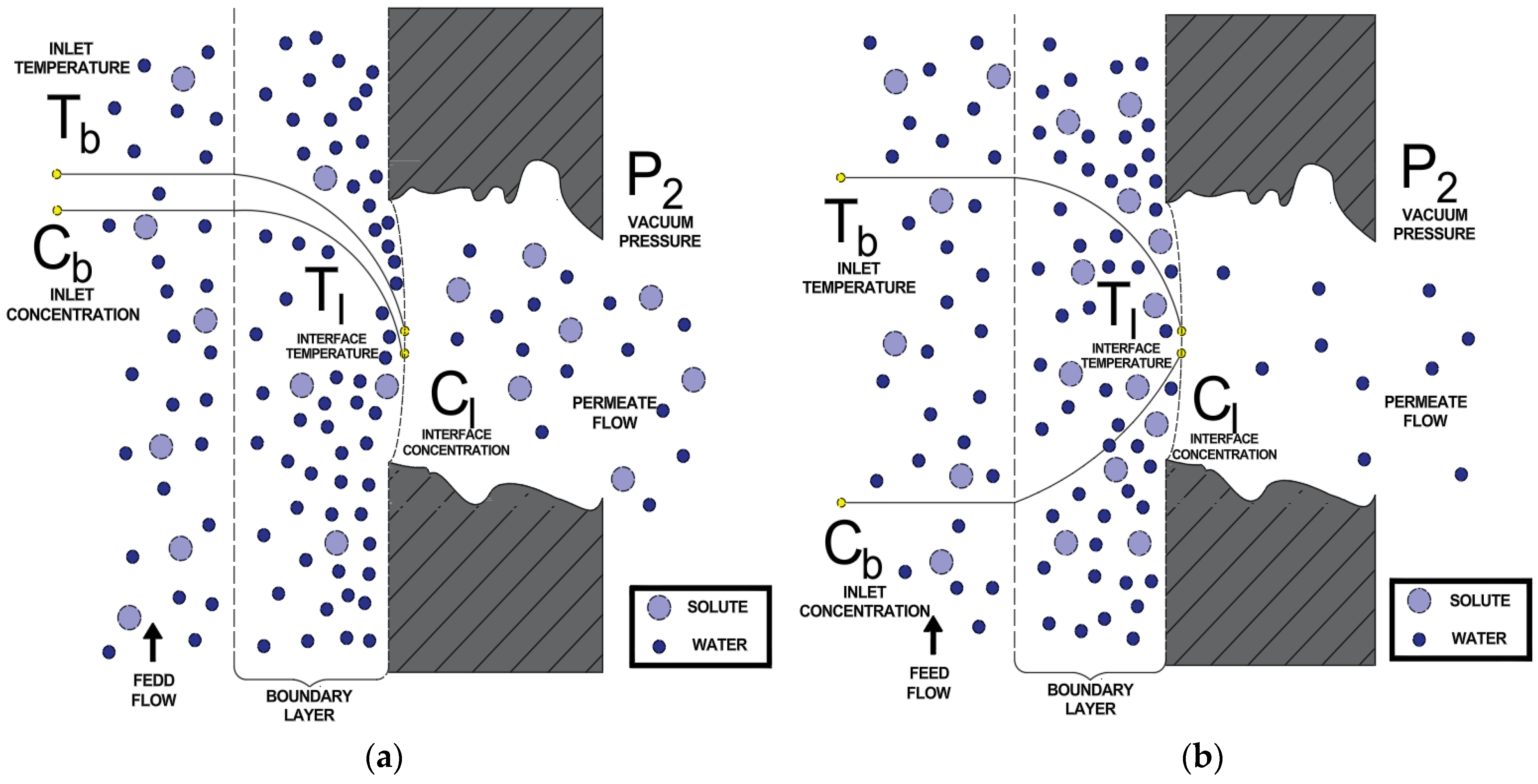Figure 2 presents the two scenarios analyzed in this study, which vary according to the feed fluid composition: (a) a solution containing VOCs, where the permeate stream has a higher VOC concentration than the feed, and the reject stream has a lower concentration of these compounds; (b) an aqueous saline solution (WS), where the permeate stream corresponds to pure water, while the reject stream exhibits a higher salt concentration than the feed stream.

1.1.1. Mass and Heat Transfer in the Liquid Phase

Mass transfer in the liquid phase during the VMD process is described using film theory, which establishes a relationship between the composition of the bulk liquid and that at the liquid–vapor interface through the mass transfer coefficient [24,25]. This theory provides a simplified representation of the concentration polarization mechanism, assuming the presence of a boundary layer of liquid adjacent to the interface through which mass transfer occurs. Within this layer, the solute diffuses, generating a concentration gradient between the bulk liquid and the interface. The mass transfer coefficient can be determined using dimensionless correlations based on the Sherwood number (see

Table 1. Mass Transfer Equations in the liquid phase of the VMD Process [26,27].

Variable	Equation (COVs)	Equation (Salts)
$N_{T1}$	$N_T=k_L·{\rho }_L·ln\left({\displaystyle \frac{w_{i,I}-w_{i,v}}{w_b-w_{i,v}}}\right)$	$N_T=k_L·{\rho }_L·ln\left({\displaystyle \frac{w_{i,I}}{w_b}}\right)$
$Sh$	$Sh={\displaystyle \frac{k_L·d}{D}}=Sh(Re,Sc,{\displaystyle \frac{d}{L}})$
$Re$	$Re={\displaystyle \frac{4·Q·\rho }{n·\pi ·d_c·\mu }}$
$Sc$	$Sc={\displaystyle \frac{\mu }{D·\rho }}$

). Depending on the module geometry, different correlations are applied, with power-law expressions being the most commonly used to calculate the relevant dimensionless numbers. Additionally,

Table 2. Equations to determine the vapor-phase concentration at the pore exit [28].

Equations
$a\cdot {y_{1,P}}^2+b\cdot y_{1,P}+c=0$
$a=(\sqrt{M_A}-\sqrt{M_B})\cdot P_P$
$b=\sqrt{M_A}·[P_I·(1-y_{1,I})-P_P]-\sqrt{M_B}\cdot [P_P+P_I·y_{1,I}]$
$c=\sqrt{M_B}\cdot P_I·y_{1,I}$

summarizes the equations employed to calculate vapor concentration at the pore outlet in the VMD process for VOC separation.

In the VMD process, heat transfer by conduction through the membrane is practically negligible due to the low pressure on the permeate side, which significantly reduces the thermal conductivity of the gas, approaching zero under near-vacuum conditions [29]. The effective thermal conductivity of the membrane decreases with decreasing pressure, as it accounts for contributions from both the solid matrix, which is unaffected by pressure, and the gas within the pores. Consequently, the heat required for the evaporation of compounds at the interface is primarily supplied by heat transfer from the liquid phase. In this context, heat transfer in the liquid phase is directly coupled to the evaporative flux through the membrane.

Table 3. Heat transfer equations in the liquid phase [4,30].

Variable	Equation (COVs and Salts)
$N_{T2}$	${\displaystyle \sum _i^n}{N}_i{\lambda }_i=h·(T_b-T_i)$
$Nu$	$Nu={\displaystyle \frac{h·d}{k}}=Nu(Re,Pr,{\displaystyle \frac{d}{L}})$
$Pr$	$Pr={\displaystyle \frac{C_p·\mu }{k}}$

presents the equations used to model heat transfer in the liquid phase during the VMD process, for both VOC separation and saline solution desalination. While the equations governing the phenomenon are equivalent in both cases, it is important to distinguish between volatile solutes in VOC-containing solutions and non-volatile solutes in saline solutions when calculating thermodynamic properties.

1.1.2. Mass Transfer Through the Membrane

Gas permeation through a porous medium can occur via three primary flow regimes, depending on operating conditions and pore size: convective flow, Knudsen flow, and transition flow. Knudsen flow arises when the pore diameter is small relative to the mean free path, defined as the average distance a molecule travels before colliding with another (

Table 4. Equation for Mass Transfer through the membrane [10,28].

Variable	Equation (COVs and Salts)
J	$J={\displaystyle \frac{d·(C_1-C_2)}{3·\delta }}·{\left({\displaystyle \frac{8·R·T}{M_A·\pi }}\right)}^{{\displaystyle \frac{1}{2}}}$
$N_{T3}$	$N_T=K_m·\sqrt{M_I}·(P_I{y}_{i,I}-P_P{y}_{i,P})$
$Kn$	$Kn={\displaystyle \frac{\lambda }{d}}$
$\lambda$	$\lambda ={\displaystyle \frac{3·\mu }{\rho }}{\left({\displaystyle \frac{\pi ·M_A}{8·R·T}}\right)}^{{\displaystyle \frac{1}{2}}}$
$\rho$	$\rho ={\displaystyle \frac{P·M_A}{R·T}}$
$\mu$	$\mu =2.6693·{10}^{-5}{\displaystyle \frac{\sqrt{M_A·T}}{{\sigma }^2·{\Omega }_{\mu }}}$
${\Omega }_{\mu }$	${\Omega }_{\mu }=0.7634219+0.8250214·{\displaystyle \frac{k·T}{\epsilon }}$
${\displaystyle \frac{\epsilon }{k}}$	${\displaystyle \frac{\epsilon }{k}}=0.77·T_c$
$\sigma$	$\sigma =2.44·{\left({\displaystyle \frac{T_c}{P_c}}\right)}^{{\displaystyle \frac{1}{3}}}$
${\alpha }_{Kn}$	${\alpha }_{Kn}={\left({\displaystyle \frac{M_B}{M_A}}\right)}^{{\displaystyle \frac{1}{2}}}$
$M$	$\sqrt{M}={\displaystyle \sum _i^n}{\displaystyle \frac{N_T}{\frac{N_i}{\sqrt{M_i}}}}$
$K_m$	$K_m={\displaystyle \frac{4·\epsilon ·d_p}{3·\tau ·\delta ·{(2·\pi ·R·T)}^{\frac{1}{2}}}}$

, 3rd row). The tortuosity of the porous medium further influences species mobility during diffusion. In this regime, molecular collisions with the pore walls dominate over intermolecular collisions. Knudsen diffusion theory provides a framework to describe gas transport through porous media (Table 4, 1st row). When the concentration gradient is expressed in terms of pressure, the resulting relationship is analogous to Darcy’s law. Additionally, a linear correlation exists between the total pressure difference and the overall mass flux N_T (Table 4, 2nd row). Consequently, the total pressure difference maintained between the liquid meniscus and the gas phase acts as the driving force for mass transfer [28].

1.1.3. Liquid–Vapor Equilibrium

Table 5. Equations for liquid–vapor equilibrium [31].

Variable	Equation (COVs and Salts)
$P_I$	$P_I={P°}_1\left(T_I\right)·x_{1,I}·{\phi }_1\left(T_1,x_{1,I}\right)+{P°}_2\left(T_I\right)·\left(1-x_{1,I}\right)·{\phi }_2\left(T_1,x_{1,I}\right)$
$Y_{1,I}$	$Y_{1,I}={\displaystyle \frac{{P°}_1\left(T_I\right)·x_{1,I}·{\phi }_1\left(T_1,x_{1,I}\right)}{P_I}}$
${\alpha }_T$	${\alpha }_T={\displaystyle \frac{w_{i,P}·(1-w_{i,P})}{w_b·(1-w_b)}}$
$P°$	$log \left(P°\right)=A-{\displaystyle \frac{B}{T+C}}$

presents the equations describing the liquid–vapor equilibrium at the interface located at the membrane pore inlet for a binary mixture.

Table 6. Antoine equation constants for water and ethanol [31].

Compound	A	B	C	Temperature Range
Water	8.0713	1730.63	233.426	1–100 [°C]
Ethanol	8.1122	1592.86	226.184	1–100 [°C]

lists the constants required to calculate vapor pressure using the Antoine equation (Table 5, 4th row). For VOC-containing solutions, the liquid–vapor equilibrium considers the presence of both components (water and ethanol) in the liquid and vapor phases at the interface. In contrast, for saline solutions, the equilibrium involves two species (water and salt) in the liquid phase, while only water is present in the vapor phase.

For the liquid–vapor equilibrium in VOC-containing solutions and considering that the binary water–organic solute mixture behaves as a non-ideal solution, the NRTL model is used to calculate the activity coefficients. This model, based on a three-parameter equation, is applicable to both liquid–vapor and liquid–liquid equilibria (see

Table 7. NRTL Model equations [32,33].

Variable	Equation
${\gamma }_I$	$ln {\gamma }_I={X_2}^2 \left[{\displaystyle \frac{{\tau }_{21}{G_{21}}^2}{(X_1+X_2·G_{21}{)}^2}}+{\displaystyle \frac{{\tau }_{12}{G}_{12}}{(X_2+X_1·G_{12}{)}^2}}\right]$
${\gamma }_2$	$ln {\gamma }_2={X_1}^2 \left[{\displaystyle \frac{{\tau }_{12}{G_{12}}^2}{(X_2+X_1·G_{12}{)}^2}}+{\displaystyle \frac{{\tau }_{21}{G}_{21}}{(X_1+X_2·G_{21}{)}^2}}\right]$
${\tau }_{12}$	${\tau }_{12}={\displaystyle \frac{A_{12}}{RT}}$
${\tau }_{21}$	${\tau }_{21}={\displaystyle \frac{A_{21}}{RT}}$
$G_{12}$	$G_{12}=exp(-{\alpha }_{12}{\tau }_{12})$
$G_{21}$	$G_{21}=exp(-{\alpha }_{21}{\tau }_{21})$

). The NRTL model is applied solely to represent the real liquid–vapor equilibrium of aqueous solutions containing volatile liquids, specifically for water–ethanol mixtures.

One of the most significant distinctions between the two processes studied lies in the presence of colligative properties in solutions containing non-volatile solutes, such as aqueous sodium chloride solutions. In the case of VMD, the relevant colligative properties are the relative lowering of vapor pressure and the elevation of the boiling point. Vapor pressure depression, resulting from the addition of a non-volatile solute to a solvent, arises from two factors: (1) a reduction in the number of solvent molecules at the liquid surface; (2) the formation of attractive interactions between solute and solvent molecules, which hinder the transition of solvent molecules from the liquid to the vapor phase. This phenomenon is critical in VMD with saline solutions, as vapor pressure directly governs the total permeate flux. Boiling point elevation refers to the increase in the solution’s boiling temperature relative to the pure solvent due to the presence of non-volatile solutes. This effect is directly related to vapor pressure depression: as vapor pressure decreases, a higher temperature is required for the solution’s vapor pressure to match the external pressure, the condition necessary for boiling. Vapor pressure depression is quantified using Raoult’s law, with its magnitude depending on the solute concentration in the liquid phase. In contrast, determining the boiling point elevation within the model is more complex, since temperature directly and indirectly affects nearly all equations in the system. Its effect is accounted for by incorporating activity coefficients, which estimate deviations from ideal behavior caused by the solute. The activity coefficient of water in a saline solution is calculated using the simplified Pitzer equation (see

Table 8. Equations for colligative properties [34].

Variable	Equation
${\gamma }_{H2O}$	$ln {\gamma }_{H2O}=-{\displaystyle \frac{A·m}{1+B·\sqrt{m}}}+C·m$
$A$	$A={\displaystyle \frac{1.327·{10}^3·\left(d^{1/2}\right)}{T^{3/2}}}$
$B$	$B=B_0+B_1·T+B_2·T^2$
$C$	$C=C_0+C_1·T+C_2·T^2$

), which describes the thermodynamic behavior of electrolyte solutions across a range of concentrations. This equation accounts for interactions between ions and the solvent. For NaCl, parameters fitted to experimental data are employed to ensure accurate representation of the system.

Finally, the estimation of transport coefficients through correlations based on dimensionless numbers is carried out using an appropriate characterization of the physical and transport properties of the liquid mixtures, as well as the geometry of the physical system. For this purpose, correlations for the properties of each compound are taken from the literature [10,35].

Considering the aforementioned information, the objective of this article is to develop and analyze a mathematical and phenomenological model of the VMD process applied to the separation of VOCs present in aqueous solutions and to the desalination of saline aqueous solutions, evaluating the influence of variables and operating conditions on separation efficiency and system productivity.

2. Materials and Methods

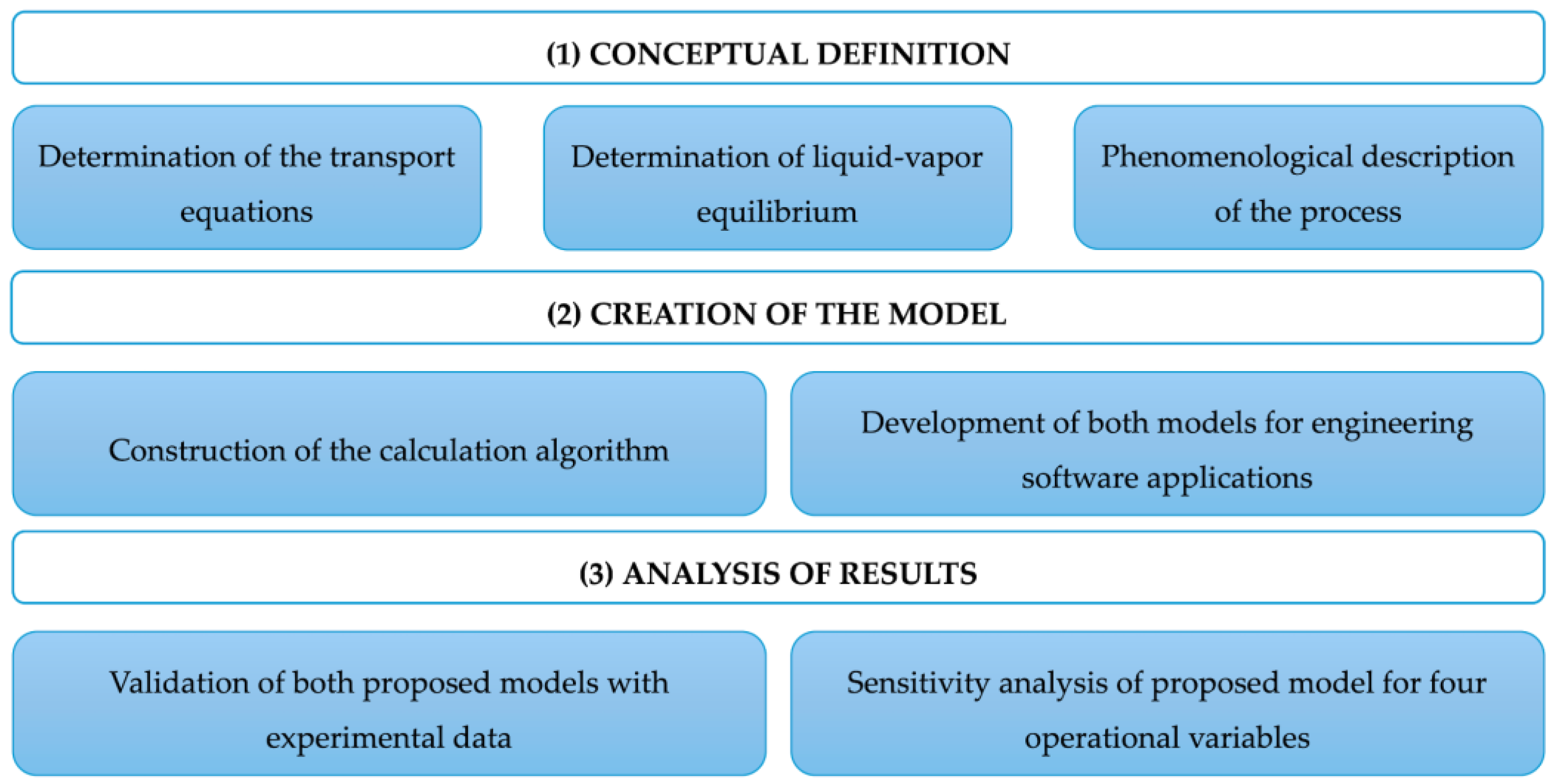
Figure 3 shows the procedure followed, which consists of three stages: (1) conceptual definition, (2) model development, and (3) results analysis. Stage 1 is based on a literature review to establish definitions, governing equations, and the assumptions required for the simulations.

Stage 2 involves the development of two models for the VMD process, according to the type of material to be separated: (1) VOCs from an aqueous solution (VMD-VOCs), and (2) water from a saline solution (VMD-WS). The VMD-VOCs model is designed for a binary system (water and VOCs), considering the NRTL thermodynamic model and a tubular geometry. On the other hand, the VMD-WS model incorporates the boiling point elevation effect, the influence of salinity on temperature polarization (mainly through its effect on the latent heat of vaporization), and assumes a tubular geometry. The process phenomena are represented in the model with the following assumptions: (a) the solute concentration at the pore outlet is zero, since the salt is a non-volatile compound in water and therefore will not pass through the membrane, and (b) selectivity cannot be calculated because the solute does not permeate the membrane. For both models, the values of the operating conditions (feed flow rate (L/min), feed temperature (°C), vacuum pressure (mbar), and feed concentration (wt.%)) depend on the type of analysis being performed, whether it is a comparison between model and experimental results, or an evaluation of the influence of operating variables.

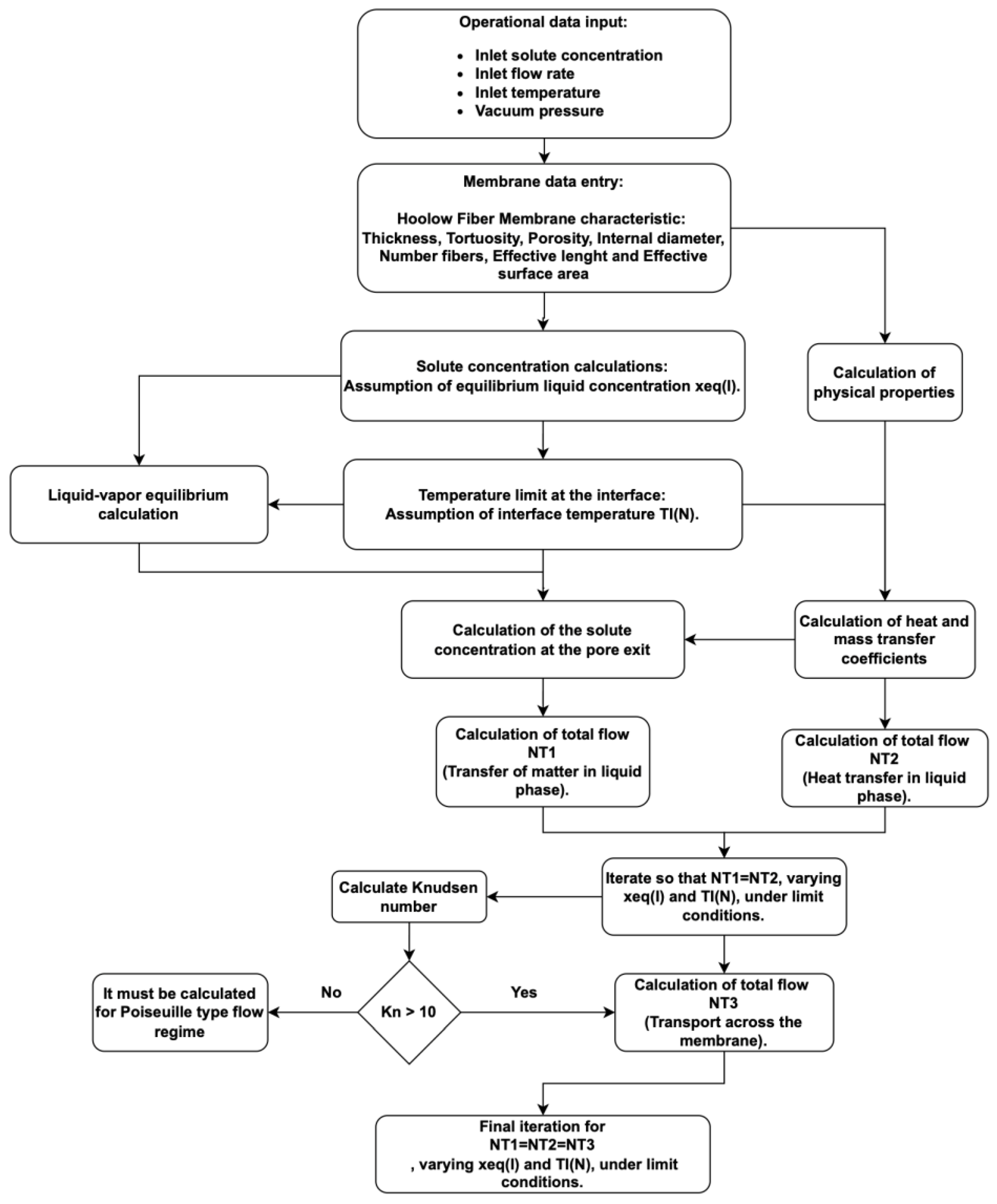
Figure 4 shows the calculation algorithm for both models, based on the previously presented methodology and the approach proposed by Silva [28], resulting in a mathematical model that describes the vacuum membrane distillation process. Both models (VMD-VOCs and VMD-WS) were developed using MATLAB R2024a (Natick, MA, USA).

In Stage 3, the models are validated by comparing the simulation results with experimental data reported in publications by other authors (see

Table 9. Experimental conditions from the studies used for model validation.

Model	Experimental Conditions for Validation	Reference Article
VMD-COVs	Aqueous solution of ethanol: 5.55 %p/p Geometry: hollow fiber Feed rate (T = 33.7 °C): 0.025–0.36 L/min Feed rate (T = 40.2 °C): 0.08–0.36 L/min Vacuum pressure: 27.8 mbar	[10]
VMD-WS	Experiment 1 Aqueous NaCl solution: 7.0 %p/p Geometry: hollow fiber, Vacuum pressure: 25 mbar Feed rate: 1 L/min Temperature: 40–70 °C	[36]
	Experiment 2 Aqueous NaCl solution: 3.5 %p/p Geometry: hollow fiber Vacuum pressure: 25 mbar Feed rate: 1 L/min Temperature: 50–70 °C	[37]

). Subsequently, the sensitivity analysis of the operating variables is performed based on the structural parameters of the membranes (see

Table 10. Structural characteristics of membranes.

Characteristics	Unit	VMD-COVs	VMD-WS
			Value [36]	Value [37]
Membrane material	-	Polypropylene	Polypropylene	Modified alumina
Average pore diameter	μm	0.03–0.05	0.5	0.22
Porosity	%	40	60	70
Thickness	μm	25	210	230
Tortuosity	-	2	1.4	1.2
Internal diameter	μm	400	340	800
Number of fibers	-	67	1300	20
Effective length	m	0.275	0.2	0.11
Effective surface area	m2	0.02315	2.8	0.006

).

Table 11. Operational values for VMD modeling.

Variable	Unit	Value
Feed temperature	°C	50
Feed flow	L/min	1
Vacuum pressure	mbar	30
Feed concentration	%p/p	7

shows the constant values assigned to each operating variable when a range is applied to the variable under study. The evaluated range is shown in each of the graphs corresponding to the respective variable.

3. Results

3.1. VMD Model Validation

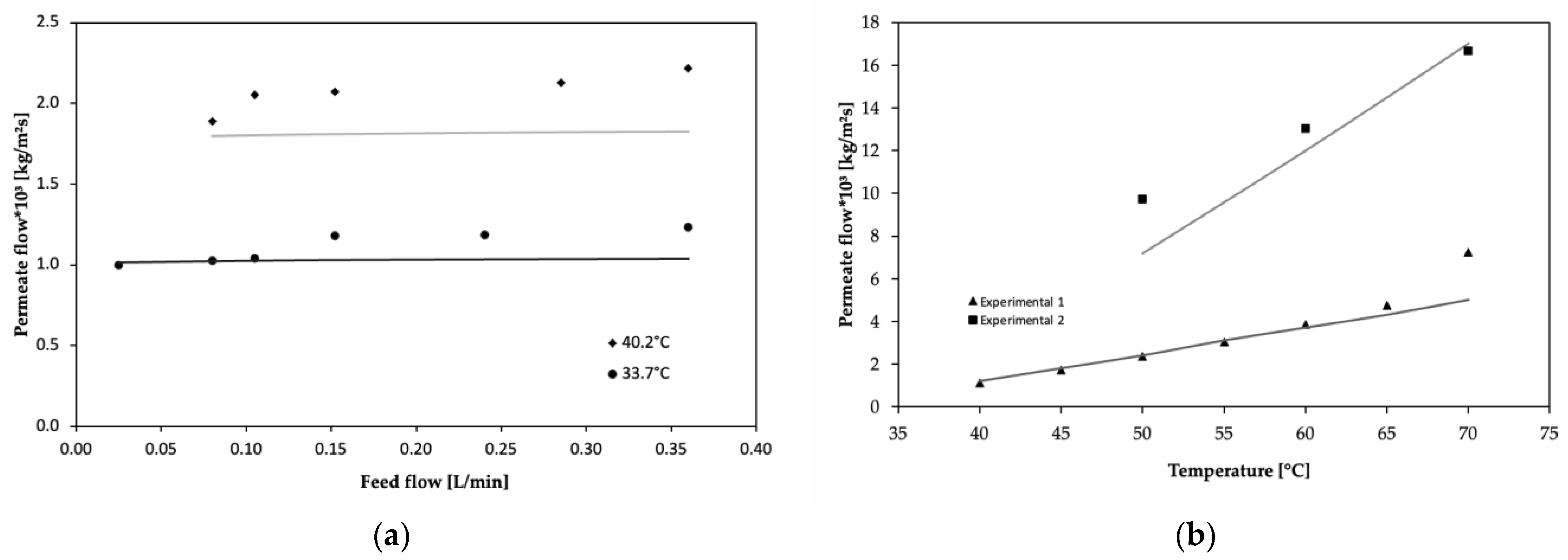
This work establishes a comparison between experimentally obtained results and those derived from a model that integrates the heat and mass transfer mechanisms in the liquid phase, within the porous membrane matrix, and the liquid–vapor equilibrium. Figure 5a,b show the validation of the VMD-VOCs and VMD-WS models, respectively. The average errors for the VMD-VOCs and VMD-WS models were 9.5% and 9.7%, respectively. For the VMD-VOCs model, applied at 33.7 °C and 40.2 °C, average errors of 7% and 12% were obtained, respectively. In both cases, the error was lower at feed flow rates near 0.1 L/min and increased at higher flow rates. The maximum recorded error at a point of the curve was 18%, which is considered acceptable for this type of simulation, since other authors conducting similar studies comparing modeling with experimental results have reported maximum point errors between 15% and 21% [38,39,40]. In these cases, as in the present manuscript, the maximum point error occurs under the conditions of the highest flow rate studied. This situation is explained by the fact that, at higher flow rates, the undeveloped condition of the laminar velocity profiles increases at the membrane module inlet, which in turn affects the temperature and concentration profiles in the corresponding boundary layers. Therefore, the VMD-VOCs model accurately describes the vacuum membrane distillation process in a tubular geometry optimized for the separation of a volatile organic compound (ethanol). In the case of the VMD-WS model, applied to Experiment 1, the simulation showed a deviation of 3.7% within the range of 40 to 65 °C. However, when including the final data point at 70 °C, the average error increased to 8.5%. For Experiment 2, an average error of 11% was obtained, demonstrating that the model fits the experimental data well for this type of membrane.

3.2. Sensitivity Analysis of Operating Variables

The sensitivity analysis aimed to quantify the behavior of the permeate flux, temperature polarization, and concentration polarization in response to variations in (a) feed temperature, (b) vacuum pressure, (c) feed flow rate, and (d) feed concentration.

3.2.1. Effect of Feed Temperature

In the VMD process, the energy required for the phase change at the interface, as well as the effect of vapor pressure, can be evaluated through careful measurement of the feed temperature, as reported by various authors [41,42,43]. This variable represents a key factor in process efficiency, as it directly influences permeation.

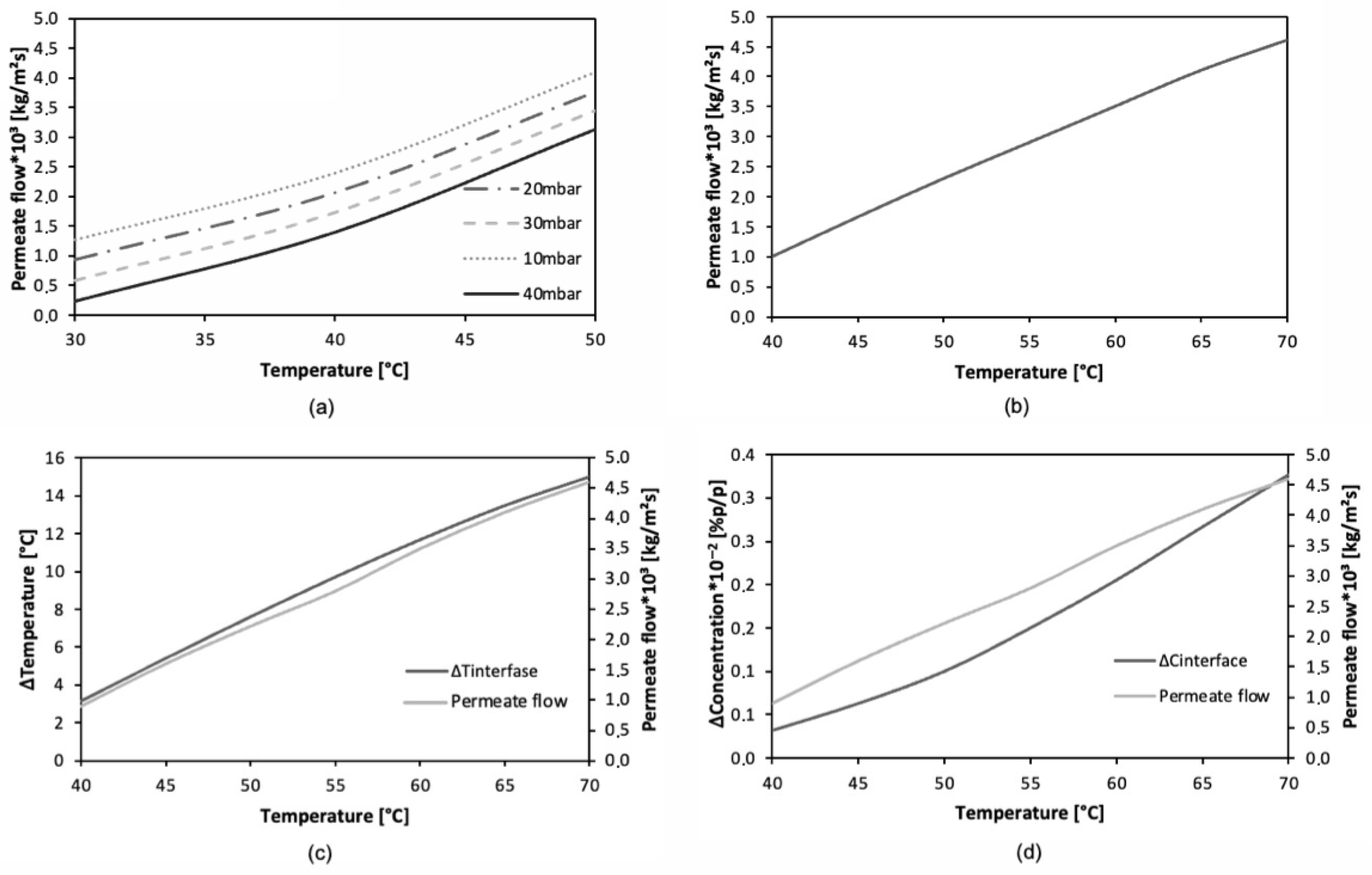
Figure 6a,b show the effect of temperature on the permeate flux for the VMD-VOCs and VMD-WS models, respectively. In the case of the VMD-VOCs and VMD-WS models, the curves exhibit an exponential increasing trend and a linear increasing trend, respectively. This difference is mainly attributed to the way colligative properties are calculated in each model’s algorithm. Another observable effect in the trend of the curves is the increase in vapor pressure with temperature, thereby validating the use of Antoine-type correlations. Additionally, Figure 6c,d show that the effect of feed temperature on temperature polarization and concentration polarization, respectively, is accurately described, as reported by other authors [44,45,46]. The temperature polarization effect reflects the energy required for the phase change to occur across the interface. Higher temperature polarization results in lower process performance, as it negatively impacts the vapor pressure that drives the permeate flux. As shown in Figure 6c (distillation of saline solution), there is a directly proportional relationship between feed temperature and temperature polarization within the analyzed temperature range. However, this effect may be mitigated by the increased permeate flux associated with higher temperatures. Nevertheless, it remains a relevant phenomenon, as highlighted in various studies focused on its mitigation [47,48,49]. As the temperature increases, this growth tends to slightly decrease. This phenomenon may be attributed to the improvement of the fluid’s thermal properties at higher temperatures, as elevated temperatures are associated with enhanced heat storage and heat transfer capabilities [50,51,52]. This allows for more efficient heat transfer in the vicinity of the membrane. In this context, it could be said that at elevated temperatures, a form of thermal gradient saturation is reached. However, this reduction in the increase in polarization does not produce significant effects on the permeate flux.

Figure 6d shows the effect of feed temperature on concentration polarization. It is observed that as the feed temperature increases, the concentration of solutes (NaCl) at the liquid–vapor interface also increases. This behavior is consistent with the previously presented polarization graphs, since the temperature rise promotes a higher evaporative flux of the more volatile component, leading to greater salt accumulation at the interface [53,54,55]. The observed trend closely resembles the behavior of temperature polarization, due to its strong dependence on this variable. Although a slight exponential trend is discernible, this pattern is directly related to the increase in feed temperature and its effect on vapor pressure, as described by the Antoine equation.

3.2.2. Effect of Vacuum Pressure

Pressure is one of the most important parameters, as the pressure differential between the pore inlet and outlet is the driving force of the VMD process [36,56,57]. This is evident in the equations presented in Section 1 of this manuscript.

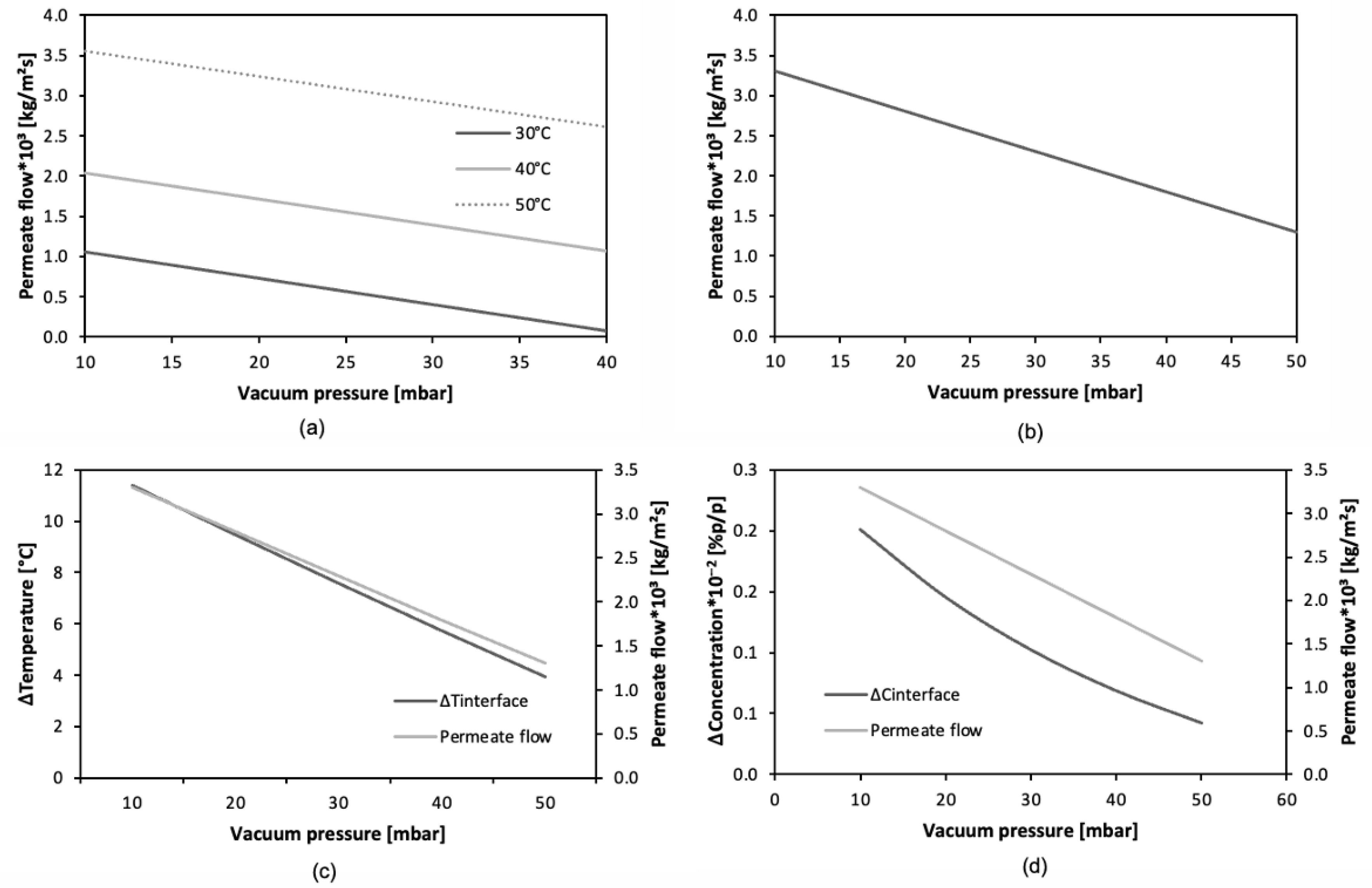
Figure 7a,b show that, for the VMD-VOCs and VMD-WS models, respectively, the permeate flux decreases as the vacuum pressure increases. This confirms that the driving force (pressure differential) is directly proportional to the permeate flux. This trend has also been observed by other authors [58,59,60]. For both membrane distillation cases (VOCs and salts), vacuum pressure plays a significant role in the variation in the permeate flux.

As previously indicated in the VMD-VOCs model, an increase in temperature maintains an upward trend in the permeate flux. On the other hand, regarding thermal polarization in the VMD-WS model (Figure 7c), a decrease in this phenomenon is observed as vacuum pressure increases. This behavior can be attributed to its direct relationship with permeate flux. When vacuum pressure decreases, the pressure differential between the vapor pressure of the feed fluid and the pressure on the vacuum side increases, resulting in an enhanced driving force and, consequently, a higher permeate flux. To sustain this increased flux, a higher evaporation rate is required, which implies greater energy consumption on the liquid side. This leads to a reduction in the interfacial temperature and, as a result, a larger thermal gradient, thereby intensifying thermal polarization. Furthermore, Figure 7d illustrates the concentration polarization phenomenon, which appears as an increase in salt concentration at the liquid–vapor interface as vacuum pressure decreases. This effect is closely related to the increase in the evaporation rate driven by the higher-pressure differential. As a result, salt particles that cannot pass through the membrane accumulate at the interface, leading to a greater difference between the interfacial and feed concentrations at low pressures, while this difference is reduced at higher pressures.

3.2.3. Effect of Feed Rate

The feed flow rate simultaneously influences both mass and heat transport in the liquid phase, which is consistent with the flow regime of the feed entering the membrane module, as quantified by the Reynolds number, which ranged from 700 to 2000.

In this regard, the flow within membrane modules used for VMD typically falls within the laminar regime. This type of flow is characterized by limited velocities, which favors more controlled mass and heat transport [61,62,63]. However, depending on the specific design of the module, this flow regime may limit fluid renewal at the liquid–vapor interface, potentially affecting the performance of the process.

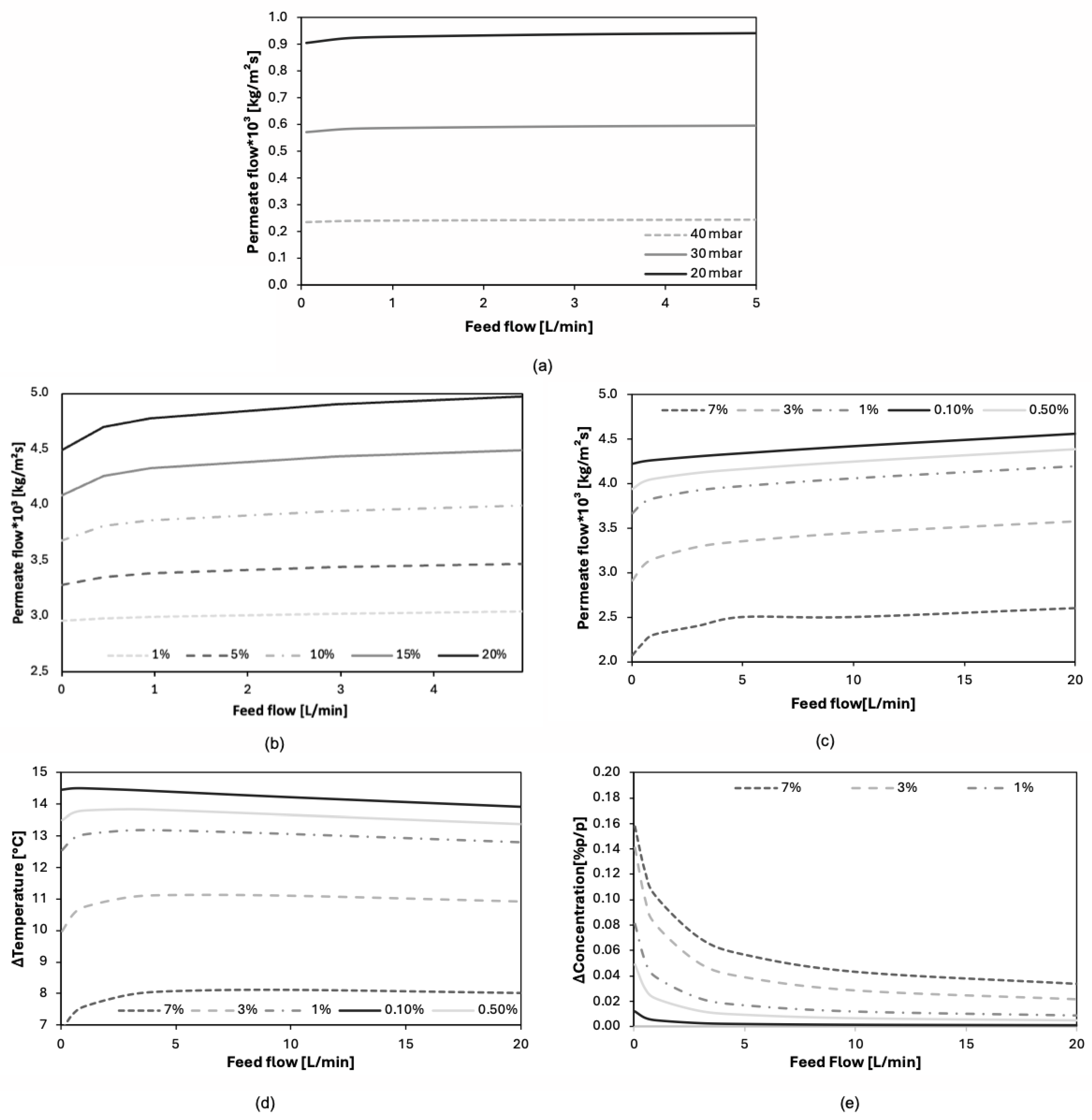
Figure 8a–c show a positive increase in permeate flux as the feed flow rate increases. For flow rates below 1 L/min, the increase in permeate flux is slight (<10%), whereas for flow rates above 1 L/min, it tends to stabilize at a relatively constant value. Higher flow rates enhance heat transfer between the fluid and the membrane and reduce concentration polarization; however, an excessive increase in flow rate also reduces the residence time of the liquid in contact with the membrane, which limits the evaporation rate. Another relevant aspect concerns the presence of undeveloped velocity profiles at the module inlet, which results in undeveloped temperature and concentration gradients. This leads to deviations from some of the dimensionless Nusselt and Sherwood correlations used to predict the transport mechanisms under study.

Figure 8d shows the trend of thermal polarization in relation to the variation in the feed flow rate. The model predicts that for flow rates below 5 L/min, thermal polarization increases, whereas for flow rates between 5 and 10 L/min, thermal polarization either stabilizes or slightly decreases. This behavior can be explained by the fact that, at low flow rates, the interfacial temperature decreases relative to the inlet temperature as the feed flow increases. The trend of thermal polarization as a function of feed flow rate is governed by the dynamics of fluid renewal at the liquid–vapor interface. At low flow rates, fluid renewal is slower, meaning the energy required for evaporation is supplied mainly by the stagnant fluid near the membrane. This causes a greater temperature to drop at the interface, as more heat is transferred from the fluid to the evaporation process. However, increasing the feed flow rate enhances the transport of fresh fluid toward the membrane, which in turn increases the evaporation rate. Thus, two opposing effects coexist: on one hand, improved fluid renewal reduces thermal polarization; on the other hand, at higher flow rates, the residence time of the fluid decreases, limiting its capacity to supply energy to the interface. This may cause the interfacial temperature to rise beyond a certain flow rate threshold. In summary, at low flow rates, the thermophysical properties of the solution have a more significant influence than convective transport effects. Conversely, at higher flow rates—as expected in processes without the presence of non-volatile compounds—the interfacial temperature tends to increase, leading to a progressive reduction in thermal polarization. On the other hand, Figure 8e shows that concentration polarization decreases asymptotically as the feed flow rate increases. This confirms that the phenomenon is influenced by the enhanced renewal of fluid at the interface, which is characteristic of high flow rates. Furthermore, it is observed that this trend is inverse to that of permeate flux with increasing flow rate, indicating that the evolution of permeate flux is strongly governed by the effect of concentration polarization.

3.2.4. Effect of Feed Concentration

Figure 9a shows that, in the VMD-COVs model, the permeate flux increases with the ethanol concentration. This is because the organic compound, being more volatile than water (the solvent), promotes a greater phase change, facilitating its transport across the interface and subsequent collection as permeate. The total product flux (permeate vapor) corresponds to the sum of water and volatile liquid. Under conditions that enhance the relative volatility of the process, the flux of VOCs increases, adding to that of the solvent (water), which accounts for the observed increase in total flux. In contrast, in the VMD-WS model, where the solute is NaCl (less volatile than water), an opposite trend is observed (see Figure 9b). In this case, increasing the salt concentration results in greater mass transfer resistance within the boundary layer, thereby reducing the permeate flux. Figure 9c indicates that thermal polarization decreases as the salt concentration in the feed increases. This behavior arises from a combination of two phenomena: (1) the ebullioscopic effect characteristic of such solutions, and (2) the non-ideal nature of the saline solution, which enhances its colligative properties. As a result, the permeate flux decreases with increasing salt concentration. Conversely, at lower salt concentrations, water exhibits a greater tendency to evaporate, leading to more pronounced cooling at the interface. This occurs because more heat is required to vaporize the larger volume of water. Therefore, increasing the concentration of the non-volatile solute raises the interfacial temperature, which reduces the evaporation rate and consequently the permeate flux. Regarding interfacial concentration, it increases as the salt concentration in the feed rises. This is mainly due to a greater tendency for NaCl to accumulate on the membrane surface, since local saturation is reached more quickly, leading to increased concentration polarization. Additionally, it is important to note that in concentrated saline solutions, the ability of particles to diffuse from regions of high to low concentration is hindered due to the higher number of NaCl particles interfering with the free movement of molecules. Consequently, mass transport from the interface to the bulk fluid becomes slower, further intensifying concentration polarization. In contrast, in more diluted solutions, the diffusion coefficient is higher, allowing for more efficient mass transport and reduced polarization. Finally, Figure 9d shows that concentration polarization remains positive across all conditions; however, for NaCl concentrations above 7 wt.%, it begins to decrease. This behavior is explained by the fact that as salt concentration increases, both heat and mass transport become more limited. As a result, the mass flux decreases, meaning less water evaporates from the solution. This causes the interfacial concentration to approach that of the feed, thus reducing the concentration gradient characteristic of concentration polarization.

3.3. Phenomenological Behavior Comparison in Both Processes

VMD is affected by two main polarization phenomena: thermal and concentration polarization. Both phenomena occur regardless of whether the solution contains VOCs or a non-volatile solute, such as salt. Polarization influences the performance of the VMD process in various ways, depending on the operational variable considered. Additionally, certain membrane properties, such as thermal conductivity and porosity, are also impacted by these phenomena. In particular, when the membrane has low thermal conductivity, thermal polarization tends to intensify. However, this effect is generally not a decisive factor in membrane design, as low thermal conductivity is prioritized to minimize heat transfer from the fluid through the pores to the membrane walls.

Figure 10 summarizes the sensitivity analysis regarding polarization phenomena and permeate flux, as described in the previous sections. It is observed that the three response variables exhibit similar behavior with increasing feed temperature and vacuum pressure. However, when the feed flow rate increases, the response variables show differentiated behavior. Regarding the effect of solute concentration in the feed, its influence depends on whether the compound is volatile (VOCs) or non-volatile (salt), as both exhibit opposite trends. Thus, in the case of VOCs, both polarization phenomena and permeate flux improve with increasing solute concentration in the feed stream. Finally, the optimal operating conditions are identified as moderately elevated feed temperatures, reduced vacuum pressures, feed flow rates within an intermediate range (adjusted according to salt concentration), and low salt concentrations in the feed stream, aimed at maximizing permeate flux.

4. Discussion

VMD is classified as a membrane distillation process, a separation technology that integrates mass transfer principles through thermal evaporation with selective transport across hydrophobic membranes. In this method, the liquid feed is subjected to a temperature increase that induces partial evaporation of the solvent. The generated vapor diffuses through a macroporous, hydrophobic membrane, which acts as a physical barrier preventing the passage of the liquid phase and allowing only the transport of the gaseous phase. The membrane’s intrinsic hydrophobicity prevents liquid penetration into the pores, resulting in the formation of a stable liquid–vapor interface at the entrance of each pore, whose existence depends on the feed pressure and the wetting properties of the system. In this study, it has been confirmed that the predominant driving force of the process is the vapor pressure difference across both sides of the membrane, generated by the thermal gradient imposed between the hot feed side and the permeate side, which operates under reduced pressure.

The validation of the VMD-VOCs and VMD-WS models demonstrated good predictive capability for simulating membrane distillation, with average errors below 10%. The VMD-VOCs model exhibited higher errors at elevated temperatures, attributed to intensified evaporation phenomena and thermal/concentration gradients, although it showed better accuracy at low flow rates. Its maximum error (18%) remains acceptable. The VMD-WS model showed better agreement across the temperature range but its accuracy decreased at 70 °C, suggesting limitations in capturing nonlinear effects. Both models are suitable for the design and optimization of VMD processes.

Feed temperature affects permeate flux differently in the VMD-VOCs and VMD-WS models, exhibiting an exponential trend in the former and a linear trend in the latter, due to differences in the calculation of colligative properties. This behavior validates the use of the Antoine equation, which relates temperature to vapor pressure. In turn, increasing temperature enhances thermal polarization, reducing process efficiency; however, this effect is attenuated at higher temperatures due to improved thermal properties of the fluid. Additionally, a higher salt concentration is observed at the liquid–vapor interface with increasing temperature, a phenomenon analogous to thermal polarization and also explainable by the Antoine equation. Suleman et al. [64] propose that it is essential to give greater attention to polarization studies focused on industrial applications, in order to optimize system efficiency and enhance the viability of the membrane distillation process in industrial environments.

Permeate flux decreases with increasing vacuum pressure, confirming that a higher driving force promotes mass transfer in membrane distillation. The VMD-VOCs model maintains a linear trend with temperature, indicating predictive stability. In the VMD-WS model, thermal polarization decreases at lower pressure due to increased evaporation and thermal gradient; however, this also entails higher energy consumption. Additionally, concentration polarization increases at low pressures due to solute accumulation at the interface, while it diminishes at higher pressures due to improved solute redistribution.

Permeate flux increases with feed flow rate, especially below 1 L/min, although this effect stabilizes at higher flow rates due to reduced fluid residence time. This behavior results from the balance between improved heat and mass transfer—which reduces concentration polarization—and decreased evaporative efficiency at elevated flow rates. Regarding thermal polarization, it is higher at low flow rates due to limited fluid renewal but decreases as flow rate increases, owing to improved circulation that mitigates the thermal gradient; however, at very high flow rates, it may be partially affected by reduced thermal residence time.

The results show opposite behaviors in the VMD-VOCs and VMD-WS models due to the volatility of the solutes. In VMD-VOCs, permeate flux increases with ethanol concentration because of its high volatility, whereas in VMD-WS, permeate flux decreases with increasing NaCl concentration due to its non-volatile nature, which increases mass transfer resistance. Additionally, thermal polarization decreases with higher salt concentration, owing to the elevated boiling point and reduced thermal gradient. Concentration polarization, although always positive, decreases above 7 wt.% NaCl as mass flux reduces and the interfacial concentration approaches that of the feed. Other authors [65,66,67] corroborate these findings regarding the effect of solute concentration on feed flow.

5. Conclusions

To reduce pointwise error, a strategy to be considered for future publications on this topic is the comparative use of other Nusselt- and Sherwood-type correlations, which would allow a better adjustment of the model results. As stated in boundary layer transport theory, the heat and mass transfer coefficients depend on inertial and viscous forces, which affect the velocity profiles [68].

There is a complex interplay between temperature, vapor pressure, and polarization phenomena in vacuum membrane distillation (VMD), highlighting the critical need to optimize operating temperature to mitigate adverse effects on process efficiency while maintaining adequate evaporation rates.

Vacuum pressure exerts a strong influence on VMD performance and the associated polarization phenomena. Lower vacuum pressures enhance permeate flux but simultaneously exacerbate both thermal and concentration polarization, which can reduce energy efficiency and shorten membrane lifespan if not properly managed. These observations underscore the necessity of tailoring vacuum pressure according to solute characteristics, thermal conditions, and overall system configuration.

From an operational standpoint, there exist optimal feed flow rates that minimize thermal and concentration polarization without significantly compromising energy efficiency. Concentration polarization decreases asymptotically with increasing flow rate, confirming that enhanced cross-flow convection effectively limits solute accumulation near the membrane surface. This inverse relationship with permeate flux emphasizes the importance of precise flow rate control in VMD system design, as maintaining an appropriate hydrodynamic regime maximizes overall performance while avoiding thermal or solute-concentration penalties that can constrain system efficiency.

The study of solute concentration effects in the feed stream reveals contrasting behaviors between VMD processes involving volatile organic compounds (VOCs) and water–salt (WS) solutions, reflecting the distinct volatility and physicochemical properties of the solutes involved.

Overall, these results highlight the importance of accounting for solute properties and operational parameters in the design and optimization of membrane distillation processes, particularly for applications involving volatile compound separation or desalination of concentrated solutions.

Ultimately, vacuum membrane distillation emerges as a highly promising technology for addressing challenges in water treatment, solution concentration, and compound recovery, providing notable advantages in energy efficiency and industrial sustainability.