A Multi-Scale Numerical Simulation Method Considering Anisotropic Relative Permeability
Abstract
1. Introduction
2. Methods
2.1. Numerical Simulation with Anisotropic Relative Permeability
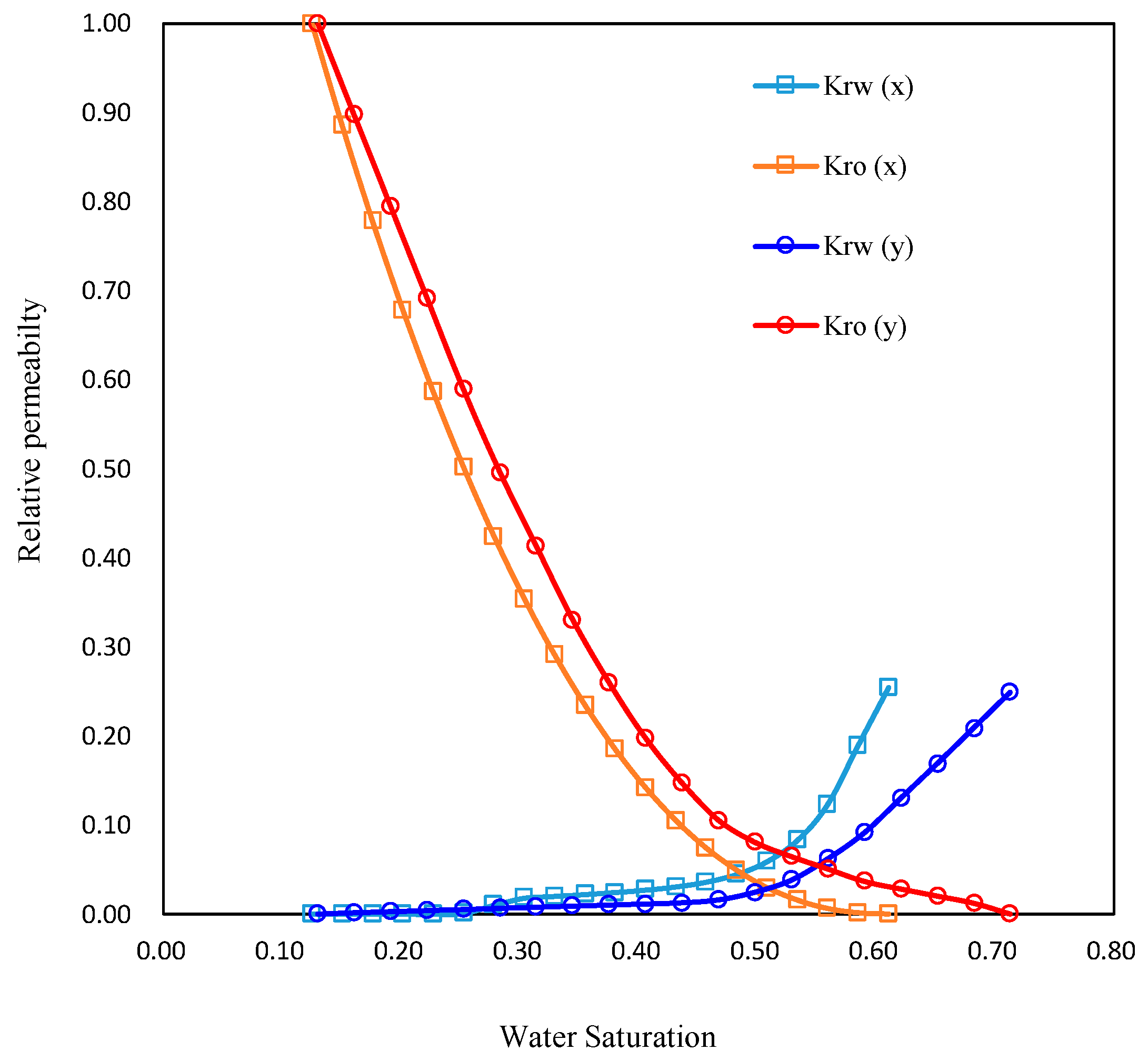
2.1.1. Anisotropic Relative Permeability
2.1.2. Fundamental Mathematical Model
- (1)
- Only oil and water phases are preset in the reservoir;
- (2)
- No mass exchange between oil and water;
- (3)
- Fluid flow conforms to Darcy’s law;
- (4)
- Reservoir is isothermal;
- (5)
- Phase equilibrium completed instantaneously.
2.1.3. The Black-Oil Model Considering Anisotropic Relative Permeability
Flow within the Reservoir
Well Models
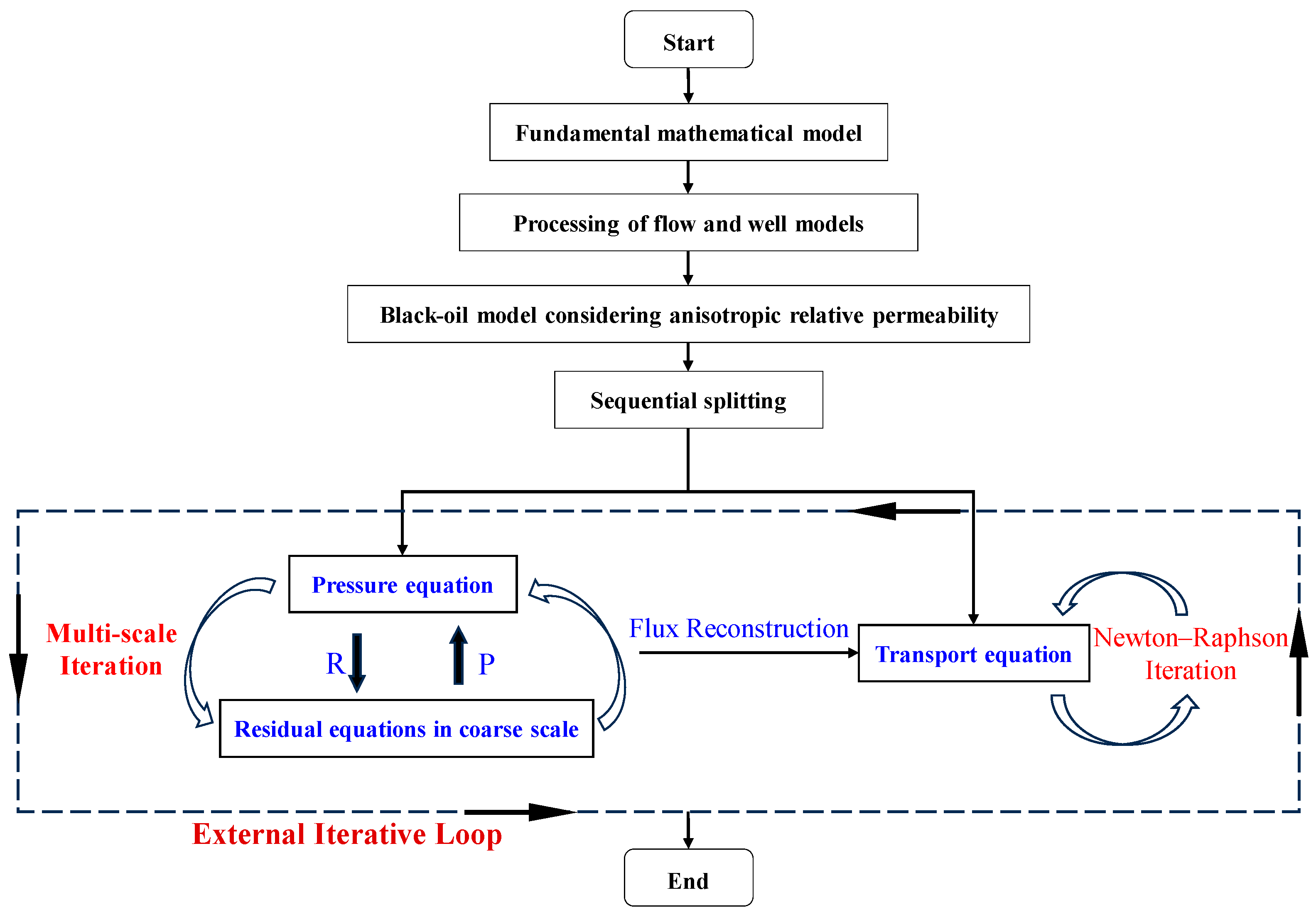
2.2. Sequential Splitting
2.2.1. The Pressure Equation
2.2.2. The Transport Equation
2.2.3. Solving the Nonlinear Problem
2.3. Multi-Scale Formulation for Pressure Equations
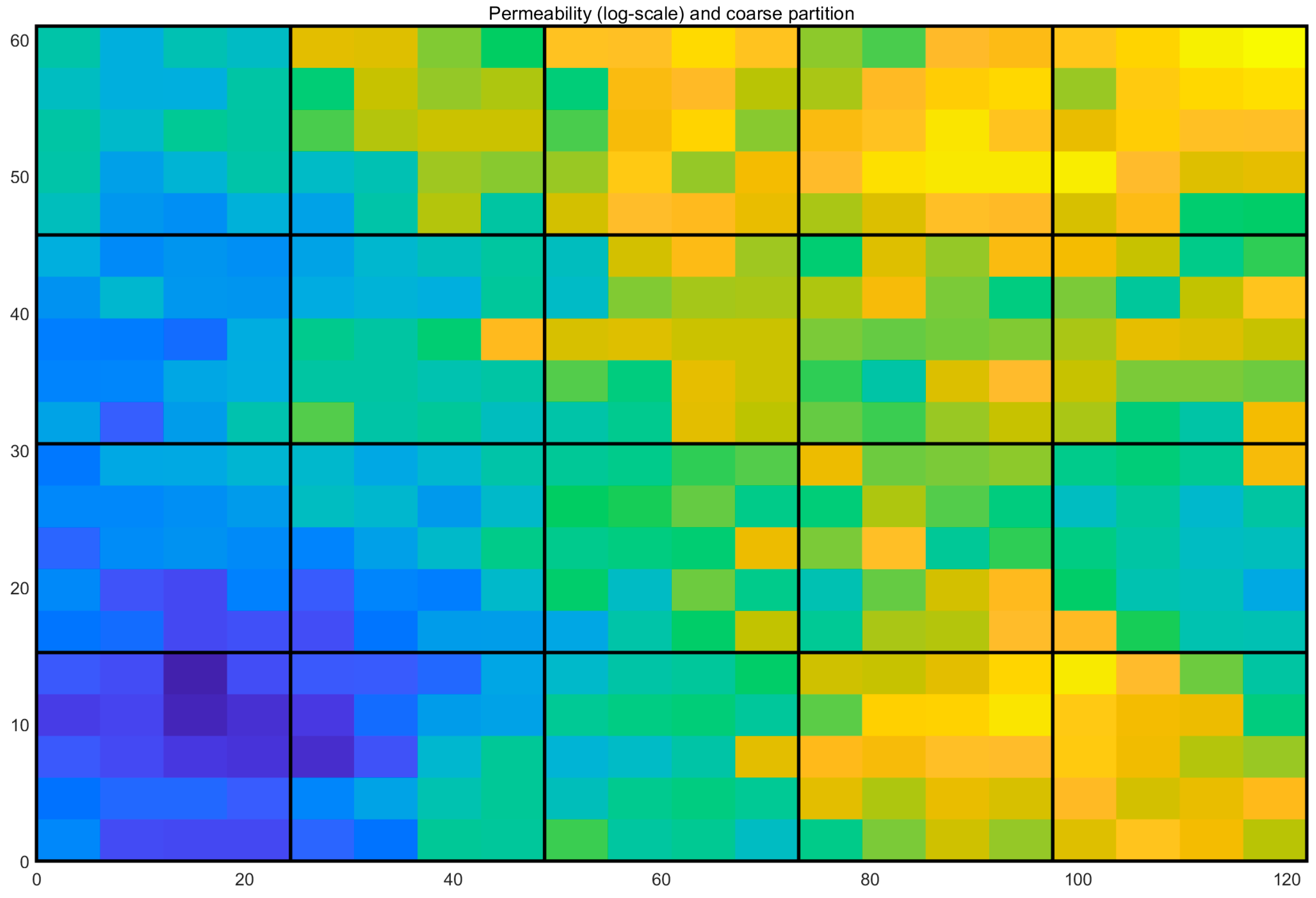
2.3.1. Multi-Scale Solver for Pressure
2.3.2. The Restriction and Iterative Prolongation Operators
2.3.3. Iterative Multi-Scale and Flux Reconstruction
3. Results and Discussion
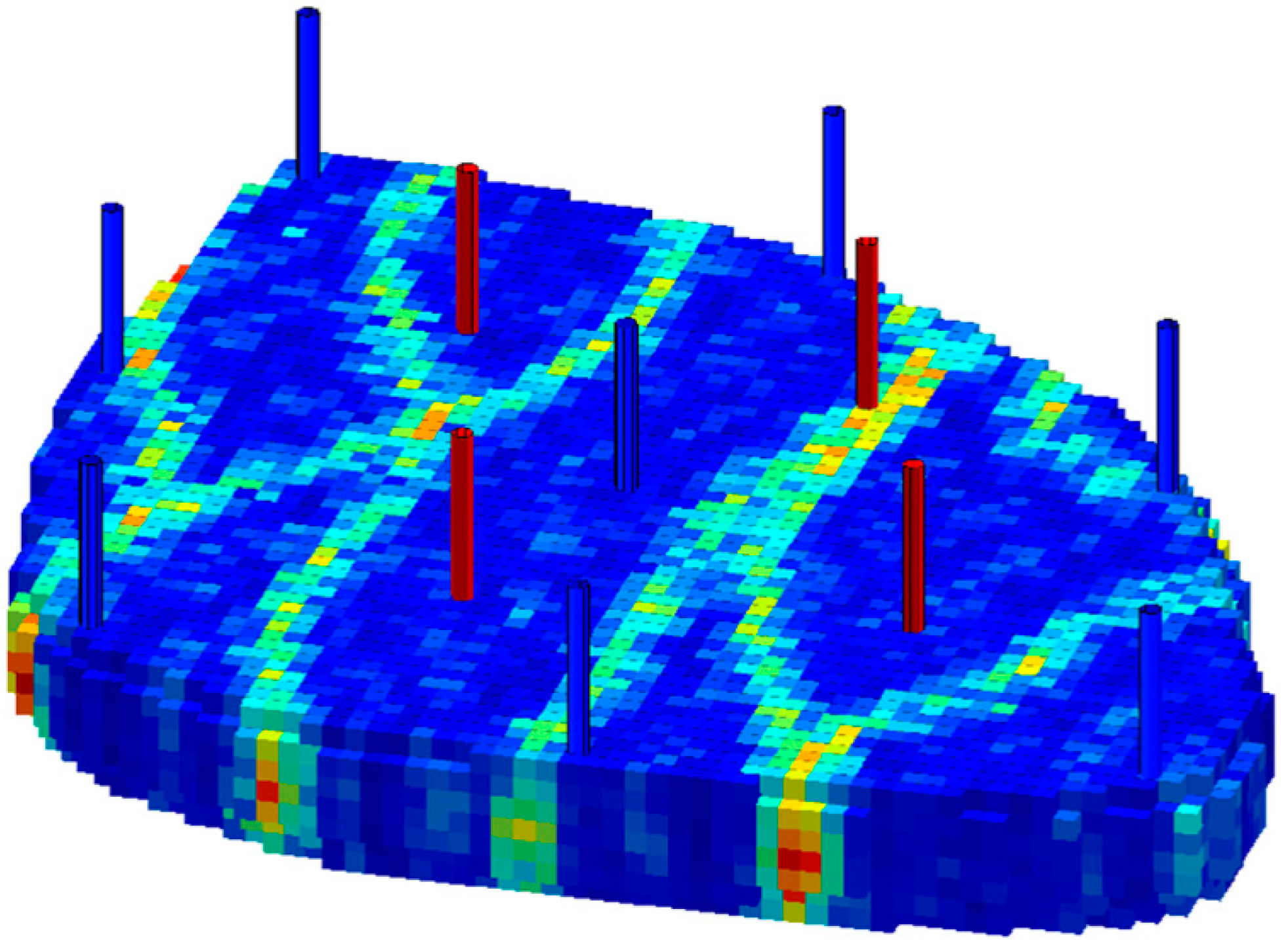
3.1. Model Validation
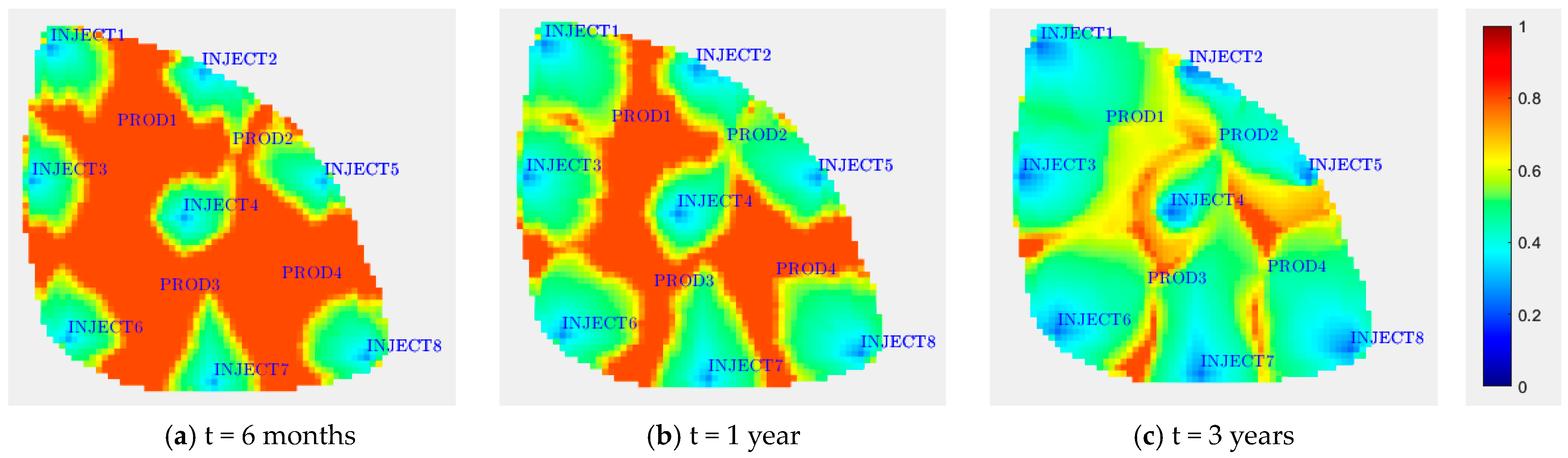
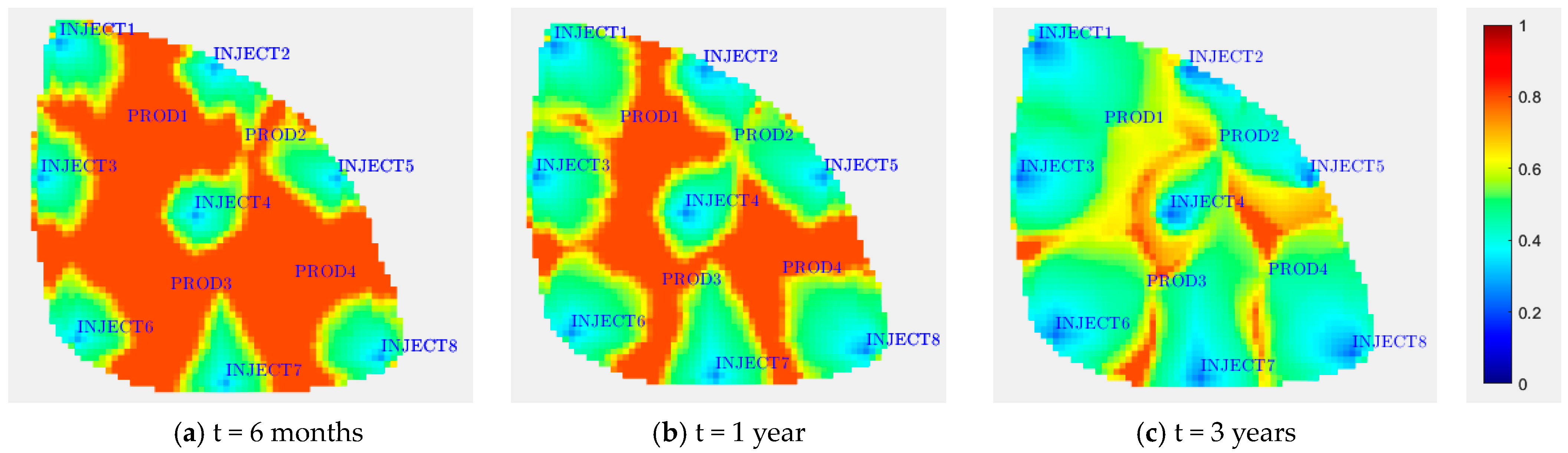
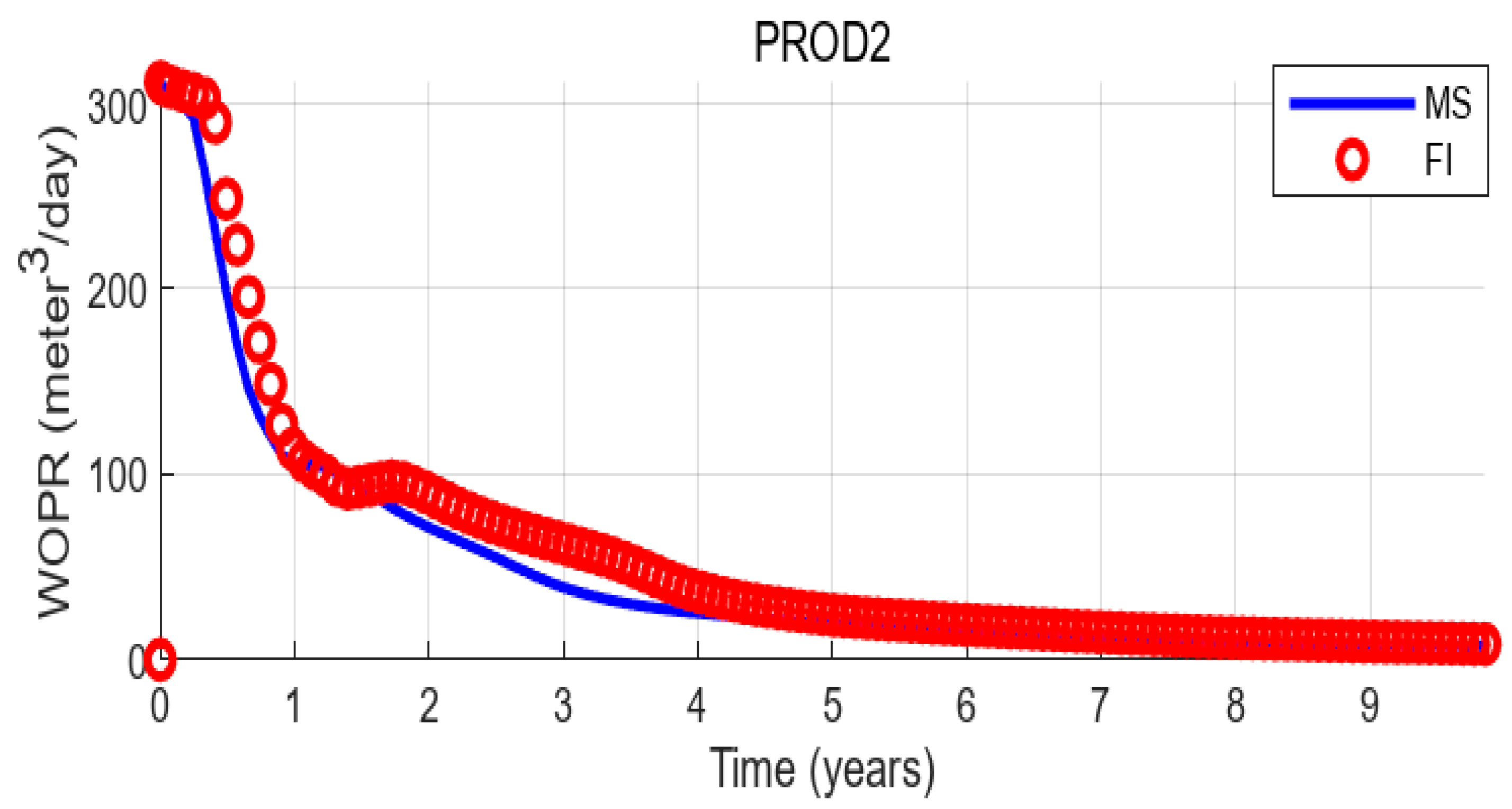
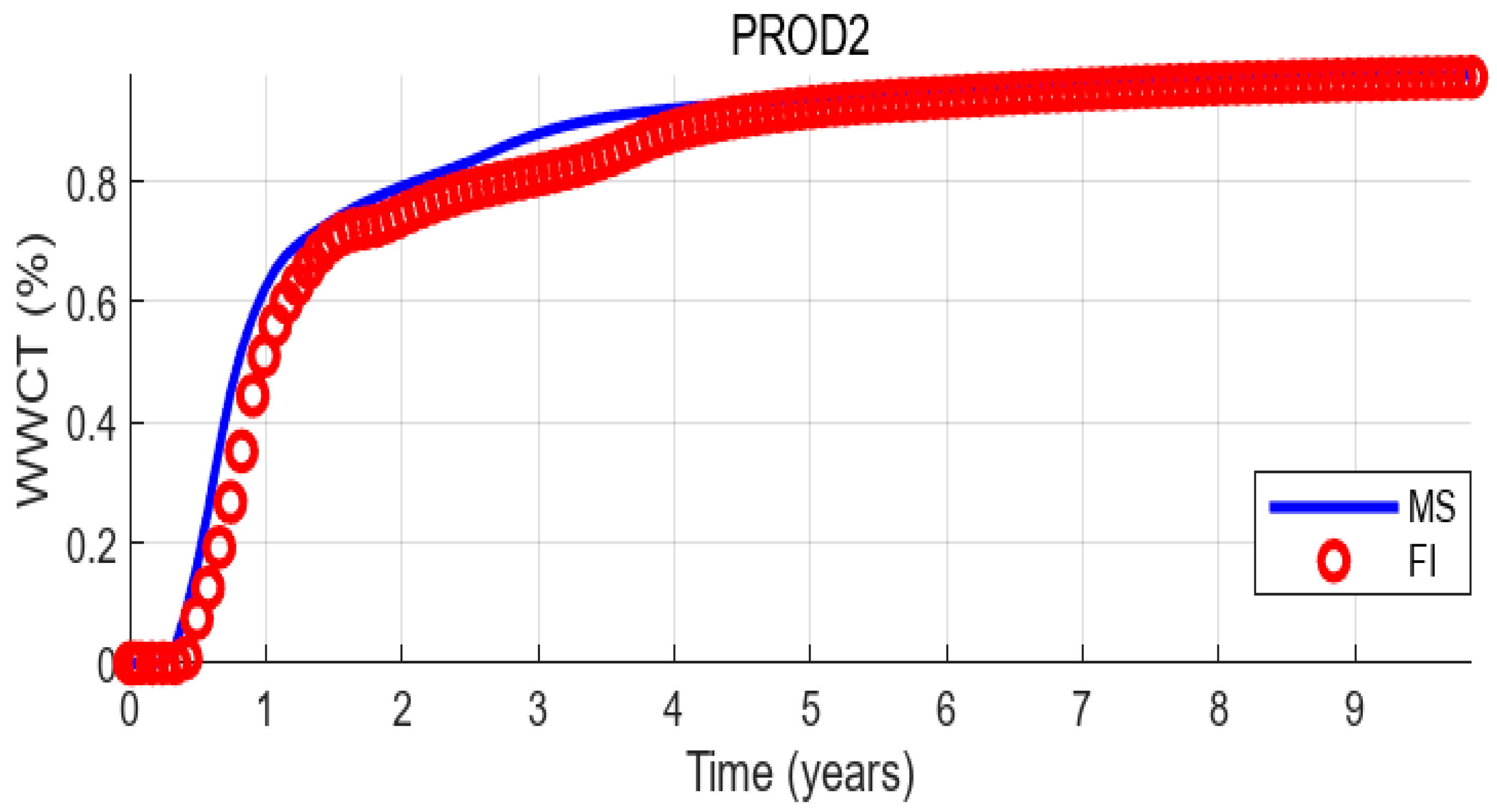
3.1.1. Accuracy
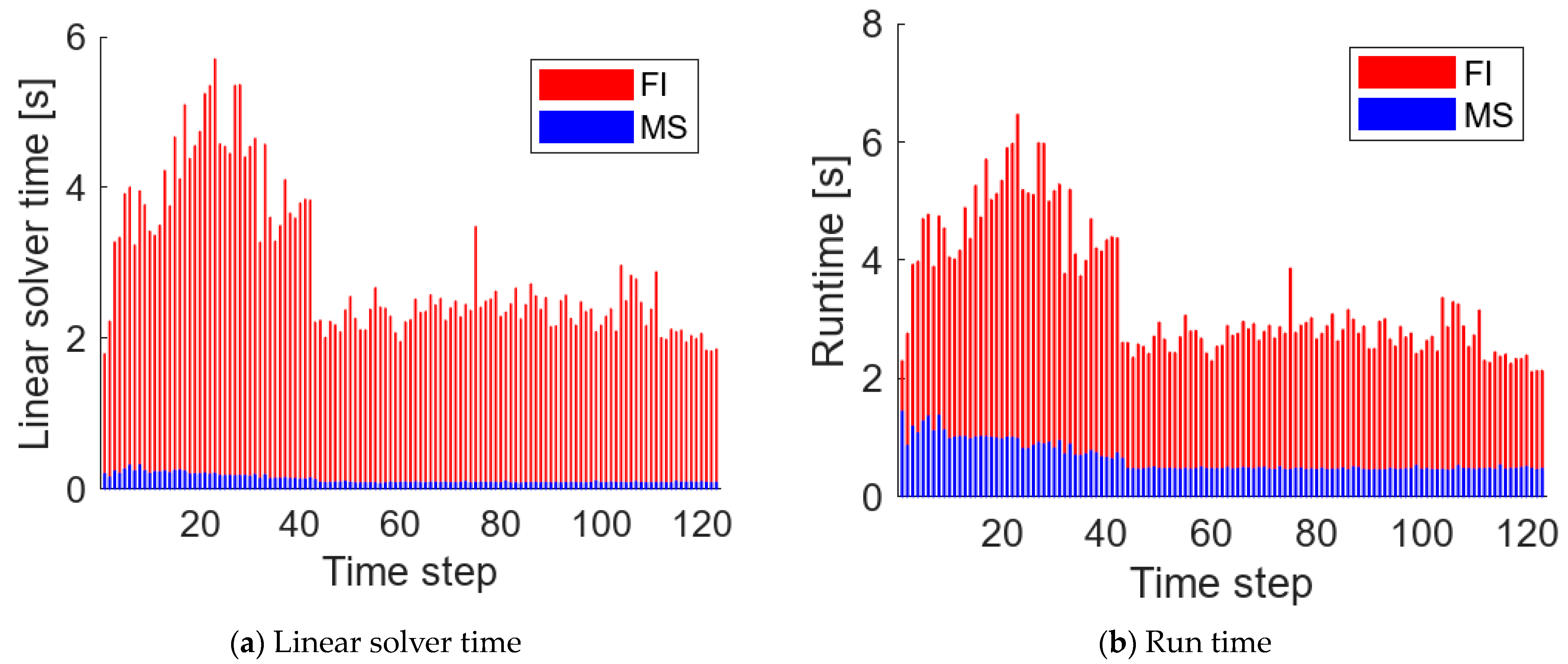
3.1.2. Efficiency
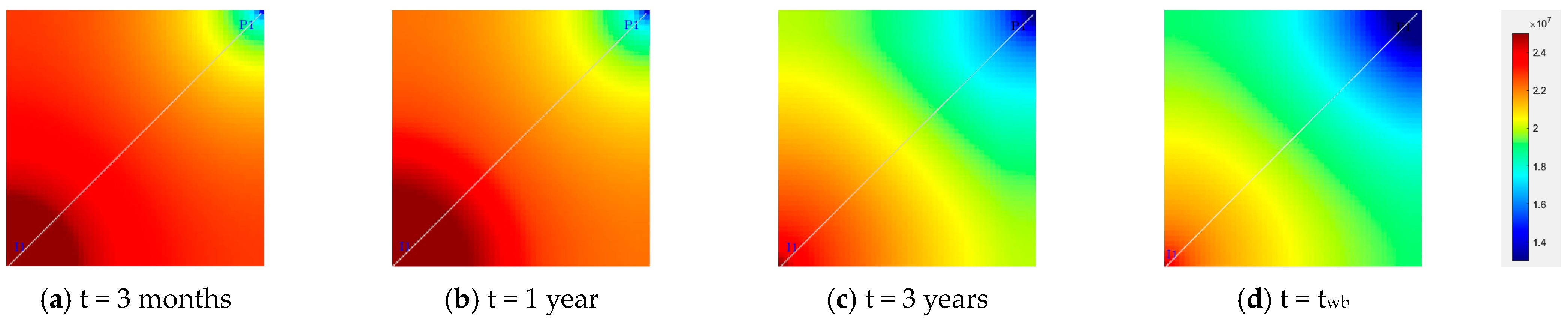
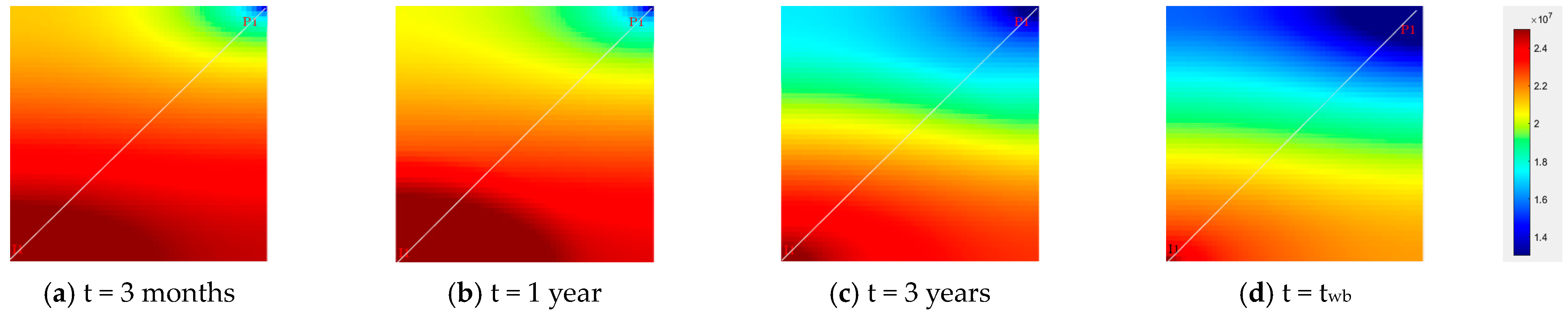
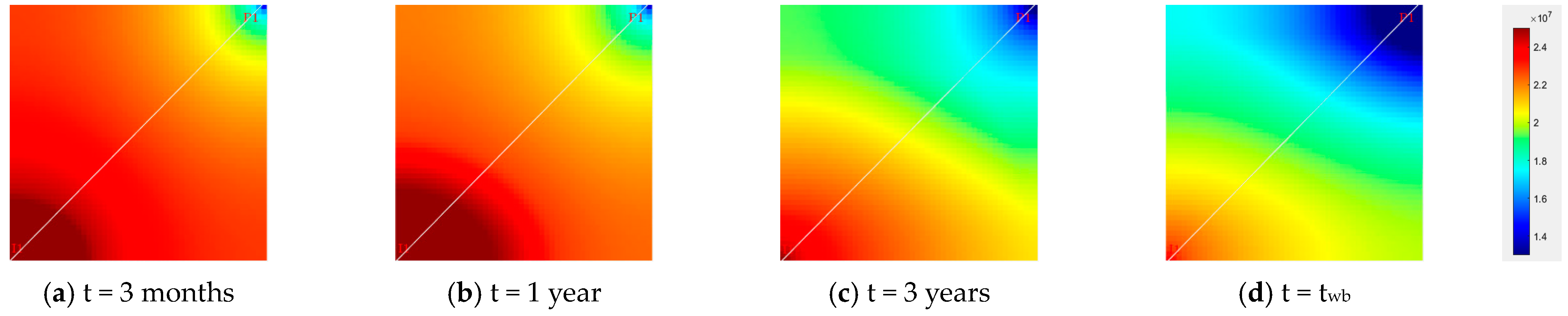
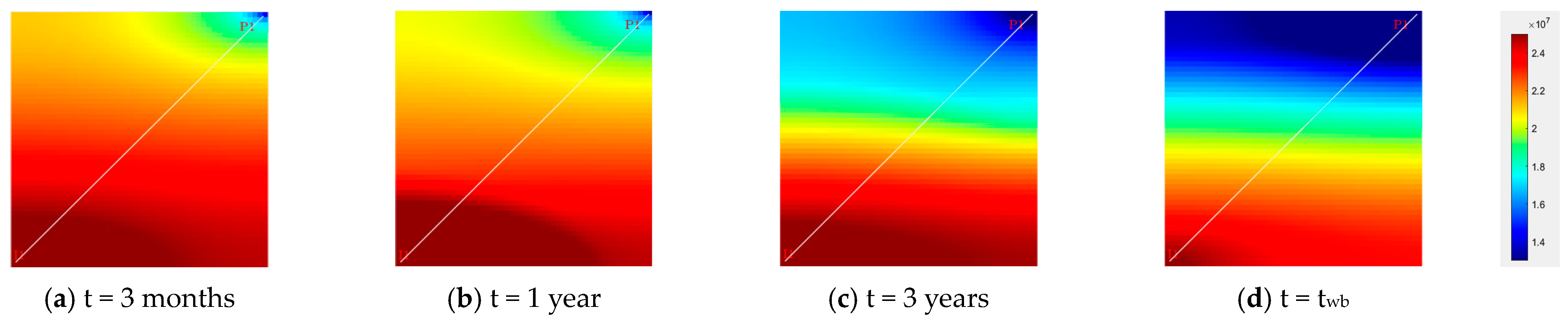
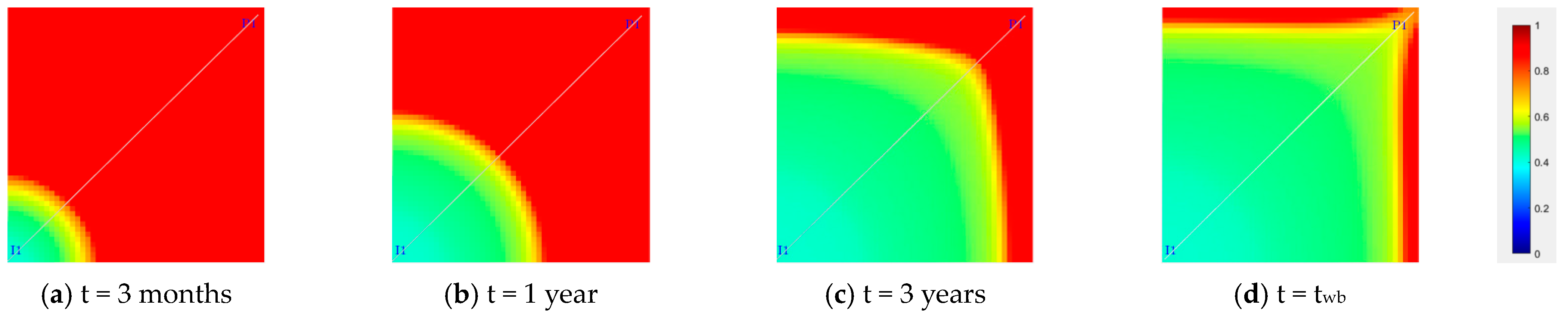
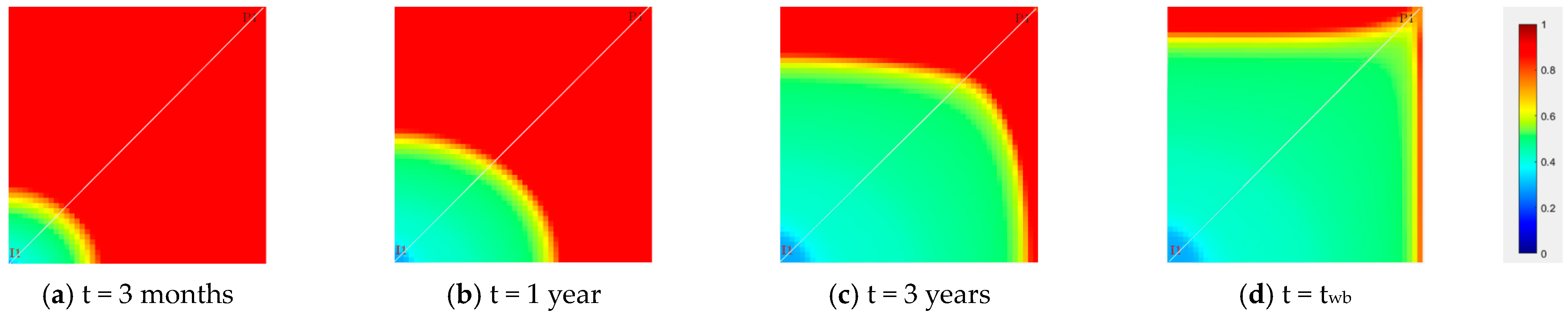
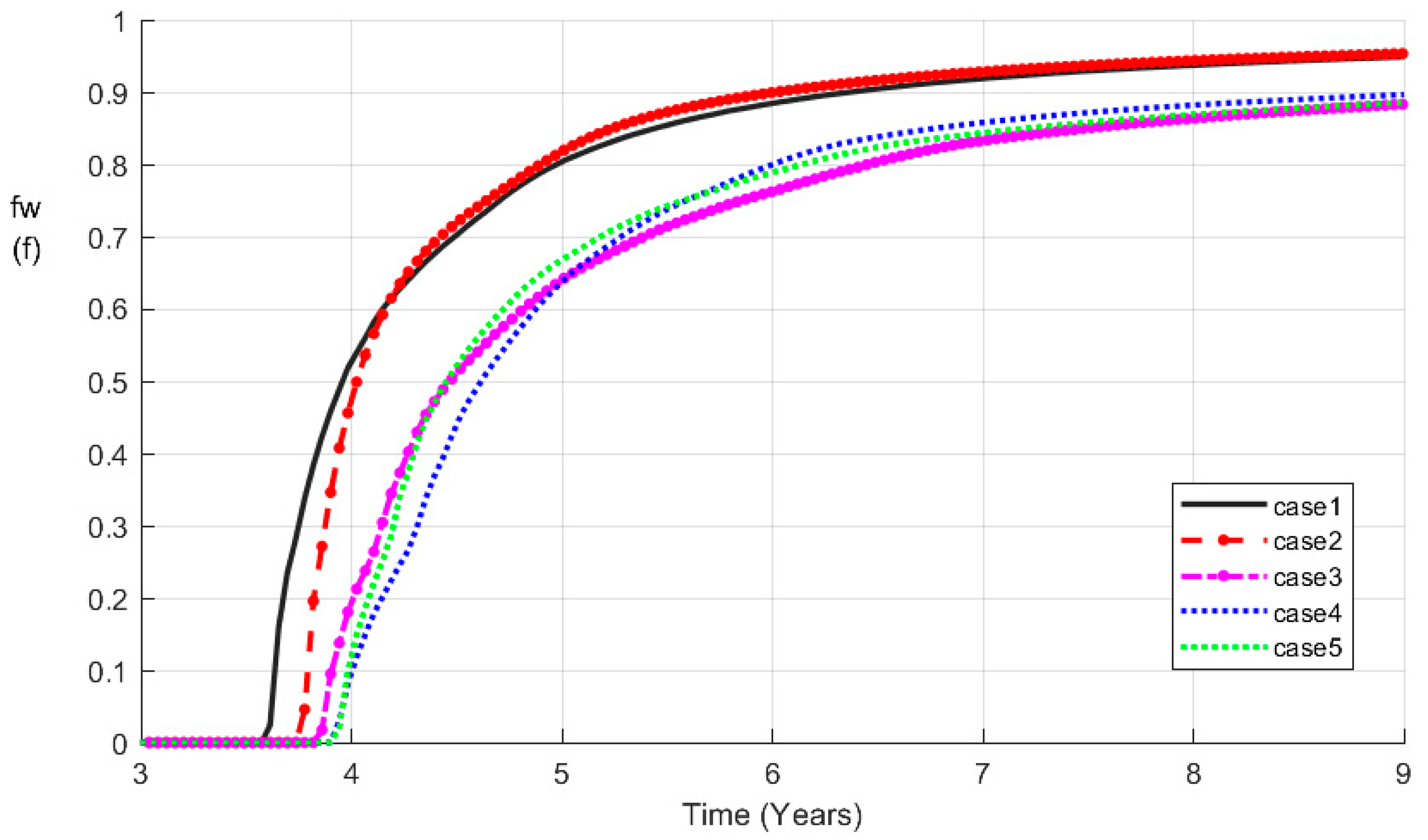
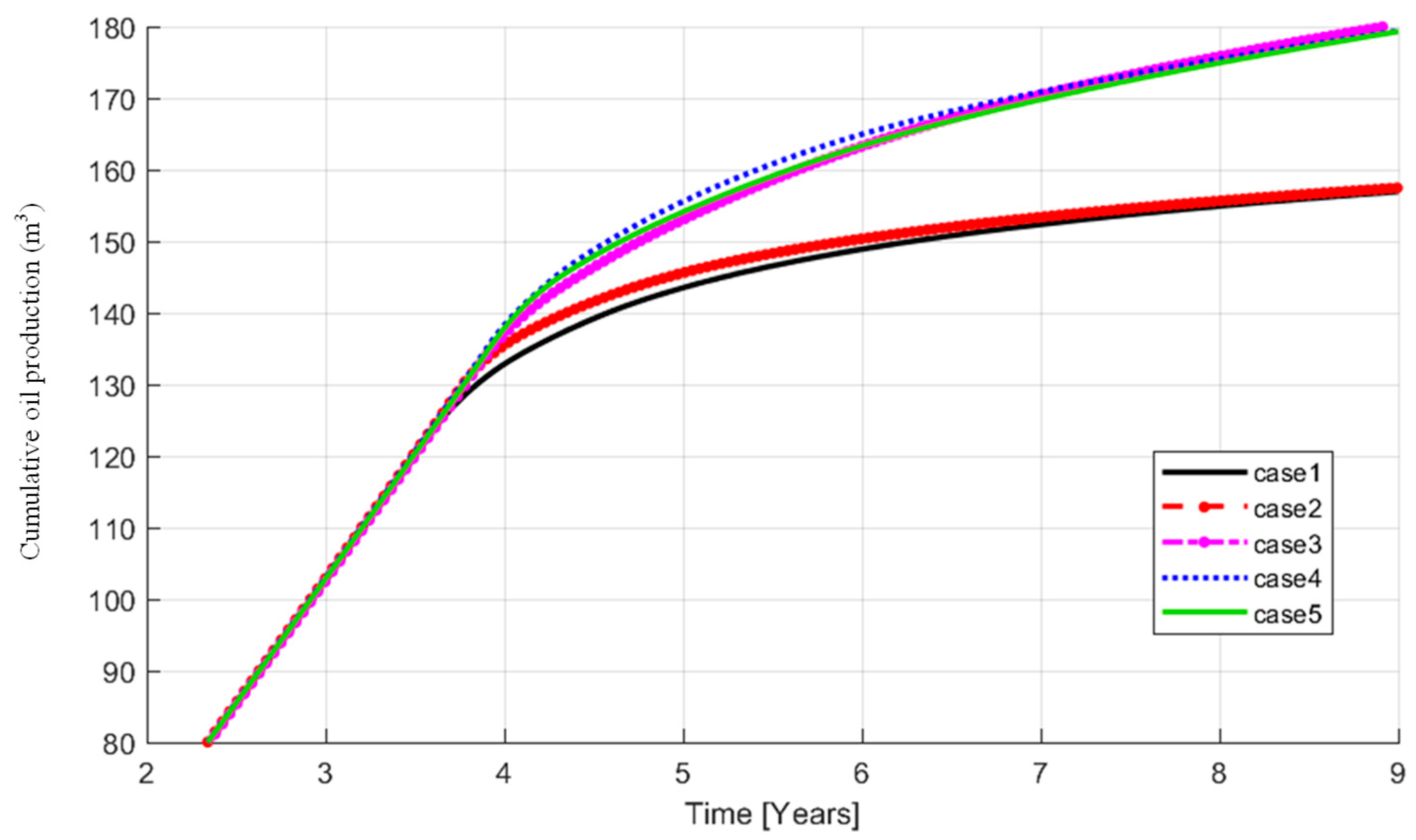
3.2. Numerical Results with Anisotropic Relative Permeability
4. Conclusions
- (1)
- The anisotropy of relative permeability has been proved, yet most existing reservoir simulators neglect its impact. This study presents a numerical simulation method, developed using MRST and based on the black-oil model, which explicitly incorporates the effects of anisotropic relative permeability;
- (2)
- Following the development of the multi-scale model, this paper adopts a sequential solution method to enhance computational efficiency. The method leverages the parallelism of the MsFV method to solve the pressure equation. The Egg model’s numerical validation confirms that the proposed IMsFV method significantly improves the iterative speed while preserving result accuracy;
- (3)
- The impact of anisotropy on waterflooding is investigated using the developed multi-scale numerical simulator. Findings indicate that anisotropic absolute and relative permeability play critical roles in waterflooding, though they operate via distinct mechanisms and cannot be equated, substituted, or entirely counterbalanced;
- (4)
- Compared to the traditional numerical simulator, the IMsFV method proposed accurately captures the anisotropy of relative permeability in reservoirs. This advancement is crucial for high-resolution numerical simulation of fluvial-phase sedimentary reservoirs, improved characterization of flow regimes, and more precise prediction of residual oil distribution.
- (1)
- This paper’s developed multi-scale reservoir numerical simulation method is limited to two-phase (oil and water) black-oil models. Future work aims to extend the model to encompass three-phase black-oil and component models, facilitating faster multi-scale solutions;
- (2)
- The analysis of relative permeability anisotropy using the established multi-scale numerical simulator employs a simplified model setup. Future research will enhance the application of this simulation method in real reservoirs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Physical Quantities | |
| Porosity, fraction | |
| Saturation of phase , volume fraction | |
| Inverse formation value factor of phase, dimensionless | |
| Darcy velocities of phase , cm/s | |
| Pressure of phase , bar | |
| Relative permeability of phase , dimensionless | |
| Relative permeability of phase in the x-direction | |
| Absolute permeability, mD | |
| Viscosity of phase , kg/ms | |
| Gravity acceleration, kg.m/s2 | |
| Vertical depth, m | |
| Volumetric production/injection rate, s–1 | |
| Density of phase , kg/m3 | |
| Capillary pressure, bar | |
| Mobility of phase , mD kg/ms | |
| Water cut, fraction | |
| Partial flow coefficient, fraction | |
| Sor | Residual oil saturation, fraction |
| Sor(x) | Residual oil saturation in the x-direction, fraction |
| Well indices, dimensionless | |
| twb | Time of water breakthrough, year |
| Domain and Grid | |
| Coarse block containing cell c containing face f | |
| c | Cell number |
| The fine-scale grid domain v | |
| The coarse-scale grid domain | |
| Discretization and Discrete Quantities | |
| Phase pressure equations in residual form | |
| Pressure equations in residual form | |
| Well production equations in residual form | |
| Well control equations in residual form | |
| Linear Algebra | |
| A, b, x | (system) matrix, left-hand side, and vector of unknowns |
| D | Diagonal matrix |
| Jacobian matrix of discrete equations | |
| P | prolongation operator (matrix) |
| Restriction operator (matrix) | |
| r | Vector of residuals |
| Vector with all unknowns in pressure equation | |
| Vector of unknown quantities for the transport equation | |
| Iterative convergence constant for the pressure equation | |
| Iterative convergence constant for the transport equation | |
| External iterative convergence constant | |
| Subscripts | |
| ) | |
| b | Basis function |
| o | Oil |
| w | Water |
| i, j, k | Cell numbers |
| bh | Bottomhole pressure |
| x, y, z | x-, y-, z-directions |
| f | Fine grid |
| c | Coarse grid |
| ref | Reference value |
| Superscripts | |
| n | Timestep |
| b | Basis function |
| 0 | Initial moment |
| s | Standard conditions |
References
- Farquharson, J.; Wadsworth, F.B. Upscaling permeability in anisotropic volcanic systems. J. Volcanol. Geotherm. Res. 2018, 364, 35–47. [Google Scholar] [CrossRef]
- Li, T.; Li, M.; Jing, X.; Xiao, W.; Cui, Q. Influence mechanism of pore-scale anisotropy and pore distribution heterogeneity on permeability of porous media. Pet. Explor. Dev. 2019, 46, 594–604. [Google Scholar] [CrossRef]
- Corey, A.T.; Rathjens, C.H. Effect of Stratification on Relative Permeability. J. Pet. Technol. 1956, 8, 69–71. [Google Scholar] [CrossRef]
- Busahmin, B.; Karri, R.R.; Tyson, S.; Jami, M. Modeling of a long sand-pack for heavy crude oil through depletion tests utilizing methane gas. Petroleum 2021, 7, 188–198. [Google Scholar] [CrossRef]
- Crotti; Rosbaco, J.A. Relative Permeability Curves: The Influence of Flow Direction and Heterogeneities. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 19–22 April 1998. [Google Scholar]
- Ezeuko, C.C.; McDougall, S.R.; Bondino, I.; Hamon, G. Anisotropic Relative Permeabilities for Characterising Heavy-Oil Depletion Experiment. In Proceedings of the International Symposium of the Society of Core Analysts, Tulsa, OK, USA, 20–23 April 2008. [Google Scholar]
- Paterson, L.; Painter, S.; Zhang, X.; Pinczewski, W.V. Simulating Residual Saturation and Relative Permeability in Heterogeneous Formations. SPE J. 1998, 3, 211–218. [Google Scholar] [CrossRef]
- Bakhshian, S.; Hosseini, S.A.; Lake, L. CO2-brine relative permeability and capillary pressure of Tuscaloosa sandstone: Effect of anisotropy. Adv. Water Resour. 2020, 135, 103464. [Google Scholar] [CrossRef]
- Lei, Z.; Liu, T.; Xie, C.; Wang, M.; Zhang, Z.-K. Predictions of Relative Permeability for Low Permeability Reservoirs and its Scale Effect. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Perth, Australia, 25–27 October 2016. [Google Scholar]
- Pergament, A.K.; Tomin, P.Y. The study of relative phase-permeability functions for anisotropic media. Math. Models Comput. Simul. 2012, 4, 1–9. [Google Scholar] [CrossRef]
- Pei, X.; Liu, Y.; Gu, W.; Jian, C. Characterization and Analysis of Anisotropic Relative Permeability. SPE J. 2021, 27, 579–596. [Google Scholar] [CrossRef]
- Raoult, N.; Beylat, S.; Salter, J.M.; Hourdin, F.; Bastrikov, V.; Ottlé, C.; Peylin, P. Exploring the Potential of History Matching for Land Surface Model Calibration. EGUsphere 2024, 2024, 1–33. [Google Scholar] [CrossRef]
- Li, C.; Wang, S.; You, Q.; Yu, C. A New Measurement of Anisotropic Relative Permeability and Its Application in Numerical Simulation. Energies 2021, 14, 4731. [Google Scholar] [CrossRef]
- Sedaghat, M.H.; Azizmohammadi, S.; Matthäi, S.K. Tensor Analysis of the Relative Permeability in Naturally Fractured Reservoirs. SPE J. 2020, 25, 162–184. [Google Scholar] [CrossRef]
- Blonsky, A.V.; Mitrushkin, D.A.; Kudryashov, I.Y.; Plynin, V.V. Computation of Absolute and Relative Permeability Full Tensors for Fractured Reservoirs. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 16–18 October 2017. [Google Scholar]
- Pei, X.; Liu, Y.; Lin, Z.; Mao, Y.; Xue, L. Anisotropic Characteristics of Relative Permeability in Sedimentary Reservoirs. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GE, USA, 25–28 June 2023. [Google Scholar]
- Li, R.; Han, Z.; Zhang, L.; Zhou, J.; Wang, S.; Huang, F. Numerical Determination of Anisotropic Permeability for Unconsolidated Hydrate Reservoir: A DEM–CFD Coupling Method. J. Mar. Sci. Eng. 2024, 12, 1447. [Google Scholar] [CrossRef]
- Keilegavlen, E.; Nordbotten, J.M.; Stephansen, A.F. Simulating Two-phase Flow in Porous Media with Anisotropic Relative Permeabilities. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 21–23 February 2011. [Google Scholar]
- Kokkinos, N.C.; Nkagbu, D.C.; Marmanis, D.I.; Dermentzis, K.; Maliaris, G. Evolution of Unconventional Hydrocarbons: Past, Present, Future and Environmental FootPrint. J. Eng. Sci. Technol. Rev. 2022, 15, 15–24. [Google Scholar] [CrossRef]
- Wang, H.; Ma, F.; Tong, X.; Liu, Z.; Zhang, X.; Wu, Z.; Li, D.; Wang, B.; Xie, Y.; Yang, L. Assessment of global unconventional oil and gas resources. Pet. Explor. Dev. 2016, 43, 925–940. [Google Scholar] [CrossRef]
- Zou, C.; Zhai, G.; Zhang, G.; Wang, H.; Zhang, G.; Li, J.; Wang, Z.; Wen, Z.; Ma, F.; Liang, Y.; et al. Formation, distribution, potential and prediction of global conventional and unconventional hydrocarbon resources. Pet. Explor. Dev. 2015, 42, 14–28. [Google Scholar] [CrossRef]
- Hisseine, O.A.; Tagnit-Hamou, A. Development of ecological strain-hardening cementitious composites incorporating high-volume ground-glass pozzolans. Constr. Build. Mater. 2020, 238, 117740. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, G.; Tao, S.; Hu, S.; Li, X.; Li, J.; Dong, D.; Zhu, R.; Yuan, X.; Hou, L.; et al. Geological features, major discoveries and unconventional petroleum geology in the global petroleum exploration. Pet. Explor. Dev. 2010, 37, 129–145. [Google Scholar] [CrossRef]
- Jia, C.; Zheng, M.; Zhang, Y. Unconventional hydrocarbon resources in China and the prospect of exploration and development. Pet. Explor. Dev. 2012, 39, 139–146. [Google Scholar] [CrossRef]
- Mao, S.; Wu, K.; Moridis, G. Integrated simulation of three-dimensional hydraulic fracture propagation and Lagrangian proppant transport in multilayered reservoirs. Comput. Methods Appl. Mech. Eng. 2023, 410, 116037. [Google Scholar] [CrossRef]
- Krogstad, S.; Lie, K.A.; Møyner, O.; Nilsen, H.M.; Raynaud, X.; Skaflestad, B. MRST-AD—An Open-Source Framework for Rapid Prototyping and Evaluation of Reservoir Simulation Problems. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 23–25 February 2015. [Google Scholar]
- Lie, K.A.; Krogstad, S.; Ligaarden, I.S.; Natvig, J.R.; Nilsen, H.M.; Skaflestad, B. Open-source MATLAB implementation of consistent discretisations on complex grids. Comput. Geosci. 2011, 16, 297–322. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of Well-Block Pressures in Numerical Reservoir Simulation with Nonsquare Grid Blocks and Anisotropic Permeability. SPE J. 1983, 23, 531–543. [Google Scholar] [CrossRef]
- Wallis, J.R. Incomplete Gaussian Elimination as a Preconditioning for Generalized Conjugate Gradient Acceleration. In Proceedings of the SPE Reservoir Simulation Symposium, San Francisco, CA, USA, 15–18 November 1983. [Google Scholar]
- Gries, S.; Stüben, K.; Brown, G.L.; Chen, D.; Collins, D. Preconditioning for Efficiently Applying Algebraic Multigrid in Fully Implicit Reservoir Simulations. SPE J. 2014, 19, 726–736. [Google Scholar] [CrossRef]
- Møyner, O.; Lie, K.-A. A Multiscale Restriction-Smoothed Basis Method for Compressible Black-Oil Models. SPE J. 2016, 21, 2079–2096. [Google Scholar] [CrossRef]
- Cusini, M.; Lukyanov, A.A.; Natvig, J.R.; Hajibeygi, H. Constrained pressure residual multiscale (CPR-MS) method for fully implicit simulation of multiphase flow in porous media. J. Comput. Phys. 2015, 299, 472–486. [Google Scholar] [CrossRef]
- Brandt, A. Algebraic multigrid theory: The symmetric case. Appl. Math. Comput. 1986, 19, 23–56. [Google Scholar] [CrossRef]
- Møyner, O.; Lie, K.A. The Multiscale Finite-Volume Method on Stratigraphic Grids. SPE J. 2014, 19, 816–831. [Google Scholar] [CrossRef]
- Møyner, O.; Lie, K.A. The Multiscale Finite Volume Method on Unstructured Grids. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 February 2013. [Google Scholar]
- Kozlova, A.; Li, Z.; Natvig, J.R.; Watanabe, S.; Zhou, Y.; Bratvedt, K.; Lee, S.H. A Real-Field Multiscale Black-Oil Reservoir Simulator. SPE J. 2016, 21, 2049–2061. [Google Scholar] [CrossRef]
- Lunati, I.; Lee, S. An Operator Formulation of the Multiscale Finite-Volume Method with Correction Function. Multiscale Model. Simul. 2009, 8, 96–109. [Google Scholar] [CrossRef]
- Mosharaf-Dehkordi, M.; Manzari, M.T. Effects of using altered coarse grids on the implementation and computational cost of the multiscale finite volume method. Adv. Water Resour. 2013, 59, 221–237. [Google Scholar] [CrossRef]
- Møyner, O.; Lie, K.A. A multiscale two-point flux-approximation method. J. Comput. Phys. 2014, 275, 273–293. [Google Scholar] [CrossRef]
- Jenny, P.; Lee, S.H.; Tchelepi, H.A. Multi-scale finite-volume method for elliptic problems in subsurface flow simulation. J. Comp. Phys. 2003, 187, 47–67. [Google Scholar] [CrossRef]
- Wang, Y.; Hajibeygi, H.; Tchelepi, H.A. Algebraic multiscale solver for flow in heterogeneous porous media. J. Comp. Phys. 2014, 259, 284–303. [Google Scholar] [CrossRef]
- Møyner, O.; Tchelepi, H. A multiscale restriction-smoothed basis method for high contrast porous media represented on unstructured grids. J. Comp. Phys. 2016, 304, 46–71. [Google Scholar] [CrossRef]
- Nwanwe, O.; Izuwa, N.C.; Ohia, N.P.; Kerunwa, A.; Nnaemeka, U. Determining optimal controls placed on injection/production wells during waterflooding in heterogeneous oil reservoirs using artificial neural network models and multi-objective genetic algorithm. Comput. Geosci. 2024. [Google Scholar] [CrossRef]
- Tian, X.; Volkov, O.; Voskov, D. An advanced inverse modeling framework for efficient and flexible adjoint-based history matching of geothermal fields. Geothermics 2024, 116, 102849. [Google Scholar] [CrossRef]
- Kor, P.; Hong, A.; Bratvold, R.B. Reservoir Production Management with Bayesian Optimization: Achieving Robust Results in a Fraction of the Time. SPE J. 2023, 1–21. [Google Scholar] [CrossRef]
- Lee, C.S.; Hamon, F.P.; Castelletto, N.; Vassilevski, P.S.; White, J.A. Multilevel well modeling in aggregation-based nonlinear multigrid for multiphase flow in porous media. J. Comput. Phys. 2024, 513, 113163. [Google Scholar] [CrossRef]
- Jansen, J.D.; Fonseca, R.M.; Kahrobaei, S.; Siraj, M.M.; Essen, v.G.; Van den Hof, P.M. The egg model—A geological ensemble for reservoir simulation. Geosci. Data J. 2014, 1, 192–195. [Google Scholar] [CrossRef]
- Zhou, H.; Lee, S.H.; Tchelepi, H.A. Multiscale Finite-Volume Formulation for the Saturation Equations. SPE J. 2011, 17, 198–211. [Google Scholar] [CrossRef]
- Chaabi, O.; Kobaisi, M.A. Algorithmic Monotone Multiscale Finite Volume Methods for Porous Media Flow. J. Comput. Phys. 2024, 499, 112739. [Google Scholar] [CrossRef]
- Cusini, M.; van Kruijsdijk, C.; Hajibeygi, H. Algebraic dynamic multilevel (ADM) method for fully implicit simulations of multiphase flow in porous media. J. Comput. Phys. 2016, 314, 60–79. [Google Scholar] [CrossRef]
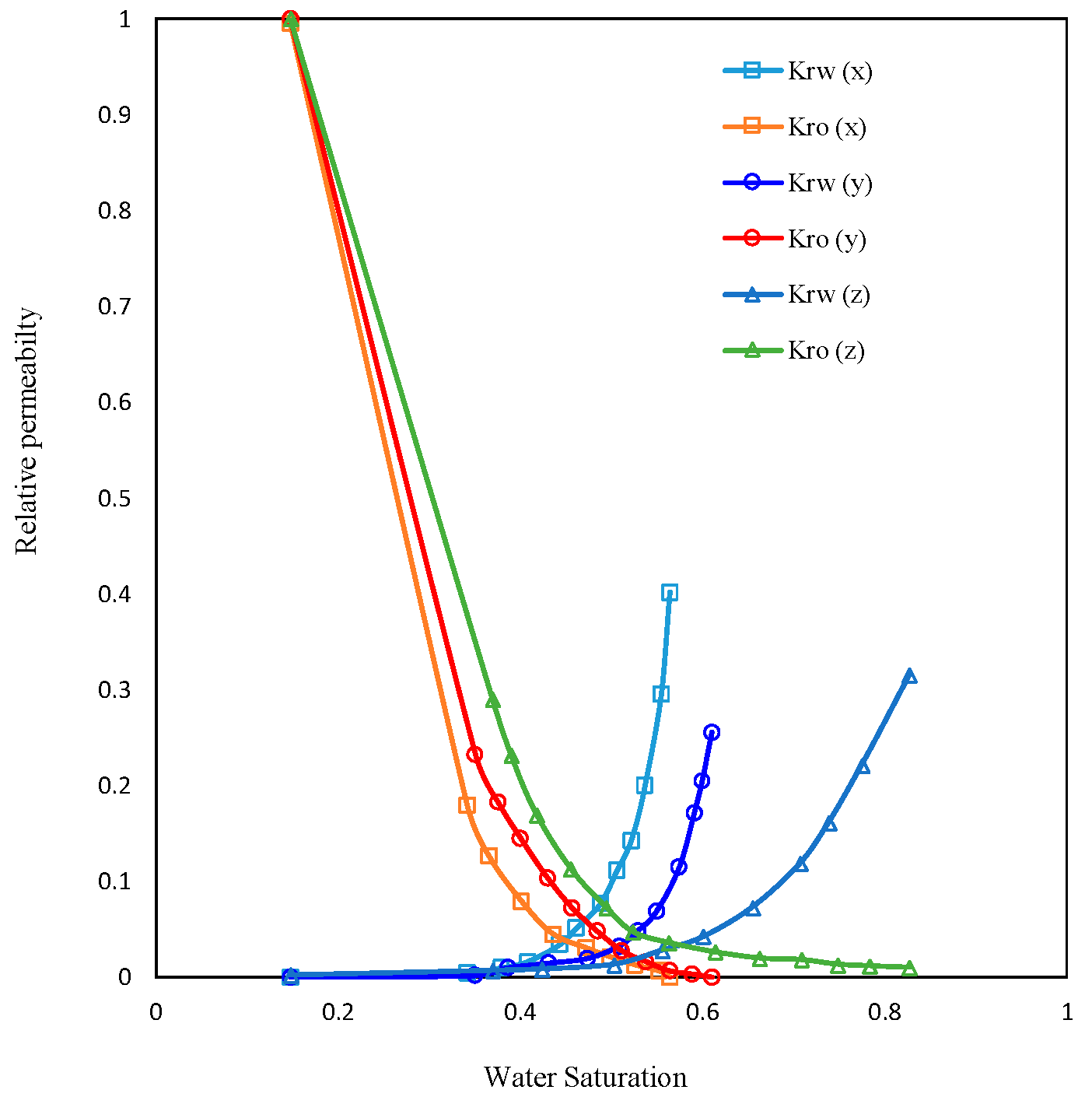



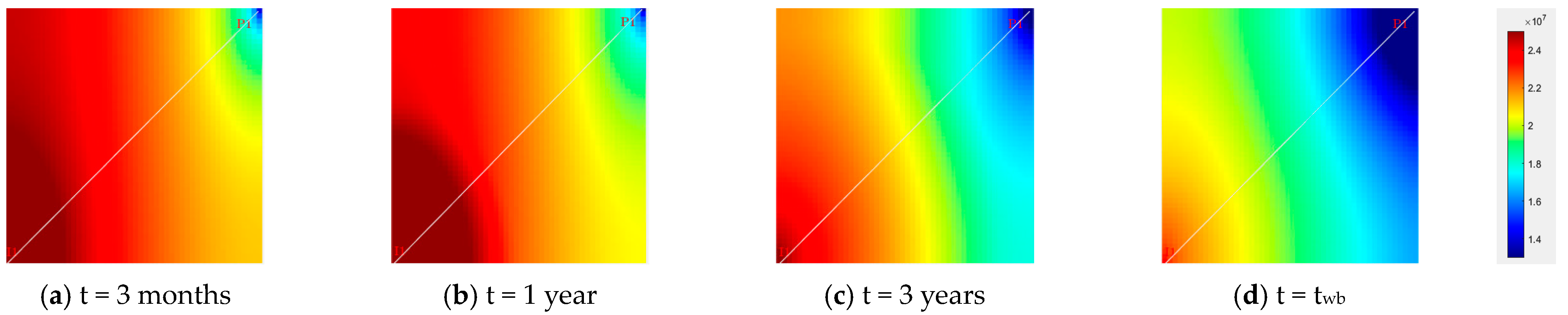



| Direction | Gas Permeability, mD | Liquid Permeability, mD | , f | ||
|---|---|---|---|---|---|
| x | 197.33 | 142.629 | 0.436 | 1 | 0.402 |
| y | 161.81 | 104.801 | 0.390 | 1 | 0.255 |
| z | 34.57 | 13.867 | 0.173 | 1 | 0.315 |
| Method | FI | MS |
|---|---|---|
| Simulation time | 534 s | 153 s |
| Total linear solver time | 360 s | 16 s |
| Grid Node | Dx (m) | Dy (m) | Dz (m) | Initial Water Saturation (f) | Porosity (f) | Permeability (10−3 μm2) | Oil Viscosity (mPa·s) |
|---|---|---|---|---|---|---|---|
| 50 × 50 × 10 | 5 | 5 | 1 | 0.125 | 0.2 | 60 | 5 |
| CASE | Models Description | Absolute Permeability | Relative Permeability |
|---|---|---|---|
| Case 1 | Isotropic homogeneous | Isotropic (Kx = Ky = 60) | Isotropic |
| Case 2 | Single Anisotropy | Anisotropy (Kx = 120, Ky = 30) | Isotropic |
| Case 3 | Single Anisotropy | Isotropic (Kx = Ky = 60) | Anisotropy |
| Case 4 | Double anisotropy | Anisotropy (Kx = 120, Ky = 30) | Anisotropy |
| Case 5 | Double anisotropy | Anisotropy (Kx = 30, Ky = 120) | Anisotropy |
| Direction | , f | , f | ||
|---|---|---|---|---|
| x | 0.125 | 0.416 | 1 | 0.189 |
| y | 0.130 | 0.318 | 1 | 0.208 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Wang, J.; Jia, D.; Zhang, R.; Zhang, J.; Yan, Y.; Wang, S. A Multi-Scale Numerical Simulation Method Considering Anisotropic Relative Permeability. Processes 2024, 12, 2058. https://doi.org/10.3390/pr12092058
Wu L, Wang J, Jia D, Zhang R, Zhang J, Yan Y, Wang S. A Multi-Scale Numerical Simulation Method Considering Anisotropic Relative Permeability. Processes. 2024; 12(9):2058. https://doi.org/10.3390/pr12092058
Chicago/Turabian StyleWu, Li, Junqiang Wang, Deli Jia, Ruichao Zhang, Jiqun Zhang, Yiqun Yan, and Shuoliang Wang. 2024. "A Multi-Scale Numerical Simulation Method Considering Anisotropic Relative Permeability" Processes 12, no. 9: 2058. https://doi.org/10.3390/pr12092058
APA StyleWu, L., Wang, J., Jia, D., Zhang, R., Zhang, J., Yan, Y., & Wang, S. (2024). A Multi-Scale Numerical Simulation Method Considering Anisotropic Relative Permeability. Processes, 12(9), 2058. https://doi.org/10.3390/pr12092058








