Evaluation of Key Development Factors of a Buried Hill Reservoir in the Eastern South China Sea: Nonlinear Component Seepage Model Coupled with EDFM
Abstract
1. Introduction
- (1)
- Equivalent continuum model (ECM)
- (2)
- Discrete fracture model (DFM)
- (3)
- Embedded Discrete Fracture Model (EDFM)
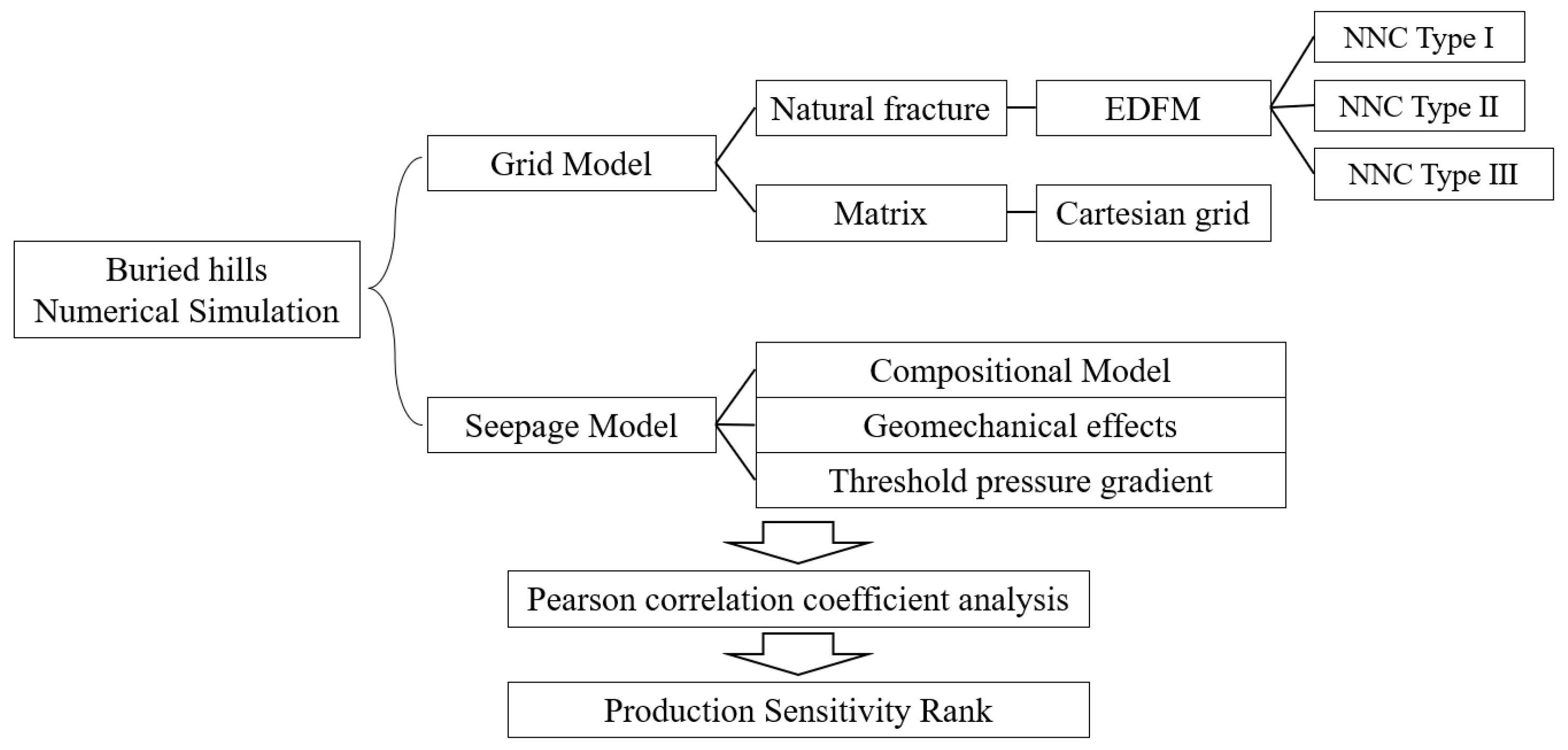
2. Materials and Methods
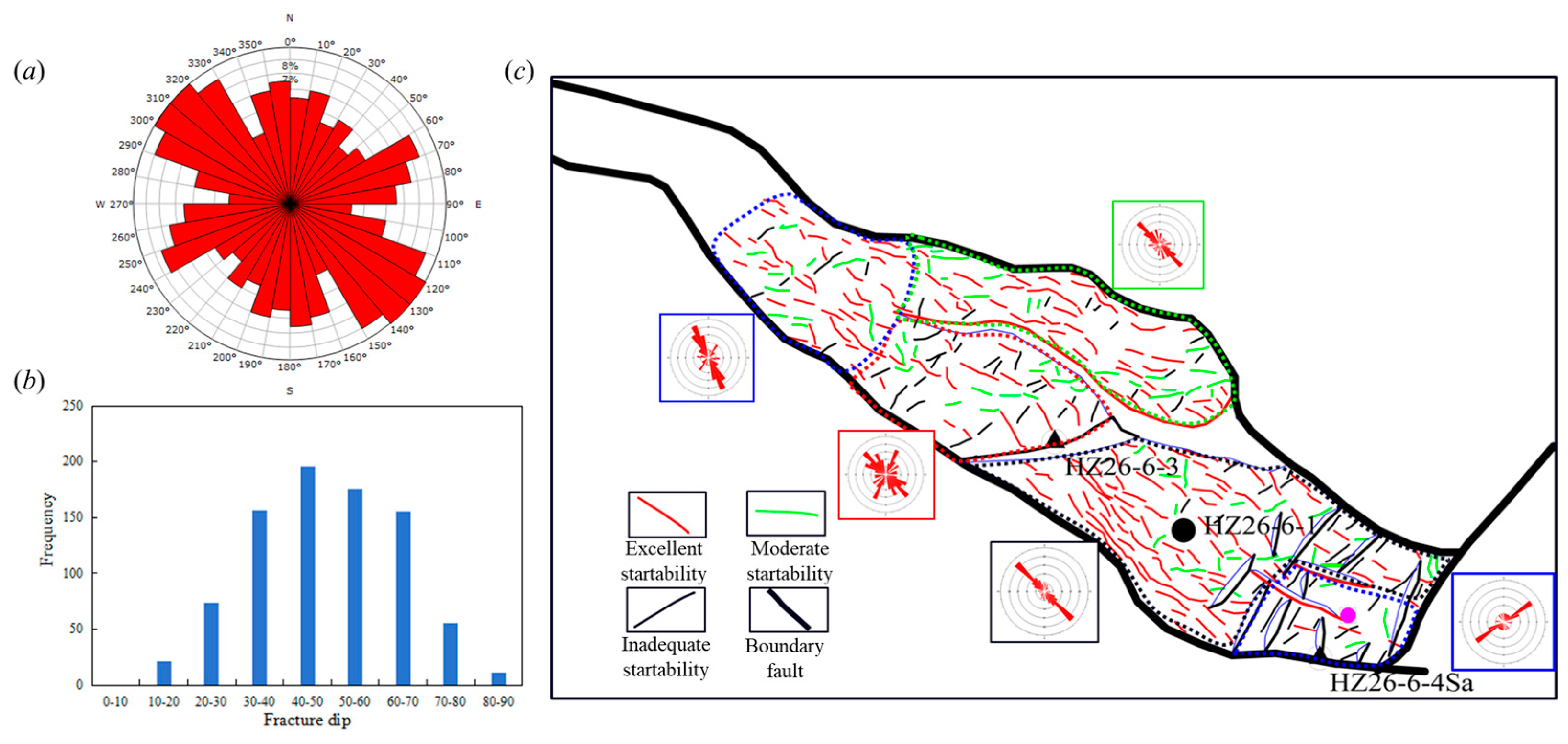
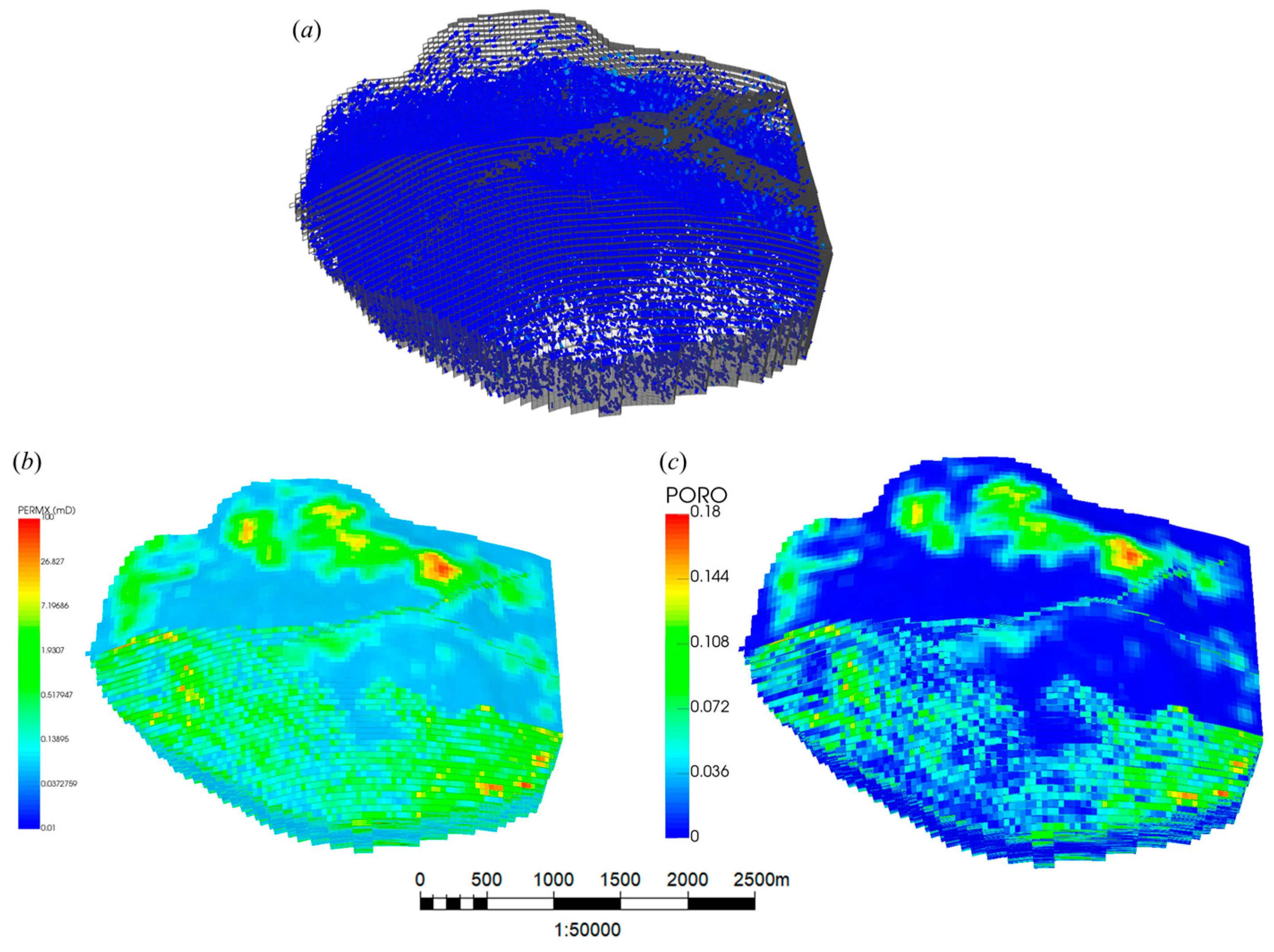
2.1. Geological Setting
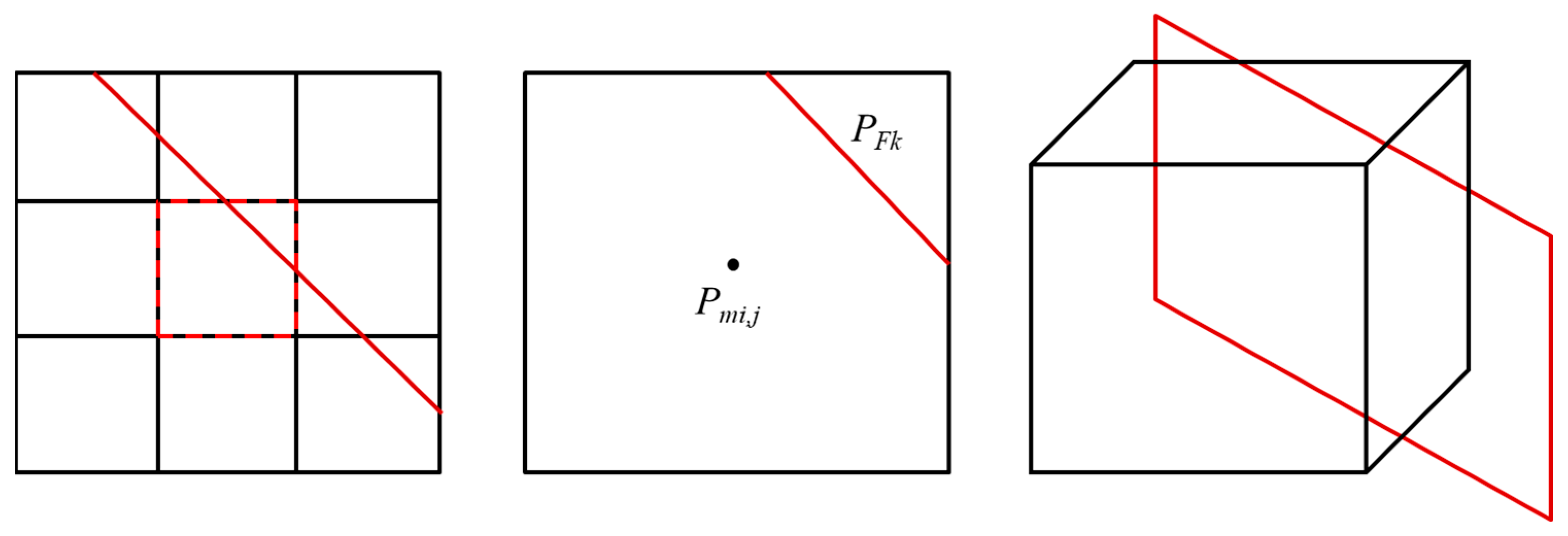
2.2. EDFM Model
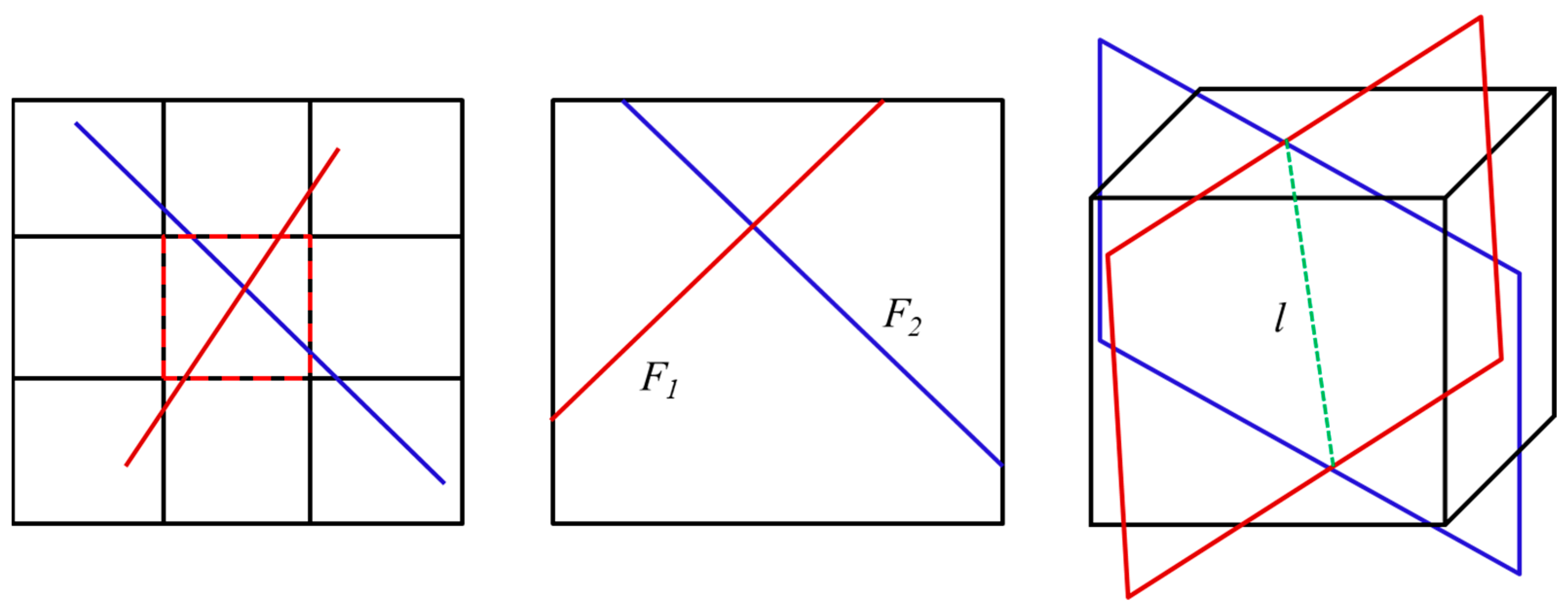
2.2.1. NNC Type I: Connection between a Fracture Segment and the Matrix Cell
2.2.2. NNC Type II: The Interconnection between Two Different Fractures within the Same Grid
2.2.3. NNC Type III: Connection of the Same Fracture within Different Grids
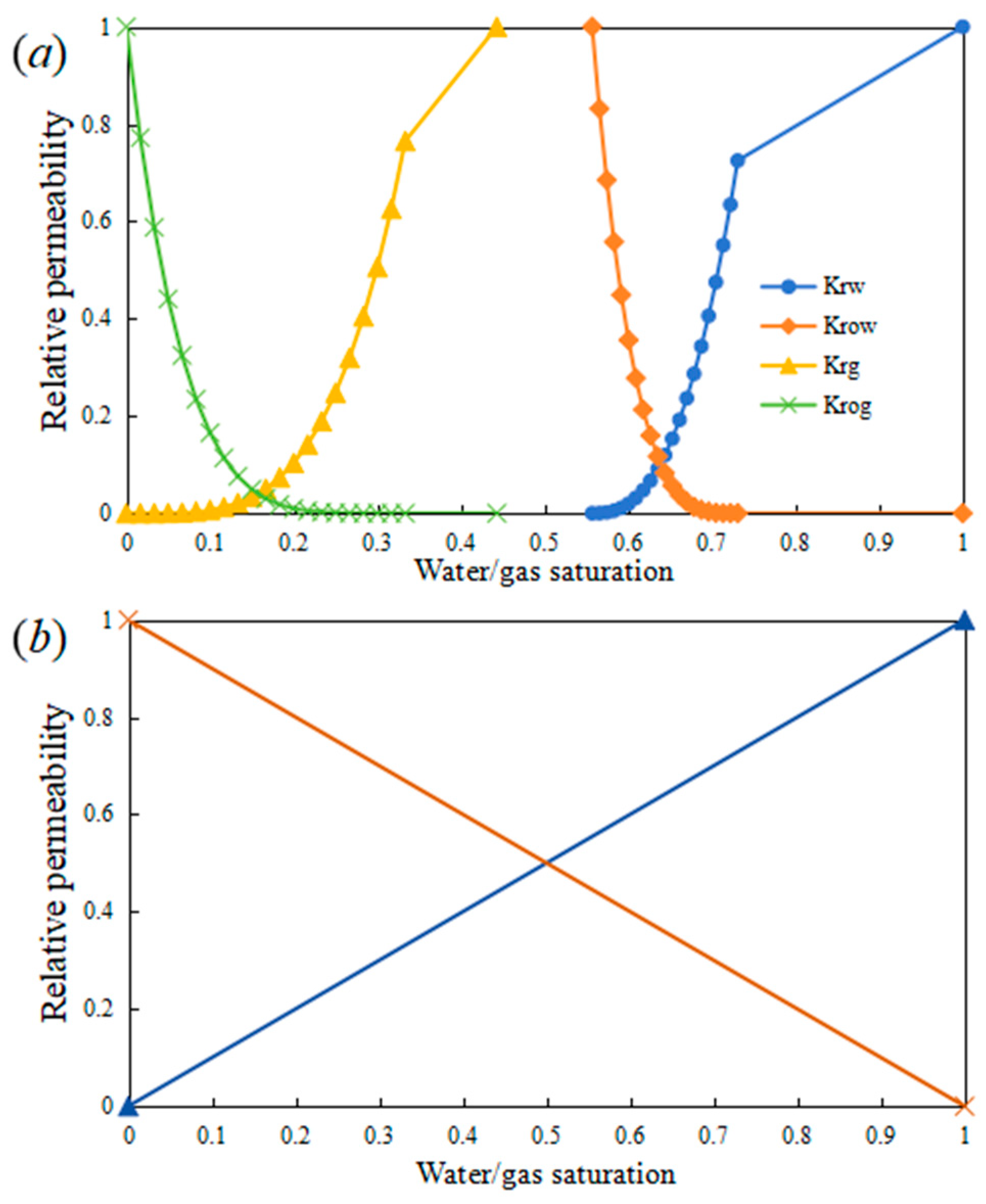
2.3. Reservoir Numerical Simulation Model
3. Discussion
- (1)
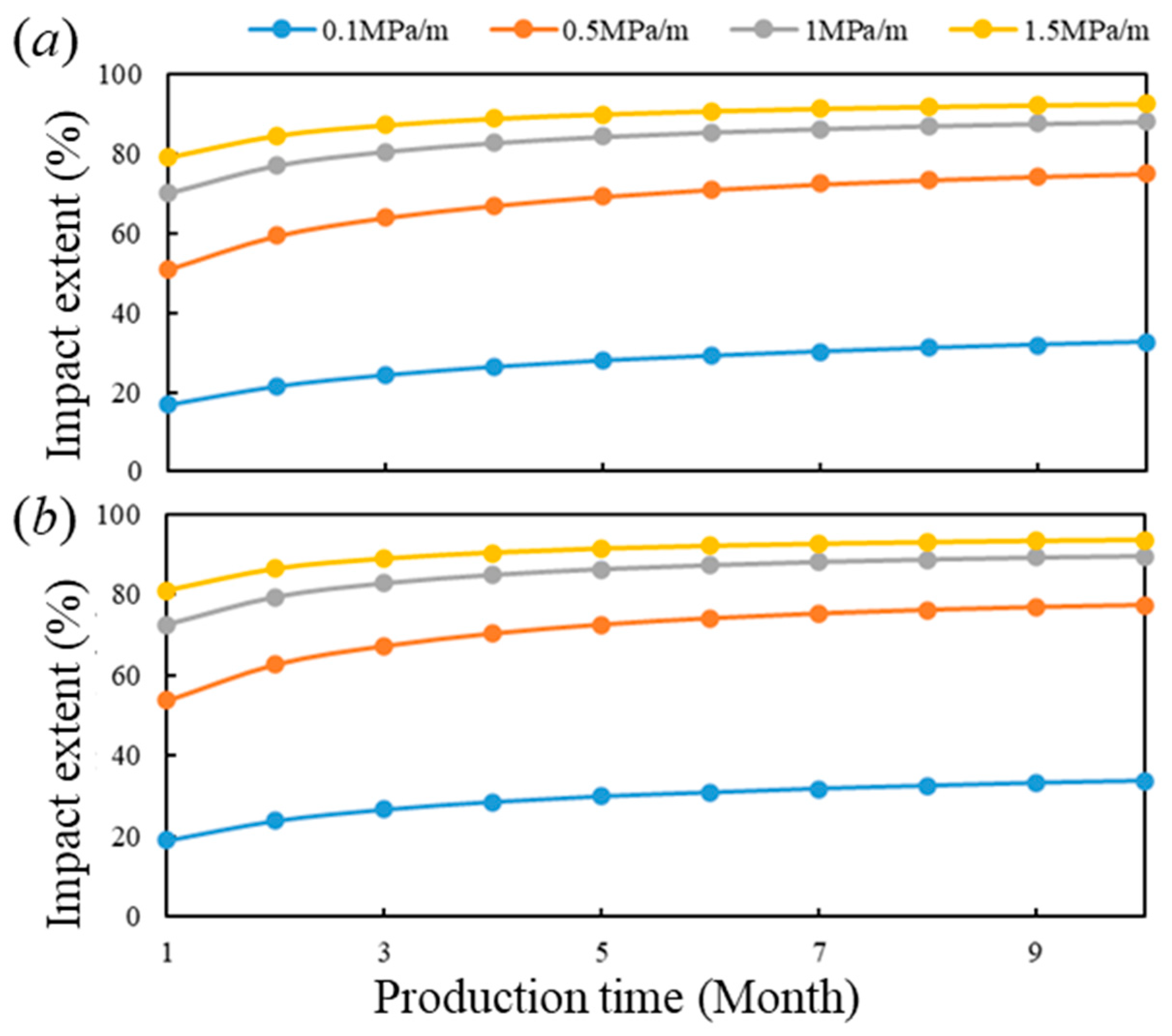
- Sensitivity analysis of threshold pressure
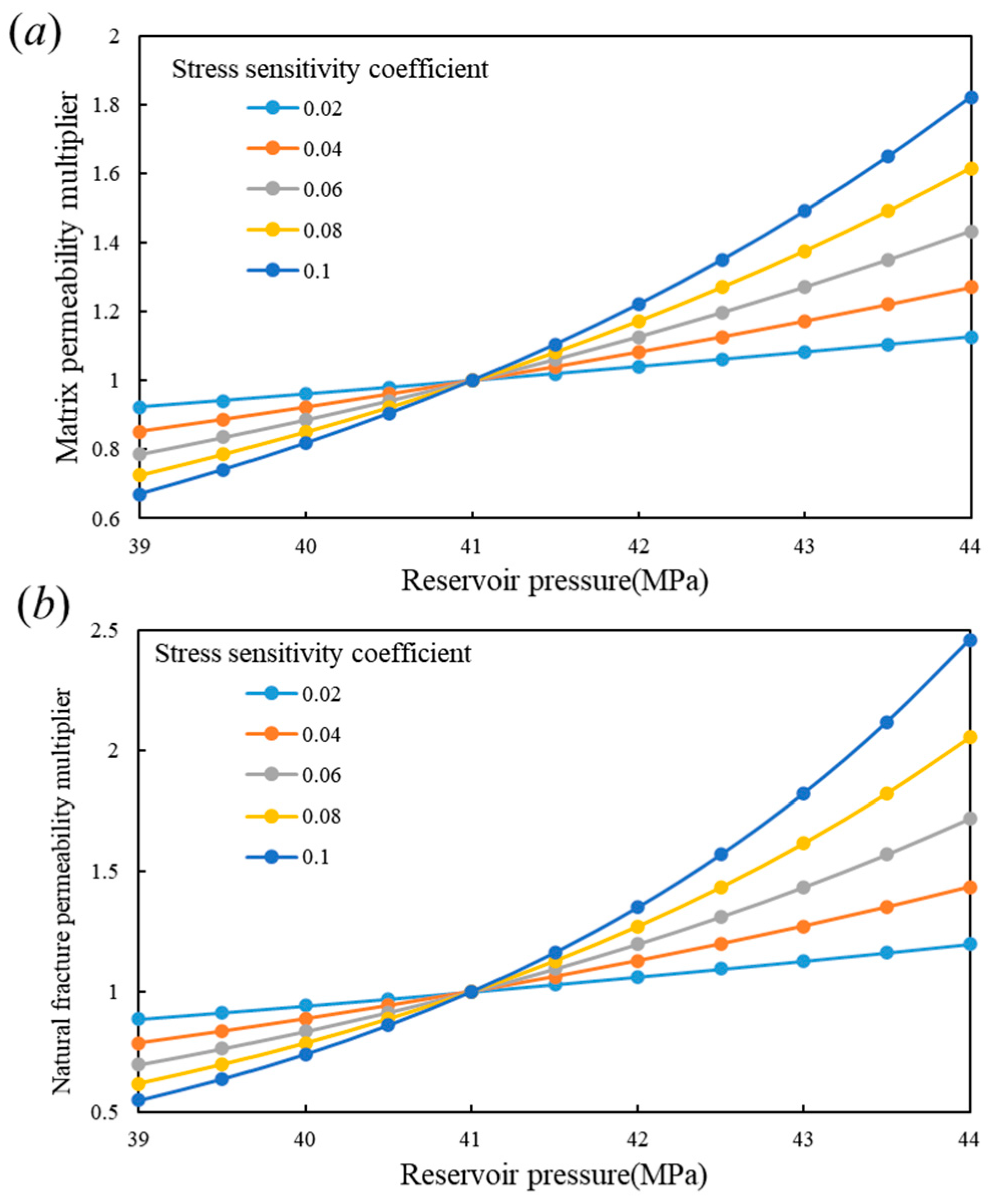
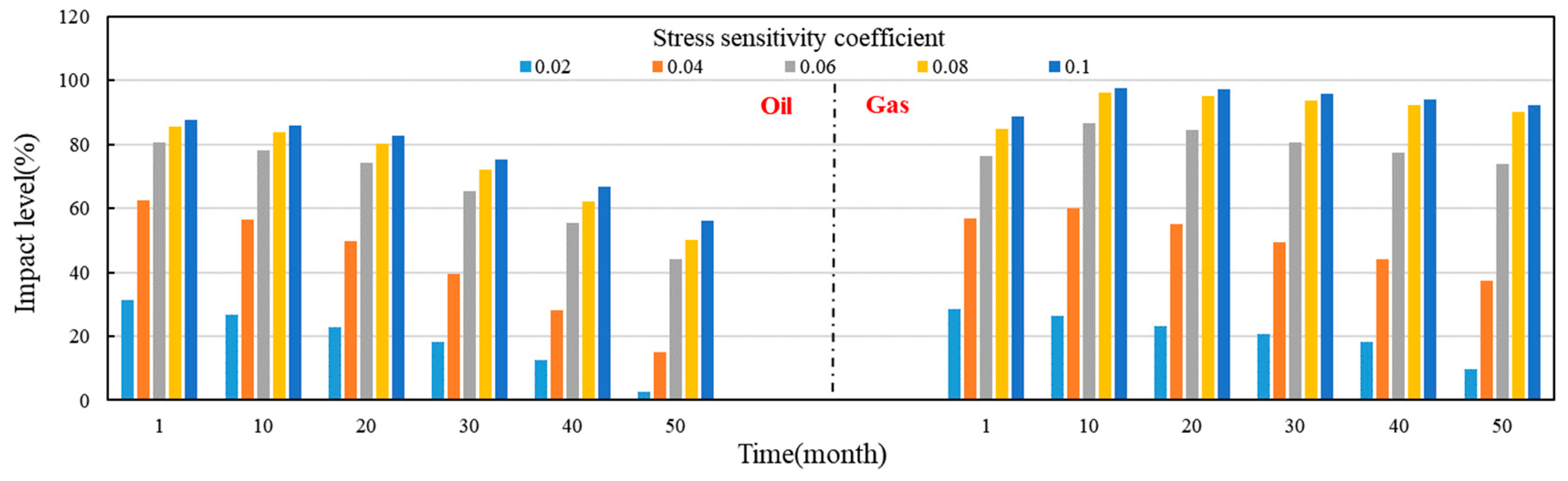
- (2)
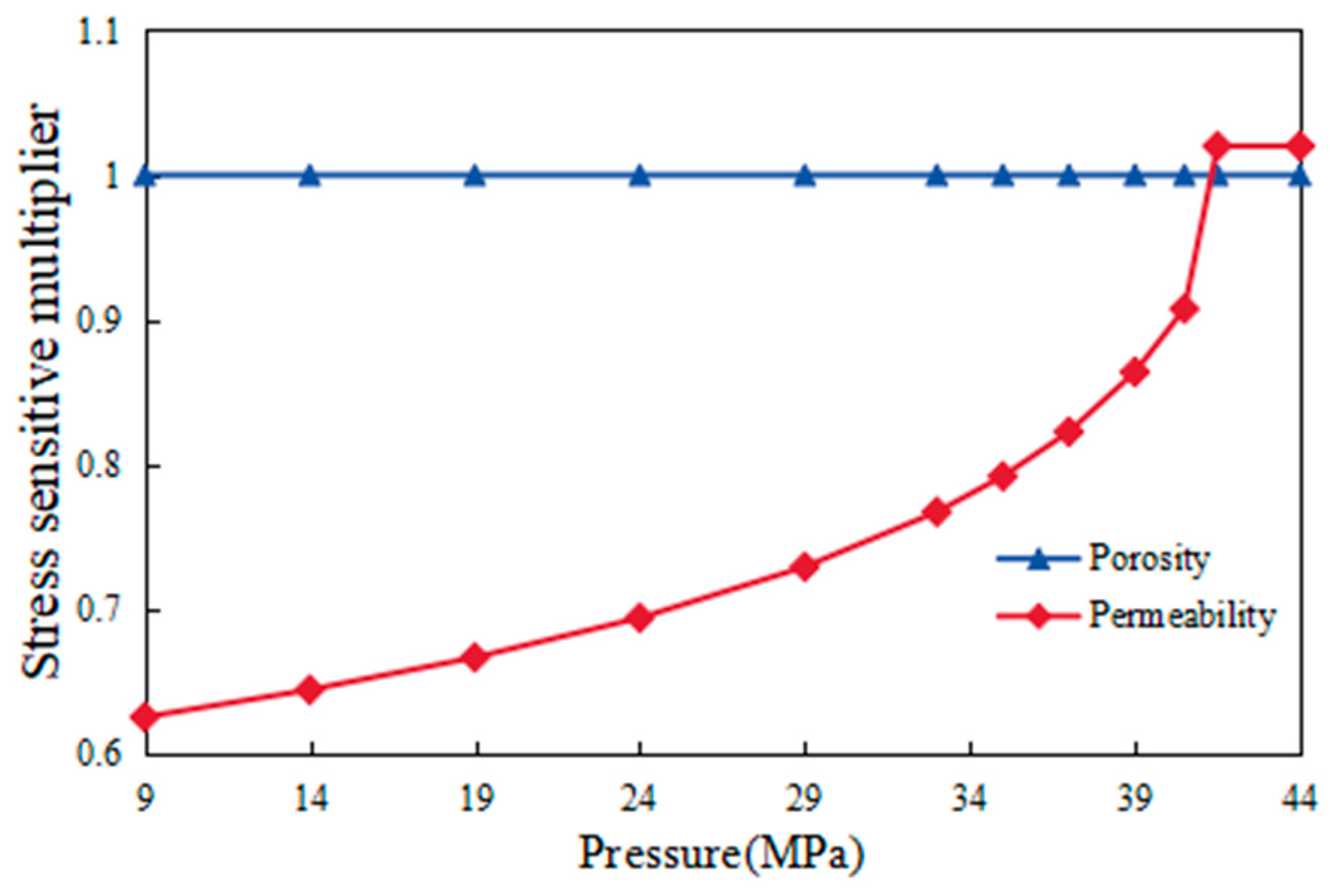
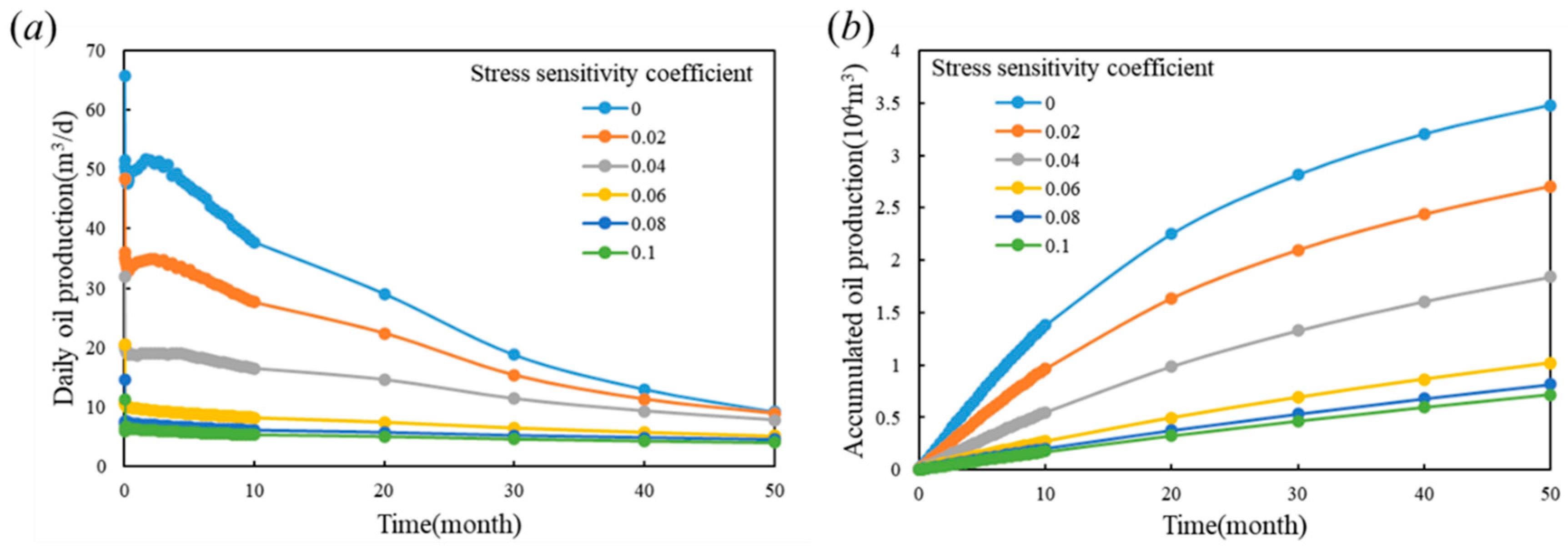
- Sensitivity analysis of geomechanical effects
- (3)
- Sensitivity analysis of natural fracture density
- (4)
- Sensitivity analysis of natural fracture length
- (5)
- Pearson Correlation Coefficient
4. Conclusions
- (1)
- This study adopts embedded discrete fracture technology and combines geomechanical effects to deeply explore the stress sensitivity of the matrix and fractures, as well as the influence of the fluid initiation pressure gradient on fracture development in tight reservoirs. Based on these theoretical foundations, we have successfully constructed a highly accurate three-dimensional numerical model at the reservoir scale, which specifically simulates the fracture development characteristics of complex reservoirs in the HZ 26-B ancient buried hills.
- (2)
- In the process of model construction, we made full use of on-site logging data and made precise corrections to the model, ensuring that the model output is highly consistent with the actual observation data. Through in-depth analysis of the model, we have revealed the impact mechanism of key factors such as the threshold pressure gradient, stress sensitivity coefficient, natural fracture density, and fracture length on reservoir productivity.
- (3)
- For the HZ 26-B buried hill reservoir, the main factors affecting productivity are the matrix permeability, geomechanical effects, and natural fracture length. The impact of the threshold pressure gradient and bottomhole flow pressure is relatively weak.
- (4)
- The research results indicate that these factors interact and together determine the development potential and production performance of oil and gas reservoirs. Especially, we found that the threshold pressure gradient has a significant impact on the initial production and pressure attenuation rate of oil and gas reservoirs, while the stress sensitivity coefficient is directly related to the degree of crack opening and expansion. In addition, the density and development characteristics of natural fractures also play a crucial role in the effective connectivity of oil and gas flow paths and reservoirs.
- (5)
- The results of this study are not applicable to all types of buried hill reservoirs and have certain limitations. However, the evaluation process for identifying primary controlling factors can be applied to any reservoir. This process allows for the accurate ranking of influencing factors with fewer simulation runs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ECM | Equivalent continuum model |
| DFM | Discrete fracture model |
| EDFM | Embedded Discrete Fracture Model |
| WOPT | Well oil production total |
| WGPT | Well gas production total |
| Km | Matrix permeability |
| lf | Natural fracture length |
| BHP | Bottomhole flow pressure |
| γ | Stress sensitivity coefficient |
| λ | Threshold pressure gradient |
References
- Su, Y.; Zhu, Z. Percolation characteristics and unstable water imiection strategy of fractured buried hill reservoirs: Taking the buried hill reservoir in Bohai JZ25-1S oilfield as an example. China Offshore Oil Gas 2019, 31, 78–85. [Google Scholar]
- Tomassi, A.; Milli, S.; Tentori, D. Synthetic seismic forward modeling of a high-frequency depositional sequence: The example of the Tiber depositional sequence (Central Italy). Mar. Pet. Geol. 2024, 160, 106624. [Google Scholar] [CrossRef]
- Deng, Y. Formation mechanism and exploration practice of large medium buried hill oil fields in Bohai Sea. Acta Pet. Sin. 2015, 36, 253–261. [Google Scholar]
- Cheng, L.; Wang, D.; Cao, R.; Xia, R. The influence of hydraulic fractures on oil recovery by water flooding processes in tight oil reservoirs: An experimental and numerical approach. J. Pet. Sci. Eng. 2020, 185, 106572. [Google Scholar] [CrossRef]
- Todd, H.B.; Evans, J.G. Improved Oil Recovery IOR Pilot Projects in the Bakken Formation. In Proceedings of the SPE Low Perm Symposium, SPE, Denver, CO, USA, 5–6 May 2016; p. SPE-180270-MS. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, L.; Huang, S.; Bai, Y.; Jia, P.; Wang, S.; Xu, B.; Chen, L. An approximate semianalytical method for two-phase flow analysis of liquid-rich shale gas and tight light-oil wells. J. Pet. Sci. Eng. 2019, 176, 562–572. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, H.; Heng, L.; Yang, J.; Chen, S. Lithofacies-controlled fracture modeling and quality control methods for complex lithology igneous buried hill rrservior: Taking igneous buried hill rrservior of Huizhou 26-6 Oilfield as an example. Sci. Technol. Eng. 2023, 23, 7671–7677. [Google Scholar]
- Taleghani, A.D.; Olson, J.E. How Natural Fractures Could Affect Hydraulic-Fracture Geometry. SPE J. 2014, 19, 161–171. [Google Scholar] [CrossRef]
- Luo, H.; Li, H.; Zhang, J.; Wang, J.; Wang, K.; Xia, T.; Zhu, X. Production performance analysis of fractured horizontal well in tight oil reservoir. J. Pet. Explor. Prod. Technol. 2018, 8, 229–247. [Google Scholar] [CrossRef]
- Qin, G.; Dai, X.; Sui, L.; Geng, M.; Sun, L.; Zheng, Y.; Bai, Y. Study of massive water huff-n-puff technique in tight oil field and its field application. J. Pet. Sci. Eng. 2021, 196, 107514. [Google Scholar] [CrossRef]
- Xu, D.; Fan, J. On the metric dimension of HDN. J. Discret. Algorithms 2014, 26, 1–6. [Google Scholar] [CrossRef]
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Warren, J.; Root, P. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Pruess, K.; Narasimhan, T.N. A Practical Method for Modeling Fluid and Heat Flow in Fractured Porous Media. Soc. Pet. Eng. J. 1985, 25, 14–26. [Google Scholar] [CrossRef]
- Sarda, S.; Jeannin, L.; Basquet, R.; Bourbiaux, B. Hydraulic Characterization of Fractured Reservoirs: Simulation on Discrete Fracture Models. SPE Reserv. Eval. Eng. 2002, 5, 154–162. [Google Scholar] [CrossRef]
- Kim, H.; Onishi, T.; Chen, H.; Datta-Gupta, A. Parameterization of embedded discrete fracture models (EDFM) for efficient history matching of fractured reservoirs. J. Pet. Sci. Eng. 2021, 204, 108681. [Google Scholar] [CrossRef]
- Helnemann, Z.E.; Brand, C.W.; Munka, M.; Chen, Y.M. Modeling Reservoir Geometry with Irregular Grids. SPE Reserv. Eng. 1991, 6, 225–232. [Google Scholar] [CrossRef]
- Denney, D. Modeling Well Performance in Shale-Gas Reservoirs. J. Pet. Technol. 2010, 62, 47–48. [Google Scholar] [CrossRef]
- Li, L.; Lee, S.H. Efficient Field-Scale Simulation of Black Oil in a Naturally Fractured Reservoir Through Discrete Fracture Networks and Homogenized Media. SPE Reserv. Eval. Eng. 2008, 11, 750–758. [Google Scholar] [CrossRef]
- Wang, K.; Liu, H.; Luo, J.; Wu, K.; Chen, Z. A Comprehensive Model Coupling Embedded Discrete Fractures, Multiple Interacting Continua, and Geomechanics in Shale Gas Reservoirs with Multiscale Fractures. Energy Fuels 2017, 31, 7758–7776. [Google Scholar] [CrossRef]
- Lee, S.H.; Lough, M.F.; Jensen, C.L. Hierarchical modeling of flow in naturally fractured formations with multiple length scales. Water Resour. Res. 2001, 37, 443–455. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of an Efficient Embedded Discrete Fracture Model for 3D Compositional Reservoir Simulation in Fractured Reservoirs. SPE J. 2013, 19, 289–303. [Google Scholar] [CrossRef]
- Yan, X.; Yu, H. Numerical simulation of hydraulic fracturing with consideration of the pore pressure distribution based on the unified pipe-interface element model. Eng. Fract. Mech. 2022, 275, 108836. [Google Scholar] [CrossRef]
- Rao, X.; Cheng, L.; Cao, R.; Jia, P.; Wu, Y.; Liu, H.; Zhao, Y.; Chen, Y. A modified embedded discrete fracture model to study the water blockage effect on water huff-n-puff process of tight oil reservoirs. J. Pet. Sci. Eng. 2019, 181, 106232. [Google Scholar] [CrossRef]
- Fiallos, M.X.; Yu, W.; Ganjdanesh, R.; Kerr, E.; Sepehrnoori, K.; Miao, J.; Ambrose, R. Modeling Interwell Interference Due to Complex Fracture Hits in Eagle Ford Using EDFM. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2019. [Google Scholar] [CrossRef]
- Qin, J.; Xu, Y.; Tang, Y.; Liang, R.; Zhong, Q.; Yu, W.; Sepehrnoori, K. Impact of Complex Fracture Networks on Rate Transient Behavior of Wells in Unconventional Reservoirs Based on Embedded Discrete Fracture Model. J. Energy Resour. Technol. 2022, 144, 083007. [Google Scholar] [CrossRef]
- Qin, J.-Z.; Zhong, Q.-H.; Tang, Y.; Yu, W.; Sepehrnoori, K. Well interference evaluation considering complex fracture networks through pressure and rate transient analysis in unconventional reservoirs. Pet. Sci. 2022, 20, 337–349. [Google Scholar] [CrossRef]








| Content | Parameter | Unit | |
|---|---|---|---|
| Grid number | 152 × 92 × 400 | ||
| Grid size | 50 × 50 × 2.5 | m | |
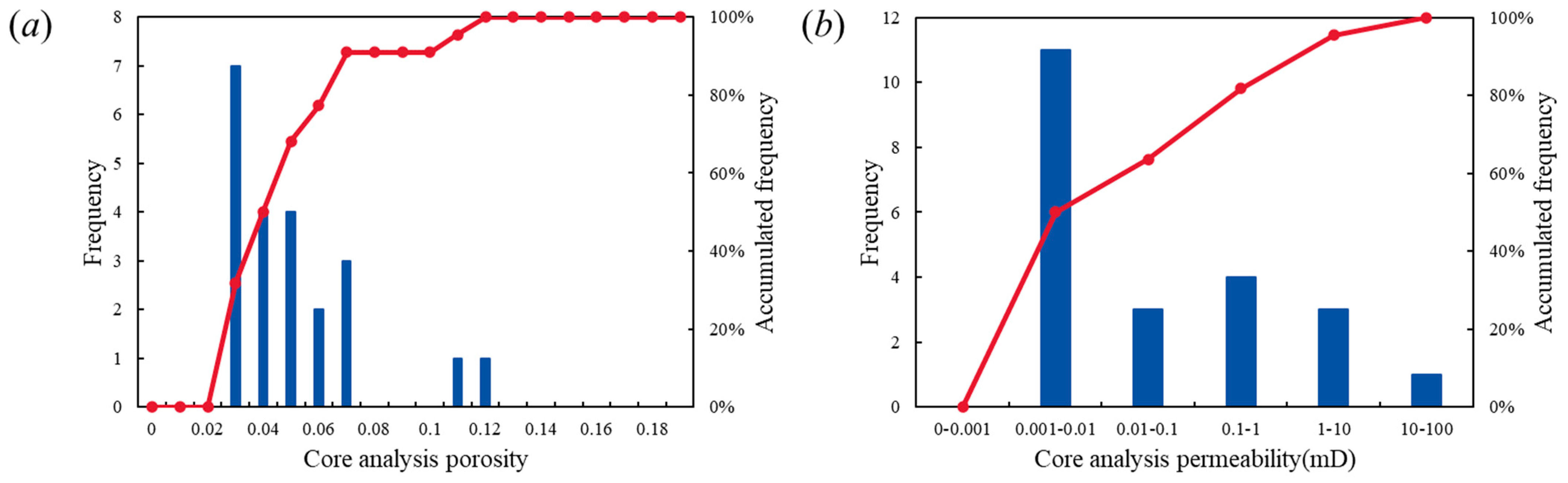
| Matrix permeability | Maximum permeability | 95.8 | mD |
| Minimum permeability | 0.06 | ||
| Average permeability | 1.2 | ||
| Matrix porosity | Minimum porosity | 0.5 | % |
| Maximum porosity | 17.9 | ||
| Average porosity | 3.7 | ||
| Natural fractures in Weathering Zones | Fracture trend | 158 | ° |
| Fracture dip angle | 52 | ° | |
| Fracture density | 4.4 | piece/m | |
| Fracture aperture | 55 | μm | |
| Natural fractures in the inner zone | Fracture trend | 138 | ° |
| Fracture dip angle | 57 | ° | |
| Fracture density | 3.7 | piece/m | |
| Fracture aperture | 49 | μm | |
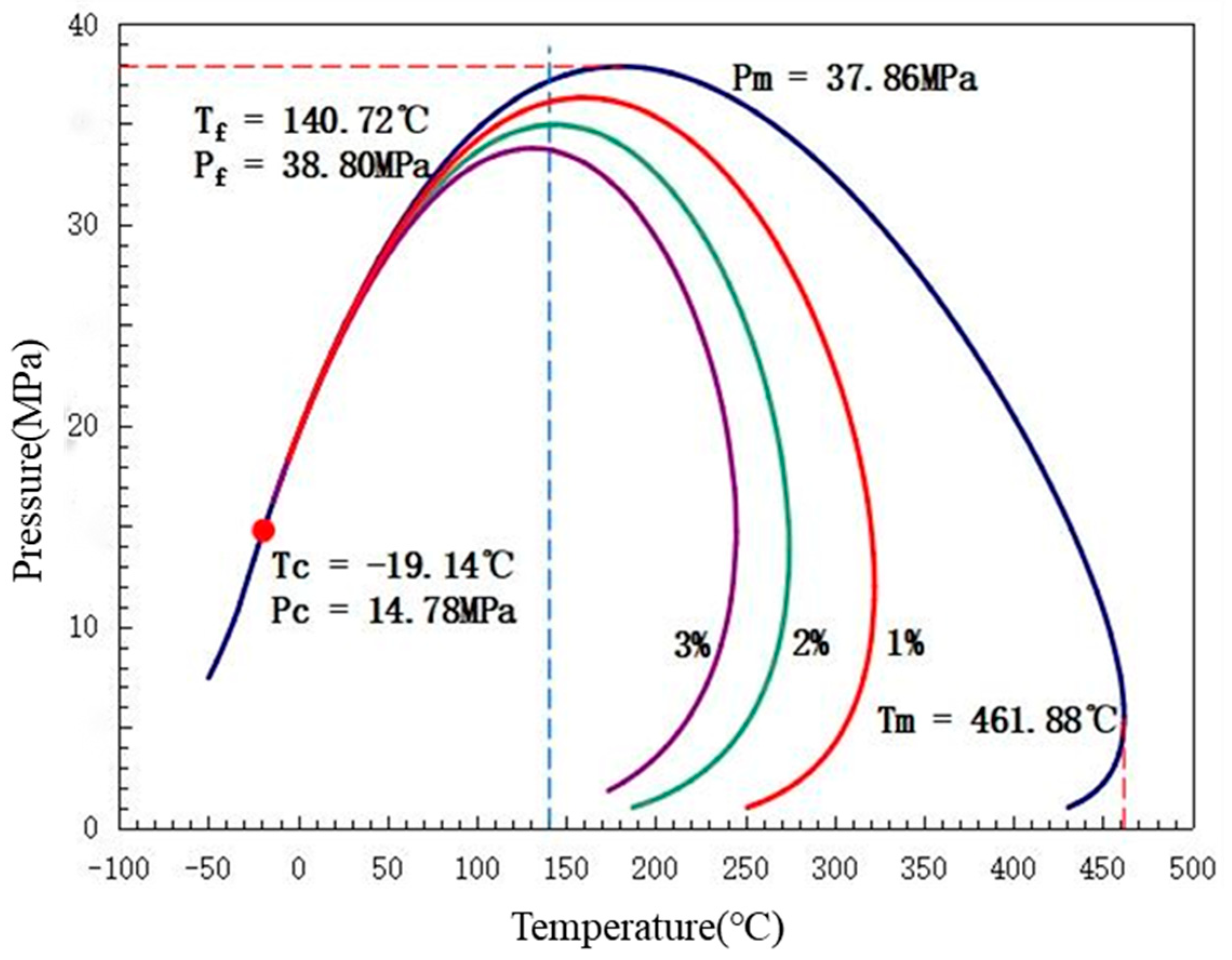
| Pseudo- Component | Critical Pressure | Critical Temperature | Critical Volume | Molar Mass | Mole Fraction |
|---|---|---|---|---|---|
| bar | K | m3/kg·mol | |||
| N2-C1 | 45.97 | 190.45 | 0.10 | 16.07 | 68.01% |
| CO2-C2 | 48.87 | 305.23 | 0.15 | 30.12 | 8.31% |
| C3 | 42.46 | 369.80 | 0.20 | 44.10 | 15.46% |
| C4-C6 | 32.76 | 471.30 | 0.32 | 73.95 | 3.09% |
| C7-C10 | 28.04 | 631.61 | 0.72 | 141.64 | 4.97% |
| C11+ | 16.07 | 975.02 | 2.47 | 530.82 | 0.15% |
| Case | Km | lf | BHP | γ | λ | WGPT | WOPT |
|---|---|---|---|---|---|---|---|
| md | m | MPa | / | MPa/m | 106 m3 | 104 m3 | |
| 1 | 0.01 | 50 | 15 | 0.02 | 0.1 | 1.04 | 0.55 |
| 2 | 0.01 | 100 | 20 | 0.04 | 0.5 | 0.55 | 0.38 |
| 3 | 0.01 | 150 | 25 | 0.06 | 1 | 0.39 | 0.31 |
| 4 | 0.01 | 200 | 30 | 0.08 | 1.5 | 0.31 | 0.24 |
| 5 | 0.01 | 250 | 35 | 0.1 | 2 | 0.22 | 0.14 |
| 6 | 0.1 | 50 | 20 | 0.06 | 1.5 | 0.92 | 2.13 |
| 7 | 0.1 | 100 | 25 | 0.08 | 2 | 0.8 | 1.79 |
| 8 | 0.1 | 150 | 30 | 0.1 | 0.1 | 1.25 | 1.49 |
| 9 | 0.1 | 200 | 35 | 0.02 | 0.5 | 1.97 | 1.39 |
| 10 | 0.1 | 250 | 15 | 0.04 | 1 | 1.77 | 2.83 |
| 11 | 1 | 50 | 25 | 0.1 | 0.5 | 4.25 | 12.68 |
| 12 | 1 | 100 | 30 | 0.02 | 1 | 10.32 | 24.21 |
| 13 | 1 | 150 | 35 | 0.04 | 1.5 | 3.6 | 10.51 |
| 14 | 1 | 200 | 15 | 0.06 | 2 | 5.69 | 17.94 |
| 15 | 1 | 250 | 20 | 0.08 | 0.1 | 5.39 | 14.54 |
| 16 | 5 | 50 | 30 | 0.04 | 2 | 22.83 | 71.07 |
| 17 | 5 | 100 | 35 | 0.06 | 0.1 | 33.17 | 55.26 |
| 18 | 5 | 150 | 15 | 0.08 | 0.5 | 21.34 | 67.38 |
| 19 | 5 | 200 | 20 | 0.1 | 1 | 17.96 | 58.28 |
| 20 | 5 | 250 | 25 | 0.02 | 1.5 | 41.74 | 114.39 |
| 21 | 10 | 50 | 35 | 0.08 | 1 | 22.3 | 70.92 |
| 22 | 10 | 100 | 15 | 0.1 | 1.5 | 33.23 | 109.12 |
| 23 | 10 | 150 | 20 | 0.02 | 2 | 63.47 | 180.52 |
| 24 | 10 | 200 | 25 | 0.04 | 0.1 | 112.13 | 174.96 |
| 25 | 10 | 250 | 30 | 0.06 | 0.5 | 48.62 | 123.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Xiang, Y.; Zhu, Y.; Wang, L.; Chen, S.; Qin, F.; Sun, B.; Deng, Y. Evaluation of Key Development Factors of a Buried Hill Reservoir in the Eastern South China Sea: Nonlinear Component Seepage Model Coupled with EDFM. Processes 2024, 12, 1736. https://doi.org/10.3390/pr12081736
Dai J, Xiang Y, Zhu Y, Wang L, Chen S, Qin F, Sun B, Deng Y. Evaluation of Key Development Factors of a Buried Hill Reservoir in the Eastern South China Sea: Nonlinear Component Seepage Model Coupled with EDFM. Processes. 2024; 12(8):1736. https://doi.org/10.3390/pr12081736
Chicago/Turabian StyleDai, Jianwen, Yangyue Xiang, Yanjie Zhu, Lei Wang, Siyu Chen, Feng Qin, Bowen Sun, and Yonghui Deng. 2024. "Evaluation of Key Development Factors of a Buried Hill Reservoir in the Eastern South China Sea: Nonlinear Component Seepage Model Coupled with EDFM" Processes 12, no. 8: 1736. https://doi.org/10.3390/pr12081736
APA StyleDai, J., Xiang, Y., Zhu, Y., Wang, L., Chen, S., Qin, F., Sun, B., & Deng, Y. (2024). Evaluation of Key Development Factors of a Buried Hill Reservoir in the Eastern South China Sea: Nonlinear Component Seepage Model Coupled with EDFM. Processes, 12(8), 1736. https://doi.org/10.3390/pr12081736






