A Novel Temporal Fusion Channel Network with Multi-Channel Hybrid Attention for the Remaining Useful Life Prediction of Rolling Bearings

Abstract

The remaining useful life (RUL) prediction of rolling bearings is crucial for optimizing maintenance schedules, reducing downtime, and extending machinery lifespan. However, existing multi-channel feature fusion methods do not fully capture the correlations between channels and time points in multi-dimensional sensor data. To address the above problems, this paper proposes a multi-channel feature fusion algorithm based on a hybrid attention mechanism and temporal convolutional networks (TCNs), called MCHA-TFCN. The model employs a dual-channel hybrid attention mechanism, integrating self-attention and channel attention to extract spatiotemporal features from multi-channel inputs. It uses causal dilated convolutions in TCNs to capture long-term dependencies and incorporates enhanced residual structures for global feature fusion, effectively extracting high-level spatiotemporal degradation information. The experimental results on the PHM2012 dataset show that MCHA-TFCN achieves excellent performance, with an average Root-Mean-Square Error (RMSE) of 0.091, significantly outperforming existing methods like the DANN and CNN-LSTM.

1. Introduction

Rolling bearings constitute fundamental mechanical components that are extensively utilized across diverse industrial applications [1]. The performance and service life of these bearings directly impact the reliability of entire systems. Traditional bearing life prediction methods, primarily based on statistical approaches and empirical formulas, have not adequately considered the influence of material characteristics on bearing performance degradation. Psuj et al. [2] revealed that the complex interplay of mechanical properties, microstructural characteristics, and surface integrity of bearing materials significantly influences their operational behavior. Through multi-sensor fusion approaches, they demonstrated precise characterization of material defects. Similarly, Alzhanov et al. [3] established that dynamic material properties directly correlate with component longevity under operational conditions. In industrial applications, bearings are subjected to complex environmental conditions and sustained high-intensity operational loads, which inevitably lead to material degradation and performance deterioration. Such degradation mechanisms can precipitate catastrophic system failures, resulting in substantial equipment damage, elevated maintenance expenditure, and significant safety hazards. Empirical studies have demonstrated that bearing-related failures constitute approximately 45% to 55% of rotating machinery malfunctions [4], emphasizing the paramount importance of systematic bearing health monitoring and management. To address these critical engineering challenges, extensive research initiatives have been directed toward the development of methodologies for predicting the remaining useful life (RUL) of bearings. Contemporary RUL prediction methodologies can be systematically categorized into model-based approaches [5] and data-driven paradigms [6,7]. Data-driven methods are currently the main research focus due to their ease of implementation and ability to avoid the high costs and complexity of model-based methods.

Data-driven methods rely on monitoring data, significantly reducing dependence on equipment degradation mechanisms and expert experience. By analyzing and processing the multi-dimensional feature information of rotating parts, potential health status or degradation features can be extracted from the data. Data-driven methods can be roughly divided into three categories: statistical methods [8,9], machine learning methods [10], and deep learning methods [11]. Deep learning methods have become mainstream in data-driven research because they reduce reliance on expert experience, empirical formulas, and physical modeling knowledge. They can directly extract degradation patterns from raw data. With the improvement in industrial data collection technology, a large amount of operational process data has been collected. Deep learning is widely used in RUL prediction due to its powerful data processing capabilities. Standard deep learning models include convolutional neural networks (CNNs) and recurrent neural networks (RNNs). Several scholars use convolutional network variants to construct mappings from vibration data to the remaining life of bearings. For example, Yang et al. [12] proposed an RUL prediction method based on a dual CNN model architecture combined with a mapping algorithm. The early fault points and RUL prediction results identified by the two CNN models were mapped using intermediate confidence variables to achieve accurate RUL prediction. Wu et al. [13] proposed a data-driven deep learning fusion model based on an attention mechanism and a parallel-branch CNN-LSTM model. The model uses a CNN and an LSTM with an attention mechanism to extract spatial and temporal features in parallel, thereby improving prediction accuracy. Du et al. [14] proposed a CNN prediction model based on the global attention mechanism (GAM), solving the problems of insufficient feature extraction and loss of critical features and achieving accurate RUL prediction for bearings.

To explore time series models, many scholars research CNN models to retain CNNs’ good spatial perception ability while incorporating time series features. Bai et al. [15] proposed a dilated causal convolution (DCC) method. It uses dilated DCC combined with causal and dilated convolution and stacks residual blocks to expand the receptive field, addressing CNNs’ limitations in capturing long-term temporal dependencies compared to RNNs. Song et al. [16] combined a temporal convolutional network (TCN) with the attention mechanism and proposed a deep learning RUL prediction method based on weighted sequence data representation. Different industrial sensors and time steps are weighted through a distributed attention mechanism. The time series is then feature-extracted using a time domain convolution module with shared weights. Zeng et al. [17] proposed a rotating machinery RUL prediction method based on a dynamic graph and spatiotemporal network (STNet), using a graph convolution network and Bi-LSTM to capture spatial and temporal correlations, improving prediction performance in single-sensor monitoring scenarios.

Additionally, with the recent development of sensor and data storage technology, a large amount of production process data has been generated, and existing methods still need to perceive adequate information in the data. Fully utilizing these data can significantly improve the reliability of equipment monitoring systems. Liang et al. [18] proposed a bearing RUL prediction method based on multi-sensor data fusion and a bidirectional temporal attention convolution network (Bi-TACN). They merged multi-sensor data into multi-channel data and combined it with channel weighting to improve the model’s feature extraction capability. Lei et al. [19] proposed an effective information extraction method for multi-dimensional data using a multi-head attention network. By adaptively evaluating and selecting features, feature information can be mined to reduce information loss. Ren [20] proposed a new industrial health indicator prediction network (MCTAN) based on multi-channel temporal attention. It uses channel attention and local attention mechanisms to effectively extract long-term temporal dependencies, improving the prediction accuracy of the multi-input model and reducing delayed predictions. In summary, the multi-input model can effectively improve the model’s data extraction capabilities.

However, despite the success of multi-branch, multi-input deep learning methods in RUL prediction for rolling bearings, some problems remain:

(1) Traditional single-channel networks can only extract features independently from each channel, which leads to a failure in fully capturing the potential correlations between different channels. The degradation process of rolling bearings is a complex and multi-dimensional phenomenon, with signals collected by different sensors often carrying complementary health condition information. Single-channel networks fail to fully utilize this information, resulting in feature extraction that is partial and not comprehensive enough.

(2) Data from different sensor channels may contain distinct fault features. If the correlations between channels are not fully explored, key information may be lost during feature fusion, leading to redundancy or missing important features. Moreover, current multi-channel networks often use static fusion methods that cannot adaptively adjust channel weights based on dynamic input, making it difficult to identify the most relevant features for RUL prediction.

This paper proposes a temporal feature fusion network based on multi-channel hybrid attention and a TCN to address these issues. It is designed to effectively fuse information from various channels and capture detailed patterns and correlations in complex datasets. This network model integrates channel attention with an enhanced TCN framework to mine spatial and temporal dependencies, achieving comprehensive feature extraction. The fusion process employs attention mechanisms and weighted aggregation, enabling the network to emphasize salient features dynamically. The contributions of this paper are as follows:

(1) A novel dual-channel fusion block is designed: The MCHA-TFCN block differs from the TCN block. The MCHA-TFCN block changes the single-channel input of the original TCN block to dual-channel and uses a Squeeze-and-Excitation Network (SENet) to extract channel weights, fusing the channel input into a single-channel output. Therefore, the MCHA-TFCN block can achieve the adaptive weighted fusion of two feature sets and reduce the number of channels. End-to-end fusion of multi-channel features is achieved by stacking MCHA-TFCN blocks.

(2) Features fused by channel attention are combined with the self-attention mechanism to improve the model’s perception of multi-dimensional degradation information, forming a spatiotemporal-level degradation perception.

(3) An MCHA-TFCN model for the RUL prediction of rolling bearings is proposed. This model consists of multiple MCHA-TFCN blocks, which integrate statistical features and deep feature mapping into the remaining service life of bearings, achieving better prediction results than advanced methods in experiments. The model’s success guides further research on multi-channel feature fusion and temporal feature learning in RUL prediction.

The rest of this paper is organized as follows: Section 2 briefly introduces the background knowledge, Section 3 details the proposed method, Section 4 verifies its performance on the bearing dataset, and Section 5 provides our conclusions.

2. Methodology

2.1. Temporal Convolutional Network

The TCN is a variant of the traditional CNN. It uses DCC and residual block stacking to expand the receptive field, addressing the limitation of the CNN in capturing long-term temporal dependencies from time series data compared to the RNN. It has recently been proven to be more accurate, simple, and precise than standard recurrent networks such as long short-term memory networks (LSTM) and CNNs on sequence data.

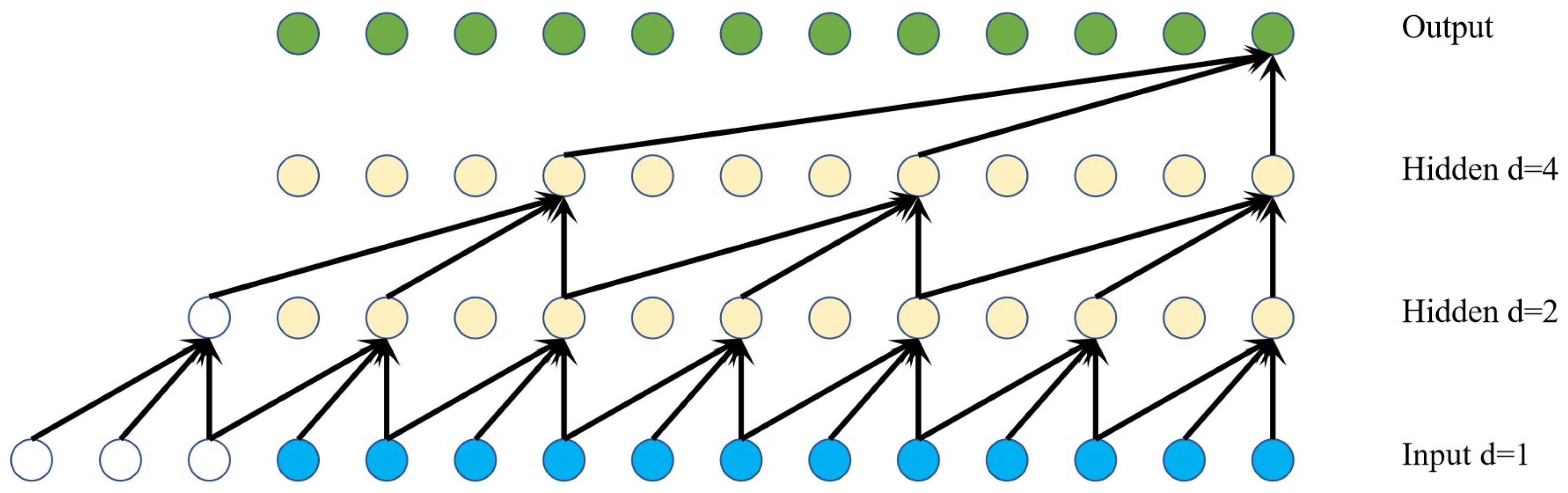
2.1.1. Dilated Convolution

Dilated convolution, also known as hole convolution, is a particular application of the convolution operation proposed by Oord et al. [21] to address the issue of the small receptive field in causal convolution. It is designed to increase the receptive field of the convolution layer, thus increasing the range of input data that each output unit of the network model can perceive. Dilated convolution expands the receptive field by inserting holes in the standard convolution kernel, thereby obtaining a more comprehensive range of input information without increasing the parameters or the computational load. As illustrated in Figure 1, a four-layer cubic convolution network is shown, where the white circles represent padding, the blue circles represent the input data, the yellow circles represent the hidden layer, and the green circles represent the output layer. The solid and dashed arrows represent the neurons directly involved in the convolution calculation. By comparing Figure 1 and Figure 2, it is evident that the receptive field corresponding to a single neuron in the output layer differs significantly. This difference increases exponentially with the number of convolution layers. The calculation formula for dilated convolution is as follows:

$$y\left(t\right)=\sum _{k=0}^{K-1}x(t+d·k)·w\left(k\right)$$

(1)

where $y\left(t\right)$ is the t-th element of the output sequence, $x\left(t\right)$ is the t-th element of the input sequence, $w\left(k\right)$ is the k-th element of the convolution kernel, d is the dilation factor, and K is the size of the convolution kernel.

2.1.2. Causal Convolution

Causal convolution was proposed by Long et al. [22] and later utilized in TCNs by Bai et al. [15]. The core concept of causal convolution is that the information at the current and preceding moments serves as the cause, while the predicted result serves as the effect. The expected outcome is solely influenced by the information at the current and preceding moments. Unlike the traditional RNN, which uses future and current data for prediction, causal convolution aligns more closely with the logic of RUL prediction. Additionally, compared to the serial structure of the RNN, causal convolution allows for parallel data processing, enhancing the efficiency of network computations. A structural diagram of dilated causal convolution combined with dilated convolution is shown in Figure 3. As illustrated in Figure 3, combining dilated causal convolution with dilated convolution increases the receptive field, enabling the model to understand better and predict dynamic changes in time series.

The calculation formula for dilated causal convolution is as follows:

$$y\left(t\right)=\underset{k=0}{\sum ^{K-1}}x(t-k)·w\left(k\right)$$

(2)

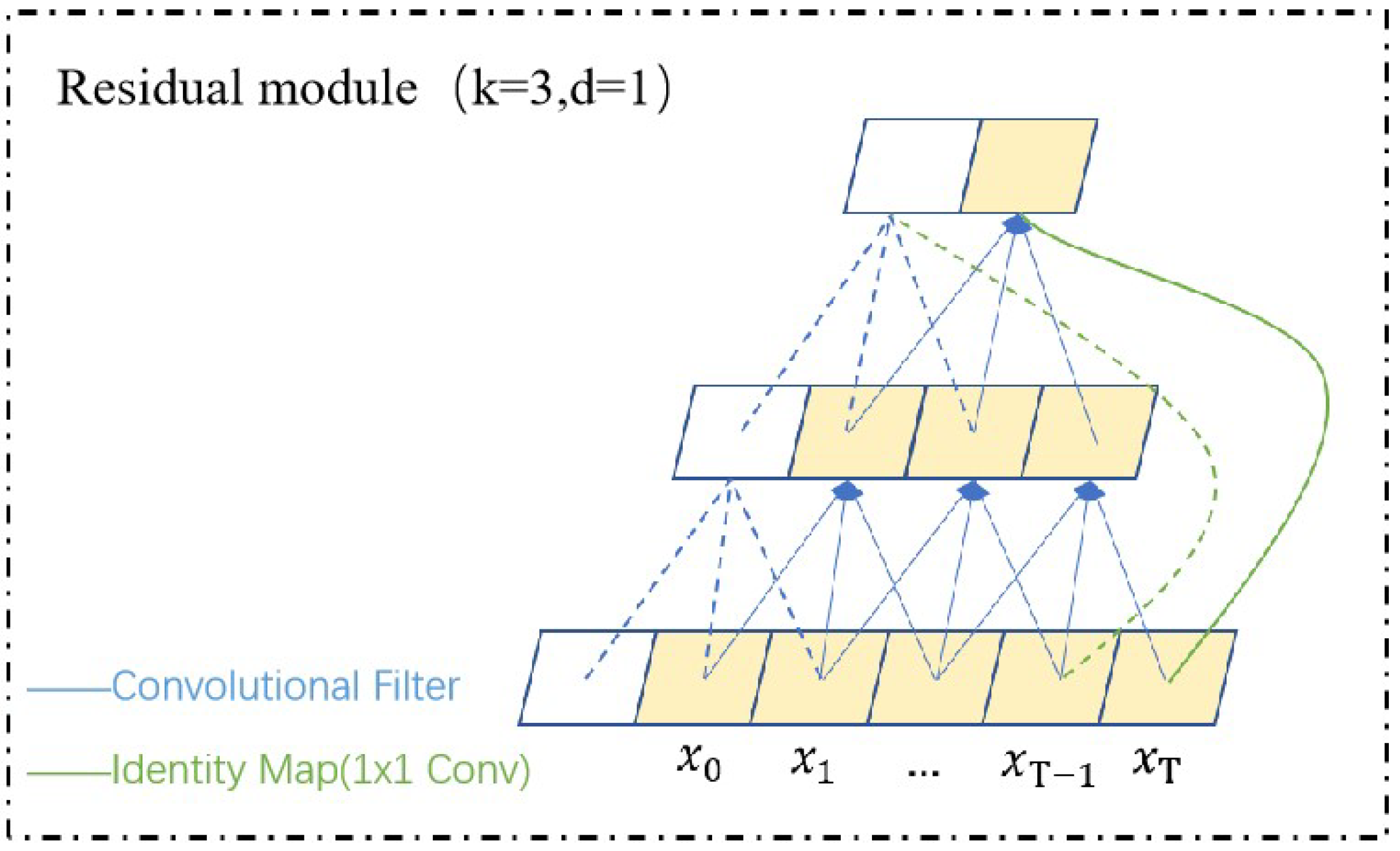
2.1.3. Residual Connection

The residual structure was first proposed by He et al. [23] to address the issues of gradient vanishing and network degradation due to increased network layers. The core idea of residual connection is to introduce a direct connection method that skips one or more layers, allowing the network input to be directly passed to the next layer. The calculation formula for residual connection is as follows:

$$y=F\left(x\right)+x$$

(3)

where $F\left(x\right)$ represents the processing of the input time series signal $x=\{x_0,x_1,x_2,\dots ,x_T\}$ by convolution, activation function, etc.

A 1 × 1 convolution block designs the residual connection to form an identity mapping. When the network gradient decreases sharply with increased network layers, the derivative can be regarded as “short-circuited”. The identity mapping replaces the original, maintaining network performance or preventing degradation. Thus, the depth of the network model can be increased effectively.

The TCN comprises several connected and stacked residual blocks, each primarily consisting of a dilated causal convolution layer, a weight normalization layer, a ReLU activation function, and a dropout layer [24]. Dropout is a commonly used regularization technique aimed at preventing neural network overfitting. The structure of the TCN residual block is illustrated in Figure 4.

The spatial topology of the TCN residual block with a dilation factor of 1 and a convolution kernel of 3 is illustrated in Figure 5.

For the multi-channel input characteristics in this study, the TCN can perform efficient parallel calculations and more stable gradient propagation than the RNN, avoiding gradient vanishing or explosion issues. Additionally, the predicted output of the TCN is not influenced by future data, aligning better with actual bearing operation data collection.

2.2. Attention Mechanism

The origins of attention mechanisms can be traced back to their successful applications in natural language processing. Inspired by the human visual system, Bahdanau et al. [25] designed an attention mechanism combined with a sequence-to-sequence (Seq2Seq) model, which enables the model to adaptively focus on the relevant part of the input sequence when generating each target word, thereby improving the translation quality. The attention mechanism has gradually diversified in recent years, and many variants and extensions have emerged. For example, the channel attention mechanism focuses on enhancing the importance of different channels in the feature map; self-attention [26] allows the model to consider the information of all positions in the sequence simultaneously when processing the sequence; and multi-head attention [27] captures the information of different subspaces in the sequence by using multiple self-attention as “heads” in parallel.

2.2.1. Channel Attention

The Squeeze-and-Excitation Network, also known as channel attention, was proposed by Hu et al. [28]. As shown in Figure 6, the channel attention mechanism mainly introduces nonlinearity by pulling up, compressing, and superimposing activation functions on the input multiple channel data and learns the weight of each channel to give high weights to channels with high influence and low weights to channels with low importance. By adjusting the contribution of multi-channel features through weighted channels, greater attention can be paid to channels that are more important to specific tasks.

The channel attention mechanism is mainly implemented through squeeze, excitation, and scale.

(1) The squeeze calculation formula is as follows:

$$z_c=F_{sq}\left(X\right)={\displaystyle \frac{1}{W}}\underset{i=1}{\sum ^W}{x}_c\left(i\right)$$

(4)

where $F_{sq}(·)$ is the squeeze function that compresses the feature matrix $X=[x_1,x_2,\dots ,x_c]\in {\mathbb{R}}^{W\times C}$ with channel count C and size $1\times W$ to a weight vector $z_C$ of size $1\times 1\times C$.

(2) The excitation calculation process is as follows:

$$s_{\mathrm{c}}=F_{ex}\left(z_c,W\right)=\sigma \left(g\left(z_c,W\right)\right)$$

(5)

where $F_{ex}(\cdot )$ is the excitation function that takes the C-dimensional vector $z_C$, obtained from global pooling in the squeeze step, and performs a fully connected operation to compress the dimensions to a $C/r$ dimensional vector. This vector is then activated by ReLU to increase nonlinearity, followed by another fully connected operation to restore it to a C-dimensional vector. Finally, sigmoid activation is applied (scaling the values between 0 and 1), resulting in the weight vector $s_{\mathrm{c}}$.

(3) The scale calculation formula is as follows:

$${\tilde{x}}_c=F_{\mathrm{scale}}\left(x_c,s_c\right)=s_c·x_c$$

(6)

where $x_c$ is a feature of channel C in the feature space X. The corresponding channel excitation value $s_c$ is applied to obtain the weighted feature ${\tilde{x}}_c$, resulting in the final weighted feature matrix

$$\tilde{X}=[{\tilde{x}}_1,{\tilde{x}}_2,\dots ,{\tilde{x}}_c]$$

2.2.2. Self-Attention Mechanism

Self-attention calculates the attention of each element relative to all other elements, allowing the model to capture the contextual relationship within the time series. Because the TCN has a vast receptive field compared to ordinary CNNs, combining self-attention can help it better learn the time series information of input features. At the same time, like the TCN, self-attention can parallelize computing and process feature information in parallel with the TCN to improve network operation efficiency. For the time series feature $X=\left\{x_1,x_2,\dots x_i,\dots ,x_n\right\},x_i\in R^d$, the query Q matrix, fundamental K matrix, value V matrix, and attention calculation formula can be expressed as

$$Q=X_f{W}^Q$$

(7)

$$K=X_f{W}^K$$

(8)

$$V=X_f{W}^V$$

(9)

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(10)

where $W^Q$, $W^K$, and $W^V$ are the weight matrices of the Q, K, and V matrices; $d_k$ represents the dimensions of Q, K, and V; $\mathrm{softmax}(·)$ is the function of the normalized attention weights; and $\mathrm{Attention}\left(Q,K,V\right)$ represents the weighted output.

3. RUL Prediction Method Based on MCHA-TFCN

3.1. Key Ideas

During the operation of mechanical equipment, sensors at different positions will generate multiple monitoring signals, which can be regarded as other characteristics of bearings. The existing life prediction methods are mostly single-channel information input, which cannot fully detect potential degradation information for feature information, and the serial processing efficiency of data is low. Therefore, it is necessary to build a multi-channel parallel computing prediction network.

This paper proposes a bearing life prediction method based on multi-channel feature fusion. By analyzing and processing different features and learning channel weight coefficients and feature weight coefficients through mixed attention, the valuable information of multi-dimensional features is retained to the maximum extent. To enhance the readability, Figure 7 outlines the main work of this paper. The process is mainly divided into three steps: (1) data processing, (2) prediction model construction, and (3) model training prediction. The details of the process are as follows.

3.2. Data Processing

The original vibration signal is usually high-dimensional and contains redundant information, making establishing an accurate degradation model difficult. Data processing can effectively reduce the data dimension and eliminate noise, which can help better capture the degradation information of the bearing. This paper processes the data to improve the prediction model’s reliability and stability. It uses the filtered time domain features combined with deep multi-scale features as the model input. The data processing process mainly includes data standardization and feature engineering. The details of the process are as follows:

(1) Data standardization:

$$x_{norm}^i\left(t\right)={\displaystyle \frac{x^i\left(t\right)-x_{mean}^i\left(t\right)}{x_{max}^i\left(t\right)-x_{min}^i\left(t\right)}}$$

(11)

where $x^i\left(t\right)$ and $x_{norm}^i\left(t\right)$ are the i-th values of the original and standardized feature sequences at time t, and $x_{mean}^i\left(t\right)$, $x_{max}^i\left(t\right)$, and $x_{min}^i\left(t\right)$ are the average, maximum, and minimum values of the i-th feature sequence values at all times, respectively. Because the life length of the bearing is inconsistent, to ensure the generalization performance of the model, the label is also standardized, and the formula is as follows:

$$Label\left(t\right)=1-{\displaystyle \frac{RU{L}_t}{RU{L}_T}}$$

(12)

where $RU{L}_t$ and $RU{L}_T$ represent the running time of the current sampling point time t and the complete failure time T, respectively.

(2) Feature engineering:

To construct a statistical feature pool, this paper uses a sliding window data processing method to extract time domain features such as the mean, variance, and root mean square from vibration data. It also uses feature screening indicators to screen out suitable time domain features. The application of feature screening enables the identification of degradation-relevant features, effectively reducing feature space dimensionality while optimizing predictive accuracy. This experiment uses correlation and monotonicity to form a comprehensive feature evaluation index to evaluate the features. The construction of feature screening indicators needs to fit the equipment degradation process, and suitable features should meet specific conditions:

(1) Correlation: the high correlation between the feature sequence and the performance change trend of the equipment.

(2) Monotonicity: degradation is an irreversible process.

Therefore, this paper uses comprehensive feature evaluation indicators to evaluate the features. The formula for comprehensive composite evaluation indicators $J\left(X\right)$ is as follows:

$$J\left(X\right)={\omega }_1{\mathrm{Cror}}_{1:k}+{\omega }_2{\mathrm{Mon}}_{1:k}$$

(13)

$$s.t\left\{\begin{array}{c}{\omega }_i>0\\ {\displaystyle \sum _i}{\omega }_i=1\end{array},i=1,2,3\right.$$

(14)

where ${\omega }_1$ and ${\omega }_2$ are the weight coefficients of the correlation coefficient index $Corr\left(\mathrm{X}\right)$ and the monotonicity index $Mon\left(\mathrm{X}\right)$, which are set to 0.6 and 0.4, respectively.

$$Corr\left(\mathrm{X}\right)={\displaystyle \frac{\left|K{\displaystyle \sum _i}{x}_i{t}_i-{\displaystyle \sum _i}{x}_i{\displaystyle \sum _i}{t}_i\right|}{\sqrt{\left[K{\displaystyle \sum _i}{x}_i^2-{\left({\displaystyle \sum _i}{x}_i\right)}^2\right]\left[K{\displaystyle \sum _i}{t}_i^2-{\left({\displaystyle \sum _i}{t}_i\right)}^2\right]}}}$$

(15)

$$Mon\left(X\right)={\displaystyle \frac{1}{K-1}}\left|{\displaystyle \sum _i}\epsilon (x_i-x_{i-1})-{\displaystyle \sum _i}\epsilon (x_{i-1}-x_i)\right|$$

(16)

where K represents the number of degradation features, $X=\left(x_1,x_2,\dots ,x_k\right)$ represents the obtained degradation feature sequence, $x_i$ represents the trend sequence of the obtained condition monitoring indicators, $\epsilon (·)$ represents the step function, ${\overline{x}}_i$ represents the smoothed degradation feature, and $T=\left(t_1,t_2,t_3\dots ,t_k\right)$ represents the corresponding time sequence.

To improve the quality of input features, enhance the performance and robustness of the model, and optimize the feature fusion effect, the filtered time domain features are combined with deep multi-scale convolution features as the input of the model. The original data are convolved with multiple convolution kernels of different sizes, and the ReLU function is introduced to provide nonlinearity and generate multi-scale deep features with different receptive fields.

The multi-scale convolution calculation formula is as follows:

$$y\left(i\right)=\sum _{m=0}^{k-1}x(i+m)\times w_j\left(m\right)$$

(17)

where, for a given one-dimensional input signal x and a one-dimensional convolution kernel of scale k, the output y of the convolution operation is the value at position i.

3.3. Construction of Prediction Model MCHA-TFCN

3.3.1. Design of Feature Fusion Module

To solve the problem of the incomplete and unbalanced feature extraction of different channel input degradation, this study proposes a novel dual-channel hybrid attention (DCHA) module by combining self-attention and channel attention mechanisms. This module aims to utilize these features better and enable the model to divide input data’s importance adaptively.

The design of the DCHA module is shown in Figure 8. In the dual-channel fusion module at the same level, one-channel attention is shared. When the dual-channel features are input, they are adaptively weighted with the input features at the same level, and the weighted features of the two are added together and then input into the self-attention module for feature fusion. This design aims to enable the high-level features obtained after fusion to consider global information better, thereby improving the model’s ability to understand and integrate information from different channels at the entire level.

$$A_i=\sigma \left(W_2\delta \left(W_1{g}_i\right)\right)$$

(18)

$$S_i=\mathrm{Attention}(F_i{W}_i^Q,F_i{W}_i^K,F_i{W}_i^V)$$

(19)

where $A_i$ represents the channel attention weight, $\delta$ represents the ReLU activation function, $\sigma$ represents the Sigmoid activation function, $g_i$ is the feature vector after pooling, $W_i^Q$, $W_i^K$, and $W_i^V$ are the weight matrices of the Q, K, and V matrices, respectively, and $S_i$ represents the corresponding self-attention feature matrix.

In the specific implementation process, self-attention captures the correlation of different positions in the input features. At the same time, channel attention helps to explore the information interaction between different channels. The DCHA module can more accurately capture the correlation between different channels by sharing channel attention weights, thereby improving the model’s feature fusion ability. This module reduces the number of model parameters while improving computational efficiency, providing an effective solution for improving the performance of the model’s adaptive partitioning of input data importance.

3.3.2. Feature Fusion Network Construction

To achieve the fusion of multiple channel features, this paper adds a DCHA module to the convolution block of the TCN and designs a dual-channel fusion module MCHA-TFCN structure based on hybrid attention. A structure diagram is shown in Figure 4, and the adaptive weighted fusion of $2^N$ features is achieved by stacking N layers of modules. Each residual block contains a multi-input dilated causal convolution layer, a dropout layer, and a batch normalization layer and uses a residual method to connect the input and output of the residual blocks of different layers; the output of the two residual blocks at each level is the input of the residual block of the next layer. The feature fusion calculation process of the MCHA-TFCN module for the input channel feature $X_i$ is shown in Formulas (20) and (21).

$$F_{\mathrm{fusion}}=A_i\odot S_i+A_{i+1}\odot S_{i+1}$$

(20)

$$o=Activation\left(X_i+X_{i+1}+F_{\mathrm{fusion}}\right)$$

(21)

where $A_i$ and $A_{i+1}$ represent the channel attention weight and the corresponding feature matrix after self-attention processing, $F_{fusion}$ represents the fused features, ⊙ means the element-by-element multiplication, $X_i$ and $X_{i+1}$ are the features to be fused, and o is the output.

Multi-channel feature fusion is achieved by continuously stacking the MCHA-TFCN dual-channel fusion module to form the MCHA-TFCN framework. The overall structure of the model is shown in Figure 9. Figure 9 describes the specific structure of the developed MCHA-TFCN, which consists of three modules, namely the feature extraction module DCHA that combines multi-head attention and channel attention, the feature fusion module of the MCHA-TFCN module for stacking, and the dense layer that maps the features to the remaining lifespan. The dense layer (Dense) consists of a fully connected layer, an activation function (PReLU), and a dropout layer, as shown in

Table 1. Parameters of dense mapping layer.

No.	Layer	Setting Value
1	Linear	2560, 256
2	BatchNorm1d	256
3	Tanh	/
4	Dropout	0.2
5	Linear	256, 1
6	PReLU	/

. The dropout layer plays a role in regularization to reduce overfitting, and the PReLU function improves the gradient disappearance problem.

According to the above network structure, the RUL prediction algorithm based on MCHA-TFCN can be simplified into a pseudo-code, as shown in Algorithm 1.

Algorithm 1 RUL prediction method based on MCHA-TFCN
Input:	Training set data for a single working condition: $X_{\mathrm{train}}$, and corresponding labels Y.
Output:	MCHA-TFCN model trained under a single working condition.
Training:
1	Initialize the network parameters of the feature acquisition module and MCHA-TFCN.
2	for epochs $=1,2,3,\dots$, max do:
3	Input training data $X_{\mathrm{train}}$ in batch order into the model to be trained.
4	Extract time domain and multi-scale depth features, and output a multi-dimensional feature sequence ${\tilde{x}}_i$ to be fused.
5	During the network forward propagation process, Formulas (18) and (19) are used to weight the input features, and Formulas (20) and (21) are used to perform feature fusion.
6	Calculate the loss of the predicted result and the actual label (MSELoss).
7	Use the Adam method to back-propagate and update the model parameters.
8	end for
9	Save the trained network structure.
Test:
10	Input the test data $X_{\mathrm{test}}$ into the model to obtain the prediction results $\widehat{Y}$.
11	Evaluate the prediction effect of the model based on the evaluation index (RMSE).

4. Verification

4.1. Dataset Description

The performance evaluation of our proposed methodology was conducted on the IEEE PHM2012 challenge dataset, with particular emphasis on feature fusion effectiveness and prediction accuracy for rolling bearing RUL estimation. Figure 10 depicts the experimental configuration.

The experimental equipment mainly consists of three functional modules: the rotation module, radial force loading module, and measurement module. The platform accelerates the degradation of the simulated bearing by applying different radial forces and using different speeds on the tested bearing. It is categorized into three working conditions based on the magnitude of the force and the speed. The division of the dataset adopts the division scheme set by the competition. The specific information is shown in

Table 2. PHM 2012 dataset partitioning.

Task	Conditions	Train	Test
Task-I	Load (N): 4000; Speed (r/min): 1800	B1_1-B1_2	B1_3-B1_7
Task-II	Load (N): 4200; Speed (r/min): 1650	B2_1-B2_2	B2_3-B2_7
Task-III	Load (N): 5000; Speed (r/min): 1500	B3_1-B3_2	B3_3

.

The measurement module mainly consists of two vibration sensors to collect the horizontal and vertical vibration signals of the tested bearing, and the axial and radial vibration signals are sampled on the bearing installation, with a sampling frequency of 25.6 kHz. The data collector collects and records 0.1 s samples every 10 s, that is, 2560 data points. The actual value of the bearing life is the time of the entire operation process of the bearing from the initial state to failure. The experimental end condition set by the accelerated experimental device is that the amplitude of the vibration signal exceeds 20 g.

4.2. Implementation Details

The input and output data structure of the proposed method and the corresponding module are shown in

Table 3. Input and output data structure of MCHA-TFCN.

Module	Input-Size	Output-Size
Feature input	32, 2, 2560	16, 32, 1, 2560
MCHA-TFCN-I	16, 32, 1, 2560	8, 32, 32, 2560
MCHA-TFCN-II	8, 32, 32, 2560	4, 32, 128, 2560
MCHA-TFCN-III	4, 32, 128, 2560	2, 32, 64, 2560
MCHA-TFCN-IV	2, 32, 64, 2560	32, 32, 2560
AdaptiveAvgPool1d	32, 32, 2560	32, 1, 2560

. The RMSE is used in this paper as the model’s loss function, and the Adam optimizer is used to update the model parameters. The grid search method is used to obtain the hyperparameters of MCHA-TFCN. The setting of the hyperparameters is shown in

Table 4. Hyperparameter settings.

Hyper-Parameter	Input-Size
Batch size	32
Max epochs	300
Initial learning rate	0.1
Gamma	0.1
Milestones	10, 100, 150, 200
Number of features to be fused	$2^n,n=4$
Kernel sizes of multiscale conv1d layers	$1\times 1,3\times 1,13\times 1,31\times 1$
Strides of multiscale conv1d layers	1, 1, 2, 2
Hidden channel list of MCHA-TFCN	[32, 128, 64, 32]
Self-attention	$a_k=2560,2560,2560$
Dropout rate	0.2

. The dynamic learning rate adjustment method changes the learning rate size when the model reaches the milestone number and the model parameters have been fine-tuned. The time domain feature input of the model is the top four time domain features selected according to the screening index, namely kurtosis, peak-to-peak value, root mean square, and mean.

4.3. Effect Verification

There are two primary purposes of the experimental part. The first is to verify the effectiveness of the proposed MCHA-TFCN method for multi-channel feature fusion. The second is to verify the accuracy of the model for RUL prediction.

(1) Effectiveness Verification

Given the effectiveness of feature fusion, the model is subjected to ablation experiments to verify the effectiveness of the proposed feature fusion module. In the ablation experiment, all test networks use the same network parameter configuration as MCHA-TFCN. Specifically, this experiment systematically compares the following three models: the MCHA-TFCN model, the TCN combined with the self-attention mechanism (i.e., TCN + SelfAT), and the essential TCN input.

To avoid randomness in the experimental results, the experiment repeated the prediction results of MCHA-TFCN five times and took the average as the final result. At the same time, for the TCN and TCN + SelfAT with single-channel input, this experiment input the filtered statistical features and multi-scale deep features into the network and, in turn, took the average of the output results. This operation was intended to eliminate the interference of prediction results caused by the difference in input data between the MCHA-TFCN and TCN. The experimental results are shown in

Table 5. Ablation experiment (condition 1).

Test	RMSE
	TCN(1)	TCN(2)	TCN-SA	MCHA-TFCN
1–3	0.355	0.194	0.157	0.109
1–4	0.303	0.115	0.105	0.044
1–5	0.209	0.188	0.130	0.118
1–6	0.220	0.155	0.139	0.126
1–7	0.097	0.150	0.109	0.057
Avg	0.237	0.151	0.128	0.091

and

Table 6. Ablation experiment (condition 2).

Test	RMSE
	TCN(1)	TCN(2)	TCN-SA	MCHA-TFCN
2–3	0.409	0.227	0.230	0.102
2–4	0.346	0.106	0.164	0.117
2–5	0.216	0.187	0.176	0.099
2–6	0.257	0.218	0.142	0.104
2–7	0.293	0.183	0.248	0.108
Avg	0.304	0.184	0.190	0.106

.

In Table 5 and Table 6, TCN(1) represents the traditional TCN whose input data are the deep features of a single channel, and TCN(2) represents the average result obtained when the input data are the time domain feature kurtosis, peak-to-peak value, root mean square, and mean value input into the traditional TCN in turn.

According to the data in the table, by comparing the results of taking the average of the deep features of the single-channel input of the TCN and the multiple time domain feature inputs with the results of the proposed method, it can be seen that MCHA-TFCN can effectively fuse multi-dimensional features, has a good feature enhancement effect, and can obtain more information related to degradation.

(2) Prediction accuracy comparison experiment

To prove the superiority of the proposed MCHA-TFCN, the MCHA-TFCN is compared with four advanced feature fusion models (i.e., CNN-LSTM, Bi-TACN [26], DANN [29], and TCN-SA [30]) in the experiment. These algorithm models are compared on the bearing test sets of working conditions 1 and 2. Comparison tables of the evaluation index RMSE results are shown in

Table 7. Comparison of RMSE results (condition 1).

Test	CNN-LSTM	DANN	TCN-SA	Bi-TACN	MCHA-TFCN
1–3	0.126	0.335	0.117	0.090	0.109
1–4	0.107	0.251	0.085	0.113	0.044
1–5	0.152	0.216	0.086	0.090	0.118
1–6	0.154	0.209	0.101	0.016	0.126
1–7	0.129	0.192	0.129	0.149	0.057
Avg	0.127	0.222	0.104	0.114	0.091

and

Table 8. Comparison of RMSE results (condition 2).

Test	CNN-LSTM	DANN	TCN-SA	Bi-TACN	MCHA-TFCN
2–3	0.174	0.168	0.230	0.203	0.102
2–4	0.136	0.106	0.064	0.137	0.117
2–5	0.150	0.228	0.150	0.176	0.099
2–6	0.167	0.237	0.154	0.142	0.104
2–7	0.183	0.192	0.263	0.248	0.108
Avg	0.162	0.186	0.172	0.181	0.106

.

From the RMSE comparison results, the RMSE of the proposed method is worse than that of the other methods. However, some individual data performance could be better than that of different methods; overall, it is better than the other methods. From the comparison of the average RMSE under working condition 1 and working condition 2, it can be seen that MCHA-TFCN can predict the degradation trend of all tested bearings, indicating that MCHA-TFCN is effective in bearing RUL prediction. Therefore, the proposed MCHA-TACN bearing RUL prediction method can fuse the bearing degradation information with time and space perception from the multi-channel feature data under a single working condition and maximize the valuable information of multi-dimensional features while improving the prediction effect of the model under a single working condition.

4.4. RUL Estimation Results and Analysis

After processing the bearing data of working condition 1 and working condition 2 in the test set, we input them into the prediction model of the corresponding working condition that was trained, and obtained the prediction result diagram shown below.

As shown in Figure 11a–e, warping occurs in the last rapid degradation stage of bearings 1–3, 1–5, and 1–6, but is slightly lacking. Still, the overall prediction result of working condition 1 has a good fit with the real-life label. It can be seen from Figure 12a–e that the bearing prediction curves all fluctuate slightly near the actual value of RUL, and the curve fitting degree is high, which shows good performance.

The proposed method can accurately reflect the degradation trend for model training under a single working condition. This shows that the high-level features fused by the MCHA-TFCN prediction model can effectively reflect the degree of bearing degradation under a single working condition.

The above experimental results show that the proposed MCHA-TFCN remaining service life prediction method not only has an excellent weighted fusion effect for multi-channel features, but also has a good ability to extract spatiotemporal features and has high accuracy in RUL prediction for a single working condition.

5. Conclusions

The RUL prediction of rolling bearings is an essential component of health management systems for rotating parts and is of great significance for reducing or even avoiding equipment failures. The proposed architecture addresses several critical challenges in RUL prediction through methodological advances. A dual-channel fusion module with Squeeze-and-Excitation Networks (SENet) enables the adaptive weighted fusion of sensor channel features, while a hybrid attention mechanism combining self-attention and channel attention enhances the model’s ability to interpret multi-dimensional degradation features. The improved temporal convolutional network (TCN) framework with attention mechanisms achieves more effective modeling of long-term temporal dependencies in bearing degradation processes. The prediction results demonstrate that the MCHA-TFCN model achieves lower RMSE and evaluation scores superior to those of several existing prediction methods.

While these preliminary results are promising, several methodological limitations require careful consideration. The multi-channel hybrid attention mechanism introduces significant computational demands, requiring substantial resources and extended training periods. The framework demonstrates sensitivity to data quality and sensor integrity, where feature extraction may be compromised by signal noise. The current validation remains limited to specific operational conditions, suggesting the need for broader evaluation across different bearing types and operating scenarios. The complex architecture also presents challenges for real-time applications, requiring a careful balance between prediction accuracy and computational efficiency in industrial settings.

Future research could address these limitations through several key approaches. The development of computationally efficient attention mechanisms and robust feature extraction methods may help maintain predictive performance while reducing computational demands. The framework’s generalization capability might be improved through transfer learning strategies and validation across diverse operational conditions. Engineering implementation could benefit from distributed computing frameworks and adaptive parameter optimization. Data quality enhancement could be pursued through advanced signal processing, while fusion optimization might be achieved through novel feature fusion strategies and multi-modal information integration.