Abstract
Self-assembly of nanoscale objects is of essential importance in materials science, condensed matter physics, and biophysics. Curvature modifies the principles and sequence of self-assembly in Euclidean space, resulting in unique and more complex structures. Understanding self-assembly behavior in curved space is not only instrumental for designing structural building blocks and assembly processes from a bottom-up perspective but is also critically important for delineating various biological systems. In this review, we summarize efforts made to unveil the physical nature of self-assembly in curved space through experiments and simulations. First, we outline the differences in the physical nature of self-assembly between curved space and Euclidean space by presenting relevant results of experiments and simulations. Second, we explore the principles of self-assembly in curved space at multiple scales and interactions, elucidating important factors that govern the self-assembly process from the perspectives of confinement and structural building blocks. Finally, we enumerate practical applications and control strategies for self-assembly in curved space and outline the challenges and prospects in this field. We hope that this review will encourage further efforts toward fundamental research and broaden the potential applications of designed assemblies in curved space.
1. Introduction
Self-assembly refers to the process by which disordered systems, without external intervention, organize into an ordered structure through interactions among their constituents [1,2,3]. This process is driven by thermodynamic equilibrium, with the organized structure possessing the lowest free energy within the system. Colloids refer to fluid mixtures in which dispersed particles have sizes ranging from 1 nm to 1 μm, which are commonly found in the natural world and biological systems. When colloidal particles aggregate, many fascinating phenomena, including self-assembly, can emerge. In contrast to atomic and molecular systems, the self-assembly of colloidal particles predominantly relies on forces such as DNA-mediated interactions [4], van der Waals forces [5], electrostatic interactions [6], and hydrophobic effects [7]. These forces are considerably weaker than chemical bonds [8] and, thereby, cannot entirely dictate the formation of the most stable structure. Thus, entropy plays an indispensable role in the self-assembly of colloidal particles. Self-assembly phenomena are abundant in biological systems, such as viruses [9], bacteria [10], and living cells [11], and a comprehensive understanding of these processes is essential for unraveling the complexity of life. These instances of self-assembly can serve as a source of inspiration for the design of biomimetic systems or play a role in medical applications like targeted drug delivery. However, biological systems often feature numerous curved interfaces, and the presence of interfaces frequently exerts a profoundly influential and determinative impact on the overall system’s properties. The introduction of curvature significantly enriches the processes and outcomes of self-assembly. Due to the mismatch between locally favorable structures and curved space or the hindrance of evolution paths by curvature, ordered structures [12,13], phase transitions [14,15], and dynamic processes [16] in curved space differ significantly from normal space. Additionally, the inherent defects brought about by topology create new order structures and generate new physics, making topology an equally important controlling factor alongside free energy. In recent years, the field of interface self-assembly at the nanoscale has gradually emerged [17,18], where curved interfaces often serve as scaffolds for nanodevices, functioning as constraints and templates [19,20,21,22]. At the same time, with the development of nanoscale synthesis methods [23], the variety of particles involved in self-assembly has greatly expanded, including grafted particles [24], Janus particles [25], various shapes of hard particles [26,27,28], mesoporous particles [29], and more. This enables more precise, complex, and widespread self-assembly. Therefore, understanding the physical processes of particle self-assembly in curved space is of great significance, aiding in the design of new heterogeneous materials or offering new perspectives on some biological processes.
In this review, we focus on the physical principles and practical applications of nanoscale particle self-assembly in curved space and propose control strategies for self-assembly systems in such space. Firstly, we introduce recent important experimental and simulation research, highlighting the physical rules of self-assembly in curved space and emphasizing the fundamental differences from Euclidean space through comparisons. Then, we delve into specific factors that influence self-assembled structures and processes, including the shape of confined interfaces, the interplay between colloidal particles and interfaces, and the properties of colloidal particles, as shown in Figure 1. Finally, we enumerate practical applications and control strategies for self-assembly in curved space and present the challenges and prospects that require further exploration in this field. It is anticipated that this review can offer new perspectives on many physical phenomena and provide theoretical guidance in the design of novel materials.
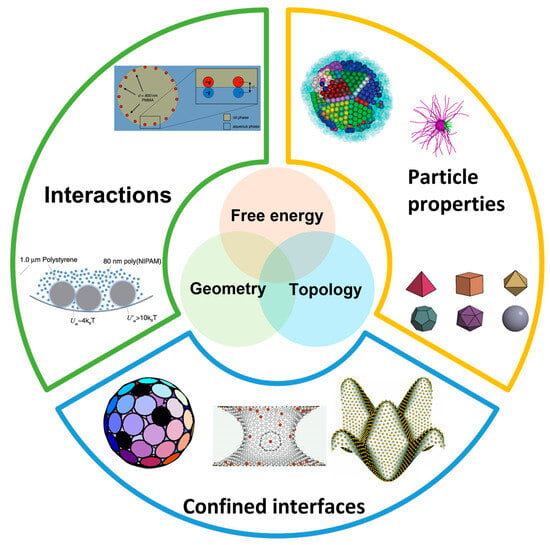
Figure 1.
Control Strategies for Self-Assembly in Curved Spaces: The regulation of self-assembly in curved space is influenced by three key factors—namely, the shape of the curved interface, particle properties, particle-particle interactions, and particle-interface interactions. These factors collectively impact the overall topological structure, local geometric arrangement, and free energy, ultimately determining the outcomes of self-assembly [9,13,14,30,31,32,33,34]. Here, “topological structure” refers to the shape of the space in which self-assembly occurs, and “geometric” refers to the local curvature size.
2. Colloids in Curved Space
In this section, we provide a brief overview of cases of colloidal particle self-assembly in two-dimensional (2D) and three-dimensional (3D) curved spaces. We summarize the fundamental physical rules of self-assembly in curved space and the influence of curvature. This helps illustrate how curvature can be used to control the outcomes and processes of self-assembly.
Consider identical hard disks packing on a 2D plane. In the densest packing arrangement, these particles naturally form a hexagonal lattice structure, with each particle having six nearest neighbors, and the hexagons can densely cover the entire 2D space. When the plane becomes curved, the introduction of curvature changes the distance distribution among the particles because the sum of the interior angles of curved triangles is not equal to π. This alteration in distance distribution results in a change in the number of nearest neighbors for the particles. By using the Voronoi partition, we can determine the number of nearest neighbors for each particle, denoted as c, which corresponds to the number of edges of the Voronoi polygons surrounding the particle. The basic idea is to create polygons around each seed point in such a way that every point within a given polygon is closer to the associated seed point than to any other seed point. Particles with a number of nearest neighbors different from 6 are referred to as defects, and the charge of a defect is defined as . On a plane, the appearance of defects is only related to the density and polydispersity of particles. Regular and dense crystals are formed at high density. Determining the type and quantity of defect particles on a curved surface requires applying Euler’s formula, which relates the number of vertices (V), edges (E), and faces (F) of Voronoi polygons in a network:
is the Euler characteristic, determined by the shape of the curved surface. If we replace V, E, and F in the Euler formula with the number of edges per Voronoi polygon c and the number of Voronoi polygons Nc, we can obtain the total defect charge determined by topology:
Indeed, you can relate curvature and the Euler characteristic using the Gauss-Bonnet theorem. The theorem states that for a closed surface M with Gaussian curvature K, the Euler characteristic is related to the total Gaussian curvature over the entire surface:
where dA represents the area element of the surface and ds is the line element of the boundary of M. This equation provides a valuable relationship between geometry and topology. For a sphere, , and 12 pentagon defects can form a regular icosahedron structure. For a cylinder and a plane, the Gaussian curvature is zero everywhere, which allows particles to form a defect-free perfect structure. For surfaces with negative curvature, , and heptagon defects may dominate. In crystallography, isolated defects that alter the rotational symmetry are referred to as disclinations [35], while defects formed by the connection of a pentagonal and heptagonal defect, disrupting translational symmetry, are known as dislocations. Dislocations, having positive and negative charges that cancel each other out, do not have a necessary topological existence. They appear to accommodate variations in curvature, driven by local geometric requirements and are consequently referred to as excess defects.
Irvine et al. [13,36] further investigated the relationship between the total defect charge and interface shape by confining fluorescent PMMA particles to interfaces of various shapes, including spherical, arched, waist-shaped, barrel-shaped, and planar, as shown in Figure 2b. The topological shape of the interface dictates the total defect charge. For interfaces of different shapes, whether with charged or neutral particles, the total defect charge is approximately equal to the integral of the interface Gaussian curvature. The presence of defects is analogously likened to pleats, and they adapt to the rapid changes in surface curvature by forming continuous dislocations. Subsequent simulations have confirmed and expanded upon these experimental findings [37]. The type, location, and orientation of defects are closely related to the curvature. Under weak curvature, excess defects like pleats appear, with their orientation following the direction of the fastest Gaussian curvature change, while under strong curvature, disclinations arise near regions of maximum (minimum) curvature.
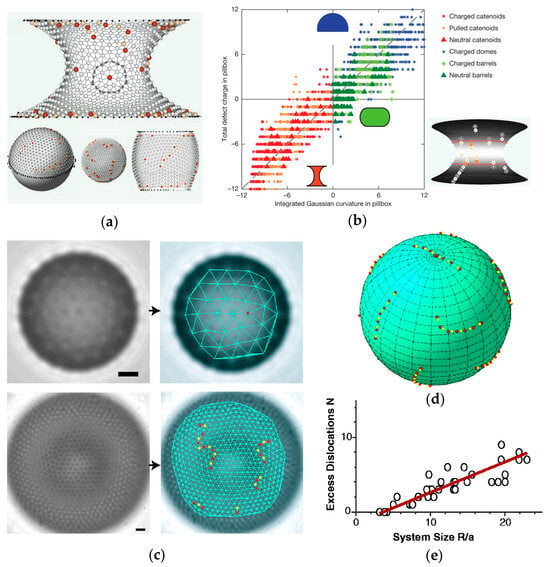
Figure 2.
Self-assembled structures in curved spaces [12,13]. (a) Interfaces are in the shape of spheres, domes, waists, and barrels on cylindrical capillary bridges. The red dots represent heptagonal defects, and the yellow dots represent pentagonal defects. (b) The total defect charge is linearly related to the Integrated Gaussian curvature. (c) Defects are identified using spherical triangulation, where disclinations appear when there are fewer particles, and scars appear when there are more particles. Bars, 5 μm. (d) The twelve scars on the spherical surface exhibit an icosahedral structure. (e) The excess number of defects is linearly related to the size of the constrained spherical surface.
Although the aforementioned studies provide a clear topological relationship between the total defect charge and interface shape, in specific systems, the number and spatial arrangement of each type of defect still depend on the potential energy interactions between particles and local geometric requirements. This is exemplified by the scar-like structures on a spherical surface. Bausch et al. [12,38] explored the self-assembly of colloidal particles with arbitrary repulsive interactions on a constrained spherical surface, where 1 µm diameter cross-linked polystyrene microspheres adhered to the surface of water droplets with a radius R. As shown in Figure 2c, when the number of particles is low, the spherical surface exhibits only 12 + 1 charge defects. However, when the number of particles exceeds a critical value (N ≈ 360), additional defect structures emerge. Defining a as the average distance between particles, it was discovered that the excess dislocation count is linearly related to R/a. In other words, on a larger constrained spherical surface, there are more defects. Observing the distribution of defects further reveals that they exist in the form of scars. On each scar, the coordination number of particles varies as … 5-7-5-7-5 … The total defect charge on each chain of defects is +1. The locations of the twelve scars correspond to a regular icosahedral structure.
On the one hand, these scars act as grain boundaries between different crystal regions, causing a change in crystal axis orientation whenever the crystal axis extends to the scar’s position to adapt to the curvature of the sphere. On the other hand, the presence of these scars serves to reduce the elastic energy loss caused by individual pentagonal defects. Using elastic theory [39], it can be calculated that the length of each scar in the ground state should be 33.56°. Therefore, the number of excess defects on the sphere follows a linear relationship with R/a.
From these studies, it can be concluded that the self-assembly in curved space results from the interplay between locally favorable structures, topology, and geometry. This principle applies to 3D space as well. Taking the example of hard sphere packing, as the packing density increases, the system enters an ordered structure at a packing density of approximately 0.64 [40] and eventually forms a face-centered cubic (FCC) or hexagonal close-packed (HCP) structure at a packing density of 0.74 [41,42,43]. Although FCC and HCP structures are energetically favorable, they cannot perfectly fill the entire spherical space, especially under strong confinement. As shown in Figure 3b, to maximize each particle’s free volume or entropy, the structure that aligns better with spherical symmetry is the icosahedron. However, as the degree of confinement decreases with a larger sphere, the system transitions from the icosahedron structure through a rhombicosidodecahedron structure to an FCC structure [31]. The observation of such structures changing with the degree of confinement has also been observed in simulations of cylindrical confinement [44]. This phenomenon is not limited to spherical confinement but is a general characteristic of self-assembly in 3D confined spaces. The dynamics of this crystallization process, as revealed through event-driven molecular dynamics (EDMD) simulations, suggest that the crystallization initiates at the spherical-constrained surface, forming multiple layered structures inward.
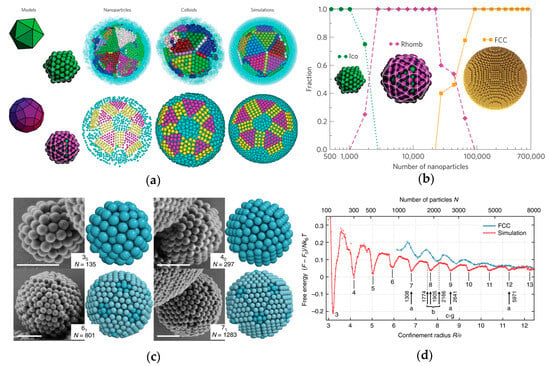
Figure 3.
Self-assembly of hard spheres by spherical confinement [31,45]. (a) Results of CoFe2O4 nanoparticles self-assembled in an emulsion and EDMD simulation. When there are fewer particles, they form an icosahedral structure. As the number of particles increases, a rhombicosidodecahedron structure forms on the surface of the icosahedral core. With further particle increase, an FCC structure is formed. The different colors represent different crystal regions distinguished by bond order parameters. (b) The fraction of various structures as a function of the number of particles. (c) Library of magic number colloidal clusters and a comparison to the model, bars, 1 μm. (d) Free energy was obtained from EDMD simulations as a function of the number of particles and the spherical confinement radius compared to the FCC structure. The free energy is at a local minimum when the number of particles matches the magic number.
In addition to the changes in self-assembled structures, another characteristic of 3D confined self-assembly is the presence of numerous local optimal structures. The number of particles at specific values forms self-assembled structures with better compatibility with spherical symmetry, known as the magic number [46,47]. Whether under attractive potentials or hard interactions, as shown in Figure 3d, these structures often have enhanced stability, higher packing densities, and average particle-free energy at a local minimum due to maximizing the number of neighboring particles [45]. Not only within a sphere but also within a cylindrical confinement, an optimal cylinder radius exists that maximizes the packing density to achieve a local maximum [48,49,50,51].
In addition to structural, the influence of curvature on self-assembly is also reflected in deeper aspects, such as phase transitions and crystallization dynamics. Phase transitions in 2D systems differ from those in 3D space, and there are various microscopic theories for 2D phase transitions, with the KTNHY theory being the most famous [52,53,54]. This theory predicts that phase transitions in 2D space are mediated by defects and involve two continuous processes: the unbinding of dislocation pairs disrupts translational symmetry while preserving orientational symmetry, leading the system from a solid phase to a hexatic phase. The separation of dislocations forms disclinations, breaking orientational symmetry and transitioning the system into a liquid phase. As shown in Figure 4, on a spherical surface, particles with dipole potentials undergo phase transitions as the dimensionless interaction parameter Γ changes, and both crystallization and melting processes follow the KTNHY theory [14,15]. However, due to the presence of inherent defects, the potential strength required for phase transitions differs from the results on a flat plane [55], and the curvature, to some extent, hinders crystallization. During the crystallization process, defects that occur in normal positions are eventually absorbed by grain boundaries, leading to the formation of the twelve scars. This has been confirmed in interstitial experiments on curved surfaces [56,57], where dislocations are more likely to move in the direction parallel to Burger’s vector [16] and are subsequently absorbed when they reach a grain boundary. However, what is surprising is that during the melting process, the positions where free dislocations are generated are unrelated to grain boundaries. Instead, they randomly occur within the regular hexagonal lattice.
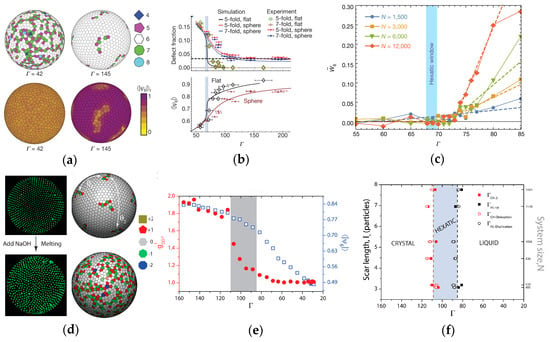
Figure 4.
KT Phase Transition on a Spherical Surface [14,15]: (a–c) depict the crystallization process, while (d–f) illustrate the melting process. (a) With increasing Γ, the number of defects decreases (top), and the bond order parameter of particles increases (bottom). (b) The variation in the fraction of defects (top) and the average bond order parameter (bottom) on both a flat plane and a spherical surface as a function of Γ. Changes on the spherical surface are slower compared to the flat plane. (c) The overall icosahedral symmetry of defects as a function of Γ, icosahedral symmetry appears in the solid phase. (d) Melting of particles on the spherical surface by screening charges with the addition of NaOH, defects obey icosahedral symmetry in the solid phase. (e) The first peak of the radial distribution function for defects and the average bond order parameter as a function of Γ indicate two distinct phase transition processes.
In Euclidean spatial crystallization, nucleation theory is often used to explain the process. In confined spaces, however, crystallization frequently initiates at the outer layers near the confining interface and progresses inward, resulting in the formation of complex multi-layered structures [26,31,58,59]. The curved interface acts as a template, influencing the final crystalline structure. When hard spheres crystallize within a sphere or a cylinder [31,44], they first form distinct crystal domains on the surface, and then the growth occurs inward. The competition and matching between the external and internal structures determine the final structure. In the case of systems with potentials, the situation is even more complex [58], and this competition exists in both thermodynamic and kinetic aspects. Crystallization initially occurs on the surface in the form of defects with icosahedral symmetry. It then grows inward through body-centered cubic (BCC) solid metastable states. Over an extended period, the structures formed by shorter-range (harder) interaction are predominantly FCC but are separated into icosahedral symmetry regions by the HCP domain. The structures formed by longer-range (softer) interactions are closer to BCC single-crystal.
3. Factors Controlling Self-Assembly in Curved Spaces
In this section, we discuss the specific control factors influencing self-assembly in curved spaces. As shown in Figure 1, there are three primary aspects: (1) interactions between particles and between particles and interfaces; (2) particle properties, including their shape and hardness; and (3) the shape of the confined interface or the curvature of the space, acting as a template, influencing the overall topological structure and local geometric properties. These three factors control the self-assembly process and resulting structures by affecting the three key factors discussed in the previous section: free energy, topological structure, and local geometry.
Interactions. Regarding self-assembly on curved interfaces, there exists a longstanding inquiry known as Thomson’s Problem [60,61,62]: Given N unit point charges positioned on the surface of a unit conducting sphere, what is the configuration that minimizes Coulombic energy? This classical problem has led to various extensions, encompassing generalized forms under different potential functions [63,64]. When particles self-assemble on a curved interface, the form of the potential significantly impacts the ground-state structure [65]. For pairwise repulsive potentials, one of the simplest forms is power-law potentials , in which e represents a generalized electric charge. The case γ = 1 corresponds to the pure Coulomb potential appropriate for charged colloids [60]. The case γ = 3 corresponds to a dipole interaction appropriate for neutral colloids at the interface between two liquids [14,15,55,66,67]. The different dielectric constants of the two liquids lead to an asymmetric distribution of charge on the colloids and a net dipole moment. The case γ = 12 is the repulsive part of the Lennard–Jones potential and is the important piece of the interaction for driving crystallization [68,69].
Particles typically form stable structures through repulsive interactions; however, when much smaller depletants are present in the system, depletion effects induce attractive interactions between colloidal particles as well as between particles and interfaces [70], causing colloidal particles to aggregate and crystallize on the interface. The depletion effect is a result of an effective, attractive force that occurs between large colloidal particles or macromolecules in the presence of smaller, non-adsorbing particles (depletants) in the surrounding solution [30]. The crystallization process on a curved surface differs from that on a flat surface. As shown in Figure 5C, on a flat surface, according to classical nucleation theory, the crystal region will spontaneously continue to grow once it exceeds the critical radius. However, on a curved surface, due to the presence of bending energy, the crystal region cannot grow indefinitely. Instead, like a brittle material pressed onto a curved surface, fractures form to create striped crystallization patterns. The overall structure does not contain defects but rather many voids (Figure 5A). If the crystal is flattened back onto a plane, the lattice axes remain mutually parallel (Figure 5B); this phenomenon is termed elastic instability [30,71].
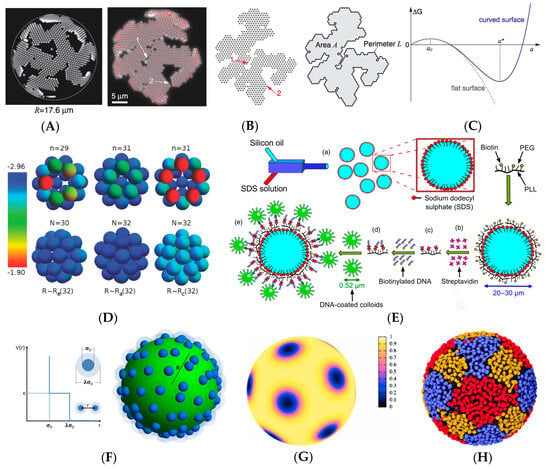
Figure 5.
The self-assembly on curved interfaces under various potential energy influences [30,68,72,73,74,75]. (A) Under depletion effects, polystyrene spheres with a diameter of 1 μm aggregate on a spherical interface, forming a crystal structure like ribbons with voids. (B) Unrolling the ribbon crystal structure onto the flat surface, where crystal axes are parallel to each other, exhibiting no defect structures. Numbers 1 and 2 mark the corresponding positions on a sphere and a plane. (C) A comparison of the free energy change for isotropic growth of crystals on flat and curved surfaces. (D) Self-assembly of particles with Lennard-Jones interactions on a spherical surface. The structure is most stable when the number of particles conforms to the magic number, and particle colors indicate potential energy magnitudes. (E) DNA-linked branches on lipid-stabilized silicon oil droplets, using this droplet as a confined spherical surface, achieving the self-assembly of DNA-functionalized nanoparticles on the confined spherical surface. The lowercase letters represent the sequence of the self-assembly process (F) Schematic representation of the core-corona potential and the resulting structure of core-corona particles self-assembly on a spherical surface. (G) Structure of block copolymers on a spherical surface predicted by self-consistent field theory, with colors representing segment fractions. (H) Self-assembly of star copolymers on a spherical substrate, forming structures that adhere to spherical topological requirements. Different colors represent different copolymers.
In addition to power-law repulsive interactions and attractive interactions, there are various specific forms of interactions with different ranges and strengths. Examples include core–corona interactions [73,76], DNA complementary base pairing [72], segment-segment interaction in copolymers [74,75,77], and volume exclusion in hard particles [78,79], among others, as shown in Figure 5. The interactions between particles influence the aggregate structure; long-range interaction systems are more dominated by enthalpy, while short-range interaction systems are more dominated by entropy.
The interactions between particles and interfaces impact the confined space for particles, determining the dimensions of self-assembly. This interaction specifically refers to the relationship among three surface energies. When the difference in surface energy between the oil phase and the water phase is greater than the difference in surface energies between the particles and the two phases, the particles will be adsorbed onto the surface, like Pickering emulsions [80,81,82]. Conversely, if the surface energy difference is larger, the particles will be located within one of the phases, depending on the particle’s affinity for either the hydrophilic or hydrophobic nature.
Particle Properties. In both experiments and simulations, the tunable properties of particles mainly include their softness/hardness and anisotropy [23,83,84]. Anisotropy refers to the variation in the physical or chemical properties of a material with different directions, exhibiting distinct properties in different directions. Traditional isotropic spherical colloidal particles typically lead to materials with simple symmetries, such as FCC and HCP packing. With advancements in synthetic techniques, like surface modification [85], addition of patchy particles [86], or grafting polymers [87], various shapes (rod-like, ellipsoidal, polyhedral, etc.) have been experimentally synthesized and self-assembled into more complex functional materials. The anisotropy of colloidal particles can be classified into surface anisotropy and shape anisotropy. Surface anisotropy refers to variations in the properties of the particle surface, such as patching and grafting chains. Shape anisotropy, on the other hand, involves the inherent non-spherical shape of particles. In this section, we emphasize the roles of configurational entropy and vibrational/rotational entropy in the self-assembly of anisotropic particles.
Configurational entropy is a crucial type of entropy in the context of large molecules with chain-like topology, such as DNA, peptides, and proteins [88]. The different spatial conformations that these chain-like molecules can adopt, owing to factors like internal bond rotations, are termed configurations. Due to thermal motion, the conformation of a molecule is constantly changing, resulting in a vast number of possible configurations for long-chain molecules. This leads to significant statistical relevance and observable configurational entropy. The configurational entropy effect of long-chain molecules plays a crucial role in the formation and evolution of the hierarchical structure in polymer systems. In the self-assembly of polymer-grafted nanoparticles, the competition or synergy between configurational entropy and enthalpy dominates the final structure [89,90].
Entropy is emergent, and it manifests its dominance prominently in confined spaces, particularly evident in the self-assembly of polymer-grafted Janus particles exhibiting surface anisotropy. In such confined spaces, optimal utilization of space is required to maximize the configurational space [4,91]. As show in Figure 6, Two types of Janus particles with surface anisotropy grafting long and short chains, when present at a planar oil-water interface, exhibit phase separation driven by the incompatibility of the two types of grafted chains. Applying pressure to this interface results in the mixing of the two types of particles, with short-chain particles interspersed between long-chain particles to achieve a larger configurational entropy. Despite the unfavorable enthalpic contribution of this process, the increase in configurational entropy compensates for the enthalpic loss [92]. In curved spaces, where the available space on either side of the interface is unequal, Janus particles grafted with two different lengths of semi-rigid chains spontaneously rotate to adjust the positions of the long-chain and short-chain ends, aiming to achieve the maximum configurational entropy. Various ordered structures emerge as the length and grafting ratio of the grafted chains vary [32].
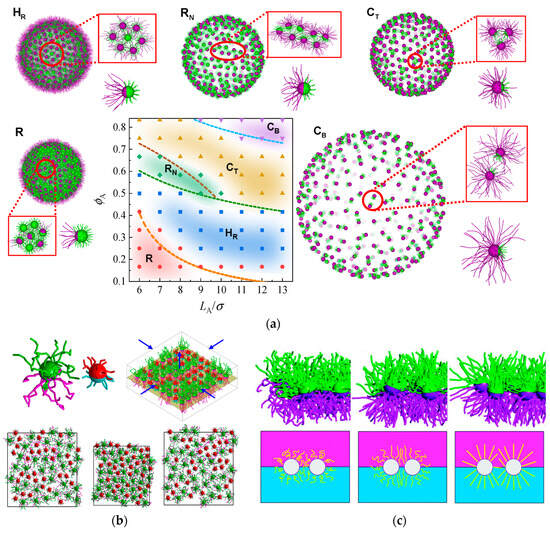
Figure 6.
Impact of Grafted Chain Conformational Entropy on Self-Assembly Structures [32,91,92]. (a) Varied structures and phase diagrams observed by altering chain length and grafting ratio of Janus particles grafted with two different lengths of polymer chains on a sphere, including binary nanocluster (CB), trinary nanocluster (CT), nanoribbon (RN), and hexagon with centered reverse (HR). (b) Amphiphilic Janus particles adsorbed at the interface, forming a mixed structure where a compressed interface leads to short-chain particles segregating long-chain particles. The arrows indicate the lateral and vertical changes of the simulation box during applying a mechanical pressure (c) Configuration of grafted chains on particles with changing rigidity, highlighting the strongest conformational entropy effect for semi-rigid chains.
Vibrational entropy and rotational entropy relate to the number of states arising from the vibrational or rotational modes of particles arranged in specific structures. The magnitude of vibrational entropy depends on the degree of freedom of particle vibrations. For colloidal particles with shape or surface anisotropy, in addition to vibration, changes in orientation at specific positions can generate rotational entropy or orientational entropy. Microstructures of typical materials, such as plastic crystal material [93], are organized by anisotropic particles with translational order but orientational disorder. Vibrational entropy and rotational entropy are particularly crucial for stabilizing colloidal assembly structures characterized by non-dense packing. In such loosely packed structures, the vibrational and rotational degrees of freedom are extensive and seemingly unstable; however, the substantial vibrational and rotational entropy produced reduces the system’s free energy, enhancing the stability of the assembly structure.
Vibrational entropy and rotational entropy typically come into play in non-dense, hard-particle systems. Similar to how spherical particles adopt FCC, HCP, or hexagonal lattice structures to maximize vibrational entropy beyond the random close packing point, non-spherical particles, in the absence of constraints, tend to form lattice structures matching their shapes as packing density increases, as shown in Figure 7. Analogous to the Onsager entropy-driven ordering phenomenon [94], non-spherical particles adopting face-to-face or edge-to-edge ordered structures contribute to an increase in overall vibrational entropy [84,95,96,97,98,99]. However, under spherical confinement, non-spherical particle systems still exhibit icosahedral symmetry structures characteristic of spherical particles, reflecting the competition between interface shape and particle shape [33,100,101]. Additionally, layered structures demonstrate how non-spherical particles mimic the behavior of spherical particles to achieve compatibility with confined spaces [26].
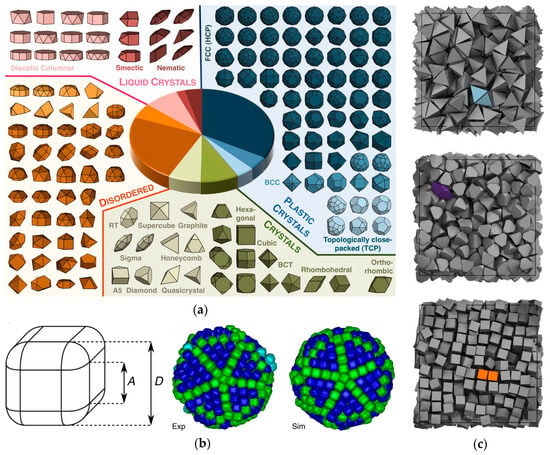
Figure 7.
Impact of shape anisotropy on self-assembly structures [26,84,95]. (a) Self-assembly results of various hard polyhedra obtained through Monte Carlo simulations, categorized into four types: crystalline, plastic crystalline, liquid crystalline, and disordered, differentiated by different colors. (b) Assembly of rounded cubes forming a structure with icosahedral symmetry under spherical confinement. The different colors represent different crystal regions distinguished by bond order parameters. (c) Face-to-face self-assembly of polyhedral particles induced by shape entropy, where polyhedral particles can be driven by entropy to form oriented ordered structures similar to patchy particles.
Curvature. Regarding the impact of curvature on self-assembly structures, it has been discussed in the previous section. Here, we focus on some modeling approaches used to predict the location and types of defects. Self-assembly of particles with repulsive interactions can be regarded as the bending of continuum elastic material [39,102], and this allows the calculation of the relationship between defect location and free energy. The portion where the formation of a defect raises the total energy is denoted as Ecore, while the drop in energy from matching the defect formation with Gaussian curvature is given by elasticity theory. The final form of free energy is thus simplified to
where g(x) is the determinant of the metric tensor, K(x) is the associated Gaussian curvature, and s(x) is the disclination density. The bending modulus of a continuum is determined by the potential energy between particles. This approach considers defects as degrees of freedom in a continuous elastic medium without distinguishing the types of defects, focusing only on the location and organizational forms of defects. Using this method, the length of scar-like defects can be calculated. The free energy of 2D crystallization in curved spaces can also be described by the Ginzburg-Landau free energy functional [34,103,104]:
where g is the determinant of the metric tensor, determined by curvature, and is the local free-energy areal density of a phase with an order parameter . For a two-phase system, this term takes the typical double-well form:
The formation of the crystal order can be analyzed through the bond-orientational order parameter . Upon crystallization, the positions of the particles can be determined through the local maxima in the order parameter function. This method combines theoretical models of microphase separation in block copolymers, allowing for the calculation of the evolution process of defects during annealing and the crystalline dynamics on various curved surfaces. These two methods can theoretically predict the location and types of defects on various surfaces [105,106,107], especially in systems with repulsive interactions or spring potentials.
4. Practical Applications and Control Strategies
Curved spaces are ubiquitous in biological systems, from viral capsid proteins [9,108,109,110] to the formation of vesicle surfaces [111]. To reduce surface energy and form stable homogeneous structures, the spherical shape is a natural choice in curved interfaces. Therefore, the most crucial application of self-assembly in curved interfaces lies in deepening our understanding of biological systems. By controlling the self-assembly process of viral capsid proteins, virus-like particles can be designed for use as vaccines, eliciting an immune response against the virus. Leveraging the self-assembly properties of vesicles allows the design of nano-sized vesicles for drug delivery. These vesicles can achieve targeted drug delivery by modifying surface properties, size, and composition, enhancing drug effectiveness while reducing side effects. In drug delivery, an important and promising application is colloidosomes. Colloidosomes refer to microcapsule shells formed by colloidal particles, typically ranging in size from nanometers to micrometers [112,113]. The synthesis of colloidosomes involves the soft template method, where emulsion droplets serve as templates. Colloidal particles adsorb at the droplet interface due to surface energy. During the evaporation of the droplet, colloidal particles aggregate and solidify, forming a stable shell structure. The number of colloidal particles on the droplet surface controls the size of colloidosomes, while the size of colloidal particles determines the pore size on the surface of colloidosomes, granting them selective permeability [81]. The self-assembly principle of colloidosomes aims to minimize the second moment of the mass distribution, defined by , rather than minimizing energy, which is related to the physical constraints and collapse process of the droplets [114]. When the number of particles is small, colloidosomes exhibit structures different from symmetric structures with long-range attractive potentials. This result indicates a general rule for clusters with short-range attraction: highly symmetric structures are highly unfavorable at equilibrium. High symmetry implies a stable state and asymmetric structures have greater configurational entropy, which dominates the formation of structures [115]. Simultaneously, the particle paths during collapse sometimes hinder the formation of the tightest structures. For example, with 13 colloidal particles, the most stable structure should be an icosahedron. However, due to the collapse process, particles cannot enter the interior of the spherical shell, so the final structure is not an icosahedron [116,117]. Moreover, many physical processes can be reinterpreted from the perspective of defect formation in curved surface self-assembly. For instance, the non-uniform particle density distribution caused by an external potential field on a flat surface with repulsive interactions can be equivalently understood as the angular projection transformation of particle positions on a curved cap [118,119]. On a macroscopic scale, the periodically corrugated pattern formed by a hard, thin film adhered to a soft substrate under compression due to mechanical instability can be explained using the continuous medium elasticity theory of defects on a curved surface [120,121,122]. In the context of the filament bundle packing problem, the stress in the cross-sectional filler can be equivalently modeled as the geometrically induced stress in a thin elastic sheet with spherical curvature [123,124,125].
The controllability of self-assembled structures drives ongoing research, development, and realization of new functional materials. Simultaneously, there is a continuous exploration of the structural changes and inherent mechanisms leading to the formation of new ordered structures during the material formation process. Understanding how to control the variation in self-assembled structures is a crucial and pivotal issue in material preparation and production, holding significant academic and practical importance. Whether they are van der Waals forces, hydrogen bonds, or electrostatic forces, these interactions fall under the category of basic interactions and can be attributed to enthalpy effects. Enthalpy effects regulate the structure at a fine particle level, allowing for precise control over particle positions and orientations. This control is based on a deep understanding of various fundamental interactions, leveraging the characteristics of a specific interaction. For example, in hydrogen bond-induced self-assembly, the design of assembly units takes full advantage of the dynamic reversibility of hydrogen bonds, enabling the resulting assembly to possess properties or functionalities such as self-healing, self-repair, and stimulus-response. In contrast to enthalpy effects, entropy effects emphasize collective particle behavior. Factors like conformational entropy, vibrational or rotational entropy, and shape entropy, as mentioned earlier, all exert influence on structure under conditions of dense particle packing. Entropy possesses characteristics of statistical macroscopicity, emergence, and unidirectional entropy increase. It can induce the generation of ordered structures, especially in extreme environments with spatial constraints, such as the stacking crystallization of colloidal hard spheres and anisotropic polyhedra. Entropy regulation often operates on a larger scale, subtly impacting the entire structure in a relatively concealed manner. Curvature, due to its unique characteristics, provides a means of structural regulation beyond entropy and enthalpy. On a large scale, it allows for the control of the entire topological structure of the self-assembled system. On a small scale, specific structural changes in self-assembly can be achieved by altering local curvature. Whether it is entropy or enthalpy, the impact on structure is global and uniform, while curvature provides a non-uniform regulatory mechanism, enabling localized functionalization. Therefore, curvature holds great significance in this context.
5. Conclusions and Outlook
The self-assembly behavior of nanoparticles in curved space is closely related to biological systems. Research on their self-assembly processes can offer new perspectives on many physical phenomena and provide theoretical guidance in the design of novel materials. In this article, we elucidate the intrinsic differences between self-assembly in curved and normal spaces by summarizing experimental and simulation studies on curved space self-assembly. The final self-assembled structure is determined by a combination of free energy, topology, and local geometry. Through an in-depth analysis of numerous research results, we discuss three structural control factors: interactions, particle shape, and curvature. We propose three self-assembly control strategies—entropy, enthalpy, and curvature—each with its characteristics and scale. These findings are crucial for understanding the behavior of nanoparticles at interfaces and their further applications.
Despite significant progress in understanding the self-assembly behavior in curved space over the years, there is still ample exploration space in this field. Due to the non-intuitiveness of entropy, a deeper understanding of its crucial role in self-assembly is needed. Additionally, efforts should be made to couple theoretical results from equilibrium states to non-equilibrium environments. In future research, a unified approach between experimental and simulation studies should be pursued to overcome these challenges, providing clear theoretical guidance for the construction of programmable materials in various environments and the study of biological and physical processes.
Author Contributions
Conceptualization: L.-T.Y.; Writing—Original Draft Preparation: Y.W. (Yuming Wang) and H.W.; Writing—Review and Editing: H.W.; Picture sorting: L.G. and Y.W. (Yibo Wu). All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge support from the National Natural Science Foundation of China (Grant Nos. 22025302 and 21873053). L.-T.Y. acknowledges financial support from the Ministry of Science and Technology of China (Grant No. 2022YFA1203203) and the State Key Laboratory of Chemical Engineering (No. SKL-ChE-23T01).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- Boles, M.A.; Engel, M.; Talapin, D.V. Self-assembly of colloidal nanocrystals: From intricate structures to functional materials. Chem. Rev. 2016, 116, 11220–11289. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N. Colloidal matter: Packing, geometry, and entropy. Science 2015, 349, 1253751. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Xu, Z.; Yang, Y.; Dai, X.; Yan, L.-T. Hierarchical crystals formed from DNA-functionalized Janus nanoparticles. ACS Nano 2018, 12, 9467–9475. [Google Scholar] [CrossRef] [PubMed]
- Choi, B.; Yu, J.; Paley, D.W.; Trinh, M.T.; Paley, M.V.; Karch, J.M.; Crowther, A.C.; Lee, C.-H.; Lalancette, R.A.; Zhu, X. Van der waals solids from self-assembled nanoscale building blocks. Nano Lett. 2016, 16, 1445–1449. [Google Scholar] [CrossRef] [PubMed]
- Willerich, I.; Gröhn, F. Molecular structure encodes nanoscale assemblies: Understanding driving forces in electrostatic self-assembly. J. Am. Chem. Soc. 2011, 133, 20341–20356. [Google Scholar] [CrossRef]
- Sánchez-Iglesias, A.; Grzelczak, M.; Altantzis, T.; Goris, B.; Perez-Juste, J.; Bals, S.; Van Tendeloo, G.; Donaldson, S.H., Jr.; Chmelka, B.F.; Israelachvili, J.N. Hydrophobic interactions modulate self-assembly of nanoparticles. ACS Nano 2012, 6, 11059–11065. [Google Scholar] [CrossRef]
- Min, Y.; Akbulut, M.; Kristiansen, K.; Golan, Y.; Israelachvili, J. The role of interparticle and external forces in nanoparticle assembly. Nat. Mater. 2008, 7, 527–538. [Google Scholar] [CrossRef]
- Zandi, R.; Reguera, D.; Bruinsma, R.F.; Gelbart, W.M.; Rudnick, J. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. USA 2004, 101, 15556–15560. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, G.; Gao, L.; Xu, D.; Wan, H.; Dai, X.; Zhang, X.; Tao, L.; Yan, L.-T. Configurational Entropy-Enabled Thermostability of Cell Membranes in Extremophiles: From Molecular Mechanism to Bioinspired Design. Nano Lett. 2023, 23, 1109–1118. [Google Scholar] [CrossRef]
- Eggeling, C.; Ringemann, C.; Medda, R.; Schwarzmann, G.; Sandhoff, K.; Polyakova, S.; Belov, V.N.; Hein, B.; Von Middendorff, C.; Schönle, A. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature 2009, 457, 1159–1162. [Google Scholar] [CrossRef] [PubMed]
- Bausch, A.R.; Bowick, M.J.; Cacciuto, A.; Dinsmore, A.D.; Hsu, M.F.; Nelson, D.R.; Nikolaides, M.G.; Travesset, A.; Weitz, D.A. Grain Boundary Scars and Spherical Crystallography. Science 2003, 299, 1716–1718. [Google Scholar] [CrossRef] [PubMed]
- Irvine, W.T.; Vitelli, V.; Chaikin, P.M. Pleats in crystals on curved surfaces. Nature 2010, 468, 947–951. [Google Scholar] [CrossRef] [PubMed]
- Guerra, R.E.; Kelleher, C.P.; Hollingsworth, A.D.; Chaikin, P.M. Freezing on a sphere. Nature 2018, 554, 346–350. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Sood, A.; Ganapathy, R. Observation of two-step melting on a sphere. Proc. Natl. Acad. Sci. USA 2022, 119, e2206470119. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, P.; Bowick, M.J.; Meinke, J.H.; Nelson, D.R.; Bausch, A.R. Direct visualization of dislocation dynamics in grain-boundary scars. Nat. Mater. 2005, 4, 407–411. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Dai, X.; Gao, L.; Xu, D.; Wan, H.; Wang, Y.; Yan, L.-T. The entropy-controlled strategy in self-assembling systems. Chem. Soc. Rev. 2023, 52, 6806–6837. [Google Scholar] [CrossRef]
- McGorty, R.; Fung, J.; Kaz, D.; Manoharan, V.N. Colloidal self-assembly at an interface. Mater. Today 2010, 13, 34–42. [Google Scholar] [CrossRef]
- Stratford, K.; Adhikari, R.; Pagonabarraga, I.; Desplat, J.-C.; Cates, M.E. Colloidal jamming at interfaces: A route to fluid-bicontinuous gels. Science 2005, 309, 2198–2201. [Google Scholar] [CrossRef]
- Herzig, E.M.; White, K.; Schofield, A.B.; Poon, W.C.; Clegg, P.S. Bicontinuous emulsions stabilized solely by colloidal particles. Nat. Mater. 2007, 6, 966–971. [Google Scholar] [CrossRef]
- Chai, Y.; Lukito, A.; Jiang, Y.; Ashby, P.D.; Russell, T.P. Fine-tuning nanoparticle packing at water–oil interfaces using ionic strength. Nano Lett. 2017, 17, 6453–6457. [Google Scholar] [CrossRef] [PubMed]
- Caciagli, A.; Singh, R.; Joshi, D.; Adhikari, R.; Eiser, E. Controlled optofluidic crystallization of colloids tethered at interfaces. Phys. Rev. Lett. 2020, 125, 068001. [Google Scholar] [CrossRef] [PubMed]
- Glotzer, S.C.; Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 2007, 6, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Akcora, P.; Liu, H.; Kumar, S.K.; Moll, J.; Li, Y.; Benicewicz, B.C.; Schadler, L.S.; Acehan, D.; Panagiotopoulos, A.Z.; Pryamitsyn, V. Anisotropic self-assembly of spherical polymer-grafted nanoparticles. Nat. Mater. 2009, 8, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Lattuada, M.; Hatton, T.A. Synthesis, properties and applications of Janus nanoparticles. Nano Today 2011, 6, 286–308. [Google Scholar] [CrossRef]
- Wang, D.; Hermes, M.; Kotni, R.; Wu, Y.; Tasios, N.; Liu, Y.; de Nijs, B.; van der Wee, E.B.; Murray, C.B.; Dijkstra, M.; et al. Interplay between spherical confinement and particle shape on the self-assembly of rounded cubes. Nat. Commun. 2018, 9, 2228. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, J.; Ge, B.; Deng, K.; Wu, X.; Xiao, T.; Jiang, T.; Quan, Z.; Cao, Y.C.; Wang, Z. Understanding Fe3O4 nanocube assembly with reconstruction of a consistent superlattice phase diagram. J. Am. Chem. Soc. 2019, 141, 3198–3206. [Google Scholar] [CrossRef]
- Henzie, J.; Andrews, S.C.; Ling, X.Y.; Li, Z.; Yang, P. Oriented assembly of polyhedral plasmonic nanoparticle clusters. Proc. Natl. Acad. Sci. USA 2013, 110, 6640–6645. [Google Scholar] [CrossRef]
- Croissant, J.G.; Fatieiev, Y.; Khashab, N.M. Degradability and clearance of silicon, organosilica, silsesquioxane, silica mixed oxide, and mesoporous silica nanoparticles. Adv. Mater. 2017, 29, 1604634. [Google Scholar] [CrossRef]
- Meng, G.; Paulose, J.; Nelson, D.R.; Manoharan, V.N. Elastic Instability of a Crystal Growing on a Curved Surface. Science 2014, 343, 634–637. [Google Scholar] [CrossRef]
- de Nijs, B.; Dussi, S.; Smallenburg, F.; Meeldijk, J.D.; Groenendijk, D.J.; Filion, L.; Imhof, A.; van Blaaderen, A.; Dijkstra, M. Entropy-driven formation of large icosahedral colloidal clusters by spherical confinement. Nat. Mater. 2015, 14, 56–60. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Wang, Y.; Gao, L.; Xu, Z.; Zhang, X.; Dai, X.; Dai, L.; Hou, C.; Yan, L.-T. Entropy-driven self-assembly of tethered Janus nanoparticles on a sphere. Fundam. Res. 2021, 1, 641–648. [Google Scholar] [CrossRef]
- Teich, E.G.; Van Anders, G.; Klotsa, D.; Dshemuchadse, J.; Glotzer, S.C. Clusters of polyhedra in spherical confinement. Proc. Natl. Acad. Sci. USA 2016, 113, E669–E678. [Google Scholar] [CrossRef] [PubMed]
- García, N.A.; Register, R.A.; Vega, D.A.; Gómez, L.R. Crystallization dynamics on curved surfaces. Phys. Rev. E 2013, 88, 012306. [Google Scholar] [CrossRef] [PubMed]
- Murayama, M.; Howe, J.; Hidaka, H.; Takaki, S. Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe. Science 2002, 295, 2433–2435. [Google Scholar] [CrossRef] [PubMed]
- Irvine, W.T.; Vitelli, V. Geometric background charge: Dislocations on capillary bridges. Soft Matter 2012, 8, 10123–10129. [Google Scholar] [CrossRef]
- Kusumaatmaja, H.; Wales, D.J. Defect motifs for constant mean curvature surfaces. Phys. Rev. Lett. 2013, 110, 165502. [Google Scholar] [CrossRef]
- Einert, T.; Lipowsky, P.; Schilling, J.; Bowick, M.J.; Bausch, A.R. Grain Boundary Scars on Spherical Crystals. Langmuir 2005, 21, 12076–12079. [Google Scholar] [CrossRef]
- Bowick, M.J.; Nelson, D.R.; Travesset, A. Interacting topological defects on frozen topographies. Phys. Rev. B 2000, 62, 8738. [Google Scholar] [CrossRef]
- Torquato, S.; Truskett, T.M.; Debenedetti, P.G. Is random close packing of spheres well defined? Phys. Rev. Lett. 2000, 84, 2064. [Google Scholar] [CrossRef]
- Hales, T.C. Sphere packings, I. In The Kepler Conjecture: The Hales-Ferguson Proof; Springer Science & Business Media: Berlin, Germany, 2011; pp. 379–431. [Google Scholar]
- Hales, T.C. Sphere packings, II. Discret. Comput. Geom. 1997, 18, 135–149. [Google Scholar] [CrossRef]
- Pusey, P.N.; Van Megen, W. Phase behaviour of concentrated suspensions of nearly hard colloidal spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Zhu, G.; Gao, L.; Xu, Z.; Dai, X.; Zhang, X.; Yan, L.-T. Entropy-Driven Unconventional Crystallization of Spherical Colloidal Nanocrystals Confined in Wide Cylinders. Nano Lett. 2021, 21, 8439–8446. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Mbah, C.F.; Przybilla, T.; Apeleo Zubiri, B.; Spiecker, E.; Engel, M.; Vogel, N. Magic number colloidal clusters as minimum free energy structures. Nat. Commun. 2018, 9, 5259. [Google Scholar] [CrossRef] [PubMed]
- Echt, O.; Sattler, K.; Recknagel, E. Magic numbers for sphere packings: Experimental verification in free xenon clusters. Phys. Rev. Lett. 1981, 47, 1121. [Google Scholar] [CrossRef]
- Martin, T.P. Shells of atoms. Phys. Rep. 1996, 273, 199–241. [Google Scholar] [CrossRef]
- Mughal, A.; Chan, H.; Weaire, D.; Hutzler, S. Dense packings of spheres in cylinders: Simulations. Phys. Rev. E 2012, 85, 051305. [Google Scholar] [CrossRef]
- Mughal, A.; Chan, H.K.; Weaire, D. Phyllotactic description of hard sphere packing in cylindrical channels. Phys. Rev. Lett. 2011, 106, 115704. [Google Scholar] [CrossRef]
- Pickett, G.T.; Gross, M.; Okuyama, H. Spontaneous chirality in simple systems. Phys. Rev. Lett. 2000, 85, 3652. [Google Scholar] [CrossRef]
- Fu, L.; Steinhardt, W.; Zhao, H.; Socolar, J.E.; Charbonneau, P. Hard sphere packings within cylinders. Soft Matter 2016, 12, 2505–2514. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181. [Google Scholar] [CrossRef]
- Nelson, D.R.; Halperin, B. Dislocation-mediated melting in two dimensions. Phys. Rev. B 1979, 19, 2457. [Google Scholar] [CrossRef]
- Young, A. Melting and the vector Coulomb gas in two dimensions. Phys. Rev. B 1979, 19, 1855. [Google Scholar] [CrossRef]
- Zahn, K.; Lenke, R.; Maret, G. Two-stage melting of paramagnetic colloidal crystals in two dimensions. Phys. Rev. Lett. 1999, 82, 2721. [Google Scholar] [CrossRef]
- Irvine, W.T.M.; Bowick, M.J.; Chaikin, P.M. Fractionalization of interstitials in curved colloidal crystals. Nat. Mater. 2012, 11, 948–951. [Google Scholar] [CrossRef]
- Bowick, M.J.; Nelson, D.R.; Shin, H. Interstitial fractionalization and spherical crystallography. Phys. Chem. Chem. Phys. 2007, 9, 6304–6312. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, Z.; Tang, S.; Tong, H.; Yanagishima, T.; Tanaka, H.; Tan, P. Morphology selection kinetics of crystallization in a sphere. Nat. Phys. 2021, 17, 121–127. [Google Scholar] [CrossRef]
- Wang, J.; Mbah, C.F.; Przybilla, T.; Englisch, S.; Spiecker, E.; Engel, M.; Vogel, N. Free energy landscape of colloidal clusters in spherical confinement. ACS Nano 2019, 13, 9005–9015. [Google Scholar] [CrossRef]
- Altschuler, E.L.; Williams, T.J.; Ratner, E.R.; Tipton, R.; Stong, R.; Dowla, F.; Wooten, F. Possible global minimum lattice configurations for Thomson’s problem of charges on a sphere. Phys. Rev. Lett. 1997, 78, 2681. [Google Scholar] [CrossRef]
- Wales, D.J.; Ulker, S. Structure and dynamics of spherical crystals characterized for the Thomson problem. Phys. Rev. B 2006, 74, 212101. [Google Scholar] [CrossRef]
- Pérez-Garrido, A.; Moore, M. Symmetric patterns of dislocations in Thomson’s problem. Phys. Rev. B 1999, 60, 15628. [Google Scholar] [CrossRef]
- Miller, W.L.; Cacciuto, A. Two-dimensional packing of soft particles and the soft generalized Thomson problem. Soft Matter 2011, 7, 7552–7559. [Google Scholar] [CrossRef]
- Bowick, M.; Cacciuto, A.; Nelson, D.R.; Travesset, A. Crystalline order on a sphere and the generalized Thomson problem. Phys. Rev. Lett. 2002, 89, 185502. [Google Scholar] [CrossRef] [PubMed]
- Bowick, M.J.; Giomi, L. Two-dimensional matter: Order, curvature and defects. Adv. Phys. 2009, 58, 449–563. [Google Scholar] [CrossRef]
- Pieranski, P. Two-dimensional interfacial colloidal crystals. Phys. Rev. Lett. 1980, 45, 569. [Google Scholar] [CrossRef]
- Gasser, U.; Eisenmann, C.; Maret, G.; Keim, P. Melting of crystals in two dimensions. ChemPhysChem 2010, 11, 963–970. [Google Scholar] [CrossRef] [PubMed]
- Luque, A.; Reguera, D.; Morozov, A.; Rudnick, J.; Bruinsma, R. Physics of shell assembly: Line tension, hole implosion, and closure catastrophe. J. Chem. Phys. 2012, 136, 184507. [Google Scholar] [CrossRef]
- Vest, J.-P.; Tarjus, G.; Viot, P. Glassy dynamics of dense particle assemblies on a spherical substrate. J. Chem. Phys. 2018, 148, 164501. [Google Scholar] [CrossRef]
- Asakura, S.; Oosawa, F. On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys. 1954, 22, 1255–1256. [Google Scholar] [CrossRef]
- Grason, G.M. Perspective: Geometrically frustrated assemblies. J. Chem. Phys. 2016, 145, 110901. [Google Scholar] [CrossRef]
- Joshi, D.; Bargteil, D.; Caciagli, A.; Burelbach, J.; Xing, Z.; Nunes, A.S.; Pinto, D.E.; Araújo, N.A.; Brujic, J.; Eiser, E. Kinetic control of the coverage of oil droplets by DNA-functionalized colloids. Sci. Adv. 2016, 2, e1600881. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Figueroa, S.E.; Gallegos-Lozano, A.; Mendoza, C.I. Packing core-corona particles on a spherical surface. Soft Matter 2022, 18, 6812–6824. [Google Scholar] [CrossRef] [PubMed]
- Chantawansri, T.L.; Bosse, A.W.; Hexemer, A.; Ceniceros, H.D.; Garcia-Cervera, C.J.; Kramer, E.J.; Fredrickson, G.H. Self-consistent field theory simulations of block copolymer assembly on a sphere. Phys. Rev. E 2007, 75, 031802. [Google Scholar] [CrossRef] [PubMed]
- Hain, T.M.; Schröder-Turk, G.E.; Kirkensgaard, J.J. Patchy particles by self-assembly of star copolymers on a spherical substrate: Thomson solutions in a geometric problem with a color constraint. Soft Matter 2019, 15, 9394–9404. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Millán, S.; García-Alcántara, C.; Ramírez-Hernández, A.; Sambriski, E.; Hernández, S. Self-Aassembly of core-corona colloids under cylindrical confinement: A Monte Carlo study. J. Mol. Liq. 2021, 335, 116219. [Google Scholar] [CrossRef]
- Kramer, E.J. Melted by mistakes. Nature 2005, 437, 824–825. [Google Scholar] [CrossRef] [PubMed]
- Tobochnik, J.; Chapin, P.M. Monte Carlo simulation of hard spheres near random closest packing using spherical boundary conditions. J. Chem. Phys. 1988, 88, 5824–5830. [Google Scholar] [CrossRef]
- Giarritta, S.P.; Ferrario, M.; Giaquinta, P. Statistical geometry of hard particles on a sphere. Phys. A 1992, 187, 456–474. [Google Scholar] [CrossRef]
- Binks, B.P.; Clint, J.H. Solid wettability from surface energy components: Relevance to Pickering emulsions. Langmuir 2002, 18, 1270–1273. [Google Scholar] [CrossRef]
- Dinsmore, A.; Hsu, M.F.; Nikolaides, M.; Marquez, M.; Bausch, A.; Weitz, D. Colloidosomes: Selectively permeable capsules composed of colloidal particles. Science 2002, 298, 1006–1009. [Google Scholar] [CrossRef]
- Kralchevsky, P.A.; Nagayama, K. Capillary interactions between particles bound to interfaces, liquid films and biomembranes. Adv. Colloid Interface Sci. 2000, 85, 145–192. [Google Scholar] [CrossRef] [PubMed]
- Travesset, A. Binary nanoparticle superlattices of soft-particle systems. Proc. Natl. Acad. Sci. USA 2015, 112, 9563–9567. [Google Scholar] [CrossRef] [PubMed]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Predictive self-assembly of polyhedra into complex structures. Science 2012, 337, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.Y.; Ross, B.M.; Hong, S.; Lee, L.P. Bioinspired nanocorals with decoupled cellular targeting and sensing functionality. Small 2010, 6, 503–507. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Glotzer, S.C. Self-assembly of patchy particles. Nano Lett. 2004, 4, 1407–1413. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, A.; Misra, B. Grafting: A versatile means to modify polymers: Techniques, factors and applications. Prog. Polym. Sci. 2004, 29, 767–814. [Google Scholar] [CrossRef]
- Frederick, K.K.; Marlow, M.S.; Valentine, K.G.; Wand, A.J. Conformational entropy in molecular recognition by proteins. Nature 2007, 448, 325–329. [Google Scholar] [CrossRef]
- Thaner, R.V.; Kim, Y.; Li, T.I.; Macfarlane, R.J.; Nguyen, S.T.; Olvera de la Cruz, M.; Mirkin, C.A. Entropy-driven crystallization behavior in DNA-mediated nanoparticle assembly. Nano Lett. 2015, 15, 5545–5551. [Google Scholar] [CrossRef]
- Rogers, W.B.; Shih, W.M.; Manoharan, V.N. Using DNA to program the self-assembly of colloidal nanoparticles and microparticles. Nat. Rev. Mater. 2016, 1, 16008. [Google Scholar] [CrossRef]
- Huang, Z.; Lu, C.; Dong, B.; Xu, G.; Ji, C.; Zhao, K.; Yan, L.-T. Chain stiffness regulates entropy-templated perfect mixing at single-nanoparticle level. Nanoscale 2016, 8, 1024–1032. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, R.; Xu, G.; Huang, Z.; Yan, L.-T. Entropy-mediated mechanical response of the interfacial nanoparticle patterning. Nano Lett. 2014, 14, 6910–6916. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Mondal, A.; Reddy, C.M. Harnessing molecular rotations in plastic crystals: A holistic view for crystal engineering of adaptive soft materials. Chem. Soc. Rev. 2020, 49, 8878–8896. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- van Anders, G.; Klotsa, D.; Ahmed, N.K.; Engel, M.; Glotzer, S.C. Understanding shape entropy through local dense packing. Proc. Natl. Acad. Sci. USA 2014, 111, E4812–E4821. [Google Scholar] [CrossRef] [PubMed]
- Haji-Akbari, A.; Engel, M.; Keys, A.S.; Zheng, X.; Petschek, R.G.; Palffy-Muhoray, P.; Glotzer, S.C. Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra. Nature 2009, 462, 773–777. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Glotzer, S.C. Entropically engineered formation of fivefold and icosahedral twinned clusters of colloidal shapes. Nat. Commun. 2022, 13, 7362. [Google Scholar] [CrossRef] [PubMed]
- Cersonsky, R.K.; van Anders, G.; Dodd, P.M.; Glotzer, S.C. Relevance of packing to colloidal self-assembly. Proc. Natl. Acad. Sci. USA 2018, 115, 1439–1444. [Google Scholar] [CrossRef]
- van Anders, G.; Ahmed, N.K.; Smith, R.; Engel, M.; Glotzer, S.C. Entropically Patchy Particles: Engineering Valence through Shape Entropy. ACS Nano 2014, 8, 931–940. [Google Scholar] [CrossRef]
- Smallenburg, F.; Löwen, H. Close packing of rods on spherical surfaces. J. Chem. Phys. 2016, 144, 164903. [Google Scholar] [CrossRef]
- de Folter, J.W.J.; Hutter, E.M.; Castillo, S.I.R.; Klop, K.E.; Philipse, A.P.; Kegel, W.K. Particle Shape Anisotropy in Pickering Emulsions: Cubes and Peanuts. Langmuir 2014, 30, 955–964. [Google Scholar] [CrossRef]
- Giomi, L.; Bowick, M. Crystalline order on Riemannian manifolds with variable Gaussian curvature and boundary. Phys. Rev. B 2007, 76, 054106. [Google Scholar] [CrossRef]
- Gómez, L.R.; García, N.A.; Vitelli, V.; Lorenzana, J.; Vega, D.A. Phase nucleation in curved space. Nat. Commun. 2015, 6, 6856. [Google Scholar] [CrossRef] [PubMed]
- Garcia, N.A.; Pezzutti, A.D.; Register, R.A.; Vega, D.A.; Gómez, L.R. Defect formation and coarsening in hexagonal 2D curved crystals. Soft Matter 2015, 11, 898–907. [Google Scholar] [CrossRef] [PubMed]
- Burke, C.J.; Mbanga, B.L.; Wei, Z.; Spicer, P.T.; Atherton, T.J. The role of curvature anisotropy in the ordering of spheres on an ellipsoid. Soft Matter 2015, 11, 5872–5882. [Google Scholar] [CrossRef]
- Sausset, F.; Tarjus, G.; Nelson, D.R. Structure and dynamics of topological defects in a glassy liquid on a negatively curved manifold. Phys. Rev. E 2010, 81, 031504. [Google Scholar] [CrossRef] [PubMed]
- Hexemer, A.; Vitelli, V.; Kramer, E.J.; Fredrickson, G.H. Monte Carlo study of crystalline order and defects on weakly curved surfaces. Phys. Rev. E 2007, 76, 051604. [Google Scholar] [CrossRef] [PubMed]
- Marzec, C.J.; Day, L.A. Pattern formation in icosahedral virus capsids: The papova viruses and Nudaurelia capensis beta virus. Biophys. J. 1993, 65, 2559–2577. [Google Scholar] [CrossRef]
- Caspar, D.L.; Klug, A. Physical principles in the construction of regular viruses. Cold Spring Harbor Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef]
- Ganser, B.K.; Li, S.; Klishko, V.Y.; Finch, J.T.; Sundquist, W.I. Assembly and analysis of conical models for the HIV-1 core. Science 1999, 283, 80–83. [Google Scholar] [CrossRef]
- Schneider, S.; Gompper, G. Shapes of crystalline domains on spherical fluid vesicles. Europhys. Lett. 2005, 70, 136. [Google Scholar] [CrossRef]
- Rossier-Miranda, F.; Schroën, C.; Boom, R. Colloidosomes: Versatile microcapsules in perspective. Colloids Surf. A 2009, 343, 43–49. [Google Scholar] [CrossRef]
- Thompson, K.L.; Williams, M.; Armes, S.P. Colloidosomes: Synthesis, properties and applications. J. Colloid Interface Sci. 2015, 447, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N.; Elsesser, M.T.; Pine, D.J. Dense packing and symmetry in small clusters of microspheres. Science 2003, 301, 483–487. [Google Scholar] [CrossRef] [PubMed]
- Meng, G.; Arkus, N.; Brenner, M.P.; Manoharan, V.N. The free-energy landscape of clusters of attractive hard spheres. Science 2010, 327, 560–563. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N.; Pine, D.J. Building materials by packing spheres. MRS Bull. 2004, 29, 91–95. [Google Scholar] [CrossRef]
- Manoharan, V.N. Colloidal spheres confined by liquid droplets: Geometry, physics, and physical chemistry. Solid State Commun. 2006, 139, 557–561. [Google Scholar] [CrossRef]
- Soni, V.; Gómez, L.R.; Irvine, W.T. Emergent geometry of inhomogeneous planar crystals. Phys. Rev. X 2018, 8, 011039. [Google Scholar] [CrossRef]
- Yao, Z.; De La Cruz, M.O. Topological defects in flat geometry: The role of density inhomogeneity. Phys. Rev. Lett. 2013, 111, 115503. [Google Scholar] [CrossRef]
- Jiménez, F.L.; Stoop, N.; Lagrange, R.; Dunkel, J.; Reis, P.M. Curvature-controlled defect localization in elastic surface crystals. Phys. Rev. Lett. 2016, 116, 104301. [Google Scholar] [CrossRef]
- Brojan, M.; Terwagne, D.; Lagrange, R.; Reis, P.M. Wrinkling crystallography on spherical surfaces. Proc. Natl. Acad. Sci. USA 2015, 112, 14–19. [Google Scholar] [CrossRef]
- Breid, D.; Crosby, A.J. Curvature-controlled wrinkle morphologies. Soft Matter 2013, 9, 3624–3630. [Google Scholar] [CrossRef]
- Bruss, I.R.; Grason, G.M. Non-Euclidean geometry of twisted filament bundle packing. Proc. Natl. Acad. Sci. USA 2012, 109, 10781–10786. [Google Scholar] [CrossRef] [PubMed]
- Grason, G.M. Defects in crystalline packings of twisted filament bundles. I. Continuum theory of disclinations. Phys. Rev. E 2012, 85, 031603. [Google Scholar] [CrossRef] [PubMed]
- Hall, D.M.; Bruss, I.R.; Barone, J.R.; Grason, G.M. Morphology selection via geometric frustration in chiral filament bundles. Nat. Mater. 2016, 15, 727–732. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).