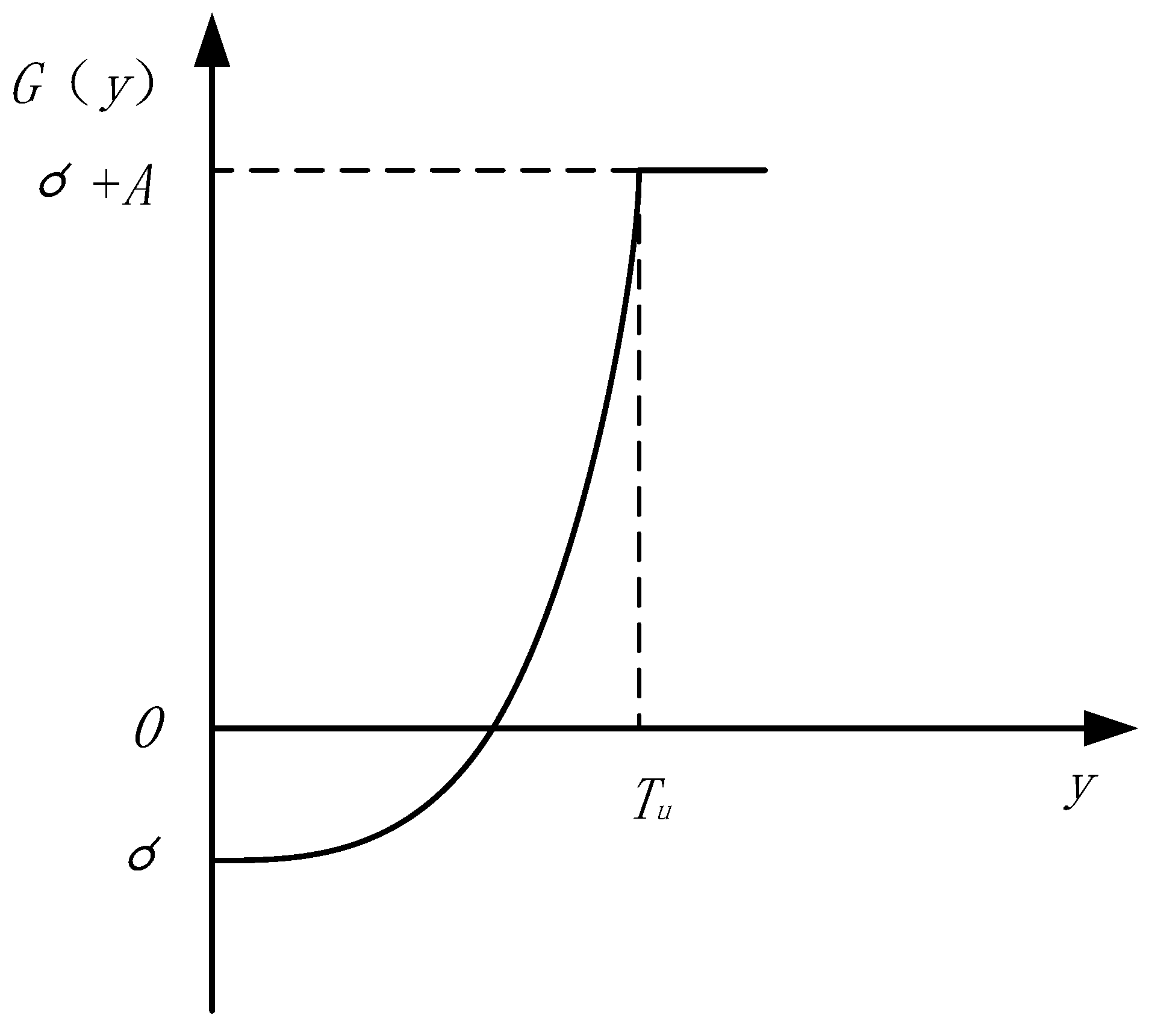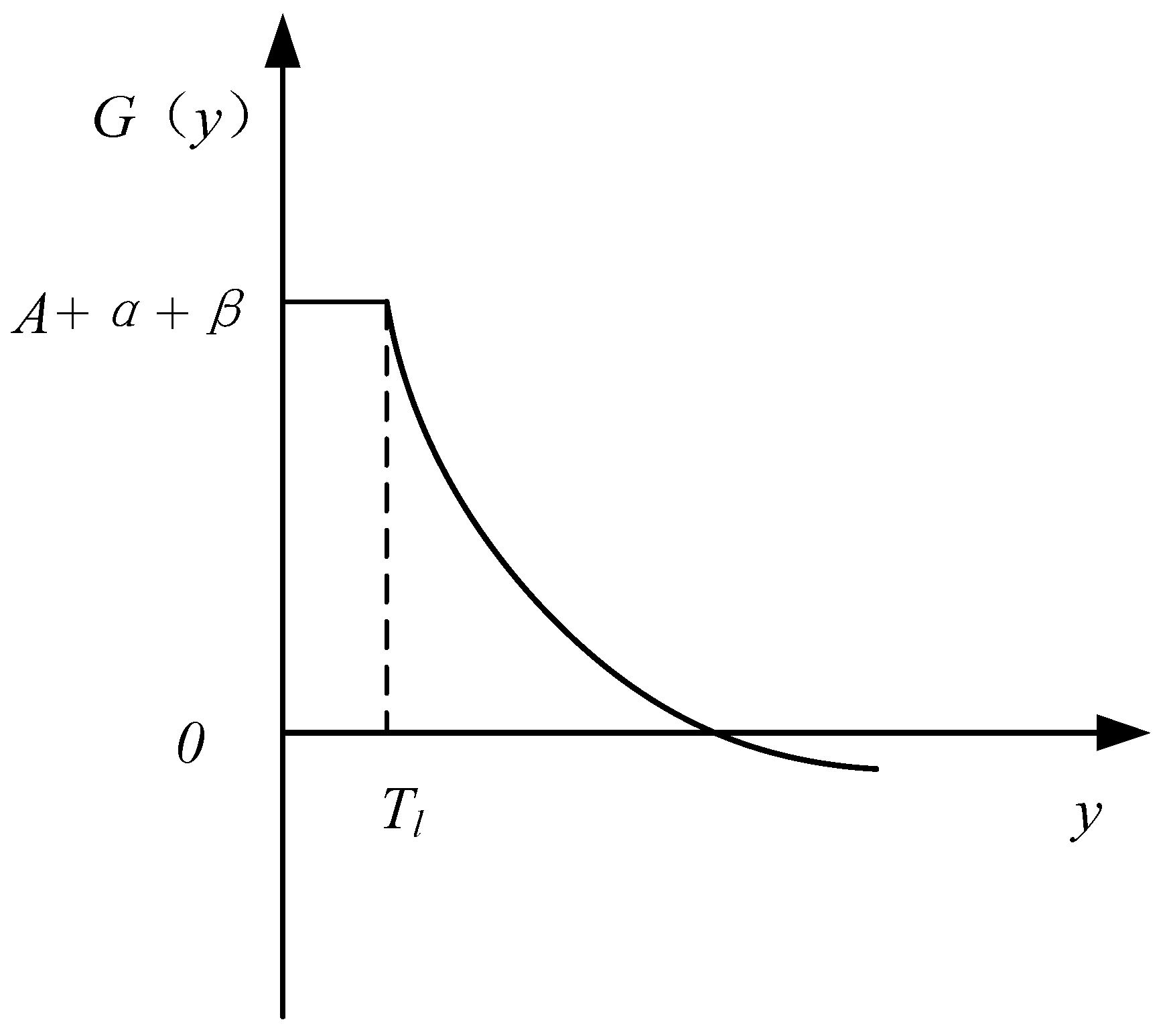1. Introduction
Dam concrete belongs to large-volume concrete, and its internal structure is relatively complex. Dam concrete bears a large load and thus causes construction quality problems, such as low concrete strength grade, bubbles, and pits. Most of the current research on concrete quality control focuses on the construction process, concrete surface inspection, and quality acceptance assessment, but there is relatively little research on construction quality control technology. This paper constructed a specification optimization model based on the concept of quality gain–loss function, and the model was analyzed from the perspective of quality loss prediction in the production process, which could provide a theoretical basis for concrete quality control.
The loss function is widely used in engineering, Xi Chen et al. [
1] proposed a kernel MSE loss function and used a deep learning approach to validate its accuracy, which is believed to quantify the prediction error of nonlinear data in a nonlinear space. Sirote Khunkitti [
2] presents a method to solve MOOPF problems based on SMA by considering fuel cost, emission, and transmission line loss as part of the objective functions to be minimized. Divish Rangasammy et al. [
3] used a deep feedforward neural network, a one-dimensional convolutional neural network, a bidirectional gated recurrent unit, and bidirectional long short-term memory to evaluate two loss functions for NASA’s commercial modular aviation propulsion system simulation data and Scania truck pressure system fault data and believed that the dynamic weighted loss function could significantly improve the remaining service life prediction and fault detection rate. This paper is developed on the basis of the Taguchi quality loss function. Taguchi’s quality concept provides a theoretical basis for product quality control. The quadratic loss function proposed by Taguchi is widely used in quality loss prediction. After decades of development, the initial success of the function has been achieved in decision-making, quality engineering, tolerance design, etc. Dr. Taguchi believed that product quality referred to the loss brought to society after a product went on the market. As long as the product deviated from the target value, losses would be caused [
4]. Considering the limitations of the Taguchi quality loss function in practical applications, Spring et al. [
5] believed that the quality loss was limited as the quality characteristic value changed. No matter how much the quality characteristic value deviated from the target value, the amount of quality loss would never exceed the maximum value. Therefore, the inverted normal quality loss function model was proposed to solve the limit problem of the traditional quality loss function. Xue [
6,
7] economically designed ARMA and VSIEWMA control charts based on the quality loss function. Li et al. [
8] improved the quality loss function to make it dimensionless in order to obtain a comparable quality loss measure when predicting the loss quality. In combination with orthogonal experiments, a random grey target model was designed for product parameters with multi-quality characteristics so as to solve the problem of product parameter selection with multi-quality characteristics. Mao et al. [
9] improved the Taguchi quality loss function according to the different growth rates on both sides of the target value of the quality loss function, and the general estimation formula of the hidden quality cost within the tolerance range was obtained with the sampling error taken into consideration. The numerical model of inherent reliability was also established. Li et al. [
10] discussed and analyzed the quality loss coefficient by raising the Taylor expansion term to the third order, and a cubic quality loss function was established as a way to calculate the implicit quality cost. Liu et al. [
11] established a cubic wear mathematical model by studying the wear law and introduced the model into the quality loss function to establish a new service quality loss model for product service life prediction. However, in actual production, there are not only quality losses but also gain effects brought by quality compensation. In response to the quality compensation effect in actual production, Wang et al. [
12] used Taylor expansion to define the constant term in the expansion as the compensation meaning and proposed the concept of quality gain–loss function.
Kapur et al. [
13,
14,
15] proposed an optimization model for determining the bounds of engineering specifications after studying inspection costs, scrap/rework costs, and changes, and the engineering specifications developed through this model could minimize the total social losses. A large number of scholars subsequently improved their specification optimization models. On the basis of research by Kapur et al., Chen [
16] assumed that the quality characteristics obeyed the exponential distribution and carried out the specification optimization design on the basis of Taguchi’s quality loss function. Wang et al. [
17] summarized the parallel, decentralized, and convergence models in the analysis of multi-process capability, and the transfer model between sub-processes in the decentralized model and the fluctuation transfer model of production in each process was established. By calculating the utility ratio, the optimal improvement method was determined, providing a basis for the optimization model of process capability with economic applicability. Zhao et al. [
18] used the concept of fuzzy matter elements to identify similar processes and adopted an improved multivariate process capability index to analyze the process capability of traditional data. Mohammad. A [
19] overcame the fuzzy definition of process loss starting from the fuzzy attribute of information in combination with the Taguchi quality loss function; Gholamreza H [
20] expanded the concept of intuitionistic fuzzy information process capability. Wang Bo et al. [
21,
22] proposed the concept of grey quality gain–loss function and analyzed two existing situations of compensation amount, and the grey quality gain–loss function was constructed under three characteristics, i.e., larger-the-better, smaller-the-better, and nominal-the-best. Six times the standard deviation was used to represent the process capability; the existing process capability indices were compared and analyzed, and a classification standard and disposal situation table was constructed. The grey quality gain–loss function was also used to calculate the optimal engineering specifications under loss and compensation, respectively.
In the second part of this paper, the expression form of the quality gain–loss function under three quality characteristics was introduced. Since the compensation amount of the mass loss function has two forms, constant compensation and functional compensation, the quadratic exponential gain–loss function model under the three quality characteristics was constructed in the third part of this paper with constant compensation as an example. In the fourth part of this paper, hyperbolic tangent compensation was used as the equational representation of functional compensation for the quadratic exponential quality gain–loss function model design, and the optimized design of engineering specifications and example verification were carried out in the latter two parts.
2. Quality Gain–Loss Function
2.1. Quality Gain–Loss Function with the Nominal-the-Best Characteristic
Genichi Taguchi believed that quality was the loss to society after a product is launched, and with the help of the Taylor expansion, he constructed the following quality loss function:
Here y represents the quality characteristic value, m represents the target value, k represents the quality loss factor, and L represents the quality loss.
However, in specific engineering construction, there are not only quality losses but also mutual compensation between two processes, i.e., the immediately preceding process and the immediately following process. Mutual compensation happens between parallel processes in engineering construction, and there is also quality compensation in the process of coupling with adaptation. Firstly, when the quality characteristic value deviates from the target value or the target interval, a quality loss term will be generated. On this basis, Wang Bo took quality compensation into account and constructed a quality gain–loss function as follows:
Here G(y) represents the quality gain–loss function with quality characteristic y, k represents the quality gain–loss factor, and g(y) represents the quality compensation function with quality characteristic y.
When the compensation amount is constant, the image of the quality gain–loss function with the desired nominal-the-best characteristic is shown in
Figure 1.
2.2. Quality Gain–Loss Function with the Larger-the-Better Characteristic
Dr. Taguchi’s quality loss function with the larger-the-better characteristic is the Taylor expansion of
L(
Y) at
Y = ∞. Based on this, Wang [
23] assumed that the quality compensation was constant, and the quality gain–loss was minimal when the quality characteristic reached infinity. The quality gain–loss function with the larger-the-better characteristic is constructed as follows:
where
Gl(
y) denotes the quality gain–loss function with the larger-the-better characteristic
y and
σ denotes the amount of quality compensation when the quality characteristic reached infinity.
When the compensation amount is constant, the image of the quality gain–loss function with the desired larger-the-better characteristic is shown in
Figure 2.
2.3. Quality Gain–Loss Function with the Smaller-the-Better Characteristic
The quality gain–loss function with the smaller-the-better characteristic was derived from the Taylor expansion at
y = 0. Based on this, Wang [
23] assumed that the quality compensation was constant, and the quality gain–loss was minimal when the quality characteristic reached 0. The quality gain–loss function with the smaller-the-better characteristic is constructed as follows:
where
Gl(
y) denotes the quality gain–loss function with the smaller-the-better characteristic
y,
k represents the quality gain–loss factor, and
σ denotes the amount of quality compensation when the quality characteristics reach 0.
When the compensation amount is constant, the image of the quality gain–loss function with the desired smaller-the-better characteristic is shown in
Figure 3.
3. Quadratic Exponential Quality Gain–Loss Function
In previous studies of asymmetric quality gain–loss functions, the magnitude of the change rate of quality loss on both sides of the target value was not considered; however, this paper argued that in specific engineering construction, the change rate of quality gain–loss on both sides of the target value of the quality gain–loss function might exist in opposite cases. Taking the temperature control system in the process of concrete placement in dams as an example, if the concrete outlet temperature was lower than the target value, the growth rate of quality gain–loss increased; if the concrete outlet temperature was higher than the target value, the growth rate of quality gain and loss would decrease and tend to be flat until the outlet temperature reached the upper limit of specifications in which case it would be reworked/scrapped. Based on this, the quadratic exponential quality gain–loss function is constructed in this paper.
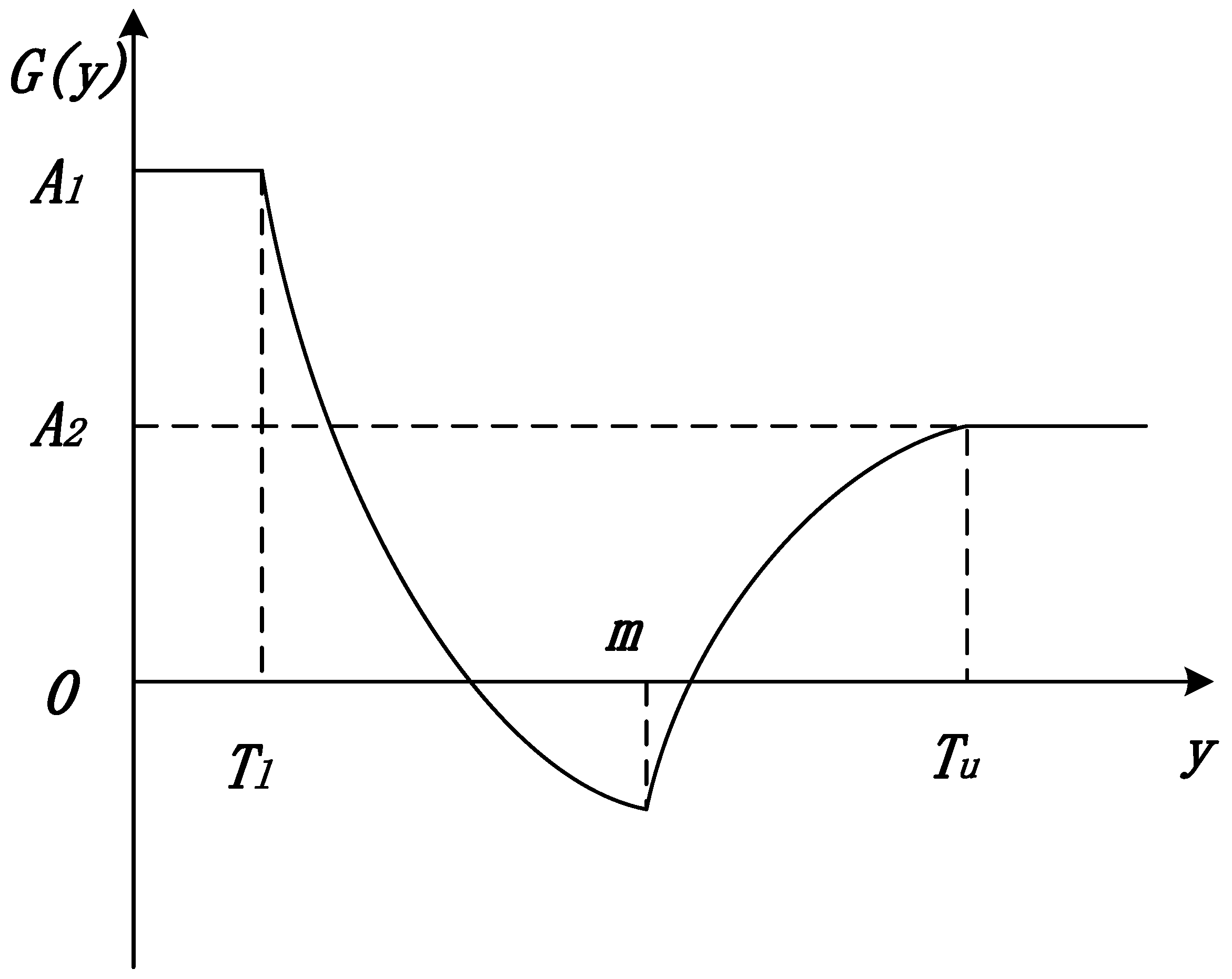
3.1. Quadratic Exponential Quality Gain–Loss Function with the Nominal-the-Best Characteristic
In this paper, considering the growth rate on both sides of the target value, the quadratic exponential quality gain–loss function with nominal-the-best characteristics was constructed.
where
g(
y) denotes the quality compensation amount,
m denotes the target characteristic value,
Tl and
Tu denote the lower functional limit and upper functional limit of the product, respectively,
A1 and
A2 denote the quality loss value when the lower functional limit and upper functional limit are reached, respectively, and the quality gain–loss coefficients
k1 and
k2 are obtained as follows:
Assuming a constant quality compensation of
σ, a schematic diagram of the quadratic exponential quality gain–loss function with the nominal-the-best characteristic is constructed as shown in
Figure 4.
The growth rates on both sides of the target values for quality gain–loss characteristics are as follows:
When the product quality characteristic value is within the range of TI–Tu, the product quality will meet the requirements; when the quality characteristic value is smaller than TI or larger than Tu, the product quality will not meet the requirements. Moreover, when the product is located in the qualified range, its quality loss growth rate will be different. When the quality characteristic value is smaller than the target value, the growth rate will become higher; when the quality characteristic value is larger than the target value, the growth rate will decrease and finally tend to level off.
3.2. Quadratic Exponential Quality Gain–Loss Function with the Larger-the-Better Characteristic
For the quadratic exponential quality gain–loss function with the larger-the-better characteristic, when the quality characteristic value is infinite, the quality gain–loss value will be the smallest; when the quality characteristic value is smaller than the lower limit of the specification, the project quality will be unqualified, and scrapping will be carried out. At this time, the quality gain–loss is a specified value, and based on this, the quadratic exponential quality gain–loss function with the larger-the-better characteristics is constructed as follows:
where
Gl(
y) denotes the quadratic exponential quality gain–loss function with the larger-the-better characteristic,
g(
y) denotes the quality compensation function,
Tl denotes the lower specification limit, and
A denotes the fixed quality loss when the lower specification limit is not reached.
Assuming a constant quality compensation of
σ, a schematic diagram of the quadratic exponential quality gain–loss function with the larger-the-better characteristic is constructed as shown in
Figure 5.
3.3. Quadratic Exponential Quality Gain–Loss Function with the Smaller-the-Better Characteristic
For the quadratic exponential quality gain–loss function with the smaller-the-better characteristic, when the quality characteristic value is 0, the quality gain–loss value will be the smallest, and considering the quality characteristic value above the upper limit of the specification, the project quality will be unqualified and scrapping will be carried out. At this time, the quality gain–loss is a specified value, and based on this, the quadratic exponential quality gain–loss function with the smaller-the-better characteristic is constructed as follows:
where
Gl(
y) denotes the quadratic exponential quality gain–loss function with the larger-the-better characteristic,
g(
y) denotes the quality compensation function,
Tu denotes the upper specification limit, and
A denotes the fixed quality loss when the upper specification limit is exceeded.
Assuming a constant quality compensation of
σ, a schematic diagram of the quadratic exponential quality gain–loss function with the smaller-the-better characteristic is constructed as shown in
Figure 6.
4. Quadratic Exponential Quality Gain–Loss Function Based on Hyperbolic Tangent Compensation
4.1. Hyperbolic Tangent Quality Compensation Function
In this paper, forms of mass compensation quantity were taken into account, and one of the forms was a constant compensation quantity, namely g(y) = σ (σ is a constant), in which the functional representation of the compensation quantity was not considered.
In order to accurately represent the change of compensation quantity in the quality control process, Wang Bo considered the finiteness of the compensation function and constructed the hyperbolic tangent compensation function according to the nature of the hyperbolic tangent function form as follows:
where
α denotes the compensation coefficient,
β denotes the maximum compensation for the quality characteristic value
y (positive compensation for
β < 0 and negative compensation for
β > 0), and
m denotes the quality characteristic target value.
From Equation (11), it can be seen that the hyperbolic tangent compensation function obtains the maximum compensation
β at the target value
m. When the value of the quality characteristic tends to be 0 or infinity, the minimum compensation is
α +
β. The image of the hyperbolic tangent quality compensation function is shown in
Figure 7.
4.2. Quadratic Exponential Quality Gain–Loss Function with the Nominal-the-Best Characteristic Based on Hyperbolic Tangent Compensation
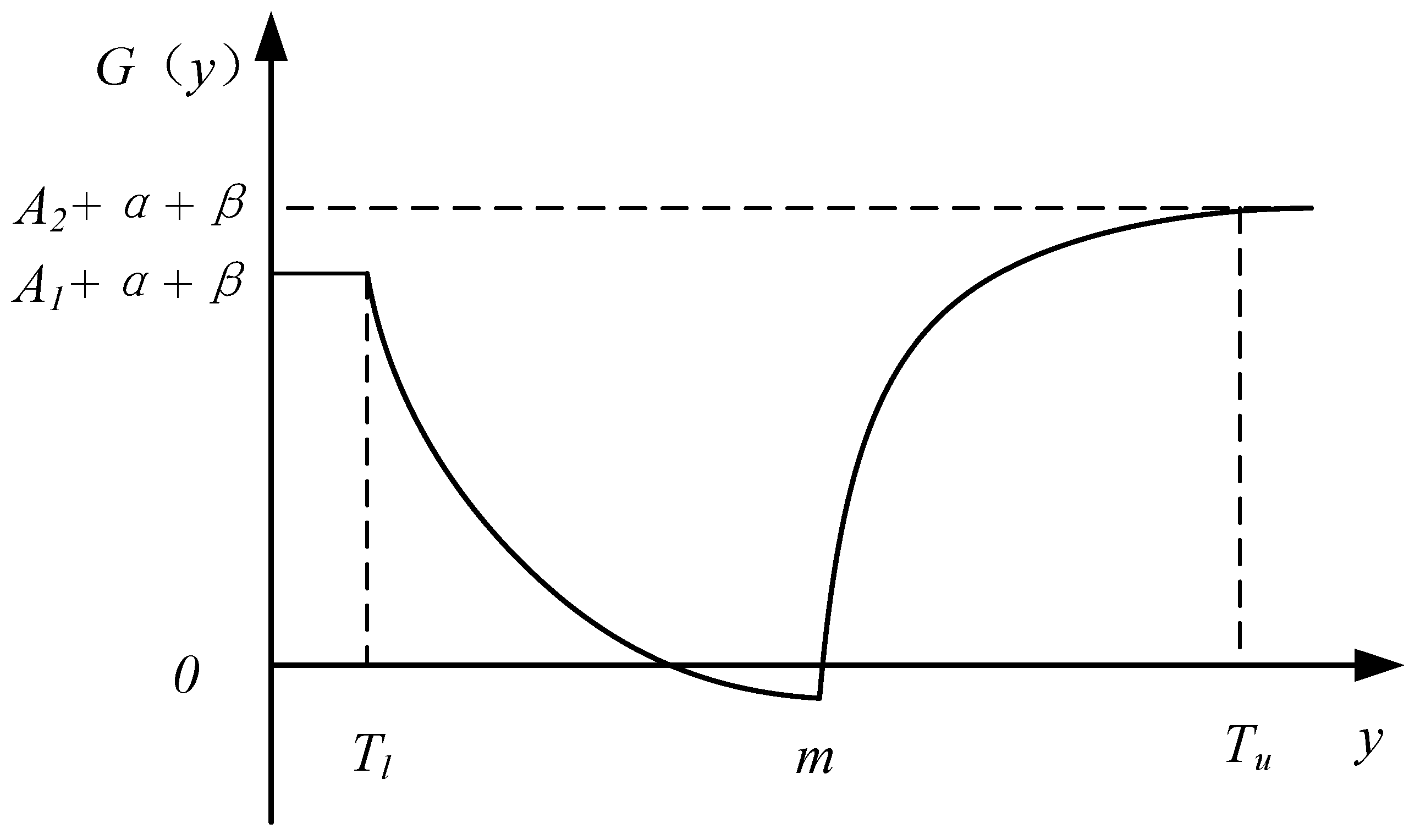
The quadratic exponential quality gain–loss function with the nominal-the-best characteristic based on hyperbolic tangent compensation is:
We constructed the schematic diagram of the quadratic exponential quality gain–loss function with the nominal-the-best characteristic under hyperbolic tangent compensation and it is shown in
Figure 8.
4.3. Quadratic Exponential Quality Gain–Loss Function with the Larger-the-Better Characteristic Based on Hyperbolic Tangent Compensation
If the compensation amount is the quality characteristic function, based on the research on hyperbolic tangent compensation in
Section 3.1, the quadratic exponential quality gain–loss function with the larger-the-better characteristic is constructed and shown in Equation (13):
When the compensation amount is hyperbolic tangent compensation, the schematic diagram of the quadratic exponential quality gain–loss function with the larger-the-better characteristic is shown in
Figure 9.
4.4. Quadratic Exponential Quality Gain–Loss Function with the Smaller-the-Better Characteristic Based on Hyperbolic Tangent Compensation
If the compensation amount is the quality characteristic function, based on the research on hyperbolic tangent compensation in
Section 3.1, the quadratic exponential quality gain–loss function with the larger-the-better characteristic is constructed and shown in Equation (14):
We constructed the schematic diagram of the quadratic exponential quality gain–loss function with the smaller-the-better characteristic under hyperbolic tangent compensation and it is shown in
Figure 10.
5. Engineering Specification Optimization
The reduction in standard deviation by improving the production equipment or production process usually requires a large cost investment. Considering the economic index of specification optimization, this paper adopted the standard limit value of the working procedure to optimize engineering specifications.
In the past, the development of engineering specifications primarily gave consideration to the impact of quality loss on the development of optimal specifications, but there was a lack of analysis of the quality compensation amount. For the quadratic exponential quality gain–loss function, the presence of the compensation amount inevitably has an impact on the development of the project specifications, which in turn affects the judgment of product quality and the assessment of expected benefits. In this chapter, an engineering specification optimization model was primarily constructed based on the quadratic exponential quality gain–loss function. In order to represent the process of establishing the optimal engineering specification more accurately, the quality loss and compensation parts were analyzed in sequence. Finally, the analysis results were summarized and derived.
5.1. Engineering Specification Optimization under Quadratic Exponential Quality Loss
In the current literature on the development of engineering specifications, a normal distribution is considered an overall range; however, after the full inspection of a product, the value of the quality characteristics for the inspected product, i.e., the product shipped to the customer, is taken in the range (
LSL,
USL) where
USL is the upper limit of the specification that meets product quality requirements and
LSL is the lower limit of the specification that meets product quality requirements. Therefore, in this section, it was assumed that the quality characteristic obeyed a truncated normal distribution, and the process average was equal to the target value, i.e.,
. Combining the loss parts of the quadratic exponential quality gain–loss function for the development of engineering specifications under loss, Kapu et al. proposed an online quality management inspection method to reduce short-term losses to users. The core aim of this method was to divide the quality losses of a product into losses to users, scrap or rework costs, and inspection costs, which can be expressed by the following Equation:
Here T denotes the average expected loss per unit of product, L(y) denotes the loss to the user, SC denotes the scrap or rework cost, and IC denotes the inspection cost. .
When a product quality characteristic
y obeys a normal distribution
,
and
are its distribution function and probability density function, respectively. The probability density function is:
where
is the process mean and
is the variance,
,
.
Consider that
y is either smaller than the lower specification limit
LSL or larger than the upper specification limit
USL, i.e.,
y is a random variable placed on the interval [
LSL, USL], and then the distribution function of this quality characteristic
y is:
The probability density is:
Here
,
,
, and
. Therefore, the loss to the customer caused by the product quality characteristics falling within the specification limits is:
When the product quality characteristics Y > USL or Y < LSL, the resulting scrap cost or rework cost is (1 − P) SC.
Therefore, the overall expected loss is:
5.2. Engineering Specification Optimization under Hyperbolic Tangent Compensation
As it is complicated to calculate the expected compensation by the hyperbolic tangent compensation function of Equation (8), the function with the same variation trend can be selected to replace the compensation specification. It is known that the independent variable
x of the hyperbolic tangent function is continuous on (−∞,+∞), and
th(
x) has a third derivative at
x = 0. According to the Taylor series expansion, we can obtain:
Because
,
,
, and
,
th(
x) can be estimated by
th*(
x):
There is an estimation deviation between
th*(
x) and
th(
x), and the deviation is larger as
x deviates further from 0. For accurate estimation,
th*(
x) is revised now:
Then the hyperbolic tangent quality compensation function can be estimated as:
Therefore, the expected quality compensation can be expressed as follows:
When
, the original type is as follows:
Here the and are the distribution function and probability density of the standard normal distribution, respectively.
6. Example Calculation
This example was based on the overlapping width specification of joints in the construction quality acceptance of the bedding material laydown process. According to the construction quality acceptance assessment table of cushion material paving and filling process compiled by the Department of Water Project Construction Management of the Ministry of Water Resources of the People’s Republic of China, formulation of the best engineering specifications was studied in combination with the design specifications and requirements.
Through the construction records, measurement of the overlap width of the joints for quality inspection was conducted every 10 linear meters to detect a group of two points per group. When the error of the checkpoint was ±10 cm, the result would meet the specification and design requirements. Therefore, 10 was taken as the target value of quality characteristics in this example. According to the design requirements and engineering practice, the joint overlap width Y is a continuous random variable and follows the normal distribution. Mean μ = 10, variance , i.e., . The quality gain–loss coefficients on both sides of the target value are k1 = 9.5 and k2 = 12.5, respectively, with a unit scrap cost of 5 and a unit inspection cost of 0.7. The compensation coefficient α = 2, and the maximum compensation amount β = −15.
Combining Equation (1) with Equation (23), the expected total loss per unit of product for the traditional quality loss function is as follows:
The desired compensation for the mass compensation component is obtained using Equation (22) as follows:
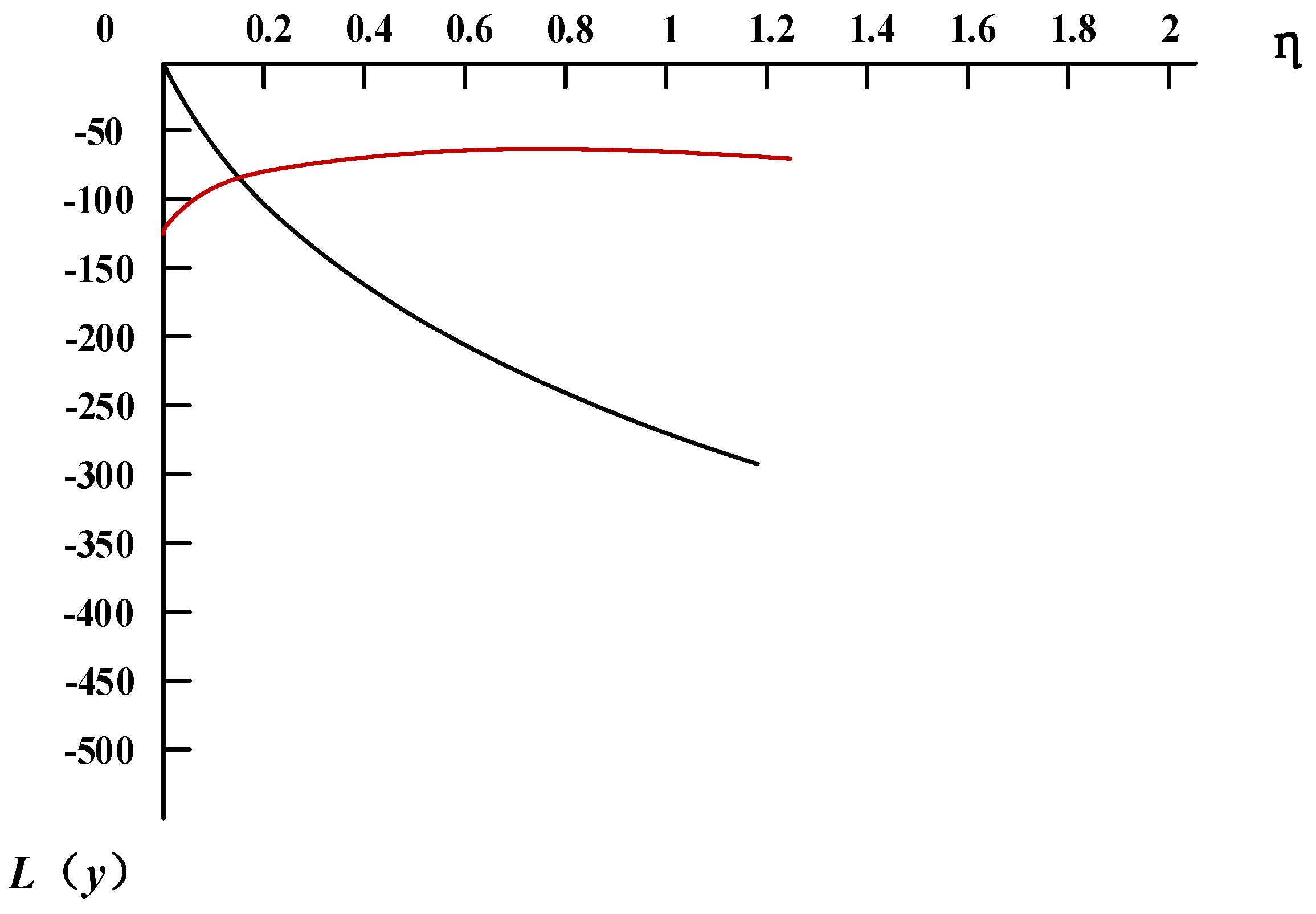
Assuming that the quality loss is positive, the quality compensation part is negative. MATLAB is used to solve and analyze the expected quality loss and expected compensation separately (with a negative compensation amount). In order to obtain an ideal state where quality compensation and quality loss are exactly equal, we allow the function image of the quality loss part to be symmetrical to the horizontal axis, as shown in
Figure 11. The optimal coefficient obtained is 0.186, and the optimal engineering specification range is:
We substitute the above data into Equation (20) to obtain the expected quality loss for users:
Therefore, the expected total loss per unit product is:
The expected compensation for the quality compensation part obtained using Equation (25) is as follows:
Assuming that the quality loss is positive and the quality compensation part is negative, MATLAB is used to solve and analyze the expected quality loss and expected compensation separately (with a negative compensation amount). In order to obtain an ideal state where quality compensation and quality loss are exactly equal, we allow the function image of the quality loss part to be symmetrical to the horizontal axis, as shown in
Figure 12. The optimal coefficient obtained is 0.162, and the optimal engineering specification range is:
Through comparison, this paper concludes that the calculation of project specifications based on the quadratic exponential quality gain–loss function is more accurate under the condition of considering quality compensation at the same time, which facilitates a more accurate determination of project specifications.
7. Conclusions
In this paper, three types of quality characteristics were introduced: Nominal-the-best characteristic, larger-the-better characteristic, and smaller-the-better characteristic. The quadratic exponential quality gain–loss function was complemented by combining the nature of hyperbolic tangent compensation, the quadratic exponential quality gain–loss function under the three characteristics was constructed, and the application scenarios of the quadratic exponential quality gain–loss function were broadened.
Considering the economic indexes in the product production process, this paper carried out engineering specification optimization design through the quadratic exponential quality gain–loss function and took the quality acceptance assessment as an example to calculate the expected total loss of the product and the expected quality compensation under hyperbolic tangent compensation, respectively. Finally, the optimal quality coefficient in product specification optimization was calculated by Matlab to be 0.162. Compared with the traditional quality profit and loss function, the optimal specification boundary was reduced from 0.744 to 0.648, achieving the effect of specification optimization.
Although the results of the study were analyzed and the above conclusions were obtained, the article still has the following shortcomings that require further research to address:
The existing research mostly focused on the theory of the quality gain–loss function under the action of a single quality characteristic, but the quality level of mass concrete construction is affected by more factors, such as the construction environment (temperature, humidity, altitude, etc.), construction equipment, construction technology, etc., which have a greater impact on the level of quality control of dam concrete construction. How to use the multivariate quality gain–loss function to represent the effect of quality control under the influence of multiple factors is the focus of future research.
This paper assumed that quality characteristics obey a normal distribution, but in actual production practice, the distribution of quality characteristics is often not unique, and subsequent research can expand the application of the quality gain–loss function under a non-normal distribution.
There are two main sources of the compensation component, one is the quality compensation brought by the coupling effect between processes and the other is the control of the construction process through specific measures to achieve the compensation. The source situation of compensation was rarely studied in this paper.
Author Contributions
Conceptualization, B.W. and Q.L.; methodology, B.W.; software, Q.L.; validation, Q.L., Q.Y. and X.N.; formal analysis, B.W.; investigation, Q.L.; resources, X.N.; data curation, J.L.; writing—original draft preparation, Q.L.; writing—review and editing, J.L.; supervision, X.N.; project administration, B.W.; funding acquisition, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
Natural Science Foundation of China (No. 51709116) and North China University of Water Resources and Electric Power Postgraduate Innovation Ability Improvement Project (NCWUYC-2023016).
Data Availability Statement
No data supporting results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, X.; Yu, R.; Ullah, S.; Wu, D.; Li, Z.; Li, Q.; Qi, H.; Liu, J.; Liu, M.; Zhang, Y. A novel loss function of deep learning in wind speed forecasting. Energy 2022, 238, 121808. [Google Scholar] [CrossRef]
- Khunkitti, S.; Siritaratiwat, A.; Premrudeepreechacharn, S. Multi-objective optimal power flow problems based on slime mould algorithm. Sustainability 2021, 13, 7448. [Google Scholar] [CrossRef]
- Rengasamy, D.; Jafarim, M.; Rothwell, B.; Chen, X.; Figueredo, G.P. Deep Learning with dynamically weighted loss function for sensor-based prognostics and health management. Sensors 2020, 20, 723. [Google Scholar] [CrossRef]
- Taguchi, G. Quality engineering in Japan. Commun. Stat.-Theory Methods 1985, 14, 2785–2801. [Google Scholar] [CrossRef]
- Spiring, F.A. The reflected normal loss function. Can. J. Stat. 1993, 21, 321–330. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, X.Y.; Xue, L. Economic design of ARMA control chart based on quality loss function. Stat. Decis. 2017, 7, 79–82. [Google Scholar]
- Xue, L. Economic Design of EWMA control charts with variable sampling intervals under preventive maintenance and quality loss functions. Oper. Res. Manag. Sci. 2020, 29, 116–121. [Google Scholar]
- Li, Y.P.; Liu, S.F.; Fang, Z.G.; Chen, H.Z. Parameter choice for multi-quality-characteristic product based on stochastic grey target model. Ind. Eng. Manag. 2017, 22, 49–54+61. [Google Scholar]
- Mao, K.; Liu, X.T.; Li, S.S.; Wang, X. Reliability analysis for mechanical parts considering hidden cost via the modified quality loss model. Qual. Reliab. Eng. Int. 2020, 37, 1373–1395. [Google Scholar] [CrossRef]
- Li, S.S.; Liu, X.T.; Wang, Y.S.; Wang, X.L. A cubic quality loss function and its applications. Qual. Reliab. Eng. Int. 2019, 35, 1161–1179. [Google Scholar] [CrossRef]
- Liu, X.T.; Mao, K.; Wang, X.L.; Wang, X.; Wang, Y.S. A modified quality loss model of service life prediction for products via wear regularity. Reliab. Eng. Syst. Saf. 2020, 204, 107187. [Google Scholar] [CrossRef]
- Wang, B. Research and Engineering Application of Quality Control Technology for Dam Concrete; China Water & Power Press: Beijing, China, 2019. [Google Scholar]
- Kapur, K.C.; Wang, C.J. Economic Design of specifications based on Taguchi’s concept of quality loss function. Qual. Des. Plan. Control. 1987, 27, 23–36. [Google Scholar]
- Kapur, K.C. An approach for development of specifications for quality improvement. Qual. Eng. 1988, 1, 63–77. [Google Scholar] [CrossRef]
- Kapur, K.C.; Cho, B.R. Economic design of the specification region for multiple quality characteristics. IIE Trans. 1994, 28, 237–248. [Google Scholar] [CrossRef]
- Chen, C.H. Specification limit under a quality loss function. J. Appl. Stat. 1999, 26, 903–908. [Google Scholar] [CrossRef]
- Wang, N.; Yan, N.; Zhang, S.; Liu, Y.M.; Yang, J.F. Analysis of multistage parallel manufacturing process capability based on utility ratio. Oper. Res. Manag. Sci. 2021, 30, 234–239. [Google Scholar]
- Zhao, J.L.; Li, J.; Xu, Y.P. An analysis of improved multivariate process capability based on entropy weight and fuzzy matter element. Ind. Eng. J. 2020, 23, 109–117. [Google Scholar]
- Mohammad, A. A fuzzy Taguchi loss-based process capability index. Int. J. Qual. Eng. Technol. 2013, 3, 303–318. [Google Scholar]
- Gholamreza, H.; Mohamadm, G.A. A process capability index for normal random variable with intuitionistic fuzzy information. Oper. Res. 2019, 21, 951–964. [Google Scholar]
- Wang, B.; Li, Q.K.; Liu, C.; Chen, Z.H.; Nie, X.T. Establishment and application of a grey quality gain-loss function model. Processes 2022, 10, 495. [Google Scholar] [CrossRef]
- Wang, B.; Yang, Q.; Liu, C.; Li, Q.K.; Nie, X.T. Optimization model of engineering specifications based on grey quality gain-loss function. Coatings 2021, 11, 1327. [Google Scholar] [CrossRef]
- Wang, B.; Fan, T.Y.; Tian, J.; Liu, M.Q.; Nie, X.T. Designing a quality gain-loss function for larger-the-better characteristic and smaller-the-better characteristic under not neglecting the linear term loss and keeping compensation amount constant. Math. Pract. Theory 2019, 49, 153–160. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).