Next Article in Journal
Dynamics of Hydrogen Storage through Adsorption: Process Simulation and Energy Analysis
Next Article in Special Issue
Melting Behavior and Densities of K2B2OF6 Melts Containing KReO4
Previous Article in Journal
Automated Production at Scale of Induced Pluripotent Stem Cell-Derived Mesenchymal Stromal Cells, Chondrocytes and Extracellular Vehicles: Towards Real-Time Release
Previous Article in Special Issue
Electrochemical Behavior of Dysprosium Ion and Its Co-Electroreduction with Nickel Ions in the Molten KCl-NaCl-CsCl Eutectic
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 11
Issue 10
10.3390/pr11102939
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Cation Nonstoichiometry on Hydration and Charge Transport Processes in Yb-Doped SrZrO3 Perovskite-Type Proton Conductor for Ceramic Electrochemical Cells

by
Adelya Khaliullina
,
Anastasia Meshcherskikh
and
Liliya Dunyushkina
*
Institute of High Temperature Electrochemistry, Ural Branch of the Russian Academy of Sciences, 20 Akademicheskaya St., Ekaterinburg 620137, Russia
*
Author to whom correspondence should be addressed.
Processes 2023, 11(10), 2939; https://doi.org/10.3390/pr11102939
Submission received: 8 September 2023 / Revised: 28 September 2023 / Accepted: 5 October 2023 / Published: 10 October 2023
(This article belongs to the Special Issue Electrochemical Technology for New Materials Synthesis and Reprocessing)
Browse Figures
Versions Notes

Abstract

:
The effect of Sr deficiency on the hydration process and ionic and electronic conductivity of Yb-doped SrZrO3 proton conductors with a perovskite-type structure was investigated. Dense SrxZr0.95Yb0.05O3-δ (x = 0.94–1.00) ceramics were prepared using solution combustion synthesis. Thermogravimetry and Raman spectroscopy methods were used to determine the concentration of bulk protonic species. Sr deficiency was found to enhance the hydration ability of the zirconate; however, lowering of Sr content to x = 0.94 deteriorated the proton uptake. The conductivity of the SrxZr0.95Yb0.05O3-δ series depending on the oxygen partial pressure at different humidities was studied by the four-probe direct current technique. Sr-deficient ceramics with x = 0.96 and 0.98 were shown to become purely protonic conductors in humid atmospheres at a temperature close to 500 °C. The ionic conductivity reaches its highest value at a Sr content of x = 0.98 (2 × 10−4 S cm−1 at 500 °C and pH2O = 3.17 kPa). The hydration behavior and transport properties of SrxZr0.95Yb0.05O3-δ are discussed in terms of the defect chemistry model that assumes the distribution of Yb ions over Sr and Zr sites at a large Sr deficiency.

1. Introduction

Proton-conducting oxides have attracted the active attention of researchers since the beginning of the 1980s, after the discovery of proton conduction in acceptor-doped SrCeO3 by Iwahara et al. [1,2,3,4]. Since then, proton conductivity has been found in many oxides with perovskite and perovskite-type structures [5,6,7,8,9,10,11]. The high interest in proton-conducting oxides is due to the possibility of their use in solid oxide fuel cells (SOFCs), solid oxide electrolysis cells (SOECs) for hydrogen generation from steam, sensors, hydrogen separation membranes, etc. Perovskite oxides are promising materials for use as both electrocatalysts and electrolytes due to the ability to optimize their properties by varying the chemical composition of the host matrix and dopants [12,13,14]. For use as electrolytes in electrochemical energy storage devices, the material must have high ionic conductivity, very low electronic conductivity and excellent chemical stability in the operating conditions of an electrochemical cell. The electronic conduction of the electrolyte leads to reducing the efficiency of a SOFC/SOEC [15,16].
The search for materials that meet these requirements remains urgent. Perovskites based on barium and strontium cerates demonstrate high ionic conductivity but suffer from notable electronic conductivity and are unstable to carbon dioxide and water vapor [17,18,19,20,21,22]. On the contrary, the zirconates of alkaline earth elements have high chemical resistance and low electronic conductivity, but their ionic conductivity is lower [20,21,23,24]. Acceptor doping of perovskite-type oxides, which results in the generation of oxygen vacancies, is known to strongly affect their hydration ability and proton conductivity [8,10,23,25]. The cation nonstoichiometry also influences the defect chemistry and transport properties of proton-conducting perovskites [26,27,28,29,30,31,32]. Protons are not a structural element of proton-conducting oxides, and proton defects are formed during the hydration of oxides in humid atmospheres. Each material has its own ability to incorporate water and accumulate bulk proton defects, which depends on the chemistry of the host matrix and dopants as well as external conditions such as temperature, oxygen partial pressure and water vapor partial pressure.
In our recent research, we reported the effect of Sr deficiency on the electrical conductivity of SrxZr0.95Yb0.05O3-δ ceramics, which was studied using the impedance spectroscopy method [32]. It was found that a small Sr deficiency improves the grain interior conductivity of the ceramics and that the conductivity increases with increasing the water vapor partial pressure, indicating that protons are involved in the charge transfer process. However, the impact of defect chemistry on the fraction of proton transfer in SrxZr0.95Yb0.05O3-δ perovskites has not been fully revealed; for a deeper understanding, the charge transfer processes in these materials, the hydration ability and the electronic and ionic (O2− and H+) conductivities depending on the cation nonstoichiometry, temperature, the partial pressures of oxygen and water vapor need to be studied. The present research aims to establish how the cation nonstoichiometry affects the concentration of bulk protonic species in SrxZr0.95Yb0.05O3-δ (x = 0.94–1.00) oxides and the contributions of ions and electrons (or holes) to the charge transfer process for the rational search for new proton-conducting solid electrolytes.

2. Defect Chemistry of SrxZr0.95Yb0.05O3-δ

2.1. Stoichiometric Yb-Doped Strontium Zirconate

The generally accepted model of defect formation can be applied to explain electrical transport in acceptor-doped strontium zirconates (see e.g., [33,34,35,36]). Replacing Zr4+ with Yb3+ is accompanied by the formation of oxygen vacancies as described by the following reaction:
Y b 2 O 3 → 2 Y b Z r / + V O • • ,
where Y b Z r / is the Yb3+ cation on Zr4+ site and V O • • is an oxygen vacancy in terms of Kröger–Vink notation.
The concentrations of oxygen vacancies and dopant ions are related by the electroneutrality condition:
[ Y b Z r / ] = 2 [ V O • • ] ,
In oxidizing atmospheres, the concentrations of defects are determined by the following reaction:
1 2 O 2 + V O • • = O O x + 2 h • ,
where O O x is an oxygen anion on its normal site and h • is an electron hole.
Taking into account the law of mass action for Reaction (3) and the electroneutrality condition (2), the following expression for the concentration of electron holes can be derived:
[ h • ] = ( 1 2 K 3 [ Y b Z r / ] ) 1 / 2 ( p O 2 ) 1 / 4 ,
where K3 is the equilibrium constant of Reaction (3).
In reducing atmospheres, oxygen vacancies and electrons are generated as a result of the release of oxygen from the oxide:
O O x = 2 e / + V O • • + 1 2 O 2 .
As follows from the law of mass action for Reaction (5) and the electroneutrality condition (2), the concentration of electrons depends on the oxygen partial pressure as follows:
[ e / ] = ( K 5 ) 1 / 2 ( 1 2 [ Y b Z r / ] ) – 1 / 2 ( p O 2 ) – 1 / 4 ,
where K5 is the equilibrium constant of Reaction (5).
Since the electrical conductivity is equal to the product of the concentration, mobility and charge of carriers, and assuming that mobility does not depend on pO2, then the electron and hole conductivities are proportional to p O 2 − 1 / 4 and p O 2 1 / 4 , respectively. The oxide-ion conductivity is assumed not to change with the oxygen partial pressure since the concentration of oxygen vacancies is determined by the acceptor dopant concentration according to Equation (2). Therefore, the electrical conductivity of an acceptor-doped strontium zirconate in dry atmospheres can be written as:
σ = σ i + σ e + σ h = σ i + σ e o p O 2 − 1 4 + σ h o p O 2 1 4 ,
where σi, σe and σh denote the ionic, electron and hole conductivities; σeo and σho are the conductivities of electrons and holes at pO2 = 1 atm.
In a humidified atmosphere, proton defects are generated in the acceptor-doped SrZrO3 as a result of the reaction of hydration:
H 2 O ( g ) + V O • • + O O × = 2 O H O • ,
where O H O •   is a proton localized on an oxygen anion.
Assuming that the concentration of electronic defects in Yb-doped SrZrO3 is low compared to that of ionic ones, the electroneutrality equation in humidified atmosphere can be written as follows:
[ Y b Z r / ] = 2 [ V O • • ] + [ O H O • ] .
The concentration of proton defects can be derived from the law of mass action for the hydration reaction (Equation (8)):
n O H = [ O H O • ] = ( K 8 [ V O • • ] ) 1 / 2 ( p H 2 O ) 1 / 2 ,
where K8 is the equilibrium constant of Reaction (8).
Combining Equations (9) and (10) yields the following expression for the concentration of proton defects:
n O H = O H O • = − 1 4   K 8   p H 2 O + ( 1 16   K 8 2 p H 2 O 2 + 1 2   K 8   p H 2 O Y b Z r / ) 1 / 2 ,
which describes the effect of the water partial pressure on the proton concentration and, accordingly, on the proton conductivity.
It follows from Equation (11) that at low pH2O, the concentration of protons is proportional to p H 2 O 1 / 2 :
n O H   =   O H O • = 2 − 1 / 2 ( K 8 [ Y b Z r / ] ) 1 / 2 ( p H 2 O ) 1 / 2 .
In highly humid atmospheres, all oxygen vacancies are occupied by proton defects so that Equation (9) can be transformed as follows:
n O H = [ O H O • ] = [ Y b Z r / ]   .
So, at high pH2O, the concentration of protons becomes equal to the concentration of the acceptor impurity and does not vary with humidity.

2.2. Sr-Deficient Yb-Doped Strontium Zirconate

In the Sr-deficient SrxZr0.95Yb0.05O3-δ (x < 1), additional oxygen vacancies are generated to maintain electrical neutrality:
− S r O → V S r / / + V O • • ,
where V S r / / is a vacancy of the Sr2+ cation.
The condition of electrical neutrality in this case can be written as:
[ V S r / / ] + [ Y b Z r / ] = 3 [ V O • • ] .
Thus, the deficiency of strontium and the associated increase in the concentration of oxygen vacancies should lead to an increase in the ionic conductivity.
In highly humid atmospheres, proton defects are expected to occupy all oxygen vacancies, and their concentration can be calculated as follows:
n O H = 2 [ V S r / / ] + [ Y b Z r / ] .
On the other hand, the deficiency of Sr may boost the incorporation of Yb3+ cations onto the sites of Sr2+ cations, which means the formation of the positively charged defects Y b S r • , the charge of which will be compensated by a decrease in the oxygen vacancy concentration. In the case of the incorporation of Yb3+ onto both Zr and Sr sites and assuming a negligible concentration of electronic defects, the electroneutrality condition can be written as follows:
[ V S r / / ] + [ Y b Z r / ] = [ Y b S r • ] + [ V O • • ] .
Accordingly, the concentration of proton defects in highly humid atmospheres will decrease as:
n O H   =   2 [ V S r / / ] + [ Y b Z r / ] − [ Y b S r • ] .
In our previous research, the conductivity of the SrxZr0.95Yb0.05O3-δ (x = 0.94–1.00) series was studied using impedance spectroscopy; it was found that a small Sr deficiency (x = 0.98) improved conductivity, which was explained by an increase in the concentration of oxygen vacancies (see Equations (2) and (15)); but with decreasing Sr content, conductivity decreased, which was supposed to be caused by the partitioning of Yb3+ ions over Sr and Zr sites and the resulting decrease in the concentration of oxygen vacancies (see Equation (17) [29]. Although our previously obtained data on the conductivity of SrxZr0.95Yb0.05O3-δ are consistent with the model of defect formation described above, to understand the processes of charge transfer in these oxides, data on the contributions of different charge carriers (oxide ions, protons, electrons/holes) to electrical transfer are required.
To gain deeper insight into the nature of the electrical conductivity of SrxZr0.95Yb0.05O3-δ, this research aims to study the hydration ability of the oxides, deconvolute the contributions of ions (O2− and H+) and electrons (or holes) to the charge transfer process and establish how the cation nonstoichiometry, temperature, the partial pressures of oxygen and water vapor affect the partial conductivities.

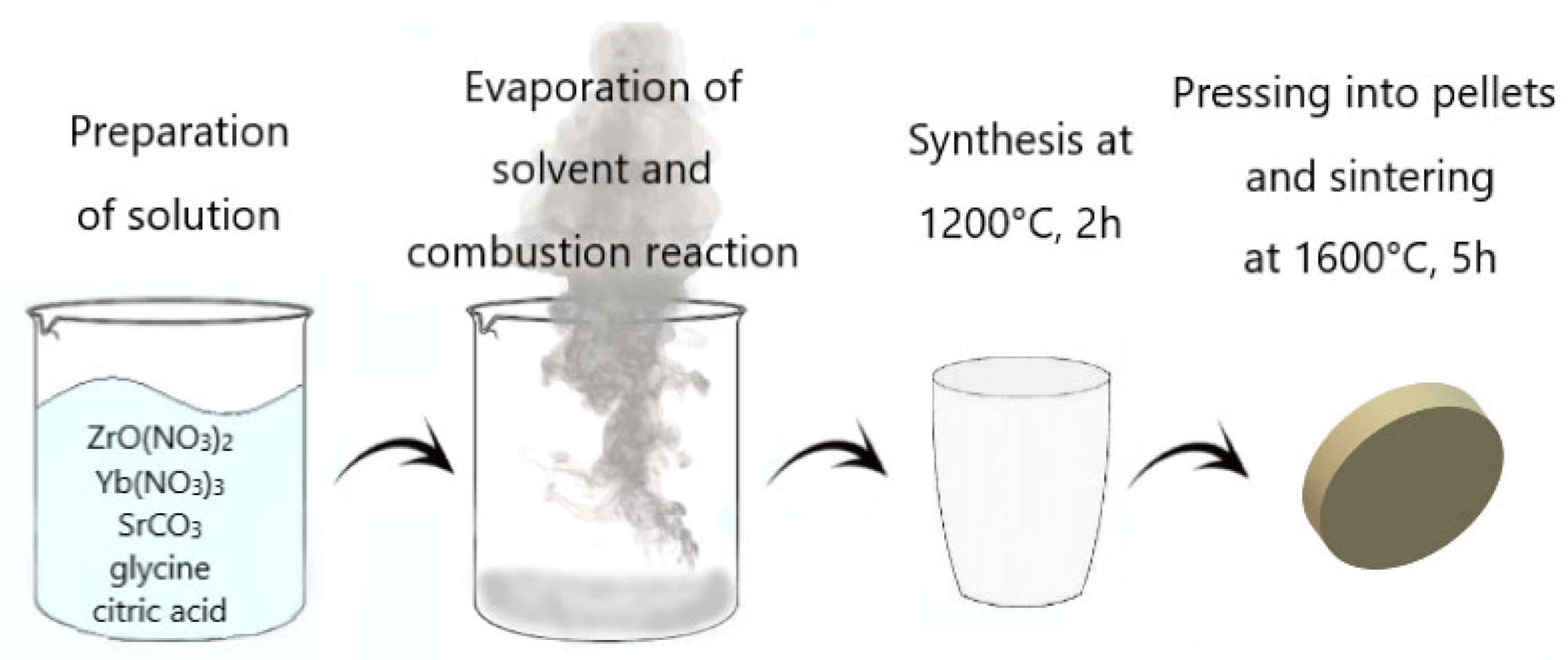
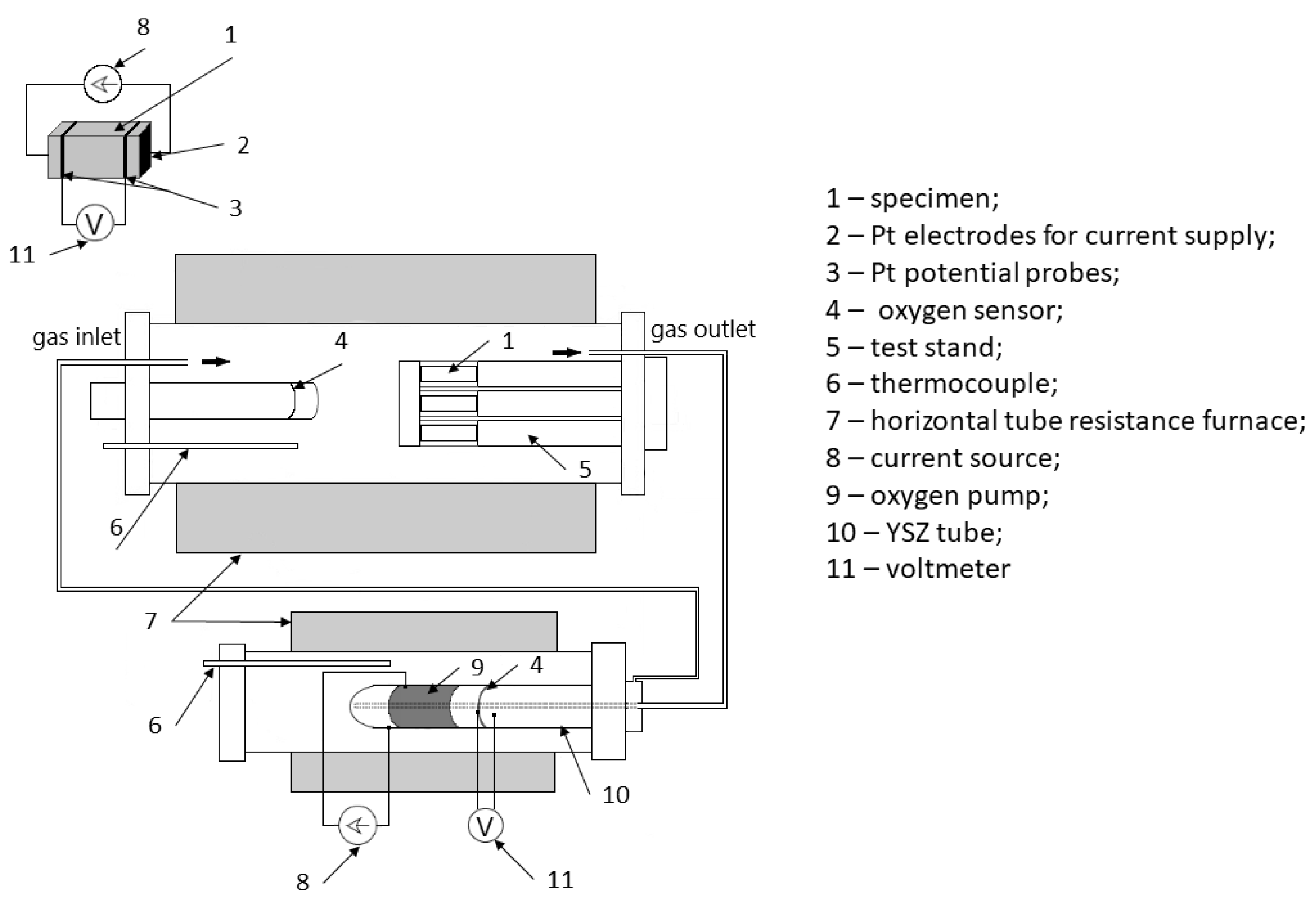
3. Materials and Methods

The powders of the SrxZr0.95Yb0.05O3-δ (x = 0.94–1.00) series were synthesized from SrCO3, ZrO(NO3)2·2H2O and Yb(NO3)3·nH2O (all with 99% purity) by using solution combustion synthesis. A schematic diagram of the synthesis is given in Figure 1. First, ZrO(NO3)2·2H2O and Yb(NO3)3·nH2O were dissolved in distilled water and ethanol, respectively. Then these solutions and the powder of SrCO3 were mixed in the ratio corresponding to nominal compositions, and citric acid (99% purity) and glycine (99% purity) were added as a complexant and a fuel, respectively; the molar ratio of the metal cations, glycine and citric acid was 2:2:1. The prepared solution was kept on a hot plate until it ignited. The obtained powder was calcined at a temperature of 1200 °C for 2 h, then thoroughly ground, pressed into pellets at 130 MPa and sintered at 1600 °C for 5 h. The density of the sintered pellets was determined by the Archimedes method and was 90–95% of the theoretical X-ray density.
The samples were characterized by the powder X-ray diffraction (XRD) method on a D/MAX-2200 Rigaku (Tokyo, Japan) diffractometer using monochromatic CuKα-radiation (λ = 1.5418 Å) at room temperature. The diffraction patterns were recorded in the range of 2q from 15° to 90° at a scanning speed of 3.33°/min with a step increment of 0.02°. Analysis of the phase composition and calculation of the crystallographic parameters were carried out using the software package MDI Jade 6.5 and database PDF-2 ICDD. Structural refinement was carried out using the FullProf 2000 (Version July2001) software [37].
The microstructure of the SrxZr0.95Yb0.05O3-δ ceramics was studied with the help of the MIRA 3 LMU (Tescan, Brno, Czechia) scanning electron microscope (SEM). The surface of the ceramic pellets was polished and annealed at 1400 °C for 4 h to obtain a clear granular pattern.
Raman spectroscopy was used to identify adsorbed impurities and their desorption temperature. Raman spectra were measured using a Renishaw U 1000 microscope-spectrometer (Renishaw, Wotton-under-Edge, UK) equipped with a 532 nm Nd:YAG laser. The measurements were carried out in backscattering geometry in the range of a Raman shift of 50–4000 cm−1 at a laser power of 50 mW upon heating from room temperature (23 °C) to 500 °C at a heating rate of 1 °C/min. For the spectroscopic measurements, the powder of Sr0.98Zr0.95Yb0.05O3-δ obtained by crushing and grinding a ceramic specimen in an agate mortar was hydrated in a flow of wet air at 700 °C for 96 h. The air flow was saturated with water vapor by blowing through a bubble with the water maintained at 25 °C (pH2O = 3.17 kPa).
The thermogravimetric (TG) method was used to determine the concentration of proton defects in SrxZr0.95Yb0.05O3-δ. The TG study was carried out by using a thermal analyzer STA Jupiter 449 F1 (Netzsch, Selb, Germany) equipped with a water vapor generator Asteam DV2MK (Adrop, Furth, Germany). For this study, the powder specimens obtained by crushing and grinding the ceramic pellets of SrxZr0.95Yb0.05O3-δ were used. A powder was placed in an alumina crucible and heated in a flow of Ar (30 mL/min) from 25 °C to 1000 °C at a heating rate of 10 °C/min and kept under these conditions for 4 h for the complete dehydration of the specimens. After dehydration, dry Ar was saturated with water vapor (pH2O = 20 kPa), and the specimen was exposed to these conditions until the constant weight was reached (8 h). After the saturation of the specimen with water, it was cooled down to 200 °C at a rate of 10 °C/min with 3 h exposures every 100 °C to equilibrate the specimen with the surrounding atmosphere. In order to take into account the effect of the crucible mass change during the experiment, we repeated the experiment with an empty crucible and subtracted the crucible mass change from the change in the mass of the crucible with a sample. The concentration of proton defects was calculated as follows:
n O H = 2   ·   ∆ m   · M o x i d e m o x i d e ·   M H 2 O   ,
where Dm and moxide denote the mass change and the mass of a specimen, respectively; Moxide and MH2O are molecular masses of the oxide and water.
The electrical conductivity of SrxZr0.95Yb0.05O3-δ was measured by using a four-probe direct current technique. A schematic view of the cell for the conductivity measurement is shown in Figure 2. For these measurements, rectangular-shaped specimens were cut from the pellets. Two porous platinum electrodes were applied on the ends of the rectangular specimens by painting Pt paste and sintering at 1050 °C for 2 h to supply current, and two platinum wires were wound around the specimens to serve as potential probes as shown in Figure 2. The specimens were installed on a test stand having room for five specimens, which ensured the same conditions for all specimens. The loaded stand was installed in a horizontal tube resistance furnace. The measurements were carried out in dried and humidified atmospheres in the temperature range of 500–800 °C. The dried atmosphere was made by passing gas through a glass pipe filled with zeolite beads. The residual water vapor pressure in the dried gas was measured by using a Baikal-3M hygrometer (JSC Etalon, Irkutsk, Russia) and was equal to 0.04 kPa. For humidification, the gas was passed through a bubbler with the water maintained at temperatures of 0 °C and 25 °C; the corresponding water vapor partial pressures were 0.61 kPa and 3.17 kPa. The conductivity was measured in a wide range of the oxygen partial pressure; the pO2 was varied by using a home-made electrochemical oxygen pump made of an yttria-stabilized zirconia (YSZ) ceramic tube and platinum electrodes. The oxygen pump was built into a gas line as shown in Figure 2. In humidified atmospheres, a pO2 value of ~10−13 Pa was achieved; while in the dried gas, it was possible to obtain a pO2 of only ~90 Pa due to the depletion of the electrochemically active component (oxygen) in the gas.

4. Results

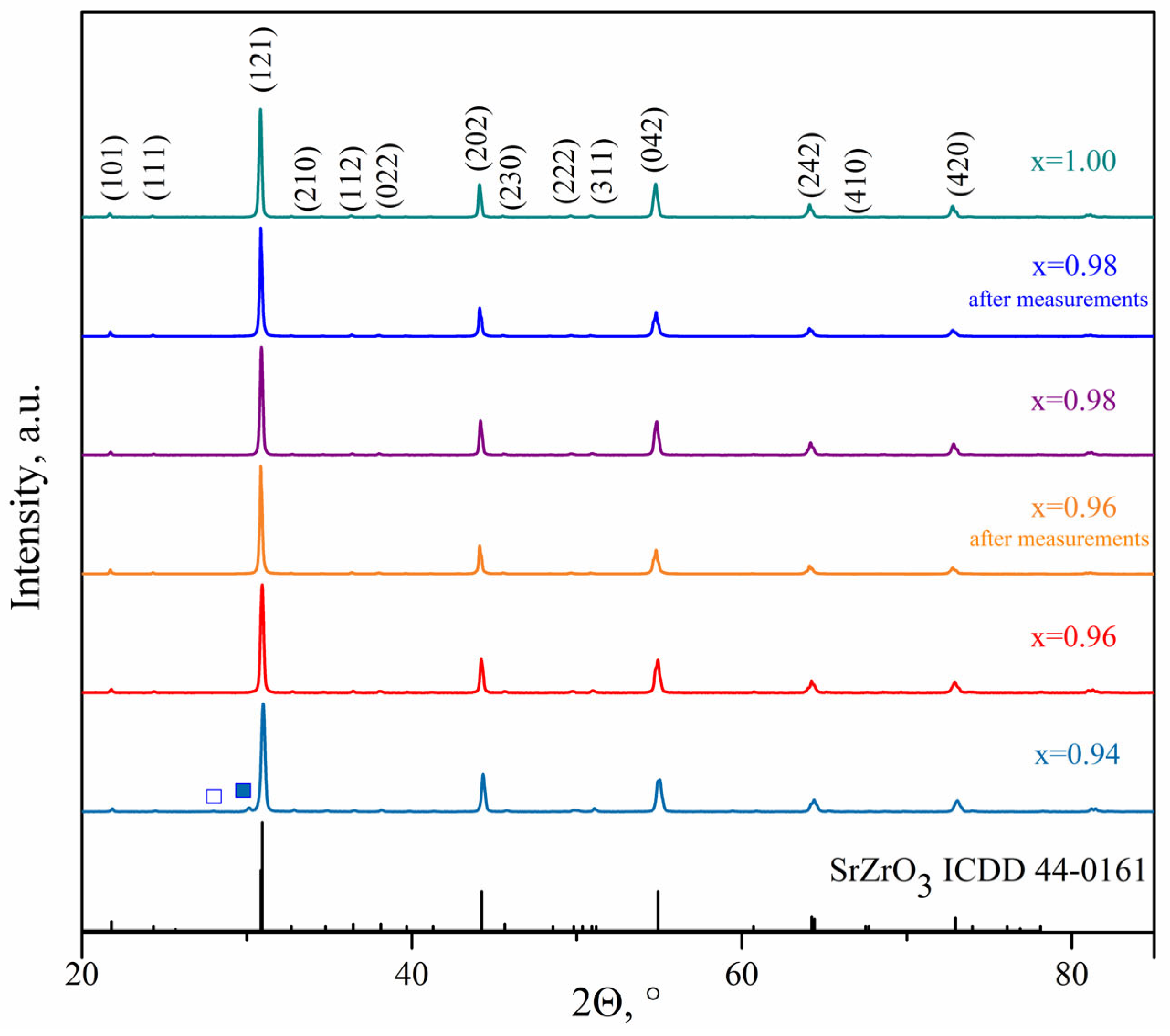
4.1. Phase Composition and Microstructure of SrxZr0.95Yb0.05O3-δ

The XRD patterns of the SrxZr0.95Yb0.05O3-δ powders shown in Figure 3 confirm the formation of an orthorhombic perovskite with space group Pnma, isostructural with SrZrO3 (PDF No. 44-0161). At a small Sr deficiency (x ≥ 0.96), the samples are monophase; however, at x = 0.94, minor ZrO2-based phases are observed. The lattice parameters and the unit cell volume as the functions of Sr content are presented in Figure 4. As can be seen, they slightly decrease with increasing Sr deficiency, which can be explained, firstly, by an increase in the concentrations of the vacancies of strontium and oxygen and, secondly, by the occupation of Sr sites by smaller Yb cations, which is facilitated by the growth of strontium deficiency.
To study the stability of the zirconates to changes in pO2 in the atmosphere, the diffraction patterns of the powders obtained by grinding the samples of SrxZr0.95Yb0.05O3-δ with x = 0.96 and 0.98, on which electrical conductivity measurements were carried out in a wide range of pO2, were recorded (see Figure 3). The XRD results confirm the steadiness of the structure of SrxZr0.95Yb0.05O3-δ upon changing the oxidizing atmosphere (air) to reducing atmosphere (pO2 = 10−13 Pa).
To establish the localization of the dopant cations, structural refinement using the full-profile analysis of the X-ray data was carried out for the composition with x = 0.96, which has a fairly large deficit of Sr and remains single-phase. We fitted the experimental XRD pattern of Sr0.96Zr0.95Yb0.05O3-δ in the frame of three models: (1) all Yb cations incorporated into Zr sites, (2) all Yb cations incorporated into Sr sites, and (3) Yb cations are distributed over the sites of Zr and Sr in equal proportions. Figure 5 shows the results of the Rietveld refinement of the X-ray diffraction data of Sr0.96Zr0.95Yb0.05O3-δ carried out in the frame of the models (1–3). The obtained values of the profile residual (Rp), weighted profile residual (Rwp), expected profile residual (Rexp) and χ2 are summarized in Table 1. As can be seen, all the parameters are very similar, which is probably because of the similarity of the atomic scattering powers of Sr and Zr. Thus, the refinement of the structure of Sr0.96Zr0.95Yb0.05O3-δ does not allow us to determine the position of the dopant ions. We expect that the use of the neutron diffraction method will be more effective because the neutron scattering length is independent of atomic number and neutron diffraction is more sensitive to lightweight atoms including oxygen. We are planning neutron diffraction experiments in the near future.
The microstructure of SrxZr0.95Yb0.05O3-δ ceramics was observed using scanning electron microscopy. As can be seen from the SEM images (Figure 6), which were originally presented in our recent research [32], the samples have a dense granular structure with a grain size of up to 2.5 microns. Strontium content does not have a noticeable effect on the microstructure. In the SEM image of the sample with x = 0.94 (Figure 6d), inclusions of light gray grains about 0.5 µm in size can be seen. This is consistent with the XRD data, according to which minor ZrO2-based phases appear at x = 0.94. The results of energy-dispersive X-ray spectroscopy (EDX) revealed that the minor phase grains contained mostly zirconium and ytterbium; it was therefore concluded that the light gray inclusions are ytterbium-doped zirconia [32].

4.2. Raman Spectra

When used in electrochemical applications, a proton-conducting electrolyte comes into contact with humid atmospheres. Upon contact with water vapor, the processes of physical and chemical adsorption and the incorporation of water into the electrolyte crystal (Reaction (8)) take place.
A common method for determining the concentration of proton defects in proton-conducting oxides is to measure the mass of a sample with a change in humidity or temperature using thermogravimetric analysis. However, the weight gain or loss of a sample may be due to a change in the concentration of both adsorbed and incorporated water. Since the concentration of bulk protonic species matters for the bulk conductivity, an understanding of H2O adsorption/desorption behavior is very important for the correct determination of the mass of the incorporated water. The adsorbed and incorporated particles have different binding energies; consequently, with increasing temperature, first, the desorption of physically adsorbed water molecules weakly bound to the surface by van der Waals forces occurs, and then, at higher temperatures, chemisorbed particles desorb, and the dehydration process predominates at even higher temperatures. A convenient way to determine the temperature at which the process of water desorption is completed is to study the oxide surface using Raman spectroscopy, which has a high sensitivity to adhered surface impurities, during heating.
For the Raman study, we prepared a powder by crushing the pellet of Sr0.98Zr0.95Yb0.05O3-δ and exposed it to humidified air (pH2O = 3.17 kPa) at a temperature of 700 °C for 24 h. The Raman spectra of the Sr0.98Zr0.95Yb0.05O3-δ powder were recorded upon heating from room temperature (23 °C) to 500 °C in the frequency range of 50–4000 cm−1; the obtained spectra are shown in Figure 7.
It is known that orthorhombic SrZrO3 is characterized by eight Raman modes observed at a Raman shift below 600 cm−1: the bands at 117, 144 and 349 cm−1 are related to B2g modes, and the bands at 169, 255, 275, 412 and 552 cm−1 correspond to Ag modes [31,38,39]. The bands observed at the Raman shift of 700–800 cm−1 lay in the region of stretching ZrO6 modes and are probably caused by the oxygen vacancies generated due to acceptor doping and strontium deficiency according to Equations (1) and (14) [31].
As can be seen in Figure 7, in addition to the Raman modes related to the orthorhombic strontium zirconate, there are strong bands at 996, 1068, 3620 and 3880 cm−1 in the spectra, which are likely due to impurities in the specimen. With increasing temperature, the intensity of the bands at 1070, 3620 and 3880 cm−1 decreases, while the peak at 996 cm−1 remains strong even at 500 °C.
The band at 996 cm−1 is probably due to the contamination of the specimen with silicon oxide during grinding in an agate mortar. The spectrum of a glassy silicate was reported to consist of two bands at ~500 and ~1000 cm−1 corresponding to the bending and stretching modes of the Si–O bond [40]. The assignment of the band at 996 cm−1 to SiO2 is consistent with the fact that the intensity of this peak does not change with increasing the temperature up to 500 °C, as it should be in the case of an adsorbed impurity.
It is known that the proton-conducting oxides containing alkaline-earth metals tend to form carbonates in CO2-containing atmospheres, which may be one of the causes of electrolyte degradation [41,42,43]. It was shown by using the first-principles approach that the SrO-terminated surfaces of strontium zirconate can trap atmospheric CO2, which results in the formation of a thin layer of CO3-like complexes [44]. The CO32− radical was reported to have a strong Raman active mode at 1063 cm−1 which was assigned to the C–O symmetric stretch [45]. The chemisorption of CO2 on the surface of strontium zirconate may result in the formation of carbonates; the Raman spectrum of SrCO3 was reported to have an intensive band at 1074 cm−1 [46].
Given the above, the Raman band at 1068 cm−1 can be assigned to both adsorbed carbonate ions and SrCO3. As can be seen in Figure 7, the intensity of this band significantly decreases with increasing temperature, but it is still observed at 500 °C. Taking into account that the thermal decomposition of strontium carbonate to produce strontium oxide and carbon dioxide takes place at a temperature of ~1200 °C [47], it is reasonable to assume that when heated from room temperature to 500 °C, mainly desorption of adsorbed CO2 occurs; therefore, the band at 1068 cm−1 is due to adsorbed CO2. However, the presence of some strontium carbonate cannot be excluded.
Group theory and the symmetry of the water molecule predict three vibration modes: the bending H–O–H mode located at 1595 cm−1 and two stretching modes corresponding to the O–H bond located at 3652 and 3756 cm−1 [48,49]. Therefore, a broad band at 3500–3750 cm−1 observed on the Raman spectra of Sr0.98Zr0.95Yb0.05O3-d can be assigned to the stretching O–H modes of water adsorbed on the surface of the specimen. This band gradually disappears with increasing temperature up to 300 °C, which indicates the completion of the process of water desorption at this temperature.
The intensity of the Raman band at 3880 cm−1 also decreases with increasing temperature, which indicates that it is due to some surface species desorbing upon heating to about 200 °C; however, we could not find literature data that would allow us to associate this peak with a specific adsorbed complex. Perhaps, this band is related to some organic impurity at the surface of the powder.
Based on the analysis of the Raman spectra of the Sr0.98Zr0.95Yb0.05O3-d powder, it can be concluded that adsorbed water mainly desorbs from the oxide surface upon heating to ~300 °C.

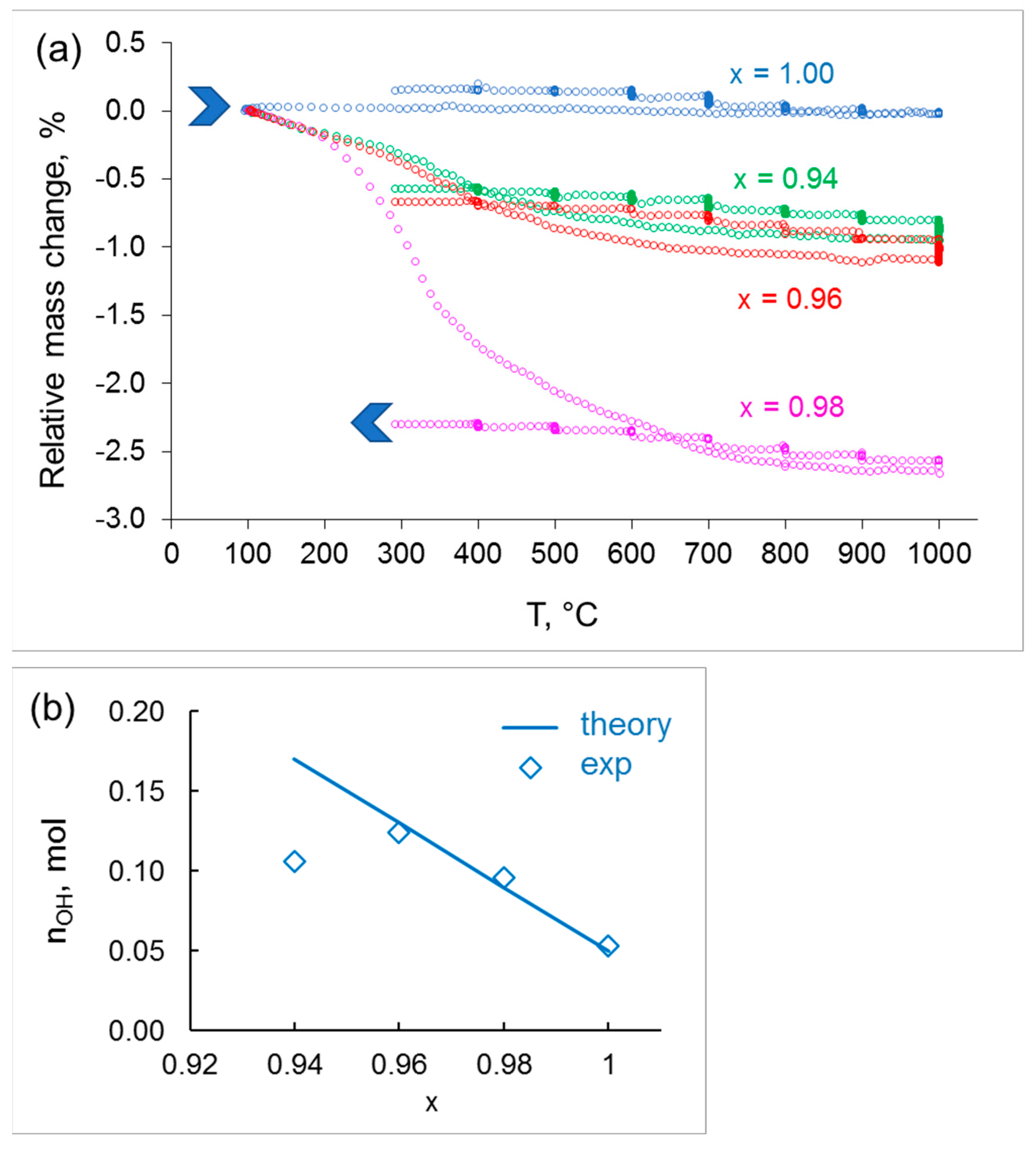
4.3. Thermogravimetry Analysis

The TG curves of the SrxZr0.95Yb0.05O3-d powders heated up to 1000 °C in a flow of Ar, kept under these conditions for 4 h for dehydration, then exposed to wet Ar (pH2O = 0.2 atm) until saturation (8 h) and cooled down to 300 °C (to avoid water adsorption as discussed in the previous section) with 3 h exposures every 100 °C are shown in Figure 8a. The samples lose weight upon heating in dry Ar due to the desorption of surface impurities and the dehydration processes and regain weight upon cooling in wet Ar due to re-hydration. The sample with x = 1.00, unlike the other samples, almost does not lose weight when heated, which indicates a small amount of adhered impurities in the original powder, but it gains weight upon cooling due to the incorporation of water. The weight of the powders nearly reaches saturation upon cooling to ~500 °C.
The concentration of proton defects in SrxZr0.95Yb0.05O3-δ versus Sr nonstoichiometry, calculated from the TG experiment using Equation (19), is presented in Figure 8b. The dependence predicted by the defect chemistry (Equation (16)) is shown by a solid line. As can be seen, the concentrations of bulk protonic species in SrxZr0.95Yb0.05O3-δ determined from TG data increase with decreasing Sr content in the range of 0.96 ≤ x ≤ 1 in accordance with Equation (16). Good agreement between the calculated values and those obtained from TG measurements indicates that the water solubility limit approaches the theoretical maximum. At x = 0.94, the proton concentration significantly falls compared to that calculated in the frame of assumption that all Yb ions are localized in Zr sites. This decrease may be due to the incorporation of a part of the dopant ions on Sr sites, where they act as a donor, which should result in a decrease in the concentration of oxygen vacancies and, accordingly, proton defects as predicted by Equation (18).

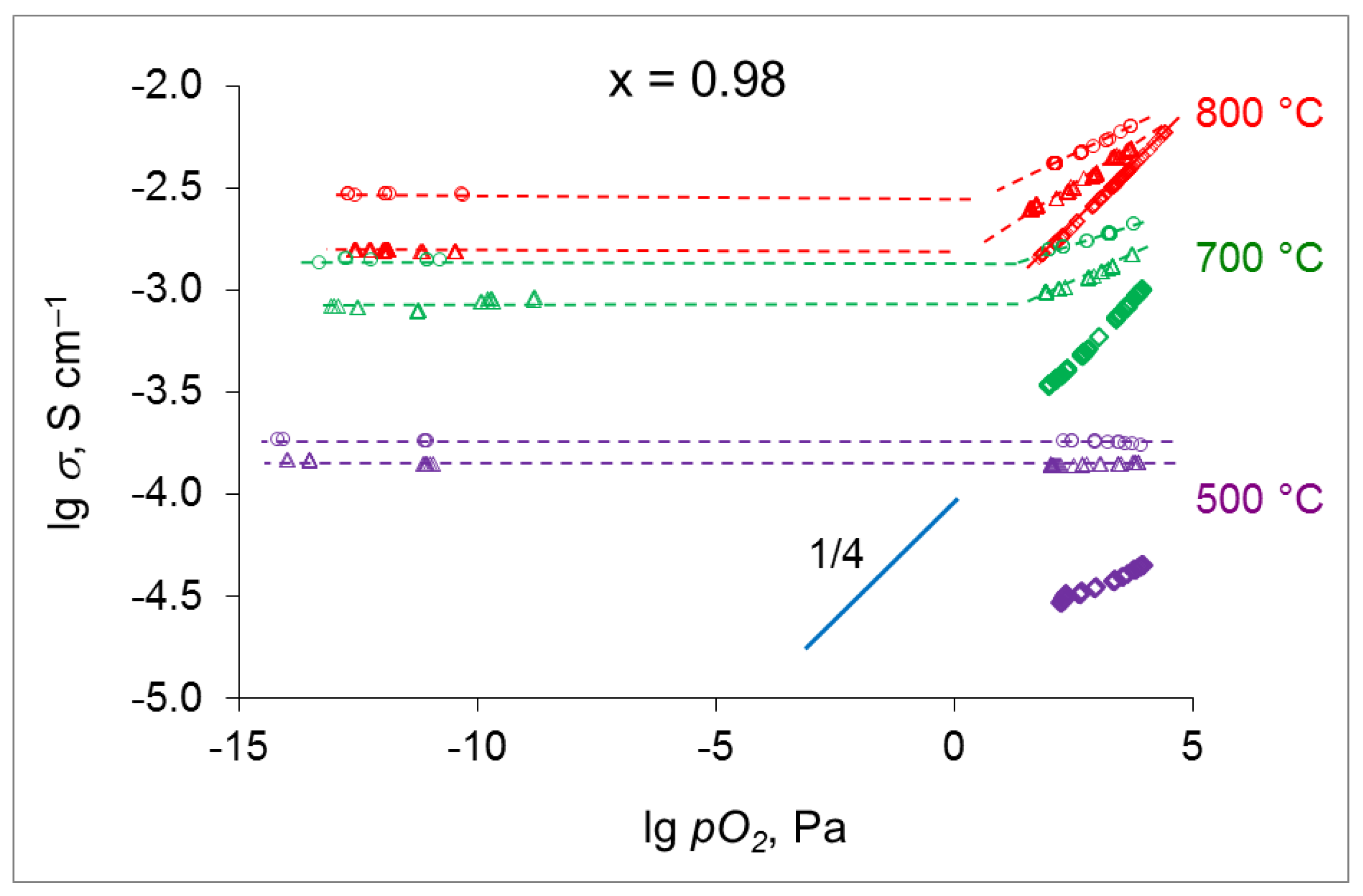
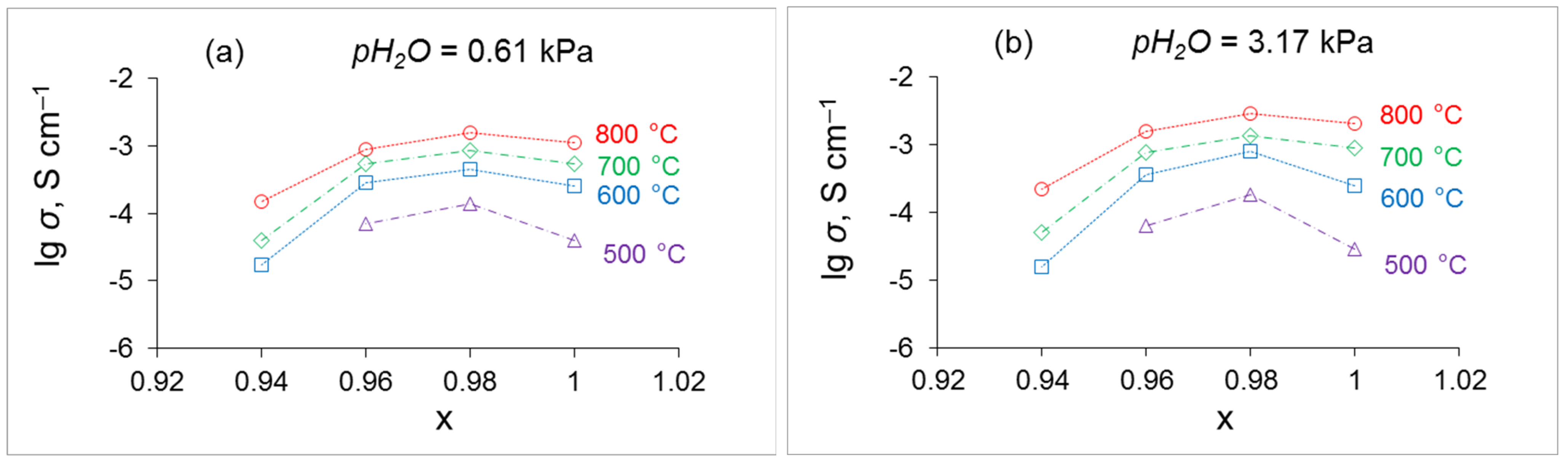
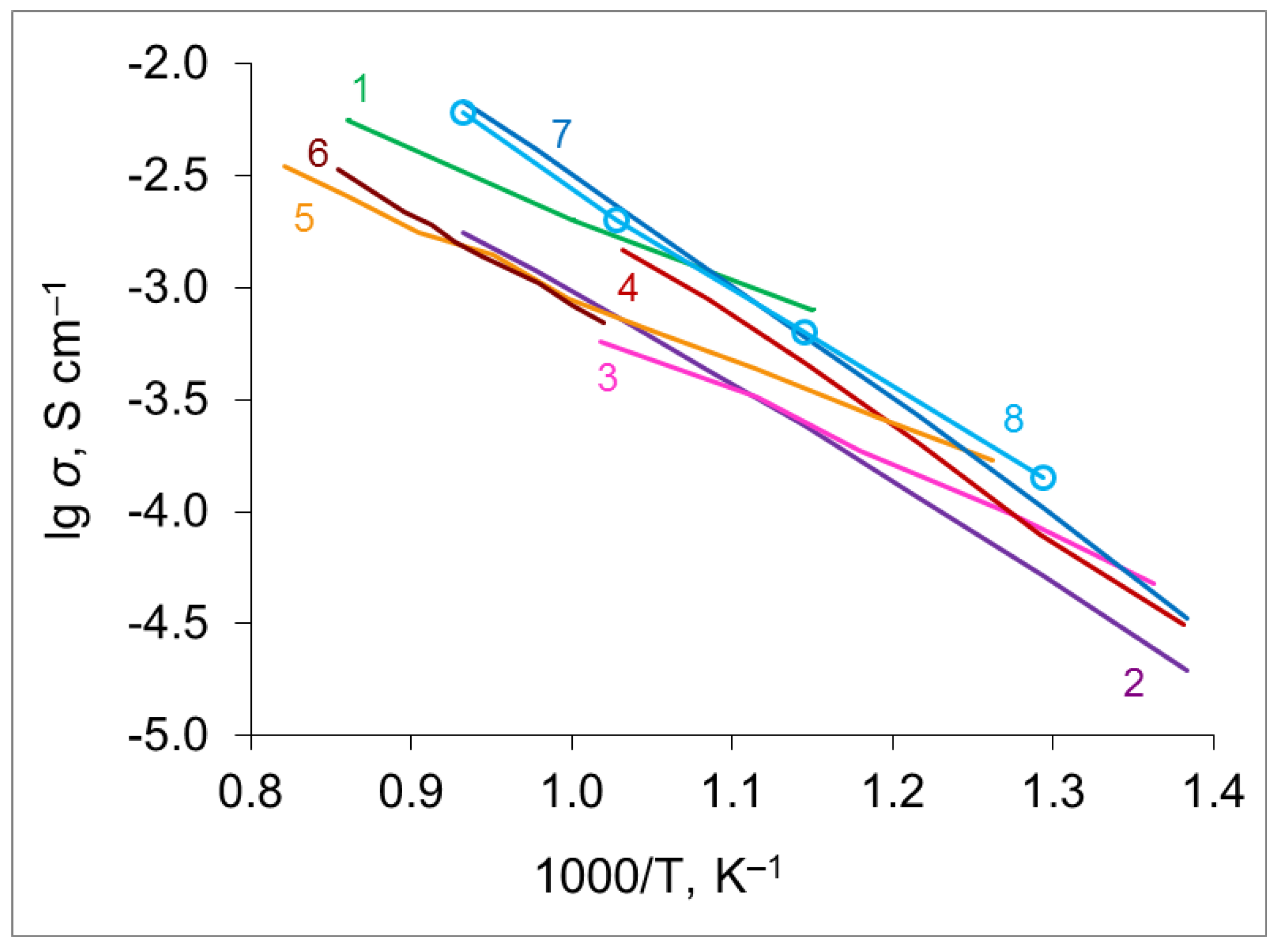
4.4. Conductivity of SrxZr0.95Yb0.05O3-d

The conductivity of SrxZr0.95Yb0.05O3-δ as a function of the oxygen partial pressure was measured at different water vapor partial pressures in the temperature range of 500–800 °C. For illustration, Figure 9 presents the conductivities obtained at different pH2O values at 800 °C. As can be seen, the conductivity of all compositions does not change in a wide range of pO2, which can be explained by the dominating oxide-ion conductivity and increases in pO2 in oxidizing conditions (pO2 > 100 Pa) indicating the dominant contribution of the hole conductivity. At the lowest pH2O (40 Pa), the slope of the lg σ–lg pO2 dependences is close to ¼, as predicted by Equation (7), but it decreases with increasing pH2O, which can be explained by an increase in the contribution of protons. The slope also decreases with decreasing temperature, approaching zero at 500 °C in humid atmospheres. For illustration, the conductivities of the specimen with x = 0.98 at different temperatures and pH2O are shown in Figure 10. The decrease in the slope with decreasing temperature is due to an increase in the solubility of water as shown by the TG experiment (see Figure 8a) and, accordingly, in the concentration of proton defects.
The ionic conductivity of SrxZr0.95Yb0.05O3-δ can be determined from the lg σ–lg pO2 dependences: it corresponds to the conductivity in the plateau region. In humid atmospheres, the “plateau” conductivity is due to the transfer of O2− and OH+ ions in the oxides. As can be seen in Figure 10, with decreasing temperature, the difference between the values of ionic conductivity at pH2O = 0.61 kPa and 3.17 kPa decreases, becoming very small at 500 °C, which indicates that the sample is almost saturated with water and protons are the predominant charge carriers. The conductivity behavior is consistent with the TG data, which show that the incorporation of water nearly reaches saturation upon cooling to ~500 °C.
In oxidizing atmospheres at high temperatures, electron holes contribute to the charge transfer. The transference number of holes at any value of pO2 can be calculated as follows:
th (pO2) = (σ(pO2) − σi)/σ(pO2),
where σ(pO2) is the total conductivity at a given pO2 and σi is the “plateau” conductivity.
The transference numbers of holes for SrxZr0.95Yb0.05O3-δ as a function of pO2 at different temperatures and pH2O, calculated from Equation (20), are shown in Figure 11. As can be seen, the holes are the predominant charge carriers in oxidizing atmospheres at high temperatures (th ≈ 0.8 in air at 800 °C), but their contribution decreases with increasing humidity, decreasing pO2 and temperature. In the Sr-deficient compositions with x = 0.96 and 0.98, the transference numbers of holes tend to zero at 500 °C. Taking into account the TG data showing that the water solubility approaches the theoretical maximum at ~500 °C (Figure 8a), which means that the oxygen vacancies are completely filled with proton defects, one can conclude that the oxides have nearly pure protonic conductivity in humid atmospheres throughout the investigated pO2 range at the temperature close to 500 °C. At higher temperatures, the hole conductivity becomes negligible at pO2 below ~100 Pa (600 °C) and ~10 Pa (700 °C).
Figure 12 shows the isotherms of the ionic conductivity of SrxZr0.95Yb0.05O3-δ at different temperatures. A slight Sr deficiency (x = 0.98) enhances the ionic conductivity, especially at low temperatures when the proton transfer is predominant. This can be explained by an increase in the concentration of oxygen vacancies to compensate for the charge of the strontium vacancies in accordance with Equation (15). However, decreasing Sr content to x = 0.94 leads to a decrease in the ionic conductivity, which can be caused by the filling of strontium vacancies with ytterbium ions, which in this case become donor defects and their positive charge is to be compensated by a decrease in the oxygen vacancy concentration according to Equation (17). Additionally, the precipitation of impurity phases as evidenced by X-ray and SEM data may slow down charge transfer.
Analysis of the hydration behavior and the electrical conductivity of the SrxZr0.95Yb0.05O3-δ (x = 0.94–1.00) series shows that the composition with x = 0.98 has the most suitable characteristics for use as a proton conducting electrolyte: it has the highest conductivity, which is purely ionic, with protons being the dominant charge carriers in both reducing and oxidizing humid atmospheres at temperatures close to 500 °C. The electrical conductivity of this composition is superior to that of strontium zirconates doped with yttrium, scandium and dysprosium [28,50,51], doped barium hafnate [52] and stannate [53] and Sc-doped calcium zirconate [54], which are considered as promising proton conducting electrolytes (see Figure 13).

5. Conclusions

The effect of Sr nonstoichiometry on the hydration and charge transport processes in SrxZr0.95Yb0.05O3-δ (x = 0.94–1.00) proton conductors with a perovskite-type structure has been studied. Dense ceramic samples were prepared using solution combustion synthesis. XRD and SEM analysis showed that the compositions with x = 0.96–1.00 are single-phase, but minor ZrO2-based phases appear at x = 0.94. The concentration of bulk protonic species in SrxZr0.95Yb0.05O3-δ was determined from TG measurements. To avoid an error in measuring the mass change due to water adsorption, the temperature of water desorption was determined from the analysis of the Raman spectra evolution upon heating the Sr0.98Zr0.95Yb0.05O3-δ powder; it was found that the process of water desorption is completed when the sample is heated to ~300 °C. In the range of 0.96 ≤ x ≤ 1, the concentration of bulk protonic species in SrxZr0.95Yb0.05O3-δ determined from the TG experiments increases with increasing Sr deficiency and correlates well with the values calculated in the frame of assumption that all Yb ions are localized in Zr sites and act as an acceptor. At x = 0.94, the proton concentration significantly falls compared to the calculated value.
A small Sr deficiency was found to enhance the ionic conductivity of SrxZr0.95Yb0.05O3-δ ceramics, which can be explained by an increase in the concentration of oxygen vacancies to compensate for the charge of strontium vacancies. However, decreasing Sr-content to x = 0.94 resulted in a decrease in the ionic conductivity, which can be caused by the distribution of Yb ions over Sr and Zr sites and the associated decrease in the oxygen vacancy concentration. Furthermore, the precipitation of minor phases as evidenced by X-ray and SEM data may slow down charge transfer.
From the analysis of the conductivity vs. pO2 dependences and the hydration ability of SrxZr0.95Yb0.05O3-δ, the conductivity of the Sr-deficient ceramics with x = 0.96 and 0.98 was proved to be almost purely protonic in humid atmospheres at a temperature of ~500 °C. The ionic conductivity reaches its highest value at Sr content of x = 0.98 (2 × 10−4 S cm−1 at 500 °C and pH2O = 3.17 kPa). The superior ionic conductivity of Sr0.98Zr0.95Yb0.05O3-δ combined with its high chemical stability makes this material a promising electrolyte for applications in proton-conducting ceramic fuel cells, electrolyzers, sensors, etc.

Author Contributions

Conceptualization, methodology, data curation, validation, supervision, project administration, writing—review and editing, L.D.; investigation, formal analysis, visualization, A.K. and A.M.; writing—original draft preparation, A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

XRD: TG and Raman spectroscopy experiments were conducted using facilities of the shared access center “Composition of compounds” (Institute of High Temperature Electrochemistry, Ural Branch of the Russian Academy of Sciences). The authors are grateful to Artem Tarutin and Rajana Abdurakhimova for their assistance with the TG and Raman spectroscopy experiments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Iwahara, H.; Esaka, T.; Uchida, H.; Maeda, N. Proton conduction in sintered oxides and its application to steam electrolysis for hydrogen production. Solid State Ion. 1981, 3–4, 359–363. [Google Scholar] [CrossRef]
  2. Iwahara, H.; Uchida, H.; Tanaka, S. High temperature type proton conductor based on SrCeO3 and its application to solid electrolyte fuel cells. Solid State Ion. 1983, 9–10, 1021–1025. [Google Scholar] [CrossRef]
  3. Iwahara, H.; Uchida, H.; Maeda, N. High temperature fuel and steam electrolysis cells using proton conductive solid electrolytes. J. Power Sources 1982, 7, 293–301. [Google Scholar] [CrossRef]
  4. Takahashi, T.; Iwahara, H. Solid state ionics: Proton conduction in perovskite type solid solutions. Rev. Chim. Min. 1980, 17, 243–253. [Google Scholar]
  5. Shimura, T.; Komori, M.; Iwahara, H. Ionic conduction in pyrochlore-type oxides containing rare earth elements at high temperature. Solid State Ion. 1996, 86–88, 685–689. [Google Scholar] [CrossRef]
  6. Labrincha, J.A.; Frade, J.R. Protonic conduction in La2Zr2O7-based pyrochlore materials. Solid State Ion. 1997, 99, 33–40. [Google Scholar] [CrossRef]
  7. Regalado Vera, C.Y.; Ding, H.; Peterson, D.; Gibbons, W.T.; Zhou, M.; Ding, D. A mini-review on proton conduction of BaZrO3-based perovskite electrolytes. J. Phys. Energy 2021, 3, 032019. [Google Scholar] [CrossRef]
  8. Hossain, S.; Abdalla, A.M.; Jamain, S.N.B.; Zaini, J.H.; Azad, A.K. A review on proton conducting electrolytes for clean energy and intermediate temperature-solid oxide fuel cells. Renew. Sustain. Energy Rev. 2017, 79, 750–764. [Google Scholar] [CrossRef]
  9. Shiraiwa, M.; Kido, T.; Fujii, K.; Yashima, M. High-temperature proton conductors based on the (110) layered perovskite BaNdScO4. J. Mater. Chem. A 2021, 9, 8607. [Google Scholar] [CrossRef]
  10. Dunyushkina, L.A.; Belyakov, S.A.; Filatov, N.M. Proton-conducting alkaline earth hafnates: A review of manufacturing technologies, physicochemical properties and electrochemical performance. J. Eur. Ceram. Soc. 2023, 43, 6681–6698. [Google Scholar] [CrossRef]
  11. Swierczek, K.; Zajac, W.; Klimkowicz, A.; Zheng, K.; Malikova, N.; Dabrowski, B. Crystal structure and proton conductivity in highly oxygen-deficient Ba1−xLax(In,Zr,Sn)O3−δ perovskites. Solid State Ion. 2015, 275, 58–61. [Google Scholar] [CrossRef]
  12. Guan, D.; Xu, H.; Zhang, Q.; Huang, Y.-C.; Shi, C.; Chang, Y.-C.; Xu, X.; Tang, J.; Gu, Y.; Pao, C.-W.; et al. Identifying a universal activity descriptor and a unifying mechanism concept on perovskite oxides for green hydrogen production. Adv. Mater. 2023. [Google Scholar] [CrossRef] [PubMed]
  13. Guan, D.; Zhong, J.; Xu, H.; Huang, Y.-C.; Hu, Z.; Chen, B.; Zhang, Y.; Ni, M.; Xu, X.; Zhou, W.; et al. A universal chemical-induced tensile strain tuning strategy to boost oxygen-evolving electrocatalysis on perovskite oxides. Appl. Phys. Rev. 2022, 9, 011422. [Google Scholar] [CrossRef]
  14. Hanif, M.B.; Rauf, S.; Motola, M.; Babar, Z.U.D.; Li, C.-J.; Li, C.-X. Recent progress of perovskite-based electrolyte materials for solid oxide fuel cells and performance optimizing strategies for energy storage applications. Mater. Res. Bull. 2022, 146, 111612. [Google Scholar] [CrossRef]
  15. Duan, C.; Kee, R.; Zhu, H.; Sullivan, N.; Zhu, L.; Bian, L.; Jennings, D.; O’Hayre, R. Highly efficient reversible protonic ceramic electrochemical cells for power generation and fuel production. Nat. Energy 2019, 4, 230–240. [Google Scholar] [CrossRef]
  16. Choi, S.; Davenport, T.C.; Haile, S.M. Protonic ceramic electrochemical cells for hydrogen production and electricity generation: Exceptional reversibility, stability, and demonstrated faradaic efficiency. Energy Environ. Sci. 2019, 12, 206–215. [Google Scholar] [CrossRef]
  17. Zajac, W.; Rusinek, D.; Zheng, K.; Molenda, J. Applicability of Gd-doped BaZrO3, SrZrO3, BaCeO3 and SrCeO3 proton conducting perovskites as electrolytes for solid oxide fuel cells. Cent. Eur. J. Chem. 2013, 11, 471–484. [Google Scholar] [CrossRef]
  18. Skubida, W.; Zheng, K.; Swierczek, K.; Michna, M.; Kondracki, L. Indium doping in SrCeO3 proton-conducting perovskites. J. Solid State Chem. 2020, 284, 121210. [Google Scholar] [CrossRef]
  19. Gorelov, V.P.; Balakireva, V.B.; Kuzmin, A.V. Charge transfer and defect structure in BaCeO3. Russ. J. Inorg. Chem. 2018, 63, 930–937. [Google Scholar] [CrossRef]
  20. Ryu, K.H.; Haile, S.M. Chemical stability and proton conductivity of doped BaCeO–BaZrO solid solutions. Solid State Ion. 1999, 125, 355–367. [Google Scholar] [CrossRef]
  21. Medvedev, D.A.; Lyagaeva, J.G.; Gorbova, E.V.; Demin, A.K.; Tsiakaras, P. Advanced materials for SOFC application: Strategies for the development of highly conductive and stable solid oxide proton electrolytes. Prog. Mater. Sci. 2016, 75, 38–79. [Google Scholar] [CrossRef]
  22. Shi, Z.; Sun, W.; Wang, Z.; Qian, J.; Liu, W. Samarium and yttrium codoped BaCeO3 proton conductor with improved sinterability and higher electrical conductivity. ACS Appl. Mater. Interfaces 2014, 6, 5175–5182. [Google Scholar] [CrossRef] [PubMed]
  23. Kreuer, K.D. Proton-Conducting Oxides. Annu. Rev. Mater. Res. 2003, 33, 333–359. [Google Scholar] [CrossRef]
  24. Pérez-Coll, D.; Heras-Juaristi, G.; Fagg, D.P.; Mather, G.C. Transport-number determination of a protonic ceramic electrolyte membrane via electrodepolarisation correction with the Gorelov method. J. Power Sources 2014, 245, 445–455. [Google Scholar] [CrossRef]
  25. Duan, C.; Huang, J.; Sullivan, N.; O’Hayre, R. Proton-conducting oxides for energy conversion and storage. Appl. Phys. Rev. 2020, 7, 011314. [Google Scholar] [CrossRef]
  26. Li, S.; Irvine, J.T.S. Non-stoichiometry, structure and properties of proton-conducting perovskite oxides. Solid State Ion. 2021, 361, 115571. [Google Scholar] [CrossRef]
  27. Yamazaki, Y.; Hernandez-Sanchez, R.; Haile, S.M. Cation non-stoichiometry in yttrium-doped barium zirconate: Phase behavior, microstructure, and proton conductivity. J. Mater. Chem. 2010, 20, 8158–8166. [Google Scholar] [CrossRef]
  28. Dunyushkina, L.A.; Khaliullina, A.S.; Meshcherskikh, A.N.; Pankratov, A.A.; Osinkin, D.A. Effect of A-site nonstoichiometry on defect chemistry and electrical conductivity of undoped and Y-doped SrZrO3. Materials 2019, 12, 1258. [Google Scholar] [CrossRef]
  29. Sharova, N.V.; Gorelov, V.P. Effect of Cation Nonstoichiometry on the Properties of Solid Electrolyte BaxCe0.97Nd0.03O3–d (0.90 ≤ x ≤ 1.10). Russ. J. Electrochem. 2004, 40, 639–645. [Google Scholar] [CrossRef]
  30. Yang, W.; Zhou, H.; Wang, L.; Li, Y.; He, Z.; Han, C.; Dai, L. The influence of Ba-site non-stoichiometry on the phase composition, sinterability, conductivity and chemical stability of BaxZr0.6Hf0.2Y0.2O3−d (0.9 ≤ x ≤ 1.03) proton conductors. Int. J. Hydrogen Energy 2021, 46, 10838–10849. [Google Scholar] [CrossRef]
  31. Shkerin, S.N.; Rudakova, A.V.; Bulanin, K.M.; Khaliullina, A.S.; Meshcherskikh, A.N.; Vovkotrub, E.G.; Dunyushkina, L.A. Raman spectroscopy of SrZrO3 based proton conducting electrolyte: Effect of Y-doping and Sr-nonstoichiometry. Int. J. Hydrogen Energy 2021, 46, 17007–17018. [Google Scholar] [CrossRef]
  32. Khaliullina, A.; Meshcherskikh, A.; Pankratov, A.; Dunyushkina, L. Effect of Sr deficiency on electrical conductivity of Yb-doped strontium zirconate. Materials 2022, 15, 4126. [Google Scholar] [CrossRef] [PubMed]
  33. Zhang, W.; Hu, Y.H. Progress in proton-conducting oxides as electrolytes for low-temperature solid oxide fuel cells: From materials to devices. Energy Sci. Eng. 2021, 9, 984–1011. [Google Scholar] [CrossRef]
  34. Kosacki, I.; Tuller, H.L. Mixed conductivity in SrCe0.95Yb0.05O3 protonic conductors. Solid State Ion. 1995, 80, 223–229. [Google Scholar] [CrossRef]
  35. Dunyushkina, L.A.; Gorelov, V.P. High temperature electrical behavior of CaTi1−xFexO3−δ (x = 0–0.5). Oxygen-ion, electronic and proton conductivity. Solid State Ion. 2013, 253, 169–174. [Google Scholar] [CrossRef]
  36. Huang, Y.; Qiu, R.; Lian, W.; Lei, L.; Liu, T.; Zhang, J.; Wang, Y.; Liu, J.; Huang, J.; Chen, F. Review: Measurement of partial electrical conductivities and transport numbers of mixed ionic-electronic conducting oxides. J. Power Sources 2022, 528, 231201. [Google Scholar] [CrossRef]
  37. Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crysstallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
  38. Kamishima, O.; Hattori, T.; Ohta, K.; Chiba, Y.; Ishigame, M. Raman scattering of single-crystal SrZrO3. J. Phys. Condens. Matter 1999, 11, 5355–5365. [Google Scholar] [CrossRef]
  39. Yang, Y.; Ning, X.; Luo, S.; Dong, F.; Li, L. Electron irradiation effects of SrZrO3 ceramic for radioactive strontium immobilization. Procedia Environ. Sci. 2016, 31, 330–334. [Google Scholar] [CrossRef]
  40. Colomban, P.; Slodczyk, A. Raman intensity: An important tool to study the structure and phase transitions of amorphous/crystalline materials. Opt. Mater. 2009, 31, 1759–1763. [Google Scholar] [CrossRef]
  41. Murphy, R.; Zhou, Y.; Zhang, L.; Soule, L.; Zhang, W.; Chen, Y.; Liu, M. A new family of proton-conducting electrolytes for reversible solid oxide cells: BaHfxCe0.8−xY0.1Yb0.1O3−δ. Adv. Funct. Mater. 2020, 30, 2002265. [Google Scholar] [CrossRef]
  42. Yang, W.; Han, C.; Li, Y.; Zhou, H.; Liu, S.; Wang, L.; He, Z.; Dai, L. Influence of rare-earth doping on the phase composition, sinterability, chemical stability and conductivity of BaHf0.8Ln0.2O3−δ (Ln = Yb, Y, Dy, Gd) proton conductors. Int. J. Hydrogen Energy 2021, 46, 35678–35691. [Google Scholar] [CrossRef]
  43. Wang, X.; Fei, M.; Zhou, C.; Li, W.; Wang, X.; Shen, X.; Liu, D.; Chen, W.; Chen, P.; Jiang, G.; et al. Enhanced proton conductivity and CO2-tolerance of intermediate-temperature protonic ceramic fuel cell with lanthanum tungstate-based composite cathode. Compos. Part B Eng. 2023, 253, 110565. [Google Scholar] [CrossRef]
  44. Sopiha, K.V.; Malyi, O.I.; Persson, C.; Wu, P. Suppression of surfaces states at cubic perovskite (001) surfaces by CO2 adsorption. Phys. Chem. Chem. Phys. 2018, 20, 18828–18836. [Google Scholar] [CrossRef] [PubMed]
  45. Tavender, S.M.; Johnson, S.A.; Balsom, D.; Parker, A.W.; Bisby, R.H. The carbonate, CO3−, in solution studied by resonance Raman spectroscopy. Laser Chem. 1999, 19, 311–316. [Google Scholar] [CrossRef]
  46. Hong, J.; Heo, S.J.; Singh, P. Water mediated growth of oriented single crystalline SrCO3 nanorod arrays on strontium compounds. Sci. Rep. 2021, 11, 3368. [Google Scholar] [CrossRef]
  47. Bagherisereshki, E.; Tran, J.; Lei, F.; AuYeung, N. Investigation into SrO/SrCO3 for high temperature thermochemical energy storage. Sol. Energy 2018, 160, 85–93. [Google Scholar] [CrossRef]
  48. Fontana, M.D.; Mabrouk, K.B.; Kauffmann, T.H. Raman spectroscopic sensors for inorganic salts. Spectrosc. Prop. Inorg. Organomet. Compd. 2013, 44, 40–67. [Google Scholar]
  49. Burikov, S.A.; Dolenko, T.A.; Fadeev, V.V. The Role of Fermi Resonance in Formation of Valence Band of Water Raman Scattering. Int. J. Opt. 2008, 2008, 204828. [Google Scholar] [CrossRef]
  50. Balakireva, V.B.; Gorelov, V.P.; Dunyushkina, L.A.; Kuzmin, A.V. Impact of Humidity on Charge Transport in Proton-Conducting Perovskites AZr0.95Sc0.05O3−δ (A = Ca, Sr, Ba) Exposed to an Oxidative Atmosphere. Phys. Solid State 2019, 61, 515–522. [Google Scholar] [CrossRef]
  51. Gharbage, B.; Marques, F.M.B.; Frade, J.R. Protonic conduction in Sr1−y(Zr1−xDyx)O3−δ Ceramics. J. Eur. Ceram. Soc. 1996, 16, 1149–1156. [Google Scholar] [CrossRef]
  52. Yang, W.; Wang, L.; Li, Y.; Zhou, H.; He, Z.; Han, C.; Dai, L. An easily sintered, chemically stable indium and tin co-doped barium hafnate electrolyte for hydrogen separation. J. Alloys Compd. 2021, 868, 159117. [Google Scholar] [CrossRef]
  53. Zvonareva, I.A.; Mineev, A.M.; Tarasova, N.A.; Fu, X.Z.; Medvedev, D.A. High-temperature transport properties of BaSn1−xScxO3−δ ceramic materials as promising electrolytes for protonic ceramic fuel cells. J. Adv. Ceram. 2022, 11, 1131–1143. [Google Scholar]
  54. Pikalova, E.Y.; Bogdanovich, N.M.; Kuz’min, A.V. Composite Electrodes for Proton Conducting Electrolyte of CaZr0.95Sc0.05O3–d. Russ. J. Electrochem. 2017, 53, 752–760. [Google Scholar] [CrossRef]
Processes 11 02939 g001
Figure 1. Scheme of the synthesis of SrxZr0.95Yb0.05O3-δ.
Figure 1. Scheme of the synthesis of SrxZr0.95Yb0.05O3-δ.
Processes 11 02939 g001
Processes 11 02939 g002
Figure 2. Schematic diagram of the four-probe method.
Figure 2. Schematic diagram of the four-probe method.
Processes 11 02939 g002
Processes 11 02939 g003
Figure 3. XRD patterns of SrxZr0.95Yb0.05O3-δ powders before and after measurements of electrical conductivity vs. pO2. White square—monoclinic ZrO2, blue square—cubic ZrO2.
Figure 3. XRD patterns of SrxZr0.95Yb0.05O3-δ powders before and after measurements of electrical conductivity vs. pO2. White square—monoclinic ZrO2, blue square—cubic ZrO2.
Processes 11 02939 g003
Processes 11 02939 g004
Figure 4. Cell parameters (a,b) and cell volume (c) of SrxZr0.95Yb0.05O3-δ as a function of Sr content x.
Figure 4. Cell parameters (a,b) and cell volume (c) of SrxZr0.95Yb0.05O3-δ as a function of Sr content x.
Processes 11 02939 g004
Processes 11 02939 g005
Figure 5. Rietveld refinement of the X-ray diffraction data of Sr0.96Zr0.95Yb0.05O3-δ based on models: (a) 1, (b) 2 and (c) 3.
Figure 5. Rietveld refinement of the X-ray diffraction data of Sr0.96Zr0.95Yb0.05O3-δ based on models: (a) 1, (b) 2 and (c) 3.
Processes 11 02939 g005
Processes 11 02939 g006
Figure 6. SEM images of SrxZr0.95Yb0.05O3-δ ceramics: (a) x = 1.00, (b) 0.98, (c) 0.96 and (d) 0.94. The minor phase grains are marked with arrows. These data were originally presented in [32].
Figure 6. SEM images of SrxZr0.95Yb0.05O3-δ ceramics: (a) x = 1.00, (b) 0.98, (c) 0.96 and (d) 0.94. The minor phase grains are marked with arrows. These data were originally presented in [32].
Processes 11 02939 g006
Processes 11 02939 g007
Figure 7. Raman spectra of Sr0.98Zr0.95Yb0.05O3-δ powder after exposition to humidified air (pH2O = 3.17 kPa) at 23 °C, 100 °C, 200 °C, 300 °C, 400 °C and 500 °C.
Figure 7. Raman spectra of Sr0.98Zr0.95Yb0.05O3-δ powder after exposition to humidified air (pH2O = 3.17 kPa) at 23 °C, 100 °C, 200 °C, 300 °C, 400 °C and 500 °C.
Processes 11 02939 g007
Processes 11 02939 g008
Figure 8. TG curves (a) and the concentrations of proton defects (b) in SrxZr0.95Yb0.05O3-δ. Solid line shows the concentrations of proton defects calculated using Equation (15).
Figure 8. TG curves (a) and the concentrations of proton defects (b) in SrxZr0.95Yb0.05O3-δ. Solid line shows the concentrations of proton defects calculated using Equation (15).
Processes 11 02939 g008
Processes 11 02939 g009
Figure 9. Conductivity of SrxZr0.95Yb0.05O3-δ vs. pO2 at 800 °C: (a) x = 1.00, (b) x = 0.98, (c) x = 0.96, (d) x = 0.94. Solid lines are guides for the eyes.
Figure 9. Conductivity of SrxZr0.95Yb0.05O3-δ vs. pO2 at 800 °C: (a) x = 1.00, (b) x = 0.98, (c) x = 0.96, (d) x = 0.94. Solid lines are guides for the eyes.
Processes 11 02939 g009
Processes 11 02939 g010
Figure 10. Conductivity of Sr0.98Zr0.95Yb0.05O3-δ vs. pO2 at different temperatures and pH2O. Diamonds, triangles and circles correspond to pH2O = 0.04, 0.61 and 3.17 kPa, respectively. Dotted lines are guides for the eyes.
Figure 10. Conductivity of Sr0.98Zr0.95Yb0.05O3-δ vs. pO2 at different temperatures and pH2O. Diamonds, triangles and circles correspond to pH2O = 0.04, 0.61 and 3.17 kPa, respectively. Dotted lines are guides for the eyes.
Processes 11 02939 g010
Processes 11 02939 g011
Figure 11. Transference numbers of holes vs. pO2 for SrxZr0.95Yb0.05O3-δ at different temperatures: (a) x = 1.00, (b) x = 0.98, (c) x = 0.96. Solid and dashed lines correspond to pH2O = 0.61 and 3.17 kPa, respectively.
Figure 11. Transference numbers of holes vs. pO2 for SrxZr0.95Yb0.05O3-δ at different temperatures: (a) x = 1.00, (b) x = 0.98, (c) x = 0.96. Solid and dashed lines correspond to pH2O = 0.61 and 3.17 kPa, respectively.
Processes 11 02939 g011
Processes 11 02939 g012
Figure 12. Ionic conductivity of SrxZr0.95Yb0.05O3-δ as a function of Sr content x at (a) pH2O = 0.61 kPa and (b) pH2O = 3.17 kPa.
Figure 12. Ionic conductivity of SrxZr0.95Yb0.05O3-δ as a function of Sr content x at (a) pH2O = 0.61 kPa and (b) pH2O = 3.17 kPa.
Processes 11 02939 g012
Processes 11 02939 g013
Figure 13. Electrical conductivity of proton-conducting electrolytes: 1—SrZr0.95Sc0.05O3-δ [50], 2—Sr0.98Zr0.95Y0.05O3-δ [28], 3—SrZr0.9Dy0.1O3-δ [51], 4—BaHf0.95In0.05Sn0.1O3-δ [52], 5—BaSn0.9Sc0.1O3-δ [53], 6—CaZr0.95Sc0.05O3-δ [54], 7—Sr0.98Zr0.95Yb0.05O3-δ [32], 8—Sr0.98Zr0.95Yb0.05O3-δ (this work).
Figure 13. Electrical conductivity of proton-conducting electrolytes: 1—SrZr0.95Sc0.05O3-δ [50], 2—Sr0.98Zr0.95Y0.05O3-δ [28], 3—SrZr0.9Dy0.1O3-δ [51], 4—BaHf0.95In0.05Sn0.1O3-δ [52], 5—BaSn0.9Sc0.1O3-δ [53], 6—CaZr0.95Sc0.05O3-δ [54], 7—Sr0.98Zr0.95Yb0.05O3-δ [32], 8—Sr0.98Zr0.95Yb0.05O3-δ (this work).
Processes 11 02939 g013
Table 1. Rietveld refinement parameters for Sr0.96Zr0.95Yb0.05O3-δ.
Table 1. Rietveld refinement parameters for Sr0.96Zr0.95Yb0.05O3-δ.
Model 1
Sr0.96Zr0.95Yb0.05O3
Pnma		Model 2
Sr0.91Yb0.05ZrO3
Pnma		Model 3
Sr0.935Yb0.025Zr0.975Yb0.025O3
Pnma
a, Å 5.8190(1)a, Å 5.8190(3)a, Å 5.8190(1)
b, Å 8.2047(1)b, Å 8.2048(8)b, Å 8.2046(9)
c, Å 5.7946(2)c, Å 5.7945(2)c, Å 5.7946(2)
V, Å3 276.65(5)V, Å3 276.65(7)V, Å3 276.65(4)
Sr0.96 (4c)x0.4753(5)Sr0.91Yb0.05 (4c)x0.4745(6)Sr0.935Yb0.025 (4c)x0.4755(7)
y0.25 y0.25 y0.2500(0)
z0.0054(6) z0.0051(1) z0.0051(7)
Occ0.48 Occ0.48 Occ0.48
Zr0.95Yb0.05 (4a)x0Zr (4a)x0Zr0.975Yb0.025 (4a)x0
y0 y0 y0
z0 z0 z0
Occ0.5 Occ0.5 Occ0.5
O1 (8c)x0.2187(4)O1 (8c)x0.2159(8)O1 (8c)x0.2195(4)
y0.0266(4) y0.0347(0) y0.0267(8)
z0.2832(5) z0.2859(0) z0.2827(3)
Occ1 Occ1 Occ1
O2 (4c)x0.5188(3)O2 (4c)x0.5170(0)O2 (4c)x0.5205(5)
y0.25 y0.25 y0.2500(0)
z0.6093(7) z0.5820(8) z0.6162(2)
Occ0.5 Occ0.5 Occ0.5
Rwp, % 10.6Rwp, % 10.7Rwp, % 10.8
Rexp, % 10.59Rexp, % 10.59Rexp, % 10.60
Rp, % 8.81Rp, % 8.66Rp, % 8.91
χ2 1.01χ2 1.02χ2 1.03
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Khaliullina, A.; Meshcherskikh, A.; Dunyushkina, L. Effect of Cation Nonstoichiometry on Hydration and Charge Transport Processes in Yb-Doped SrZrO3 Perovskite-Type Proton Conductor for Ceramic Electrochemical Cells. Processes 2023, 11, 2939. https://doi.org/10.3390/pr11102939

AMA Style

Khaliullina A, Meshcherskikh A, Dunyushkina L. Effect of Cation Nonstoichiometry on Hydration and Charge Transport Processes in Yb-Doped SrZrO3 Perovskite-Type Proton Conductor for Ceramic Electrochemical Cells. Processes. 2023; 11(10):2939. https://doi.org/10.3390/pr11102939

Chicago/Turabian Style

Khaliullina, Adelya, Anastasia Meshcherskikh, and Liliya Dunyushkina. 2023. "Effect of Cation Nonstoichiometry on Hydration and Charge Transport Processes in Yb-Doped SrZrO3 Perovskite-Type Proton Conductor for Ceramic Electrochemical Cells" Processes 11, no. 10: 2939. https://doi.org/10.3390/pr11102939

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop