Influence of Particle Shape on Tortuosity of Non-Spherical Particle Packed Beds
Abstract
1. Introduction
2. Tortuosity Models
3. Methods
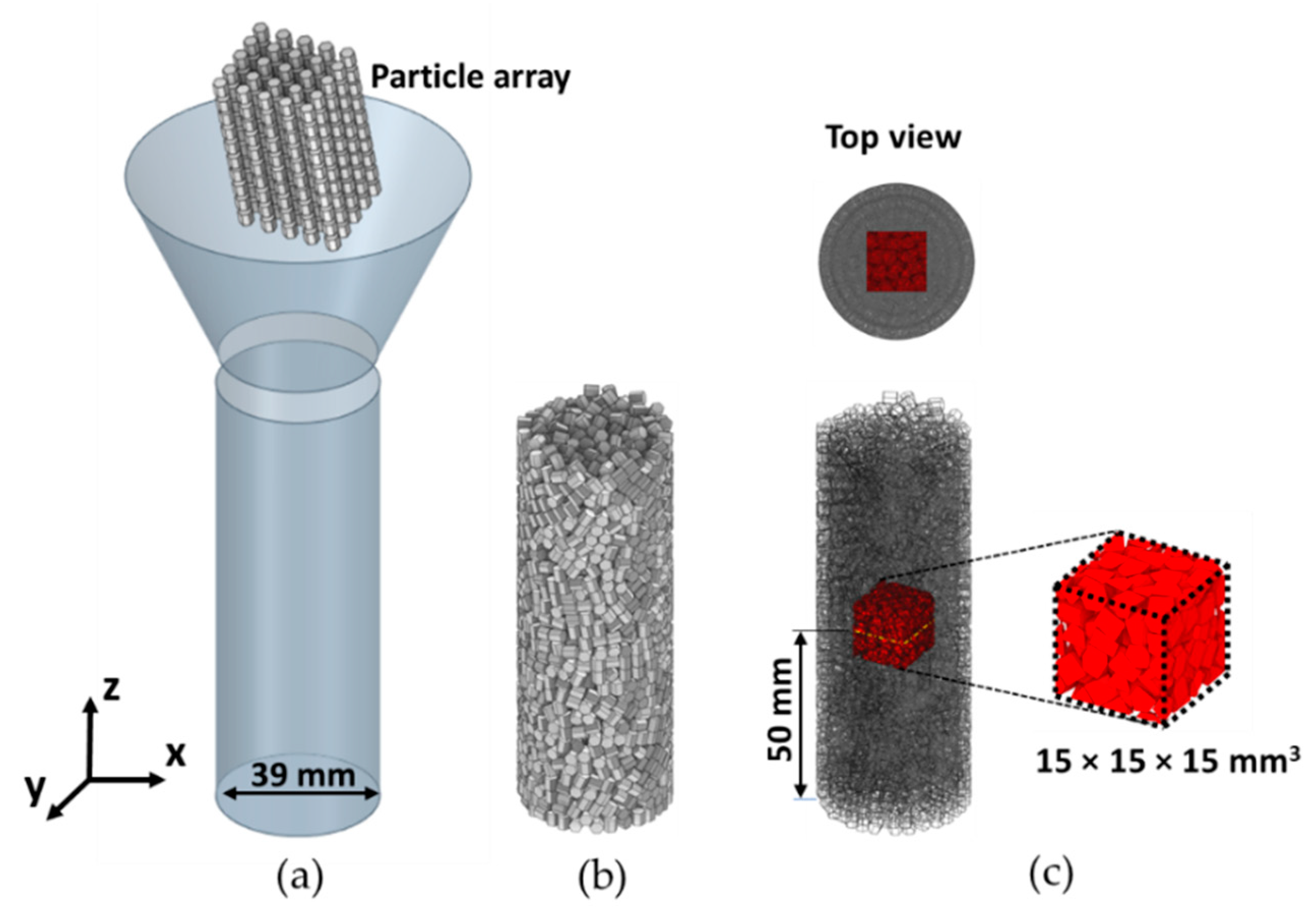
3.1. Particle Shape and Packing Generation
3.2. Domain and Thermal Simulations
4. Results and Discussion
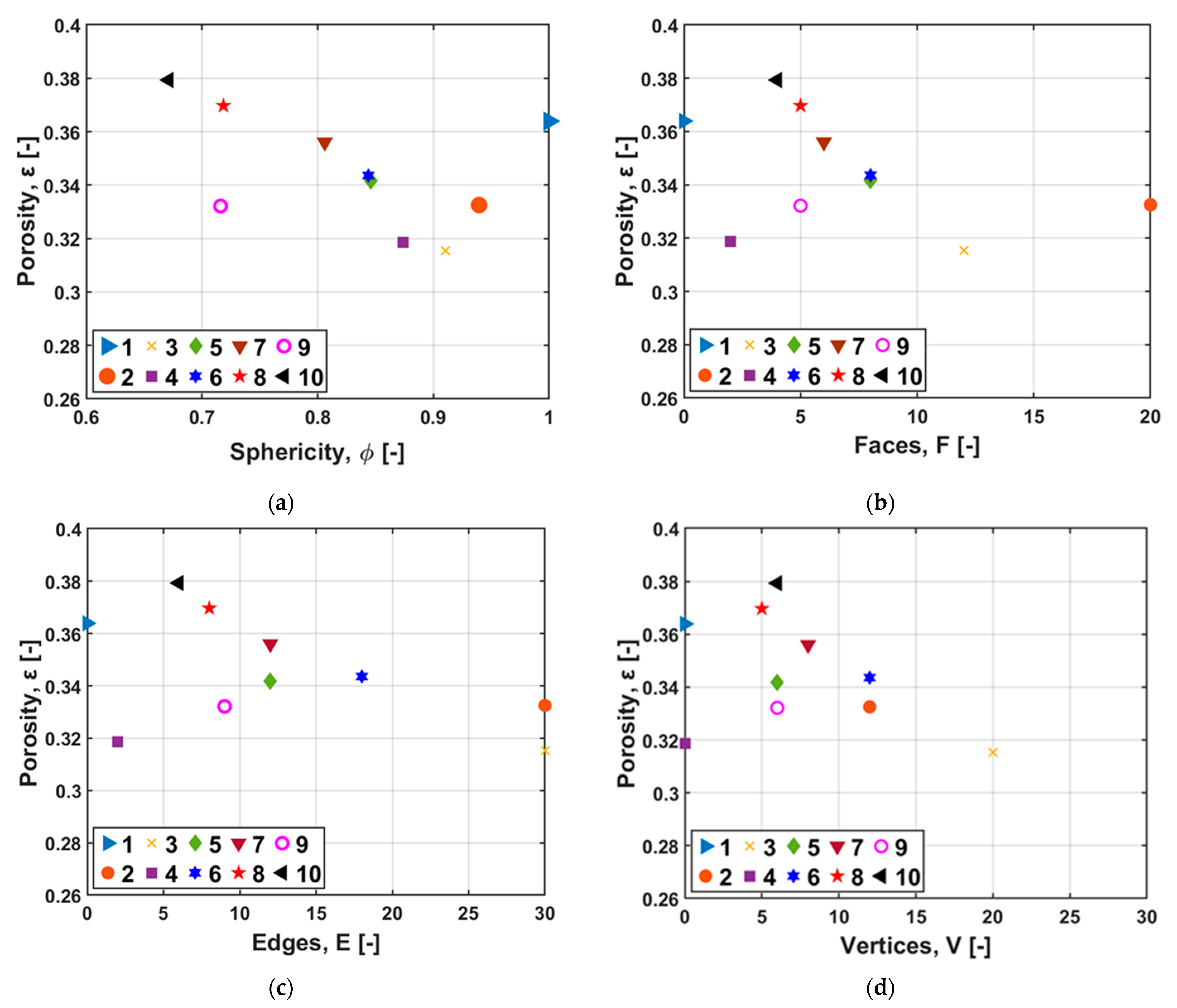
4.1. Packing Results
4.2. Thermal Results
4.2.1. Mesh Independence Study for All Shapes
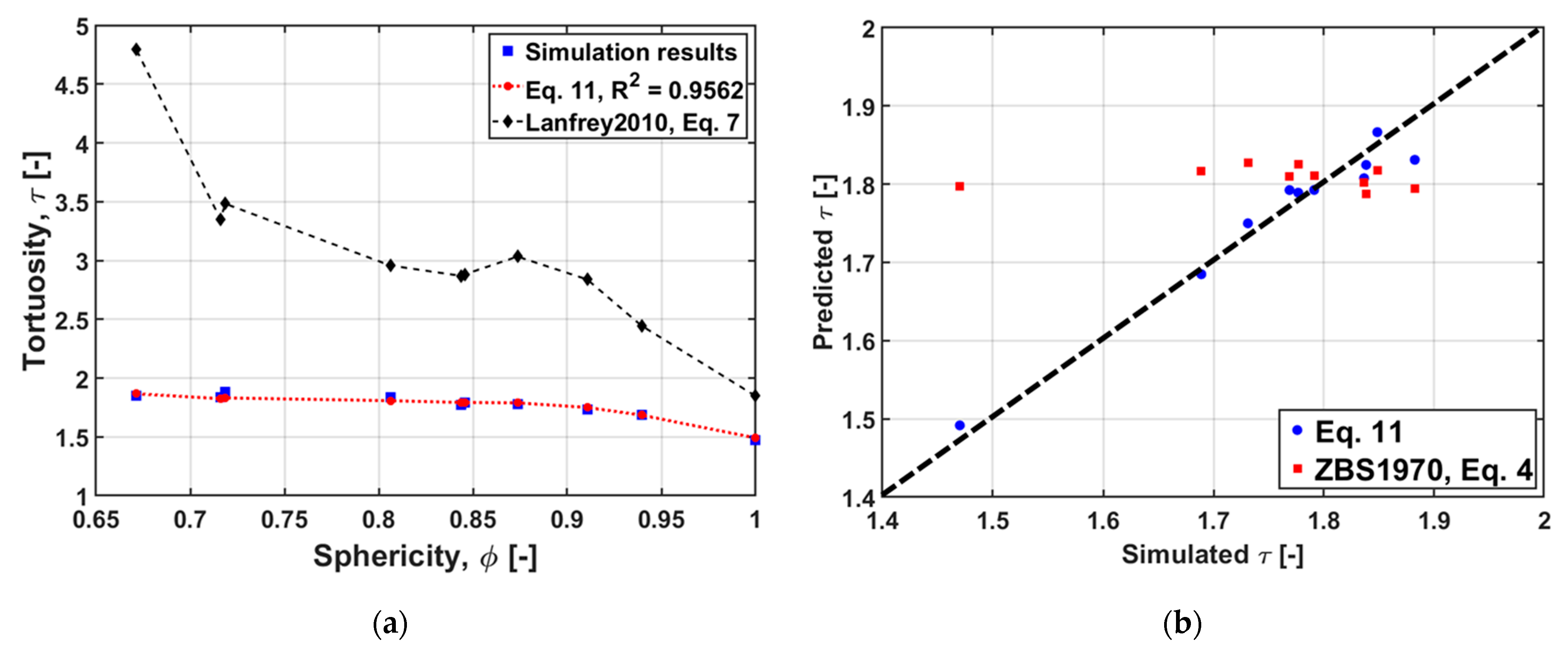
4.2.2. Comparison of Results with Old Models
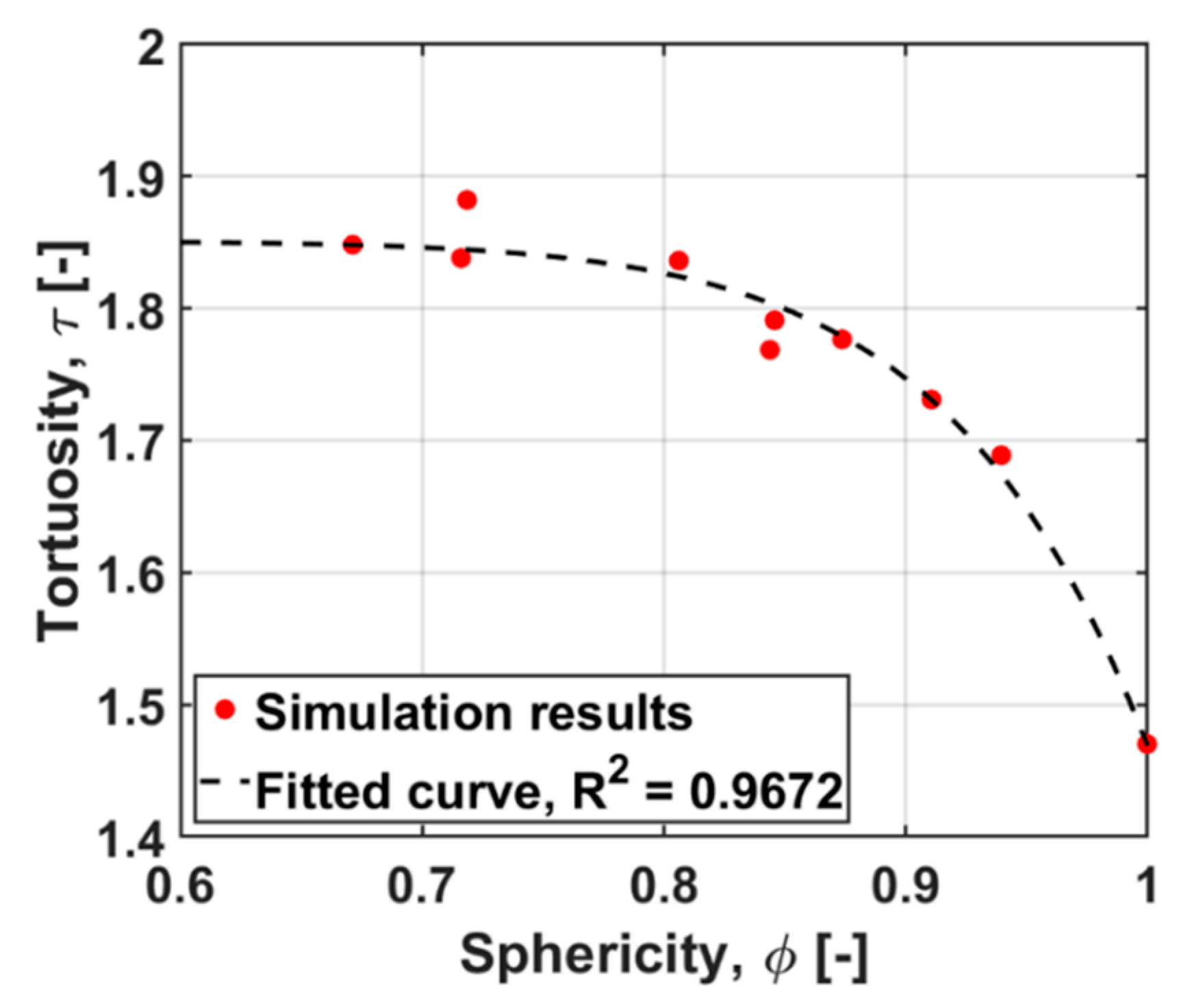
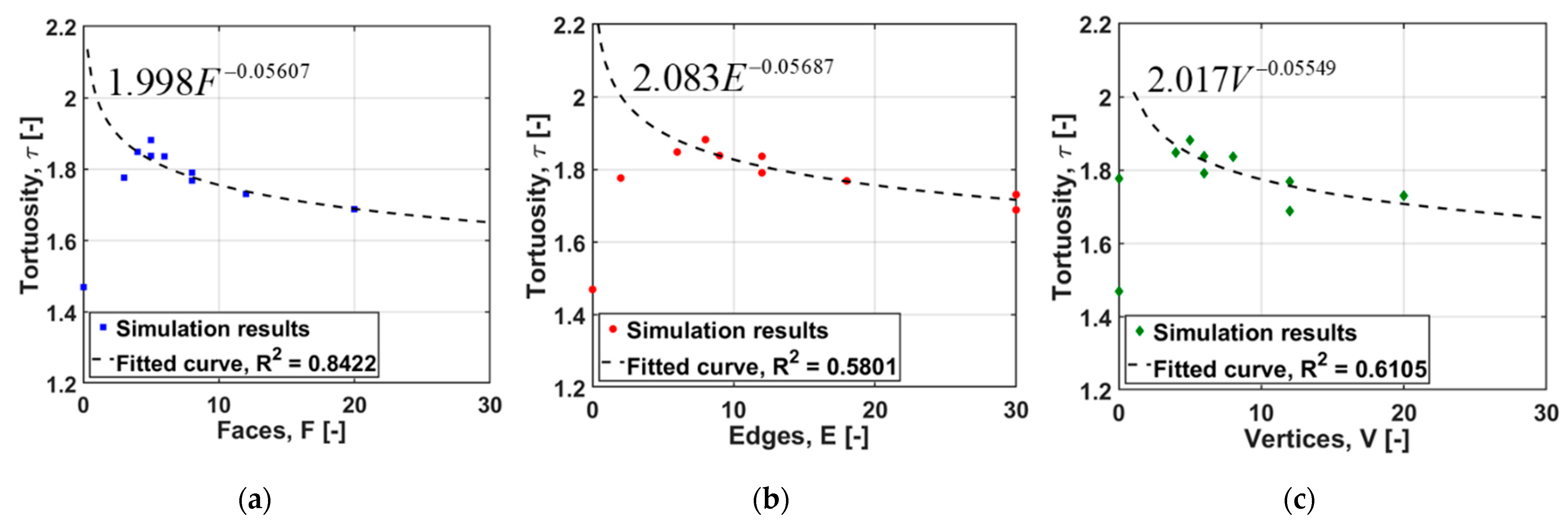
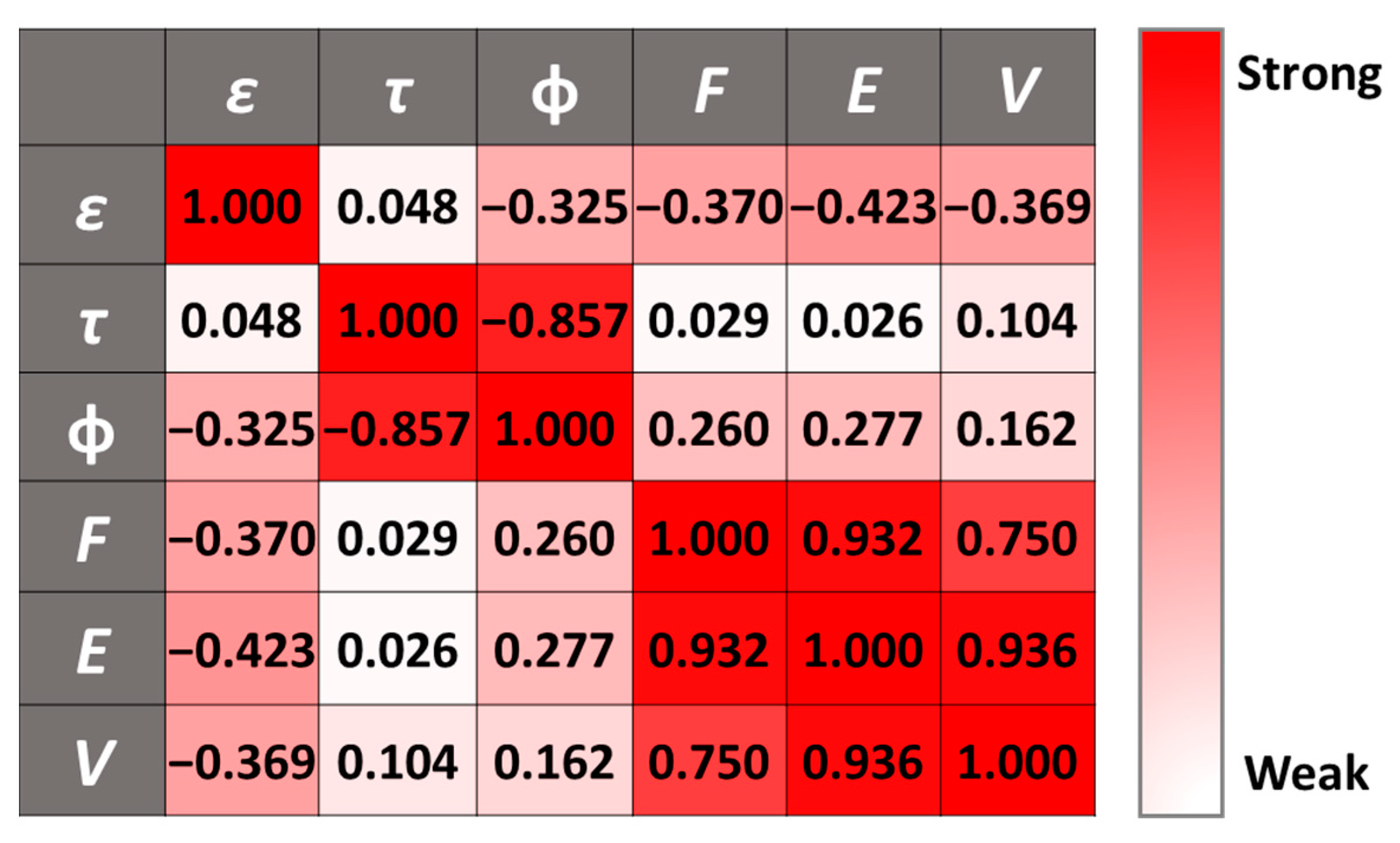
4.3. Effect of Particle Shape on Tortuosity
4.4. Modification of Tortuosity Equation—ZBS Model
- -
- Porosity for our range of simulations was found to have a weak correlation to tortuosity, which is also observed in Figure 6b. Hence, the effect of other parameters is essential.
- -
- When considering , , and , these variables are strongly interrelated to each other but weakly related to tortuosity. With porosity, they are moderately inversely related. This effect is detected in Figure 4, where higher porosities can be seen for lower values of , , and .
- -
- As already indicated, sphericity dominates the correlation coefficient analysis for tortuosity, with those variables being proportional to each other.
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| fitting coefficients, Equation (10) | - | |
| particle surface area | m2 | |
| specific surface area | m−1 | |
| adjusting parameter [39] | - | |
| cylinder/bed diameter | m | |
| coefficient of unconfined diffusion | m2/s | |
| effective diffusion coefficient | m2/s | |
| diameter of equivalent volume sphere | m | |
| number of particle edges | - | |
| number of particle faces | - | |
| ratio of particle-to-gas conductivity | - | |
| ratio of bed-to-gas conductivity | - | |
| empirical constant, Equation (11) | - | |
| empirical constant, Equation (11) | - | |
| number of mesh elements | - | |
| total directional heat flux | W/m2 | |
| directional heat flux of element | W/m2 | |
| bed radius | m | |
| volume fraction of mesh element | - | |
| number of particle vertices | - | |
| particle volume | m3 | |
| porosity | - | |
| particle conductivity | W/(mK) | |
| gas conductivity | W/(mK) | |
| effective bed conductivity | W/(mK) | |
| tortuosity | - | |
| tortuosity from the ZBS model, Equation (4) [47] | - | |
| sphericity | - |
References
- Sharma, R.K.; Cresswell, D.L.; Newson, E.J. Effective Diffusion Coefficients and Tortuosity Factors for Commercial Catalysts. Ind. Eng. Chem. Res. 1991, 30, 1428–1433. [Google Scholar] [CrossRef]
- Das, S.; Deen, N.G.; Kuipers, J.A.M. Multiscale Modeling of Fixed-Bed Reactors with Porous (Open-Cell Foam) Non-Spherical Particles: Hydrodynamics. Chem. Eng. J. 2018, 334, 741–759. [Google Scholar] [CrossRef]
- Welsh, Z.G.; Khan, M.I.H.; Karim, M.A. Multiscale Modeling for Food Drying: A Homogenized Diffusion Approach. J. Food Eng. 2021, 292, 110252. [Google Scholar] [CrossRef]
- Lammens, J.; Goudarzi, N.M.; Leys, L.; Nuytten, G.; van Bockstal, P.-J.; Vervaet, C.; Boone, M.N.; de Beer, T. Spin Freezing and its Impact on Pore Size, Tortuosity and Solid State. Pharmaceutics 2021, 13, 2126. [Google Scholar] [CrossRef]
- Muhammed, N.S.; Haq, B.; Al Shehri, D.; Al-Ahmed, A.; Rahman, M.M.; Zaman, E. A Review on Underground Hydrogen Storage: Insight into Geological Sites, Influencing Factors and Future Outlook. Energy Rep. 2022, 8, 461–499. [Google Scholar] [CrossRef]
- Boudreau, B.P.; Meysman, F.J.R. Predicted Tortuosity of Muds. Geology 2006, 34, 693. [Google Scholar] [CrossRef]
- Peng, S.; Marone, F.; Dultz, S. Resolution Effect in X-Ray Microcomputed Tomography Imaging and Small Pore’s Contribution to Permeability for a Berea Sandstone. J. Hydrol. 2014, 510, 403–411. [Google Scholar] [CrossRef]
- del Castillo, L.F.; Hernández, S.I.; Compañ, V. Obtaining the Tortuosity Factor as a Function of Crystallinity in Polyethylene Membranes; Maciel-Cerda, A., Ed.; Springer: Cham, Switzerland, 2017; pp. 77–86. [Google Scholar] [CrossRef]
- Maerki, M.; Wehrli, B.; Dinkel, C.; Müller, B. The Influence of Tortuosity on Molecular Diffusion in Freshwater Sediments of High Porosity. Geochim. Cosmochim. Acta 2004, 68, 1519–1528. [Google Scholar] [CrossRef]
- Tjaden, B.; Brett, D.J.L.; Shearing, P.R. Tortuosity in Electrochemical Devices: A Review of Calculation Approaches. Int. Mater. Rev. 2018, 63, 47–67. [Google Scholar] [CrossRef]
- Lee, J.K.; Bazylak, A. Optimizing Porous Transport Layer Design Parameters via Stochastic Pore Network Modelling: Reactant Transport and Interfacial Contact Considerations. J. Electrochem. Soc. 2020, 167, 013541. [Google Scholar] [CrossRef]
- Espinoza, M.; Andersson, M.; Yuan, J.; Sundén, B. Compress Effects on Porosity, Gas-Phase Tortuosity, and Gas Permeability in a Simulated PEM Gas Diffusion Layer. Int. J. Energy Res. 2015, 39, 1528–1536. [Google Scholar] [CrossRef]
- Ostadi, H.; Rama, P.; Liu, Y.; Chen, R.; Zhang, X.X.; Jiang, K. 3D Reconstruction of a Gas Diffusion Layer and a Microporous Layer. J. Memb. Sci. 2010, 351, 69–74. [Google Scholar] [CrossRef]
- Usseglio-Viretta, F.L.E.; Finegan, D.P.; Colclasure, A.; Heenan, T.M.M.; Abraham, D.; Shearing, P.; Smith, K. Quantitative Relationships Between Pore Tortuosity, Pore Topology, and Solid Particle Morphology Using a Novel Discrete Particle Size Algorithm. J. Electrochem. Soc. 2020, 167, 100513. [Google Scholar] [CrossRef]
- Cooper, S.J.; Eastwood, D.S.; Gelb, J.; Damblanc, G.; Brett, D.J.L.; Bradley, R.S.; Withers, P.J.; Lee, P.D.; Marquis, A.J.; Brandon, N.P.; et al. Image Based Modelling of Microstructural Heterogeneity in LiFePO 4 Electrodes for Li-Ion Batteries. J. Power Sources 2014, 247, 1033–1039. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in Porous Media: A Critical Review. Soil Sci. Soc. Am. J. 2013, 77, 1461. [Google Scholar] [CrossRef]
- Fu, J.; Thomas, H.R.; Li, C. Tortuosity of Porous Media: Image Analysis and Physical Simulation. Earth-Science Rev. 2021, 212, 103439. [Google Scholar] [CrossRef]
- Cooper, S.J.; Bertei, A.; Shearing, P.R.; Kilner, J.A.; Brandon, N.P. TauFactor: An Open-Source Application for Calculating Tortuosity Factors from Tomographic Data. SoftwareX 2016, 5, 203–210. [Google Scholar] [CrossRef]
- Sobieski, W.; Matyka, M.; Gołembiewski, J.; Lipiński, S. The Path Tracking Method as an Alternative for Tortuosity Determination in Granular Beds. Granul. Matter 2018, 20, 72. [Google Scholar] [CrossRef]
- Stenzel, O.; Pecho, O.; Holzer, L.; Neumann, M.; Schmidt, V. Predicting Effective Conductivities Based on Geometric Microstructure Characteristics. AIChE J. 2016, 62, 1834–1843. [Google Scholar] [CrossRef]
- Pardo-Alonso, S.; Vicente, J.; Solórzano, E.; Rodriguez-Perez, M.Á.; Lehmhus, D. Geometrical Tortuosity 3D Calculations in Infiltrated Aluminium Cellular Materials. Procedia Mater. Sci. 2014, 4, 145–150. [Google Scholar] [CrossRef]
- Al-Raoush, R.I.; Madhoun, I.T. TORT3D: A MATLAB Code to Compute Geometric Tortuosity from 3D Images of Unconsolidated Porous Media. Powder Technol. 2017, 320, 99–107. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid Flow through a Granular Bed. Trans. Inst. Chem. Eng. 1937, 75, 150–167. [Google Scholar] [CrossRef]
- Kozeny, J. Ueber kapillare Leitung des Wassers im Boden. R. Acad. Sci. Vienna Proc. Cl. I 1927, 136, 271–306. [Google Scholar]
- Matyka, M.; Khalili, A.; Koza, Z. Tortuosity-Porosity Relation in Porous Media Flow. Phys. Rev. E 2008, 78, 026306. [Google Scholar] [CrossRef]
- Piller, M.; Schena, G.; Nolich, M.; Favretto, S.; Radaelli, F.; Rossi, E. Analysis of Hydraulic Permeability in Porous Media: From High Resolution X-Ray Tomography to Direct Numerical Simulation. Transp. Porous Media 2009, 80, 57–78. [Google Scholar] [CrossRef]
- Luo, L.; Yu, B.; Cai, J.; Zeng, X. Numerical Simulation of Tortuosity for Fluid Flow in Two-Dimensional Pore Fractal Models of Porous Media. Fractals 2014, 22, 1450015. [Google Scholar] [CrossRef]
- Jin, G.; Patzek, T.W.; Silin, D.B. Direct In Proceedings of the Prediction of the Absolute Permeability of Unconsolidated and Consolidated Reservoir Rock. SPE Annual Technical Conference and Exhibition Proceeding, Houston, TX, USA, 26 September 2004. [Google Scholar] [CrossRef]
- Degruyter, W.; Burgisser, A.; Bachmann, O.; Malaspinas, O. Synchrotron X-ray Microtomography and Lattice Boltzmann Simulations of Gas Flow through Volcanic Pumices. Geosphere 2010, 6, 470–481. [Google Scholar] [CrossRef]
- Ahmadi, M.M.; Mohammadi, S.; Hayati, A.N. Analytical Derivation of Tortuosity and Permeability of Monosized Spheres: A Volume Averaging Approach. Phys. Rev. E 2011, 83, 026312. [Google Scholar] [CrossRef]
- Guo, P. Lower and Upper Bounds for Hydraulic Tortuosity of Porous Materials. Transp. Porous. Med. 2015, 109, 659–671. [Google Scholar] [CrossRef]
- Saomoto, H.; Katagiri, J. Direct Comparison of Hydraulic Tortuosity and Electric Tortuosity Based on Finite Element Analysis. Theor. Appl. Mech. Lett. 2015, 5, 177–180. [Google Scholar] [CrossRef]
- Brown, L.D.; Abdulaziz, R.; Tjaden, B.; Inman, D.; Brett, D.J.L.; Shearing, P.R. Investigating Microstructural Evolution during the Electroreduction of UO2 to U in LiCl-KCl Eutectic Using Focused Ion Beam Tomography. J. Nucl. Mater. 2016, 480, 355–361. [Google Scholar] [CrossRef]
- Maxwell, J.C. Treatise on Electricity and Magnetism; Clarendon Press: London, UK, 1873. [Google Scholar]
- Wakao, N.; Smith, J.M. Diffusion in Catalyst Pellets. Chem. Eng. Sci. 1962, 17, 825–834. [Google Scholar] [CrossRef]
- Weissberg, H.L. Effective Diffusion Coefficient in Porous Media. J. Appl. Phys. 1963, 34, 2636–2639. [Google Scholar] [CrossRef]
- Tsotsas, E.; Martin, H. Thermal Conductivity of Packed Beds: A Review. Chem. Eng. Process. 1987, 22, 19–37. [Google Scholar] [CrossRef]
- Kim, J.H.; Ochoa, J.A.; Whitaker, S. Diffusion in Anisotropic Porous Media. Transp. Porous Media 1987, 2, 327–356. [Google Scholar] [CrossRef]
- Comiti, J.; Renaud, M. A New Model for Determining Mean Structure Parameters of Fixed Beds from Pressure Drop Measurements: Application to Beds Packed with Parallelepipedal Particles. Chem. Eng. Sci. 1989, 44, 1539–1545. [Google Scholar] [CrossRef]
- Boudreau, B.P. The Diffusive Tortuosity of Fine-Grained Unlithified Sediments. Geochim. Cosmochim. Acta 1996, 60, 3139–3142. [Google Scholar] [CrossRef]
- du Plessis, E.; Woudberg, S.; Prieur du Plessis, J. Pore-Scale Modelling of Diffusion in Unconsolidated Porous Structures. Chem. Eng. Sci. 2010, 65, 2541–2551. [Google Scholar] [CrossRef]
- Pisani, L. Simple Expression for the Tortuosity of Porous Media. Transp. Porous Media 2011, 88, 193–203. [Google Scholar] [CrossRef]
- Currie, J.A. Gaseous Diffusion in Porous Media. Part 2: Dry Granular Materials. Br. J. Appl. Phys. 1960, 11, 318–324. [Google Scholar] [CrossRef]
- Wyllie, M.R.J.; Spangler, M.B. Application of Electrical Resistivity Measurements to Problem of Fluid Flow in Porous Media. Am. Assoc. Pet. Geol. Bull. 1952, 36, 359–403. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Lanfrey, P.Y.; Kuzeljevic, Z.V.; Dudukovic, M.P. Tortuosity Model for Fixed Beds Randomly Packed with Identical Particles. Chem. Eng. Sci. 2010, 65, 1891–1896. [Google Scholar] [CrossRef]
- Zehner, P.; Schlünder, E.U. Waermeleitfahigkeit von Schuettungen bei maessigen Temperaturen. Chemie Ing. Tech. 1970, 42, 933–941. [Google Scholar] [CrossRef]
- Blender Foundation, Blender 2.90. Available online: https://www.blender.org/ (accessed on 31 August 2020).
- Rodrigues, S.J.; Vorhauer-Huget, N.; Tsotsas, E. Effective Thermal Conductivity of Packed Beds Made of Cubical Particles. Int. J. Heat Mass Transf. 2022, 194, 122994. [Google Scholar] [CrossRef]
- Bender, J.; Erleben, K.; Trinkle, J. Interactive Simulation of Rigid Body Dynamics in Computer Graphics. Comput. Graph. Forum 2014, 33, 246–270. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- George, G.R.; Bockelmann, M.; Schmalhorst, L.; Beton, D.; Gerstle, A.; Lindermeir, A.; Wehinger, G.D. Influence of Foam Morphology on Flow and Heat Transport in a Random Packed Bed with Metallic Foam Pellets-An Investigation Using CFD. Materials. 2022, 15, 3754. [Google Scholar] [CrossRef]
- Fernengel, J.; Weber, R.; Szesni, N.; Fischer, R.W.; Hinrichsen, O. Numerical Simulation of Pellet Shrinkage within Random Packed Beds. Ind. Eng. Chem. Res. 2021, 60, 6863–6867. [Google Scholar] [CrossRef]
- Partopour, B.; Dixon, A.G. An Integrated Workflow for Resolved-Particle Packed Bed Models with Complex Particle Shapes. Powder Technol. 2017, 322, 258–272. [Google Scholar] [CrossRef]
- Ambekar, A.S.; Mondal, S.; Buwa, V.V. Pore-Resolved Volume-of-Fluid Simulations of Two-Phase Flow in Porous Media: Pore-Scale Flow Mechanisms and Regime Map. Phys. Fluids 2021, 33, 102119. [Google Scholar] [CrossRef]
- Tsotsas, E. Particle-Particle Heat Transfer in Thermal DEM: Three Competing Models and a New Equation. Int. J. Heat Mass Transf. 2019, 132, 939–943. [Google Scholar] [CrossRef]
- You, E.; Sun, X.; Chen, F.; Shi, L.; Zhang, Z. An Improved Prediction Model for the Effective Thermal Conductivity of Compact Pebble Bed Reactors. Nucl. Eng. Des. 2017, 323, 95–102. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Liu, W.; Liu, Z. Numerical Study on Heat Transfer Performance in Packed Bed. Energies 2019, 12, 414. [Google Scholar] [CrossRef]
- Bu, S.; Wang, J.; Sun, W.; Ma, Z.; Zhang, L.; Pan, L. Numerical and Experimental Study of Stagnant Effective Thermal Conductivity of a Graphite Pebble Bed with High Solid to Fluid Thermal Conductivity Ratios. Appl. Therm. Eng. 2020, 164, 114511. [Google Scholar] [CrossRef]
- Bu, S.; Chen, B.; Li, Z.; Jiang, J.; Chen, D. An Explicit Expression of Empirical Parameter in ZBS Model for Predicting Pebble Bed Effective Thermal Conductivity. Nucl. Eng. Des. 2021, 376, 111106. [Google Scholar] [CrossRef]
- von Seckendorff, J.; Hinrichsen, O. Review on the Structure of Random Packed-Beds. Can. J. Chem. Eng. 2021, 99, S703–S733. [Google Scholar] [CrossRef]
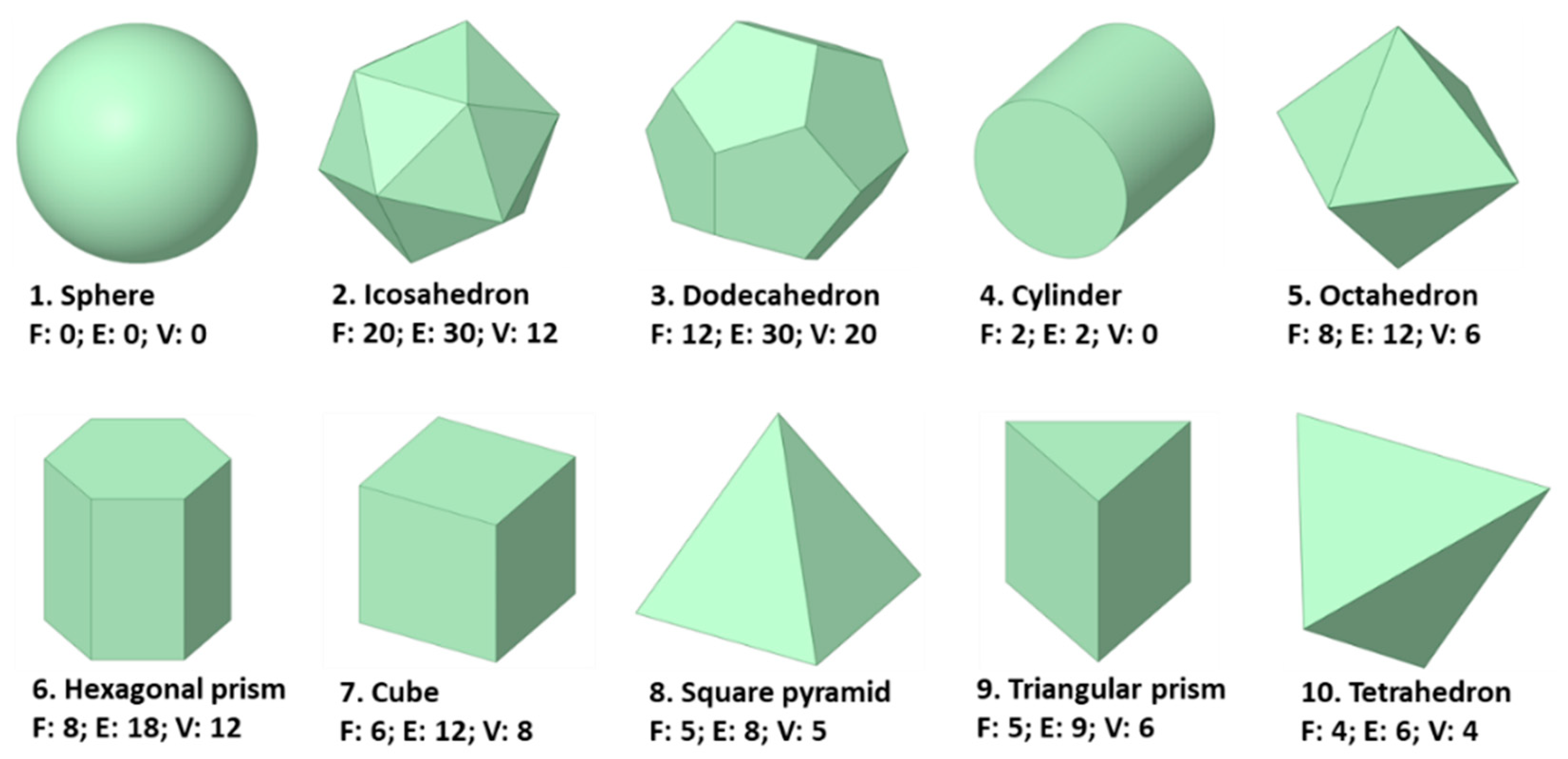




| Particle ID | Particle Type | ||
|---|---|---|---|
| 1 | Sphere | 43.54 | 1.000 |
| 2 | Icosahedron | 46.34 | 0.939 |
| 3 | Dodecahedron | 47.81 | 0.911 |
| 4 | Cylinder | 49.83 | 0.874 |
| 5 | Octahedron | 51.47 | 0.846 |
| 6 | Hexagonal prism | 51.59 | 0.844 |
| 7 | Cube | 54.00 | 0.806 |
| 8 | Square pyramid | 60.58 | 0.719 |
| 9 | Triangular prism | 60.79 | 0.716 |
| 10 | Tetrahedron | 64.85 | 0.671 |
| Particle ID | Particle Type | |||
|---|---|---|---|---|
| 1 | Sphere | 0.364 ± 0.0084 | 0.248 ± 0.0062 | 1.470 ± 0.0105 |
| 2 | Icosahedron | 0.333 ± 0.0016 | 0.197 ± 0.0123 | 1.689 ± 0.0115 |
| 3 | Dodecahedron | 0.315 ± 0.0117 | 0.182 ± 0.0067 | 1.731 ± 0.1417 |
| 4 | Cylinder | 0.319 ± 0.0011 | 0.179 ± 0.0074 | 1.777 ± 0.0597 |
| 5 | Octahedron | 0.342 ± 0.0044 | 0.191 ± 0.0064 | 1.791 ± 0.0292 |
| 6 | Hexagonal prism | 0.344 ± 0.0135 | 0.194 ± 0.0080 | 1.769 ± 0.0129 |
| 7 | Cube | 0.356 ± 0.0030 | 0.194 ± 0.0049 | 1.836 ± 0.1276 |
| 8 | Square pyramid | 0.370 ± 0.0046 | 0.196 ± 0.0055 | 1.882 ± 0.0359 |
| 9 | Triangular prism | 0.332 ± 0.0075 | 0.206 ± 0.0116 | 1.838 ± 0.0465 |
| 10 | Tetrahedron | 0.379 ± 0.0098 | 0.180 ± 0.0009 | 1.848 ± 0.0296 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, S.J.; Vorhauer-Huget, N.; Richter, T.; Tsotsas, E. Influence of Particle Shape on Tortuosity of Non-Spherical Particle Packed Beds. Processes 2023, 11, 3. https://doi.org/10.3390/pr11010003
Rodrigues SJ, Vorhauer-Huget N, Richter T, Tsotsas E. Influence of Particle Shape on Tortuosity of Non-Spherical Particle Packed Beds. Processes. 2023; 11(1):3. https://doi.org/10.3390/pr11010003
Chicago/Turabian StyleRodrigues, Simson Julian, Nicole Vorhauer-Huget, Thomas Richter, and Evangelos Tsotsas. 2023. "Influence of Particle Shape on Tortuosity of Non-Spherical Particle Packed Beds" Processes 11, no. 1: 3. https://doi.org/10.3390/pr11010003
APA StyleRodrigues, S. J., Vorhauer-Huget, N., Richter, T., & Tsotsas, E. (2023). Influence of Particle Shape on Tortuosity of Non-Spherical Particle Packed Beds. Processes, 11(1), 3. https://doi.org/10.3390/pr11010003







