Efficient Microwave Processing of Thin Films Based on Double-Ridged Waveguide
Abstract
1. Introduction
2. Methodology
2.1. Theory of the Double-Ridged Waveguide
2.2. Geometry
2.3. Governing Equations
2.4. Input Parameters and Boundary Conditions
3. Results and Discussions
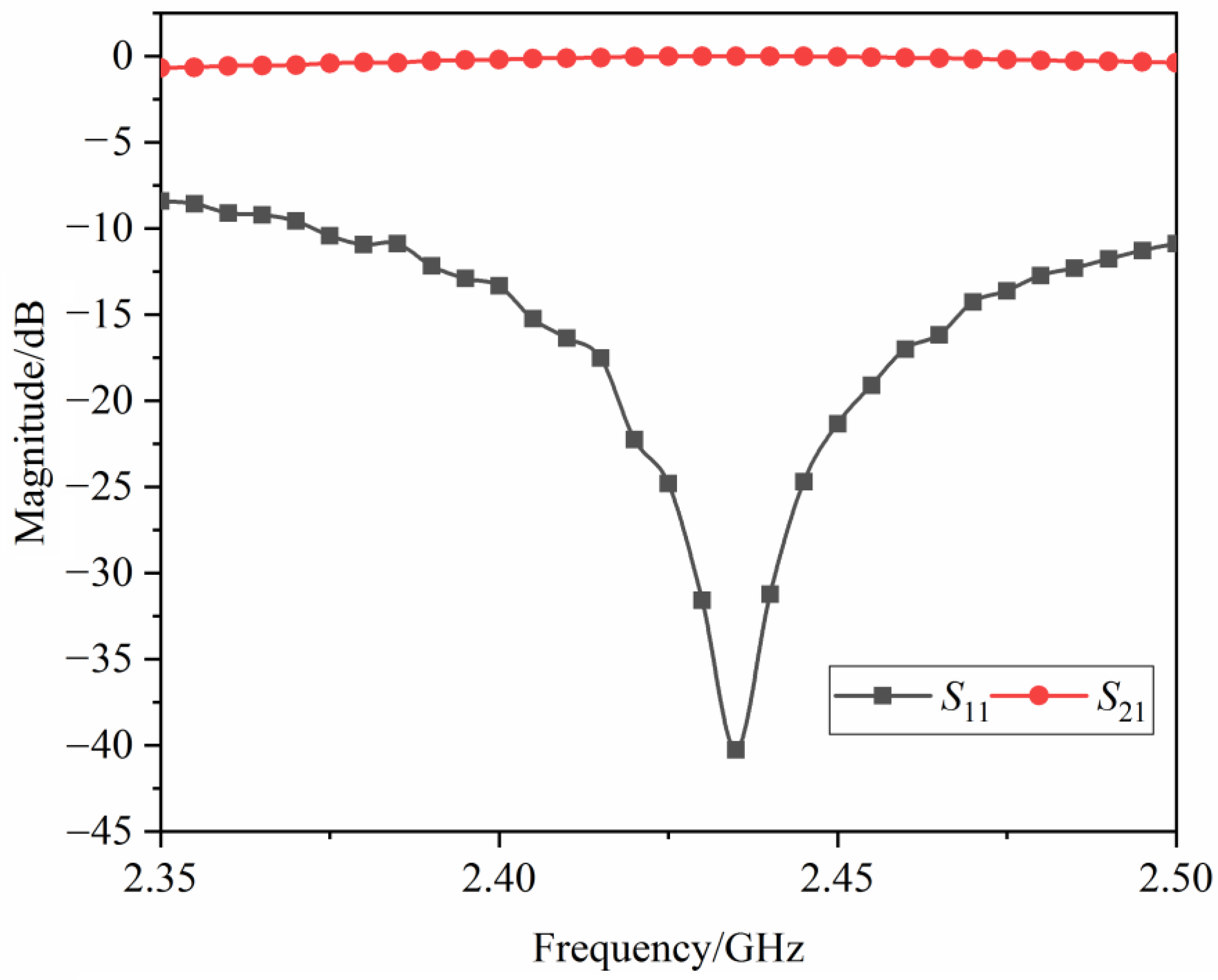
3.1. Transmission Performance
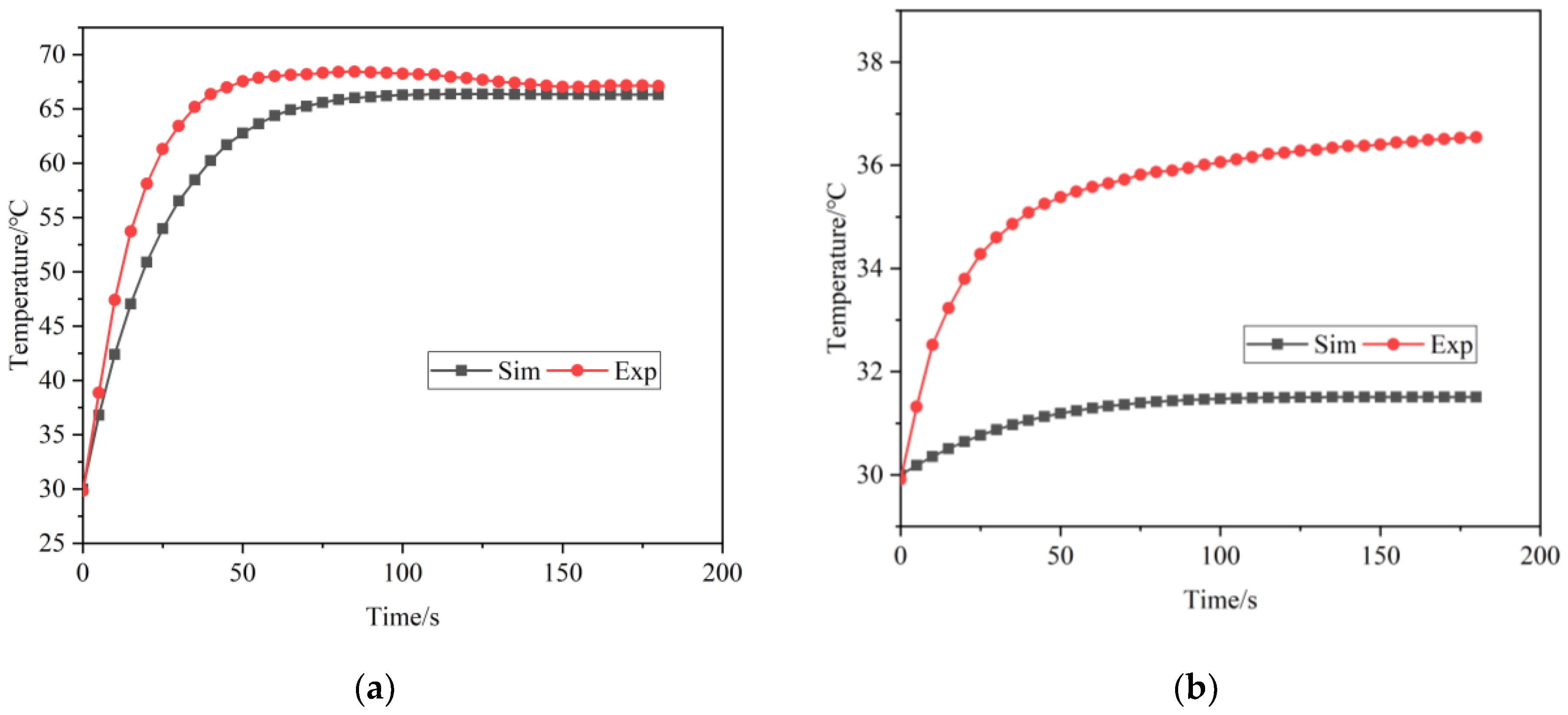
3.2. Experimental Validation
3.3. Sensitivity Analysis
3.3.1. Effect of the Working State on Heating Performance
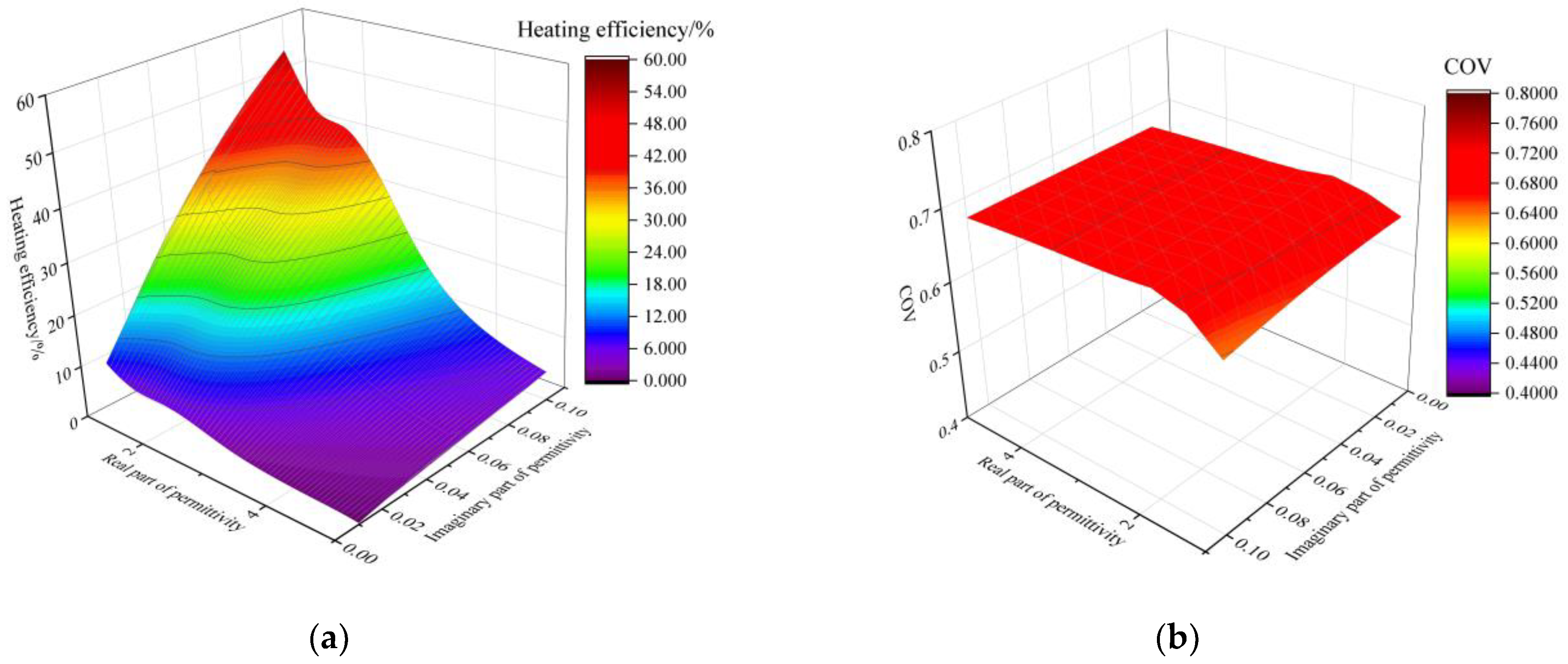
3.3.2. Effect of the Material Permittivity on Heating Performance
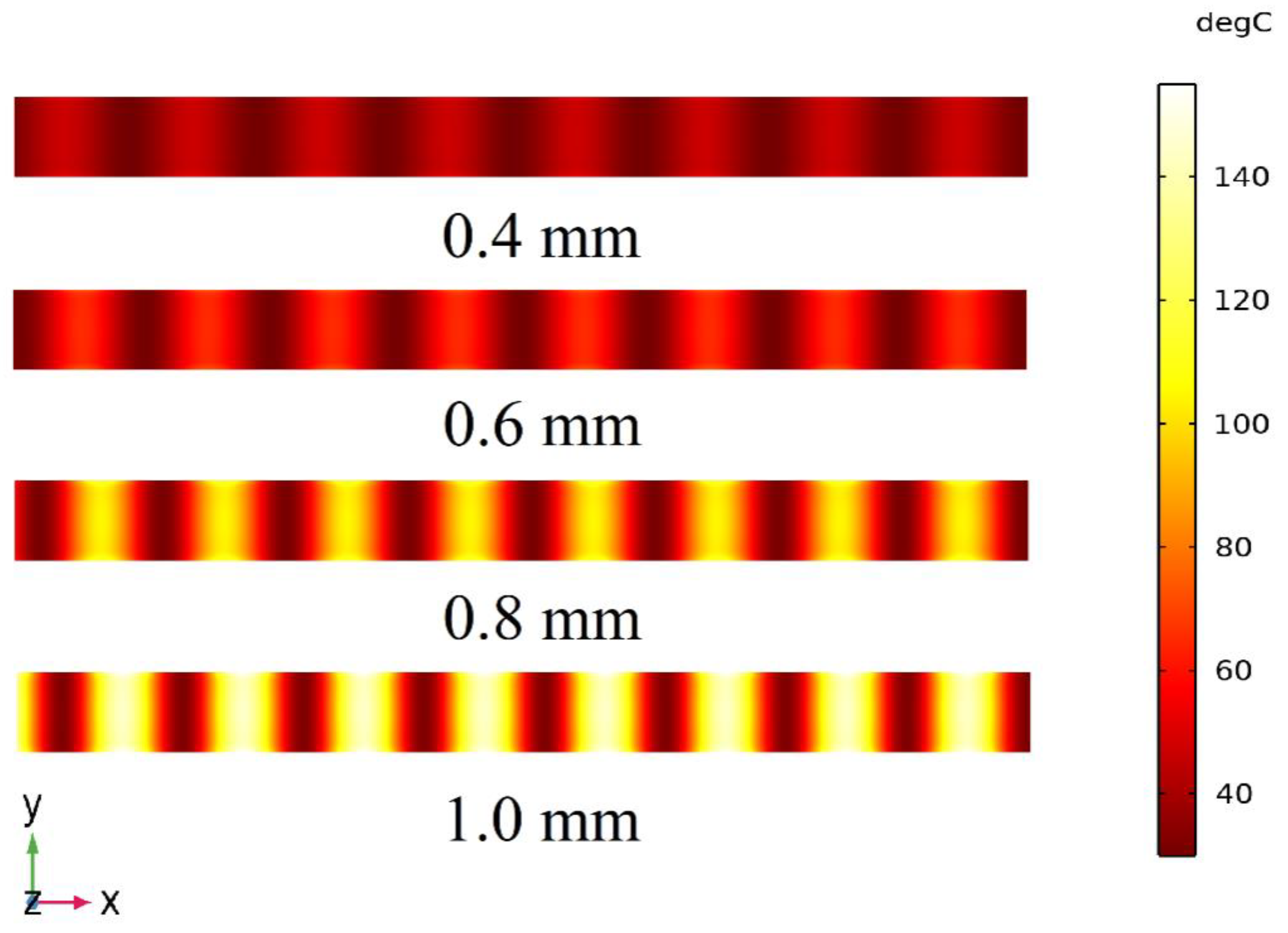
3.3.3. Effect of the Film Thickness on Heating Performance
3.3.4. Effect of the Distance between Two Ridges on Heating Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, Z.; Zhang, S.; Hong, T.; Zhu, H.; Huang, K. Frequency-selected microwave heating: Its mathematical physics basis and characteristics. Int. J. RF Microw. Comput. 2020, 30, e22131. [Google Scholar] [CrossRef]
- Chen, J.; Li, L.; Chen, G.; Peng, J.; Srinivasakannan, C. Rapid thermal decomposition of manganese ore using microwave heating. J. Alloy. Compd. 2017, 699, 430–435. [Google Scholar] [CrossRef]
- Ekezie, F.G.C.; Sun, D.W.; Han, Z.; Cheng, J.H. Microwave-assisted food processing technologies for enhancing product quality and process efficiency: A review of recent developments. Trends Food Sci. Technol. 2017, 67, 58–69. [Google Scholar] [CrossRef]
- Beckler, B.; Cowan, A.; Farrar, N.; Murawski, A.; Robinson, A.; Diamanduros, A.; Scarpinato, K.; Sittaramane, V.; Quirino, R.L. Microwave Heating of antibody-functionalized carbon nanotubes as a feasible cancer treatment. Biomed. Phys. Eng. Expr. 2018, 4, 045025. [Google Scholar] [CrossRef]
- Chen, H.L.; Li, T.; Liang, Y.; Sun, B.; Li, Q.L. Experimental study of temperature distribution in rubber material during microwave heating and vulcanization process. Heat Mass Transf. 2017, 53, 1051–1060. [Google Scholar] [CrossRef]
- Vakhin, A.V.; Khelkhal, M.A.; Tajik, A.; Ignashev, N.E.; Krapivnitskaya, T.O.; Peskov, N.Y.; Glyavin, M.Y.; Bulanova, S.A.; Slavkina, O.V.; Schekoldin, K.A. Microwave Radiation Impact on Heavy Oil Upgrading from Carbonate Deposits in the Presence of Nano-Sized Magnetite. Processes 2021, 9, 2021. [Google Scholar] [CrossRef]
- Murzakhanov, F.; Ponomarev, A.; Khelkhal, M.A.; Amziane, O.; Vakhin, A.V.; Gafurov, M. Conventional and high-field pulsed EPR experimental studies on Bazhenov oil formation under the influence of 50 Hz electromagnetic field. Fuel 2023, 334, 126580. [Google Scholar] [CrossRef]
- Sun, J.; Wang, W.; Yue, Q. Review on microwave-matter interaction fundamentals and efficient microwave-associated heating strategies. Materials 2016, 9, 231. [Google Scholar] [CrossRef]
- Asami, S. Surface Drying by High Frequency Dielectric and Microwave Heating. J. Surf. Finish. Soc. Jpn. 2015, 66, 305–310. (In Japanese) [Google Scholar] [CrossRef]
- Antony, P.; Paoloni, F. Heating of lossy films on a metal surface using a dielectric loaded T-septum waveguide. J. Microw. Power Electromagn. Energy 1992, 27, 112–116. [Google Scholar] [CrossRef]
- Song, Z.; Jing, C.; Yao, L.; Zhao, X.; Wang, W.; Mao, Y.; Ma, C. Microwave drying performance of single-particle coal slime and energy consumption analyses. Fuel Process Technol. 2016, 143, 69–78. [Google Scholar] [CrossRef]
- Chen, H.; Li, T.; Li, K.; Li, Q. Experimental and numerical modeling research of rubber material during microwave heating process. Heat Mass Tran. 2018, 54, 1289–1300. [Google Scholar] [CrossRef]
- Erchiqui, F.; Kaddami, H.; Dituba-Ngoma, G.; Slaoui-Hasnaoui, F. Comparative study of the use of infrared and microwave heating modes for the thermoforming of wood-plastic composite sheets. Int. J. Heat Mass Tran. 2020, 158, 119996. [Google Scholar] [CrossRef]
- Huang, K.; Li, J.; Zhang, Y. Research on Dry Microwave Heating Infectious Aerosols or Droplets on Respirators. IEEE Trans. Microw. Theory Technol. 2021, 69, 4246–4255. [Google Scholar] [CrossRef]
- Dębowski, M.A. Low temperature microwave processing of silicone resin coatings containing microwave susceptors. Surf. Coat. Technol. 2017, 320, 13–17. [Google Scholar] [CrossRef]
- Sastry, S.K.; Palaniappan, S. The temperature difference between a microorganism and a liquid medium during microwave heating. J. Food Process Pres. 1991, 15, 225–230. [Google Scholar] [CrossRef]
- Clark, D.E.; Folz, D.C.; West, J.K. Processing materials with microwave energy. Mater. Sci. Eng. A 2000, 287, 153–158. [Google Scholar] [CrossRef]
- Leclerc, P.; Doucet, J.; Chaouki, J. Development of a microwave thermogravimetric analyzer and its application on polystyrene microwave pyrolysis kinetics. J. Anal. Appl. Pyrol. 2018, 130, 209–215. [Google Scholar] [CrossRef]
- Huang, K.M.; Lin, Z.; Yang, X. Numerical simulation of microwave heating on chemical reaction in dilute solution. Prog. Electromagn. Res. 2004, 49, 273–289. [Google Scholar] [CrossRef][Green Version]
- Liao, Y.H.; Zhu, H.C.; Huang, K.M. Fast algorithm for electromagnetic pulse heating on dispersive medium. Int. J. Appl. Electromagn. Mech. 2016, 50, 275–282. [Google Scholar] [CrossRef]
- Huang, K.M.; Liao, Y.H. Transient power loss density of electromagnetic pulse in debye media. IEEE Trans. Microw. Theory Technol. 2014, 63, 135–140. [Google Scholar] [CrossRef]
- Hong, K.; Fu, W.; Guang, M.; Zhang, Y.; Li, B. Microwave heating performances of low density polyethylene (LDPE) plastic particles. J. Anal. Appl. Pyrol. 2021, 160, 105356. [Google Scholar] [CrossRef]
- Bleackley, W.J.; Vankoughnett, A.L.; Wyslouzil, W. Ridged waveguide microwave applicators. J. Microw. Power 1972, 7, 23–28. [Google Scholar] [CrossRef]
- El-Sayed, E.D.M.; Hashem, A.M. Wave propagation in rectangular waveguides with symmetrically placed tapered ridges. J. Microw. Power 1984, 19, 35–46. [Google Scholar] [CrossRef]
- El-Sayed, E.D.M.; Hashem, A.M. Ridged waveguide applicators for uniform microwave heating of sheet materials. J. Microw. Power 1984, 19, 111–117. [Google Scholar] [CrossRef]
- Liu, F.; Turner, I.; Siores, E.; Groombridge, P. A numerical and experimental investigation of the microwave heating of polymer materials inside a ridge waveguide. J. Microw. Power Electromagn. Energy 1996, 31, 71–82. [Google Scholar] [CrossRef]
- Zhou, P.; Yang, X.; Huang, K.; Jia, G. Microwave-Assisted Continuous-Flow Reactor Based on a Ridged Waveguide. Chem. Eng. Technol. 2015, 38, 1334–1339. [Google Scholar] [CrossRef]
- Helszajn, J.; Caplin, M. Impedance and propagation in ridge waveguide. Microw. Eng. Eur. 1997, 49–50. [Google Scholar]
- Hradecký, Z.; Mazánek, M. Nonstandard Double Ridged Waveguide Mode Study. Available online: https://www.researchgate.net/profile/M-Mazanek/publication/266584704_NONSTANDARD_DOUBLE_RIDGED_WAVEGUIDE_MODE_STUDY/links/54e253c50cf2c3e7d2d37564/NONSTANDARD-DOUBLE-RIDGED-WAVEGUIDE-MODE-STUDY.pdf (accessed on 10 October 2022).
- Marcuvitz, N. Waveguide Handbook; IET Digital Library: Hertfordshire, UK, 1986. [Google Scholar]
- Hoefer, W.J.; Burton, M.N. Closed-form expressions for the parameters of finned and ridged waveguides. IEEE Trans. Microw. Theory Technol. 1982, 30, 2190–2194. [Google Scholar] [CrossRef]
- Dang, Z.; Zhu, H.F.; Huang, J.; He, H.D. An ultra-wideband power combining in ridge waveguide for millimeter wave. IEEE Trans. Microw. Theory Technol. 2020, 68, 1376–1389. [Google Scholar] [CrossRef]
- Geedipalli, S.S.R.; Rakesh, V.; Datta, A.K. Modeling the heating uniformity contributed by a rotating turntable in microwave ovens. J. Food Eng. 2007, 82, 359–368. [Google Scholar] [CrossRef]
- Lin, B.Q.; Li, H.; Dai, H.M.; Zhu, C.J.; Yao, H. Three-dimensional simulation of microwave heating coal sample with varying parameters. Appl. Therm. Eng. 2016, 93, 1145–1154. [Google Scholar]
- Xing, K. Study on Heat Transfer Characteristics of Rubber Vulcanization with Cords by Microwave Heating. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2017. [Google Scholar]
- Zhu, S.L. Investigation on Heat Transfer Characteristics and Temperature Control of Rubber in Microwave Vulcanization Process. Ph.D. Thesis, Qingdao University of Science and Technology, Qingdao, China, 2020. [Google Scholar]
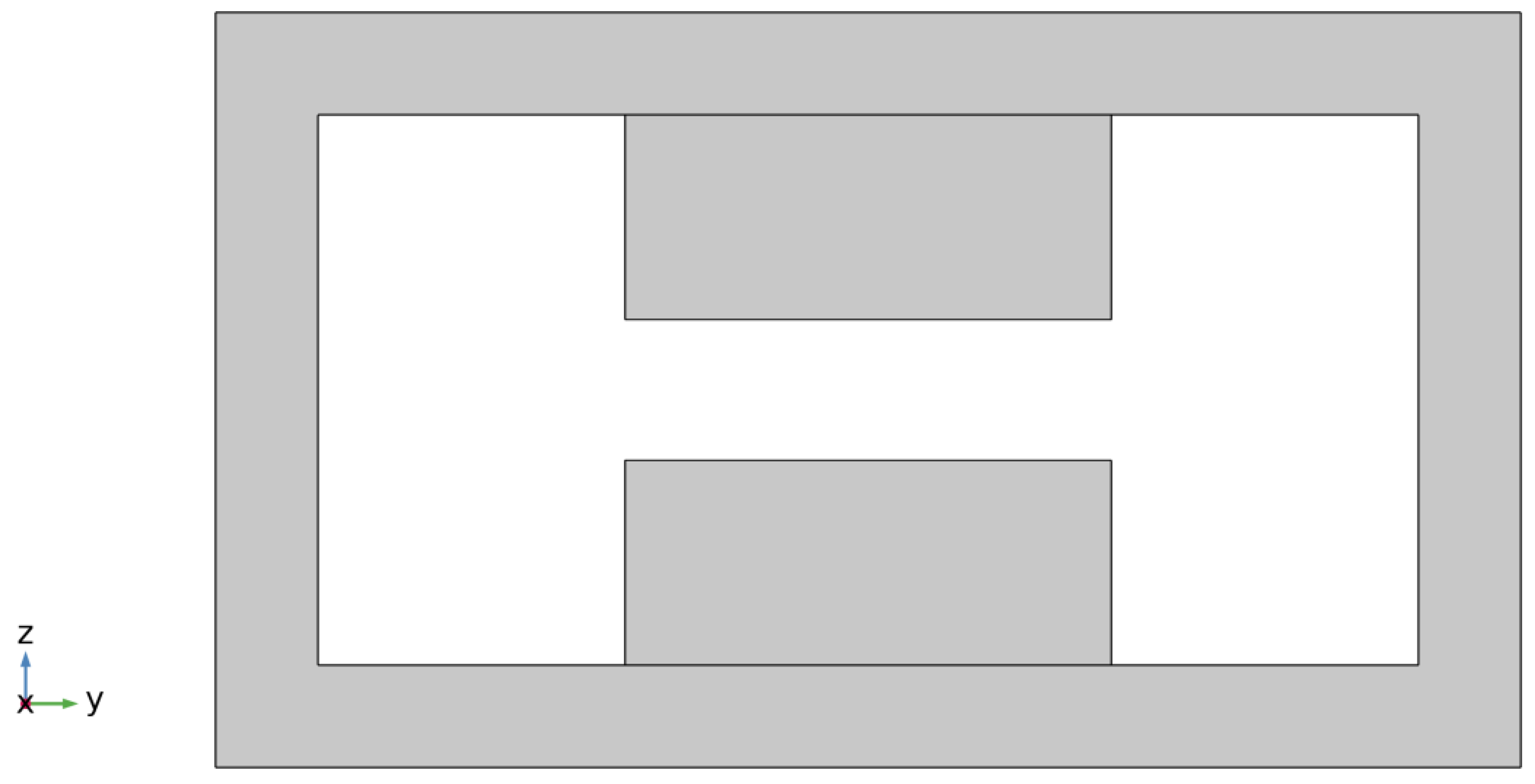

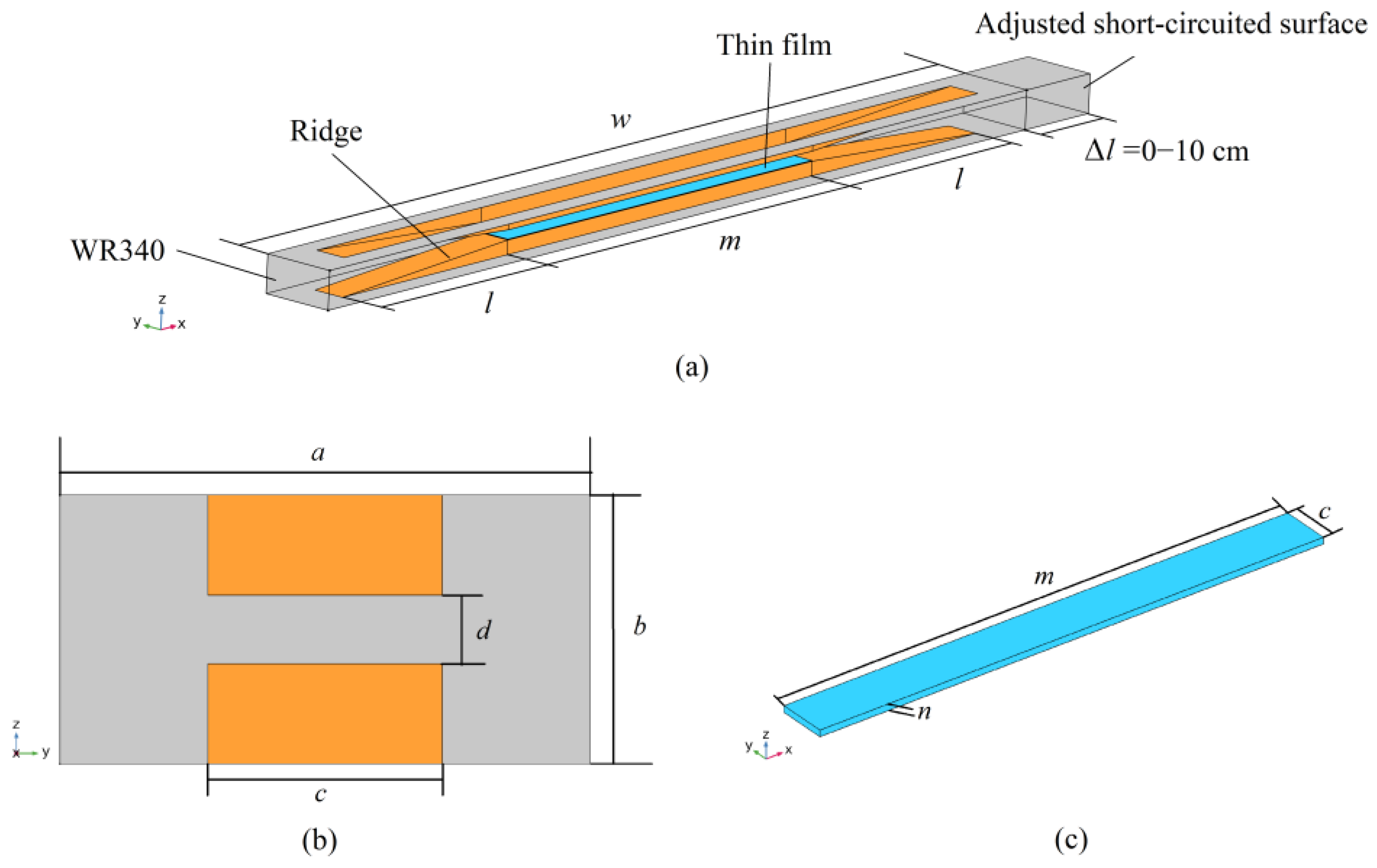






| a | b | c | d | m | l | w | n |
|---|---|---|---|---|---|---|---|
| 86.36 | 43.18 | 38 | 3 | 480 | 260 | 1100 | 0.8 |
| Property | Domain | Value | Unit | Source |
|---|---|---|---|---|
| Relative permittivity | Thin film Air | 2.17–0.05 × j 1 | - - | Measurement - |
| Relative permeability | Thin film Air | 1 1 | - - | [35] - |
| Conductivity | Thin film Air | 0 0 | S/m | [35] - |
| Heat capacity at constant pressure | Thin film | 1671.8 | [36] | |
| Density | Thin film | 1309.1 | [36] | |
| Heat conductivity coefficient | Thin film | 0.25 | [36] |
| Working State | COV | Heating Efficiency/% |
|---|---|---|
| Traveling wave | 0.306 | 7.12 |
| Standing wave | 0.690 | 23.29 |
| Thickness/mm | COV | Heating Efficiency/% |
|---|---|---|
| 0.4 | 0.694 | 4.68 |
| 0.6 | 0.703 | 9.34 |
| 0.8 | 0.704 | 19.18 |
| 1.0 | 0.687 | 29.11 |
| Distance/mm | COV | Heating Efficiency/% |
|---|---|---|
| 1 | 0.644 | 52.14 |
| 3 | 0.674 | 17.22 |
| 5 | 0.688 | 8.79 |
| 7 | 0.671 | 4.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Chen, H.; Huang, Z.; Yang, Y.; Zhu, H.; Hong, T. Efficient Microwave Processing of Thin Films Based on Double-Ridged Waveguide. Processes 2023, 11, 145. https://doi.org/10.3390/pr11010145
Wang Q, Chen H, Huang Z, Yang Y, Zhu H, Hong T. Efficient Microwave Processing of Thin Films Based on Double-Ridged Waveguide. Processes. 2023; 11(1):145. https://doi.org/10.3390/pr11010145
Chicago/Turabian StyleWang, Qiulin, Hang Chen, Zihan Huang, Yang Yang, Huacheng Zhu, and Tao Hong. 2023. "Efficient Microwave Processing of Thin Films Based on Double-Ridged Waveguide" Processes 11, no. 1: 145. https://doi.org/10.3390/pr11010145
APA StyleWang, Q., Chen, H., Huang, Z., Yang, Y., Zhu, H., & Hong, T. (2023). Efficient Microwave Processing of Thin Films Based on Double-Ridged Waveguide. Processes, 11(1), 145. https://doi.org/10.3390/pr11010145







