Abstract
mRNA-based therapeutics are predicted to have a bright future. Recently, a B2C study was published highlighting the critical bottlenecks of mRNA manufacturing. The study focused on supply bottlenecks of various chemicals as well as shortages of skilled personnel. The assessment of existing messenger ribonucleic acid (mRNA) vaccine processing shows the need for continuous manufacturing processes that are capable of about 80% chemical reduction and more than 70% personnel at factor five more efficient equipment utilization. The key technology to solve these problems is both a higher degree of automation and the maximization of process throughput. In this paper, the application of a quality-by-design process development approach is demonstrated, using process models as digital twins. Their systematic application leads to both robust optimized process parameters, with an increase in productivity of up to 108%, and sophisticated control concepts, preventing batch failures and minimizing the operating workload in terms of personnel and chemicals’ consumption. The approach thereby provides a data-driven decision basis for the industrialization of such processes, which fulfills the regulatory requirements of the approval authorities and paves the way for PAT integration. In the process investigated, it was shown that conventional PID-based controls can regulate fluctuations in the input streams sufficiently well. Model-based control based on digital twins may have potential above all in a further increase in productivity, but is not mandatory to implement for the industrialization of continuous mRNA manufacturing.
1. Introduction
The relevance of mRNA-based vaccines is steadily growing due to the coronavirus pandemic, especially in view of the promising results published on the updated mRNA vaccine against the omicron variant [1,2]. Furthermore, the extensive automatization of the production processes is planned to increase throughput and allow production of the pharmaceutical at non-specific sites [3].
The pDNA/mRNA process is generally split into two main steps. Firstly, the manufacturing and purification of the pDNA, secondly the in vitro transcription (IVT) for the formation of the mRNA target molecule, including its subsequent purification [4,5,6]. In a previously published study [7], the optimization potential in the mRNA process was shown to lie in the use of bead-based solutions. This showed an increase in productivity of 10.7% for the mixed-mode step, mainly due to an increase in yield from 86.9% to 98.65%. As a basis of comparison for this work, the purity specification was increased to 99.5%, at which the batch process has a productivity of 115 g/l*d, with a yield of 78.5%. In the reversed phase periodic countercurrent chromatography (RP-PCC), a productivity increase of 5% was achieved compared with the batch process in the previously published study. This productivity increase is based on the better utilization of the chromatography resin. Yield and purity did not change here and were constant at >99.9%, which is associated with the process control where the mRNA molecules are specifically bound, while the impurities are found in the flowthrough. As in prior works, in this paper we focus on the manufacturing of mRNA, as it is the main bottleneck in the production of the pharmaceutical [7]. The methods, however, can be easily applied to the manufacturing of pDNA as well.
In the context of the above-mentioned process intensification and increased automation, the process development based on Quality-by-Design (QbD) gives rise to highly robust design and control spaces that ensure the inherent quality of the product [7,8]. In the exemplified process development, the demonstrated QbD methods lay out a clear path for the robust design of the manufacturing process and culminate in a reliable process control strategy utilizing traditional control strategies based on proportional–integral–derivative (PID) control and advanced process control (APC) strategies based on model predictive control (MPC).
1.1. Process Overview
As mentioned above, the pDNA/mRNA production process is split into two parts. A process overview is given in Figure 1. The first part is the production of pDNA, including its harvest and purification, using two orthogonal chromatography steps: one based on anion-exchange chromatography and the other on hydrophobic-interaction chromatography. The second part is the production of mRNA and its purification using a combination of mixed-mode (MMC) and reversed-phase chromatography (RP). This process is presented in more detail in previous papers by our working group, and functional digital twins for each process step have been developed [4,7]. Additionally, continuous process design has been evaluated based on the developed models [7,9].
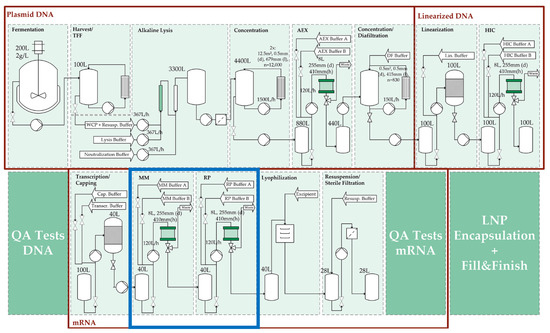
Figure 1.
Process overview for the pDNA/mRNA production. The blue highlighted process steps are the chromatographic purification processes, discussed in this work.
In the developed process, chromatography is the main purification step, as it is also commonly applied in different industrially realized processes [4,6,10,11]. To realize the aspired highly automated manufacturing of active agents, a high level of process control is required, decreasing the number of decisions made by the operating personnel and therefore decreasing manpower requirement.
1.2. Contol Approach for Chromatography
After chromatography established itself as a large-scale manufacturing process, control studies have been developed by academia with various methods such as fuzzy control, artificial neuronal networks (ANN) and MPC for either batch or SMB and MCSGP operations [12,13,14,15,16,17]. However, none of these efficient solutions have been realized on an industrial scale. Neither equipment vendors nor manufacturers have been willing to establish these new methods under regulatory constraints in recent decades.
Today, the situation has changed with the FDA and EMA demanding continuous manufacturing [8] and opening up registration paths based on a rigorous QbD approach [18,19].
2. Materials and Methods
2.1. QbD-Based Process Design
The goal of the QbD-based process design approach is to enable a robust manufacturing process, operating in optimal ranges to ensure quality by design. For this purpose, established quality management methods are used, which are applied at the different stages of the process design [18]. The first prominent example of process development in the context of QbD-process design would be the A-mAb case study of the CMC Biotech Working Group [20].
The first step of a QbD-based process development is the identification of critical quality attributes (CQA) derived from the quality target product profile (QTPP). This identification is necessary, so that these characteristics can be studied and controlled. Furthermore, compliance with the CQAs is a prerequisite for product release according to the regulators [19]. The second step is the identification of key process parameters (KPP), critical process parameters (CPP) and material attributes (MA), which contribute to the compliance with the CQAs. Thirdly, the influence of these factors on the CQAs is evaluated in a multidimensional combination of the factors called design space [18]. Inside the design space there exists a space in which the CQA lies in the acceptable range, which is called the proven acceptable range (PAR). Based on the design space and the PAR, a space is defined, in which the process can be controlled and, by design, the compliance to a defined set of CQAs is ensured. This space is the intersection of the design space and the PAR and is called the control space. In the control space, there exists the optimum for the CQAs, CPPs and KPPs, which should be the setpoints for the input variables. This approach is demonstrated for two chromatography processes in this study as examples.
2.2. Process Model
The extensive study of a design space to observe the influence of different input variables, the KPPs and MAs, can either be performed experimentally or model based. However, to evaluate the influences and interactions of different parameters on the CQAs, vast amounts of experiments are necessary. For example, to evaluate the influence of ten parameters in a two-step design of experiment (DoE) scheme, 1056 experiments are needed. To meet this high demand for data, a model-based approach is a prerequisite for success [8].
The chromatographic model used in this study is a lumped pore diffusion model, see Equation (1), and a Langmuirian adsorption model, see Equation (2) [21]; this is explained in detail in previous works concerning the mRNA material system [4,7].
The model parameters are obtained from experimental data; their determination was demonstrated in a previous publication [4]. Details on the employed resins, methods and the continuous plant setup can also be found in previous publications [4,7]. As critical quality attributes, we defined the product purity and optimized the design space to ensure purity for a maximized productivity. The purity is defined by the quotient of the target component concentration and the sum of all component concentrations in the product fraction, as given in Equation (3). The productivity is given by the mass of the target component in the product fraction , the column volume and the required time for a cycle , including regeneration and re-equilibration steps measured in days.
The models used in this study are modular and built in blocks analogous to the real plant. The structure of the model is shown schematically in Figure 2. The dynamic models of the column and the plant dead volume are marked in red. The actuators are shown in blue and the detectors in green. The solid black arrows represent the information flow along the process stream. Signal paths are indicated by dashed arrows.
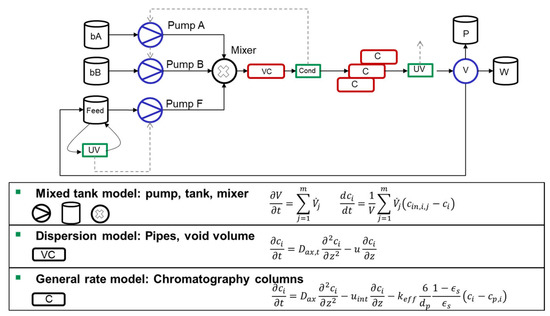
Figure 2.
Model overview for the continuous chromatography models.
The tanks shown define the concentrations of the different streams. The pumps specify the flow in the system. The flow ratio between pump A and B allows the gradient to be mixed during chromatography. In this model, the pump heads have a dead volume of 100 mL and are represented by a mixed tank model. Changes in the flow rate are mapped with a delay according to Equation (5) in order to map the start-up process of the motor. Here, is the desired flow rate, is the delay and is the current flow rate. From experience, it was decided to assume a of five seconds
2.2.1. Continuous Twin Column Chromatography Model (CTCC)
The use of MCSGP chromatography is well established in academia as a continuous biomanufacturing technique [22,23]. It allows for significant productivity and yield increases for gradient chromatography of up to 3.4 times for the productivity [24]. The CTCC is a MCSGP-like interconnection of two chromatography columns, but the columns are not synchronized. Instead, fractions to be reloaded are temporarily stored in tanks to increase the productivity of the process. The setup of this configuration is depicted in Figure 3. The productivity gain is rooted in the fact that in an MCSGP process the columns have to be synchronized in such a way that the pre-fraction of the peak and the post-fraction of the peak elute when the feed in the other column starts or ends, respectively. This requires the flowrate to be decreased. For ideal feed volumes and gradients, this can be easily done; in this process, however, the addition of storage tanks results in a productivity gain, as the elution can be operated in a more ideal flowrate. In comparison with the batch process, the productivity increases by 20% from 115 to 139 .
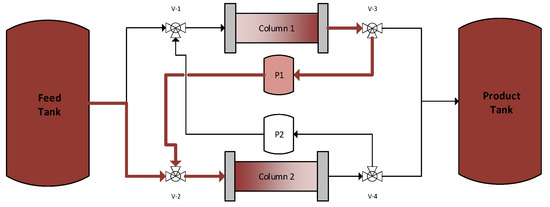
Figure 3.
Decoupled setup for the MCSGP process. The pre- and post-fractions from the MCSGP separation are stored in P1 and P2.
The CTCC model is constructed analogously to the setup shown in Figure 2. The fractionation is implemented based on real processes by a combination of the UV sum signal and the time. The first intersection point for determining the pre-fraction is detected with the aid of the UV signal. The length of the product fraction and the post-fraction was determined in column volume and varied as KPP. To reach a simulated cyclic steady state, five cycles for each chromatographic separation were modeled.
2.2.2. Periodic Countercurrent Chromatography (PCC)
PCC was modeled as a 3-column PCC. For dynamic adjustment of the switching times in the DoE, the columns were switched according to the breakthrough of the currently loaded column, which therefore represents a key process parameter and is investigated in the DoE. The fractionation of the product fraction takes place as in the CTCC process on the basis of the UV signal.
2.3. Proportional-Integral-Derivative (PID) Control
Since, in this case, a model of the process to be controlled is available and therefore unstable behavior cannot cause any damage, the Ziegler–Nichols method is suitable for determining the control parameters [25,26]. To determine the parameters, which are the proportional gain , the integrator and the derivative time constant , the step response of the target variable in the uncontrolled state is recorded in the process. Subsequently, the amplification , the reset time and the derivative time are determined from the step response, from which the control parameters can be calculated heuristically. The control parameters were calculated here using the tuning rules according to Chien, Hrones and Reswick [26,27], a refinement of the Ziegler–Nichols tuning rules, as a shorter control time was achieved with these parameters. The parameters are calculated according to Table 1 for a PID controller with an aperiodic control curve.

Table 1.
Tuning rules according to Chien, Hrones and Reswick [21,23].
2.4. Quality Management Tools
In order to identify process parameters and material attributes that influence the critical quality attributes, it is advised to use quality management tools [18,20]. In a first step, an Ishikawa diagram was created to identify potential variables. In this diagram, the influences on the quality attributes are divided according to different groups, such as the buffer preparation or process parameters [28].
During the different stages of process development, different failure-mode-analysis (FMEA)-derived tools are used. In the earlier parts of the process development, expected impacts of the identified variables are ranked on the CQAs: the purity and the process attribute (PA) and the productivity. The impact was assessed by the expected main effect and the expected effect in the interaction with other process parameters as shown in the CMC case study [20]. The ranking is given in Table 2. In the first iteration, the interaction of the parameters is estimated based on prior knowledge. The impact, however, can be directly quantitatively evaluated once the model is verified and validated with the process data. A one-factor-at-a-time (OFAT)-study lends itself to this. The determined value for the impact and the interaction is then multiplied and, based on the scores given in Table 2, either a univariate or a multivariate examination on the parameter is performed. The result of the multiplication of the impact and the interaction is later called “severity”. Variables with a score of ≤2 are not studied; those with scores 4–8 can be studied univariately or multivariately; those with higher scores are studied multivariately. The decision of whether variables with 4–8 scores have to be studied univariately or multivariately must be properly justified.

Table 2.
Ratings for the impact and the interaction assessment of potential variables on the process attributes and the CQAs.
The resulting multivariate study is the design space for the chromatographic process. The endpoints of this multidimensional space are modeled in a full-factorial DoE and the resulting design space can be evaluated statistically. Based on this evaluation, the previous assessment on the impact and the interaction can be improved. If the resolution of the DoE is too low, the use of models allows for easy expansion of the space under study, allowing for better regression and thus a better description of the experimental space. This extension was performed for both studied systems for different reasons. The rationale and the observed parameters will be discussed later.
3. Results
3.1. Critical Process Parameter Identification
As described above, the first step is to identify the critical and key process parameters that are responsible for the quality of the process. Here, quality means both compliance with the CQA and efficient production, i.e., compliance with the PA, in this case productivity. The identified process parameters are divided into five different groups in Figure 4: first, the parameters that determine the equipment; in a second group, the process variables, such as the temperature, the pH value or the conductivity of the buffer; in addition, manipulated variables, such as the gradient length; the remaining groups are organization, environment and the column parameters. When using the model, only the process is considered, the choice of the column material has already been made before, thus the other parameters cannot be represented in the model.
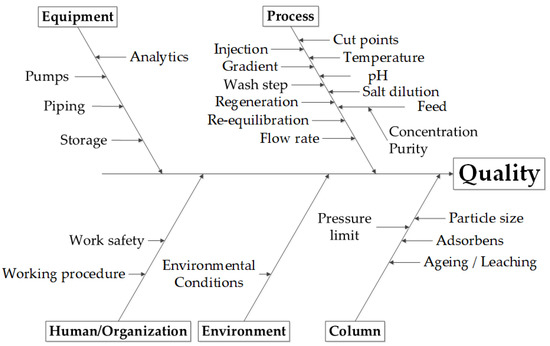
Figure 4.
Ishikawa diagram for the identification of critical and key process parameters in the chromatography processes.
3.2. Continuous Twin Column Chromatography (CTCC)
3.2.1. One-Factor-at-a-Time (OFAT)
In the first step of the process development of the CTCC process, the parameters that have an influence on the chromatography were determined. These parameters were then investigated in a one-factor-at-a-time (OFAT) study; their influence on the CQAs and KPPs are evaluated and summarized in Table 3. In the OFAT study, 65 runs were simulated. The identified parameters were varied over wide ranges to identify even small influences on the target variables. From this OFAT study, the values in the “Main Effect” columns are obtained; their significance has been previously presented in Table 1. For values between 4 and 8, it must be justified that these variables are only examined univariately.

Table 3.
Result of the impact assessment for the CTCC process step after the evaluation of the OFAT study.
Based on these numerical values, it was decided not to multivariately investigate the flow rate, since no interaction of the parameters related to the CQA is expected. With regard to PA, a large influence on productivity is expected, however, this influence is linear and can be expected.
The start of fractionation is also not investigated multivariately, since the steep front of the peaks in an overloaded chromatogram makes this detection very reliable.
3.2.2. Design and Control Space
Based on the OFAT study, the DoE for the CTCC process was created. The parameters considered influential were varied; these are the injection volume, feed concentration, salt concentration at the start of the gradient, salt concentration at the end of the gradient, gradient length, length of the pre-, product- and post-fraction and porosity, based on the severity score as described in Section 2.4. Including the center points, this results in 1025 trials in the simulated DoE space. In a first DoE, the parameters were varied in a wide range to cover a wide design space. This setup allows to identify robust areas of the process and to determine the edge of failure. The resulting contour plots for the statistically most significant parameters on purity as CQA and productivity as KPP are shown in Figure 5.
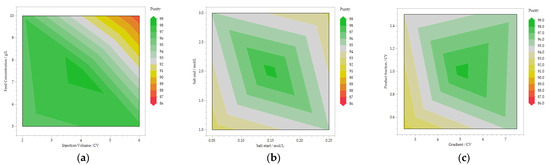
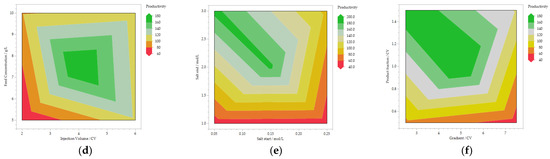
Figure 5.
Contour plots of the wider DoE-scheme for the CQA, purity (a–c) and the KPP, productivity (d–f), depicting the influence of the most significant variables.
The influences of the parameters on the purity (a, b and c) show a rather small acceptable range in which the desired purity (>99%) is achieved. This defines the range of suitable parameters. High productivities are also found in this range, as shown by the contour plots depicting the effect on this KPP (d, e and f). However, it should be noted here that, although a good overview of the data can be obtained in contour plots, the interactions in this space must also be considered for the evaluation of an optimal production range. In order to be able to perform a reliable optimization, the created model must be able to represent the investigated space well. However, this is only possible for the purity in the observed range with a regression coefficient of 0.48 for the purity. The description of productivity is better achieved with an R2 of 0.8. Therefore, based on the findings of the contour plots, a narrower space was constructed in order not to cover the edge of failure and to create a space that is easier to describe. The refined space consisted of 513 additional simulations. The edges of the reduced space are shown in Table 4.

Table 4.
Edges of the reduced DoE.
The regression of the resulting ordinary least squares (OLS) model is shown in Figure 6. It can be seen that the correlation for productivity is slightly better than for purity, with an R2 of 0.98 compared with 0.97. Furthermore, the distribution across the bisector, which is the ideal distribution, tends to be split into two groups for purity, which may indicate that one area of the data is more poorly correlated.
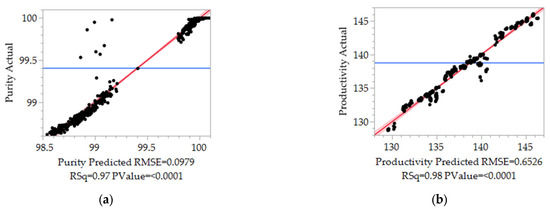
Figure 6.
Regression for the refined DoE of the CTCC process. (a) Shows the results for the purity, (b) shows the results for productivity.
As before, Figure 7 shows the contour profiles for the significant parameters. It should be noted that the legend of the purity plots (a, b and c) is more finely resolved. It can be seen that the system designed in this way is particularly robust with respect to variable variables, such as feed concentration, feed volume and salt concentration of the buffers. The CQA, the purity, is fulfilled in the entire investigated range, thus batch failures are reduced even in the case of fluctuations. The KPP is strongly influenced in this range; this does not affect the batch release but the economic efficiency of the process step. This shows that the control space, even with unrealistically large fluctuations between 10 and 20%, see Table 3, represents a process in which the CQAs are fulfilled at every point. This extremely robust process control leads to a minimization of batch failures and thus to a maximization of process economy. The robustness of the process is depicted in Figure 8. From these graphs, it becomes clear that the only significant influence on the CQA is the product fraction length, which can be easily controlled by a timed valve switch. The productivity is depended on changes to the feed volume and concentration, as these linearly influence the total mass that is loaded in the column in a fixed production time.
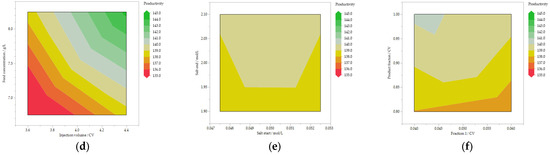
Figure 7.
Contour plots for the finer DoE. Influences on the purity are given in (a–c). Influences on the productivity are given in (d–f).
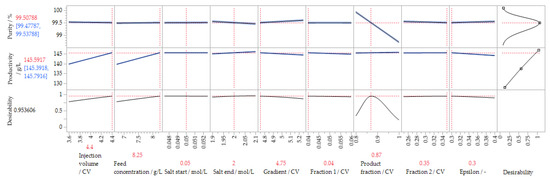
Figure 8.
Optimization for the finer DoE space, with the marked optimum for productivity and purity.
3.3. Periodic Countercurrent Chromatgrapyh (PCC)
3.3.1. One-Factor-at-a-Time (OFAT)
The OFAT study for the PCC process was conducted using the same methodology as for the CTCC process. The results are given in Table 5. In total, the PCC-OFAT study consisted of 49 simulations. Compared with the CTCC process, some process parameters were adapted to the modified procedure. Due to the process, the threshold for product fractionation was adjusted, as the steep peak front allows for an easy detection. Therefore, the parameter variation was increased to enable the observation of its influence. The product fraction length was replaced with another UV-based cut, as no center cut was performed. This enables the detection of the peak end, as the side components are not-binding, without employing any further PAT systems. This behavior is also the reason why most process parameters have little influence on the CQA for the process development of the PCC. This results in the optimization focusing mainly on productivity, instead of purity. It should be noted, however, that the wash length may have a strong influence on the purity, as too short wash durations can cause the side components to mix into the product fraction. Based on the results of the OFAT study, the following variables were studied multivariately: the bed height, diameter, flow rate, feed concentration, wash length, acetonitrile concentration and fractionation start threshold.

Table 5.
Results of the impact assessment for the PCC process step after the evaluation of the OFAT study.
3.3.2. Design and Control Space
In the first step, a full factorial experimental design was constructed from the above-mentioned parameters in two stages and three center points, corresponding to 129 simulations. However, the DoE developed in this way could not correctly represent the progression of purity over the wash duration, as purity drops from the center point (>99%) and the upper limit (>99%) to the lower limit at ~66%. For this reason, the DoE for the wash duration was refined to four stages and, with the plan thus extended to 513 simulations, a successful regression could be performed based on the data. The DoE was stepwise adjusted to the regression coefficient.
To check the consistency of the simulated data and to increase the understanding of the process, it is useful to look at the contour plots. Figure 9 shows the influences of the most significant parameters on the target values. A frequently observed behavior in chromatography is shown in the contour plots (a) and (b). It shows that a high yield is usually accompanied by a lower purity. The productivity also shows realistically expected correlations. Thus, productivity increases with increased flow rate and decreases with increasing column height. With regard to the washing step, consequently the acetonitrile concentration and the washing time, a correlation to the yield is primarily evident, which is also to be expected. Overall, the data indicate a realistic description of the experimental space and confirm the statements of further statistical analyses.
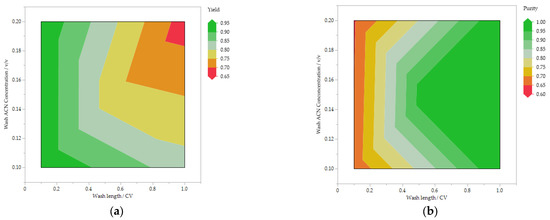
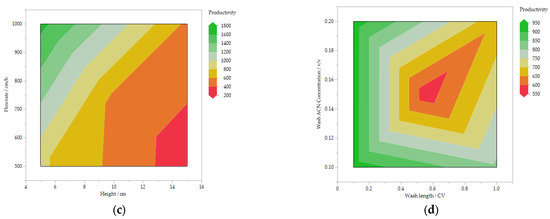
Figure 9.
Contour plots of the most significant influences on yield (a), purity (b) and productivity (c,d).
Figure 10 shows the regression results for DoE. The regressions for yield and productivity show very good regression coefficients and low P-values. This is also true for the purity regression; however, the design space seems to be split in two. Therefore, it is possible that the range between the groups cannot be depicted correctly.
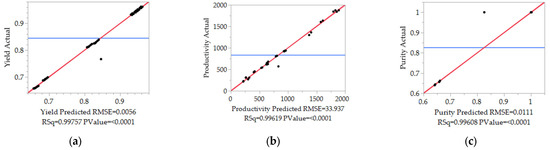
Figure 10.
Regression for the refined DoE in the PCC process, (a) for the product yield, (b) for the productivity and (c) for the purity.
In order to investigate this possibility, Figure 11 shows the course of the model over the significant parameters with regard to purity. The acetonitrile concentration, as well as the fraction start, do not appear to be significant in this range. The wash length on the other hand shows a significant influence on purity. Nevertheless, it is noticeable that in parts of the investigated experimental space the purity is above one, which is not physically possible. This means that the optimum of the DoE does not represent the optimum of the simulations. Besides the purity, the predictions between the DoE points also do not match the model results.
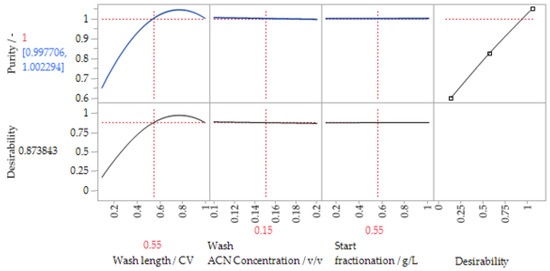
Figure 11.
Purity profile based on the constructed DoE.
For this reason, an artificial neural network (ANN) was trained as an alternative to predict the optimum and to better describe the experimental space. To describe the experimental space, 20 tanh(x) neurons were used. For validation, a nested cross-validation (k = 5, L = 4) was used. The results of the ANN are given in Figure 12. The ANN generally depicts a realistic behavior of the observed CQA and KPPs. Especially, the course for purity is depicted closely to the observed values in the design space, with an R2 > 0.9999 for the training, validation and test set. The optimum calculated by the ANN is very robust for wash durations between 0.6 and 1. In addition, it agrees with the results of the simulations in this range, which proves a good description of the design space.
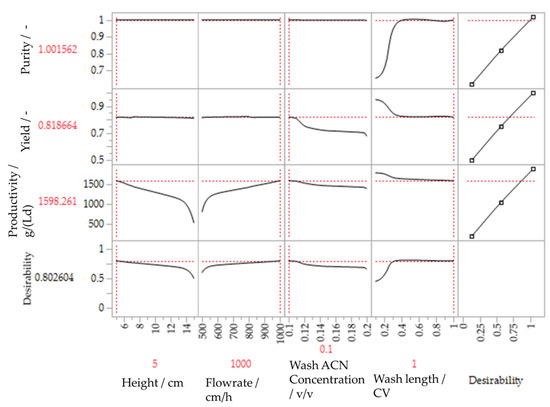
Figure 12.
Purity, yield and productivity profile for the ANN, shortened to the significant parameters.
3.4. Control Strategy
As described before, some control systems are already implemented for investigation in the DoE. For PCC, this is the breakthrough detection, which controls the switching of the columns. In addition, the fractionation is controlled by UV detection, which initiates and terminates the fractionation of the product peak in the gradient. Based on the previously obtained knowledge, it is clear that the washing time, as well as the acetonitrile concentration, has the greatest influence on the CQA. This relationship is clearly shown in Figure 9a,b,d. The findings obtained from the neural network also show the influence of these parameters. The control of the washing time is not a control loop and the flow rate control of the pumps is state-of-the-art in production plants and widely established. However, the composition of the buffer is not checked, so a conductivity measurement was introduced here, which automatically compensates for a possible fluctuation in the buffer concentration. The conductivity measurement is used as a control variable in the controller, which has the volume flow of pump B as its manipulated variable (see Figure 2). In order to prevent fluctuations in the total volume flow, the manipulated variable is deducted from the volume flow of pump A.
Figure 13a shows the step response to a jump in concentration in buffer B. The amplification, the reset time and the derivative time can be determined by the inflection point tangent (red) according to Chien, Hrones and Reswick. From the values for , and , the proportional gain is then determined to be 2491.77%/%, the integrator time constant to be 18.30 s and the derivative time constant to be 1.81 s. The system set in this way can quickly regulate out different fluctuations in the buffer concentration without oscillation. The control response (green) to different error cases is shown in Figure 13b–d. In none of the observed cases does the variation of the buffer lead to changes in the chromatogram and consequently neither to changes in the CQAs and PAs.
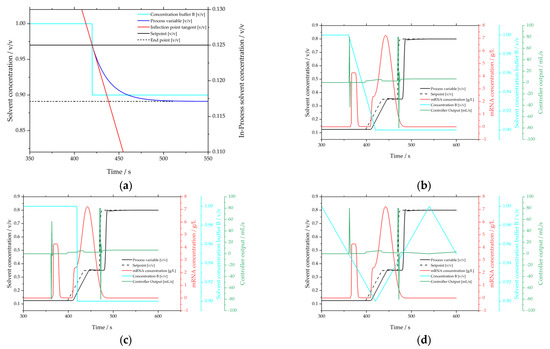
Figure 13.
Step response of the process variable for evaluation using the Chien, Hrones and Reswick-parameters (a) and the response of the controlled system on a buffer concentration shift (b), step (c) or a zigzag pattern (d).
This implemented control and the implemented process optimum leads to an increase in productivity of 38% with consistent high purity and yield. The key figures of the optimized and controlled process are shown in Table 6 in comparison with the batch process.

Table 6.
Influence of different process setups for the reversed phase chromatography step.
The control tasks in the CTCC process behave in the same way as in the PCC process. Fractionation is started by means of a UV signal, and the length of the subsequent fraction can be reliably controlled over time. The fluctuations expected from the previous process show no influence on the CQA in the expected fluctuation range, as shown in Figure 8, and thus do not lead to batch failures. Nevertheless, like the PCC process, the process is susceptible to fluctuations in buffer concentration. This dependence has already been discussed and is shown in Figure 6b. The variation of 10% in buffer B assumed in PCC would drop the purity here to <98%, which means that the product does not comply with the CQA. For this reason, a comparable control to the PCC was implemented, based on the measurement of the conductivity upstream of the column. The effect of the control is shown in Figure 14. Here, only the worst case, i.e., a sudden change in the buffer concentration, is shown; this can nevertheless be quickly compensated for by the system and does not lead to a change in the chromatogram, so that there is no need to worry about a change in the CQA. This makes it clear that, even with the unrealistic variation of 10% in the concentration of buffer B, purity is achieved by gradient control. In addition, due to the effective control, no change in the chromatogram can be seen and therefore the productivity in the controlled process is still at the optimum. The covariation of other process parameters (e.g., feed concentration or feed volume) was not investigated, since, based on the previous DoE studies, an interaction with respect to the CQA in this area is not expected, see Figure 8.
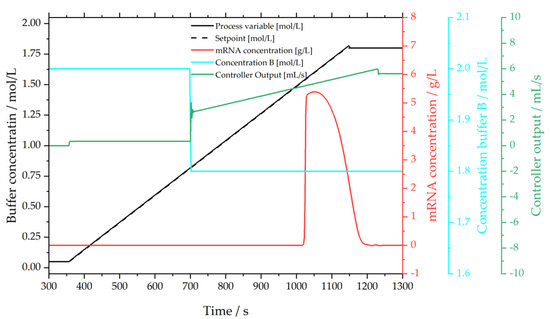
Figure 14.
Chromatogram of the CTCC step with the implemented control system.
In addition to the process control already described, the implementation of model predictive control is possible. Based on the modeling of the chromatography process, the fraction cuts can be determined in advance to ensure optimal separation of the components in the chromatography. A similar result could be achieved if it were possible to determine the side component concentrations online using PAT systems. The possibility of this measurement has already been demonstrated for other stock systems [29]. These techniques are particularly interesting for application in the mixed-mode CTCC step, since a center cut is performed here. In our opinion, there is no advantage for the PCC step, since only one component is expected in the elution. The implementation of this control in the model leads to an increase in productivity of 108%, see Table 7, with the same yield and purity. This increase is due to the possible increase in column loading and the reduction in column length, where the prediction-based automated fractionation can still ensure purity.

Table 7.
Influence of different process setups for the mixed-mode chromatography step.
4. Discussion
In this paper, as well as in the overview paper in which the whole process for mRNA manufacturing from in vitro transcription and membrane processes up to lipid nano particle formulation (LNP) were discussed in detail, the aim was to demonstrate the regulatory method for the development of a pharmaceutical process on the basis of model data. Reference was made to the ICH guidelines of the European Union [18,19]. During process development, it was shown that the use of quality management tools, as already demonstrated by the CMC BioTech Working Group for monoclonal antibody production [20], among others, can increase process understanding and also provide for planned process robustness. Processes can be designed, as shown in the example of CTCC, in such a way that expected fluctuations of a variable not intended as an inline measurement, in this case feed concentration, lead to compliance with the previously set critical quality attributes (CQA).
It was shown that, to identify the parameters to be studied multivariately, a one-factor-at-a-time (OFAT) study is well suited to estimate the magnitude of the influences. The findings of this OFAT study subsequently led to a more precise specification of the parameter influence ranking. Based on this refined assessment of the parameter influences on the CQAs and key process parameters (KPP), the parameters to be investigated multivariately were identified and examined in a DoE design. The advantages of this design in this study is that a full-factorial sampling method is widely employed in experimentally based process development and such the approach is easily transferable to the more conventional design approach. To obtain additional knowledge about the design space a Latin-hypercube sampling could be employed. This would likely lead to higher accuracy in the statistical model, but would also increase the required computation time, as the number of experiments would most likely increase. The use of process models in such a procedure is ideal, because the model parameters can be determined with a manageable amount of effort and a valid model is then available as a digital twin [30]. This model, as demonstrated in this study, allows the substitution of a large number of experiments to be performed in a short period of time that would not be feasible in the laboratory, thus elevating process understanding to a level that cannot be achieved by conventional laboratory experiments. The precise knowledge of the design space thus spanned also enables the optimization of various KPPs or CQAs, which could be arbitrarily extended to include, for example, economics. For the optimization of these CQAs and KPPs, it has been shown in this study that, in some cases, the reliability of the ordinary least squares models decreases, especially in cases such as the purity curve in the PCC model, which is >99.9% in wide ranges, but decreases abruptly for short wash durations. However, these nonlinear relationships could be well represented by a low-complexity neural network, showing a high prediction quality for the system under investigation and allows for the optimization of the investigated CQA and KPP.
In addition to the importance for process design, the models also showed as digital twins the possibility of evaluating possibilities for process control following process development. Here, simple empirical approaches can be used to compensate for fluctuations in a timely manner. Other control tasks, especially in chromatography, are limited to controls without loops. Here, the use of UV sum signals was employed to control switching times and fractionation. The overall process control concept is depicted in Figure 15. The different control loops are marked in color. In red is the previously modeled gradient control with the use of a PID control loop. In green, the breakthrough control is shown, which is based on a UV threshold. In the blue control loop, the gradient at the end of the column is measured and used to determine the current porosity and axial dispersion in order to determine the drift via the column aging and to define a termination criterion for the column change, a technique already demonstrated in [31]. The fractionation control is shown in orange. As already discussed, the data of the orange control loop also offer the possibility to describe the drift of the isothermal parameters by applying artificial neural networks and thus to define a further termination criterion for the column change, as well as to enable a model-predictive control over the aging process.
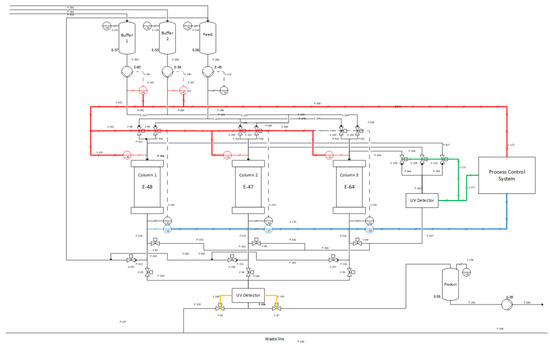
Figure 15.
Process control concept of the PCC separation. Highlighted are the gradient control loop (red), the breakthrough control (green), the column ageing control (blue) and the fractionation control (orange).
It could be pointed out that there is a potential for optimization in the area of advanced process control (APC), for example, through the implementation of soft sensors, which can be used to test the CQA with regard to real-time release testing. This technology allows the inline measurement of target and side components in mAb and model systems and it is conceivable that this technology can also be established for the mRNA system [29,32,33].
The potential of model-based control lies particularly in the further optimization of various process parameters. On the one hand, this technology has the potential to increase productivity by determining the concentration of the components in the feed solution or, alternatively, by obtaining the concentration from the release testing of the previous unit operation. With the help of this concentration, the loading flow rate in the loading can be adjusted accordingly to increase productivity. On the other hand, based on the previous determination of the minor components, the separation method can be optimized via the gradient [16].
Process influences that cannot be influenced by control were also examined for their influence in this study. In chromatography, these are mainly porosity, axial diffusion and isothermal parameters. Due to column aging and fouling, these parameters can change during the process. However, in order to deal with the fluctuation of these process parameters, a termination criterion can be defined with the help of the design space investigated, above which the column must be repacked. The shift of the column’s fluid dynamics can be controlled by analyzing the fluid dynamics’ influences on the gradient. This analysis is done with the conductivity sensors installed behind the columns, see Figure 15 marked in blue. Advances in the field of parameter determination with the aid of neural networks are particularly useful for the purpose of determining the isothermal parameters [34,35]. These methods offer the possibility to map the parameter shift over time very precisely, which results in a better termination parameter for the column than a simple cycle number. This allows the column to continue to be used as long as it is in specification, thus making better use of the resin increasing the economic efficiency of the process.
5. Conclusions
This work uses the actual mRNA therapeutics’ production process to demonstrate the regulatory demanded approach for continuous bioprocess development. The process development performed in this way results in robustly designed processes, minimizing batch failures and reducing the consumption of human and chemical resources. In individual steps, the influence of various process parameters is first estimated. This leads to a known design space in which a control space is defined. It was shown that for the processes considered here, control with the aid of UV-level sum signal circuits and simple PID control loops is sufficient for process success with regard to the CQAs. This shows that the industrialization of the PID control concept as well as the continuous biomanufacturing techniques are straightforward with state-of-the-art technology.
These robustly designed continuous chromatography processes for mixed mode in a CTCC and reversed phase in a PCC setup allow separation in compliance with the CQAs and KPPs. This is possible, despite rather extreme variations in the process parameters of, for example, 10% in the concentration of buffer B, 37.5% in the injection volume or 13% in the feed concentration. Covariation of the process parameters would most likely not influence the CQA, as no interaction regarding purity was observed in the statistical analysis. There is, however, an influence to be expected regarding productivity, as a change in feed concentration and feed volume would decrease the available feed per hour and therefore must influence the productivity. By optimizing the process in the design space, productivity could be increased by 21% for the CTCC process. Furthermore, an additional optimization potential through the integration of model predictive control or PAT technologies of 108% compared with the batch process and 72% compared with the simple CTCC process was identified. The PCC process showed an optimization potential of 38% compared with the batch process. Compliance with the CQA, the purity, was achieved in both processes with 99.5% and >99.9%, respectively. From this data, it becomes clear that the most promising technology for CTCC is the determination of the optimal fraction cuts employing model predictive control. The alternative simultaneous determination of major and minor components using chemometric methods and the resulting fraction cut-point determination would achieve a comparable productivity gain. In addition, the implementation of these technologies would enable a further step towards the final goal of real-time release testing. The industrial implementation of these additional technologies would naturally lead to higher capital investment costs in the construction of the plant and the following maintenance. Nevertheless, the worst-case costs of a few hundred thousand euros would be more than compensated by the increased productivity and yield, as well as possible personnel and chemical savings and the increased out-of-spec safety.
Author Contributions
Conceptualization, J.S.; methodology, F.L.V. and S.Z.-R.; software, F.L.V. and S.Z.-R.; validation, F.L.V., S.Z.-R., A.S. and J.S.; investigation, F.L.V. and S.Z.-R.; writing—original draft preparation, F.L.V.; writing—review and editing, J.S., J.P.B.M. and B.N.; supervision, J.S.; project administration, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institute for Separation and Process Technology from Clausthal University of Technology and received no external funding.
Data Availability Statement
Data cannot be made publicly available.
Acknowledgments
The authors would like to acknowledge their institute’s laboratory colleagues, especially Frank Steinhäuser, Nils Hoffmann and Volker Strohmeyer as well as the PCS team Thomas Knebel with Christian Siemers, Automation Technology for the longterm cooperation, and Christian Bohn, Control Engineering, with his co-workers Mirjam Holm and Stephan Beitler at Clausthal University of Technology for PID controller design method support. We kindly acknowledge the support of Open Access Publishing Fund of the Clausthal University of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- BioNTech. Pfizer and BioNTech Announce Omicron-Adapted COVID-19 Vaccine Candidates Demonstrate High Immune Response Against Omicron; BioNTech: Mainz, Germany; New York, NY, USA, 2022. [Google Scholar]
- Moderna. Moderna Announces Omicron-Containing Bivalent Booster Candidate mRNA-1273.214 Demonstrates Superior Antibody Response Against Omicron; Moderna: Cambridge, MA, USA, 2022. [Google Scholar]
- BioNTech. BioNTech Introduces First Modular mRNA Manufacturing Facility to Promote Scalable Vaccine Production in Africa; BioNTech: Mainz, Germany, 2022. [Google Scholar]
- Schmidt, A.; Helgers, H.; Vetter, F.L.; Juckers, A.; Strube, J. Digital Twin of mRNA-Based SARS-COVID-19 Vaccine Manufacturing towards Autonomous Operation for Improvements in Speed, Scale, Robustness, Flexibility and Real-Time Release Testing. Processes 2021, 9, 748. [Google Scholar] [CrossRef]
- Štrancar, A. High Yield mRNA Production Process from E. coli to Highly Pure mRNA. 2020. Available online: https://www.biaseparations.com/en/library/seminars-webinars/1098/high-yield-mrna-production-process-from-ecoli-to-highly-pure-mrna (accessed on 6 July 2022).
- Von der Mülbe, F.; Reidel, L.; Ketterer, T.; Gontcharova, L.; Bauer, S.; Pascolo, S.; Probst, J.; Schmid, A. Method for Producing RNA. U.S. Patent 10,017,826, 10 July 2018. [Google Scholar]
- Schmidt, A.; Helgers, H.; Vetter, F.L.; Juckers, A.; Strube, J. Fast and Flexible mRNA Vaccine Manufacturing as a Solution to Pandemic Situations by Adopting Chemical Engineering Good Practice—Continuous Autonomous Operation in Stainless Steel Equipment Concepts. Processes 2021, 9, 1874. [Google Scholar] [CrossRef]
- Zobel-Roos, S.; Schmidt, A.; Mestmäcker, F.; Mouellef, M.; Huter, M.; Uhlenbrock, L.; Kornecki, M.; Lohmann, L.; Ditz, R.; Strube, J. Accelerating Biologics Manufacturing by Modeling or: Is Approval under the QbD and PAT Approaches Demanded by Authorities Acceptable Without a Digital-Twin? Processes 2019, 7, 94. [Google Scholar] [CrossRef]
- Helgers, H.; Hengelbrock, A.; Schmidt, A.; Strube, J. Digital Twins for Continuous mRNA Production. Processes 2021, 9, 1967. [Google Scholar] [CrossRef]
- GenScript ProBio. Accelerating Vaccine Development against COVID-19. 2020. Available online: https://www.genscriptprobio.com/gsfiles/techfiles/GPB-COVID19-GMP%20plasmid-GPB_052020.pdf (accessed on 8 July 2022).
- Kis, Z.; Kontoravdi, C.; Shattock, R.; Shah, N. Resources, Production Scales and Time Required for Producing RNA Vaccines for the Global Pandemic Demand. Vaccines 2020, 9, 3. [Google Scholar] [CrossRef]
- Klatt, K.-U.; Hanisch, F.; Dünnebier, G.; Engell, S. Model-based optimization and control of chromatographic processes. Comput. Chem. Eng. 2000, 24, 1119–1126. [Google Scholar] [CrossRef]
- Toumi, A.; Engell, S. Optimization-based control of a reactive simulated moving bed process for glucose isomerization. Chem. Eng. Sci. 2004, 59, 3777–3792. [Google Scholar] [CrossRef]
- Engell, S.; Toumi, A. Optimisation and control of chromatography. Comput. Chem. Eng. 2005, 29, 1243–1252. [Google Scholar] [CrossRef]
- Grossmann, C.; Ströhlein, G.; Morari, M.; Morbidelli, M. Optimizing model predictive control of the chromatographic multi-column solvent gradient purification (MCSGP) process. J. Process Control 2010, 20, 618–629. [Google Scholar] [CrossRef]
- Espinoza, D.; Andersson, N.; Nilsson, B. Binary separation control in preparative gradient chromatography using iterative learning control. J. Chromatogr. A 2022, 1673, 463078. [Google Scholar] [CrossRef]
- Armstrong, A.; Horry, K.; Cui, T.; Hulley, M.; Turner, R.; Farid, S.S.; Goldrick, S.; Bracewell, D.G. Advanced control strategies for bioprocess chromatography: Challenges and opportunities for intensified processes and next generation products. J. Chromatogr. A 2021, 1639, 461914. [Google Scholar] [CrossRef]
- European Medicines Agency. ICH Guideline Q11 on Development And Manufacture of Drug Substances (Chemical Entities and Biotechnological/Biological Entities); European Medicines Agency: Amsterdam, The Netherlands, 2012. [Google Scholar]
- European Medicines Agency. ICH Guideline Q8 (R2) on Pharmaceutical Development; European Medicines Agency: Amsterdam, The Netherlands, 2017. [Google Scholar]
- CMC Biotech Working Group. A-Mab: A Case Study in Bioprocess Development. 2009. Available online: https://qbdworks.com/storage/2014/06/A-MabCaseStudyVersion.pdf (accessed on 8 July 2022).
- Guiochon, G.; Felinger, A.; Shirazi, D.G.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography, 2nd ed.; Elsevier Academic Press: Amsterdam, The Netherlands; ISBN 9780123705372.
- Papathanasiou, M.M.; Steinebach, F.; Stroehlein, G.; Müller-Späth, T.; Nascu, I.; Oberdieck, R.; Morbidelli, M.; Mantalaris, A.; Pistikopoulos, E.N. A control strategy for periodic systems–application to the twin-column MCSGP. In 12th International Symposium on Process Systems Engineering and 25th European Symposium on Computer Aided Process Engineering; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1505–1510. ISBN 9780444634290. [Google Scholar]
- Aumann, L.; Morbidelli, M. A continuous multicolumn countercurrent solvent gradient purification (MCSGP) process. Biotechnol. Bioeng. 2007, 98, 1043–1055. [Google Scholar] [CrossRef] [PubMed]
- Persson, O.; Andersson, N.; Nilsson, B. Design of two-column batch-to-batch recirculation to enhance performance in ion-exchange chromatography. J. Chromatogr. A 2018, 1531, 112–121. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. J. Dyn. Syst. Meas. Control 1993, 115, 220–222. [Google Scholar] [CrossRef]
- Zacher, S.; Reuter, M. Regelungstechnik für Ingenieure; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017; ISBN 978-3-658-17631-0. [Google Scholar]
- Chien, K.L.; Hrones, J.; Reswick, J.B. On the Automatic Control of Generalized Passive Systems. Trans. Am. Soc. Mech. Eng. 1952, 74, 175–185. [Google Scholar] [CrossRef]
- Ishikawa, K. Guide to Quality Control, 13th ed; Asian Productivity Organization: Tokyo, Japan, 1996; ISBN 92-833-1036-5. [Google Scholar]
- Vetter, F.L.; Zobel-Roos, S.; Strube, J. PAT for Continuous Chromatography Integrated into Continuous Manufacturing of Biologics towards Autonomous Operation. Processes 2021, 9, 472. [Google Scholar] [CrossRef]
- Zobel-Roos, S.; Mouellef, M.; Ditz, R.; Strube, J. Distinct and Quantitative Validation Method for Predictive Process Modelling in Preparative Chromatography of Synthetic and Bio-Based Feed Mixtures Following a Quality-by-Design (QbD) Approach. Processes 2019, 7, 580. [Google Scholar] [CrossRef]
- Helling, C.; Dams, T.; Gerwat, B.; Belousov, A.; Strube, J. Physical characterization of column chromatography: Stringent control over equipment performance in biopharmaceutical production. Trends Chromatogr. 2013, 8, 55–71. [Google Scholar]
- Zobel-Roos, S.; Mouellef, M.; Siemers, C.; Strube, J. Process Analytical Approach towards Quality Controlled Process Automation for the Downstream of Protein Mixtures by Inline Concentration Measurements Based on Ultraviolet/Visible Light (UV/VIS) Spectral Analysis. Antibodies 2017, 6, 24. [Google Scholar] [CrossRef]
- Mendhe, R.; Thukkaram, M.; Patil, N.; Rathore, A.S. Comparison of PAT based approaches for making real-time pooling decisions for process chromatography-use of feed forward control. J. Chem. Technol. Biotechnol. 2015, 90, 341–348. [Google Scholar] [CrossRef]
- Mouellef, M.; Szabo, G.; Vetter, F.L.; Siemers, C.; Strube, J. Artificial Neural Network for Fast and Versatile Model Parameter Adjustment Utilizing PAT Signals of Chromatography Processes for Process Control under Production Conditions. Processes 2022, 10, 709. [Google Scholar] [CrossRef]
- Mouellef, M.; Vetter, F.L.; Zobel-Roos, S.; Strube, J. Fast and Versatile Chromatography Process Design and Operation Optimization with the Aid of Artificial Intelligence. Processes 2021, 9, 2121. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).