Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—Analysis and Modeling Based on Isocratic Analytical-Scale Investigations
Abstract
1. Introduction
2. Theoretical Background
2.1. Thermodynamic Retention Model
2.2. Column Model Based on Discrete Convolution
3. Experimental
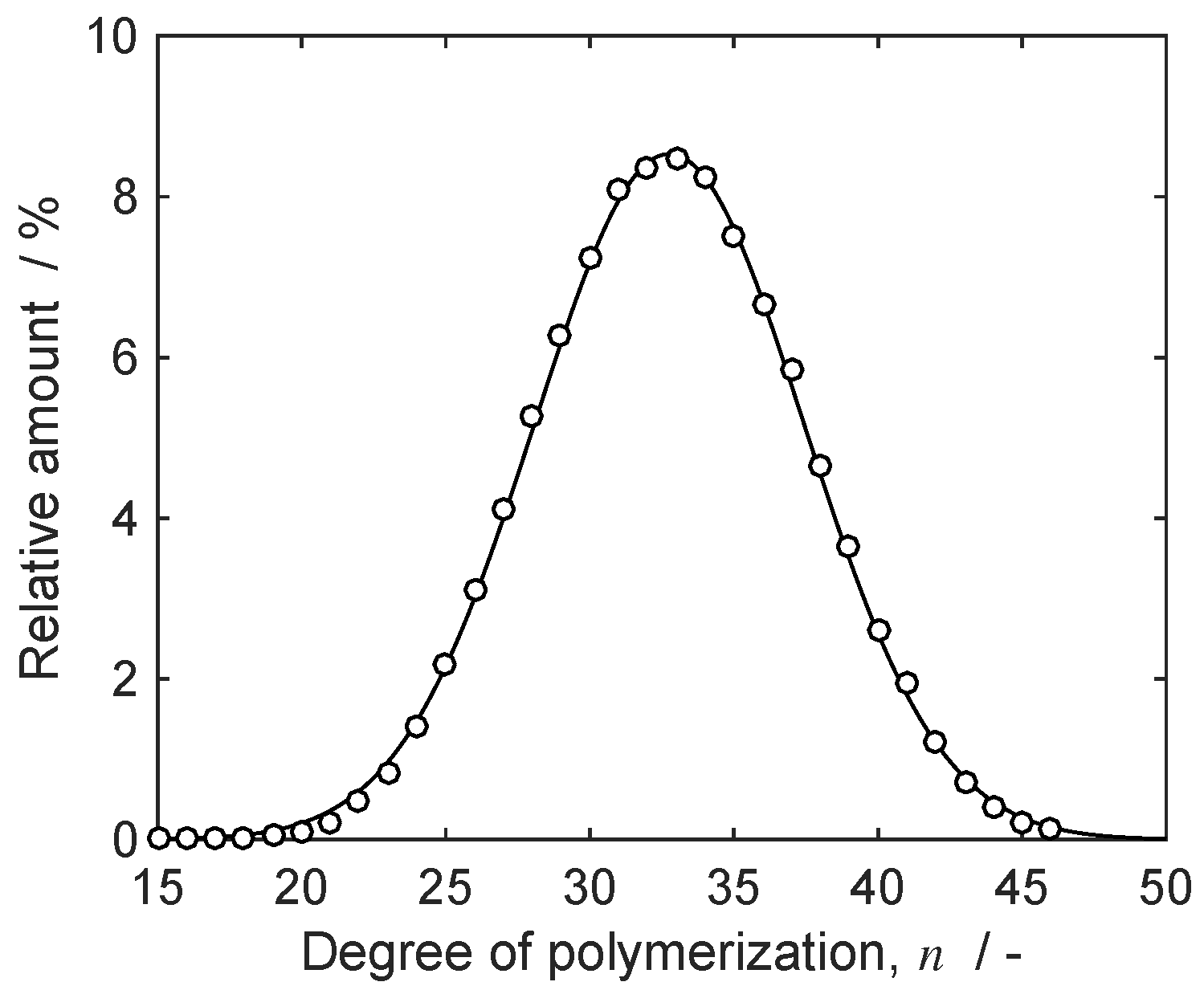
3.1. Materials
3.2. Chromatographic Separation
4. Results and Discussion
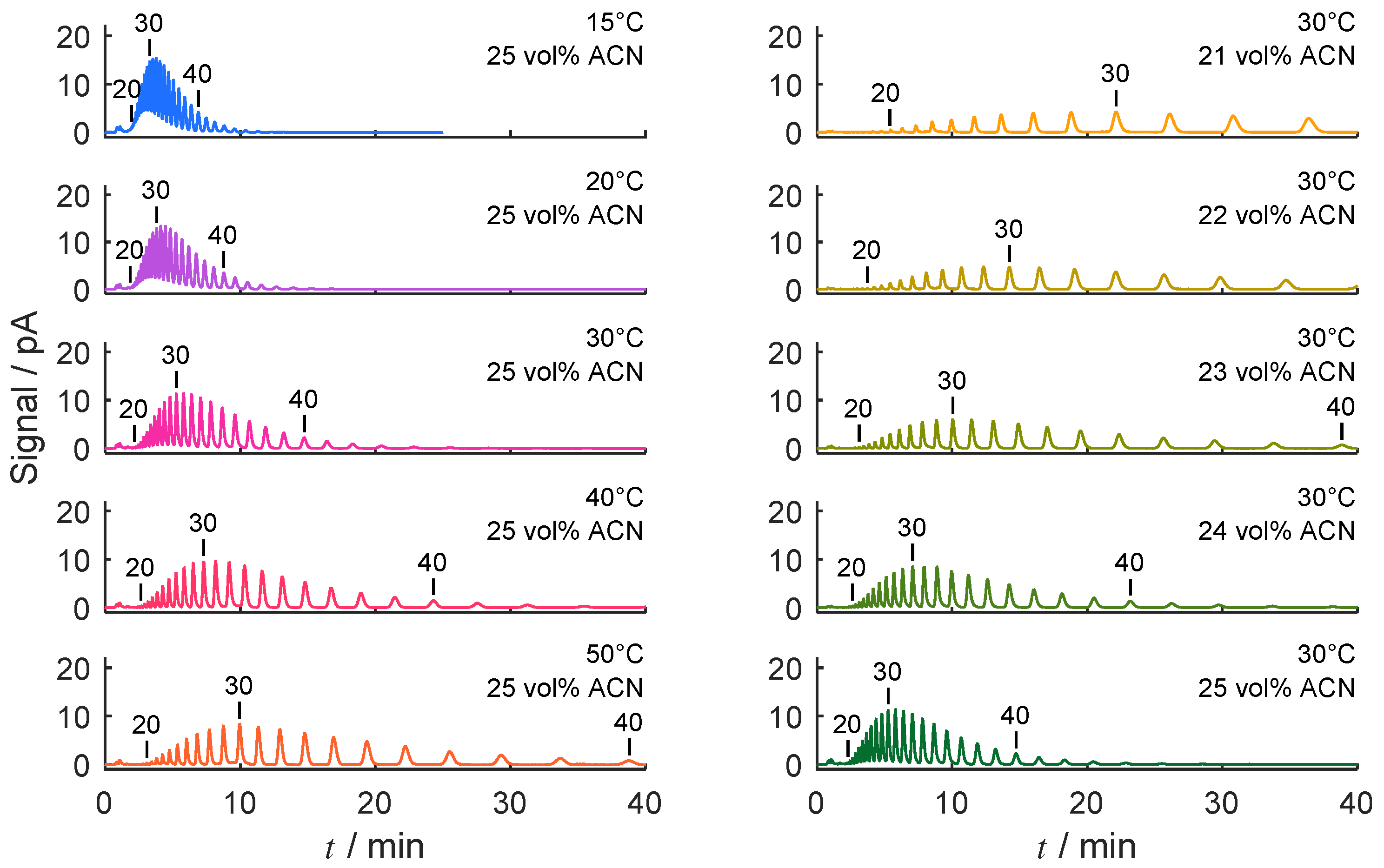
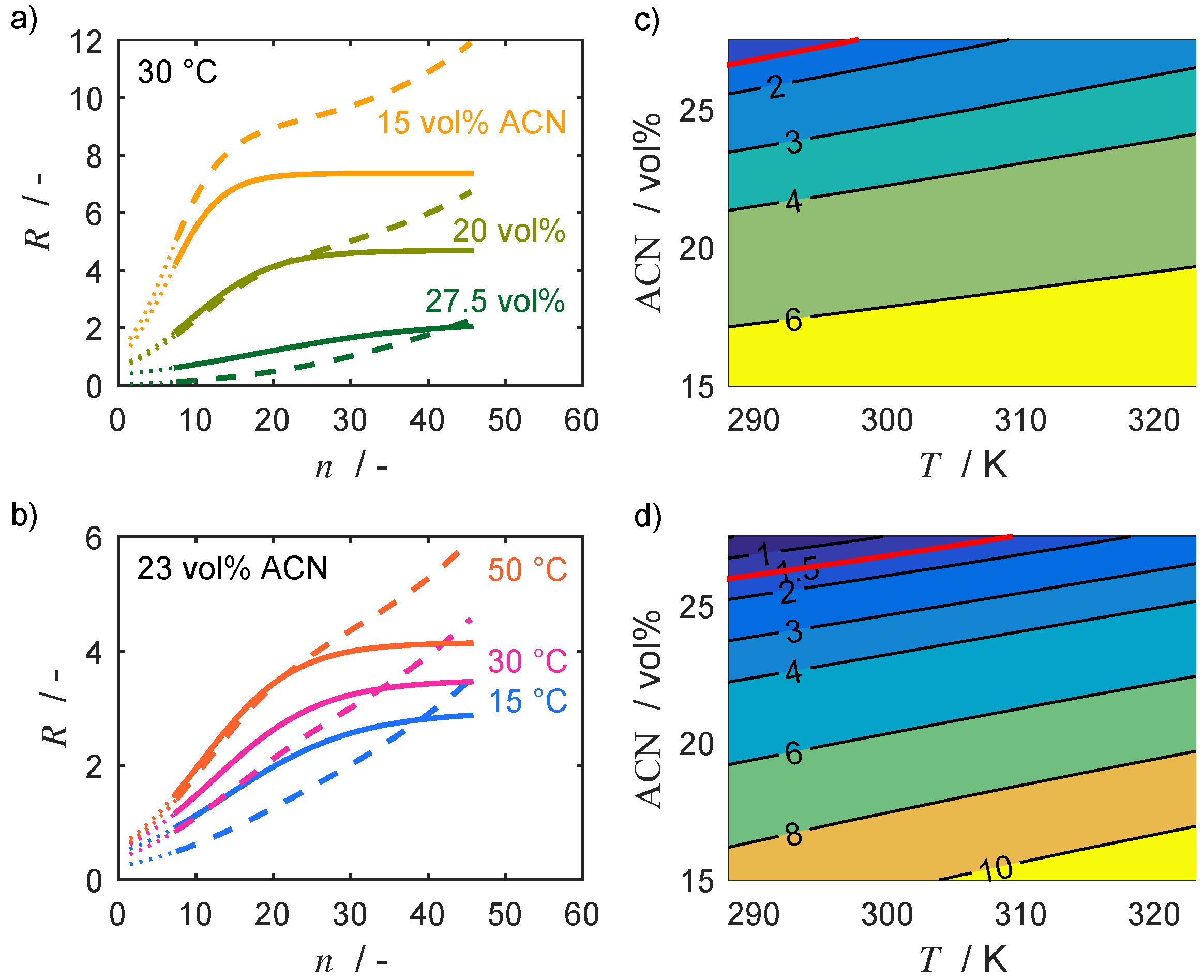
4.1. Separation Problem and Role of Operating Conditions
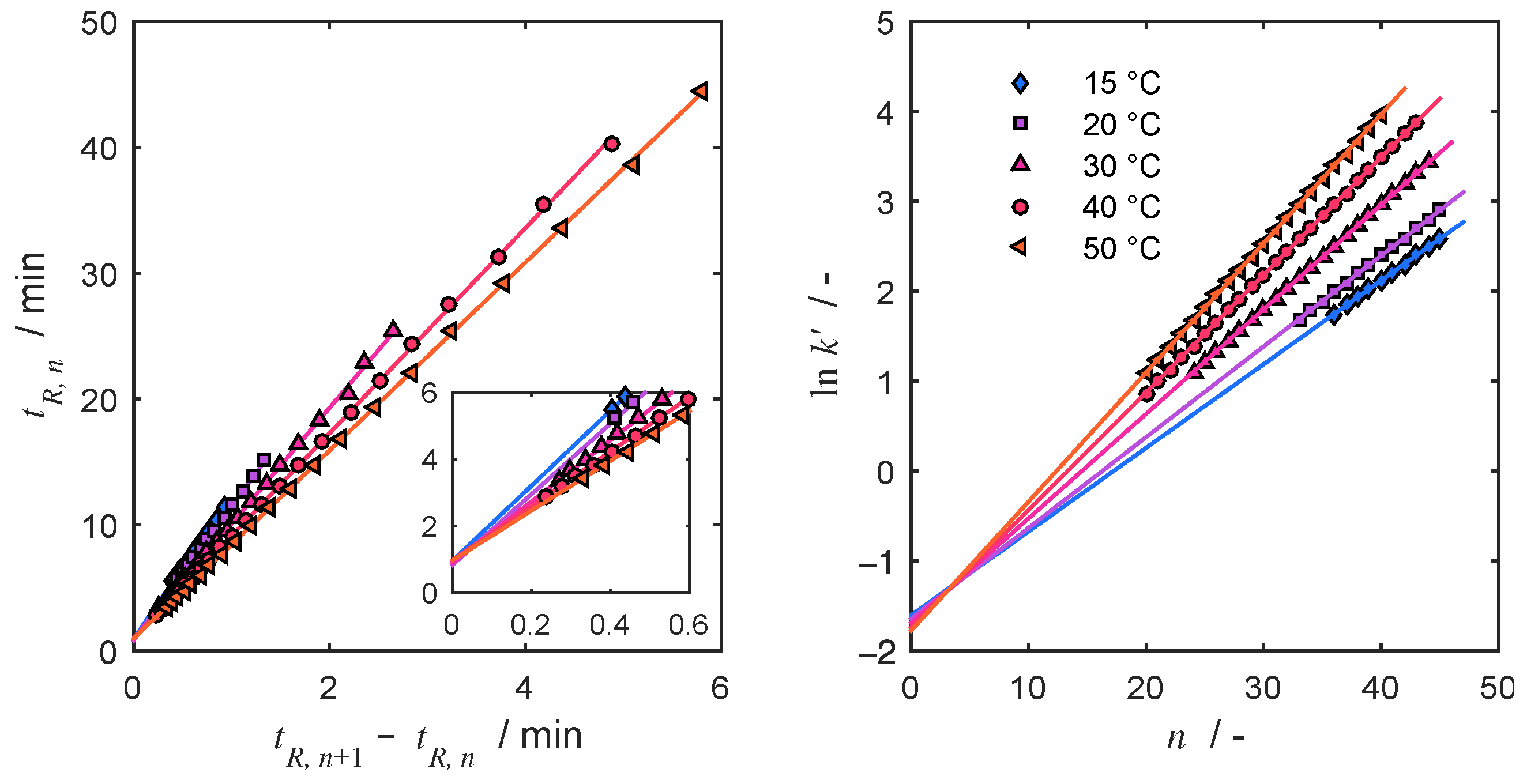
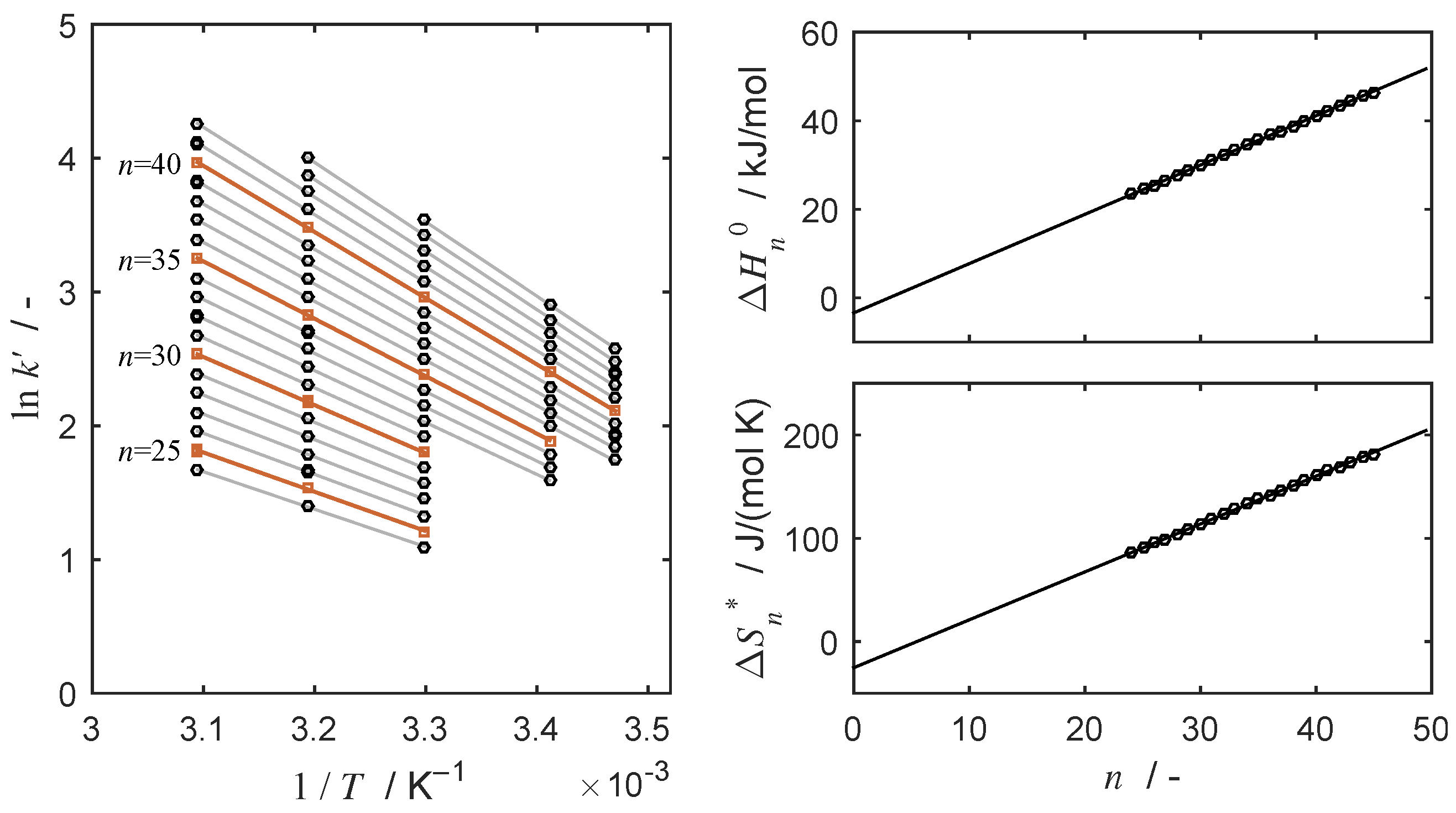
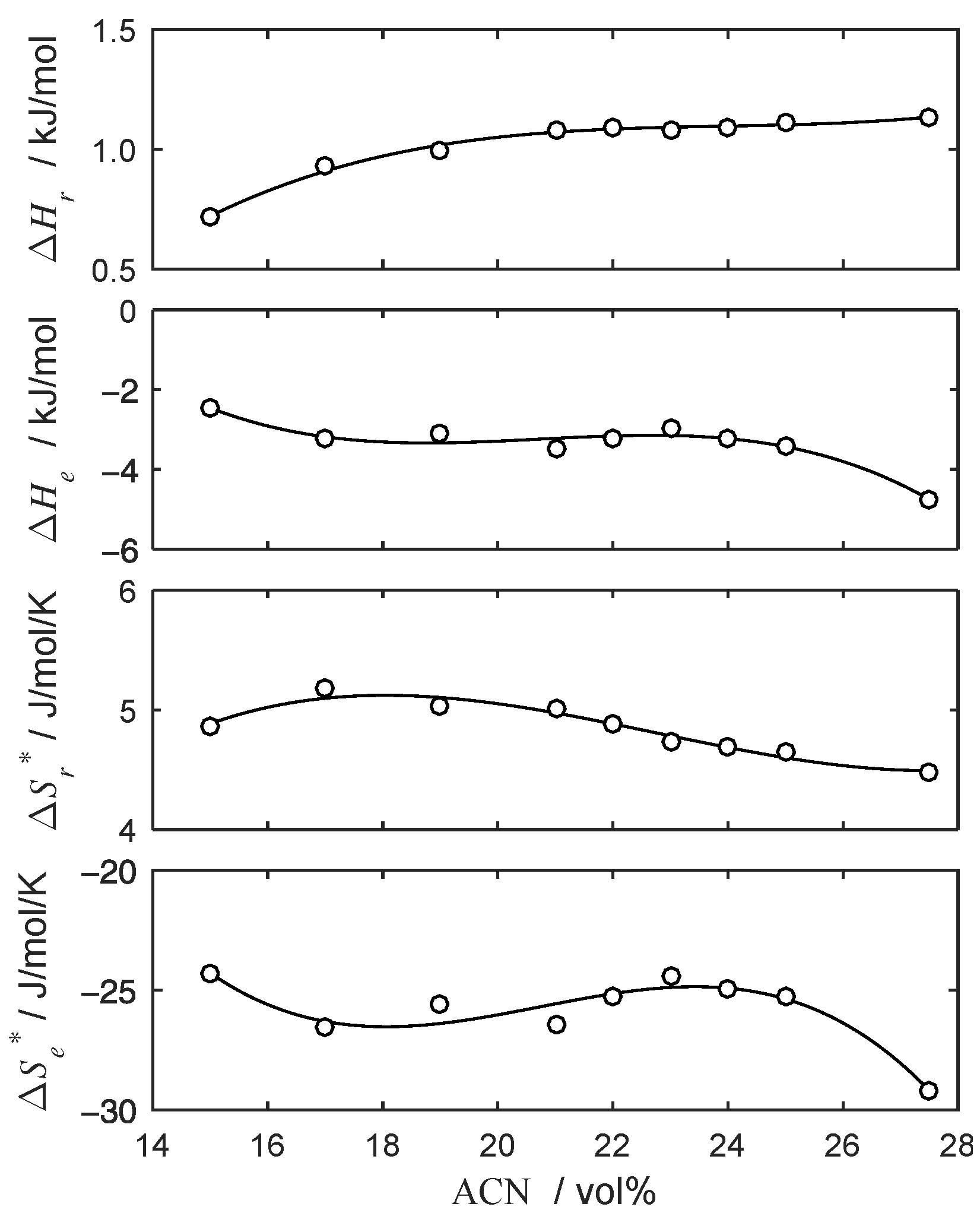
4.2. Thermodynamic Parameters
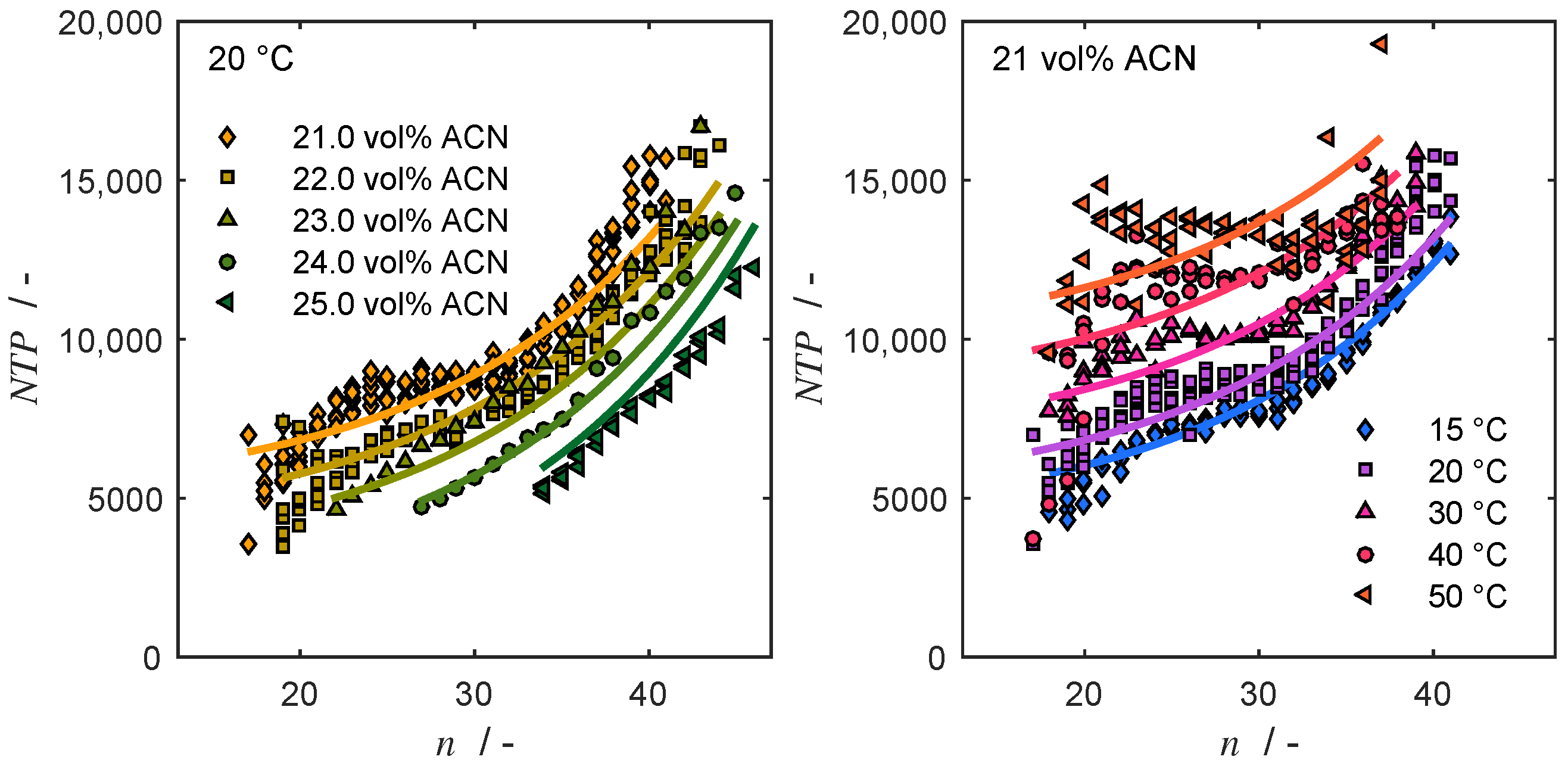
4.3. Column Efficiency
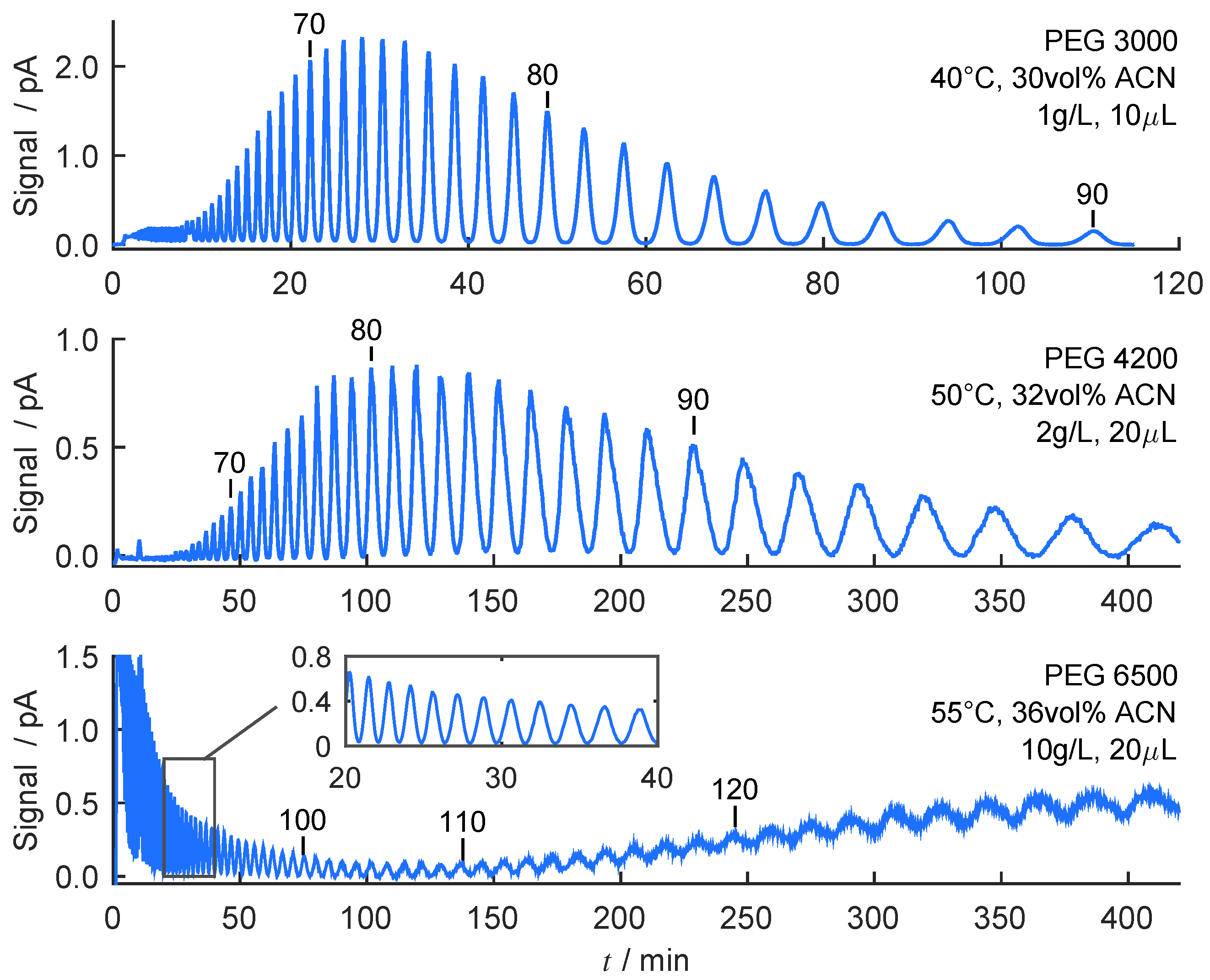
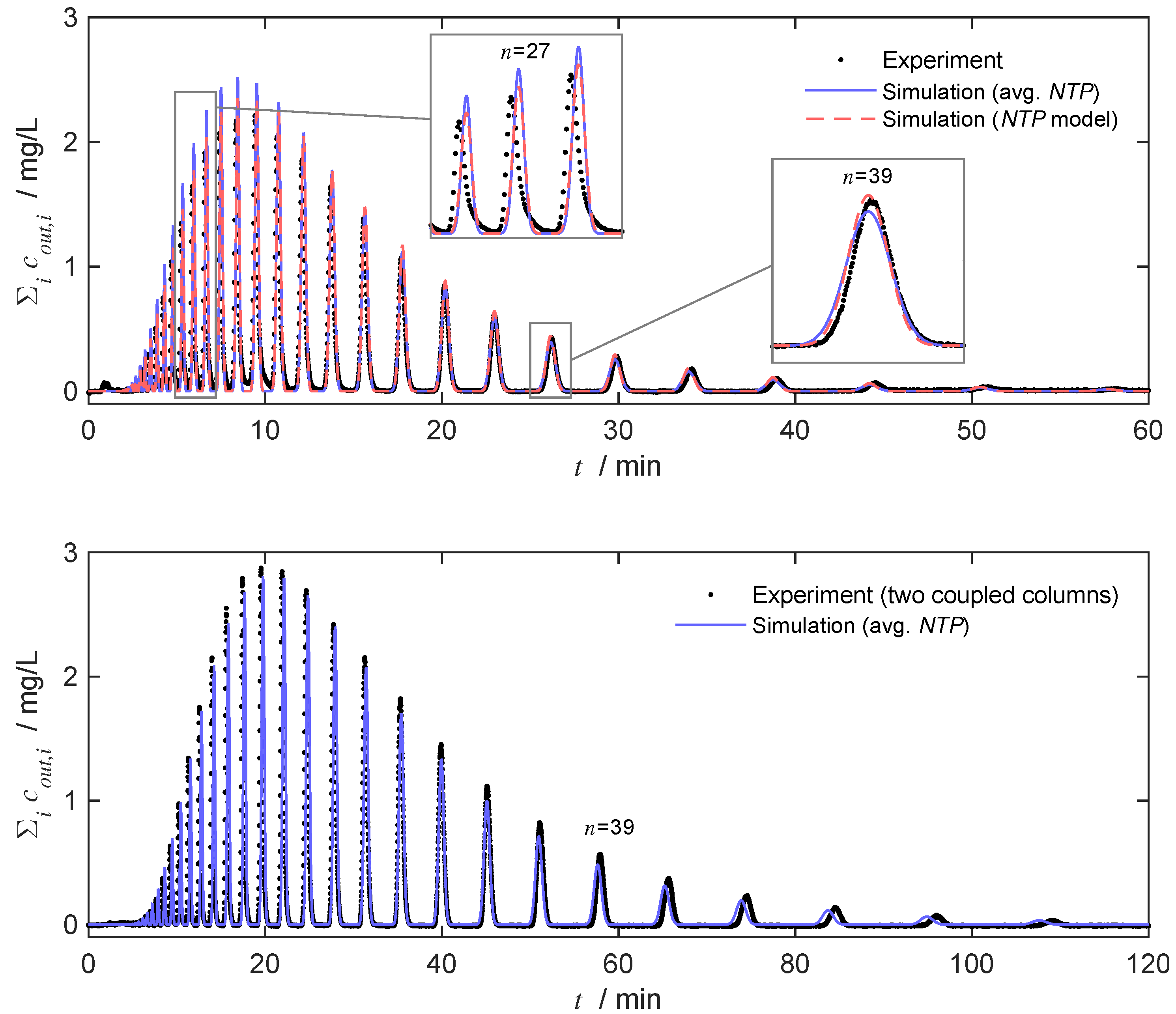
4.4. Evaluation and Prediction of Separation under Analytical Conditions
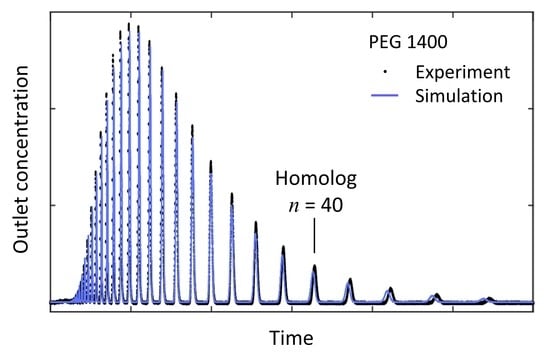
4.5. Prediction of Chromatograms Based on Convolution Model
5. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guiochon, G.; Shirazi, D.G.; Felinger, A.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography, 2nd ed.; Academic Press: Boston, MA, USA, 2006. [Google Scholar]
- Süß, S.; Michaud, V.; Amsharov, K.; Akhmetov, V.; Kaspereit, M.; Damm, C.; Peukert, W. Quantitative Evaluation of Fullerene Separation by Liquid Chromatography. J. Phys. Chem. C 2019, 123, 16747–16756. [Google Scholar] [CrossRef]
- Trathnigg, B.; Veronik, M. A thermodynamic study of retention of poly(ethylene glycol)s in liquid adsorption chromatography on reversed phases. J. Chromatogr. A 2005, 1091, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Chen, K.; He, S.; Liu, X.; Zheng, X.; Jiang, Z.X. Drug Development through Modification of Small Molecular Drugs with Monodisperse Poly(ethylene glycol)s. Org. Process Res. Dev. 2020, 24, 1364–1372. [Google Scholar] [CrossRef]
- Vicent, M.J.; Dieudonné, L.; Carbajo, R.J.; Pineda-Lucena, A. Polymer conjugates as therapeutics: Future trends, challenges and opportunities. Expert Opin. Drug Deliv. 2008, 5, 593–614. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Bo, S.; Wang, H.; Li, Y.; Yang, Z.; Huang, Y.; Jiang, Z.X. Application of Monodisperse PEGs in Pharmaceutics: Monodisperse Polidocanols. Mol. Pharm. 2017, 14, 3473–3479. [Google Scholar] [CrossRef] [PubMed]
- Bohn, P.; Meier, M.A.R. Uniform poly(ethylene glycol): A comparative study. Polym. J. 2020, 52, 165–178. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Shi, Q.; Li, Y.; Xia, G.; Chen, L.; Yang, Z.; Jiang, Z.X. Highly Efficient Synthesis of Monodisperse Poly(ethylene glycols) and Derivatives through Macrocyclization of Oligo(ethylene glycols). Angew. Chem. Int. Ed. 2015, 54, 3763–3767. [Google Scholar] [CrossRef]
- Wu, W.; Supper, M.; Rausch, M.H.; Kaspereit, M.; Fröba, A.P. Mutual Diffusivities of Binary Mixtures of Water and Poly(ethylene) Glycol from Heterodyne Dynamic Light Scattering. Int. J. Thermophys. 2022, 43, 177. [Google Scholar] [CrossRef]
- Meyer, T.; Harms, D.; Gmehling, J. Analysis of polyethylene glycols with respect to their oligomer distribution by high-performance liquid chromatography. J. Chromatogr. A 1993, 645, 135–139. [Google Scholar] [CrossRef]
- Rissler, K. High-performance liquid chromatography and detection of polyethers and their mono(carboxy)alkyl and -arylalkyl substituted derivatives. J. Chromatogr. A 1996, 742, 1–54. [Google Scholar] [CrossRef]
- Rissler, K. Improved separation of polyethylene glycols widely differing in molecular weight range by reversed-phase high performance liquid chromatography and evaporative light scattering detection. Chromatographia 1999, 49, 615–620. [Google Scholar] [CrossRef]
- Lochmüller, C.; Moebus, M.A.; Liu, Q.; Jiang, C.; Elomaa, M. Temperature Effect on Retention and Separation of Poly(ethylene glycol)s in Reversed-Phase Liquid Chromatography. J. Chromatogr. Sci. 1996, 34, 69–76. [Google Scholar] [CrossRef][Green Version]
- Chang, T.; Lee, H.C.; Lee, W.; Park, S.; Ko, C. Polymer characterization by temperature gradient interaction chromatography. Macromol. Chem. Phys. 1999, 200, 2188–2204. [Google Scholar] [CrossRef]
- Cho, D.; Park, S.; Hong, J.; Chang, T. Retention mechanism of poly(ethylene oxide) in reversed-phase and normal-phase liquid chromatography. J. Chromatogr. A 2003, 986, 191–198. [Google Scholar] [CrossRef]
- Trathnigg, B.; Skvortsov, A. Determination of the accessible volume and the interaction parameter in the adsorption mode of liquid chromatography. J. Chromatogr. A 2006, 1127, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Trathnigg, B.; Jamelnik, O. Characterization of different reversed phase systems in liquid adsorption chromatography of polymer homologous series. J. Chromatogr. A 2007, 1146, 78–84. [Google Scholar] [CrossRef]
- Nguyen Viet, C.; Trathnigg, B. Determination of thermodynamic parameters in reversed phase chromatography for polyethylene glycols and their methyl ethers in different mobile phases. J. Sep. Sci. 2010, 33, 464–474. [Google Scholar] [CrossRef]
- Wang, M.; Mallette, J.; Parcher, J.F. Comparison of void volume, mobile phase volume and accessible volume determined from retention data for oligomers in reversed-phase liquid chromatographic systems. J. Chromatogr. A 2011, 1218, 2995–3001. [Google Scholar] [CrossRef]
- Xu, L.; Shahid, S.; Shen, J.; Emanuelsson, E.A.C.; Patterson, D.A. A wide range and high resolution one-filtration molecular weight cut-off method for aqueous based nanofiltration and ultrafiltration membranes. J. Membr. Sci. 2017, 525, 304–311. [Google Scholar] [CrossRef]
- Shimada, K.; Sato, K.; Lusenkova, M.A.; Kinugasa, S.; Kudo, K.; Yamauchi, Y. Separation of Oligomers by Supercritical Fluid Chromatography. Kobunshi Ronbunshu 2001, 58, 541–547. [Google Scholar] [CrossRef][Green Version]
- Takahashi, K.; Kinugasa, S.; Senda, M.; Kimizuka, K.; Fukushima, K.; Matsumoto, T.; Shibata, Y.; Christensen, J. Quantitative comparison of a corona-charged aerosol detector and an evaporative light-scattering detector for the analysis of a synthetic polymer by supercritical fluid chromatography. J. Chromatogr. A 2008, 1193, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K. Advanced reference materials for the characterization of molecular size and weight. J. Phys. Mater. 2020, 1193, 146–150. [Google Scholar] [CrossRef]
- Sun, C.; Baird, M.; Simpson, J. Determination of poly(ethylene glycol)s by both normal-phase and reversed-phase modes of high-performance liquid chromatography. J. Chromatogr. A 1998, 800, 231–238. [Google Scholar] [CrossRef]
- Martin, A.J.P. Some Theoretical Aspects of Partition Chromatography. Symp. Biochem. Soc. 1949, 3, 4–20. [Google Scholar]
- Colin, H.; Krstulović, A.M.; Gonnord, M.F.; Guiochon, G.; Yun, Z.; Jandera, P. Investigation of selectivity in reversed-phase liquid chromatography-effects of stationary and mobile phases on retention of homologous series. Chromatographia 1983, 17, 9–15. [Google Scholar] [CrossRef]
- Yanagihara, Y.; Yasukawa, K.; Tamura, U.; Uchida, T.; Noguchi, K. Characteristics of a new HPLC column packed with octadecyl-bonded polymer gel. Chromatographia 1987, 24, 701–704. [Google Scholar] [CrossRef]
- Kim, Y.; Ahn, S.; Chang, T. Martin’s Rule for High-Performance Liquid Chromatography Retention of Polystyrene Oligomers. Anal. Chem. 2009, 81, 5902–5909. [Google Scholar] [CrossRef]
- Chester, T.L.; Coym, J.W. Effect of phase ratio on van’t Hoff analysis in reversed-phase liquid chromatography, and phase-ratio-independent estimation of transfer enthalpy. J. Chromatogr. A 2003, 1003, 101–111. [Google Scholar] [CrossRef]
- Thompson, J.F.; Honda, S.I.; Hunt, G.E.; Krupka, R.M.; Morris, C.J.; Powell, L.E.; Silberstein, O.O.; Towers, G.H.N.; Zacharius, R.M. Partition Chromatography and Its Use in the Plant Sciences. Bot. Rev. 1959, 25, 1–263. [Google Scholar] [CrossRef]
- Skvortsov, A.; Trathnigg, B. Martin’s rule revisited: Its molecular sense and limitations. J. Chromatogr. A 2003, 1015, 31–42. [Google Scholar] [CrossRef]
- Tomlinson, E.; Poppe, H.; Kraak, J. Thermodynamics of functional groups in reversed-phase high performance liquid-solid chromatography. Int. J. Pharm. 1981, 7, 225–243. [Google Scholar] [CrossRef]
- Golshan-Shirazi, S.; Guiochon, G. Modeling of preparative liquid chromatography. J. Chromatogr. A 1994, 658, 149–171. [Google Scholar] [CrossRef]
- Kalbfuss, B.; Flockerzi, D.; Seidel-Morgenstern, A.; Reichl, U. Size-exclusion chromatography as a linear transfer system: Purification of human influenza virus as an example. J. Chromatogr. B 2008, 873, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.S.; Kaspereit, M.; Sainio, T. Intermittent recycle-integrated reactor-separator for production of well-defined non-digestible oligosaccharides from oat β-glucan. Chem. Eng. J. 2021, 410, 128352. [Google Scholar] [CrossRef]
- Villermaux, J. Chemical engineering approach to dynamic modelling of linear chromatography: A flexible method for representing complex phenomena from simple concepts. J. Chromatogr. A 1987, 406, 11–26. [Google Scholar] [CrossRef]
- Nicoud, R.M. Chromatographic Processes: Modeling, Simulation, and Design; Cambridge Series in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Villermaux, J. Deformation of Chromatographic Peaks Under the Influence of Mass Transfer Phenomena. J. Chromatogr. Sci. 1974, 12, 822–831. [Google Scholar] [CrossRef]
- Martin, A.J.P.; Synge, R.L.M. A new form of chromatogram employing two liquid phases. Biochem. J. 1941, 35, 1358–1368. [Google Scholar] [CrossRef]
- Smit, H.C.; Smit, J.C.; de Jager, E.M. The role of the theoretical plate concept and gamma density functions in studies on mass transport and mass loadability of chromatographic columns. Chromatographia 1986, 22, 123–131. [Google Scholar] [CrossRef]
- Spitzer, M.; Sabadini, E.; Loh, W. Entropically driven partitioning of ethylene oxide oligomers and polymers in aqueous/organic biphasic systems. J. Phys. Chem. B 2002, 106, 12448–12452. [Google Scholar] [CrossRef]
- Rafferty, J.L.; Siepmann, J.I.; Schure, M.R. A molecular simulation study of the effects of stationary phase and solute chain length in reversed-phase liquid chromatography. J. Chromatogr. A 2012, 1223, 24–34. [Google Scholar] [CrossRef]
- Lindsey, R.K.; Rafferty, J.L.; Eggimann, B.L.; Siepmann, J.I.; Schure, M.R. Molecular simulation studies of reversed-phase liquid chromatography. J. Chromatogr. A 2013, 1287, 60–82. [Google Scholar] [CrossRef] [PubMed]
- Foley, J.P. Resolution equations for column chromatography. Analyst 1991, 116, 1275–1279. [Google Scholar] [CrossRef]
- Bombaugh, K.J.; Levangie, R.F. High Resolution Gel Permeation Chromatography-Using Recycle. Sep. Sci. 1970, 5, 751–763. [Google Scholar] [CrossRef]
- Seidel-Morgenstern, A.; Guiochon, G. Theoretical Study of Recycling in Preparative Chromatography. AIChE J. 1993, 39, 809–819. [Google Scholar] [CrossRef]
- Bailly, M.; Tondeur, D. Recycle optimization in non-linear productive chromatography—I Mixing recycle with fresh feed. Chem. Eng. Sci. 1982, 37, 1199–1212. [Google Scholar] [CrossRef]
- Grill, C.M. Closed-loop recycling with periodic intra-profile injection: A new binary preparative chromatographic technique. J. Chromatogr. A 1998, 796, 101–113. [Google Scholar] [CrossRef]
- Kaspereit, M.; Sainio, T. Simplified Design of Steady-State Recycling Chromatography Under Ideal and Nonideal Conditions. Chem. Eng. Sci. 2011, 66, 5428–5438. [Google Scholar] [CrossRef]
- Lochmüller, C.H.; Jiang, C.; Liu, Q.; Antonucci, V.; Elomaa, M. High-Performance Liquid Chromatography of Polymers: Retention Mechanisms and Recent Advances. Crit. Rev. Anal. Chem. 1996, 26, 29–59. [Google Scholar] [CrossRef]
| Sample | ACN | ||||
|---|---|---|---|---|---|
| vol% | kJ/mol | kJ/mol | J/(mol K) | J/(mol K) | |
| PEG 1400 | 15.0 | 0.715 | −2.465 | 4.861 | −24.285 |
| (this work) | 17.0 | 0.929 | −3.241 | 5.171 | −26.520 |
| 19.0 | 0.994 | −3.076 | 5.027 | −25.629 | |
| 21.0 | 1.083 | −3.509 | 5.006 | −26.432 | |
| 22.0 | 1.090 | −3.245 | 4.893 | −25.299 | |
| 23.0 | 1.077 | −2.992 | 4.742 | −24.434 | |
| 24.0 | 1.094 | −3.320 | 4.684 | −24.950 | |
| 25.0 | 1.114 | −3.410 | 4.639 | −25.263 | |
| 27.5 | 1.132 | −4.771 | 4.481 | −29.251 | |
| PEG 600 [18] | 11.1 | 1.1 | −2.8 | 5.9 | −13.0 |
| PEG 2300 [15] | 35.0 | 1.23 | 14.0 | 4.39 | 30.0 |
| 45.0 | 0.52 | - | 1.68 | - |
| 0.000472 | −0.033848 | 0.814105 | −5.467108 | |
| −0.006433 | 0.399831 | −8.210674 | 52.4509195 | |
| 0.001490 | −0.101743 | 2.216156 | −10.494034 | |
| −0.021576 | 1.342734 | −27.387407 | 157.230293 |
| /- | / | /vol% | /- | /- |
|---|---|---|---|---|
| −19,664.2 | 159.82 | −1059.81 | 436.453 | 0.07349 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Supper, M.; Heller, K.; Söllner, J.; Sainio, T.; Kaspereit, M. Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—Analysis and Modeling Based on Isocratic Analytical-Scale Investigations. Processes 2022, 10, 2160. https://doi.org/10.3390/pr10112160
Supper M, Heller K, Söllner J, Sainio T, Kaspereit M. Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—Analysis and Modeling Based on Isocratic Analytical-Scale Investigations. Processes. 2022; 10(11):2160. https://doi.org/10.3390/pr10112160
Chicago/Turabian StyleSupper, Malvina, Kathleen Heller, Jakob Söllner, Tuomo Sainio, and Malte Kaspereit. 2022. "Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—Analysis and Modeling Based on Isocratic Analytical-Scale Investigations" Processes 10, no. 11: 2160. https://doi.org/10.3390/pr10112160
APA StyleSupper, M., Heller, K., Söllner, J., Sainio, T., & Kaspereit, M. (2022). Separation of Molar Weight-Distributed Polyethylene Glycols by Reversed-Phase Chromatography—Analysis and Modeling Based on Isocratic Analytical-Scale Investigations. Processes, 10(11), 2160. https://doi.org/10.3390/pr10112160