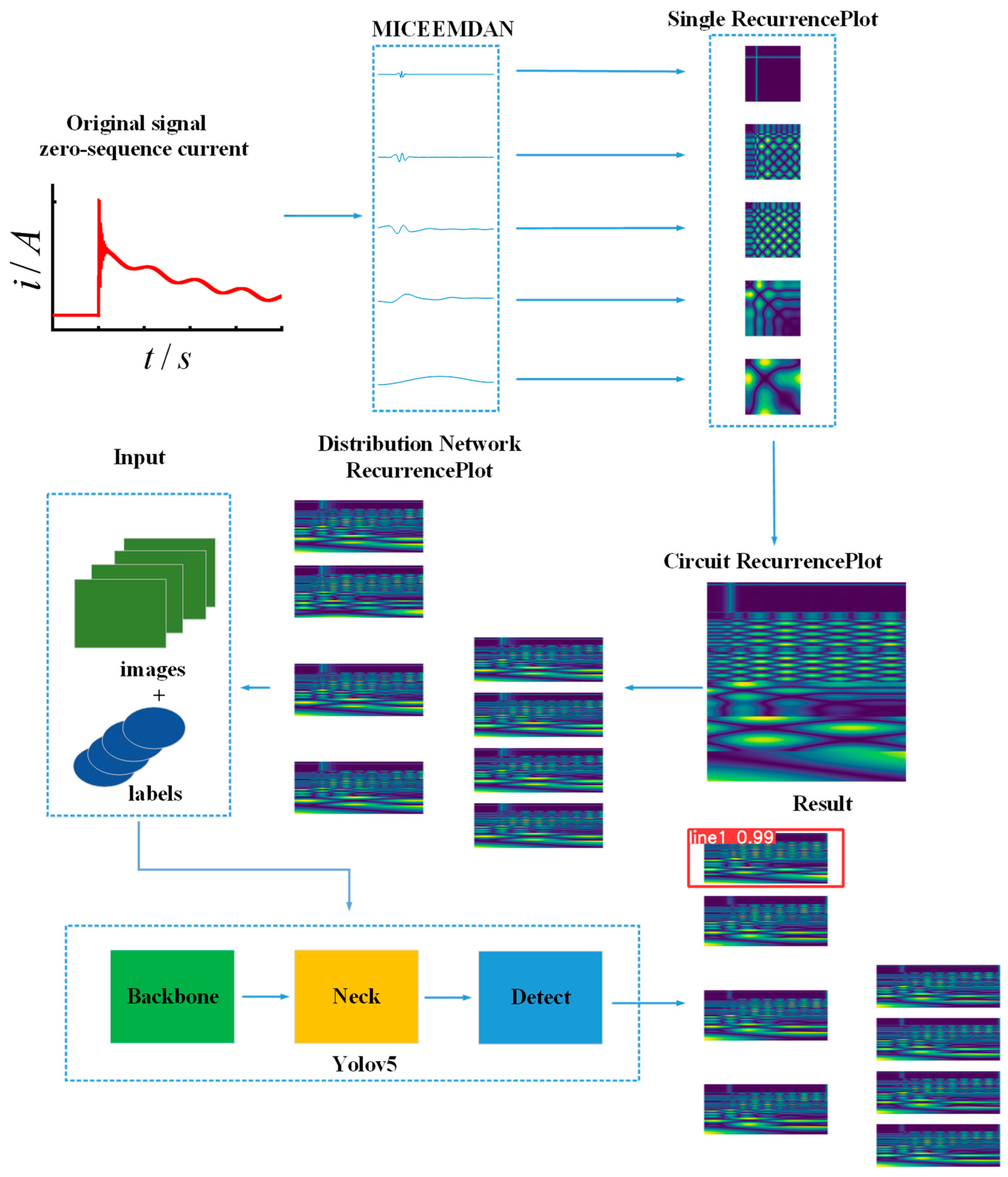
Distribution Network Fault-Line Selection Method Based on MICEEMDAN–Recurrence Plot–Yolov5
Abstract
1. Introduction
2. Multi-Scale Weighted Permutation Entropy
2.1. Multi-Scale Permutation Entropy
2.2. Multi-Scale Weighted Permutation Entropy
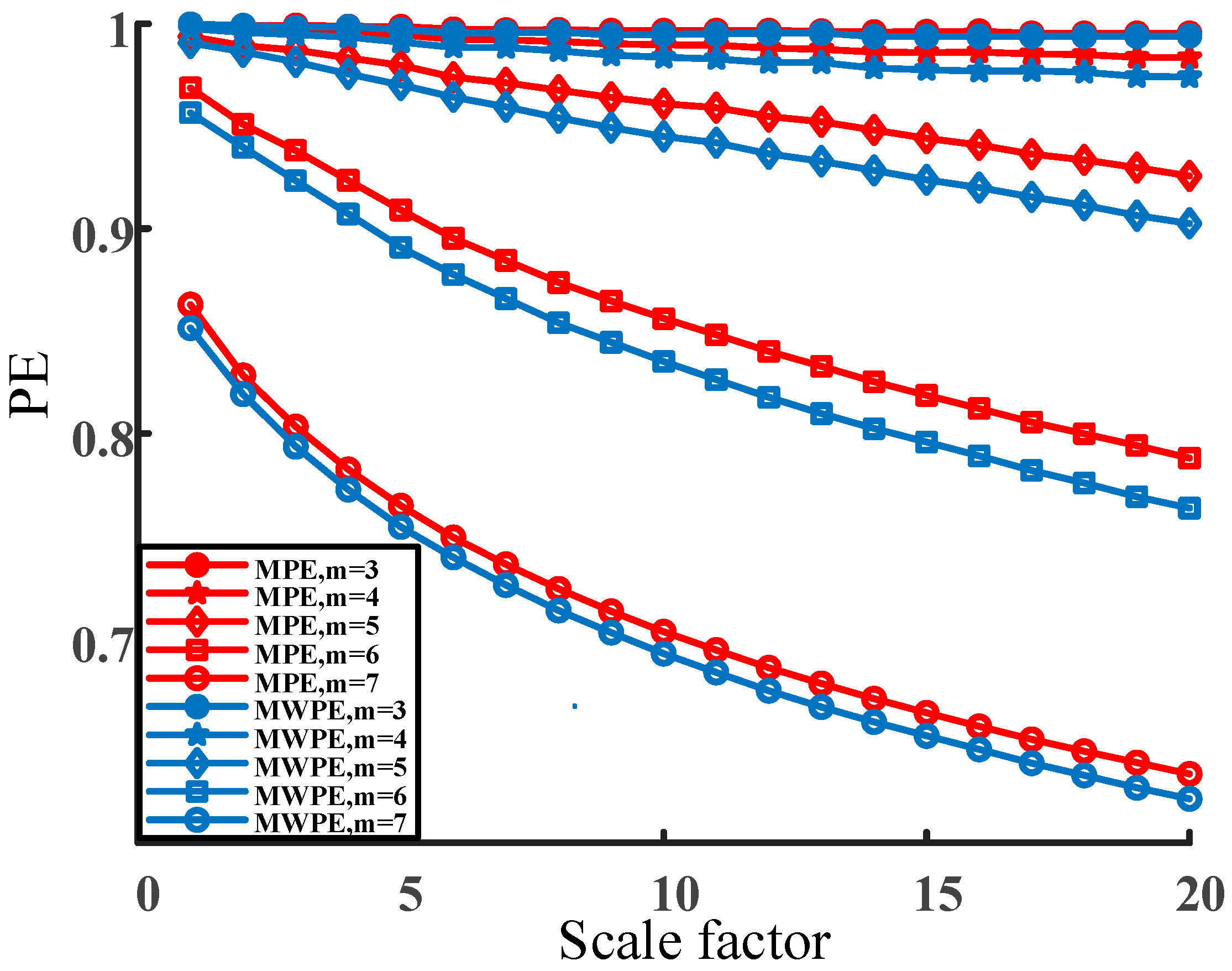
2.3. Parameter Selection and Analysis Comparison
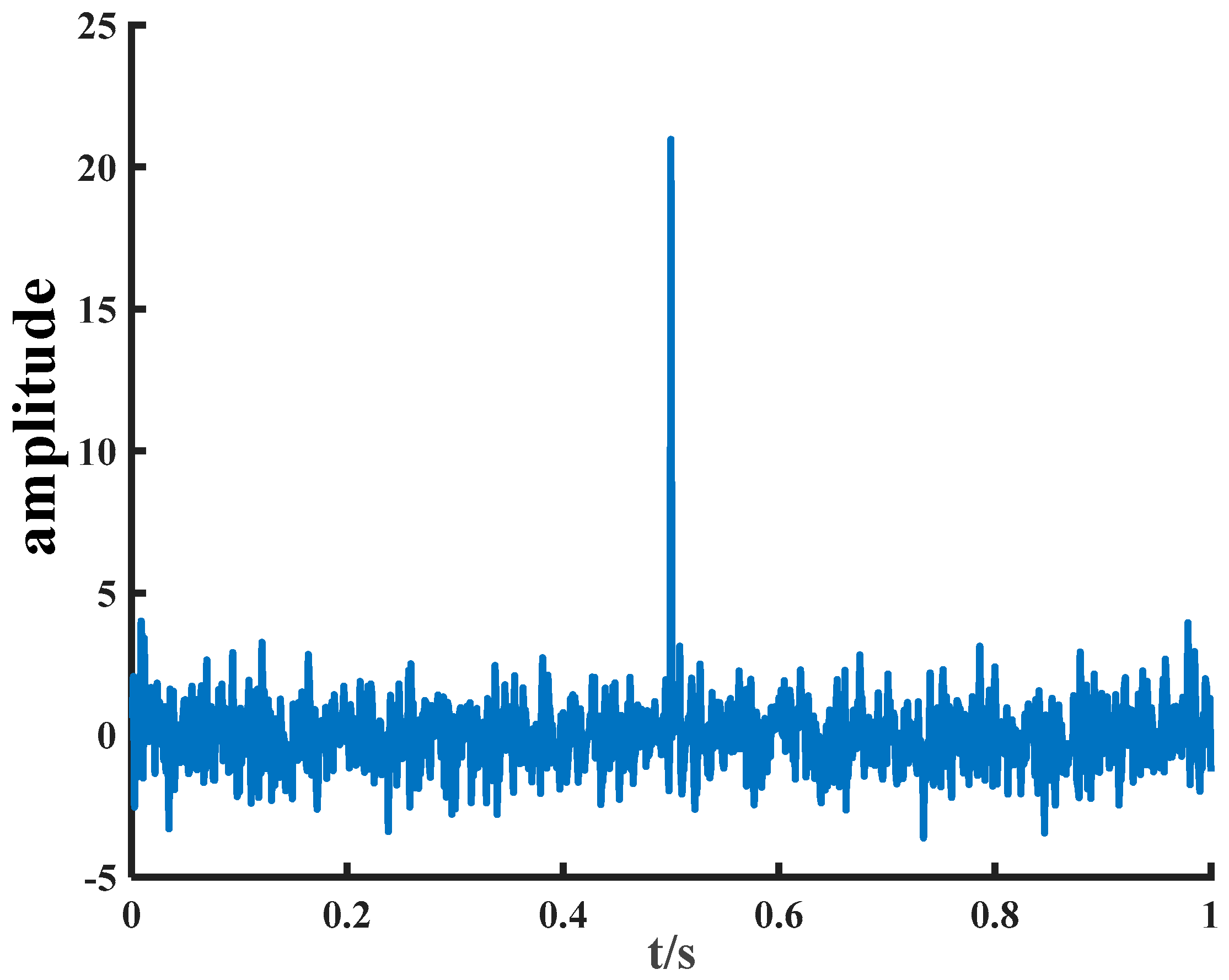
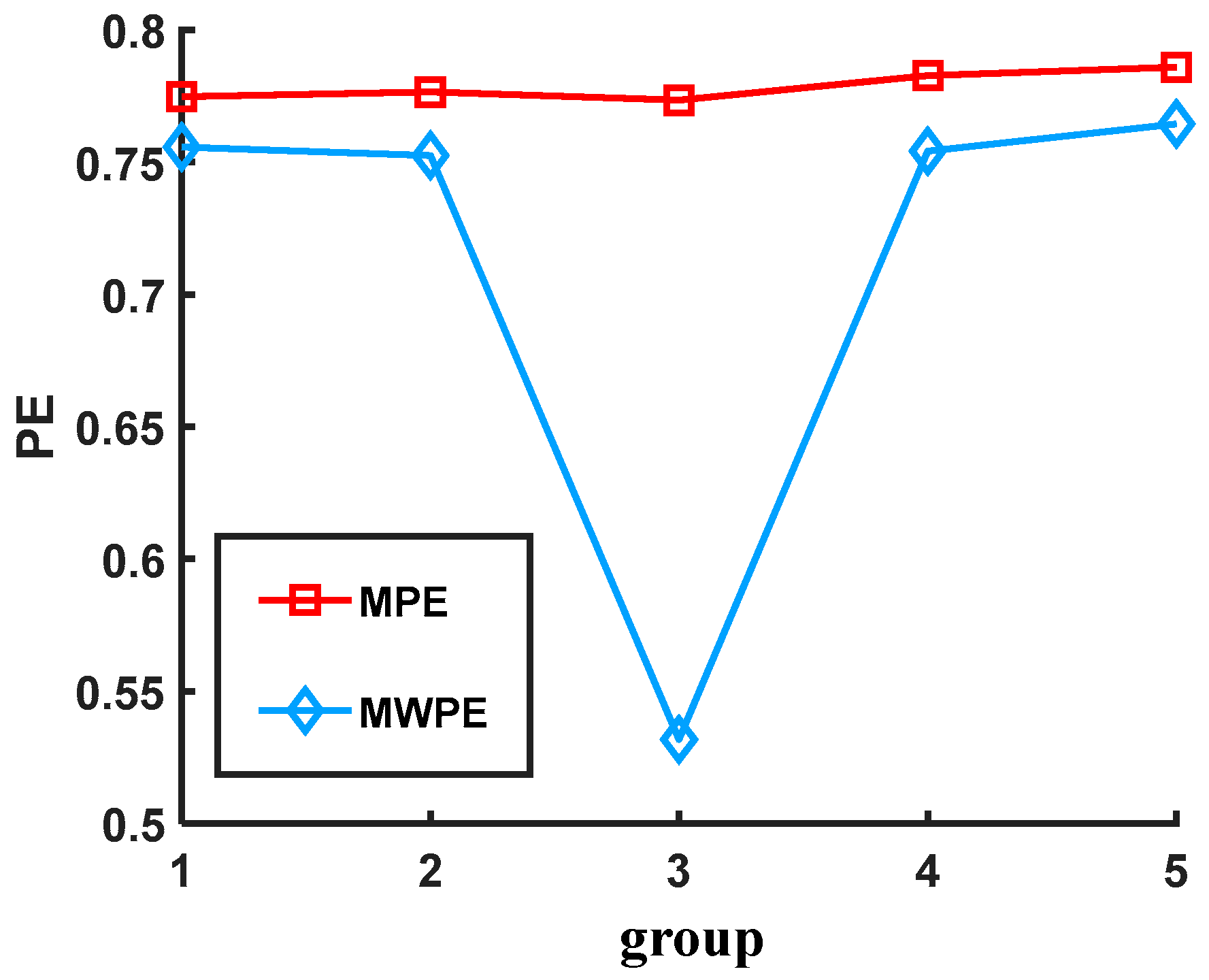
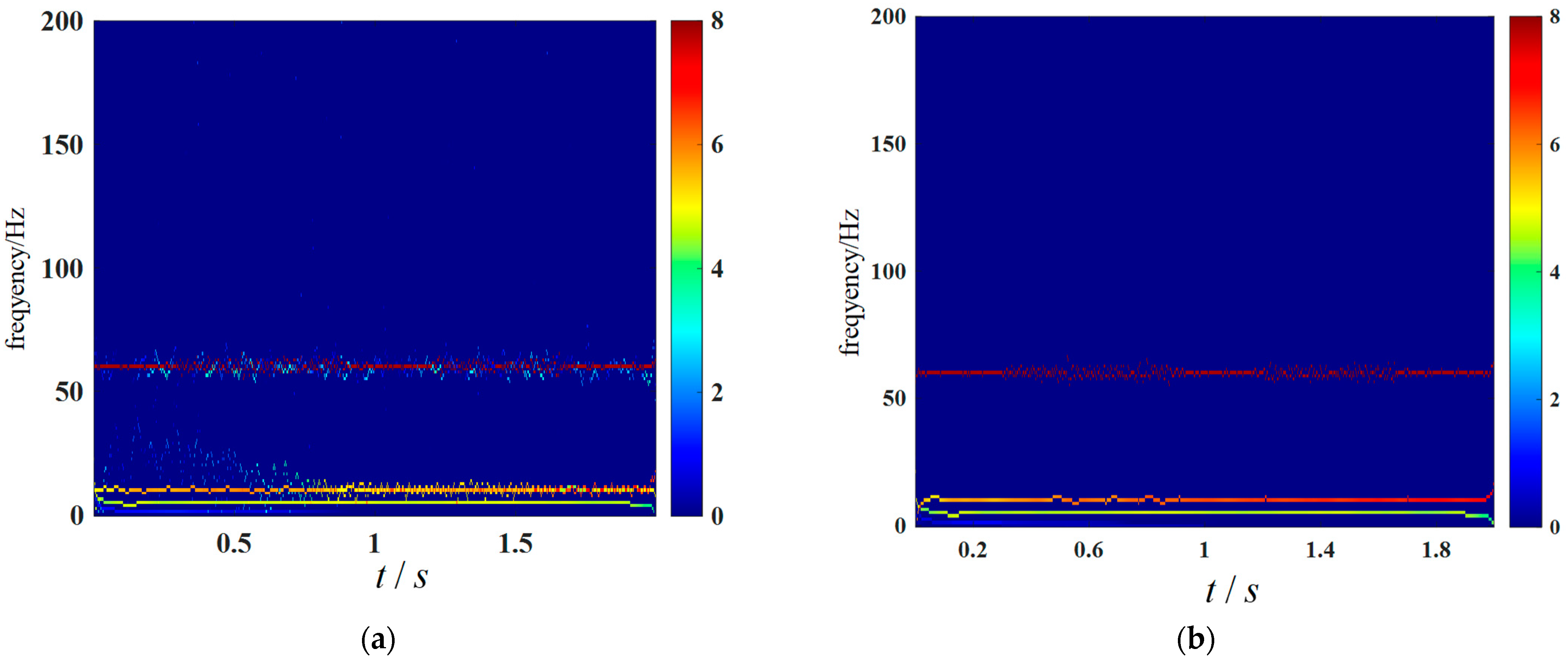
2.4. Noise Signal Detection
3. MICEEMDAN Signal Decomposition
3.1. ICEEMDAN Signal Decomposition
- (1)
- Add Group I white noise to the original signal; i.e.,where x is the signal to be decomposed; β0 is the intensity factor of the white noise; E(·) denotes the kth order modal component generated by the EMD decomposition; and w(i) is the Gaussian noise.
- (2)
- The first set of residuals is obtained.where N(·) denotes the local mean value of the generated signal.
- (3)
- Calculate the first modal component d1 = x − R1.
- (4)
- Continuing with the addition of white noise, the second set of residuals R2 = R1 + β1E(w(i)) is calculated using the local mean decomposition, and the second modal component d2 = R1 − R2 is defined.
- (5)
- Calculate the Kth residual RK = (N(RK−1 + βK−1E(w(i)))) and the modal component dK = RK−1 − RK.
- (6)
- All modalities and residual numbers are obtained until the end of the computational decomposition.
3.2. ICEEMDAN Signal Decomposition
- (1)
- The ICEEMDAN decomposition of the original signal I(t) is performed to obtain the K modal components IMF.
- (2)
- The MWPE calculation is performed for each decomposition of the resulting modal component IMF to obtain the entropy value PE for each modal component.where, i = 1, 2, …, K.
- (3)
- When the entropy value obtained from the MWPE calculation is more significant than 0.6, the decomposition signal is considered a noisy signal and is removed from the original signal.where R(t) is the remaining signal after noise removal and IMFj, j = 1, 2, …, p is the noise component obtained by decomposition.
- (4)
- The IMF of MICEEMDAN is obtained by decomposing R(t) using EMD, and the results are arranged in high to low frequencies.
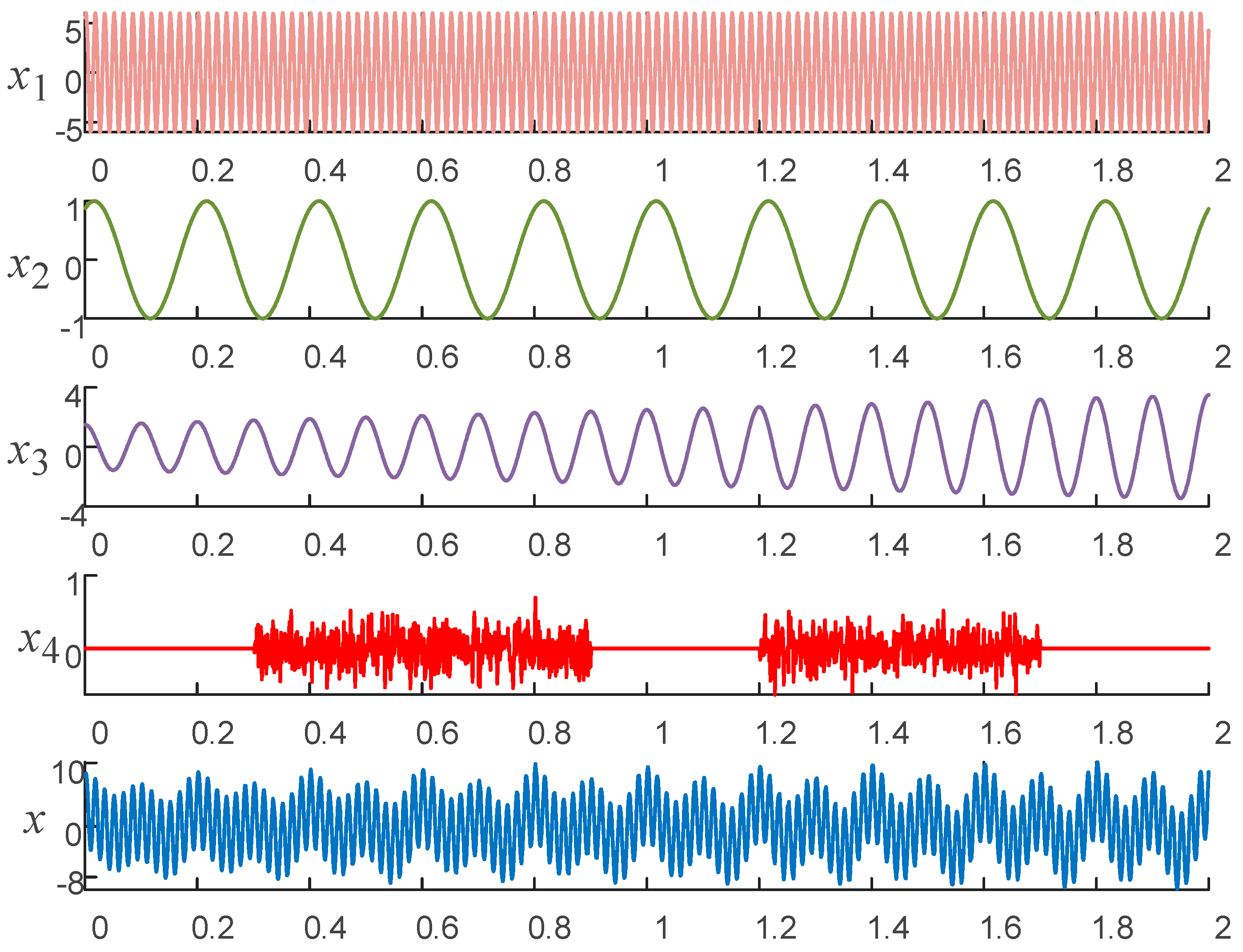
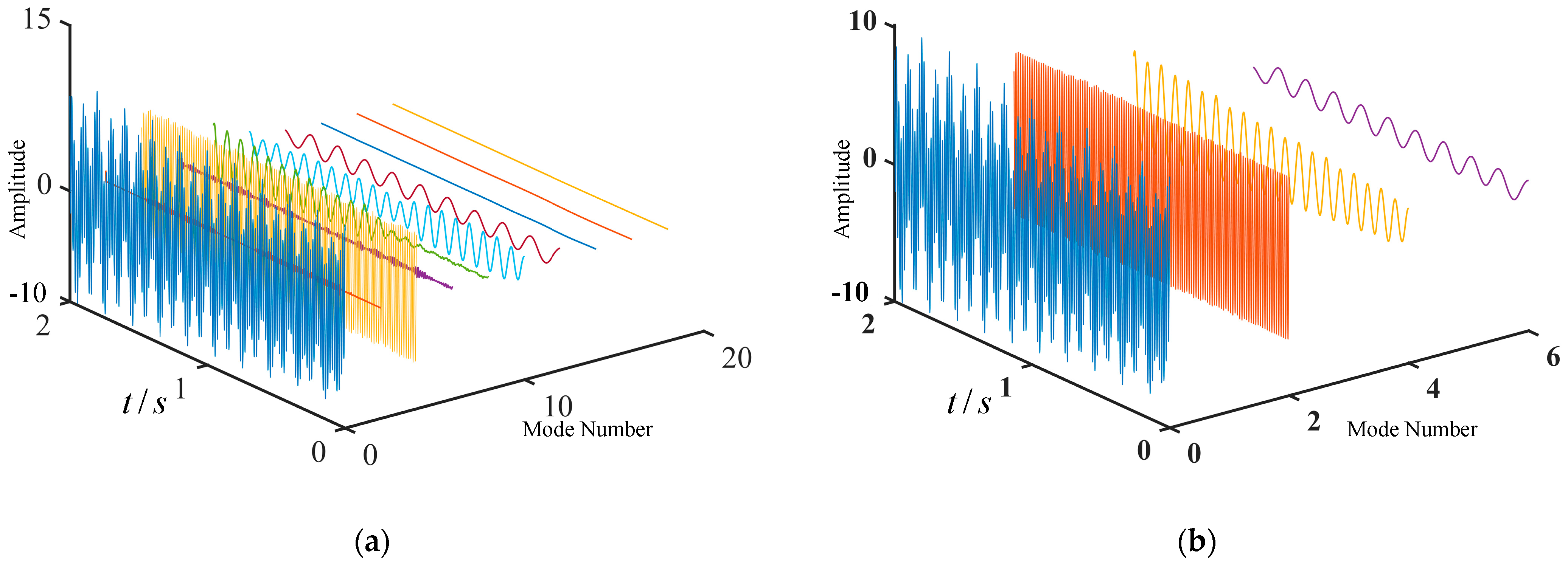
3.3. Decomposition of Simulation Signals Using ICEEMDAN and MICEEMDAN
4. Signal Feature Extraction
4.1. Recurrence Plot
- (1)
- MICEEMDAN decomposition of the zero-sequence current signal during a distribution network fault is performed to obtain its modal components IMF1, IMF2…
- (2)
- For a given time series {x(i), i = 1, 2, …, n}, the extracted trajectories arewhere i = 1, 2, …, n − (m − 1), m is the dimension of the trajectory and Γ is the delay; in this paper, let m = 1, Γ = 1.
- (3)
- Calculate the distance di,j between any two points on the trajectory.
- (4)
- Calculate the recurrence matrix Ri,j.where ε is the threshold value of the minimum distance. The size chosen in this paper is 15% of the standard deviation of the data, and Θ is the Heaviside function, the expression of which is
- (5)
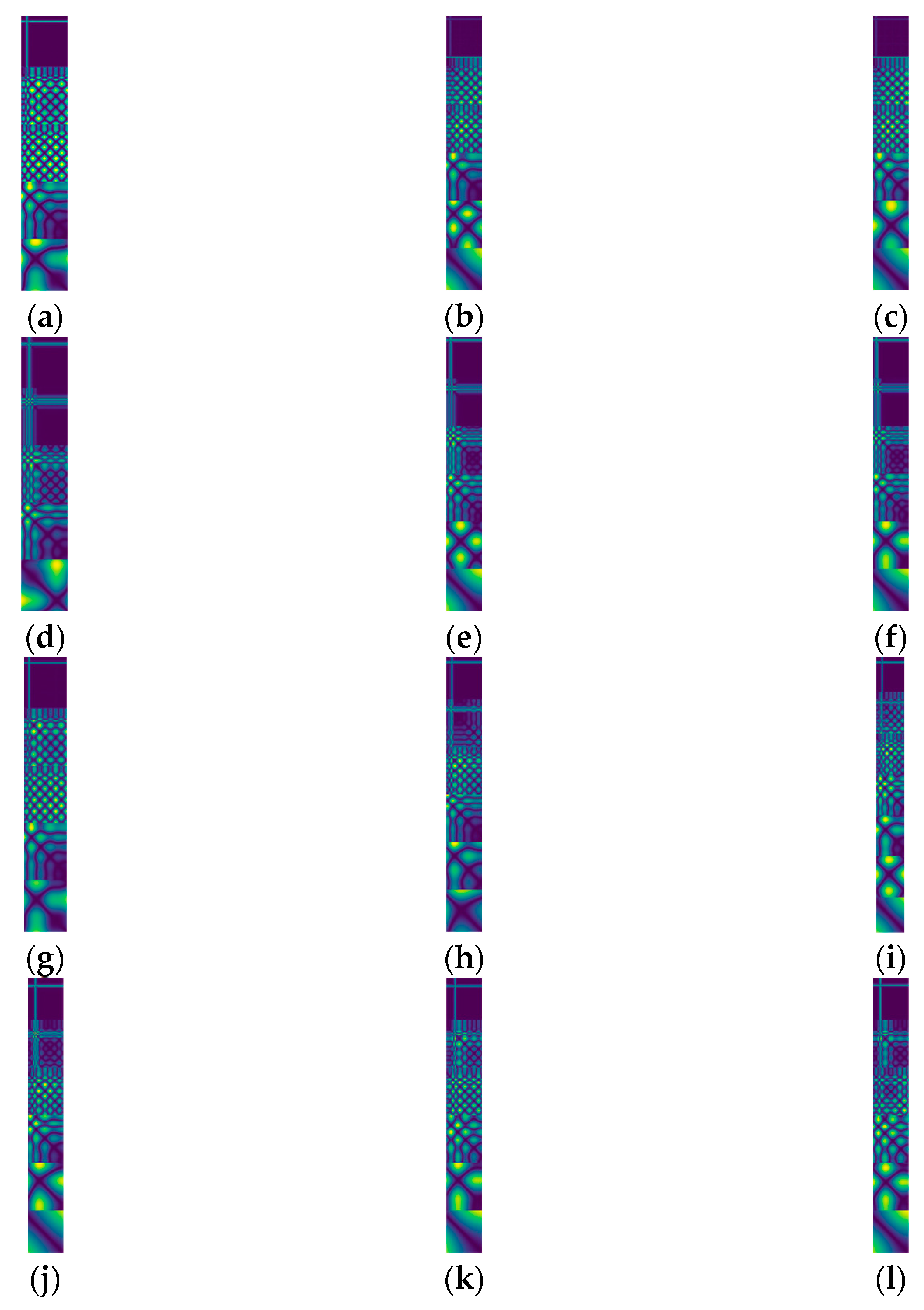
- The modal components obtained from the decomposition are all Recurrence Plot transformed and stitched from top to bottom.
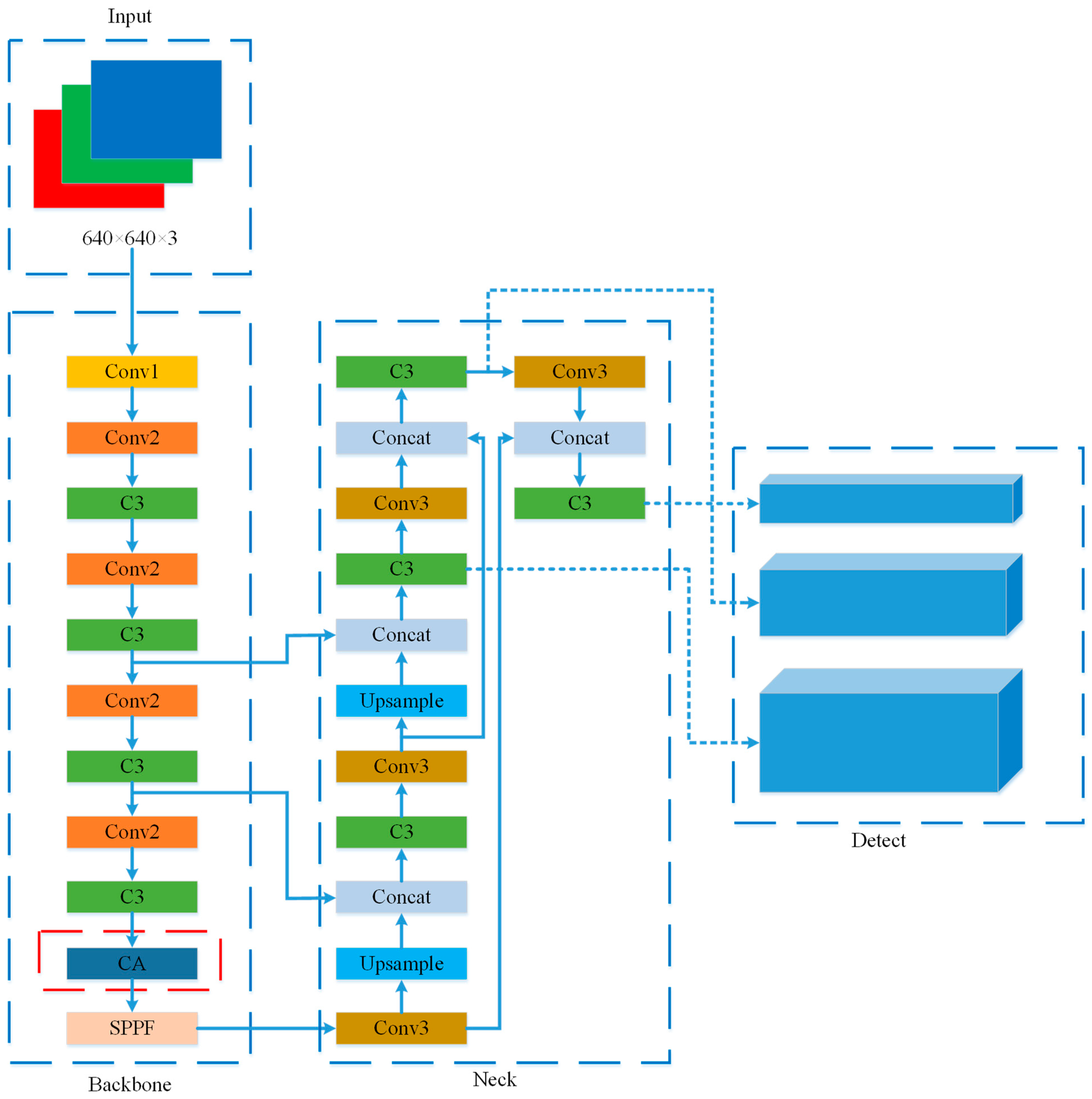
4.2. CA Attention Mechanism
- (1)
- Divide the input feature map into two directions, width and height, and perform global average pooling to obtain the feature maps in both the width and height directions, as shown in Equation (21).
- (2)
- The feature maps in the width and height directions of the obtained global perceptual field are stitched together, after which they are fed into the convolution module with a shared convolution kernel of 1 × 1 to reduce their dimension to the original C/r, where C is the channel number and r is the reduction rate, and then the batch normalized feature map F1 is fed into the Sigmoid activation function to obtain the feature map shaped as 1 × (W + H) × C/r feature map f, as shown in Equation (22).
- (3)
- The feature map f is convolved with a convolution kernel of 1 × 1 according to the original height and width to obtain the feature maps Fh and Fw, with the same number of channels as the original one. The attention weights gh for the feature maps in the height and width and gw in the width direction are obtained after the Sigmoid activation function, as shown in Equation (23).
- (4)
- After the above calculation, the attention weight gh in the height direction and the attention weight gw in the width direction of the input feature map will be obtained. Finally, the final feature map with attention weights in the width and height directions is obtained by multiplying and weighting the original feature map with the formula shown in (24).
4.3. Improved Yolov5 Neural Network
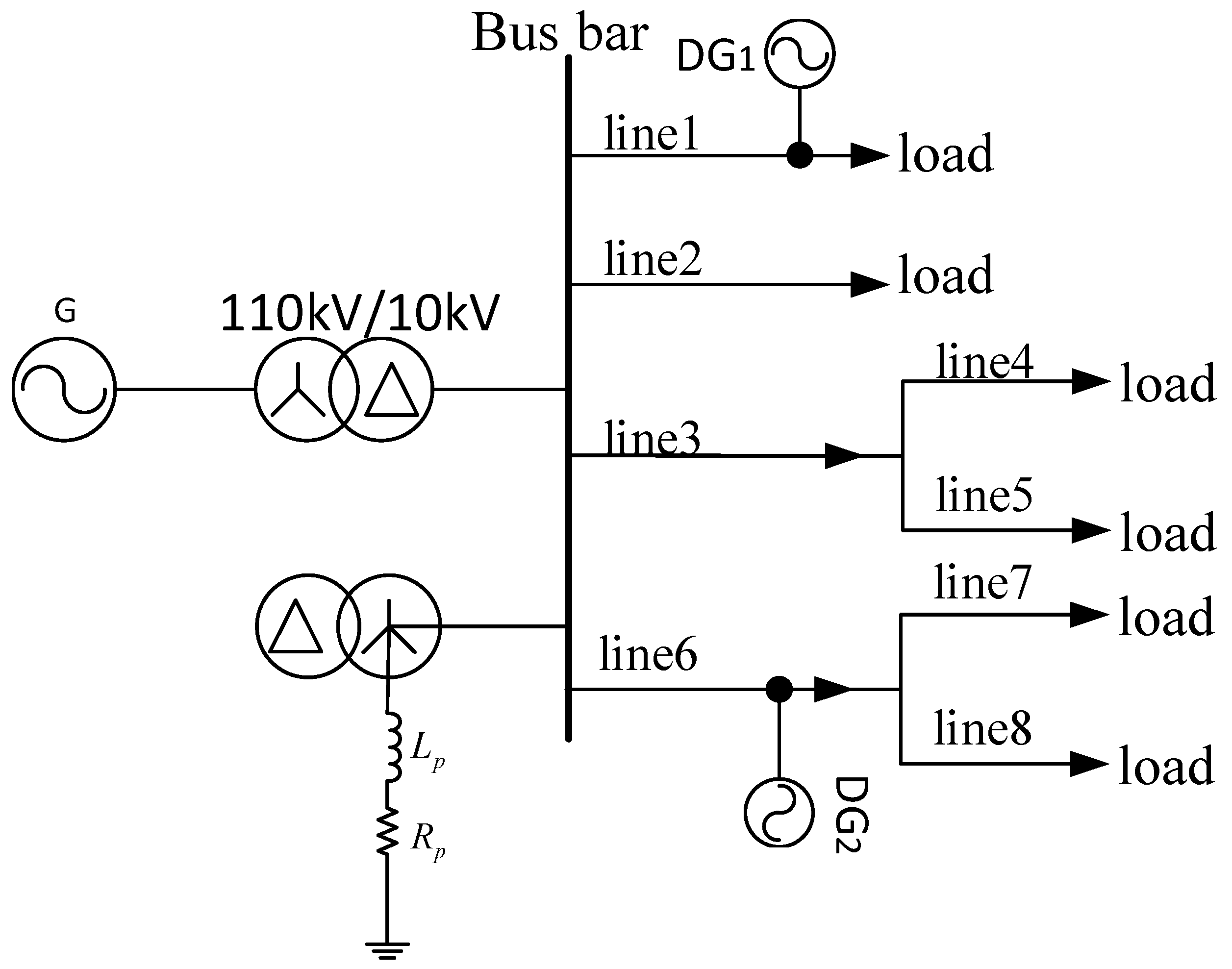
5. Fault-Line Selection Process
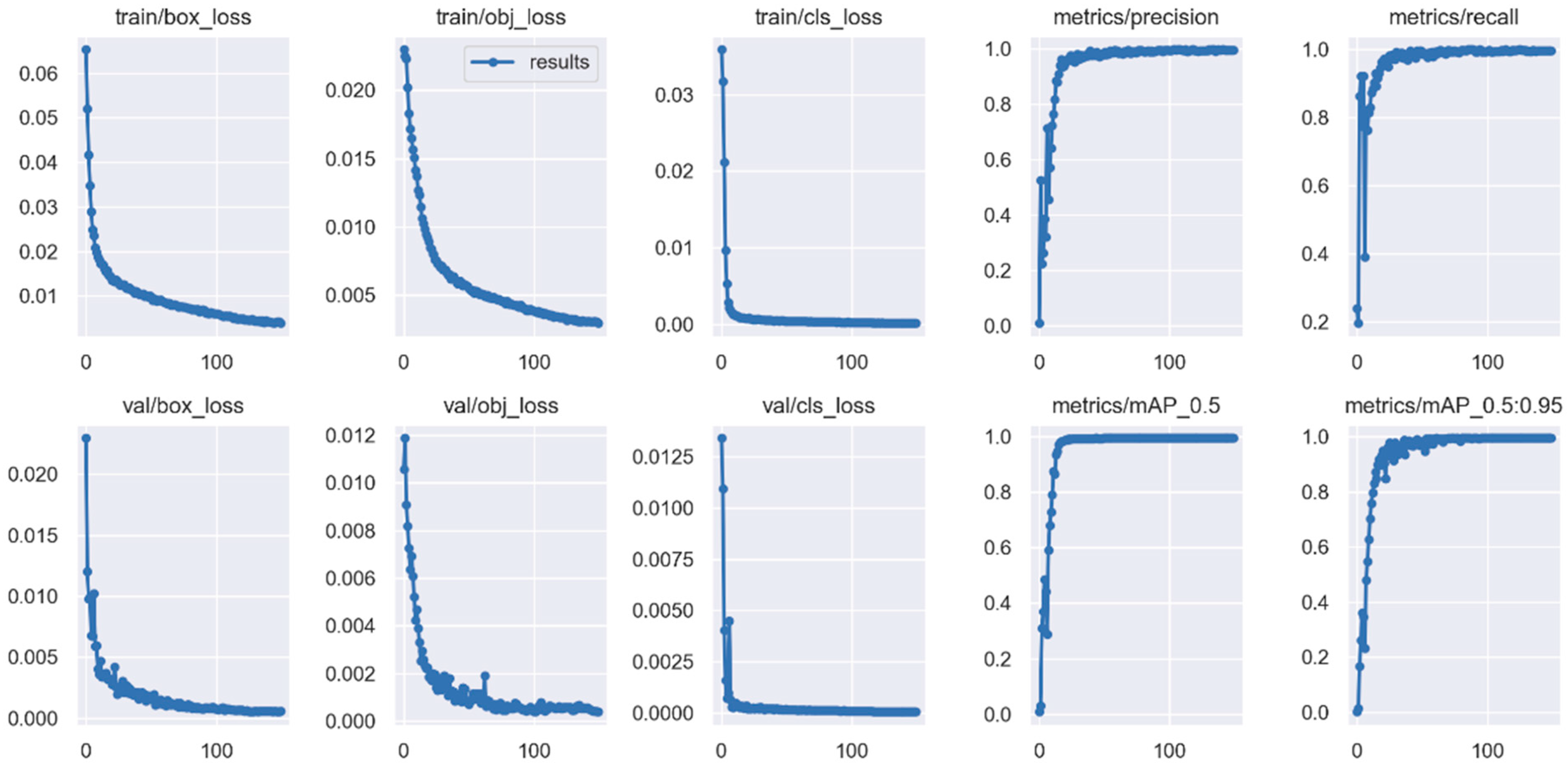
6. Experimental Verification and Analysis
6.1. Simulation Environment
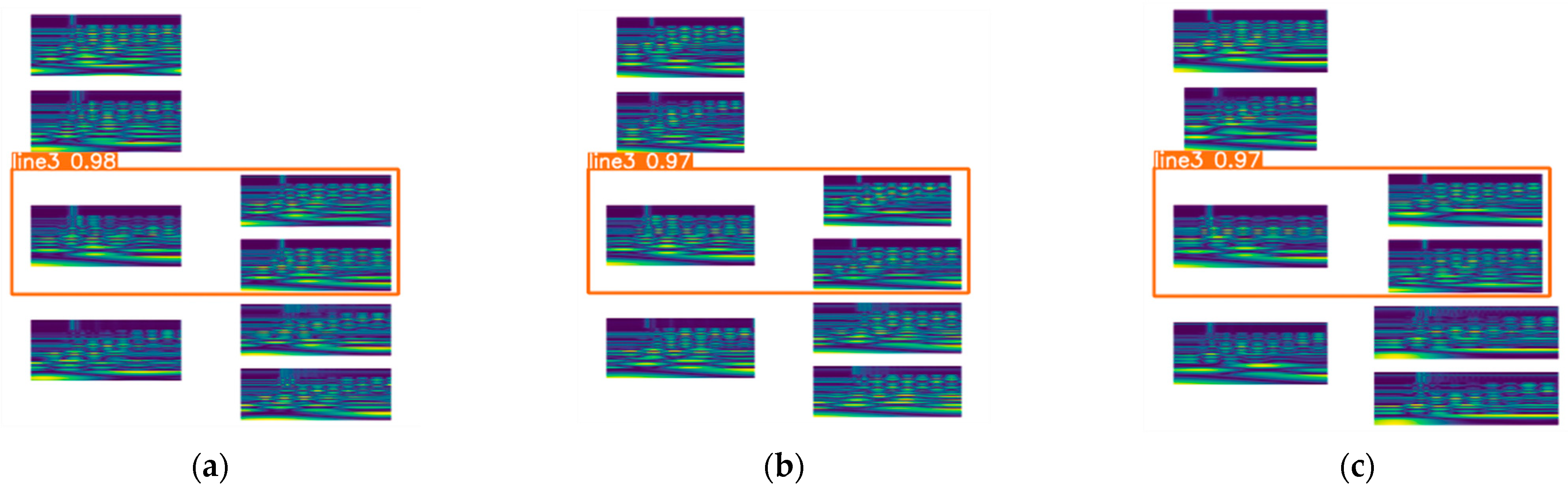
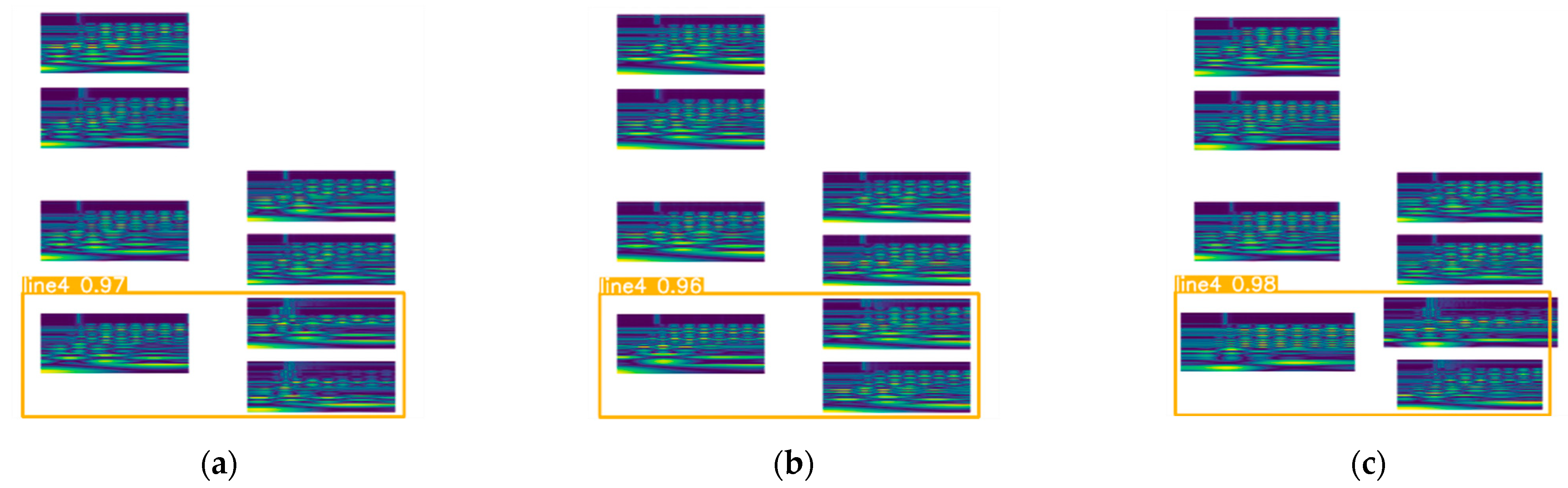
6.2. Feature Image Acquisition
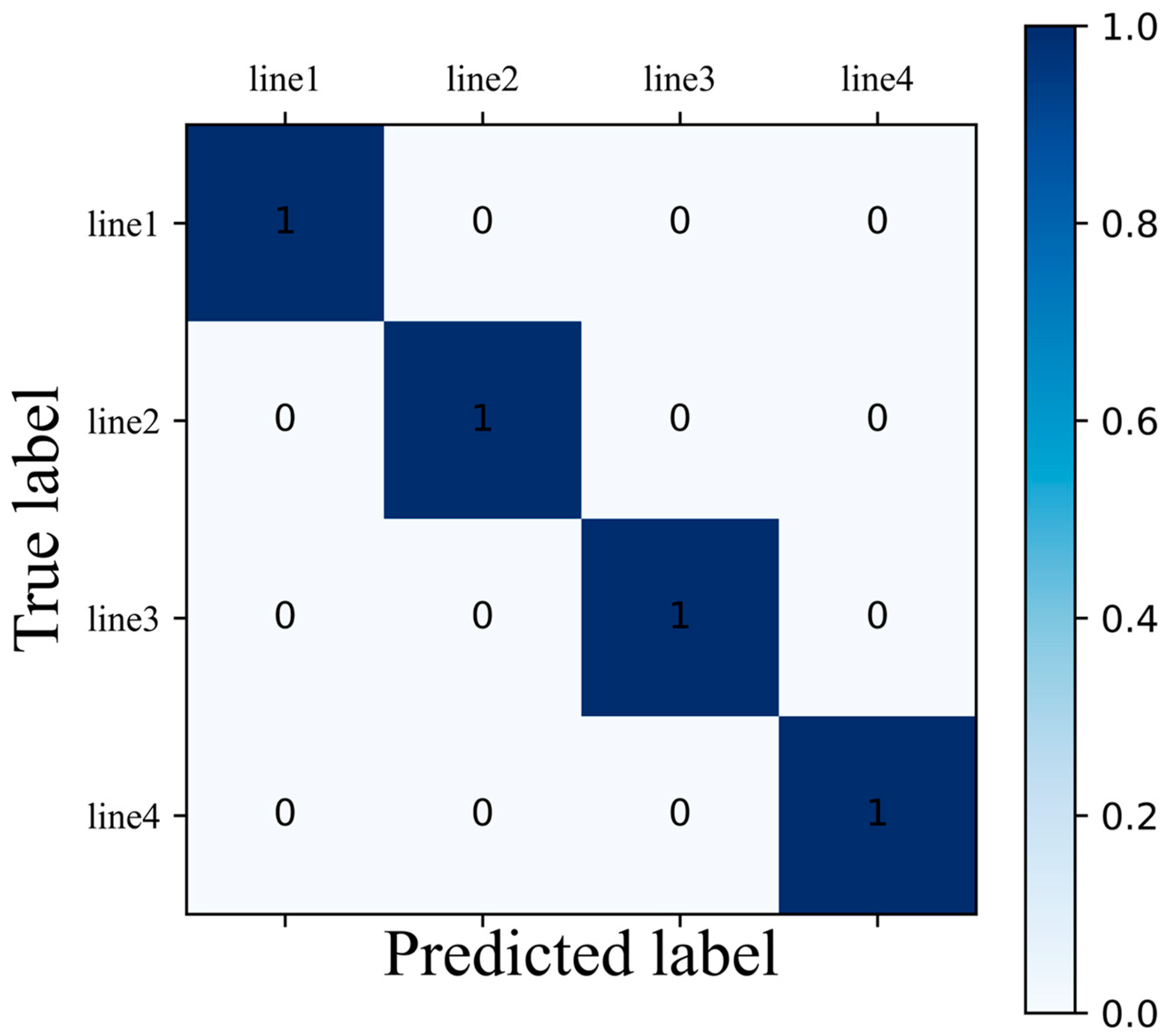
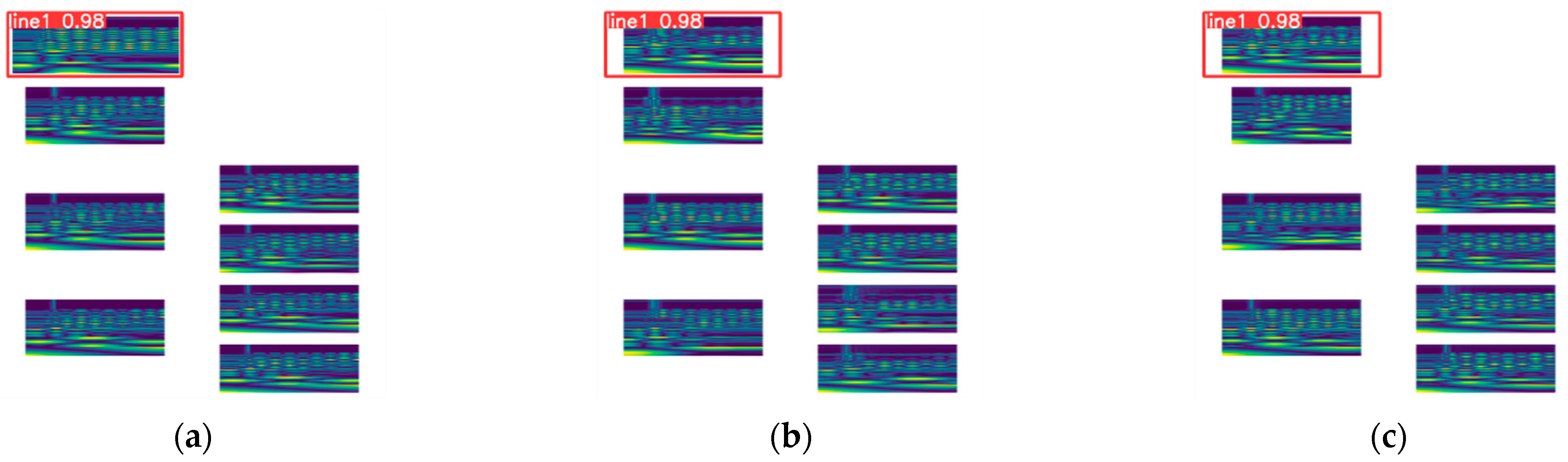
6.3. Line Selection Results in Verification and Analysis
6.4. Comparison Verification
6.4.1. Comparative Verification of Different Neural Networks
6.4.2. Anti-Noise Comparison Verification
6.4.3. High-Resistance Grounding Comparison Verification
6.4.4. Distributed Generators Access
6.4.5. Dynamic Mold Experiment
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ICEEMDAN | Improved Complete Ensemble Empirical Mode Decomposition Adaptive Noise |
| MICEEMDAN | modifying the Improved Complete Ensemble Empirical Mode Decomposition Adaptive Noise |
| PE | permutation entropy |
| MPE | multi-scale permutation entropy |
| MWPE | multi-scale weighted permutation entropy |
| IMFs | intrinsic mode functions |
| VMD | variational modal decomposition |
| CNN | convolutional neural network |
| CA | coordinate attention |
References
- Zhang, X.; Tai, N.; Wu, P.; Zheng, X.; Huang, W. A fault line selection method for DC distribution network using multiple observers. Energies 2019, 12, 1245. [Google Scholar] [CrossRef]
- Su, X.; Wei, H. A fault-line selection method for small-current grounded system based on deep transfer learning. Energies 2022, 15, 3467. [Google Scholar] [CrossRef]
- Cheng, H.-J.; Meng, H.; Jiang, P.-J. Research on fault line selection in small-current neutral grounding power system. In Proceedings of the 2013 IEEE International Conference on Vehicular Electronics and Safety, Dongguan, China, 28–30 July 2013; pp. 206–209. [Google Scholar] [CrossRef]
- Liao, K.; Du, Y.; Dong, K.; Fan, H.; Zhao, X. Identification of Fault Line Selection and Section for Single-Phase Ground Fault in Small Current Grounding System. In Proceedings of the 2020 5th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 12–14 September 2020; pp. 267–271. [Google Scholar] [CrossRef]
- Shuping, G.; Bicong, D.; Guobing, S.; Mingxing, S. Fault line selection method of DC distribution network based on transient current fault component. In Proceedings of the 2020 7th International Forum on Electrical Engineering and Automation (IFEEA), Hefei, China, 25–27 September 2020; pp. 433–437. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, Z. Single-Phase ground fault traveling wave line selection method and line selection device field test. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Zhengyi, L.; Changhong, D.; Huamei, Y.; Hu, F. A LSTM line selection method of single-phase ground fault based on big-data platform. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 776–780. [Google Scholar] [CrossRef]
- Liu, B.; Ma, H.; Xu, H.; Ju, P. Single-phase-to-ground fault detection with distributed parameters analysis in non-direct grounded systems. CSEE J. Power Energy Syst. 2019, 5, 139–147. [Google Scholar] [CrossRef]
- Chang, Z.; Song, G.; Huang, W.; Guo, S.; Zhang, W. Phase voltage and current fault components based fault segment location method under single-phase earth fault in distribution network. Power Syst. Technol. 2020, 41, 2363–2369. [Google Scholar] [CrossRef]
- Yang, X.; Liu, W. A new line selection method based on intrinsic mode energy of phase current change. J. Electr. Power Sci. Technol. 2018, 33, 149–154. [Google Scholar] [CrossRef]
- Yang, F.; Liu, X.X.; Shen, Y. Low-resistance grounding system high-resistance ground fault protection based on zero sequence current projection coefficient. Power Syst. Technol. 2020, 44, 1128–1133. [Google Scholar]
- Gao, L.; Wu, S.; Wang, M.; Wang, Z.; Yang, Y. Single-line-to-ground fault line selection method in distribution network based on multi-scale wavelet decomposition of transient signals. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 15–17 April 2022; pp. 2052–2057. [Google Scholar] [CrossRef]
- Qingshan, Q.; Xiuying, X.; Chongyi, T.; Ruiqi, W. Single-phase ground fault location of distribution network with DG based on CEEMD. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29–31 May 2020; pp. 587–591. [Google Scholar] [CrossRef]
- Hou, S.; Guo, W. Optimal denoising and feature extraction methods using modified CEEMD combined with duffing system and their applications in fault line selection of non-solid-earthed network. Symmetry 2020, 12, 536. [Google Scholar] [CrossRef]
- Ray, P.; Mishra, D.P.; Dey, K.; Mishra, P. Fault detection and classification of a transmission line using discrete wavelet transform & artificial neural network. In Proceedings of the 2017 International Conference on Information Technology (ICIT), Bhubaneswar, India, 21–23 December 2017; pp. 178–183. [Google Scholar] [CrossRef]
- Luo, G.; Tan, Y.; Li, M.; Cheng, M.; Liu, Y.; He, J. Stacked auto-encoder-based fault location in distribution network. IEEE Access 2020, 8, 28043–28053. [Google Scholar] [CrossRef]
- Jayamaha, D.K.J.S.; Lidula, N.W.A.; Rajapakse, A.D. Wavelet-multi resolution analysis based ANN architecture for fault detection and localization in DC microgrids. IEEE Access 2019, 7, 145371–145384. [Google Scholar] [CrossRef]
- Tabatabaei, A.; Mosavi, M.R.; Farajiparvar, P. A traveling-wave fault location technique for three-terminal lines based on wavelet analysis and Recurrent Neural Network using GPS timing. In Proceedings of the 2013 Smart Grid Conference (SGC), Tehran, Iran, 17–18 December 2013; pp. 268–272. [Google Scholar] [CrossRef]
- Liang, J. Research on rapid diagnosis method of single-phase grounding fault in distribution network based on deep learning. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 20–24. [Google Scholar] [CrossRef]
- Cheng, X.-R.; Cui, B.-J.; Hou, S.-Z. Fault line selection of distribution network based on modified CEEMDAN and GoogLeNet neural network. IEEE Sens. J. 2022, 22, 13346–13364. [Google Scholar] [CrossRef]
- Hou, S.; Guo, W. Fault identification method for distribution network based on parameter optimized variational mode decomposition and convolutional neural network. IET Gener. Transm. Distrib. 2022, 16, 737–749. [Google Scholar] [CrossRef]
- Zhang, H.; He, S.-S. Analysis and comparison of permutation entropy, approximate entropy and sample entropy. In Proceedings of the 2018 International Symposium on Computer, Consumer and Control (IS3C), Taichung, Taiwan, 6–8 December 2018; pp. 209–212. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, X.; Cao, J.; Liu, B. Recognition of biological tissue denaturation based on improved multiscale permutation entropy and GK fuzzy clustering. Information 2022, 13, 140. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, T.; Meng, R.; Liu, Q. Generalized composite multiscale permutation entropy and PCA based fault diagnosis of rolling bearings. J. Vib. Shock 2018, 37, 61–66. [Google Scholar]
- Zheng, J.D.; Cheng, J.H.; Yang, Y. Modified EEMD algorithm and its applications. J. Vib. Shock 2013, 32, 21–26. [Google Scholar]
- Zhao, Y.; Adjallah, K.H.; Sava, A. Influence study of the intermittent wave amplitude vs. the sampling frequency ratio on ICEEMDAN mode mixing alleviation performance. In Proceedings of the 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 19–21 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Das, A.B.; Bhuiyan, M.I.H. Discrimination of focal and non-focal EEG signals using entropy-based features in EEMD and CEEMDAN domains. In Proceedings of the 2016 9th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 20–22 December 2016; pp. 435–438. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Song, G.; Cheng, Q.; Wei, X.; Wei, Y. Faulty line selection method for distribution network based on variable scale bistable system. J. Sens. 2016, 2016, 1–17. [Google Scholar] [CrossRef]
- Wang, Z.; Qiao, P.; Shi, B. Nonpenetrating damage identification using hybrid lamb wave modes from Hilbert-Huang spectrum in thin-walled structures. Shock Vib. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Moraes, A.L.; Fernandes, R.A.S. Recurrence Plots: A novel feature engineering technique to analyze power quality disturbances. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate attention for efficient mobile network design. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13708–13717. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, F.; Xu, Z.; Wang, J.; Liu, K.; Qin, L. Insulator and damage detection and location based on Yolov5. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 25–27 February 2022; pp. 17–24. [Google Scholar] [CrossRef]








| Signal | Multi-Scale Permutation Entropy | Multi-Scale Weighted Permutation Entropy |
|---|---|---|
| White noise | 0.9087 | 0.8918 |
| Gaussian white noise | 0.9112 | 0.8896 |
| High-frequency sinusoidal signal | 0.4310 | 0.4162 |
| Fundamental frequency sinusoidal signal | 0.1176 | 0.1053 |
| AM signal | 0.5152 | 0.4541 |
| FM signal | 0.3753 | 0.3809 |
| AM/FM signal | 0.5371 | 0.4981 |
| Intermittent signal | 0.5888 | 0.8402 |
| Circuit Type | Resistance/ (Ω·km−1) | Inductance/ (mH·km−1) | Grounding Capacitance/ (μF·km−1) | |||
|---|---|---|---|---|---|---|
| Positive Phase | Zero Phase | Positive Phase | Zero Phase | Positive Phase | Zero Phase | |
| Overhead line | 0.178 | 0.25 | 1.21 | 5.54 | 0.015 | 0.012 |
| Cable line | 0.27 | 2.7 | 0.255 | 1.02 | 0.339 | 0.28 |
| Methods | Training Rounds | Accuracy/% |
|---|---|---|
| Yolov5 | 300 | 99.31 |
| Yolov5 + CA | 150 | 99.98 |
| Line | Number of Samples | Accuracy/% | ||
|---|---|---|---|---|
| Method 1 | Method 2 | Method of This Paper | ||
| Line 1 | 500 | 92.91 | 96.89 | 99.98 |
| Line 2 | 600 | 93.18 | 95.94 | 99.99 |
| Line 3 | 800 | 90.72 | 93.87 | 99.97 |
| Line 4 | 800 | 91.86 | 93.89 | 99.98 |
| Signal-to-Noise Ratio/dB | Line | Number of Samples | Accuracy/% | ||
|---|---|---|---|---|---|
| Ref. [14] | Ref. [19] | This Paper | |||
| 35 | Line 1 | 500 | 96.91 | 98.33 | 99.98 |
| Line 2 | 600 | 96.83 | 98.30 | 99.99 | |
| Line 3 | 800 | 94.21 | 97.51 | 99.97 | |
| Line 4 | 800 | 94.73 | 97.54 | 99.98 | |
| 30 | Line 1 | 500 | 94.71 | 95.31 | 99.97 |
| Line 2 | 600 | 94.67 | 95.12 | 99.98 | |
| Line 3 | 800 | 93.11 | 92.78 | 99.97 | |
| Line 4 | 800 | 93.02 | 93.02 | 99.98 | |
| 25 | Line 1 | 500 | 90.67 | 91.25 | 99.96 |
| Line 2 | 600 | 88.32 | 91.12 | 99.98 | |
| Line 3 | 800 | 87.91 | 90.42 | 99.95 | |
| Line 4 | 800 | 87.05 | 90.61 | 99.95 | |
| 20 | Line 1 | 500 | 84.84 | 88.15 | 99.94 |
| Line 2 | 600 | 84.32 | 88.32 | 99.95 | |
| Line 3 | 800 | 82.59 | 86.89 | 99.93 | |
| Line 4 | 800 | 82.51 | 85.91 | 99.94 | |
| Grounding Resistance/Ω | Line | Line Selection Results | ||
|---|---|---|---|---|
| Ref. [14] | Ref. [19] | This Paper | ||
| 1000 | Line 1 | Line 1 | Line 1 | Line 1 |
| Line 2 | Line 2 | Line 2 | Line 2 | |
| Line 3 | Line 2 | Line 3 | Line 3 | |
| Line 4 | Line 4 | Line 4 | Line 4 | |
| 1500 | Line 1 | Line 1 | Line 1 | Line 1 |
| Line 2 | Line 2 | Line 2 | Line 2 | |
| Line 3 | Line 2 | Line 3 | Line 3 | |
| Line 4 | Line 3 | Line 3 | Line 4 | |
| Line | Number of Samples | Accuracy/% | |
|---|---|---|---|
| Original Model | New Model | ||
| Line 1 | 500 | 97.93 | 99.75 |
| Line 2 | 600 | 98.19 | 99.87 |
| Line 3 | 800 | 98.12 | 99.79 |
| Line 4 | 800 | 97.86 | 99.69 |
| Fault Type | Fault Line | Fault Point | Transition Resistance | Fault Close Angle | Fault Line Selection Result |
|---|---|---|---|---|---|
| AG | Line 1 | F1 | 0 Ω | 0° | Line 1 |
| BG | Line 1 | F2 | 500 Ω | 30° | Line 1 |
| CG | Line 1 | F3 | 1000 Ω | 60° | Line 1 |
| AG | Line 2 | F1 | 400 Ω | 60° | Line 2 |
| BG | Line 2 | F2 | 800 Ω | 120° | Line 2 |
| CG | Line 2 | F3 | 200 Ω | 30° | Line 2 |
| BG | Line 2 | F4 | 500 Ω | 150° | Line 2 |
| AG | Line 3 | F1 | 0 Ω | 0° | Line 3 |
| CG | Line 3 | F2 | 400 Ω | 60° | Line 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, S.; Xu, Y.; Guo, W. Distribution Network Fault-Line Selection Method Based on MICEEMDAN–Recurrence Plot–Yolov5. Processes 2022, 10, 2127. https://doi.org/10.3390/pr10102127
Hou S, Xu Y, Guo W. Distribution Network Fault-Line Selection Method Based on MICEEMDAN–Recurrence Plot–Yolov5. Processes. 2022; 10(10):2127. https://doi.org/10.3390/pr10102127
Chicago/Turabian StyleHou, Sizu, Yan Xu, and Wei Guo. 2022. "Distribution Network Fault-Line Selection Method Based on MICEEMDAN–Recurrence Plot–Yolov5" Processes 10, no. 10: 2127. https://doi.org/10.3390/pr10102127
APA StyleHou, S., Xu, Y., & Guo, W. (2022). Distribution Network Fault-Line Selection Method Based on MICEEMDAN–Recurrence Plot–Yolov5. Processes, 10(10), 2127. https://doi.org/10.3390/pr10102127





