Optimizing the Geometric Parameters of a Stepped Labyrinth Seal to Minimize the Discharge Coefficient
Abstract
1. Introduction
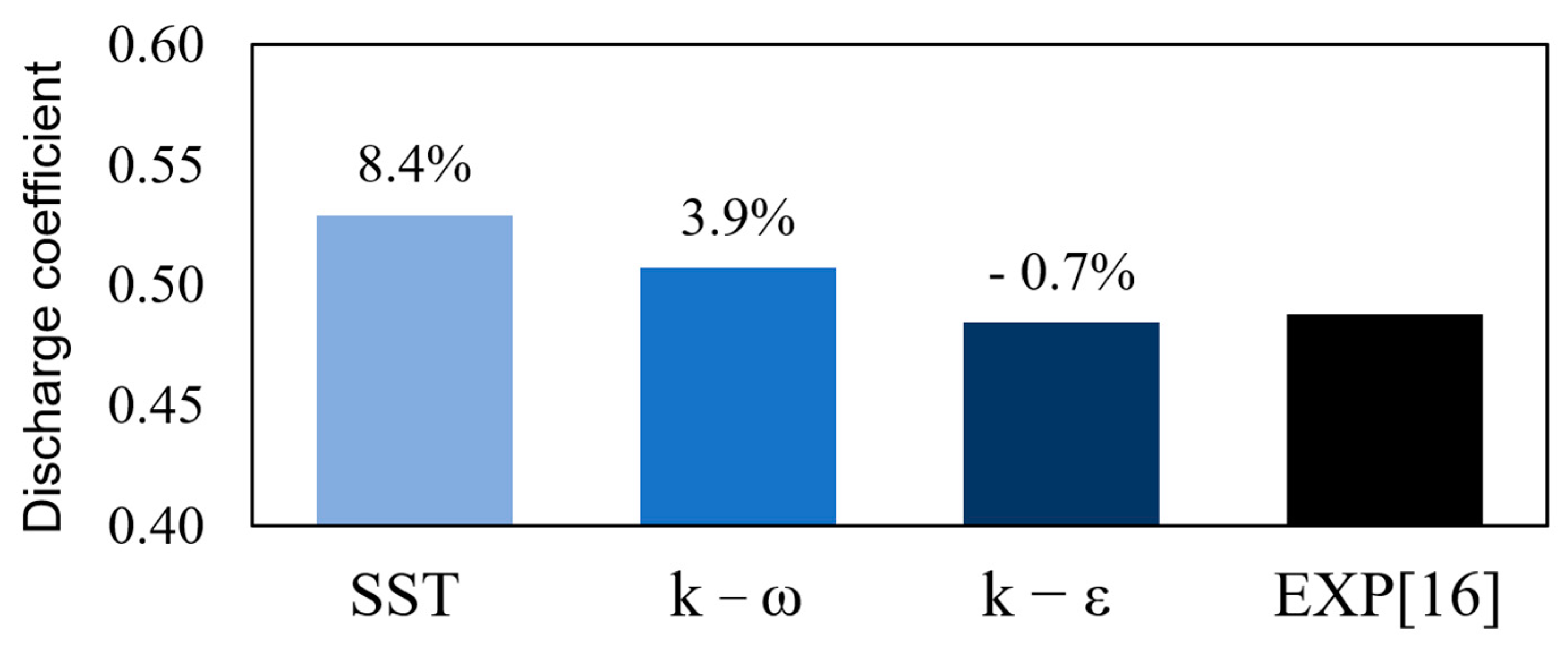
2. Numerical Method and Verification
3. Results and Discussion
4. Conclusions
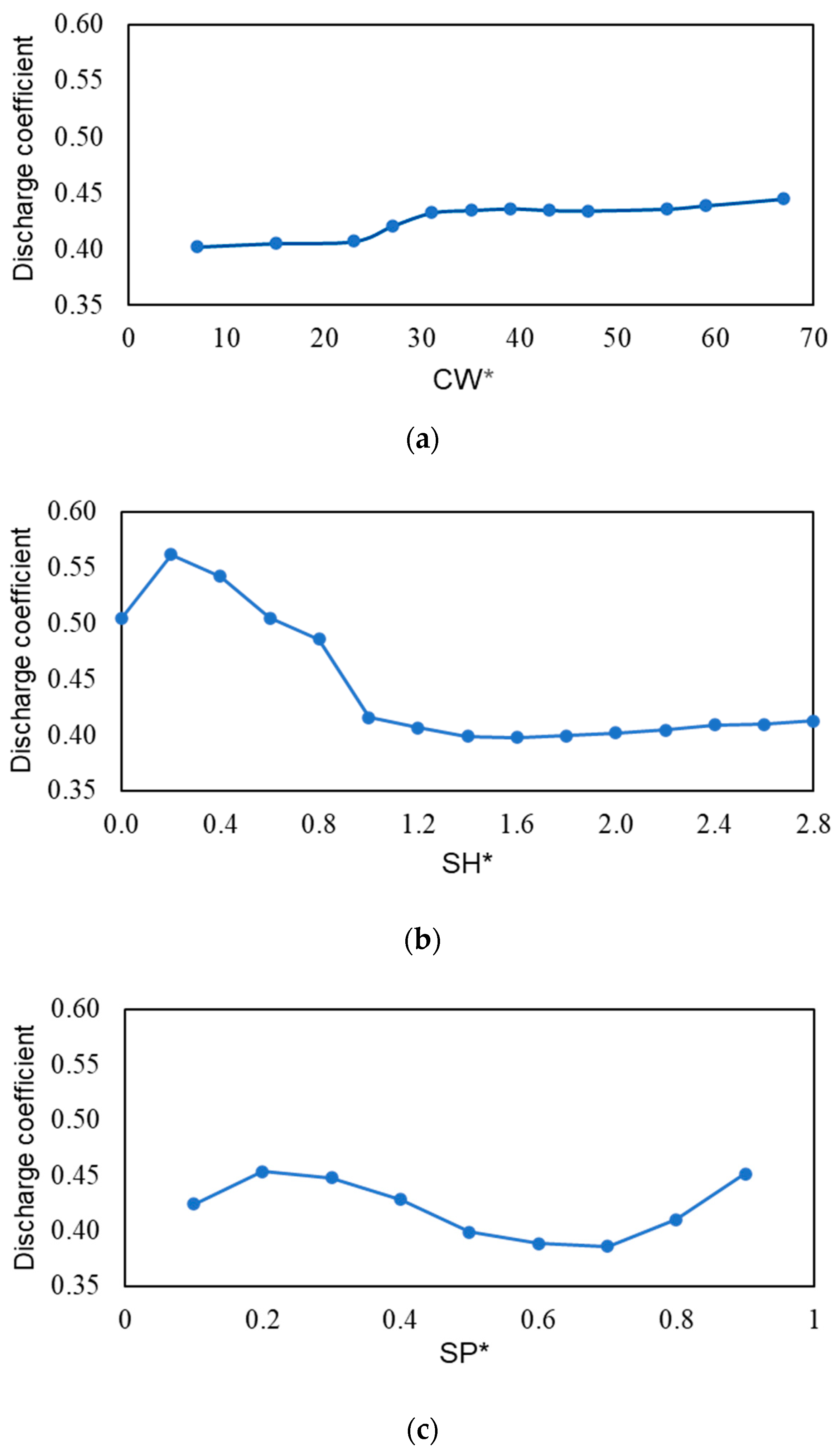
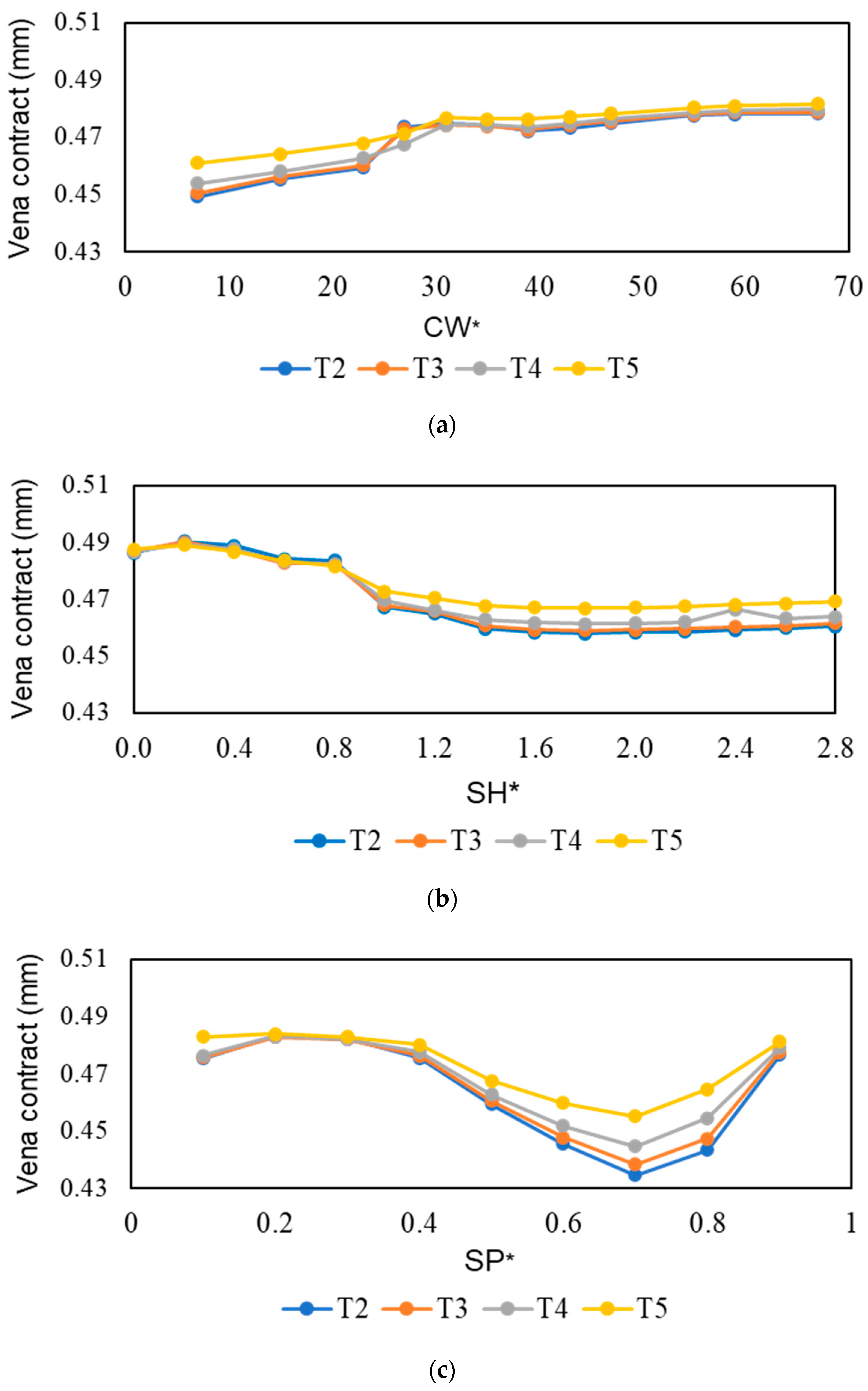
- In the stepped labyrinth seal, when CW, SH, and SP were varied, the discharge coefficient of SH was the most sensitive at a factor of approximately 30%;
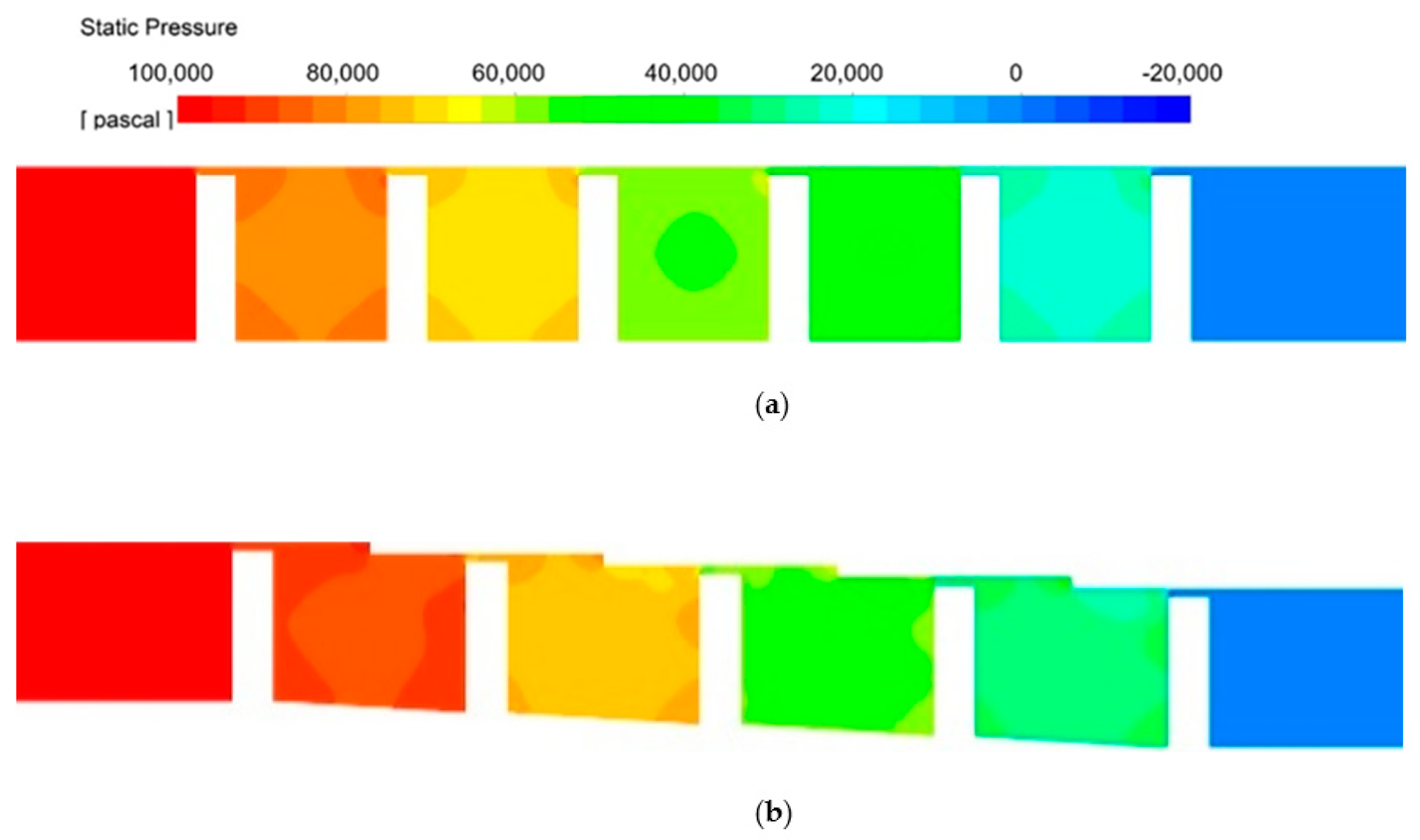
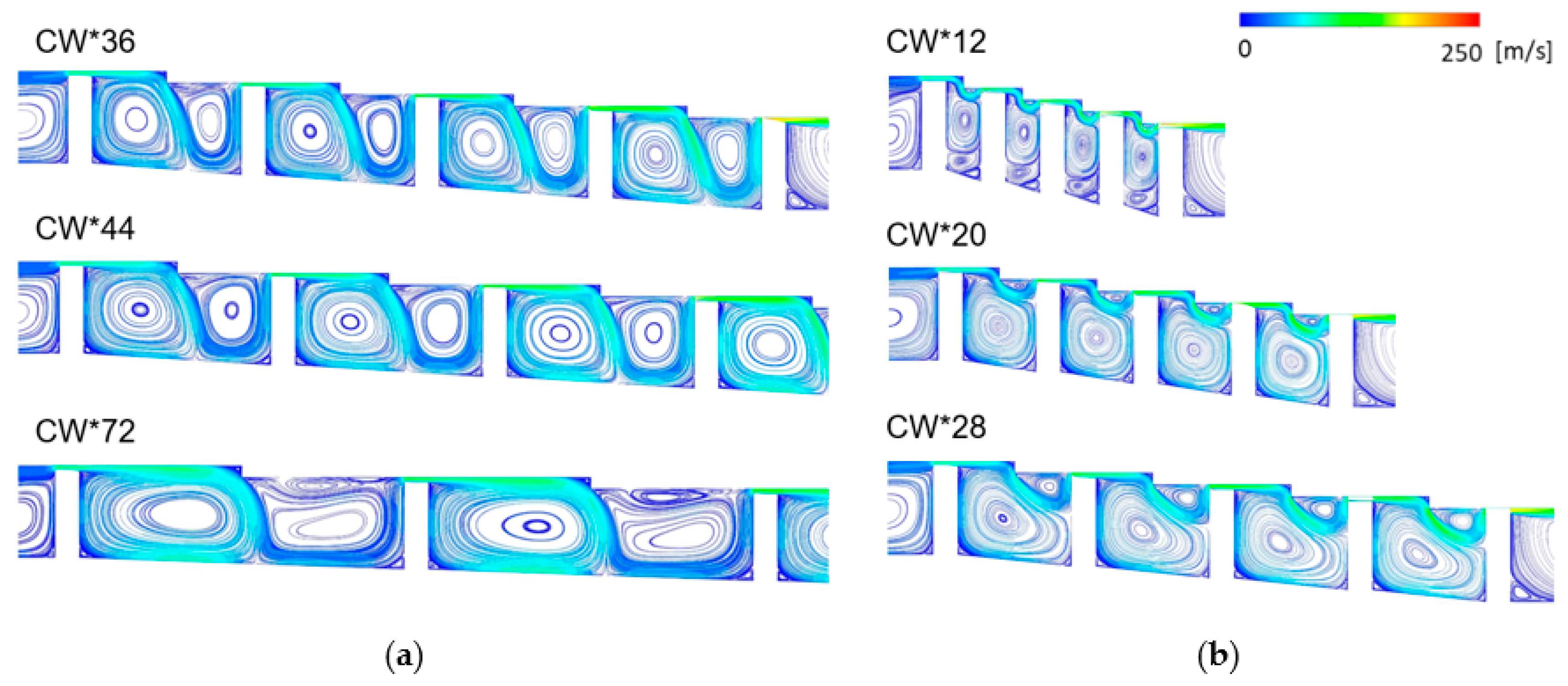
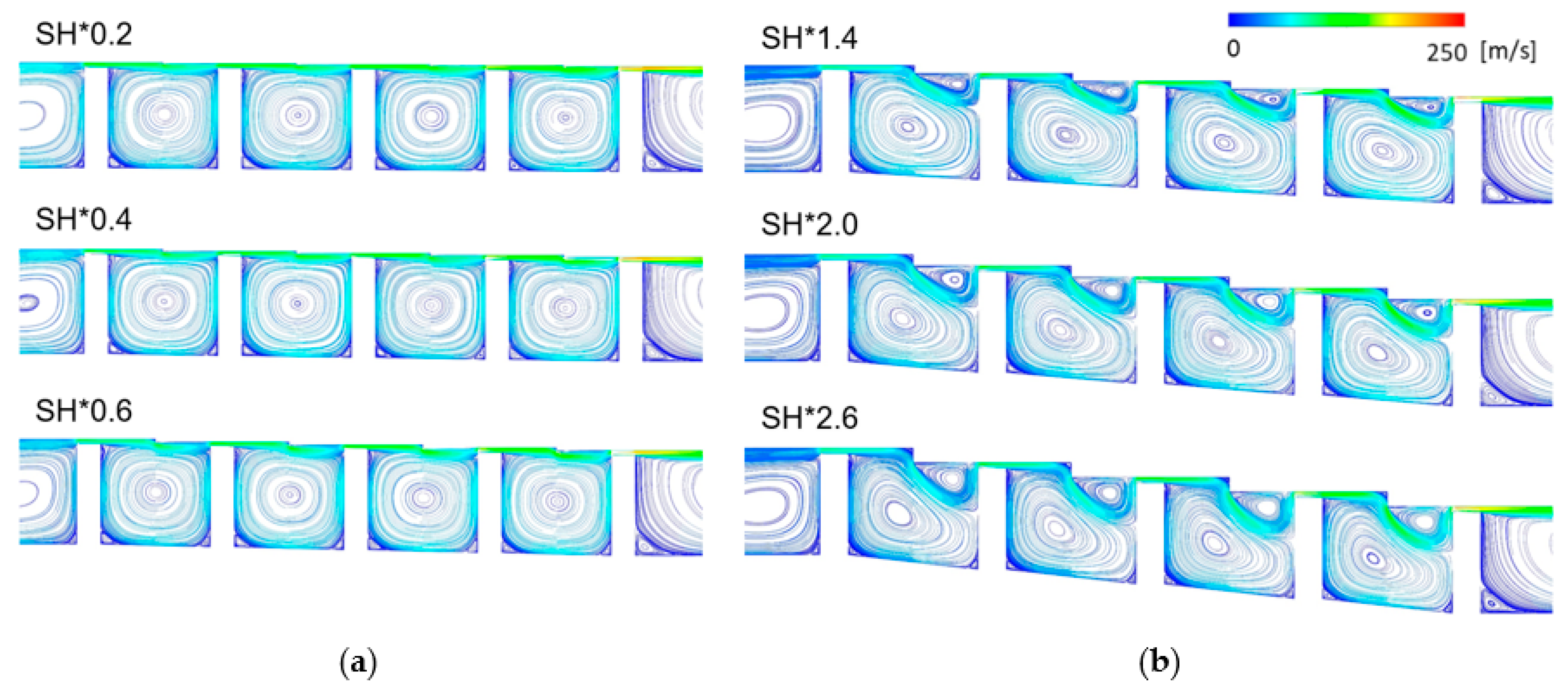
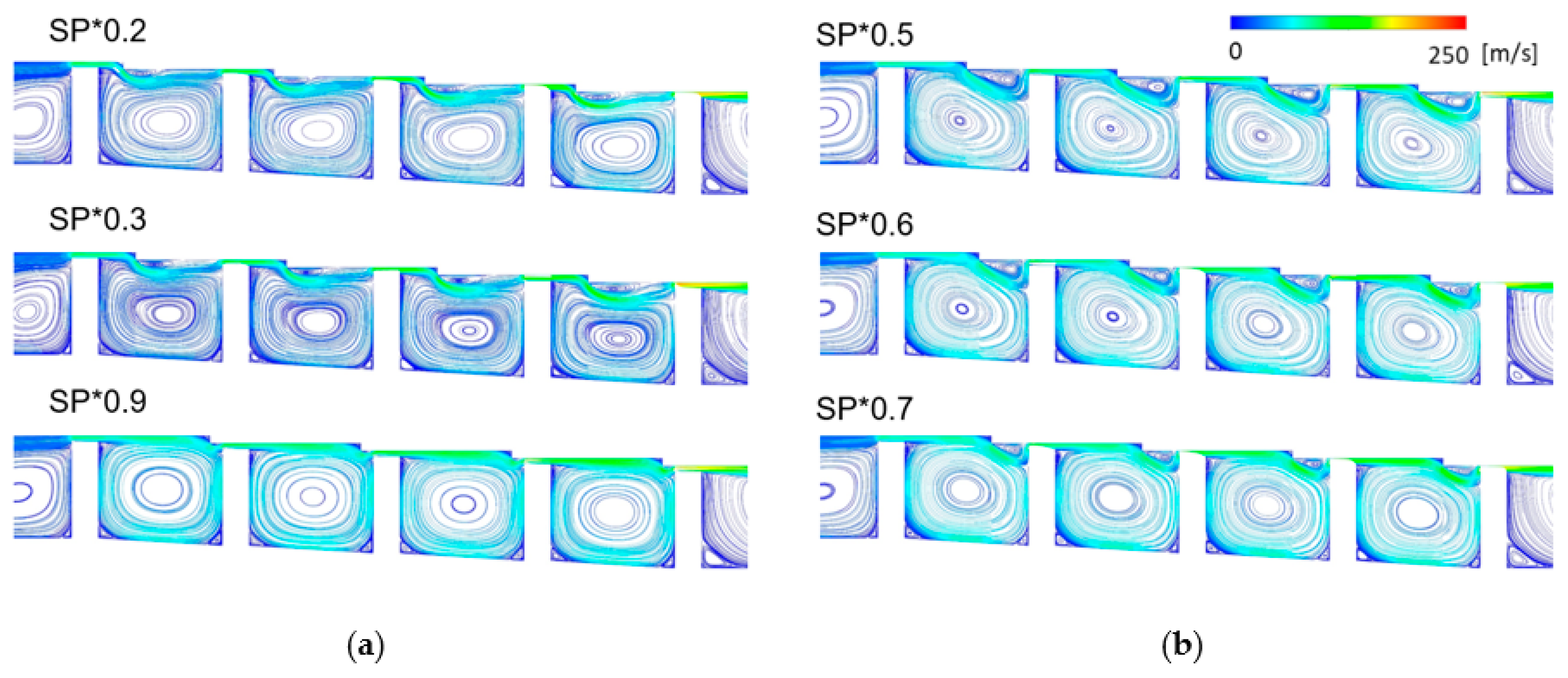
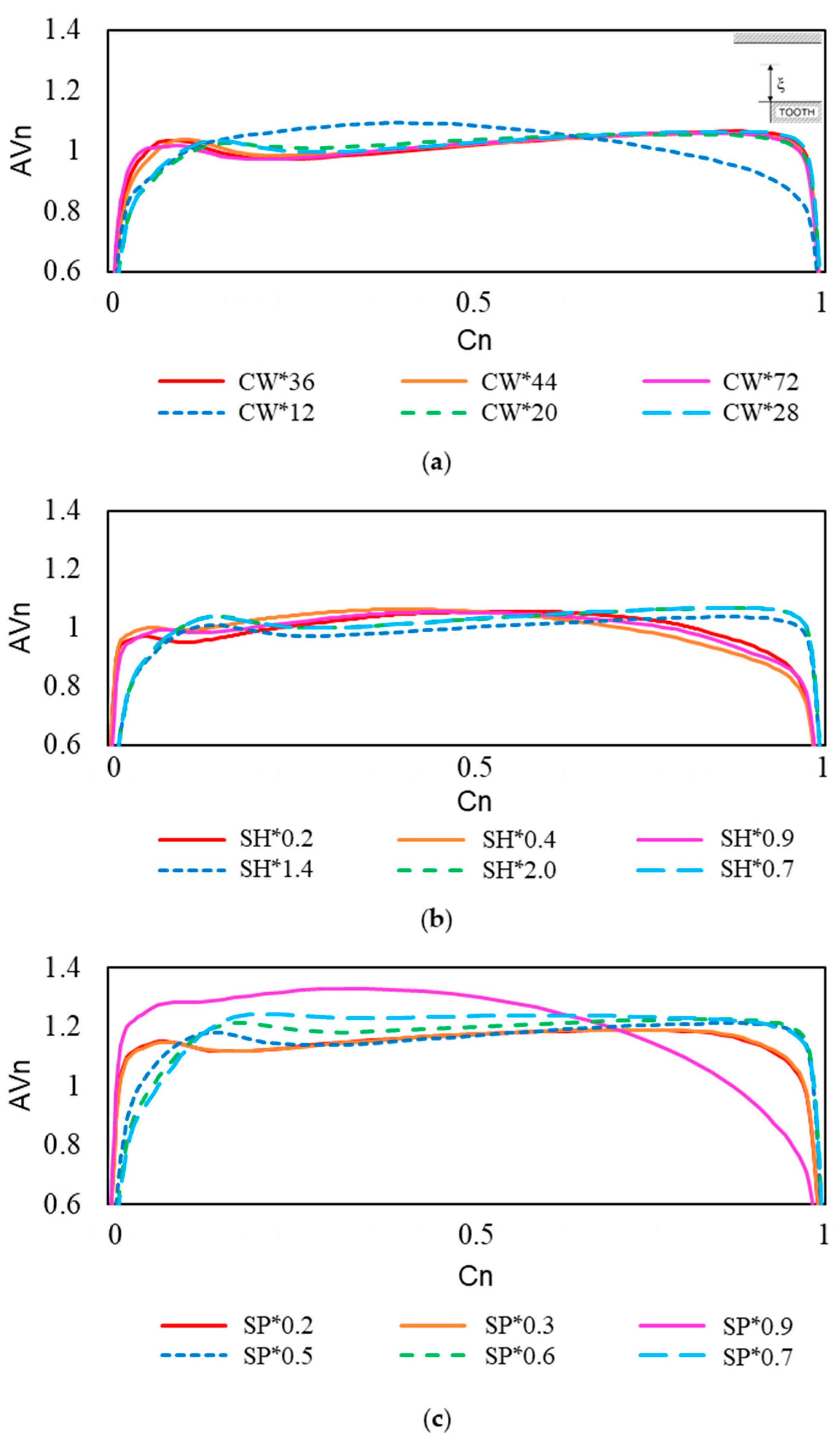
- In the stepped labyrinth seal, when a small recirculation flow appeared at the clearance inlet, the clearance inlet pressure was reduced, and the axial velocity gently increased, which reduced the size of the vena contracta. The shapes with these characteristics exhibited a small discharge coefficient;
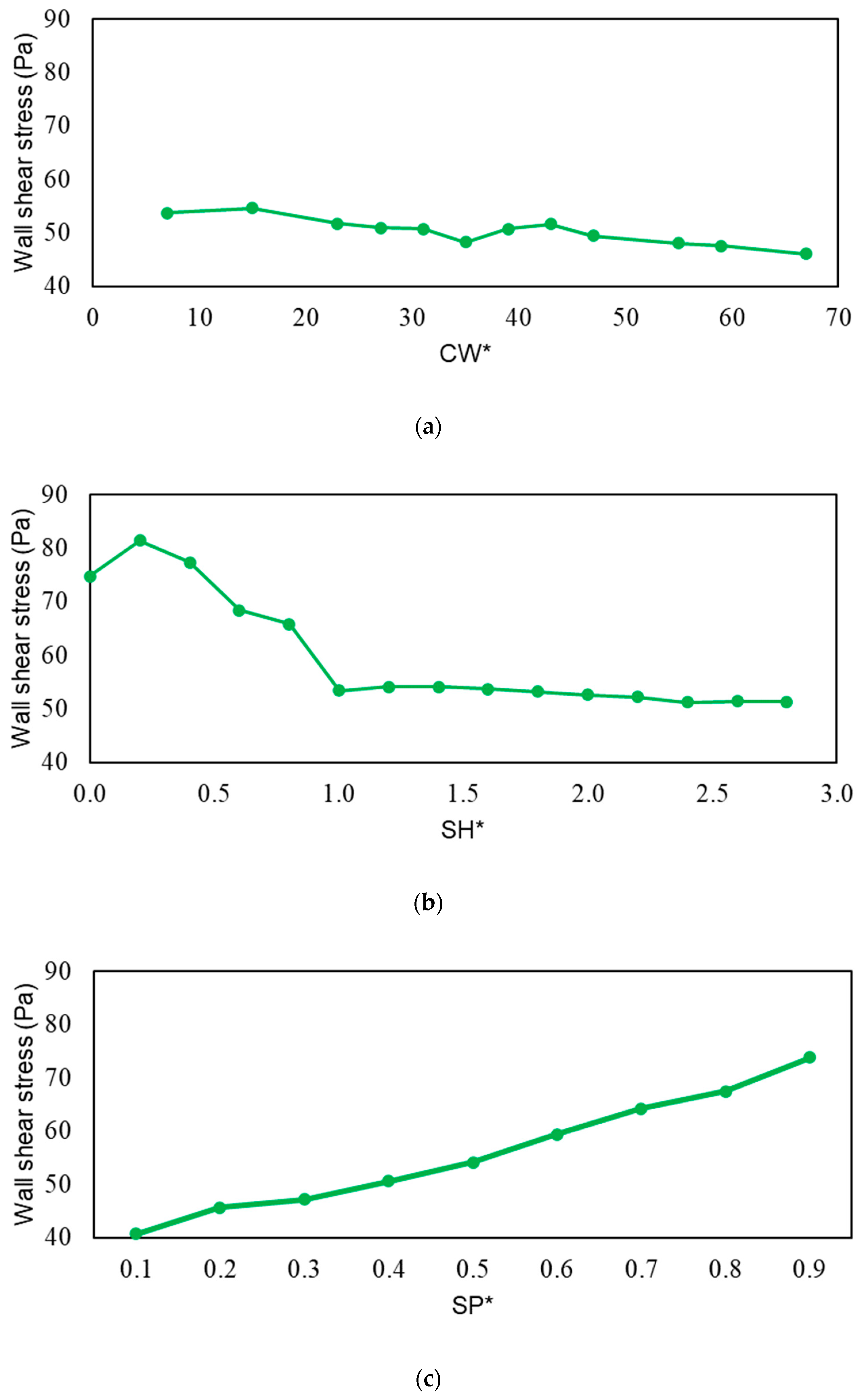
- The wall shear stress and discharge coefficient trends were very similar for the SH changes of the stepped labyrinth seal. However, no correlations existed between the wall shear stress and the discharge coefficient for CW and SP changes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cross-sectional area of labyrinth seal () | |
| AVn | Normalized axial velocity |
| Discharge coefficient | |
| Normalized clearance | |
| CW | Cavity width |
| Mass flow rate (kg/s) | |
| P | Pressure (Pa) |
| R | Specific gas constant |
| SH | Step height |
| SP | Step position |
| T | Temperature (K) |
| W | Width of tooth |
| Greek Symbols | |
| Isentropic coefficient | |
| ξ | Coordinate from tooth tip |
| Subscripts | |
| id | Ideal |
| in | Inlet |
| out | Outlet |
| Superscript | |
| * | Normalized |
References
- Boyce, M.P. Gas Turbine Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Ahn, J.; Song, J.C.; Lee, J.S. Fully Coupled Large Eddy Simulation of Conjugate Heat Transfer in a Ribbed Channel with a 0.1 Blockage Ratio. Energies 2021, 14, 2096. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Eckert, E.R.G.; Ramsey, J.W. Film Cooling with Injection Through Holes: Adiabatic Wall Temperatures Down-394 Stream of a Circular Hole. J. Eng. Power 1968, 90, 384–393. [Google Scholar] [CrossRef]
- Zhou, B. PowerGen Gas Turbine Losses and Condition Monitoring: A Loss Data-Based Study. ASCE-ASME J. Risk Uncertain. Eng. Syst. B: Mech. Eng. 2016, 2, 021007. [Google Scholar] [CrossRef]
- Sultanian, B.K. Gas Turbines Internal Flow Systems Modeling; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Martin, H.M. Labyrinth Packings. Engineer 1908, 85, 35–36. [Google Scholar]
- Zhang, W.; Zhang, Y.; Yang, J.; Li, C. Influence of Tilting Rotor on Characteristics of Fluid-Induced Vibration for Labyrinth Seals. J. Vibroeng 2016, 18, 5416–5431. [Google Scholar] [CrossRef][Green Version]
- Holle, G.; Krishnan, M. Gas Turbine Engine Brush Seal Applications. In Proceedings of the 26th Joint Propulsion Conference, Orlando, FL, USA, 18 July 1990. [Google Scholar]
- Bondarenko, G.A.; Khizhnyak, L.A. Experimental Investigation of a Honeycomb Seal. Chem. Petrol. Eng. 1978, 14, 793–795. [Google Scholar] [CrossRef]
- Becker, E. Strömungsvorgänge in Ringformigen Spalten (Labyrinth-Dichtungen). Ver. Deut Ing. 1907, 51, 1133–1141. [Google Scholar]
- Stodola, A. Steam and Gas Turbines, 6th ed.; McGraw-Hill: New York, NY, USA, 1927; pp. 189–194. [Google Scholar]
- Egli, A. The Leakage of Steam Through Labyrinth Seals. Trans. ASME 1935, 57, 115–122. [Google Scholar]
- Dollin, F.; Brown, W.S. Flow of Fluids Through Openings in Series. Engineer 1937, 164, 223–224. [Google Scholar]
- Hodkinson, B. Estimation of the Leakage Through a Labyrinth Gland. Proc. Inst. Mech. Eng. 1939, 141, 283–288. [Google Scholar] [CrossRef]
- Jeri, J. Flow Through Straight-Through Labyrinth Seals. In Proceedings of the Seventh International Congress on Applied Mechanics, London, UK, 5–11 September 1948; 1948; Volume 2, pp. 70–82. [Google Scholar]
- Wittig, S.; Schelling, U.; Kim, S.; Jacobsen, K. Numerical Predictions and Measurements of Discharge Coefficients in Labyrinth Seals. In Proceedings of the ASME 1987 International Gas Turbine Conference and Exhibition, Anaheim, CA, USA, 31 May–4 June 1987. [Google Scholar]
- Denecke, J.; Dullenkopf, K.; Wittig, S.; Bauer, H.-J. Experimental Investigation of the Total Temperature Increase and Swirl Development in Rotating Labyrinth Seals. ASME J. Turbomach. 2005, 3, 1161–1171. [Google Scholar]
- Szymanski, A.; Dykas, S.; Wroblewski, W.; Fraczek, D. Experimental and Numerical Validation Study of the Labyrinth Seal Configurations. In Proceedings of the 12th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics ETC12, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Baek, S.I.; Ahn, J. Optimizing the Geometric Parameters of a Straight-Through Labyrinth Seal to Minimize the Leakage Flow Rate and the Discharge Coefficient. Energies 2021, 14, 705. [Google Scholar] [CrossRef]
- Eser, D.; Kazakia, J.Y. Air Flow in Cavities of Labyrinth Seals. Int. J. Eng. Sci. 1995, 33, 2309–2326. [Google Scholar] [CrossRef]
- Wein, L.; Kluge, T.; Seume, J.R.; Hain, R.; Fuchs, T.; Kähler, C.; Schmierer, R.; Herbst, F. Validation of RANS Turbulence Models for Labyrinth Seal Flows by Means of Particle Image Velocimetry. In Proceedings of the ASME Turbo/Expo, Virtual, Online, 21–25 September 2020; ASME: New York, NY, USA, 2020; Volume 10A. [Google Scholar]
- Gao, F.; Chew, J.W.; Beard, P.F.; Amirante, D.; Hills, N.J. Numerical Studies of Turbine Rim Sealing Flows on a Chute Seal Configuration. In Proceedings of the ETC 12, Stockholm, Sweden, 3–7 April 2017; Rolls-Royce Plc: Derby, UK, 2017. [Google Scholar]
- Stocker, H.L. Determining and Improving Labyrinth Seal Performance in Current and Advanced High Performance Gas Turbines. AGARD Conf. Proc. 1978, 237, 13/1–13/22. [Google Scholar]
- Wittig, S.; Jacobsen, K.; Schelling, U.; Kim, S. Heat Transfer in Stepped Labyrinth Seals. J. Eng. Gas Turbines Power 1988, 110, 63–69. [Google Scholar] [CrossRef]
- Vakili, A.D.; Meganathan, A.J.; Michaud, M.; Radhakrishnan, S. An Experimental and Numerical Study of Labyrinth Seal Flow. In Proceedings of the Turbo Expo, Reno, NV, USA, 6–9 June 2005; pp. 1121–1128. [Google Scholar]
- Joachimmiak, D.; Krzyśłak, P. Analysis of the Gas Flow in a Labyrinth Seal of Variable Pitch. J. Appl. Fluid Mech. 2019, 12, 921–930. [Google Scholar] [CrossRef]
- Hur, M.S.; Lee, S.I.; Moon, S.W.; Kim, T.S.; Kwak, J.S.; Kim, D.H.; Jung, I.Y. Effect of Clearance and Cavity Geometries on Leakage Performance of a Stepped Labyrinth Seal. Processes 2020, 8, 1496. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, C. Shape Optimization of Labyrinth Seals to Improve Sealing Performance. Aerospace 2021, 8, 92. [Google Scholar] [CrossRef]
- Kim, J.H.; Ahn, J. Large Eddy Simulation of Leakage Flow in a Stepped Labyrinth Seal. Processes 2021, 9, 2179. [Google Scholar] [CrossRef]
- Deng, S.; Wang, D.; Chen, X. Experimental Investigation of Geometry Effect on Discharge Characteristic for Stepped Labyrinth Seal. In Proceedings of the Montreal 2018 Global Power and Propulsion Forum, Montreal, QC, Canada, 7–9 May 2018. [Google Scholar]
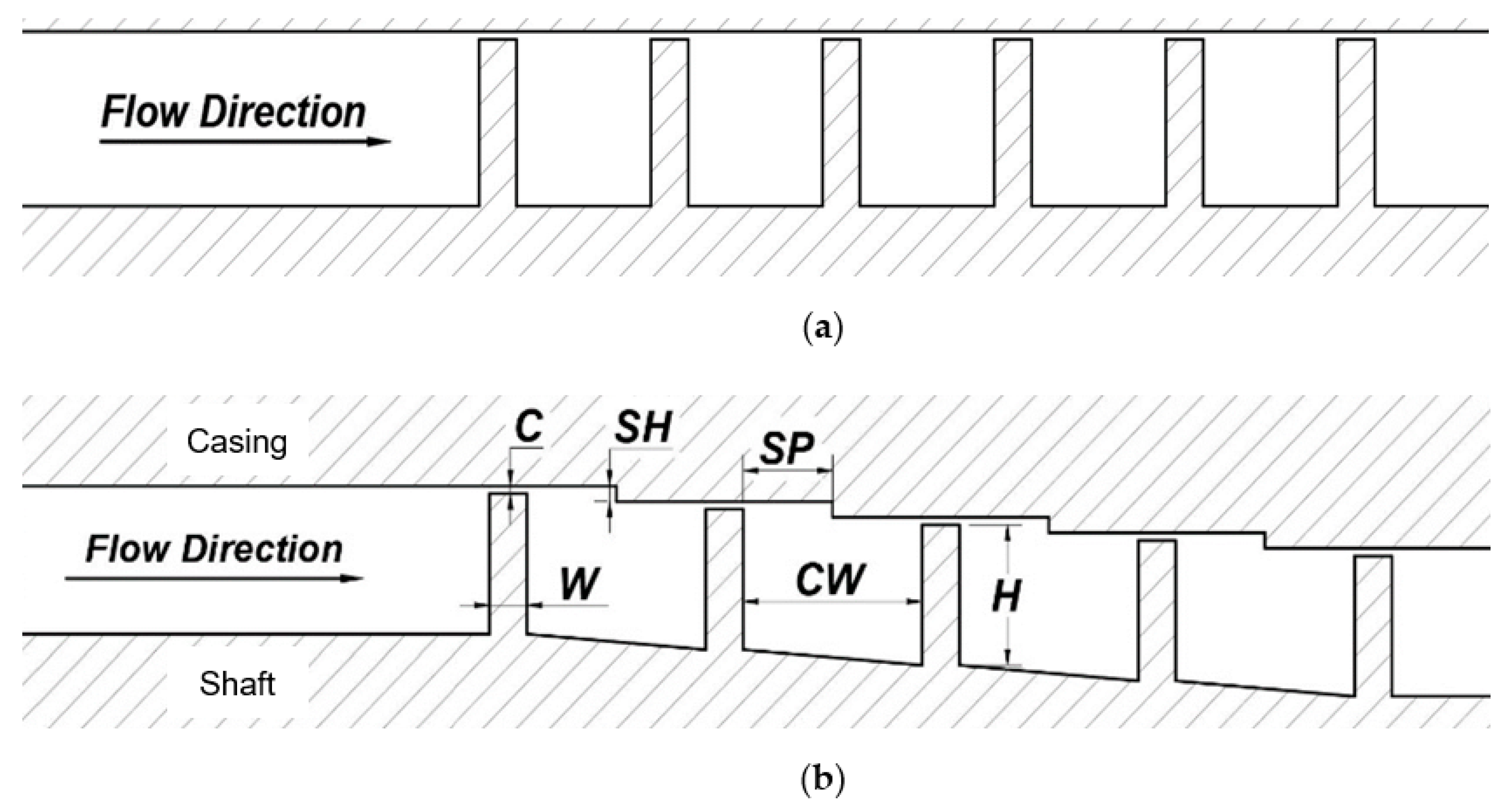
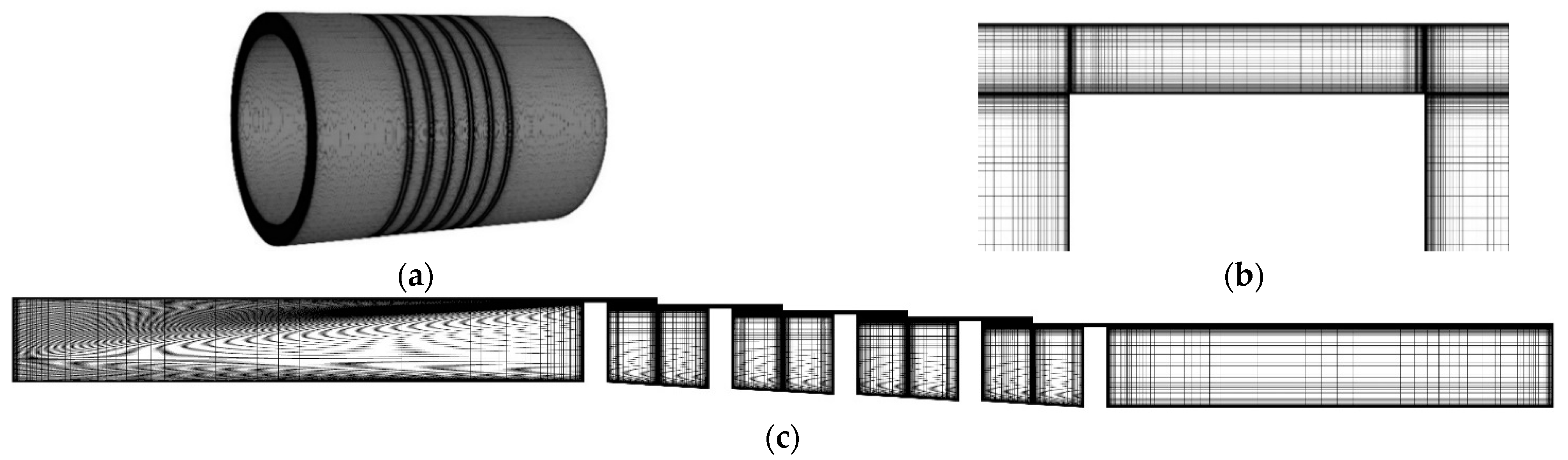
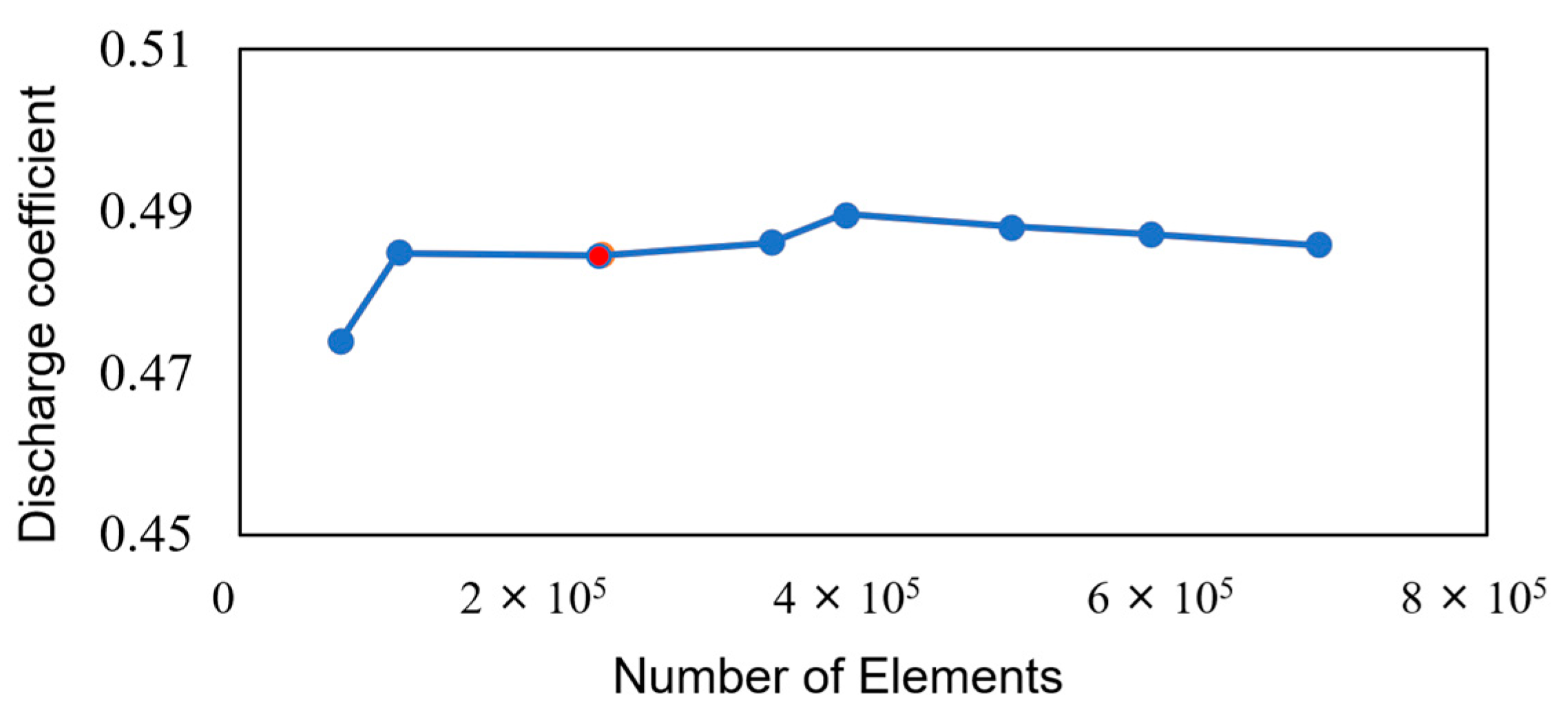
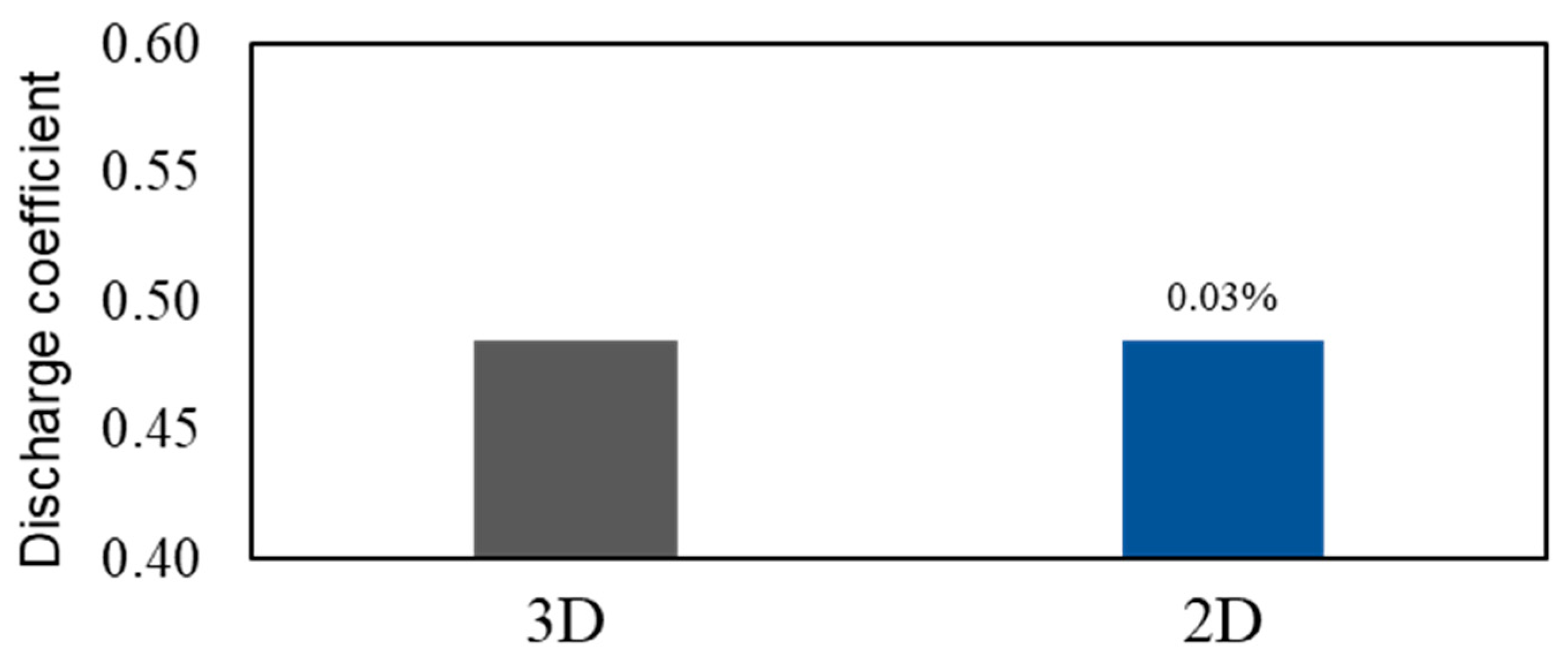
| Geometry Parameter | Straight-Through Seal [16] | Stepped Seal |
|---|---|---|
| Number of teeth (N) | 6 | 5 |
| Clearance (C) | 0.5 mm | 0.5 mm |
| Tooth width (T) | 2.5 mm | 2.5 mm |
| Tooth height (H) | 10.5 mm | 10.5 mm |
| Cavity width (CW) | 9.5 mm | 3.5–33.5 mm |
| Step height (SH) | - | 0–5.6 mm |
| Step position (SP) | - | 0.15–10.35 mm |
| Surface | Boundary Condition |
|---|---|
| Inlet | Pressure inlet, 300 K, 202,650 (Pa, absolute pressure) |
| Outlet | Pressure outlet, 300 K, 101,325 (Pa, absolute pressure) |
| Shaft | 0 RPM, adiabatic wall |
| Casing | 0 RPM, adiabatic wall |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chun, Y.H.; Ahn, J. Optimizing the Geometric Parameters of a Stepped Labyrinth Seal to Minimize the Discharge Coefficient. Processes 2022, 10, 2019. https://doi.org/10.3390/pr10102019
Chun YH, Ahn J. Optimizing the Geometric Parameters of a Stepped Labyrinth Seal to Minimize the Discharge Coefficient. Processes. 2022; 10(10):2019. https://doi.org/10.3390/pr10102019
Chicago/Turabian StyleChun, Ye Hwan, and Joon Ahn. 2022. "Optimizing the Geometric Parameters of a Stepped Labyrinth Seal to Minimize the Discharge Coefficient" Processes 10, no. 10: 2019. https://doi.org/10.3390/pr10102019
APA StyleChun, Y. H., & Ahn, J. (2022). Optimizing the Geometric Parameters of a Stepped Labyrinth Seal to Minimize the Discharge Coefficient. Processes, 10(10), 2019. https://doi.org/10.3390/pr10102019







