Three-Dimensional Dynamic Formation of Second-Order Multi-Agent System Based on Rigid Graphs
Abstract
:1. Introduction
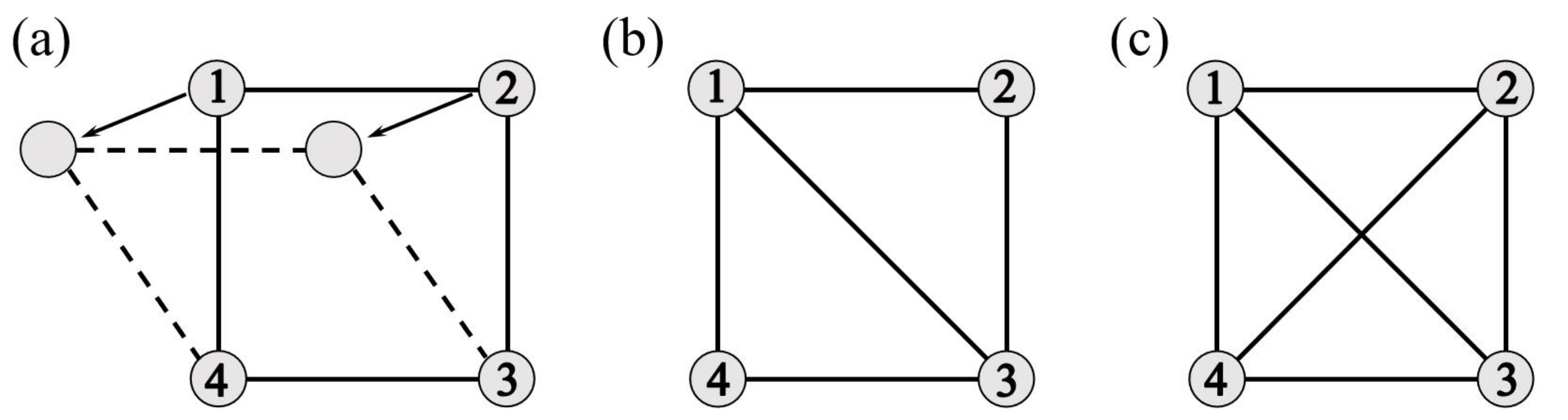
2. Notations and Basic Concepts
3. Problem Statement
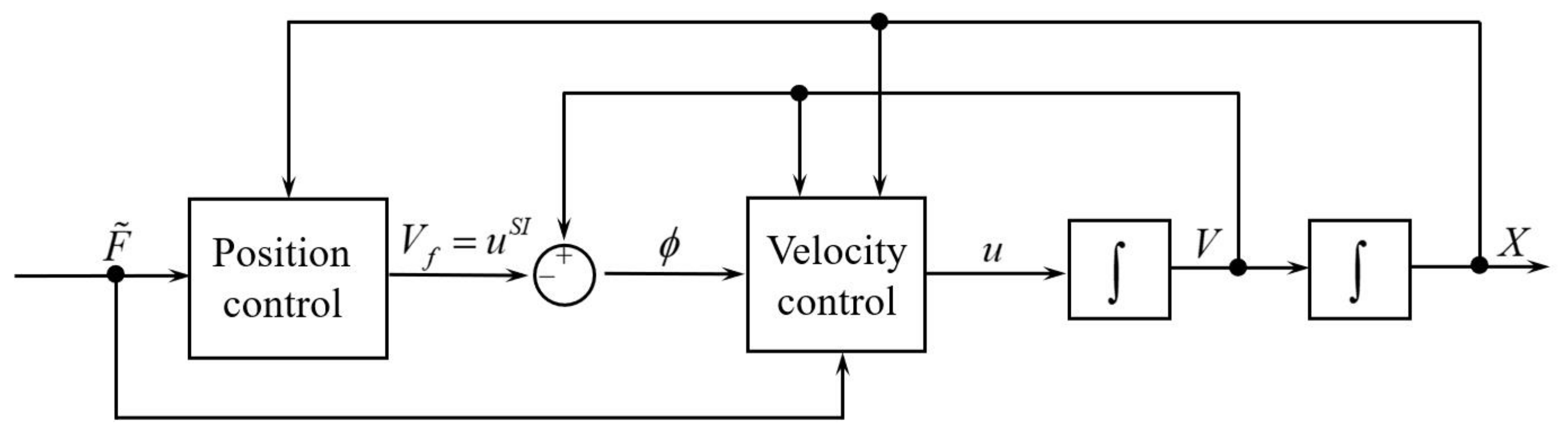
4. Design for Control Inputs
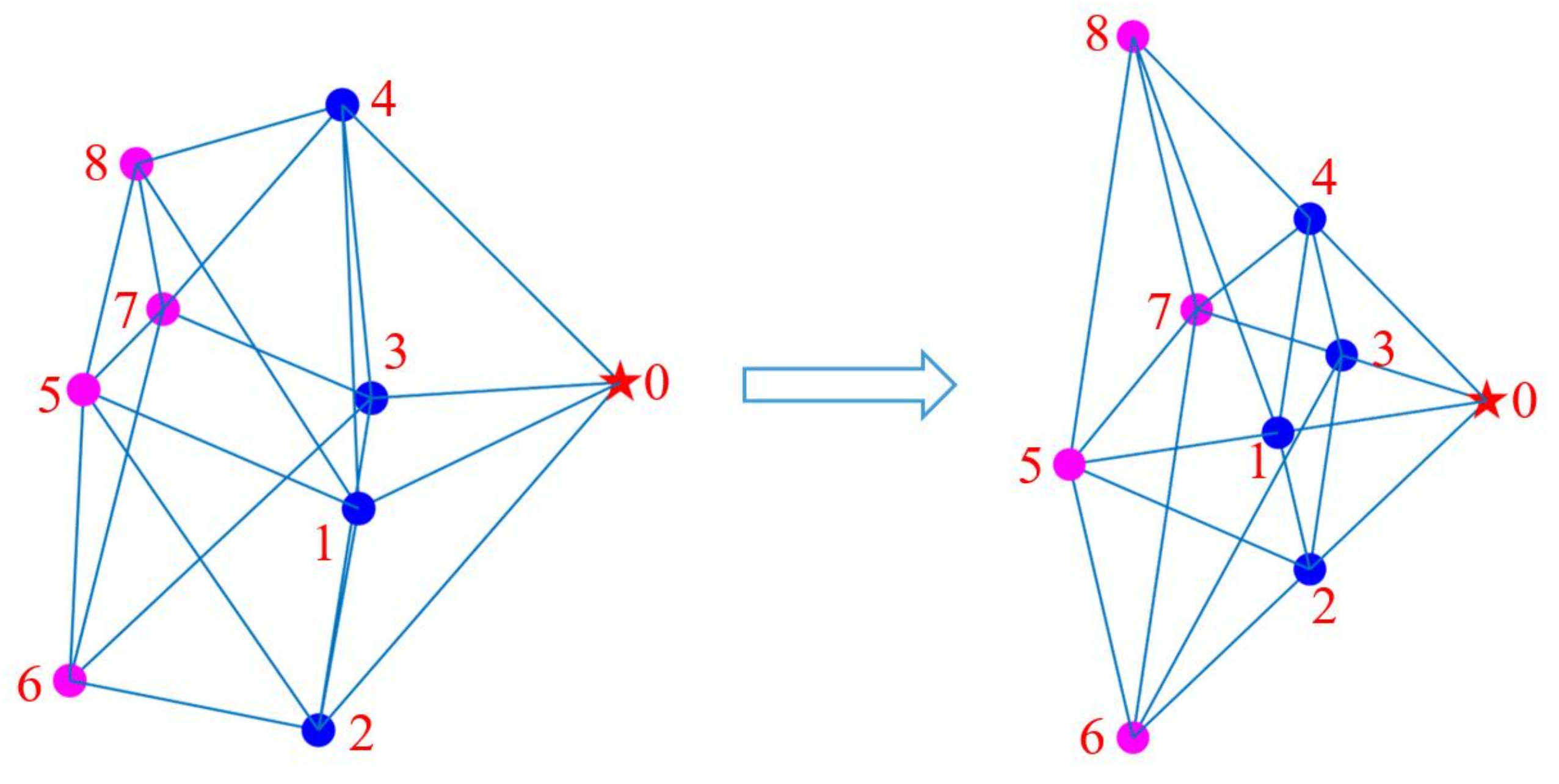
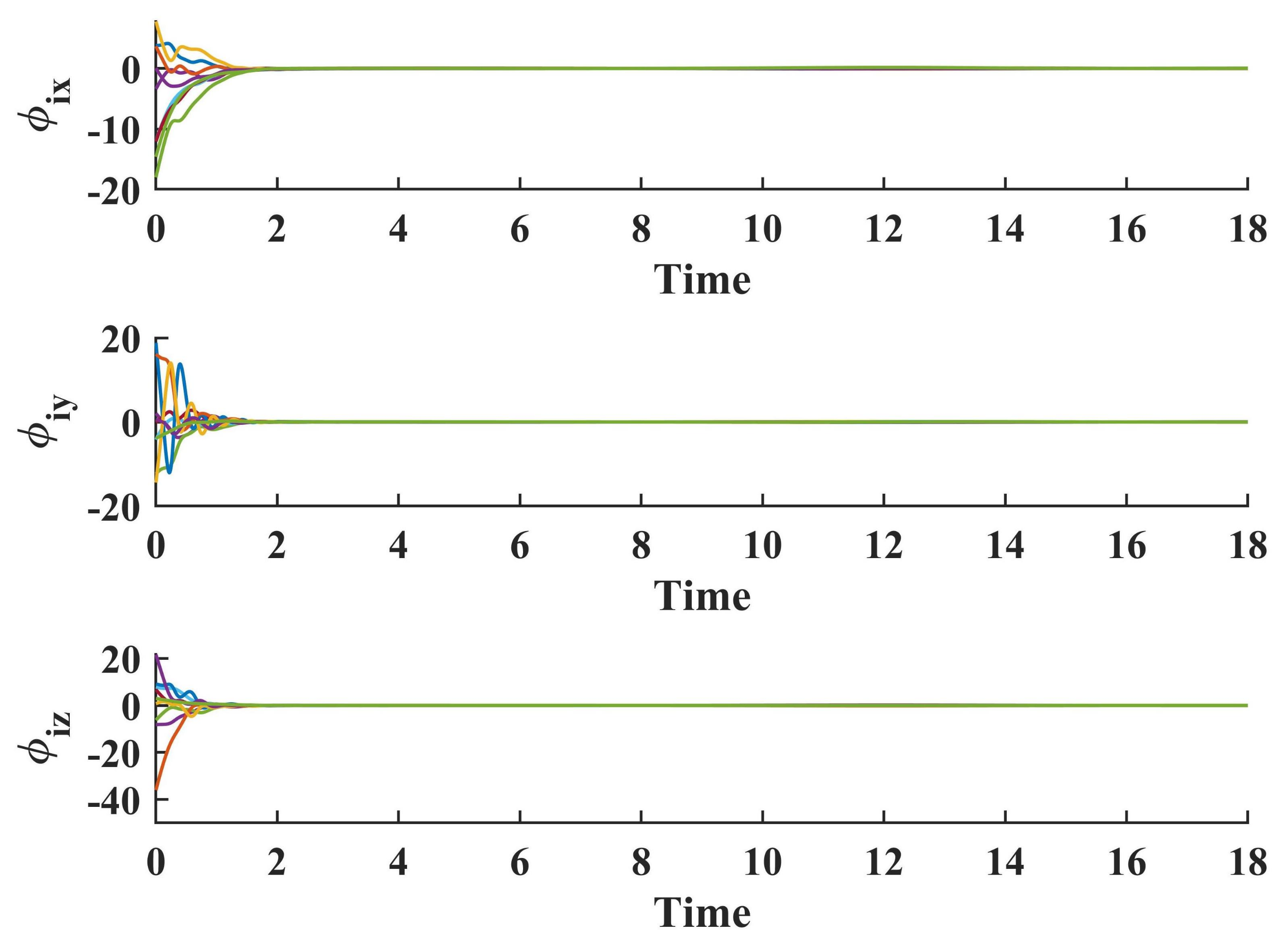
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Animasaun, I.L.; Shah, N.A.; Wakif, A.; Mahanthesh, B.; Sivaraj, R.; Koriko, O.K. Conceptual and Empirical Reviews I. In Ratio of Momentum Diffusivity to Thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization; Chapman and Hall/CRC: New York, NY, USA, 2022. [Google Scholar]
- Wen, G.; Zheng, W.X. On Constructing Multiple Lyapunov Functions for Tracking Control of Multiple Agents with Switching Topologies. IEEE Trans. Automat. Control 2019, 64, 3796–3803. [Google Scholar] [CrossRef]
- Yongzhao, H.; Xiwang, D.; Qingdong, L.; Zhang, R. Distributed Fault-Tolerant Time-Varying Formation Control for Second-Order Multi-Agent Systems with Actuator Failures and Directed Topologies. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 774–778. [Google Scholar]
- Meng, Z.; Anderson, B.; Hirche, S. Formation control with mismatched compasses. Automatica 2016, 69, 232–241. [Google Scholar] [CrossRef]
- Deng, J.; Wang, L.; Liu, Z. Attitude synchronization and rigid formation of multiple rigid bodies over proximity networks. Automatica 2018, 125, 109388. [Google Scholar]
- Olfatisaber, R.; Murray, R.M. Graph rigidity and distributed formation stabilization of multi-vehicle systems. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002. [Google Scholar]
- Krick, L.; Broucke, M.E.; Francis, B.A. Stabilization of infinitesimally rigid formations of multi-robot networks. Int. J. Control 2009, 82, 423–439. [Google Scholar] [CrossRef]
- Oh, K.K.; Ahn, H.S. Formation control of mobile agents based on inter-agent distance dynamics. Automatica 2011, 47, 2306–2312. [Google Scholar] [CrossRef]
- Cai, X.; de Queiroz, M. Multi-agent formation maneuvering and target interception with double-integrator model. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014. [Google Scholar]
- Cai, X.; de Queiroz, M. Multi-agent formation maintenance and target tracking. In Proceedings of the American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Zhang, P.; Queiroz, M.D.; Cai, X. Three-Dimensional Dynamic Formation Control of Multi-Agent Systems Using Rigid Graphs. J. Dyn. Syst. Meas. Control 2015, 137, 111006. [Google Scholar] [CrossRef]
- Deghat, M.; Anderson, B.; Lin, Z. Combined Flocking and Distance-Based Shape Control of Multi-Agent Formations. IEEE Trans. Automat. Control 2016, 61, 1824–1837. [Google Scholar] [CrossRef]
- Cai, X.; Queiroz, M.D. Rigidity-Based Stabilization of Multi-Agent Formations. J. Dyn. Syst. Meas. Control 2013, 136, 014502. [Google Scholar] [CrossRef]
- Oh, K.K.; Ahn, H.S. Distance-based undirected formations of single-integrator and double-integrator modeled agents in n-dimensional space. Int. J. Robust Nonlinear Control 2013, 24, 1809–1820. [Google Scholar] [CrossRef]
- Cao, M.; Morse, A.S.; Yu, C.; Anderson, B.; Dasgupta, S. Maintaining a Directed, Triangular Formation of Mobile Autonomous Agents. Commun. Inf. Syst. 2011, 11, 1–16. [Google Scholar]
- Park, M.C.; Anderson, B.; Sun, Z.; Ahn, H.S. Stability analysis on four agent tetrahedral formations. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2015; pp. 631–636. [Google Scholar]
- Sun, Z.; Mou, S.; Anderson, B.; Morse, A.S. Non-robustness of gradient control for 3-D undirected formations with distance mismatch. In Proceedings of the Australian Control Conference, Fremantle, WA, Australia, 4–5 November 2013. [Google Scholar]
- Babazadeh, R.; Selmic, R. Distance-Based Multiagent Formation Control with Energy Constraints Using SDRE. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 41–56. [Google Scholar] [CrossRef]
- Queiroz, M.D.; Cai, X. Formation Maneuvering and Target Interception for Multi-Agent Systems via Rigid Graphs. Asian J. Control 2015, 17, 1174–1186. [Google Scholar]
- Khaledyan, M.; Liu, T.; Queiroz, M.D. Flocking and Target Interception Control for Formations of Nonholonomic Kinematic Agents. IEEE Trans. Control Syst. Technol. 2019, 28, 1603–1610. [Google Scholar] [CrossRef] [Green Version]
- Cao, M.; Morse, A.S.; Yu, C.; Anderson, B.D.O.; Dasguvta, S. Maintaining a Directed, Triangular Formation of Mobile Autonomous Agents. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3603–3608. [Google Scholar]
- Dorfler, F.; Francis, B. Geometric Analysis of the Formation Problem for Autonomous Robots. IEEE Trans. Automat. Control 2010, 55, 2379–2384. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Distributed cooperative control of multiple vehicle formations using structural potential functions. IFAC Proc. Vol. 2002, 35, 495–500. [Google Scholar] [CrossRef]
- Sun, Z.; Park, M.-C.; Anderson, B.D.O.; Ahn, H.-S. Distributed stabilization control of rigid formations with prescribed orientation. Automatica 2017, 78, 250–257. [Google Scholar] [CrossRef]
- Anderson, B.; Yu, C.; Fidan, B.; Hendrickx, J. Rigid graph control architectures for autonomous formations. Control Syst. IEEE 2008, 28, 48–63. [Google Scholar]
- Asimow, L.; Roth, B. The rigidity of graphs, II. J. Math. Anal. Appl. 1979, 68, 171–190. [Google Scholar] [CrossRef]
- Vu, V.T.; Tran, Q.H.; Pham, T.L.; Dao, P.N. Online Actor-critic Reinforcement Learning Control for Uncertain Surface Vessel Systems with External Disturbances. Int. J. Control Autom. 2022, 20, 1029–1040. [Google Scholar] [CrossRef]
- Vu, V.T.; Pham, T.L.; Dao, P.N. Disturbance observer-based adaptive reinforcement learning for perturbed uncertain surface vessels. ISA Trans. 2022, in press. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, G.; Liu, L.; Yang, C.; Cui, Y.; Hou, K.; Liu, D.; Xue, C. Three-Dimensional Dynamic Formation of Second-Order Multi-Agent System Based on Rigid Graphs. Processes 2022, 10, 1961. https://doi.org/10.3390/pr10101961
Tian G, Liu L, Yang C, Cui Y, Hou K, Liu D, Xue C. Three-Dimensional Dynamic Formation of Second-Order Multi-Agent System Based on Rigid Graphs. Processes. 2022; 10(10):1961. https://doi.org/10.3390/pr10101961
Chicago/Turabian StyleTian, Gailing, Lu Liu, Chenyu Yang, Yu Cui, Kaiyan Hou, Dan Liu, and Chenyang Xue. 2022. "Three-Dimensional Dynamic Formation of Second-Order Multi-Agent System Based on Rigid Graphs" Processes 10, no. 10: 1961. https://doi.org/10.3390/pr10101961
APA StyleTian, G., Liu, L., Yang, C., Cui, Y., Hou, K., Liu, D., & Xue, C. (2022). Three-Dimensional Dynamic Formation of Second-Order Multi-Agent System Based on Rigid Graphs. Processes, 10(10), 1961. https://doi.org/10.3390/pr10101961





