Abstract
In this research, we investigate the influence of a load-balancing strategy and parametrization on the speed-up of discrete element method simulations using Lethe-DEM. Lethe-DEM is an open-source DEM code which uses a cell-based load-balancing strategy. We compare the computational performance of different cell-weighing strategies based on the number of particles per cell (linear and quadratic). We observe two minimums for particle to cell weights (at 3, 40 for quadratic, and 15, 50 for linear) in both linear and quadratic strategies. The first and second minimums are attributed to the suitable distribution of cell-based and particle-based functions, respectively. We use four benchmark simulations (packing, rotating drum, silo, and V blender) to investigate the computational performances of different load-balancing schemes (namely, single-step, frequent and dynamic). These benchmarks are chosen to demonstrate different scenarios that may occur in a DEM simulation. In a large-scale rotating drum simulation, which shows the systems in which particles occupy a constant region after reaching steady-state, single-step load-balancing shows the best performance. In a silo and V blender, where particles move in one direction or have a reciprocating motion, frequent and dynamic schemes are preferred. We propose an automatic load-balancing scheme (dynamic) that finds the best load-balancing steps according to the imbalance of computational load between the processes. Furthermore, we show the high computational performance of Lethe-DEM in the simulation of the packing of particles on 4800 processes. We show that simulations with optimum load-balancing need ≈40% less time compared to the simulations with no load-balancing.
1. Introduction
Granular materials are prevalent in nature and global industry [1,2,3]. Due to their abundance and wide range of applications, the study of granular flows is an active research area where multiple challenges remain unanswered [4,5]. Generally, researchers use continuum (Eulerian) or discrete (Lagrangian) approaches to model granular systems. Although computationally efficient, continuum approaches can be inaccurate because the flow of granular systems may deviate significantly from that of continuous matter [6]. The Discrete Element Method (DEM) is a Lagrangian model which simulates the motion of all the particles and their collisions with other particles and boundaries in a system [4]. Since DEM tracks every particle individually, it is more accurate than continuum-based models. This accuracy, of course, comes with a high computational cost [7].
The computational cost for the best-designed DEM codes is of the order of , where is the number of simulated particles [7,8]. This limits the number of particles in a simulation based on the available computational resources. In the last two decades, parallel computing has helped researchers simulate granular systems containing millions of particles [4,8,9,10,11,12,13]. To this end, several parallel DEM softwares using multiple central processing units (CPU) to carry-out a single simulation have been developed [5,9,12,14,15,16]. These parallel DEM softwares generally employ a single program, multiple data (SPMD) approach to parallelize the simulations. SPMD is based on spatial domain decomposition in which the simulation domain is divided between the parallel processes and communication between the processes is ensured through the Message Passing Interface (MPI) [6]. As the particles move inside the simulation domain and migrate between the subdomains, the computational load on the processes changes [10]. Migration of particles between the subdomains may lead to load imbalance, in which the computational load on the processes is significantly different. This overburdens some cores while leaving others idle and thus slows down the simulation. Load-balancing can mitigate this problem.
Load-balancing re-equalizes the computational loads by re-distributing the simulation between the processes [10]. In the DEM, load-balance is mainly interpreted as having an equal number of particles on each process [6]. Compared to Computational Fluid Dynamics (CFD) [17], less attention has been paid to load-balancing in DEM. Fleissner et al. [13,18] used an orthogonal recursive bisection domain partitioning algorithm [19] in their simulations. This algorithm recursively subdivides the simulation domain using planes and moves these planes in order to reach a homogeneous computational load [10]. LIGGGHTS uses a recursive multi-sectioning algorithm on a Cartesian simulation grid for load-balancing [20]. Cintra et al. [21,22] used a recursive coordinate bisection in a simulation of hopper discharge and landslide using the DEMOOP software. The performances of different load-balancing algorithms were compared in other works [10,11,23]. Markauskas and Kačeniauskas [23] simulated the discharge of spherical particles on 128–2048 cores and reported a speed-up of 1785 on 2048 cores. They observed that complex adaptations of the k-way graph partitioning method do not improve the parallel performance. Our work in Lethe-DEM [8], using a forest of tree approach for load-balancing, aims at solving the limitations and challenges of load-balancing in DEM simulations.
2. Problem Definition
This work focuses on the load-balancing aspects of the DEM. The fundamentals of DEM are not reviewed here. Interested readers may find the fundamentals of DEM and the details of its implementation elsewhere [8]. We use an open-source DEM software, Lethe-DEM, which is parallelized using MPI [8]. This code is based on the deal.II finite element library [24,25] and uses its particles capabilities [26]. In this code, the Hertz–Mindlin, limiting the tangential overlap and limiting the tangential force, and Hertz and Hookean contact models are implemented. In the analyses in this research, we use the Hertz–Mindlin with limiting the tangential overlap model. Lethe-DEM uses a background grid in which the particles are mapped frequently. This grid, and consequently the particles, are distributed between the processes in a parallel simulation. Lethe-DEM handles the mesh partitioning using the p4est library via deal.II [27,28]. Initially, we create a coarse triangulation (which consists of not more than 100–10,000 cells in most cases) using deal.II or GMSH [29]. Lethe-DEM replicates this triangulation on all the processes, refines it locally to reach a desired element size in a forest-of-tree manner, and partitions the final triangulation through p4est. Each subdomain in the input triangulation is assigned to a process. A halo layer of the width of a single cell surrounds each subdomain. The cells in this halo are referred to as ghost cells and the particles that reside in these ghost cells as ghost particles. In Figure 1 the concepts of distributed triangulation and subdomains, ghost cells) and ghost particles) are explained.
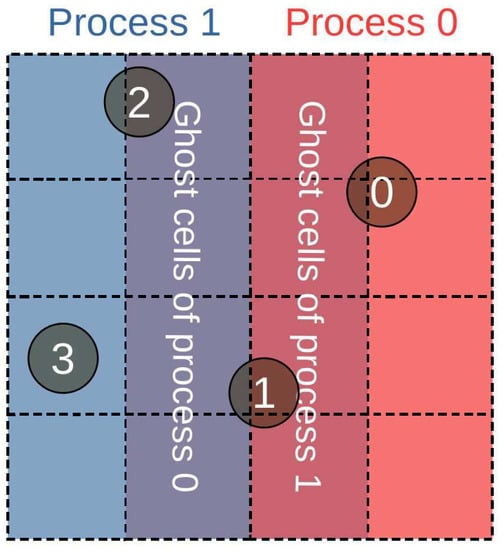
Figure 1.
A triangulation distributed between two processes (Processes 0 and 1) and four particles. The ghost cells are highlighted for each process. Particles 0 and 3 are local particles for processes 0 and 1, respectively, while particle 1 is a ghost particle of process 1 and particle 2 is a ghost particle of process 0.
According to these definitions, we categorize the particle-particle contacts into local-local and local-ghost contacts. Local-local collisions are fully handled by the process owning the particle, while in local-ghost contacts, each process only handles the calculations on the particle which is local to it. This means that calculations of local-ghost contacts are performed on the processes for which one particle is local. As the particles move in the simulation domain and change subdomain, we need three functions to: update the owner cells (and subdomain) of the particles, create and update the ghost particles, and update the properties and location of the ghost particles.
Load-balancing in Lethe-DEM is performed by assigning a weight to each cell according to its computational load and redistributing the cells between the processes such that all the processes have equal weight. The computational cost of some functions (for example, the function used to update the owner cells and subdomain) in the DEM software is proportional to , while other functions (for example, particle-wall and particle-particle contact force) have computational costs proportional to and . Because these functions have different costs, assigning a weight to each cell based on the number of particles is a complicated task. We can use different strategies to assign the cell weight. Two intuitive strategies are linear and quadratic weighting:
where and are weights of particles and cells. We investigate the performances of linear and quadratic weight models as well as the effects of and . Furthermore, load-balancing itself is an expensive operation. In other words, calling load-balancing too frequently adds extra computational cost to a simulation. Consequently, we have to call load-balancing depending on the dynamics of the granular flow. To this end, we introduce three different load-balancing schemes in Lethe-DEM:
- single-step (also referred to as once in this article): In this load-balancing strategy, we only call load-balancing once per simulation at a given iteration;
- frequent: In frequent load-balancing, the software calls load-balancing at a constant frequency (every iterations);
- dynamic: In dynamic load-balancing, the software automatically detects if load-balancing is required by measuring the load imbalance. At a predefined frequency, the software checks the computational weights of all the processes. If the weight difference between the processes with the highest and lowest loads exceeds a threshold based on the average load (if , where is a defined threshold), load-balancing is performed. L and denote the total process load (summation of the weights of the cells, in Equations (1) and (2), owned by each process) and a user-defined dynamic load-balancing threshold, respectively.
The goal of this study is to characterize and quantify the impact of both the weighting strategy as well as the load-balancing scheme. Using four benchmarks, namely:
- Packing of particles;
- A rotating drum;
- A silo;
- A V-blender.
We demonstrate that load-balancing can greatly reduce computational time even for simulations including a moving geometry. We quantify the load-balancing cost and identify the best load-balancing schemes for different types of granular flows frequently simulated with the DEM. Instead of focusing on the load-balance algorithms, which have been studied and compared in the literature [10,11,13,18,20,21,22,23,30], we study the weighting strategies and consistent load-balancing schemes in different scenarios that may occur in DEM simulations. This research is useful to the researchers interested in using the DEM simulations and of particle-based methods to optimize the computational costs of their parallel simulations. Furthermore, all the benchmarks and examples are accessible on the Lethe GitHub page (https://github.com/lethe-cfd/lethe/wiki, accessed on 21 December 2021).
3. Results and Discussion
3.1. Benchmark Cases
We use four benchmark cases. The first case is the packing of particles in a rectangular box. We use this case to compare the computational performances of linear and quadratic weights as well as the load-balancing costs of large-scale simulations. The second case is the granular flow in a rotating drum. This is an example of the cases in which particles reside in a constant region of the simulation domain after the flow has reached pseudo steady-state. In the third case, we simulate the motion of particles during a silo discharge. This simulation is an example of cases in which the particles move in one direction inside the simulation domain. The last case is a V blender in which particles have a continuous reciprocating motion. We specify the physical properties in Table 1 by using the experimental research in the literature [31,32], and interested readers can find the parameter handler files of these simulations in the examples section of the Lethe Github repository: https://github.com/lethe-cfd/lethe, (accessed on 21 December 2021). Figure 2 illustrates the simulation geometries and configurations.

Table 1.
Simulation and physical properties of the packing in rectangular box, rotating drum, silo and V-blender simulations.
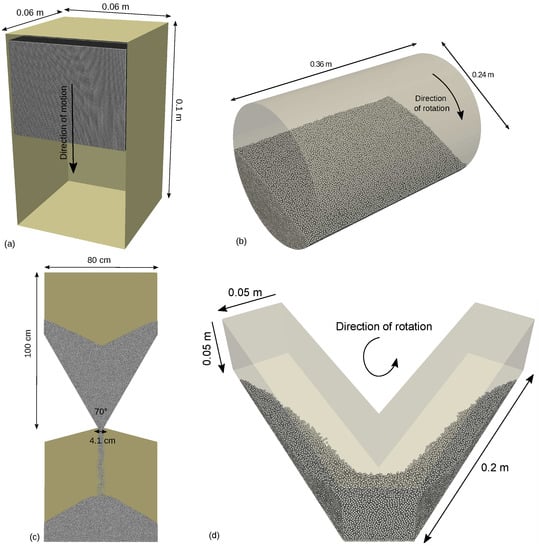
Figure 2.
Configurations of the benchmark cases used in this work: (a) packing of particles in a rectangular box, (b) rotating drum [32], (c) silo filling and discharge [31], (d) V blender.
3.2. Influence of the Weighting Strategy (Linear and Quadratic)
We compare the simulation times of the packing case with particles with a linear and quadratic load-balancing weighting strategy. We compare the simulation times at different ratios of . We select the range of 1–100 for where the former value (1) corresponds to the situation in which the weight of owned cells is equal to the weight of owned particles (in favor of the number of cells), and the latter value (100) belongs to the situation where the weight of owned cells is almost negligible compared to that of the particles. We use frequent load-balancing with , and repeat each simulation three times and report the average simulation time. Figure 3 shows the results of this comparison. Both linear and quadratic weighting strategies show the decreasing-increasing-decreasing-increasing trends. The linear weighting strategy shows two minimums at and 50, and the quadratic weighting strategy shows two minimums at and 40. The first minimums are attributed to the suitable distribution of cell-based functions, and the second minimums are attributed to the appropriate distribution of particle-based functions over the processes. The global minimum occurs at for linear load-balancing.
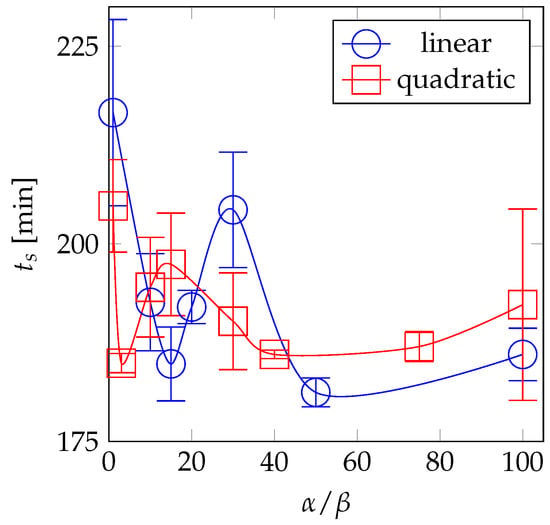
Figure 3.
Influence of the load balancing strategy on the simulation time for the packing case. Error bars show standard deviation.
3.3. Packing in Box
Figure 4a shows the comparison between the load-balancing times (for a single load-balancing operation) of four packing simulations in Table 1. We do not compare the simulation times of these simulations since we have performed strong and weak scaling analyses of Lethe-DEM in previous research [8]. We perform the simulations of the packing of , , , and particles on 8, 48, 480, and 4800 processes, respectively ( 20,000). This figure shows that the cost of load-balancing increases as the number of particles increases in a simulation. Figure 4b shows the load-balancing times (for a single load-balancing operation) for the simulation of packing of particles on 32, 64, 96 and 128 processes. The cost of load-balancing decreases as the number of processes increases in the simulation. This decrease is super-linear. This indicates that the cost of load-balancing does not scale linearly with the number of particles per core. Consequently, load-balancing becomes more and more viable as the number of cores is increased.
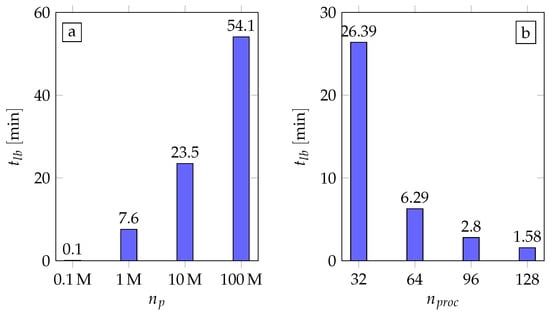
Figure 4.
Required time to perform a single load-balancing for simulations of packing of (a) , , , and particles on 8, 48, 480, and 4800 processes, and (b) particles on 32, 64, 96, and 128 processes.
Figure 5 shows the simulation times of the packing of particles on 64 processes with frequent load-balancing (, 20, 100, 200 and ). The total simulation time decreases from to , and then increases as the load-balancing frequency increases. Not only the total cost of load-balancing increases with increasing the load-balancing frequency, it also shows that more frequent load-balancing cannot decrease the simulation time. This happens because some operations, such as the mapping of particles into subdomains and cells and the updating of the ghost particles has to be performed right after each load-balancing step. These operations add an extra computational cost to the total simulation time. In summary, we conclude that the time required to load-balance is non-negligible, especially for large-scale systems or a small number of processes and does not scale well with the number of particles and cells. As a result, we have to avoid any non-necessary load-balancing in the simulations. Indeed, for a larger number of particles, load balancing can become prohibitively expensive.
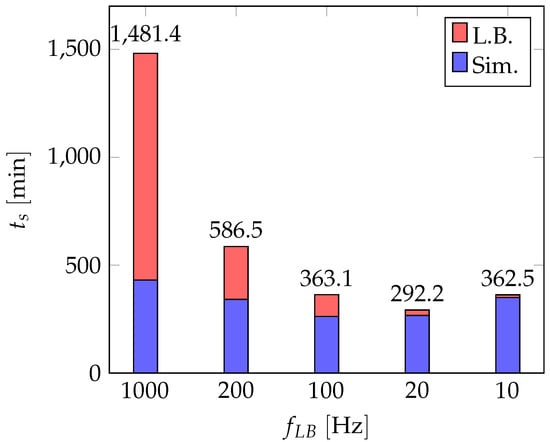
Figure 5.
Simulation times of the packing of particles benchmark on 64 processes with frequent load-balancing at , 20, 100, 200 and . Load-balancing time is illustrated using the red color.
Figure 6 shows screenshots of packing simulations of , , , particles on 8, 48, 480, and 4800 processes at . Interested readers may find an animation of the simulation of particles in the supplementary materials Video S1 (packing.mp4). As the particles move towards the bottom wall of the rectangular box, load-balancing moves the subdomain of processes with the bulk of the particles to equalize the computational load on each process. Finally, one process handles the majority of the cells on top of the particle bed, while the rest of the processes are distributed evenly amongst the cells located in the bed of particles. Since 10,000 time-steps exist between two consecutive load-balance steps (), load-balancing compensates its computational cost by increasing the speed of the DEM throughout the simulations. Consequently, a trade-off exists between the load-balancing time and the time it saves.
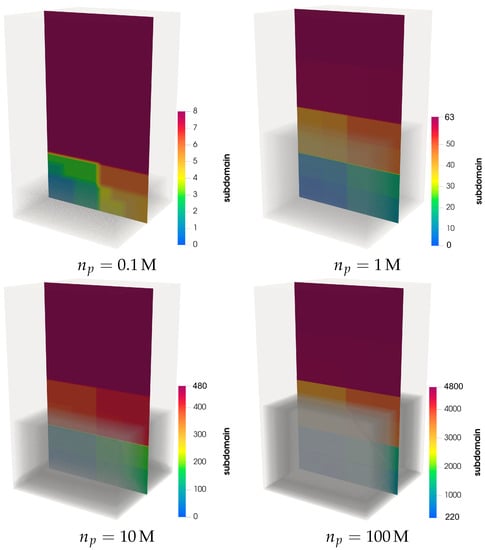
Figure 6.
Simulation screenshots of packing of , , , particles on 8, 48, 480, and 4800 processes at .
3.4. Rotating Drum
We performed the rotating drum simulation with three load-balancing strategies: single-step load-balancing at , frequent load-balancing with , and dynamic load-balancing with and . Since the system reaches the steady-state at approximately , we call load-balancing at when using the single-step scheme. The simulation with the frequent scheme calls the load-balancing 100 times during the simulation, while the simulation with the dynamic scheme calls load-balancing eight times. Figure 7 shows the distribution of subdomains before (at ) and after (at ) load-balancing. This distribution does not significantly change after , when the granular flow reaches pseudo steady-state.
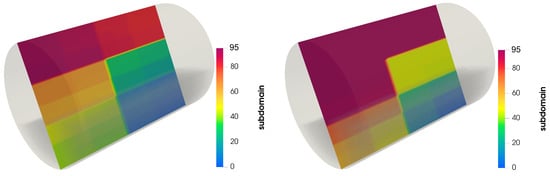
Figure 7.
Distribution of particles and subdomains in the simulation of a rotating drum on 64 processes. (left): before load-balancing at , and (right): after load-balancing at .
Figure 8 shows the simulation times (including load-balancing time) with different load-balancing schemes. The simulation times without load-balancing, with single-step, frequent, and dynamic load-balancing schemes are 1337, 894.1, 762.4, and 868.3 min, respectively. These results show that frequent load balancing leads to a lower simulation time than the alternative strategy. However, these simulations include a small number of particles () for which the load balancing cost is small. According to the trends in Figure 4 and Figure 5, for a similar simulation but with a higher particle count, minimizing the number of load-balancing operations using the single-step or dynamic strategy yields better results than frequent load-balancing. In general, at a small number of particles, cores and cells dynamic load-balancing is the most efficient scheme, while at a large number of particles (), cores and cells, single-step load-balancing is preferred for rotating drum simulations. Interested readers can find the animation of this simulation in the supplementary materials Video S2 (drum.mp4).
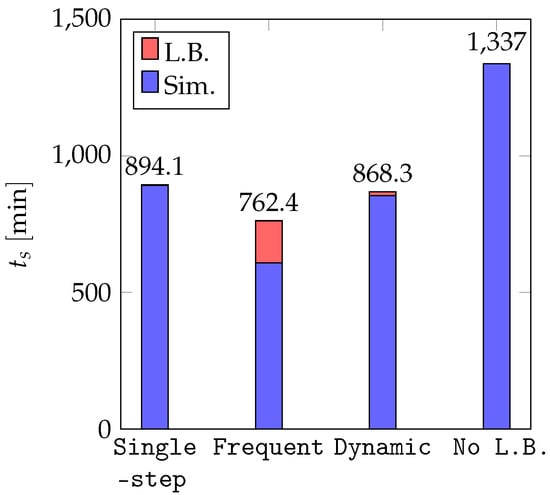
Figure 8.
Simulation times of the rotating drum benchmark with different load-balancing schemes. Load-balancing time is illustrated using the red color.
3.5. Silo
In the silo simulation, particles are packed on top of a stopper in the filling phase. Then in the discharge phase, the stopper is removed and particles leave the hopper and move into the bottom container. Figure 9 shows the distribution of subdomains and particles in the silo simulation. Interested readers may find an animation of the silo simulation in the supplementary materials Video S3 (silo.mp4). At the beginning of the filling phase (), the particles and all the subdomains of processes except process 0 are in the hopper. As the discharge phase begins and particles leave the hopper, the simulation moves the subdomain of processes towards the bottom container. When all the particles completely leave the hopper (), all the particles and subdomains are located in the bottom of the geometry and one single process handles the hopper.
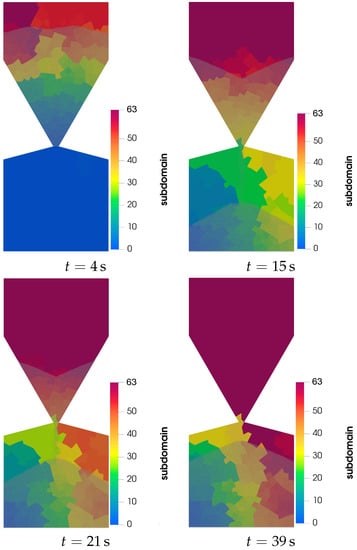
Figure 9.
Distribution of subdomains and particles in the simulation of silo on 64 processes with .
Using the single-step load-balancing for this simulation is meaningless. Figure 10 shows the simulation times (including load-balancing time) without and with frequent and dynamic load-balancing schemes. Figure 10 shows the simulation times of the silo simulation with no load-balancing, and with frequent and dynamic load-balancing schemes. Frequent (with ) and dynamic schemes (with and a threshold of 0.8) call load-balancing 40 and 35 times, respectively, throughout this simulation. The simulation times are 154.1, 96.2 and 98.8 hours for no load-balancing, frequent and dynamic schemes, respectively. Load-balancing times are negligible compared to the total simulation time for this small-scale simulation (). The dynamic scheme does not call load-balancing when the particles get packed on top of the stopper and in the bottom of the container (when the load-balancing is not necessary). Silo simulation results show that in systems where the particles move in one direction, frequent and dynamic load-balancing show the best computational performance.
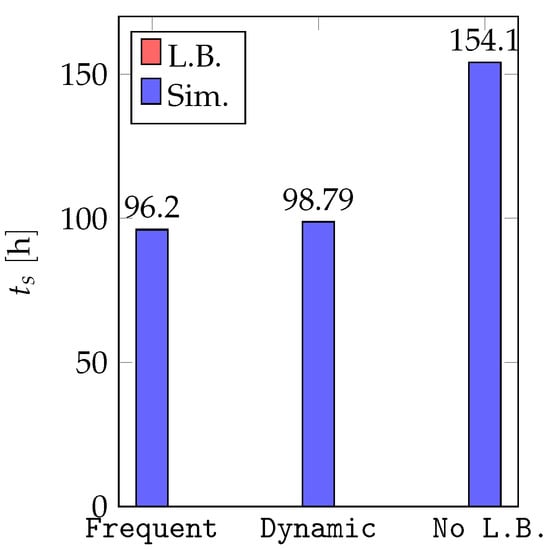
Figure 10.
Simulation times of the silo benchmark without and with dynamic and frequent load-balancing schemes.
3.6. V Blender
In a V blender, particles have a reciprocating motion. Similar to the silo, using a single-step load-balancing is meaningless here. We simulate the V blender with frequent (with ) and dynamic (with and ) load-balancing schemes. Frequent and dynamic schemes call load-balancing 200 and 192 times, respectively. Figure 11 shows the distribution of the subdomains during the simulation on 64 processes with the frequent load-balancing scheme. Interested readers may find an animation of this simulation in the supplementary materials Video S4 (VBlender.mp4). Particles continuously move inside the V blender. As a result, frequent and dynamic load-balancing schemes are required to obtain the best performance in such systems. The simulations without load-balancing, and with frequent and dynamic schemes, take 3402.6, 2536.1, and 2325.1 min, respectively. In systems with reciprocating granular flow, dynamic and frequent schemes show the best performance.
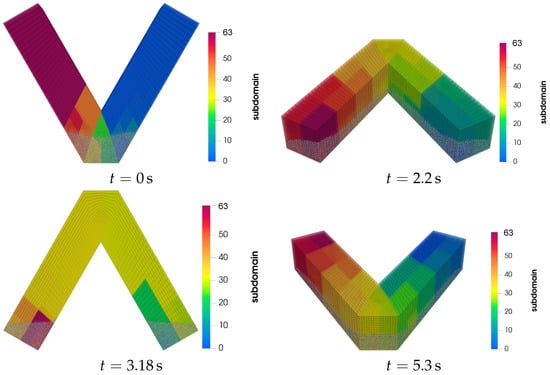
Figure 11.
Distribution of subdomains and position of particles during the simulation of V blender on 64 processes with frequent scheme.
4. Conclusions
In this research, we compared the computational performances of linear and quadratic load-balancing weighting strategies as well as three different load-balancing schemes. Linear and quadratic strategies showed two minimums in the computational cost at particle weigh to cell weigh of 15, 50 and 3, 40, respectively. The first minimum is attributed to cell-based functions, while the second minimum is attributed to particle-based functions. We compared the load-balancing times in packing simulations. We observed that increasing the number of particles and cells and decreasing the number of processes in a simulation increases the load-balancing cost. As a result, we should avoid any non-necessary load-balancing in large-scale simulations. Afterwards, we evaluated the performances of different load-balancing schemes, namely single-step, frequent and dynamic, in systems with different behaviors. We observed that in large-scale systems in which particles reside in a constant region after reaching steady-state (for instance, the rotating drum), single-step load-balancing shows the best performance. In the simulations where particles move in one direction (for example, the silo) or where particles have a reciprocating motion (for example, the V blender) frequent and dynamic load-balancing schemes are favorable. Dynamic load-balancing is a scheme that calls load-balancing according to the imbalance between the computational load on the processes. Using dynamic load-balancing, we can avoid unnecessary load-balancing operations. In the packing simulation, we were able to simulate the packing of particles on 4800 processes, which shows the high computational performance of Lethe-DEM. On average, the computational cost of simulations with optimum load-balancing is 60% of simulations without load-balancing.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/pr10010079/s1, Video S1: packing.mp4, Video S2: drum.mp4, Video S3: silo.mp4, Video S4: VBlender.mp4.
Author Contributions
S.G.: Data curation, Formal analysis, Investigation, Software, Validation, Methodology, Visualization, Writing—original draft; B.B.: Funding acquisition, Software, Validation, Methodology, Project administration, Resources, Supervision, Writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This project was partially funded by the Natural Sciences and Engineering Research Council via NSERC Grant RGPIN-2020-04510.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Lethe-DEM is an open source DEM software available on GitHub https://github.com/lethe-cfd/lethe, (accessed on 21 December 2021).
Acknowledgments
The authors would like to acknowledge support received by the deal.II community. The authors would like to acknowledge the support received from Calcul Québec and Compute Canada. Computations shown in this work were made on the supercomputer Beluga, Cedar and Graham managed by Calcul Québec and Compute Canada. The operation of these supercomputers is funded by the Canada Foundation for Innovation (CFI), the ministère de l’Économie, de la science et de l’innovation du Québec (MESI) and the Fonds de recherche du Québec—Nature et technologies (FRQ-NT).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Particle diameter | |
| Time-step | |
| e | Coefficient of restitution |
| Load-balancing frequency | |
| L | Total computational load of a process |
| Number of cells | |
| Number of particles | |
| Number of processes | |
| t | Time |
| Simulation time | |
| Load-balancing time | |
| Simulation time | |
| Cell weight | |
| Y | Young’s modulus |
| Greek letters | |
| Particle weight | |
| Cell weight | |
| Dynamic load-balancing threshold | |
| Coefficient of friction | |
| Coefficient of rolling friction | |
| Density of particle | |
| Poisson’s ratio |
References
- Richard, P.; Nicodemi, M.; Delannay, R.; Ribiere, P.; Bideau, D. Slow relaxation and compaction of granular systems. Nat. Mater. 2005, 4, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Ketterhagen, W.R.; am Ende, M.T.; Hancock, B.C. Process modeling in the pharmaceutical industry using the discrete element method. J. Pharm. Sci. 2009, 98, 442–470. [Google Scholar] [CrossRef]
- Boac, J.M.; Ambrose, R.K.; Casada, M.E.; Maghirang, R.G.; Maier, D.E. Applications of discrete element method in modeling of grain postharvest operations. Food Eng. Rev. 2014, 6, 128–149. [Google Scholar] [CrossRef] [Green Version]
- Blais, B.; Vidal, D.; Bertrand, F.; Patience, G.S.; Chaouki, J. Experimental methods in chemical engineering: Discrete element method—DEM. Can. J. Chem. Eng. 2019, 97, 1964–1973. [Google Scholar] [CrossRef]
- Golshan, S.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N.; Blais, B.; Kuipers, J. Review and implementation of CFD-DEM applied to chemical process systems. Chem. Eng. Sci. 2020, 221, 115646. [Google Scholar] [CrossRef]
- Sawley, M.L.; Cleary, P.W. A parallel discrete element method for industrial granular flow simulations. EPFL Supercomput. Rev. 1999, 11, 23–29. [Google Scholar]
- Norouzi, H.R.; Zarghami, R.; Sotudeh-Gharebagh, R.; Mostoufi, N. Coupled CFD-DEM Modeling: Formulation, Implementation and Application to Multiphase Flows; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Golshan, S.; Munch, P.; Gassmoller, R.; Kronbichler, M.; Blais, B. Lethe-DEM: An open-source parallel discrete element solver with load balancing. arXiv 2021, arXiv:2106.09576. [Google Scholar]
- Norouzi, H.; Zarghami, R.; Mostoufi, N. New hybrid CPU-GPU solver for CFD-DEM simulation of fluidized beds. Powder Technol. 2017, 316, 233–244. [Google Scholar] [CrossRef]
- Eibl, S.; Rüde, U. A systematic comparison of runtime load balancing algorithms for massively parallel rigid particle dynamics. Comput. Phys. Commun. 2019, 244, 76–85. [Google Scholar] [CrossRef] [Green Version]
- Rettinger, C.; Rüde, U. Dynamic load balancing techniques for particulate flow simulations. Computation 2019, 7, 9. [Google Scholar] [CrossRef] [Green Version]
- Tsuzuki, S.; Aoki, T. Large-scale granular simulations using Dynamic load balance on a GPU supercomputer. In Proceedings of the Poster at the 26th IEEE/ACM International Conference on High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014. [Google Scholar]
- Fleissner, F.; Eberhard, P. Load balanced parallel simulation of particle-fluid dem-sph systems with moving boundaries. Parallel Comput. Archit. Algorithms Appl. 2007, 48, 37–44. [Google Scholar]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD–DEM. Prog. Comput. Fluid Dyn. Int. J. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Weinhart, T.; Orefice, L.; Post, M.; van Schrojenstein Lantman, M.P.; Denissen, I.F.; Tunuguntla, D.R.; Tsang, J.; Cheng, H.; Shaheen, M.Y.; Shi, H.; et al. Fast, flexible particle simulations—An introduction to MercuryDPM. Comput. Phys. Commun. 2020, 249, 107129. [Google Scholar] [CrossRef]
- Forgber, T.; Toson, P.; Madlmeir, S.; Kureck, H.; Khinast, J.G.; Jajcevic, D. Extended validation and verification of XPS/AVL-Fire™, a computational CFD-DEM software platform. Powder Technol. 2020, 361, 880–893. [Google Scholar] [CrossRef]
- Blais, B.; Barbeau, L.; Bibeau, V.; Gauvin, S.; El Geitani, T.; Golshan, S.; Kamble, R.; Mikahori, G.; Chaouki, J. Lethe: An open-source parallel high-order adaptative CFD solver for incompressible flows. SoftwareX 2020, 12, 100579. [Google Scholar] [CrossRef]
- Fleissner, F.; Eberhard, P. Parallel load-balanced simulation for short-range interaction particle methods with hierarchical particle grouping based on orthogonal recursive bisection. Int. J. Numer. Methods Eng. 2008, 74, 531–553. [Google Scholar] [CrossRef]
- Warren, M.S.; Salmon, J.K. A parallel hashed oct-tree n-body algorithm. In Proceedings of the 1993 ACM/IEEE Conference on Supercomputing, Portland, OR, USA, 19 November 1993; pp. 12–21. [Google Scholar]
- Berger, R.; Kloss, C.; Kohlmeyer, A.; Pirker, S. Hybrid parallelization of the LIGGGHTS open-source DEM code. Powder Technol. 2015, 278, 234–247. [Google Scholar] [CrossRef]
- Cintra, D.T.; Willmersdorf, R.B.; Lyra, P.R.M.; Lira, W.W.M. A hybrid parallel DEM approach with workload balancing based on HSFC. Eng. Comput. 2016, 33, 2264–2287. [Google Scholar] [CrossRef]
- Cintra, D.T.; Willmersdorf, R.B.; Lyra, P.R.M.; Lira, W.W.M. A parallel DEM approach with memory access optimization using HSFC. Eng. Comput. 2016, 33, 2463–2488. [Google Scholar] [CrossRef]
- Markauskas, D.; Kačeniauskas, A. The comparison of two domain repartitioning methods used for parallel discrete element computations of the hopper discharge. Adv. Eng. Softw. 2015, 84, 68–76. [Google Scholar] [CrossRef]
- Arndt, D.; Bangerth, W.; Blais, B.; Clevenger, T.C.; Fehling, M.; Grayver, A.V.; Heister, T.; Heltai, L.; Kronbichler, M.; Maier, M.; et al. The deal. II library, version 9.2. J. Numer. Math. 2020, 28, 131–146. [Google Scholar] [CrossRef]
- Arndt, D.; Bangerth, W.; Blais, B.; Fehling, M.; Gassmöller, R.; Heister, T.; Heltai, L.; Köcher, U.; Kronbichler, M.; Maier, M.; et al. The deal. II library, version 9.3. J. Numer. Math. 2021, 29, 171–186. [Google Scholar] [CrossRef]
- Gassmöller, R.; Lokavarapu, H.; Heien, E.; Puckett, E.G.; Bangerth, W. Flexible and scalable particle-in-cell methods with adaptive mesh refinement for geodynamic computations. Geochem. Geophys. Geosystems 2018, 19, 3596–3604. [Google Scholar] [CrossRef]
- Burstedde, C.; Wilcox, L.C.; Ghattas, O. p4est: Scalable algorithms for parallel adaptive mesh refinement on forests of octrees. SIAM J. Sci. Comput. 2011, 33, 1103–1133. [Google Scholar] [CrossRef] [Green Version]
- Bangerth, W.; Burstedde, C.; Heister, T.; Kronbichler, M. Algorithms and Data Structures for Massively Parallel Generic Adaptive Finite Element Codes. Acm Trans. Math. Softw. 2012, 38, 1–38. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Owen, D.; Feng, Y.; Han, K.; Peric, D. Dynamic domain decomposition and load balancing in parallel simulation of finite/discrete elements. In Proceedings of the ECCOMAS 2000, Barcelona, Spain, 11–14 September 2000. [Google Scholar]
- Golshan, S.; Esgandari, B.; Zarghami, R.; Blais, B.; Saleh, K. Experimental and DEM studies of velocity profiles and residence time distribution of non-spherical particles in silos. Powder Technol. 2020, 373, 510–521. [Google Scholar] [CrossRef]
- Alizadeh, E.; Dubé, O.; Bertrand, F.; Chaouki, J. Characterization of mixing and size segregation in a rotating drum by a particle tracking method. AIChE J. 2013, 59, 1894–1905. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).