Abstract
The digital era introduces a significant issue concerning the preservation of individuals’ privacy. Each individual has two autonomous traits, privacy concern which indicates how anxious that person is about preserving privacy, and privacy behavior which refers to the actual actions the individual takes to preserve privacy. The significant gap between these two traits is called the privacy paradox. While the existence and the extensive distribution of the privacy paradox is widely-considered in both academic and public discussion, no convincing explanation of the phenomenon has been provided. In this study we harness a new mathematical approach, “soft logic,” to better represent the reality of the privacy paradox. Soft numbers extend zero from a singularity to an infinite one-dimensional axis, thus enabling the representation of contradictory situations that exist simultaneously, i.e., a paradox. We develop a mathematical model for representing the privacy paradox with soft numbers, and demonstrate its application empirically. This new theory has the potential to address domains that mix soft human reality with robust technological reality.
1. Introduction
We currently live in the “digital era” or “age of information,” in which a significant portion of our activities, perhaps a majority of them, have transitioned onto digital platforms [1]. This transition is increasing incessantly, as the use of digital platforms, mainly the Internet, continues to expand [2,3]. However, while digital means are highly beneficial for their users, they also introduce significant risks of privacy loss. For example, sensitive personal information is often disclosed when using e-commerce [4], using of Internet of Things (IoT) applications may expose habits and daily routines [5,6], and eHealth wearable technologies may also leak sensitive information [7,8]. The right to privacy is considered essential for a liberal society, and is described as a basic human right [9,10]. Privacy protection is regulated by governments, e.g., the EU’s (European Union) General Data Protection Regulation (GDPR) [11], and the USA Health Insurance Portability and Accountability Act (HIPAA) [12].
The growing use of digital platforms intensifies privacy awareness among users [13], and shapes their decisions [14]. This phenomenon is driven by the natural existence of privacy concern [15]. “Privacy concern” (or “privacy attitude”) may be defined as “concern about the safeguarding and usage of personal data provided to an entity (such as a firm)” or “anxiety or sensitivity related to the loss of personal intimacy” [16]. Privacy concerns appear in the vast majority of digital fields, e.g., when shopping online [17], using electronic medical records in the healthcare sector [18], using online social networks like Facebook [19], searching the Internet using search engines like Google [20], and using mobile applications [21]. The last example, use of mobile application, has attracted extensive public attention lately because of attempts to curtail the COVID-19 pandemic by using Bluetooth and GPS location spotting for surveillance of the public [22].
Privacy concerns, in turn, influence users’ actions, resulting in their privacy behavior, which may be defined as the way privacy protection or risk of privacy violations alter users’ behavior [23]. As with privacy concern, privacy behavior is relevant to the vast majority of digital platforms. For example, setting privacy preferences of Facebook or other social networks [24], customers’ trust in an eCommerce platform that results in their consent to complete a transaction [4], the consideration of privacy concerns when installing (or not) some mobile applications [25], the amount of personal information disclosed on the Internet [26], and the willingness to purchase an IoT device [27].
Privacy behavior then, is, or should be, a consequence of privacy concern, and one might expect that a user’s privacy behavior would reflect their privacy concern. In fact, however, this is not necessarily so; this is the phenomenon widely-known as the “privacy paradox.” This term was first coined in 2001 by Barry Brown, a Hewlett-Packard employee, regarding customers’ use of supermarket loyalty cards in ways that contradict their privacy concern [28]. In general, “privacy paradox” refers to contradictions between privacy behavior and privacy concern, or the ways in which privacy behavior deviates from privacy concern. Susan Barnes [29] claimed, “In America, we live in a paradoxical world of privacy. On one hand, teenagers reveal their intimate thoughts and behaviors online and, on the other hand, government agencies and marketers are collecting personal data about us.” Another example for the privacy paradox is that consumers freely provide personal data despite their complaints and concerns regarding their ability to control their personal information in the digital marketplace [30]. With respect to the general population, it was found that most users of online platforms rarely make efforts to protect their data, despite considering privacy an important issue; sometimes, they even give information away voluntarily [31]. In the digital era, information sharing has become a prevalent activity, and surveys show low correlation between individuals’ self-stated privacy concerns and their number of data-sharing authorizations [32]. Mobile Health (mHealth) applications that use mobile devices to support the practice of medicine and public health is another domain in which the privacy paradox is observed. There is conflict between growing privacy concerns and the inherent need of mHealth application to collect personal data [33]. The privacy paradox phenomenon is also evident with smart wearables, considering the tension between the benefits of this technology and their cost in privacy loss [34]. In general, ignoring the privacy paradox may be an indicator of neglecting the human factor, specifically cognition in digital systems environment. When a system is fully automated, cognition usual does not play a role. However, when a human user is involved, for example when manually configuring privacy preferences, cognition may affect decision making, and therefore must be considered within the model [35].
Many attempts have been made to explain the privacy paradox. For example, by applying the privacy calculus theory, which argues that users make decisions on privacy issues by weighing the benefits vs. the risk of disclosing personal or sensitive information [36]. However, most users overweigh benefits rather than risks, sometimes even if they have experienced an invasion of privacy [37]. Some researches argue that users’ decisions are an outcome of both rational and emotional mental perceptions created during the process [38], while other explanations are based on structuration theory [39] which claims, for example, that individual deciding about location-sharing are not acting as free agents, but rather are influenced by contextual factors [40]. A one leading explanation relates to ability of the user to understand the complicated technological environment and the consequences of his actions [41]. This capability, known as the user’s “technological literacy,” might be is expected to prevent the privacy paradox. However, it was found out that even when technological literacy is present, the privacy paradox still exists [42].
Originally, literacy was defined as the ability to read and write [43]. Technological literacy is the “ability to use, manage, understand, and assess technology” [44]. The variation in technological literacy across the population correlates with diversity, e.g., a younger population usually handles technological issues better than an older population [45]. The lack of technological literacy is a hurdle hampering users ability to make privacy decisions efficiently, according to his or her preferences [46]. Thus, acquiring technological literacy is necessary for protecting privacy. For example, Desimpelaere et al. [47] showed that training children in privacy literacy improves their privacy protection. Technological literacy (or computer literacy) may even be used as a predictor of user behavior regarding privacy and security [48]. Thus, technological literacy has a direct impact on the privacy paradox, e.g., it was shown that the privacy paradox effect is lower among students studying information science students than among students in other fields [49]. Users who are unfamiliar with technical terms, adopt opinions based on instantaneous reactions, and lack thoughtfulness [50]. In fact, the level of the technological literacy plays a major role in setting whether privacy related decisions are taken “blindly” or “consciously” [51].
As the word “paradox” suggests, the privacy paradox reflects the existence of several contradictory states within the same person simultaneously. Considering the factors that influence the privacy paradox–privacy concern, privacy behavior, and technological literacy–creates a need for a mathematical model adequate for representing a paradox. This study offers a novel representation of the privacy paradox based on soft logic. The mathematical theory of soft logic is based on extending the current singular number zero to form a continuous axis, i.e., there are infinite zero values. The development of soft logic was motivated by the need to work with paradoxical states, and therefore might be fruitful when for studying the privacy paradox. The model is formalized below, and empirically demonstrated on a sample population.
2. Literature Review
There are theories that explain and even model the privacy paradox, e.g., using a construal level theory [52]. Another approach relates the privacy paradox to parallelism, and argues that it may be “explained by the lack of explicit conceptualization and operationalization at multiple levels” [53]. An attempt has even been made to prove and explain the privacy paradox, for example, in a seller scenario [54]. Some individual traits are frequently related to the privacy paradox, e.g., trust [55] or impulsivity, which was found to explain more of the variance in information disclosure than the “Big Five factors,” namely openness, conscientiousness, extraversion, agreeableness, and neuroticism [56]. Li et al. [57] argue that “online consumers are more likely to disclose personal information when they have positive cognitive appraisals,” which may explain the privacy paradox in some scenarios. Risk aversion, a well-known player in decision making processes, is introduced as a possible factor causing people to deviate from the rational calculus for decisions, thus contributing to the privacy paradox [58]. Other factors stem from the platform architecture rather than individual traits, e.g., the way personalized advertisements effect people’s perceptions of benefits and costs [59]. Razzano [60] approaches the privacy paradox from a collective rights perspective, conceptualizing it in terms of public rather than individual dimensions. Ichihashi [61] claimed, “consumers become ‘addicted’ to the platform, whereby they lose privacy and receive low payoffs, but continue to choose high activity levels”.
The two-factor theory (or Herzberg’s motivation-hygiene theory) argues that positive aspects of satisfaction (“enablers”), and negative aspects of dissatisfaction (“inhibitors”), may coexist independently [62]. This theory was harnessed to interpret the privacy paradox regarding the IoT (Internet of Things) technology [63]. The lemming effect was suggested as a cause for what seems to be an arbitrary behavior that leads to the privacy paradox in information security [64]. The vast majority of approaches are consistent with the idea that an inherent, internal contradiction is present, and cannot be explained by a classical logic or rationalism.
The privacy paradox is basically a qualitive factor, but is often treated quantitively, e.g., when trying to optimize data acquisition [65]. However, in the prevailing research literature, it is usually peripheral components that are quantified, e.g., laziness is introduced as a possible cause for the privacy paradox [66], as is fatigue [67]. Hou and Qingyan [68] accommodated perceived benefit and perceived risk in a model that analyzes utility maximization, and proved the existence of the privacy paradox. The privacy paradox may also be measured using statistical tools. For example, Norton (Symantec Corporation), a provider of cybersecurity software, argues that among Americans, 72% feel most of their online activities are tracked, 79% showed concerns regarding the use of data collected by companies, and 81% consider this data with a higher potential risk than benefits, yet “people aren’t necessarily prioritizing their privacy online” [69]. While these measures provide more evidence for the existence of the privacy paradox, they do not evaluate it specifically, and cannot represent its distribution among individuals.
Gimpel, et al. [70] introduced a metric for measuring the privacy paradox, and specified seven requirements: quantifiability, precision, comparability (use of standard units), obtainability, interpretability (easiness of interpretation by users), usefulness, economy (efficiency with regard to costs and benefit). While this development addresses the core issue of the current study, the metric presented ignores the distinction between the components of paradoxical (antinomy) and non-paradoxical (or veridical paradox) situations. Concerning the seven requirements, we disagree only with the interpretability requirement, because this issue is inherently complicated, and privacy paradox metrics are intended primarily for system architects and regulators, not end-users.
We adopt soft logic theory to represent the privacy paradox. The development of soft logic was largely inspired by the research of Marcelo Dascal who wrote about and described the work of the great mathematician and philosopher Gottfried Wilhelm Leibniz [71]. Leibniz aspired to discover and develop a new mathematical language that would provide a softer logic, and thereby overcome the limitations of the true/false dichotomy, which is a central concept in classical logic. According to Dascal, language is a tool for thought, but also influences thinking. On many occasions, Leibniz argued that classical logic, which contains only the two states, true and false (conveniently represented by “1” and “0” in computational systems) is insufficient for grasping the full meaning of human reasoning and conscious. However, he did not develop this idea any further, and established only the fundamentals of this theory. Leibniz, one of the founding fathers of calculus as a branch of mathematics referred to infinitesimals as ideal numbers that might be infinitely small [72]. William Clifford [73] concretized this concept by developing dual numbers, with the form: , where , are real numbers and . The mathematician Felix Klein developed a geometric-algebraic model that he called “blow-up,” by exploding the point of origin of a coordinate (e.g., Cartesian) system [74] and adding all of the possible revolutions around the point of origin, thereby creating a circle around the point of origin, which is connected with lines to each point on the circle. Rotating the circle by degrees turns it back on itself but in the opposite direction. When this procedure is applied in a three-dimensional space, reversing the direction by 180 degrees creates the Möbius strip twist. This blow-up concept was adopted in the soft logic field, by extending the zero point to an axis.
3. The Concept of Soft Logic
3.1. Soft Logic Basics
Soft logic is a new mathematical concept developed to enable the representation of paradoxical situations, i.e., contradictory states that exist at the same time. While traditional (binary or classical) logic is based on two states, true and false that cannot coexist, real life is more colorful than this black and white scenario [75]. Soft logic may be a member of the paraconsistent logic family, which relates to a dialethic paradoxes when a state is both true and false at the same time [76]. The Möbius strip, depicted in Figure 1, exemplifies one of these paradoxes [77]. From any local point of view, the strip has two sides, but from a global perspective, it has only one side. Therefore, it raises an unanswered question (from a human perspective); does it have one side or two? Thus it introduces a paradoxical situation. This inconclusive situation leads to developing an alternative approach, which maintains that both contradicting states coexist.

Figure 1.
Paradoxical concept: The Möbius strip.
Shifting from abstract examples to the real world, the current era is dynamic and characterized by a duality. People face parallel experiences, the real world and the digital world [78]. The fusion of these two worlds creates a new dimension of existence. To understand and describe this situation accurately, a new mathematical concept is required. Soft logic addresses this requirement by introducing a new type of numbers, which have been named “soft numbers”, which aim to represent such situations [79]. In other words, soft logic is useful in representing inherent uncertainty. The concept of soft logic relies on a blow-up of the zero number, an approach that distinguish between multiples of this number [80]. In soft logic, the zero is no longer a singular point, but an axis with infinite number of points, forming the zero axis. As explained above, the roots of the soft logic are found in the thinking of Leibniz (who aspired to overcome the true and false dichotomy) and Klein (who developed the “blow up” concept), and were further developed by the Digital Living 2030 project, which is a collaboration between Tel Aviv University and Stanford University. The project was motivated by a desire to create a mathematical bridge between the real world and the digital world. Based on the concept of the zero-axis, we define a new type of number called soft number, which contains two distinct components: (a) The component (on the one-axis, with old, classic numbers) that may, for example, represent the real objective world; and (b) The component (the new zero-axis) that may, for example, represents subjective human interpretation. Before formalizing soft numbers, their axioms are introduced.
Soft logic theory may sometimes be confused with other “soft” theories like fuzzy logic. Both fuzzy logic and soft logic break the dichotomy of true and false logic, allowing the use of a real number instead of a discrete 2-value binary one. However, the two theories address totally different realities: Fuzzy logic theory relates to cases in which we can assume a hidden, singular situation, but due to uncertainty cannot define them with a singular value. It is closely related to the probabilistic mathematics. The membership function of an element of a fuzzy set is extended from obtaining the value or to the entire range of numbers in the segment . In this sense, fuzzy set/logic allows multiplications of the number 1 with some real number between 0 and 1. On the other hand, soft logic do not assume the existence of singularity, and allow multiple contradicting situation to be exist at the same time. As a rule of thumb, it may be said that we will consider the use of fuzzy logic when we lack some information, and soft logic when we face a paradox. Fuzzy logic is a member of the soft computing family, a term that was coined by Lotfi A. Zadeh. While there is no exact definition to soft computing, we do think that soft logic can be a member of this family as well.
3.2. Axioms of Soft Numbers
According to classical mathematics, the expression is undefined, although in fact any real number could represent this expression, since for all real numbers , therefore, ). This insight opens a new range and fertile ground for investigation. To address this, we assume the existence of a continuum of distinct multiples , where a is any real number and is an object called a “soft zero”. The multiples , which are the multiplications of , are also called “soft zeros.” We denote the real number by , and all other real numbers are conceived as its multiples. We also define the term absolute zero as: . Now, let a, b be any real numbers and two corresponding soft zeros as defined above. The axioms of soft logic are:
Axiom 1 (Distinction).
Ifthen
In soft logic, we extend the zero from a singular point to a line (axis). This creates a distinction between different multiples of . This axiom calls for an order definition: If then . The soft zeros which are multiplication of have natural order according to the order of the multiplication factor.
Axiom 2 (Addition).
Under the assumption that the multiples of are located on a straight line, we can define the addition of multiples of as the addition of their corresponding real multipliers. The axis behaves regularly: .
Axiom 3 (Nullity).
.
Numbers on the zero axis “collapse” under multiplication. Addition has significance and meaning, but multiplication does makes no distinction whatsoever.
Axiom 4 (Bridging).
, .
There exists a relation between the real number and the soft zero, which is called a “bridge”, and is notated mathematically with the sign . The existence of the bridge enables the creation of the soft number.
Axiom 5 (Non-commutativity).
Bridging is directionally oriented; therefore, the order of the bridging operation is significant (unless, or , which in this case the sides are equal) and the result is not commutative. Note that even .
3.3. Formal Definition of a Soft Number
A soft number is a construction of the following form:
In Equation (1): are any real numbers. The new operator is a type of addition that considers the two-appearance left and right of a bridge number ( and . The symbol may be omitted from the soft number representation, therefore, . A soft number can be visualized in a specific coordinate system. For example, the Möbius strip is described when the zero axis is parallel to the real axis. Now, let denotes the set of all soft numbers so that:
It is noteworthy that, according to the non-commutativity axiom, any soft number in the set has a mirror image number created by reversing its bridging order, i.e., is mirrored by and vice versa. The two mirrored numbers have different meanings.
3.4. Basic Arithmetic of Soft Numbers
The addition operator of two soft numbers is defined by the following rule:
According to this definition, the set is a group under addition , when the + sign represents the addition operation for this group.
The multiplication of two soft numbers is defined by the following rule:
This operation is commutative and satisfies the laws of associativity and distribution. With these two operations, and , soft numbers create the ring , in which the and signs represent the addition and multiplication operators of the ring.
The inverse of a soft number exists when , and is defined as:
Therefore, is almost a field, an algebraic structure with two operations, addition and multiplication that satisfy certain rules (“almost”, because the inverse is undefined only when ).
3.5. Advanced Mathematical Operations of Soft Numbers
The -th power of a soft number is:
where is any natural number (.
The square root of a soft number only exists when , and has two values:
The -th root of a soft number satisfies the following statements:
for and an odd :
for and an even :
The projection of soft numbers to calculus is expressed in the following equation:
To generalize the basic calculus equation, if is a real polynomial function, then any soft number satisfies:
4. Representing the Privacy Paradox Using Soft Logic
4.1. The Privacy Paradox Space
The privacy paradox, currently viewed as a combination of an antinomy and a veridical paradox but not a falsidical paradox, is intuitively suitable for representation by soft logic theory. Before achieving this goal, we describe the privacy-paradox space that defines the situations in which the paradox exists, and its magnitude.
Thema: A privacy-paradox space of an individual acting in an online environment is spanned by three factors:
- Privacy Concern: The magnitude of the user’s care/anxiety/awareness of privacy, e.g., users of e-commerce transactions who claim that they will not disclose personal information, even for a significant discount.
- Privacy Behavior: The amount of privacy preservation actually reflected in user’s behavior, e.g., a user of e-commerce transactions discloses personal information, and the seller gains user’s trust even when a minor discount is offered.
- Technological Literacy: The ability of the user to manage technology efficiently, in this case to control online activities, e.g., understanding the privacy-setting mechanism on Facebook, and the consequences of each action.
It should be noted that all three factors can be measured and expressed on a tangible, quantitative scale. In this study, we will use a discrete scale for practical reasons, although the averaging operator applied to the population yields a continuous scale. A significant gap between privacy concerns and privacy behavior introduces an inconstancy. This phenomenon becomes a real paradox (antinomy) when technological literacy is high, hence the inconstancy cannot be rationally explained. For the sake of convenience, we will refer to the real paradox as a “paradoxical situation,” and the other states as “non-paradoxical situations.” The space spanned by the aforementioned factors can be described by a three-dimensional model, as depicted in Figure 2.
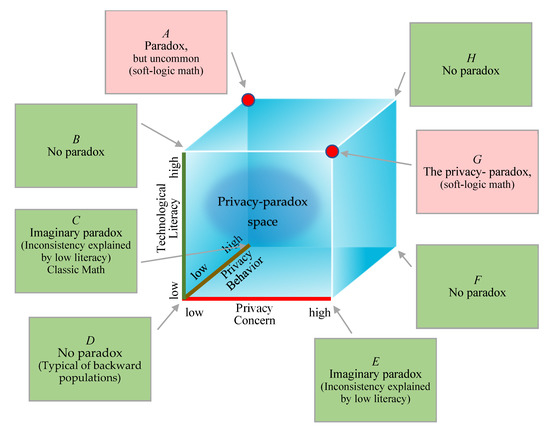
Figure 2.
Three-dimensional model of the privacy paradox.
To explain the privacy-paradox space, we identify the vertices of the cube: (A) High privacy behavior but low privacy concern and high literacy. This situation is paradoxical (because the high literacy should lineup with the behavior and the concern), but is uncommon and do not represent the classic privacy paradox; (B) Low privacy behavior and low privacy concern, with high literacy. There is no paradox regardless of the literacy level; (C) High privacy behavior but low privacy concern and low literacy. This situation is not paradoxical, or introduces an imaginary paradox (because low literacy explains the deviation); (D) Low privacy behavior and low privacy concern, with low literacy. There is no paradox regardless of the literacy level; (E) Low privacy behavior but high privacy concern and low literacy. This situation is not paradoxical, or introduces an imaginary paradox (because low literacy explains the deviation); (F) High privacy behavior and high privacy concern, with low literacy. There is no paradox regardless of the literacy level; (G) Low privacy behavior, high privacy concern and high literacy. This is the classic privacy paradox in which privacy behavior deviates downward from privacy concern despite a high literacy level. Therefore, the deviation cannot be explained; (H) High privacy behavior and high privacy concern, with high literacy. There is no paradox regardless of the literacy level. The privacy paradox of an individual is expressed in the privacy-paradox space. Soft logic math is beneficial in the two ranges that introduce a true paradox (the spaces that are close to either point A and/or point G). These ranges are described in psychology by the “double bind theory” [81]. A collection of individuals forms a distribution which is the privacy-paradox sphere.
4.2. Applying Soft Logic to the Privacy Paradox
To represent the privacy paradox with the mathematics of soft logic, let be privacy Concern, let be privacy Behavior, and let be technological Literacy, such that , when indicates no literacy at all and indicates maximal literacy. The expression indicates the lack of a literacy level.
Let , a factor that measures the gap between privacy behavior and privacy concern. The value represents adequate behavior, i.e., when privacy concern is consistent with privacy behavior, and there is no significant gap between them. This value is expected when (significant literacy), otherwise we face a paradox. The value is expected (or may be explained) only when (minimal literacy). The absolution of the difference causes the loss of some information, whether the individual has a frivolous pattern (), or a paranoid pattern ().
We now introduce two representations for placing an individual in the privacy paradox space:
Representation A:
In this representation as defined by Equation (12), (The letter ψ was selected for two reasons: (a) It is often used to represent the word “psychology” or study of psychology; and (b) It has the shape of a trident, i.e., a central line with deviations in two directions.) stands for an individual state where:
- The is the baseline and expresses as the rational component of the number.
- The unexplained deviation from privacy concern () is the “soft” component of the number.
These two components may also be thought of as expectancy and standard deviation.
In a world where the privacy paradox does not exist, the “soft” component of is redundant, and is actually rational. In this world, where . However, in the real world, because ( is not necessarily a function of ), the paradox does exist.
Representation B:
In this representation, as defined by Equation (13), stands for an individual deviation level:
- The unexplained deviation from privacy concern () is the “soft” component of the number.
- The explained deviation from privacy concern () is the rational component of the number.
4.3. Privacy Paradox: Distribution of Soft Numbers
For the purpose of developing this section, let us assume that , and are normally distributed ( ). When the three parameters indeed distribute normally, this system can be modeled by normalizing their values to a standard normal distribution .
We are interested in the distribution of , and specifically the distribution of .
The sum of two normally distributed random variables also distribute normally as follows: if and then .
Therefore,
Considering the random variable of the product , we address absolution by adding the assisting random variable , which can have the values or with equal probability (of ). The random variable is defined as:
and, it is clear that:
Therefore:
Let us define:
The product of two independent normal variables follows a modified Bessel function, and the density function is given by:
where is the Bessel function:
Therefore, the distribution is given by:
5. Empirical Study
The empirical study aimed to demonstrate how the methodology for using soft logic to represent the privacy paradox can be implemented.
5.1. Design
To conduct the empirical study, we developed a questionnaire designed to collect information from an individual on the three major factors: privacy concerns (), privacy behavior (), and technological literacy (). The empirical study paired privacy concerns and privacy behavior in seven scenarios:
- Using secure web sites when purchasing goods with an e-commerce transaction. A screenshot depicting this scenario was shown to the participants.
- Publishing a post on Facebook online social network about a car accident that an individual experienced.
- Consent to provide personal information in response to a national survey. A screenshot depicting this scenario was shown to the participants.
- An offer to receive a significant discount on purchasing electronics in return for providing the email address. A screenshot depicting this scenario was shown to the participants.
- Browsing a web site by clicking a URL that was provided as a winning message of free cinema tickets.
- The importance of keeping the antivirus updated and genuine.
- Reading the privacy notice when installing a new application on a smartphone.
Scenario (a) above is depicted in Figure 3. In the screen shown on the left, the participants are introduced with an e-commerce purchasing scenario on a non-secured site to evaluate privacy behavior; the screen on the right side, questions participants regarding their attitude on this issue, evaluating privacy concern. As explained below, all of these pairs of questions were shuffled randomly to minimize the possible linking by the participants.
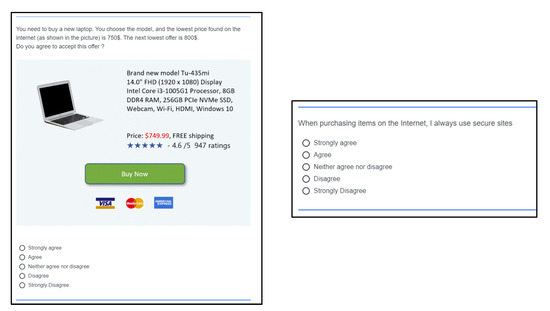
Figure 3.
Evaluating privacy concern vs. privacy behavior when using secure web sites when purchasing goods with an e-commerce transaction.
For each of the above scenarios, a pair of questions was introduced, one to evaluate the individual’s actual action in this scenario (), and the other to evaluate her/his attitude towards the scenario (). Both and C were ranked on a scale of 1 to 5. The answers were normalized for all scenarios, so that 1 represents minimal value and 5 represents maximal value. To achieve this, the scale was reversed for some questions (depending on the context), e.g., in scenario (b) about publishing a post on a car accident, selecting the “public” publishing option represents a minimal value of 1, and the answer not to publish at all represents a maximal value of 5.
Let be the user index (given participants, ), and let be the user scenario number (), the variable indicates the answer of participant to scenario regarding of the privacy concern question (), and the variable indicates the answer of participant to scenario regarding for the privacy behavior question (). Since the questions are paired by content, the for participant is given by: . To minimize the linking of two paired questions by the user, the questions in this section of the questionnaire were shuffled randomly.
A separate section of the questionnaire included five questions for evaluating the technological literacy of the participants. Each of these questions can be answered correctly (indicated by 1) incorrectly (indicated by 0). Let indicate the question number (), and let be the answer of participant to question (), so that the overall technological literacy of user is given by: ().
The four-part questionnaire opened with (1) general information about this study (without revealing the motivation of estimating the gap ). The conditions for participation were presented and consent was required to continue. This was followed by (2) demographic questions; (3) seven pairs of questions regarding the scenarios (shuffled randomly); and (4) five questions regarding the technological literacy. Participation was anonymous, and the participants were required to be at least 18 years old. The research was approved by the institutional ethics committee.
5.2. Participants
The participants were recruited using the crowdsourcing platform Amazon Mechanical Turk (MTurk). MTurk has proven to be suitable for studies of this type [82]. The MTurk qualification mechanism was applied to guarantee that each participant would be assigned to one experiment only, and thereby preventing a carryover effect. The compensation includes a fee of $0.2 for carrying out the Human Intelligence Task (HIT) on MTurk, an accepted and fair combination for this task [83]. The questionnaire was created using the Qualtrics online survey platform.
The study included valid participants (12 responses were disqualified for various reasons). Of the participants, 38% were female and 62% were male; 13% were 18–25 years old, 26% were 26–30 years old, 36% were 31–40 years old, 16% were 41–50 years old, and 9% were older than 50; 70% had a bachelor’s degree, 10% had a high school diploma, and 17% had a master’s degree. The vast majority of the participants (83%) were employees, 14% were self-employed, and 4% were unemployed or currently looking for work.
5.3. Results
The overall privacy concern () was relatively high (, privacy behavior () was medium (, and the technological literacy () was average (. The distributions of these three factors are depicted in Figure 4 a, b, and c respectively. As a preliminary result, the visual differences between the privacy concern (Figure 4a) and the privacy behavior (Figure 4b) demonstrate that the gap is significantly positive (). Potentially, if literacy is significant, the privacy paradox does indeed exist.
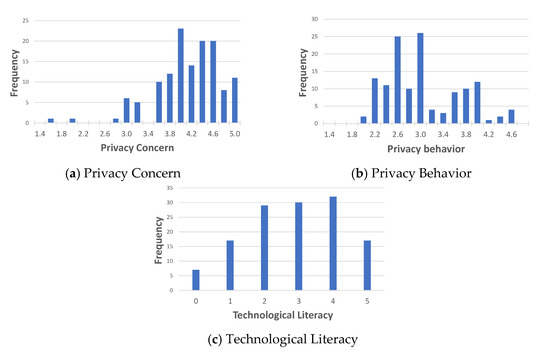
Figure 4.
Distributions of privacy concern, privacy behavior, and technological literacy.
The spread of the results in the privacy-paradox space is depicted in Figure 5. The X axis (horizontal and stretched from right to left) describes privacy concern, the Y axis (the other horizontal axis) describes privacy behavior, and the Z axis (vertical) describes technological literacy. Each vertex in the three-dimensional space describes a single participant point, and the surfaces were drawn to assist with orientation in the three-dimensional space (otherwise it is difficult to locate each point at an exact location). The bottom diagonal green line represents a perfect balance between privacy concern and privacy behavior (), i.e., all the points which are above this line are not paradoxical at all. The more remote a point is from the green line horizontally, the higher the potential paradox is (the distance from the line is given by: ). However, if a point is low on the Z axis (technological literacy), the paradox can be explained, and therefore it is not a paradox. It can be clearly seen that many points do represent a significant privacy paradox.
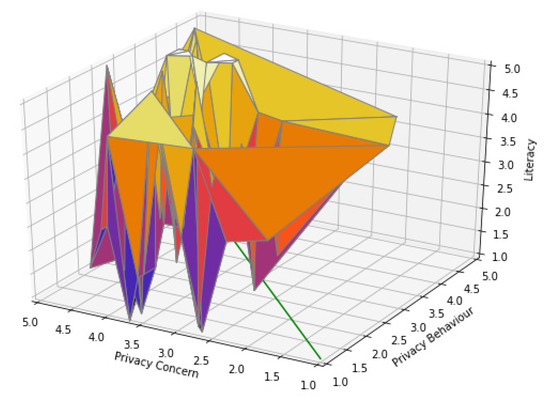
Figure 5.
The spread of the results in the privacy paradox space.
5.4. Representation with Soft Logic
Each participant’s result generates a single soft number with representation A () or representation B (). To balance both components of , the raw results of , , and were normalized to the range by dividing each by the maximal range (which was 5 in this study). For example, the theoretical result of yields:
and:
To show the spread of the results, and are displayed on two-dimensional graphs shown in Figure 6a and Figure 6b respectively. In Figure 6a (representation A denoted by ), the X-axis describes concern (C) which is the base line, and expresses the component of the soft number, while the Y-axis describes the paradoxical part () which expresses the component of the soft number. In Figure 6b (representation B denoted by ), the X-axis describes the non-paradoxical element () which is the component of the soft number, while the Y-axis describes the paradoxical part () which expresses the component of the soft number.
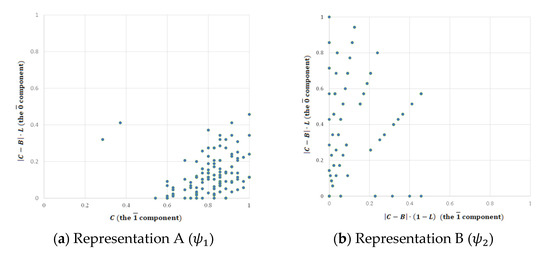
Figure 6.
Graphical representations of the soft numbers yielded by the empirical study.
6. Discussion
The existence of a significant gap between the privacy concerns and privacy behavior of an individual is known as the privacy paradox. While this phenomenon is prevalent, researchers have only explained it with speculation [84]. A gap between privacy concern and privacy behavior can reconciled when the individual has low technological literacy, and could introduce a true paradoxical situation when technological literacy is high. Therefore, privacy concern, privacy behavior and technological literacy may be correlated to the privacy paradox. For example, it has been argued, “Internet technical literacy negatively related to the Internet privacy concerns” [85]. Both situations, the veridical paradox and the true paradox (antinomy in classical logic or a dialetheia in a paraconsistent logic) requires attention, because the users are not acting in accordance with their true privacy preferences. The privacy paradox may be considered part of the attempts to integrate the human factors into digital systems. Previous steps towards achieving this goal include, for example, considering user behavior in a financial information system [86], but this study is focused on paradoxical situations which are difficult to model.
In this study, we offer a mathematical formalization of the privacy-paradox space which unifies both the non-paradoxical (falsidical paradox) and the paradoxical states in general, and specifically addresses the paradox. To achieve this, we applied a new mathematical theory: soft logic. The concept of soft logic tolerates the simultaneous existence of paradoxical situations; for example, it can represent a scenario when a singular point in space and time has two different temperature values. Naturally, this situation is impossible, at least in classical physics, however, the current case deals with cognition, in which paradoxical situations may be observed, as described above. We formulated and represented the privacy paradox using the language of soft logic in two different ways. Finally, we conducted an empirical study that included valid participants, and demonstrated how the privacy paradox space (of a group of individuals) can be represented and handled mathematically by using soft logic. This methodology may pave the way for developing algorithms that can enhance privacy. For example, when low technological literacy exists, i.e., in low paradox situations, literacy education is required. On the other hand, when high technological literacy exists, i.e., in significantly paradoxical situations, the solution may require other means. From the applicative point of view, this methodology can make a significant contribution to privacy-enhancing technology (PET) [87]. The soft logic approach defines paradoxical situations well, in situation where few opposites exist in the same time and place (a single individual in our case), and also enables carrying out mathematical operations on the discrete values. The availability of these operators is important; e.g., the absolute value of subtracting two values in the privacy-paradox space should describe the gap between two individuals. Without the zero axis, the paradox cannot be represented adequately, especially the holistic realty of joining the paradoxical and non-paradoxical components.
Paradoxes have become more prevalent and more powerful in the digital era, possibly due to the complexity of the environment. For example, the paradox of the parts and the whole [88], the efficiency paradox [89], and the paradox of complexity [90]. As privacy is a key issue in public discussion, the privacy paradox is certainly a prominent paradox, if not the most prominent one. The failure to provide a convincing explanation for the privacy paradox, suggests that two contradicting situations exist simultaneously, a situation that cannot be well-represented using the mathematical tools of classical logic. Therefore, current reality calls for a new theory to better address this issue. This study developed and empirically demonstrated the methodology of adopting soft logic for understand the privacy paradox. Since the privacy paradox is by its nature a classic paradox, we assume that the theory can be extended to many other paradoxical situations, in some cases with only minor adjustment. The idea of dualism is not new, for example, Immanuel Kant introduced understanding and sensibility as a pair and coined the terms “noumenon” for the object that exists independently of human sense, and “phenomenon” for the observable object [91]. The noumenal world is known to be exist but unknown to us because it is not sensible, an idea that is identified with Kant’s concept of the “thing-in-itself.”
While the paradoxical domain is one possible dimension for extending the theory, another dimension would be the type of the problem to be solved. For example, it has been shown how soft logic can be applied to decision trees dealing for a reality that combines a cognitive process with a more robust (e.g., machine-based) process [92]. Taking a wider view, the human and the machine worlds collide in the digital era, and soft logic representation might be a holistic way to represent this unnatural fusion.
While soft logic representation theory is elegant and promising, its effectiveness for developing applications to protect and refine privacy has still to be proved empirically. This could be achieved in a further study focused on specific domains or components of a system, for example setting defaults for applications such that they are optimized for the majority of the population [93]. Moreover, the proposed mathematics may require further development, especially to accommodate a wide variety of distributions, because the problem is stochastic by its nature. The empirical demonstration presented here might be slightly biased by sophisticated participants who could have noticed that the same issue (privacy concern and privacy behavior) appeared repeatedly in the questionnaire. A further study that analyzes real behavior in non-simulated activities could reduce this bias. Another issue with this study is the absolution of the gap between privacy-concern values and privacy-behavior values. As mentioned, while this absolution introduces a more elegant and unified model, it may also cause a loss of some information. This information encapsulates the essence of the problem: whether the user is exaggerating his or her anxiety about privacy, resulting in an unnecessary reduction of its benefits, or rather is underestimating privacy protection, causing undesired privacy loss. This simplification of the model might be addressed in a future study by extending the mathematical model to also include negative values in the gap. Lastly, the empirical part of this study is bounded to a demonstration of a soft logic representation of a real dataset. However, a more applicable study could implement this methodology in an application. For example, when installing a new smartphone application, the model can be assimilated in the configuration session, so that the selected choices and option reflect the user’s true preferences more adequately.
Bringing together human preferences and sensitivities concerning privacy (which is a fuzzy domain) and the technological environment (which is a robust domain) requires an effective bridge. The theory of soft logic provides this bridge, thereby contributing to the construction of new foundations for solving problems in this field. The evolution of technology and humanity may correspond to the evolution of the zero number. This historical journey started with ignoring zero as a number, then defining a singular zero that addresses well-defined mathematical domains such as Newtonian physics, and now zero is being extended to become an axis that addresses the fusion of humanity and technology.
7. Conclusions
While paradoxical situations are often unavoidable, especially when soft human factors like cognition are an inherent part of the model, they can be represented mathematically by using soft logic. This result is the most important contribution of this research, and may be helpful, for example, when developing applications in these environments. The functionally and usability of the soft logic representation are expected due to their success enabling mathematical manipulations, and therefore algorithms, without the need to describe and construct the causality of the paradox.
Author Contributions
Conceptualization, R.S.H., M.K. and O.M.; Methodology, R.S.H., M.K. and O.M.; Software, R.S.H.; Validation, R.S.H.; Formal analysis, R.S.H. and M.K.; Investigation, R.S.H., M.K. and O.M.; Resources, R.S.H.; Data Curation, R.S.H. and M.K.; Writing—Original Draft, R.S.H. and M.K.; Writing—Review & Editing, R.S.H., M.K. and O.M.; Visualization, R.S.H.; Funding acquisition, R.S.H. and O.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ariel Cyber Innovation Center in conjunction with the Israel National Cyber Directorate in the Prime Minister Office, and also, by the Koret Foundation Grant for Smart Cities and Digital Living 2030 awarded to Stanford University and Tel Aviv University.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of Ariel University (authorization number: AU-ENG-RH-20210830, date of approval: 30/Aug/2021).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shepherd, J. What is the digital era? In Social and Economic Transformation in the Digital Era; IGI Global: Hershey, PA, USA, 2004; pp. 1–18. [Google Scholar]
- ITU. New ITU Statistics Show More than Half the World Is Now Using the Internet. eTrade for all. 2018. Available online: https://etradeforall.org/news/new-itu-statistics-show-more-than-half-the-world-is-now-using-the-internet/ (accessed on 9 June 2022).
- Dwivedi, Y.K.; Rana, N.P.; Jeyaraj, A.; Clement, M.; Williams, M.D. Re-examining the unified theory of acceptance and use of technology (UTAUT): Towards a revised theoretical model. Inf. Syst. Front. 2019, 21, 719–734. [Google Scholar] [CrossRef]
- Jones, B. Understanding eCommerce Consumer Privacy from the Behavioral Marketers’ Viewpoint. 2019. Available online: https://www.proquest.com/dissertations-theses/understanding-ecommerce-consumer-privacy/docview/2323168353/se-2?accountid=14765 (accessed on 9 June 2022).
- Yang, Y.; Wu, L.; Yin, G.; Li, L.; Zhao, H. A survey on security and privacy issues in Internet-of-Things. IEEE Internet Things J. 2017, 4, 120–1258. [Google Scholar] [CrossRef]
- Lomotey, R.K.; Sofranko, K.; Orji, R. Enhancing privacy in wearable IoT through a provenance architecture. Multimodal Technol. Interact. 2018, 2, 18. [Google Scholar] [CrossRef]
- Bellekens, X.; Seeam, A.; Hamilton, A.W.; Seeam, P.; Nieradzinska, K. Pervasive eHealth Services a Security and Privacy Risk Awareness Survey; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Price, W.N.; Cohen, I.G. Privacy in the age of medical big data. Nat. Med. 2019, 25, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Regan, P.M. Privacy as a common good in the digital world. Inf. Commun. Soc. 2002, 5, 382–405. [Google Scholar] [CrossRef]
- Mokrosinska, D. Privacy and Autonomy: On Some Misconceptions Concerning the Political Dimensions of Privacy. Law Philos. 2018, 37, 117–143. [Google Scholar] [CrossRef]
- Li, H.; Yu, L.; He, W. The impact of GDPR on global technology development. J. Glob. Inf. Technol. Manag. 2019, 22, 1–6. [Google Scholar] [CrossRef]
- Moore, W.; Frye, S. Review of HIPAA, part 1: History, protected health information, and privacy and security rules. J. Nucl. Med. Technol. 2019, 47, 269–272. [Google Scholar] [CrossRef]
- Correia, J.; Compeau, D. Information privacy awareness (IPA): A review of the use, definition and measurement of IPA. In Proceedings of the 50th Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 4–7 January 2017. [Google Scholar]
- Wagner, C.; Trenz, M.; Veit, D. How do Habit and Privacy Awareness Shape Privacy Decisions? Association for Information Systems: Atlanta, GA, USA, 2020. [Google Scholar]
- Anic, I.D.; Budak, J.; Rajh, E.; Recher, V.; Skare, V.; Skrinjaric, B. Extended model of online privacy concern: What drives consumers’ decisions? Online Inf. Rev. 2019, 43, 799–817. [Google Scholar] [CrossRef]
- IGI Global. What is Privacy Concern. 2021. Available online: https://www.igi-global.com/dictionary/privacy-concern/40729 (accessed on 9 June 2022).
- Sheehan, K.B.; Hoy, M.G. Dimensions of privacy concern among online consumers. J. Public Policy Mark. 2000, 19, 62–73. [Google Scholar] [CrossRef]
- Enaizan, O.; Alwi, N.; Zaizi, N. Privacy and Security Concern for Electronic Medical Record Acceptance and Use: State of the Art. J. Adv. Sci. Eng. Res. 2017, 7, 23–34. [Google Scholar]
- Lin, S.-W.; Liu, Y.-C. The effects of motivations, trust, and privacy concern in social networking. Serv. Bus. 2012, 6, 411–424. [Google Scholar] [CrossRef]
- Aljifri, H.; Navarro, D.S. Search engines and privacy. Comput. Secur. 2004, 23, 379–388. [Google Scholar] [CrossRef]
- Xu, H.; Gupta, S.; Rosson, M.B.; Carroll, J.M. Measuring Mobile Users’ Concerns for Information Privacy; Citeseer: Princeton, NJ, USA, 2012. [Google Scholar]
- Cohen, I.G.; Gostin, L.O.; Weitzner, D.J. Digital smartphone tracking for COVID-19: Public health and civil liberties in tension. Jama 2020, 323, 2371–2372. [Google Scholar] [CrossRef]
- Acquisti, A.; Brandimarte, L.; Loewenstein, G. Privacy and human behavior in the age of information. Science 2015, 347, 509–514. [Google Scholar] [CrossRef]
- Read, K.; van der Schyff, K. Modelling the intended use of Facebook privacy settings. South Afr. J. Inf. Manag. 2020, 22, 1–9. [Google Scholar] [CrossRef]
- Tay, S.W.; Teh, P.S.; Payne, S.J. Reasoning about privacy in mobile application install decisions: Risk perception and framing. Int. J. Hum. Comput. Stud. 2021, 145, 102517. [Google Scholar] [CrossRef]
- Yu, L.; Li, H.; He, W.; Wang, F.-K.; Jiao, S. A meta-analysis to explore privacy cognition and information disclosure of internet users. Int. J. Inf. Manag. 2020, 51, 102015. [Google Scholar] [CrossRef]
- Emami-Naeini, P.; Dheenadhayalan, J.; Agarwal, Y.; Cranor, L.F. Which Privacy and Security Attributes Most Impact Consumers’ Risk Perception and Willingness to Purchase IoT Devices? IEEE: Piscataway, NJ, USA, 2021; pp. 1937–1954. [Google Scholar]
- The Privacy Issue. Decoding the Privacy Paradox. 2021. Available online: https://theprivacyissue.com/privacy-and-society/decoding-privacy-paradox (accessed on May 2022).
- Barnes, S.B. A privacy paradox: Social networking in the United States. First Monday 2006, 11. [Google Scholar] [CrossRef]
- Norberg, P.A.; Horne, D.R.; Horne, D.A. The privacy paradox: Personal information disclosure intentions versus behaviors. J. Consum. Aff. 2007, 41, 100–126. [Google Scholar] [CrossRef]
- Gerber, N.; Gerber, P.; Volkamer, M. Explaining the privacy paradox: A systematic review of literature investigating privacy attitude and behavior. Comput. Secur. 2018, 77, 226–261. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y.; Ouyang, S.; Xiong, W. The Data Privacy Paradox and Digital Demand; National Bureau of Economic Research (NBER): Cambridge, MA, USA, 2011. [Google Scholar]
- Zhu, M.; Wu, C.; Huang, S.; Zheng, K.; Young, S.D.; Yan, X.; Yuan, Q. Privacy paradox in mHealth applications: An integrated elaboration likelihood model incorporating privacy calculus and privacy fatigue. Telemat. Inform. 2021, 61, 101601. [Google Scholar] [CrossRef]
- Kang, H.; Jung, E.H. The smart wearables-privacy paradox: A cluster analysis of smartwatch users. Behav. Inf. Technol. 2020, 40, 1755–1768. [Google Scholar] [CrossRef]
- Shiau, W.-L.; Wang, X.; Zheng, F.; Tsang, Y.P. Cognition and emotion in the information systems field: A review of twenty-four years of literature. Enterp. Inf. Syst. 2022, 16, 1992675. [Google Scholar] [CrossRef]
- Min, J.; Kim, B. How are people enticed to disclose personal information despite privacy concerns in social network sites? The calculus between benefit and cost. J. Assoc. Inf. Sci. Technol. 2015, 66, 839–857. [Google Scholar] [CrossRef]
- Kokolakis, S. Privacy attitudes and privacy behaviour: A review of current research on the privacy paradox phenomenon. Comput. Secur. 2017, 64, 122–134. [Google Scholar] [CrossRef]
- Mohammed, Z.A.; Tejay, G.P. Examining the privacy paradox through individuals’ neural disposition in e-commerce: An exploratory neuroimaging study. Comput. Secur. 2021, 104, 102201. [Google Scholar] [CrossRef]
- Stones, R. Structuration Theory; Macmillan International Higher Education: London, UK, 2005. [Google Scholar]
- Zafeiropoulou, A.M.; Millard, D.E.; Webber, C.; O’Hara, K. Unpicking the privacy paradox: Can structuration theory help to explain location-based privacy decisions? In Proceedings of the 5th Annual ACM Web Science Conference, Paris, France, 2–4 May 2013; pp. 463–472. [Google Scholar]
- Hargittai, E.; Marwick, A. What can I really do?” Explaining the privacy paradox with online apathy. Int. J. Commun. 2016, 10, 21. [Google Scholar]
- Barth, S.; de Jong, M.D.; Junger, M.; Hartel, P.H.; Roppelt, J.C. Putting the privacy paradox to the test: Online privacy and security behaviors among users with technical knowledge, privacy awareness, and financial resources. Telemat. Inform. 2019, 41, 55–69. [Google Scholar] [CrossRef]
- Marvin, C. Constructed and reconstructed discourse: Inscription and talk in the history of literacy. Commun. Res. 1984, 11, 563–594. [Google Scholar] [CrossRef]
- International Technology and Engineering Educators Association. Standards for Technological Literacy: Content for the Study of Technology; ITEEA: Reston, VA, USA, 2000. [Google Scholar]
- Harley, D.A.; Kurniawan, S.H.; Fitzpatrick, G.; Vetere, F. Age matters: Bridging the generation gap through technology-mediated interaction. In CHI’09 Extended Abstracts on Human Factors in Computing Systems; ACM: Birmingham, UK, 2009; pp. 4799–4802. [Google Scholar] [CrossRef]
- Furnell, S.; Moore, L. Security literacy: The missing link in today’s online society? Comput. Fraud. Secur. 2014, 5, 12–18. [Google Scholar] [CrossRef]
- Desimpelaere, L.; Hudders, L.; Van de Sompel, D. Knowledge as a strategy for privacy protection: How a privacy literacy training affects children’s online disclosure behaviour. In Computers in Human Behavior; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Dincelli, E.; Goel, S. Can privacy and security be friends? a cultural framework to differentiate security and privacy behaviors on online social networks. In Proceedings of the 50th Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 4–7 January 2017. [Google Scholar]
- Weinberger, M.; Bouhnik, D.; Zhitomirsky-Geffet, M. Factors affecting students’ privacy paradox and privacy protection behavior. Open Inf. Sci. 2017, 1, 3–20. [Google Scholar] [CrossRef]
- Baek, Y.M. Solving the privacy paradox: A counter-argument experimental approach. Comput. Hum. Behav. 2014, 38, 33–42. [Google Scholar] [CrossRef]
- Arpetti, J.; Delmastro, M. The privacy paradox: A challenge to decision theory? J. Ind. Bus. Econ. 2021, 48, 505–525. [Google Scholar] [CrossRef]
- Hallam, C.; Zanella, G. Online self-disclosure: The privacy paradox explained as a temporally discounted balance between concerns and rewards. Comput. Hum. Behav. 2017, 68, 217–227. [Google Scholar] [CrossRef]
- Davazdahemami, B.; Hammer, B.; Luse, A.; Kalgotra, P. The role of parallelism in resolving the privacy paradox of information disclosure in social networks. In Proceedings of the Thirty Ninth International Conference on Information Systems, San Francisco, CA, USA, 13–16 December 2018. [Google Scholar]
- Madarasz, K.; Pycia, M. Towards a Resolution of the Privacy Paradox; SSRN: Rochester, NY, USA, 2020. [Google Scholar]
- Bilal, A.; Wingreen, S.; Sharma, R. Virtue ethics as a solution to the privacy paradox and trust in emerging technologies. In Proceedings of the 2020 the 3rd International Conference on Information Science and System, Cambridge, 19–22 March 2020; pp. 224–228. [Google Scholar]
- Aivazpour, Z.; Rao, V.S. Information Disclosure and Privacy Paradox: The Role of Impulsivity. ACM SIGMIS Database DATABASE Adv. Inf. Syst. 2020, 51, 14–36. [Google Scholar] [CrossRef]
- Li, H.; Luo, X.R.; Zhang, J.; Xu, H. Resolving the privacy paradox: Toward a cognitive appraisal and emotion approach to online privacy behaviors. Inf. Manag. 2017, 54, 1012–1022. [Google Scholar] [CrossRef]
- Mantilla, E.; Robles-Flores, J.A. The Role of Risk Aversion in the Privacy Paradox on Internet Users; Esan University: Lima, Peru, 2021. [Google Scholar]
- Idberg, L.; Orfanidou, S.; Karppinen, O. Privacy for sale!: An exploratory study of personalization privacy paradox in consumers’ response to personalized advertisements on social networking sites. Diva-Portal 2021, 71. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:lnu:diva-105022 (accessed on 9 June 2022).
- Razzano, G. Understanding the Theory of Collective Rights: Redefining the Privacy Paradox. Africaportal. 2021. Available online: https://www.africaportal.org/publications/understanding-theory-collective-rights-redefining-privacy-paradox/ (accessed on 9 June 2022).
- Ichihashi, S. Dynamic privacy choices. In Proceedings of the the 21st ACM Conference on Economics and Computation, Virtual Event, Hungary, 13–17 July 2020; pp. 539–540. [Google Scholar]
- Alshmemri, M.; Shahwan-Akl, L.; Maude, P. Herzberg’s two-factor theory. Life Sci. J. 2017, 14, 12–16. [Google Scholar]
- Lee, A.-R. Investigating the Personalization--Privacy Paradox in Internet of Things (IoT) Based on Dual-Factor Theory: Moderating Effects of Type of IoT Service and User Value. Sustainability 2021, 13, 10679. [Google Scholar] [CrossRef]
- Snyman, D.P.; Kruger, H.; Kearney, W.D. I shall, we shall, and all others will: Paradoxical information security behaviour. Inf. Comput. Secur. 2018, 26, 290–305. [Google Scholar] [CrossRef]
- Liao, G.; Su, Y.; Ziani, J.; Wierman, A.; Huang, J. The Privacy Paradox and Optimal Bias-Variance Trade-offs in Data Acquisition. ACM SIGMETRICS Perform. Eval. Rev. 2022, 49, 6–8. [Google Scholar] [CrossRef]
- Wirth, J.; Maier, C.; Laumer, S.; Weitzel, T. Laziness as an explanation for the privacy paradox: A longitudinal empirical investigation. Internet Res. 2021, 32, 24–54. [Google Scholar] [CrossRef]
- Choi, H.; Park, J.; Jung, Y. The role of privacy fatigue in online privacy behavior. Comput. Hum. Behav. 2018, 81, 42–51. [Google Scholar] [CrossRef]
- Hou, Z.; Qingyan, F. The Privacy Paradox on Social Networking Sites: A Quantitative Model Based on Privacy Calculus and An Experimental Study On Users’ Behavior of Balancing Perceived Benefit and Risk. Data Anal. Knowl. Discov. 2021, 1. [Google Scholar]
- Stouffer, C. The Privacy Paradox: How Much Privacy Are We Willing to Give Up Online? 2021. Available online: https://us.norton.com/internetsecurity-privacy-how-much-privacy-we-give-up.html (accessed on April 2022).
- Gimpel, H.; Kleindienst, D.; Waldmann, D. The disclosure of private data: Measuring the privacy paradox in digital services. Electron. Mark. 2018, 28, 475–490. [Google Scholar] [CrossRef]
- Dascal, M. Leibniz’s Two-Pronged Dialectic. In Leibniz: What Kind of Rationalist? Epistemology, and the Unity of Science; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Jesseph, D.M. Leibniz on the foundations of the calculus: The question of the reality of infinitesimal magnitudes. Perspect. Sci. 1998, 6, 6–40. [Google Scholar] [CrossRef]
- Clifford, W. Preliminary Sketch of Bi-quaternions. Proc. Lond. Math. Soc. 1873, 4, 381–395. [Google Scholar]
- Griffiths, P.; Harris, J. Principles of Algebraic Geometry; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Barker, M.-J.; Iantaffi, A. Life Isn’t Binary; Jessica Kingsley Publishers: London, UK, 2019. [Google Scholar]
- Priest, G. Paraconsistent logic. In Handbook of Philosophical Logic; Springer: Berlin/Heidelberg, Germany, 2002; pp. 287–393. [Google Scholar]
- Starostin, E.; Van Der Heijden, G. The shape of a Möbius strip. Nat. Mater. 2007, 6, 563–567. [Google Scholar] [CrossRef]
- Belk, R.W. Extended self in a digital world. J. Consum. Res. Oxf. Univ. Press 2013, 40, 477–500. [Google Scholar] [CrossRef]
- Klein, M.; Maimon, O. Fundamentals of Soft Logic. New Math. Nat. Comput. 2021, 17, 703–737. [Google Scholar] [CrossRef]
- Álvarez, M.J.; Ferragut, A.; Jarque, X. A survey on the blow up technique. Int. J. Bifurc. Chaos 2011, 21, 3103–3118. [Google Scholar] [CrossRef]
- Bateson, G.; Jackson, D.D.; Haley, J.; Weakland, J. Toward a theory of schizophrenia. Behav. Sci. 1956, 1, 251–264. [Google Scholar] [CrossRef]
- Paolacci, G.; Chandler, J.; Ipeirotis, P.G. Running experiments on Amazon Mechanical Turk. Judgm. Decis. Mak. 2010, 5, 411–419. [Google Scholar]
- Burleigh, T. What Is Fair Payment on MTurk? 2019. Available online: https://tylerburleigh.com/blog/what-is-fair-payment-on-mturk/ (accessed on May 2022).
- Solove, D.J. The myth of the privacy paradox. Georg. Wash. Law Rev. 2021, 89, 1–51. [Google Scholar] [CrossRef]
- Dinev, T.; Hart, P. Internet privacy, social awareness, and Internet technical literacy. An exploratory investigation. BLED 2004 Proc. 2004, 24. [Google Scholar]
- Maita, I.; Saide, S.; Putri, Y.G.; Megawati, M.; Munzir, M.R. Information system and behavioural intention: Evaluating the user behaviour of financial information system in the developing country of Indonesia. Technol. Anal. Strateg. Manag. 2022, 34, 594–607. [Google Scholar] [CrossRef]
- Van Blarkom, G.; Borking, J.J.; Olk, J.E. Handbook of Privacy and Privacy-Enhancing Technologies—The case of Intelligent Software Agents; PISA Consortium: The Hague, The Netherlands, 2003. [Google Scholar]
- Stange, K.C. The paradox of the parts and the whole in understanding and improving general practice. Int. J. Qual. Health Care 2002, 14, 267–268. [Google Scholar] [CrossRef][Green Version]
- Fox, E.M. The efficiency paradox. NYU Law Econ. Res. Pap. 2008, 77. [Google Scholar]
- Mossman, K.L. The Complexity Paradox: The More Answers We Find, the More Questions We Have; OXFORD University Press: Oxford, UK, 2014. [Google Scholar]
- Williams, J.J. Kant on the original synthesis of understanding and sensibility. Br. J. Hist. Philos. 2018, 26, 66–86. [Google Scholar] [CrossRef]
- Fivel, O.; Klein, M.; Maimon, O. Decision Trees with Soft Numbers. Int. J. Circuits Syst. Signal Process. 2021, 15. [Google Scholar] [CrossRef]
- Hirschprung, R.S.; Toch, E.; Maimon, O. Simplifying data disclosure configurations in a cloud computing environment. ACM Trans. Intell. Syst. Technol. (TIST) 2015, 6, 1–26. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).