Convolutional Neural Networks for Human Activity Recognition Using Body-Worn Sensors
Abstract
:1. Introduction
2. Related Work
3. Convolutional Neural Networks for HAR
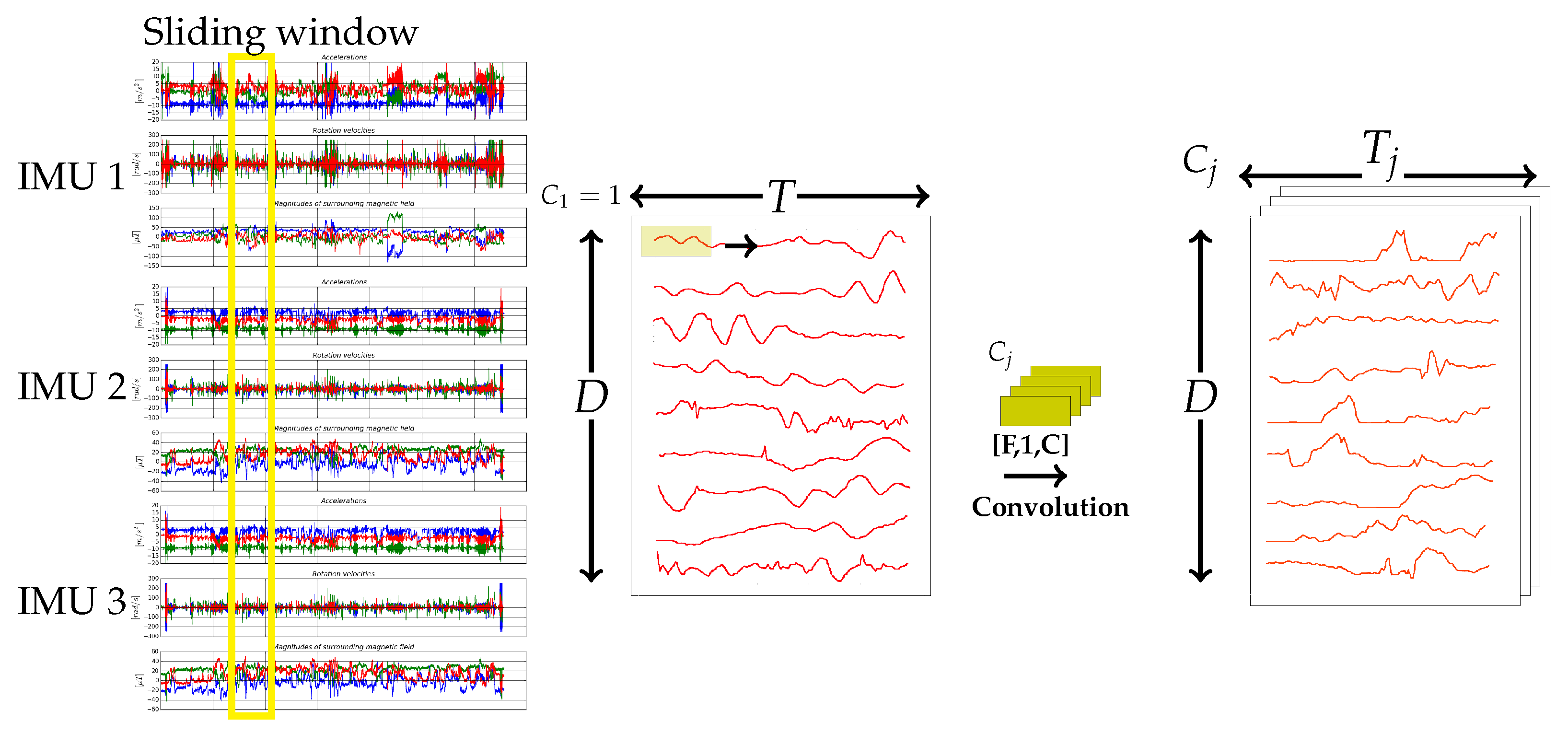
3.1. Temporal Convolution and Pooling Operations
3.2. Deep Architectures
4. Materials and Methods
4.1. Opportunity Dataset
4.2. Pamap2 Dataset
4.3. Order Picking Dataset
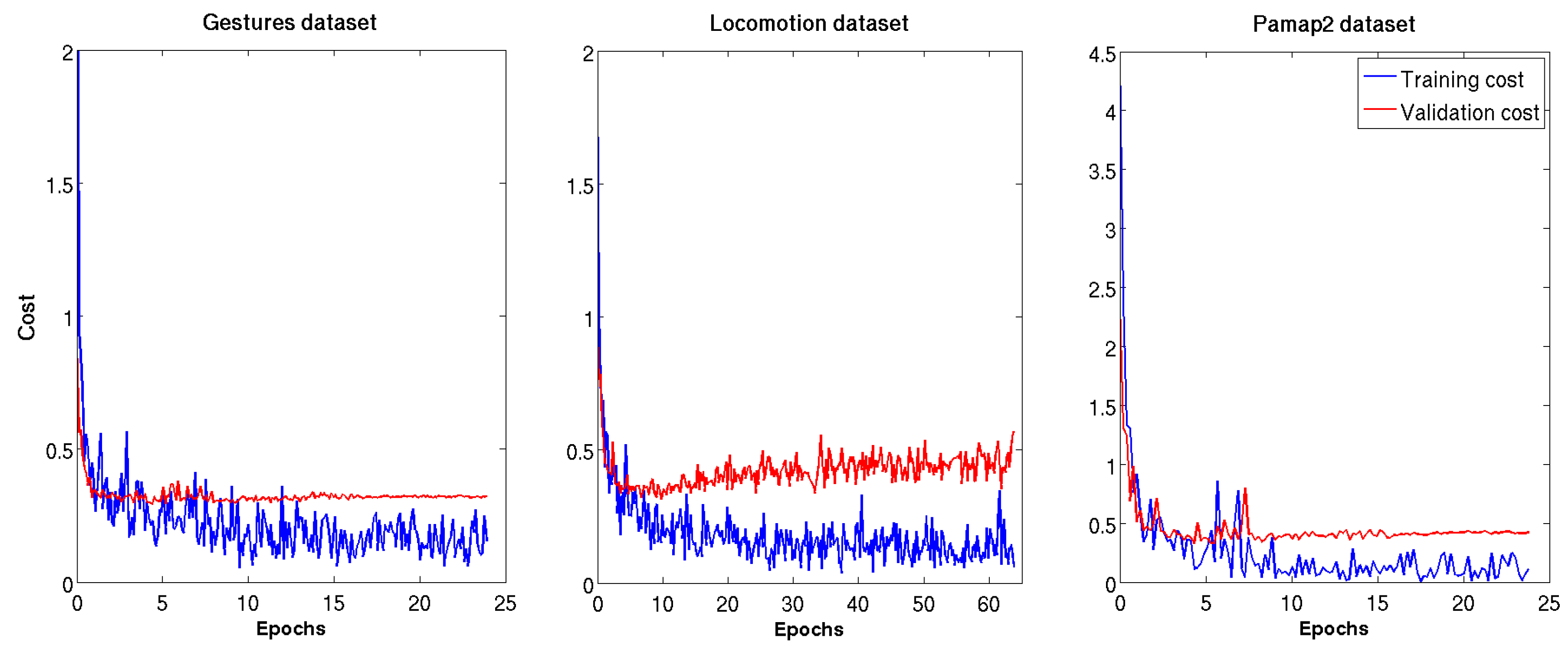
4.4. Implementation Details
5. Results and Discussion
5.1. Opportunity-Gestures
5.2. Opportunity-Locomotion
5.3. Pamap2
5.4. Order Picking
5.5. Comparison with the State-of-the-Art
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Feichtenhofer, C.; Pinz, A.; Zisserman, A. Convolutional two-stream network fusion for video action recognition. arXiv, 2016; arXiv:1604.06573. [Google Scholar]
- Zeng, M.; Nguyen, L.T.; Yu, B.; Mengshoel, O.J.; Zhu, J.; Wu, P.; Zhang, J. Convolutional neural networks for human activity recognition using mobile sensors. In Proceedings of the 2014 6th International Conference on Mobile Computing, Applications and Services (MobiCASE), Austin, TX, USA, 6–7 November 2014; IEEE: New York, NY, USA, 2014; pp. 197–205. [Google Scholar]
- Ronao, C.A.; Cho, S.B. Deep convolutional neural networks for human activity recognition with smartphone sensors. In Proceedings of the International Conference on Neural Information Processing, Istanbul, Turkey, 9–12 November 2015; Springer: New York, NY, USA, 2015; pp. 46–53. [Google Scholar]
- Yang, J.; Nguyen, M.N.; San, P.P.; Li, X.; Krishnaswamy, S. Deep Convolutional Neural Networks on Multichannel Time Series for Human Activity Recognition. In Proceedings of the 24th International Conference on Artificial Intelligence (IJCAI’15 ), Buenos Aires, Argentina, 25–31 July 2015; pp. 3995–4001. [Google Scholar]
- Ordóñez, F.J.; Roggen, D. Deep convolutional and LSTM recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Bulling, A.; Blanke, U.; Schiele, B. A tutorial on human activity recognition using body-worn inertial sensors. ACM Comput. Surv. (CSUR) 2014, 46, 33. [Google Scholar] [CrossRef]
- Lara, O.D.; Labrador, M.A. A Survey on Human Activity Recognition Using Wearable Sensors. IEEE Commun. Surv. Tutor. 2013, 15, 1192–1209. [Google Scholar] [CrossRef]
- Feldhorst, S.; Masoudenijad, M.; ten Hompel, M.; Fink, G.A. Motion Classification for Analyzing the Order Picking Process using Mobile Sensors. In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods, Rome, Italy, 24–26 February 2016; SCITEPRESS-Science and Technology Publications, Lda: Setúbal, Portugal, 2016; pp. 706–713. [Google Scholar]
- Hammerla, N.Y.; Halloran, S.; Ploetz, T. Deep, convolutional, and recurrent models for human activity recognition using wearables. arXiv, 2016; arXiv:1604.08880. [Google Scholar]
- Yao, R.; Lin, G.; Shi, Q.; Ranasinghe, D.C. Efficient Dense Labelling of Human Activity Sequences from Wearables using Fully Convolutional Networks. Pattern Recogn. 2018, 78, 252–266. [Google Scholar] [CrossRef]
- Grzeszick, R.; Lenk, J.M.; Moya Rueda, F.; Fink, G.A.; Feldhorst, S.; ten Hompel, M. Deep Neural Network based Human Activity Recognition for the Order Picking Process. In Proceedings of the 4th International Workshop on Sensor-based Activity Recognition and Interaction, Rostock, Germany, 21–22 September 2017; ACM: New York, NY, USA, 2017. [Google Scholar]
- Roggen, D.; Cuspinera, L.P.; Pombo, G.; Ali, F.; Nguyen-Dinh, L.V. Limited-memory warping LCSS for real-time low-power pattern recognition in wireless nodes. In Proceedings of the European Conference on Wireless Sensor Networks, Porto, Portugal, 9–11 February 2015; Springer: New York, NY, USA, 2015; pp. 151–167. [Google Scholar]
- Ordonez, F.J.; Englebienne, G.; De Toledo, P.; Van Kasteren, T.; Sanchis, A.; Krose, B. In-home activity recognition: Bayesian inference for hidden Markov models. IEEE Pervasive Comput. 2014, 13, 67–75. [Google Scholar] [CrossRef]
- Huynh, T.; Schiele, B. Analyzing features for activity recognition. In Proceedings of the 2005 Joint Conference on Smart Objects and Ambient Intelligence: Innovative Context-Aware Services: Usages and Technologies, Grenoble, France, 12–14 October 2005; ACM: New York, NY, USA, 2005; pp. 159–163. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems; Lake Tahoe, NV, USA, 3–6 December 2012, pp. 1097–1105.
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Badrinarayanan, V.; Handa, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for robust semantic pixel-wise labelling. arXiv, 2015; arXiv:1505.07293. [Google Scholar]
- Almazán, J.; Gordo, A.; Fornés, A.; Valveny, E. Word spotting and recognition with embedded attributes. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2552–2566. [Google Scholar] [CrossRef] [PubMed]
- Sudholt, S.; Fink, G.A. PHOCNet: A Deep Convolutional Neural Network for Word Spotting in Handwritten Documents. In Proceedings of the International Conference on Frontiers in Handwriting Recognition, Shenzhen, China, 23–26 October 2016. [Google Scholar]
- Wu, C.; Ng, R.W.; Torralba, O.S.; Hain, T. Analysing acoustic model changes for active learning in automatic speech recognition. In Proceedings of the 2017 International Conference on Systems, Signals and Image Processing (IWSSIP), Poznan, Poland, 22–24 May 2017; IEEE: New York, NY, USA, 2017; pp. 1–5. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A. Generating sequences with recurrent neural networks. arXiv, 2013; arXiv:1308.0850. [Google Scholar]
- Ravi, D.; Wong, C.; Lo, B.; Yang, G.Z. Deep learning for human activity recognition: A resource efficient implementation on low-power devices. In Proceedings of the 2016 IEEE 13th International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Francisco, CA, USA, 14–17 June 2016; IEEE: New York, NY, USA, 2016; pp. 71–76. [Google Scholar]
- Ravi, D.; Wong, C.; Lo, B.; Yang, G.Z. A deep learning approach to on-node sensor data analytics for mobile or wearable devices. IEEE J. Biomed. Health Inform. 2017, 21, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, K.; Miyake, S. Neocognitron: A new algorithm for pattern recognition tolerant of deformations and shifts in position. Pattern Recogn. 1982, 15, 455–469. [Google Scholar] [CrossRef]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems (ISCAS), Paris, France, 30 May–2 June 2010; IEEE: New York, NY, USA, 2010; pp. 253–256. [Google Scholar]
- OPPORTUNITY Activity Recognition Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/opportunity+activity+recognition (accessed on 6 March 2018).
- PAMAP2 Physical Activity Monitoring Data Set. Available online: http://archive.ics.uci.edu/ml/datasets/pamap2+physical+activity+monitoring (accessed on 30 November 2017).
- Roggen, D.; Calatroni, A.; Rossi, M.; Holleczek, T.; Förster, K.; Tröster, G.; Lukowicz, P.; Bannach, D.; Pirkl, G.; Ferscha, A.; et al. Collecting complex activity datasets in highly rich networked sensor environments. In Proceedings of the 2010 Seventh International Conference on Networked Sensing Systems (INSS), Kassel, Germany, 15–18 June 2010; IEEE: New York, NY, USA, 2010; pp. 233–240. [Google Scholar]
- Chavarriaga, R.; Sagha, H.; Calatroni, A.; Digumarti, S.T.; Tröster, G.; Millán, J.d.R.; Roggen, D. The Opportunity challenge: A benchmark database for on-body sensor-based activity recognition. Pattern Recogn. Lett. 2013, 34, 2033–2042. [Google Scholar] [CrossRef]
- Reiss, A.; Stricker, D. Introducing a new benchmarked dataset for activity monitoring. In Proceedings of the 2012 16th International Symposium on Wearable Computers (ISWC), Newcastle, UK, 18–22 June 2012; IEEE: New York, NY, USA, 2012; pp. 108–109. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional Architecture for Fast Feature Embedding. arXiv, 2014; arXiv:1408.5093. [Google Scholar]
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv, 2013; arXiv:1312.6120. [Google Scholar]
- Rippel, O.; Snoek, J.; Adams, R.P. Spectral representations for convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 7–12 December 2015; pp. 2449–2457. [Google Scholar]
- Ojala, M.; Garriga, G.C. Permutation Tests for Studying Classifier Performance. J. Mach. Learn. Res. 2010, 11, 1833–1863. [Google Scholar]
- Moya Rueda, F. CNN IMU. Available online: https://github.com/wilfer9008/CNN_IMU (accessed on 16 April 2018).

| Activity Class | Warehouse A | Warehouse B |
|---|---|---|
| walking | 21,465 | 32,904 |
| searching | 344 | 1776 |
| picking | 9776 | 33,359 |
| scanning | 0 | 6473 |
| info | 4156 | 19,602 |
| carrying | 1984 | 0 |
| acknowledge | 5792 | 0 |
| Unknown | 1388 | 264 |
| flip | 1900 | 2933 |
| Dataset | Epochs | |
|---|---|---|
| Baseline CNN | CNN-IMU | |
| Gestures | 12 | 8 |
| Locomotion | 12 | 12 |
| Pamap2 | 12 | 12 |
| Order Picking | 20 | 20 |
| Architecture | Max-Pooling | Acc | |
|---|---|---|---|
| baseline CNN [5] | No | 90.96 | 91.11 |
| CNN-2 | Yes | 91.49 | 91.52 |
| CNN-IMU | No | 92.13 | 91.88 |
| CNN-IMU-2 | Yes | 91.80 | 91.57 |
| Architecture | Max-Pooling | Acc | |
| baseline CNN [5] | No | 83.43 | 75.89 |
| CNN-2 | Yes | 83.43 | 75.89 |
| CNN-IMU | No | 92.24 | 92.01 |
| CNN-IMU-2 | Yes | 92.13 | 92.00 |
| Architecture | ||||
|---|---|---|---|---|
| Acc | Acc | |||
| baseline CNN [5] | 90.96 | 91.11 | 83.43 | 75.89 |
| CNN-2 | 91.49 | 91.52 | 83.43 | 75.89 |
| CNN-IMU | 92.13 | 91.88 | 92.24 | 92.01 |
| CNN-IMU-2 | 91.8 | 91.57 | 92.13 | 92.0 |
| Architecture | ||||||
|---|---|---|---|---|---|---|
| No Decrease | @ | @ | ||||
| Acc | Acc | Acc | ||||
| baseline CNN [5] | 90.96 | 91.11 | 91.68 | 91.94 | 91.72 | 91.88 |
| CNN-2 | 91.49 | 91.52 | 91.51 | 91.62 | 91.22 | 91.45 |
| CNN-IMU | 92.13 | 91.88 | 92.46 | 92.38 | 92.22 | 92.14 |
| CNN-IMU-2 | 91.80 | 91.57 | 92.40 | 92.29 | 92.44 | 92.31 |
| Architecture | ||||||
| No Decrease | @ | @ | ||||
| Acc | Acc | Acc | ||||
| baseline CNN [5] | 83.43 | 75.89 | - | - | - | - |
| CNN-2 | 83.43 | 75.89 | - | - | - | - |
| CNN-IMU | 92.24 | 92.01 | 91.52 | 91.38 | 91.25 | 90.81 |
| CNN-IMU-2 | 92.13 | 92.00 | 91.64 | 91.29 | 91.31 | 90.93 |
| Architecture | Max-Pooling | Acc | |
|---|---|---|---|
| baseline CNN [5] | No | 88.05 | 88.02 |
| CNN-2 | Yes | 89.66 | 89.57 |
| CNN-IMU | No | 88.61 | 88.61 |
| CNN-IMU-2 | Yes | 88.11 | 88.05 |
| Architecture | Max-Pooling | Acc | |
| baseline CNN [5] | No | 89.78 | 89.67 |
| CNN-2 | Yes | 89.68 | 89.56 |
| CNN-IMU | No | 88.76 | 88.59 |
| CNN-IMU-2 | Yes | 88.67 | 88.53 |
| Architecture | ||||
|---|---|---|---|---|
| Acc | Acc | |||
| baseline CNN [5] | 88.05 | 88.02 | 89.78 | 89.67 |
| CNN-2 | 89.66 | 89.57 | 89.68 | 89.56 |
| CNN-IMU | 88.61 | 88.61 | 88.76 | 88.59 |
| CNN-IMU-2 | 88.11 | 88.05 | 88.67 | 88.53 |
| Architecture | ||||||
|---|---|---|---|---|---|---|
| No Decrease | @ | @ | ||||
| Acc | Acc | Acc | ||||
| baseline CNN [5] | 88.05 | 88.02 | 88.06 | 87.92 | 86.57 | 86.40 |
| CNN-2 | 89.66 | 89.57 | 88.39 | 88.25 | 89.29 | 88.17 |
| CNN-IMU | 88.61 | 88.61 | 88.48 | 88.39 | 87.45 | 87.31 |
| CNN-IMU-2 | 88.11 | 88.05 | 88.65 | 88.55 | 87.62 | 87.55 |
| Architecture | ||||||
| No Decrease | @ | @ | ||||
| Acc | Acc | Acc | ||||
| baseline CNN [5] | 89.78 | 89.67 | 87.14 | 89.02 | 88.19 | 88.07 |
| CNN-2 | 89.68 | 89.56 | 89.45 | 89.35 | 87.75 | 87.67 |
| CNN-IMU | 88.76 | 88.59 | 88.18 | 88.05 | 87.50 | 87.35 |
| CNN-IMU-2 | 88.67 | 88.53 | 87.76 | 87.59 | 86.85 | 86.69 |
| Architecture | Max-Pooling | Acc | |
|---|---|---|---|
| baseline CNN [5] | No | 89.90 | 89.60 |
| CNN-2 | Yes | 92.55 | 92.60 |
| CNN-IMU | No | 90.12 | 89.94 |
| CNN-IMU-2 | Yes | 90.78 | 90.76 |
| Architecture | Max-Pooling | Acc | |
| baseline CNN [5] | No | 84.75 | 84.99 |
| CNN-2 | Yes | 91.15 | 91.22 |
| CNN-IMU | No | 90.22 | 89.94 |
| CNN-IMU-2 | Yes | 91.22 | 91.25 |
| Architecture | ||||
|---|---|---|---|---|
| Acc | Acc | |||
| baseline CNN [5] | 89.90 | 89.60 | 84.75 | 84.99 |
| CNN-2 | 92.55 | 92.60 | 91.15 | 91.22 |
| CNN-3 | 92.54 | 92.62 | 93.0 | 93.15 |
| CNN-IMU | 90.12 | 89.94 | 90.22 | 89.84 |
| CNN-IMU-2 | 90.78 | 90.76 | 91.22 | 91.25 |
| CNN-IMU-3 | 91.30 | 91.53 | 92.52 | 92.62 |
| Architecture | ||||||
|---|---|---|---|---|---|---|
| No Decrease | @ | @ | ||||
| Acc | Acc | Acc | ||||
| baseline CNN [5] | 89.90 | 89.60 | 89.87 | 89.93 | 90.17 | 90.11 |
| CNN-2 | 92.55 | 92.60 | 91.75 | 91.67 | 91.81 | 83.52 |
| CNN-3 | 92.54 | 92.62 | 91.36 | 91.33 | 91.70 | 91.72 |
| CNN-IMU | 90.12 | 89.94 | 91.70 | 91.68 | 91.22 | 91.23 |
| CNN-IMU-2 | 90.78 | 90.76 | 88.27 | 88.84 | 92.81 | 96.01 |
| CNN-IMU-3 | 91.30 | 91.53 | 91.89 | 91.93 | 89.93 | 89.95 |
| Architecture | ||||||
| No Decrease | @ | @ | ||||
| Acc | Acc | Acc | ||||
| baseline CNN [5] | 84.75 | 84.99 | 89.27 | 89.13 | 88.35 | 88.18 |
| CNN-2 | 91.15 | 91.22 | 89.77 | 89.62 | 88.64 | 88.52 |
| CNN-3 | 93.0 | 93.15 | 92.23 | 92.10 | 91.81 | 91.49 |
| CNN-IMU | 90.22 | 89.84 | 89.72 | 89.58 | 90.06 | 90.09 |
| CNN-IMU-2 | 91.22 | 91.25 | 91.94 | 92.04 | 93.13 | 93.21 |
| CNN-IMU-3 | 92.52 | 92.62 | 90.61 | 90.64 | 92.92 | 92.99 |
| Architecture | Person 1 | Person 2 | Person 3 | Warehouse A | |||||
|---|---|---|---|---|---|---|---|---|---|
| Acc | Acc | Acc | Acc | ||||||
| Baseline CNN | 64.69 | 65.23 | 70.2 | 67.36 | 65.62 | 60.72 | 66.84 ± 2.95 | 64.44 ± 3.39 | |
| Baseline CNN | 63.72 | 62.71 | 69.81 | 65.32 | 66.34 | 61.5 | 66.62 ± 3.06 | 63.18 ± 1.95 | |
| CNN-2 | 66.66 | 63.58 | 73.33 | 59.15 | 68.05 | 63.61 | 69.35 ± 3.52 | 65.45 ± 3.21 | |
| CNN-2 | 68.2 | 65.77 | 69.53 | 66.46 | 67.74 | 61.97 | 68.49 ± 0.93 | 64,73 ± 2.42 | |
| CNN-IMU | 66.48 | 64.54 | 70.22 | 67.26 | 66.8 | 62.25 | 67.83 ± 2.07 | 64.68 ± 2.51 | |
| CNN-IMU | 67.36 | 65.20 | 73.34 | 68.67 | 67.24 | 63.22 | 69.31 ± 3.49 | 65.22 ± 2.76 | |
| CNN-IMU-2 | 68.34 | 66.23 | 74.39 | 69.09 | 69.68 | 63.97 | 70.80 ± 3.18 | 66.43 ± 2.56 | |
| CNN-IMU-2 | 67.43 | 68.04 | 72.05 | 69.69 | 70.60 | 66.20 | 70.03 ± 2.36 | 67.97 ± 1.75 | |
| Architecture | Person 1 | Person 2 | Person 3 | Warehouse A | |||||
|---|---|---|---|---|---|---|---|---|---|
| Acc | Acc | Acc | Acc | ||||||
| Baseline CNN | 45.98 | 36.04 | 60.78 | 53.05 | 77.15 | 75.6 | 61.30 ± 15.59 | 54.89 ± 19.84 | |
| Baseline CNN | 43.9 | 35.53 | 59.66 | 52.27 | 77.68 | 76.35 | 60.41 ± 16.9 | 54.72 ± 20.52 | |
| CNN-2 | 49.39 | 43.8 | 58.57 | 52.42 | 77.56 | 76.61 | 61.84 ± 13.37 | 57.61 ± 17.01 | |
| CNN-2 | 47.42 | 40.16 | 62.64 | 56.53 | 77.97 | 76.70 | 62.68 ± 15.27 | 57.80 ± 18.30 | |
| CNN-IMU | 49.79 | 46.94 | 59.21 | 51.28 | 76.38 | 75.48 | 61.79 ± 13.48 | 57.9 ± 15.37 | |
| CNN-IMU | 67.23 | 63.21 | 60.87 | 53.99 | 80.0 | 77.76 | 69.36 ± 9.74 | 64.98 ± 11.98 | |
| CNN-IMU-2 | 43.06 | 52.68 | 61.11 | 68.65 | 78.32 | 79.97 | 60.83 ± 17.63 | 67.10 ± 13.71 | |
| CNN-IMU-2 | 54.31 | 45.66 | 61.71 | 53.78 | 89.93 | 78.13 | 68.65 ± 18.79 | 59.86 ± 16.12 | |
| Architecture | Datasets | |||||
|---|---|---|---|---|---|---|
| Gestures | Locomotion | Pamap2 | ||||
| Acc | Acc | Acc | ||||
| baseline CNN [5] | 91.58 | 90.67 | 90.07 | 90.03 | 89.90 | 90.04 |
| CNN-2 | 91.26 | 91.32 | 89.71 | 89.64 | 91.09 | 90.97 |
| CNN-3 | - | - | - | - | 91.94 | 91.82 |
| CNN-IMU | 92.22 | 92.07 | 88.10 | 88.05 | 92.52 | 92.54 |
| CNN-IMU-2 | 91.85 | 91.58 | 87.99 | 87.93 | 93.68 | 93.74 |
| CNN-IMU-3 | - | - | - | - | 93.53 | 93.62 |
| CNN-Ordonez [5] | - | 88.30 | - | 87.8 | - | - |
| Hammerla [9] | - | 89.40 | - | - | - | 87.8 |
| DeepCNNLSTM Ordonez [5] | - | 91.7 | - | 89.5 | - | - |
| Dense labeling Yao [10] * | 89.9 | 59.6 | 87.1 | 88.7 | - | - |
| Architecture | Person 1 | Person 2 | Person 3 | Warehouse A | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Acc | Acc | Acc | Acc | |||||||
| Statistical features | Bayes | 64.8 | - | 51.3 | - | 69.9 | - | 62.0 ± 7.8 | - | |
| Random Forest | 64.3 | - | 52.9 | - | 63.5 | - | 60.2 ± 5.2 | - | ||
| SVM linear | 66.6 | - | 63.5 | - | 64.1 | - | 63.6 ± 2.6 | - | ||
| CNN | CNN-IMU-2 | 68.34 | 66.23 | 74.39 | 69.09 | 69.68 | 63.97 | 70.80 ± 3.18 | 66.43 ± 2.56 | |
| Architecture | Person 1 | Person 2 | Person 3 | Warehouse B | ||||||
| Acc | Acc | Acc | Acc | |||||||
| Statistical features | Bayes | 58.0 | - | 62.4 | - | 81.8 | - | 67.4 ± 10.3 | - | |
| Random Forest | 49.5 | - | 70.1 | - | 79.0 | - | 66.2 ± 12.4 | - | ||
| SVM linear | 39.7 | - | 62.8 | - | 77.2 | - | 59.9 ± 15.4 | - | ||
| CNN | CNN-IMU | 67.23 | 63.21 | 60.87 | 53.99 | 80.0 | 77.76 | 69.36 ± 9.74 | 64.98 ± 11.98 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moya Rueda, F.; Grzeszick, R.; Fink, G.A.; Feldhorst, S.; Ten Hompel, M. Convolutional Neural Networks for Human Activity Recognition Using Body-Worn Sensors. Informatics 2018, 5, 26. https://doi.org/10.3390/informatics5020026
Moya Rueda F, Grzeszick R, Fink GA, Feldhorst S, Ten Hompel M. Convolutional Neural Networks for Human Activity Recognition Using Body-Worn Sensors. Informatics. 2018; 5(2):26. https://doi.org/10.3390/informatics5020026
Chicago/Turabian StyleMoya Rueda, Fernando, René Grzeszick, Gernot A. Fink, Sascha Feldhorst, and Michael Ten Hompel. 2018. "Convolutional Neural Networks for Human Activity Recognition Using Body-Worn Sensors" Informatics 5, no. 2: 26. https://doi.org/10.3390/informatics5020026
APA StyleMoya Rueda, F., Grzeszick, R., Fink, G. A., Feldhorst, S., & Ten Hompel, M. (2018). Convolutional Neural Networks for Human Activity Recognition Using Body-Worn Sensors. Informatics, 5(2), 26. https://doi.org/10.3390/informatics5020026





