Abstract
This paper serves as a survey and empirical evaluation of the state-of-the-art in activity recognition methods using accelerometers. The paper is particularly focused on long-term activity recognition in real-world settings. In these environments, data collection is not a trivial matter; thus, there are performance trade-offs between prediction accuracy, which is not the sole system objective, and keeping the maintenance overhead at minimum levels. We examine research that has focused on the selection of activities, the features that are extracted from the accelerometer data, the segmentation of the time-series data, the locations of accelerometers, the selection and configuration trade-offs, the test/retest reliability, and the generalisation performance. Furthermore, we study these questions from an experimental platform and show, somewhat surprisingly, that many disparate experimental configurations yield comparable predictive performance on testing data. Our understanding of these results is that the experimental setup directly and indirectly defines a pathway for context to be delivered to the classifier, and that, in some settings, certain configurations are more optimal than alternatives. We conclude by identifying how the main results of this work can be used in practice, specifically in experimental configurations in challenging experimental conditions.
1. Introduction
In this paper we are concerned with accelerometer-based Activity Recognition (AR). Firstly, we need to clarify the difference between activity tracking and activity recognition: whereas the former is only concerned with estimating general levels of activity (e.g., estimating calorie consumption or monitoring (non-)sedentary behaviour [1]), the latter is attempting to discern the actual activities occurring. It is the latter of these which will be examined here. Tri-axial accelerometers provide a low-power and high-fidelity measurement of force along the x, y, and z directions, and thus provide a view into the movement of the person wearing the device. Although there is significant potential for accurately predicting activities of daily living with accelerometers, many open problems exist due to the sheer volume of reasonable configurations available. For example, accelerometers may be configured with specific sampling rates, sample resolution and accelerometer range, features can be extracted from windows of any size, and the selection of the ultimate data analysis and classification pipeline is also non-trivial. All configurations can have an impact on both the battery lifetime and the predictive performance of an AR classifier, and so these parameters must be chosen with care. For instance, the sampling frequency dictates a performance trade-off between prediction accuracy and energy consumption. Indeed, human movements produce acceleration signals with most of the energy below 15 Hz, yet lower sampling frequencies may be preferable for long experiments to reduce the energy consumption.
This study is mostly focused specifically on body-worn accelerometers, although there has been recent interest in using mobile phone accelerometers for activity recognition [2,3,4,5]. AR can benefit from other on-body sensors, including gyroscopes (that measure angular rotation) and magnetometer sensors (that measure orientation with respect to the magnetic poles). Since these sensors typically consume several orders of magnitude more power than accelerometers, we do not consider these here. Note also that although outside the scope of this study, there is recent research in the area of Activities of Daily Living (ADL) recognition using other types of sensor, such as Red/Green/Blue-Depth (RGB-D) sensors [6] or other environmental sensors [7], or the fusion thereof [8].
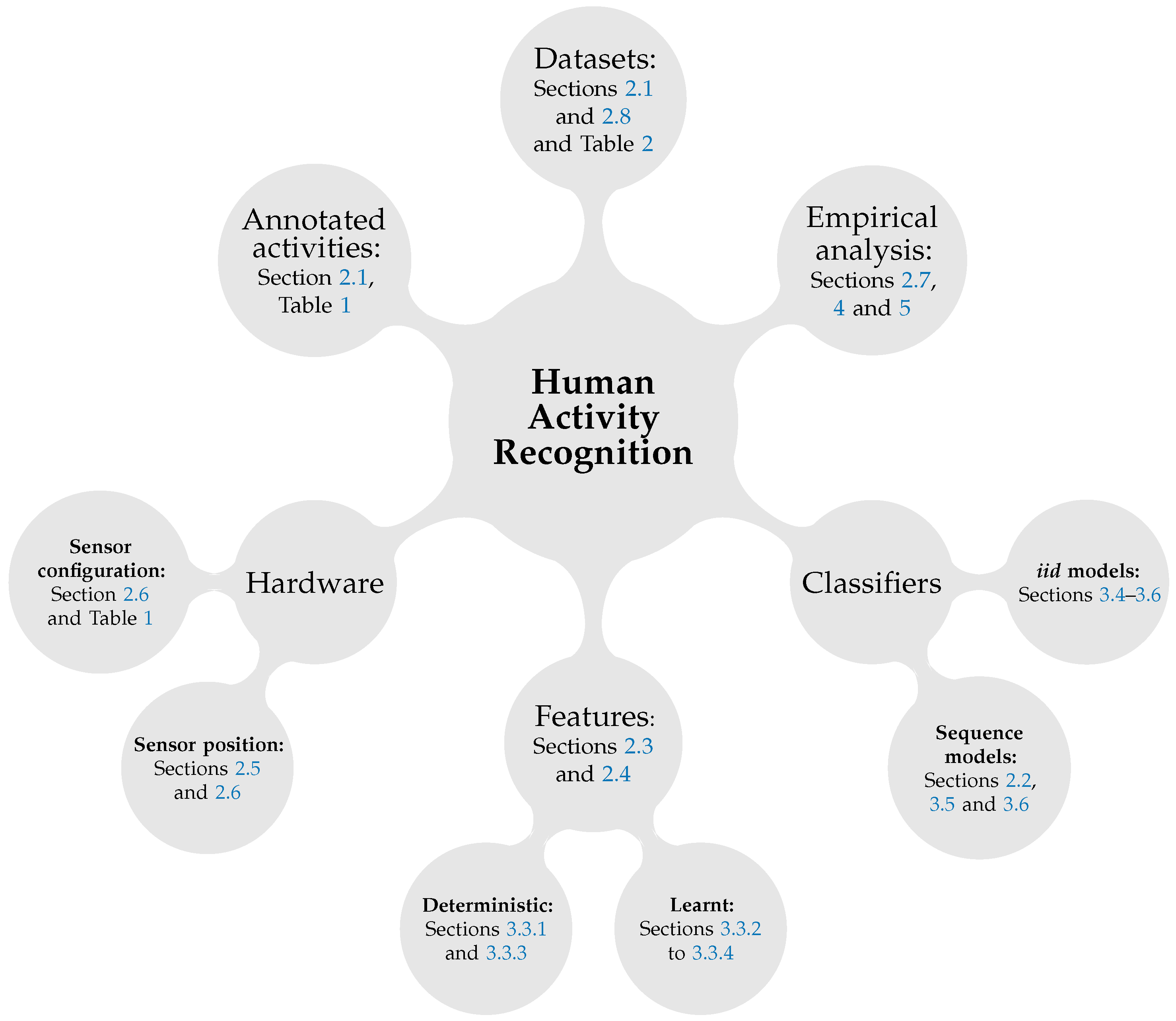
In this paper we address some of the open questions in the accelerometer-based AR, and particularly focus both on a comprehensive summary of the field and also an extensive experimental evaluation of possible configurations. Therefore, the rest of the paper is structured as follows: We summarise the recent research from the field and identify some open questions in Section 2. In Section 4 we address some of the open questions from Section 2 and present our main results with the classification models, feature representations and configurations that were described in Section 3. Finally, in Section 5 we conclude our main results. We summarise the structure of this paper in Figure 1 where the six important aspects of human activity recognition are shown: hardware, activity set, datasets features, classifiers and empirical performance evaluation. For each category (and subsequent child categories) we provide references to the sections and tables that introduce and discuss these topics.
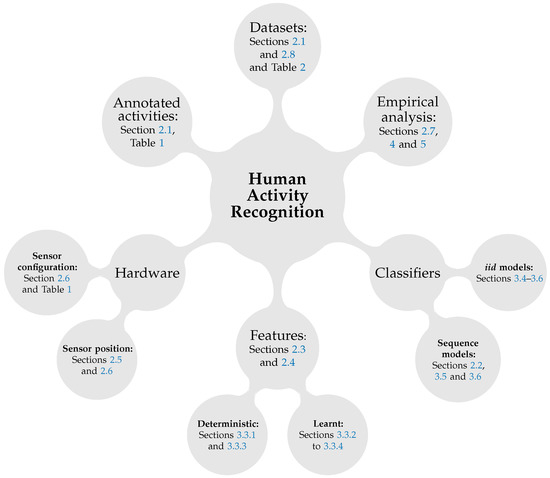
Figure 1.
This figure illustrates the main topics that are covered by this paper and lists the relevant sections and tables where each concept is discussed and introduced.
2. Summary of Research Directions and Open Questions
It is natural to consider the use of accelerometers for activity recognition, since it is clear that certain activities will have clear movement patterns for different parts of the body, whilst the sensors are relatively low-cost, low-power, and have wide user acceptance [9]. However, there are certain distinct issues that need to be addressed:
- What activities are we interested in? (Section 2.1)
- Are structured models (that model the sequential nature of the data) required for classification? (Section 2.2)
- What are the relevant features in the accelerometer data that are useful for prediction? (Section 2.3)
- How is the time series segmented? (Section 2.4)
- What are the optimal locations of accelerometers for the recognition of various activities? (Section 2.5)
- What are the trade-offs when selecting and configuring the accelerometers (e.g., sampling rate)? (Section 2.6)
- How robust are the predictions within an individual, and across individuals and sensor placements? (Section 2.7)
These issues are shared with many other settings where Machine Learning (ML) is applied to Digital Signal Processing (DSP), and as such this is a fairly mature research area [10,11]. More details regarding the specific questions we will be answering are given in Section 3. We note that whilst research has often focused on which ML algorithm performs best for the given dataset, we will assume instead here that virtually any state-of-the-art ML algorithm (e.g., kernel Support Vector Machines (SVMs) [12], Decision Trees [13], Bayesian classifiers [14]) can be made to perform equivalently given the appropriate feature set. Therefore, we employ simpler algorithms in order to increase our understanding of the problem.
It should be noted that vastly different accuracies are reported depending on the activity examined (e.g., a range of ≈41% to ≈97% in a study by [15]) and one should be aware that accelerometers may not be appropriate for some activities. Further to this, the positioning of sensors also plays an important role, and it is likely that this will be a limiting factor for many applications, since the positioning of sensors is often largely driven by user acceptance rather than optimality of ADL recognition performance [9]. It is worth mentioning here, however, that in some settings, such as in the scenario described in the Sensor Platform for HEalthcare in Residential Environment (SPHERE) project [16,17,18], we may not limited to the use of accelerometers alone, and other sensor modalities may be more appropriate for the activities that are hard to classify using (e.g., wrist-worn) accelerometers.
2.1. Activities
The first work to investigate performance of recognition algorithms with multiple, wire-free accelerometers on a large set (20) of activities using datasets annotated by the subjects themselves was by [15].
Another study by [19] examined eight activities: the first six from [15], as well as climbing down stairs, and sit-ups. [20] examined two activities and various postures. Table 1 shows the activities that we have identified in the literature while completing this review. Note that some in some sense encompass others (e.g., “eating lunch” is a subset of “eating”).

Table 1.
Activities found ADL studies using accelerometers.
Since each study defines a different set of activities, and indeed how certain activities are defined, it makes it somewhat difficult to compare the absolute classification results between studies and hence evaluate the different methodologies taken by researchers. In a given context, one might be interested in for example ADL for health-related purposes (c.f. the SPHERE project [16]), which would provide a specific driver for which activities are selected.
2.2. Structured vs. Unstructured Models
When performing classification on sequential data, it is common to ignore the sequential nature of the data and instead treat the data as if it were “independently and identically distributed” (iid), and subsequently use a standard ML algorithm that is designed for iid data. Intuitively, we might imagine that the strength of the temporal dependence in the sequence will determine how effective this approximation is, and this will in turn depend on how the data is pre-processed (i.e., is raw data presented to the classifier, or are features instead computed from the time series?). It has been shown [21] that under certain conditions structured models (e.g., Hidden Markov Models (HMMs) [22] or Conditional Random Fields (CRFs) [23]) and unstructured models (e.g., SVMs [12]) can yield equivalent predictive performance on sequential tasks, whilst unstructured models are also typically much cheaper to compute.
CRFs have been successfully employed for activity recognition in a smart-home environment [24], which although using environmental sensors rather than body-worn sensors would appear to have the same temporal characteristics. An approach based on semi-Markov CRFs that allows for overlapping activities was introduced by [25], whose results indicated that the proposed approach worked well even for complicated (higher-level) activities such eating and driving a car. The average precision and recall were both over , higher than were obtained by using HMMs or Topic Models (TMs).
The theoretical analysis in [21] related the excess risk incurred by unstructured models to the rate of decay of correlations within the sequence. It would therefore be advisable to perform the a-priori procedures outlined in [21] to determine whether activity recognition from accelerometer data, using the various types of feature construction discussed in Section 2.3, is a setting that requires structured models or not.
2.3. Survey of Feature Extraction Pipelines
Rather than attempt to classify every single data point (at e.g., 50Hz sampling rate), it makes sense to compute features of the data that are based on some kind of temporal window. This reduces the computational burden of the classification algorithms, reduces the effects of noise, and reduces the temporal dependence of subsequent examples, so that they can be treated as if they were iid. In fact, such temporal dependence still exists, but this is mostly ignored in the literature—c.f. the discussion in Section 2.2. There is a trade-off here: the longer the window length, the more these positive benefits are realised; however if the window length becomes too large, the probability that a given window contains more than one activity is increased, the delay before a classification output can be generated is increased, and the number of training examples for the classifier will also be reduced.
In both [15,19], feature extraction based on windows with overlap were used: [15] used window sizes of 512 samples with 256 samples of overlap at a sampling rate of 76.25 Hz, equating to a window length of 6.7 s; [19] used window sizes of 256 samples with 128 samples of overlap at a sampling rate of 50 Hz, equating to a window length of 5.12 s. Typically features are computed in each of the accelerometer directions independently, although in some cases features that combine the axes are also used.
Typical features can be split into two types: time domain features such as the mean, standard deviation, and correlation within the window; frequency domain features that are gathered after computing a Fast Fourier Transform (FFT) over the window. The frequency domain features include entropy, energy, and coherence (correlation in the frequency domain). Using a short window length enables near real-time inference of the user’s current activity and ensures the detection can rapidly adapt to changes.
According to [26], mid-sized time windows (from 5 to 7 s long) perform best from a range of windows from 1 to 15 s for wrist-placed accelerometers. The results are slightly different for other accelerometer placements, but the trend of mid-size windows performing best holds [26].
In [27], the authors approach the problem of acceleration-based activity recognition using strategies that are typical in speech processing, such as Mel Frequency Cepstral Coefficientss (MFCCs) and Perceptual Linear Predictions (PLPs) coefficients. Their framework extracts a total of 561 time-domain and frequency-domain features. While the proposed approach is interesting, it is worth mentioning that the MFCC features were directly inspired by deliberately modelling the response of the human ear to sound. Thus the practical justification of these features for AR is unclear.
Not all features are equally useful in discriminating activities. Feature selection methods such as filter, wrapper, or embedded selection [28] can be applied to reduce the number of features. For example, [29] reports on applying Relief-F, a filter-based approach, to select accelerometer features for activity recognition. Alternatively, methods such as Principal Component Analysis (PCA) are used to map the original features into a lower dimensional subspace with mutually uncorrelated components. Reducing the number of features significantly reduces the computational effort of the classification process [26].
A recent study showed on a variety of datasets that extremely simple histogram-like features [30] can still achieve good recognition performance. It would be interesting to test these features more comprehensively against other feature types mentioned above. The statistical features that were extracted were comprehensive, but many sets of features widely adopted by the community (e.g., [30]) were omitted.
Using only simple features has the appealing property that the computational burden is extremely low, which brings in the possibility of performing low-power feature extraction on the sensing device before transmission. This idea was investigated in depth in [31], where the authors presented a comparative performance evaluation study of a large number of features from acceleration data computed on embedded hardware platforms. The features were evaluated in the dimensions of cost and accuracy, and the paper concluded that simple time domain features computed in fixed-point arithmetic have the best cost/accuracy trade-off. The results showed that computing and transmitting a few of these time-domain features instead of sending the full acceleration data allows for the reduction of energy consumption by an order of magnitude, while still achieving acceptable accuracy. Other work in this area includes [32] in which low-complexity estimators of complex features are efficiently produced from carefully architected neural networks.
Recently, [33,34] examined the possibility of learning features automatically. Feature learning is a well-studied approach for static data (e.g., object recognition in computer vision). In contrast to heuristic feature design, where domain specific expert knowledge is exploited to manually design features such as described above, the goal is to automatically discover meaningful representations of data. This is usually done by optimising an objective function that captures the appropriateness of the features, such as by energy minimisation or so-called “deep learning” (see [35] for a review) Building on this [36] developed sparse-coding framework for activity recognition exploits unlabelled sample data, whilst learning meaningful sparse feature representations. The authors give results on a benchmark dataset showing that their feature learning approach outperforms state-of-the-art approaches to analysing ADL, and claim that their approach will generalise well (see Section 2.7 for further discussion of this).
Finally, an interesting approach using Bayesian non-parametric methods was taken by [37], in which they employed an Hierarchical Dirichlet Process (HDP) model [38] (a form of TM) to infer physical activity levels from the raw accelerometer data, and used the extracted mixture proportions as features to perform the multi-label activity classification. They then showed that the correlation between inferred physical activity levels to the users’ daily routine was better than when using FFT-based features. This is similar in nature to an earlier study by [39], who used an Expectation Maximisation (EM)-based clustering algorithm to generate features for their classifier which they used to recognise nine sporting activities, and reported a ≈5% improvement over a standard classification approach.
2.4. Segmentation of Accelerometer Data Streams
Explicit segmentation of the sensor data stream is in itself a non-trivial problem, and approaches can roughly be partitioned into methods that rely on a sliding window [40], and probabilistic methods based on HMMs (e.g., [41]). The goal of the segmentation problem is to infer a hidden state at each time, as well as the parameters describing the emission distribution associated with each hidden state. Typically in the segmentation problem, self-transition probabilities among states are assumed to be high, such that the system remains in each state for non-negligible time. More robust parameter-learning methods involve placing HDP priors over the HMM transition matrix [38].
Typically the approaches taken to activity recognition based on accelerometer data have taken the approach described earlier of [15,19], extracting small windows of consecutive sensor readings from the continuous sensor data stream. It has been claimed by [33] that this circumvents the need for explicit segmentation. On the basis of the discussion in Section 2.2, we would argue that this is only true if the window length is long enough so that the dynamics of the system (i.e., the rate of decay in the auto-correlation) are accurately captured, and that rigorous analysis of this is yet to be performed.
2.5. Location of Sensors on the Body
Many positions for the placement of accelerometers have been considered, including: (1) hip (belt); (2) wrist; (3) upper arm; (4) ankle; (5) thigh; (6) chest/trunk; (7) armpit; (8) trouser pocket; (9) shirt pocket; (10) necklace.
The results of [15], which considered locations 1–5 of the above, suggested that multiple accelerometers aided in recognition, since conjunctions between acceleration feature values at different sites were useful for discriminating many activities. However, they also found that with just two biaxial accelerometers–thigh and wrist–the recognition performance dropped only slightly.
In another study [42], which considered locations 1, 2, 8, 9, and 10 of the above—placement in a bag was also considered although this is no longer “body worn”—it was found that any of the positions were good for detecting walking, standing, sitting and running. Ascending and descending the stairs was difficult to distinguish from walking in all positions, since the classifier was trained for multiple persons. Their general conclusion was that the wrist performed best overall because the feature set was optimised for the wrist position.
As there are numerous placement locations on the body another questions arises: will activity recognition benefit from taking into account data from different on-body locations? In [43] a study was performed to determine if a model trained on the combined on-body locations performed better than a model that is aware of the location of the sensor. They report that classification models aware of the on-body location perform better than location independent models indicating that data collected from other on-body locations may not be beneficial if the sensor location is known or fixed (as in the case of wrist-worn wearables).
More recently, deep architectures have also been proposed, which build on data from multiple body-worn sensors [44,45]. Such architectures have the capability of automatically learning representations from raw sensor data. This is an attractive feature of these architectures since it removes the necessity of a practitioner to define features. However, since these models can model arbitrarily complex functions [46] care must be taken to minimise the risk of overfitting. Again we should stress that the optimal positioning of a sensor will also be driven by user acceptance, as well as by the resultant classification accuracy. A meta-analysis of user preferences in the design of wearables indicated that they would like to wear the sensor on the wrist, followed in descending order by the trunk, belt, ankle and finally the armpit [9].
2.6. Accelerometer Selection and Configuration
Digital accelerometers are configurable, allowing their users to tailor the raw data generation to the needs of their application. Different configuration options include the number of axes, the range of the acceleration, the resolution of the analog-to-digital converter (ADC), and the sampling frequency. Looking into the literature, there appears to be no consensus in the research community on what is the best choice for these configuration parameters for given types of activities. For instance, in the literature that is reviewed in this paper, summarised in Table 2, we see the use of both biaxial and triaxial accelerometers; sensors with a range of acceleration from g to g; and sampling frequencies that range from 1 to 100 Hz. On several occasions, these configuration parameters are often omitted or provided without justification. Moreover, little interest is shown to the energy consumption of the acceleration sensors. Whilst energy consumption is not a challenge when data is collected in controlled environments, it constitutes a major challenge when data is collected in natural environments, particularly when the duration of the experiment exceeds the battery lifetime of the sensor, as it can lead to loss of blocks of raw data [47]. However, low power accelerometers consume several orders of magnitude less power than low power gyroscopes. For example, the SPW-2 wearable sensor [48] employs the ADXL362 accelerometer and the LSM6DS0 gyroscope; ADXL362 consumes approximately 8 W at 50 Hz while LSM6DS0 consumes approximately mW at Hz.

Table 2.
Publicly available data-sets for activity recognition based on body-worn accelerometers. For activities see Table 1. Data formats: T = Time domain, F = Frequency domain. Sensor placements: L = Lower arm (wrist), U = Upper arm, W = Waist, C = Chest, B = Back, A = Ankle. N/A = Not applicable, N/K = Not known. The dataset number (#) is a hyperlink to a download page in the pdf version of this document.
Digital accelerometers incorporate an ADC. The resolution of the raw samples depends on the configuration of these parameters. The size of each sample is defined by the bit-resolution n of the ADC, (, 12 and 16 bits are typical). The resolution of the measurement also depends on the maximum acceleration range of the sensor (R) and is derived by . Thus, these configuration parameters control a trade-off between being able to sense high acceleration and the resolution of the measurements. The sampling frequency, the bit-resolution, along with the number of axes, also control the amount of data that is produced. Regardless of whether the raw data is transmitted wirelessly to the infrastructure or stored to a local flash memory, energy consumption scales with the amount of produced data. Indeed, different configurations of the acceleration sensor can make the battery lifetime of the wearable sensor last from a few days to few years [48]. Therefore, in cases of long experiments where battery lifetime is a concern, accelerometers should not use higher resolution and sampling frequency than necessary.
In [42], the authors investigate whether the high frequency information in the signal is relevant to the classification problem, and if not what level of down-sampling can be applied without affecting classification performance. In particular, the sampling frequency of 50 Hz was down-sampled to lower frequencies (without a low-pass filter) from 1 to 30 Hz. Accuracy was seen to increase with higher sampling rates, stabilising between 15–20 Hz, and only improved marginally above this. However, it should be noted that this was a biaxial rather than triaxial accelerometer, and that a fairly limited subset of features (no spectral features) were used, so it is difficult to draw a solid conclusion from this single study. More recent works also demonstrate that simple classification tasks can be effectively conducted at very low sampling frequency and resolution, increasing the battery lifetime of wearable sensors by more than an order of magnitude [49]. Khan et al. [50] performed a comprehensive study on optimising the sampling frequency of accelerometers in the context of human activity recognition. Their work concludes that the sampling rates that are used in the literature are up to higher than what is needed, leading to the waste of precious resources.
2.7. Methods to Estimate Generalisation Performance
In [19], trained classification algorithms from data collected in four different settings are assessed in the following ways:
- A single subject over different days, mixed together and cross-validated.
- Multiple subjects over different days, mixed together and cross-validated.
- A single subject on one day used as training data, and data collected for the same subject on another day used as testing data.
- One subject for one day used as training data, and data collected on another subject on another day used as testing data.
These aim to target test/retest reliability (for single and multiple subjects), within subjects and between subjects generalisation performance respectively. The authors showed that using Fourier features as described in Section 2.3 and off-the-shelf classifiers, they were able to achieve near perfect accuracy (>99%) in settings 1 and 2, ≈90% accuracy in setting 3, and only ≈65% accuracy in setting 4.
These results were corroborated by those of [15], which showed that although some activities are recognised well with subject-independent training data, others appear to require subject-specific training data (such as “stretching” and “riding an elevator”—see Section 2.1).
Another issue is that of laboratory versus naturalistic settings. An early study [51] reported an overall accuracy of for data collected in a laboratory setting but recognition rates dropped to for data collected in naturalistic settings, which demonstrated that the performance of algorithms tested only on laboratory data (or data acquired from the experimenters themselves) may suffer when tested on data collected under less-controlled (i.e., naturalistic) circumstances.
A recent activity recognition challenge [52] introduced a new semi-naturalistic dataset with several interesting features. Firstly, the data sequences were annotated by several annotators. Interestingly, this demonstrates the presence of annotation ambiguity on activity recognition datasets both in terms of the temporal alignment of the labels and the specification of the activities. Indeed, the regions of highest ambiguity are those with the highest rates of activity transitions. Since the labels themselves are ambiguous, evaluation of performance also becomes ambiguous in this setting. To overcome these difficulties, performance evaluation was based on proper measures between probability distributions.
2.8. Publically Available Data-Sets
In Table 2 we provide a summary of some of the most commonly cited publicly available data-sets, along with their characteristics. Note that we have focused on data-sets for activity recognition based on body-worn accelerometers–since accelerometer data is now readily available from smart-homes, there may be many more datasets available that do not focus on ADL, such as those focusing on lower-level “gestures” or gait analysis. We note that there are vast differences in the quantity of data, the number of subjects, the accelerometer sampling rates and ranges, and the settings of the recordings. This makes it especially difficult to compare results from different data-sets.
3. Materials and Methods
The previous section outlined several open questions in accelerometer-based activity recognition. In this section we discuss the methods that we will use to answer these questions. In particular we focus on assessing the effect of sampling rate, feature extraction, window length and sequential classification for activity recognition, and the resources, models, and experimental protocol are described below.
3.1. Data-Sets Used in This Work
A list of publicly available datasets for AR based on accelerometers is given in Table 2, with details regarding the collection of the data, annotations, setting, and hardware. Of these, datasets 1, 11, 12 are used in this study, with the following to be noted:
- har
- This was collected by attaching a smart-phone (with accelerometer and gyroscope) in a waist-mounted holder, with 30 participants conducting 6 activities in a controlled laboratory environment. Six activities were annotated in this dataset: walking, walking up stairs, walking down stairs, sitting, standing and lying down. The acceleration was sampled at 50 Hz on triaxial accelerometers and gyroscopes. Since gyroscopes can consume several orders of magnitude more power than accelerometers (c.f. Section 1), we only assess the accelerometer data in our treatment of this work. More details can be found in [4].
- uschad
- This was recorded by 14 subjects (7 male, 7 female) performing 12 activities (walking forward, walking left, walking right, walking upstairs, walking downstairs, running forward, jumping, sitting, standing, sleeping, elevator up, elevator down) in a controlled laboratory environment (with accelerometers and gyroscopes), with ground truth annotation performed by an observer standing nearby. The accelerometer, gyroscope and magnetometer data were sampled at 100 Hz, and data from the Microsoft Kinect accompanies this dataset. In our analysis we do not consider the Microsoft Kinect, magnetometer or gyroscope data, and use only the accelerometer data. More details can be found in [62].
- pamap2
- This contains data of 18 different physical activities (lying, sitting, standing, walking, running, cycling, Nordic walking, watching TV, computer work, car driving, ascending stairs, descending stairs, vacuum cleaning, ironing, folding laundry, house cleaning, playing soccer, rope jumping) performed by 9 subjects wearing 3 inertial measurement units (over the wrist on the dominant arm, on the chest, and on the dominant side’s ankle) and a heart rate monitor. Data were sampled at 100 Hz in this work and we use only the accelerometer data, although magnetometer and gyroscope data are also available. More details can be found in [63].
In all the data-sets, sensors were either placed on the waist (W) or lower-arm/wrist (L), and in some cases additional sensors were placed on other parts of the body. For the purposes of this study, we are limiting our analysis to the W and L placements, since a meta-analysis of user preferences in the design of wearables indicated that these were two of the most preferable locations (along with on the chest/trunk) [9].
All of these data-sets are artificial in the sense that they were collected in controlled laboratory environments, although varying degrees of effort have been made to make the environment as naturalistic as possible. There is clearly a trade-off here between ease of data collection (including ground-truth labelling) and the degree of realism that can be achieved. In order to ensure that performance is comparable between datasets, we have limited the set of activity labels that we consider to activities 1–6 in Table 1.
3.2. Calibration of Raw Accelerometer Data
Some datasets provide acceleration readings that are in raw digital format rather than ones calibrated against gravity. Digital codewords can be converted to gravity units with offset (o) and scale (s) parameters which specify the 0 g position and the number of bits that represent 1 g respectively [64]. For an accelerometer with a sensitivity of g with b-bits of precision, one might expect and (i.e., accelerations are evenly distributed over the range of codewords). However, these are insufficient estimates in general, due to variance in the manufacturing process, sensitivity towards environmental conditions and other confounding factors [64]. Therefore, we propose to learn these offset and scale parameters by first noting that the norm of the accelerations at rest must equal 1 g. We define the offset and scale vectors as and respectively. With these a tri-axial digital codeword, , is converted to acceleration with the following operation , where ⊘ is the element-wise division operator. The norm of this vector, , is a scalar which will equal 1 g at rest.
Given a dataset of N digital codewords, , we define a squared error loss as
where denotes the squared 2-norm of the i-th instance.The gradient of the loss with respect to the offset and scale vectors can be shown to be
and these may trivially be incorporated with with any state-of-the-art optimisation algorithms to find the optimal and .
We select only the subset of instances for which the accelerometer is at rest to ensure that gravity is the only factor contributing to recorded acceleration. For example, data within a window will be selected if the maximum variance of the three axis within this window is below a low threshold. Many datasets consist of multiple participants and we calibrated digital codewords on a per-participant basis as it was not clear whether the same accelerometer was consistently used.
3.3. Features Used in This Study
In this sub-section we will describe the types of features that will be used in our experimental comparison.
3.3.1. Hand-Crafted Features
The purpose of feature extraction is to present a learning algorithm with informative representations of the data so that induction can be performed effectively. Firstly, the raw acceleration was separated into ‘body’ and ‘gravity’ streams with the use of low-and high-pass filters. From these two streams the acceleration and jerk (derivative of body acceleration) on each axis were presented to the feature extraction algorithm. Statistical measures were extracted (for a full list see [4]) from the time, frequency and information theoretic domains.
A large number of features were extracted here (321 in total), but, as we incorporate sparse regularisation, the least informative features will be eliminated, performing feature selection. Often practitioners will incorporate domain knowledge to specify appropriate features a priori, but we prefer to investigate those that were deemed most informative by the learning procedure.
Another set of features that we consider in this work are the Empirical Cumulative Distribution Function (ECDF) features that were introduced in [30]. These features are computed from the empirical cumulative distribution of all axes. A practitioner specifies the percentiles of interest (e.g., k values between 0 and 100), and these values are interpolated from the ECDF. This produces k features per axis, and excellent performance is reported by the authors.
3.3.2. Sparse Coding and Dictionary Learning
Dictionary Learning, also known as Sparse Coding [65] is a class of unsupervised methods for learning sets of over-complete bases to represent data in a parsimonious manner. The aim of sparse coding is to find a set of vectors , known as a dictionary, such that we can represent an input vector as a linear combination of these vectors:
While there exist efficient techniques to learn a complete set of vectors (i.e., a basis) such as PCA [66], an over-completeness can achieve a more stable, robust, and compact decomposition than using a basis [67]. However, with an over-complete basis, the coefficients are no longer uniquely determined by the input vector . Therefore, in sparse coding, we introduce additional sparsity constraints to resolve the degeneracy introduced by over-completeness.
Sparsity is defined as having few non-zero components or many that are close to zero. The sparse coding cost function on a set of m input vectors arranged in the columns of the matrix as
where is the set of basis vectors (dictionary), is the set of coefficients for each example, and is a sparsity inducing regularisation function, and the scaling constant determines the relative importance of good reconstructions and sparsity. The most direct measure of sparsity is the quasi-norm , but it is non-differentiable and difficult to optimise in general. A common choice for the sparsity cost is the penalty (see [68] for a review). Since it is also possible to make the sparsity penalty arbitrarily small by scaling down and scaling up by some large constant, is constrained to be less than some constant C.
Since the optimisation problem is not jointly convex in and , sparse coding consists of performing two separate optimisations: (1) over coefficients for each training example with fixed; and (2) over basis vectors across the whole training set with fixed. Using an sparsity penalty, sub-problem (1) reduces to solving an regularised least squares problem which is convex in which can be solved using standard convex optimisation software such as CVX [69]. With a differentiable such as the log penalty, conjugate gradient methods can also be used. Sub-problem (2) reduces to a least squares problem with quadratic constraints which is convex in , for which again there are standard methods available. Other approaches to solving this problem include Bayesian methods wherein the joint uncertainty over the dictionary elements and reconstruction coefficients is captured [70].
Since the data is decomposed as a linear superposition of the dictionary elements, classifiers can use the reconstruction coefficients, , directly as features [70]. Since sparsity is imposed on the representation of the data, only a few bases will be ‘active’ for any given instance.
3.3.3. Fixed Dictionaries
It is worth noting that of course the sparse coding problem is a simpler optimisation problem if the dictionary is fixed rather than learnt. In this case, one can use dictionaries that are based on basis functions from a specific class, such as the Fourier basis or wavelet bases. Here we briefly introduce the Fourier basis and Gabor wavelet basis as described in [11].
Fourier analysis represents any finite continuous energy function as a sum of sinusoidal waves ,
The more regular the function is, the faster the decay of the amplitude as increases. If is defined only over an interval, e.g., , the Fourier transform becomes a decomposition into an orthonormal basis: of . If the signal is uniformly regular, then the Fourier transform can represent the signal using very few nonzero coefficients. Hence this class of signal is said to be sparse in the Fourier basis. The wavelet basis was introduced by Haar [71] as an alternative way of decomposing signals into a set of coefficients on a basis. The Haar wavelet basis defines a sparse representation of piecewise regular signals, and has therefore received much attention from the image processing community. An orthonormal basis on can be formed by dilating and translating these atoms as follows,
The definition of a time-frequency dictionary is that it is composed of waveforms of unit norm () which have a narrow spread in time (u) and frequency (). Choice of the dictionary should, if possible, be based on knowledge of properties of the signal. One of the most common choices for a general class of real-world signals is the Gabor dictionary, as it can represent a wide range of smooth signals. Gabor time-frequency atoms are scaled, translated and modulated Gaussian functions [72]. Without loss of generality, discrete real Gabor atoms will be considered, which are given by
where Z is a normalisation factor (to ensure that for each atom ), denotes the series of parameters of the functions of the dictionary, and is the Gaussian window.
A sampling pattern is dyadic if the daughter wavelets are generated by dilating the mother wavelet as in Equation (7) by and translating it by , i.e., . Dyadic sampling is optimal because the space variable is sampled at the Nyquist rate for any given frequency. The dictionary is then defined as,
where is the discrete Gabor atom as defined in Equation (8). An example of this sampling scheme is given in Table 3 for a signal of length 128 and dilation factor .

Table 3.
Example of the dyadic sampling scheme for a signal of length 128 and .
3.3.4. Convolutional Sparse Coding
The canonical approach to sparse coding intrinsically assumes independence between observations during learning. For many natural signals however, sparse coding is applied to “patches” of the signal, which violates this assumption (e.g., since data will generally not be aligned in phase). Convolutional Sparse Coding (CSC) explicitly models local interactions through the convolution operator [73], however the resulting optimisation problem is considerably more complex than traditional sparse coding. Fast CSC (FCSC) was introduced by [73], who used an optimisation approach that exploits the separability of convolution bands across the frequency spectrum which resulted in an efficient dictionary learning algorithm. It was initially designed for two dimensional image patches, where the convolutions are therefore within the 2-dimensional space of the image, but the approach can be readily applied to lower or higher dimensional problems.
The objective for convolutional sparse coding is
where is the k-th filter, is the corresponding sparse feature map, and is an image.
Recently, there have been attempts to use shift-invariant sparse coding to learn features for activity recognition [74]. In this work the authors used a shift invariant form of Non-negative Matrix Factorisation (NMF) [75], which is closely related to CSC, except that the signals are required to be non-negative. For NMF to work it was necessary to double the signal dimensions with negative copies, and then for classification the approach was to sum the activations over the temporal dimension of the frame, yielding the summed activations for each feature as a feature vector that is passed to the classifier (note that coefficients are non-negative). In this case, the algorithm was applied to raw (normalised) signals, which is of course dependent on the placement and orientation of the accelerometer.
A related approach was taken by [36], using a sparse-coding framework for human activity recognition. In this case the authors used a clustering approach to group together sparse codes, rather than full CSC. In this case, only the magnitude of the accelerometer readings was used, which worked well for the range of activities they were analysing. The authors make the point that an advantage of sparse-coding type approaches is the ability to leverage unlabelled data to improve representation power.
3.3.5. Classification Using Sparse Codes
For all of the sparse coding techniques above, the coefficients that are learnt on each signal become the features for the classification algorithm, as proposed by [36]. We note that there has been some work in unifying dictionary learning and classification in a single optimisation framework [76], which has the potential to learn bases that are simultaneously useful for reconstruction and classification, we will leave this as a possible avenue for future work.
In theory, dictionaries learnt from the data as in Section 3.3.2 should be more tailored to the signals present within the data, and hence should be able to represent (and hence reconstruct) the signals with fewer active components. In addition, smaller dictionaries should be sufficient. Of course there is nothing in Equation (5) that enforces discriminative power in the coefficients. In our experiments we will consider only learnt dictionaries since the fixed dictionaries performance was very poor and are more expensive, and the performance of CSC was unstable.
3.4. Classification Models Used in This Work
We consider three classifiers in this work: Random Forest (RF), Logistic Regression (LR), and Multi-layer Perceptron (MLP). Although our datasets are sequential, we sill simplify our notation in this section and assume the data are iid.
3.4.1. Mathematical Notation
Each observation is a sequence of length and each position of the sequence is a D-vector, i.e., . Given a target label space, , consisting of Y values, every sequence has an associated target vector, . A dataset then consists of M observation-target pairs, . For the m-th observation, its n-th position is selected with (‘tokens’) and the corresponding label for this position (‘tags’) is identified by .
Concretely, taking activity recognition as an example, represents the data sequence of length , whereas represents the n-th window of the sequence with the associated tag .
3.4.2. Random Forest
The RF algorithm is a popular and effective method for classification and regression problems. At a high level, a RF can be viewed as an ensemble of decision trees. The original formulation of a RF [77] implements each of the trees as a Classification or Regression Tree (CART) [78] and uses the Gini impurity measure as the splitting criteria. The Gini impurity measures the probability of an incorrect classification given the class distribution. Thus there is a direct relationship between the (im)purity of the split and the probability of an incorrect classification making it an effective splitting criterion. The subset of features each split has available to choose from is randomly selected (typically , where n is the number of features) in a process referred to as ‘feature bagging’. Given a large number of trees in the RF this leads to correlation between any dominating features across the many trees in the forest. The data available to each tree is a bootstrap sample (with replacement) which helps avoid overfitting. In order to produce a prediction, each input is passed through all trees and their predictions aggregated, with the final prediction chosen through a majority vote.
3.4.3. Logistic Regression
LR is a discriminative probabilistic model. In general, given a weight vector , LR models the probability distribution as
where . The parameters of this model () are optimised to minimise the negative log likelihood of the labels given the data. Many optimisation techniques can be used here, including Stochastic Gradient Descent (SGD), Limited-Memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithms etc. We use L-BFGS in our work. Regularisation is performed on the weight matrix.
3.4.4. Multi-Layer Perceptron
Neural Networks (NNs) are a very popular non-linear classification technique that are based on cascading several nonlinear functions. These techniques are described in great detail in, e.g., [79], and here we will discuss the selected architecture of the network.
The architecture of the network (i.e., the number of layers, and number of hidden units per layer) can be selected to trade off computational complexity and feature accuracy. On highly resource-constrained devices, for example, the practitioner may target networks with little capacity. All experiments in this paper involve one hidden layer with 100 hidden units.
Hence, with activation functions , the output of a two-layer NN is compactly written:
where is the activation function of the first layer (rectified unit) and is the activation function of the output layer (softmax). The network is optimised by maximum likelihood, and regularisation is imposed on the weights, and , but not the biases.
3.5. Convolutional Neural Networks
Convolutional Neural Networks (CNNs), also referred to as ConvNets, are a widely used extension of MLPs which have seen great success in computer vision tasks [80]. A key difference between CNNs and other NNs are the use of convolutions in layers of the network that induces weight sharing in the network. These convolutional layers learn feature representations with neurons in a layer arranged into feature maps, of which each neuron has a receptive field connecting it to a small region of neurons in a previous layer. CNNs also typically have pooling layers for downsampling, usually performing average or max pooling in order to reduce the spatial resolution of the feature maps. These layers are usually stacked on top of each other and used in conjunction with dense layers creating a deep architecture. The architecture of CNNs, which typically refers to the number of layers, the size of each layer, the choice of activation functions etc, are varied. Further information on the architectures evaluated in this work are detailed in Section 3.7.
3.6. Recurrent Neural Networks
Recurrent Neural Networks (RNNs) build upon feedforward NNs by allowing recurrent edges, i.e., edges which span adjacent timesteps in the network. This is useful in problems where data is not independent in time or space as RNNs can choose to pass specific information across different timesteps. Perhaps the most widely used RNNs in the practice are Long Short-Term Memory (LSTM) [81] networks. LSTMs introduced the concept of a memory cell replacing the traditional nodes in hidden layers, storing state for given periods of time. LSTMs have been shown to successfully learn time dependencies and perform well in a variety of tasks [82]. The details of the architecture used is detailed in Section 3.7.
3.6.1. Conditional Random Fields (CRFs)
All models so far have made iid assumptions about the data points. Since activity recognition is by definition a sequential problem, we investigate the benefits of modelling the sequential nature of the data with CRFs.
Conditional Random Fields (CRFs) [23,83] constitute a structured classification model of the distribution of conditional on . The most common form of CRF is the linear-chain CRF which are applied to sequential data, e.g., natural language, but more general CRFs can be learnt on trees and indeed arbitrary structures. In general, the probability distribution over the n-th node is influenced by the neighbouring nodes with graphical models, and this influence is propagated over the structure using algorithms based on message passing [84]. In this section, we introduce the CRF, but refer the reader to other texts (e.g., [21,23,83]) for more detail.
The general equation for estimating the probability of a sequence is given by:
where denotes the length of the m-th instance and n iterates over the sequence. The model requires specification of feature functions that are (often binary) functions of the current and previous labels, and (optionally) the sequence .
We will use the vectors , , , and matrices during inference in CRFs. Subscripts are used to denote the position along the sequence, e.g., is a vector that pertains to the n-th position of the sequence, and parentheses are used to specify an element in the vectors, e.g., the y-th value of the n-th alpha vector is given by . Matrices are indexed by two positions, and the -th element of is specified by .
In order to reduce the time complexity of inference, we describe a dynamic programming routine based on belief propagation here. We first calculate localised ‘beliefs’ about the target distributions, and these are called potentials. The accumulation of local potentials at node n is termed the ‘node potential’. This -vector where the y-th position is defined as , where fj is the j-th feature function. Similarly, the accumulation of local potentials at the n-th edge is termed the ‘edge potential’. This is a matrix of size where the -th element is given by . Node potentials are depicted as the edges between observation and targets in Figure 2, while in the same figure, edge potentials are depicted by edges between pairs of target nodes.

Figure 2.
In this figure we show how marginal inference is performed over node with Conditional Random Field (CRF) models, where we have related the theoretical foundations of CRFs described in this section to a graphical representation of a short sequence. Note, the CRF is an undirected graphical model, and the arrows shown in this image indicate the direction of the passed messages when performing inference on .
Given these potentials, we can apply the forward and backward algorithm on the CRFs chain. By defining the intermediate variables , and (where ⊙ denotes the element-wise product between vectors) the forward and backward vectors are recursively defined as:
with the base cases and . The un-normalised probability of the n-th position in the sequence can be calculated with
Finally, in order to convert this to a probability distribution, values from Equation (16) must be normalised by computing the ‘partition function’. This is a real number, and may be calculated at any position n with . The partition function is a universal normaliser on the sequence, and its value will be the same when computed at any position in the sequence. With this, we can now calculate the probability distribution on the n-th position
In this work, we incorporate the methodology of [85] for our analysis of CRFs where unigram potentials of the CRF derive from the class-membership probability estimates of a base classifier. Intuitively, this technique will introduce significant contextual information to the CRF (since the decision boundary will not necessarily be linear) but additionally the model can propagate the localised beliefs along the whole sequence. Empirically, this approach has been reported to not lose predictive power but learning also converges at a significantly higher rate. This approach has not been used in activity recognition work previously, to the best of the author’s knowledge.
Another technique that is popular in the activity recognition field for adding sequential dependence in classifiers involves using the predicted probabilities of the previous time step as additional features for the current time window. We do not consider this since the CRF described here offers a more principled approach for propagating belief and uncertainty.
3.7. Empirical Experiments in this Work
As explained in the previous section, three datasets are considered in our experiments: HAR, USCHAD, and PAMAP2. The primary contributions of this work derive from studying the classification performance of the LR, RF, and MLP classifiers over several different window length and sampling rate configurations.
3.7.1. Sensor Configuration Analysis
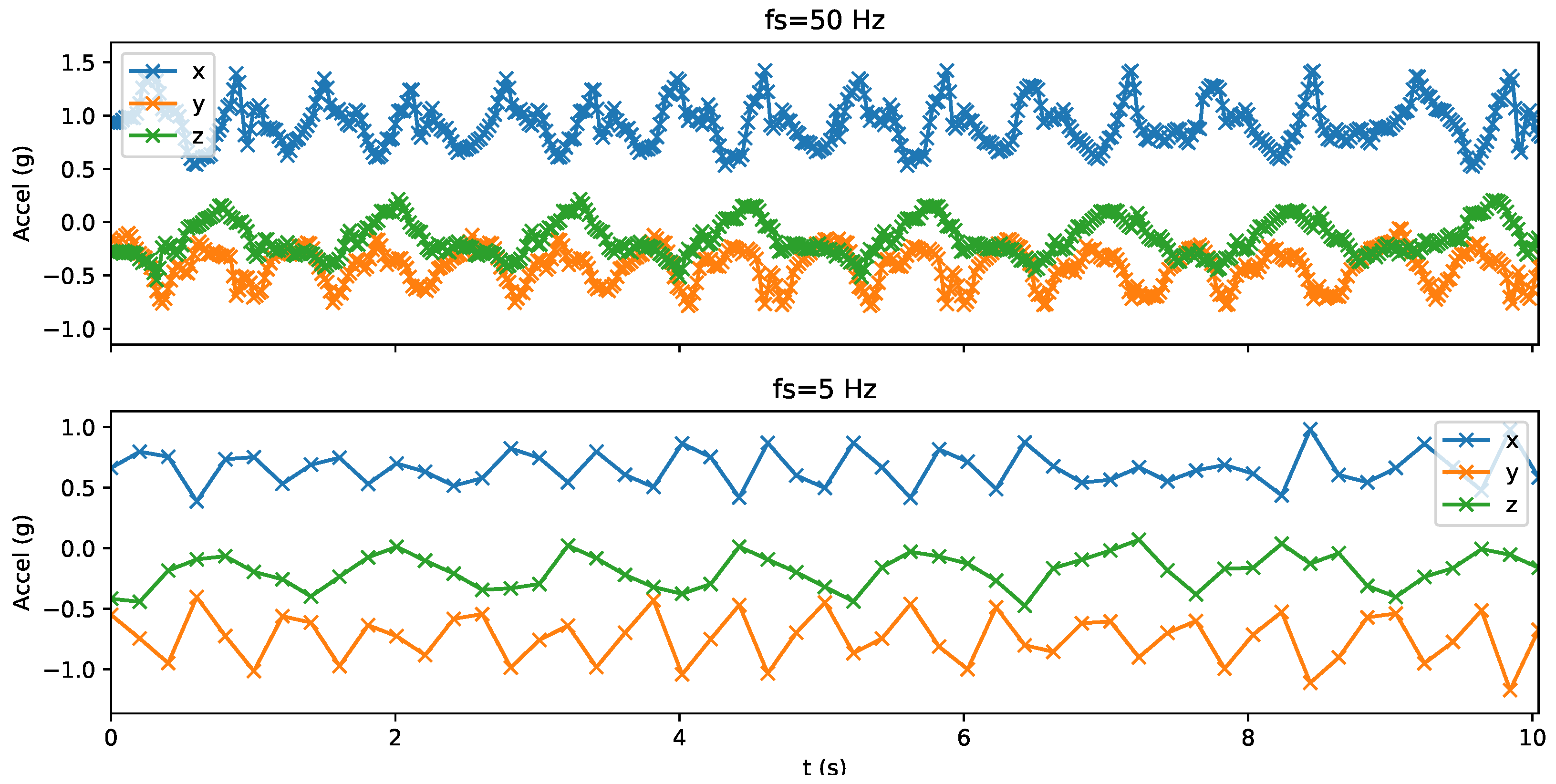
Our analysis first resamples the data to Hz. We illustrate the effect of resampling the data in Figure 3. In this figure we observe that the lower sampling rates tend to ‘lose’ the high-frequency aspects of the accelerometer, as expected. Particularly, we highlight the almost total loss of peaks between 6 and 8 s period with the 5 Hz sampling frequency in Figure 3 on the x-channel. However, between 4 and 6 s, the integrity of the ‘peaks’ appears to be high, indicating inconsistent data representations at the different sampling rates. Window lengths of length 1.5 s, 3.0 s, 4.5 s and 6.0 s are considered for feature extraction. Three classes of feature are extracted: statistical [4], dictionary [70] and ECDF [30] features are extracted. We selected these three since they represent a diverse set of features that are both pre-specified and learnt from data.
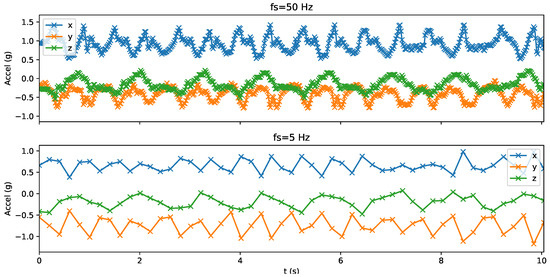
Figure 3.
The raw data (top) at 50 Hz, and resampled 5 Hz (bottom). Notice that the high-frequency aspects of the accelerometer data are removed with lower sampling frequencies. Samples are marked with × symbols. The x, y and z axes are depicted in blue, orange and green respectively.
3.7.2. Experimentation with iid Classifiers
For every experiment described here, we perform cross validation for hyper parameter selection. The data were stratified so that no data from training participants were used in testing (i.e., different subjects data used in training and testing). We employ 5-fold cross validation on all classifiers over set of parameters:
- RF:
- Ensemble size: ; Max depth of tree: .
- LR:
- L2 regulariser:
- MLP:
- L2 regulariser: Empirically we found values outside of this range performed very poorly, so we concentrated our search space over a smaller interval than with LR.
3.7.3. Experimentation with Sequential Classifiers
Additionally, we consider the effect of incorporating structured models [21] in AR. We incorporate the classification procedure described by [85] in our analysis.
3.7.4. Experimentation with Neural Network Models
We also consider more advanced neural network based models for AR with CNNs and also investigate the utility of convolutions and recurrency for feature learning and prediction. Two popular methods of incorporating recurrency in Deep Neural Networks (DNNs) include LSTM [81] and Gated Recurrent Unit (GRU) [86]. These two techniques achieve state-of-the-art performance on sequence prediction tasks since they directly parameterise the influence of nearby data points on predicting the current time point, and the neighbourhood of influence is optimised during the learning phase. Our experiments use LSTM since they have been shown to perform similarly to other methods (e.g., GRU) in many settings [87].
The CNN and LSTM models, unlike the feature experiments, take as inputs accelerometer data directly. Thus, we provide these models with the body and gravity components of the x, y, and z axes instead of determinisitcally extracted features. In this way our work demonstrates the capability of the networks to learn representations of the accelerometer data. Note, however, that we focus our analyses on only one accelerometer configuration (sampling rate of 30 Hz, window length of 3 s) which, as we will see later, is selected based on the results of the feature experiments. Moreover, this configuration is chosen since a complete analysis of CNNs and LSTMs over all sensor configurations would necessitate particular care in specifying the network architectures. Such an analysis is outside the scope of this paper and will be considered in future work.
For the recurrent experiments, we perform 5-fold parameter selection on the training set over the following configurations:
- Dropout rate:
- Training epochs:
Both CNN and LSTM models share the same basic architecture and use Rectified Linear Unit (ReLU) activations in all hidden layers. The architecture for CNN is as follows
- Convolutional layer with 64 units, a kernel size of 9 (i.e., 0.3 s), and dropout (selected in cross validation)
- Convolutional layer with 32 units, a kernel size of 9, and dropout (selected in cross validation)
- Flattening layer
- Fully connected with 16 units; ReLU activations and dropout
- Output layer with softmax
and for LSTM
- LSTM layer with 64 units and dropout (selected in cross validation)
- LSTM layer with 32 units and dropout (selected in cross validation)
- Flattening layer
- Fully connected with 16 units; ReLU activations and dropout
- Output layer with softmax
All networks were trained with the Adam optimiser [88] and parameters are tuned to minimise categorical cross entropy. Additionally, we also investigate the contribution of CRFs on CNN and LSTM models using the same methodology from the feature experiments. Although CNN and LSTM models propagate information relating to the state of the neighbouring features, thus they do not naturally model label sequences. As a concrete example, one can trivially impose constraints on the set of legal transitions over a sequence with CRFs (e.g., one cannot transition from ‘lying’ to ‘walking’ without an intermediate activity). Such constraints cannot be imposed with vanilla LSTM models, for example, since beliefs on neighbouring predictions (i.e., the final node) are not propagated over the sequences. CRFs, on the other hand, can compel such consistency [21] thus motivating the use of CRFs on the predictions of CNN and LSTM.
4. Results and Discussion
4.1. Validation of Calibration
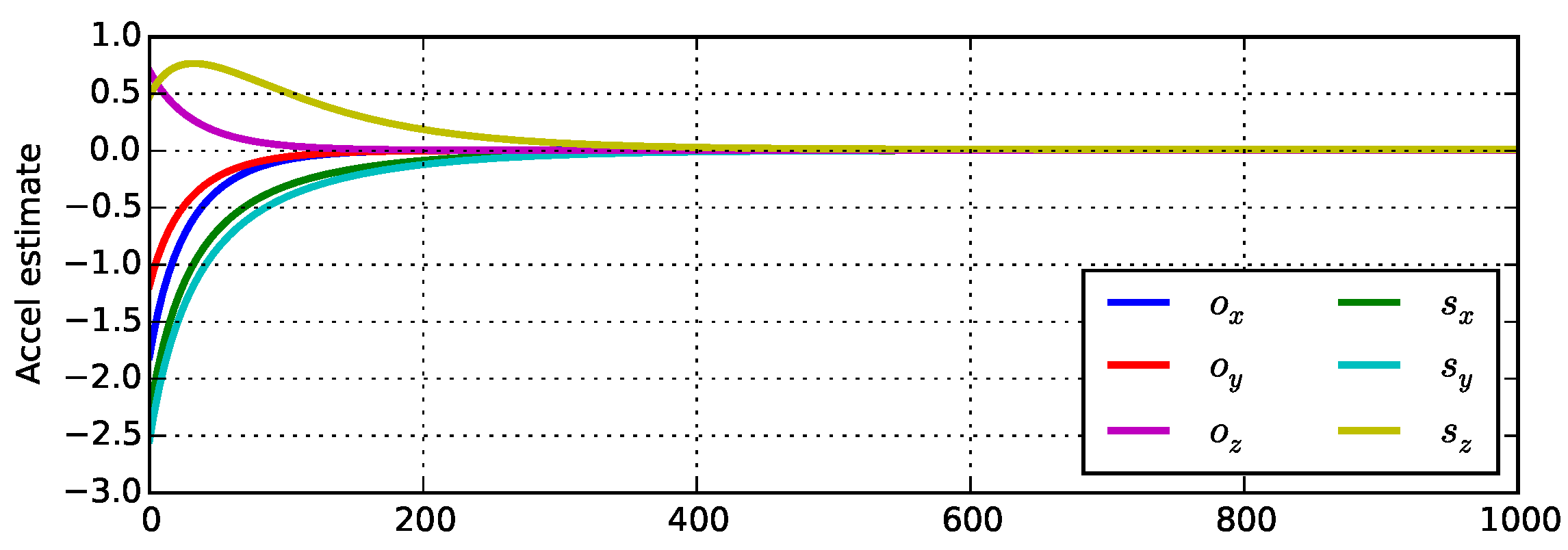
In Figure 4 we show the difference between the true and estimated offset and scale parameters for a synthetically generated dataset as function of the number of learning iterations. Convergence was determined when the norm of the gradient fell below an arbitrary small threshold (), and we can see that the estimated parameters have converged to their true values within approximately 400 iterations and that even after one iteration the estimated values were in a good approximation region.
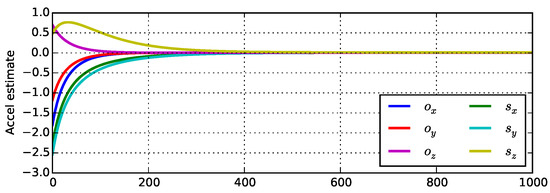
Figure 4.
Error of estimated calibration parameters as a function of iteration number. Values at zero indicates perfect estimation.
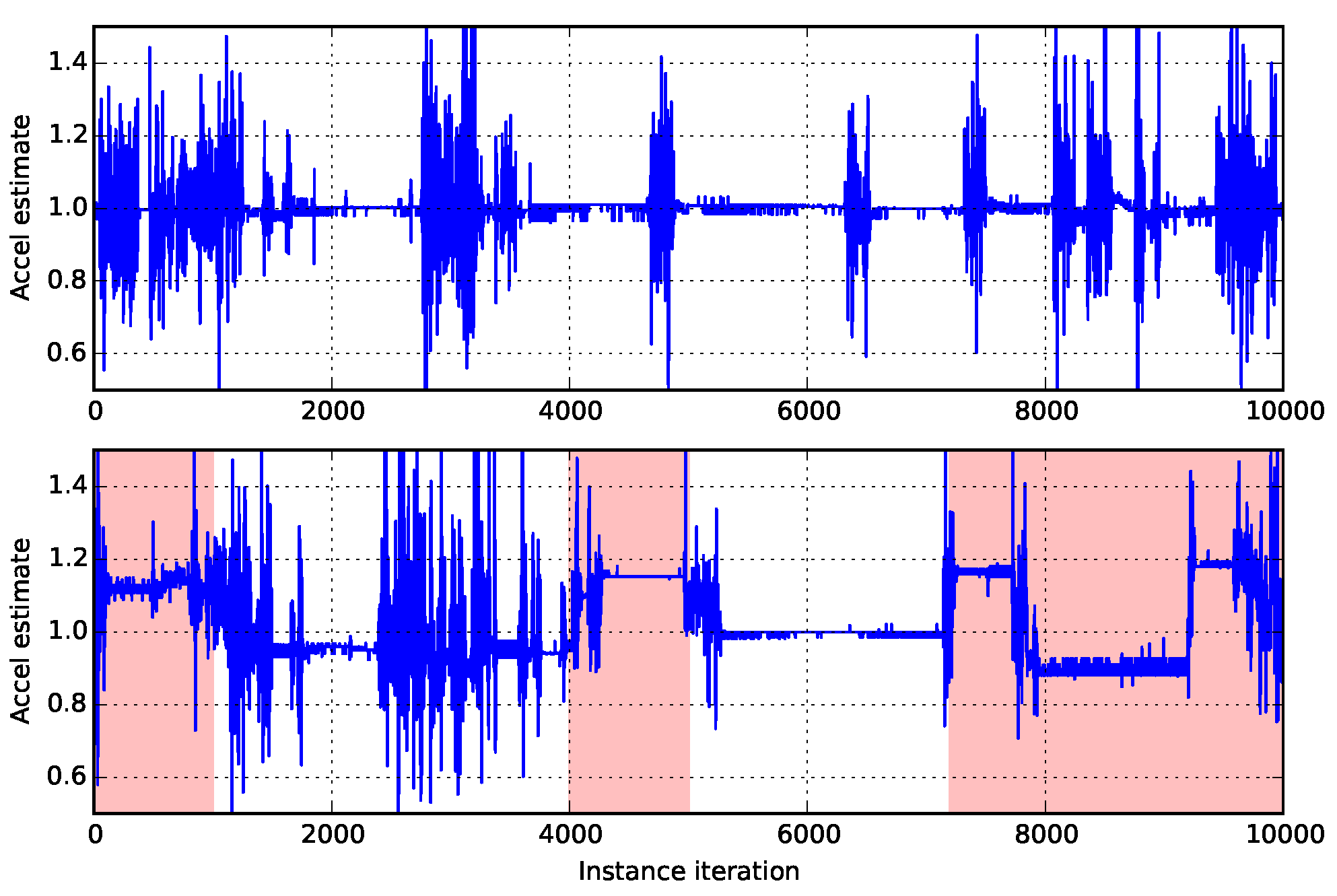
Convergence errors cannot be shown for the real datasets as the true parameters are not available. However, visual inspection of the norm of the accelerations show that good approximations are made (Figure 5 (top)), but that when using the parameters from one recording on another, the norm is offset from the 1 g position, see Figure 5 (bottom).
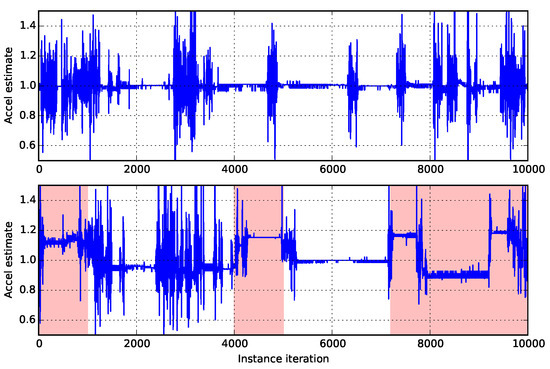
Figure 5.
Calibrated accelerometer readings (upper) that were derived from raw (uncalibrated) accelerometer values (lower). The intervals shaded in red were used to perform calibration.
4.2. Analysis of Sensor Configurations
Our analysis covers the following contexts: three datasets (har, uschad, pamap2), six classifiers (LR, MLP, RF; and these three classifiers chained together with CRFs), three classes of feature representation (statistical, dictionary-learnt, and ECDF), six sampling rates (5 Hz, 10 Hz, 20 Hz, 30 Hz, 40 Hz, and 50 Hz), four window lengths (1.5 s, 3.0 s, 4.5 s and 6 s). In total, this produces approximately 1 300 results to discuss. We will structure our analysis of these results by first presenting the analysis for one particular dataset (har). We will then discuss inter-and intra-dataset analyses.
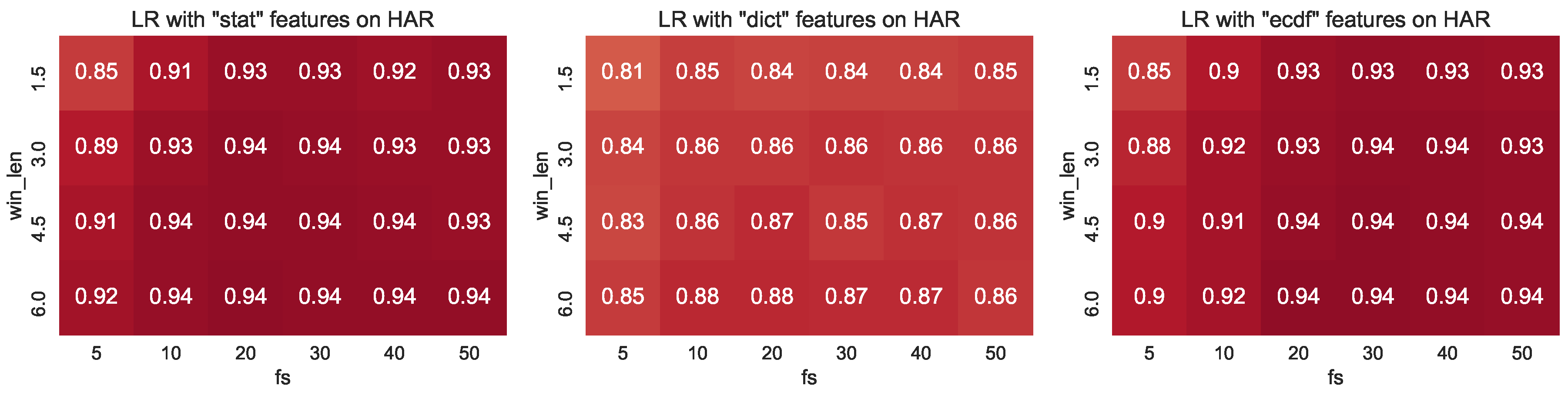
4.3. LR Performance on HAR
Figure 6 shows the classification performance of LR on the har dataset. This figure illustrates predictive accuracy over all sampling rates (rows), window lengths (columns), and features (stat features shown on left, dict features in middle, and ecdf features on the right). The colour of the subplot illustrates classification performance (0% is shown in blue, and 100% accuracy is shown in dark red). Since we will use this style of figure throughout this discussion, we adopt the following convention: will indicate the column relating to a sampling rate of 5 Hz, will relate to the row associated with a window length of 1.5 s, and corresponds to the element associated with a window length of 3 s and a sampling rate of 10 Hz.
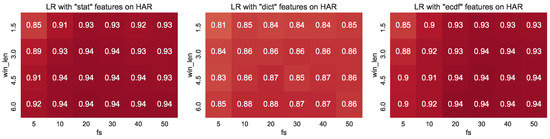
Figure 6.
Visualisation of the classification performance on the har dataset for stat features (left), dict features (middle) and ecdf features (right) over varying window lengths (rows) and sampling rates (columns). Darker red colours indicate better performance.
With the stat features (left column in Figure 6), we observe relatively consistent performance over all configurations. The performance at is the lowest of all configurations investigated by approximately 0.1. Intuitively, this performance gap makes sense: with such a low sampling rate many of the characteristics of the signal are no longer present (c.f. Figure 3), and this is further compounded by the short window. As the window length and sampling rate grow, we can observe a general trend of improving classification performance (with the maximal performance at ). Interestingly, our results show that this performance can be achieved with the following configurations relatively low-valued and . This is perhaps somewhat surprising since the data is significantly under-sampled here.
The dict features produce test performance that is, overall, significantly worse than the stat features, with maximal performance of . We can also observe the general trend of improved results with increasing window length and sampling rate that we observed with the stat features. It is surprising that the dict features are not as performant as the stat or ecdf features, particularly since these features arise from an intuitive basis. We hypothesise that since these features are learnt from data itself, and since we used a well-known heuristic of specifying the regularisation at that this heuristic is not optimal for this configuration. Additionally, the bases employed are not optimised for discrimination between classes. However, with six classes of approximately equal counts, a random classifier would achieve accuracy of ≈, indicating that these features are representing the data and labels well.
Finally, the figure on the right hand side of Figure 6 shows the classification performance of the ecdf features on the har dataset. Here, we observe classification performance that is very similar to that obtained by the stat features. This is a satisfactory result since the ecdf features are very simple and fast to extract from the raw data. This figure also demonstrates that classification performance increases with context (i.e., longer window lengths and higher sampling rates), and once again the performance seems to ‘saturate’ beyond .
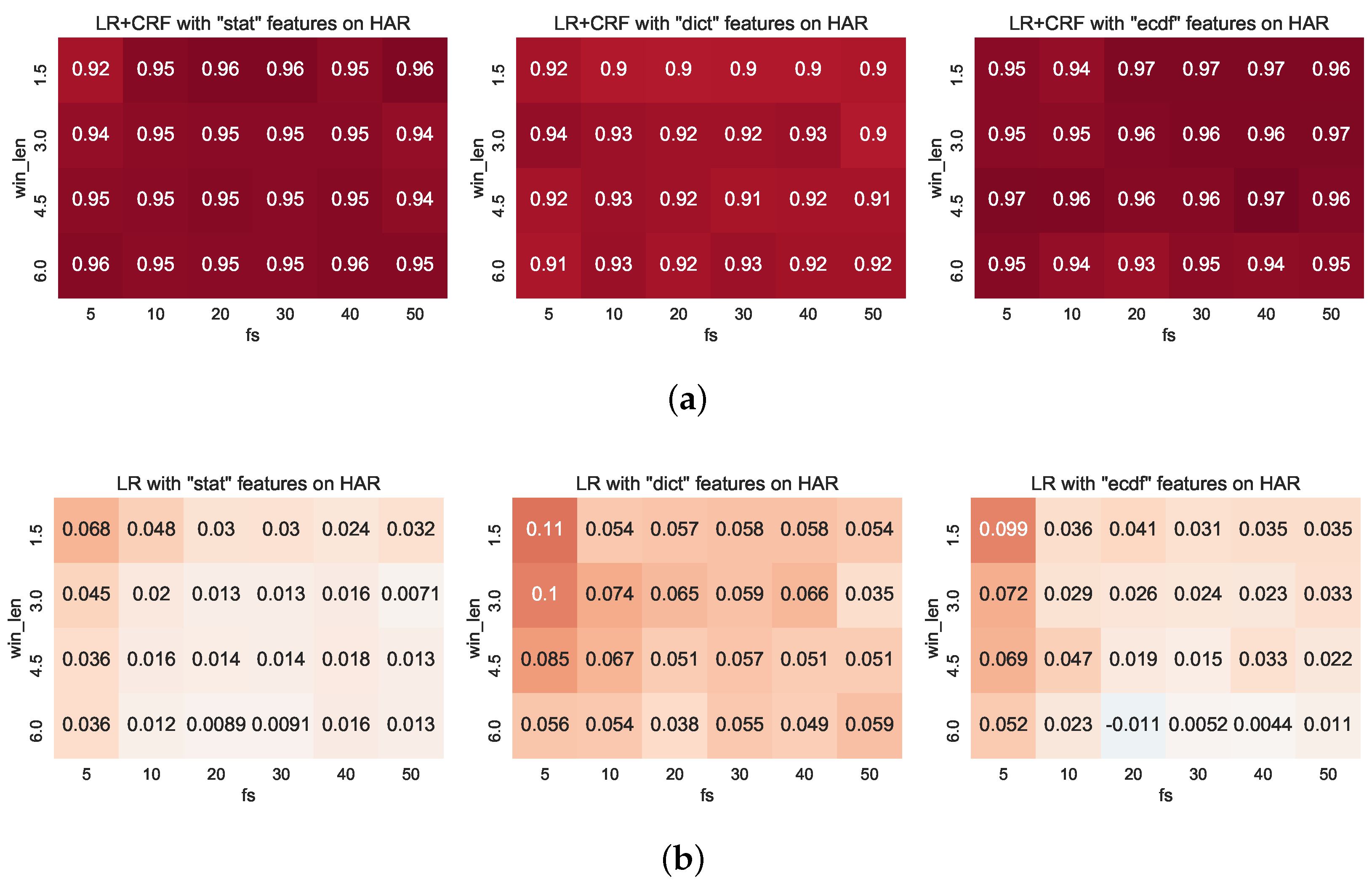
4.4. LR-CRF Performance on HAR
Figure 7 shows the classification performance that is obtained when modelling the sequences with CRFs and with LR probability estimates as the node potentials. We will identify this pairing succinctly as ‘LR-CRF’, with corresponding parings with RF and MLP denoted as RF-CRF and MLP-CRF respectively. In Figure 7a the absolute performance is shown. By comparing the performance shown on this figure with that shown on Figure 6 (note the colour scale is shared between these two figures) we can see that in general there is an improvement on classification performance over most of the configurations. Indeed, introducing the CRF has lifted the minimal classification performance by ≈9% to over 90%. The difference between the LR-CRF and the basic LR models are depicted in Figure 7b. In this figure, the red hues indicate that the LR-CRF model was more performant than the basic LR model, blue colours indicate superior performance by the basic LR model, and white colours specify that both classifiers perform comparably.
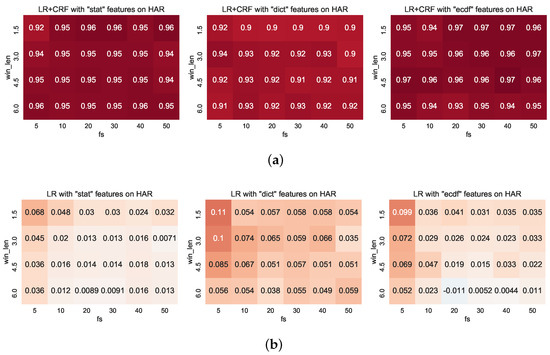
Figure 7.
Classification performance obtained by Logistic Regression-Conditional Random Field (LR-CRF) on the har dataset. (a) LR-CRF classification performance over the three feature categories considered. (b) Difference between LR-CRF and LR classification performance. Red indicates LR-CRF outperforms the basic LR model.
This figure shows that in nearly all configurations investigated modelling the structure of the data improves classification performance. Interestingly, the impact of CRFs on classification accuracy is most dramatic at low sampling rates and small window lengths. For example, for each of the three feature sets considered, the largest increase of performance is obtained at with increases to performance of ≈7–11%. This is an intuitive result since these are the settings with least context, and CRFs provide a mechanism for transferring context through chains. The incorporation of structured classifiers is known to positively impact classification performance in settings such as these [21].
4.5. Overall Impact of CRFs on Predictive Performance
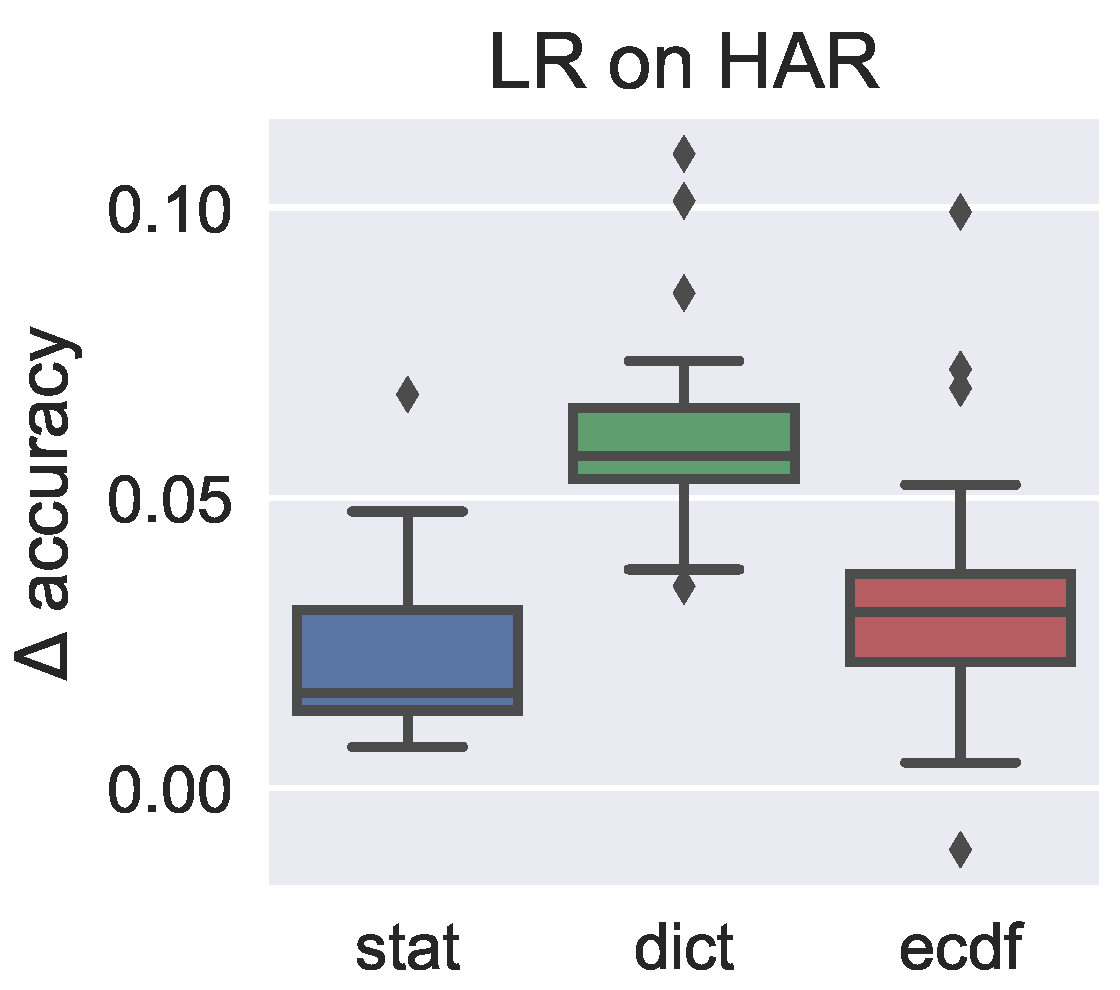
We summarise the improvement in classification performance in the box plots shown in Figure 8, and we can see here that the highest average improvement is obtained by the dict features where over 70% of configurations receive over 5% improvement in accuracy.
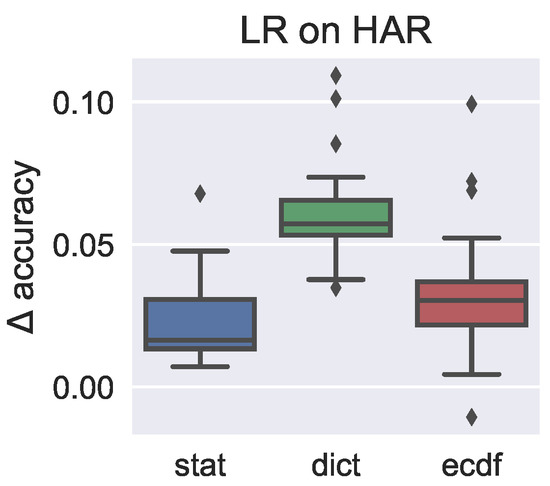
Figure 8.
Improvement in classification accuracy obtained by incorporating structure on the classification task with Conditional Random Fields (CRFs).
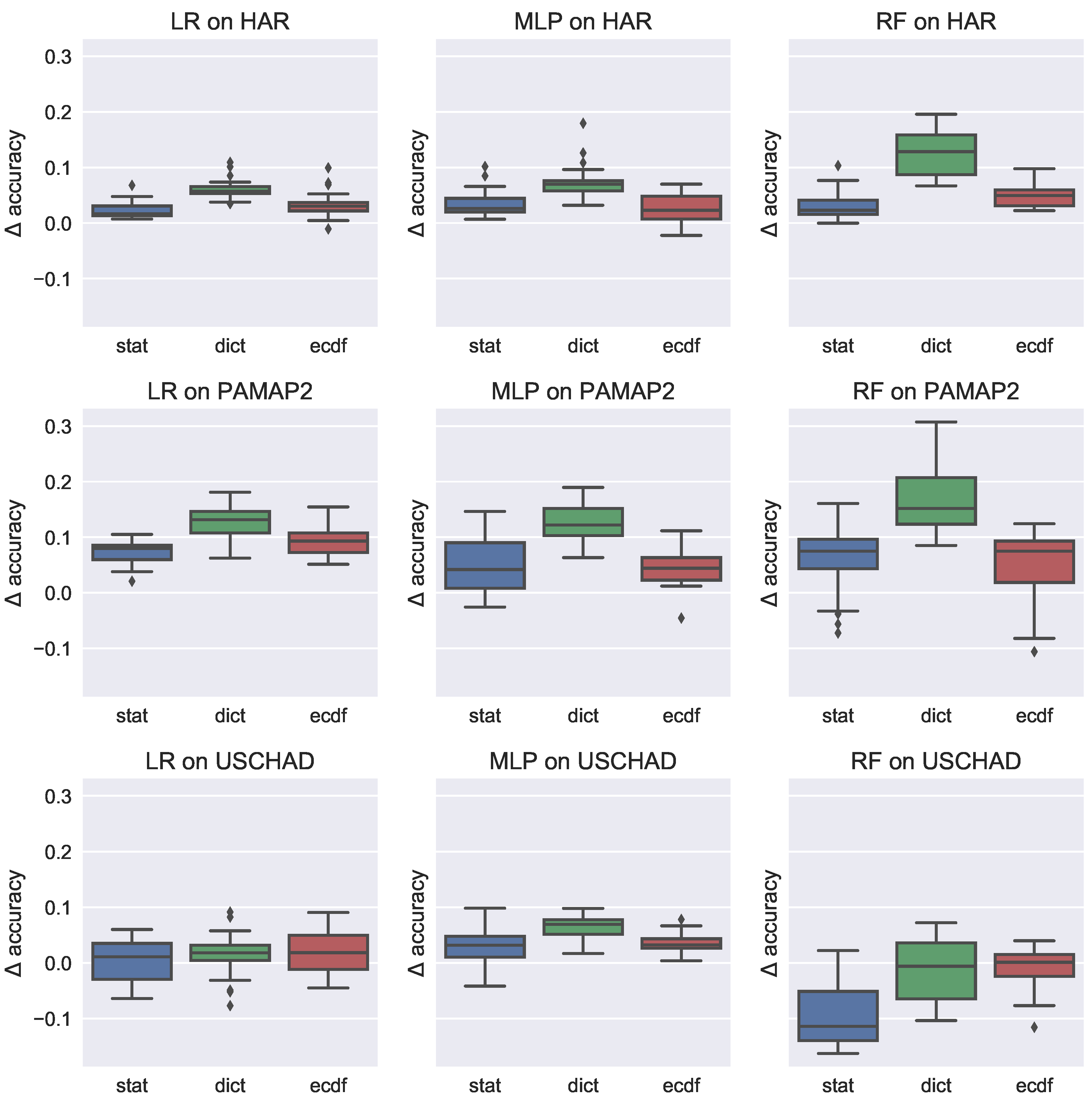
In Figure 9 we visualise the effect over all configurations. Results on HAR are shown on the top row, Results on PAMAP2 in the middle row, and USCHAD on the bottom row. The first column presents the results of LR-CRFs, the middle column on MLP-CRFs and the final column on RF-CRFs.
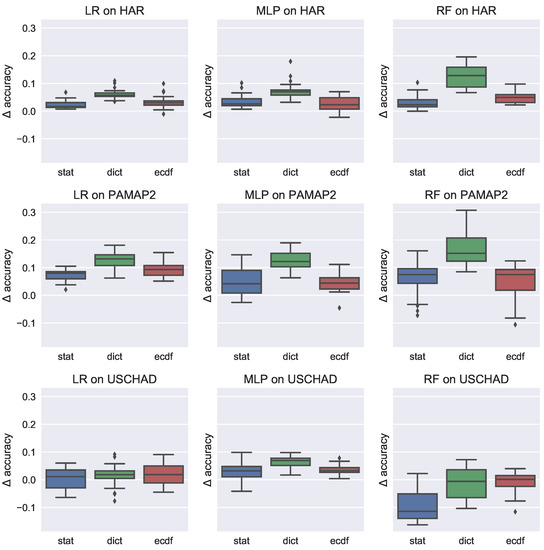
Figure 9.
Box plots over changes to performance in accuracy when using Conditional Random Field (CRF) models to capture sequential dynamics. Results on har are shown on the top row, Results on pamap2 in the middle row, and uschad on the bottom row. The first column presents the results of Logistic Regression (LR) CRFs, the middle column on Multi-layer Perceptron (MLP) CRFs and the final column on Random Forest CRFs.
In general with the HAR and PAMAP2 datasets we observe improvements to performance on all features and all classifiers. The most pronounced average improvement is observed with RF on the PAMAP2 dataset with a median improvement of approximately 0.18, with a minimal improvement of 0.1.
Interestingly, the USCHAD, on average, does not benefit from the application of CRFs on the task, particularly with the RF classifier from which we report a large negative change in accuracy. It is difficult to explain this aspect of our results. We hypothesise that since the USCHAD dataset is small that our models are overfitting to the data, despite our extensive cross validation on hyperparameters. This is, perhaps, one weakness of using probability estimates as features in the CRF namely that the indicative bias of the CRF is strongly influenced by the beliefs of an independent classifier rather than being derived solely from the raw features themselves. However, one of the advantages of the model is that it permits us to trivially learn non-linear sequence models in a principled manner. We must also recognise the general advantages of using a sequential model on this data, however, as indicated in Figure 9.
Finally, we illustrate another visualisation of the contributions of the CRFs in Figure 10. Here we perform aggregation over datasets (Figure 10a) and features (Figure 10b). In effect these figures are the ‘marginal’ distributions over the datasets and features in Figure A1, Figure A2 and Figure A3.
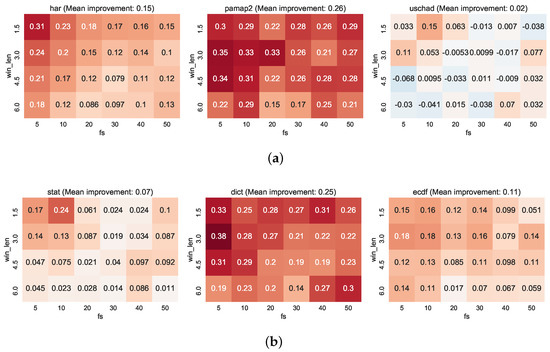
Figure 10.
Mean aggregated change in performance when aggregated over datasets (a) and features (b). (a) Mean improvement of Conditional Random Fields (CRFs) aggregated over datasets. (b) Mean improvement of Conditional Random Fields (CRFs) aggregated over features.
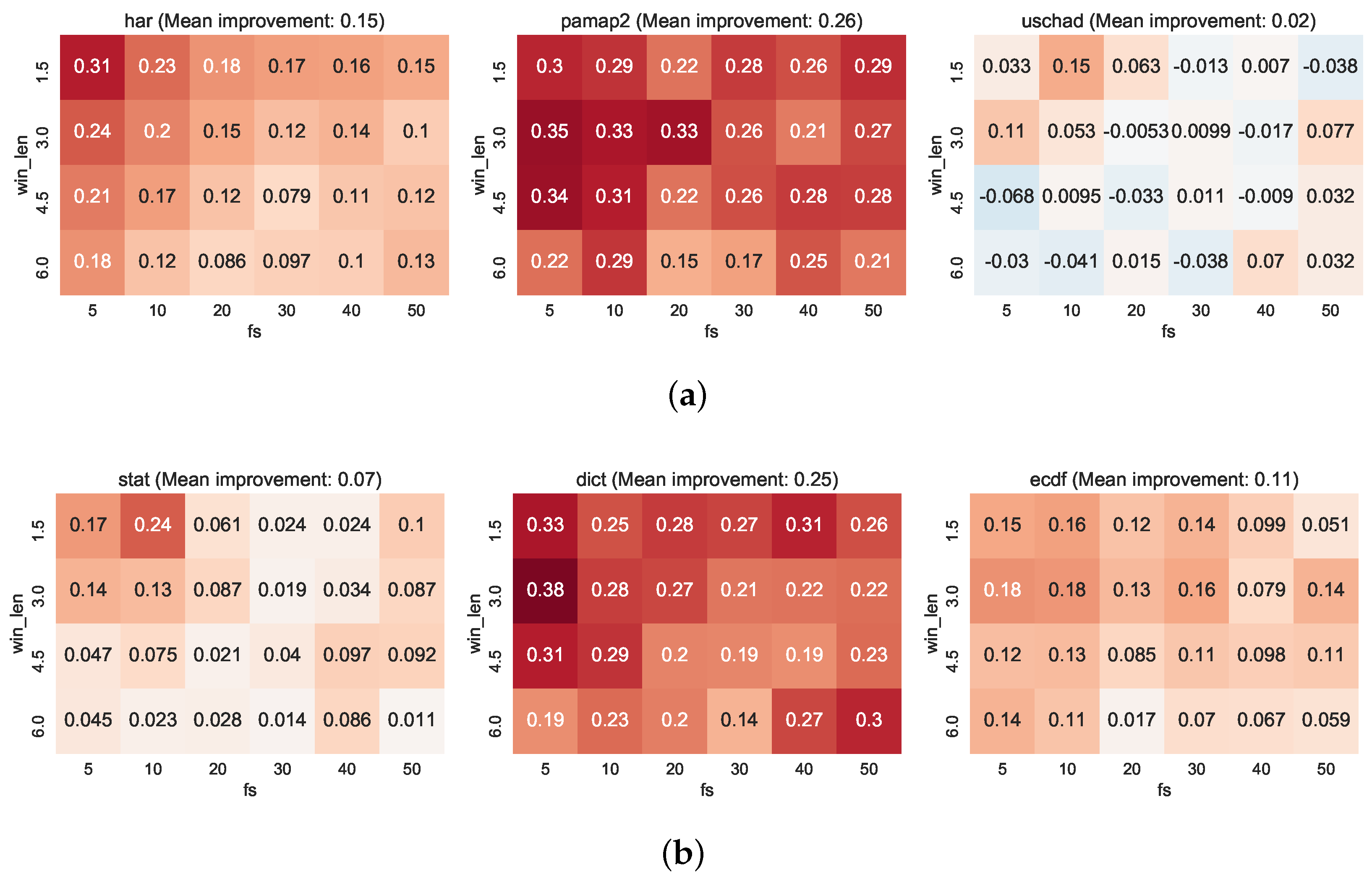
Figure 10a shows that incorporating a CRF on the datasets for the har and pamap2 datasets results in a net improvement in classification performance over all window and sampling rate configurations, with more moderate improvements shown on the uschad dataset overall. In general, the dict features make the largest contributions to this figure. There is also a general tendency for more improvement on the configurations with less context, which is a natural effect of propagating localised beliefs through the CRF structure. As reported earlier, the uschad dataset reports negligible improvements on average (with approximately 2% improvement on average). In Figure 10b, we can see that the dict features benefit most from the introduction of sequential context.
4.6. Comparison between Datasets and Classifiers
In the appendix we present the complete set of results obtained for this work that we omit from the main text owing to their size. Figure A1 shows the full set of results of the har dataset, Figure A2 shows the full results for the pamap2 dataset, and Figure A3 shows the full results for the uschad dataset. In all cases, the first subfigure corresponds to the results obtained from LR, the middle subfigure derives from MLP classifiers, and the final subfigure presents the results obtained from a RF.
On average, we can see that the har dataset receives the highest overall performance, particularly with the stat and ecdf features where the performance is often over 0.9. Since the performance of this dataset is consistently high, we speculate that the dataset may present less of a challenge from a classification perspective than the other two datasets that we consider. Several aspects will contribute to this. Firstly, in this dataset the activities were recorded in a very controlled laboratory environment, and the manner in which some of the activities were recorded is far from natural (e.g., people will rarely walk a staircase for a period of minutes). Hence, while this dataset provides a powerful resource for the analysis of common activities, it is difficult to know how models learnt on this data will generalise in naturalistic settings.
Other datasets (e.g., the SPHERE challenge [52] and Opportunity [61]) capture data and annotations in less controlled settings, but do not yet capture the aspects of activity required to be considered naturalistic. However, the SPHERE project is endeavouring to capture and release these datasets [16,17]. One of the challenges that will need to be addressed in this setting is that of acquiring labelled data, since the cohort that contribute to the data collection campaigns occur in the homes of the participants. However, un-and semi-supervised techniques [89,90] and others involving active and transfer learning [91,92,93] can be utilised in these settings.
Both pamap2 and uschad appear to be much more challenging to classify. For one thing, the average classification performance is much less than har, and often there is significantly more variation across configuration contexts, particularly with RFs. Interestingly, with these datasets, it seems that the highest performance is often obtained with the longest window lengths (i.e., ). Although this is the longest window that we considered, we did not include longer windows (e.g., or ) in our analysis since we believed that in many real settings, some activities will not last for longer than this (e.g., walking between rooms in a home environment).
A unifying result that is common to most experimental results is that the features with the least context (i.e., ) tend to achieve the lowest predictive accuracy on the test set. Often, this trait can be compensated for by increasing the window length, but with the uschad dataset (Figure A3) it is possible to see that with stat and ecdf features, only small improvements are achieved by increasing the window length for . In all of the settings of low context, significant improvements are made by introducing a model over the sequence. Interestingly, since CRFs have been shown to improve predictive performance on low-fidelity data contexts, we believe that the design pattern of chaining simple features (extracted perhaps over longer windows) and simple classifiers with CRFs can increase predictive reliability in resource-constrained settings, e.g., embedded settings for Internet of Things (IoT). Additionally, there is a pleasing interpretation to our results that taking windows of at least 3 s produces consistently strong results: in walking activity windows of 3 s will capture approximately 6 steps, if one walks at a rate of 2 steps per second. In Fourier analyses, this then permits the model to quantify the dominant frequencies of the signal reliably.
4.7. Analysis of CNN and LSTM Models
Table 4 presents the results obtained from the CNN and LSTM models on the har (left) pamap2 (middle) and uschad (right). As baseline methods we also present the results of logistic regression on the stat and ecdf features at the configuration , .

Table 4.
Classification results obtained by the statistical models (top two rows) and the advanced neural network models (bottom two rows) on the har (left), pamap2 (middle) and uschad (right) datasets with the configuration for window lengths of 3 s and accelerometer data sampled at 30 Hz. Results also show the results obtained with iid and Conditional Random Field models.
If we consider the har dataset first (left column of Table 4), we can see that in both iid and CRF settings the statistical and ECDF features perform similarly in terms of their classification performance (with a difference of 0.003 in favour of the ECDF features). Although the performance of LSTM is lower than the other models the classification performance is still high. Interestingly, we can see that all models benefit from chaining their predictions together with CRFs, and the LSTM model (which achieved the least performance in the iid setting) achieves the highest classification performance with CRFs, and in so doing its classification error reduced by approximately %.
More modest classification performance is achieved on the pamap2 dataset (middle column of Table 4), and we also observe higher variance in the predictive accuracy across the classifiers considered (with a range of ≈). In the iid and CRF settings, we can observe that the stat features achieve highest classification performance, and the model with the next highest classification performance (LSTM) is ≈ lower. It is difficult to understand why there is such a large performance gap between the stat features and the others on this dataset. We can, however, observe this pattern across all considered configurations, c.f. performance images in the Appendix.
Finally, the results of uschad dataset are shown in the right column of Table 4. We can see that the results obtained from the statistical and ECDF features are competitive to those obtained by LSTM and CNN respectively. In particular, the LSTM model obtains joint equal performance on this dataset in these configurations. We can also observe that test accuracy increases in all cases when incorporating a CRF over the base classifier’s predictions.
We conclude our analysis on the CNN and LSTM models for AR with a comment on the overall performance in comparison the the stat and ecdf features. We note that no single approach dominates the others, with stat features sometimes out performing all others, and at other times LSTM models achieve the best performance. A consistent and repeatable result that CRFs have been shown to improve classification performance nearly all settings, and sometimes (e.g., with LSTM on the har dataset) reduced classification error by ≈60%. NNs-based approaches do bring several advantages, however. We note that computation of the stat features in particular is costly in terms of CPU time. Although the CNN and LSTM models are also costly in training, one advantage of these is that they are not costly to test.
Although the main focus and contributions of this work is within-paper comparisons (i.e., how features, classifiers and sensor configurations affect classification performance over consistent data partitions and activity labels) we briefly take this opportunity to compare our results with existing literature. First, we will restate that we enforced clean partitions between subjects on train and test folds. This means that data from the test participants were never used in training. This is a much harder task than when the split is done with each participant.
The authors of the har dataset [4] also introduced the stat features that we used in this work. With these features test-set accuracy of as obtained, which is very similar to the results that we achieved with stat and ecdf features and CNN and LSTM models. However, we make improvements on these baseline results when we chain adjacent data points together with a CRF. Additionally, the authors used additional sensors in their analysis: a gyroscope. As we have discussed in the Introduction (Section 1), these sensors can consume an order of magnitude more power than accelerometers, and so we did not consider these in our analysis but yet obtained comparable performance.
The baseline performance of the pamap2 dataset [94] is approximately 80–90%. Our performance on this dataset ranges from approximately 0.7 to 0.85 in the iid setting, but we achieve predictive performance competitive accuracy of 0.91 with the CRF-chained stat-LR model. However, the baseline method considered here also incorporated a total of three accelerometer sensors while we have only used one.
With uschad, the baseline method yields a mean accuracy of approximately 67%, but have considered a much larger set of activities than our work. Additionally, the authors had access to supplementary sensors (including a Microsoft Kinect) which provides significant additional information. It is challenging to compare our results with these owing to the difference in sensor data and activity labels that were considered, but we have demonstrated that test-set accuracy of approximately 0.9 can be achieved over the configurations that we considered.
4.8. Analysis of Misclassification Errors
In this section, we show that by analysing classification errors ‘reasonable’ misclassifications generally are produced, i.e., ‘moving’ activities (walking, walking upstairs, and walking downstairs) are rarely misclassified as ‘stationary’ activities (lying, sitting, and standing). As a concrete example, with the har dataset we show the contingency tables on the test set over the six activities. The contingency tables from LR and LR+CRF are shown in Figure 11a,b respectively. In these figures, the rows indicate the ground truth and the columns the predictions, i.e., element indicates that label i is predicted as j. The contingency table of a perfect classifier will have only zero-valued off-diagonal components.
Figure 11.
Contingency tables of activities recognised on the har dataset with Linear Regression (LR) (a) and LR with Conditional Random Fields (CRFs) (b) with a window length of 3 s, and a sampling rate of 20 Hz. Rows indicate the ground truth and columns indicate predictions. (a) Contingency table for LR. (b) Contingency table for LR + CRF.
We can broadly categorise the target activities as ‘moving’ (consisting of walking, walking upstairs and walking downstairs) and ‘sedentary’ (sitting, standing and lying). Both contingency tables considered demonstrate a strong ability to separate between the activity categories, but we can see that incorporating the CRF has corrected some of the errors that occurred when using the iid classification model.
Distinguishing between the stationary activities is determined to be a harder classification task in our evaluation (particularly between sitting and standing). It is interesting to see that in the iid setting, lying can be confused as walking upstairs and walking downstairs since there is little in common between these two activities. We believe this to be because when walking up and down stairs the accelerometer will be horizontal on the banister, which is a similar pose that would occur when lying down. However, we can also observe that by introducing the CRF to the problem, these errors have been corrected, based on the incorporation of the neighbouring context.
5. Conclusions
In this paper we have examined state-of-the-art methods in activity recognition methods using accelerometers. Our particular interest is in long-term activity recognition in real-world environments, in which abundance of data, such as high frequency sampling and multiple body sensors, are not available due to maintenance restrictions in data collection. Using three publicly available data-sets, we have attempted to answer some open questions in the literature: Should we be using structured models, or is it sufficient to consider the data as if it were iid? Are the approaches taken so far genuinely robust across different contexts across a wide variety of activities that summarise activities of daily living? What are the most appropriate features and how robust are these across activities? What is the minimum sampling rate required to get good classification performance? Do advanced neural network models out-perform more classical feature-based representations?
Our results provide evidence for answering many of the questions posed at the beginning of this paper. First, we have noted that incorporating lower sampling frequencies does not worsen classification performance. That low sampling frequencies do not deteriorate classification is of particular interest for machine learning and sensor researchers. We also conclude that the use of longer feature windows for feature extraction can help the classification, as such configurations may capture a greater proportion of the temporal context of the activities. This context can alternatively be captured by introducing structured models, and we showed examples where structured models are preferable to unstructured models.
One of the principal contributions of this work is that, somewhat surprisingly, many disparate experimental configurations yield comparable predictive performance on testing data. We understand these results arising from the experimental setup directly and indirectly define a pathway for context to be delivered to the classifier, and that, in some settings, certain configurations are more optimal than alternatives. Interestingly, our experiments show that regardless of how context arrives to a classifier (whether via high sampling rate, wide feature windows or by modelling sequences) competitive performance can be achieved. In particular we summarise our analysis with the following observations:
- Context can be delivered to classification models by increasing the sampling rate, selecting wide feature windows for feature extraction, modelling the temporal dependence between features.
- Classification performance tends to improve when these configurations are independently ‘increased’ (i.e., more context introduced).
- There tends to be a performance plateau for any given dataset (i.e., maximal performance) and our results indicate this can be achieved on several device, feature and classifier configurations.
With these observations in mind, our recommendations are that practitioners that use low sampling rates (e.g., in IoT settings) utilise sequential classifiers in prediction. On less constrained data acquisition contexts, however, there is more freedom for the practitioner to specify their pipeline. However, given the consistency of our empirical evaluation we would still recommend incorporating sequential information on the task in general.
Additionally, we conclude that since most accelerometer-based activity recognition datasets have been collected in controlled lab environments, it is difficult to estimate performance of these methods in the wild. Therefore, there is a pressing need for naturalistic datasets, but several challenges are impeding the collection and release of naturalistic activity recognition datasets.
Future work will include deeper analysis into the definition and explicit specification of the most important features for activity recognition, particularly in natural settings. This will include the incorporation of fully Bayesian models in which both the means and variances of the posterior distribution will be informative towards this goal, e.g., Gaussian Process models using Automatic Relevance Determination (ARD) [95]. The introduction of such methods will reduce the risk of overfitting, but Bayesian models can naturally be adapted to hierarchical models which can naturally lead to transfer learning frameworks [96]. All future experiments will be validated against these datasets and others.
Author Contributions
N.T. and T.D. conceived and designed the experiments; N.T. performed the experiments; N.T. and T.D. analysed the data; All authors wrote and edited the paper.
Acknowledgments
This work was performed under the Sensor Platform for HEalthcare in a Residential Environment (SPHERE) Interdisciplinary Research Collaboration (IRC) funded by the UK Engineering and Physical Sciences Research Council (EPSRC), Grant EP/K031910/1. N.T is funded by the Continuous Behavioural Biomarkers of Cognitive Impairment (CUBOId) project funded by the UK Medical Research Council Momentum Awards under Grant MC-PC-16029. R.M is funded by EurValve (Personalised Decision Support for Heart Valve Disease), Project Number: H2020 PHC-30-201.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This section tabulates the complete set of results. Each table provides the classification accuracy of the three feature sets considered (stat, ecdf and dict) with LR, RF and MLP. Each table tabulates classification performance over 24 independent sensor configurations discussed in Section 3.7.
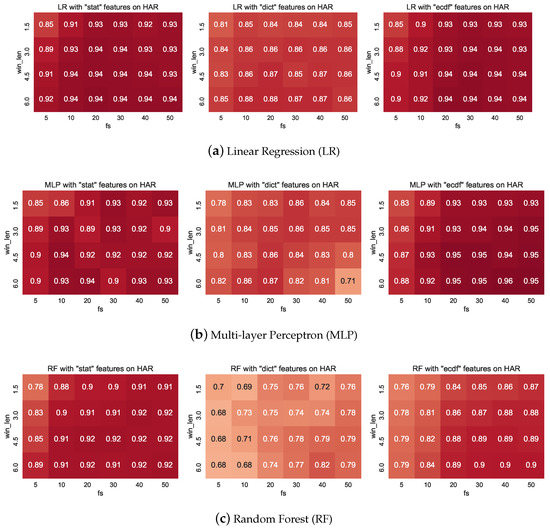
Figure A1.
Classification performance on the har dataset with all iid feature configurations.
Figure A1.
Classification performance on the har dataset with all iid feature configurations.
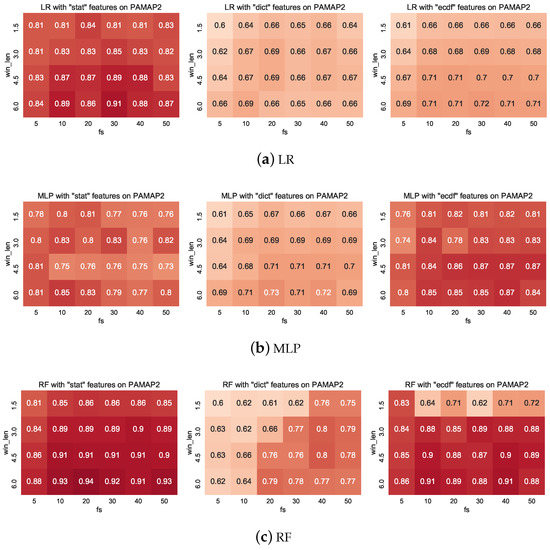
Figure A2.
Classification performance on the PAMAP2 dataset with all iid feature configurations.
Figure A2.
Classification performance on the PAMAP2 dataset with all iid feature configurations.
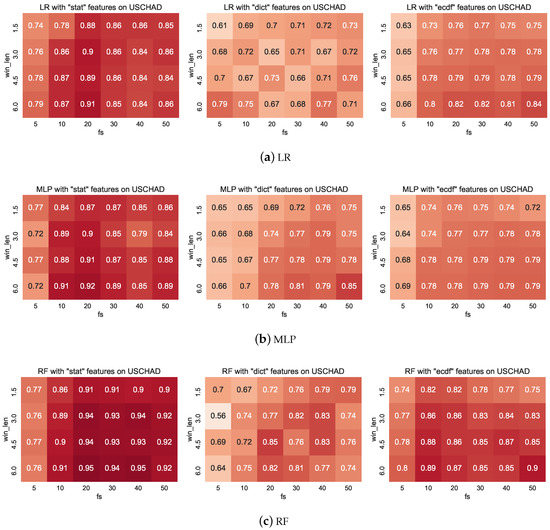
Figure A3.
Classification performance on the USCHAD dataset with all iid feature configurations.
Figure A3.
Classification performance on the USCHAD dataset with all iid feature configurations.
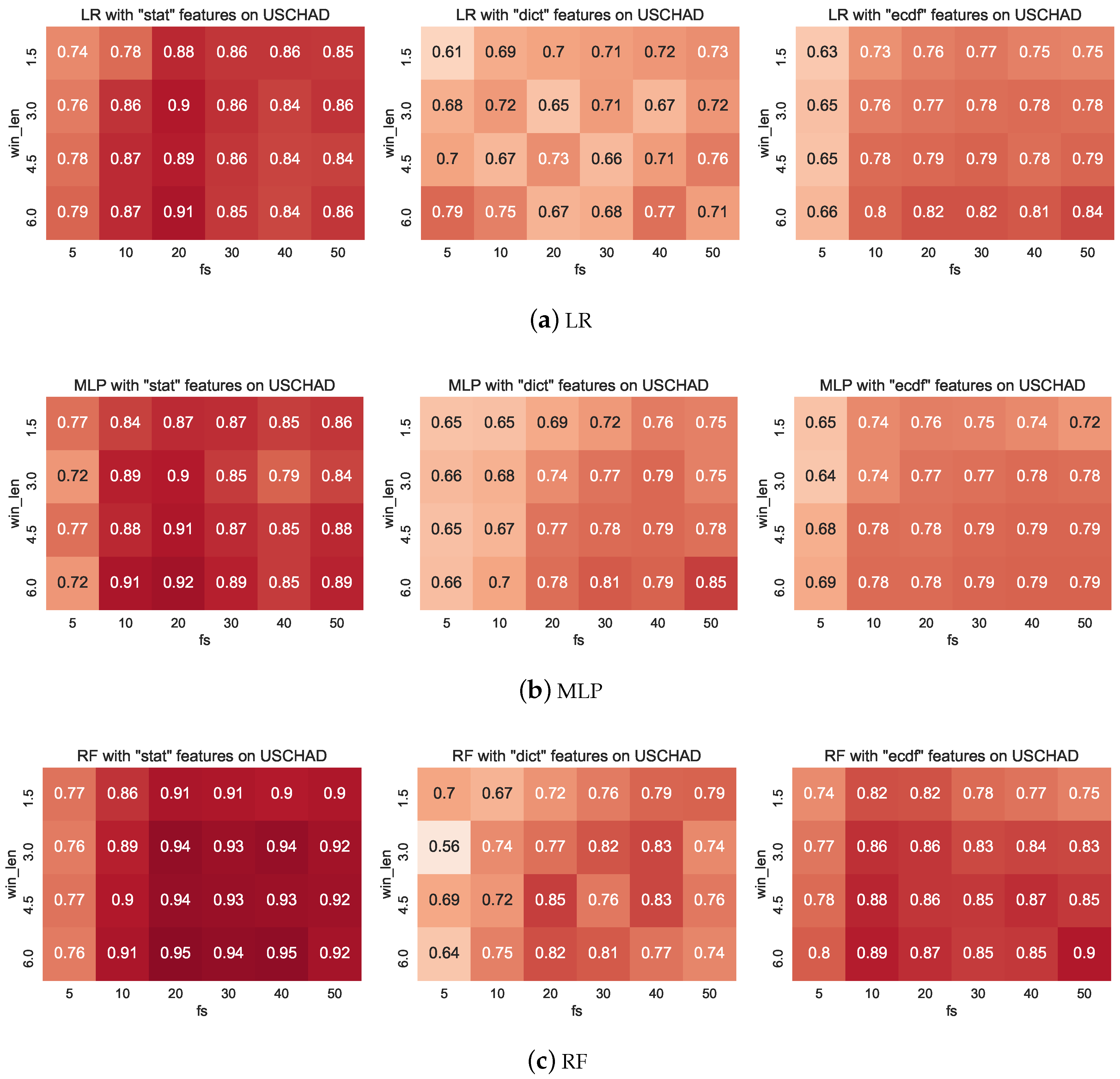
References
- Biddle, S.; Biddle, S.J.H.; Pearson, N.; Ross, G.M.; Braithwaite, R. Tracking of sedentary behaviours of young people: A systematic review. Prev. Med. 2010, 51, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Kwapisz, J.; Weiss, G.; Moore, S. Activity recognition using cell phone accelerometers. ACM SigKDD Explor. Newsl. 2011, 12, 74–82. [Google Scholar] [CrossRef]
- Siirtola, P.; Röning, J. Recognizing Human Activities User-Independently on Smartphones Based on Accelerometer Data. Int. J. Int. Multimed. Artif. Intell. 2012, 1, 38–45. [Google Scholar] [CrossRef]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. A public domain dataset for human activity recognition using smartphones. In Proceedings of the 21th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 24–26 April 2013. [Google Scholar]
- Brezmes, T.; Gorricho, J.L.; Cotrina, J. Activity recognition from accelerometer data on a mobile phone. In Distributed Computing, Artificial Intelligence, Bioinformatics, Soft Computing, and Ambient Assisted Living; Springer: Heidelberg/Berlin, Germany, 2009; pp. 796–799. [Google Scholar]
- Piyathilaka, L.; Kodagoda, S. Gaussian mixture based HMM for human daily activity recognition using 3D skeleton features. In Proceedings of the 8th IEEE Conference on Industrial Electronics and Applications (ICIEA), Melbourne, Australia, 19–21 June 2013; pp. 567–572. [Google Scholar]
- Krishnan, N.; Cook, D. Activity recognition on streaming sensor data. Perv. Mob. Comput. 2014, 10, 138–154. [Google Scholar] [CrossRef] [PubMed]
- Diethe, T.; Twomey, N.; Kull, M.; Flach, P.; Craddock, I. Probabilistic sensor fusion for ambient assisted living. arXiv 2017, arXiv:1702.01209. [Google Scholar]
- Bergmann, J.; McGregor, A. Body-worn sensor design: What do patients and clinicians want? Ann. Biomed. Eng. 2011, 39, 2299–2312. [Google Scholar] [CrossRef] [PubMed]
- Bulling, A.; Blanke, U.; Schiele, B. A tutorial on human activity recognition using body-worn inertial sensors. ACM Comput. Surv. 2014, 46, 33. [Google Scholar] [CrossRef]
- Diethe, T.R. Sparse Machine Learning Methods With Applications in Multivariate Signal Processing. Ph.D. Thesis, UCL Advances, University College London, London, UK, 2010. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Support Vector Machines; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Quinlan, J. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Williams, C.; Barber, D. Bayesian classification with Gaussian processes. Patt. Anal. Mach. Intell. 1998, 20, 1342–1351. [Google Scholar] [CrossRef]
- Bao, L.; Intille, S. Activity Recognition From User-Annotated Acceleration Data. In Pervasive Computing; Springer: Heidelberg/Berlin, Germany, 2004; pp. 1–17. [Google Scholar]
- Zhu, N.; Diethe, T.; Camplani, M.; Tao, L.; Burrows, A.; Twomey, N.; Kaleshi, D.; Mirmehdi, M.; Flach, P.; Craddock, I. Bridging e-Health and the Internet of Things: The SPHERE Project. Intelli. Syst. IEEE 2015, 30, 39–46. [Google Scholar] [CrossRef]
- Woznowski, P.; Burrows, A.; Diethe, T.; Fafoutis, X.; Hall, J.; Hannuna, S.; Camplani, M.; Twomey, N.; Kozlowski, M.; Tan, B.; et al. SPHERE: A sensor platform for healthcare in a residential environment. In Designing, Developing, and Facilitating Smart Cities; Springer: Heidelberg/Berlin, Germany, 2017; pp. 315–333. [Google Scholar]
- Woznowski, P.; Fafoutis, X.; Song, T.; Hannuna, S.; Camplani, M.; Tao, L.; Paiement, A.; Mellios, E.; Haghighi, M.; Zhu, N.; et al. A Multi-modal Sensor Infrastructure for Healthcare in a Residential Environment. In Proceedings of the 2015 IEEE International Conference on Communication Workshop, London, UK, 8–12 June 2015. [Google Scholar]
- Ravi, N.; Dandekar, N.; Mysore, P.; Littman, M.L. Activity Recognition from Accelerometer Data. In Proceedings of the 17th Conference on Innovative Applications of Artificial Intelligence, Pittsburgh, PA, USA, 9–13 July 2005; Volume 3, pp. 1541–1546. [Google Scholar]
- Karantonis, D.M.; Narayanan, M.R.; Mathie, M.; Lovell, N.H.; Celler, B.G. Implementation of a real-time human movement classifier using a triaxial accelerometer for ambulatory monitoring. IEEE Trans. Inf. Technol. Biomed. 2006, 10, 156–167. [Google Scholar] [CrossRef] [PubMed]
- Twomey, N.; Diethe, T.; Flach, P. On the need for structure modelling in sequence prediction. Mach. Learn. 2016, 104, 291–314. [Google Scholar] [CrossRef]
- Rabiner, L.; Juang, B.H. An introduction to hidden Markov models. ASSP Mag. IEEE 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Lafferty, J.; McCallum, A.; Pereira, F. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. In Proceedings of the Eighteenth International Conference on Machine Learning, Williamstown, MA, USA, 28 June–1 July 2001; pp. 282–289. [Google Scholar]
- Nazerfard, E.; Das, B.; Holder, L.B.; Cook, D.J. Conditional random fields for activity recognition in smart environments. In Proceedings of the 1st ACM International Health Informatics Symposium, Arlington, VA, USA, 11–12 November 2010; pp. 282–286. [Google Scholar]
- Lee, S.; Le, H.X.; Ngo, H.Q.; Kim, H.I.; Han, M.; Lee, Y.K. Semi-Markov conditional random fields for accelerometer-based activity recognition. Appl. Intell. 2011, 35, 226–241. [Google Scholar]
- Janidarmian, M.; Roshan Fekr, A.; Radecka, K.; Zilic, Z. A comprehensive analysis on wearable acceleration sensors in human activity recognition. Sensors 2017, 17, 529. [Google Scholar] [CrossRef] [PubMed]
- San-Segundo, R.; Montero, J.M.; Barra-Chicote, R.; Fernández, F.; Pardo, J.M. Feature extraction from smartphone inertial signals for human activity segmentation. Signal Process. 2016, 120, 359–372. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Gupta, P.; Dallas, T. Feature selection and activity recognition system using a single triaxial accelerometer. IEEE Trans. Biomed. Eng. 2014, 61, 1780–1786. [Google Scholar] [CrossRef] [PubMed]
- Hammerla, N.; Kirkham, R.; Andras, P.; Ploetz, T. On Preserving Statistical Characteristics of Accelerometry Data Using Their Empirical Cumulative Distribution. In Proceedings of the 2013 International Symposium on Wearable Computers, Zurich, Switzerland, 8–12 September 2013; pp. 65–68. [Google Scholar]
- Elsts, A.; McConville, R.; Fafoutis, X.; Twomey, N.; Piechocki, R.; Santos-Rodriguez, R.; Craddock, I. On-Board Feature Extraction from Acceleration Data for Activity Recognition. In Proceedings of the International Conference on Embedded Wireless Systems and Networks (EWSN), Madrid, Spain, 14–16 February 2018. [Google Scholar]
- Santos-Rodriguez, R.; Twomey, N. Efficient approximate representations of computationally expensive features. In Proceedings of the European Symposium on Artificial Neural Networks (ESANN), Bruges, Belgium, 25–27 April 2018. [Google Scholar]
- Plötz, T.; Hammerla, N.; Olivier, P. Feature Learning for Activity Recognition in Ubiquitous Computing. In Proceedings of the 22nd Intenational Joint Conference on Artificial Intelligence (IJCAI), Barcelona, Spain, 19–22 July 2011; pp. 1729–1734. [Google Scholar]
- Alsheikh, M.A.; Selim, A.; Niyato, D.; Doyle, L.; Lin, S.; Tan, H.P. Deep Activity Recognition Models with Triaxial Accelerometers. arXiv 2016, arXiv:1511.04664v2. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Nurmi, P.; Hammerla, N.; Plötz, T. Using unlabeled data in a sparse-coding framework for human activity recognition. Perv. Mob. Comput. 2014, 15, 242–262. [Google Scholar] [CrossRef]
- Nguyen, T.; Gupta, S.; Venkatesh, S.; Phung, S. A Bayesian Nonparametric Framework for Activity Recognition Using Accelerometer Data. In Proceedings of the 2014 22nd International Conference on Pattern Recognition, 24–28 August 2014; pp. 2017–2022. [Google Scholar]
- Teh, Y.; Jordan, M.I.; Beal, M.J. Hierarchical Dirichlet Processes. J. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
- Siirtola, P.; Laurinen, P.; Haapalainen, E.; Roning, J. Clustering-based activity classification with a wrist-worn accelerometer using basic features. In Proceedings of the Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009; pp. 95–100. [Google Scholar]
- Keogh, E.; Chu, S.; Hart, D.; Pazzani, M. Segmenting time series: A survey and novel approach. Data Min. Time Series Databases 2004, 57, 1–22. [Google Scholar]
- Fox, E.; Sudderth, E.B.; Jordan, M.I.; Willsky, A.S. An HDP-HMM for systems with state persistence. In Proceedings of the 25th Intenationna Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 312–319. [Google Scholar]
- Maurer, U.; Sudderth, E.B.; Jordan, M.I.; Willsky, A.S. Activity recognition and monitoring using multiple sensors on different body positions. In Proceedings of the International Workshop on Wearable and Implantable Body Sensor Networks (BSN), Cambridge, MA, USA, 3–5 April 2006; pp. 113–116. [Google Scholar]
- Sztyler, T.; Stuckenschmidt, H. On-body localization of wearable devices: An investigation of position-aware activity recognition. In Proceedings of the 2016 IEEE International Conference on Pervasive Computing and Communications (PerCom), Sydney, Australia, 14–19 March 2016; pp. 1–9. [Google Scholar]
- Ordóñez, F.J.; Roggen, D. Deep convolutional and lstm recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Ha, S.; Choi, S. Convolutional neural networks for human activity recognition using multiple accelerometer and gyroscope sensors. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 381–388. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neur. Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Fafoutis, X.; Elsts, A.; Piechocki, R.; Craddock, I. Experiences and Lessons Learned from Making IoT Sensing Platforms for Large-Scale Deployments. IEEE Access 2018, 6, 3140–3148. [Google Scholar] [CrossRef]
- Fafoutis, X.; Vafeas, A.; Janko, B.; Sherratt, R.S.; Pope, J.; Elsts, A.; Mellios, E.; Hilton, G.; Oikonomou, G.; Piechocki, R.; et al. Designing Wearable Sensing Platforms for Healthcare in a Residential Environment. Trans. Perv. Health Technol. 2017, 17. [Google Scholar] [CrossRef]
- Fafoutis, X.; Marchegiani, L.; Elsts, A.; Pope, J.; Craddock, I. Extending the Battery Lifetime of Wearable Sensors with Embedded Machine Learning. In Proceedings of the 4th IEEE World Forum on Internet of Things (IEEE WF-IoT), Singapore, 5–8 February 2018; pp. 269–274. [Google Scholar]
- Khan, A.; Hammerla, N.; Mellor, S.; Plötz, T. Optimising sampling rates for accelerometer-based human activity recognition. Patt. Recognit. Lett. 2016, 73, 33–40. [Google Scholar] [CrossRef]
- Foerster, F.; Smeja, M.; Fahrenberg, J. Detection of posture and motion by accelerometry: A validation study in ambulatory monitoring. Comput. Hum. Behav. 1999, 15, 571–583. [Google Scholar] [CrossRef]
- Twomey, N.; Diethe, T.; Kull, M.; Song, H.; Camplani, M.; Hannuna, S.; Fafoutis, X.; Zhu, N.; Woznowski, P.; Flach, P.; et al. The SPHERE challenge: Activity recognition with multimodal sensor data. arXiv 2016, arXiv:1603.00797. [Google Scholar]
- Casale, P.; Pujol, O.; Radeva, P. Personalization and user verification in wearable systems using biometric walking patterns. Person. Ubiquit. Comput. 2012, 16, 563–580. [Google Scholar] [CrossRef]
- Borazio, M.; Van Laerhoven, K. Using time use with mobile sensor data: A road to practical mobile activity recognition? In Proceedings of the 12th International Conference on Mobile and Ubiquitous Multimedia, Lulea, Sweden, 2–5 December 2013; p. 20. [Google Scholar]
- Huynh, T.; Fritz, M.; Schiele, B. Discovery of activity patterns using topic models. In Proceedings of the 10th International Conference on Ubiquitous Computing, Seoul, Korea, 21–24 September 2008; pp. 10–19. [Google Scholar]
- Stikic, M.; Schiele, B. ADL recognition based on the combination of RFID and accelerometer sensing. In Proceedings of the 2nd International Conference on Pervasive Computing Technologies for Healthcare, Tampere, Finland, 30 Janury–1 February 2008; pp. 258–263. [Google Scholar] [CrossRef]
- Van Laerhoven, K.; Berlin, E.; Schiele, B. Enabling efficient time series analysis for wearable activity data. In Proceedings of the 2009 International Conference on Machine Learning and Applications, Miami Beach, FL, USA, 13–15 December 2009; pp. 392–397. [Google Scholar]
- Van Laerhoven, K.; Kilian, D.; Schiele, B. Using rhythm awareness in long-term activity recognition. In Proceedings of the 12th IEEE International Symposium on Wearable Computers, Pittsburgh, PA, USA, 28 September–1 October 2008; pp. 63–66. [Google Scholar]
- Borazio, M.; Berlin, E.; Kücükyildiz, N.; Scholl, P.; Laerhoven, K.V. Towards Benchmarked Sleep Detection with Wrist-Worn Sensing Units. In Proceedings of the 2014 IEEE International Conference on Healthcare Informatics, Verona, Italy, 15–17 September 2014; IEEE Computer Society: Washington, DC, USA; pp. 125–134. [Google Scholar]
- Borazio, M.; Van Laerhoven, K. Combining wearable and environmental sensing into an unobtrusive tool for long-term sleep studies. In Proceedings of the 2nd ACM SIGHIT International Health Informatics Symposium, Miami, FL, USA, 28–30 January 2012; pp. 71–80. [Google Scholar]
- Chavarriaga, R.; Sagha, H.; Calatroni, A.; Digumarti, S.T.; Roggen, D. The Opportunity challenge: A benchmark database for on-body sensor-based activity recognition. Patt. Recognit. Lett. 2013, 34, 2033–2042. [Google Scholar] [CrossRef]
- Zhang, M.; Sawchuk, A.A. USC-HAD: A Daily Activity Dataset for Ubiquitous Activity Recognition Using Wearable Sensors. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, PA, USA, 5–8 September 2012; ACM: New York, NY, USA; pp. 1036–1043. [Google Scholar]
- Reiss, A.; Stricker, D. Creating and Benchmarking a New Dataset for Physical Activity Monitoring. In Proceedings of the 5th International Conference on PErvasive Technologies Related to Assistive Environments, Heraklion, Greece, 6–8 June 2012; pp. 40:1–40:8. [Google Scholar]
- Twomey, N.; Faul, S.; Marnane, W. Comparison of accelerometer-based energy expenditure estimation algorithms. In Proceedings of the 4th International Conference on Pervasive Computing Technologies for Healthcare (PervasiveHealth), Munich, Germany, 22–25 March 2010; pp. 1–8. [Google Scholar]
- Olshausen, B.A.; Field, D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 1996, 381, 607–609. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.I. A tutorial on principal components analysis. Cornell Univ. USA 2002, 51, 65. [Google Scholar]
- Balan, R.; Casazza, P.G.; Heil, C.; Landau, Z. Density, overcompleteness, and localization of frames. I. Theory. J. Fourier Anal. Appl. 2006, 12, 105–143. [Google Scholar] [CrossRef]
- Bach, F.; Jenatton, R.; Mairal, J.; Obozinski, G. Optimization with sparsity-inducing penalties. Found. Trends Mach. Learn. 2012, 4, 1–106. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. Available online: http://cvxr.com/cvx (accessed on 29 May 2018).
- Diethe, T.; Twomey, N.; Flach, P. BDL. NET: Bayesian dictionary learning in Infer. NET. In Proceedings of the 2016 IEEE 26th International Workshop on Machine Learning for Signal Processing (MLSP), Salerno, Italy, 13–16 September 2016; pp. 1–6. [Google Scholar]
- Haar, A. Zur theorie der orthogonalen funktionensysteme. Math. Ann. 1910, 69, 331–371. [Google Scholar] [CrossRef]
- Mallat, S.; Zhang, Z. Matching pursuit with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Bristow, H.; Eriksson, A.; Lucey, S. Fast convolutional sparse coding. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, Oregon, 25–27 June 2013; pp. 391–398. [Google Scholar]
- Vollmer, C.; Gross, H.M.; Eggert, J. Learning Features for Activity Recognition with Shift-Invariant Sparse Coding. In Artificial Neural Networks and Machine Learning ICANN 2013; Springer: Heidelberg/Berlin, Germany, 2013; Volume 8131, pp. 367–374. [Google Scholar]
- Eggert, J.; Wersing, H.; Korner, E. Transformation-invariant representation and NMF. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 4, pp. 2535–2539. [Google Scholar]
- Mairal, J.; Ponce, J.; Sapiro, G.; Zisserman, A.; Bach, F.R. Supervised Dictionary Learning. In Advances in Neural Information Processing Systems 21; Koller, D., Schuurmans, D., Bengio, Y., Bottou, L., Eds.; Curran Associates, Inc.: New York, NY, USA, 2009; pp. 1033–1040. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Wadsworth and Brooks: Monterey, CA, USA, 1984. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: New York, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neur. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lipton, Z.C. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Sutton, C.; McCallum, A. An introduction to conditional random fields. Mach. Learn. 2011, 4, 267–373. [Google Scholar] [CrossRef]
- Pearl, J. Reverend Bayes on inference engines: A distributed hierarchical approach. In Proceedings of the Second AAAI Conference on Artificial Intelligence, Pittsburgh, PA, USA, 18–20 August 1982; pp. 133–136. [Google Scholar]
- Hoefel, G.; Elkan, C. Learning a two-stage SVM/CRF sequence classifier. In Proceedings of the 17th ACM Conference on Information and Knowledge Management, Napa Valley, CA, USA, 26–30 October 2008; ACM: Menlo Park, CA, USA, 2008; pp. 271–278. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Twomey, N.; Diethe, T.; Craddock, I.; Flach, P. Unsupervised learning of sensor topologies for improving activity recognition in smart environments. Neurocomputing 2017, 234, 93–106. [Google Scholar] [CrossRef]
- Chen, Y.; Diethe, T.; Flach, P. ADLTM: A Topic Model for Discovery of Activities of Daily Living in a Smart Home. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016. [Google Scholar]
- Diethe, T.; Twomey, N.; Flach, P. Active transfer learning for activity recognition. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 27–29 April 2016. [Google Scholar]
- Twomey, N.; Diethe, T.; Flach, P. Bayesian active learning with evidence-based instance selection. In Proceedings of the Workshop on Learning over Multiple Contexts, European Conference on Machine Learning (ECML15), Porto, Portugal, 7–11 September 2015. [Google Scholar]
- Diethe, T.; Twomey, N.; Flach, P. Bayesian Active Transfer Learning in Smart Homes. In Proceedings of the Workshop on Active Learning, International Conference on Machine Learning (ICML15), Lille, France, 10 July 2015. [Google Scholar]
- Reiss, A.; Stricker, D. Introducing a new benchmarked dataset for activity monitoring. In Proceedings of the 16th International Symposium on Wearable Computers (ISWC), Newcastle, UK, 18–22 June 2012; pp. 108–109. [Google Scholar]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).