Artificial Neural Networks and Particle Swarm Optimization Algorithms for Preference Prediction in Multi-Criteria Recommender Systems

Abstract

Recommender systems are powerful online tools that help to overcome problems of information overload. They make personalized recommendations to online users using various data mining and filtering techniques. However, most of the existing recommender systems use a single rating to represent the preference of user on an item. These techniques have several limitations as the preference of the user towards items may depend on several attributes of the items. Multi-criteria recommender systems extend the single rating recommendation techniques to incorporate multiple criteria ratings for improving recommendation accuracy. However, modeling the criteria ratings in multi-criteria recommender systems to determine the overall preferences of users has been considered as one of the major challenges in multi-criteria recommender systems. In other words, how to additionally take the multi-criteria rating information into account during the recommendation process is one of the problems of multi-criteria recommender systems. This article presents a methodological framework that trains artificial neural networks with particle swarm optimization algorithms and uses the neural networks for integrating the multi-criteria rating information and determining the preferences of users. The proposed neural network-based multi-criteria recommender system is integrated with k-nearest neighborhood collaborative filtering for predicting unknown criteria ratings. The proposed approach has been tested with a multi-criteria dataset for recommending movies to users. The empirical results of the study show that the proposed model has a higher prediction accuracy than the corresponding traditional recommendation technique and other multi-criteria recommender systems.

1. Introduction

Recommender systems are intelligent decision support systems that have made it possible for online users to access various information and services, receive product recommendations from online shops, and interact with people through social networking websites [1,2]. One of the significant advantages of these systems has been to help in addressing the problems of information overload for improving the relationships between users and management [3]. Recommender systems have different different application domains. Lu et al. [3] conducted a constructive review of the areas of applications of recommender systems and how they improve and make our daily activities easier. Some of these application domains include e-learning, tourism, e-government, e-commerce, social networking sites, and so on. However, majority of the existing recommender systems use single ratings to determine preferences of users on items. Nevertheless, this technique has been considered inefficient as users might express their opinions based on several attributes of items.

Multi-criteria recommendation has been recently proposed to use multiple ratings for various attributes of items to provide more accurate estimations of users’ opinions. Its importance has been recognized by the recommender systems research community to improve the quality of recommendations the systems might give to users. Along with this growth in multi-criteria rating information, however, there is increasing concern over efficient ways of modeling the criteria ratings for determining the overall preferences of users. The two major approaches used are heuristic-based and model-based approaches [4]. In the heuristic-based approach, the similarity computation of traditional collaborative filtering is extended to consider the criteria rating information [5]. The similarities are computed separately based on each criterion and then apply some statistical and data mining techniques to combine them for estimating the overall similarity. On the other hand, the model-based approach uses a predictive model to learn the relationships between multi-criteria rating information. The model-based approach can be used to develop multi-criteria recommender systems irrespective of the single rating technique used to estimate ratings for individual criteria, while the heuristic-based approach can only work with similarity-based single rating technique. Given the wider scope of model-based approach, this paper proposed a model that integrates single rating techniques with artificial networks for improving the recommendation accuracy. However, the efficiency of applying artificial neural networks in solving prediction problems depends mostly on the algorithms used to train the networks. The gradient descent-based back-propagation algorithm is one of the more commonly used algorithms for training neural networks, but it suffers from problems of slow convergence and has a high probability of getting trapped in local minima [6,7]. Several optimization techniques have been proposed to train neural networks, such as genetic algorithms [8], particle swarm optimization algorithms [9], simulated annealing algorithms [10], bee colony algorithms [11], and others. However, research has shown that genetic and simulated annealing algorithms have the tendency to avoid local minima, but their major drawback is slow convergence rates [12]. Particle swarm optimization algorithms have been recognized as the most efficient training algorithms as they avoid getting trapped at local minima, and more interestingly, they have fast convergence rates [13,14]. Therefore, the neural networks used in this study have been trained using particle swarm optimization algorithms. As no previous study has investigated the use of neural networks to model the criteria ratings in multi-criteria recommender systems [15], the major objective of this study was to investigate the significance of particle swarm optimization-based neural networks in improving the prediction and recommendation accuracy of the systems.

This paper has been divided into eight sections including this introductory section. Section 2 contains a survey of related works. The third and fourth sections offer overviews of recommender systems and particle swarm optimization algorithms, respectively. Section 5 contains the summary of the proposed approach, and the experimental methodology is given in Section 6. Section 7 gives the empirical results of the study. Lastly, Section 8 concludes the paper and proposes some potential future research.

2. Related Work

Though research on recommender systems has a long history in relation to information filtering and retrieval, the study of recommender systems as an independent research field began with the emergence of papers on collaborative filtering in the mid-1990s [16,17,18,19]. Furthermore, in 2005, Michael et al. [20] proposed a decision-making support system that combines text-mining techniques with multi-criteria analysis techniques for recommending movies to users. Their paper was among the studies that marked the beginning of extending traditional collaborative filtering techniques to multi-criteria recommendation problems [21].

Adomavicius and Kwon [22] proposed new techniques for incorporating the criteria ratings. They presented several techniques of extending item-based collaborative filtering into a form that can handle the multi-criteria rating information. According to their experimental findings, the proposed methods have significantly improved the accuracy of the systems. Although different techniques that used similarities between items based on each criteria were used, the main drawbacks of their experiments were the metrics they used for measuring the similarities and the size of the neighborhood [21].

In restaurant recommendation, Fernando et al. [23] proposed a new recommendation approach based on the concept of item view [24]. Another interesting study on multiple-aspect recommendations of restaurants is the work of Fu et al. [25] who proposed a probabilistic model that measures users preferences on restaurants based on multiple aspects ratings. The aspects ratings reflect the quality of services provided by the restaurants. Moreover, the study of Fu et al. involves considering the geographical location of the user for context-awareness recommendations. Several studies already existed that used matrix factorization technique [26] and integrated it with geographical location, such as the fused matrix factorization approach by Cheng et al. [27]. However, the most exciting part of the work of Fu et al. [25] was the ability of the model to capture the geographical influence in addition to multiple-aspect recommendations of restaurants. Similarly, in the tourism domain, Nilashi et al. [28] proposed a multi-criteria modeling approach called the Principal Component Analysis-Adaptive Neuro-Fuzzy Inference System (PCA-ANFIS), with aims of improving the prediction accuracy of the multi-criteria recommender system. They used Gaussian mixture model [29] with Expectation– Maximization (EM) clustering and ANFIS. They also used PCA for dimensionality reduction and to tackle the problems of multicollinearity and interdependences between the criteria. In another piece of research, an attempt was made to apply fuzzy clustering means (fuzzy C-means) for data clustering in the tourism domain for addressing sparsity problems [30]. Recently, Fumba et al. [31] applied Choquet integrals of a fuzzy [32] to develop a recommendation model to determine the total ordering of the criteria ratings and measures preferences of users based on multi-criteria ratings. In a movie recommendation domain, Klenthi et al. [33] developed a utility-based multi-criteria recommendation framework that worked based on the principle of preference disaggregation. In their approach, preferences of users are modeled as a set of additive utility functions of the criteria ratings. The model works with a utility additive algorithm.

In [34], an effort was put in place towards using a particle swarm optimization algorithm and applying different similarity measures to develop a multi-criteria recommender system. The particle swarm optimization algorithm was used to optimize the function of the similarities between users based on each criterion. Equation (1) shows how the overall similarity ($sim(u,v)$) between users u and v is estimated based on their similarity $si{m}_k(u,v)$ for each criterion k. The ${\omega }_i$ is the weight of the similarity $si{m}_i(u,v)$, optimized using particle swarm optimization algorithm. Though the potential of particle swarm optimization algorithm has been tested in this study, the algorithm was used only to optimize the weights of the similarity values for each criterion, not the weight of the criteria ratings. Hence, the model cannot be applied to model-based collaborative filtering techniques such as the matrix factorization technique [26].

$$sim(u,v)=\sum _{k\in [1,n]}{\omega }_{k}si{m}_k(u,v)$$

(1)

As seen from most of the previous work mentioned above, the majority of the existing research on multi-criteria recommender systems followed a heuristic-based approach, and potentials of the powerful machine algorithms are not well explored. Among the initial attempts that applied machine learning algorithms is the work of Jannach et al. [35], who applied support vector regression to model the criteria ratings. However, using support vector regression has some drawbacks, because it requires the careful choice of hyperparameters that could allow for sufficient generalization of performance. The algorithm also uses a kernel trick, and choosing the suitable kernel function could be problematic as well [36].

3. Recommender Systems

Recommender systems (RSs) aim to estimate preferences of users towards items and suggest items that users might be interested in [37]. RSs assume the two sets U and I, representing the set of all users of the system and the set of items that could be recommended to them, respectively. Traditionally, RSs predict a single rating r to serve as the degree to which a user u may accept an item i. Their utility functions are of the form $f(u\times i)\to r$. To determine how the utility function would predict the value of r, there are four common recommendation techniques that can be applied [38]. For instance, as reviewed by Yera and Martınez in [39], fuzzy tools can be applied in various ways to develop RSs.

A collaborative filtering recommendation technique is one of the three main techniques for building RSs and is the most widely used technique [3]. Other techniques are demographic filtering, content-based filtering, and a hybrid-based filtering technique that combines the collaborative filtering technique with content-based filtering or the demographic filtering technique in different ways [40]. The collaborative filtering technique is further divided into memory-based and model-based filtering [41]. The memory-based filtering uses similarities between users or items to predict the values for r and uses them to recommend items that users with similar opinions liked in the past. The model-based approach predicts the values for r by building a predictive model using machine learning and data mining techniques [42].

Multi-criteria RSs (MCRSs) extend the traditional recommendation technique by assigning multiple ratings $r_k$ for $k=1,2,\dots ,n$ called the criteria ratings and an overall rating $r_o$ to various attributes of the items for enhancing the prediction accuracy of the system. An example of MCRSs is the movie recommender system that recommends movies to users based on action, direction, story, and visual effect of the movies.

Table 1. Example of rating matrix in MCRSs.

	${\mathit{M}}_1$	${\mathit{M}}_2$	${\mathit{M}}_3$	${\mathit{M}}_4$	…	${\mathit{M}}_{\mathit{n}}$
$U_1$	54,5,3,5	55,5,4,5	34,2,3,3	34,3,3,3	…	12,1,3,1
$U_2$	24,1,3,1	55,5,5,5	55,4,4,4	34,2,3,5	…	44,3,3,5
$U_3$	21,5,2,4	55,5,5,5	54,5,4,4	32,5,4,3	…	43,5,4,3
$U_4$	24,1,5,1	22,2,2,2	55,4,3,4	35,3,3,5	…	45,2,3,5
.
.
.
$U_m$	33,3,3,2	21,1,1,5	55,4,5,4	44,4,3,5	…	12,1,1,1

shows example of the $m\times n$ rating matrix of MCRSs measured in a scale of 5 (1 to 5). It can be seen from the table that the first number of each entry is bigger and bolder. These large, bolded numbers are the overall ratings, while the subscript numbers are the criteria ratings for the action, direction, story, and visual effect, respectively. From the table, we can also see that even though some users have the same overall ratings, their criteria ratings are entirely different. For instance, both $U_3$ and $U_4$ have an overall rating of 2 on $M_1$, but $U_3$ and $U_4$ have different opinions about $M_1$. This is because $U_3$ gives little importance to the ratings of the second and fourth criteria, as the overall rating is closer the ratings of the first and third criteria. However, $U_4$ has a counter-consideration concerning the influence of the criteria ratings with respect to the overall rating.

Furthermore, Table 1 also illustrates some of the main characteristics of the utility function of MCRSs. Their utility functions are of the form $f(u\times i)\to r_o,r_1,r_2,\dots ,r_n$ [37]. The value of $r_o$ can be estimated using either model-based or heuristic-based approaches. The model-based approach computes $r_o$ as a function of the criteria ratings (see Equation (2)).

$$r_o=f(r_1,r_2,\dots ,r_n)$$

(2)

The heuristic-based approach measures the similarities between users on each criterion k and uses them to computes the overall similarity and $r_o$. The similarities between users on each criterion can be estimated using any suitable similarity metrics such as Pearson correlation similarity (see Equation (3)), cosine rule (see Equation (4)), and so on. The unknown rating ${\widehat{r}}_{ui}$ will be predicted using Equation (5), where $si{m}_o$ is the resulting overall similarity between u and v that is calculated based on the similarities between all the criteria ratings. The $si{m}_o$ can be computed using several techniques, such as the averaging technique, the worst similarity technique, or by using weighted similarity techniques to estimate the weights of the similarities based on each criterion k [15].

$$sim(u,v)=\frac{{\sum }_{i\in I_{uv}}(r_{ui}-{\overline{r}}_u)(r_{vi}-{\overline{r}}_v)}{\sqrt{{\sum }_{i\in I_{uv}}{(r_{ui}-{\overline{r}}_u)}^2{\sum }_{i\in I_{uv}}{(r_{vi}-{\overline{r}}_v)}^2}}$$

(3)

$$sim(u,v)=\frac{r_u·r_v}{\parallel r_u{\parallel }_2{\parallel r_v\parallel }_2}=\frac{{\sum }_i{r}_{ui}{r}_{vi}}{\sqrt{{\sum }_i{r}_{ui}^2}\sqrt{{\sum }_i{r}_{vi}^2}}$$

(4)

$${\widehat{r}}_{ui}={\overline{r}}_u+\frac{{\sum }_{v\in N_i\left(u\right)}si{m}_o(u,v)(r_{ui}-{\overline{r}}_v)}{{\sum }_{v\in N_i\left(u\right)}\left|si{m}_o(u,v)\right|}$$

(5)

4. Particle Swarm Optimization (PSO)

Particle swarm optimization (PSO) is a population-based computational algorithm proposed by Eberhart and Kennedy [43], which is inspired by the way bird flocking or fish schooling behaves. PSO is an intelligent optimization algorithm that resembles the genetic algorithm. It starts with an initial population of solutions called particles and tries to find an optimal solution. The main difference between PSO algorithms and genetic algorithms is that the PSO does not require operations like mutation and crossover, which makes it easier to implement with a low computation time. The particles, which are similar to chromosomes in genetic algorithms, fly across the problem space by moving along the direction of the current optimal particle [6,44]. At iteration t, every particle k keeps track of its current position $p_k^t$; the best fitness it has attained so far is called $pbest$, and the global fitness of all the particles is called $gbest$. Each particle has velocity $v_k^t$ associated to it for following the fittest particle.

Similar to chromosomes in genetic algorithm, the particles are initially generated at random and $pbest$ for each particle will be calculated and compared to determine $gbest$. The two basic operations of the PSO algorithm are updating the velocity $v_k^{t+1}$ and the position $p_k^{t+1}$ in order to obtain the fitness after the iteration $t+1$. The $v_k^{t+1}$ and $p_k^{t+1}$ are computed using Equations (6) and (7), respectively.

$$v_k^{t+1}=\omega v_k^t+c_1\times rand\times (gbes{t}_k-p_k^t)+c_2\times rand\times (gbes{t}_k-p_k^t)$$

(6)

$$p_k^{t+1}=p_k^t+v_k^{t+1}$$

(7)

The first item in Equation (6) provides the ability for the PSO algorithm to search the whole problem space, and $\omega$ is the weighting function, $c_1$ and $c_2$ are constants called acceleration coefficients usually in the range [0, 4], and the function $rand$ generates a random number in the interval [0, 1] [6,45].

5. The Proposed Model and Approach

The proposed method follows an aggregation function approach to estimate preferences of users on items based on the multi-criteria rating information as shown in Equation (2). Generally, following the aggregation function requires at least four necessary steps as follows.

• Decompose the n-dimensional multi-criteria rating problem into n distinct single rating problems.
• Choose a prediction function or algorithm that can learn the relationships between the criteria ratings and the overall rating.
• Integrate the prediction algorithm with the distinct single rating techniques of step 1 for predicting the criteria ratings and the overall rating.
• Provide a list of recommendations.

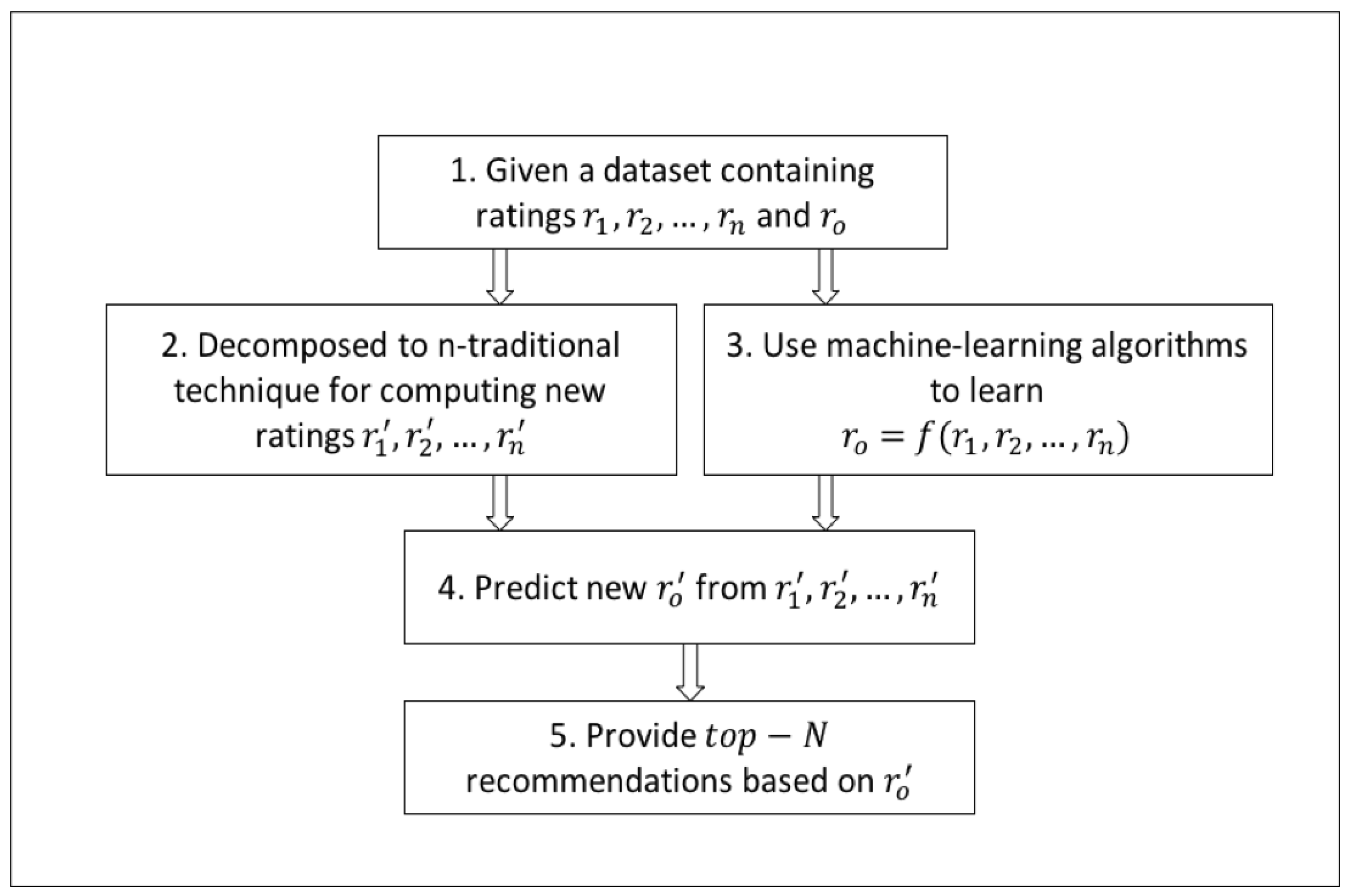
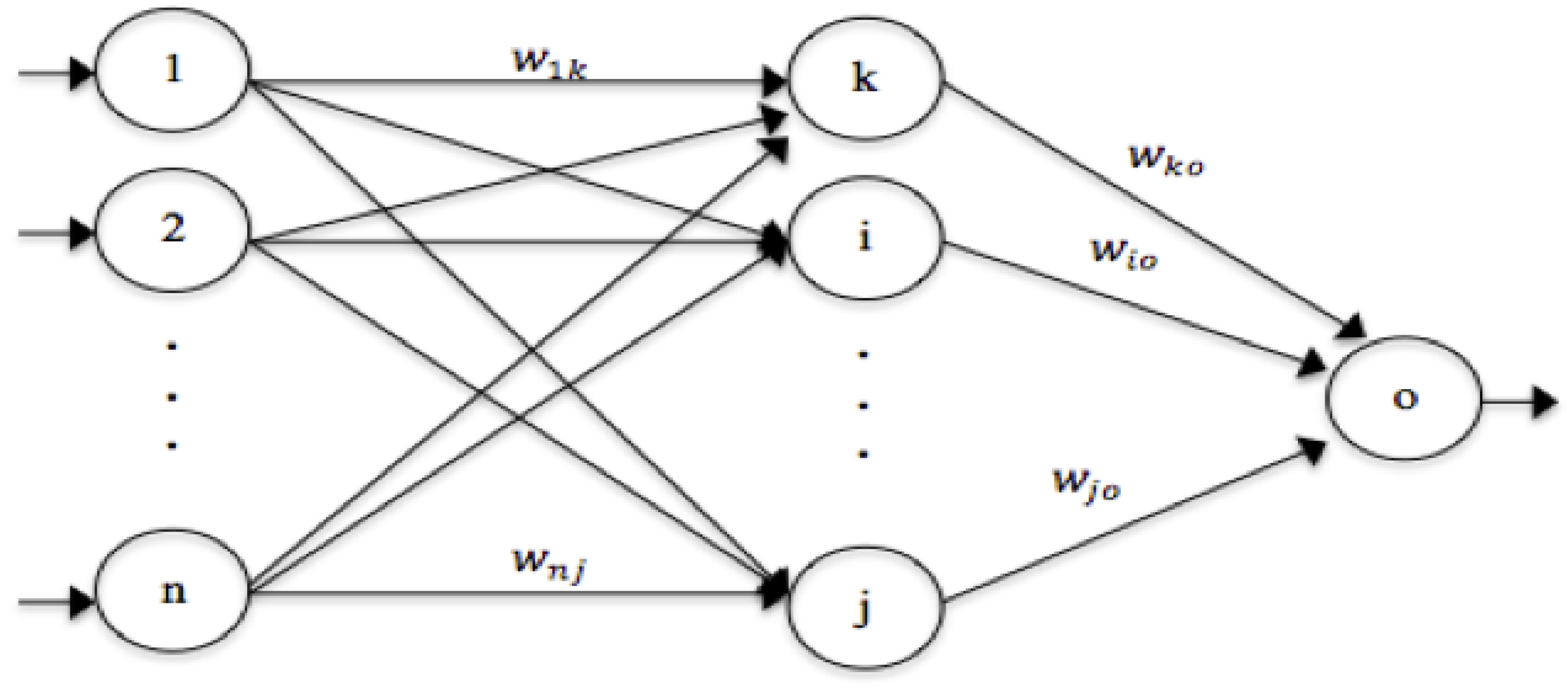
Similarly, modeling the criteria ratings using the proposed approach to provide the top-N recommendations requires five basic steps, as shown in Figure 1 [22]. The machine learning algorithm in step 3 of the figure is an artificial neural network (ANN) containing an input layer, a hidden layer, and an output layer (see Figure 2). While working with an artificial neural network, activation functions need to be defined for each node except at the input layer to determine the outputs of the neurons in the network. This is done by defining two activation functions: a sigmoid activation function and a linear activation function for all neurons in the hidden and output layers respectively. For instance, the activation function of neuron k defined in Equation (8) takes the weighted sum of the inputs $r_a$ of the neuron a (1 ≤ a ≤ n) from the input layer. Similarly, the linear activation function at the output neuron o is defined in Equation (9)

$$f\left(k\right)=\frac{1}{1+exp(-{\sum }_{a=1}^n{\omega }_{ak}{r}_a)}$$

(8)

$$f\left(o\right)=\sum _{k=1}^n{\omega }_{ko}f\left(k\right)$$

(9)

Finally, the learning error E between the actual output $y_k$ of the network for the $k^{th}$ feature set and the real output $t_k$ from the dataset was evaluated after every iteration using the mean square error metric in Equation (10).

$$E=\frac{1}{N}\sum _{k=1}^N{(y_k-t_k)}^2$$

(10)

In training the neural network with the PSO algorithm, we defined the particles to be the matrix of weights connecting the input layer and the hidden layer (${\omega }_{1k}$ to ${\omega }_{nj}$) and the weights connecting the hidden layer and the output layer (${\omega }_{ko}$ to ${\omega }_{jo}$).

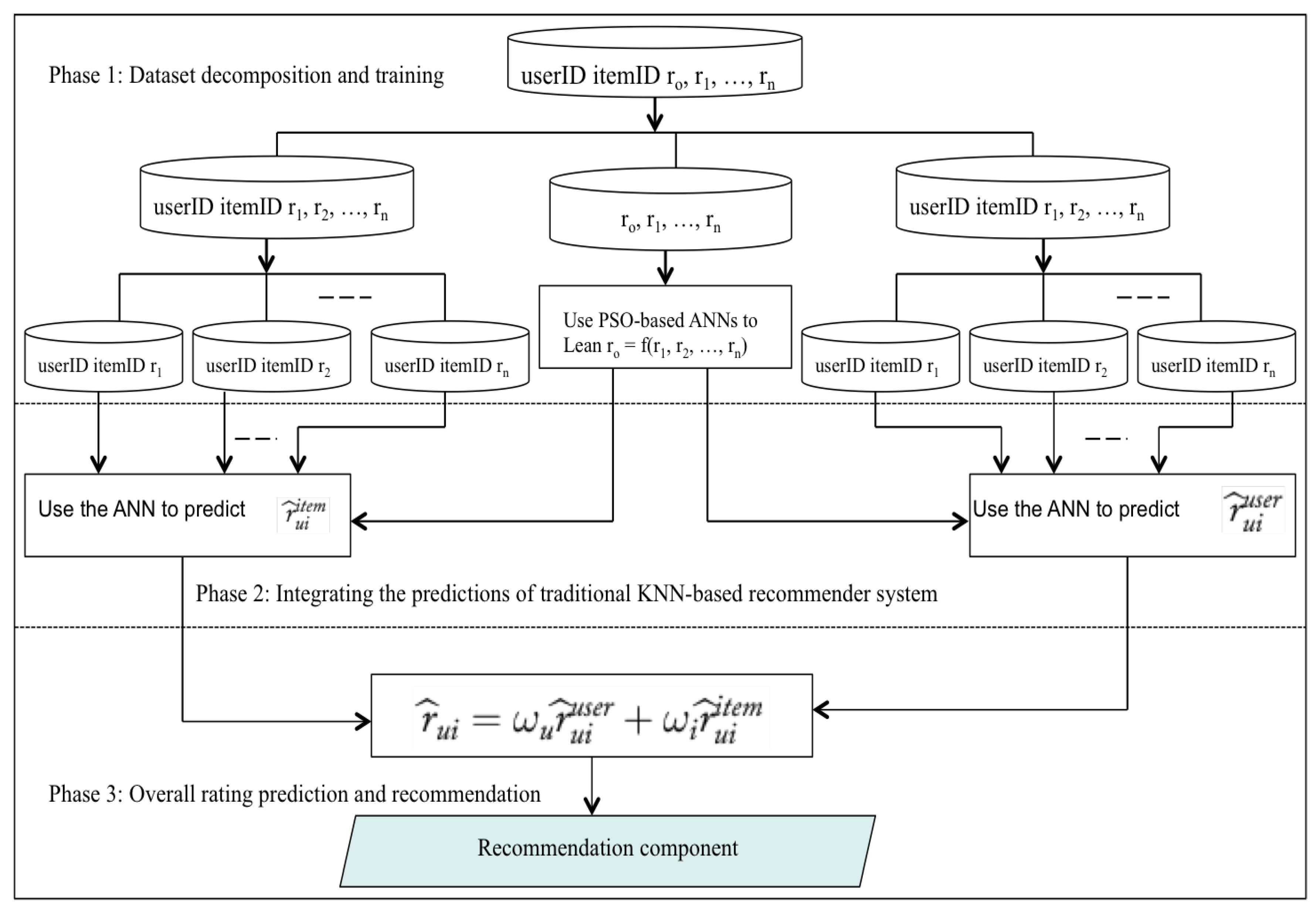
To give a specific explanation of the proposed approach, Figure 3 shows the architecture of our proposed model. The model consists of three phases, which are briefly explained as follows: In phase 1, the multi-criteria rating dataset is decomposed into to three components (note that the two components at the left- and right-hand sides contain the same data). As shown in the figure, each of the components at the left- and right-hand sides contains user ID, item ID, and the criteria ratings $r_1,r_2,\dots ,r_n$. The component in the middle consists of the criteria ratings together with their corresponding overall ratings (that is $r_o,r_1,\dots ,r_n$), and no item ID and user ID.

The two similar components are further decomposed into subcomponents containing user ID, item ID, and single rating $r_k$ for the $k^{th}$ criterion so that each one of them can be treated as a traditional problem shown in Equation (5). We, therefore, used k instances of item-based traditional k-nearest neighborhood (kNN) -based recommender systems for the subcomponents at the left-hand side, and similarly, k instances of user-based traditional kNN-based recommender systems for the subcomponents at the right-hand side. The purpose of the instances of kNN-based traditional recommender systems is to compute learn how to computer unknown ratings for the $k^{th}$ criterion.

The neural network is trained using the middle component to learn the relationships between $r_o$ and the criteria ratings as given in Equation (2). We trained to instances of the neural networks so that each one can be used to integrate the k predicted values for the instances of the item- and user-based traditional kNN-based recommender systems explained in the previous paragraph. In phase 2 of the model, the learned neural networks received these predicted values to estimate the overall ratings ${\widehat{r}}_{ui}^{item}$ and ${\widehat{r}}_{ui}^{user}$ respectively. Finally, in phase 3, the ${\widehat{r}}_{ui}^{item}$ and ${\widehat{r}}_{ui}^{user}$ are combined as illustrated in Equation (11) to calculate the overall rating ${\widehat{r}}_{ui}$ for user u on item i.

$${\widehat{r}}_{ui}={\omega }_u{\widehat{r}}_{ui}^{user}+{\omega }_i{\widehat{r}}_{ui}^{item}$$

(11)

The calculated ${\widehat{r}}_{ui}$ for users on new items are then used by the recommendation component to provide a list of top-N recommendations.

6. Experimental Methodology

To evaluate the performance of our proposed method, we used a Yahoo!Movie dataset for recommending movies to users. The Yahoo!movie dataset is a multi-criteria dataset where preference information on movies was provided by users on the strength of four different attributes of movies namely, the direction, the action, the story, and the visual effect of the movie. The dataset was provided by Yahoo!Movies website http://movies.yahoo.com, containing users’ ratings of movies based on the four criteria. However, as the Yahoo!Movies website no longer provides the dataset, we therefore collected the dataset from Kleanthi Lakiotaki [33], who initially extracted the dataset. We named the rating for the direction, the action, the story, and the visual effect of the movies as $r_1$, $r_2$, $r_3$, and $r_4$ respectively. Ratings for each criterion were measured on a 13-fold scale starting from F representing the lowest preference to $A^{+}$, which represents the highest preference of the user. The 13 scales are: $A^{+}$, A, $A^{-}$, $B^{+}$, B, $B^{-}$, $C^{+}$, C, $C^{-}$, $D^{+}$, D, $D^{-}$, and F. In addition to the criteria ratings, an overall rating ($r_o$) that measures the final acceptability of users on movies was also included in the dataset, and it was equally measured on the same scales ($A^{+}$ to F).

Table 2. Sample of the original dataset.

User	Movie	Direction	Action	Story	Visual	Overall
ID	ID	$\left({\mathit{r}}_1\right)$	$\left({\mathit{r}}_2\right)$	$\left({\mathit{r}}_3\right)$	$\left({\mathit{r}}_4\right)$	$\left({\mathit{r}}_{\mathit{o}}\right)$
101	1	$A^{+}$	C	$C^{-}$	$B^{-}$	$C^{-}$
	3	B	$B^{+}$	$B^{+}$	$A^{-}$	$B^{-}$
	5	$B^{-}$	$A^{-}$	$B^{+}$	$A^{-}$	$A^{-}$
102	3	$A^{+}$	$A^{+}$	$A^{+}$	$A^{+}$	$A^{+}$
	5	$C^{-}$	C	$A^{+}$	$A^{+}$	$A^{+}$
	6	C	B	$C^{+}$	$B^{-}$	$B^{-}$

shows the original sample of the dataset, where $r_1$, $r_2$, $r_3$, and $r_4$ are the rating for the action, direction, visual, and story of the movies respectively, along with an overall rating $r_o$. In order to work with numerical data, the ratings (A⁺ to F) were transformed to numbers from 13 to 1, respectively.

For instance, A⁺→13, A→12, A⁻→11, B⁺→10, …, D→3, D⁻→2, and F→1.

Table 3. Sample of the numerical representation of the dataset.

User	Movie	Direction	Action	Story	Visual	Overall
ID	ID	$\left({\mathit{r}}_1\right)$	$\left({\mathit{r}}_2\right)$	$\left({\mathit{r}}_3\right)$	$\left({\mathit{r}}_4\right)$	$\left({\mathit{r}}_{\mathit{o}}\right)$
101	1	13	6	5	8	5
	3	9	10	10	11	8
	5	8	11	10	11	11
102	3	13	13	13	13	13
	5	5	6	13	13	13
	6	6	9	7	8	8

presents the transformed numerical ratings of Table 2. The dataset contains a total of 62,156 ratings of 6078 users for 976 movies. We also used Pearson correlation coefficient to measure the correlations between the criteria ratings and the overall rating. The percentage correlations for the action, direction, story, and he visual effects of the movies are approximately 86.5%, 91.1%, 90.5%, and 84.4% respectively. This shows the strength of the relationship between the criteria ratings and the overall rating. According to these calculated correlations, users are more interested in the story and direction of the movies than visual effects and actions of the movies.

Moreover, to conduct the experiment, we need to provide parameters to our model so that part of the dataset would be used for the training and the remaining portion of the dataset for testing the performance of the model. However, how should a dataset be divided into training and test sets? If the training dataset is small, our parameter estimates will have higher variance, whereas with a low amount of test data, our performance statistic will have higher variance. The question now is with respect to the best way of dividing the dataset. There are many techniques for splitting the dataset into training and test set such as the leave one out (LOO) Monte Carlo test, disjoint set test, and n-fold cross-validation, etc. [46,47]. To measure the performance of our predictive model, we used n-fold cross-validation for selecting the parameters of the model [48,49,50]. The n-fold cross-validation divides the experimental dataset into n subsamples, where one of these subsamples will serve as the validation set for testing the model. The combination of the remaining $n-1$ subsamples will be the training set. This process is repeated n times so that each of the subsamples will have the chance to serve as the test set. In this study, we used 10-fold cross-validation (that is n = 10) throughout the experiments.

To develop the MCRSs illustrated in Figure 3, we used two k-nearest neighborhood (kNN) single rating RSs and integrated them with PSO-based neural networks in different ways. The role played by kNN is to predict the criteria ratings that will serve as the input to the neural network for computing the overall rating. The experiment was conducted with six RSs as follows:

• Single_U: A user-based kNN recommender system that computes similarities between users using Equation (3)
• Single_I: An item-based kNN recommender system that computes similarities between items using a modified version of Equation (3) to find similarities between item i and item j.
• MCRSs_Sim: A heuristic-based MCRS that computes $r_o$ based on the average similarities between users using Equation (12), where $si{m}_k(u,v)$ is the similarity between u and v based on the $k^{th}$ criterion that could be obtained using Equation (3). $r_o$ will be computed using Equation (5) (in this case $r_o$ = ${\widehat{r}}_{ui}$ while $sim(u,v)$ = $si{m}_{avg}$).

  $$si{m}_{avg}(u,v)=\frac{1}{n+1}\sum _{k=0}^{n}si{m}_k(u,v)$$

  (12)
• ANNs_U: A model-based MCRSs that integrates PSO-based ANNs with Single_U in item 1 to estimate the overall rating. We named the rating provided by this model as ${\widehat{r}}_{ui}^{user}$.
• ANNs_I: A model-based MCRSs that integrates PSO-based ANNs with Single_I in item 2 to estimate the overall rating. We named the rating provided by this model as ${\widehat{r}}_{ui}^{item}$.
• ANNs_W: This approach combines items number 4 and 5 above in a weighted form [51] to estimate the overall rating as a weighted sum of the ratings from items 4 and 5 as given in Equation (11), where ${\omega }_u$ and ${\omega }_i$ are the weights that are estimated using the gradient descent algorithm [35].

As can be seen in the results and discussion section, different values of k (the neighborhood size) were tested to monitor the performance of our model and to make comparative analyses with the traditional techniques based on the values of k. Other experimental parameters used were Pearson’s correlation coefficient with a minimum similarity threshold of 0.0, minimum number of neighbors set to 1, and minimum overlap (co-rated items) set to 2. The selection of these parameters followed several trials to determine the ones that provided optimal results.

Furthermore, to analyze the accuracy of the systems, we used several evaluation metrics to investigate their prediction and recommendation accuracy. The evaluation metrics used were:

• Mean average error (MAE)
• Root mean square error (RMSE)
• Precision, recall, and F-measure
• Fraction of concordant pairs (FCP)
• Normalized discounted cumulative gain (NDCG)
• Mean reciprocal ranking (MRR)
• Gini coefficient.

Though PSO algorithm did not require many experimental parameters compared to other optimization algorithms, it became necessary for experiments with optimization algorithms to carefully select parameters that could provide the desired solutions and terminate the execution of the program when certain conditions were satisfied. These parameters are the number of particles to be generated for training, the initialization of the learning factors, the maximum velocity, number of iterations, and the target training error. The number of particles used for the experiment was chosen to be 100, initialized randomly to matrices and vectors of real numbers within the interval [0, 1]. The learning factors ($c_1$ and $c_2$ in Equation (6)) were each selected as an integer 2. The velocity limit that a particle can move at was set to 0.2 in order to prevent overshooting. Finally, the termination condition was based on the minimum error E in Equation (10) which was chosen to be 0.001, or when the number of iterations was up to 200 training cycles. The experimental parameters were selected after several test runs.

7. Results and Discussion

To evaluate the advantages and effectiveness of the proposed method, we developed our methodological framework usinh two kNN-based RSs to calculate the average similarities between users/items based on each criterion, and the overall ratings are estimated using PSO-based ANN. The experimental results are then compared with traditional techniques and a heuristic-based MCRS The two kNN-based traditional RSs (Single_U and Single_I) used the overall rating to learn the similarities between users and items, respectively. Moreover, the three ANN-based MCRSs were ANNs_U that integrates the Single_U with the PSO-based neural network, ANNs_I that integrates the Single_I with the PSO-based neural network, and lastly, the ANNs_W, which is a hybrid of ANNs_U and ANNs_I. The evaluation metrics introduced in the previous section were equally applied to the six RSs.

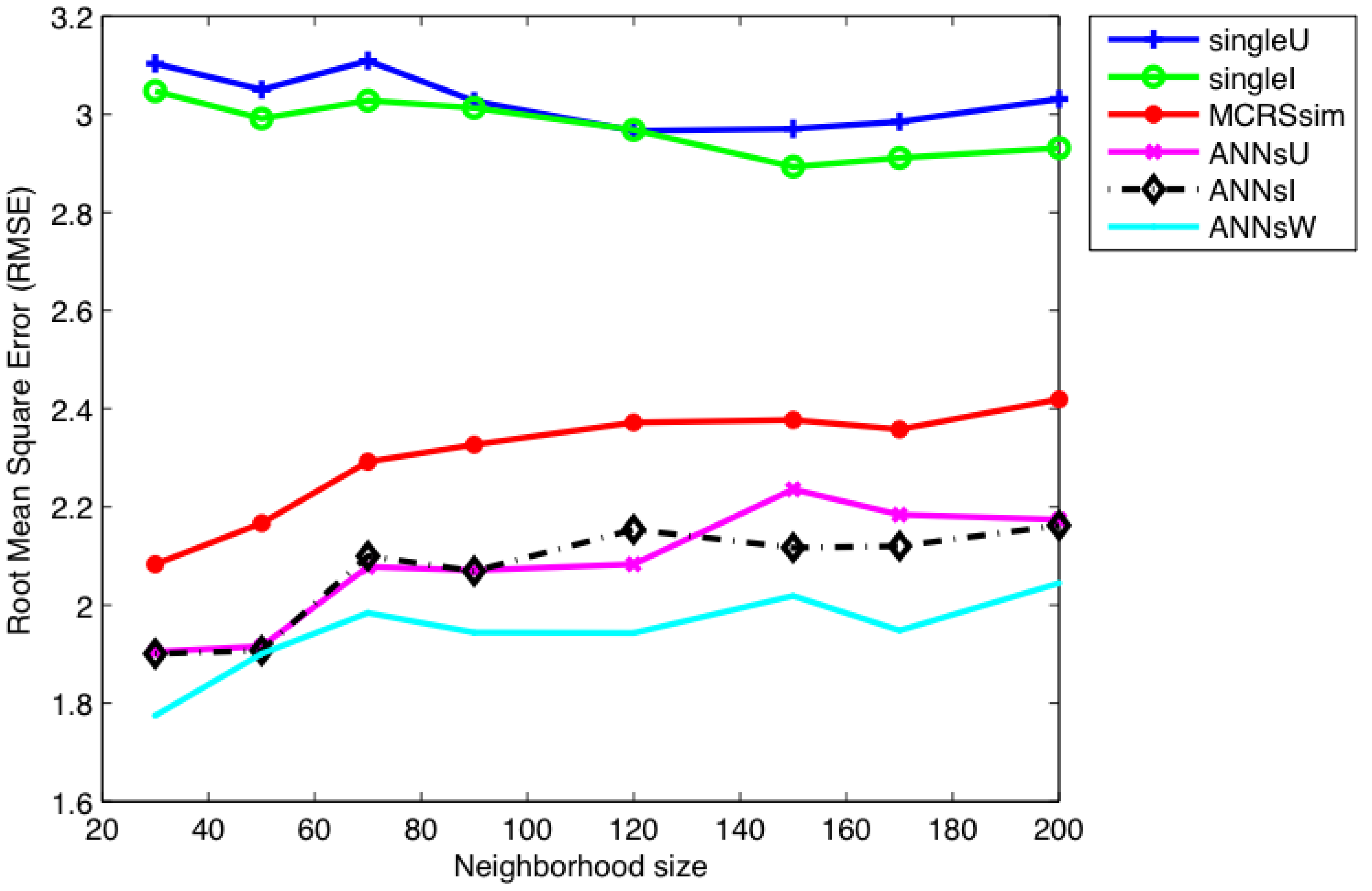
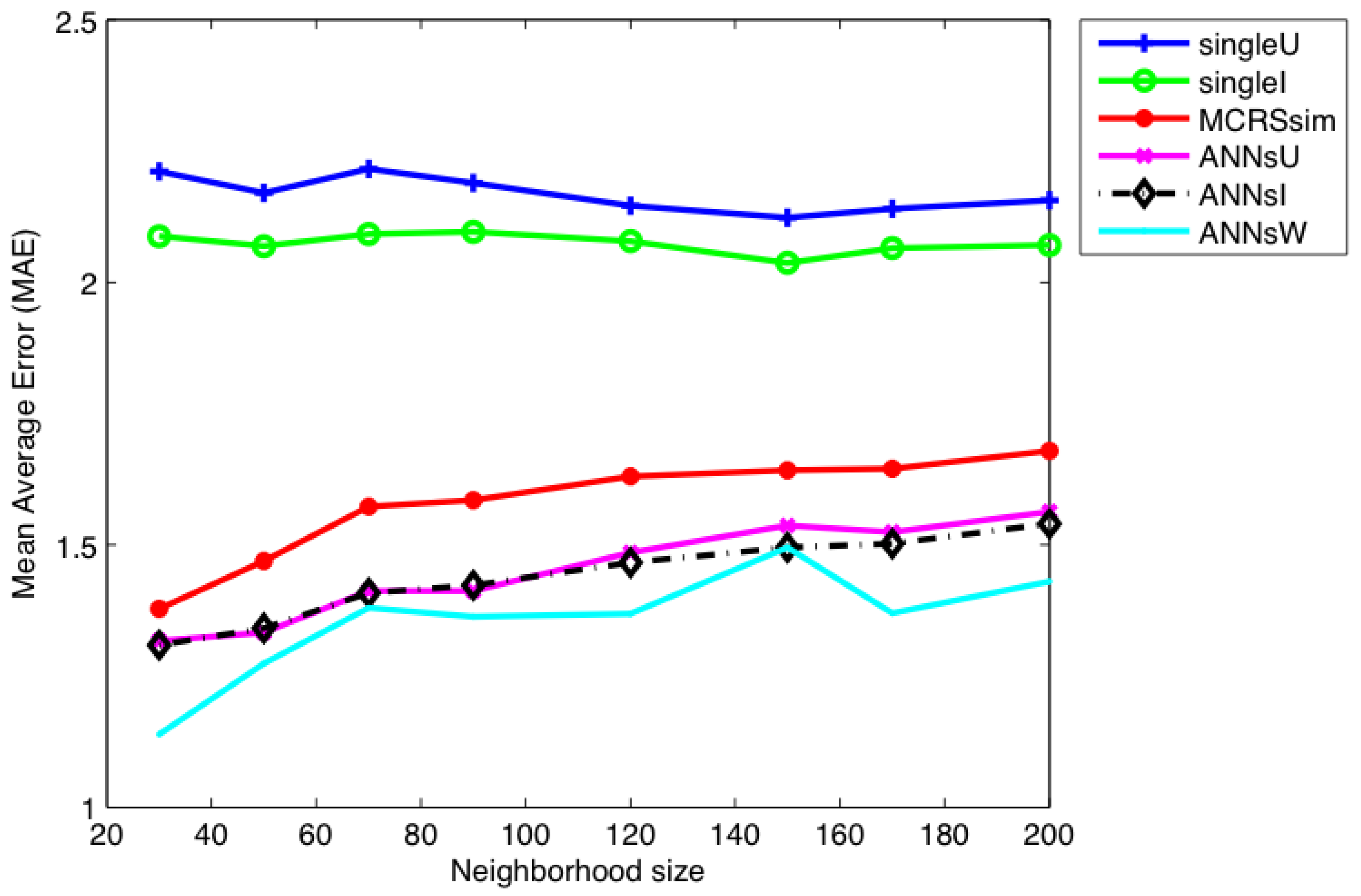
Furthermore, as choosing the value of k in kNN-based RSs remains one of the main determining factors of the accuracy of the systems [52], we performed several experiments with different-sized neighborhoods to consider various number of clusters to effectively analyzed and compared the performance of the RSs. The experiments began with a moderately small neighborhood size of 30 neighbors, and increased up to the size of 200 neighbors per cluster. The resulting RMSEs and MAEs for the RSs have been analyzed and presented in Figure 4 and Figure 5, respectively. The figures show the prediction errors of each system based on the neighborhood sizes. Although it is apparent from the data in the figures that all the MCRSs have the least prediction errors, it is interesting is that the hybrid (ANNs_W) has smaller errors than the rest of the systems.

Additionally, the results also indicate that all the ANN-based systems are much better than heuristic-based systems (MCRSs_Sim). The differences between ANNs_U and ANNs_I could be attributed to the nature of the experimental dataset, where when the number of items is lower than the number of users, it might be difficult for some users to have neighbors, and vice versa. As the dataset contains 6078 users and 976 items, then the item-based RSs (Single_I) will likely have higher accuracy than the Single_U. This finding has important implications for developing both traditional and multi-criteria RSs. Therefore, since deciding on the item- or user-based RSs depends on the $user\times item$ ratio, it is recommended that the hybridization of two techniques could provide a better solution for this drawback. Further, if we now look at the results by the neighborhood sizes, it can be seen that unlike the traditional techniques, the four MCRSs have better prediction accuracy with smaller sizes.

For further comparison, we calculated the average performance of the six RSs based on the evaluation metrics mentioned in the last section. The results obtained from the preliminary analysis of their accuracy are summarized in

Table 4. Evaluation results. FCP: fraction of concordant pairs; MRR: mean reciprocal ranking; NDCG: normalized discounted cumulative gain.

Size of K	Single_I	Single_U	MCRSs_Sim	ANNs_I	ANNs_U	ANNs_W
RMSE	3.030	2.973	2.300	2.081	2.066	1.945
MAE	2.169	2.075	1.575	1.448	1.436	1.353
Precision	0.795	0.802	0.817	0.828	0.835	0.838
Recall	0.800	0.805	0.810	0.821	0.824	0.833
F1	0.797	0.803	0.813	0.824	0.829	0.835
MRR × 10−2	0.109	0.122	0.166	0.280	0.170	0.570
NDCG	0.887	0.902	0.925	0.961	0.921	0.975
Gini	0.739	0.768	0.832	0.836	0.839	0.858
FCP	0.620	0.641	0.738	0.816	0.822	0.839

. The results were computed by taking the average of the eight experiments based on the neighborhood sizes. The data on the table illustrates some of the leading characteristics of all the systems. It can be seen that except for the NDCG and MRR where MCRSs_Sim slightly outperformed ANNs_U and ANNs_I respectively, the proposed ANN-based systems reported the highest predictions, classification, and ranking accuracy. This table is quite revealing in several ways. First, it shows the ability of the proposed techniques to provide the recommended ranking of items that matches how the systems’ users would have ranked the same items. Also, the table demonstrates that the proposed techniques have high frequencies with which they can make correct decisions on whether an item can be accepted by a user. Lastly, similar to Figure 4 and Figure 5, the table confirms that the proposed techniques can predict ratings that are close to the actual user ratings.

Finally, to measure the extent of the existence of linear relationships between the predictions of the six RSs and the actual ratings from the dataset, we extracted some of their predicted values and applied Pearson’s correlation coefficient formula to estimate the inter-correlations among them and also their correlations with the corresponding actual ratings.

Table 5. Correlation matrix between the actual rating and the predicted values.

	Actual	Single_I	Single_U	MCRSs_Sim	ANNs_I	ANNs_U	ANNs_W
Actual	1.000	0.834	0.739	0.894	0.916	0.896	0.935
Single_I	0.834	1.000	0.664	0.921	0.956	0.759	0.891
Single_U	0.739	0.664	1.000	0.666	0.737	0.872	0.793
MCRSs_Sim	0.894	0.921	0.666	1.000	0.968	0.794	0.903
ANNs_I	0.916	0.956	0.737	0.968	1.000	0.814	0.943
ANNs_U	0.896	0.759	0.872	0.794	0.814	1.000	0.922
ANNs_W	0.935	0.891	0.793	0.903	0.943	0.922	1.000

presents the summary statistics of the correlations results. Strong evidence can be seen from the table when we compare the data presented in the second row or second column of the table. The second row shows the correlations between actual ratings and the predictions of all the RSs. The findings in this table are consistent with those of Figure 4 and Figure 5, and Table 4.

8. Conclusions and Future Work

This study was undertaken to design a methodological framework for user modeling in multi-criteria recommendation problems and to evaluate the effectiveness of the proposed method. In this investigation, the aim was to train feed-forward neural networks with the particle swarm optimization (PSO) algorithm and use the neural network as an aggregation function for predicting the preferences of the users on items. The proposed method was made up of user- and item-based traditional RSs (kNN-based RSs) integrated with neural networks to learn the relationships between ratings for predicting and recommending relevant items to users. Several experiments have been conducted to determine the effects of neural networks in modeling the criteria rating information. The experimental results of the current study have supported the relevance of using artificial neural networks for modeling users’ preferences in multi-criteria decision-making problems. It was also shown that the hybrid user- and item-based model has by far improved the accuracy of the systems. Moreover, this study has demonstrated, for the first time, that a neural network trained with the PSO algorithm could be used to model multi-criteria recommendation problems and to improve the accuracy of the systems.

Although the PSO algorithm has been proved to be one of the most efficient and practical optimization techniques [6] and has the capacity to overcome the problems of slow convergence and getting trapped in local minima, investigation of the efficiency of the systems when modeling with a hybrid of the PSO algorithm and other optimization algorithms like the genetic algorithm, gravitational search algorithm, ant colony algorithm, and so is necessary.