Multidimensional Data Exploration by Explicitly Controlled Animation
Abstract
1. Introduction
- a novel representation of the view space based on a small multiple metaphor
- a set of interaction techniques to continuously navigate the view space and combine partial insights obtained from different views
2. Related Work
2.1. Element-Based Plots
2.2. Navigating Multidimensional Data Visualizations
- Genericity: We handle all types of element-based plots (Section 2.1), e.g., scatterplots, graph/trail drawings, and DR projections, in an uniform way and by a single implementation.
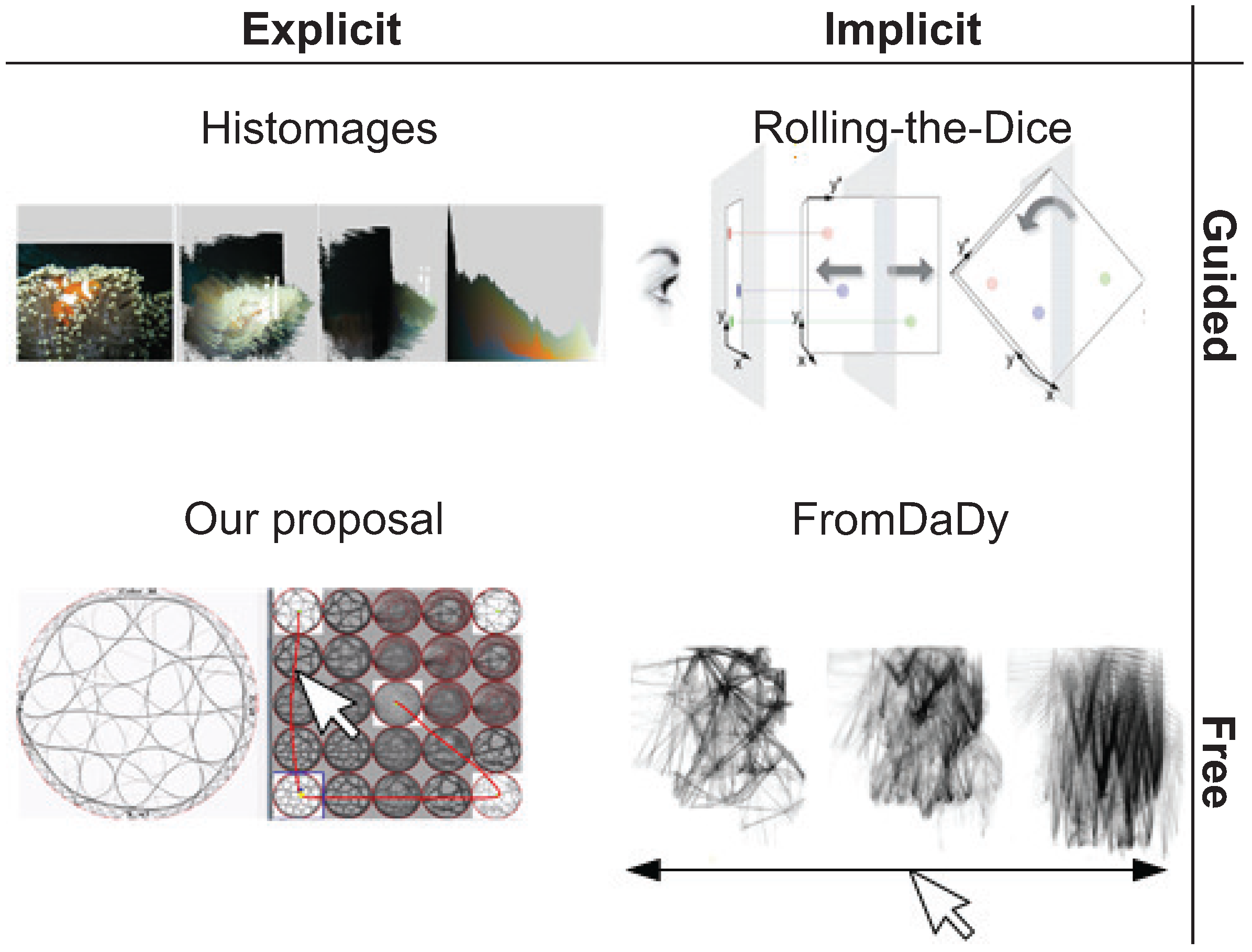
- View by example: We provide an explicit small-multiple-like depiction of the view space .
- Continuity: We allow a continuous change of the current view based on smooth interpolation between the small-multiple views without having to bother about understanding the explicit abstract parameter space . This allows generating an infinite set of intermediary views in .
- Free navigation: The view generation is in the same time controlled by the user (one sees along which existing views one navigates) and unconstrained (one can freely and fully control the shape of the navigation path).
- Ease of use and scalability: We generate our intermediary views by simple click-and-drag of a point in the view space; these views are generated in real-time for large datasets D (millions of elements).
- Control: Most importantly, and novel with respect to all approaches discussed so far, we propose a simple mechanism for changing only parts of the current view, while keeping other parts fixed. This enables us to combine insights from different views on-the-fly, to accumulate insights on the input dataset D.
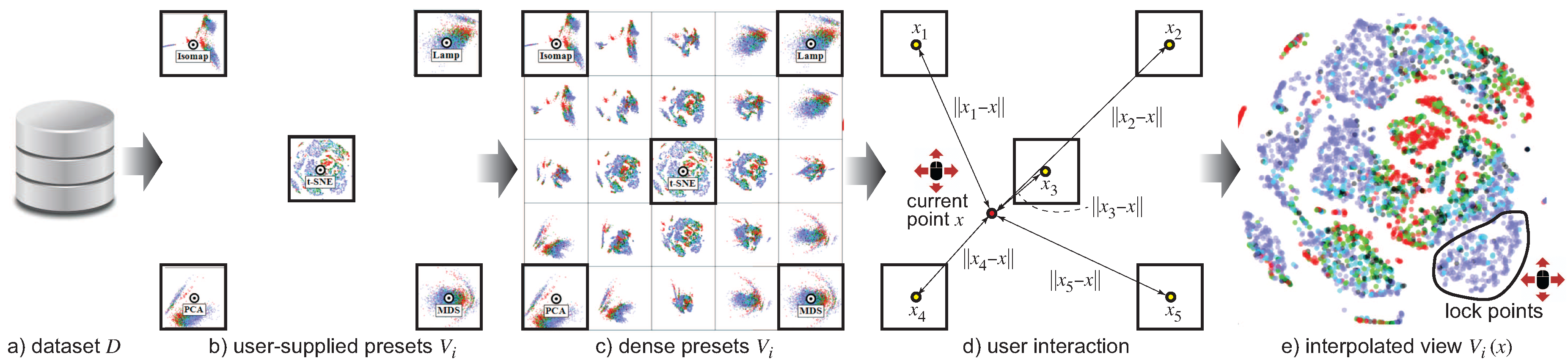
3. Proposed Method
- Guided: The set of preset views between which the user can choose is limited by construction, and depends on the dimensionality of the input dataset D.
- Free: The set of preset views is fully configurable by the user, who can choose any number and type of views in to animate between.
- Implicit: Once the transition (animation) between and is triggered by the user, the generation of intermediate views between and happens automatically (usually via some type of linear interpolation). The user can specify and , but not the path in the view-space along which the animation evolves nor can he slow/accelerate/pause the animation.
- Explicit: The user can choose the path along which the animation evolves, and also the speed thereof.
3.1. Our Proposal
- Allow one to freely sketch the interpolation path between two such view presets , in an interactive and visual way (as in [57]), rather than automatically controlling the interpolation via a linear formula.
3.2. Implementation Details
4. Applications
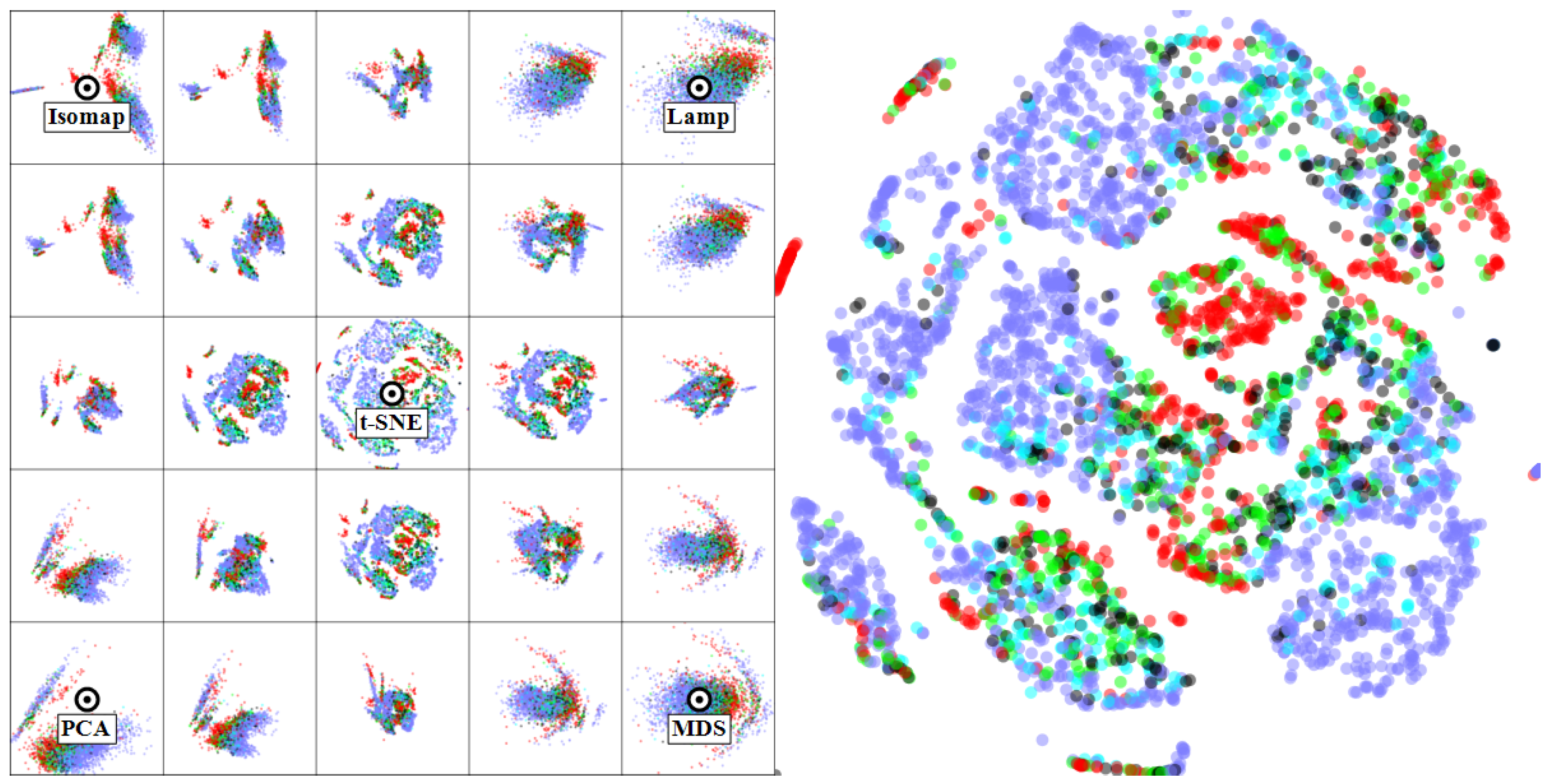
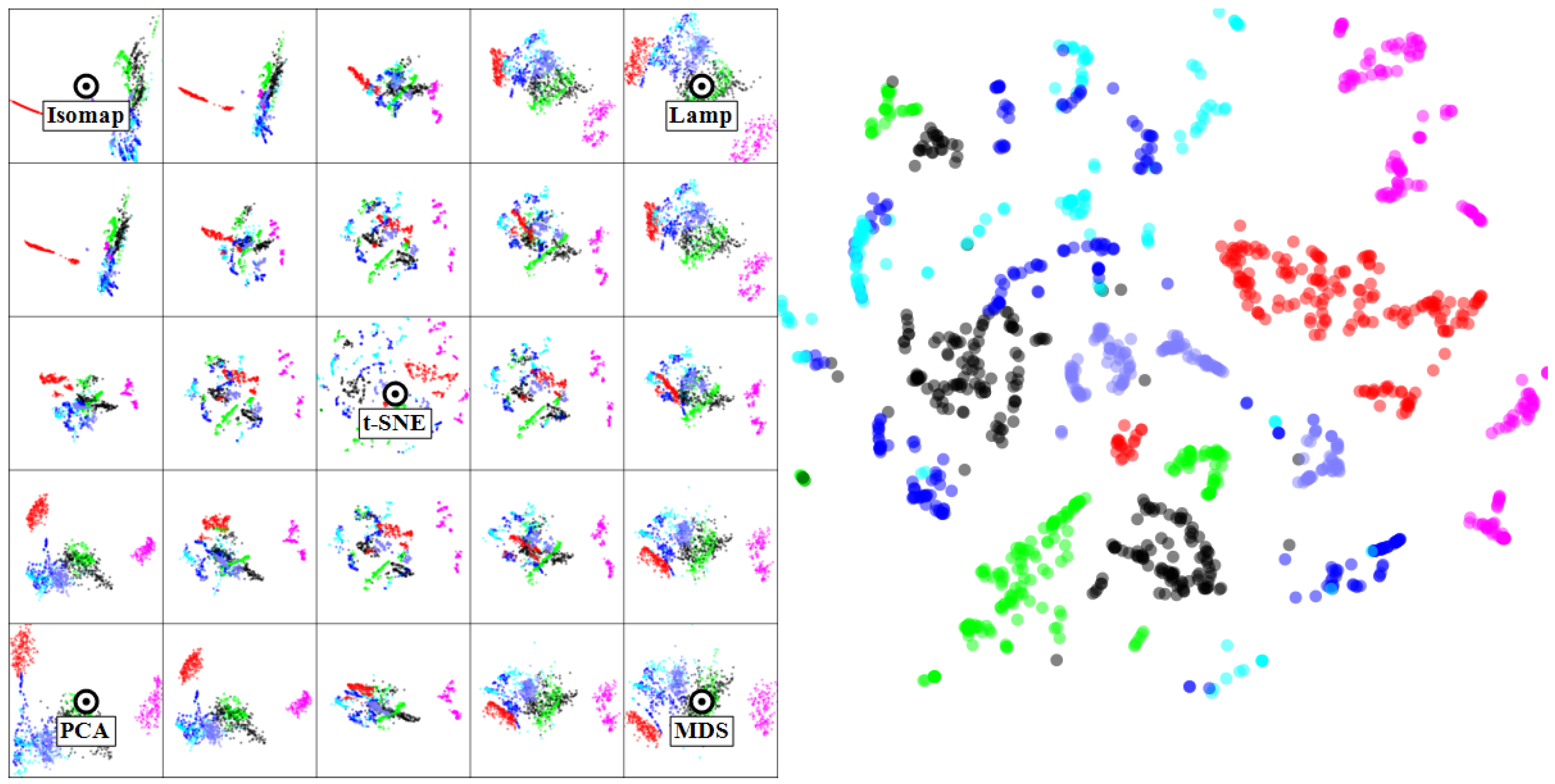
4.1. Multidimensional Projections
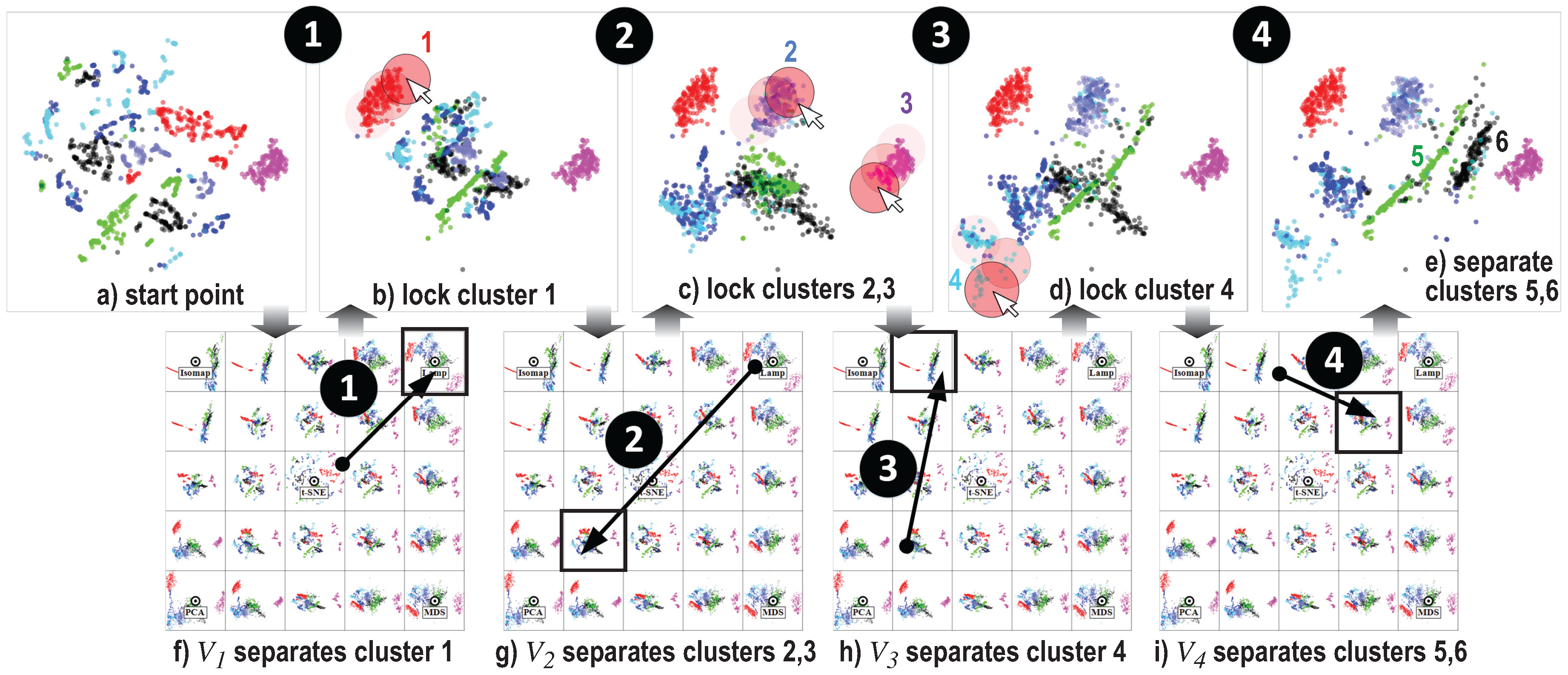
4.1.1. Software Dataset
4.1.2. Segmentation Dataset
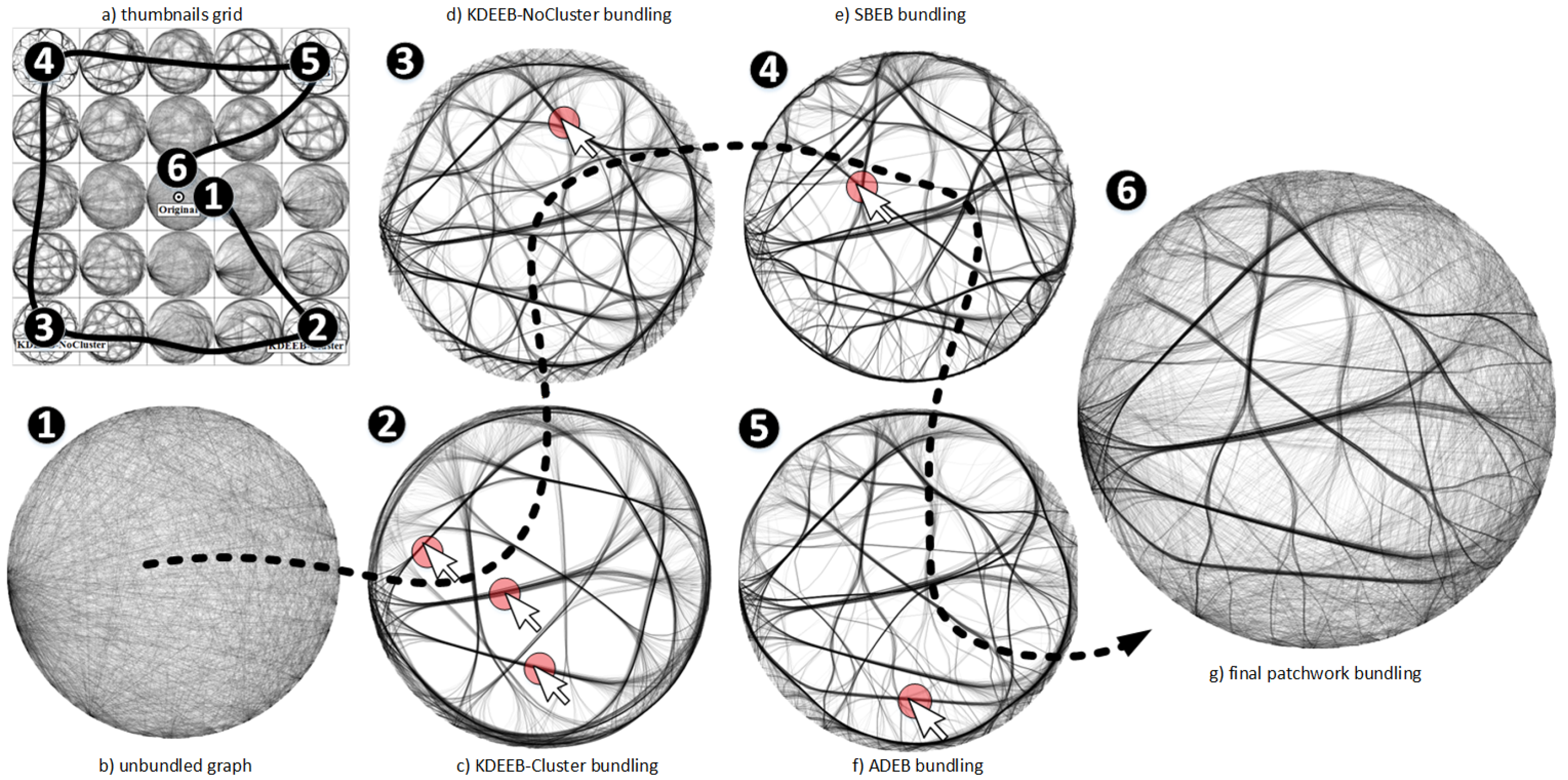
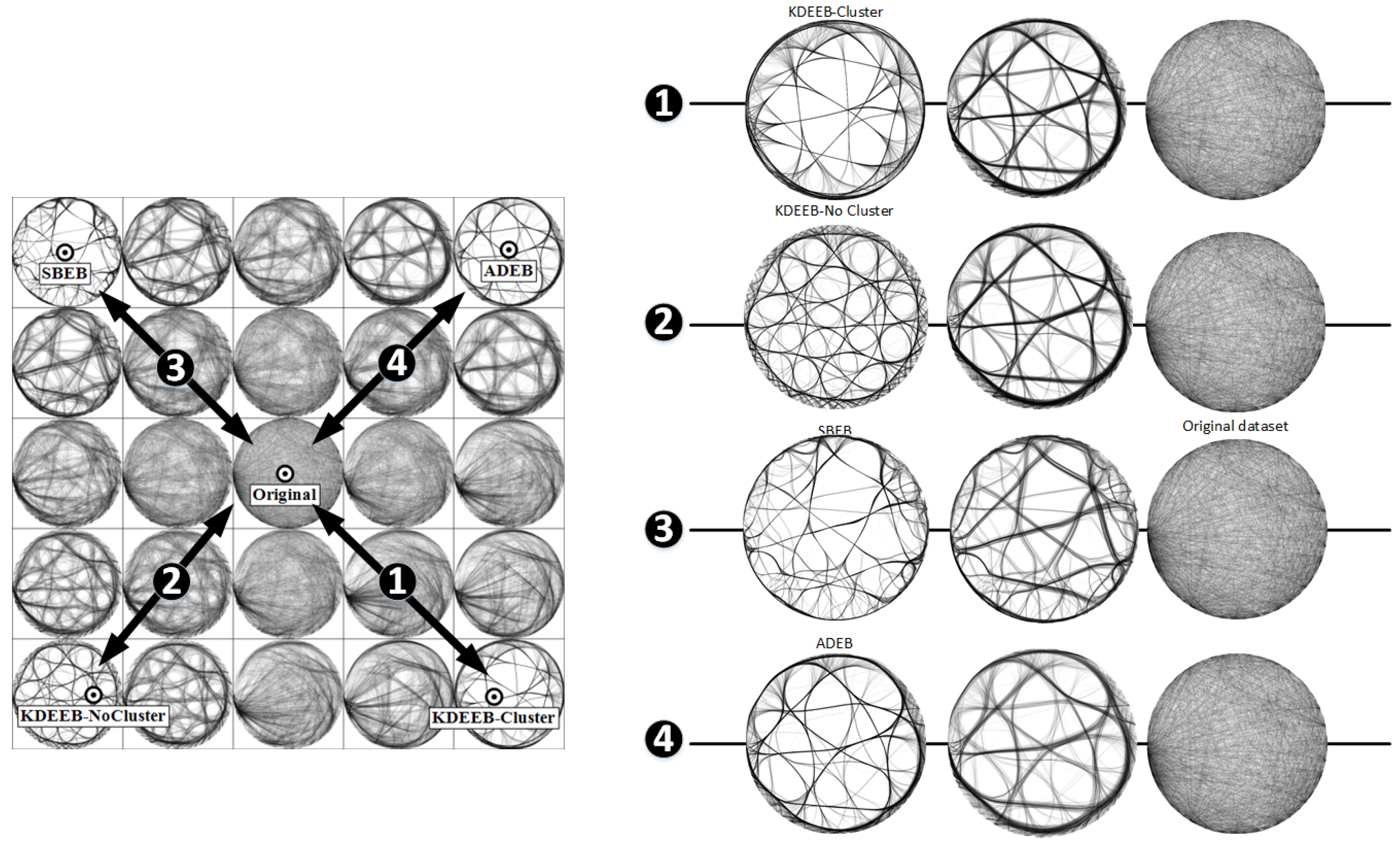
4.2. Bundled Graph Drawings
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Readings in Information Visualization: Using Vision to Think; Card, S.K., Mackinlay, J.D., Shneiderman, B., Eds.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1999. [Google Scholar]
- Hurter, C.; Telea, A.; Ersoy, O. MoleView: An attribute and structure-based semantic lens for large element-based plots. IEEE TVCG 2011, 17, 2600–2609. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.; Card, S.K. The Table Lens: Merging Graphical and Symbolic Representations in an Interactive Focus+Context Visualization for Tabular Information. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Boston, MA, USA, 24–28 April 1994; pp. 318–322. [Google Scholar]
- Telea, A. Combining Extended Table Lens and Treemap Techniques for Visualizing Tabular Data. In Proceedings of the Eighth Joint Eurographics/IEEE VGTC conference on Visualization, Lisbon, Portugal, 8–10 May 2006; pp. 51–58. [Google Scholar]
- Brosz, J.; Nacenta, M.A.; Pusch, R.; Carpendale, S.; Hurter, C. Transmogrification: Causal manipulation of visualizations. In Proceedings of the 26th Annual ACM Symposium on User Interface Software and Technology, St. Andrews, UK, 8–11 October 2013; pp. 97–106. [Google Scholar]
- Hurter, C.; Taylor, R.; Carpendale, S.; Telea, A. Color tunneling: Interactive exploration and selection in volumetric datasets. In Proceedings of the 2014 IEEE Pacific Visualization Symposium, Yokohama, Japan, 4–7 March 2014; pp. 225–232. [Google Scholar]
- Lhuillier, A.; Hurter, C.; Telea, A. State of the Art in Edge and Trail Bundling Techniques. Comput. Graph. Forum 2017. [Google Scholar] [CrossRef]
- Inselberg, A. The plane with parallel coordinates. Vis. Comput. 1985, 1, 69–91. [Google Scholar] [CrossRef]
- Inselberg, A. Parallel Coordinates; Springer: Berlin, Germany, 2009. [Google Scholar]
- Cleveland, W.S. Visualizing Data; Hobart Press: Summit, NJ, USA, 1993. [Google Scholar]
- Borg, I.; Groenen, P. Modern Multidimensional Scaling: Theory and Applications, 2nd ed.; Springer: Berlin, Germany, 2005. [Google Scholar]
- Van der Maaten, L.J.P.; Hinton, G.E. Visualizing High-dimensional Data using t-SNE. JMLR 2008, 9, 2579–2605. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Joia, P.; Coimbra, D.; Cuminato, J.; Paulovich, F.; Nonato, L.G. Local Affine Multidimensional Projection. IEEE TVCG 2011, 17, 2563–2571. [Google Scholar] [CrossRef] [PubMed]
- Kandogan, E. Visualizing Multi-Dimensional Clusters, Trends, and Outliers Using Star Coordinates. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001. [Google Scholar]
- Kandogan, E. Star Coordinates: A Multi-Dimensional Visualization Technique with Uniform Treatment of Dimensions. In Proceedings of the IEEE InfoVis 2000, Salt Lake City, UT, USA, 9–10 October 2000. [Google Scholar]
- Lehmann, D.J.; Theisel, H. Orthographic Star Coordinates. IEEE TVCG 2013, 19, 2615–2624. [Google Scholar] [CrossRef] [PubMed]
- Rubio-Sánchez, M.; Sanchez, A.; Lehmann, D.J. Adaptable Radial Axes Plots for Improved Multivariate Data Visualization. CGF 2017, 36, 389–399. [Google Scholar] [CrossRef]
- Gabriel, K.R. The biplot graphic display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
- Rubio-Sanchez, M.; Raya, L.; Diaz, F.; Sanchez, A. A comparative study between RadViz and Star Coordinates. IEEE TVCG 2016, 22, 619–628. [Google Scholar] [CrossRef] [PubMed]
- Daniels, K.M.; Grinstein, G.; Russell, A.; Glidden, M. Properties of normalized radial visualizations. Inf. Visual. 2012, 11, 273–300. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Martins, R.; Coimbra, D.; Minghim, R.; Telea, A. Visual analysis of dimensionality reduction quality for parameterized projections. Comput. Graph. 2014, 41, 26–42. [Google Scholar] [CrossRef]
- Tollis, I.; Battista, G.D.; Eades, P.; Tamassia, R. Graph Drawing: Algorithms for the Visualization of Graphs; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Kruiger, J.F.; Rauber, P.; Martins, R.; Kerren, A.; Kobourov, S.; Telea, A. Graph Layouts by t-SNE. CGF 2017, 36, 1745–1756. [Google Scholar] [CrossRef]
- Holten, D. Hierarchical edge bundles: Visualization of adjacency relations in hierarchical data. IEEE TVCG 2006, 12, 741–748. [Google Scholar] [CrossRef] [PubMed]
- Ersoy, O.; Hurter, C.; Paulovich, F.; Cantareiro, G.; Telea, A. Skeleton-based edge bundling for graph visualization. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2364–2373. [Google Scholar] [CrossRef] [PubMed]
- Hurter, C.; Ersoy, O.; Telea, A. Graph bundling by kernel density estimation. Comput. Graph. Forum 2012, 31, 865–874. [Google Scholar] [CrossRef]
- Peysakhovich, V.; Hurter, C.; Telea, A. Attribute-Driven Edge Bundling for General Graphs with Applications in Trail Analysis. In Proceedings of the 2015 IEEE Pacific Visualization Symposium (PacificVis), Hangzhou, China, 14–17 April 2015; pp. 39–46. [Google Scholar]
- Lhuillier, A.; Hurter, C.; Telea, A. FFTEB: Edge Bundling of Huge Graphs by the Fast Fourier Transform. In Proceedings of the 10th IEEE Pacific Visualization Symposium, PacificVis 2017, Seoul, Korea, 18–21 April 2017. [Google Scholar]
- Hofmann, J.; Groessler, M.; Pichler, P.P.; Lehmann, D.J. Visual Exploration of Global Trade Networks with Time-Dependent and Weighted Hierarchical Edge Bundles on GPU. Comput. Graph. Forum 2017, 36, 1545–1556. [Google Scholar] [CrossRef]
- van der Zwan, M.; Codreanu, V.; Telea, A. CUBu: Universal real-time bundling for large graphs. IEEE TVCG 2016, 22, 2550–2563. [Google Scholar] [CrossRef] [PubMed]
- Tversky, B.; Morrison, J.B.; Betrancourt, M. Animation: Can It Facilitate? Int. J. Hum.-Comput. Stud. 2002, 57, 247–262. [Google Scholar] [CrossRef]
- Chevalier, F.; Riche, N.H.; Plaisant, C.; Chalbi, A.; Hurter, C. Animations 25 Years Later: New Roles and Opportunities. In Proceedings of the International Working Conference on Advanced Visual Interfaces (AVI ’16), Bari, Italy, 7–10 June 2016; pp. 280–287. [Google Scholar]
- Bertin, J. Semiology of Graphics; University of Wisconsin Press: Madison, WI, USA, 1983. [Google Scholar]
- Elmqvist, N.; Stasko, J.; Tsigas, P. DataMeadow: A visual canvas for analysis of large-scale multivariate data. Inf. Vis. 2008, 7, 18–33. [Google Scholar] [CrossRef]
- Archambault, D.; Purchase, H.; Pinaud, B. Animation, Small Multiples, and the Effect of Mental Map Preservation in Dynamic Graphs. IEEE TVCG 2011, 17, 539–552. [Google Scholar] [CrossRef] [PubMed]
- Elmqvist, N.; Dragicevic, P.; Fekete, J.D. Rolling the dice: Multidimensional visual exploration using scatterplot matrix navigation. IEEE TVCG 2008, 14, 1141–1148. [Google Scholar] [CrossRef] [PubMed]
- Asimov, D. The grand tour: A tool for viewing multidimensional data. SIAM J. Sci. Stat. Comput. 1985, 6, 128–143. [Google Scholar] [CrossRef]
- Dhillon, I.S.; Modha, D.S.; Spangler, W. Class visualization of high-dimensional data with applications. Comput. Stat. Data Anal. 2002, 41, 59–90. [Google Scholar] [CrossRef]
- Huber, P.J. Projection pursuit. Ann. Stat. 1985, 13, 435–475. [Google Scholar] [CrossRef]
- Huh, M.Y.; Kim, K. Visualization of Multidimensional Data Using Modifications of the Grand Tour. J. Appl. Stat. 2002, 29, 721–728. [Google Scholar] [CrossRef]
- Pagliosa, P.; Paulovich, F.; Minghim, R.; Levkowitz, H.; Nonato, G. Projection inspector: Assessment and synthesis of multidimensional projections. Neurocomputing 2015, 150, 599–610. [Google Scholar] [CrossRef]
- Ma, K.L. Image graphs—A novel approach to visual data exploration. In Visualization’99: Proceedings of the IEEE Conference on Visualization; Ebert, D., Gross, M., Hamann, B., Eds.; IEEE Computer Society: Washington, DC, USA, 1999; pp. 81–88. [Google Scholar]
- Friedman, J.H.; Tukey, J.W. A projection pursuit algorithm for exploratory data analysis. IEE Trans. Comput. 1974, 100, 881–890. [Google Scholar] [CrossRef]
- Lehmann, D.J.; Theisel, H. Optimal Sets of Projections of High-Dimensional Data. IEEE TVCG 2015, 22, 609–618. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; Shneiderman, B. A rank-by-feature framework for unsupervised multidimensional dataexploration using low dimensional projections. In Proceedings of the IEEE Symposium on Information Visualization, Austin, TX, USA, 10–12 October 2004; pp. 65–72. [Google Scholar]
- Sips, M.; Neubert, B.; Lewis, J.P.; Hanrahan, P. Selecting good views of high-dimensional data using class consistency. CGF 2009, 28, 831–838. [Google Scholar] [CrossRef]
- Schreck, T.; von Landesberger, T.; Bremm, S. Techniques for precision-based visual analysis of projected data. Inf. Vis. 2010, 9, 181–193. [Google Scholar] [CrossRef]
- Lehmann, D.J.; Albuquerque, G.; Eisemann, M.; Magnor, M.; Theisel, H. Selecting coherent and relevant plots in large scatterplot matrices. CGF 2012, 31, 1895–1908. [Google Scholar] [CrossRef]
- Marks, J.; Andalman, B.; Beardsley, P.; Freeman, W.; Gibson, S.; Hodgins, J.; Kang, T.; Mirtich, B.; Pfister, H.; Ruml, W.; et al. Design Galleries: A General Approach to Setting Parameters for Computer Graphics and Animation. In ACM SIGGRAPH’97: Proceedings of the International Conference on Computer Graphics and Interactive Techniques; Whitted, T., Ed.; ACM Press/Addison-Wesley Publishing Co. : New York, NY, USA, 1997; pp. 389–400. [Google Scholar]
- Biedl, T.; Marks, J.; Ryall, K.; Whitesides, S. Graph Multidrawing: Finding Nice Drawings Without Defining Nice. In GD’98: Proceedings of the International Symposium on Graph Drawing; Whitesides, S.H., Ed.; Springer: Berlin, Germany, 1998; Volume 1547, pp. 347–355. [Google Scholar]
- Wu, Y.; Xu, A.; Chan, M.Y.; Qu, H.; Guo, P. Palette-Style Volume Visualization. In Proceedings of the EG/IEEE Conference on Volume Graphics, Prague, Czech Republic, 3–4 September 2007; pp. 33–40. [Google Scholar]
- Jankun-Kelly, T.; Ma, K.L. Visualization exploration and encapsulation via a spreadsheet-like interface. IEEE Trans. Vis. Comput. Graph. 2001, 7, 275–287. [Google Scholar] [CrossRef]
- Shapira, L.; Shamir, A.; Cohen-Or, D. Image Appearance Exploration by Model-Based Navigation. Comput. Graph. Forum 2009, 28, 629–638. [Google Scholar] [CrossRef]
- Van Wijk, J.J.; van Overveld, C.W. Preset based interaction with high dimensional parameter spaces. In Data Visualization; Springer: Berlin, Germany, 2003; pp. 391–406. [Google Scholar]
- Hurter, C.; Tissoires, B.; Conversy, S. FromDaDy: Spreading data across views to support iterative exploration of aircraft trajectories. IEEE TVCG 2009, 15, 1017–1024. [Google Scholar] [PubMed]
- Hurter, C. Image-Based Visualization: Interactive Multidimensional Data Exploration. Synth. Lect. Vis. 2015, 3, 1–127. [Google Scholar] [CrossRef]
- Paulovich, F.V.; Nonato, L.G.; Minghim, R.; Levkowitz, H. Least square projection: A fast high-precision multidimensional projection technique and its application to document mapping. IEEE TVCG 2008, 14, 564–575. [Google Scholar] [CrossRef] [PubMed]
- Paulovich, F.V.; Silva, C.T.; Nonato, L.G. Two-phase mapping for projecting massive data sets. IEEE TVCG 2010, 16, 12811290. [Google Scholar] [CrossRef] [PubMed]
- Pekalska, E.; de Ridder, D.; Duin, R.; Kraaijveld, M. A new method of generalizing Sammon mapping with application to algorithm speed-up. In Proceedings of the Annual Conference Advanced School for Computer Image (ASCI), Heijen, The Netherlands, 15–17 June 1999; pp. 221–228. [Google Scholar]
- Morrison, A.; Chalmers, M. A pivot-based routine for improved parent-finding in hybrid MDS. Inf. Vis. 2004, 3, 109–122. [Google Scholar] [CrossRef]
- Faith, J. Targeted Projection Pursuit for Interactive Exploration of High-Dimensional Data Sets. In Proceedings of the 11th International Conference on Information Visualization, Zurich, Switzerland, 4–6 July 2007. [Google Scholar]
- Roberts, J.C. Exploratory Visualization with Multiple Linked Views. In Exploring Geovisualization; Elsevier: Amsterdam, The Netherlands, 2004; pp. 149–170. [Google Scholar]
- North, C.; Shneiderman, B. A Taxonomy of Multiple Window Coordination; Technical Report T.R. 97-90; School of Computing, Univercity of Maryland: College Park, MD, USA, 1997. [Google Scholar]
- Baldonaldo, M.; Woodruff, A.; Kuchinsky, A. Guidelines for using multiple views in information visualization. In Proceedings of the Working Conference on Advanced Visual Interfaces (AVI), Palermo, Italy, 24–26 May 2000; pp. 110–119. [Google Scholar]
- Becker, R.; Cleveland, W. Brushing scatterplots. Technometrics 1987, 29, 127–142. [Google Scholar] [CrossRef]
- Schulz, H.J.; Hadlak, S. Preset-based Generation and Exploration of Visualization Designs. J. Vis. Lang. Comput. 2015, 31, 9–29. [Google Scholar] [CrossRef]
- Liu, B.; Wünsche, B.; Ropinski, T. Visualization by Example—A Constructive Visual Component-based Interface for Direct Volume Rendering. In Proceedings of the International Conference on Computer Graphics Theory and Applications, Angers, France, 17–21 May 2010; pp. 254–259. [Google Scholar]
- Chevalier, F.; Dragicevic, P.; Hurter, C. Histomages: Fully Synchronized Views for Image Editing. In Proceedings of the 25th Annual ACM Symposium on User Interface Software and Technology, Cambridge, MA, USA, 7–10 October 2012; pp. 281–286. [Google Scholar]
- Shepard, D. A Two-dimensional Interpolation Function for Irregularly-Spaced Data. In Proceedings of the 23rd ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Schulz, H.J.; Nocke, T.; Heitzler, M.; Schumann, H. A Design Space of Visualization Tasks. IEEE TVCG 2013, 19, 2366–2375. [Google Scholar] [CrossRef] [PubMed]
- Shneiderman, B. The Eyes Have It: A Task by Data Type Taxonomy for Information Visualizations. In Proceedings of the 1996 IEEE Symposium on Visual Languages, Boulder, CO, USA, 3–6 September 1996; pp. 336–343. [Google Scholar]
- Kruiger, H.; Hassoumi, A.; Schulz, H.-J.; Telea, A.; Hurter, C. Video Material for the Animation-Based Exploration. 2017. Available online: http://recherche.enac.fr/~hurter/SmallMultiple/ (accessed on 17 August 2017).
- Meirelles, P.; Santos, C., Jr.; Miranda, J.; Kon, F.; Terceiro, A.; Chavez, C. A study of the relationships between source code metrics and attractiveness in free software projects. In Proceedings of the 2010 Brazilian Symposium on Software Engineering, Bahia, Brazil, 27 September–1 October 2010; pp. 11–20. [Google Scholar]
- Coimbra, D.; Martins, R.; Neves, T.; Telea, A.; Paulovich, F. Explaining three-dimensional dimensionality reduction plots. Inf. Vis. 2016, 15, 154–172. [Google Scholar] [CrossRef]
- Lichman, M. UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences. 2013. Available online: http://archive.ics.uci.edu/ml (accessed on 17 August 2017).
- Rauber, P.E.; Falcao, A.X.; Telea, A.C. Projections as Visual Aids for Classification System Design. Inf. Vis. 2017. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruiger, J.F.; Hassoumi, A.; Schulz, H.-J.; Telea, A.; Hurter, C. Multidimensional Data Exploration by Explicitly Controlled Animation. Informatics 2017, 4, 26. https://doi.org/10.3390/informatics4030026
Kruiger JF, Hassoumi A, Schulz H-J, Telea A, Hurter C. Multidimensional Data Exploration by Explicitly Controlled Animation. Informatics. 2017; 4(3):26. https://doi.org/10.3390/informatics4030026
Chicago/Turabian StyleKruiger, Johannes F., Almoctar Hassoumi, Hans-Jörg Schulz, AlexandruC Telea, and Christophe Hurter. 2017. "Multidimensional Data Exploration by Explicitly Controlled Animation" Informatics 4, no. 3: 26. https://doi.org/10.3390/informatics4030026
APA StyleKruiger, J. F., Hassoumi, A., Schulz, H.-J., Telea, A., & Hurter, C. (2017). Multidimensional Data Exploration by Explicitly Controlled Animation. Informatics, 4(3), 26. https://doi.org/10.3390/informatics4030026







