Abstract
Massive open online courses (MOOCs) represent an innovative online learning paradigm that has garnered considerable popularity in recent years, attracting a multitude of learners to MOOC platforms due to their accessible and adaptable instructional structure. However, the elevated dropout rate in current MOOCs limits their advancement. Current dropout prediction models predominantly employ fixed-size convolutional kernels for feature extraction, which insufficiently address temporal dependencies and consequently demonstrate specific limitations. We propose a Lie Group-based feature context-local fusion attention model for predicting dropout in MOOCs. This model initially extracts shallow features using Lie Group machine learning techniques and subsequently integrates multiple parallel dilated convolutional modules to acquire high-level semantic representations. We design an attention mechanism that integrates contextual and local features, effectively capturing the temporal dependencies in the study behaviors of learners. We performed multiple experiments on the XuetangX dataset to evaluate the model’s efficacy. The results show that our method attains a precision score of 0.910, exceeding the previous state-of-the-art approach by 3.3%.
1. Introduction
Recently, Massive Open Online Courses (MOOCs) have emerged as an innovative teaching paradigm. The internet facilitates new avenues for knowledge acquisition and innovative learning methods, thereby significantly transforming the educational sector [1,2]. High dropout rates continue to pose a significant challenge to the advancement of MOOCs, despite the provision of enhanced platforms and learning pathways for learners. Prior studies demonstrate that completion rates for MOOCs typically remain under 10% [3]. Identifying learners at risk of dropout allows instructors to implement early interventions through personalized guidance, thus decreasing the likelihood of dropout. A critical area of research in online education involves analyzing learner behavior to identify key factors contributing to dropout rates, improving MOOC completion rates, and enhancing the overall quality of online education [4]. Accurate dropout prediction is crucial for advancing the sustainable and high-quality development of MOOCs.
Current models for predicting dropout rates in MOOCs are categorized into three primary types [5]: (1) models based on traditional machine learning, (2) models based on deep learning, and (3) models based on attention mechanisms. Conventional machine learning models focus on the clickstream data of learners, framing dropout prediction as a regression problem and employing classifiers as predictive models for dropout [6]. Yujiao et al. [7] introduced a feature weighting method that integrates Pearson correlation with a Support Vector Machine (SVM) for modeling purposes. The experimental results across various datasets indicated that by differentiating the significance of distinct behavioral features, this model surpassed traditional equal-weight feature models in predictive performance. Chen et al. [8] introduced a non-iterative hybrid algorithm that integrates decision trees with extreme learning machines, employing entropy theory to enhance model structure optimization. This successfully reduced behavioral variance and addressed training time challenges in predicting MOOC dropout. Behr et al. [9] employed a Random Forest (RF) approach, grounded in conditional inference trees, which integrates variables from learners’ early university experiences to predict dropout rates in extensive higher education datasets. Despite these advancements, traditional machine learning approaches often encounter limitations in processing complex data, frequently failing to identify deep, underlying patterns.
In this context, researchers have suggested methods based on deep learning, which utilize their capacity for automatic feature learning and have been extensively employed for dropout prediction. Xia and Qi [10] developed a multi-layer fully convolutional network aimed at predicting dropout. Niu et al. [11] introduced a new neural network model, CNNAE-LSTM, which integrates a convolutional autoencoder with a Long Short-Term Memory (LSTM) network to extract essential features and conduct time series modeling. Cam et al. [12] designed DeepS3VM, a hybrid model for dropout prediction. This model employs a Recurrent Neural Network (RNN) to analyze trends in learner behavior over time and integrates SVM for the classification of learners at risk of dropout. Chen et al. [13] addressed the challenges of insufficient early-stage data and sample imbalance by integrating a Convolutional Neural Network (CNN) with LSTM for dropout prediction, enhancing prediction accuracy. Deep learning methods predominantly utilize convolutional operations that emphasize local features, resulting in difficulties in capturing long-range dependencies and constraining their capacity to process global context.
With the continuous development of related research, scholars have introduced attention mechanisms into dropout prediction models. Attention mechanisms have increasingly been employed as practical approaches in dropout prediction owing to their ability to model long-range dependencies. Kumar et al. [14] developed the EDLN model, which incorporates various deep learning modules and utilizes a static attention mechanism to allocate attention weights to high-dimensional behavioral vectors. Wen and Juan [15] developed a model that combines self-attention mechanisms, a CNN, and LSTM, where the self-attention mechanism dynamically weights features and captures temporal correlations among them. Lee et al. [16] presented a deep learning model called DAS, which employs the attention mechanism of the Transformer to thoroughly examine the continuous behavioral changes in learners throughout a single learning session, ultimately forecasting the likelihood of session completion by the learners. In addition, Chen et al. [17] utilized a multi-head self-attention mechanism to forecast learner performance.
Despite the satisfactory results achieved by the aforementioned models, several challenges persist:
- Existing models predominantly utilize fixed convolution kernels, leading to constrained feature information extraction. The use of large-scale convolution kernels would significantly increase feature dimensions, thereby increasing the computational burden.
- Current attention mechanisms do not adequately capture the behavioral patterns of learners, especially in terms of temporal correlations. This method elevates computational demands but diminishes prediction accuracy.
- Most existing models exhibit intricate architectures, elevated feature dimensions, and significant computational complexity.
This study proposes a Lie Group-based feature context-local fusion attention model to predict MOOCs dropout and address key challenges. First, the model initially projects data samples onto a Lie Group manifold space, extracting multiscale feature maps through parallel dilated convolution. Second, it introduces a context-local feature fusion attention mechanism designed to capture features and their correlations across temporal and feature dimensions. Finally, it forecasts dropout rates. This study’s main contributions are summarized below:
- This study introduces a feature extraction method employing Lie Group machine learning, leveraging the computational advantages of Lie Groups and Lie algebras to effectively minimize feature dimensions and model complexity. Unlike conventional vector spaces that treat learning behaviors as discrete points, the manifold structure of Lie Groups can characterize the temporal continuity and non-linear evolutionary features of these behaviors.
- We present a context-local feature fusion attention mechanism that integrates contextual and local features. The mechanism empowers the model to more effectively extract region-specific details and contextual features while minimizing irrelevant features. Furthermore, it facilitates cross-layer interaction between shallow and high-level features, enhances the diversity of feature representations, and thereby improves the model’s prediction accuracy.
- Our model architecture utilizes mechanisms, including Lie Group and attention, to minimize feature dimensions efficiently. This method enhances both prediction accuracy and computational performance. Comprehensive experiments utilizing the publicly accessible XuetangX dataset demonstrate that our model outperforms leading methodologies in feature extraction and classification accuracy.
2. Related Work
2.1. Traditional Machine Learning-Based Dropout Prediction Model
Jin [18] employed an enhanced quantum particle swarm optimization algorithm to optimize the Support Vector Regression (SVR) model, successfully predicting dropout for the subsequent week. In comparison to traditional SVR models, Logistic Regression (LR) and other methodologies produced advantageous experimental outcomes. In dropout prediction models utilizing traditional machine learning, addressing sample imbalance among learners presents a significant challenge. Masood et al. [19] employed the Synthetic Minority Oversampling Technique to address this issue. Marcolino et al. [20] employed Adaptive Synthetic Sampling to generate dropout learner samples and detected dropouts through the CatBoost algorithm. Many research investigations have integrated different machine learning methods to forecast dropout rates. Blundo et al. [21] employed various classifiers for predicting dynamic weekly dropout. Kim et al. [22] introduced a dropout prediction model that integrates XGBoost and CatBoost, thereby improving prediction accuracy. Alghamdi et al. [23] integrated AdaBoost, RF, XGBoost, and additional models for dropout prediction, resulting in a 2% enhancement in accuracy compared to individual models. Feature selection and processing are both essential components in machine learning methodologies. Qiu et al. [24] utilized mutual information and random forests to identify the highest-scoring feature sets as inputs, subsequently applying logistic regression for dropout prediction. Kabathova and Drlik aggregated features of learning activities, selecting course engagement and test scores as inputs, and achieved favorable results across multiple classifiers [25].
2.2. Deep Learning-Based Dropout Prediction Model
Classical machine learning models depend largely on expert domain knowledge and experience, which introduces specific limitations. Deep learning models have gained significant attention and have been applied to dropout prediction due to their capacity for autonomous feature learning. Xu et al. [5] introduced a convolutional neural network approach utilizing feature extraction within Lie Group spaces for the purpose of dropout prediction. Shou et al. [26] utilized a parallel Fully Convolutional Network to extract multiscale features for predicting dropout. Zhang et al. [27] applied a Temporal Convolutional Network for modeling time-series features of learning behavior. Numerous studies integrate conventional machine learning techniques with deep learning methodologies. Alruwais [28] proposed the DeepFM model, which integrates Factorization Machines with a Deep Neural Network (DNN), resulting in a dropout prediction accuracy of 99%. Zheng et al. [29] utilized a C5.0 decision tree model to assign weights to key features, which were then used to train a CNN model. In dropout prediction research, learning behavior is analyzed as time-series data, utilizing LSTM for predictive modeling [30]. Talebi et al. [31] introduced six ensemble dropout prediction models that combine CNN and LSTM, resulting in an average accuracy of 92%. Mubarak et al. [32] designed a CNN–LSTM hyper-model, utilizing a tailored cost-sensitive loss function to enhance performance on minority class samples.
2.3. Attention-Based Dropout Prediction Model
To understand the behaviors of learners, identify factors contributing to dropout, and improve predictive model performance, some researchers have implemented attention mechanisms to predict dropout rates. Zheng et al. [33] designed a four-module dropout prediction architecture, utilizing a self-attention mechanism in the second module to assess correlations among local features and produce new feature representations. Fu et al. [34] proposed an ensemble model called CLSA. This model initially extracts features through a CNN and subsequently processes the sequential inputs bidirectionally with a Bidirectional Long Short-Term Memory network (Bi-LSTM). A static attention mechanism is integrated into the vectors to execute fixed-weight summation of features, allowing the model to emphasize the critical features associated with learner dropout. This model attained a dropout prediction accuracy of 87.6%. Yin et al. [35] incorporated multiple self-attention layers to enhance representational capacity and employed a decoupled attention mechanism to reduce computational complexity. Liu et al. [36] employed Bi-LSTM in conjunction with attention mechanisms to extract features for video learning, integrating these with additional characteristics for dropout prediction. Liang et al. [37] concurrently examined individual student behavior together with peer relationships related to dropout prediction. The extraction of individual behavioral features involved the use of self-attention mechanisms to identify essential characteristics. Furthermore, Capuano et al. put forward a series of attention-based classification and prediction methods for MOOCs data [38,39,40].
3. Methodology
3.1. Method Overview
Figure 1 illustrates the complete framework of the model. The process begins by representing samples within a Lie Group space to facilitate the extraction of features from both behavioral and temporal dimensions. Next, various modules utilizing parallel dilated convolutions are implemented to extract advanced abstract semantic features. Building on these features, we proposed an attention mechanism that integrates contextual and local features to extract key characteristics from samples while discarding irrelevant features and performing feature fusion. Finally, we perform dropout prediction on the samples.
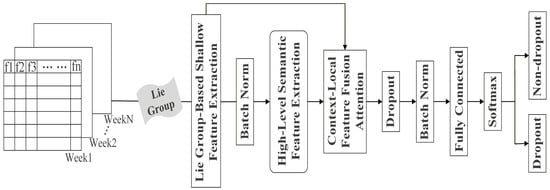
Figure 1.
Overview of the proposed model architecture.
3.2. Lie Group-Based Shallow Feature Extraction
In conventional vector spaces, models tend to treat learning behaviors at each time step as independent points or vectors, overlooking the continuity between them. However, in authentic learning scenarios, learner behaviors often exhibit continuity and dynamic dependencies. For instance, a student’s actions—from watching instructional videos and participating in online quizzes to submitting assignments—are not mutually isolated. Rather, they form a continuous process that evolves over time. The manifold structure of Lie Groups is better equipped to capture non-linear relationships and can model the temporal evolution of learner behavior more accurately than linear spaces.
Initially, the data samples are projected onto the Lie Group manifold, producing their corresponding representations. This transformation can be expressed as follows:
where represents the frequency of engagement by a learner in learning behavior of type on day , and denotes the element in the Lie Group manifold that corresponds to the statistical outcome of the learner’s behavior of type .
Each data sample associated with the Lie Group can have its attributes represented as , with denoting the Lie Group representations derived from the sample, as formulated below:
where denotes the mapping function that transforms raw data samples into d-dimensional Lie Group feature vectors. For any region within the Lie Group space, the mapping function produces a set of feature vectors for each sample point within that region, , where . This indicates that the region contains n sample points. Each sample point is represented by a d-dimensional feature vector, corresponding to days and types of learning behavior features.
To intuitively illustrate the mathematical process of the Lie Group mapping, as shown in Figure 2, we use the learner behavior matrix on the left as an example to demonstrate how it obtains its corresponding Lie Group representation via the logarithmic mapping.
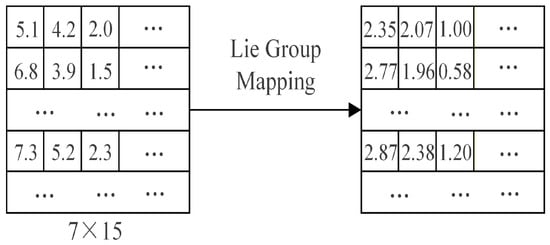
Figure 2.
Illustration of the Lie Group logarithmic mapping process.
Research on dropout prediction frequently emphasizes learner academic performance, neglecting the intricacies of their engagement and self-management skills. To effectively capture behavioral patterns associated with dropout, we extracted features across four dimensions, defined as follows:
The final feature vector for each learner related to a course is represented as a set that includes course access behavior (), video learning behavior (), assignment practice behavior (), and community interaction behavior (). Table 1 provides detailed definitions and mathematical representations of all features.

Table 1.
Feature definitions.
3.3. High-Level Semantic Feature Extraction
Figure 1 illustrates that Batch Normalization (BN) was applied prior to convolution. The objective is to modify the distribution of data samples via normalization and scaling. Prior studies [41] demonstrate that these operations can enhance the model’s convergence speed.
With the increasing depth of models, challenges such as vanishing gradients [42] and performance degradation [43] may occur. We employ a feature extraction method that incorporates blocks of multiple parallel dilated convolutions along with residual connections to address these challenges, as demonstrated in Figure 3.
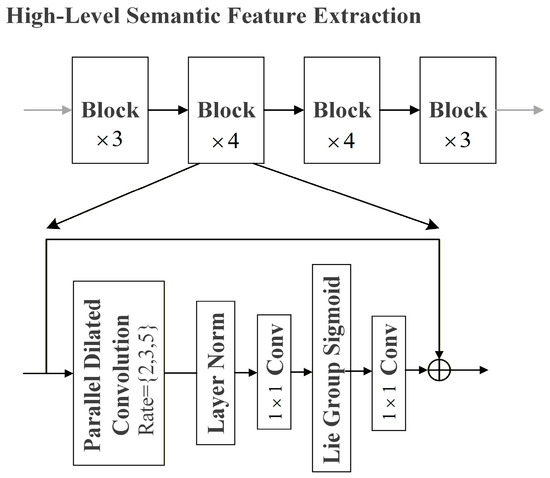
Figure 3.
The procedure for extracting high-level semantic features.
Figure 3 illustrates the Block module, with its formula articulated as follows:
where x refers to the input sample, denotes parallel dilated convolution, indicates layer normalization, represents convolution, and signifies the Lie Group activation function.
Prior studies [44] demonstrate that increasing the size of the convolution kernel to expand the model’s receptive field substantially increases the parameter count, consequently elevating the risk of overfitting. To tackle this issue, we utilize parallel dilated convolution with three dilation rates () to enhance the receptive field while managing the number of training parameters, as illustrated in Figure 4. The input feature map is processed by parallel dilated convolution as illustrated below:
where denotes the output of parallel dilated convolution with dilation rate . denotes the dilated convolution function, signifies shared parameters, and refers to the concatenation of the input feature map with the feature map derived from convolution.
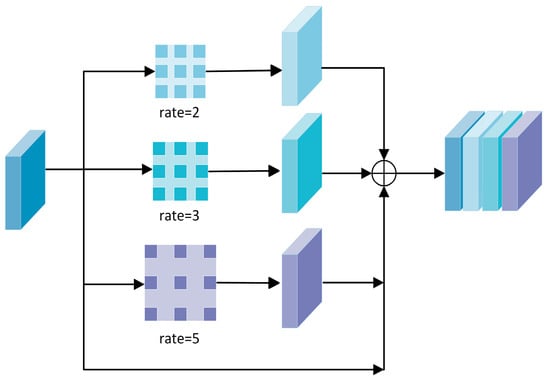
Figure 4.
Illustration of the parallel dilated convolution module. The last row represents the original features prior to convolution operations.
Subsequently, we employed layer normalization to accelerate the model’s convergence speed. We employed convolutions to integrate information across channels. Given that traditional kernel functions are inadequate for Lie Group samples in the model [41,45], we utilize the Lie Group sigmoid to enhance the robustness of the learned representations. To mitigate the issue of vanishing gradients, we implement residual connections following each block, combining the features extracted by parallel dilated convolutions with the block’s input features.
3.4. Context–Local Feature Fusion Attention Module
In the early stages of the model, numerous convolutions are applied to the data samples to extract high-level semantic features. Excessive emphasis on features processed through convolutions may lead to the neglect of significant earlier features [46], thereby impacting dropout prediction. Learning behaviors typically span several weeks, and dropout is often associated with specific behavioral patterns observed in the preceding week. We employ an attention mechanism that fuses both contextual and local features, allowing the model to learn the contextual dependencies of learning behavior features [47]. As shown in Figure 5, our proposed attention mechanism structurally differentiates the attention sources for features at different levels. This achieves a synergistic modeling of both global dependencies and local variations in learning behavior. Unlike traditional attention mechanisms that only perform self-attention aggregation within the same feature layer, we utilize shallow-level features to generate the Query, which is used to perceive short-term behavioral dependencies and local dynamic changes. Meanwhile, high-level semantic features serve as the Key and Value to capture the long-term global temporal context. This cross-layer interaction structure enables the model to fuse local and global features, thereby enhancing the diversity of its feature representations.
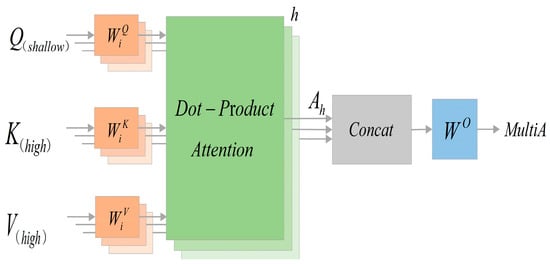
Figure 5.
Multi-head attention.
Figure 5 illustrates the multi-head attention mechanism adopted by the model [48,49]. The underlying calculation of one attention module is described as follows:
where is derived by applying a linear transformation to the Lie Group shallow features through the matrix . High-level semantic features are mapped to and through the matrices and , respectively. The similarity between and is computed to form the attention weights, which are subsequently applied to via weighted summation to yield the output features. Multi-head attention concurrently allocates input dimensions across several single-head attention modules for processing. Each module contains distinct matrices , , and , which compute the attention outputs . The final concatenated result is presented below:
The integration of contextual and local multi-head attention modules enabled the model to identify specific learning behavior features at critical time points for dropout prediction. To reduce overfitting while improving generalization ability, 30% of neurons were randomly deactivated during training. To address the oscillations caused by the dropout layer, we integrated a BN layer to enhance stability and accelerate training. The features acquired by the model are subsequently aligned with a score distribution. The scores are subsequently transformed into probability values using a softmax function for dropout prediction.
4. Experiments
4.1. Dataset
XuetangX, founded by Tsinghua University in 2013, ranks among the leading MOOC platforms in China. It provides an extensive selection of online courses from top domestic and international institutions. The XuetangX dataset [50] comprises multimodal information pertinent to online learning, including user behavior, course content, interaction records, and additional elements. Owing to its comprehensive scope, the dataset is extensively utilized in recommendation systems, behavioral modeling, and dropout prediction tasks. The dataset is notable for its large scale, sparse learner behavior data, and pronounced temporal characteristics, which pose considerable challenges for model development and practical application.
Table 2 presents statistical data from the XuetangX dataset, indicating that only about 23% of learners complete courses on the MOOCs platform. For our experiments, 15 features were selected: the 14 learning behavior features listed in Table 1, supplemented by an additional feature representing the learner’s active learning time. This feature reflects the extent of learner engagement and willingness to participate in the course, which can significantly influence dropout prediction. To ensure consistency and comparability between tests, we used an 80% training set and 20% test set data partition ratio, in accordance with other research on the XuetangX dataset. To mitigate the randomness introduced by a single data partition, we employed a Monte Carlo cross-validation strategy, in which the dataset was randomly divided into 80% training and 20% testing subsets ten times. The model was repeatedly trained and evaluated on each split, and the final results were reported as the average performance over the ten runs. In addition, to address the class imbalance between dropout and non-dropout learners, a class-weighted loss function was applied during training to achieve balanced optimization.

Table 2.
Details of the dataset.
4.2. Experimental Settings and Evaluation Metrics
The model’s effectiveness was evaluated through a series of experiments and comparative analyses. All baseline models and the proposed model used the same data partitioning, computational environment settings, and data preprocessing procedures. The configuration details of the experimental environment are provided in Table 3.

Table 3.
Experimental environment parameters.
Dropout prediction is formulated as a classification task. In such tasks, samples are typically categorized into positive and negative outcomes, which can be further grouped into four cases: true positive (), true negative (), false positive (), and false negative (). Based on these scenarios, we employ the following evaluation metrics:
4.3. Results and Analysis
Seven baseline models were employed to investigate the viability and effectiveness of our methodology, as summarized in Table 4. Our method yielded an F1-score of 0.901, representing improvements of 17.1% and 9.6% over LR and SVM, respectively. In terms of accuracy, our model reached 0.897, surpassing XGBoost and AdaBoost by 4.1% and 5.8%, and outperforming kNN by 7.3%. For precision, the proposed method attained 0.910, exceeding RF and GBDT by 8.3% and 5%, respectively. We incorporated parallel dilated convolutions into our model, enabling the extraction of features at multiple scales through varying dilation rates to effectively capture multi-level feature information. Traditional machine learning methods mainly rely on shallow statistical representations, which restrict their capacity to capture high-level semantics. The experimental results confirm the efficacy of our method. Furthermore, we integrated an attention mechanism to enhance the model’s ability to concentrate on essential behavioral features in the scene while minimizing the impact of irrelevant features.

Table 4.
Comparison of results with the baseline model.
Alongside the baseline model, we also selected several dropout prediction models from recent studies for comparative analysis, as summarized in Table 5. Our model achieved an F1-score of 0.901, representing improvements of 11% and 10.8% over SAVSNet and the CNN, respectively. SAVSNet employs a fixed-size 1D convolutional kernel of size 3 to extract local features from three consecutive time steps, while the CNN similarly relies on fixed-size convolutional kernels for feature extraction. In contrast, our model utilizes multi-branch parallel dilated convolutions featuring variable kernel sizes and dilation rates of 2, 3, and 5. Smaller kernels emphasize short-term behavioral changes in learning, whereas larger kernels identify long-term learning patterns. The outputs of all parallel branches are fused along the feature dimension, enabling effective interaction and representation learning across multiple scales. This method efficiently extracts more distinctive features, circumvents the limitations of fixed-size kernel feature extraction, and enhances the overall representational capacity of the model.

Table 5.
Performance comparison of dropout prediction models.
An accuracy of 0.897 was attained by our model, representing improvements of 3.5% and 2.3% over FWTS-CNN and MFCN-VIB, respectively. The proposed model utilizes an attention mechanism to prioritize behavioral features, giving greater weight to those behaviors that are significantly correlated with dropout prediction. Compared with the attention-free FWTS-CNN and MFCN-VIB models, our method shows a notable enhancement in accuracy, suggesting that the attention mechanism facilitates more accurate identification of dropout students.
On the precision metric, our model achieved 0.910, representing improvements of 4.8% and 4.2% over CLSA and Cross-TabNet, respectively. CLSA employs static attention, computing attention weights once across the feature dimension, which prevents dynamic weight updates. Cross-TabNet adopts sequential attention to progressively filter key features. This mechanism focuses attention on the feature dimension rather than the temporal dimension, resulting in weaker capture of learners’ cross-temporal learning behaviors. In contrast, our model employs an attention module that integrates contextual and local features. Local attention identifies short-term, high-frequency behavioral patterns within adjacent time steps, whereas contextual attention discerns long-term learning patterns throughout the entire learning cycle. By fusing contextual and local features, the model achieves complementary multiscale information processing, enabling more accurate dropout prediction. Furthermore, attention weights in our model are dynamically adjusted according to the input sequence, ensuring adaptive feature representation.
We employed SHAP to analyze the influence of each feature. As shown in Figure 6, our experimental findings reveal that the feature action_problem_check_correct holds considerable importance. Learners who successfully complete related exercises exhibit a strong understanding of the material, which fosters a positive reinforcement effect, encouraging continued engagement in their studies. Conversely, repeated failures to complete exercises correctly lead to frustration, reduced interest in learning, and a markedly increased likelihood of dropout. Additionally, frequent pausing of videos on MOOC platforms often signifies challenges in understanding the content, compelling learners to pause for reflection or reference. This persistent action_pause_video behavior undermines motivation and elevates the risk of dropout.
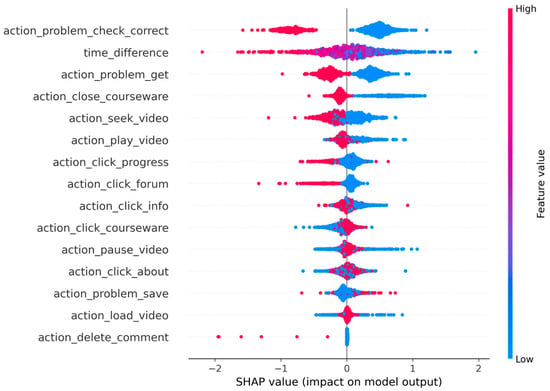
Figure 6.
Feature importance visualization based on SHAP. SHAP summary plot showing the contribution of learning behavior features to dropout prediction. Along the horizontal axis, SHAP values are presented to quantify feature importance, whereas the vertical axis enumerates the features.
4.4. Ablation Study
4.4.1. Effect of Lie Group Feature Learning on Dropout Prediction
This subsection presents a comparative analysis between models with and without the Lie Group feature learning module to evaluate its significance. Table 6 reports the experimental results, indicating that the exclusion of the Lie Group feature learning component causes a 2.5% drop in prediction accuracy relative to the full model. These findings demonstrate that Lie Group machine learning substantially strengthens the model’s capacity for learning salient features, thereby boosting predictive performance.

Table 6.
Influence of Lie Group.
4.4.2. Effect of Parallel Dilated Convolutions on Dropout Prediction
To validate the importance of parallel dilated convolutions, we conducted experimental analyses using two different convolution methods, as shown in Table 7. The accuracy obtained with traditional convolutions was 0.860, while the accuracy with parallel dilated convolutions increased to 0.897. This represents a 3.7% improvement, indicating that parallel dilated convolutions can more effectively extract features from learner behavior. In addition, they facilitate the fusion of features across multiple scales, thereby further strengthening feature learning.

Table 7.
Influence of parallel dilated convolution.
4.4.3. Effect of the Attention Mechanism on Dropout Prediction
To investigate the role of attention mechanisms in dropout prediction, we conducted experiments under three settings: (1) using only local feature attention, (2) using only contextual feature attention, and (3) using both attention mechanisms simultaneously. As shown in Table 8, the accuracy achieved with the joint application of both mechanisms was 0.897, representing improvements of 2.2% and 0.8% over using only local feature attention and only contextual feature attention, respectively. From the experiments, we observe that the integration of contextual and local features within the attention mechanism enables the capture of both learners’ overall learning trajectories and local behavioral patterns, which in turn strengthens the model’s representational power.

Table 8.
Influence of context-local feature fusion attention.
4.4.4. Effect of the Class Weighting Strategy on Dropout Prediction
To investigate the impact of the class weighting strategy on experimental results, we conducted comparative experiments between the model utilizing class weighting and the model without this strategy. The results are shown in Table 9. Upon introducing the class weighting strategy, the model achieved a Recall of 0.900, which is 2.8% higher than the model without this strategy. This indicates that under class imbalance conditions, the unweighted model tends to bias predictions towards the majority class (non-dropouts), resulting in an increased missed detection rate for dropouts. Conversely, with the inclusion of class weighting, the loss function assigns greater weight to the minority class, effectively mitigating the bias caused by class imbalance and enhancing the model’s robustness.

Table 9.
Influence of class weighting strategy.
5. Conclusions
This study proposes a Lie Group-based feature context-local fusion attention model for predicting dropout in MOOCs. First, the model utilizes Lie Group machine learning to model the learner’s behavioral sequences, capturing the continuous evolution of learning behavior over time while maintaining geometric consistency. Subsequently, the model introduces a context–local fusion attention mechanism to capture both the learner’s long-term contextual dependencies and their short-term behavioral trends. The two core modules work in concert to accurately pinpoint the key features leading to dropout, thereby identifying potential dropouts. For example, learners who fail to correctly complete post-class exercises are often more likely to abandon their studies later. We carried out extensive evaluations on the XuetangX dataset to validate the model’s effectiveness and robustness. The results indicate that the proposed method surpasses the PCMT model, with a 4.4% gain in accuracy and a 3.3% improvement in precision.
While our approach demonstrates improvements in metrics such as accuracy and precision, it still has certain limitations. For instance, the computational burden of the model could be further minimized. Future research will explore integrating Lie Group machine learning with Graph Neural Network architectures. This aims to enhance the model’s relational reasoning capabilities and scalability while simultaneously further improving accuracy and reducing computational complexity.
Beyond its predictive performance, the proposed model holds significant practical value in online learning scenarios. The model can be integrated into MOOC early warning systems to identify at-risk learners at an early stage, enabling instructors to implement timely and targeted interventions. This is further supported by the model’s SHAP-based interpretability analysis, which can identify key behavioral indicators associated with dropout risk. Consequently, the system can automatically generate alerts when students show early signs of disengagement.
Author Contributions
Y.L. conceived and designed the study; methodology was jointly developed by Y.L. and C.X.; D.Y. carried out the software implementation; Y.L. and C.X. prepared the initial draft; C.X. was responsible for manuscript revision and editing; and Y.S. secured the funding. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (62262074), the Science and Technology Plan Project of Yunnan Province (202405AC350083), the National Natural Science Foundation of China (62363015), the National Natural Science Foundation of China (42261068), and the Natural Science Foundation of Jiangxi Province (20242BAB25112).
Data Availability Statement
The XuetangX dataset analyzed during the current study is publicly available in the MoocData repository at http://moocdata.cn/data/user-activity (accessed on 18 November 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Moreno-Marcos, P.M.; Muñoz-Merino, P.J.; Maldonado-Mahauad, J.; Pérez-Sanagustín, M.; Alario-Hoyos, C.; Delgado Kloos, C. Temporal Analysis for Dropout Prediction Using Self-Regulated Learning Strategies in Self-Paced MOOCs. Comput. Educ. 2020, 145, 103728. [Google Scholar] [CrossRef]
- Fidalgo-Blanco, Á.; Sein-Echaluce, M.L.; García-Peñalvo, F.J. From Massive Access to Cooperation: Lessons Learned and Proven Results of a Hybrid xMOOC/cMOOC Pedagogical Approach to MOOCs. Int. J. Educ. Technol. High. Educ. 2016, 13, 24. [Google Scholar] [CrossRef]
- De Freitas, S.I.; Morgan, J.; Gibson, D. Will MOOCs Transform Learning and Teaching in Higher Education? Engagement and Course Retention in Online Learning Provision. Br. J. Educ. Technol. 2015, 46, 455–471. [Google Scholar] [CrossRef]
- Rawat, S.; Kumar, D.; Kumar, P.; Khattri, C. A Systematic Analysis Using Classification Machine Learning Algorithms to Understand Why Learners Drop out of MOOCs. Neural Comput. Appl. 2021, 33, 14823–14835. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Ye, J.; Shu, J. Educational Data Mining: Dropout Prediction in XuetangX MOOCs. Neural Process. Lett. 2022, 54, 2885–2900. [Google Scholar] [CrossRef]
- Jin, C. Dropout Prediction Model in MOOC Based on Clickstream Data and Student Sample Weight. Soft Comput. 2021, 25, 8971–8988. [Google Scholar] [CrossRef]
- Yujiao, Z.; Ang, L.W.; Shaomin, S.; Palaniappan, S. Dropout Prediction Model for College Students in MOOCs Based on Weighted Multi-Feature and SVM. J. Inform. Web Eng. 2023, 2, 29–42. [Google Scholar] [CrossRef]
- Chen, J.; Feng, J.; Sun, X.; Wu, N.; Yang, Z.; Chen, S. MOOC Dropout Prediction Using a Hybrid Algorithm Based on Decision Tree and Extreme Learning Machine. Math. Probl. Eng. 2019, 2019, 8404653. [Google Scholar] [CrossRef]
- Behr, A.; Giese, M.; Teguim, K.H.D.; Theune, K. Early Prediction of University Dropouts—A Random Forest Approach. Jahrb. Natl. Stat. 2020, 240, 743–789. [Google Scholar] [CrossRef]
- Xia, X.; Qi, W. Dropout Prediction and Decision Feedback Supported by Multi Temporal Sequences of Learning Behavior in MOOCs. Int. J. Educ. Technol. High. Educ. 2023, 20, 32. [Google Scholar] [CrossRef]
- Niu, K.; Lu, G.; Peng, X.; Zhou, Y.; Zeng, J.; Zhang, K. CNN Autoencoders and LSTM-Based Reduced Order Model for Student Dropout Prediction. Neural Comput. Appl. 2023, 35, 22341–22357. [Google Scholar] [CrossRef]
- Nguyen Thi Cam, H.; Sarlan, A.; Arshad, N.I. A Hybrid Model Integrating Recurrent Neural Networks and the Semi-Supervised Support Vector Machine for Identification of Early Student Dropout Risk. PeerJ Comput. Sci. 2024, 10, e2572. [Google Scholar] [CrossRef]
- Chen, H.-C.; Prasetyo, E.; Tseng, S.-S.; Putra, K.T.; Prayitno; Kusumawardani, S.S.; Weng, C.-E. Week-Wise Student Performance Early Prediction in Virtual Learning Environment Using a Deep Explainable Artificial Intelligence. Appl. Sci. 2022, 12, 1885. [Google Scholar] [CrossRef]
- Kumar, G.; Singh, A.; Sharma, A. Ensemble Deep Learning Network Model for Dropout Prediction in MOOCs. Int. J. Electr. Comput. Eng. Syst. 2023, 14, 187–196. [Google Scholar] [CrossRef]
- Wen, X.; Juan, H. Early Prediction of MOOC Dropout in Self-Paced Students Using Deep Learning. Interact. Learn. Environ. 2024, 32, 7102–7119. [Google Scholar] [CrossRef]
- Lee, Y.; Shin, D.; Loh, H.; Lee, J.; Chae, P.; Cho, J.; Park, S.; Lee, J.; Baek, J.; Kim, B.; et al. Deep Attentive Study Session Dropout Prediction in Mobile Learning Environment. arXiv 2021, arXiv:2002.11624. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, G.; Liu, J.; Chen, Y.; Zheng, Q.; Tian, F.; Zhu, H.; Wang, Q.; Wu, Y. A Prediction Model of Student Performance Based on Self-Attention Mechanism. Knowl. Inf. Syst. 2023, 65, 733–758. [Google Scholar] [CrossRef]
- Jin, C. MOOC Student Dropout Prediction Model Based on Learning Behavior Features and Parameter Optimization. Interact. Learn. Environ. 2023, 31, 714–732. [Google Scholar] [CrossRef]
- Masood, S.W.; Gogoi, M.; Begum, S.A. Optimised SMOTE-Based Imbalanced Learning for Student Dropout Prediction. Arab. J. Sci. Eng. 2025, 50, 7165–7179. [Google Scholar] [CrossRef]
- Rebelo Marcolino, M.; Reis Porto, T.; Thompsen Primo, T.; Targino, R.; Ramos, V.; Marques Queiroga, E.; Munoz, R.; Cechinel, C. Student Dropout Prediction through Machine Learning Optimization: Insights from Moodle Log Data. Sci. Rep. 2025, 15, 9840. [Google Scholar] [CrossRef]
- Blundo, C.; Loia, V.; Orciuoli, F. A Time-Aware Approach for MOOC Dropout Prediction Based on Rule Induction and Sequential Three-Way Decisions. IEEE Access 2023, 11, 113189–113198. [Google Scholar] [CrossRef]
- Kim, S.; Choi, E.; Jun, Y.-K.; Lee, S. Student Dropout Prediction for University with High Precision and Recall. Appl. Sci. 2023, 13, 6275. [Google Scholar] [CrossRef]
- Alghamdi, S.; Soh, B.; Li, A. ISELDP: An Enhanced Dropout Prediction Model Using a Stacked Ensemble Approach for In-Session Learning Platforms. Electronics 2025, 14, 2568. [Google Scholar] [CrossRef]
- Qiu, L.; Liu, Y.; Liu, Y. An Integrated Framework With Feature Selection for Dropout Prediction in Massive Open Online Courses. IEEE Access 2018, 6, 71474–71484. [Google Scholar] [CrossRef]
- Kabathova, J.; Drlik, M. Towards Predicting Student’s Dropout in University Courses Using Different Machine Learning Techniques. Appl. Sci. 2021, 11, 3130. [Google Scholar] [CrossRef]
- Shou, Z.; Chen, P.; Wen, H.; Liu, J.; Zhang, H. MOOC Dropout Prediction Based on Multidimensional Time-Series Data. Math. Probl. Eng. 2022, 2022, 2213292. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Zhao, J.; Zhang, B.; Zhang, F. IC-BTCN: A Deep Learning Model for Dropout Prediction of MOOCs Students. IEEE Trans. Educ. 2024, 67, 974–982. [Google Scholar] [CrossRef]
- Alruwais, N.M. Deep FM-Based Predictive Model for Student Dropout in Online Classes. IEEE Access 2023, 11, 96954–96970. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, Z.; Wang, Y.; Fu, Q. MOOC Dropout Prediction Using FWTS-CNN Model Based on Fused Feature Weighting and Time Series. IEEE Access 2020, 8, 225324–225335. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, H.; Zhang, N.; Yan, H.; Tang, F.; Zhang, W. Dropout Rate Prediction of Massive Open Online Courses Based on Convolutional Neural Networks and Long Short-Term Memory Network. Mob. Inf. Syst. 2022, 2022, 8255965. [Google Scholar] [CrossRef]
- Talebi, K.; Torabi, Z.; Daneshpour, N. Ensemble Models Based on CNN and LSTM for Dropout Prediction in MOOC. Expert Syst. Appl. 2024, 235, 121187. [Google Scholar] [CrossRef]
- Mubarak, A.A.; Cao, H.; Hezam, I.M. Deep Analytic Model for Student Dropout Prediction in Massive Open Online Courses. Comput. Electr. Eng. 2021, 93, 107271. [Google Scholar] [CrossRef]
- Zheng, Y.; Shao, Z.; Deng, M.; Gao, Z.; Fu, Q. MOOC Dropout Prediction Using a Fusion Deep Model Based on Behaviour Features. Comput. Electr. Eng. 2022, 104, 108409. [Google Scholar] [CrossRef]
- Fu, Q.; Gao, Z.; Zhou, J.; Zheng, Y. CLSA: A Novel Deep Learning Model for MOOC Dropout Prediction. Comput. Electr. Eng. 2021, 94, 107315. [Google Scholar] [CrossRef]
- Yin, S.; Lei, L.; Wang, H.; Chen, W. Power of Attention in MOOC Dropout Prediction. IEEE Access 2020, 8, 202993–203002. [Google Scholar] [CrossRef]
- Liu, H.; Chen, X.; Zhao, F. Learning Behavior Feature Fused Deep Learning Network Model for MOOC Dropout Prediction. Educ. Inf. Technol. 2024, 29, 3257–3278. [Google Scholar] [CrossRef]
- Liang, G.; Qian, Z.; Wang, S.; Hao, P. MOOCs Dropout Prediction via Classmates Augmented Time-Flow Hybrid Network. In Neural Information Processing; Luo, B., Cheng, L., Wu, Z.-G., Li, H., Li, C., Eds.; Communications in Computer and Information Science; Springer Nature: Singapore, 2024; Volume 1969, pp. 405–416. ISBN 978-981-99-8183-0. [Google Scholar]
- Capuano, N.; Caballé, S.; Conesa, J.; Greco, A. Attention-Based Hierarchical Recurrent Neural Networks for MOOC Forum Posts Analysis. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 9977–9989. [Google Scholar] [CrossRef]
- Sebbaq, H.; El Faddouli, N. An Explainable Attention-Based Bidirectional GRU Model for Pedagogical Classification of MOOCs. Interact. Technol. Smart Educ. 2022, 19, 396–421. [Google Scholar] [CrossRef]
- Al-azazi, F.A.; Ghurab, M. ANN-LSTM: A Deep Learning Model for Early Student Performance Prediction in MOOC. Heliyon 2023, 9, e15382. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. A Combination of Lie Group Machine Learning and Deep Learning for Remote Sensing Scene Classification Using Multi-Layer Heterogeneous Feature Extraction and Fusion. Remote Sens. 2022, 14, 1445. [Google Scholar] [CrossRef]
- Galimberti, C.L.; Furieri, L.; Xu, L.; Ferrari-Trecate, G. Hamiltonian Deep Neural Networks Guaranteeing Non-Vanishing Gradients by Design. IEEE Trans. Autom. Control. 2023, 68, 3155–3162. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA; pp. 770–778. [Google Scholar]
- Xu, C.; Zhu, G.; Shu, J. A Lightweight and Robust Lie Group-Convolutional Neural Networks Joint Representation for Remote Sensing Scene Classification. Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, G.; Shu, J. Robust Joint Representation of Intrinsic Mean and Kernel Function of Lie Group for Remote Sensing Scene Classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 796–800. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y.; Zhang, J.; Gao, P.; Song, G.; Liu, Y.; Li, H.; Qiao, Y. UniFormer: Unifying Convolution and Self-Attention for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 12581–12600. [Google Scholar] [CrossRef]
- Apostolidis, E.; Balaouras, G.; Mezaris, V.; Patras, I. Combining Global and Local Attention with Positional Encoding for Video Summarization. In Proceedings of the 2021 IEEE International Symposium on Multimedia (ISM), Naple, Italy, 29 November–1 December 2021; IEEE: Piscataway, NJ, USA; pp. 226–234. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Ghazimoghadam, S.; Hosseinzadeh, S.A.A. A Novel Unsupervised Deep Learning Approach for Vibration-Based Damage Diagnosis Using a Multi-Head Self-Attention LSTM Autoencoder. Measurement 2024, 229, 114410. [Google Scholar] [CrossRef]
- Feng, W.; Tang, J.; Liu, T.X. Understanding Dropouts in MOOCs. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 517–524. [Google Scholar] [CrossRef]
- Pan, T.; Feng, G.; Liu, X.; Wu, W. Using Feature Interaction for Mining Learners’ Hidden Information in MOOC Dropout Prediction. In Augmented Intelligence and Intelligent Tutoring Systems; Lecture Notes in Computer Science; Frasson, C., Mylonas, P., Troussas, C., Eds.; Springer Nature: Cham, Switzerland, 2023; Volume 13891, pp. 507–517. ISBN 978-3-031-32882-4. [Google Scholar]
- Basnet, R.B.; Johnson, C.; Doleck, T. Dropout Prediction in Moocs Using Deep Learning and Machine Learning. Educ. Inf. Technol. 2022, 27, 11499–11513. [Google Scholar] [CrossRef]
- Pan, F.; Huang, B.; Zhang, C.; Zhu, X.; Wu, Z.; Zhang, M.; Ji, Y.; Ma, Z.; Li, Z. A Survival Analysis Based Volatility and Sparsity Modeling Network for Student Dropout Prediction. PLoS ONE 2022, 17, e0267138. [Google Scholar] [CrossRef]
- Niu, K.; Zhou, Y.; Lu, G.; Tai, W.; Zhang, K. PMCT: Parallel Multiscale Convolutional Temporal Model for MOOC Dropout Prediction. Comput. Electr. Eng. 2023, 112, 108989. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).