Percolation–Stochastic Model for Traffic Management in Transport Networks
Abstract
1. Introduction
- Percolation analysis can effectively characterize the spatiotemporal evolution of congestion for the purpose of traffic signal control.
- Dynamic signal adjustment based on percolation-driven congestion analysis successfully balances traffic, thereby increasing overall network throughput.
- Dynamic percolation-based perimeter control significantly outperforms conventional fixed-perimeter control in terms of network traffic efficiency.
2. Mathematical Framework of the Proposed Model
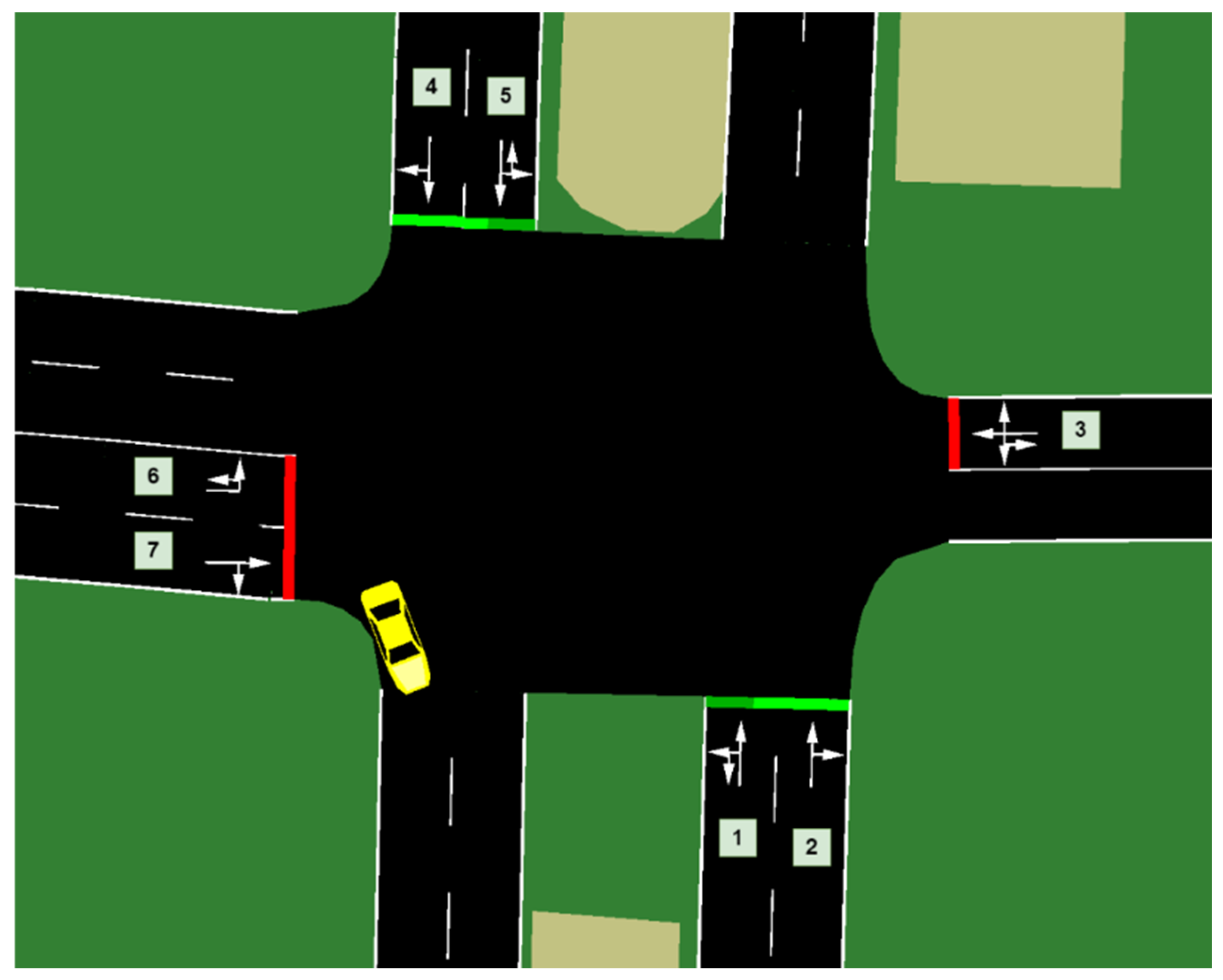
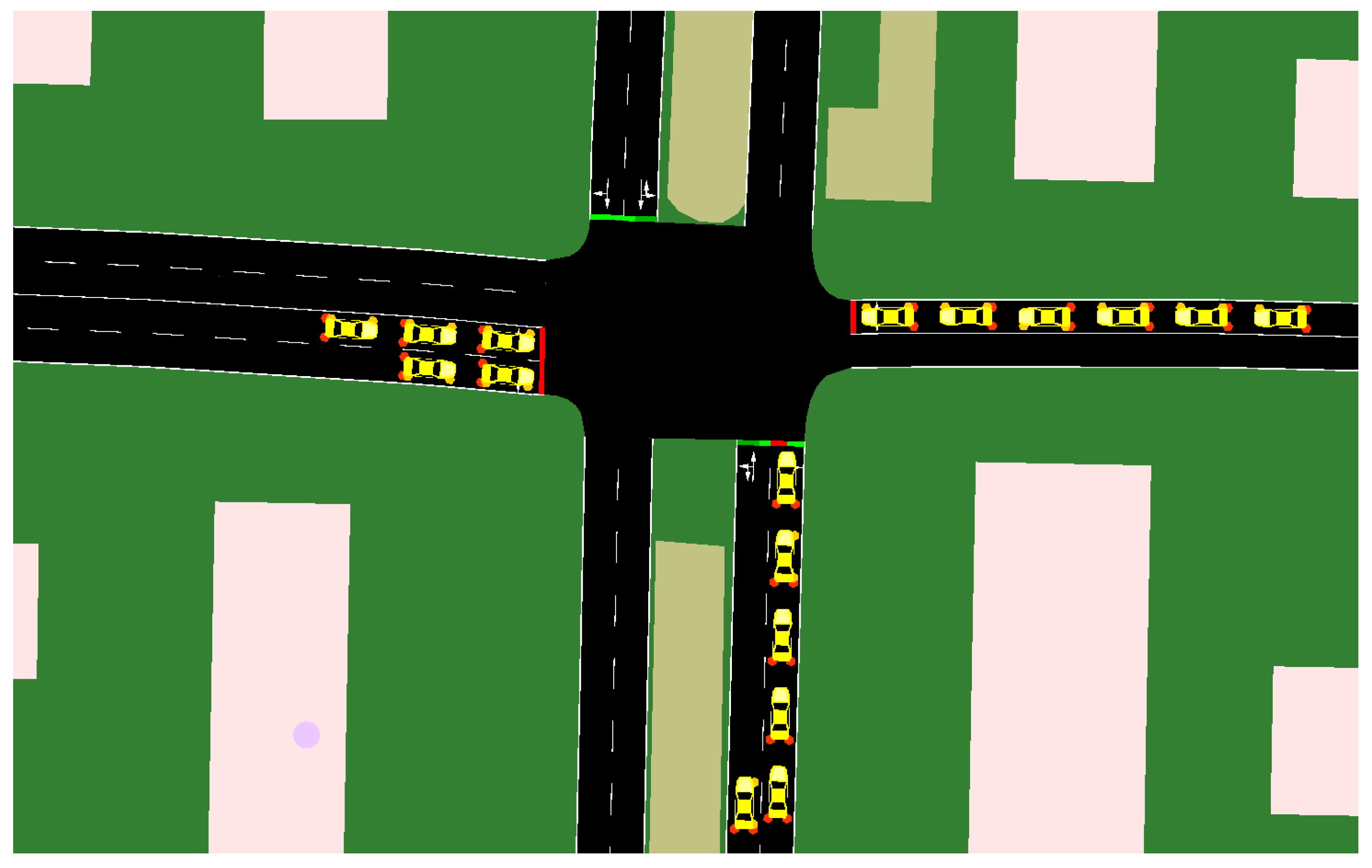
2.1. Description of Intersection Operation
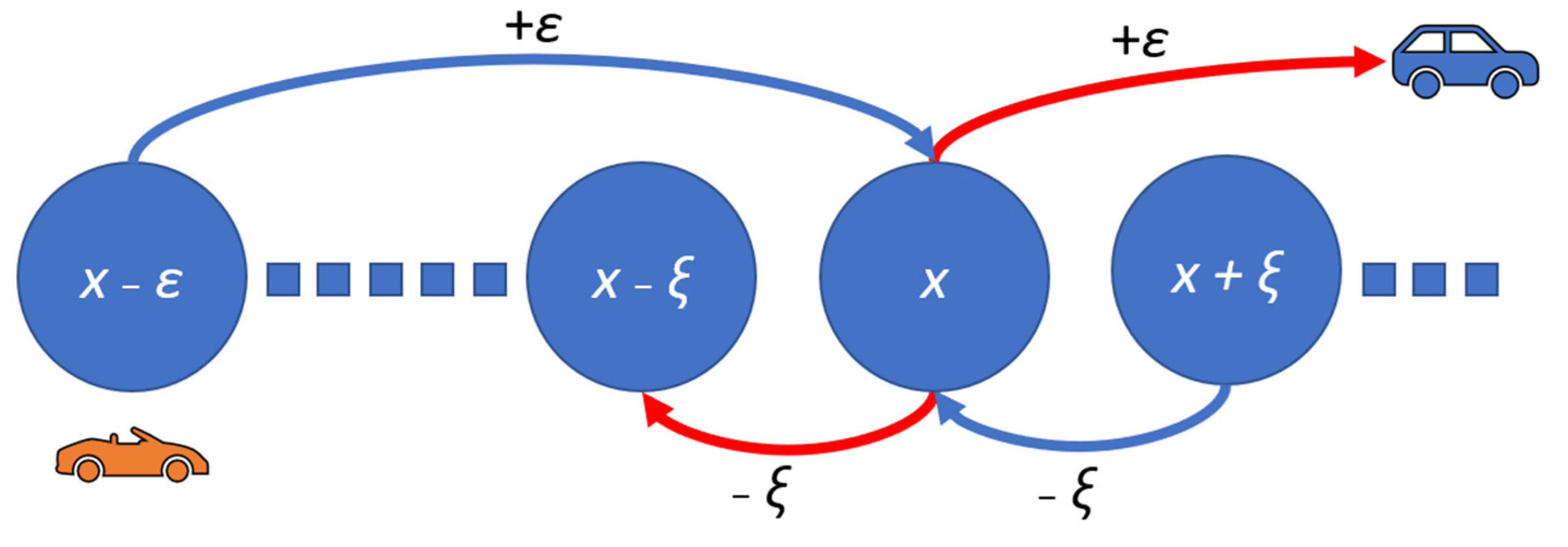
2.2. Fundamental Principles of Percolation Theory
2.3. Stochastic Dynamics Model of Traffic Light Operation
3. Algorithm for Generating Control of Traffic Signal Phases
- Use the stochastic dynamics model to compute the times at which departure lanes are expected to overload. If such lanes are found, select the lane with the nearest predicted time to the overloaded/blocked state. Verify that an exit lane is available (not overloaded) for the selected departure lane and confirm that the exit lane has sufficient capacity for the waiting vehicles.
- Among the directions where a green phase is admissible, find the lane that has not been opened for the longest time and select it as the candidate lane.
- If, considering the lanes closed by red signals, no candidate can be found, then select a candidate disregarding the restriction imposed by the closed red signals.
- The time needed to clear the current queue from the lane,
- The capacity of the exit lane, i.e., how much time is available before this lane becomes filled,
- The maximum permissible duration of the green signal,
- The minimum of these calculated values.
4. Verification of the Developed Traffic Flow Model and Analysis of Simulation Results
4.1. Selection of Cities for Simulation
- The initialization can be performed simultaneously across all simulated city areas.
- A certain number of traffic jams are formed initially, but the roads (including unsignalized segments) are not completely blocked.
4.2. Simulation Methodology
- Choice of a city area and import of data from OpenStreetMap.
- Construction of the urban environment for traffic simulation based on the imported data.
- Random generation of route sets for the selected areas.
- For each selected area (6 cities) and for each route set (2 sets), separate simulations are created (2 simulations):
- a.
- Simulation of static control of traffic signal phase switching.
- b.
- Calculation of the percolation threshold and simulation of dynamic control of traffic signal phase switching (see Table 3).
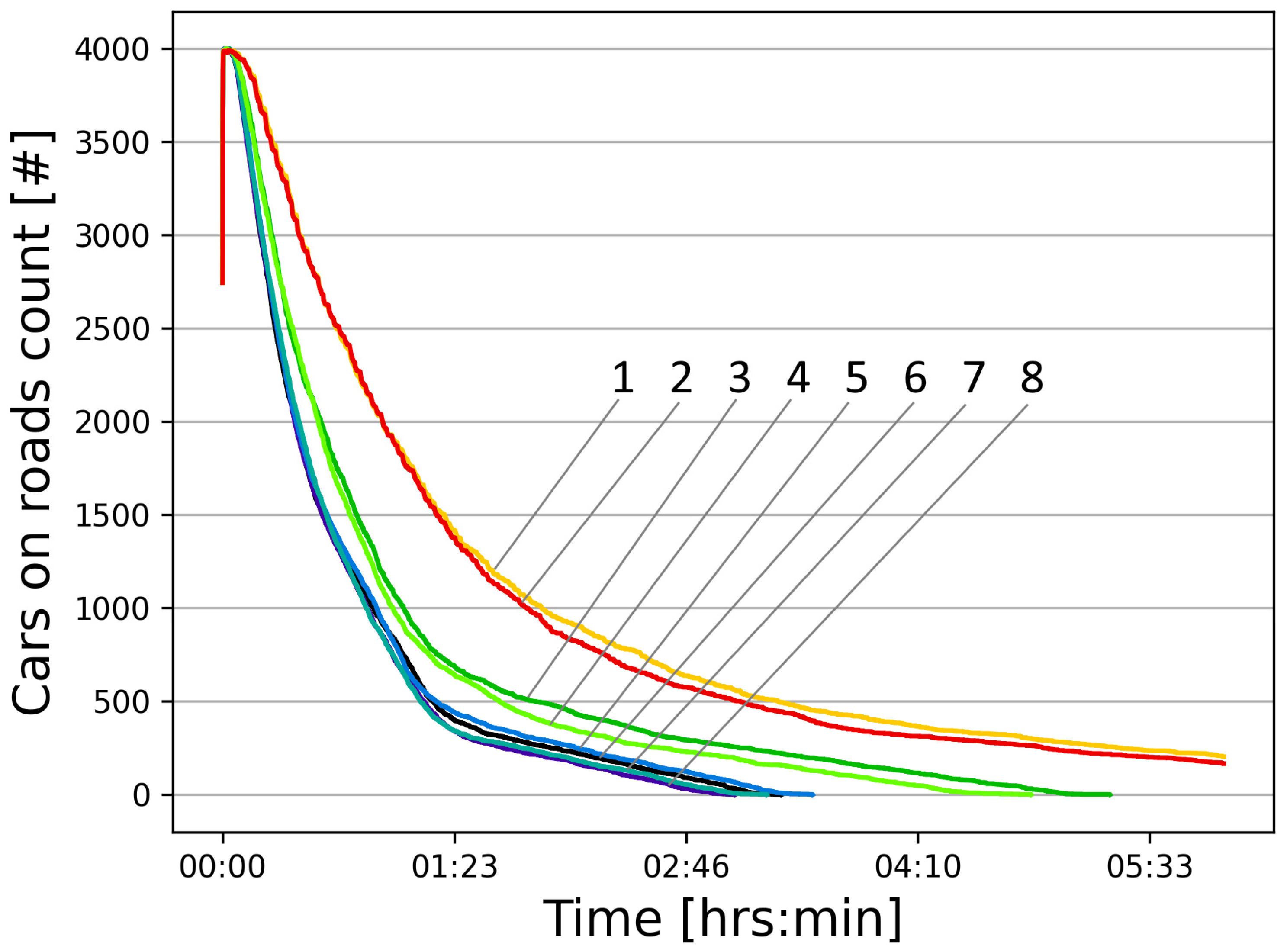
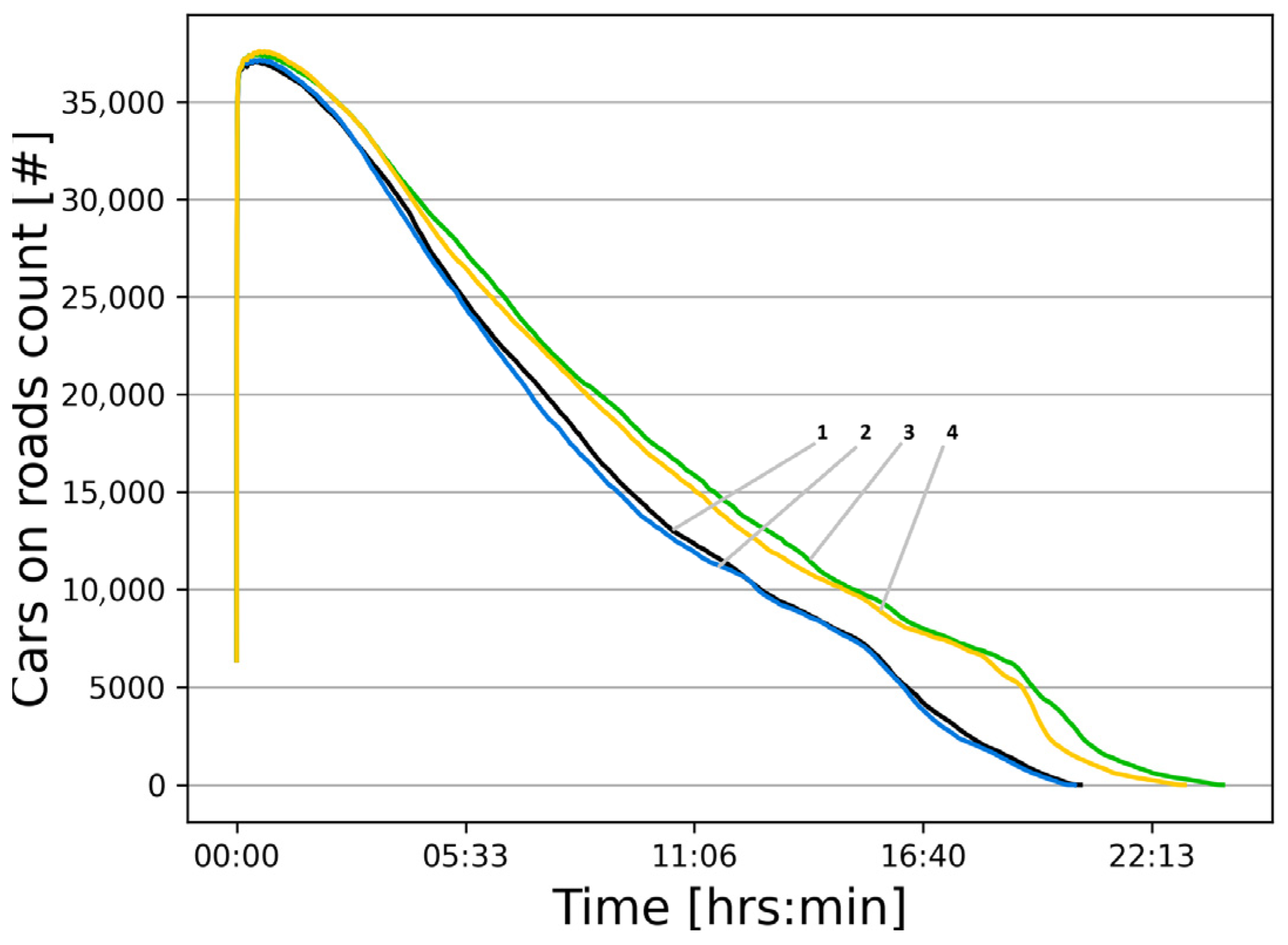
- Curve 1—NY-1-120 (route set No. 1, switching cycle 120 s);
- Curve 2—NY-2-120 (route set No. 2, switching cycle 120 s);
- Curve 3—NY-1-60 (route set No. 1, switching cycle 60 s);
- Curve 4—NY-2-60 (route set No. 2, switching cycle 60 s);
- Curve 5—NY-1-30 (route set No. 1, switching cycle 30 s);
- Curve 6—NY-2-30 (route set No. 2, switching cycle 30 s);
- Curve 7—NY-1-15 (route set No. 1, switching cycle 15 s);
- Curve 8—NY-2-15 (route set No. 2, switching cycle 15 s).
4.3. Simulation Results and Their Analysis
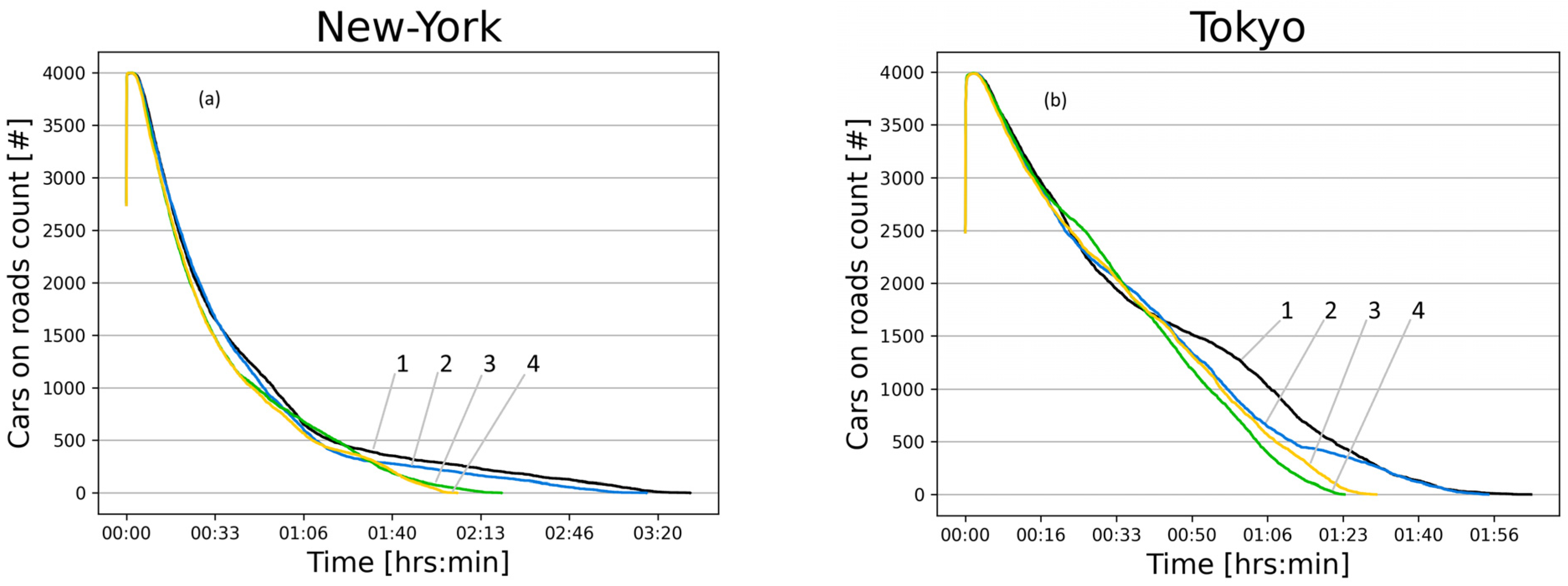
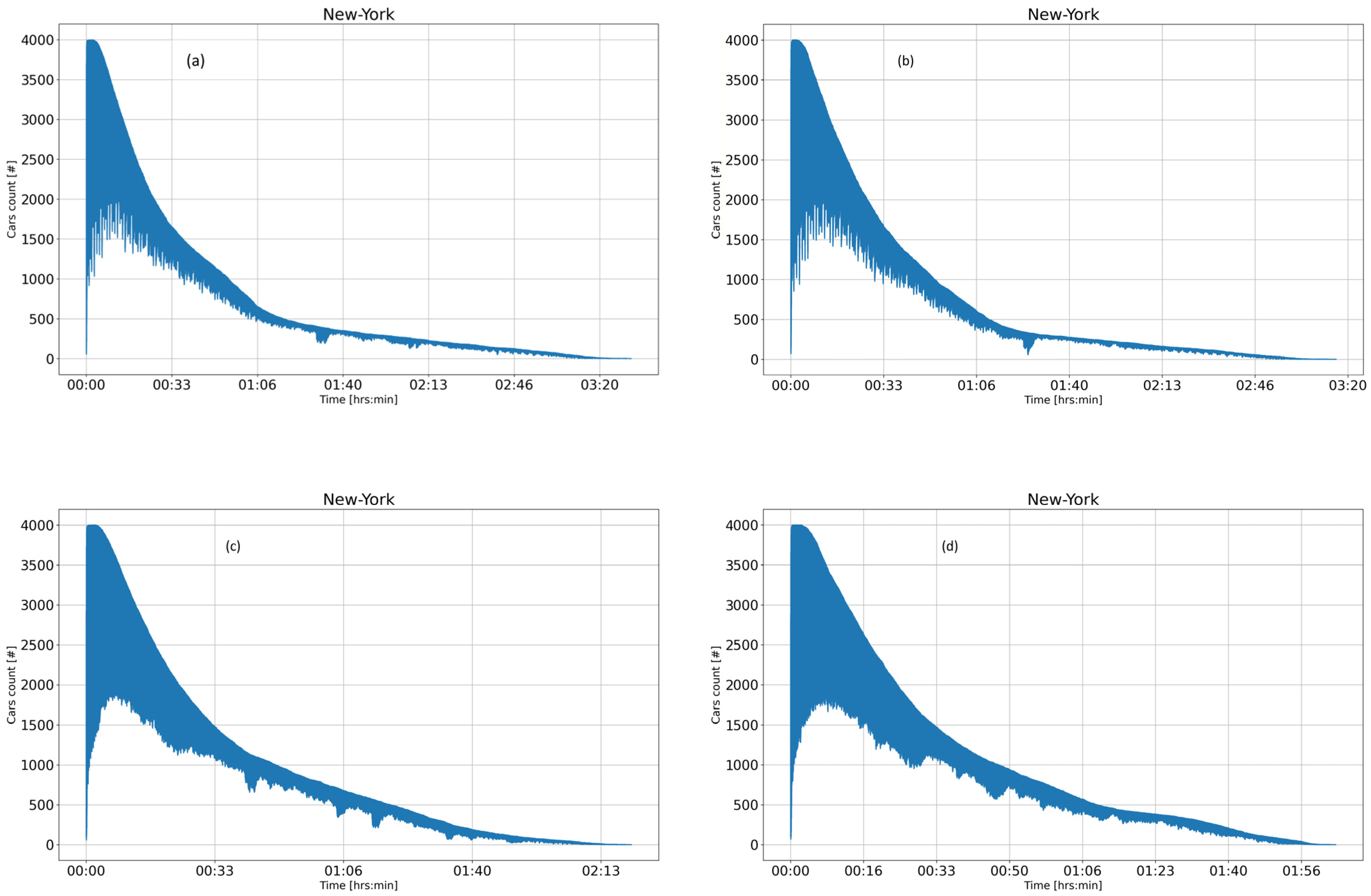
- Figure 12a shows the simulation results for static cyclic traffic signal switching with route set No. 1.
- Figure 12b shows the simulation results for static cyclic traffic signal switching with route set No. 2.
- Figure 12c shows the simulation results for dynamic traffic signal switching with route set No. 1.
- Figure 12d shows the simulation results for dynamic traffic signal switching with route set No. 2.
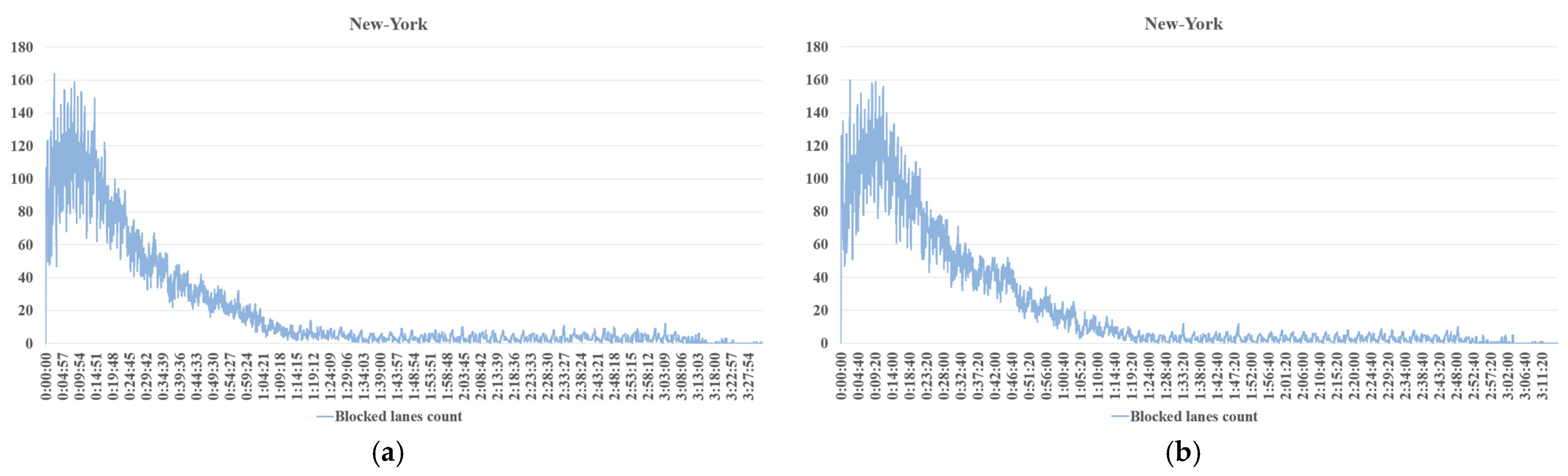
- Figure 13 presents the graphs showing the statistics of fully occupied traffic lanes during the simulation for route sets 1 and 2 under static (cyclic) and dynamic traffic signal control, using New York as an example. The graphs for Tokyo, Moscow, Mexico City, Berlin, and Shanghai show a similar pattern.
- Figure 13a shows the simulation results for static cyclic traffic signal switching with route set No. 1.
- Figure 13b shows the simulation results for static cyclic traffic signal switching with route set No. 2.
- Figure 13c shows the simulation results for dynamic traffic signal switching with route set No. 1.
- Figure 13d shows the simulation results for dynamic traffic signal switching with route set No. 2.

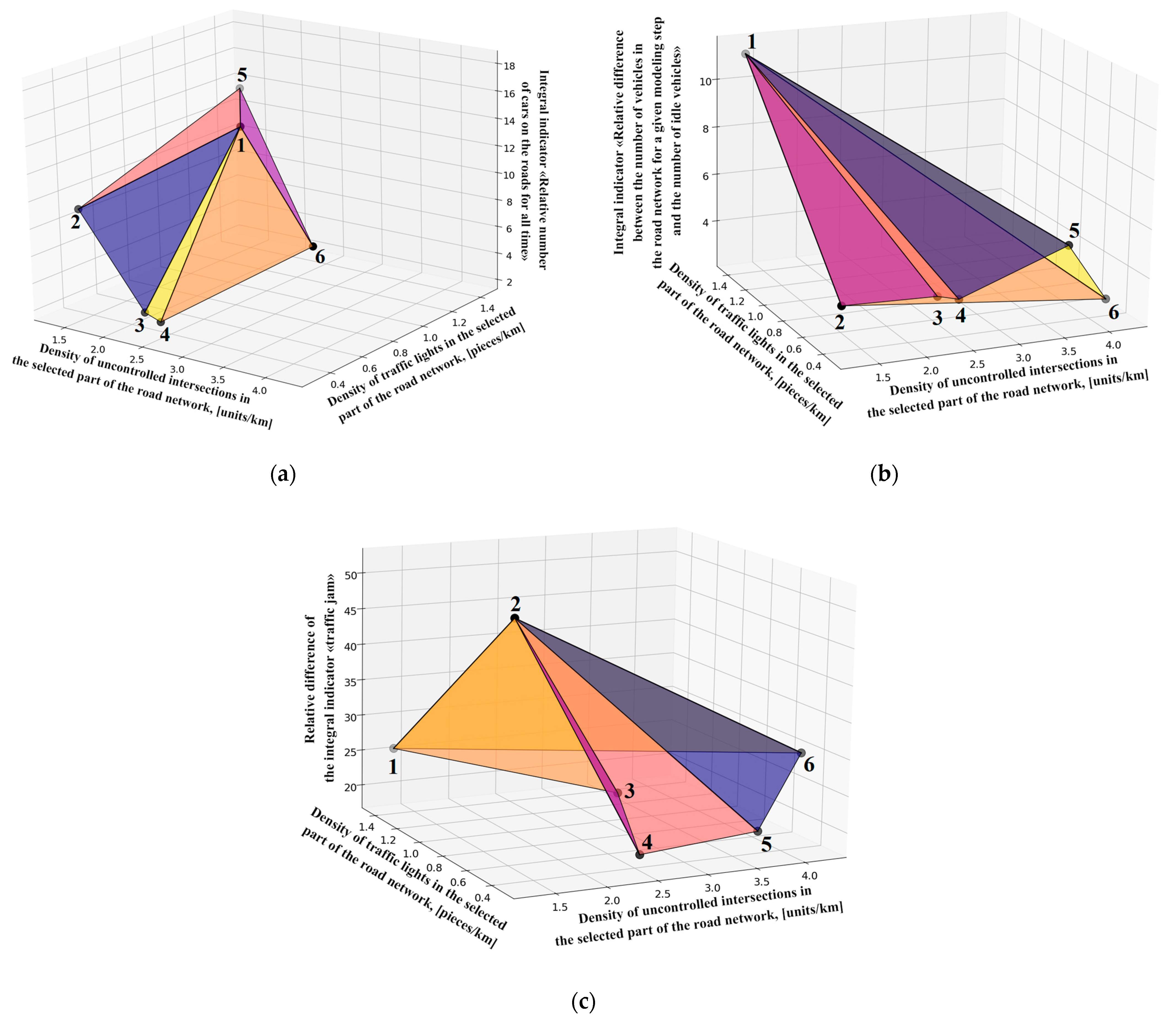
4.4. Determination of Near-Optimal Values of Traffic Light Density and Unsignalized Intersections in the Transport Network
- Connect the nearest points with straight lines to form a perimeter enclosing the domain of the integral indicator.
- Select the point with the maximum value of the integral indicator (the vertex), treating it as the maximum within its domain.
- Connect the corner points of the perimeter with the selected maximum point.
- For each column of integral indicators in Table 8, the maximum value of the indicator was taken as unity, and normalization was performed (so that each indicator ranges from 0 to 1).
- —density of unsignalized intersections in the selected road network section [units/km].
- —density of traffic lights in the selected road network section [units/km].
- —numerical value of the overall quality function.
5. Conclusions
6. Directions for Further Research
- The approach proposed in this article will be compared with other models and systems, including adaptive control systems, such as SCATS and SCOOT.
- Model studies will be conducted when the number of vehicles (possible routes) is increased to 50,000 using static switching cycles of 90, 120 and more seconds. To analyze the performance of our model, we used the SUMO simulation tool with a static 24 s cycle as a benchmark for comparison. The results obtained from this comparison can be used to compare different models with each other, i.e., to use it as a standard measure for each model. However, this represents a certain limitation of the results obtained, as does the number of routes used in modeling (4000). In addition, to collect more comprehensive statistics, it is planned to conduct experiments with larger routes sets.
- A detailed study of the model’s accuracy through indirect measurements will be conducted based on the method of constructing the surface of the overall quality function (described in Section 4.4). To construct this surface, it is planned to use, among other things, the data obtained when increasing the number of vehicles to 50,000 and the duration of static cycles of switching traffic lights.
- The proposed modeling technique will be studied using the Fokker-Planck Equation (13) and fractional differential Equation (14):
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paulus, R.; Agrawal, A. Intelligent traffic light design and control in smart cities: A survey on techniques and methodologies. Int. J. Veh. Inf. Commun. Syst. 2020, 5, 436. [Google Scholar] [CrossRef]
- Nurmukhanbetov, S.N.; Nurmagambetov, G.B. The Efficiency of Smart Traffic Light in the “Smart City” Concept Based on Neural Networks for Object and Image Recognition. Sci. Aspect 2023, 20, 2549–2560. [Google Scholar]
- Alvarez Lopez, P.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.-P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018. [Google Scholar] [CrossRef]
- Ziemke, D.; Kaddoura, I.; Nagel, K. The MATSim Open Berlin Scenario: A multimodal agent-based transport simulation scenario based on synthetic demand modeling and open data. Procedia Comput. Sci. 2019, 151, 870–877. [Google Scholar] [CrossRef]
- Großmann, T.; Schrab, K.; Protzmann, R.; Radusch, I. Modeling Bus Traffic for the Berlin SUMO Traffic Scenario. SUMO Conf. Proc. 2025, 6, 101–115. [Google Scholar] [CrossRef]
- Pradhananga, R.; Williams, S.; Aygun, S.; Chen, L.; Tu, Y.; Crow, W.; Aakur, S.; Tzeng, N.F. Digital Twin-Aided Municipal Traffic Control. SUMO Conf. Proc. 2025, 6, 149–161. [Google Scholar] [CrossRef]
- Ostendorf, N.; Garlichs, K.; Wolf, L. HaTS-Hanover Traffic Scenario for SUMO. SUMO Conf. Proc. 2025, 6, 117–132. [Google Scholar] [CrossRef]
- Kwon, Y.; Jung, J.-H.; Eom, Y.-H. Global efficiency and network structure of urban traffic flows: A percolation-based empirical analysis. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 113104. [Google Scholar] [CrossRef]
- Hamedmoghadam, H.; Zheng, N.; Li, D.; Vu, H. Percolation-based dynamic perimeter control for mitigating congestion propagation in urban road networks. Transp. Res. Part C Emerg. Technol. 2022, 145, 103922. [Google Scholar] [CrossRef]
- Konstantinov, S.; Kazaryan, D.; Diveev, A.; Sofronova, E.; Daryina, A.; Seliverstov, Y.; Baskin, L. Utilizing multi-source real data for traffic flow optimization in CTraf. Comput. Res. Model. 2024, 16, 147–159. [Google Scholar] [CrossRef]
- Soori, S. Optimization techniques in traffic management. Int. J. Multidiscip. Res. 2025, 7, 1–11. [Google Scholar] [CrossRef]
- Prasan, U.; Vital, T.; Khyati, B.; Deepika, K.; Nitya, C.; Harshavardhan, P.; Himanthkumar, C. Deep Learning Approaches to Intelligent Traffic Signal Systems. GRENZE Int. J. Eng. Technol. 2025, 11, 1182–13788. [Google Scholar]
- Kumar, G.A. AI Traffic Monitoring. Int. J. Sci. Res. Eng. Manag. 2025, 9, 1–19. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, J. Research on traffic state prediction method based on traffic flow prediction under multi-time granularity. Sci. Rep. 2025, 15, 24317. [Google Scholar] [CrossRef] [PubMed]
- Abduljabbar, R.; Dia, H.; Liyanage, S. Machine Learning Traffic Flow Prediction Models for Smart and Sustainable Traffic Management. Infrastructures 2025, 10, 155. [Google Scholar] [CrossRef]
- Sun, W.; Cui, H.; Zhu, M. Traffic Congestion Analysis and Probability Estimation Based on Stochastic Characteristics of Traffic Arrival. Promet Traffic Transp. 2025, 37, 585–597. [Google Scholar] [CrossRef]
- Shokrolah Shirazi, M.; Chang, H.-F. Evaluation of traffic signals for daily traffic pattern. J. Smart Cities Soc. 2025, 4, 137–151. [Google Scholar] [CrossRef]
- He, Y.; Xia, J. Comprehensive Evaluation on Traffic Safety of Mixed Traffic Flow in a Freeway Merging Area Based on a Cloud Model: From the Perspective of Traffic Conflict. Symmetry 2025, 17, 855. [Google Scholar] [CrossRef]
- Alyoshkin, A. The Influence of Transport Link Density on Conductivity If Junctions and/or Links Are Blocked. Mathematics 2021, 9, 1278. [Google Scholar] [CrossRef]
- Alyoshkin, A.; Zhukov, D. Percolation in Road Networks. In Proceedings of the 2022 4th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russia, 9–11 November 2022; pp. 158–163. [Google Scholar] [CrossRef]
- Alyoshkin, A.; Zhukov, D. Percolation Model of Road Line Overloading. In Proceedings of the 2023 5th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russia, 8–10 November 2023; pp. 861–864. [Google Scholar] [CrossRef]
- Grimmet, G. Percolation, 2nd ed.; Springer: Berlin, Germany, 1999; 444p. [Google Scholar] [CrossRef]
- Sahimi, M. Applications of Percolation Theory; Tailor & Francis: London, UK, 1994; 276p. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Tailor & Francis: London, UK, 1992; 192p. [Google Scholar] [CrossRef]
- Feder, J. Fractals, 3rd ed.; Plenum Press: New York, NY, USA; London, UK, 2013; 284p. [Google Scholar] [CrossRef]
- Kramarov, S.O.; Popov, O.R.; Dzhariev, I.E.; Petrov, E.A. Percolation and connectivity formation in the dynamics of data citation networks in high energy physics. Russ. Technol. J. 2025, 13, 16–27. [Google Scholar] [CrossRef]
- Zhukov, D.; Khvatova, T.; Lesko, S.; Zaltsman, A. Managing social networks: Applying the Percolation theory methodology to understand individuals’ attitudes and moods. Technol. Forecast. Soc. Change 2017, 123, 234–245. [Google Scholar] [CrossRef]
- Zhukov, D.O.; Khvatova, T.Y.; Lesko, S.A.; Zaltsman, A.D. The influence of connection density on clusterization and percolation threshold during information distribution in social networks. Inform. I Primen. (Inform. Their Appl.) 2018, 12, 90–97. [Google Scholar] [CrossRef]
- Lesko, S.; Aleshkin, A.; Zhukov, D. Reliability Analysis of the Air Transportation Network when Blocking Nodes and/or Connections Based on the Methods of Percolation Theory. IOP Conf. Ser. Mater. Sci. Eng. 2020, 714, 012016. [Google Scholar] [CrossRef]
- Zhukov, D.O.; Andrianova, E.G.; Lesko, S.A. The Influence of a Network’s Spatial Symmetry, Topological Dimension, and Density on Its Percolation Threshold. Symmetry 2019, 11, 920. [Google Scholar] [CrossRef]
- Wu, N. German Highway Capacity Manual (HBS2015). In Proceedings of the World Transport Convention 2018, Beijing, China, 18–21 June 2018. [Google Scholar] [CrossRef]
- Wu, N. Traffic Quality Assessment at Signalized Intersections—Procedures in the New German Highway Capacity Manual (HBS 2015). In Proceedings of the 15th COTA International Conference of Transportation Professionals (CICTP 2015), Beijing, China, 24–27 July 2015; pp. 2474–2485. [Google Scholar] [CrossRef]




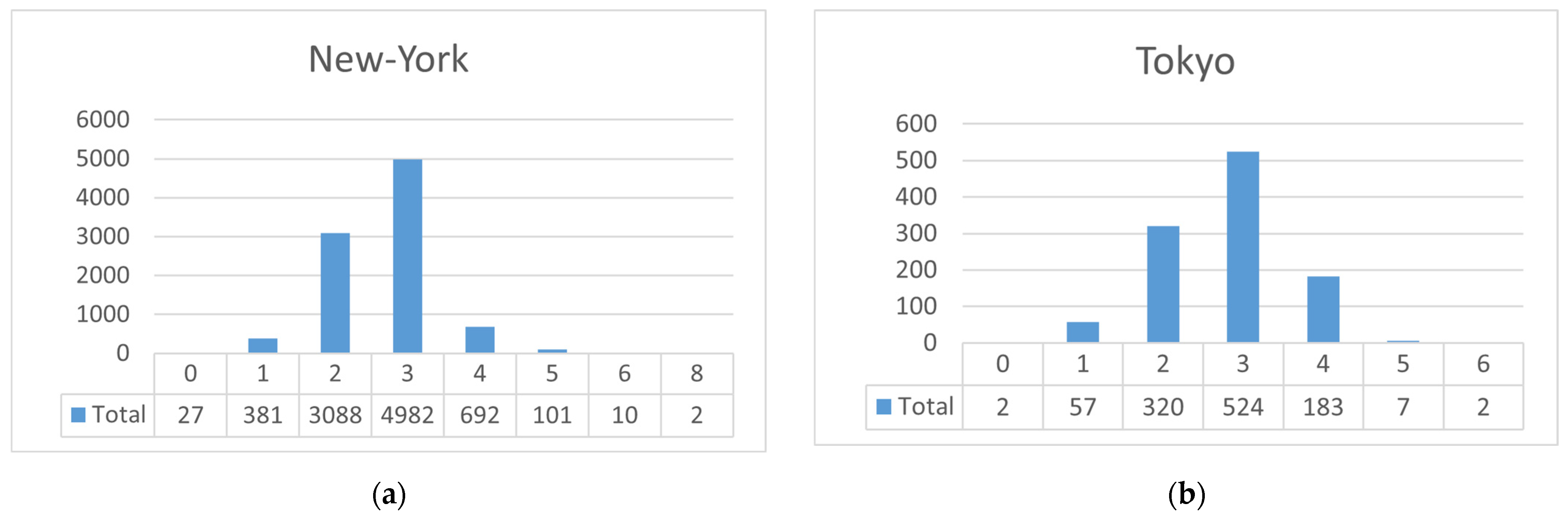



| City | Coordinates | Number of Vehicles in the Experiment | Number of Traffic Lights | Number of Unsignalized Intersections | Ratio of Signalized to Unsignalized Intersections |
|---|---|---|---|---|---|
| New York | −74.023056, 40.735354, −73.906099, 40.830413 | 4000 | 1957 | 1802 | 1.09 |
| Moscow | 37.565399, 55.734592, 37.679815, 55.779358 | 4000 | 192 | 1220 | 0.16 |
| Tokyo | 139.697486, 35.678460, 139.757845, 35.742650 | 4000 | 220 | 2188 | 0.10 |
| Berlin | 13.323501, 52.498585, 13.428170, 52.536943 | 4000 | 187 | 1336 | 0.14 |
| Shanghai | 121.405481, 31.179804, 121.573106, 31.277710 | 4000 | 992 | 3081 | 0.32 |
| Mexico City | −99.191556, 19.293875, −99.080280, 19.438003 | 4000 | 835 | 9804 | 0.09 |
| Number of Outgoing Connections | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Calculated percolation threshold (N) | 0.19 | 0.44 | 0.59 | 0.68 | 0.74 | 0.78 | 0.82 | 0.84 |
| City | Length of the Selected Road Network Section [km] | Number of Traffic Lights in the Selected Section | Traffic Light Density in the Selected Section [units/km] | Number of Unsignalized Intersections | Density of Unsignalized Intersections in the Selected Section [units/km] | Density of the Selected Road Network ( ) | Calculated Percolation Threshold (N) |
|---|---|---|---|---|---|---|---|
| New York | 1355.66 | 1957 | 1.44 | 1802 | 1.33 | 2.51 | 0.53 |
| Moscow | 563.36 | 192 | 0.36 | 1220 | 2.26 | 2.37 | 0.50 |
| Tokyo | 518.97 | 220 | 0.42 | 2188 | 4.22 | 2.79 | 0.56 |
| Berlin | 539.06 | 187 | 0.35 | 1336 | 2.48 | 2.54 | 0.53 |
| Shanghai | 2351.26 | 992 | 0.42 | 3081 | 1.31 | 2.75 | 0.55 |
| Mexico City | 2705.93 | 835 | 0.31 | 9804 | 3.62 | 2.64 | 0.54 |
| Line in the Picture | Switching Duration | End of Movement Time [s] | End of Movement Time [h:mm:ss] | Vehicles Remaining on the Roads |
|---|---|---|---|---|
| NY-1-120 | 120 s | 21,600 | 6:00:00 | 203 |
| NY-2-120 | 120 s | 21,600 | 6:00:00 | 165 |
| NY-1-60 | 60 s | 19,148 | 5:19:08 | 0 |
| NY-2-60 | 60 s | 17,446 | 4:50:46 | 0 |
| NY-1-30 | 30 s | 12,731 | 3:32:11 | 0 |
| NY-2-30 | 30 s | 11,744 | 3:15:44 | 0 |
| NY-1-15 | 15 s | 12,063 | 3:21:03 | 0 |
| NY-2-15 | 15 s | 11,058 | 3:04:18 | 0 |
| City | Route Set 1, Static Control | Route Set 2, Static Control | Route Set 1, Dynamic Control | Route Set 2, Dynamic Control | Relative Number of Vehicles on the Roads over the Entire Simulation Period [%] |
|---|---|---|---|---|---|
| New York | 9,942,909 | 9,319,843 | 8,458,108 | 8,222,975 | 13.40% |
| Moscow | 4,456,490 | 5,331,339 | 4,635,557 | 4,883,271 | 2.75% |
| Tokyo | 9,997,552 | 9,374,439 | 8,640,626 | 8,843,160 | 9.75% |
| Berlin | 8,020,844 | 7,908,250 | 7,581,441 | 7,964,433 | 2.41% |
| Shanghai | 7,449,906 | 6,492,959 | 6,670,030 | 6,045,126 | 8.81% |
| Mexico City | 6,812,375 | 6,668,035 | 5,622,640 | 5,458,987 | 17.79% |
| City | Route Set 1, Static Control | Route Set 2, Static Control | Route Set 1, Dynamic Control | Route Set 2, Dynamic Control | Relative Difference Between the Number of Vehicles in the Road Network at a Given Simulation Step and the Number of Idling Vehicles [%] |
|---|---|---|---|---|---|
| New York | 3,118,471 | 3,105,098 | 3,439,251 | 3,479,512 | 11.17% |
| Moscow | 2,137,707 | 2,217,376 | 2,227,865 | 2,297,077 | 3.90% |
| Tokyo | 1,913,071 | 1,928,052 | 1,983,877 | 1,959,000 | 2.65% |
| Berlin | 2,460,474 | 2,422,737 | 2,550,934 | 2,513,340 | 3.71% |
| Shanghai | 2,185,179 | 2,187,322 | 2,250,599 | 2,287,545 | 3.79% |
| Mexico City | 2,183,887 | 2,170,988 | 2,321,269 | 2,272,104 | 5.48% |
| City | Route Set 1, Static Control | Route Set 2, Static Control | Route Set 1, Dynamic Control | Route Set 2, Dynamic Control | Relative Difference in the Integral “Congestion” Indicator [%] |
|---|---|---|---|---|---|
| New York | 253,520 | 257,974 | 182,383 | 198,230 | 25.59% |
| Moscow | 91,511 | 112,587 | 72,453 | 75,454 | 27.53% |
| Tokyo | 408,372 | 379,448 | 264,090 | 290,184 | 29.64% |
| Berlin | 212,144 | 213,756 | 166,060 | 178,822 | 19.02% |
| Shanghai | 241,414 | 188,795 | 106,077 | 104,441 | 51.07% |
| Mexico City | 146,641 | 163,328 | 123,475 | 122,070 | 20.78% |
| City | Dataset Number (Points in Figure 15 and Figure 16) | Ratio of Signalized to Unsignalized Intersections | Density of Unsignalized Intersections in the Selected Road Network Section [units/km] | Density of Traffic Lights in the Selected Road Network Section [units/km] | Integral Indicator “Relative Number of Vehicles on the Roads over the Entire Period” | Integral Indicator “Relative Difference Between the Number of Vehicles in the Road Network at a Given Simulation Step and the Number of Idling Vehicles” | Relative Difference in the Integral “Congestion” Indicator [%] |
|---|---|---|---|---|---|---|---|
| New York | 1 | 1.09 | 1.33 | 1.44 | 13.40% | 11.17% | 25.59% |
| Shanghai | 2 | 0.32 | 1.31 | 0.42 | 8.81% | 3.79% | 51.07% |
| Moscow | 3 | 0.16 | 2.26 | 0.36 | 2.75% | 3.90% | 27.53% |
| Berlin | 4 | 0.14 | 2.48 | 0.35 | 2.41% | 3.71% | 19.02% |
| Mexico City | 5 | 0.09 | 3.62 | 0.31 | 17.79% | 5.48% | 20.78% |
| Tokyo | 6 | 0.10 | 4.22 | 0.42 | 9.75% | 2.65% | 29.64% |
| Parameter | Shanghai—Section A | Shanghai—Section B | San Francisco | Toronto |
|---|---|---|---|---|
| Total road length | 547.31 | 591.95 | 1301.76 | 1275.76 |
| Number of traffic lights | 480 | 156 | 954 | 556 |
| Number of unsignalized intersections | 803 | 670 | 3350 | 3465 |
| Traffic light density [units/km] | 0.88 | 0.26 | 0.73 | 0.44 |
| Unsignalized intersection density [units/km] | 1.47 | 1.13 | 2.57 | 2.72 |
| Density of the selected road network section | 2.66 | 2.79 | 2.91 | 2.71 |
| Percolation threshold | 0.55 | 0.56 | 0.58 | 0.55 |
| Integral indicator “Relative number of vehicles on the roads over the entire period” (normalized value in parentheses, with respect to the maximum value given in the table) | 1.32% (0.07) | 0.27% (0.02) | 9.35% (0.52) | 21.81% (1.23) |
| Integral indicator “Relative difference between the total number of vehicles in the road network at a given simulation step and the number of idling vehicles” (normalized value in parentheses, with respect to the maximum value given in the table) | 10.42% (0.94) | 3.60% (0.32) | 8.30% (0.74) | 1.00% (0.09) |
| Relative difference in the integral “congestion” indicator (normalized value in parentheses, with respect to the maximum value given in the table) | 46.74% (0.92) | 0.98% (0.02) | 23.07% (0.45) | 50.75% (0.99) |
| Numerical value of the overall quality function Z | 0.64 | 0.12 | 0.57 | 0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aleshkin, A.; Zhukov, D.; Zhmud, V. Percolation–Stochastic Model for Traffic Management in Transport Networks. Informatics 2025, 12, 122. https://doi.org/10.3390/informatics12040122
Aleshkin A, Zhukov D, Zhmud V. Percolation–Stochastic Model for Traffic Management in Transport Networks. Informatics. 2025; 12(4):122. https://doi.org/10.3390/informatics12040122
Chicago/Turabian StyleAleshkin, Anton, Dmitry Zhukov, and Vadim Zhmud. 2025. "Percolation–Stochastic Model for Traffic Management in Transport Networks" Informatics 12, no. 4: 122. https://doi.org/10.3390/informatics12040122
APA StyleAleshkin, A., Zhukov, D., & Zhmud, V. (2025). Percolation–Stochastic Model for Traffic Management in Transport Networks. Informatics, 12(4), 122. https://doi.org/10.3390/informatics12040122







