Hybrid Approach Using Dynamic Mode Decomposition and Wavelet Scattering Transform for EEG-Based Seizure Classification
Abstract
1. Introduction
2. Related Works
- The hybrid approach enhances seizure classification by combining DMD with the WST for EEG analysis, which effectively leverages the strengths of both methods to improve feature extraction.
- DMD modes capture the dynamic behaviour and temporal evolution of EEG signals. They decompose complex EEG recordings into a set of interpretable, low-rank dynamic modes that reflect key frequency and growth patterns associated with seizure activity, while the WST extracts a stable and translational invariant representation of modes of the signal.
- The proposed hybrid method addresses the challenge of seizure classification by combining the dynamic sensitivity of DMD with the structural robustness of WST. The model produces accurate and efficient seizure classification across a diverse range of patients.
- The proposed hybrid approach was evaluated on three publicly accessible datasets. The results showed that these features employed for classification outperform state-of-the-art methods. The robustness of the proposed method is further validated through statistical hypothesis testing, which demonstrates that the improvements achieved by the proposed approach are statistically significant.
3. Materials and Methods
3.1. Dataset Description
3.1.1. CHB-MIT Dataset
3.1.2. Bern Barcelona Dataset
3.1.3. Khas Dataset
3.2. Dynamic Mode Decomposition
Mathematics of DMD
- Compute SVD of :
- Calculate :
- Evaluate the eigen decomposition of :
- Calculate the DMD mode matrix :
3.3. Wavelet Scattering Transform
- 1.
- Zeroth-order scattering coefficients:At level 0, the low-frequency scattering coefficient is calculated by convolution of signal f using :
- 2.
- First-order scattering coefficients:At level 1, the signal f is convolved with wavelet functions at different scales:and number of wavelet used is k. By taking the modulus of these convolutions, the first-order coefficients are derived. The f is convolved with wavelet functions similar to CWT. The nonlinear modulus operation is applied to these coefficients and convolving the result with the scaling function to obtain the scattering coefficients at level 1:
- 3.
- Second-order scattering coefficients:At level 2, the coefficients in level 1 are further convolved with the wavelet functions at various scales and modulus operation is performed on each.The scattering network energy is dissipated in each layer. The zeroth-order coefficient averages input signal, so mainly low-frequency information is obtained from this layer [40]. The averaging procedure causes a loss of high-frequency information. The omitted features in the initial step are acquired in the following layers through the use of a CWT, resulting in scalogram coefficients. The coefficients undergo a nonlinear operation and are applied to a low-pass filter to obtain scattering coefficients [41]. Figure 10 shows the layers of the wavelet scattering network. Finally scattering coefficients are concatenated to form a feature matrix
3.4. Classification
3.4.1. Naive Bayes
3.4.2. Support Vector Machine (SVM)
3.4.3. Random Forest
3.4.4. Boosting Algorithms
3.4.5. Bagging Algorithms
3.4.6. K-Nearest Neighbours (K-NN)
4. Proposed Methodology
4.1. Preprocessing of EEG Signals
4.2. Extraction of Dynamic Modes
Hankelization
4.3. WST-Based Feature Extraction
| Algorithm 1 Proposed hybrid DMD-WST algorithm |
|
4.4. Classification Using ML Model
5. Experimental Results
5.1. Evaluation Metrics
5.1.1. Precision
5.1.2. Sensitivity
5.1.3. F1 Score
5.1.4. Accuracy
5.1.5. Cohen’s Kappa
5.1.6. Matthews Correlation Coefficient (MCC)
5.1.7. G-Mean
5.1.8. Confusion Matrix
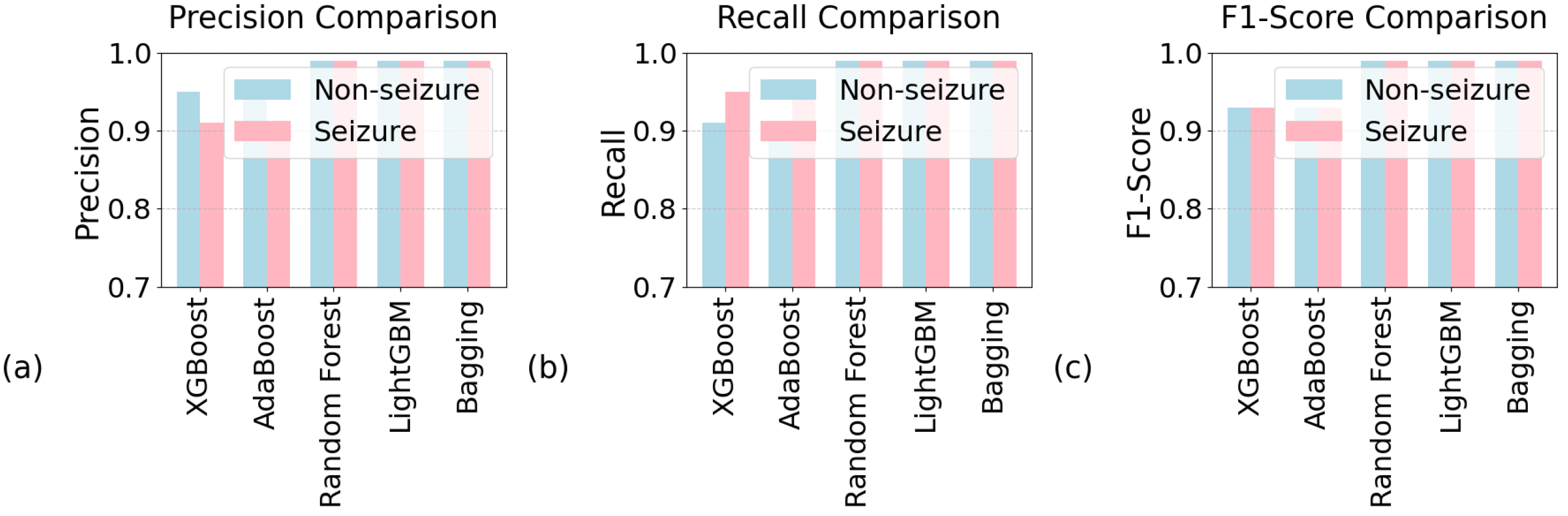
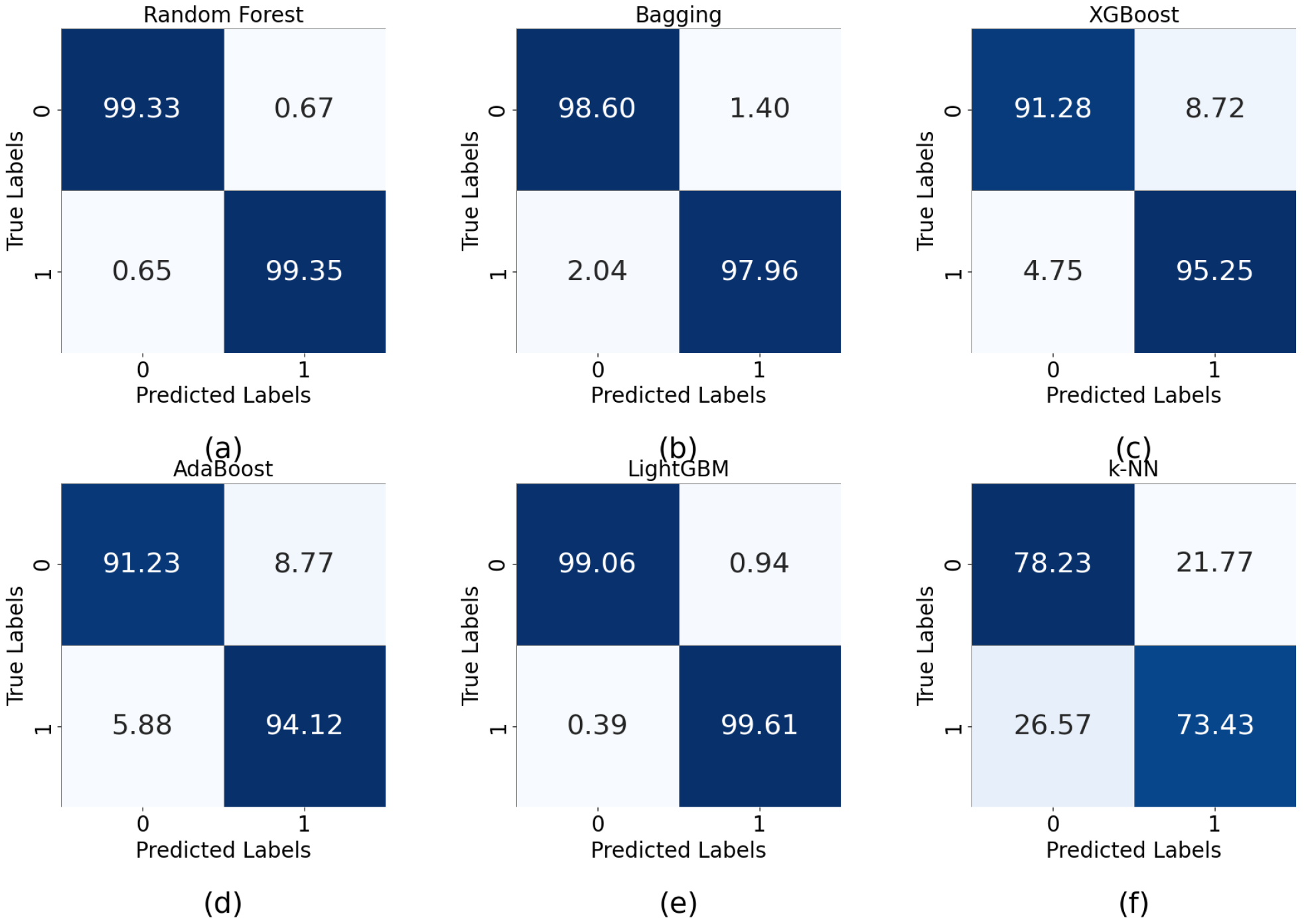
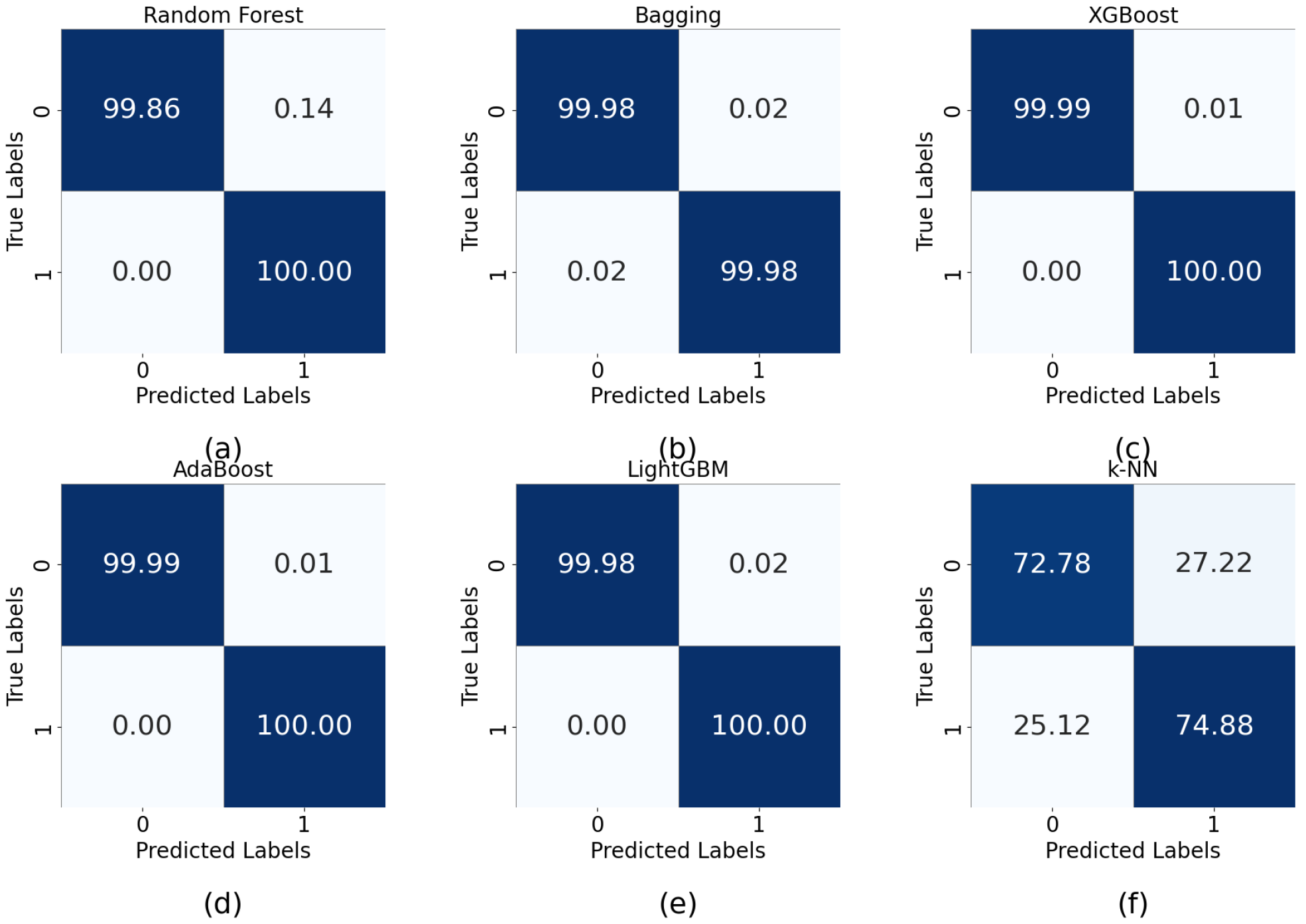
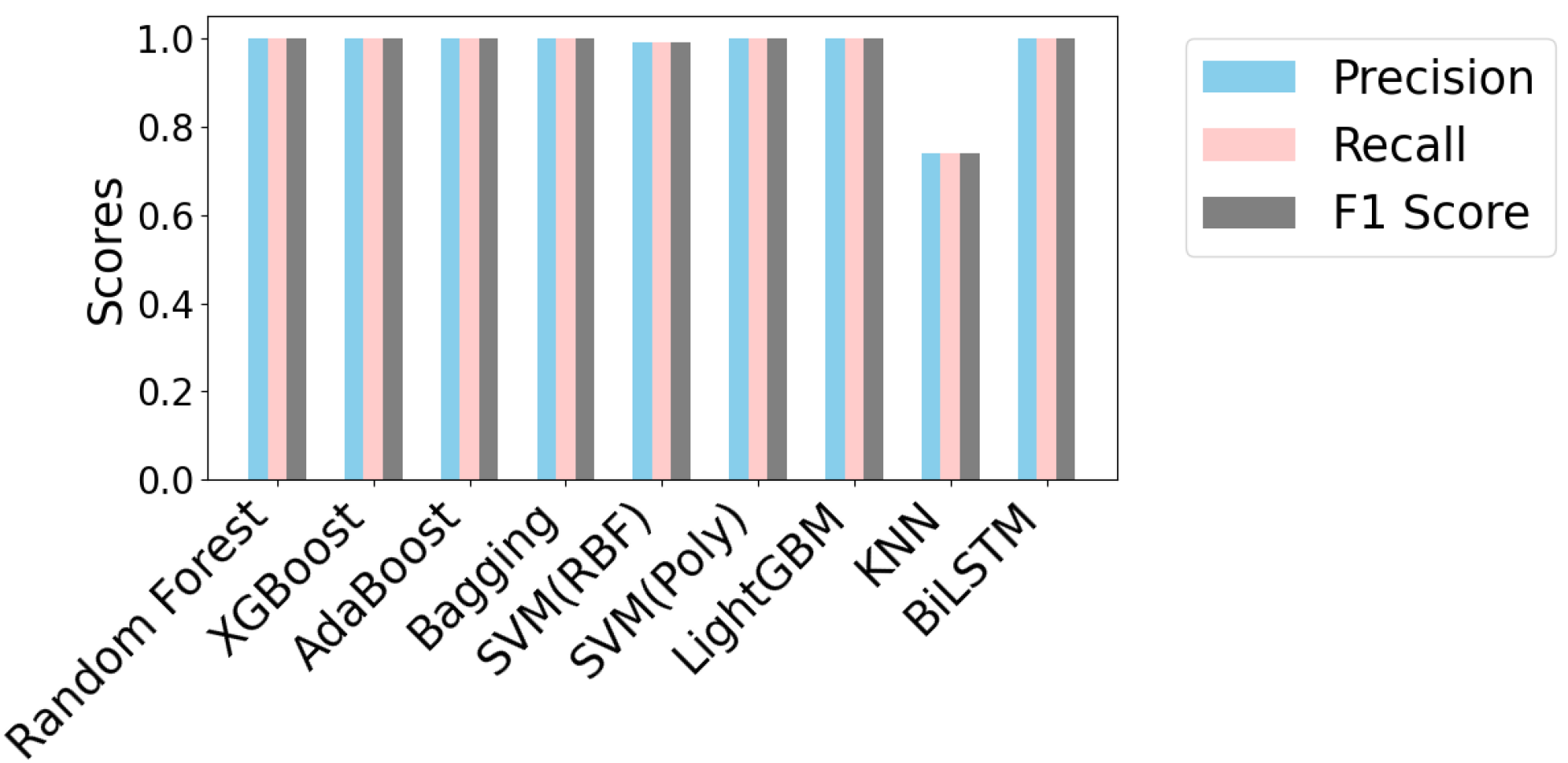
5.2. Performance Analysis
6. Discussion
6.1. Confidence Score and Confidence Intervals
6.2. Statistical Hypothesis Tests
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization (WHO), Global Campaign Against Epilepsy. Atlas: Epilepsy Care in the World; World Health Organization (WHO) Department of Mental Health and Substance Abuse, International Bureau for Epilepsy: Geneva, Switzerland, 2005. [Google Scholar]
- Brodie, M.J.; Zuberi, S.M.; Scheffer, I.E.; Fisher, R.S. The 2017 ILAE classification of seizure types and the epilepsies: What do people with epilepsy and their caregivers need to know? Epileptic Disord. 2018, 20, 77–87. [Google Scholar] [CrossRef]
- Wang, L.; Xue, W.; Li, Y.; Luo, M.; Huang, J.; Cui, W.; Huang, C. Automatic epileptic seizure detection in EEG signals using multi-domain feature extraction and nonlinear analysis. Entropy 2017, 19, 222. [Google Scholar] [CrossRef]
- Alharthi, M.K.; Moria, K.M.; Alghazzawi, D.M.; Tayeb, H.O. Epileptic Disorder Detection of Seizures Using EEG Signals. Sensors 2022, 22, 6592. [Google Scholar] [CrossRef] [PubMed]
- Du, R.; Huang, J.; Zhu, S. EEG-Based Epileptic Seizure Detection Model Using CNN Feature Optimization. In Proceedings of the 2022 15th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Beijing, China, 5–7 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Schindler, K.; Rummel, C. Nonrandomness, nonlinear dependence, and nonstationarity of electroencephalographic recordings from epilepsy patients. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2012, 86, 046206. [Google Scholar] [CrossRef]
- Swami, P.; Panigrahi, B.; Nara, S.; Bhatia, M.; Gandhi, T. EEG Epilepsy Datasets. 2016. Available online: https://www.researchgate.net/publication/308719109_EEG_Epilepsy_Datasets (accessed on 24 September 2025).
- Hussain, S.J. Epileptic Seizure Detection Using Wavelets and EMD. In Proceedings of the 2018 Fourth International Conference on Biosignals, Images and Instrumentation (ICBSII), Chennai, India, 22–24 March 2018; pp. 206–212. [Google Scholar]
- Quintero-Rincón, A.; Pereyra, M.; d’Giano, C.; Risk, M.; Batatia, H. Fast Statistical Model-Based Classification of Epileptic EEG Signals. Biocybern. Biomed. Eng. 2018, 38, 877–889. [Google Scholar] [CrossRef]
- Li, M.; Sun, X.; Chen, W. Patient-Specific Seizure Detection Method Using Nonlinear ModeDecomposition for Long-Term EEG Signals. Med. Biol. Eng. Comput. 2020, 58, 3075–3088. [Google Scholar] [CrossRef]
- Aayesha; Qureshi, M.B.; Afzaal, M.; Qureshi, M.S.; Fayaz, M. Machine learning-based EEG signals classification model for epileptic seizure detection. Multimed. Tools Appl. 2021, 80, 17849–17877. [Google Scholar] [CrossRef]
- Varlı, M.; Yılmaz, H. Multiple classification of EEG signals and epileptic seizure diagnosis with combined deep learning. J. Comput. Sci. 2023, 67, 101943. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pachori, R.B. A Multivariate Approach for Patient-Specific EEG Seizure Detection Using Empirical Wavelet Transform. IEEE Trans. Biomed. Eng. 2017, 64, 2003–2015. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Wen, P.; Song, B.; Li, Y. An EEG based real-time epilepsy seizure detection approach using discrete wavelet transform and machine learning methods. Biomed. Signal Process. Control 2022, 77, 103820. [Google Scholar] [CrossRef]
- Subasi, A.; Jukic, S.; Kevric, J. Comparison of EMD, DWT and WPD for the localization of epileptogenic foci using random forest classifier. Measurement 2019, 146, 846–855. [Google Scholar] [CrossRef]
- Solaija, M.S.J.; Saleem, S.; Khurshid, K.; Hassan, S.A.; Kamboh, A.M. Dynamic Mode Decomposition Based Epileptic Seizure Detection from Scalp EEG. IEEE Access 2018, 6, 38683–38692. [Google Scholar] [CrossRef]
- Cura, O.K.; Akan, A. Analysis of epileptic EEG signals by using dynamic mode decomposition and spectrum. Biocybern. Biomed. Eng. 2021, 41, 28–44. [Google Scholar] [CrossRef]
- Mallat, S. Understanding deep convolutional networks. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150203. [Google Scholar] [CrossRef]
- Yamaguchi, C. Fourier and wavelet analyses of normal and epileptic electroencephalogram (EEG). In Proceedings of the First International IEEE EMBS Conference on Neural Engineering, Capri Island, Italy, 20–22 March 2003; pp. 406–409. [Google Scholar] [CrossRef]
- Amin, M.G.; Feng, K.D. Short-time Fourier transforms using cascade filter structures. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1995, 42, 631–641. [Google Scholar] [CrossRef]
- Peng, P.; Song, Y.; Yang, L.; Wei, H. Seizure prediction in EEG signals using STFT and domain adaptation. Front. Neurosci. 2022, 15, 825434. [Google Scholar] [CrossRef]
- Kıymık, M.K.; Güler, İ.; Dizibuyuk, A.; Akın, M. Comparison of STFT and Wavelet Transform Methods in Determining Epileptic Seizure Activity in EEG Signals for Real-Time Application. Comput. Biol. Med. 2005, 35, 603–616. [Google Scholar] [CrossRef]
- Gosala, B.; Kapgate, P.D.; Jain, P.; Chaurasia, R.N.; Gupta, M. Wavelet Transforms for Feature Engineering in EEG Data Processing: An Application on Schizophrenia. Biomed. Signal Process. Control 2023, 85, 104811. [Google Scholar] [CrossRef]
- Rafiuddin, N.; Khan, Y.U.; Farooq, O. A Novel Wavelet Approach for Multiclass iEEG Signal Classification in Automated Diagnosis of Epilepsy. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Aydin, N. Wavelet scattering transform based Doppler signal classification. Comput. Biol. Med. 2023, 167, 107611. [Google Scholar] [CrossRef]
- Khan, Y.U.; Gotman, J. Wavelet-based automatic seizure detection in intracerebral electroencephalogram. Clin. Neurophysiol. 2003, 114, 898–908. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, W.; Yuan, Q.; Chen, S. Automatic Seizure Detection Using Wavelet Transform and SVM in Long-Term Intracranial EEG. IEEE Trans. Neural Syst. Rehabil. 2012, 20, 749–755. [Google Scholar] [CrossRef]
- Amin, H.U.; Malik, A.S.; Ahmad, R.F.; Badruddin, N.; Kamel, N.; Hussain, M.; Chooi, W.-T. Feature extraction and classification for EEG signals using wavelet transform and machine learning techniques. Australas. Phys. Eng. Sci. Med. 2015, 38, 139–149. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pachori, R.B.; Upadhyay, A.; Acharya, U.R. Tunable-Q Wavelet Transform Based Multiscale Entropy Measure for Automated Classification of Epileptic EEG Signals. Appl. Sci. 2017, 7, 85. [Google Scholar] [CrossRef]
- Alickovic, E.; Kevric, J.; Subasi, A. Performance evaluation of empirical mode decomposition, discrete wavelet transform, and wavelet packed decomposition for automated epileptic seizure detection and prediction. Biomed. Signal Process. Control 2018, 39, 94–102. [Google Scholar] [CrossRef]
- Omidvar, M.; Zahedi, A.; Bakhshi, H. EEG signal processing for epilepsy seizure detection using 5-level Db4 discrete wavelet transform, GA-based feature selection and ANN/SVM classifiers. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 10395–10403. [Google Scholar] [CrossRef]
- Karabiber Cura, O.; Kocaaslan Atli, S.; Senay, H.; Akan, A. Epileptic seizure classifications using empirical mode decomposition and its derivative. Biomed. Eng. Online 2020, 19, 10. [Google Scholar] [CrossRef]
- Xia, Y.; Zhou, W.; Li, C.; Yuan, Q.; Geng, S. Seizure detection approach using S-transform and singular value decomposition. Epilepsy Behav. 2015, 52, 187–193. [Google Scholar] [CrossRef]
- Subasi, A.; Gursoy, M.I. EEG signal classification using PCA, ICA, LDA and support vector machines. Expert Syst. Appl. 2010, 37, 8659–8666. [Google Scholar] [CrossRef]
- Das, A.B.; Bhuiyan, M.I.H. Discrimination and classification of focal and non-focal EEG signalsusing entropy-based features in the EMD-DWT domain. Biomed. Signal Process. Control 2016, 29, 11–21. [Google Scholar] [CrossRef]
- Qin, X.; Xu, D.; Dong, X.; Cui, X.; Zhang, S. EEG signal classification based on improved variational modedecomposition and deep forest. Biomed. Signal Process. Control 2023, 83, 104650. [Google Scholar] [CrossRef]
- Brunton, B.W.; Johnson, L.A.; Ojemann, J.G.; Kutz, J.N. Extracting spatial–temporal coherent patterns in large-scale neural recordings using dynamic mode decomposition. J. Neurosci. Methods 2016, 258, 1–15. [Google Scholar] [CrossRef]
- Hocepied, G.; Kacha, A.; Grenez, F.; Nonclercq, A. Stability analysis of epileptic EEG signals. In Proceedings of the 8th IEEE International Conference on Bioinformatics and Bioengineering (BIBE), Athens, Greece, 8–10 October 2008; pp. 1–5. [Google Scholar]
- Bilal, M.; Rizwan, M.; Saleem, S.; Khan, M.M.; Alkatheir, M.S.; Alqarni, M. Automatic Seizure Detection Using Multi-Resolution Dynamic Mode Decomposition. IEEE Access 2019, 7, 61180–61194. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, G.; Zhang, Q.; Zhang, J.; Zeng, X. Wavelet scattering transform for ECG beat classification. Comput. Math. Methods Med. 2020, 2020, 3215681. [Google Scholar] [CrossRef]
- Al-Taee, A.; Khushaba, R.; Zia, T.; Al-Jumaily, A. Feature Extraction Using Wavelet Scattering Transform Coefficients for EMG Pattern Classification. In Proceedings of the AI 2021: Advances in Artificial Intelligence, AI, Sydney, NSW, Australia, 2–4 February 2022; Long, G., Yu, X., Wang, S., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2022; Volume 13151. [Google Scholar] [CrossRef]
- Susu, A.A.; Agboola, H.A.; Solebo, C.; Lesi, F.E.; Aribike, D.S. Wavelet Time Scattering Based Classification of Interictal and Preictal EEG Signals. J. Brain Res.—J. Fur Hirnforsch. 2020, 3, 115. [Google Scholar]
- Jiang, Y.; Chen, W.; You, Y. Scattering transform-based features for the automatic seizure detection. Biocybern. Biomed. Eng. 2020, 40, 77–89. [Google Scholar] [CrossRef]
- Mohammadpoory, Z.; Nasrolahzadeh, M.; Amiri, S.A. Patient-independent epileptic seizure detection using weighted visibility graph features and wavelet decomposition. Multimed. Tools Appl. 2025, 84, 3197–3221. [Google Scholar] [CrossRef]
- Liu, G.; Tian, L.; Zhou, W. Patient-independent seizure detection based on channel-perturbation convolutional neural network and bidirectional long short-term memory. Int. J. Neural Syst. 2022, 32, 2150051. [Google Scholar] [CrossRef]
- Zarei, A.; Mohammadzadeh, B. Automatic seizure detection using orthogonal matching pursuit, discrete wavelet transform, and entropy based features of EEG signals. Comput. Biol. Med. 2021, 131, 104250. [Google Scholar] [CrossRef]
- Pattnaik, S.; Rao, B.N.; Rout, N.K.; Sabut, S.K. Transfer learning based epileptic seizure classification using scalogram images of EEG signals. Multimed. Tools Appl. 2024, 83, 84179–84193. [Google Scholar] [CrossRef]
- Tripathi, P.M.; Kumar, A.; Kumar, M.; Komaragiri, R.S. Automatic seizure detection and classification using super-resolution superlet transform and deep neural network-A preprocessing-less method. Comput. Methods Programs Biomed. 2023, 240, 107680. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, T.; Li, T. Detecting Epileptic Seizures in EEG Signals with Complementary Ensemble Empirical Mode Decomposition and Extreme Gradient Boosting. Entropy 2020, 22, 140. [Google Scholar] [CrossRef]
- Moctezuma, L.A.; Molinas, M. Classification of low-density EEG for epileptic seizures by energy and fractal features based on EMD. J. Biomed. Res. 2020, 34, 180–190. [Google Scholar] [CrossRef]
- Peng, H.; Lei, C.; Zheng, S.; Zhao, C.; Wu, C.; Sun, J.; Hu, B. Automatic epileptic seizure detection via Stein kernel-based sparse representation. Comput. Biol. Med. 2021, 132, 104338. [Google Scholar] [CrossRef]
- Amiri, M.; Aghaeinia, H.; Amindavar, H.R. Automatic Epileptic Seizure Detection in EEG Signals Using Sparse Common Spatial Pattern and Adaptive Short-Time Fourier Transform-Based Synchrosqueezing Transform. Biomed. Signal Process. Control 2023, 79, 104022. [Google Scholar] [CrossRef]
- Dalal, M.; Tanveer, M.; Pachori, R.B. Automated identification system for focal EEG signals using fractal dimension of FAWT-based sub-bands signals. In Proceedings of the Machine Intelligence and Signal Analysis; Springer: Singapore, 2019; pp. 583–596. [Google Scholar]
- Sharma, R.; Sircar, P.; Pachori, R.B. Automated focal EEG signal detection based on third order cumulant function. Biomed. Signal Process. Control 2020, 58, 101856. [Google Scholar] [CrossRef]
- Sairamya, N.J.; Subathra, M.S.P.; Suviseshamuthu, E.S.; George, S.T. A new approach for automatic detection of focal EEG signals using wavelet packet decomposition and quad binary pattern method. Biomed. Signal Process. Control 2021, 63, 102096. [Google Scholar] [CrossRef]
- Mehla, V.K.; Singhal, A.; Singh, P. An Efficient Classification of Focal and Non-Focal EEG Signals Using Adaptive DCT Filter Bank. Circuits Syst. Signal Process. 2023, 42, 4691–4712. [Google Scholar] [CrossRef]
- Qaisar, S.M.; Hussain, S.F. Effective epileptic seizure detection by using level-crossing EEG sampling sub-bands statistical features selection and machine learning for mobile healthcare. Comput. Methods Programs Biomed. 2021, 203, 106034. [Google Scholar] [CrossRef]
- Chawla, P.; Rana, S.B.; Kaur, H.; Singh, K. Local Mean Decomposition Based Epileptic Seizure Classification Using Ensemble Machine Learning. In Proceedings of the International Conference on Advances and Applications of Artificial Intelligence and Machine Learning, Noida, India, 16–17 September 2022; Springer: Singapore; pp. 305–316. [Google Scholar]
- Li, C.; Zhang, X.; Zhang, Z.; Liu, Z. Seizure Onset Detection Using Empirical Mode Decomposition and Common Spatial Pattern. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 458–467. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Mohan, N.; Soman, K.P. A data-driven technique for harmonics monitoring in emerging power grids using noise-aware dynamic mode decomposition. Meas. Sci. Technol. 2019, 31, 015016. [Google Scholar] [CrossRef]
- Ingabire, H.N.; Wu, K.; Amos, J.T.; He, S.; Peng, X.; Wang, W.; Li, M.; Chen, J.; Feng, Y.; Rao, N.; et al. Analysis of ECG Signals by Dynamic Mode Decomposition. IEEE J. Biomed. Health Inform. 2022, 26, 2124–2135. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef]
- Andén, J.; Mallat, S. Deep scattering spectrum. IEEE Trans. Signal Process. 2014, 62, 4114–4128. [Google Scholar] [CrossRef]
- Parmar, S.; Paunwala, C. A novel and efficient Wavelet Scattering Transform approach for primitive-stage dyslexia-detection using electroencephalogram signals. Healthc. Anal. 2023, 3, 100194. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. A survey of ensemble learning: Concepts, algorithms, applications, and prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Joshi, S.C.; Jana, G.C.; Agrawal, A. A multi-view representation learning approach for seizure detection over multi-channel EEG signals. In Proceedings of the International Conference on Frontiers of Intelligent Computing: Theory and Applications, Aizawl, Mizoram, India, 18–19 June 2022; Springer: Singapore, 2022; pp. 375–385. [Google Scholar]
- Jana, R.; Mukherjee, I. Deep learning based efficient epileptic seizure prediction with EEG channel optimization. Biomed. Signal Process. Control 2021, 68, 102767. [Google Scholar] [CrossRef]
- Krake, T.; Reinhardt, S.; Hlawatsch, M.; Eberhardt, B.; Weiskopf, D. Visualization and selection of Dynamic Mode Decomposition components for unsteady flow. Vis. Inform. 2021, 5, 15–27. [Google Scholar] [CrossRef]
- Somogyi, Z.; Somogyi, Z. Performance Evaluation of Machine Learning Models. In Proceedings of the Application of Artificial Intelligence: Step-by-Step Guide from Beginner to Expert; Springer: Cham, Switzerland, 2021; pp. 87–112. [Google Scholar]
- Abhishek, S.; Kumar, S.; Mohan, N.; Soman, K.P. EEG Based Automated Detection of Seizure Using Machine Learning Approach and Traditional Features. Expert Syst. Appl. 2024, 251, 123991. [Google Scholar] [CrossRef]
- Cramér, H. Mathematical Methods of Statistics; Princeton Mathematical Series; Princeton University Press: Princeton, NJ, USA, 1999; Volume 43. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Matthews Correlation Coefficient (MCC) is More Informative Than Cohen’s Kappa and Brier Score in Binary Classification Assessment. IEEE Access 2021, 9, 78368–78381. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, S.; Chen, W.; Du, G.; Fu, Q.; Jiang, H. A scheme combining feature fusion and hybrid deep learning models for epileptic seizure detection and prediction. Sci. Rep. 2024, 14, 16916. [Google Scholar] [CrossRef]
- Kumar, P.; Upadhyay, P.K. EpiCNN-LSTMDetect: A Combined Deep Learning Method for Identifying Epileptic Seizures. In Proceedings of the 2025 3rd International Conference on Intelligent Systems, Advanced Computing and Communication (ISACC), Silchar, India, 27–28 February 2025; pp. 852–857. [Google Scholar]
- Jiang, Y.; Chen, W.; Li, M.; Zhang, T.; You, Y. Synchroextracting chirplet transform-based epileptic seizures detection using EEG. Biomed. Signal Process. Control 2021, 68, 102699. [Google Scholar] [CrossRef]
- Tian, X.; Deng, Z.; Ying, W.; Choi, K.S.; Wu, D.; Qin, B.; Wang, J.; Shen, H.; Wang, S. Deep multi-view feature learning for EEG-based epileptic seizure detection. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1962–1972. [Google Scholar] [CrossRef]
- Xiang, J.; Li, C.; Li, H.; Cao, R.; Wang, B.; Han, X.; Chen, J. The detection of epileptic seizure signals based on fuzzy entropy. J. Neurosci. Methods 2015, 243, 18–25. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Akbari, H.; Ur Rehman, A.; Nishtar, Z.; Masood, B.; Ghazvini, M.; Too, J.; Hamedi, N.; Kaabar, M.K. Exploiting feature selection and neural network techniques for identification of focal and nonfocal EEG signals in TQWT domain. J. Healthc. Eng. 2021, 2021, 6283900. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.R.; Rao, Y.S. Epileptic seizures classification in EEG signal based on semantic features and variational mode decomposition. Clust. Comput. 2019, 22, 13521–13531. [Google Scholar] [CrossRef]
- San-Segundo, R.; Gil-Martín, M.; D’Haro-Enríquez, L.F.; Pardo, J.M. Classification of epileptic EEG recordings using signal transforms and convolutional neural networks. Comput. Biol. Med. 2019, 109, 148–158. [Google Scholar] [CrossRef]
- Al-Salman, W.; Li, Y.; Wen, P.; Miften, F.S.; Oudah, A.Y.; Al Ghayab, H.R. Extracting epileptic features in EEGs using a dual-tree complex wavelet transform coupled with a classification algorithm. Brain Res. 2022, 1779, 147777. [Google Scholar] [CrossRef]
- Supriya, S.; Siuly, S.; Wang, H.; Zhang, Y. New feature extraction for automated detection of epileptic seizure using complex network framework. Appl. Acoust. 2021, 180, 108098. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, Y.; Liu, Z.; Guo, J.; Cao, G.; Ouyang, M.; Liu, D.; Shan, Y.; Kang, G.; Zhao, G. Computer-Aided Intracranial EEG Signal Identification Method Based on a Multi-Branch Deep Learning Fusion Model and Clinical Validation. Brain Sci. 2021, 11, 615. [Google Scholar] [CrossRef]
- Akbari, H.; Sadiq, M.T. Detection of focal and non-focal EEG signals using non-linear features derived from empirical wavelet transform rhythms. Phys. Eng. Sci. Med. 2021, 44, 157–171. [Google Scholar] [CrossRef]
- Anuragi, A.; Sisodia, D.S.; Pachori, R.B. Classification of focal and non-focal EEG signals using optimal geometrical features derived from a second-order difference plot of FBSE-EWT rhythms. Artif. Intell. Med. 2023, 139, 102542. [Google Scholar] [CrossRef]
- Srinath, R.; Gayathri, R.; Shalini, C.; Maragathavalli, P. Epilepsy Disease Detection Using the Proposed CNN-FCM Approach. In Proceedings of the International Conference on Innovations in Data Analytics, Kolkata, India, 29–30 November 2023; pp. 371–380. [Google Scholar]
- Fasil, O.K.; Rajesh, R. Time-domain exponential energy for epileptic EEG signal classification. Neurosci. Lett. 2019, 694, 1–8. [Google Scholar] [CrossRef]
- Chakraborty, M.; Mitra, D. A computationally efficient automated seizure detection method based on the novel idea of multiscale spectral features. Biomed. Signal Process. Control 2021, 70, 102990. [Google Scholar] [CrossRef]
- Shanmugam, S.; Dharmar, S. Implementation of a non-linear SVM classification for seizure EEG signal analysis on FPGA. Eng. Appl. Artif. Intell. 2024, 131, 107826. [Google Scholar] [CrossRef]
- Buldu, A.; Kaplan, K.; Kuncan, M. A Hybrid Study for Epileptic Seizure Detection Based on Deep Learning using EEG Data. J. Univers. Comput. Sci. 2024, 30, 909–934. [Google Scholar] [CrossRef]
- Kyeremateng-Boateng, H.; Josyula, D.; Conn, M. Computing Confidence Score for Neural Network Predictions from Latent Features. In Proceedings of the 2023 International Conference on Control, Communication and Computing, Thiruvananthapuram, India, 19–21 May 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Nemenyi, P.B. Distribution-Free Multiple Comparisons. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1963. [Google Scholar]


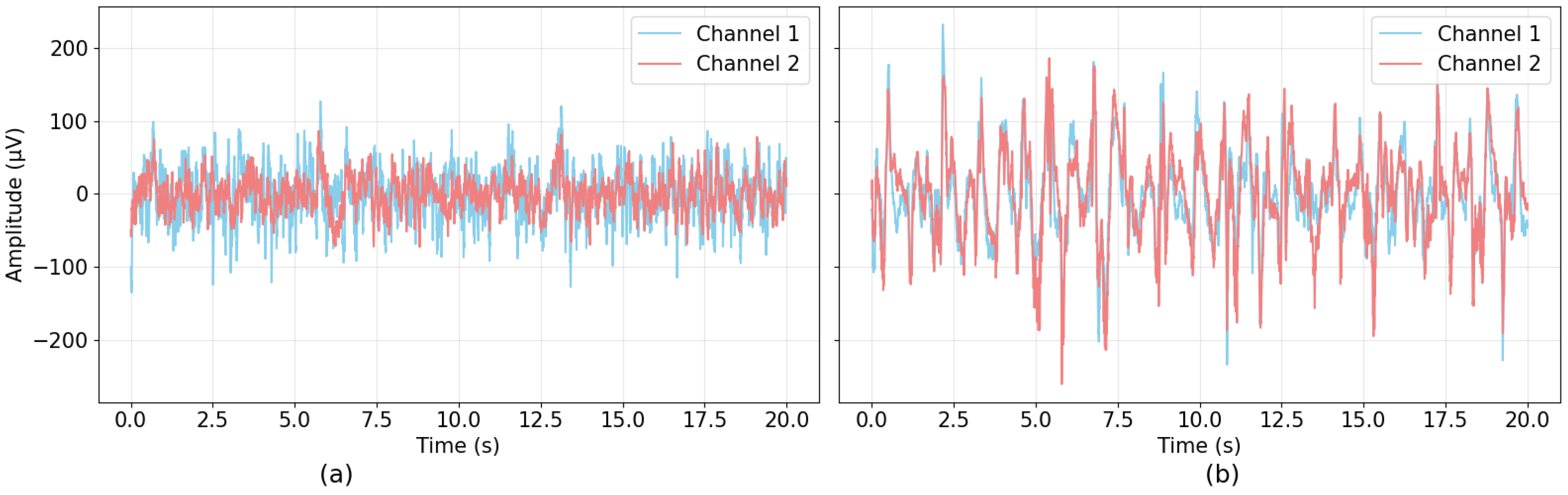

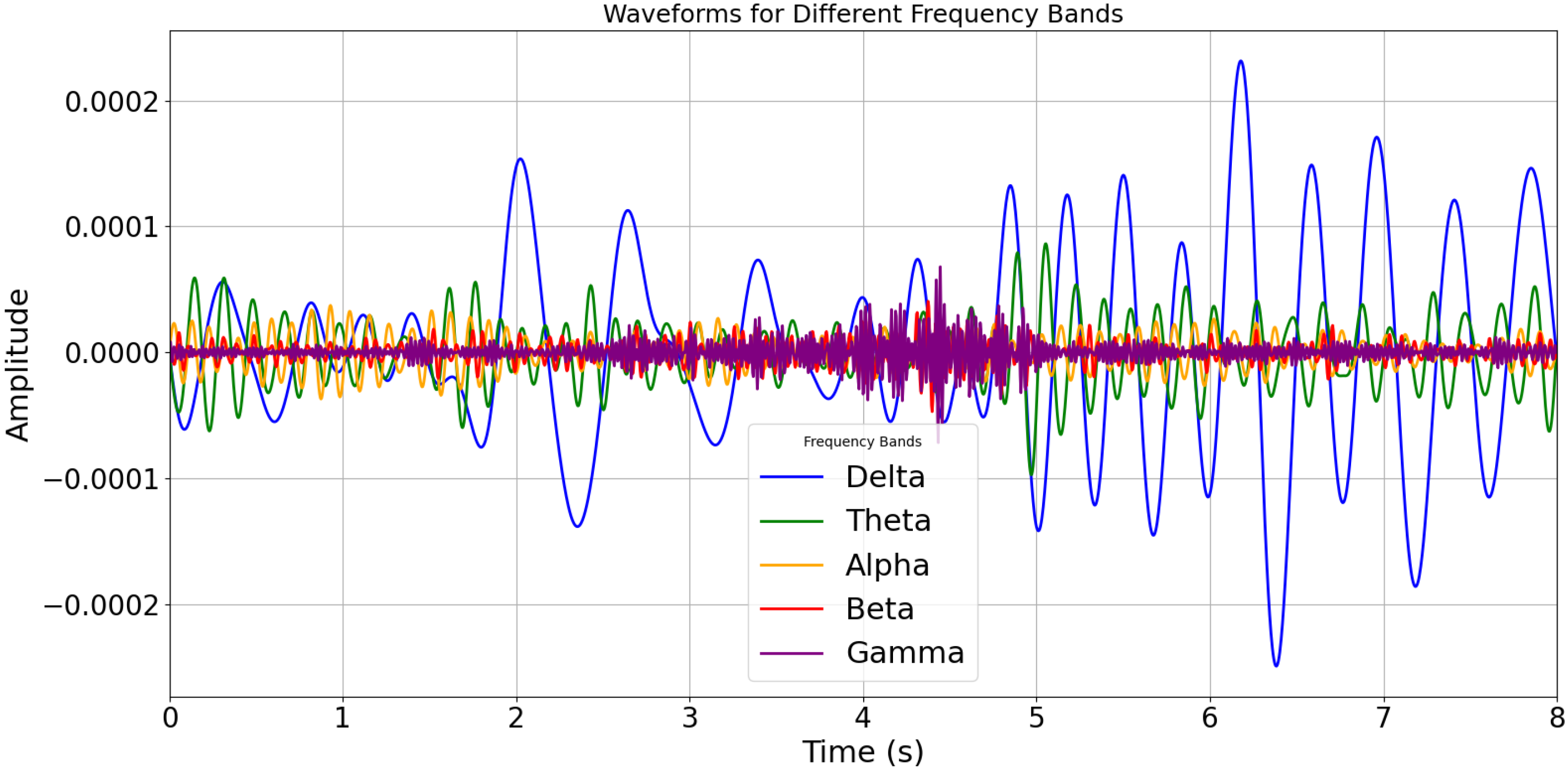




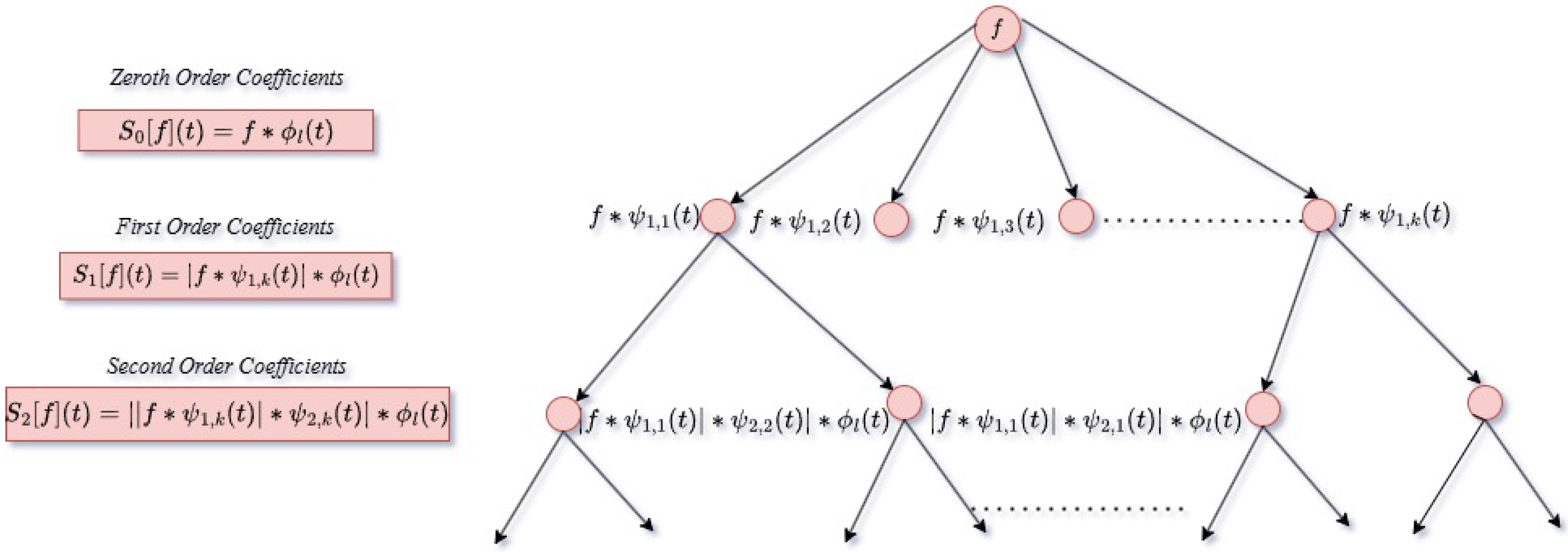
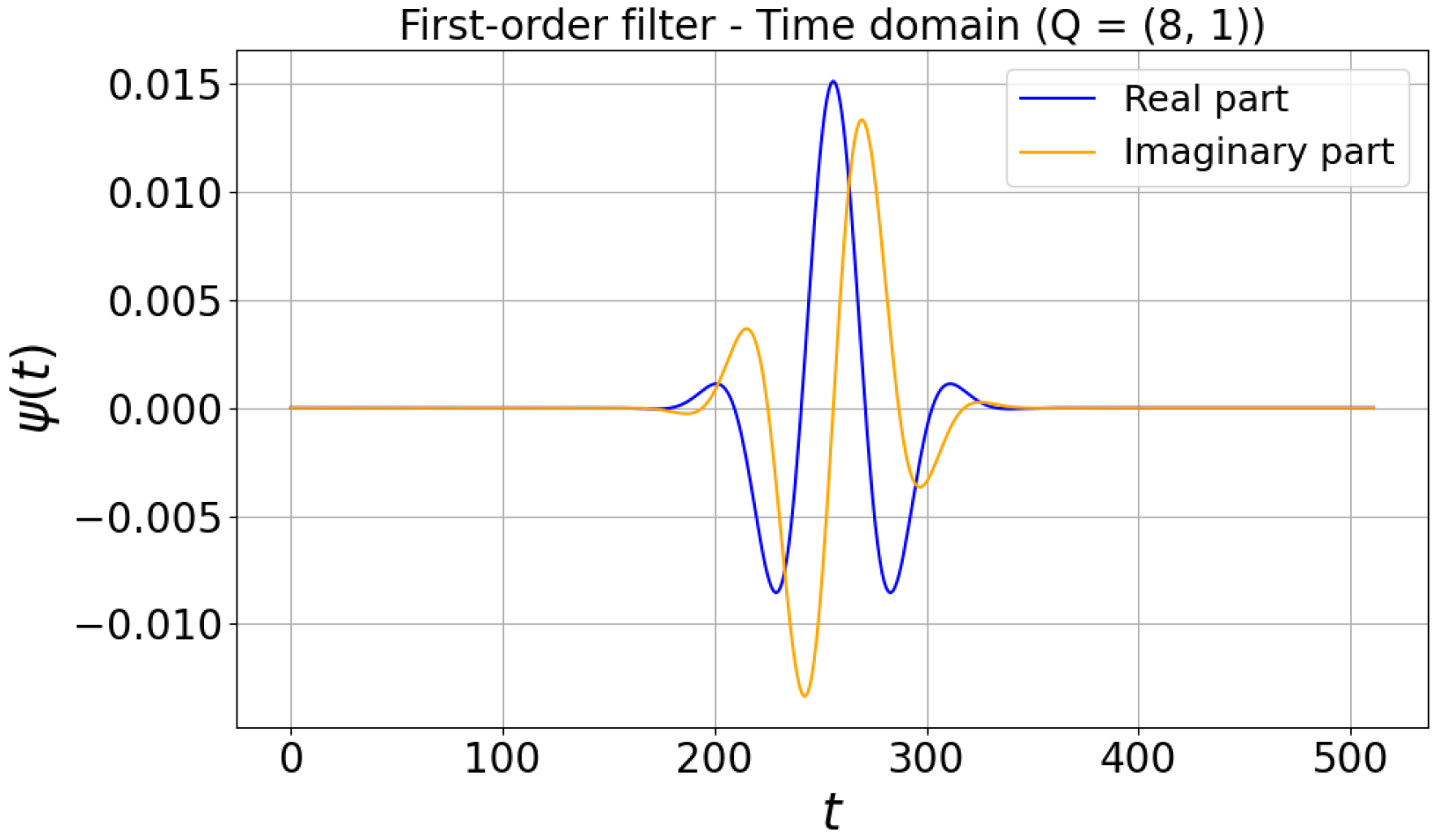







| Author | Methodology | Dataset | Performance |
|---|---|---|---|
| Quintero-Rincon et al. (2018) [9] | EEG signals are decomposed into five brain rhythms using WT. Each brain signal is reduced to a low dimension with a Gaussian statistical model and classified by linear discriminant analysis. | CHB-MIT | Accuracy 97–99%,Sensitivity 98%, Specificity 88% |
| Hussain et al. (2018) [8] | EEG signals are decomposed by EMD. Each IMF feature is extracted based on the mean weighted frequency and classified using a neural network. | CHB-MIT | Accuracy 97%,Sensitivity 97%,Specificity 97% |
| Li et al. (2020) [10] | EEG is fragmented into nonlinear modes using the NM decomposition algorithm. The fractional central moment is computed from the modes and used as a feature vector for K-NN classifiers. | CHB-MIT | Accuracy 99%,Sensitivity 98.40%, Specificity 99.10% |
| Wu et al. (2020) [49] | Complementary EEMD and features obtained from EEG signals; XGBoost is used for classification. | CHB-MIT | Accuracy 95%,Sensitivity 95%,Specificity 95% |
| Moctezuma and Molinas (2020) [50] | Applied EMD; features like teager and instantaneous energy, Higuchi and Petrosian fractal dimensions used; classified using K-means. | CHB-MIT | Accuracy 93% |
| Peng et al.(2021) [51] | Symmetric positive definite matrices are used for seizure classification. | CHB-MIT | Accuracy 98.21%, Sensitivity 97.85%, Specificity 98.57% |
| Aayesha et al. (2021) [11] | Temporal spectral features obtained from DWT; fuzzy rough nearest neighbour used for classification. | CHB-MIT | Accuracy 92.79% |
| Amiri et al.(2023) [52] | Seizures detected using spatial pattern adaptive STFT-based synchrosqueezing transform. | CHB-MIT | Accuracy 98%,Sensitivity 98.44%,Specificity 99.19% |
| Subashi et al. (2019) [15] | Localized focal regions using EMD, DWT, and WPD; statistical features classified using SVM. | Bern, Barcelona | Accuracy 99%,F1 score 0.99 |
| Dalal et al. (2019) [53] | EEG signals decomposed using flexible analytic wavelet transform; fractal dimensions classified using robust energy-based least squares twin SVM. | Bern, Barcelona | Accuracy 90% |
| Sharma et al.(2020) [54] | Nonlinear third-order cumulant used for non-focal vs. focal classification. | Bern, Barcelona | Accuracy 99%,Sensitivity 98.68%, Specificity 99.32% |
| Sairamya et al.(2021) [55] | WPD, entropies, and quad binary pattern applied to EEG signals to identify non-focal and focal classes. | Bern, Barcelona | Accuracy 95% |
| Mehla et al.(2023) [56] | Signal decomposed into Fourier intrinsic band function using DCT. Features like variance, mean frequency, complexity, kurtosis, etc., extracted. | Bern, Barcelona | Accuracy 99%, Sensitivity 99%, Specificity 99% |
| Varli et al. (2023) [12] | Two DL models trained separately on images created by STFT and CWT methods. | Bern, Barcelona, CHB-MIT | Accuracy 93–95%, 95–96% |
| Qaisar and Hussain(2021) [57] | EEG analysed using adaptive rate DWT and subband statistical features; info gain-based dimensionality reduction applied. | Khas | Accuracy 100%,F1 score 1.00 |
| Du et al. (2022) [5] | Optimized CNN-based feature extraction; seizure states classified using SVM. | Khas | Accuracy 98%,F1 score 0.97 |
| Chawla et al. (2020) [58] | EEG signals disintegrated using local mean decomposition. Hjorth parameters calculated as features | Khas | Accuracy 96%, Sensitivity 96%,Specificity 97.6% |
| Classifiers | Parameter |
|---|---|
| Random forest | n_estimators = 100, random_state = 42 |
| XGBoost | n_estimators = 500, learning_rate=1.0, max_depth = 3, random_state=42 |
| adaBoost | n_estimators = 100, learning_rate = 0.1, random_state = 42 |
| bagging | n_estimators = 100, random_state = 42 |
| SVM (linear) | C_value = 100, random_state = 42 |
| SVM (RBF) | C_value = 100, gamma_value = 0.01 |
| SVM (Poly) | C_value = 100, gamma_value = 0.01, degree_value = 3, coef_value = 1 |
| LightGBM | n_estimators = 100, learning_rate = 0.1, random_state = 42 |
| Algorithm | Precision | Sensitivity | F1 Score | Accuracy (%) |
|---|---|---|---|---|
| Random forest | 0.99 | 0.99 | 0.99 | 99 |
| XGBoost | 0.93 | 0.93 | 0.93 | 93 |
| AdaBoost | 0.93 | 0.93 | 0.93 | 93 |
| Bagging | 0.99 | 0.99 | 0.99 | 98.8 |
| SVM (linear) | 0.67 | 0.68 | 0.68 | 68 |
| SVM (RBF) | 0.88 | 0.91 | 0.89 | 89 |
| SVM (Poly) | 0.95 | 0.95 | 0.95 | 94.61 |
| LightGBM | 0.99 | 0.99 | 0.99 | 99 |
| K-NN | 0.76 | 0.76 | 0.76 | 77 |
| Naive Bayes | 0.80 | 0.79 | 0.79 | 80 |
| Algorithm | Cohen’s Kappa | MCC | G-Mean |
|---|---|---|---|
| Random forest | 0.98 | 0.98 | 0.99 |
| XGBoost | 0.86 | 0.87 | 0.93 |
| AdaBoost | 0.85 | 0.85 | 0.925 |
| Bagging | 0.98 | 0.98 | 0.99 |
| LightGBM | 0.99 | 0.99 | 0.99 |
| SVM (RBF) | 0.77 | 0.79 | 0.89 |
| SVM(Poly) | 0.89 | 0.89 | 0.95 |
| Algorithm | Precision | Sensitivity | F1 Score | Accuracy (%) |
|---|---|---|---|---|
| Random forest | 1.00 | 1.00 | 1.00 | 100 |
| XGBoost | 1.00 | 1.00 | 1.00 | 100 |
| AdaBoost | 1.00 | 1.00 | 1.00 | 100 |
| Bagging | 1.00 | 1.00 | 1.00 | 100 |
| SVM (linear) | 0.65 | 0.65 | 0.65 | 65 |
| SVM (RBF) | 0.99 | 0.99 | 0.99 | 98 |
| SVM (Poly) | 1.00 | 1.00 | 1.00 | 100 |
| LightGBM | 1.00 | 1.00 | 1.00 | 100 |
| K-NN | 0.74 | 0.74 | 0.74 | 77 |
| Naive Bayes | 0.49 | 0.49 | 0.50 | 50 |
| Algorithm | Cohen’s Kappa | MCC | G-Mean |
|---|---|---|---|
| Random forest | 1.00 | 1.00 | 1.00 |
| XGBoost | 1.00 | 1.00 | 1.00 |
| AdaBoost | 1.00 | 1.00 | 1.00 |
| Bagging | 1.00 | 1.00 | 1.00 |
| LightGBM | 1.00 | 1.00 | 1.00 |
| SVM (RBF) | 0.98 | 0.98 | 0.99 |
| SVM (Poly) | 1.00 | 1.00 | 1.00 |
| Algorithm | Precision | Sensitivity | F1 Score | Accuracy (%) |
|---|---|---|---|---|
| Random forest | 1.00 | 1.00 | 1.00 | 100 |
| XGBoost | 1.00 | 1.00 | 1.00 | 100 |
| AdaBoost | 1.00 | 1.00 | 1.00 | 100 |
| Bagging | 1.00 | 1.00 | 1.00 | 100 |
| SVM (linear) | 0.62 | 0.62 | 0.62 | 62 |
| SVM (RBF) | 0.97 | 0.97 | 0.97 | 96.87 |
| SVM (Poly) | 0.99 | 0.99 | 0.99 | 99 |
| LightGBM | 0.99 | 0.99 | 0.99 | 99 |
| K-NN | 0.57 | 0.58 | 0.58 | 58 |
| Naive Bayes | 0.57 | 0.57 | 0.57 | 57 |
| Author | Feature Extraction | Classification | Performance |
|---|---|---|---|
| Bhattacharya and Pachori et al. (2017) [13]. | Empirical WT | Random forest, linear Naive bayesK-NN classifiers | Accuracy 0.99 Sensitivity 0.97 |
| Li et al. (2021) [59] | Common spatial pattern wavelet transform and EMD | SVM | Sensitivity 0.97 |
| Shen et al. (2022) [14] | DB16-DWT | RUSBoosted tree ensemble models | Accuracy 0.96,Sensitivity 0.96 |
| Zarei et al. (2021) [46] | DWT, orthogonal matching pursuit, statistical features, entropy features | SVM | Accuracy 0.97Sensitivity 0.97 |
| Jiang et al. (2021) [76] | Synchroextracting chirplet transform | SVM | Accuracy 0.99 MCC 0.97 |
| Alharati et al. (2021) [4] | DWT | CNN | Accuracy 0.96 Sensitivity 0.96 |
| Tian et al. (2021) [77] | FFT and WPD | CNN | Accuracy 0.98 Sensitivity 0.96 |
| Bilal et al. (2019) [39] | MRDMD and temporal features | RUSBoost | Sensitivity 0.937 |
| Zhang, Jincan and Zheng et al. (2024) [74] | DWT and time–frequency domain and nonlinear features | CNN-gated recurrent unit-attention mechanism | Accuracy 0.99 Sensitivity 0.99 |
| Kumar Priyaranjan et al. (2025) [75] | Mean, skewness, kurtosis, and STFT | EpiCNN-LSTM | Accuracy 0.99 Sensitivity 0.99 |
| Solaija et al. (2018) [16] | DMD, DMD power and curve-length | RUSBoost | Sensitivity 0.87 |
| Xiang et al. (2015) [78] | Fuzzy entropy and sample entropy | SVM | Accuracy 0.98 Sensitivity 0.98 |
| Cura and akan et al. (2021) [17] | Higherorder, DMD spectral moments, DMD sub-band power. | Random forest | Accuracy 0.96 Sensitivity 0.92 |
| Zeynab et al. (2025) [44] | Weighted visibility graph (WVG) features | Random forest | Accuracy 0.94 Sensitivity 0.92 |
| Proposed method | DMD-WST | Random forest | Accuracy 0.99 Sensitivity 0.99 MCC 0.98 |
| Author | Feature Extraction | Classification | Performance |
|---|---|---|---|
| Sadiq et al. (2021) [79] | Tunable Q-factor wavelet transform (TQWT) entropy features | Cascade-forward neural network | Accuracy 0.97 Sensitivity 0.97 |
| Kumar and Rao et al. (2019) [80] | VMD differential entropy | Random forest | Accuracy 0.78 |
| San-Srgundo et al. (2019) [81] | EMD | DNN | Accuracy 0.989 |
| al salmon et al. (2022) [82] | Dual-tree complex WT and fast fourier transform | Least squareSVM | Accuracy 0.968 |
| Supriya et al. (2021) [83] | Edge weight fluctuation (EWF) | SVM | Accuracy 0.99 Sensitivity 1.00 |
| Wang et al. (2021) [84] | Multi-branch DL fusion model | CNN | Accuracy 0.97 Sensitivity 0.97 |
| akbari and Sadiq et al. (2021) [85] | Kruskal–Wallis statistical test | SVM | accuracy 0.93 Sensitivity 0.96 |
| anuragi et al. (2023) [86] | Fourier–Bessel series expansion-based EWT | Least squareSVM | Accuracy 0.98 |
| Srinath and Gayathri et al. (2023) [87] | EMD | CNN FCM | Accuracy 0.99 |
| Fasil and Rajesh et al. (2019) [88] | Exponential energy features | SVM | Accuracy 0.89 |
| Proposed method | DMD-WST | Random forest | Accuracy 1.00 Sensitivity 1.00MCC 1.00 |
| Author | Feature Extraction | Classification | Performance |
|---|---|---|---|
| Chakraborty et al. (2021) [89] | Multiscale spectralfeatures | Random forest | Accuracy 0.989 sensitivity 0.981 |
| Du et al. (2022) [5] | Optimized feature CNN model for feature extraction | SVM | Accuracy 0.98 Sensitivity 1.00 |
| Shanmughan et al. (2024) [90] | DWT | Non-Linear SVM | Accuracy 0.88 Sensitivity 1.00 |
| Buldu et al. (2024) [91] | CWT | CNN | accuracy 0.95Sensitivity 0.96 |
| Proposed method | DMD-WST | Random forest | Accuracy 1.00Sensitivity 1.00 |
| Dataset | Friedman Test Statistic | p Value | Kendall’s W [95% CI] |
|---|---|---|---|
| CHB-MIT | 15.846 | 0.00036 | 0.208 [0.202, 0.2451] |
| Bern Barcelona | 6.500 | 0.0387 | 0.026 [0.002, 0.0868] |
| Khas dataset | 15.250 | 0.00048 | 0.164 [0.116, 0.208] |
| Dataset | Comparison | Corrected p-Value | Cliff’s [95% CI] | Significance |
|---|---|---|---|---|
| CHB-MIT | Random Forest vs Bagging | 0.78047 | [−0.62, 0.38] | NSF |
| Random Forest vs LightGBM | 0.00716 | 1.00 [1.0, 1.0] | SDF | |
| Bagging vs LightGBM | 0.00066 | 1.00 [1.0, 1.0] | SDF | |
| Bern Barcelona | Random Forest vs LightGBM | 0.37206 | −0.40 [−0.7, −0.1] | NSF |
| Random Forest vs XGBoost | 0.57290 | −0.30 [−0.7, 0.1] | NSF | |
| LightGBM vs XGBoost | 0.93987 | 0.10 [0.0, 0.3] | NSF | |
| Khas | Random Forest vs AdaBoost | 0.00497 | 1.00 [1.0, 1.0] | SDF |
| Random Forest vs XGBoost | 0.97281 | −0.02 [−0.52, 0.44] | NSF | |
| AdaBoost vs XGBoost | 0.01021 | −0.95 [−1.0, −0.8] | SDF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
C, S.; Mohan, N.; S, S.K.; Harikumar, A. Hybrid Approach Using Dynamic Mode Decomposition and Wavelet Scattering Transform for EEG-Based Seizure Classification. Informatics 2025, 12, 117. https://doi.org/10.3390/informatics12040117
C S, Mohan N, S SK, Harikumar A. Hybrid Approach Using Dynamic Mode Decomposition and Wavelet Scattering Transform for EEG-Based Seizure Classification. Informatics. 2025; 12(4):117. https://doi.org/10.3390/informatics12040117
Chicago/Turabian StyleC, Sreevidya, Neethu Mohan, Sachin Kumar S, and Aravind Harikumar. 2025. "Hybrid Approach Using Dynamic Mode Decomposition and Wavelet Scattering Transform for EEG-Based Seizure Classification" Informatics 12, no. 4: 117. https://doi.org/10.3390/informatics12040117
APA StyleC, S., Mohan, N., S, S. K., & Harikumar, A. (2025). Hybrid Approach Using Dynamic Mode Decomposition and Wavelet Scattering Transform for EEG-Based Seizure Classification. Informatics, 12(4), 117. https://doi.org/10.3390/informatics12040117






