Evaluating and Enhancing Artificial Intelligence Models for Predicting Student Learning Outcomes
Abstract
1. Introduction
- RQ1: How do machine learning and deep learning models compare in predicting student outcomes to improve AI’s use in education?
- RQ2: How does the Lasso feature selection affect the accuracy and performance of AI models in predicting student outcomes?
- RQ3: How do hyperparameter tuning techniques like Bayesian optimisation and cross-validation enhance the adaptability of AI-based educational prediction models?
- First, we comprehensively assess ten different predictive models. These contain seven machine learning architectures and three deep learning architectures covering fundamental and cutting-edge approaches. All models are implemented using Python on two public benchmark student datasets.
- Second, we examine the influence of Lasso-based regularisation on model performance improvement. In this investigation, the accuracy and efficiency of the models across all ten models are evaluated in terms of feature selection through Lasso regularisation.
- Third, we use hyperparameter tuning techniques to optimise model configurations. Bayesian hyperparameter optimisation is employed to fine-tune the deep learning models, while cross-validation is utilised to determine the optimal threshold for Lasso regularisation.
- Fourth, our evaluation methodology includes a dual approach, using both k-fold cross-validation and holdout validation methods. This robust assessment strategy ensures that the performance of our models is evaluated thoroughly.
- Finally, the insights obtained from our research provide educators, researchers, and policymakers with essential information. This knowledge allows them to make informed decisions regarding personalised educational plans based on the capabilities of predictive models.
2. Related Works
2.1. Prediction of Student Performance
2.2. Evaluating Student Progression
2.3. Developing a Model of Adaptive Feedback
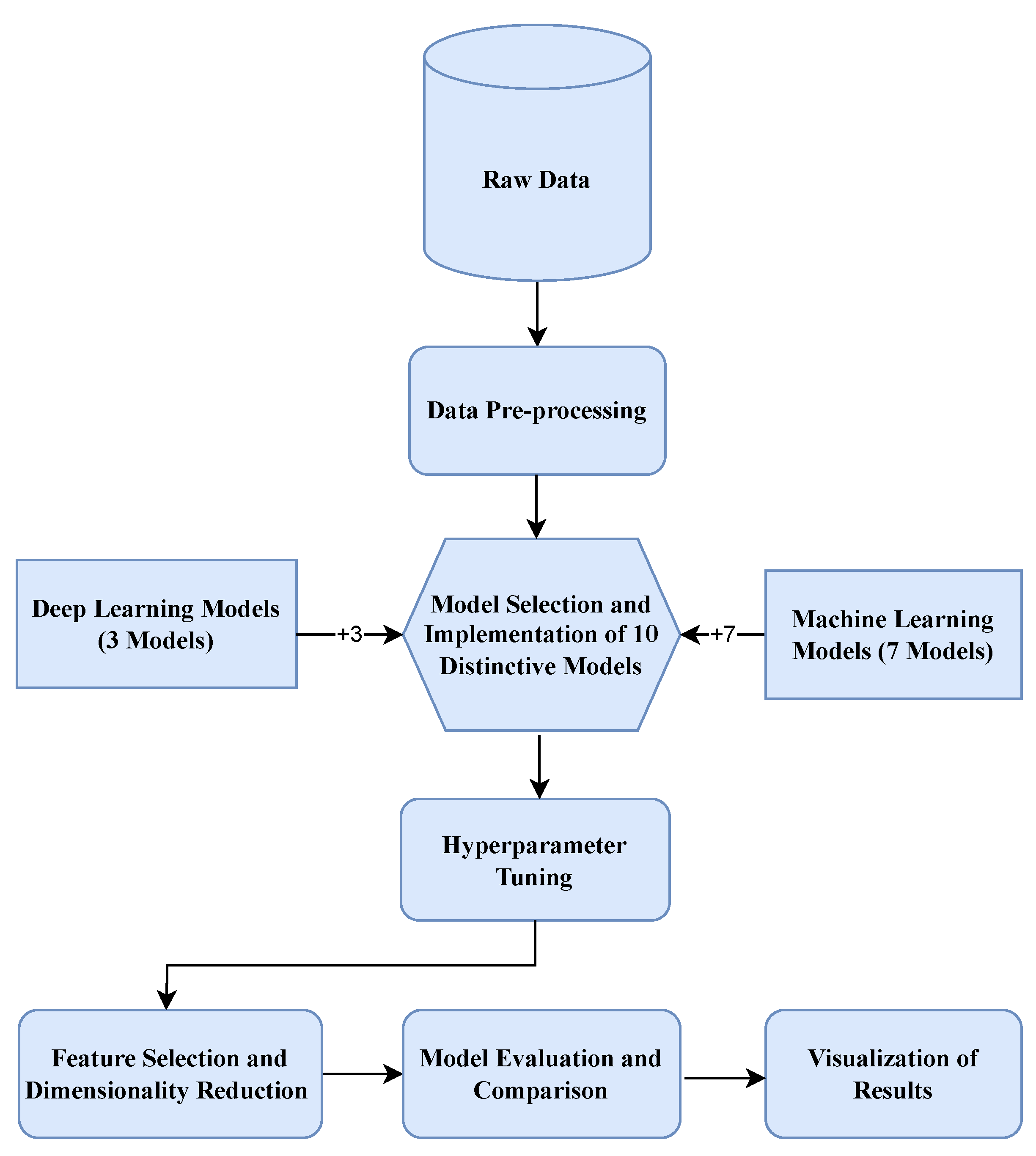
3. Methods
3.1. Data Acquisition and Preparation
3.2. Data Preprocessing
3.3. Model Selection and Implementation
3.4. Hyperparameter Tuning
3.5. Model Evaluation and Comparison
3.6. Feature Selection and Dimensionality Reduction
3.7. Visualisation of Results
4. Results
4.1. Machine Learning Models with Holdout Evaluation
4.2. Machine Learning Models with k-Fold Cross-Validation
4.3. Deep Learning Models with Holdout Evaluation
4.4. Deep Learning Models with k-Fold Cross-Validation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaswan, K.S.; Dhatterwal, J.S.; Ojha, R.P. AI in personalized learning. In Advances in Technological Innovations in Higher Education; CRC Press: Boca Raton, FL, USA, 2024; pp. 103–117. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Pernaa, J.; Ikävalko, T.; Takala, A.; Vuorio, E.; Pesonen, R.; Haatainen, O. Artificial Intelligence Chatbots in Chemical Information Seeking: Narrative Educational Insights via a SWOT Analysis. Informatics 2024, 11, 20. [Google Scholar] [CrossRef]
- Xie, H.; Chu, H.C.; Hwang, G.J.; Wang, C.C. Trends and development in technology-enhanced adaptive/personalized learning: A systematic review of journal publications from 2007 to 2017. Comput. Educ. 2019, 140, 103599. [Google Scholar] [CrossRef]
- Fahad Mon, B.; Wasfi, A.; Hayajneh, M.; Slim, A.; Abu Ali, N. Reinforcement Learning in Education: A Literature Review. Informatics 2023, 10, 74. [Google Scholar] [CrossRef]
- Ouyang, F.; Wu, M.; Zheng, L.; Zhang, L.; Jiao, P. Integration of artificial intelligence performance prediction and learning analytics to improve student learning in online engineering course. Int. J. Educ. Technol. High. Educ. 2023, 20, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Casey, K.; Azcona, D. Utilizing student activity patterns to predict performance. Int. J. Educ. Technol. High. Educ. 2017, 14, 1–15. [Google Scholar] [CrossRef]
- Pallathadka, H.; Wenda, A.; Ramirez-Asís, E.; Asís-López, M.; Flores-Albornoz, J.; Phasinam, K. Classification and prediction of student performance data using various machine learning algorithms. Mater. Today Proc. 2023, 80, 3782–3785. [Google Scholar] [CrossRef]
- KNN. Sklearn-Neighbors-KNeighborsClassifier-Python-Libraray. 2023. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html (accessed on 1 November 2023).
- SVM. Sklearn-Svm-SVC-Python-Libraray. 2023. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html (accessed on 1 November 2023).
- Decision-Tree-Classifier. Scikit-Learn-Python-Libraray. 2023. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html (accessed on 1 November 2023).
- LinearRegression. Sklearn-Linear-Model-LinearRegression-Python-Libraray. 2023. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html/ (accessed on 1 November 2023).
- Logestic-Regression. Sklearn-Linear-Model-LogisticRegression-Python-Libraray. 2023. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html (accessed on 1 November 2023).
- RandomForest. Sklearn-Ensemble-RandomForestClassifier-Python-Libraray. 2023. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html (accessed on 1 November 2023).
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- TF.keras.Sequential. TensorFlow-v2.14.0-Python-Libraray. 2023. Available online: https://www.tensorflow.org/api_docs/python/tf/keras/Sequential (accessed on 1 November 2023).
- TF.keras.layers.Conv1D. TensorFlow-v2.14.0-Python-Libraray. 2023. Available online: https://www.tensorflow.org/api_docs/python/tf/keras/layers/Conv1D (accessed on 1 November 2023).
- Emami, S.; Martínez-Muñoz, G. Sequential Training of Neural Networks with Gradient Boosting. IEEE Access 2023, 11, 42738. [Google Scholar] [CrossRef]
- Emami, S.; Martýnez-Muñoz, G. Source-Code-GitHub-Sequential Training of Neural Networks with Gradient Boosting. 2022. Available online: https://github.com/GAA-UAM/GBNN (accessed on 1 November 2023).
- Brownlee, J. What is the Difference between a Batch and an Epoch in a Neural Network. Mach. Learn. Mastery 2018, 20, 1–5. [Google Scholar]
- Victoria, A.H.; Maragatham, G. Automatic tuning of hyperparameters using Bayesian optimization. Evol. Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Mockus, J.; Mockus, J. The Bayesian Approach to Local Optimization; Springer: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Roberts, S.; Nowak, G. Stabilizing the lasso against cross-validation variability. Comput. Stat. Data Anal. 2014, 70, 198–211. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Yadav, S.; Shukla, S. Analysis of k-fold cross-validation over hold-out validation on colossal datasets for quality classification. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; pp. 78–83. [Google Scholar]
- Kaggle. Student Grade Prediction-Dataset-from-Paulo Cortez. 2018. Available online: https://www.kaggle.com/datasets/dipam7/student-grade-prediction/ (accessed on 1 November 2023).
- Cortez, P. Student Performance. UCI Machine Learning Repository. 2014. [Google Scholar] [CrossRef]
- Cortez, P.; Silva, A.M.G. Using data mining to predict secondary school student performance. In Proceedings of the 5th Annual Future Business Technology Conference, Porto, Portugal, 5–12 April 2008. [Google Scholar]
- Amrieh-Hamtini-Aljarah. Students’ Academic Performance Dataset (xAPI-Edu-Data). 2016. Available online: https://www.kaggle.com/datasets/aljarah/xAPI-Edu-Data?resource=download (accessed on 3 May 2024).
- Amrieh, E.A.; Hamtini, T.; Aljarah, I. Mining educational data to predict student’s academic performance using ensemble methods. Int. J. Database Theory Appl. 2016, 9, 119–136. [Google Scholar] [CrossRef]
- Amrieh, E.A.; Hamtini, T.; Aljarah, I. Preprocessing and analyzing educational data set using X-API for improving student’s performance. In Proceedings of the 2015 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Amman, Jordan, 3–5 November 2015; pp. 1–5. [Google Scholar]
- Code, C.S. Comparative-Study-Deep-Learning-Machine-Learning. 2023. Available online: https://github.com/aideveloper63/Comparative-Study-DL-ML (accessed on 1 July 2024).
- Riestra-González, M.; del Puerto Paule-Ruíz, M.; Ortin, F. Massive LMS log data analysis for the early prediction of course-agnostic student performance. Comput. Educ. 2021, 163, 104108. [Google Scholar] [CrossRef]
- Shabani, N.; Beheshti, A.; Farhood, H.; Bower, M.; Garrett, M.; Rokny, H.A. icreate: Mining creative thinking patterns from contextualized educational data. In Proceedings of the International Conference on Artificial Intelligence in Education, Durham, UK, 27–31 July 2022; pp. 352–356. [Google Scholar]
- Shabani, N.; Beheshti, A.; Farhood, H.; Bower, M.; Garrett, M.; Alinejad-Rokny, H. A Rule-Based Approach for Mining Creative Thinking Patterns from Big Educational Data. AppliedMath 2023, 3, 243–267. [Google Scholar] [CrossRef]
- Arroway, P.; Morgan, G.; O’Keefe, M.; Yanosky, R. Learning Analytics in Higher Education; Technical Report, Research Report; ECAR: Louisville, CO, USA, 2016. [Google Scholar]
- Gligorea, I.; Cioca, M.; Oancea, R.; Gorski, A.T.; Gorski, H.; Tudorache, P. Adaptive Learning Using Artificial Intelligence in e-Learning: A Literature Review. Educ. Sci. 2023, 13, 1216. [Google Scholar] [CrossRef]
- Hartley, K.; Hayak, M.; Ko, U.H. Artificial Intelligence Supporting Independent Student Learning: An Evaluative Case Study of ChatGPT and Learning to Code. Educ. Sci. 2024, 14, 120. [Google Scholar] [CrossRef]
- Di Mitri, D.; Schneider, J.; Drachsler, H. Keep me in the loop: Real-time feedback with multimodal data. Int. J. Artif. Intell. Educ. 2021, 32, 1–26. [Google Scholar] [CrossRef]
- Lutz, W.; Rubel, J.A.; Schwartz, B.; Schilling, V.; Deisenhofer, A.K. Towards integrating personalized feedback research into clinical practice: Development of the Trier Treatment Navigator (TTN). Behav. Res. Ther. 2019, 120, 103438. [Google Scholar] [CrossRef]
- Tabares-Soto, R.; Orozco-Arias, S.; Romero-Cano, V.; Bucheli, V.S.; Rodríguez-Sotelo, J.L.; Jiménez-Varón, C.F. A comparative study of machine learning and deep learning algorithms to classify cancer types based on microarray gene expression data. PeerJ Comput. Sci. 2020, 6, e270. [Google Scholar] [CrossRef]
- Swathy, M.; Saruladha, K. A comparative study of classification and prediction of Cardio-Vascular Diseases (CVD) using Machine Learning and Deep Learning techniques. ICT Express 2022, 8, 109–116. [Google Scholar] [CrossRef]
- Theofilatos, A.; Chen, C.; Antoniou, C. Comparing machine learning and deep learning methods for real-time crash prediction. Transp. Res. Rec. 2019, 2673, 169–178. [Google Scholar] [CrossRef]
- Singh, M.; Verma, C.; Kumar, R.; Juneja, P. Towards enthusiasm prediction of Portuguese school’s students towards higher education in realtime. In Proceedings of the 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, United Arab Emirates, 9–10 January 2020; pp. 421–425. [Google Scholar]
- Hamoud, A. Selection of best decision tree algorithm for prediction and classification of students’ action. Am. Int. J. Res. Sci. Technol. Eng. Math. 2016, 16, 26–32. [Google Scholar]
- Ünal, F. Data mining for student performance prediction in education. Data-Min.-Methods Appl. Syst. 2020, 28, 423–432. [Google Scholar]
- Liu, C.; Wang, H.; Du, Y.; Yuan, Z. A predictive model for student achievement using spiking neural networks based on educational data. Appl. Sci. 2022, 12, 3841. [Google Scholar] [CrossRef]
- Ünal, F.; Birant, D. Educational data mining using semi-supervised ordinal classification. In Proceedings of the 2021 3rd International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 11–13 June 2021; pp. 1–5. [Google Scholar]
- Cerda, P.; Varoquaux, G.; Kégl, B. Similarity encoding for learning with dirty categorical variables. Mach. Learn. 2018, 107, 1477–1494. [Google Scholar] [CrossRef]
- Rodríguez, P.; Bautista, M.A.; Gonzalez, J.; Escalera, S. Beyond one-hot encoding: Lower dimensional target embedding. Image Vis. Comput. 2018, 75, 21–31. [Google Scholar] [CrossRef]
- Okada, S.; Ohzeki, M.; Taguchi, S. Efficient partition of integer optimization problems with one-hot encoding. Sci. Rep. 2019, 9, 13036. [Google Scholar] [CrossRef] [PubMed]
- scikit learn. Libraray-Machine-Learning-in-Python. 2023. Available online: https://scikit-learn.org/stable/ (accessed on 1 November 2023).
- Dmlc Xgboost. Xgboost-for-a-Binary-Classification-Task. 2022. Available online: https://xgboost.readthedocs.io/en/stable/get_started.html (accessed on 1 November 2023).
- Mateo, J.; Rius-Peris, J.; Maraña-Pérez, A.; Valiente-Armero, A.; Torres, A. Extreme gradient boosting machine learning method for predicting medical treatment in patients with acute bronchiolitis. Biocybern. Biomed. Eng. 2021, 41, 792–801. [Google Scholar] [CrossRef]
- Dhieb, N.; Ghazzai, H.; Besbes, H.; Massoud, Y. Extreme gradient boosting machine learning algorithm for safe auto insurance operations. In Proceedings of the 2019 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Cairo, Egypt, 4–6 September 2019; pp. 1–5. [Google Scholar]
- Warsito, B.; Santoso, R.; Suparti; Yasin, H. Cascade forward neural network for time series prediction. J. Phys. Conf. Ser. 2018, 1025, 012097. [Google Scholar] [CrossRef]
- Singh, N.; Singh, A.; Tripathy, M. Selection of hidden layer neurons and best training method for ffnn in application of long term load forecasting. J. Electr. Eng. 2012, 63, 153–161. [Google Scholar] [CrossRef]
- Hosseini, H.G.; Luo, D.; Reynolds, K.J. The comparison of different feed forward neural network architectures for ECG signal diagnosis. Med. Eng. Phys. 2006, 28, 372–378. [Google Scholar] [CrossRef]
- Martinez, J.; Carroll, R.; Muller, S.; Sampson, J.; Chatterjee, N. Empirical performance of crossvalidation with oracle methods in a genomics context. Am. Stat. 2011, 64, 223–228. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Ojero, J.O.; Tackie-Otoo, B.N.; Taki, M.Y. Application of gradient boosting regression model for the evaluation of feature selection techniques in improving reservoir characterisation predictions. J. Pet. Sci. Eng. 2022, 208, 109244. [Google Scholar] [CrossRef]
- Chetverikov, D.; Liao, Z.; Chernozhukov, V. On cross-validated lasso in high dimensions. Ann. Stat. 2021, 49, 1300–1317. [Google Scholar] [CrossRef]
- Buragohain, D.; Punpeng, G.; Jaratjarungkiat, S.; Chaudhary, S. Impact of e-learning activities on English as a second language proficiency among engineering cohorts of Malaysian higher education: A 7-month longitudinal study. Informatics 2023, 10, 31. [Google Scholar] [CrossRef]
- Couronné, R.; Probst, P.; Boulesteix, A.L. Random forest versus logistic regression: A large-scale benchmark experiment. BMC Bioinform. 2018, 19, 270. [Google Scholar] [CrossRef]
- Muthukrishnan, R.; Rohini, R. LASSO: A feature selection technique in predictive modeling for machine learning. In Proceedings of the 2016 IEEE International Conference on Advances in Computer Applications (ICACA), Coimbatore, India, 24 October 2016; pp. 18–20. [Google Scholar]

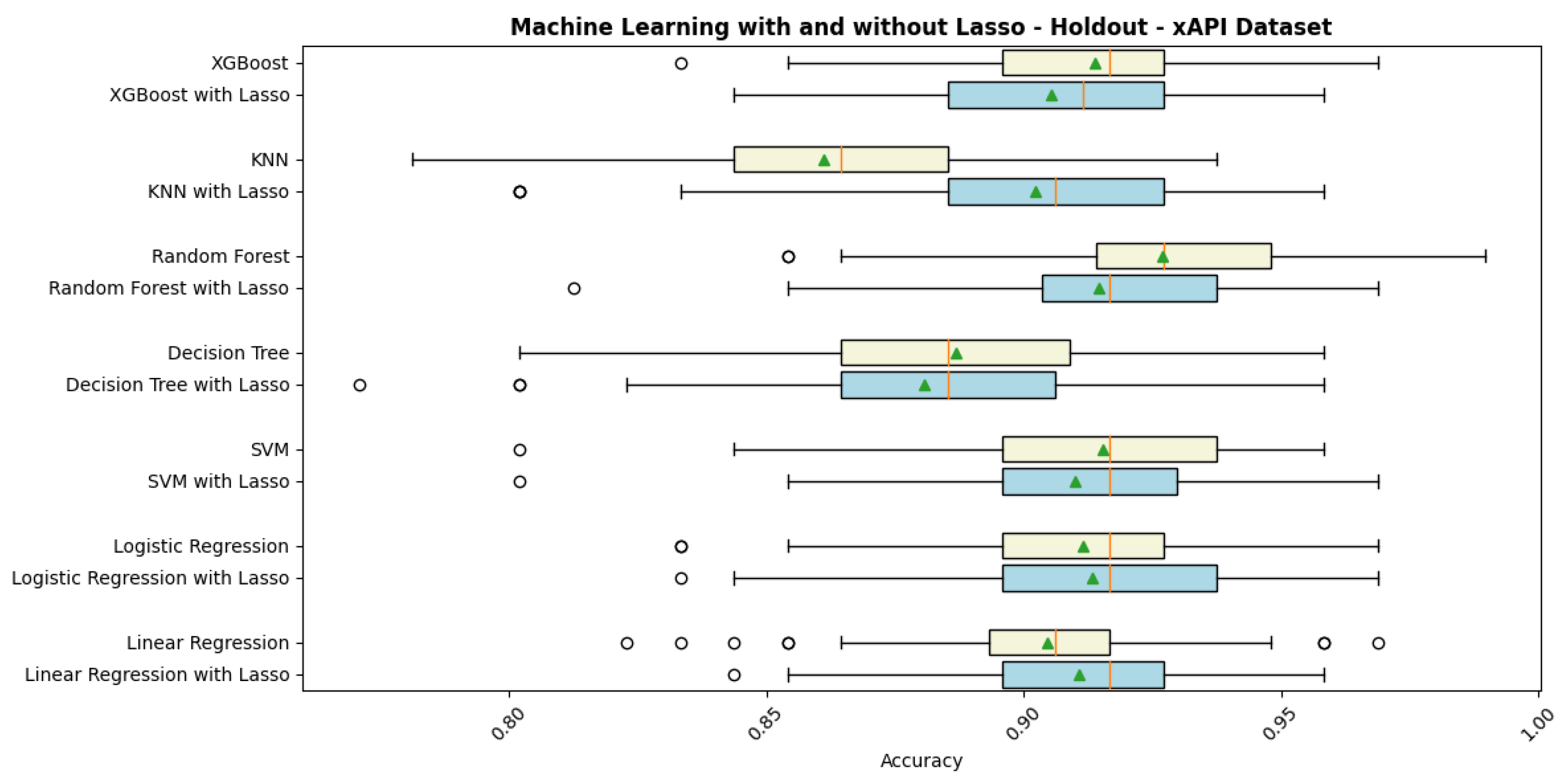

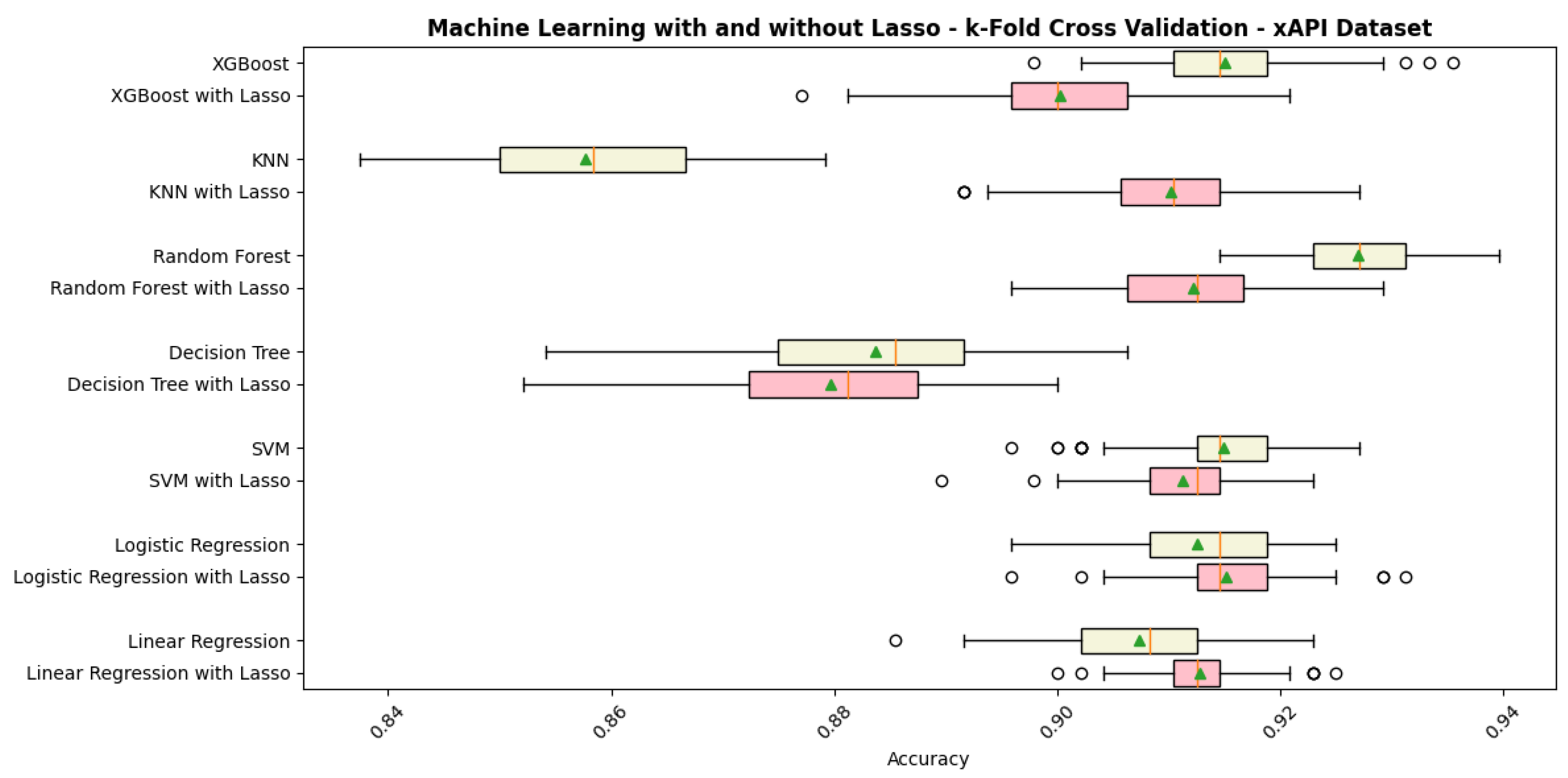
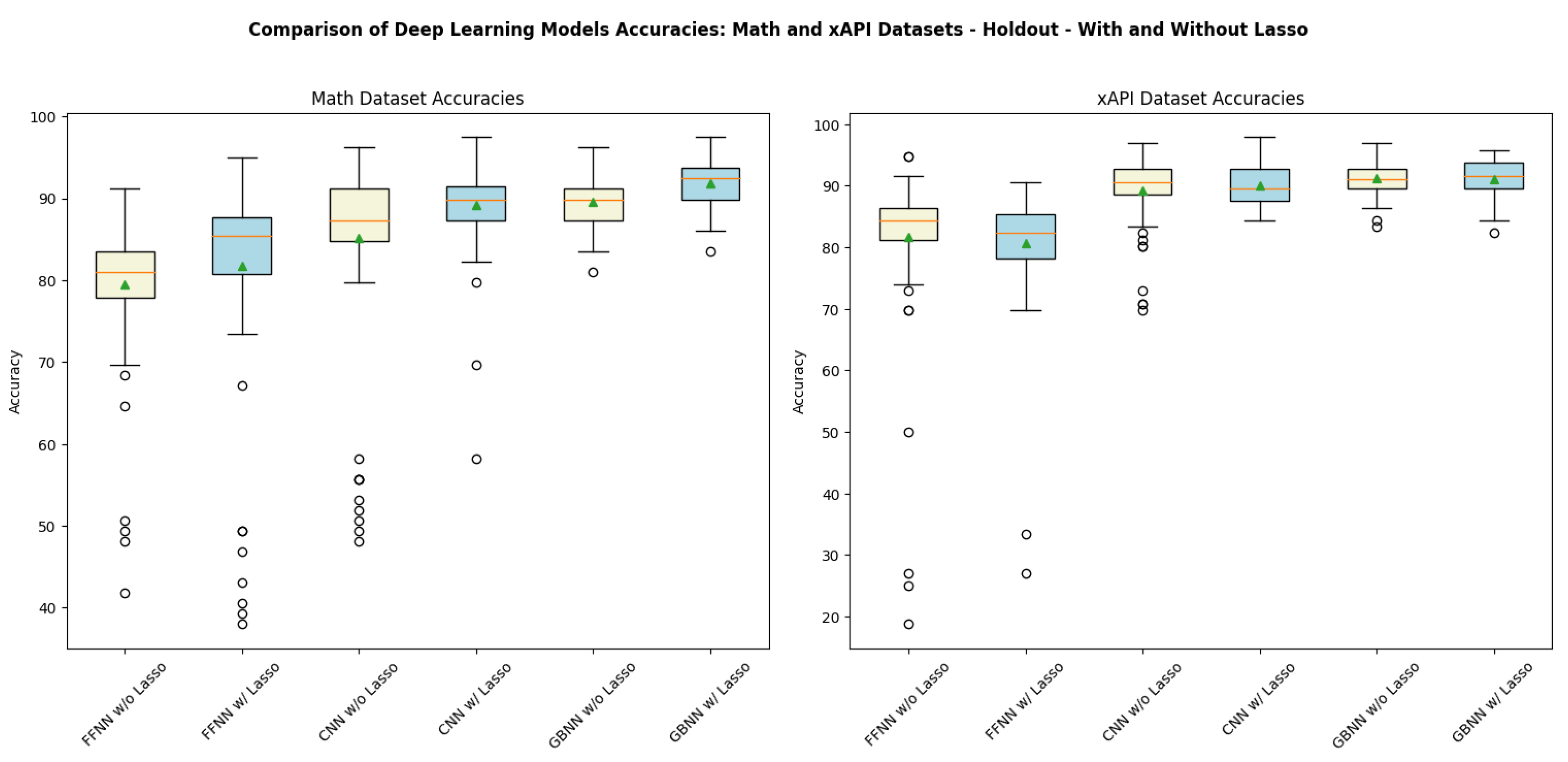
| Machine Learning Model | Without Lasso (Math) | With Lasso (Math) | Without Lasso (xAPI) | With Lasso (xAPI) |
|---|---|---|---|---|
| Decision Tree | 89.62% | 89.65% | 88.69% | 88.07% |
| kNN | 73.05% | 82.41% | 86.10% | 90.23% |
| Linear Regression | 87.80% | 89.46% | 90.47% | 91.07% |
| Logistic Regression | 89.94% | 91.54% | 91.15% | 91.34% |
| Random Forest | 93.58% | 92.87% | 92.69% | 91.46% |
| SVM | 87.30% | 89.85% | 91.53% | 91.00% |
| XGBoost | 93.49% | 92.10% | 91.37% | 90.54% |
| Machine Learning Model | Math Dataset | xAPI Dataset | ||
|---|---|---|---|---|
| Without Lasso | With Lasso | Without Lasso | With Lasso | |
| Decision Tree | 89.94% | 89.49% | 88.36% | 87.96% |
| kNN | 73.44% | 83.48% | 85.77% | 91.01% |
| Linear Regression | 87.75% | 89.27% | 90.73% | 91.28% |
| Logistic Regression | 89.94% | 91.39% | 91.26% | 91.51% |
| Random Forest | 93.82% | 92.94% | 92.70% | 91.22% |
| SVM | 87.59% | 89.98% | 91.49% | 91.12% |
| XGBoost | 93.53% | 91.94% | 91.51% | 90.03% |
| Deep Learning Model | Math Dataset | xAPI Dataset | ||
|---|---|---|---|---|
| Without Lasso | With Lasso | Without Lasso | With Lasso | |
| CNN | 85.15% | 89.13% | 89.28% | 90.09% |
| FFNN | 79.49% | 81.76% | 81.67% | 80.72% |
| GBNN | 89.52% | 91.87% | 91.18% | 91.08% |
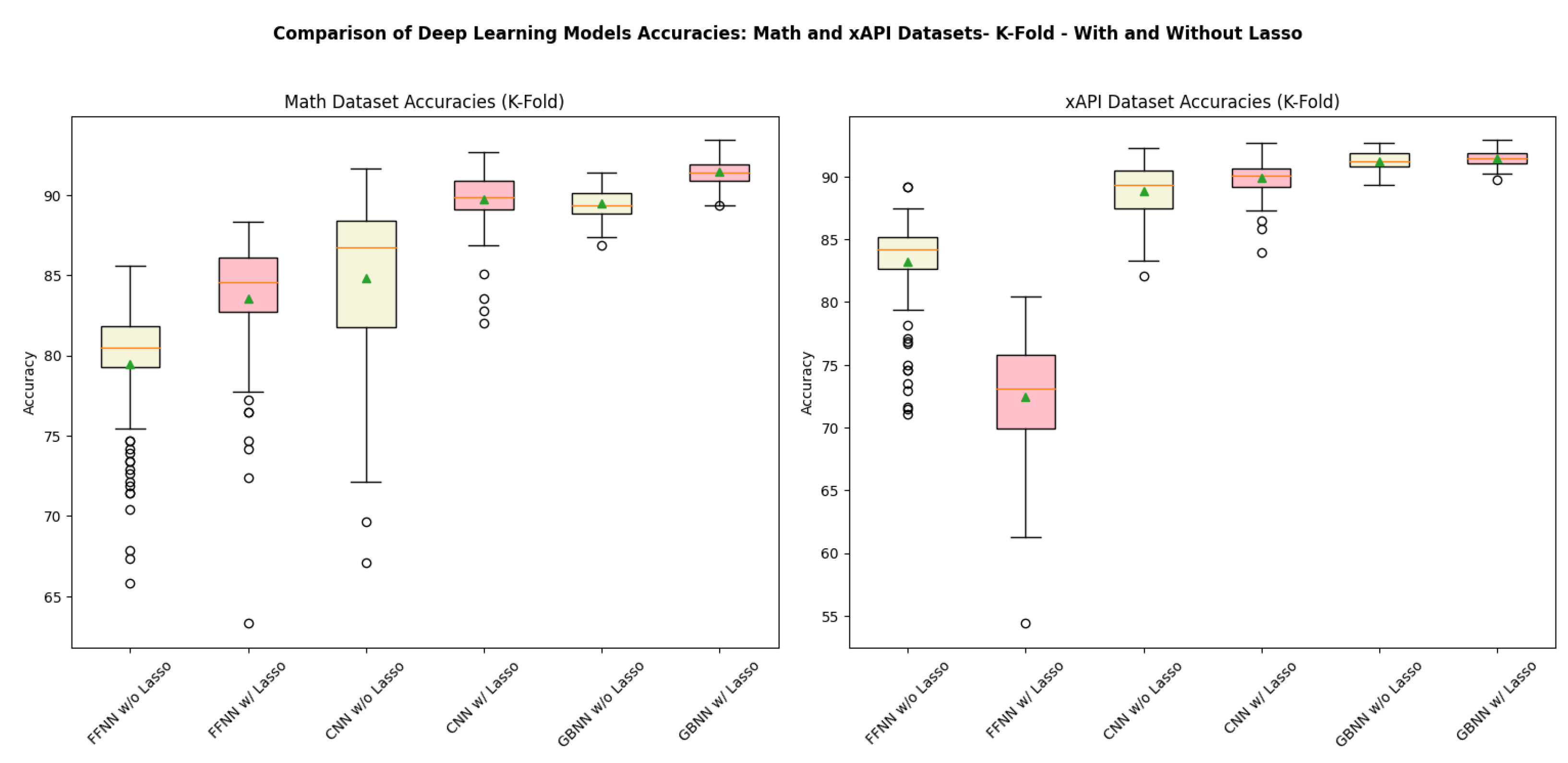
| Deep Learning Model | Math Dataset | xAPI Dataset | ||
|---|---|---|---|---|
| Without Lasso | With Lasso | Without Lasso | With Lasso | |
| CNN | 84.84% | 89.71% | 88.88% | 89.90% |
| FFNN | 79.48% | 83.56% | 83.23% | 72.46% |
| GBNN | 89.51% | 91.43% | 91.21% | 91.44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhood, H.; Joudah, I.; Beheshti, A.; Muller, S. Evaluating and Enhancing Artificial Intelligence Models for Predicting Student Learning Outcomes. Informatics 2024, 11, 46. https://doi.org/10.3390/informatics11030046
Farhood H, Joudah I, Beheshti A, Muller S. Evaluating and Enhancing Artificial Intelligence Models for Predicting Student Learning Outcomes. Informatics. 2024; 11(3):46. https://doi.org/10.3390/informatics11030046
Chicago/Turabian StyleFarhood, Helia, Ibrahim Joudah, Amin Beheshti, and Samuel Muller. 2024. "Evaluating and Enhancing Artificial Intelligence Models for Predicting Student Learning Outcomes" Informatics 11, no. 3: 46. https://doi.org/10.3390/informatics11030046
APA StyleFarhood, H., Joudah, I., Beheshti, A., & Muller, S. (2024). Evaluating and Enhancing Artificial Intelligence Models for Predicting Student Learning Outcomes. Informatics, 11(3), 46. https://doi.org/10.3390/informatics11030046






