Information-Theoretic Measures and Modeling Stock Market Volatility: A Comparative Approach
Abstract
1. Introduction
2. Methodology
2.1. Volatility
2.2. GARCH Models
- The process is called GARCH (p, q) process if and ;
- The random variables are identical and independent, is the residual series and its conditional variance;
- , are real parameters and ensures that at all times.
- where and. and represent sign effect and leverage effect;
- For leverage effect must be statistically significant and negative;
- Returns are stationary if and EGARCH captures serial dependence and leverage effects in returns;
- If is small, then decreases. For large , the value of increases;
- Due to log-transformation of variance, it guarantees positivity of variance without any restriction on parameters.
- where andindicates asymmetry of returns;
- assumes value equals to 1 for (negative-shock), and zero otherwise;
- For positive and significant , leverage effect exists.
- where are real parameters;
- The variable is strictly positive and denotes the conditional standard deviation of ;
- The current volatility depends on both the modulus and the sign of the past returns through and ;
- For 0, the effect of the bad news is greater than those of the good news;
- The GJR-GARCH model due to Glosten et al. (1993) is a version of TGARCH, which corresponds to squaring the variables involved in Equation (8).
Conditional Distributions and GARCH Modeling
- whereand are location, scale, and shape parameters, respectively, and is a Gamma function.
- where are location and scale parameters, respectively, and represents the tail-thickness parameter;
- For the distribution converges to the standard normal distribution, and for , it has thicker tails than the normal distribution.
- where denoted skewness and shape parameters, respectively. For negative skewness , and for positive skewness . The parameter ;
- For the skewed-GED distribution converges to the GED;
- The sign function equals to −1 for negative values of its argument and equals to 1 for positive values;
- The values of , and
- where denotes the asymmetry coefficient, are mean and the standard deviation, respectively.
- The density is skewed to the right if and skewed to the left if .
2.3. Information Theoretic Measures and Volatility Modeling
2.3.1. Shannon Entropy Measure
- where, the convention holds, and , represents the probability of , for . therefore, and
- The entropy reaches to its maximum value if all events follow the equally likely assumption;
- The entropy corresponding to an event with probability less than one has a positive sign.
- (1)
- Maximum Likelihood (ML);
- (2)
- effreys: Bayesian estimate with a = 1/2;
- (3)
- Laplace: Bayesian estimate with a = 1;
- (4)
- Schurmann–Grassberger (SG): Bayesian estimate with a = 1/(length of underlying asset prices series);
- (5)
- Minimax with a = sqrt (sum (underlying asset prices series))/(length of underlying asset prices series);
- (6)
- Shrink entropy: Uses James–Stein-type shrinkage at the level of cell frequencies.
2.3.2. Tsallis Entropy
- where and Rare events of interests denote , and frequently encountered have ;
- The q-exponential function , whose inverse is the q-logarithmic function ;
- Gell-Mann and Tsallis (2004) suggested q1.4 for high-frequency financial returns;
- The value of the parameter q decreases to 1 as the frequency of the data decreases. The values emphasize highly volatile signals.
2.3.3. Approximate and Sample Entropy
- Suppose the underlying time series, of length ;
- For , let and be two vectors of length and denotes distance between the two vectors. Therefore,
- Two vectors and are called similar if , where denotes the specified tolerance. Now compute the relative frequency for each of the .
- where denote number of vectors similar to for a fixed and Now computing the average frequency
- Finally, ApEn can be computed by using the following statistics.
- where denotes number of vectors pairs of length and with ;
- denotes total number of templates equals to length with
3. Empirical Analysis
3.1. Stationarity and Normality Tests
3.2. Testing the ARCH Effect
3.3. Volatility Estimation Using GARCH Models
3.4. Volatility Assessment Using Shannon and Tsallis Entropy
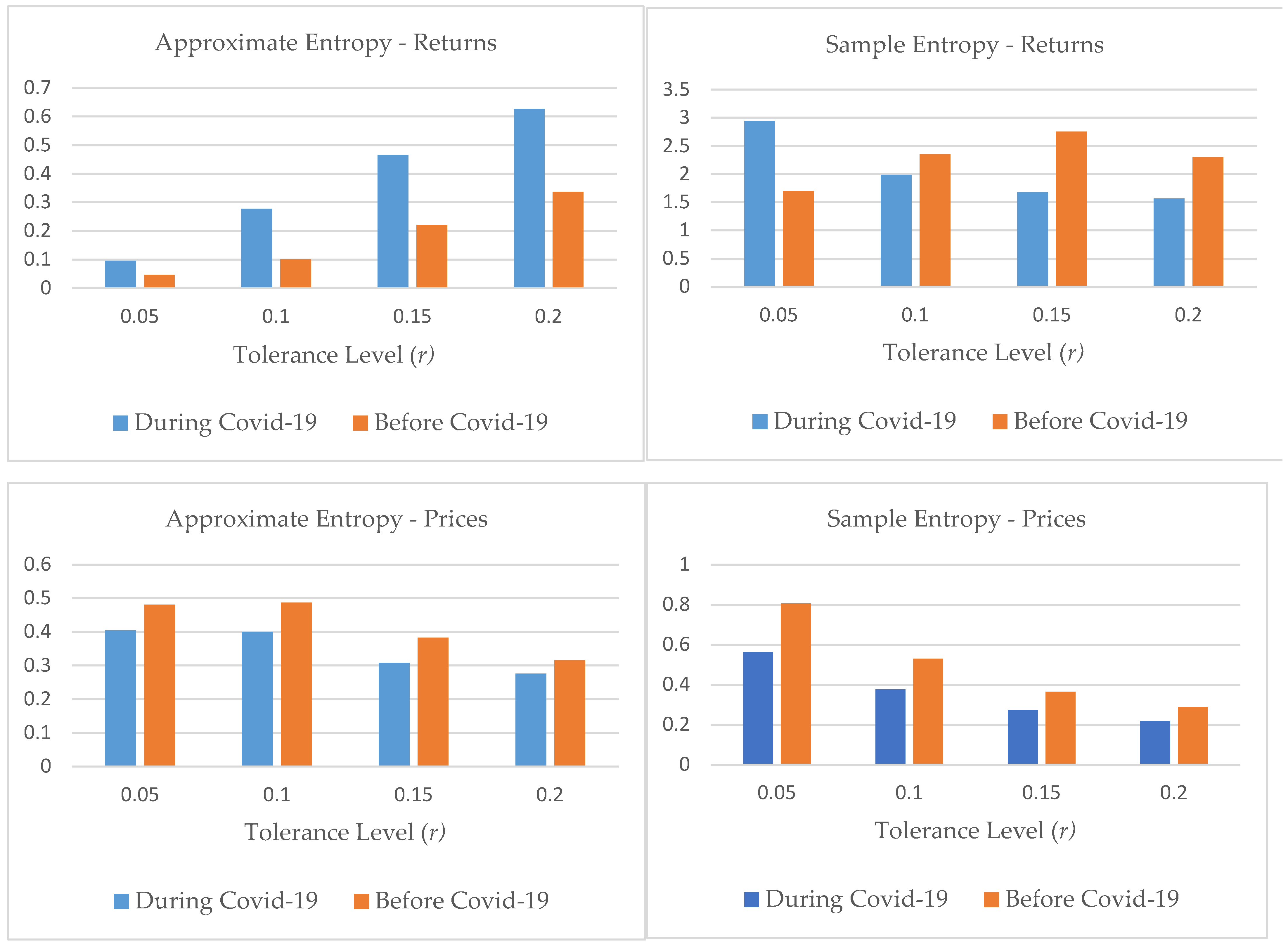
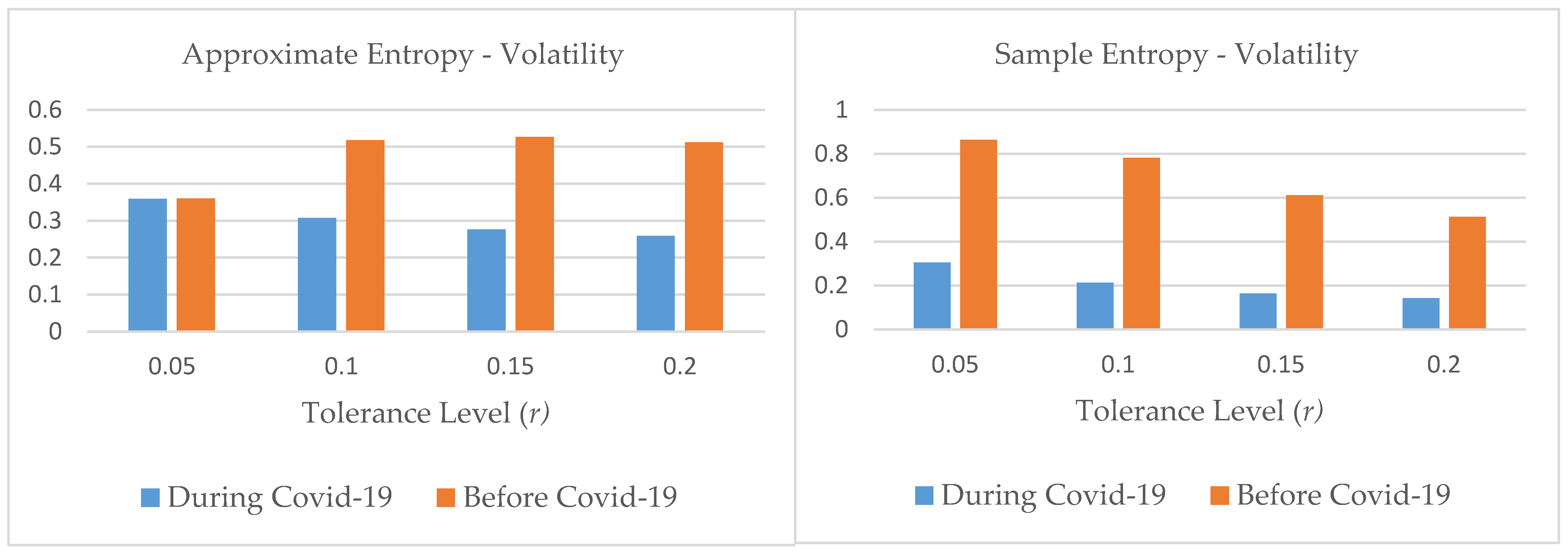
3.5. Regularity and Randomness Using Approximate Entropy and Sample Entropy
4. Discussion and Conclusions
- Both best-fitted models suggested the remarkable existence of the leverage effect in the Pakistan Stock Exchange;
- A high variation in the estimated volatility of the pandemic period has observed, and extreme downturns in prices are expected;
- The behavior of the variance is asymmetric for PSX-100 closing returns of both examined periods;
- The GARCH volatility modeling shows a usual behavior of the Pakistani market response towards bad news.
- We have pointed out that no remarkable difference between the randomness of volatility series before and during the COVID-19 pandemic, based on Shannon and Tsallis entropy estimates;
- All values of entropies are positive on both periods, and volatility shows non-linear dynamics;
- The overall relative difference of estimated entropies is not significant;
- The overall relative difference of estimated entropies is not significant under both the Shannon and Tsallis entropies;
- In the case of closing prices of the PSX-100, the Shannon entropy shows almost similar behavior under all estimation methods;
- In the case of ApEn and SampEn, the market shows mixed behavior, and the results are more sensitive. The sample entropy results reported more randomness in the pre-pandemic period for the Pakistani Stock Market. We detected both entropies are very sensitive to the selection of parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model | LOGLIK. | BIC | SIC | HQIC | AIC |
|---|---|---|---|---|---|
| Student T | |||||
| GJRGARCH | 745.2045 | −5.9935 | −5.8795 | −5.9956 | −5.9476 |
| EGARCH | 741.4358 | −5.9629 | −5.8489 | −5.9649 | −5.917 |
| TGARCH | 740.9011 | −5.9585 | −5.8446 | −5.9606 | −5.9126 |
| Asymmetric Student T | |||||
| GJRGARCH | 746.4149 | −5.9952 | −5.867 | −5.9978 | −5.9436 |
| EGARCH | 742.1684 | −5.9607 | −5.8325 | −5.9633 | −5.9091 |
| TGARCH | 741.6314 | −5.9564 | −5.8281 | −5.9589 | −5.9047 |
| Generalized Error | |||||
| GJRGARCH | 745.4326 | −5.9954 | −5.8814 | −5.9974 | −5.9495 |
| EGARCH | 742.1894 | −5.969 | −5.855 | −5.971 | −5.9231 |
| TGARCH | 741.8362 | −5.9661 | −5.8522 | −5.9682 | −5.9202 |
| Skewed GED | |||||
| GJRGARCH | 746.4959 | −5.9959 | −5.8677 | −5.9985 | −5.9443 |
| EGARCH | 742.675 | −5.9648 | −5.8366 | −5.9674 | −5.9132 |
| TGARCH | 742.3509 | −5.9622 | −5.834 | −5.9648 | −5.9106 |
| Model | LOGLIK. | BIC | SIC | HQIC | AIC |
|---|---|---|---|---|---|
| Student T | |||||
| GJRGARCH | 611.1641 | −6.1547 | −6.0209 | −6.1579 | −6.1006 |
| EGARCH | 611.0953 | −6.1438 | −5.9933 | −6.1478 | −6.0829 |
| TGARCH | 611.8439 | −6.1617 | −6.0279 | −6.1648 | −6.1075 |
| Asymmetric Student T | |||||
| GJRGARCH | 612.1173 | −6.1543 | −6.0037 | −6.1582 | −6.6851 |
| EGARCH | 615.0001 | −6.1939 | −6.0601 | −6.197 | −6.1075 |
| TGARCH | 614.4997 | −6.1786 | −6.028 | −6.1825 | −6.0933 |
| Generalized Error | |||||
| GJRGARCH | 616.2783 | −6.2069 | −6.0731 | −6.2101 | −6.1075 |
| EGARCH | 616.9883 | −6.204 | −6.0534 | −6.2079 | −6.0933 |
| TGARCH | 612.136 | −6.1647 | −6.0309 | −6.1678 | −6.1397 |
| Skewed GED | |||||
| GJRGARCH | 612.2701 | −6.1558 | −6.0053 | −6.1598 | −6.0933 |
| EGARCH | 612.6194 | −6.1696 | −6.0358 | −6.1727 | −6.1397 |
| TGARCH | 613.2739 | −6.1661 | −6.0155 | −6.1700 | −6.1176 |
References
- Abdalla, Suliman Zakaria Suliman, and Zakaria Suliman. 2012. Modelling stock returns volatility: Empirical evidence from Saudi Stock Exchange. International Research Journal of Economics 85: 166–79. [Google Scholar]
- Ahmed, Nawaz, Rizwan Raheem Ahmed, Jolita Vveinhardt, and Dalia Streimikiene. 2016. Empirical analysis of stock returns and volatility: Evidence from Asian stock market. Technological and Economic Development of Economy 22: 808–29. [Google Scholar]
- Ahn, Kwangwon, Daeyong Lee, Sungbin Sohn, and Biao Yang. 2019. Stock Market Uncertainty and Economic Fundamental: An Entropic Based Approach. Quantitative Finance 19: 1151–63. [Google Scholar] [CrossRef]
- Alamgir, Farzana, and Sakib Bin Amin. 2021. The nexus between oil price and stock market: Evidence from South Asia. Energy Reports 7: 693–703. [Google Scholar] [CrossRef]
- Ali, Rizwan, Inayat Ullah Mangla, Ramiz Ur Rehman, Wuzhao Xue, Muhammad Akram Naseem, and Muhammad Ishfaq Ahmad. 2020. Exchange rate, gold price, and stock market nexus: A quantile regression approach. Risks 8: 86. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2001. The distribution of realized exchange rate volatility. Journal of American Statistical Association 96: 42–57. [Google Scholar] [CrossRef]
- Aruga, Kentaka. 2021. Changes in human mobility under the COVID-19 pandemic and the Tokyo fuel market. Journal of Risk and Financial Management 14: 163. [Google Scholar] [CrossRef]
- Bali, Turan G, and Panayiotis Theodossiou. 2006. A Conditional-SGT-VaR Approach with alternative GARCH models. Annals of Operations Research 151: 241–67. [Google Scholar] [CrossRef]
- Bartiromo, Rosario. 2010. Shared information in the stock market. Quantitative Finance 11: 229–35. [Google Scholar] [CrossRef]
- Bentes, Sonia R., and Rui Menezes. 2012. Entropy A New Measure of Stock Market Volatility. Journal of Physics: Conference Series 394: 012033. [Google Scholar] [CrossRef]
- Bhowmik, Roni, and Shouyang Wang. 2020. Stock market volatility and return analysis: A systematic literature review. Entropy 22: 522. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–327. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. A conditionally heteroskedastic time series model for speculative prices and rates of return. Review of Economics and Statistics 69: 542–47. [Google Scholar] [CrossRef]
- Cao, Charles Q., and Ruey S. Tsay. 1992. Nonlinear time-series analysis of stock volatilities. Journal of Applied Econometrics 7: S165–S185. [Google Scholar] [CrossRef]
- Chkili, Walid, Chaker Aloui, and Duc K. Nguyen. 2012. Asymmetric effects and long memory in dynamic volatility relationships between stock returns and exchange rates. Journal of International Financial Markets, Institutions and Money 22: 738–57. [Google Scholar] [CrossRef]
- Darbellay, Georges A., and Diethelm Wuertz. 2000. The entropy as a tool for analyzing statistical dependence in financial time series. Physica A 287: 429–39. [Google Scholar] [CrossRef]
- Dhanaiah, Gangineni, and Siviram R. Prasad. 2017. Volatility and co-movement models: A literature review and synthesis. International Journal of Engineering Management Research 7: 1–25. [Google Scholar]
- Ding, Zhuanxin, Clive WJ Granger, and Robert F. Engle. 1993. A long memory property of stock market returns and a new model. Journal of Empirical Finance 1: 83–106. [Google Scholar] [CrossRef]
- Engle, Robert.F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Fan, Ying, Yu-Jun Zhang, Hsein-Tang Tsai, and Yi-Ming Wei. 2008. Estimating ‘value at risk’ of crude oil price and its spillover effect using the ged-garch approach. Energy Economics 30: 3156–71. [Google Scholar] [CrossRef]
- Figlewski, Stephen. 1997. Forecasting volatility. Financial Markets, Institutions, and Instruments 6: 1–88. [Google Scholar] [CrossRef]
- Figlewski, Stephen, and Clifton T. Green. 1999. Market risk and model risk for a financial institution writing options. Journal of Finance 54: 1465–999. [Google Scholar] [CrossRef]
- Francq, Christian, and Jean-Michel Zakoian. 2010. GARCH Models:Structure, Statistical Inferences and Financial Applications. West Sussex: Wiley. [Google Scholar]
- Gell-Mann, Murray, and Constantino Tsallis. 2004. Nonextensive Entropy: Interdisciplinary Applications. Oxford: Oxford University Press. [Google Scholar]
- Gençay, Ramaza, and Nikola Gradojevic. 2008. Overnight interest rates and aggregate market expectations. Economic Letters 100: 27–30. [Google Scholar]
- Gençay, Ramazan, and Nikola Gradojevic. 2010. Crash of 087—Was it expected? Aggregate market fears and long-range dependence. Journal of Empirical Finance 17: 270–82. [Google Scholar] [CrossRef]
- Gençay, Ramaza, and Nikola Gradojevic. 2017. The Tale of Two Financial Crises: An Entropic Perspective. Entropy 19: 244. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Gosset, William Sealy. 1908. The probable error of a mean. Biometrika 6: 1–25. [Google Scholar]
- Gulko, Less. 1999. The entropy theory of stock option pricing. International Journal of Theoretical and Applied Finance 2: 331–55. [Google Scholar] [CrossRef]
- Harrison , Barry, and Winston R. Moor. 2012. Forecasting stock market volatility in central and eastern European countries. Journal of Forecasting 31: 490–503. [Google Scholar] [CrossRef]
- Hansen, Bruce E. 1994. Autoregressive conditional density estimation. International Economic Review 35: 705–30. [Google Scholar] [CrossRef]
- Hussain, Sartaj, Bhanu K. V. Murthy, and Amit Kumar Singh. 2019. Stock market volatility: A review of the empirical literature. IUJ Journal of Management 7: 96–105. [Google Scholar]
- Joyo, Ahmed Shafique, and Lin Lefin Lin. 2019. Stock Market Integration of Pakistan with Its Trading Partners: A Multivariate DCC-GARCH Model Approach. Sustainability 11: 303. [Google Scholar] [CrossRef]
- Kolmogorov, Andrei Nikolaevich. 1958. A New Metric Invariant of Transient Dynamical Systems and Automorphisms in Lebesgue Spaces. Doklady Akademii Nauk, Russian Academy of Sciences: Moscow, Russai 119: 861–64. [Google Scholar]
- Lahmiri, Salim, and Stelios Bekiros. 2020a. Randomness, Informational Entropy, and Volatility Interdependencies among the Major World Markets: The Role of the COVID-19 Pandemic. Entropy 22: 833. [Google Scholar] [CrossRef] [PubMed]
- Lahmiri, Salim, and Stelios Bekiros. 2020b. Nonlinear analysis of Casablanca Stock Exchange, Dow Jones and S&P500 industrial sectors with a comparison. Physica A 539: 122923. [Google Scholar]
- Lambert, Philippe, and Sebastien Laurent. 2001. Modleing Financial Time Series Using Garch-Type Models and a Skewed-Student t-Density. Ottignies-Louvain-la-Neuve: Universit’e Catholique de Louvain, Institut de Statistique. [Google Scholar]
- Lee, Gary G. J., and Robert F. Engle. 1999. A permanent and transitory component model of stock return volatility. In Cointegration Causality and Forecasting A Festschrift in Honor of Clive WJ Granger. New York: Oxford University Press, pp. 475–97. [Google Scholar]
- Liu, Zhifeng, Toan Luu Duc Huynh, and Peng-Fei Dai. 2021. The impact of COVID-19 on the stock market crash risk in China. Research in international Business and Finance 57: 101419. [Google Scholar] [CrossRef]
- Mabrouk, Samir, and Samir Saadi. 2012. Parametric value-at-risk analysis: Evidence from stock indices. The Quarterly Review of Economics and Finance 52: 305–321. [Google Scholar] [CrossRef]
- Mandelbort, Benoit. 1963. The Variation of Certain Speculative Prices. The Journal of Business 36: 394–419. [Google Scholar] [CrossRef]
- McMillan, David N., Alan Speight, and Owain Apgwilym. 2000. Forecasting UK stock market volatility. Applied Financial Economics 10: 435–48. [Google Scholar] [CrossRef]
- Mensi, Walid. 2013. Ranking efficiency for twenty-six emerging stock markets and financial crisis: Evidence from the Shannon entropy approach. International Journal of Management Science and Engineering 7: 53–63. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Economics 59: 347–70. [Google Scholar] [CrossRef]
- Ng, Hock Guan, and Michael McAleer. 2004. Recursive modelling of symmetric and asymmetric volatility in the presence of extreme observations. International Journal of Forecasting 20: 115–29. [Google Scholar] [CrossRef]
- Okicic, Jasmina. 2015. An empirical analysis of stock returns and volatility: The case of stock markets from Central and Eastern Europe and South East. European Journal of Economics Business 9: 7–15. [Google Scholar] [CrossRef]
- Ong, Marcus A. 2015. An information theoretic analysis of stock returns, volatility and trading volumes. Applied Economics 47: 3891–906. [Google Scholar] [CrossRef]
- Patev, Plamen, and Nigokhos Kanaryan. 2008. Stock Market Volatility Changes in Central Europe Caused by Asian and Russian Crisis. International Journal of Economic Research 5: 13–35. [Google Scholar]
- Pele, Daniel Traian, Emese Lazar, and Alfonso Dufour. 2017. Information entropy and measure of market risk. Entropy 19: 226. [Google Scholar] [CrossRef]
- Pincus, Steven M. 1991. Approximate entropy as a measure of system complexity. Proceedings of the National Academy of Sciences of the United States of America 88: 2297–301. [Google Scholar] [CrossRef]
- Pincus, Steve M. 2008. Approximate Entropy as an Irregularity Measure for Financial Data. Econometric Reviews 27: 329–62. [Google Scholar] [CrossRef]
- Poon, Ser-Huang, and Clive Granger. 2005. Practical issues in forecasting volatility. Financial Analysts Journal 61: 45–56. [Google Scholar] [CrossRef]
- Preda, Vasile, and Costel Balcau. 2010. Entropy Optimization with Applications. Bucharest: The Publishing House of the Romanian Academy. [Google Scholar]
- Preda, Vasile, and Muhammad Sheraz. 2015. Risk-neutral densities in entropy theory of stock options using Lambert function and a new approach. Proceedings of The Romanian Academy Series A 16: 20–27. [Google Scholar]
- Preda, Vasile, Silvia Dedu, and Muhammad Sheraz. 2014. New measure selection for Hunt-Devolder semi-Markov regime switching interest rate models. Physica A: Statistical Mechanics and Its Applications 407: 350–59. [Google Scholar] [CrossRef]
- Rényi, Alfred. 1961. On measures of entropy and information. In Proceedings of the 4th Berkely Sympodium on Mathematics of Statistics and Probability. Berkeley: University of California Press, vol. 1, pp. 547–61. [Google Scholar]
- Ribeiro, Maria, Teresa Henriques, Luísa Castro, André Souto, Luís Antunes, Cristina Costa-Santos, and Andreia Teixeira. 2021. The entropy Universe. Entropy 23: 222. [Google Scholar] [CrossRef] [PubMed]
- Richman, Joshua S., and J. Randall Moorman. 2000. Physiological time-series analysis using approximate entropy and sample entropy. American Journal of Physiology Heart and Circulatory Physiology 278: 2039–49. [Google Scholar] [CrossRef]
- Shannon, Claude E. 1948. A mathematical theory of communication. The Bell System Technical Journal 27: 379–423. [Google Scholar] [CrossRef]
- Sheraz, Muhammad, Silvia Dedu, and Vasile Preda. 2015. Entropy measures for assessing volatile markets. Procedia Economics and Finance 22: 655–62. [Google Scholar] [CrossRef]
- Sheraz, Muhammad, Vasile Preda, and Silvia Dedu. 2019. Non-Extensive Minimal Entropy Martingale Measures, and semi-Markov Regime Switching Interest Rate Modeling. AIMS Mathematics 5: 300–10. [Google Scholar] [CrossRef]
- Szczygielski, Jan Jakub, Princess Rutendo Bwanya, Ailie Charteris, and Janusz Brzeszczyński. 2021. The only certainty is uncertainty: An analysis of the impact of COVID-19 uncertainty on regional stock markets. Finance Research Letters, 101945. [Google Scholar] [CrossRef] [PubMed]
- Tapiero, Oren J. 2013. The relationship between risk and incomplete states uncertainty: A Tsallis entropy perspective. Algorithmic Finance 2: 141–50. [Google Scholar] [CrossRef]
- Taylor, Stephen J. 1986. Modelling Financial Time Series. Chichester: John Wiley & Sons Ltd. [Google Scholar]
- Taylor, Stephen J. 1987. Forecasting of the volatility of currency exchange rates. International Journal of Forecasting 3: 159–70. [Google Scholar] [CrossRef]
- Taylor, James W. 2004. Volatility forecasting with smooth transition exponential smoothing. International Journal of Forecasting 20: 273–86. [Google Scholar] [CrossRef]
- Toma, Aida. 2014. Model selection criteria using divergences. Entropy 16: 2686–98. [Google Scholar] [CrossRef]
- Topcu, Mert, and Omer Serkan Gulal. 2020. The impact of COVID-19 on emerging stock markets. Finance Research Letters 36: 101691. [Google Scholar] [CrossRef]
- Tsallis, Constantino. 1988. Possible generalization of Boltzmann-Gibbs statistics. Journal of Statistical Physics 52: 479–87. [Google Scholar] [CrossRef]
- Umar, Muhammad, Nawazish Mirza, Syed Kumail Abbas Rizvi, and Mehreen Furqan. 2021. Asymmetric Volatility Structure of Equity Returns: Evidence from an Emerging Market. The Quarterly Review of Economics and Finance. [Google Scholar] [CrossRef]
- Waheed, Rida, Suleman Sarwer, Sahar Sarwer, and Muhammad Kaleem Khan. 2020. The impact of COVID-19 on Karachi stock exchange: Quantileon-quantile approach using secondary and predicted data. Journal of Public Affairs 20: e2290. [Google Scholar] [CrossRef] [PubMed]
- Wiśniewska, Małgorzata, and Agnieszka Wyłomańska. 2017. A Garch process with ged distribution. In Cyclostationarity: Theory and Methods. Cham: Springer, vol. III, pp. 83–103. [Google Scholar]
- Xu, Libo. 2021. Stock Return and the COVID-19 pandemic: Evidence from Canada and the US. Finance Research Letters 38: 101872. [Google Scholar] [CrossRef]
- Yentes, Jennifer M., Nathaniel Hunt, Kendra K. Schmid, Jeffrey P. Kaipust, Denise McGrath, and Nicholas Stergiou. 2012. The appropriate use of approximate entropy and sample entropy with short data sets. Annals of Biomedical Engineering 41: 349–65. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar] [CrossRef]
- Zhou, Rongxi, Ru Cai, and Guanqun Tong. 2013. Applications of entropy in finance: A review. Entropy 15: 4909–31. [Google Scholar] [CrossRef]
- Zhu, Dongmin, and Jhon W. Galbraith. 2011. Modeling and forecasting expected shortfall with the generalized asymmetric student-t and asymmetric exponential power distributions. Journal of Empirical Finance 18: 765–78. [Google Scholar] [CrossRef]
- Zimon, Grzegorz, and Hossein Tarighi. 2021. Effects of the COVID-19 global crisis on the working capital management policy: Evidence from Poland. Journal of Risk Financial Management 14: 169. [Google Scholar] [CrossRef]
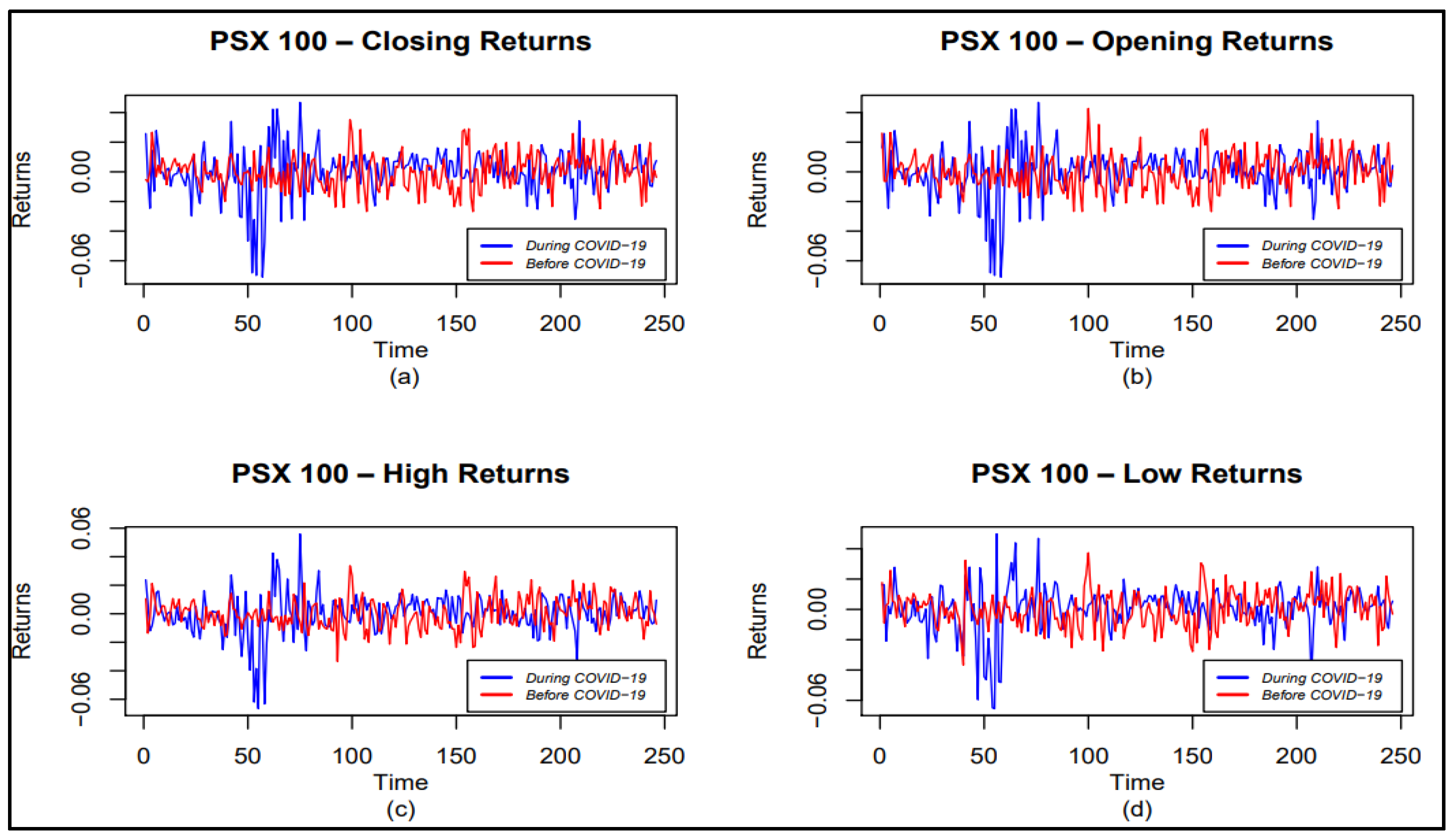
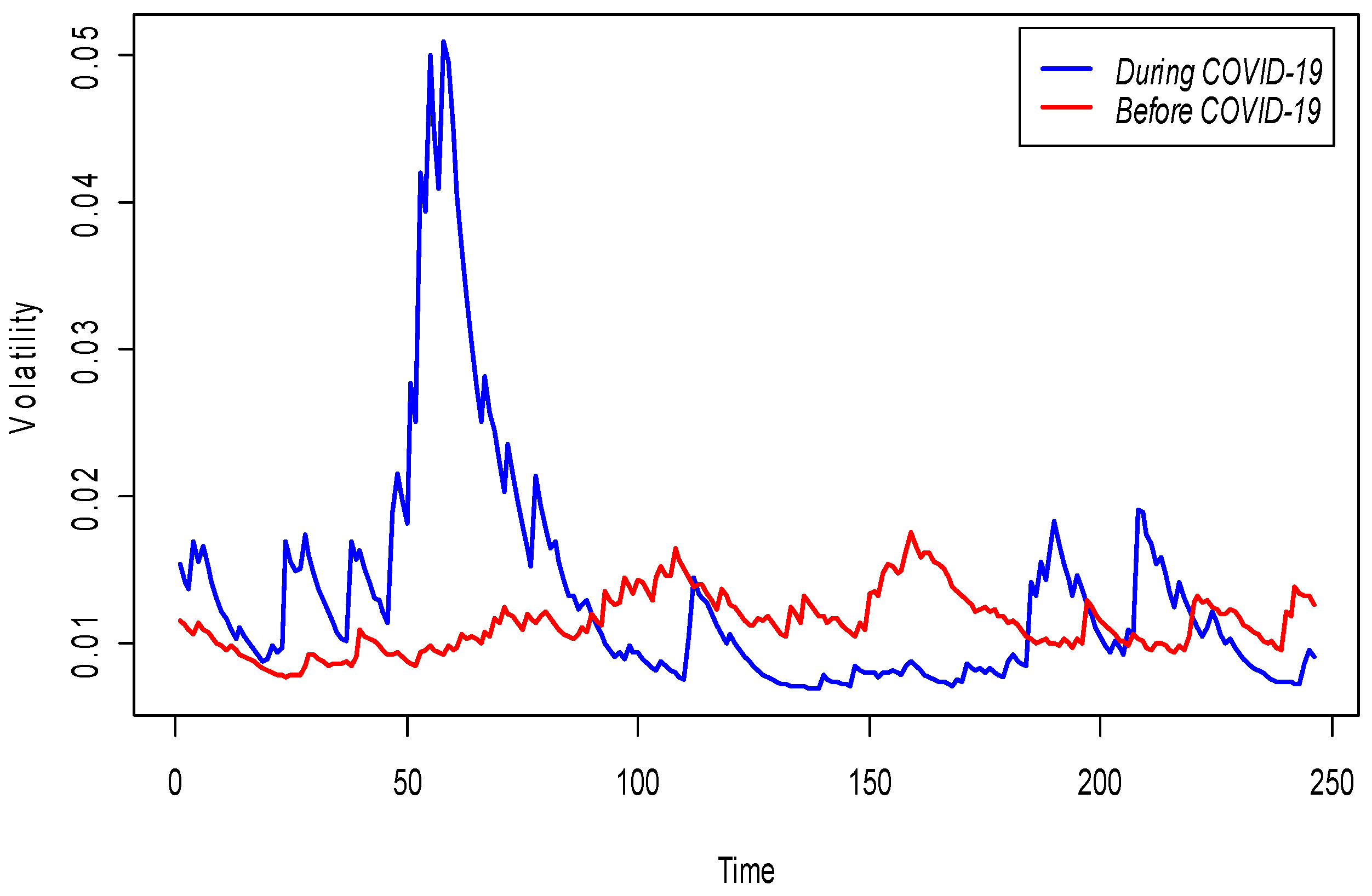
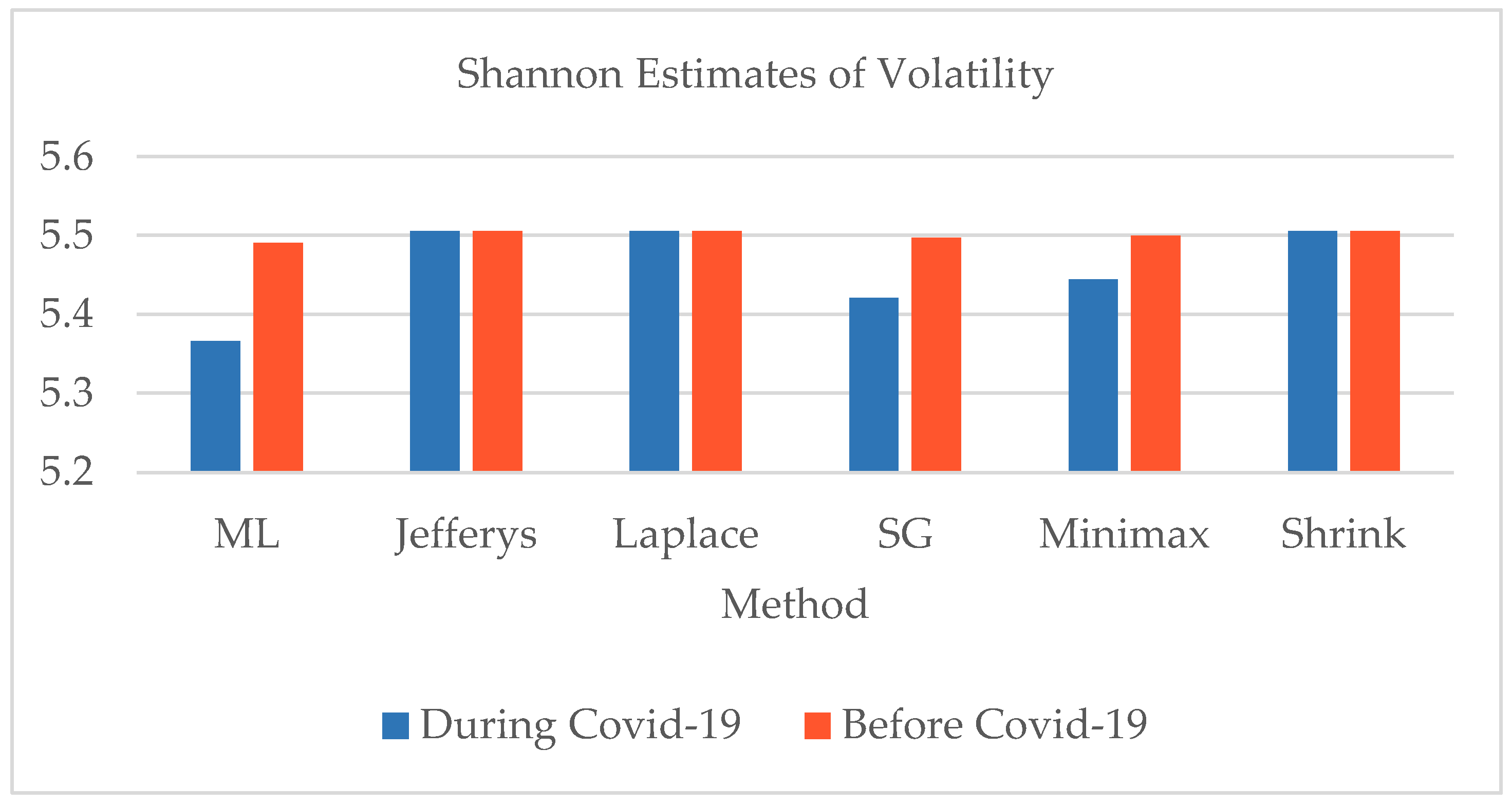
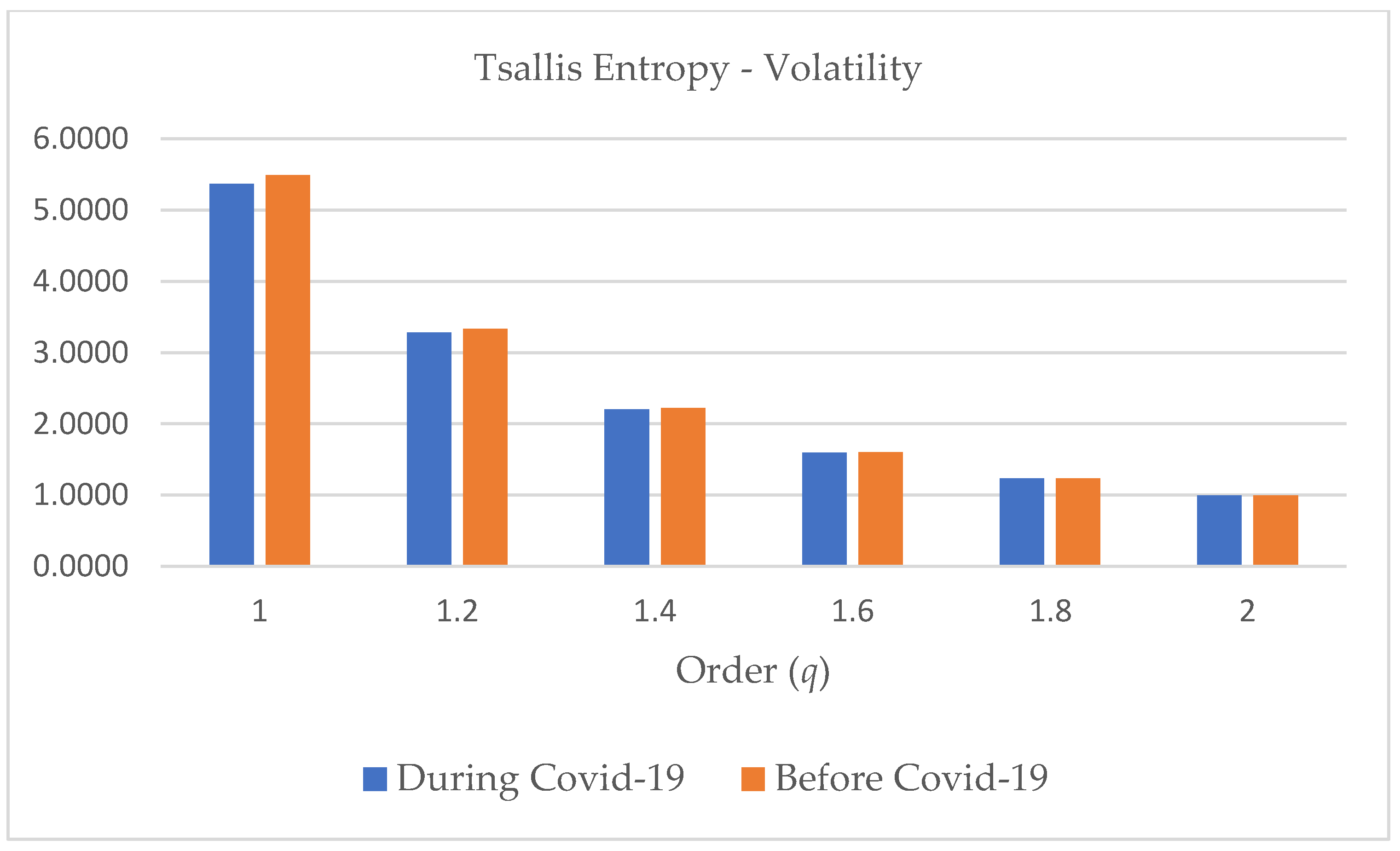
| Returns | Before COVID-19 | COVID-19 | ||||||
|---|---|---|---|---|---|---|---|---|
| Closing | Opening | High | Low | Closing | Opening | High | Low | |
| Minimum | −0.0268 | −0.0268 | −0.0335 | −0.0367 | −0.071 | −0.071 | −0.0666 | −0.0655 |
| 1st Quartile | −0.0071 | −0.0078 | −0.0068 | −0.0065 | −0.0054 | −0.0054 | −0.0064 | −0.0054 |
| Median | 0.0001 | 0.0004 | 0.0001 | 0.0012 | 0.0012 | 0.0012 | 0.0011 | 0.0022 |
| Mean | 0.0003 | 0.0004 | 0.0003 | 0.0004 | 0.0002 | 0.0002 | 0.0002 | 0.0002 |
| 3rd Quartile | 0.0075 | 0.0079 | 0.007 | 0.0075 | 0.0085 | 0.0086 | 0.0075 | 0.0082 |
| Maximum | 0.0351 | 0.0427 | 0.0337 | 0.0374 | 0.0468 | 0.0468 | 0.056 | 0.0498 |
| Skewness | 0.1326 | 0.1736 | 0.1744 | −0.0276 | −1.151 | −1.1479 | −0.9461 | −1.1668 |
| Kurtosis | 3.1178 | 3.206 | 3.3096 | 3.4331 | 8.0603 | 8.0203 | 9.1404 | 7.7247 |
| SD | 0.0116 | 0.0122 | 0.0107 | 0.0118 | 0.0155 | 0.0156 | 0.0138 | 0.0152 |
| CV | 0.0243 | 0.0327 | 0.0282 | 0.0323 | 0.0125 | 0.0147 | 0.0144 | 0.015 |
| Range | 0.0619 | 0.0696 | 0.0672 | 0.0741 | 0.1179 | 0.1179 | 0.1226 | 0.1153 |
| Inter−Quartile range | 0.0145 | 0.0157 | 0.0138 | 0.0141 | 0.0139 | 0.014 | 0.0139 | 0.0136 |
| JB Stats | 0.7971 | 1.5441 | 2.0296 | 1.6715 | 303.1570 | 298.9304 | 404.2784 | 272.5008 |
| Lilliefors Stats | 0.0479 | 0.0336 | 0.0298 | 0.0375 | 0.1281 | 0.1276 | 0.0986 | 0.1193 |
| Pearson Chi Sq. Test | 19.8455 | 10.5772 | 13.3577 | 17.6829 | 66.4959 | 66.1870 | 43.9431 | 70.3577 |
| Period of Variables | Stationary Tests | ARCH Effect | |||
|---|---|---|---|---|---|
| Variable | ADF Stats | Philip Perron Stats | KPSS Stats | LM Stats | LB Stats |
| Closing Returns—Before COVID-19 | −12.9559 (0.0001) | −12.9191 (0.0001) | 0.4042 (0.0753) | 36.728 (0.0002) | 8.3691 (0.0038) |
| Closing Returns—COVID-19 | −13.4422 (0.0100) | −13.7433 (0.0001) | 0.3249 (0.0100) | 73.918 (0.0000) | 5.8386 (0.0157) |
| GJR-GARCH-SGED COVID-19 Period | ||||||||
| mu | ar1 | ma1 | skew | shape | ||||
| 0.0002 (0.0010) | 0.8163 (0.1413) | −0.7490 (0.1661) | 0.0000 (0.0000) | 0.0000 (0.0126) | 0.8222 (0.0312) | 0.2437 (0.0820) | 0.8801 (0.1162) | 1.6361 (0.3015) |
| EGARCH-STD before-COVID-19 Period | ||||||||
| mu | ar1 | ma1 | shape | |||||
| −0.0013 (0.0000) | −0.1308 (0.0000) | 0.3022 (0.0000) | −0.1310 (0.0000) | −0.1792 (0.0000) | 0.9854 (0.0001) | −0.1452 (0.0000) | 18.7972 (0.0030) | |
| Estimation | Volatility | Prices | ||
|---|---|---|---|---|
| Method | COVID-19 | Before COVID-19 | COVID-19 | Before COVID-19 |
| ML | 5.3661 | 5.4902 | 5.5037 | 5.5050 |
| Jeffreys | 5.5052 | 5.5053 | 5.5037 | 5.5050 |
| Laplace | 5.5053 | 5.5053 | 5.5037 | 5.5050 |
| SG | 5.4207 | 5.4971 | 5.5037 | 5.5050 |
| minimax | 5.4439 | 5.4994 | 5.5037 | 5.5050 |
| Shrink | 5.5053 | 5.5053 | 5.5037 | 5.5050 |
| Parameter | Volatility | Prices | ||
|---|---|---|---|---|
| q | COVID-19 | Before COVID-19 | COVID-19 | Before COVID-19 |
| 1 | 5.3661 | 5.4902 | 5.5037 | 5.5050 |
| 1.2 | 3.2792 | 3.3314 | 3.3365 | 3.3370 |
| 1.4 | 2.1998 | 2.2212 | 2.2232 | 2.2234 |
| 1.6 | 1.5958 | 1.6045 | 1.6052 | 1.6053 |
| 1.8 | 1.2309 | 1.2344 | 1.2346 | 1.2347 |
| 2 | 0.9944 | 0.9958 | 0.9959 | 0.9959 |
| Returns | Volatility | Prices | |||||
|---|---|---|---|---|---|---|---|
| COVID-19 | Before COVID-19 | COVID-19 | Before COVID-19 | COVID-19 | Before COVID-19 | ||
| 0.05 | 1 | 2.0077 | 1.9918 | 0.5665 | 1.051 | 0.8225 | 0.876 |
| 2 | 0.6347 | 0.5192 | 0.475 | 0.7457 | 0.5948 | 0.6834 | |
| 3 | 0.0958 | 0.047 | 0.3587 | 0.3605 | 0.4043 | 0.4813 | |
| 0.1 | 1 | 1.9011 | 2.0217 | 0.4579 | 0.9009 | 0.5764 | 0.5923 |
| 2 | 0.9052 | 0.7616 | 0.3918 | 0.7500 | 0.482 | 0.565 | |
| 3 | 0.2774 | 0.1014 | 0.3073 | 0.5177 | 0.3998 | 0.4872 | |
| 0.15 | 1 | 1.7757 | 1.9621 | 0.4091 | 0.7828 | 0.4231 | 0.4143 |
| 2 | 0.995 | 0.9847 | 0.3325 | 0.6667 | 0.3639 | 0.4258 | |
| 3 | 0.4658 | 0.222 | 0.2761 | 0.5267 | 0.3085 | 0.3828 | |
| 0.2 | 1 | 1.6367 | 1.8465 | 0.3535 | 0.6795 | 0.3358 | 0.3074 |
| 2 | 1.0500 | 1.1772 | 0.3105 | 0.6127 | 0.3141 | 0.3251 | |
| 3 | 0.6265 | 0.3374 | 0.2585 | 0.5123 | 0.2757 | 0.3164 | |
| r | l | Returns | Volatility | Prices | |||
|---|---|---|---|---|---|---|---|
| COVID-19 | Before COVID-19 | COVID-19 | Before COVID-19 | COVID-19 | Before COVID-19 | ||
| 0.05 | 1 | 2.4511 | 2.6077 | 0.3638 | 1.0016 | 0.7022 | 0.8336 |
| 2 | 2.3931 | 2.4849 | 0.3316 | 1.0452 | 0.613 | 0.8029 | |
| 3 | 2.9444 | 1.7047 | 0.3039 | 0.8627 | 0.5625 | 0.8052 | |
| 0.1 | 1 | 2.0316 | 2.4002 | 0.2712 | 0.7824 | 0.4747 | 0.5476 |
| 2 | 1.875 | 2.4022 | 0.2397 | 0.8176 | 0.4061 | 0.5454 | |
| 3 | 1.9879 | 2.3514 | 0.2128 | 0.7807 | 0.3757 | 0.5301 | |
| 0.15 | 1 | 1.7655 | 2.165 | 0.2215 | 0.6359 | 0.3431 | 0.385 |
| 2 | 1.5924 | 2.1313 | 0.19 | 0.6476 | 0.2913 | 0.3878 | |
| 3 | 1.678 | 2.7515 | 0.1632 | 0.6107 | 0.2723 | 0.3644 | |
| 0.2 | 1 | 1.5554 | 1.9543 | 0.1939 | 0.5431 | 0.271 | 0.2969 |
| 2 | 1.434 | 2.0363 | 0.1655 | 0.5518 | 0.2335 | 0.2982 | |
| 3 | 1.5666 | 2.3026 | 0.143 | 0.5125 | 0.2184 | 0.2895 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheraz, M.; Nasir, I. Information-Theoretic Measures and Modeling Stock Market Volatility: A Comparative Approach. Risks 2021, 9, 89. https://doi.org/10.3390/risks9050089
Sheraz M, Nasir I. Information-Theoretic Measures and Modeling Stock Market Volatility: A Comparative Approach. Risks. 2021; 9(5):89. https://doi.org/10.3390/risks9050089
Chicago/Turabian StyleSheraz, Muhammad, and Imran Nasir. 2021. "Information-Theoretic Measures and Modeling Stock Market Volatility: A Comparative Approach" Risks 9, no. 5: 89. https://doi.org/10.3390/risks9050089
APA StyleSheraz, M., & Nasir, I. (2021). Information-Theoretic Measures and Modeling Stock Market Volatility: A Comparative Approach. Risks, 9(5), 89. https://doi.org/10.3390/risks9050089






