Alleviating Class Imbalance in Actuarial Applications Using Generative Adversarial Networks
Abstract
1. Introduction
1.1. Background
1.2. Aims and Objectives
- deep overview of generative models and why GANs are of better quality than other generative models;
- an overview of GANs with practical applications in a number of areas with emphasis for actuarial use; and
- provide a practical example of a popular GAN use for alleviating class imbalance, data augmentation, and improving predictive models.
1.3. Contribution
1.4. Structure of the Paper
2. Class Imbalance
2.1. Definition
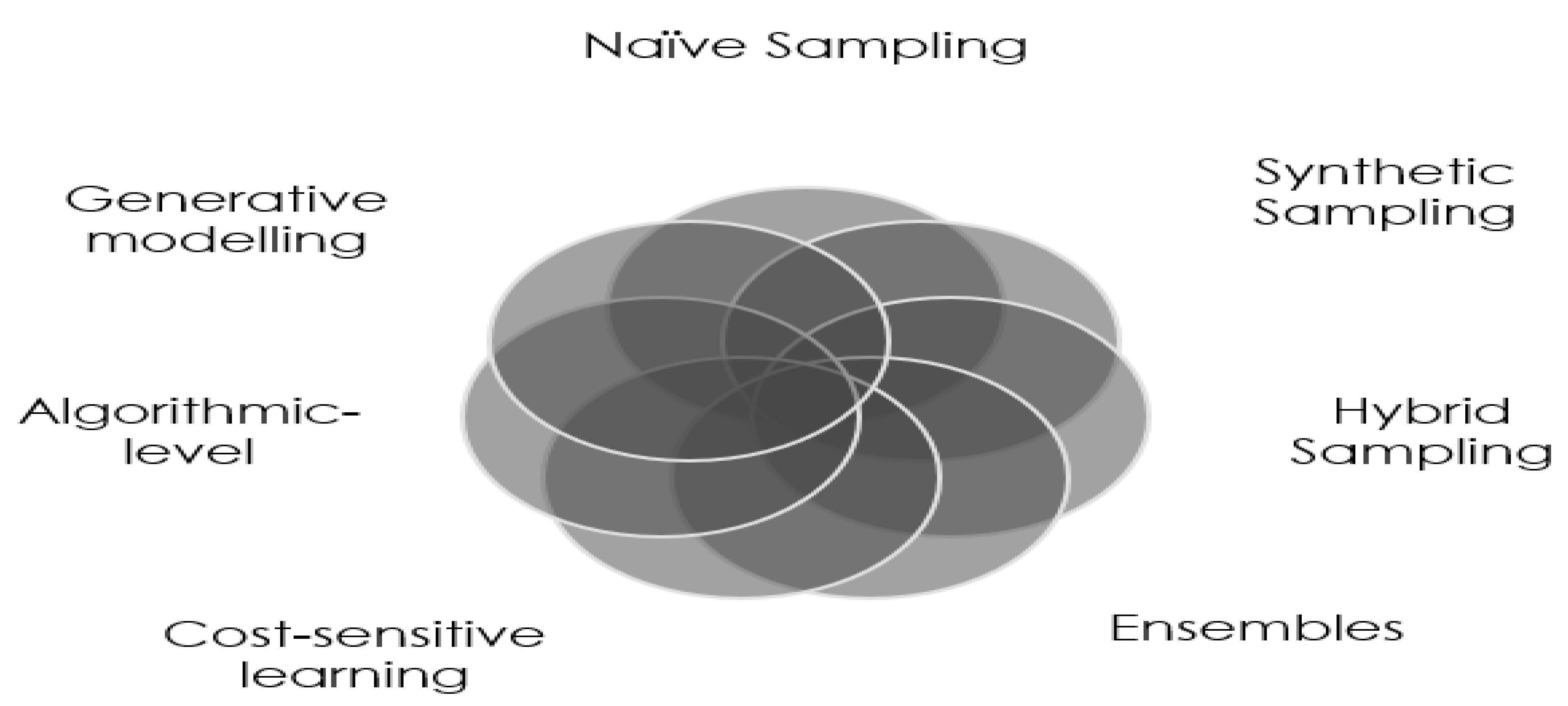
2.2. Techniques to Alleviate Class Imbalance
2.2.1. Re-Sampling
2.2.2. Synthetic Sampling
2.2.3. Ensembles
2.2.4. Other Methods
3. Generative Models
3.1. Definition
3.2. Explicit Models
3.2.1. FVBNs
3.2.2. Non-Linear ICA
3.2.3. Variational Autoencoders
3.2.4. Boltzmann Machines
3.3. Implicit Models
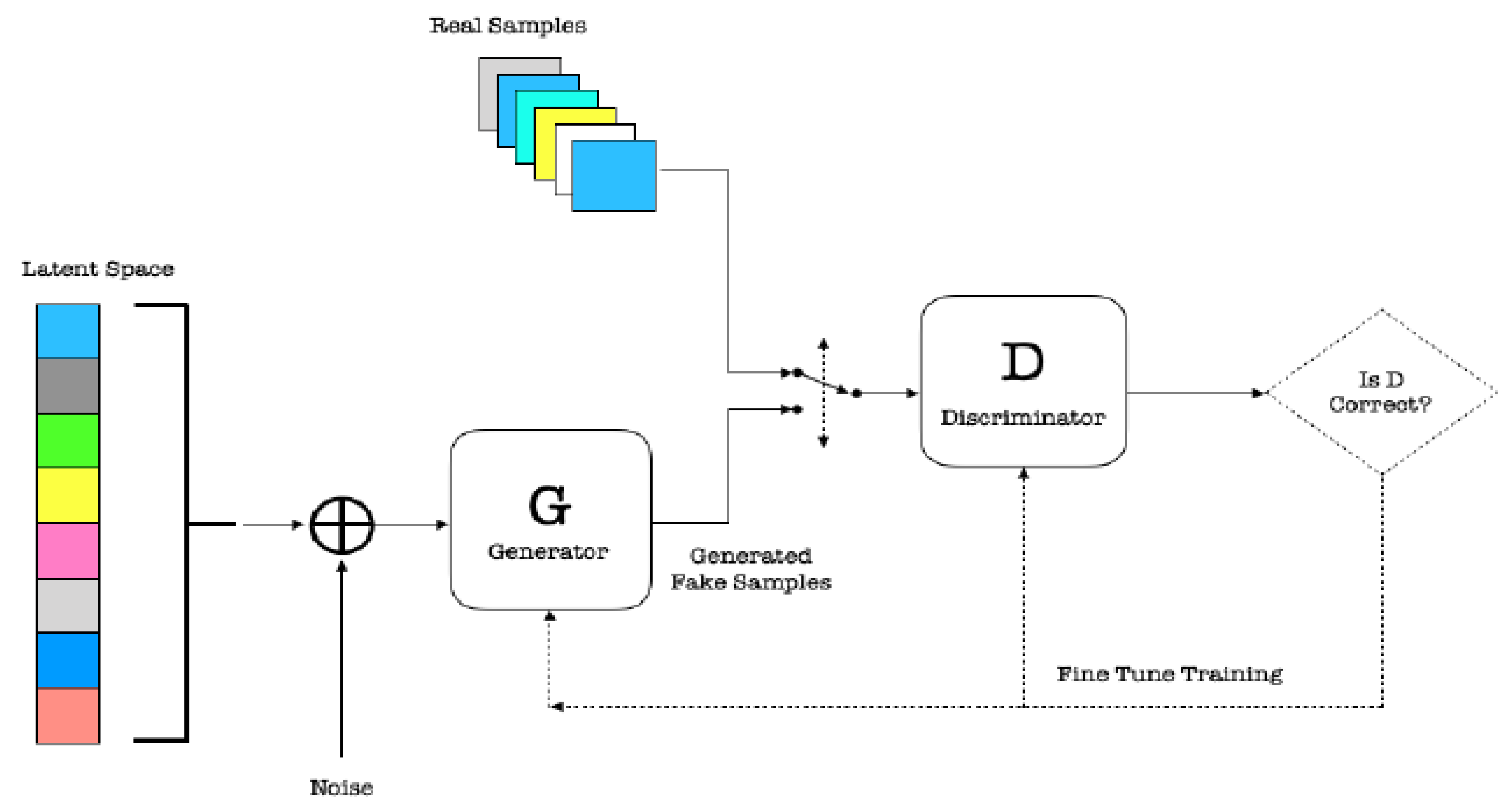
3.3.1. GANs
- G picks z from the prior latent space Z and then generates samples from this distribution using ANN;
- D receives generated samples from G and the true data examples, and it must distinguish between the two for authenticity.
3.3.2. GMMNs
3.4. Summary
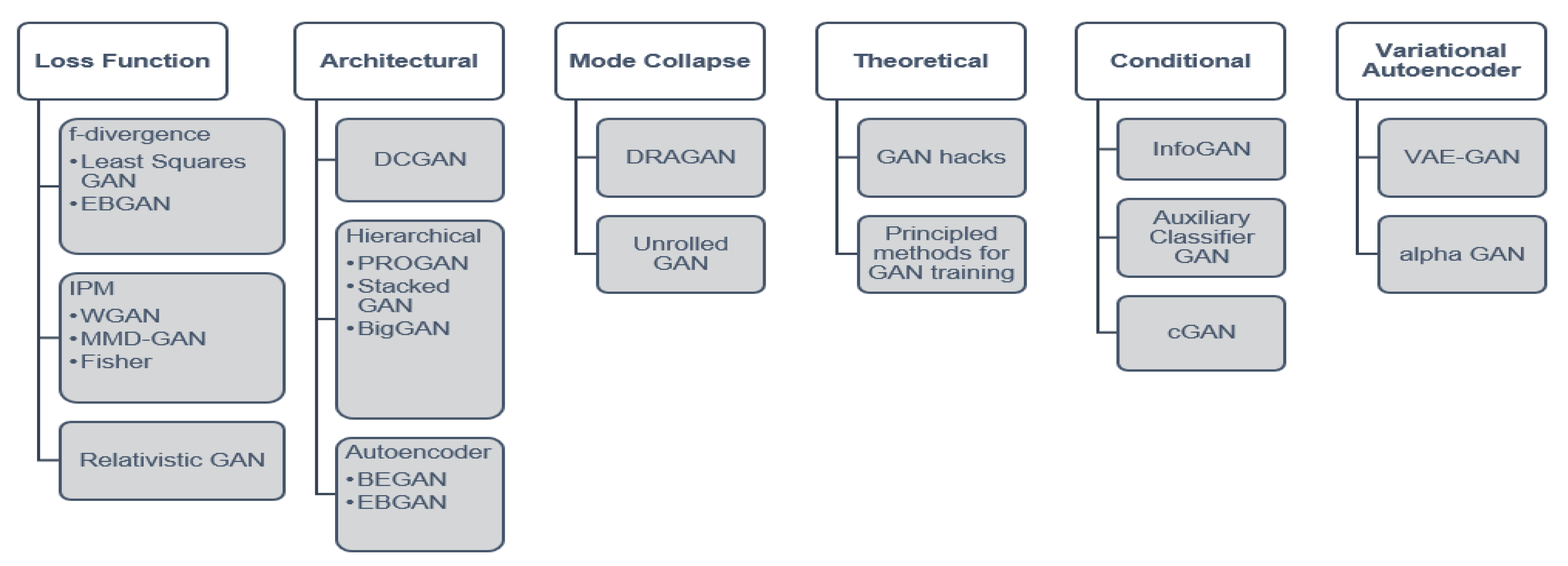
4. Applications of GANs
4.1. Data Augmentation
4.2. Anomaly Detection
4.3. Time Series
4.4. Privacy Preservation
4.5. Missing Data Imputation
4.6. Semi-Supervised Learning
4.7. Domain Adaptation
4.8. Summary
5. Methodology
5.1. SMOTE
5.2. Vanilla GAN
5.2.1. The Discriminator
5.2.2. The Generator
5.2.3. GAN Loss
| Algorithm 1: Mini-batch SG ascent of GANs with the original objective for MM-GAN. The number of steps to apply to D, k, is a hyper-parameter. For every training of G, we train D k times. Goodfellow et al. (2014) used . |
|
5.2.4. Non-Saturating GAN
5.2.5. Optimal Solution
5.3. Challenges with GANs
5.3.1. Mode Collapse
5.3.2. Vanishing Gradient
5.4. Improved GAN Training
5.4.1. Conditional GANs
5.4.2. Deep Convolutional GAN
5.4.3. Loss Variants
5.5. WGAN
5.5.1. Wasserstein Distance
5.5.2. The Critic
5.6. Improved WGAN Training
6. Experiments
6.1. Data Sets
6.1.1. Credit Card Fraud
6.1.2. Pima Indians Diabetes
6.1.3. German Credit Scoring
6.1.4. Breast Cancer Wisconsin
6.1.5. Glass Identification
6.2. Scaling the Data
6.3. Train-Test Split
6.4. SMOTE Implementation
6.5. GAN Implementation
6.5.1. Software
6.5.2. The Generator
6.5.3. The Critic
6.5.4. Labels
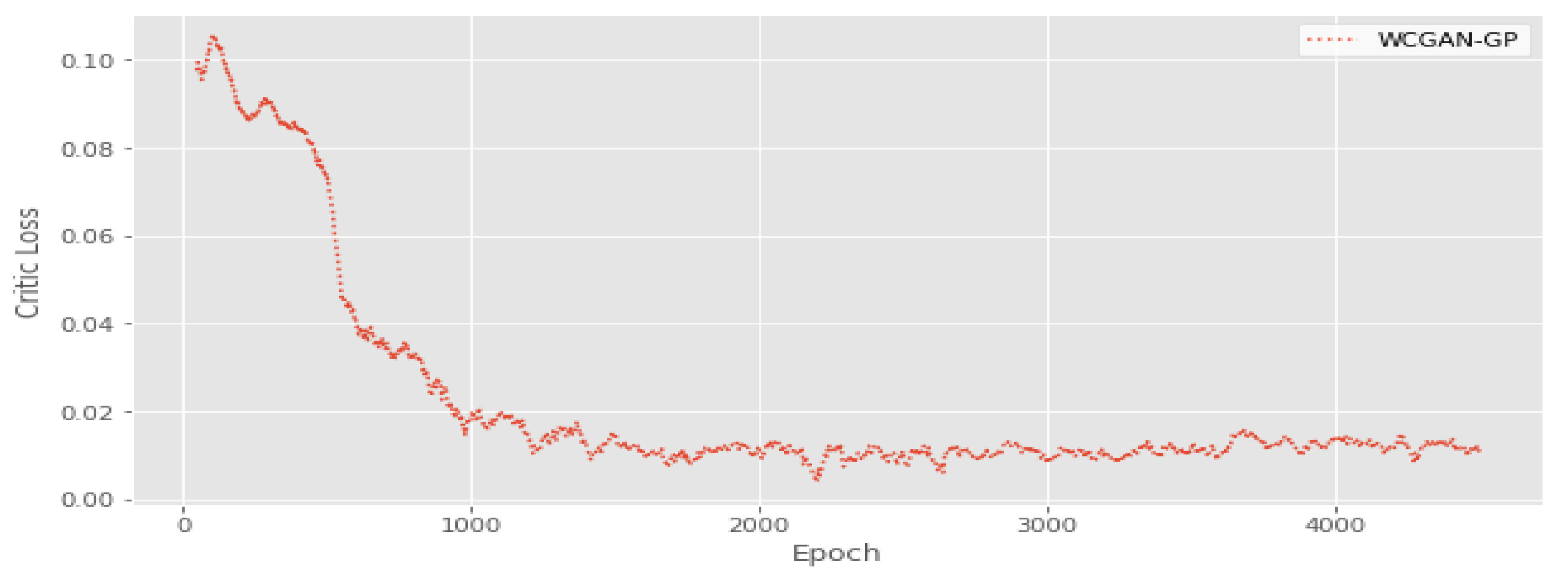
6.5.5. Training WGAN-GP
6.5.6. Generating Synthetic Samples
6.6. Logistic Regression
6.7. Evaluation
6.8. Statistical Hypothesis Testing
6.8.1. Friedman Test
6.8.2. Post-Hoc Nemenyi Test
6.8.3. Implementation
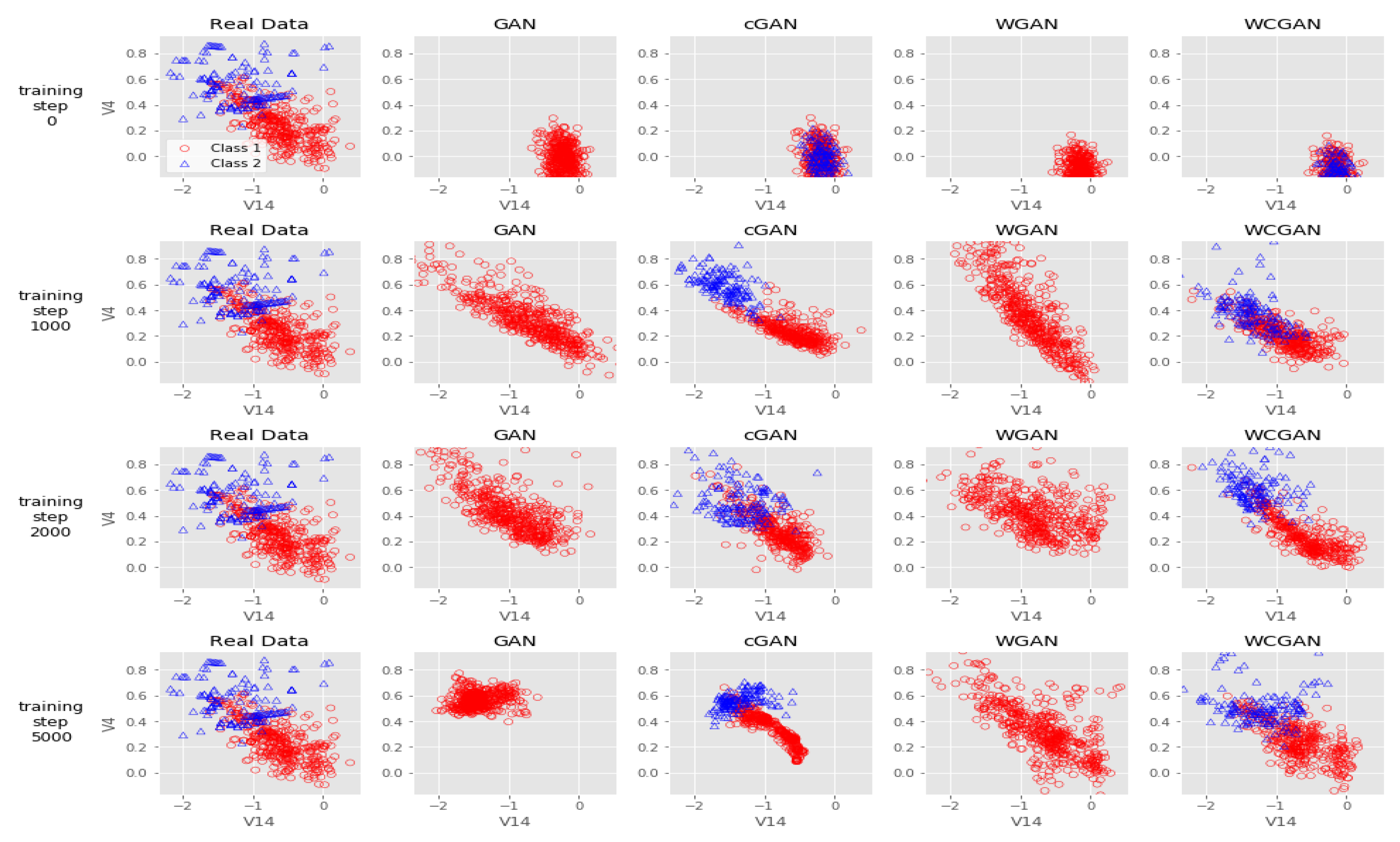
7. Results
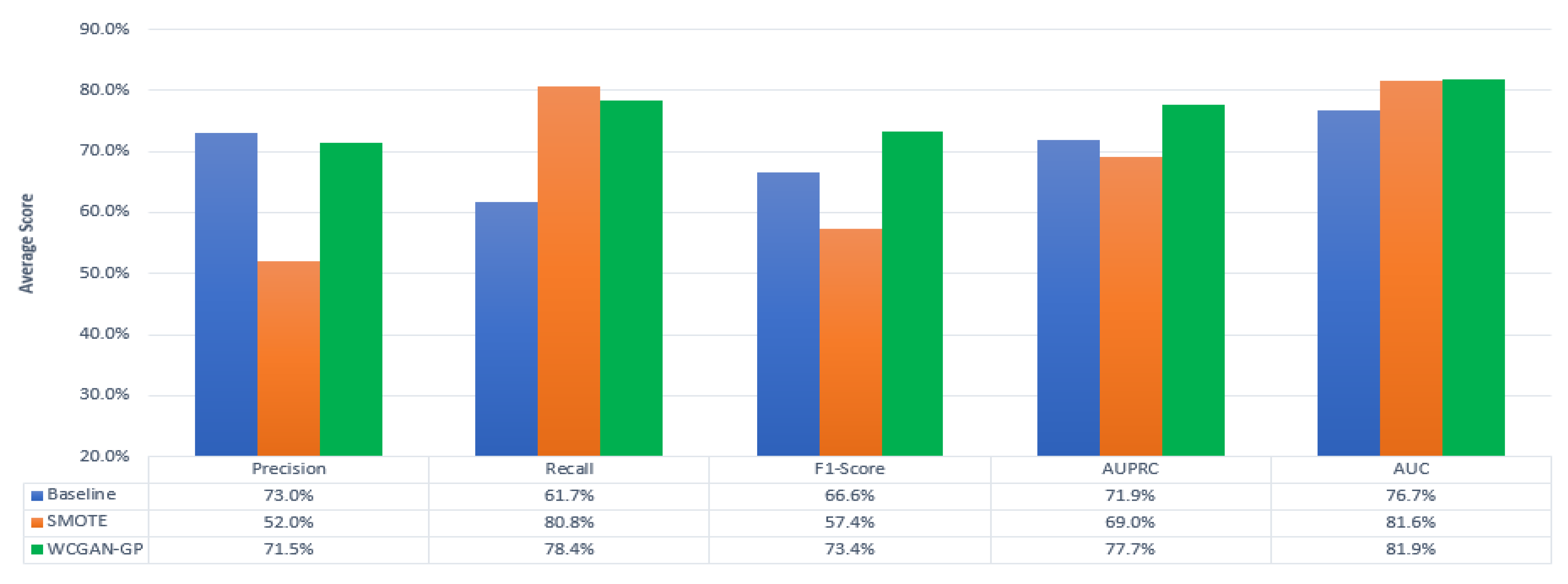
7.1. Comparisons
7.1.1. AUC
7.1.2. AUPRC
7.2. Statistical Hypothesis Testing
8. Discussion
8.1. Results
8.2. Implications for Actuaries
9. Conclusions, Limitations and Future Research
9.1. Conclusions
9.2. Summary of Applications
9.3. Limitations and Future Research
- Consideration on other data sets to apply the same techniques, especially complex data sets that include small disjuncts, over-lapping, mixed data types, and multiple classes, particularly actuarial data sets.
- Alternative consideration for other ML algorithms would show which ML technique is best and for which data set and domain.
- Empirical comparison of these results with other tabular data sets where GANs were applied.
- Implementation and leveraging of the GANs in R or Python for actuarial use.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goodfellow, Ian, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherzil Ozair, Aaron Courville, and Yoshua Bengio. 2014. Generative adversarial nets. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 2672–80. [Google Scholar]
- Ackley, David H., Geoffrey Everest Hinton, and Terrence Joseph Sejnowski. 1985. A learning algorithm for boltzmann machines. Cognitive Science 9: 147–69. [Google Scholar] [CrossRef]
- Akcay, Samet, Amir Atapour-Abarghouei, and Toby P. Breckon. 2018. Ganomaly: Semi-supervised anomaly detection via adversarial training. In Asian Conference on Computer Vision. Cham: Springer, pp. 622–37. [Google Scholar]
- Antoniou, Antreas, Amos Storkey, and Harrison Edwards. 2017. Data augmentation generative adversarial networks. arXiv arXiv:1711.04340. [Google Scholar]
- Arjovsky, Martin, Soumith Chintala, and Leon Bottou. 2017. Wasserstein gan. arXiv arXiv:1701.07875. [Google Scholar]
- Armanious, Karim, Chenming Jiang, Marc Fischer, Thomas Küstner, Tobias Hepp, Konstantin Nikolaou, Sergio Gatidis, and Bin Yang. 2018. Medgan: Medical image translation using gans. arXiv arXiv:1806.06397. [Google Scholar] [CrossRef] [PubMed]
- Batista, Gustavo Enrique, Ronaldo Cristiano Prati, and Maria-Carolina Monard. 2004. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explorations Newsletter 6: 20–29. [Google Scholar] [CrossRef]
- Beaulieu-Jones, Brett K., Zhiwei Steven Wu, Chris Williams, Ran Lee, Sanjeev P. Bhavnani, James Brian Byrd, and Casey S. Greene. 2019. Privacy-preserving generative deep neural networks support clinical data sharing. Circulation: Cardiovascular Quality and Outcomes 12: e005122. [Google Scholar] [CrossRef]
- Bekkar, Mohamed, Hasiba Kheliouane Djemaa, and Akrouf Alitouche Taklit. 2013. Evaluation measures for models assessment over imbalanced data sets. Journal of Information Engineering and Applications 3: 27–38. [Google Scholar]
- Bellinger, Collin, Chris Drummond, and Nathalie Japkowicz. 2016. Beyond the boundaries of smote. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin: Springer, pp. 248–63. [Google Scholar]
- Bellinger, Collin, Nathalie Japkowicz, and Chris Drummond. 2015. Synthetic oversampling for advanced radioactive threat detection. Paper presented at the IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, December 9–11; pp. 948–53. [Google Scholar]
- Bengio, Yoshua, Eric Thibodeau-Laufer, Guillaume Alain, and Jason Yosinski. 2014. Deep generative stochastic networks trainable by backprop. Paper presented at the International Conference on Machine Learning, Bejing, China, June 22–24; pp. 226–34. [Google Scholar]
- Bradley, Andrew P. 1997. The use of the area under the roc curve in the evaluation of machine learning algorithms. Pattern Recognition 30: 1145–59. [Google Scholar] [CrossRef]
- Brock, Andrew, Jeff Donahue, and Karen Simonyan. 2018. Large scale gan training for high fidelity natural image synthesis. arXiv arXiv:1809.11096. [Google Scholar]
- Chawla, Nitesh Vijay. 2009. Data mining for imbalanced datasets: An overview. In Data Mining and Knowledge Discovery Handbook. Berlin: Springer, pp. 875–86. [Google Scholar]
- Chawla, Nitesh Vijay, Kevin Bowyer, Lawrence Hall, and W. Phillip Kegelmeyer. 2002. Smote: synthetic minority over-sampling technique. Journal of Artificial Intelligence Research 16: 321–57. [Google Scholar] [CrossRef]
- Chawla, Nitesh Vijay, Alecsander Lazarevic, Lawrence Hall, and Kevin Bowyer. 2003. Smoteboost: Improving prediction of the minority class in boosting. In European Conference on Principles of Data Mining and Knowledge Discovery. Berlin: Springer, pp. 107–19. [Google Scholar]
- Choi, Yunjei, Minje Choi, Munyoung Kim, Jung-Woo Ha, Sunghun Kim, and Jaegul Choo. 2018. Stargan: Unified generative adversarial networks for multi-domain image-to-image translation. Paper presented at the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, June 18–23; pp. 8789–97. [Google Scholar]
- Chongxuan, Lee, Kun Xu, Jun Zhu, and Bo Zhang. 2017. Triple generative adversarial nets. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 4088–98. [Google Scholar]
- Creswell, Antonia, Tom White, Vincent Dumoulin, Kai Arulkumaran, Biswa Sengupta, and Anil Bharath. 2018. Generative adversarial networks: An overview. IEEE Signal Processing Magazine 35: 53–65. [Google Scholar] [CrossRef]
- Das, Barnan, Narayana Chatapuram Krishnan, and Diane J. Cook. 2015. Racog and wracog: Two probabilistic oversampling techniques. IEEE Transactions on Knowledge and Data Engineering 27: 222–34. [Google Scholar] [CrossRef] [PubMed]
- Ding, Zihan, Xiao-Yang Liu, Miao Yin, Wei Liu, and Linghe Kong. 2019. Tgan: Deep tensor generative adversarial nets for large image generation. arXiv arXiv:1901.09953. [Google Scholar]
- Douzas, George, and Fernando Bação. 2018. Effective data generation for imbalanced learning using conditional generative adversarial networks. Expert Systems With Applications 91: 464–71. [Google Scholar] [CrossRef]
- Dua, Dheeru, and Graff Casey. 2017. UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences. Available online: https://archive.ics.uci.edu/ml (accessed on 18 May 2019).
- Esteban, Cristóbal, Stephanie L. Hyland, and Gunnar Rätsch. 2017. Real-valued (medical) time series generation with recurrent conditional gans. arXiv arXiv:1706.02633. [Google Scholar]
- Ester, Martin, Hans-Peter Kriegel, Joerg Sander, and Xiaowei Xu. 1996. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 96: 226–31. [Google Scholar]
- Evett, I. W., and E. J. Spiehler. 1987. Rule induction in forensic science. In KBS in Goverment. Burlington: Jones & Bartlett Publishers, pp. 107–18. [Google Scholar]
- Fernández, Alberto, Salvador Garcia, Francisco Herrera, and Nitesh Vijay Chawla. 2018. Smote for learning from imbalanced data: progress and challenges, marking the 15-year anniversary. Journal of Artificial Intelligence Research 61: 863–905. [Google Scholar] [CrossRef]
- Fiore, Ugo, Alfredo De Santis, Francesca Perla, Paolo Zanetti, and Francesco Palmieri. 2019. Using generative adversarial networks for improving classification effectiveness in credit card fraud detection. Information Sciences 479: 448–55. [Google Scholar] [CrossRef]
- François, Chollet. 2015. keras. Available online: https://github.com/fchollet/keras (accessed on 20 August 2019).
- Frey, Brendan J., Geoffrey Everest Hinton, and Peter Dayan. 1996. Does the wake-sleep algorithm produce good density estimators? In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 661–667. [Google Scholar]
- Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2001. The Elements Of Statistical Learning. Springer Series in Statistics New York; New York: Springer, vol. 1. [Google Scholar]
- Friedman, Milton. 1937. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association 32: 675–701. [Google Scholar] [CrossRef]
- Fu, Rao, Jie Chen, Shutian Zeng, Yiping Zhuang, and Agus Sudjianto. 2019. Time series simulation by conditional generative adversarial net. arXiv arXiv:1904.11419. [Google Scholar] [CrossRef]
- Ganganwar, Vaishali. 2012. An overview of classification algorithms for imbalanced datasets. International Journal of Emerging Technology and Advanced Engineering 2: 42–47. [Google Scholar]
- Gao, Ming, Xia Hong, Sheng Chen, C. J. Harris, and Emad Khalaf. 2014. Pdfos: Pdf estimation based over-sampling for imbalanced two-class problems. Neurocomputing 138: 248–59. [Google Scholar] [CrossRef]
- Geyer, Charles J. 1992. Practical markov chain monte carlo. Statistical Science 7: 473–83. [Google Scholar] [CrossRef]
- Glorot, Xavier, Antoine Bordes, and Yoshua Bengio. 2011. Deep sparse rectifier neural networks. Paper presented at the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, April 11–13; pp. 315–23. [Google Scholar]
- Goodfellow, Ian. 2016. Nips 2016 tutorial: Generative adversarial networks. arXiv arXiv:1701.00160. [Google Scholar]
- Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. Cambridge: MIT Press, vol. 1. [Google Scholar]
- Gulrajani, Ishaan, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron Courville. 2017. Improved training of wasserstein gans. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 5767–77. [Google Scholar]
- Han, Hui, Wenyuan Wang, and Binghuan Mao. 2005. Borderline-smote: A new over-sampling method in imbalanced data sets learning. In International Conference on Intelligent Computing. Berlin: Springer, pp. 878–87. [Google Scholar]
- Hanley, James A., and Barbara J. McNeil. 1982. The meaning and use of the area under a receiver operating characteristic (roc) curve. Radiology 143: 29–36. [Google Scholar] [CrossRef] [PubMed]
- Hartigan, J. A., and M. A. Wong. 1979. Algorithm as 136: A k-means clustering algorithm. Journal of the Royal Statistical Society. Series c (Applied Statistics) 28: 100–8. [Google Scholar] [CrossRef]
- He, Haibo, and Edwardo A. Garcia. 2008. Learning from imbalanced data. IEEE Transactions on Knowledge & Data Engineering 21: 1263–84. [Google Scholar]
- He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jain Sun. 2015. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. Paper presented at the IEEE International Conference on Computer Vision, Santiago, Chile, December 7–13; pp. 1026–34. [Google Scholar]
- Hinton, Geoffrey Everest. 2002. Training products of experts by minimizing contrastive divergence. Neural Computation 14: 1771–800. [Google Scholar] [CrossRef]
- Hinton, Geoffrey Everest, Simon Osindero, and Yee-Why Teh. 2006. A fast learning algorithm for deep belief nets. Neural Computation 18: 1527–54. [Google Scholar] [CrossRef]
- Hinton, Geoffrey Everest, and Ruslan Russ Salakhutdinov. 2006. Reducing the dimensionality of data with neural networks. Science 313: 504–7. [Google Scholar] [CrossRef]
- Hinton, Geoffrey Everest, and Tiejman Tieleman. 2012. Lecture 6.5—Rmsprop, Coursera: Neural Networks for Machine Learning. Available online: https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (accessed on 28 August 2019).
- Hitawala, Saifuddin. 2018. Comparative study on generative adversarial networks. arXiv arXiv:1801.04271. [Google Scholar]
- Hoffman, Judy, Eric Tzeng, Taesung Park, Jun-Yan Zhu, Phillip Isola, Kate Saenko, Alexei Efros, and Trevor Darrell. 2017. Cycada: Cycle-consistent adversarial domain adaptation. arXiv arXiv:1711.03213. [Google Scholar]
- Hong, Weixiang, Zhenzhen Wang, Ming Yang, and Junsong Yuan. 2018. Conditional generative adversarial network for structured domain adaptation. Paper presented at the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, June 18–23; pp. 1335–44. [Google Scholar]
- Hong, Yongjun, Uiwon Hwang, Jaeyoon Yoo, and Sungroh Yoon. 2019. How generative adversarial networks and their variants work: An overview of GAN. ACM Computing Surveys (CSUR) 52: 10. [Google Scholar] [CrossRef]
- Ioffe, Sergey, and Christian Szegedy. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv arXiv:1502.03167. [Google Scholar]
- Jolicoeur-Martineau, Alexia. 2018. The relativistic discriminator: A key element missing from standard gan. arXiv arXiv:1807.00734. [Google Scholar]
- Karras, Terro, Samuli Laine, and Timo Aila. 2019. A style-based generator architecture for generative adversarial networks. Paper presented at the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, June 15–20; pp. 4401–10. [Google Scholar]
- Kim, Taeskoo, Moonsu Cha, Hyunsoo Kim, Jungkwon Lee, and Jiwon Kim. 2017. Learning to discover cross-domain relations with generative adversarial networks. Paper presented at 34th International Conference on Machine Learning, Sydney, Australia, August 6–11, vol. 70, pp. 1857–65. [Google Scholar]
- Kingma, Diederik Pieter, and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv arXiv:1412.6980. [Google Scholar]
- Kingma, Diederik Pieter, and Max Welling. 2013. Auto-encoding variational bayes. arXiv arXiv:1312.6114. [Google Scholar]
- Kullback, Solomon. 1997. Information Theory and Statistics. North Chelmsford: Courier Corporation. [Google Scholar]
- Kullback, Solomon, and Richard Arthur Leibler. 1951. On information and sufficiency. The Annals of Mathematical Statistics 22: 79–86. [Google Scholar] [CrossRef]
- Larsen, Anders Boesen Lindbo, Søren Kaae Sønderby, Hugo Larochelle, and Ole Winther. 2015. Autoencoding beyond pixels using a learned similarity metric. arXiv arXiv:1512.09300. [Google Scholar]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting us mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Li, Stevan Cheng-Xian, Bo Jiang, and Benjamin Marlin. 2019. Misgan: Learning from incomplete data with generative adversarial networks. arXiv arXiv:1902.09599. [Google Scholar]
- Li, Yujia, Kevin Swersky, and Richard Zemel. 2015. Generative moment matching networks. Paper presented at the 32nd International Conference on Machine Learning, Lille, France, July 6–11; pp. 1718–27. [Google Scholar]
- Lin, Jianhua. 1991. Divergence measures based on the shannon entropy. IEEE Transactions on Information Theory 37: 145–51. [Google Scholar] [CrossRef]
- Liu, Zhiyue, Jiahai Wang, and Zhiwei Liang. 2019. Catgan: Category-aware generative adversarial networks with hierarchical evolutionary learning for category text generation. arXiv arXiv:1911.06641. [Google Scholar] [CrossRef]
- Longadge, Rushi, and Snehalata Dongre. 2013. Class imbalance problem in data mining review. arXiv arXiv:1305.1707. [Google Scholar]
- López, Victoria, Alberto Fernández, Salvado García, Vasile Palade, and Francisco Herrera. 2013. An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics. Information Sciences 250: 113–41. [Google Scholar] [CrossRef]
- Lucic, Mario, Karol Kurach, Marcin Michalski, Sylvain Gelly, and Olivier Bousquet. 2018. Are gans created equal? a large-scale study. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 700–9. [Google Scholar]
- Van der Maaten, Laurens, and Geoffrey Everest Hinton. 2008. Visualizing data using t-sne. Journal of Machine Learning Research 9: 2579–605. [Google Scholar]
- Makhzani, Alireza, Jonathon Shlens, Navdeep Jaitly, Ian Goodfellow, and Brendan Frey. 2015. Adversarial autoencoders. arXiv arXiv:1511.05644. [Google Scholar]
- Manisha, Padala, and Sujit Gujar. 2018. Generative adversarial networks (gans): What it can generate and what it cannot? arXiv arXiv:1804.00140. [Google Scholar]
- Mariani, Giovanni, Florian Scheidegger, Roxana Istrate, Costas Bekas, and Cristiano Malossi. 2018. Bagan: Data augmentation with balancing gan. arXiv arXiv:1803.09655. [Google Scholar]
- Mathew, Josey, Ming Luo, Chee Khiang Pang, and Hian Leng Chan. 2015. Kernel-based smote for svm classification of imbalanced datasets. Paper presented at the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, November 9–12; pp. 1127–32. [Google Scholar]
- McCullagh, Peter. 1984. Generalized linear models. European Journal of Operational Research 16: 285–92. [Google Scholar] [CrossRef]
- Mirza, Mehdi, and Simon Osindero. 2014. Conditional generative adversarial nets. arXiv arXiv:1411.1784. [Google Scholar]
- Mitchell, Tom M. 2006. The Discipline of Machine Learning. Pittsburgh: Machine Learning Department, School of Computer Science, Carnegie Mellon University, vol. 9. [Google Scholar]
- Miyato, Takeru, Shin-ichi Maeda, Masanori Koyama, and Shin Ishii. 2018. Virtual adversarial training: a regularization method for supervised and semi-supervised learning. IEEE Transactions on Pattern Analysis and Machine Intelligence 41: 1979–93. [Google Scholar] [CrossRef] [PubMed]
- Mottini, Alejandro, Alix Lheritier, and Rodrigo Acuna-Agost. 2018. Airline passenger name record generation using generative adversarial networks. arXiv arXiv:1807.06657. [Google Scholar]
- Müller, Alfred. 1997. Integral probability metrics and their generating classes of functions. Advances in Applied Probability 29: 429–43. [Google Scholar]
- Nemenyi, Peter. 1962. Distribution-free multiple comparisons. In Biometrics. Princeton: Princeton University, vol. 18, p. 263. [Google Scholar]
- Nowozin, Sebastian, Botond Cseke, and Ryota Tomioka. 2016. f-gan: Training generative neural samplers using variational divergence minimization. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 271–279. [Google Scholar]
- Odena, Augustus. 2016. Semi-supervised learning with generative adversarial networks. arXiv arXiv:1606.01583. [Google Scholar]
- Odena, Augustus, Christopher Olah, and Jonathon Shlens. 2017. Conditional image synthesis with auxiliary classifier gans. Paper presented at the 34th International Conference on Machine Learning, Sydney, Australia, August 6–11, vol. 70, pp. 2642–51. [Google Scholar]
- O’Malley, B. R., Robert E. Dorrington, Stephen C. Jurisich, J. A. Valentini, T. M. Cohen, and B. J. Ross. 2005. An investigation of the mortality of south african assured lives, 1995–1998. South African Actuarial Journal 5: 27–59. [Google Scholar] [CrossRef]
- Park, Noseong, Mahmoud Mohammadi, Kshitij Gorde, Sushil Jajodia, Hongkyu Park, and Youngmin Kim. 2018. Data synthesis based on generative adversarial networks. Proceedings of the Very Large Data Bases Endowment 11: 1071–83. [Google Scholar] [CrossRef]
- Pohlert, Thorsten. 2014. The pairwise multiple comparison of mean ranks package (pmcmr). R Package 27: 10. [Google Scholar]
- Pozzolo, Andrea Dal. 2015. Adaptive Machine Learning for Credit Card Fraud Detection. Edited by Machine Learning Group. Brussels: Université Libre de Bruxelles. [Google Scholar]
- Python Software Foundation. 2017. Python Language Reference (Version 3.6. 3.). Amsterdam: Python Software Foundation. [Google Scholar]
- Qian, Ning. 1999. On the momentum term in gradient descent learning algorithms. Neural Networks 12: 145–51. [Google Scholar] [CrossRef]
- Radford, Alec, Luke Metz, and Soumith Chintala. 2015. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv arXiv:1511.06434. [Google Scholar]
- Reed, Scott, Zeynep Akata, Xinchen Yan, Lajanugen Logeswaran, Bernt Schiele, and Honglak Lee. 2016. Generative adversarial text to image synthesis. arXiv arXiv:1605.05396. [Google Scholar]
- Rezende, Danilo Jimenez, Shakir Mohamed, and Daan Wierstra. 2014. Stochastic backpropagation and approximate inference in deep generative models. arXiv arXiv:1401.4082. [Google Scholar]
- Multiple Imputation for Nonresponse in Surveys. Hoboken: John Wiley & Sons, vol. 81.
- Rubner, Yossi, Carlo Tomasi, and Leonidas Guibas. 2000. The earth mover’s distance as a metric for image retrieval. International Journal of Computer Vision 40: 99–121. [Google Scholar] [CrossRef]
- Ruder, Sebastian. 2016. An overview of gradient descent optimization algorithms. arXiv arXiv:1609.0474. [Google Scholar]
- Rumelhart, David Everett, Geoffrey Everest Hinton, and Ronald J. Williams. 1986. Learning representations by back-propagating errors. Nature 323: 533. [Google Scholar] [CrossRef]
- Saito, Takaya, and Mark Rehmsmeier. 2015. The precision-recall plot is more informative than the roc plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE 10: e0118432. [Google Scholar] [CrossRef]
- Salakhutdinov, Ruslan Russ, and Geoffrey Everest Hinton. 2009. Deep boltzmann machines. In Artificial Intelligence and Statistics. Berlin: Springer, pp. 448–55. [Google Scholar]
- Salimans, Tim, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, and Xi Chen. 2016. Improved techniques for training gans. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 2234–42. [Google Scholar]
- Schafer, Joseph L., and Maren K. Olsen. 1998. Multiple imputation for multivariate missing-data problems: A data analyst’s perspective. Multivariate Behavioral Research 33: 545–71. [Google Scholar] [CrossRef]
- Schlegl, Thomas, Philipp Seeböck, Sebastian M. Waldstein, Ursula Schmidt-Erfurth, and Georg Langs. 2017. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In International Conference on Information Processing in Medical Imaging. Cham: Springer, pp. 146–157. [Google Scholar]
- Shang, Chao, Aaron Palmer, Jiangwen Sun, Ko-Shin Chen, Jin Lu, and Jinbo Bi. 2017. Vigan: Missing view imputation with generative adversarial networks. Paper presented at 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, December 11–14; pp. 766–75. [Google Scholar]
- Smith, Jack W., James E. Everhart, W. C. Dickson, William C. Knowler, and Robert Scott Johannes. 1988. Using the adap learning algorithm to forecast the onset of diabetes mellitus. In Proceedings of the Annual Symposium on Computer Application in Medical Care. Bethesda: American Medical Informatics Association, pp. 261–65. [Google Scholar]
- Sricharan, Kumar, Raja Bala, Matthew Shreve, Hui Ding, Kumar Saketh, and Jin Sun. 2017. Semi-supervised conditional gans. arXiv arXiv:1708.05789. [Google Scholar]
- Street, W. Nick, William H. Wolberg, and O. L. Mangasarian. 1993. Nuclear feature extraction for breast tumor diagnosis. In Biomedical Image Processing and Biomedical Visualization. Washington, DC: International Society for Optics and Photonics, vol. 1905, pp. 861–70. [Google Scholar]
- Tzeng, Eric, Judy Hoffman, Kate Saenko, and Trevor Darrell. 2017. Adversarial discriminative domain adaptation. Paper presented at the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, July 21–26; pp. 7167–76. [Google Scholar]
- Van den Oord, Aaron, Nal Kalchbrenner, Lasse Espeholt, Oriol Vinyals, and Alex Graves. 2016. Conditional image generation with pixelcnn decoders. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 4790–4798. [Google Scholar]
- Vondrick, Carl, Hamed Pirsiavash, and Antonio Torralba. 2016. Generating videos with scene dynamics. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 613–621. [Google Scholar]
- Voorhees, ELLEN M. 1986. Implementing agglomerative hierarchic clustering algorithms for use in document retrieval. Information Processing & Management 22: 465–76. [Google Scholar]
- Wang, Kunfeng, Chao Gou, Yanjie Duan, Yilun Lin, Xinhu Zheng, and Fei-Yue Wang. 2017. Generative adversarial networks: introduction and outlook. IEEE/CAA Journal of Automatica Sinica 4: 588–98. [Google Scholar] [CrossRef]
- Wang, Shuo, and Xin Yao. 2009. Diversity analysis on imbalanced data sets by using ensemble models. Paper presented at 2009 IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, March 30–April 2; pp. 324–31. [Google Scholar]
- Xu, Lei, Maria Skoularidou, Alfredo Cuesta-Infante, and Kalyan Veeramachaneni. 2019. Modeling tabular data using conditional gan. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 7335–45. [Google Scholar]
- Yang, Li-Chia, Szu-Yu Chou, and Yi-Hsuan Yang. 2017. Midinet: A convolutional generative adversarial network for symbolic-domain music generation. arXiv arXiv:1703.10847. [Google Scholar]
- Yi, Zili, Hao Zhang, Ping Tan, and Minglun Gong. 2017. Dualgan: Unsupervised dual learning for image-to-image translation. Paper presented at the IEEE International Conference on Computer Vision, Venice, Italy, October 22–29; pp. 2849–57. [Google Scholar]
- Yoon, Jinsung, Daniel Jarrett, and Mihaela Van der Schaar. 2019. Time-series generative adversarial networks. In Advances in Neural Information Processing Systems. Cambridge: The MIT Press, pp. 5508–18. [Google Scholar]
- Yoon, Jinsung, James Jordon, and Mihaela Van Der Schaar. 2018. Gain: Missing data imputation using generative adversarial nets. arXiv arXiv:1806.02920. [Google Scholar]
- Zhang, Huaxiang, and Mingfang Li. 2014. Rwo-sampling: A random walk over-sampling approach to imbalanced data classification. Information Fusion 20: 99–116. [Google Scholar] [CrossRef]
- Zhou, Xingyu, Zhisong Pan, Guyu Hu, Siqi Tang, and Cheng Zhao. 2018. Stock market prediction on high-frequency data using generative adversarial nets. Mathematical Problems in Engineering 2018: 4907423. [Google Scholar] [CrossRef]
- Zhu, Jun-Yan, Taesung Park, Phillip Isola, and Alexei A. Efros. 2017. Unpaired image-to-image translation using cycle-consistent adversarial networks. Paper presented the IEEE International Conference on Computer Vision, Venice, Italy, October 22–29; pp. 2223–32. [Google Scholar]
| 1. | The imblearn package in Python can also do SMOTE and its notable variants. Other packages exist in R, such as ROSE, unbalanced, smotefamily, DMwR, ebmc, and IRIC. |
| 2. | Pytorch and Tensorflow are also popular packages available in Python for implementing GANs. |
| 3. | The version of the WCGAN was incorporated with an improved WGAN training using the GP term as per the paper by Gulrajani et al. (2017). |
| Explicit Density | Approximate | Variational Inference | Variational Autoencoder |
| Markov chain | Deep Belief Network | ||
| Restricted Boltzmann Machine | |||
| Tractable | Full Visible Belief Net | NADE | |
| MADE | |||
| PixelRNN/CNN | |||
| Change of variable models | Nonlinear ICA | ||
| Implicit Density | Direct | Generative Adversarial Network | Minimax GAN |
| Non-saturating GAN | |||
| GAN variants | |||
| Generative Moment Matching Network | GMMN | ||
| Markov | Generative Stochastic Network | GSN |
| Actuarial Discipline | Description |
|---|---|
| Product Design, Propensity and Customer Behavior | Create wider and more model points; Boost propensity models with more data per cell, leading to better and accurate models. |
| Actuarial Models | Experience monitoring and experience rates derived using a large credible data set. Boost models using data augmentation, semi-supervised learning, missing data imputation and domain adaptation for pricing, assumption setting, anomaly detection, risk estimation, time series and attention prediction in insurance, reinsurance, banking, investment, healthcare, and enterprise risk management. |
| Projections | Network modeling by looking at driving dependencies rather than correlation assumptions, i.e., use generative models. Strategic flexible and more decision-based models based on the environment. More GAN-based time series models driven by the environment. Enhanced solvency projection models and stress tests which are based on rich data sets. |
| Reserving | Make projections more predictive through a large enough credible data at all model points, i.e., accurate assumptions per risk cell with less margins. |
| Surplus Distribution | More granular individual information from alternative data sources through leveraging generative models. |
| Investment Strategy | Granular data for asset/liability modeling, i.e., use GANs to simulate scenarios that depend entirely on the adopted investment strategy and boosting the model. Enhanced market risk monitoring. Improvements to portfolio optimization. |
| Data Cleaning | Reduce errors; fill in gaps using imputation; increase the sample size; query other data sets and verify patterns using Cycle GANs. |
| Research | Make actuarial data sets more publicly available through synthesized data generated by GANs, boosting industry data. This is helpful for creating accurate and more up-to-date standard tables and encouraging actuarial research. |
| External Data Sources | Leverage other data sets through combining multiple data sets. For example, DualGAN or CycleGAN can be leveraged to learn a representation that encompasses different data sets. |
| Imbalanced Data Set | Majority Cases | Minority Cases | Number of Features | Numeric Features | Ordinal Features |
|---|---|---|---|---|---|
| Credit Card Fraud | 284,807 | 492 | 31 | 31 | 0 |
| Pima Indians Diabetes | 500 | 268 | 8 | 8 | 0 |
| Glass Identification | 144 | 70 | 9 | 9 | 0 |
| German Credit Scoring | 700 | 300 | 20 | 14 | 6 |
| Breast Cancer Wisconsin | 357 | 212 | 28 | 28 | 0 |
| Data Set | Value of k-NN |
|---|---|
| Credit Card Fraud | 6 |
| Pima Indians Diabetes | 9 |
| Glass Identification | 10 |
| German Credit Scoring | 12 |
| Breast Cancer Wisconsin | 10 |
| Parameter | Value |
|---|---|
| Confusion Matrix | Predicted: Minority | Predicted: Majority |
|---|---|---|
| Actual: Minority | True Positive (TP) | False Negative (FN) |
| Actual: Majority | False Positive (FP) | True Negative (TN) |
| Metric | Formula |
|---|---|
| Accuracy | |
| Precision | |
| Recall | |
| F1-Score | 2 |
| Method | Precision | Recall | F1-Score | AUPRC | AUC |
|---|---|---|---|---|---|
| Credit Card Fraud | |||||
| Baseline | |||||
| SMOTE | |||||
| WCGAN-GP | |||||
| Pima Indians Diabetes | |||||
| Baseline | |||||
| SMOTE | 53.54% | 80.30% | 64.24% | 68.18% | 75.48% |
| WCGAN-GP | |||||
| German Credit Scoring | |||||
| Baseline | |||||
| SMOTE | 47.83% | 70.51% | 56.99% | 58.84% | 69.61% |
| WCGAN-GP | |||||
| Glass Identification | |||||
| Baseline | |||||
| SMOTE | 73.91% | 70.83% | 72.34% | 87.29% | 72.86% |
| WCGAN-GP | 78.57% | ||||
| Breast Cancer Wisconsin | |||||
| Baseline | |||||
| SMOTE | 92.59% | 100.00% | 96.15% | 98.56% | 96.45% |
| WCGAN-GP |
| Data Set | p-Value | Significance |
|---|---|---|
| Credit Card Fraud | 2.9560 × | Yes |
| Pima Indians Diabetes | 0.188386 | No |
| German Credit Scoring | 1.0683 × | Yes |
| Glass Identification | 0.465622 | No |
| Breast Cancer Wisconsin | 4.0085 × | Yes |
| Test | Credit Card Fraud | German Credit | Breast Cancer |
|---|---|---|---|
| WCGAN-GP vs. SMOTE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngwenduna, K.S.; Mbuvha, R. Alleviating Class Imbalance in Actuarial Applications Using Generative Adversarial Networks. Risks 2021, 9, 49. https://doi.org/10.3390/risks9030049
Ngwenduna KS, Mbuvha R. Alleviating Class Imbalance in Actuarial Applications Using Generative Adversarial Networks. Risks. 2021; 9(3):49. https://doi.org/10.3390/risks9030049
Chicago/Turabian StyleNgwenduna, Kwanda Sydwell, and Rendani Mbuvha. 2021. "Alleviating Class Imbalance in Actuarial Applications Using Generative Adversarial Networks" Risks 9, no. 3: 49. https://doi.org/10.3390/risks9030049
APA StyleNgwenduna, K. S., & Mbuvha, R. (2021). Alleviating Class Imbalance in Actuarial Applications Using Generative Adversarial Networks. Risks, 9(3), 49. https://doi.org/10.3390/risks9030049






