Pricing, Risk and Volatility in Subordinated Market Models
Abstract
1. Introduction
1.1. Time Subordination in Financial Modelling
1.2. Contributions of the Paper
- (a)
- demonstrate that the recent pricing formulas for the VG, NIG and FD models are precise and fast converging, and can be successfully used for other applications (e.g., calculations of volatility curve);
- (b)
- provides efficient closed-form formulas for first and second-order risk sensitivities (Delta, Gamma) and compare them with numerical techniques; and,
- (c)
- deduce from these formulas several practical features regarding delta-hedging policies and portfolio performance.
1.3. Structure of the Paper
2. Exponential Lévy Processes
2.1. Basics of Lévy Processes
2.2. Exponential Lévy Motions
2.3. Option Pricing
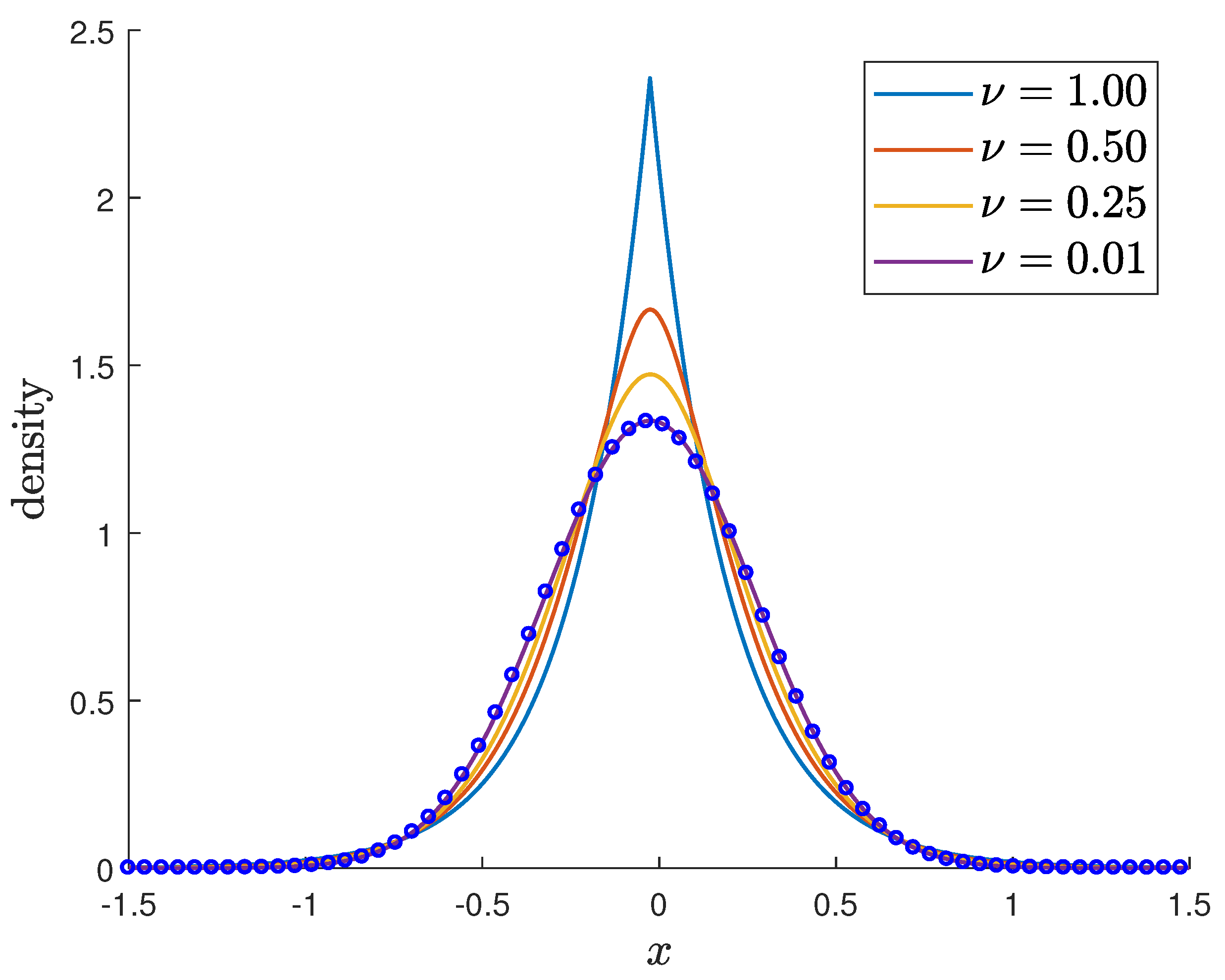
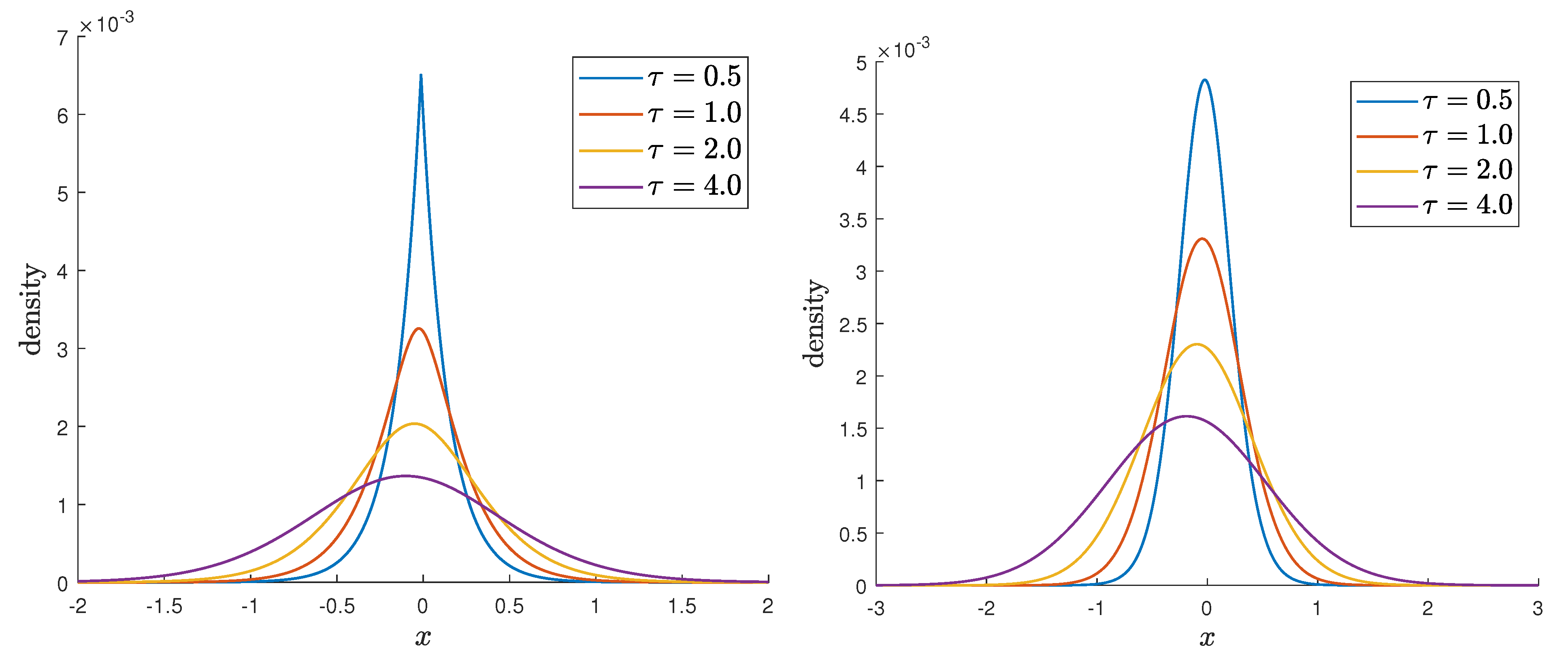
3. Subordinated Models
3.1. Exponential VG Model
3.1.1. Model Characteristics
3.1.2. Financial Applications
3.2. Exponential NIG Model
3.2.1. Model Characteristics
3.2.2. Financial Applications
3.3. Fractional Diffusion Model
3.3.1. Lévy-Stable Processes and Fractional Derivatives
3.3.2. Model Characteristics
3.3.3. Financial Applications
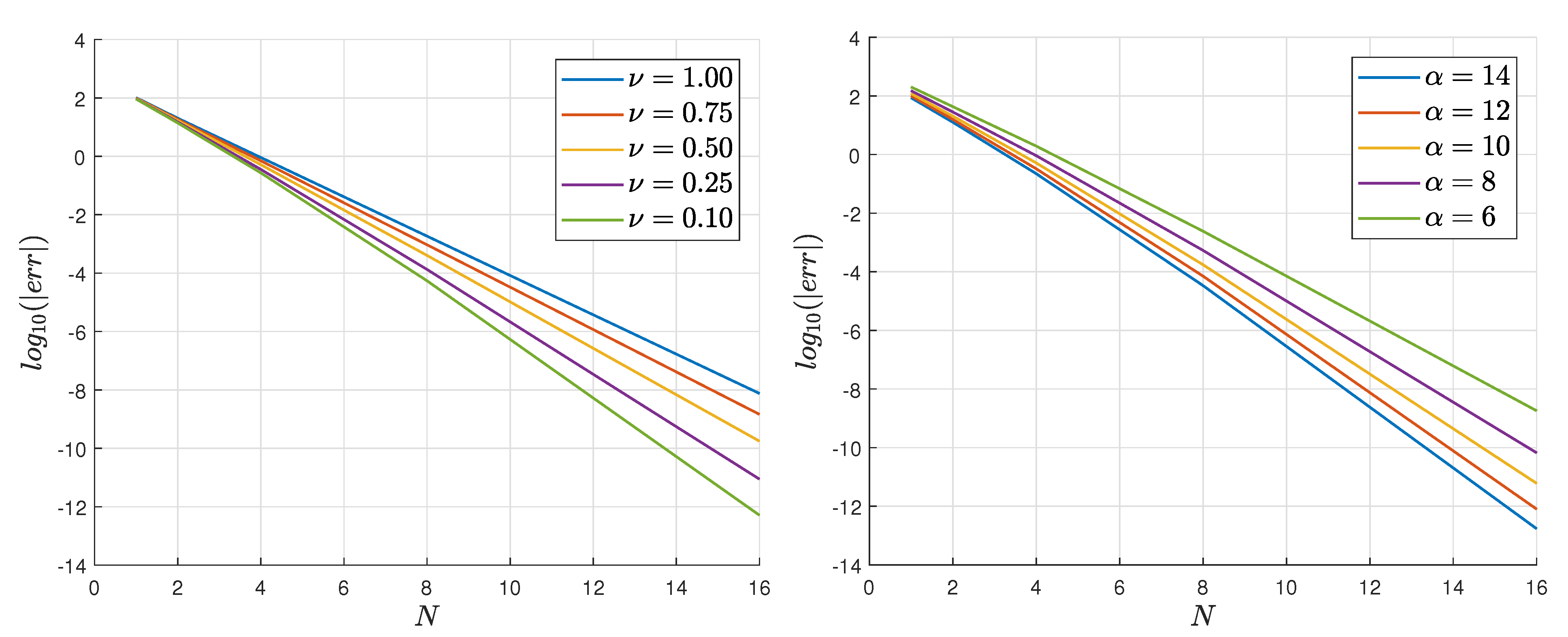
4. Pricing and Volatility Modelling
- -
- (OTM price) If ,
- -
- (ITM price) If ,
- -
- (ATM price) If ,
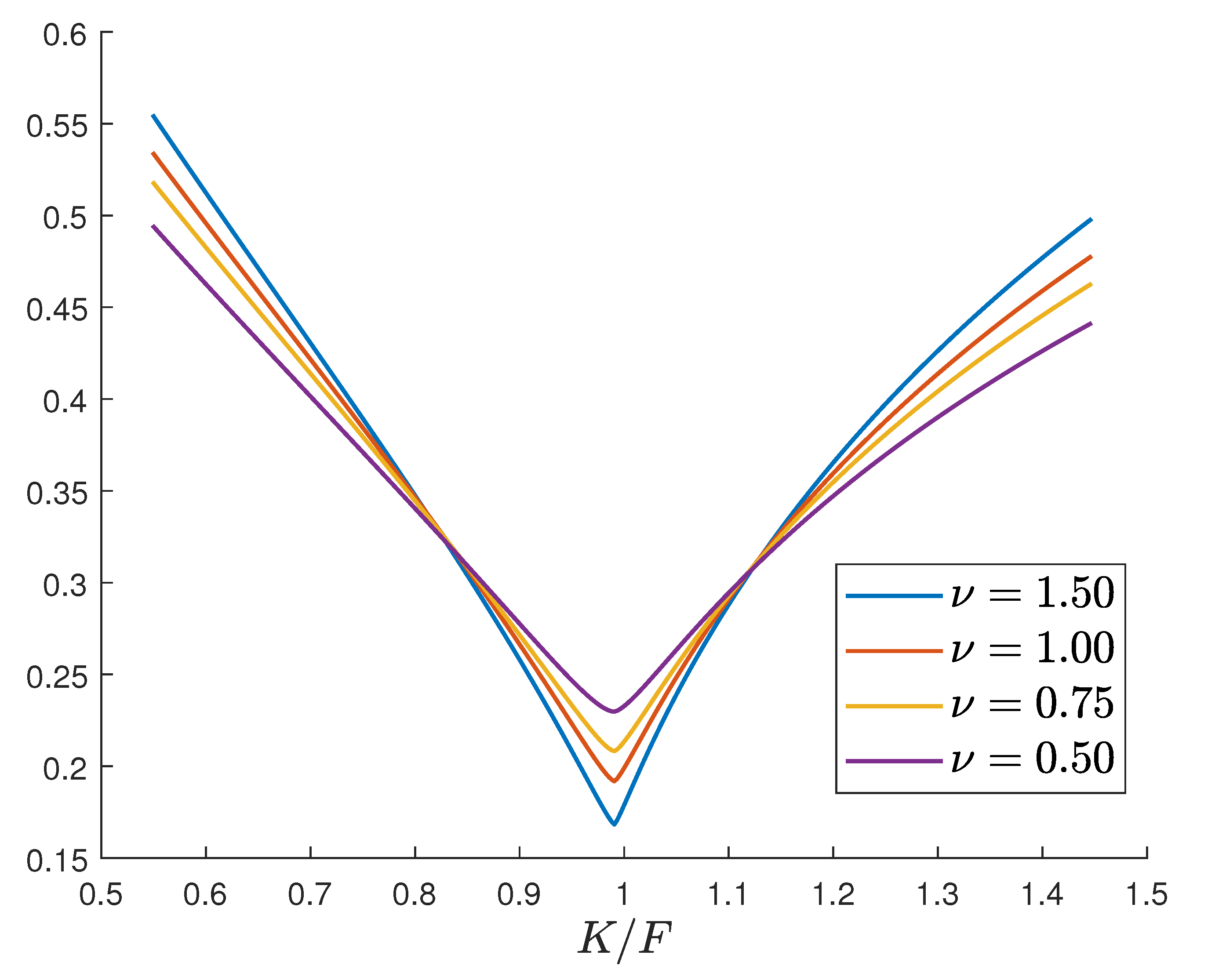
4.1. At-the-Money Forward Approximations
4.2. Implied Volatility
5. First-Order Sensitivities
- -
- (OTM sensitivity) If ,
- -
- (ITM sensitivity) If ,
- -
- (ATM sensitivity) If ,
5.1. Delta Hedging
5.2. Comparisons with Numerical Techniques
6. Second-Order Sensitivities and Portfolio Performance
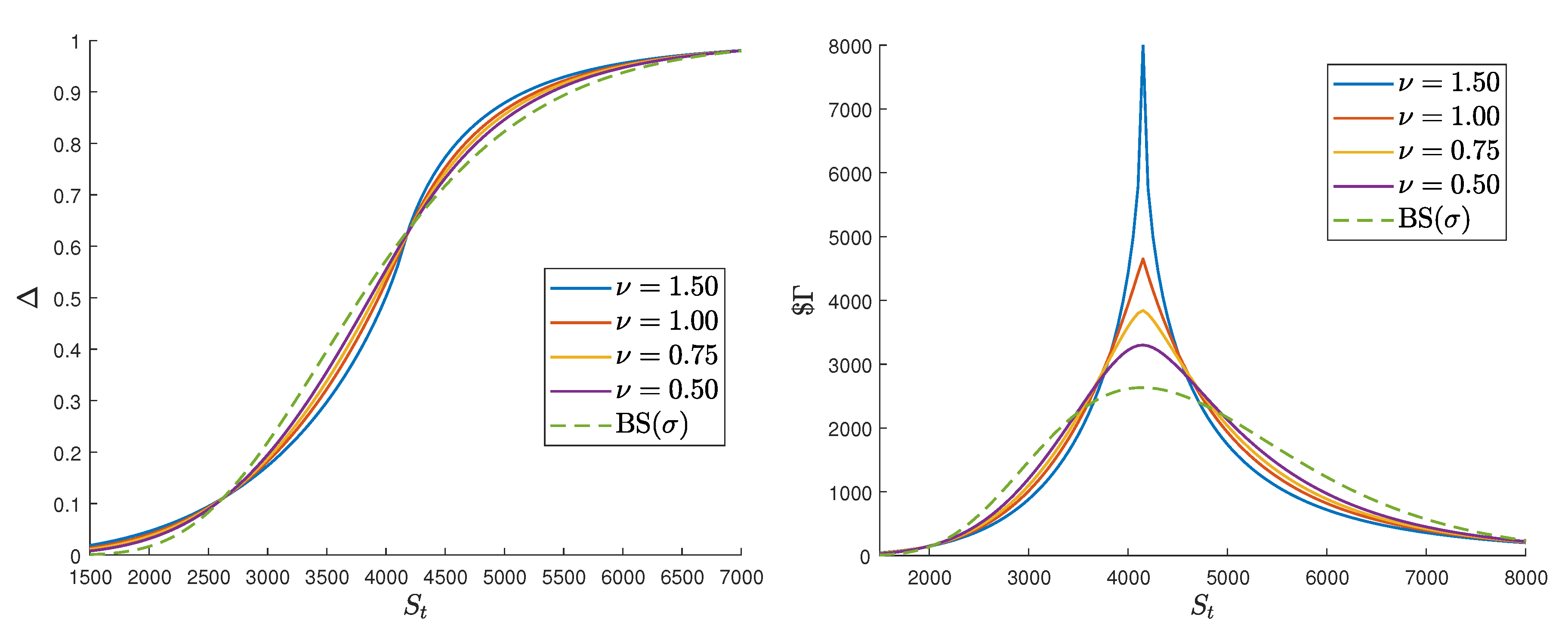
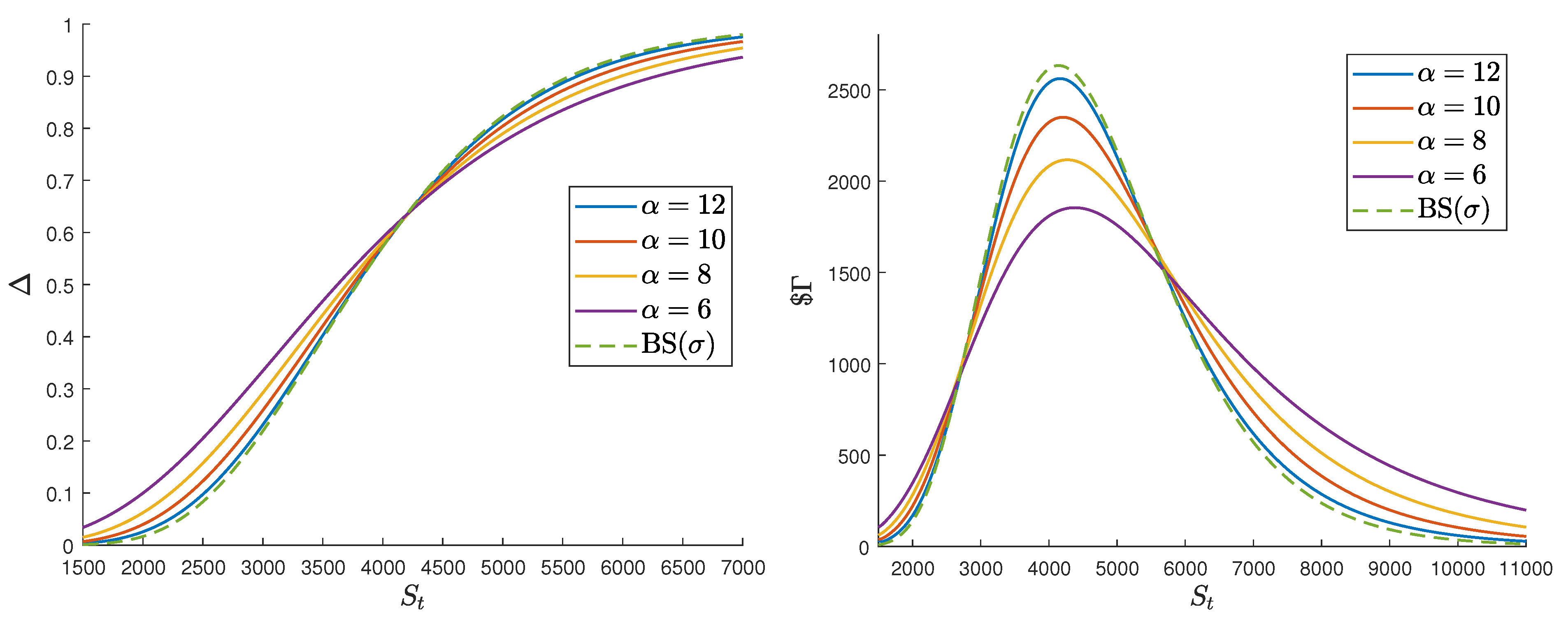
6.1. Gamma, Dollar Gamma
- -
- (OTM sensitivity) If ,
- -
- (ITM sensitivity) If ,
- -
- (ATM sensitivity) If ,
6.2. Properties and Particular Cases
7. Concluding Remarks
- (a)
- The pricing formulas are smooth and fast converging, and provide excellent agreement with efficient numerical techniques (such as the PROJ method). Moreover, these formulas can provide useful approximations for at-the-money options, and allow for the construction of volatility curves.
- (b)
- We have derived several analytical formulas for risk sensitivities and shown that they also provide excellent agreement with standard numerical (Fourier) evaluations.
- (c)
- Thanks to these formulas, we were able to show that the presence of a time subordination in the VG, NIG, and FD models has a minimal impact on the delta hedging policy of an at-the-money option, but, on the contrary, has a direct impact on the P&L of the delta hedged portfolio.
Author Contributions
Funding
Conflicts of Interest
References
- Abramowitz, Milton, and Irene Stegun. 1972. Handbook of Mathematical Functions. Mineola: Dover Publications. [Google Scholar]
- Aguilar, Jean-Philippe. 2020a. Some pricing tools for the Variance Gamma model. International Journal of Theoretical and Applied Finance 23: 2050025. [Google Scholar] [CrossRef]
- Aguilar, Jean-Philippe. 2020b. Explicit option valuation in the exponential NIG model. arXiv arXiv:2006.04659. [Google Scholar]
- Aguilar, Jean-Philippe. 2020c. Pricing Path-Independent Payoffs with Exotic Features in the Fractional Diffusion Model. Fractal Fract 4: 2. [Google Scholar] [CrossRef]
- Aguilar, Jean-Philippe, Cyril Coste, and Jan Korbel. 2018. Series representation of the pricing formula for the European option driven by space-time fractional diffusion. Fractional Calculus and Applied Analysis 21: 981–1004. [Google Scholar] [CrossRef]
- Andrews, Larry. 1992. Special Functions of Mathematics for Engineers. New York: McGraw & Hill. [Google Scholar]
- Barndorff-Nielsen, Ole. 1977. Exponentially decreasing distributions for the logarithm of particle size. Proceedings of the Royal Society of London 353: 401–19. [Google Scholar]
- Barndorff-Nielsen, Ole, John Kent, and Michael Sørensen. 1982. Normal Variance-Mean Mixtures and z Distributions. International Statistical Review 50: 145–59. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole. 1997. Normal inverse Gaussian distributions and stochastic volatility models. Scandinavian Journal of Statistics 24: 1–133. [Google Scholar] [CrossRef]
- Bertoin, Jean. 1999. Subordinators: Examples and Applications. In Lectures on Probability Theory and Statistics. Lecture Notes in Mathematics. Edited by Bernard Pierre. Berlin and Heidelberg: Springer, vol. 1717. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The Pricing of Options and Corporate Liabilities. The Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bochner, Salomon. 1949. Diffusion equation and stochastic processes. Proceedings of the National Academy of Science of the United States of America 35: 368–70. [Google Scholar]
- Boyarchenko, Svetlana, and Sergei Levendorskiĭ. 2000. Option pricing for truncated Lévy Processes. International Journal of Theoretical and Applied Finance 3: 549–52. [Google Scholar] [CrossRef]
- Brenner, Menahem, and Marti G. Subrahmanyam. 1994. A simple approach to option valuation and hedging in the Black-Scholes Model. Financial Analysts Journal 50: 25–28. [Google Scholar] [CrossRef]
- Calvet, Laurent, and Adlai Fischer. 2008. Multifractal Volatility: Theory, Forecasting and Pricing. Burlington: Academic Press. [Google Scholar]
- Carr, Peter, and Dilip Madan. 1999. Option valuation using the Fast Fourier Transform. Journal of Computational Finance 2: 61–73. [Google Scholar] [CrossRef]
- Carr, Peter, Hélyette Geman, Dilip Madan, and Marc Yor. 2002. The Fine Structure of Asset Returns: An Empirical Investigation. Journal of Business 75: 305–32. [Google Scholar] [CrossRef]
- Carr, Peter, and Liurn Wu. 2003. The Finite Moment Log Stable Process and Option Pricing. The Journal of Finance 58: 753–77. [Google Scholar] [CrossRef]
- Carr, Peter, and Liuren Wu. 2004. Time-changed Lévy processes and option pricing. Journal of Financial Economics 71: 113–41. [Google Scholar] [CrossRef]
- Cartea, Alavaro, and Diego del-Castillo-Negrete. 2007. Fractional diffusion models of option prices in markets with jumps. Physica A 374: 749–63. [Google Scholar] [CrossRef]
- Cont, Rama, and Peter Tankov. 2004. Financial Modelling with Jump Processes. New York: Chapman & Hall. [Google Scholar]
- Cont, Rama. 2007. Volatility Clustering in Financial Markets: Empirical Facts and Agent-Based Models. In Long Memory in Economics. Edited by Teyssière Gilles and Kirman Alan. Berlin and Heidelberg: Springer. [Google Scholar]
- Clark, Peter K. 1973. A subordinated stochastic process model with fixed variance for speculative prices. Econometrica 41: 135–55. [Google Scholar] [CrossRef]
- Cui, Zhenyu, Justin L. Kirkby, and Duy Nguyen. 2017. Equity-linked annuity pricing with cliquet-style guarantees in regime-switching and stochastic volatility models with jumps. Insurance: Mathematics and Economics 74: 46–62. [Google Scholar] [CrossRef]
- Cui, Zhenyu, Justin L. Kirkby, and Duy Nguyen. 2019. A general framework for time-changed Markov processes and applications. European Journal of Operational Research 273: 785–800. [Google Scholar] [CrossRef]
- de Jonge, Bram, Ruud Teunter, and Tiedo Tinga. 2017. The influence of practical factors on the benefits of condition-based maintenance over time-based maintenance. Reliability Engineering & System Safety 158: 21–30. [Google Scholar]
- Eberlein, Ernst, and Ulrich Keller. 1995. Hyperbolic distributions in finance. Bernoulli 1: 281–99. [Google Scholar] [CrossRef]
- Eberlein, Ernst, Kathrin Glau, and Antonis Papapantoleon. 2010. Analysis of Fourier Transform Valuation Formulas and Applications. Applied Mathematical Finance 17: 211–40. [Google Scholar] [CrossRef]
- Fang, Fang, and Cornelis W. Oosterlee. 2008. A novel pricing method for European options based on Fourier cosine series expansions. SIAM Journal on Scientific Computing 31: 826–48. [Google Scholar] [CrossRef]
- Figueroa-López, José E., Steven R. Lancette, Kiseop Lee, and Yanhui Mi. 2012. Estimation of NIG and VG models for high frequency financial data. In Handbook of Modeling High-Frequency Data in Finance. Edited by Viens Frederi, Mariani Maria and Florescu Ionut. Hoboken: John Wiley & Sons. [Google Scholar]
- Fiorani, Filippo, Elisa Luciano, and Patrizia Semeraro. 2007. Single and Joint Default in a Structural Model with Purely Discontinuous Assets. Carlo Alberto Notebooks Working Paper 41. Available online: https://EconPapers.repec.org/RePEc:cca:wpaper:41 (accessed on 8 November 2020).
- Geman, Hélyette. 2009. Stochastic Clock and Financial Markets. Handbook of Numerical Analysis 15: 649–63. [Google Scholar]
- Gorenflo, Rudolf, Francesco Mainardi, and Alessandro Vivoli. 2006. Discrete and Continuous Random Walk Models for Space-Time Fractional Diffusion. Journal of Mathematical Sciences 132: 614–28. [Google Scholar] [CrossRef]
- Ivanov, Roman. 2018. Option pricing in the variance-gamma model under the drift jump. International Journal of Theoretical and Applied Finance 21: 1–19. [Google Scholar] [CrossRef]
- Jizba, Petr, Jan Korbel, Hynek Lavička, Martin Prokš, Václav Svoboda, and Christian Beck. 2018. Transition between superstatistical regimes: Validity, breakdown and applications. Physica A 493: 29–46. [Google Scholar] [CrossRef]
- Kirkby, Justin L. 2015. Efficient Option Pricing by Frame Duality with the Fast Fourier Transform. SIAM Journal on Financial Mathematics 6: 713–47. [Google Scholar] [CrossRef]
- Kleinert, Hagen, and Jan Korbel. 2016. Option Pricing Beyond Black-Scholes Based on Double-Fractional Diffusion. Physica A 449: 200–14. [Google Scholar] [CrossRef]
- Korbel, Jan, and Yuri Luchko. 2016. Modeling of financial processes with a space-time fractional diffusion equation of varying order. Fractional Calculus and Applied Analysis 19: 1414–33. [Google Scholar] [CrossRef]
- Kou, Steven. 2002. A jump-diffusion model for option pricing. Management Science 48: 1086–101. [Google Scholar] [CrossRef]
- Krawiecki, Andrzej, Janusz A. Holyst, and Dirk Helbing. 2002. Volatility Clustering and Scaling for Financial Time Series due to Attractor Bubbling. Physical Review Letters 89: 158701. [Google Scholar] [CrossRef] [PubMed]
- Lam, Kin, Eric Chang, and Matthew C. Lee. 2002. An empirical test of the variance gamma option pricing model. Pacific-Basin Finance Journal 10: 267–85. [Google Scholar] [CrossRef]
- Lewis, Alan. 2001. A Simple Option Formula for General Jump-Diffusion and Other Exponential Lévy Processes. SSRN. SSRN 282110. Available online: https://ssrn.com/abstract=282110 (accessed on 8 November 2020).
- Li, Changpin, Deliang Qian, and YangQuan Chen. 2011. On Riemann-Liouville and Caputo Derivatives. Discrete Dynamics in Nature and Society 2011: 562494. [Google Scholar] [CrossRef]
- Li, Lingfei, and Vadim Linetsky. 2014. Time-Changed Ornstein-Uhlenbeck processes and their applications in commodity derivative models. Mathematical Finance 24: 289–330. [Google Scholar] [CrossRef]
- Linders, Daniel, and Ben Stassen. 2015. The multivariate Variance Gamma model: Basket option pricing and calibration. Quantitative Finance 16: 555–72. [Google Scholar] [CrossRef]
- Luchko, Yuri, Jean-Philippe Aguilar, and Jan Korbel. 2019. Applications of the Fractional Diffusion Equation to Option Pricing and Risk Calculations. Mathematics 7: 796. [Google Scholar]
- Luciano, Elisa, and Wim Schoutens. 2006. A multivariate jump-driven financial asset model. Quantitative Finance 6: 385–402. [Google Scholar] [CrossRef]
- Luciano, Elisa. 2009. Business Time and New Credit Risk Models. Convegno Economia e Incertezza. Available online: https://ideas.repec.org/p/icr/wpmath/16-2010.html#download (accessed on 1 October 2020).
- Luciano, Elisa, and Patrizia Semeraro. 2010. Multivariate time changes for Lévy asset models: Characterization and calibration. Journal of Computational and Applied Mathematics 223: 1937–53. [Google Scholar] [CrossRef][Green Version]
- Lux, Thomas, and Michele Marchesi. 2000. Volatility Clustering in Financial Markets: A MicroSimulation of Interacting Agents. International Journal of Theoretical and Applied Finance 3: 675–702. [Google Scholar] [CrossRef]
- Madan, Dilip, Peter Carr, and Eric Chang. 1998. The Variance Gamma Process and Option Pricing. European Finance Review 2: 79–105. [Google Scholar] [CrossRef]
- Madan, Dilip, and Eugene Seneta. 1990. The Variance Gamma (V.G.) Model for Share Market Returns. The Journal of Business 63: 511–24. [Google Scholar] [CrossRef]
- Madan, Dilip, and Elton A. Daal. 2005. An Empirical Examination of the Variance Gamma Model for Foreign Currency Options. The Journal of Business 78: 2121–52. [Google Scholar]
- Mainardi, Francesco, Yuri Luchko, and Gianni Pagnini. 2001. The fundamental solution of the space-time fractional diffusion equation. Fractional Calculus and Applied Analysis 4: 153–92. [Google Scholar]
- Mandelbrot, Benoit. 1963. The Variation of Certain Speculative Prices. The Journal of Business 36: 384–419. [Google Scholar] [CrossRef]
- Merton, Robert. 1976. Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics 3: 125–44. [Google Scholar] [CrossRef]
- Mittnik, Svetlozar, and Stefan Rachev. 2000. Stable Paretian Models in Finance. Hoboken: John Wiley & Sons. [Google Scholar]
- Niu, Hongli, and Jun Wang. 2013. Volatility clustering and long memory of financial time series and financial price model. Digital Signal Processing 23: 489–98. [Google Scholar] [CrossRef]
- Phelan, Carolyn E., Daniele Marazzina, Gianluca Fusai, and Guido Germano. 2019. Hilbert transform, spectral filters and option pricing. Annals of Operations Research 282: 273–98. [Google Scholar] [CrossRef]
- Ruijter, Marjon, Mark Versteegh, and Cornelis W. Oosterlee. 2015. On the application of spectral filters in a Fourier option pricing technique. Journal of Computational Finance 19: 76–106. [Google Scholar] [CrossRef]
- Rydberg, Tina Hviid. 1997. The Normal inverse Gaussian Lévy process: Simulation and approximation. Communications in Statistics. Stochastic Models 13: 887–910. [Google Scholar] [CrossRef]
- Samko, Stefan, Anatoly A. Kilbas, and Oleg Marichev. 1993. Fractional Integrals and Derivatives, Theory and Applications. Yverdon: Gordon and Breach Science Publishers. [Google Scholar]
- Sato, Ken-iti. 1999. Lévy Processes and Infinitely Divisible Distributions. Cambridge: Cambridge University Press. [Google Scholar]
- Schoutens, Wim. 2003. Lévy Processes in Finance: Pricing Financial Derivatives. Hoboken: Wiley & Sons. [Google Scholar]
- Semeraro, Patrizia. 2008. A multivariate Variance Gamma model for financial applications. International Journal of Theoretical and Applied Finance 11: 1–18. [Google Scholar] [CrossRef]
- Takahashi, Akihiko, and Akira Yamazaki. 2008. Efficient static replication of European options under exponential Lévy models. The Journal of Futures Markets 29: 1–15. [Google Scholar] [CrossRef]
- Tarasov, Vasily E. 2019. On history of mathematical economics: Application of fractional calculus. Mathematics 7: 509. [Google Scholar] [CrossRef]
- Tomovski, Živorad, Johan L. A. Dubbeldam, and Jan Korbel. 2020. Applications of Hilfer-Prabhakar operator to option pricing financial model. Fractional Calculus and Applied Analysis 23: 996–1012. [Google Scholar] [CrossRef]
- Venter, Johannes, and Riaan de Jongh. 2002. Risk estimation using the Normal inverse Gaussian distribution. The Journal of Risks 2: 1–25. [Google Scholar] [CrossRef]
- Zolotarev, Vladimir. 1986. One-dimensional Stable Distributions. Providence: American Mathematical Soc. [Google Scholar]
| Subordinated Model | Limiting Regimes |
|---|---|
| VG | VG BS |
| NIG | NIG BS |
| FD | FD FMLS BS |
| sub-BS(,) FD | sub-BS BS |
| ATMF Implied Volatility (European Options) | |
|---|---|
| Exponential VG | |
| Low variance regime (): | |
| Exponential NIG | Solve |
| Large steepness regime (): | |
| At order : | |
| sub-BS | |
| Non-fractional regime (): | |
| Exponential VG Model [, ] | |||||
|---|---|---|---|---|---|
| Formula (2) | Lewis (74) | ||||
| Deep OTM () | 2.1823 | 0.6347 | 0.0941 | 0.0940 | 0.0940 |
| OTM () | 0.4113 | 0.2567 | 0.2455 | 0.2455 | 0.2455 |
| ATM () | 0.5703 | 0.5718 | 0.5719 | 0.5719 | 0.5719 |
| ITM () | 0.7569 | 0.8113 | 0.8134 | 0.8134 | 0.8134 |
| Deep ITM () | 0.4729 | 0.8589 | 0.9206 | 0.9206 | 0.9206 |
| Exponential NIG Model [, ] | |||||
| Formula (2) | Lewis (74) | ||||
| Deep OTM () | 0.2921 | 0.2722 | 0.2747 | 0.2748 | 0.2748 |
| OTM () | 0.4289 | 0.4309 | 0.4311 | 0.4311 | 0.4311 |
| ATM () | 0.6336 | 0.6410 | 0.6412 | 0.6412 | 0.6412 |
| ITM () | 0.6936 | 0.7030 | 0.7033 | 0.7033 | 0.7033 |
| Deep ITM () | 0.7827 | 0.7966 | 0.7971 | 0.7971 | 0.7971 |
| 1st Order () | 2nd Order () | |
|---|---|---|
| Exponential VG | ||
| Low variance regime (): | ||
| Exponential NIG | ||
| Large steepness regime (): | ||
| FD | ||
| sub-BS | ||
| Non fractional regime (): | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, J.-P.; Kirkby, J.L.; Korbel, J. Pricing, Risk and Volatility in Subordinated Market Models. Risks 2020, 8, 124. https://doi.org/10.3390/risks8040124
Aguilar J-P, Kirkby JL, Korbel J. Pricing, Risk and Volatility in Subordinated Market Models. Risks. 2020; 8(4):124. https://doi.org/10.3390/risks8040124
Chicago/Turabian StyleAguilar, Jean-Philippe, Justin Lars Kirkby, and Jan Korbel. 2020. "Pricing, Risk and Volatility in Subordinated Market Models" Risks 8, no. 4: 124. https://doi.org/10.3390/risks8040124
APA StyleAguilar, J.-P., Kirkby, J. L., & Korbel, J. (2020). Pricing, Risk and Volatility in Subordinated Market Models. Risks, 8(4), 124. https://doi.org/10.3390/risks8040124






