Exploiting Distributional Temporal Difference Learning to Deal with Tail Risk
Abstract
1. Introduction
2. Nontechnical Overview
2.1. Machine Learning
2.2. Reinforcement Learning
2.3. Our Contribution
3. Preliminaries
3.1. TD Learning
3.2. Distributional Reinforcement Learning (disRL)
4. Leptokurtosis
- Leptokurtosis of the reward distribution. disRL simply integrates over the distribution in order to estimate the true Q value. Traditional TD Learning uses a recursive estimate. Both are inefficient under leptokurtosis. Indeed, in general there exist much better estimators than the sample average, whether calculated using the entire sample, or calculated recursively. The most efficient estimator is the one that reaches the Cramér-Rao lower bound, or if this bound is invalid, the Chapman-Robbins lower bound (Casella and Berger 2002; Schervish 2012). Under conditions where maximum likelihood estimation (MLE) is consistent, MLE will provide the asymptotically most efficient estimator with the lowest variance: it reaches the Cramér-Rao lower bound (Casella and Berger 2002). Often, the MLE estimator of the mean is very different from the sample average. This is the case, among others, under leptokurtosis.
- Heterogeneity of the prediction error. The prediction error (TD error) is the sum of two components, the period reward and the (discounted) increment in values . As the agent has learned the optimal policy and the state transition probabilities, Q values converge to expectations of sums of rewards. These expectations should eventually depend only on states and actions. Since the distribution of state transitions is generally assumed to be non-leptokurtic (e.g., Poisson), the increment in Q values will no longer exhibit leptokurtosis. At the same time, rewards continue to be drawn from a leptokurtic distribution. As a result, the prediction error is a sum of a leptokurtic term and an asymptotically non-leptokurtic term. The resulting heterogeneity needs to be addressed. Measures to deal with leptokurtosis may inadversely affect the second term.8 The two terms have to be decoupled during updating. This is done neither in traditional TD Learning nor in disRL.
- Non-stationarity of the distribution of values. As the agent learns, the empirical distribution of Q values shifts. These shifts can be dramatic, especially in a leptokurtic environment. This is problematic for implementations disRL that proceed as if it the distribution of Q values is stationary. Categorical disRL, for instance, represents the distribution by means of histogram defined over a pre-set range. Outlier rewards may challenge the set range (i.e., outliers easily push the estimated Q-values beyond the set range). One could use a generous range, but this reduces the precision with which the middle of the distribution is estimated. We will illustrate this with an example when presenting results from our simulation experiments. Recursive procedures, like those used in the Kalman filter or in conventional TD learning, are preferred when a distribution is expected to change over time. Versions of disRL that fix probability levels (e.g., by fixing probability levels, as in quantile disRL; Dabney et al. (2018)) allow the range to flexibly adjust, and therefore can accommodate nonstationarity. These would provide viable alternatives as well.
5. Proposed Solution
5.1. Environment
5.2. Efficient disRL (e-disRL)
- e-disRL-: Rewards and discounted action-value updates are separated; standard recursive TD learning is applied to the latter, and standard disRL to the former (i.e., the mean is estimated by simple integration over the empirical reward distribution).
- e-disRL: Same as e-disRL-, but we use an efficient estimator for the mean of the reward distribution.
| Algorithm 1: Pseudo-Code for e-disRL- and e-disRL. |
 |
5.3. Convergence
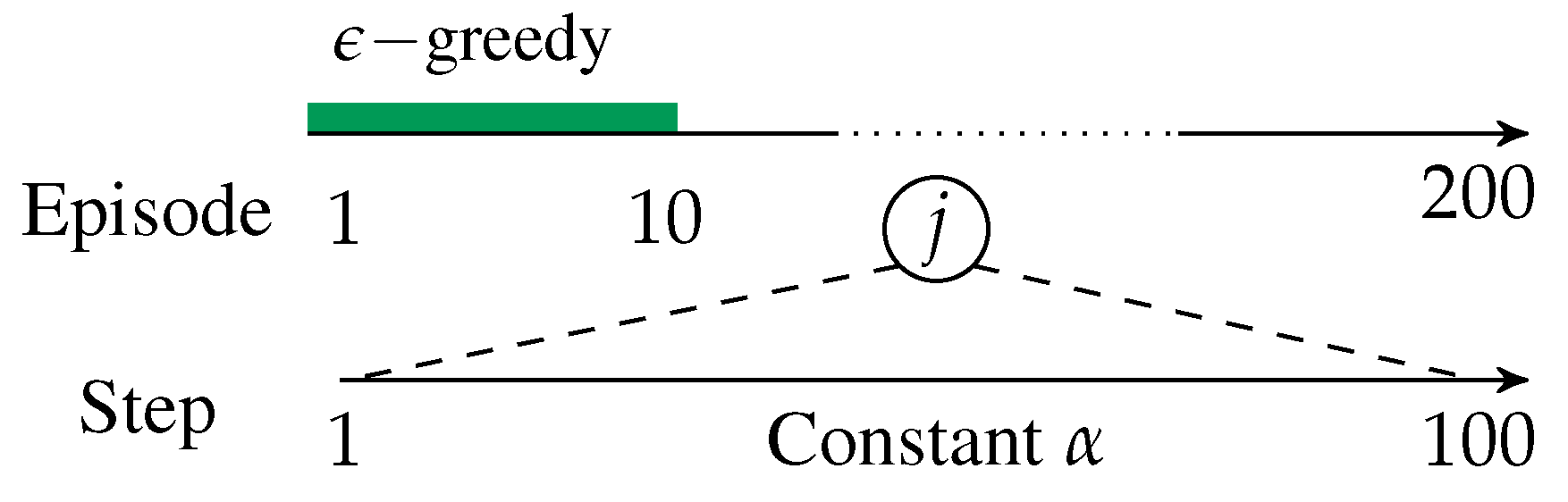
6. Simulation Experiments
6.1. Methods
6.2. The Gaussian Environment
6.3. The Leptokurtic Enviroment I: t-Distribution
6.4. The Leptokurtic Environment II: Drawing Rewards from the Empirical Distribution of S&P 500 Daily Returns
6.5. Impact of Outlier Risk on Categorical Distributional RL
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alberg, Dima, Haim Shalit, and Rami Yosef. 2008. Estimating stock market volatility using asymmetric garch models. Applied Financial Economics 18: 1201–8. [Google Scholar] [CrossRef]
- Bellemare, Marc G., Will Dabney, and Rémi Munos. 2017. A distributional perspective on reinforcement learning. Paper presented at 34th International Conference on Machine Learning, Sydney, Australia, August 7, vol. 70, pp. 449–58. [Google Scholar]
- Bellman, Richard Ernest. 1957. Dynamic Programming. Princeton, New Jersey, USA: Princeton University Press. [Google Scholar]
- Bogle, John C. 2016. The index mutual fund: 40 years of growth, change, and challenge. Financial Analysts Journal 72: 9–13. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. A conditionally heteroskedastic time series model for speculative prices and rates of return. Review of Economics and Statistics 69: 542–47. [Google Scholar] [CrossRef]
- Bossaerts, Peter. 2005. The Paradox of Asset Pricing. Princeton: Princeton University Press. [Google Scholar]
- Casella, George, and Roger L. Berger. 2002. Statistical Inference. Pacific Grove: Duxbury, vol. 2. [Google Scholar]
- Cichy, Radoslaw M., and Daniel Kaiser. 2019. Deep neural networks as scientific models. Trends in Cognitive Sciences 23: 305–17. [Google Scholar] [CrossRef] [PubMed]
- Corhay, Albert, and A. Tourani Rad. 1994. Statistical properties of daily returns: Evidence from european stock markets. Journal of Business Finance & Accounting 21: 271–82. [Google Scholar]
- Curto, José Dias, José Castro Pinto, and Gonçalo Nuno Tavares. 2009. Modeling stock markets’ volatility using garch models with normal, student’s t and stable paretian distributions. Statistical Papers 50: 311. [Google Scholar] [CrossRef]
- Dabney, Will, Georg Ostrovski, David Silver, and Rémi Munos. 2018. Implicit quantile networks for distributional reinforcement learning. Paper presented at International Conference on Machine Learning, Stockholm, Sweden, July 10. [Google Scholar]
- Dabney, Will, Mark Rowland, Marc G. Bellemare, and Rémi Munos. 2018. Distributional reinforcement learning with quantile regression. Paper presented at Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, February 2. [Google Scholar]
- d’Acremont, Mathieu, and Peter Bossaerts. 2016. Neural mechanisms behind identification of leptokurtic noise and adaptive behavioral response. Cerebral Cortex 26: 1818–30. [Google Scholar] [CrossRef]
- Franses, Philip Hans, Marco Van Der Leij, and Richard Paap. 2007. A simple test for garch against a stochastic volatility model. Journal of Financial Econometrics 6: 291–306. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2013. Monte Carlo Methods in Financial Engineering. New York: Springer Science & Business Media, vol. 53. [Google Scholar]
- Jurczenko, Emmanuel, and Bertrand Maillet. 2012. The four-moment capital asset pricing model: Between asset pricing and asset allocation. In Multi-Moment Asset Allocation and Pricing Models. Hoboken: John Wiley, pp. 113–63. [Google Scholar]
- Liu, Chuanhai, and Donald B. Rubin. 1995. Ml estimation of the t distribution using em and its extensions, ecm and ecme. Statistica Sinica 5: 19–39. [Google Scholar]
- Ludvig, Elliot A., Marc G. Bellemare, and Keir G. Pearson. 2011. A primer on reinforcement learning in the brain: Psychological, computational, and neural perspectives. In Computational Neuroscience for Advancing Artificial Intelligence: Models, Methods and Applications. Hershey: IGI Global, pp. 111–44. [Google Scholar]
- Lyle, Clare, Pablo Samuel Castro, and Marc G. Bellemare. 2019. A comparative analysis of expected and distributional reinforcement learning. Paper presented at International Conference on Artificial Intelligence and Statistics, Naha, Japan, April 16. [Google Scholar]
- Madan, Dilip B. 2017. Efficient estimation of expected stock price returns. Finance Research Letters 23: 31–38. [Google Scholar] [CrossRef]
- Mittnik, Stefan, Marc S. Paolella, and Svetlozar T. Rachev. 1998. Unconditional and conditional distributional models for the nikkei index. Asia-Pacific Financial Markets 5: 99. [Google Scholar] [CrossRef]
- Mnih, Volodymyr, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin Riedmiller. 2013. Playing atari with deep reinforcement learning. arXiv arXiv:1312.5602. [Google Scholar]
- Moravčík, Matej, Martin Schmid, Neil Burch, Viliam Lisỳ, Dustin Morrill, Nolan Bard, Trevor Davis, Kevin Waugh, Michael Johanson, and Michael Bowling. 2017. Deepstack: Expert-level artificial intelligence in heads-up no-limit poker. Science 56: 508–13. [Google Scholar] [CrossRef] [PubMed]
- Nowak, Piotr, and Maciej Romaniuk. 2013. A fuzzy approach to option pricing in a levy process setting. International Journal of Applied Mathematics and Computer Science 23: 613–22. [Google Scholar] [CrossRef]
- Poggio, Tomaso, and Thomas Serre. 2013. Models of visual cortex. Scholarpedia 8: 3516. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2000. Optimization of conditional value-at-risk. Journal of Risk 2: 21–42. [Google Scholar] [CrossRef]
- Rowland, Mark, Marc G. Bellemare, Will Dabney, Rémi Munos, and Yee Whye Teh. 2018. An analysis of categorical distributional reinforcement learning. arXiv arXiv:1802.08163. [Google Scholar]
- Rowland, Mark, Robert Dadashi, Saurabh Kumar, Rémi Munos, Marc G. Bellemare, and Will Dabney. 2019. Statistics and samples in distributional reinforcement learning. arXiv arXiv:1902.08102v1. [Google Scholar]
- Savage, Leonard J. 1972. The Foundations of Statistics. North Chelmsford: Courier Corporation. [Google Scholar]
- Scherer, Matthias, Svetlozar T. Rachev, Young Shin Kim, and Frank J. Fabozzi. 2012. Approximation of skewed and leptokurtic return distributions. Applied Financial Economics 22: 1305–16. [Google Scholar] [CrossRef]
- Schervish, Mark J. 2012. Theory of Statistics. New York, New York, USA: Springer Science & Business Media. [Google Scholar]
- Schultz, Wolfram, Peter Dayan, and P. Read Montague. 1997. A neural substrate of prediction and reward. Science 275: 1593–99. [Google Scholar] [CrossRef]
- Silver, David, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, and et al. 2016. Mastering the game of go with deep neural networks and tree search. Nature 529: 484–89. [Google Scholar] [CrossRef] [PubMed]
- Simonato, Jean-Guy. 2012. Garch processes with skewed and leptokurtic innovations: Revisiting the johnson su case. Finance Research Letters 9: 213–19. [Google Scholar] [CrossRef]
- Singh, Satinder, and Peter Dayan. 1998. Analytical mean squared error curves for temporal difference learning. Machine Learning 32: 5–40. [Google Scholar] [CrossRef]
- Sun, Qiang, Wen-Xin Zhou, and Jianqing Fan. 2020. Adaptive huber regression. Journal of the American Statistical Association 115: 254–65. [Google Scholar] [CrossRef]
- Sutton, Richard S., and Andrew G. Barto. 2018. Reinforcement Learning: An Introduction, 2nd ed. Cambridge: MIT Press. [Google Scholar]
- Taleb, Nassim Nicholas. 2007. The Black Swan: The Impact of the Highly Improbable. New York: Random House, vol. 2. [Google Scholar]
- Toenger, Shanti, Thomas Godin, Cyril Billet, Frédéric Dias, Miro Erkintalo, Goëry Genty, and John M. Dudley. 2015. Emergent rogue wave structures and statistics in spontaneous modulation instability. Scientific Reports 5: 10380. [Google Scholar] [CrossRef]
- Watkins, Christopher J. C. H., and Peter Dayan. 1992. Q-learning. Machine Learning 8: 279–92. [Google Scholar] [CrossRef]
| 1. | The term “return” refers to the percentage investment gain/loss obtained over a certain time frame (e.g., daily). It should not be confused with the term “return” referred to in the RL literature. However, the two terms are related as they both refer to some feedback from the environment/market to agents/investors. Likewise, we should be aware of the context (finance/RL) for proper interpretation of the terms “payoffs” or “rewards.” |
| 2. | SARSA is short for State-Action-Reward-State-Action. |
| 3. | The distribution can be remembered parsimoniously in various ways, e.g., as histograms, in terms of a specific set of quantiles or truncated expectations (“expectiles”). Compare, e.g., Bellemare et al. (2017); Dabney et al. (2018); Rowland et al. (2019). |
| 4. | Technically, this is not exactly true for many versions of disRL in the literature. Only parametrically fitted histograms, quantiles or expectiles are remembered, reducing memory load. |
| 5. | It is also referred as semi-supervised learning as it sits in-between the above two types. |
| 6. | We focus here on techniques that use the empirical distribution, since it is a consistent estimate of the true distribution, while the histogram is not consistent as an estimate of the true density. |
| 7. | To simplify things, we suppress the stochastic index “” which is used in probability theory to capture randomness. only affects the rewards, and not the value function Q. This distinction will be important when we discuss de-coupling of the terms of the RL updating equations. |
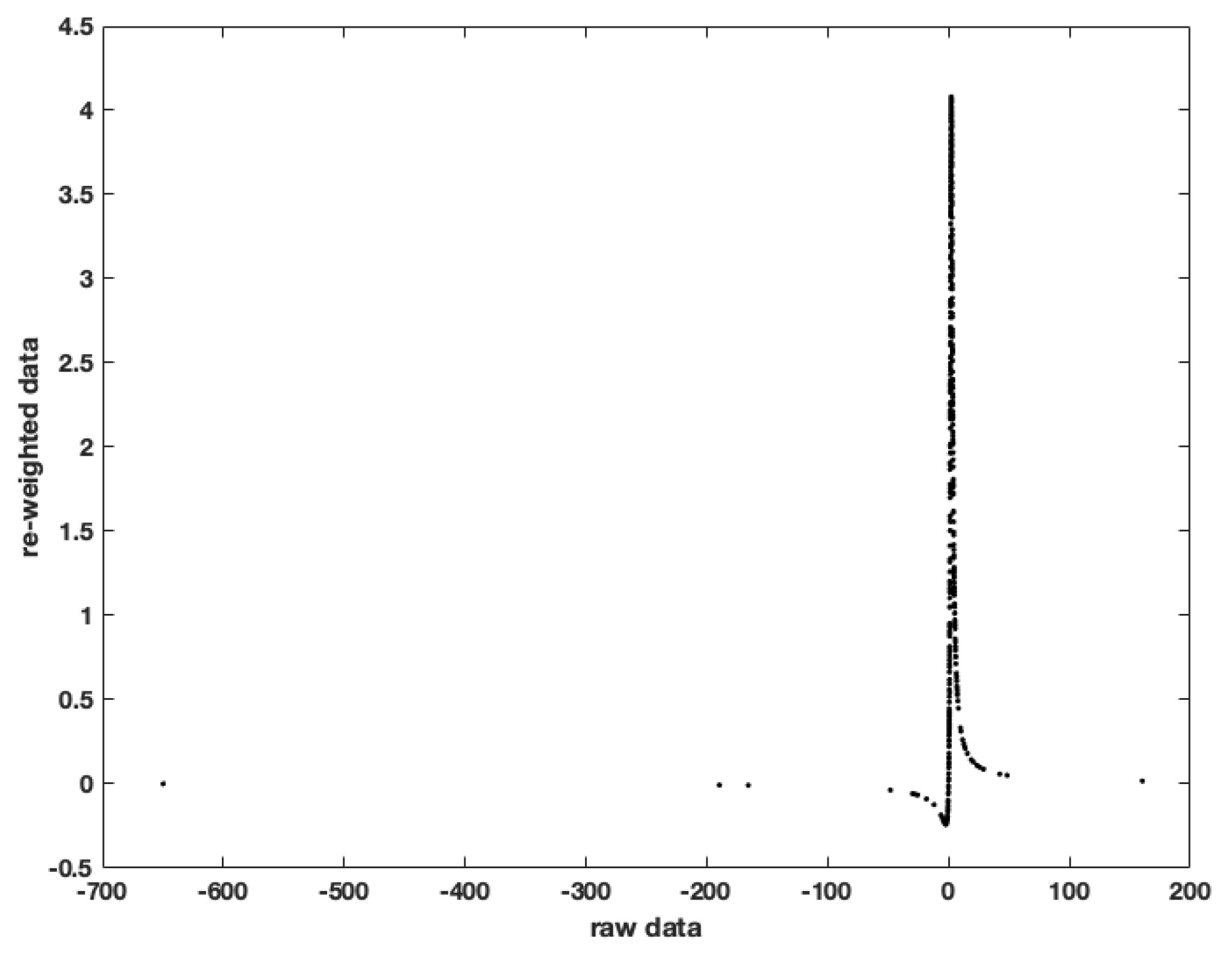
| 8. | Maximum likelihood estimation of the mean of a leptokurtic distribution, the t distribution for instance, eliminates the influence of outliers by setting them (close to) zero, as we shall document later (see Figure 2). The resulting estimator is less efficient than the simple sample average when the distribution is not leptokurtic, since observations are effectively discarded. |
| 9. | Traditional disRL approximates the empirical distribution of Q values with a parametric family of distribution, in order to capture complex relationships between a large state space and state-action values. This approximation complicates convergence proofs; see, e.g., Bellemare et al. (2017); Dabney et al. (2018); Rowland et al. (2018). |
| 10. | The quantiles or expectiles versions of disRL are not subject this influence. Like the empirical distribution approach we use in e-disRL, unbounded ranges are possible. |
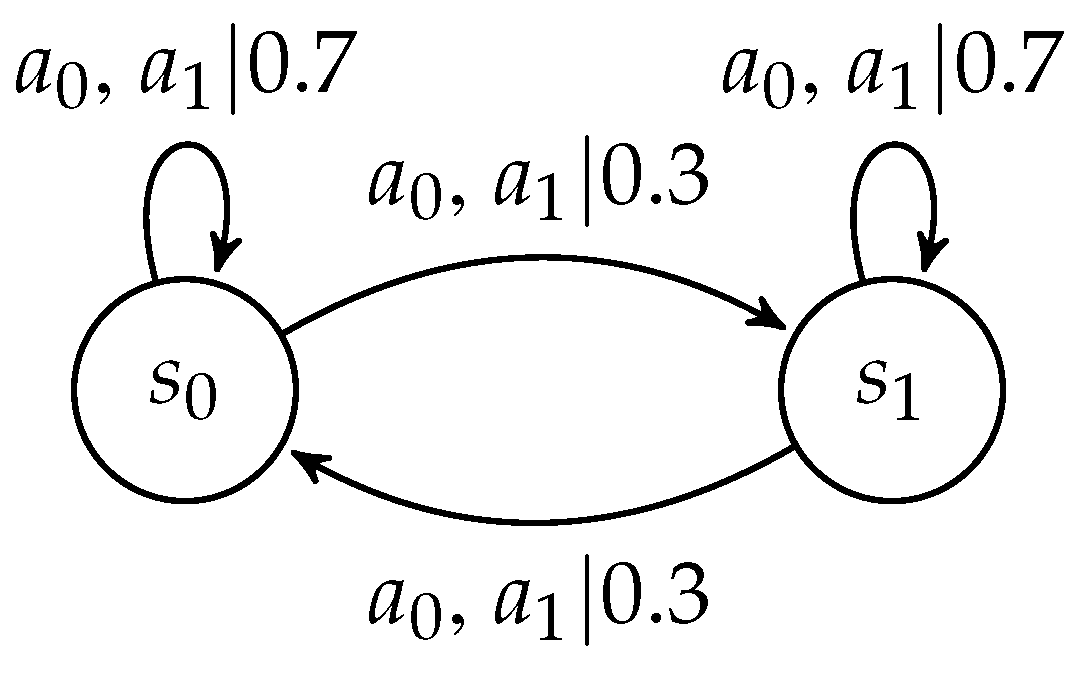
| 11. | The Q values of the optimal state-action pairs can readily be computed by taking the infinite sum of maximal expected rewards (2.0) discounted with a discount factor equal to 0.9. That is, the Q values equal . |
| 12. | For suboptimal state-action pairs, the Q values equal the immediate expected reward from a sub-optimal action, namely, 1.5, plus the expected infinite sum of discounted rewards when switching to the optimal policy in the subsequent trial and beyond. That is, the Q value equals . |
| 13. | See previous footnote for calculations. |
| 14. | Expectiles are related to expected shortfall/Conditional Value at Risk (CVaR) in finance. CVaR is the expected loss in the tails of a distribution (Rockafellar and Uryasev 2000). |
| 15. | The Cramèr-Rao lower bound does not exist for the shifted-exponential distribution, which is why we refer here to the Chapman-Robbins bound. |



| Reward Distribution | ||||||
|---|---|---|---|---|---|---|
| Gaussian | Leptokurtic | Empirical S&P 500 | ||||
| Convergence Robustness | Gaussian | Leptokurtic | Empirical S&P 500 |
|---|---|---|---|
| TD | 67(%) | 1(%) | 42(%) |
| disRL | 5 | 1 | 1 |
| e-disRL- e-disRL | 100 | 16 80 | 100 100 |
| Learning | Robust | Average Convergence | |||
|---|---|---|---|---|---|
| Procedure | State | Convergence | Mean | St Error | (Min, Max) |
| TD Learning | 1(%) | 54(%) | 3(%) | (0(%), 100(%)) | |
| 1 | 56 | 3 | (0, 100) | ||
| disRL | 1 | 55 | 4 | (0, 100) | |
| 1 | 45 | 4 | (0, 100) | ||
| e-disRL- | 20 | 59 | 4 | (0, 100) | |
| 12 | 63 | 4 | (0, 100) | ||
| e-disRL | 77 | 95 | 2 | (0, 100) | |
| 83 | 98 | 1 | (5, 100) | ||
| Learning | Robust | Average Convergence | |||
|---|---|---|---|---|---|
| Procedure | State | Convergence | Mean | St Error | (Min, Max) |
| TD Learning | 37(%) | 99(%) | <0.5(%) | (95(%), 100(%)) | |
| 47 | 99 | <0.5 | (97, 100) | ||
| disRL | 1 | 69 | 3 | (3, 100) | |
| 1 | 62 | 3 | (1, 100) | ||
| e-disRL- | 100 | 100 | 0 | (100, 100) | |
| 100 | 100 | 0 | (100, 100) | ||
| e-disRL | 100 | 100 | 0 | (100, 100) | |
| 100 | 100 | 0 | (100, 100) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bossaerts, P.; Huang, S.; Yadav, N. Exploiting Distributional Temporal Difference Learning to Deal with Tail Risk. Risks 2020, 8, 113. https://doi.org/10.3390/risks8040113
Bossaerts P, Huang S, Yadav N. Exploiting Distributional Temporal Difference Learning to Deal with Tail Risk. Risks. 2020; 8(4):113. https://doi.org/10.3390/risks8040113
Chicago/Turabian StyleBossaerts, Peter, Shijie Huang, and Nitin Yadav. 2020. "Exploiting Distributional Temporal Difference Learning to Deal with Tail Risk" Risks 8, no. 4: 113. https://doi.org/10.3390/risks8040113
APA StyleBossaerts, P., Huang, S., & Yadav, N. (2020). Exploiting Distributional Temporal Difference Learning to Deal with Tail Risk. Risks, 8(4), 113. https://doi.org/10.3390/risks8040113






