Comparing Two Different Option Pricing Methods

Abstract

Motivated by new financial markets where there is no canonical choice of a risk-neutral measure, we compared two different methods for pricing options: calibration with an entropic penalty term and valuation by the Esscher measure. The main aim of this paper is to contrast the outcomes of those two methods with real-traded call option prices in a liquid market like NASDAQ stock exchange, using data referring to the period 2019–2020. Although the Esscher measure method slightly underperforms the calibration method in terms of absolute values of the percentage difference between real and model prices, it could be the only feasible choice if there are not many liquidly traded derivatives in the market.

1. Introduction

Empirical studies show that real financial markets are incomplete, which means that not all derivative securities like options are replicable by means of some initial capital plus the value process of some self-finance trading strategy, and therefore hold unhedgeable and undiversifiable risks. The second fundamental theorem of asset pricing implies that in incomplete markets there typically exist several martingale measures consistent with the no-arbitrage principle that can be chosen as pricing measures (see, e.g., Jeanblanc et al. 2009; Shreve 2004). In fact, the range of option prices composes the total range between the inf and the sup of expected values with respect to martingale measures, and is therefore too large for practical purposes, see (Eberlein and Hammerstein 2004, Theorem 11.55).

Therefore, it makes sense to select a particular martingale measure for pricing purposes. In this study, we introduce, discuss, and compare two methods for the simulation of European call option prices: one based on the Esscher martingale measure and the other on the calibration to real-traded securities with an entropic penalty term. We implemented them in the programming language R and contrast the simulated derivative prices with real data retrieved from NASDAQ option chains. The objective of the paper was to provide a good fit between real and simulated contingent claim prices, consequently suggesting a choice for risk-neutral pricing measures in incomplete markets. In order to fulfill this aim, we constructed a model rich enough to describe stock prices but feasible for practice and connected to option prices. In this context, it is natural to exogenously specify different, suitable underlying asset price dynamics on a case-by-case basis.

The Esscher transform, invented by the Swedish actuary F. Esscher and introduced in Esscher (1932), is a time-honored tool in actuarial science for approximating the distribution of the aggregate claims of a portfolio. It consists of an exponential tilting procedure. More recently, it has been used as a premium calculation principle, see Van Heerwaarden et al. (1989), in option pricing, see Gerber and Shiu (1994), and also in pricing defaultable assets, see Lee and Rheinländer (2012). In our financial setting, the agent has the option to invest in a financial market via admissible strategies. Hereby we exclude strategies leading to arbitrage opportunities. The corresponding theory has been developed by Kallsen and Shiryaev, see Kallsen and Shiryaev (2002). In Benth and Schmeck (2014), the authors used an Esscher transform incorporated in a two-factor model to derive futures prices in electricity markets. Furthermore, pricing methodology for weather derivatives in a specific two-factor model is established in Hell et al. (2012).

The idea of calibration is to consider a set of liquid option prices, and to find a market martingale measure such that the expected values of the option payoffs are as close as possible to the observed prices. This approximation problem is typically ill-posed, and one has to include a regularization term, we opted for an entropic penalty term in this regard. A general exposition about the calibration method can be found in Cont and Tankov, see Cont and Tankov (2004a).

Section 2 and Section 3 are divided into a theoretical and a numerical part. The second section is devoted to the geometric Esscher measure and Laplace cumulant processes. In this part, we modeled the log–prices of the stock with a $COGARCH$ process (introduced in Klüppelberg et al. (2004)) and present a sufficient condition for the existence of such a measure. Assuming the driving Lévy process to have a $NIG$ (normal inverse Gaussian) distribution, which is infinitely divisible and thus corresponds to a Lévy process, we explain the original procedure—relying on the canonical representation theorem for semimartingales—followed by simulating the paths of the stock pricesunder the martingale measure. We pinpoint that, as Lemma 1 shows, the choice of the $NIG$ distribution in the $COGARCH$ model is crucial, since it allows for generating the risk-neutral trajectories of the underlying asset price.

In the third section, the calibration method is explained; using the fundamental concepts of relative entropy of distributions and Lévy processes on the Skorohod space (presented in Appendix E), we chose a martingale measure under which the dynamics of the stock prices follow an exponential Lévy process. In this part we mainly follow Cont and Tankov (2004a), even if the mathematical structure was refined and generalized, and the numerical approximation machinery was tailored to our goals.

In order to make the readers familiar with the theory and the notation that stands behind the main concepts of these two methods, in the appendix we also present a construction of the $NIG$ distribution and some essential results on Lévy processes, highlighting the connection with the characteristics of semimartingales.

The main point of the present paper is as follows: if there are many liquid options around, like plain vanilla calls and puts on liquid stocks, we would expect the calibration method to perform best, therefore, we chose it as the benchmark method. However, in new financial markets, like insurance derivatives, cryptocurrencies, energy, or electricity markets, there are often only a few derivatives or any at all available, or the underlying (like electricity) is difficult to trade in since it is not storable. In these cases the calibration method is not implementable, and there is not much choice other than to use the Esscher method which has been done, e.g., in the book by Benth, Benth, and Koekebakker about electricity and related markets, see Benth et al. (2008). Besides that, there are few, if at all, studies about practical implementation of hedging strategies in incomplete markets, therefore our study fills a gap in this direction. Our main result thus is that while the Esscher martingale measure based pricing method in a liquid market does underperform the calibration method, as is to be expected, it does so only by less than 5%. So it might be a feasible choice of method in new financial markets.

2. Esscher Measure Method

In this section, the dynamics of the stock prices are introduced and sufficient conditions for the existence of the Esscher measure, which was used to simulate European call options prices, are established. We refer to Appendix D for a brief summary of the theory, which is necessary to construct the geometric Esscher measure. In the following, we use notation that can be found, e.g., in the books (Rheinländer and Sexton 2011; Shiryaev and Jacod 2003), as well as references therein.

2.1. The Model

On a probability space $\left(\mathsf{\Omega },\mathcal{F},P\right)$ we introduce a driving, $\mathbb{R}$-valued Lévy process $L={\left\{L_t\right\}}_t$ with generating triplet $\left({\sigma }^2,\nu ,{\gamma }_h\right)$ with respect to a truncation function h (see Appendix B and Appendix C). We endow this space with $\mathbb{F}$, the augmented filtration of L. Define the dynamics of the spot prices by the process $S={\left\{S_t\right\}}_t$, where $S:=S_{0}exp\left(G\right),S_0\in {\mathbb{R}}^{+},$ with the log-prices $G={\left\{G_t\right\}}_t$ which follow a $COGARCH$ process, introduced in Klüppelberg et al. (2004):

$$d{G}_t={\sigma }_{t-}d{L}_t,G_0=0.$$

(1)

The volatility process ${\sigma }^2={\left\{{\sigma }_t^2\right\}}_t$ is given by

$${\sigma }_t^2:=\left(k{\int }_0^t{e}^{X_s}ds+{\sigma }_0^2\right)e^{-X_{t-}},t\ge 0,$$

(2)

with ${\sigma }_0^2\in {\mathbb{R}}^{+}$ and an adapted, right-continuous with left limits (RCLL) process $X={\left\{X_t\right\}}_t$ defined by

$$X_t:=\eta log\delta -\sum _{0<s\le t}log\left[1+\mathsf{\Phi }{\left(\Delta L_s\right)}^2\right],t\ge 0,$$

where $k>0,\eta >0,\mathsf{\Phi }\ge 0$. We recall that a process is said to be RCLL if it has, almost surely, right-continuous trajectories with left limits. Although ${\sigma }^2$ is a left-continuous process, as shown by (2), we use ${\sigma }_{-}$ with the aim to highlight that we are working with a process which is adapted and left-continuous, therefore predictable.

For an adapted process $r={\left\{r_t\right\}}_t$ modeling the interest rate, the discounted spot price process is given by $\tilde{S}={\left\{{\tilde{S}}_t\right\}}_t$, where ${\tilde{S}}_t:=exp\left(-{\int }_0^t{r}_{s}ds\right)S_t,t\ge 0$. Thus, we consider the process $G^{\prime }={\left\{G_t^{\prime }\right\}}_t$, where $G_t^{\prime }:=-{\int }_0^t{r}_{s}ds+G_t$ for every $t\ge 0$, whose dynamics follow $d{G}_t^{\prime }=-r_{t}dt+d{G}_t$. At this point, we can express $\tilde{S}=S_{0}exp\left(G^{\prime }\right)$ and we want to find a process $\theta \in L\left(G^{\prime }\right)$ such that $\tilde{S}$ is a $P^{\theta }$–local martingale: $P^{\theta }$ denotes the geometric Esscher measure, or Esscher martingale transform, for the exponential process $\tilde{S}$ (see Appendix D).

Remark 1.

From (1), it is clear that G jumps at the same times as L does, and $\Delta G_t={\sigma }_{t-}\Delta L_t$ for every $t\ge 0$. For $t\in {\mathbb{R}}^{+}$ and $\omega \in \mathsf{\Omega }$, the measure associated with its jumps is

$$\begin{array}{cc}\hfill {\mu }^G\left(\omega ;\left(0,t\right]\times A\right)& =\sum _{s\le t}{1}_{\left\{x\ne 0\right\}\cap A}\left(\Delta G_s\left(\omega \right)\right)=\sum _{s\le t}{1}_{\left\{x\ne 0\right\}}\left(\Delta L_s\left(\omega \right)\right)1_{{\left({\sigma }_{s-}\left(\omega \right)\right)}^{-1}A}\left(\Delta L_s\left(\omega \right)\right)\hfill \\ & ={\mu }^L\left(\omega ;\left(0,t\right]\times {\left({\sigma }_{-}\left(\omega \right)\right)}^{-1}A\right),A\in \mathcal{B}\left(\mathbb{R}\right).\hfill \end{array}$$

Furthermore ${\mu }^{G^{\prime }}={\mu }^G$, hence $F_{\left(t,\omega \right)}^{G^{\prime }}\left(dy\right)=\nu {\left({\sigma }_{t-}\left(\omega \right)·\right)}^{-1}\left(dy\right)$, meaning that

$$F_{\left(t,\omega \right)}^{G^{\prime }}\left(A\right)={\int }_{\mathbb{R}}{1}_A\left({\sigma }_{t-}\left(\omega \right)y\right)\nu \left(dy\right),A\in \mathcal{B}\left(\mathbb{R}\right).$$

Theorem 1.

Let $\theta \in L\left(G^{\prime }\right)$ be such that $\theta ·G^{\prime }$ is exponentially special and $Z^{\theta }$ is a uniformly integrable martingale. If also $\left(\theta +1\right)·G^{\prime }$ is exponentially special and θ satisfies

$$\left({\theta }_t+\frac{1}{2}\right){\sigma }_{t-}^2{\sigma }^2-r_t+{\sigma }_{t-}{\gamma }_h+{\int }_{\mathbb{R}}\left(e^{\left({\theta }_t+1\right){\sigma }_{t-}y}-e^{{\theta }_t{\sigma }_{t-}y}-{\sigma }_{t-}h\left(y\right)\right)\nu \left(dy\right)=0$$

(3)

for every $t\ge 0$, then $\tilde{S}$ is a $P^{\theta }$-local martingale.

Note that $G^{\prime }$ is a 1-dimensional process, thus the geometric Esscher measure is unique.

Proof. 

Let

$$\widetilde{G^{\prime }}{\left(h\right)}_t:=\sum _{s\le t}\left[\Delta G_s^{\prime }-h\left(\Delta G_s^{\prime }\right)\right]={\left(\left(x-h\left(x\right)\right)🟉{\mu }^G\right)}_t,t\ge 0$$

and $G^{\prime }{\left(h\right)}_t:=G_t^{\prime }-\widetilde{G^{\prime }}{\left(h\right)}_t,t\ge 0$. By Remark 1, we get

$$\begin{array}{cc}\hfill d{G}^{\prime }{\left(h\right)}_t& =d{G}_t^{\prime }-d\widetilde{G^{\prime }}{\left(h\right)}_t=-r_{t}dt+d{G}_t-\left(x-h\left(x\right)\right){\mu }^G\left(dt,dx\right)\hfill \\ & =-r_{t}dt+{\sigma }_{t-}d{L}_t-\left({\sigma }_{t-}y-h\left({\sigma }_{t-}y\right)\right){\mu }^L\left(dt,dy\right).\hfill \end{array}$$

Taking into account Lemma A1 in Appendix D, which provides

$${\delta }^L{\left({\sigma }_{-}\right)}_t={\sigma }_{t-}{\gamma }_h+{\int }_{\mathbb{R}}{\sigma }_{t-}\left(y-h\left(y\right)\right)\nu \left(dy\right),t\ge 0,$$

and considering that ${\left({\sigma }_{-}·L\right)}^c={\sigma }_{-}·L^c$ and $⟨{\sigma }_{-}·L^c,{\sigma }_{-}·L^c⟩=\int {\sigma }_{-}^2{\sigma }^{2}dt$, we obtain the characteristics of $G^{\prime }$ under P with respect to h:

$$\left\{\begin{array}{c}{b}_t^{G^{\prime }}=-r_t+{\sigma }_{t-}{\gamma }_h+{\int }_{\mathbb{R}}\left(h\left({\sigma }_{t-}y\right)-{\sigma }_{t-}h\left(y\right)\right)\nu \left(dy\right)\hfill \\ c_t^{G^{\prime }}={\sigma }_{t-}^2{\sigma }^2\hfill \\ F_t^{G^{\prime }}\left(dy\right)=\nu {({\sigma }_{t-}·)}^{-1}\left(dy\right)\hfill \end{array}\right.,t\ge 0.$$

(4)

Thus, if $\theta$ satisfies $\tilde{\kappa }\left(\theta +1\right)-\tilde{\kappa }\left(\theta \right)=0$, thanks to Theorem A2 we can conclude that $\tilde{S}$ is a $P^{\theta }$-local martingale. In fact, using (A11) we have

$$\begin{array}{cc}\hfill & \tilde{\kappa }{\left(\theta +1\right)}_t-\tilde{\kappa }{\left(\theta \right)}_t\hfill \\ & =b_t^{G^{\prime }}+\frac{1}{2}{\sigma }_{t-}^2{\sigma }^2+{\theta }_t{\sigma }_{t-}^2{\sigma }^2+{\int }_{\mathbb{R}}\left(e^{\left({\theta }_t+1\right)x}-e^{{\theta }_{t}x}-h\left(x\right)\right)F_t^{G^{\prime }}\left(dx\right)\hfill \\ \hfill & =\left({\theta }_t+\frac{1}{2}\right){\sigma }_{t-}^2{\sigma }^2-r_t+{\sigma }_{t-}{\gamma }_h+{\int }_{\mathbb{R}}\left(e^{\left({\theta }_t+1\right){\sigma }_{t-}y}-e^{{\theta }_t{\sigma }_{t-}y}-{\sigma }_{t-}h\left(y\right)\right)\nu \left(dy\right)\hfill \\ & =0,t\ge 0,\hfill \end{array}$$

where the last equality holds by (3). □

The next lemma provides us with the candidate solutions to Equation (3) when L follows a $NIG$ distribution (see Appendix A).

Lemma 1.

Let $L={\left\{L_t\right\}}_t$ be a $NIG$-distributed Lévy process with parameters $\left(\alpha ,\beta ,\mu ,\delta \right)$ and define the truncation function $h\left(x\right):=x{1}_D\left(x\right),x\in \mathbb{R}.$ If a process $\theta ={\left\{{\theta }_t\right\}}_t$ such that

$$\left({\sigma }_{t-}{\theta }_t\right)\left(\omega \right),{\sigma }_{t-}\left({\theta }_t+1\right)\left(\omega \right)\in \left[-\alpha -\beta ,\alpha -\beta \right],t\in {\mathbb{R}}_0^{+},\omega \in \mathsf{\Omega }$$

(5)

fulfills Equation (3), then for every $t\ge 0$ we have

$$\begin{array}{cc}\hfill {\theta }_t^{1,2}=\frac{1}{2\left(R_t^2+{\delta }^2{\sigma }_{t-}^2\right){\sigma }_{t-}}(& -{\delta }^2{\sigma }_{t-}^3-2\beta {\delta }^2{\sigma }_{t-}^2-R_t^2\left({\sigma }_{t-}+2\beta \right)\hfill \\ & \pm \sqrt{4{\alpha }^2{\delta }^2{R}_t^2{\sigma }_{t-}^2+4R_t^4{\alpha }^2-R_t^2{\delta }^2{\sigma }_{t-}^4-\frac{R_t^6}{{\delta }^2}-2{\sigma }_{t-}^2{R}_t^4}),\hfill \end{array}$$

(6)

with $R_t:=-r_t+\mu {\sigma }_{t-}$.

Proof. 

Since $L_1\sim NIG\left(\alpha ,\beta ,\mu ,\delta \right)$, we apply (A6) and (A9) (see Appendix A and Appendix B) to obtain

$$E\left[e^{z{L}_1}\right]=exp\left[\mu z+{\gamma }_{1}z+{\int }_{\mathbb{R}}\left(e^{zx}-1-zx{1}_D\left(x\right)\right)\nu \left(dx\right)\right],z\in \left[-\alpha -\beta ,\alpha -\beta \right],$$

where ${\displaystyle {\gamma }_1:=\frac{2\delta \alpha }{\pi }{\int }_0^{1}sinh\left(\beta x\right)K_1\left(\alpha x\right)dx}$ and ${\displaystyle \nu \left(dx\right)=\frac{\delta \alpha }{\pi \left|x\right|}{e}^{\beta x}{K}_1\left(\alpha \left|x\right|\right)dx.}$ Using (A5), we get

$$\delta \left(\sqrt{{\alpha }^2-{\beta }^2}-\sqrt{{\alpha }^2-{\left(\beta +z\right)}^2}\right)={\gamma }_{1}z+{\int }_{\mathbb{R}}\left(e^{zx}-1-zx{1}_D\left(x\right)\right)\nu \left(dx\right)$$

(7)

for $z\in \left[-\alpha -\beta ,\alpha -\beta \right]$. Proceeding as in the proof of Theorem 1, we have

$$\begin{array}{cc}\hfill 0& =\tilde{\kappa }{\left(\theta +1\right)}_t-\tilde{\kappa }{\left(\theta \right)}_t\hfill \\ & =R_t+{\sigma }_{t-}{\gamma }_1+{\int }_{\mathbb{R}}\left[e^{\left({\theta }_t+1\right){\sigma }_{t-}x}-1-{\sigma }_{t-}\left({\theta }_t+1\right)x{1}_D\left(x\right)\right]\nu \left(dx\right)\hfill \\ & -{\int }_{\mathbb{R}}\left(e^{{\theta }_t{\sigma }_{t-}x}-1-{\sigma }_{t-}{\theta }_{t}x{1}_D\left(x\right)\right)\nu \left(dx\right),t\ge 0.\hfill \end{array}$$

(8)

Since ${\sigma }_{-}{\gamma }_1={\sigma }_{-}\left[\left(\theta +1\right)-\theta \right]{\gamma }_1$, we expand on the chain of equalities in (8):

$$\begin{array}{cc}\hfill 0& =R_t+\left[{\sigma }_{t-}\left({\theta }_t+1\right){\gamma }_1+{\int }_{\mathbb{R}}\left(e^{\left({\theta }_t+1\right){\sigma }_{t-}x}-1-{\sigma }_{t-}\left({\theta }_t+1\right)x{1}_D\left(x\right)\right)\nu \left(dx\right)\right]\hfill \\ & -\left[{\sigma }_{t-}{\theta }_t{\gamma }_1+{\int }_{\mathbb{R}}\left(e^{{\theta }_t{\sigma }_{t-}x}-1-{\sigma }_{t-}{\theta }_{t}x{1}_D\left(x\right)\right)\nu \left(dx\right)\right]\hfill \\ & =R_t+\delta \left(\sqrt{{\alpha }^2-{\left(\beta +{\sigma }_{t-}{\theta }_t\right)}^2}-\sqrt{{\alpha }^2-{\left(\beta +{\sigma }_{t-}\left({\theta }_t+1\right)\right)}^2}\right),t\ge 0,\hfill \end{array}$$

where the last equality is obtained by combining (5) and (7). At this point it remains to find the possible solutions for every $t\ge 0$ to the equation

$$R_t+\delta \left(\sqrt{{\alpha }^2-{\left(\beta +{\sigma }_{t-}{\theta }_t\right)}^2}-\sqrt{{\alpha }^2-{\left(\beta +{\sigma }_{t-}\left({\theta }_t+1\right)\right)}^2}\right)=0,$$

which can be written as ${\displaystyle \sqrt{{\alpha }^2-{\left(\beta +{\sigma }_{t-}\left({\theta }_t+1\right)\right)}^2}=\frac{R_t}{\delta }+\sqrt{{\alpha }^2-{\left(\beta +{\sigma }_{t-}{\theta }_t\right)}^2}.}$ Squaring both sides we get

$$2\frac{R_t}{\delta }\sqrt{{\alpha }^2-{\left(\beta +{\sigma }_{t-}{\theta }_t\right)}^2}=-\left({\sigma }_{t-}^2+2\beta {\sigma }_{t-}+\frac{R_t^2}{{\delta }^2}\right)-2{\sigma }_{t-}^2{\theta }_t,$$

(9)

and repeating once again the same operation of squaring we end up with an equation of second degree in $\theta$:

$$4{\sigma }_{t-}^2\left({\sigma }_{t-}^2+\frac{R_t^2}{{\delta }^2}\right){\theta }_t^2+4{\sigma }_{t-}\left({\sigma }_{t-}^3+2\beta {\sigma }_{t-}^2+\frac{R_t^2}{{\delta }^2}{\sigma }_{t-}+2\beta \frac{R_t^2}{{\delta }^2}\right){\theta }_t+c_t=0,$$

(10)

where $c_t:={\left({\sigma }_{t-}^2+2\beta {\sigma }_{t-}+\frac{R_t^2}{{\delta }^2}\right)}^2-4\frac{R_t^2}{{\delta }^2}\left({\alpha }^2-{\beta }^2\right)$. Computing algebraically the solutions of (10) we get the expressions in (6). □

We have empirically tested both possible branches of solutions in (6), and we have chosen

$$\begin{array}{cc}\hfill {\theta }_t=\frac{1}{2\left(R_t^2+{\delta }^2{\sigma }_{t-}^2\right){\sigma }_{t-}}(& -{\delta }^2{\sigma }_{t-}^3-2\beta {\delta }^2{\sigma }_{t-}^2-R_t^2\left({\sigma }_{t-}+2\beta \right)\hfill \\ & -\sqrt{4{\alpha }^2{\delta }^2{R}_t^2{\sigma }_{t-}^2+4R_t^4{\alpha }^2-R_t^2{\delta }^2{\sigma }_{t-}^4-\frac{R_t^6}{{\delta }^2}-2{\sigma }_{t-}^2{R}_t^4})\hfill \end{array}$$

(11)

to run the simulation because it prevents the risk-neutral dynamics from “exploding”, i.e., from skyrocketing to unrealistically high prices in a short time.

Remark 2.

Unfortunately, it does not seem possible for us to prove, from an analytical point of view, that either candidate solution in (6) solves (3), i.e., that it is a true solution. What the simulations suggest is that only the process in (11) is indeed a solution of (3). This insight is confirmed by the numerical experiments to a greater extent. In fact, it turns out that both processes ${\theta }^{1,2}$ satisfy Condition (5). However, ${\theta }^1$ makes the right hand side in (9) negative, and this implies that it does not solve (3). On the contrary, the process ${\theta }^2$—the one we pick in (11)—makes such term positive, hence it solves (3), indeed.

2.1.1. Simulation of the $P^{\theta }$-Dynamics

The goal of this section is to carefully describe a procedure to generate the risk-neutral dynamics of the underlying asset price. This allows us to compute the simulated European call option prices with the Monte Carlo method.

Let $r\in {\mathbb{R}}^{+}$ represent the constant annual interest rate. We assume that the driving Lévy process L is $NIG$-distributed and that the hypothesis of Theorem 1 hold (with respect to the truncation function $\overline{h}\left(x\right)=x{1}_D\left(x\right),x\in \mathbb{R}$). Using the R-package yuima (see Iacus 2011) we estimate the parameters of the model from the time series of the underlying asset log-prices. Next, we simulated a sufficiently large number of paths of the variance process ${\sigma }^2$ with the found parameters: by (11), from each of them we can get a trajectory of $\theta$. The issue reduces to generating the paths of G, but note that, after the change of measure, L is not a Lévy process anymore because $F_t^{\theta }\left(dx\right)=e^{{\theta }_{t}x}\nu \left(dx\right),t\ge 0$. Consequently, G is not a $COGARCH$ process under the martingale measure. Then, in order to simulate its trajectories we use the canonical representation for semimartingales (Shiryaev and Jacod (2003), Chapter II, Theorem 2.34): for a d-dimensional semimartingale $X={\left\{X_t\right\}}_t$ with characteristics $\left(B,C,{\nu }^X\right)$ relative to the truncation function h, it holds:

$$X=X_0+X^c+B+h\left(x\right)🟉({\mu }^X-{\nu }^X)+\left(x-h\left(x\right)\right)🟉{\mu }^X.$$

(12)

The symbol 🟉 denotes the integration with respect to a random measure: we refer to (Shiryaev and Jacod (2003), Chapter II, Section 1) for an extensive study of this topic. For the reader’s convenience, we provide the basic definition.

Definition 1.

Let μ be a random measure on ${\mathbb{R}}_0^{+}\times \mathbb{R}$ and $W:\mathsf{\Omega }\times {\mathbb{R}}_0^{+}\times \mathbb{R}\to \mathbb{R}$ be measurable function with respect to the product σ-algebra $\mathcal{O}\otimes \mathcal{B}\left(\mathbb{R}\right)$, where $\mathcal{O}$ denotes the optional σ-algebra on $\mathsf{\Omega }\times {\mathbb{R}}_0^{+}$. The integral process $W🟉\mu$ is defined by

$$W🟉{\mu }_t\left(\omega \right):=\left\{\begin{array}{cc}{\int }_{\left[0,t\right]\times \mathbb{R}}W\left(\omega ;s,x\right)\mu \left(\omega ;ds,dx\right),\hfill & \mathit{if}{\int }_{\left[0,t\right]\times \mathbb{R}}\left|W\left(\omega ;s,x\right)\right|\mu \left(\omega ;ds,dx\right)<\infty \hfill \\ \infty ,\hfill & \mathit{otherwise}\hfill \end{array}\right..$$

For an arbitrarily chosen $ϵ\le 1$, fix the truncation function $h\left(x\right):=x{1}_{\left\{\left|z\right|<ϵ\right\}}\left(x\right)$ for $x\in \mathbb{R}$, and let $\left(0,\nu ,{\gamma }_h\right)$ be the corresponding generating triplet of L. From the proof of Theorem 1, specifically from (4), we readily get the characteristics $\left(b_t,0,\nu {\left({\sigma }_{t-}·\right)}^{-1}\left(dx\right)\right)$ of G under P, and invoking (A12) and Remark A2 in Appendix D we find them under $P^{\theta }$:

$$\left\{\begin{array}{c}{b}_t^{\theta }=b_t+{\int }_{\mathbb{R}}h\left(x\right)\left(e^{{\theta }_{t}x}-1\right)F_t\left(dx\right)\hfill \\ c_t^{\theta }=0\hfill \\ F_t^{\theta }\left(dx\right)=e^{{\theta }_{t}x}\nu {({\sigma }_{t-}·)}^{-1}\left(dx\right)\hfill \end{array}\right.,t\ge 0.$$

(13)

We now represent G by (12), noting that $G_0=0$ and $G^c=0$ since $c^{\theta }=0$. As regards the term $B={\left\{B_t\right\}}_t$, we expand on the computations in (13), getting

$$\begin{array}{c}{\displaystyle b_t^{\theta }={\sigma }_{t-}{\gamma }_h+{\int }_{\left|x\right|<ϵ/{\sigma }_{t-}}{\sigma }_{t-}y\frac{\delta \alpha }{\pi \left|y\right|}{e}^{\left({\theta }_t{\sigma }_{t-}+\beta \right)y}{K}_1\left(\alpha \left|y\right|\right)dy}\hfill \\ \hfill {\displaystyle -{\int }_{\left(-ϵ,ϵ\right)}{\sigma }_{t-}y\frac{\delta \alpha }{\pi \left|y\right|}{e}^{\beta y}{K}_1\left(\alpha \left|y\right|\right)dy,t\ge 0,}\end{array}$$

and obtain the variables of the process B by $B_t={\int }_{\left(0,t\right)}{b}_s^{\theta }ds,t\ge 0.$

At this point we need to approximate a trajectory of the process $h\left(x\right)🟉({\mu }^G-{\nu }^G)$. In order to do so, we neglect the contribution of the jumps of G with absolute value smaller than $ϵ$, focusing just on the term

$$\begin{array}{cc}\hfill h\left(x\right)🟉({\mu }^G-{\nu }^G)& \approx -h\left(x\right)🟉{\nu }^G=-{\int }_{\left(0,t\right)}ds{\int }_{\mathbb{R}}x{1}_{\left\{\left|z\right|<ϵ\right\}}\left(x\right)F_s^{\theta }\left(dx\right)\hfill \\ \hfill & {\displaystyle =-{\int }_{\left(0,t\right)}ds{\int }_{\left|x\right|<ϵ/{\sigma }_{s-}}{\sigma }_{s-}y\frac{\delta \alpha }{\pi \left|y\right|}{e}^{\left({\theta }_s{\sigma }_{s-}+\beta \right)y}{K}_1\left(\alpha \left|y\right|\right)dy,t\ge 0,}\hfill \end{array}$$

which in turn cancels out with one of the addends defining B. Heuristically speaking, in this approach we are assuming that the small jumps of the underlying asset price do not contribute to the determination of the option value in a significant way. However, we may refer to Asmussen and Rosiński (2001) for a more sophisticated procedure taking into account the variation of such small jumps in the case of Lévy processes.

Finally we concentrate on the term $\left(x-h\left(x\right)\right)🟉{\mu }^G$: we simulate its paths similarly to the Lévy–Itô decomposition theorem (see Sato 1999, Theorem 19.2). According to this result, if $\tilde{L}$ is a Lévy process with generating triplet $\left(A,\nu ,\gamma \right)$ and $D_{a,\infty }:=\left\{x\in {\mathbb{R}}^d:a<\left|x\right|<\infty \right\}$ for $a>0$, then ${\left\{{\left(\left(x-x{1}_D\left(x\right)\right)🟉{\mu }^{\tilde{L}}\right)}_t\right\}}_t$ is a compound Poisson process with constant $\nu \left(D_{1,\infty }\right)$ and distribution

$$\varphi \left(B\right):=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}B\subset D\hfill \\ \frac{\nu \left(B\cap D_{1,\infty }\right)}{\nu \left(D_{1,\infty }\right)},\hfill & \mathrm{otherwise}\hfill \end{array}\right.,B\in \mathcal{B}\left({\mathbb{R}}^d\right).$$

Thus, we take a nonhomogeneous Poisson process with time-varying intensity

$$\begin{array}{cc}\hfill {\lambda }_t& :={\displaystyle F_t^{\theta }\left(\left\{\left|x\right|>ϵ\right\}\right)={\int }_{\mathbb{R}}{e}^{{\theta }_t{\sigma }_{t-}y}{1}_{D_{ϵ,\infty }}\left({\sigma }_{t-}y\right)\frac{\delta \alpha }{\pi \left|y\right|}{e}^{\beta y}{K}_1\left(\alpha \left|y\right|\right)dy}\hfill \\ & {\displaystyle ={\int }_{\left|x\right|>ϵ/{\sigma }_{t-}}\frac{\delta \alpha }{\pi \left|y\right|}{e}^{\left({\theta }_t{\sigma }_{t-}+\beta \right)y}{K}_1\left(\alpha \left|y\right|\right)dy,t\ge 0}\hfill \end{array}$$

and impose the time-varying jumps sizes to follow

$${\displaystyle c_t:={\int }_{\mathbb{R}}x\frac{1_{D_{ϵ,\infty }}\left(x\right)}{{\lambda }_t}{F}_t^{\theta }\left(dx\right)=\frac{1}{{\lambda }_t}{\int }_{\left|x\right|>ϵ/{\sigma }_{t-}}{\sigma }_{t-}y\frac{\delta \alpha }{\pi \left|y\right|}{e}^{\left({\theta }_t{\sigma }_{t-}+\beta \right)y}{K}_1\left(\alpha \left|y\right|\right)dy,t\ge 0.}$$

The jump times of this process have been simulated by the thinning algorithm described in Lewis and Shedler (1979).

Denote by N the number of iterations we run and by $S^i$, for $i=1,\dots ,N$, the corresponding, simulated trajectories of the spot price under the pricing measure $P^{\theta }$. We obtain the value of an European call option with strike K and maturity T following the Monte Carlo method, i.e., computing the sample mean of the vector of components $e^{-rT}{\left(S^i\left(T\right)-K\right)}^{+},i=1,\dots ,N.$

2.1.2. Empirical Results

We have empirically tested the Esscher method on the prices of call options on Apple Inc. stock (ticker symbol: AAPL) with fixed strike at $\$320$. In Figure 1a, the simulated option prices are shown as function of their maturities. The average of the absolute values of percentage difference is $3.1646\%$.

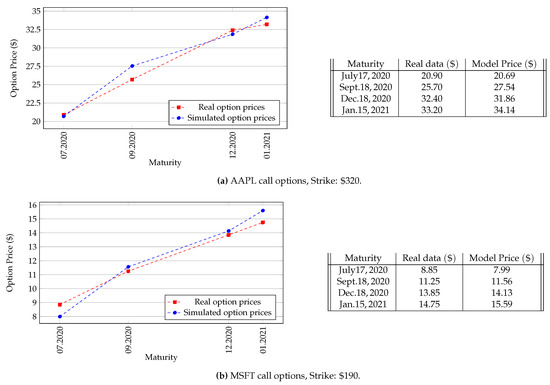
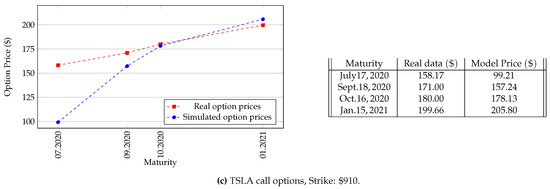
Figure 1. Numerical experiments for the Esscher method.

Furthermore, we applied this method to the prices of call options on Microsoft Corporation stock (ticker symbol: MSFT) with strike $\$190$: we plot the outcomes in Figure 1b. In this case, the mean of absolute values of percentage difference settles down at $5.0518\%$.

Finally we report the results of a test on call options with strike $\$910$ with Tesla, Inc. (ticker symbol: TSLA) as underlying stock. In Figure 1c we can notice a big discrepancy between the real price and the predicted value for the shortest-term maturity taken into account, the latter being $37.2755\%$ smaller than the former. However, if we neglect this first term we recover a result in line with the previous experiments, namely an average for the absolute values of percentage difference of $4.0555\%$.

In all the three cases, we set the number of Monte Carlo iterations $N={10}^4$ and we used the time series of the $log-$prices associated to the trading year before 19 February 2020, to estimate the parameters of the $COGARCH$ model (see Section 2.1.1). Therefore, the simulations were run prior to Apple’s stock split (on 28 August 2020) and Tesla’s stock split (on 31 August 2020).

Remark 3.

The real data was obtained from https://old.nasdaq.com, where American options are traded. Although our approximation generates the prices in an European model, it can be accepted as meaningful since:

• the analyzed derivatives have short-term maturities, so we are allowed to ignore the dividend yield (however, TSLA does not pay dividends);
• the time values of the options were always positive, implying that it is convenient to sell the option rather than exercising the call right.

3. Calibration with Entropic Penalty Term Method

In the Esscher method, the density process is completely defined by the spot prices: this is an intuitive drawback in liquid markets, because it does not use all the available information (e.g., the time series of derivative prices). This is a motivation to consider the Calibration Method, which consists in modeling the spot prices dynamics directly under a martingale measure “chosen” by the market.

3.1. The Model

We start the practical analysis by taking into account a driving, $\mathbb{R}$-valued Lévy process $L={\left\{L_t\right\}}_t$ with generating triplet $\left({\sigma }^2,\nu ,\gamma \right)$ on a probability space $\left(\mathsf{\Omega },\mathcal{F},Q\right)$ endowed with the augmented filtration of L, which satisfies the usual conditions and is denoted by $\mathbb{G}$. We describe the stock prices $S={\left\{S_t\right\}}_t$ with an exponential Lévy model: $S_t:=S_{0}exp\left(rt+L_t\right),t\ge 0,$ with $S_0\in {\mathbb{R}}^{+}$ and $r\in {\mathbb{R}}^{+}$ representing the constant annual interest rate. The discounting process $R={\left\{R_t\right\}}_t$ reduces to the deterministic function $R_t:=exp\left(-rt\right),t\ge 0.$ Since we need Q to be a martingale measure for S we require:

(i)

there exists a $t>0$ such that $E^Q[exp\left(L_t\right)]<\infty$;

(ii)

$\mathsf{\Psi }\left(1\right)=\frac{1}{2}{\sigma }^2+\gamma +{\int }_{\mathbb{R}}\left(e^x-1-x{1}_D\left(x\right)\right)\nu \left(dx\right)=0$.

With these assumptions, Remark A1 in Appendix B proves that ${\left\{exp\left(L_t\right)\right\}}_t$ is a martingale with $E^Q\left[exp\left(L_t\right)\right]=1$ for every $t>0$. Considering the discounted spot prices process $\tilde{S}={\left\{{\tilde{S}}_t\right\}}_t$, defined by ${\tilde{S}}_t:=R_t{S}_t=S_{0}exp\left(L_t\right),t\ge 0$, we can state that it is a Q-martingale with constant expectation equal to $S_0$.

In our discussion the driving Lévy process L will be a pure jump process, so its generating triplet simplifies as ${\sigma }^2=0$. In particular, due to assumption (ii) we get the next relation:

$$\gamma =-{\int }_{\mathbb{R}}\left(e^x-1-x{1}_D\left(x\right)\right)\nu \left(dx\right).$$

(14)

Assume that there are N European call options with fixed maturity T available in the market, and for each $j=1,\dots ,N$ let $K_j$ and $C^j$ be the strike price and the observed price of the j-th derivative, respectively. It is convenient to consider the quantities $k_j=log\left(K_j\right),j=1,\dots ,N$. In this setting, S is the price process of the underlying asset. Since Q is a martingale measure for S, we can use it to price options: $C_{\nu }^j:=exp\left(-rT\right)E^Q\left[{\left(S_T-exp\left(k_j\right)\right)}^{+}\right],j=1,\dots ,N$. Denoting by $Q_{L_T}$ the pushforward distribution on $\mathbb{R}$ generated by $L_T$ we have

$$C_{\nu }^j=exp\left(-rT\right){\int }_{\mathbb{R}}{\left(S_0{e}^{rT+y}-e^{k_j}\right)}^{+}{Q}_{L_T}\left(dy\right),j=1,\dots ,N.$$

Thus, knowing the Lévy measure $\nu$, the whole generating triplet could be recovered and therefore the option prices computed.

The reasoning which leads the calibration is choosing $\nu$ such that $C_{\nu }^j$ is “close” to $C^j$ for any $j=1,\dots ,N$. Hence we pick the Lévy measure of the model by a least-squares procedure:

$$\overline{\nu }=arg\underset{\nu }{min}\left\{\sum _{j=1}^N{\left|C_{\nu }^j-C^j\right|}^2\right\}.$$

(15)

Since the problem expressed in (15) is ill posed (see Cont and Tankov 2004a, Chp. 13), we introduce a regularization term. Let $L^0={\left\{L_t^0\right\}}_t$ be a, pure jump, driving Lévy process with generating triplet $\left(0,{\nu }_0,{\gamma }_0\right)$ statistically estimated from the time series of the underlying asset price. Furthermore, let $Q^{L^0}$ and $Q^L$ be the distributions on the Skorohod space $\left(\mathfrak{D},{\mathcal{F}}_{\mathfrak{D}};\mathbb{F}\right)$ generated by $L^0$ and L, respectively, which are supposed to be equivalent on ${\mathcal{F}}_t$ for every $t>0$ (see Appendix E). We use the relative entropy as a measure of the distance from $Q^{L_0}$, so that by Remark A3 the issue is reduced to solving the optimization problem:

$$\overline{\nu }=arg\underset{\nu \in \mathbf{Q}}{min}\left\{\sum _{j=1}^N{\left|C_{\nu }^j-C^j\right|}^2+\alpha {\int }_{\mathbb{R}}\left(\frac{d\nu }{d{\nu }^0}log\frac{d\nu }{d{\nu }^0}+1-\frac{d\nu }{d{\nu }^0}\right)d{\nu }^0\right\},$$

(16)

for $\mathbf{Q}:=\left\{\nu :Q^L{|}_{{\mathcal{F}}_t}\sim {\left.Q^{L^0}\phantom{|}\right|}_{{\mathcal{F}}_t},t>0\right\}$. The term $\alpha$ is a regularization parameter: the higher it is, the more we trust the initial distribution and the less importance we give to calibration. The existence of a solution to (16) has been studied, among others, in the paper Cont and Tankov (2004b). We are going to relax the assumptions in (16), considering the minimization in the set of the Lévy measures equivalent to ${\nu }^0$.

3.1.1. Numerical Approximation

The goal of this section is to describe in each and every detail a discretization procedure that allows us to tackle the optimization problem in (16). To this aim, it is necessary to express the objective functional in (16) as a function of the masses of the discretized Lévy measures. The steps of our argument are the following:

I.

estimate the parameters of the prior Lévy process $L^0$ from the time series of log–returns;

II.

introduce a discretization grid for the prior Lévy measure ${\nu }^0$ and the driving Lévy measure $\nu$ (in what follows, the points of such a grid are denoted by $y_1<\cdots <y_{N_d}$). Their discretized versions are denoted by ${\nu }_d^0$ and ${\nu }_d$, respectively;

III.

compute the discrete version of the entropy term in (16) as a function of the masses of ${\nu }_d$;

IV.

use an approach based on the Fourier inversion theorem to get an approximation of the modified time values of the options at the log–strikes under scrutiny. This allows us to obtain (23), a discretized version of the objective functional in (16);

V.

calculate explicitly the derivatives of the discretized objective functional to speed up the simulations;

VI.

choose the regularization parameter $\alpha$.

Fix a maturity T and define the grid $x_j\in {\mathbb{R}}^{+}$, $j=1,\dots ,N$, with $x_1<x_2<\dots <x_N$: these points represent the log–strike prices of the options available on the market. Moreover, from the time series of the log–returns we obtain the parameters of the historical, $NIG$-distributed Lévy process $L^0={\left\{L_t^0\right\}}_t$ by a maximum likelihood procedure using the R-package ghyp. Note that, in this case, one can select any pure jump, infinitely divisible distribution: we opt for the NIG by analogy with the Esscher’s method, and our choice is satisfactory, as the final goodness of fit between real data and model prices shows. First we introduce a discretization grid consisting in the points $y_h,h=1,\dots ,N_d$, with $y_1<y_2<\dots <y_{N_d}$, which constitutes a partition of the interval $\left[-M,M\right]$ for some $M>0$, and then we approximate the Lévy measure of $L^0$ with the discrete version ${\nu }_d^0\left(dy\right)={\sum }_{h=1}^{N_d}{\nu }_h^0{\delta }_{\left(y_h\right)}\left(dy\right)$, where ${\delta }_{\left(\overline{a}\right)}$ denotes the Dirac measure at a point $\overline{a}$ and

$${\nu }_1^0={\int }_{\left(-\infty ,y_1\right]}d{\nu }^0;{\nu }_h^0={\int }_{\left(y_{h-1},y_h\right]}d{\nu }^0,h=2,\dots ,N_d-1;{\nu }_{N_d}^0={\int }_{\left(y_{N_d-1},\infty \right)}d{\nu }^0.$$

Now we take into account another measure which has the same mass points as the previous one: ${\nu }_d\left(dy\right)={\sum }_{h=1}^{N_d}{\nu }_h{\delta }_{\left(y_h\right)}\left(dy\right),$ with ${\nu }_h\in {\mathbb{R}}^{+}$ for every $h=1,\dots ,N_d$. We note that the calibrated measures ${\nu }_d$ and ${\nu }_d^0$ are equivalent, but ${\nu }_d$ and the prior ${\nu }^0$ are not. We understand the measure ${\nu }_d$ as the discretized Lévy measure of the driving, pure jump Lévy processes $L={\left\{L_t\right\}}_t$. We now want to compute the Radon–Nikodym derivative $\frac{d{\nu }_d}{d{\nu }_d^0}$ with the aim to explicitly express the entropy term of (16) in the discrete version

$${\int }_{\mathbb{R}}\left(\frac{d{\nu }_d}{d{\nu }_d^0}log\frac{d{\nu }_d}{d{\nu }_d^0}+1-\frac{d{\nu }_d}{d{\nu }_d^0}\right)d{\nu }_d^0.$$

(17)

Set $y_0=-\infty$ and define the function

$$f\left(y\right):=\left\{\begin{array}{cc}\frac{{\nu }_h}{{\nu }_h^0},\hfill & \mathrm{if}{y}_{h-1}<y\le y_h,h=1,\dots ,N_d\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right..$$

For every $A\in \mathcal{B}\left(\mathbb{R}\right)$ it results

$$\begin{array}{cc}\hfill {\int }_{\mathbb{R}}f{1}_{A}d{\nu }_d^0& =\sum _{h=1}^{N_d}\frac{{\nu }_h}{{\nu }_h^0}{\int }_{\left(y_{h-1},y_h\right]}{1}_A\left(y\right){\nu }_d^0\left(dy\right)=\sum _{h=1}^{N_d}\frac{{\nu }_h}{{\nu }_h^0}{\nu }_d^0\left(\left(y_{h-1},y_h\right]\cap A\right)\hfill \\ \hfill & =\sum _{h=1}^{N_d}\frac{{\nu }_h}{{\nu }_h^0}{\nu }_h^0{1}_A\left(y_h\right)={\nu }_d\left(A\right),\hfill \end{array}$$

as ${\nu }_d^0\left(\left(y_{h-1},y_h\right]\cap A\right)={\nu }_h^0{1}_A\left(y_h\right),h=1,\dots ,N_d$. Therefore, $\frac{d{\nu }_d}{d{\nu }_d^0}=f$. Moving back to the integral (17), we get:

$$\begin{array}{cc}\hfill & {\int }_{\mathbb{R}}\left(\frac{d{\nu }_d}{d{\nu }_d^0}log\frac{d{\nu }_d}{d{\nu }_d^0}+1-\frac{d{\nu }_d}{d{\nu }_d^0}\right)d{\nu }_d^0={\int }_{\left(-\infty ,y_{N_d}\right]}\left(\frac{d{\nu }_d}{d{\nu }_d^0}log\frac{d{\nu }_d}{d{\nu }_d^0}+1-\frac{d{\nu }_d}{d{\nu }_d^0}\right)d{\nu }_d^0\hfill \\ & =\sum _{h=1}^{N_d}\left[\frac{{\nu }_h}{{\nu }_h^0}log\frac{{\nu }_h}{{\nu }_h^0}+1-\frac{{\nu }_h}{{\nu }_h^0}\right]{\nu }_d^0\left(\left(y_{h-1},y_h\right]\right)=\sum _{h=1}^{N_d}\left[{\nu }_h\left(log{\nu }_h-log{\nu }_h^0\right)+{\nu }_h^0-{\nu }_h\right].\hfill \end{array}$$

Following the Carr and Madan approach (see Carr and Madan 1999, Section 3.2) for further details), we are able to to express the quantity ${\sum }_{j=1}^N{\left|C_{\nu }^j-C^j\right|}^2$ as a function of ${\nu }_1,\dots ,{\nu }_{N_d}$. The option price $C_{\nu }\left(k\right)$ is not an integrable function, as a swift application of Lebesgue’s convergence theorem shows that it converges to $S_0$ as $k\to -\infty$. Therefore, we focus on the modified time value $z_T$, defined by $z_T\left(k\right):=C_{\nu }\left(k\right)-{\left(S_0-e^{k-rT}\right)}^{+},k\in \mathbb{R}.$ We suppose that $z_T$ and its inverse Fourier transform ${\zeta }_T$ are integrable, so by inversion (see, e.g., Rudin 1987, Theorem 9.11) we have

$$z_T\left(k\right)=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}{e}^{-iku}{\zeta }_T\left(u\right)dua.e.$$

(18)

Fix $k\in \mathbb{R}$; we first analyze the term

$$\begin{array}{cc}\hfill {\left(S_0-e^{k-rT}\right)}^{+}& =\left(S_0-e^{k-rT}\right)1_{\left\{z\le log{S}_0+rT\right\}}\left(k\right)\hfill \\ & =e^{-rT}{\int }_{\mathbb{R}}\left(e^{log{S}_0+rT}-e^k\right)1_{\left\{z\le log{S}_0+rT\right\}}\left(k\right)Q_{L_T}\left(dy\right).\hfill \end{array}$$

In a similar way we get

$$C_{\nu }\left(k\right)=e^{-rT}{\int }_{\mathbb{R}}\left(e^{y+log{S}_0+rT}-e^k\right)1_{\left\{z\le y+log{S}_0+rT\right\}}\left(k\right)Q_{L_T}\left(dy\right).$$

This provides the following expression for $z_T\left(k\right)$:

$$\begin{array}{c}\hfill z_T\left(k\right)=e^{-rT}{\int }_{\mathbb{R}}\left[\left(S_0{e}^{rT+y}-e^k\right)1_{\left\{z\ge k-log{S}_0-rT\right\}}\left(y\right)-\left(S_0{e}^{rT}-e^k\right)1_{\left\{z\le log{S}_0+rT\right\}}\left(k\right)\right]Q_{L_T}\left(dy\right).\end{array}$$

The assumption (ii) ensures that ${\int }_{\mathbb{R}}{e}^y{Q}_{L_T}\left(dy\right)=1,$ so we finally obtain

$$\begin{array}{c}\hfill z_T\left(k\right)=e^{-rT}{\int }_{\mathbb{R}}\left[\left(S_0{e}^{rT+y}-e^k\right)\left(1_{\left\{z\ge k-log{S}_0-rT\right\}}\left(y\right)-1_{\left\{z\le log{S}_0+rT\right\}}\left(k\right)\right)\right]Q_{L_T}\left(dy\right),k\in \mathbb{R}.\end{array}$$

The insight here is to use the Fourier transform and its inverse to estimate the values $z_T\left(x_j\right)$ for every $j=1,\dots ,N$. Hence we fix a point $u\in \mathbb{R}$ and introduce the inverse Fourier transform

$${\zeta }_T\left(u\right):=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}{e}^{iuk}{z}_T\left(k\right)dk.$$

Under suitable conditions which allow us to switch the order of integration we have

$$\begin{array}{cc}\hfill {\zeta }_T\left(u\right)& =-\frac{e^{-rT}}{\sqrt{2\pi }}{\int }_{\left(-\infty ,0\right]}\left[{\int }_{\left(y+log{S}_0+rT,log{S}_0+rT\right)}{e}^{iuk}\left(S_0{e}^{rT+y}-e^k\right)dk\right]Q_{L_T}\left(dy\right)\hfill \\ & +\frac{e^{-rT}}{\sqrt{2\pi }}{\int }_{\left(0,\infty \right)}\left[{\int }_{\left(log{S}_0+rT,y+log{S}_0+rT\right)}{e}^{iuk}\left(S_0{e}^{rT+y}-e^k\right)dk\right]Q_{L_T}\left(dy\right).\hfill \end{array}$$

(19)

We turn our attention on the computation of the first term of the sum (19). An explicit calculation of the inner integral (respect to the Lebesgue measure) of such addend, indicated by $I_1$, gives

$$\begin{array}{cc}\hfill I_1\left(y\right)& =S_0\frac{e^{rT+y+iu\left(log{S}_0+rT\right)}}{iu(iu+1)}\left[iu\left(1-e^{-y}+1-e^{iuy}\right)\right]\hfill \\ \hfill & =S_0\frac{e^{rT+iu\left(log{S}_0+rT\right)}}{iu+1}\left(e^y-1\right)+S_0\frac{e^{rT+iu\left(log{S}_0+rT\right)}}{iu\left(iu+1\right)}{e}^y-S_0\frac{e^{iulog{S}_0}{e}^{\left(iu+1\right)rT}}{iu\left(iu+1\right)}{e}^{y+iuy},y\in \left(-\infty ,0\right].\hfill \end{array}$$

The same strategy allows us to compute the inner integral $I_2$ of the second addend in (19), as well. Precisely, for every $y\in \left(0,\infty \right)$ we get

$$I_2\left(y\right)=-S_0\frac{e^{rT+iu\left(log{S}_0+rT\right)}}{iu+1}\left(e^y-1\right)-S_0\frac{e^{rT+iu\left(log{S}_0+rT\right)}}{iu\left(iu+1\right)}{e}^y+S_0\frac{e^{iulog{S}_0}{e}^{\left(iu+1\right)rT}}{iu\left(iu+1\right)}{e}^{y+iuy}.$$

Therefore we are able to represent the inverse Fourier transform as

$${\zeta }_T\left(u\right)=\frac{S_0}{\sqrt{2\pi }}\frac{e^{iu\left(log{S}_0+rT\right)}}{iu+1}\left[{\int }_{\mathbb{R}}\left(1-e^y\right)Q_{L_T}\left(dy\right)-\frac{1}{iu}{\int }_{\mathbb{R}}{e}^y{Q}_{L_T}\left(dy\right)+\frac{1}{iu}{\int }_{\mathbb{R}}{e}^{y+iuy}{Q}_{L_T}\left(dy\right)\right].$$

Both (A9) in Appendix B and assumption (i) make us conclude that

$${\zeta }_T\left(u\right)=\frac{S_0}{\sqrt{2\pi }}\frac{e^{iu\left(log{S}_0+rT\right)}}{iu\left(iu+1\right)}\left[e^{T\mathsf{\Psi }\left(iu+1\right)}-1\right],u\in \mathbb{R}.$$

(20)

By the definition of $\mathsf{\Psi }$ in (A8) (see Appendix B), substituting the discrete version ${\nu }_d$ for the Lévy measure $\nu$ associated to L, as a consequence of (14) we get, for every $u\in R$,

$$\mathsf{\Psi }\left(iu+1\right)\simeq {\int }_{\mathbb{R}}\left(e^{\left(iu+1\right)y}-iu{e}^y-e^y+iu\right){\nu }_d\left(dy\right)=\sum _{h=1}^{N_d}{e}^{y_h}\left(e^{iu{y}_h}-1\right){\nu }_h+iu\sum _{h=1}^{N_d}\left(1-e^{y_h}\right){\nu }_h.$$

(21)

Plugging (21) into (20) we obtain, for $u\in \mathbb{R}$, the final approximation

$${\zeta }_T\left(u\right)\simeq \frac{S_0}{\sqrt{2\pi }}\frac{e^{iu\left(log{S}_0+rT\right)}}{iu\left(iu+1\right)}\left[exp\left(T\sum _{h=1}^{N_d}{e}^{y_h}\left(e^{iu{y}_h}-1\right){\nu }_h+iuT\sum _{h=1}^{N_d}\left(1-e^{y_h}\right){\nu }_h\right)-1\right].$$

(22)

With the aim to approximate $z_T$ at the points $x_j$, for $j=1,\dots ,N$, we construct a new, uniform grid with mesh d containing the log-strike one. Specifically, fixed $\tilde{N}\in \mathbb{N}$, we set

$${\tilde{x}}_n:=\frac{2\pi n}{\tilde{N}\Delta },n=-\tilde{N},\dots ,-1,0,1,\dots ,\tilde{N},$$

for $\Delta :=\frac{A}{\tilde{N}}$, with $A:=\frac{2\pi }{d}$, which is the size of the discretization interval. We carry out our construction so that for every $j=1,\dots ,N$ and $h=1,\dots ,N_d$ there exists a $n_{hj}\in \left\{-\tilde{N}+1,\dots ,\tilde{N}-1\right\}$ such that $x_j-y_h={\tilde{x}}_{n_{hj}}$. We eventually introduce the points of the discretization grid as

$$u_k:=-\frac{A}{2}+k\Delta ,k=0,\dots ,\tilde{N}.$$

We then compute

$$\begin{array}{cc}\hfill z_T\left({\tilde{x}}_n\right)& \simeq \frac{1}{\sqrt{2\pi }}{\int }_{\left(-A/2,A/2\right)}{e}^{-iu{\tilde{x}}_n}{\zeta }_T\left(u\right)du\simeq \frac{1}{\sqrt{2\pi }}\frac{A}{\tilde{N}}\sum _{k=0}^{\tilde{N}-1}{e}^{-i{u}_k{\tilde{x}}_n}{\tilde{w}}_k{\zeta }_T\left(u_k\right)\hfill \\ & =\frac{1}{\sqrt{2\pi }}\frac{A}{\tilde{N}}{e}^{i\frac{A}{2}{\tilde{x}}_n}\sum _{k=0}^{\tilde{N}-1}exp\left(-i\frac{2\pi n}{\tilde{N}}k\right){\tilde{w}}_k{\zeta }_T\left(u_k\right),n=0,\dots ,\tilde{N}-1,\hfill \end{array}$$

where ${\tilde{w}}_k$ are chosen by the trapezoidal rule, i.e.,

$${\tilde{w}}_k:=\left\{\begin{array}{cc}\frac{1}{2},\hfill & \mathrm{if}k=0,\tilde{N}-1\hfill \\ 1,\hfill & \mathrm{if}k=1,\dots ,\tilde{N}-2\hfill \end{array}\right..$$

Therefore, knowing ${\zeta }_T\left(u_k\right)$ for $k=0,\dots ,\tilde{N}-1$, we can use a fast Fourier transform (FFT) to estimate the values $z_T\left({\tilde{x}}_n\right)$, for $n=0,\dots ,\tilde{N}-1$, and, due to the symmetry of the grid, an inverse discrete Fourier transform to get $z_T\left({\tilde{x}}_n\right)$ for $n=-\tilde{N}+1,\dots ,-1$. Thus, we reduce the optimization problem (16) to the minimization in ${\left({\mathbb{R}}^{+}\right)}^d$ of the objective functional:

$$\mathcal{F}\left({\nu }_1,\dots ,{\nu }_{N_d}\right)=\sum _{j=1}^N{\left|z_t\left(x_j\right)+{\left(S_0-e^{x_j-rT}\right)}^{+}-C^j\right|}^2+\alpha \sum _{h=1}^{N_d}\left[{\nu }_h\left(log{\nu }_h-log{\nu }_h^0\right)+{\nu }_h^0-{\nu }_h\right].$$

(23)

The optimization is run under the L-BFGS-B algorithm, so we compute the derivatives of $\mathcal{F}$ to speed it up. We focus on deriving the first addend in (23), since calculating the entropic term is straightforward. Denote by $g\left({\nu }_1,\dots ,{\nu }_{N_d}\right)$ the argument of the exponential in (22) and define

$$C_u:=\frac{S_0}{\sqrt{2\pi }}\frac{e^{iu\left(log{S}_0+rT\right)}}{iu\left(iu+1\right)},u\in \mathbb{R}.$$

Under suitable integrability condition, for every $u\in \mathbb{R}$ and $h=1,\dots ,N_d$ we have

$$\begin{array}{cc}\hfill \frac{\partial {\zeta }_T\left(u\right)}{\partial {\nu }_h}& \left({\nu }_1,\dots ,{\nu }_{N_d}\right)=C_{u}T{e}^{g\left({\nu }_1,\dots ,{\nu }_{N_d}\right)}\left[e^{y_h}\left(e^{iu{y}_h}-1\right)+iu\left(1-e^{y_h}\right)\right]\hfill \\ & =\frac{S_0}{\sqrt{2\pi }}\frac{T}{iu+1}{e}^{iu\left(log{S}_0+rT\right)}\left(1-e^{y_h}\right)e^{g\left({\nu }_1,\dots ,{\nu }_{N_d}\right)}+T{e}^{y_h}{\zeta }_T\left(u\right)\left(e^{iu{y}_h}-1\right)+T{e}^{y_h}{C}_u\left(e^{iu{y}_h}-1\right).\hfill \end{array}$$

Direct calculation from (18) leads, for every $k\in \mathbb{R}$ and $h=1,\dots ,N_d$, to

$$\begin{array}{cc}\hfill & \frac{\partial z_T\left(k\right)}{\partial {\nu }_h}\left({\nu }_1,\dots ,{\nu }_{N_d}\right)=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}{e}^{-iuk}\frac{\partial {\zeta }_T\left(u\right)}{\partial {\nu }_h}\left({\nu }_1,\dots ,{\nu }_{N_d}\right)du\hfill \\ \hfill & =\frac{S_0}{2\pi }T\left(1-e^{y_h}\right){\int }_{\mathbb{R}}\frac{e^{-iuk}}{iu+1}{e}^{iu\left(log{S}_0+rT\right)}{e}^{g\left({\nu }_1,\dots ,{\nu }_{N_d}\right)}du\hfill \\ & +T{e}^{y_h}\left[z_T\left(k-y_h\right)+{\left(S_0-e^{k-rT-y_h}\right)}^{+}-z_T\left(k\right)-{\left(S_0-e^{k-rT}\right)}^{+}\right].\hfill \end{array}$$

(24)

Taking $k={\tilde{x}}_n$, for $n=0,\dots ,\tilde{N}-1$, we can approximate the first addend in (24) with an FFT:

$${\int }_{\mathbb{R}}\frac{e^{-iu{\tilde{x}}_n}}{iu+1}{e}^{iu\left(rT+log{S}_0\right)}{e}^{g\left({\nu }_1,\dots ,{\nu }_{N_d}\right)}\simeq \frac{A}{\tilde{N}}\sum _{k=0}^{\tilde{N}-1}{e}^{-i{u}_k{\tilde{x}}_n}{\tilde{w}}_{k}f\left(u_k\right)=\frac{A}{\tilde{N}}{e}^{i\frac{A}{2}{\tilde{x}}_n}\sum _{k=0}^{\tilde{N}-1}exp\left(-i\frac{2\pi n}{\tilde{N}}k\right){\tilde{w}}_{k}f\left(u_k\right),$$

where

$$f\left(u\right):=\frac{\sqrt{2\pi }}{S_0}iu{\zeta }_T\left(u\right)+\frac{e^{iu\left(log{S}_0+rT\right)}}{iu+1},u\in \mathbb{R}.$$

Summarizing, we can numerically calculate the derivatives of $\mathcal{F}$:

$$\frac{\partial \mathcal{F}}{\partial {\nu }_h}\left({\nu }_1,\dots ,{\nu }_{N_d}\right)=2\sum _{j=1}^N\left[z_T\left(x_j\right)+{\left(S_0-e^{x_j-rT}\right)}^{+}-C^j\right]\frac{\partial z_T\left(x_j\right)}{\partial {\nu }_h}\left({\nu }_1,\dots ,{\nu }_{N_d}\right)+\alpha \left(log{\nu }_h-log{\nu }_h^0\right)$$

for any $h=1,\dots ,N_d$.

The regularization parameter $\alpha$ should be eventually determined; to this aim, we follow a procedure loosely inspired by the Morozov discrepancy principle (see the classical Morozov (1966)). We start off by minimizing the quadratic pricing error (15), ignoring the entropy term and using the discretized Lévy measure of $L^0$ as starting point. The value ${ϵ}_0$ of the functional at the found minimum $\overline{\nu }$ is interpreted as the distance between the market and the selected model class. After that we consider the bid–ask spread of the options on the market and denote by $ϵ$ its Euclidean norm. The absolute value of the difference between these two quantities is then allowed to be slightly greater, although it must maintain the same order of magnitude. This leads to the introduction of another term $\widetilde{ϵ}:=\left|{ϵ}_0-ϵ\right|$, where c is a positive constant to be picked. At this point the functional in (16) is strictly increasing in $\alpha$, so we choose the regularization parameter as follows:

$$\alpha :=\widetilde{ϵ}{\left({\int }_{\mathbb{R}}\left(\frac{d\overline{\nu }}{d{\nu }^0}log\frac{d\overline{\nu }}{d{\nu }^0}+1-\frac{d\overline{\nu }}{d{\nu }^0}\right)d{\nu }^0\right)}^{-1}.$$

For our applications, taking $c\approx 2$ has proven to be a satisfactory choice in terms of goodness of fit.

3.1.2. Empirical Results

The final step is to empirically apply this method on prices of real-traded options. In particular, we have tested it with derivatives on the same stocks as those considered for the Esscher’s method. In order to estimate the parameters of the historical Lévy process, we used the same time series of log–prices as those of the Esscher’s method (see Section 2.1.2) All the call options under scrutiny expire in January 2021: 11 months from the time of simulation.

In the case of call options on Apple Inc. stock (AAPL) we obtained an average of the absolute values of percentage difference of $3.5794\%$: Figure 2a displays the results of such implementation. As regards call options on Microsoft Corporation stock (MSFT), the absolute values of percentage difference is $1.6425\%$ and the results are shown in Figure 2b. Finally we calibrated our method to the prices of call options on Tesla, Inc. stock (TSLA): Figure 2c shows the outcomes. Here the mean of absolute values of percentage difference settles down at $0.9148\%$.

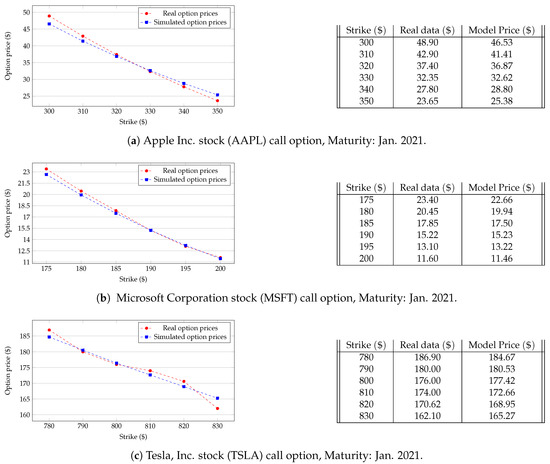
Figure 2. Numerical experiments for the calibration method.

This time we retrieved the real prices from https://finance.yahoo.com, but the same considerations as Remark 3 apply.

4. Conclusions

The main purpose of this research is to quantify the performances of two option pricing methods in a liquid market like NASDAQ. The first approach is based on the Esscher measure, the second one on the calibration to real-traded call option prices with an entropic penalty term.

Our experimental analysis shows that, from a computational point of view, the Esscher method with ${10}^4$ Monte Carlo iterations is far faster than the calibration method: the table in Figure 3 reports the exact execution times that we have obtained with an Asus ZenBook UX31A. This fact is especially noticeable when we need to simulate the prices of options with different maturities and same strike. On the other hand, the calibration method allows generating the entire option chain for a fixed maturity with great precision. Moreover, it is more stable than the previous one, as it provides results closer to real data for a larger range of stock prices.

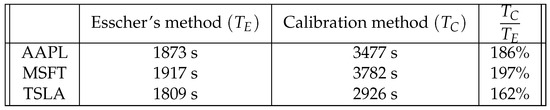
Figure 3. Computational times (in seconds) of both methods (with an Asus ZenBook UX31A).

Comparing averages of absolute values for percentage difference between real and simulated prices, the calibration procedure offers better outcomes than Esscher’s, with the only exception of AAPL call options, where the latter outperforms the former by approximately 42 basis points. Nevertheless, the Esscher method only needs the historical time series of the underlying asset price to be applied, so it is feasible also in markets with few derivatives. This study shows that the Esscher measure is an appealing and efficient solution to price call options in illiquid—or low liquid—financial markets.

5. Future Research

Considering the future work on the subject, one of the directions worth investigating is the Linear Esscher measure method. The importance of focusing on this approach is given by its intrinsic link to the minimal entropy Hellinger martingale measure, as indicated by Rheinländer and Sexton in (Rheinländer and Sexton 2011, Chp. 9), and, in much more detail, by Choulli and Stricker in Choulli and Stricker (2006). Moreover, it would be interesting to extend our study to other asset classes like metal futures, and to compare it with the results obtained in Chen (2011).