Retirement Ages by Socio-Economic Class
Abstract
1. Introduction
2. Our Utilitarian Framework
2.1. The Pension Schemes
2.2. The Model Specifications
- Disutility of workIn this case, the lifetime utility for class i, , given the retirement age reached at time t, is defined as:with s designating the system, either DB or NDC, the individual time preference, the CRRA utility function , for the risk aversion coefficient (if , then ) and , where v is a constant (as done by Knell and Nationalbank (2016)). The function gives the utility of consumption, while represents the disutility of work.
- Utility of leisureIn the case of the utility of leisure, the lifetime utility for class i, at the retirement age is determined as:with the utility of leisure (following Lacomba and Lagos (2006)). The utility function is defined as mentioned above.
2.3. Data Description and Assumptions
2.4. Results
2.4.1. Disutility of Work
2.4.2. Utility of Leisure
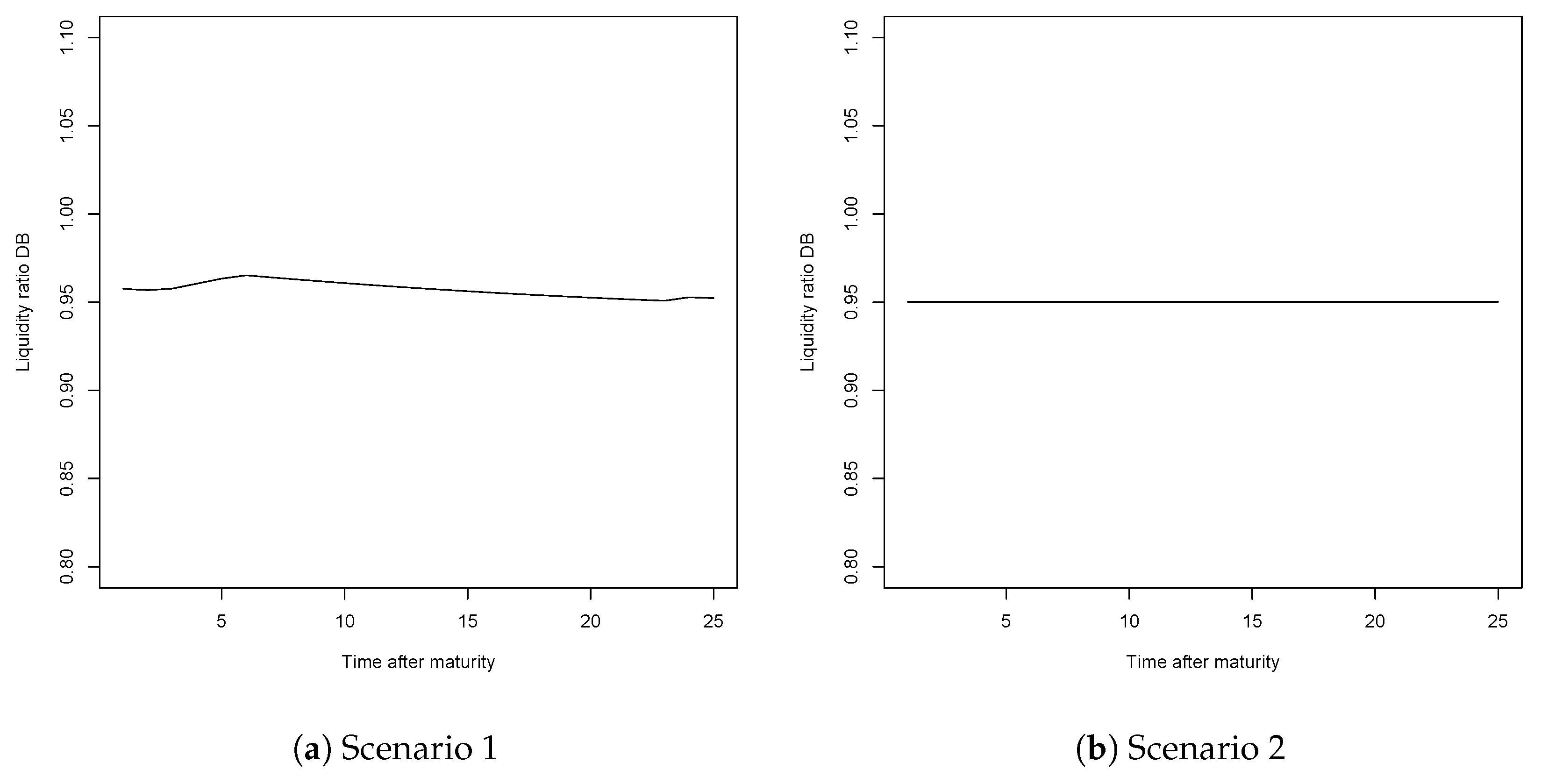
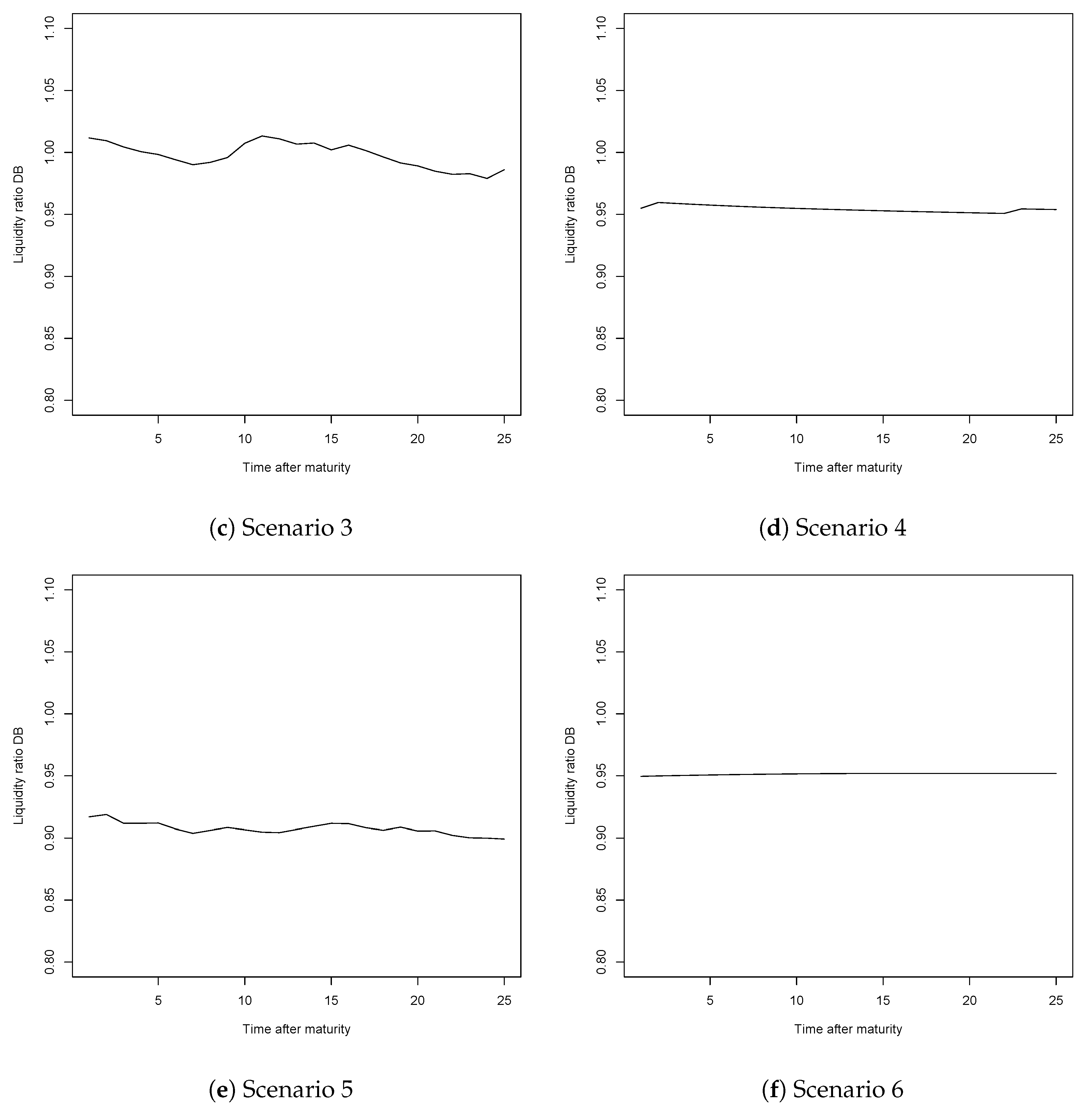
3. Actuarial Framework
3.1. Optimisation Problem
3.2. Results
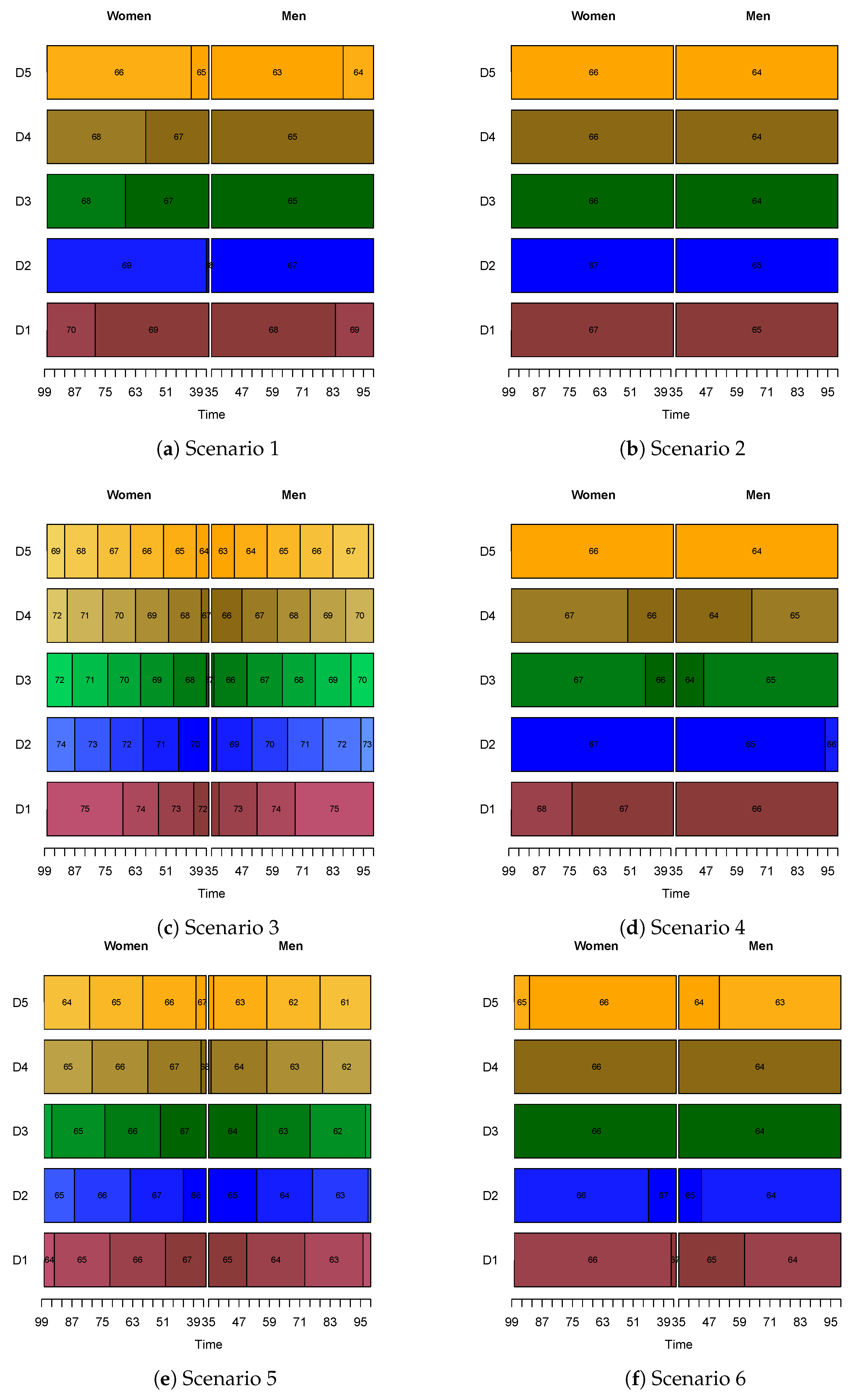
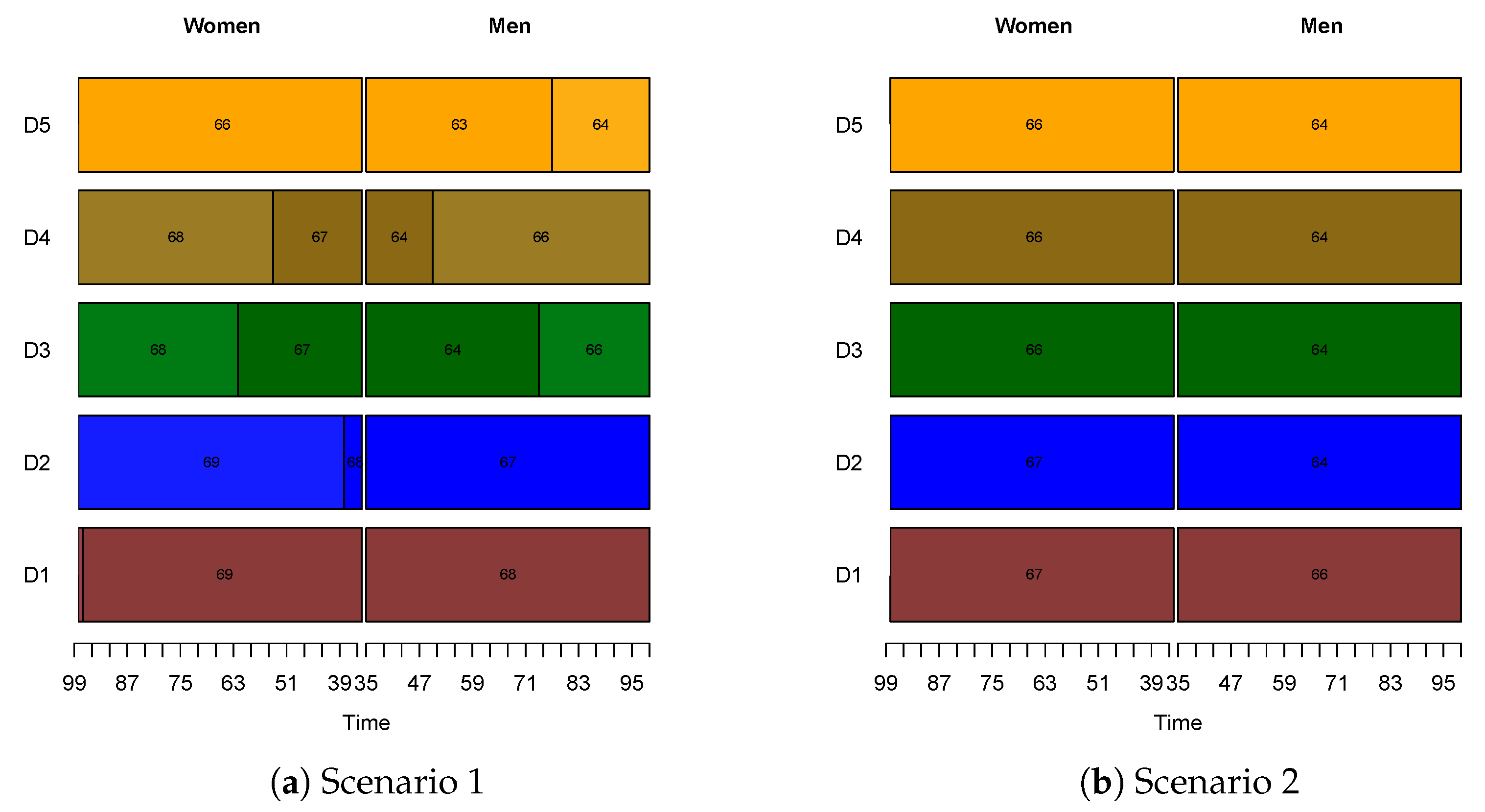
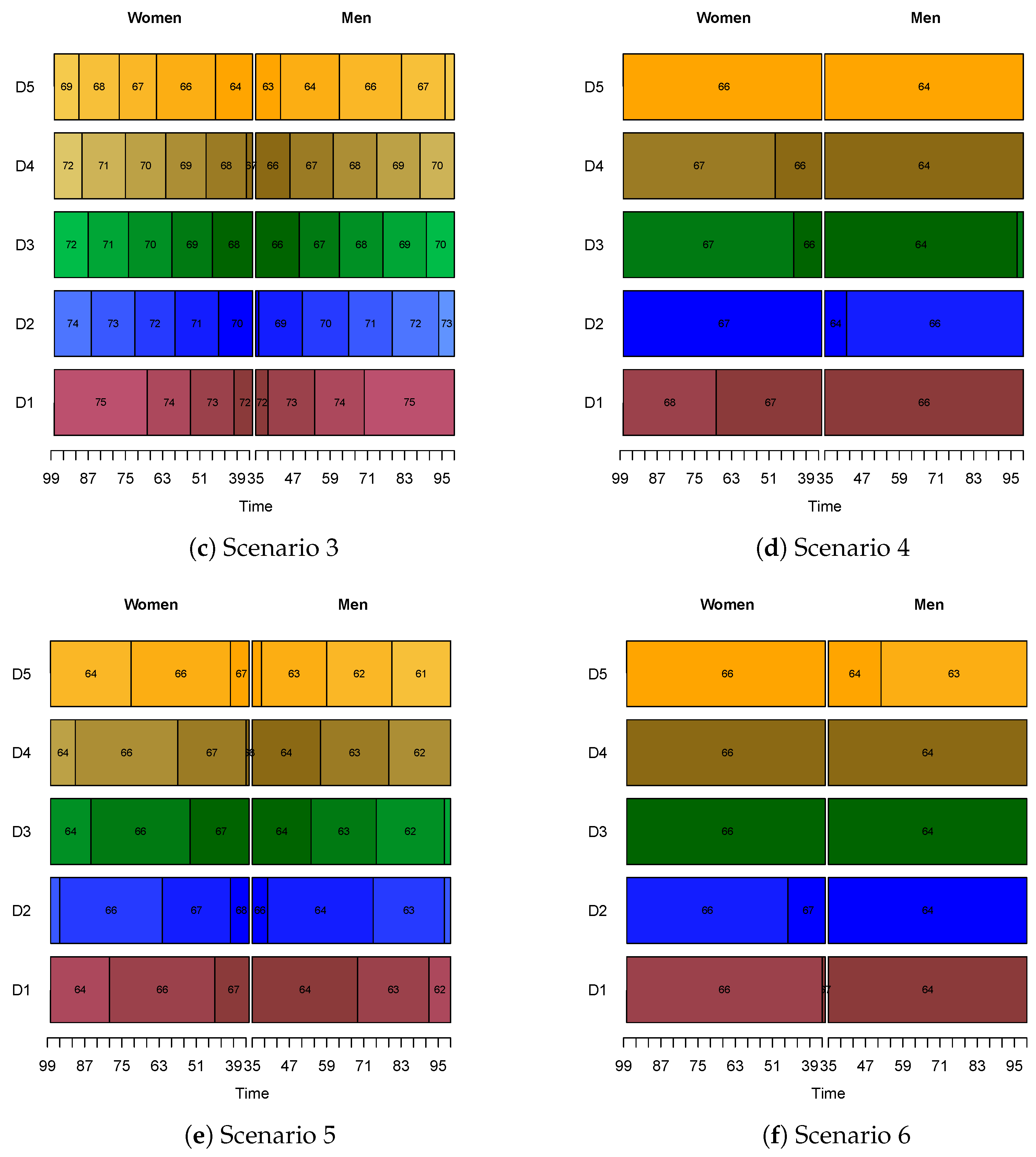
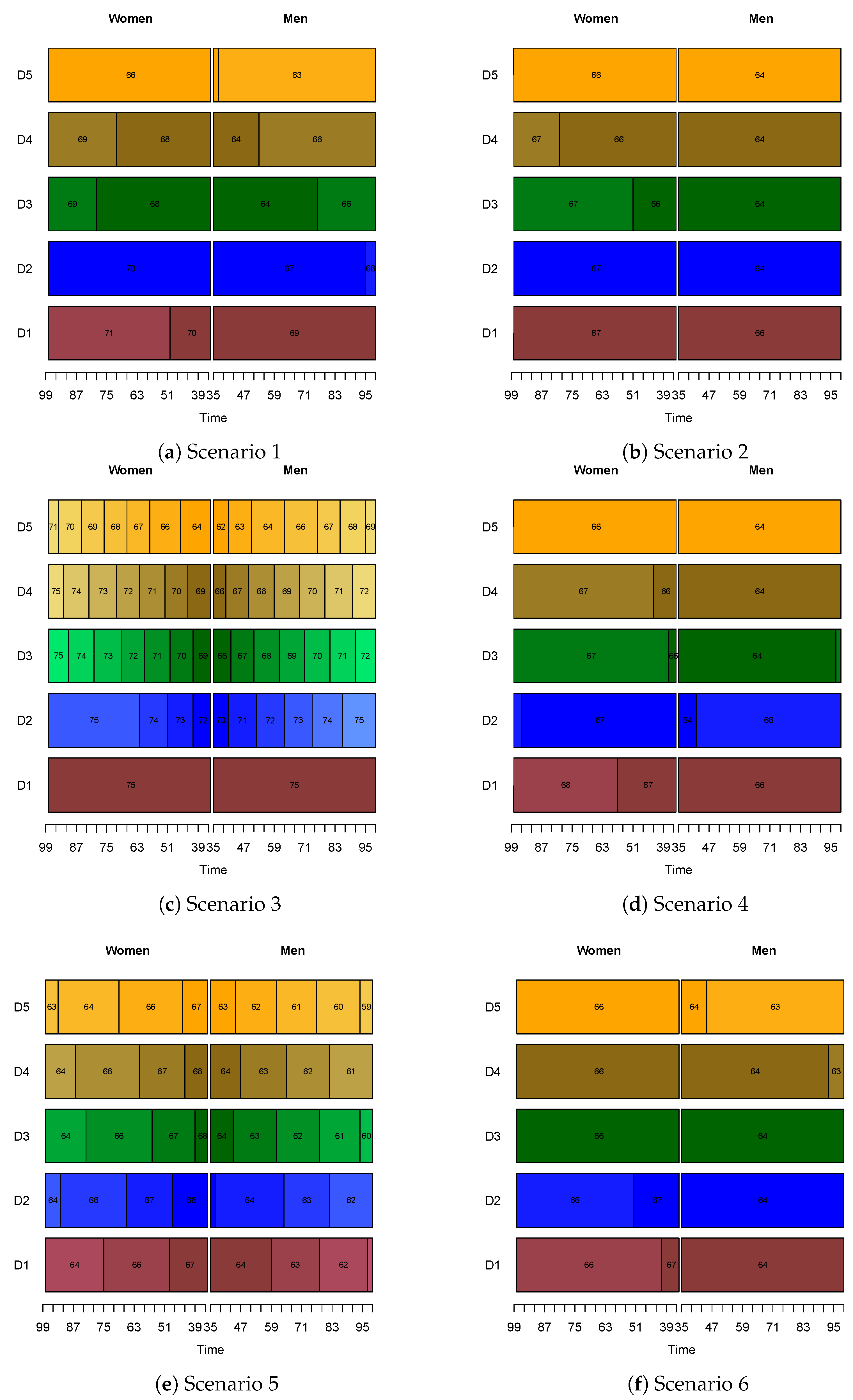
3.2.1. Class-Specific Retirement Ages
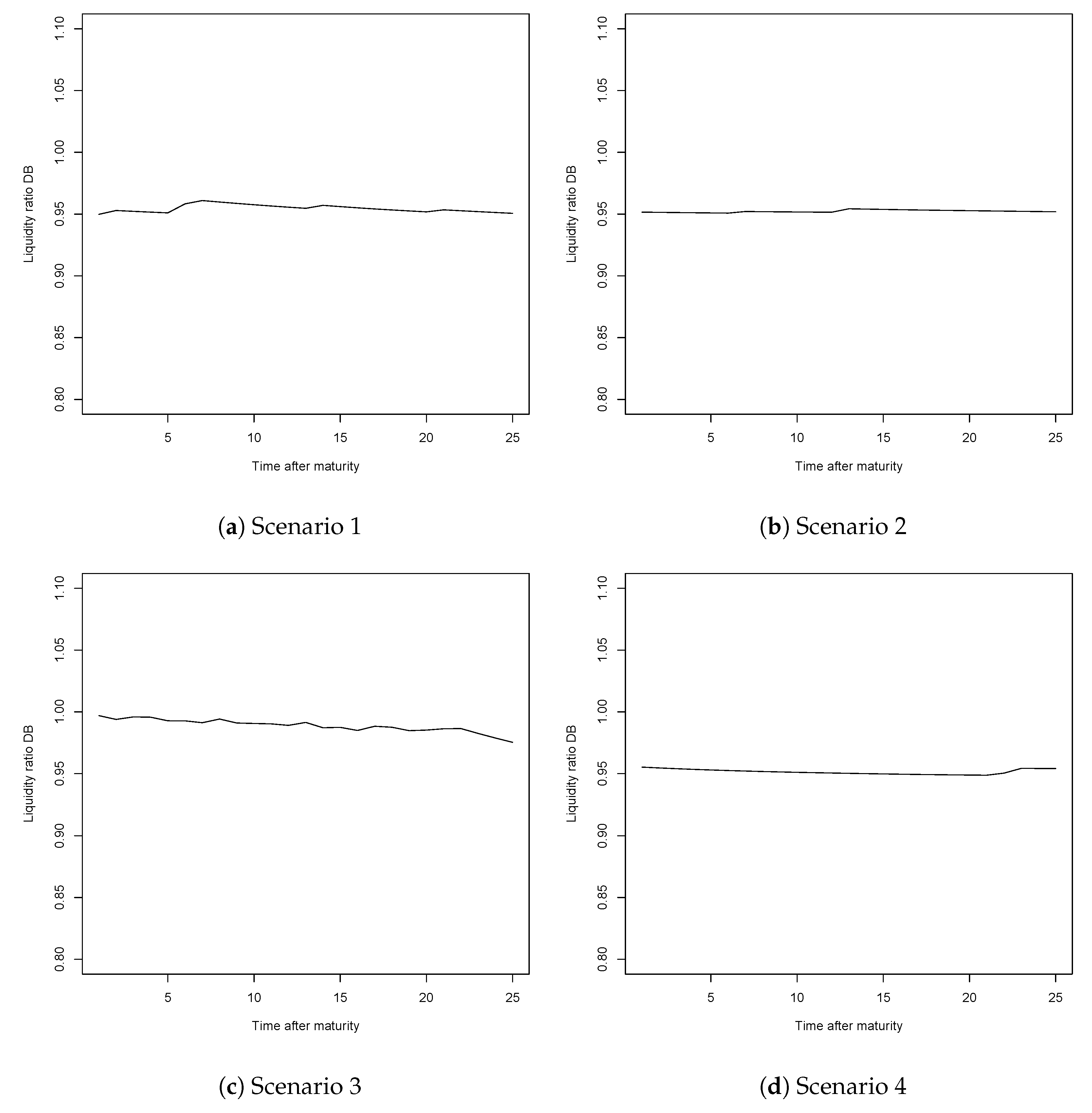
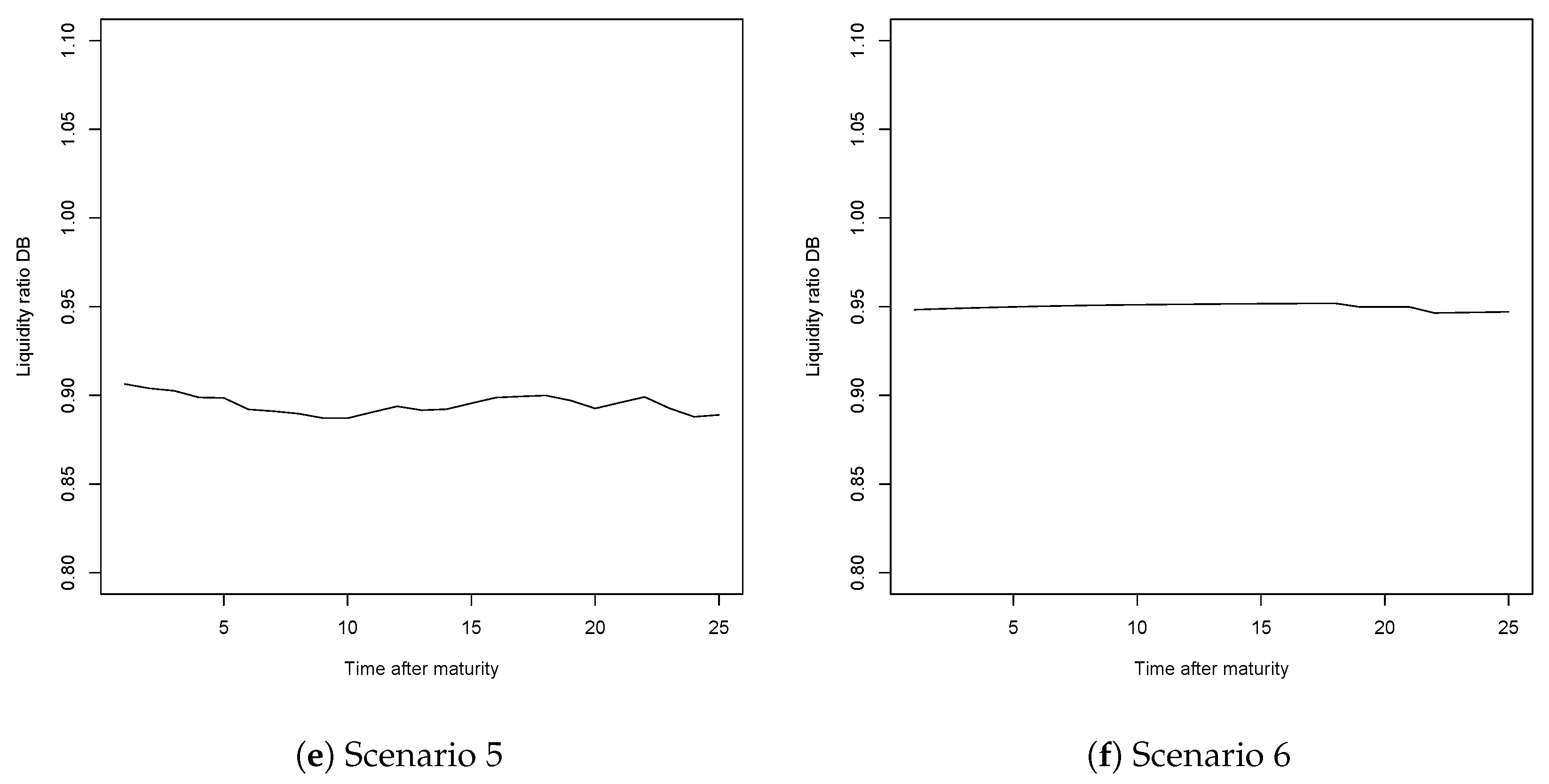
3.2.2. Further Discussion
Mortality Evolving throughout Time
No Gender Distinction
3.3. Mortality Differences Impacting the Retirement Age by One Year
3.4. A Real Case Study: The Swiss System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
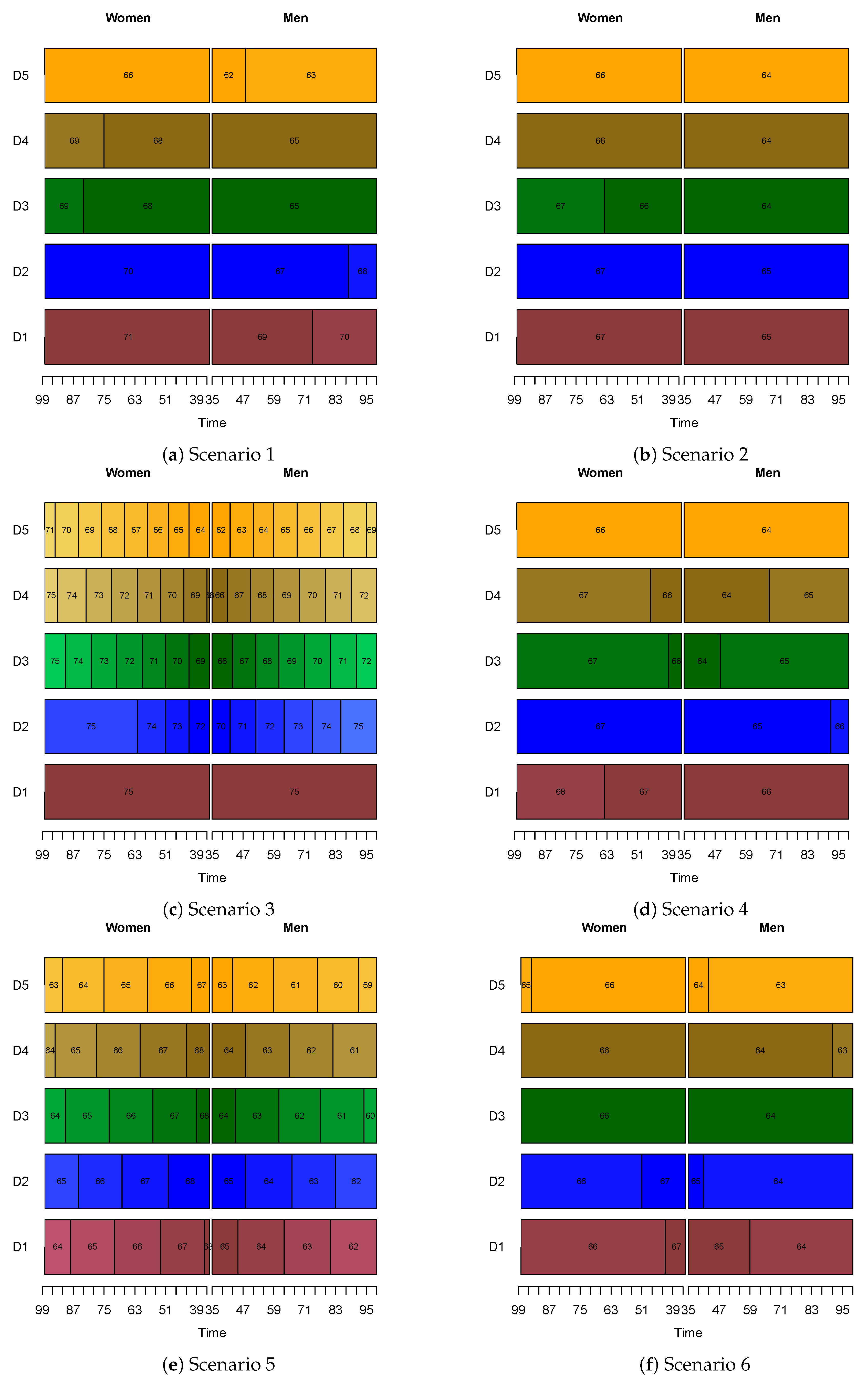
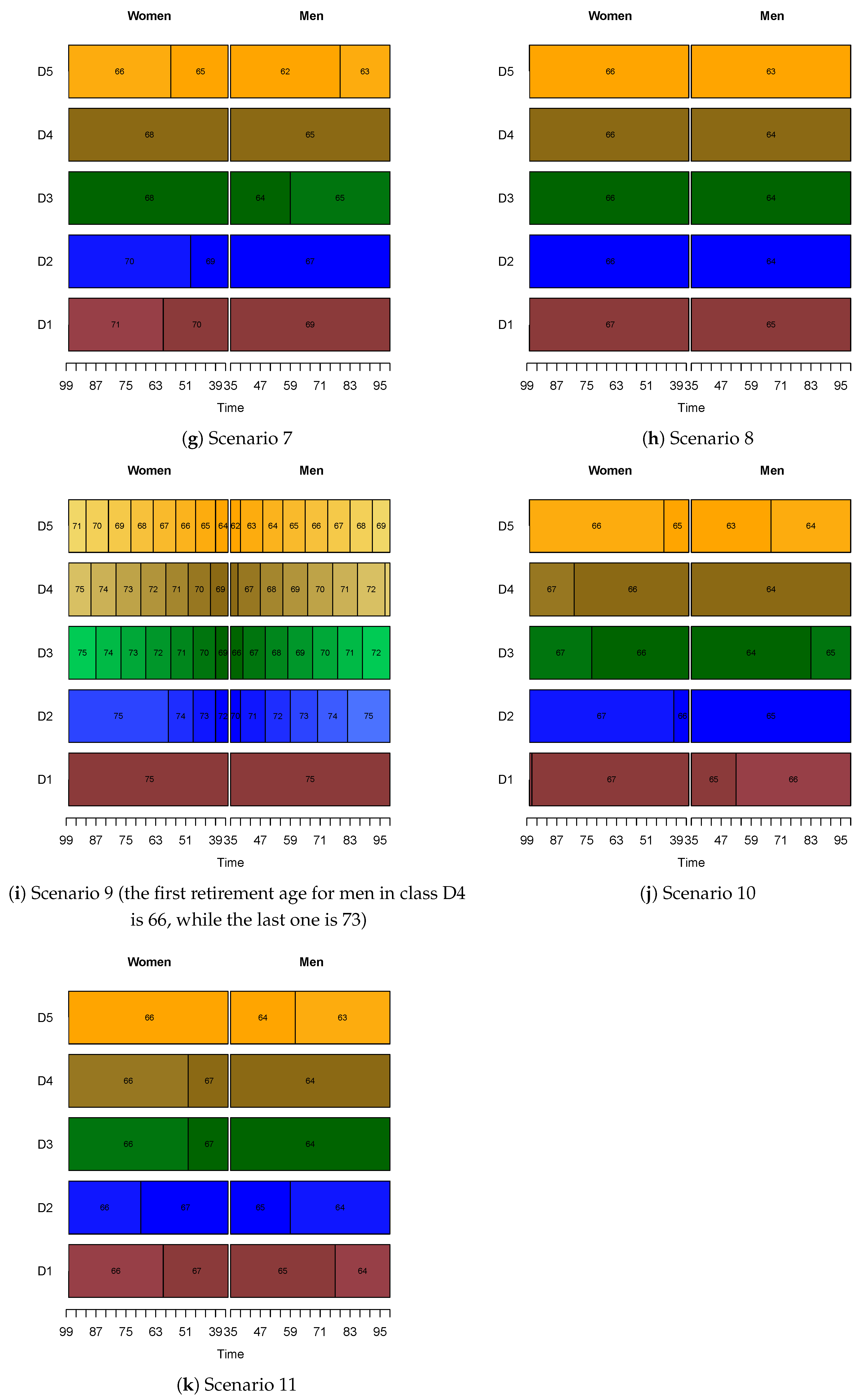
Appendix A. Results for the Model Using the Disutility of Work

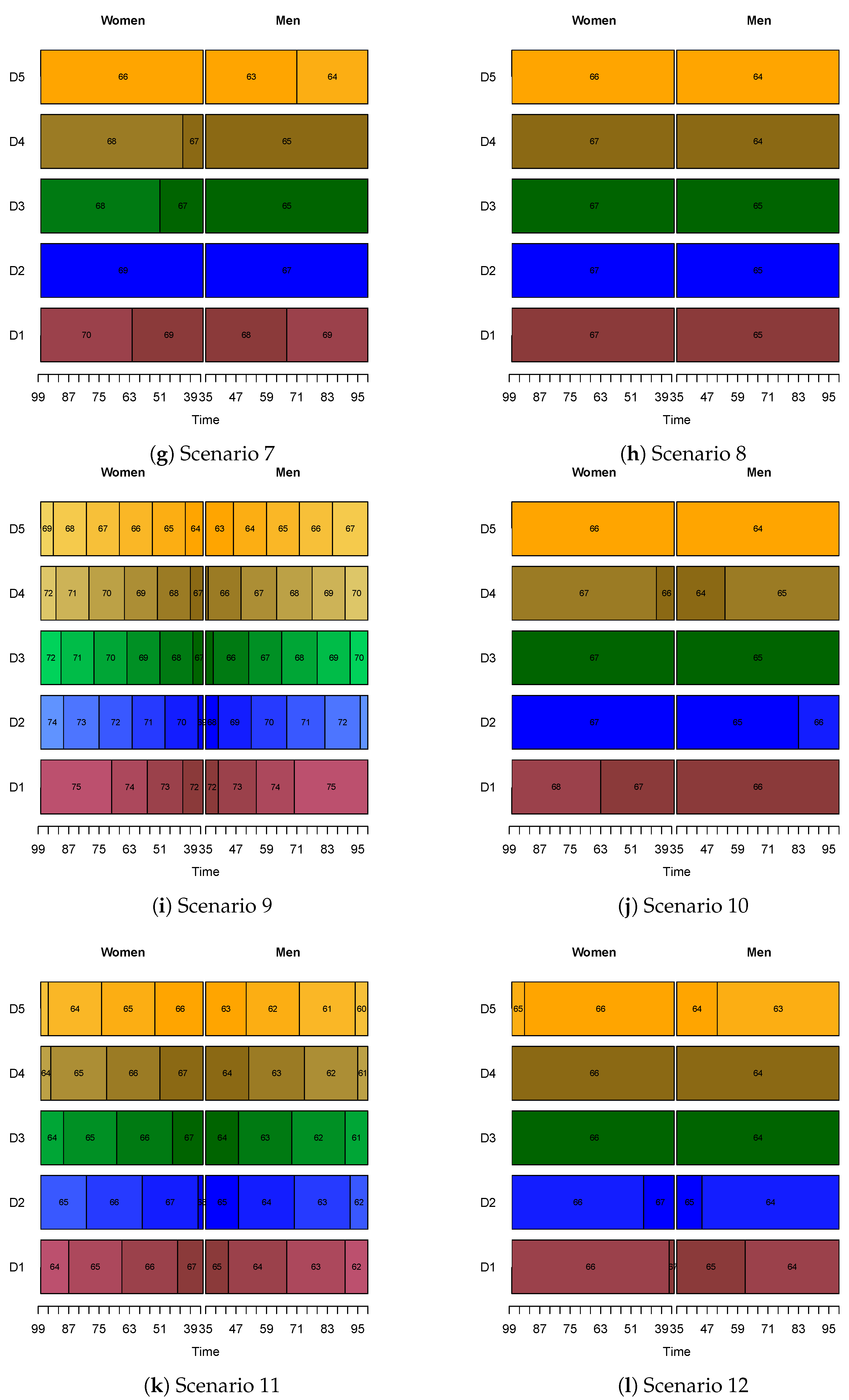
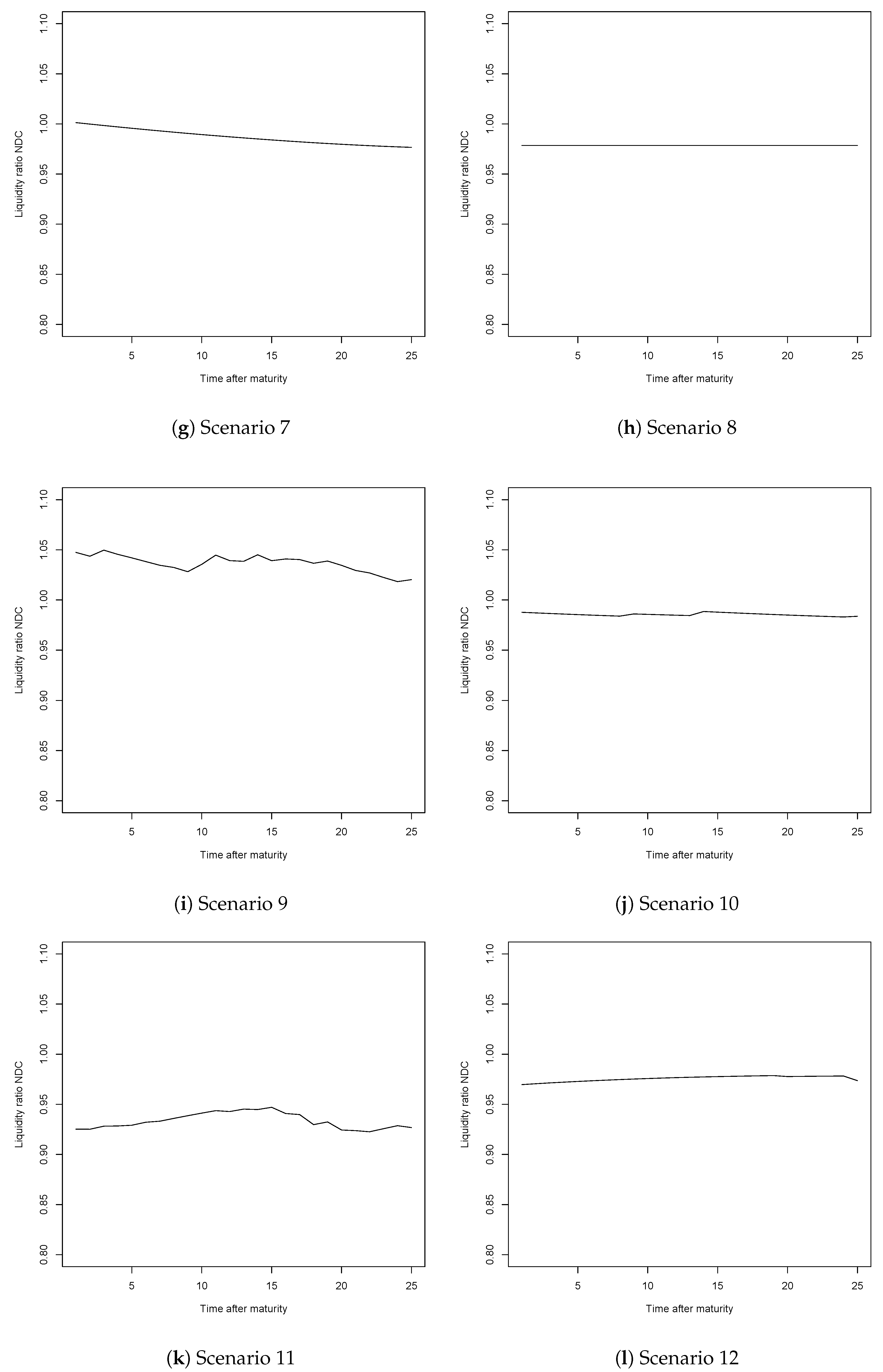
Appendix B. Results for the Model Using the Utility of Leisure
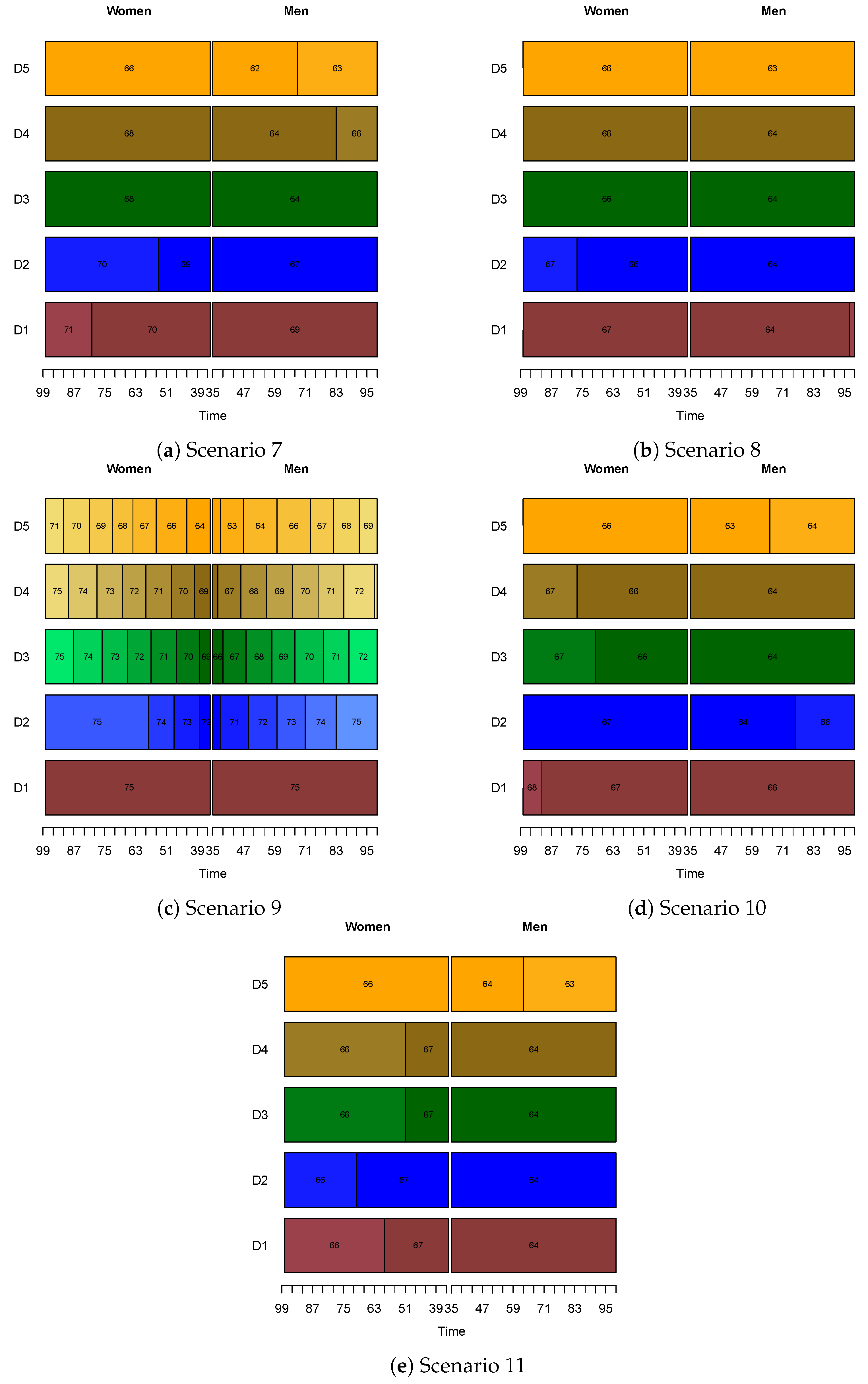
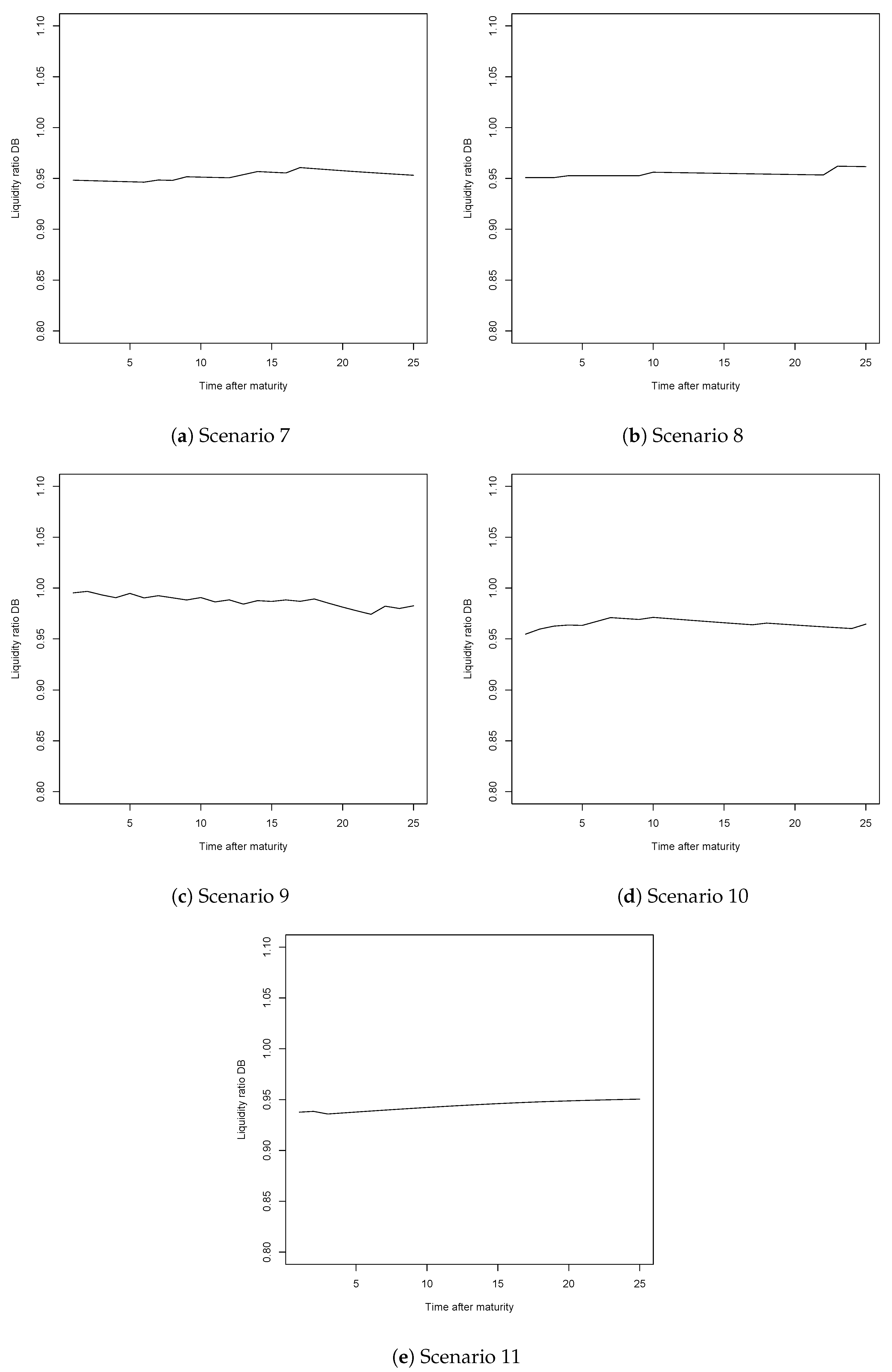
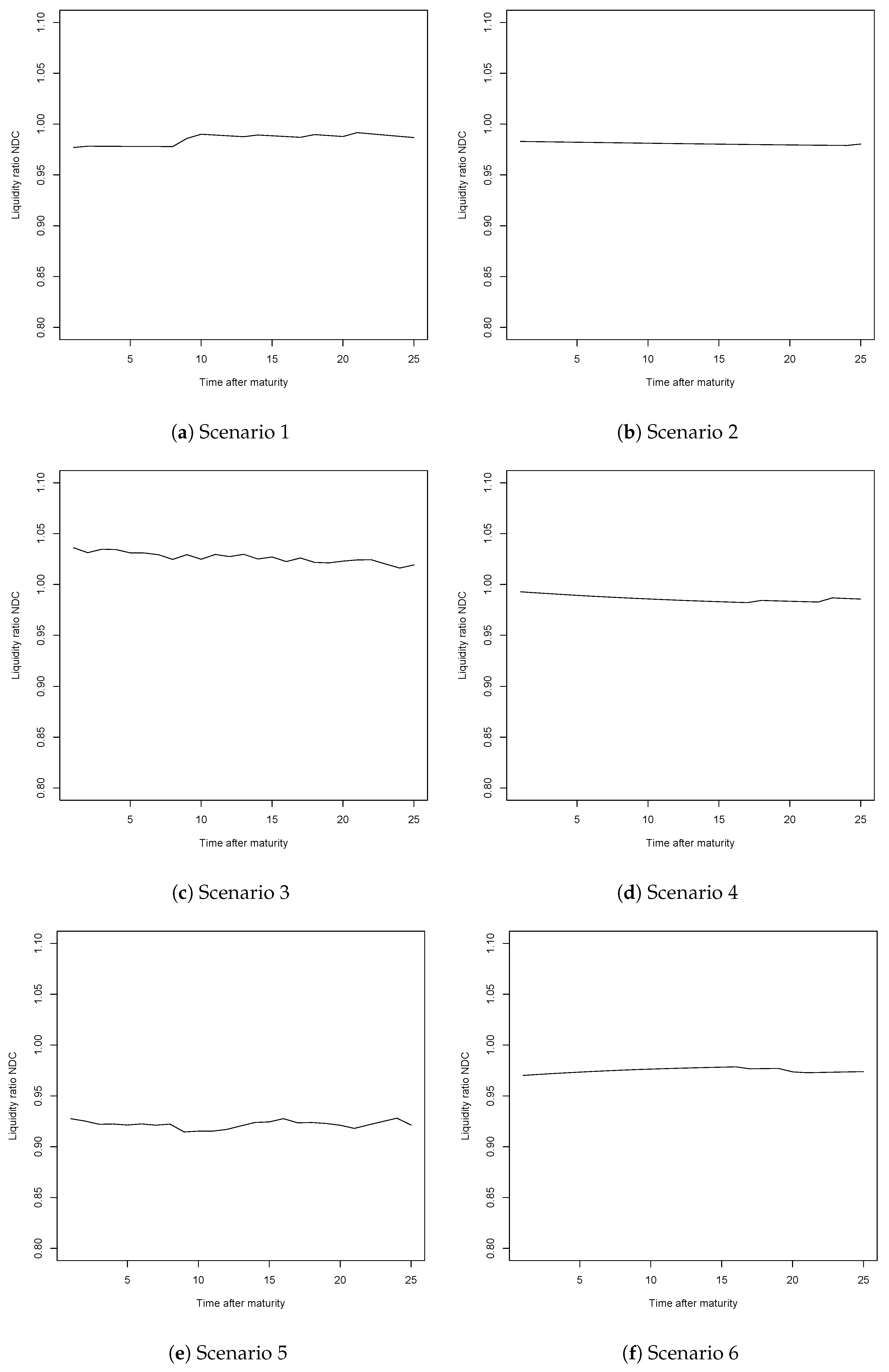
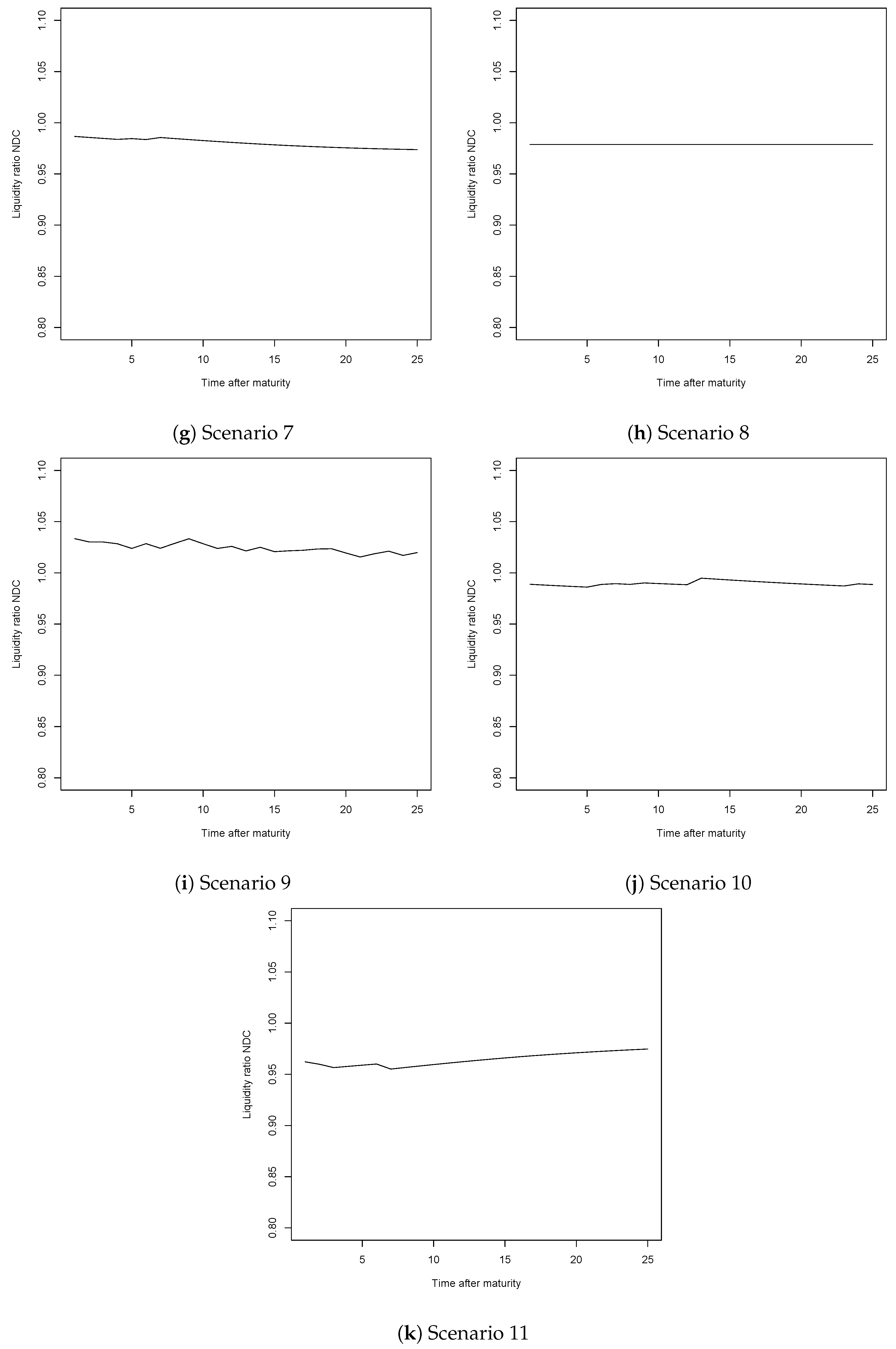
Appendix C. Mortality Rates by Socio-Economic Class

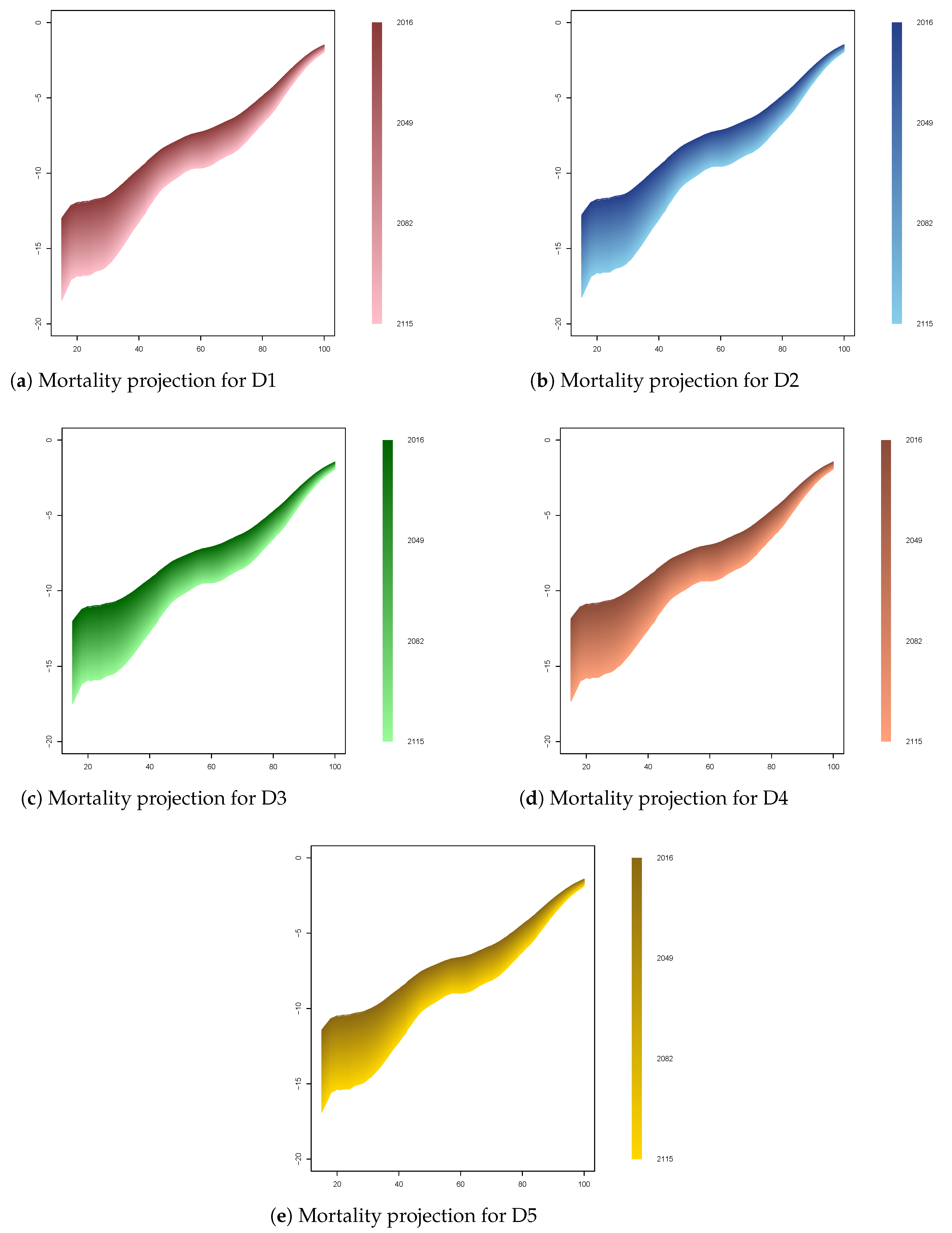
References
- Arnold, Séverine, María del Carmen Boado-Penas, and Humberto Godínez-Olivares. 2016. Longevity Risk in Notional Defined Contribution Pension Schemes: A Solution. The Geneva Papers on Risk and Insurance-Issues and Practice 41: 24–52. [Google Scholar] [CrossRef]
- Azar, Samih Antoine. 2010. Bounds to the coefficient of relative risk aversion. Banking and Finance Letters 2: 391–98. [Google Scholar]
- Bagliano, Fabio C., and Giuseppe Bertola. 2004. Models for Dynamic Macroeconomics. Oxford: Oxford University Press on Demand. [Google Scholar]
- Bisetti, Emilio, and Carlo Favero. 2014. Measuring the impact of longevity risk on pension systems: The case of Italy. North American Actuarial Journal 18: 87–103. [Google Scholar] [CrossRef]
- Bloom, David, David Canning, and Michael Moore. 2014. Optimal retirement with increasing longevity. The Scandinavian Journal of Economics 116: 838–58. [Google Scholar] [CrossRef]
- Bodie, Zvi, Alan Marcus, and Robert Merton. 1988. Defined benefit versus defined contribution pension plans: What are the real trade-offs? In Pensions in the US Economy. Chicago: University of Chicago Press, pp. 139–62. [Google Scholar]
- Börsch-Supan, Axel. 2006. What are NDC Systems? What do they bring to Reform Strategies? In Pension Reform: Issues and Prospects for Non-Financial Defined Contribution (NDC) Schemes. Washington: The World Bank, pp. 35–55. [Google Scholar]
- Bowers, Newton, Hans Gerber, James Hickman, Donald Jones, and Cecil Nesbitt. 1997. Actuarial Mathematics. Schaumburg: Society of Actuaries. [Google Scholar]
- Chetty, Raj. 2006. A new method of estimating risk aversion. American Economic Review 96: 1821–34. [Google Scholar] [CrossRef]
- Chetty, Raj, Michael Stepner, Sarah Abraham, Shelby Lin, Benjamin Scuderi, Nicholas Turner, Augustin Bergeron, and David Cutler. 2016. The association between income and life expectancy in the united states, 2001–2014. JAMA 315: 1750–66. [Google Scholar] [CrossRef]
- Hakola, Tuulia. 1999. Race for Retirement. Technical Report. Helsinki: VATT Institute for Economic Research. [Google Scholar]
- Hansen, Casper, and Lars Lonstrup. 2009. The Optimal Legal Retirement Age in Olg Model with Endogenous Labour Supply. Discussion Papers on Business and Economics. Odense: University of Southern Denmark. [Google Scholar]
- Hardy, Melissa. 1984. Effects of education on retirement among white male wage-and-salary workers. Sociology of Education 57: 84–98. [Google Scholar] [CrossRef]
- Hörner, Wolfgang, Hans Döbert, Lutz Reuter, and Botho Kopp. 2007. The Education Systems of Europe. Dordrecht: Springer, 7 vols. [Google Scholar]
- Hunt, Andrew, and David Blake. 2017. Modelling mortality for pension schemes. ASTIN Bulletin: The Journal of the IAA 47: 601–29. [Google Scholar] [CrossRef]
- Jang, Bong-Gyu, Seyoung Park, and Yuna Rhee. 2013. Optimal retirement with unemployment risks. Journal of Banking & Finance 37: 3585–604. [Google Scholar]
- Jijiie, Anca, Jennifer Alonso-García, and Séverine Arnold. 2019. Mortality by Socio-Economic Class and Its Impact on the Retirement Schemes: How to Render the Systems Fairer? Working Paper. Sydney: ARC Centre of Excellence in Population Ageing Research (CEPAR). [Google Scholar]
- Knell, Markus, and Oesterreichische Nationalbank. 2016. Increasing longevity and ndc pension systems. Journal of Pension Economics and Finance 17: 1–30. [Google Scholar]
- Lacomba, Juan, and Francisco Lagos. 2006. Population aging and legal retirement age. Journal of Population Economics 19: 507–19. [Google Scholar] [CrossRef]
- Li, Nan, and Ronald Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the Lee-Carter method. Demography 42: 575–94. [Google Scholar] [CrossRef] [PubMed]
- Lumsdaine, Robin, James Stock, and David Wise. 1992. Three models of retirement: Computational complexity versus predictive validity. In Topics in the Economics of Aging. Chicago: University of Chicago Press, pp. 21–60. [Google Scholar]
- Määttänen, Niku, Andres Võrk, Magnus Piirits, Robert Gal, Elena Jarocinska, Anna Ruzik, and Theo Nijman. 2014. The Impact of Living and Working Longer on Pension Income in Five European Countries: Estonia, Finland, Hungary, the Netherlands and Poland. Case Report No. 476/2014. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2496799 (accessed on 16 June 2019).
- MacDonald, Bonnie-Jeanne, and Andrew JG Cairns. 2011. Three retirement decision models for defined contribution pension plan members: A simulation study. Insurance: Mathematics and Economics 48: 1–18. [Google Scholar] [CrossRef]
- Magnani, Riccardo. 2018. What’s Gone Wrong in the Design of PAYG Systems? CEPN Working Papers 2018-13. Paris: Centre d’Economie de l’Université de Paris Nord. [Google Scholar]
- Meara, Ellen, Seth Richards, and David Cutler. 2008. The gap gets bigger: Changes in mortality and life expectancy, by education, 1981–2000. Health Affairs 27: 350–60. [Google Scholar] [CrossRef]
- Munnell, Alicia, Anthony Webb, and Anqi Chen. 2016. Does Socioeconomic Status Lead People to Retire Too Soon? Age 60: 65. [Google Scholar] [CrossRef]
- Nelissen, Jan. 1999. Mortality differences related to socioeconomic status and the progressivity of old-age pensions and health insurance: The Netherlands. European Journal of Population/Revue européenne de Démographie 15: 77–97. [Google Scholar] [CrossRef]
- OECD. 2014. Mortality Assumptions and Longevity Risk. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- OECD. 2015. Pensions at a Glance 2015. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- Oeppen, Jim, and James Vaupel. 2002. Broken Limits to Life Expectancy. Science 296: 1029–31. [Google Scholar] [CrossRef]
- Olshansky, Jay, Toni Antonucci, Lisa Berkman, Robert Binstock, Axel Boersch-Supan, John Cacioppo, Bruce Carnes, Laura Carstensen, Linda Fried, Dana Goldman, and et al. 2012. Differences in life expectancy due to race and educational differences are widening, and many may not catch up. Health Affairs 31: 1803–13. [Google Scholar] [CrossRef] [PubMed]
- Ostaszewski, Krzysztof, Hong Mao, and Yuling Wang. 2011. The Determination of Optimal Retirement Age Using Optimal Control Theory. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1888016 (accessed on 16 June 2019).
- Palme, Mårten, and Ingemar Svensson. 2004. Income security programs and retirement in sweden. In Social Security Programs and Retirement Around the World: Micro-Estimation. Chicago: University of Chicago Press, pp. 579–642. [Google Scholar]
- Palmer, Edward. 2006. What’s ndc? In Pension Reform: Issues and Prospects for Non-Financial Defined Contribution (NDC) Schemes. Edited by Robert Holzmann and Edward Palmer. Washington: World Bank Publications, Chapter 2. pp. 17–35. [Google Scholar]
- Panis, Constantijn, Michael Hurd, David Loughran, Julie Zissimopoulos, Steven Haider, Patricia St Clair, Delia Bugliari, Serhii Ilchuk, Gabriela Lopez, Philip Pantoja, and et al. 2002. The Effects of Changing Social Security Administration’s Early Entitlement Age and the Normal Retirement Age. Santa Monica: RAND. [Google Scholar]
- Piekkola, Hannu, and Matthias Deschryvere. 2004. Retirement Decisions and Option Values: Their Application Regarding Finland, Belgium and Germany. Technical Report, ETLA Discussion Papers. Helsinki: The Research Institute of the Finnish Economy (ETLA). [Google Scholar]
- Rogerson, Richard, and Johanna Wallenius. 2009. Retirement in a Life Cycle Model of Labor Supply with Home Production. Michigan Retirement Research Center Research Paper 2009-205). Ann Arbor: University of Michigan. [Google Scholar]
- Rutledge, Matthew, Geoffrey Sanzenbacher, Steven Sass, Gal Wettstein, Caroline Crawford, Christopher Gillis, Anek Belbase, Alicia Munnell, Anthony Webb, Anqi Chen, and et al. 2018. What Explains the Widening Gap in Retirement Ages by Education? Center for Retirement Research Issue Brief, 18–10. [Google Scholar]
- Samuelson, Paul. 1958. An exact consumption-loan model of interest with or without the social contrivance of money. Journal of Political Economy 66: 467–82. [Google Scholar] [CrossRef]
- Samwick, Andrew. 1998. New evidence on pensions, social security, and the timing of retirement. Journal of Public Economics 70: 207–36. [Google Scholar] [CrossRef]
- Sheshinski, Eytan. 1977. A model of social security and retirement decisions. Journal of Public Economics 10: 337–60. [Google Scholar] [CrossRef]
- Shkolnikov, Vladimir, Rembrandt Scholz, Dmitri Jdanov, Michael Stegmann, and Hans-Martin Von Gaudecker. 2007. Length of life and the pensions of five million retired German men. European Journal of Public Health 18: 264–69. [Google Scholar] [CrossRef] [PubMed]
- Stenberg, Anders, and Olle Westerlund. 2013. Education and retirement: Does University education at mid-age extend working life? IZA Journal of European Labor Studies 2: 16. [Google Scholar] [CrossRef]
- Stock, James, and David Wise. 1990. Pensions, the option value of work, and retirement. Econometrica 58: 1151–80. [Google Scholar] [CrossRef]
- Venti, Steven, and David Wise. 2015. The long reach of education: Early retirement. The Journal of the Economics of Ageing 6: 133–48. [Google Scholar] [CrossRef][Green Version]
- Vidal-Meliá, Carlos, María del Carmen Boado-Penas, and Francisco Navarro-Cabo. 2015. Notional defined contribution pension schemes: Why does only Sweden distribute the survivor dividend? Journal of Economic Policy Reform 19: 200–20. [Google Scholar] [CrossRef]
- Villegas, Andrés, and Steven Haberman. 2014. On the modeling and forecasting of socioeconomic mortality differentials: An application to deprivation and mortality in England. North American Actuarial Journal 18: 168–93. [Google Scholar] [CrossRef]
- Wilcox, David. 2006. Reforming the defined-benefit pension system. Brookings Papers on Economic Activity 2006: 235–304. [Google Scholar] [CrossRef]
| 1. | |
| 2. | This list is, of course, non-exhaustive. |
| 3. | Besides the advantage of its simple form, this function fulfils the requirements imposed by the inter-temporal separability (or time additivity) condition of the lifetime utility. See, for instance, Bagliano and Bertola (2004). |
| 4. | Defining the socio-economic class with respect to the level of education allows us to limit the potential transitions between classes, as well as the incentives to switch classes close to retirement. |
| 5. | Although the option value model is of particular interest for retirement decision problems, as it can account for more individual preferences, we focus in this study on the life-cycle model instead. Two reasons stand behind this choice. Firstly, the option-value model includes random factors in the construction of the utility functions. Because we are interested in social security systems, we feel that a model including random processes would veer too far from methods that could be implemented in practice. Moreover, in order to implement this type of model, individual data is required for the calibration of its many coefficients, including those pertinent to the random variables. At this moment, we do not have at our disposal the necessary data to perform a reliable study for this kind of model. |
| 6. | |
| 7. | For a more detailed description of NDC schemes, please see (Palmer 2006; Börsch-Supan 2006; Vidal-Meliá et al. 2015; Arnold et al. 2016). |
| 8. | There are multiple ways of defining the NDC pension. Thus, we could consider only the people alive at age x and time t belonging to each class (). However, since we are using unisex mortality tables for calculating the value of the annuity, we take into account all the people alive based on the unisex mortality rates, which allows us both to be closer to the practice and to ease the comprehension of our model. |
| 9. | As opposed to most utilitarian models, we do not split earnings between consumption and savings. Indeed, to simplify the model, and as it would not change the main conclusions of the paper, we decided to set consumption equal to the total earnings, after payment of the contributions to the retirement system. |
| 10. | Pensions indexation provides protection against price inflation, in which case the indexation rates follow the inflation rates, or against wage inflation, with the indexation following the growth rate of salaries. Both mechanism are known and used in practice. In our case, the pension indexation provides protection against wage inflation and ensures that the standard of living for pensioners is maintained on par with the one of the active population. |
| 11. | |
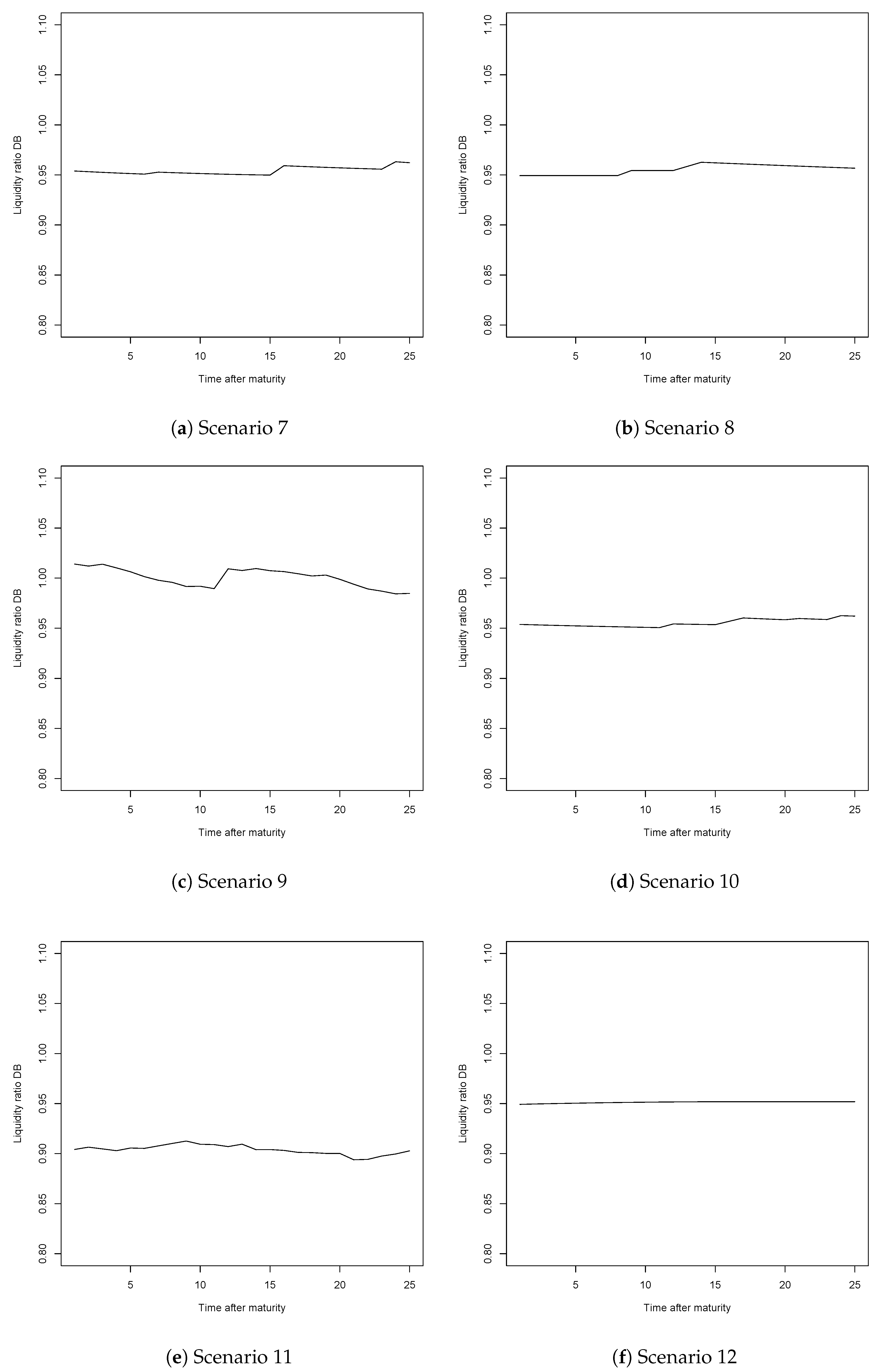
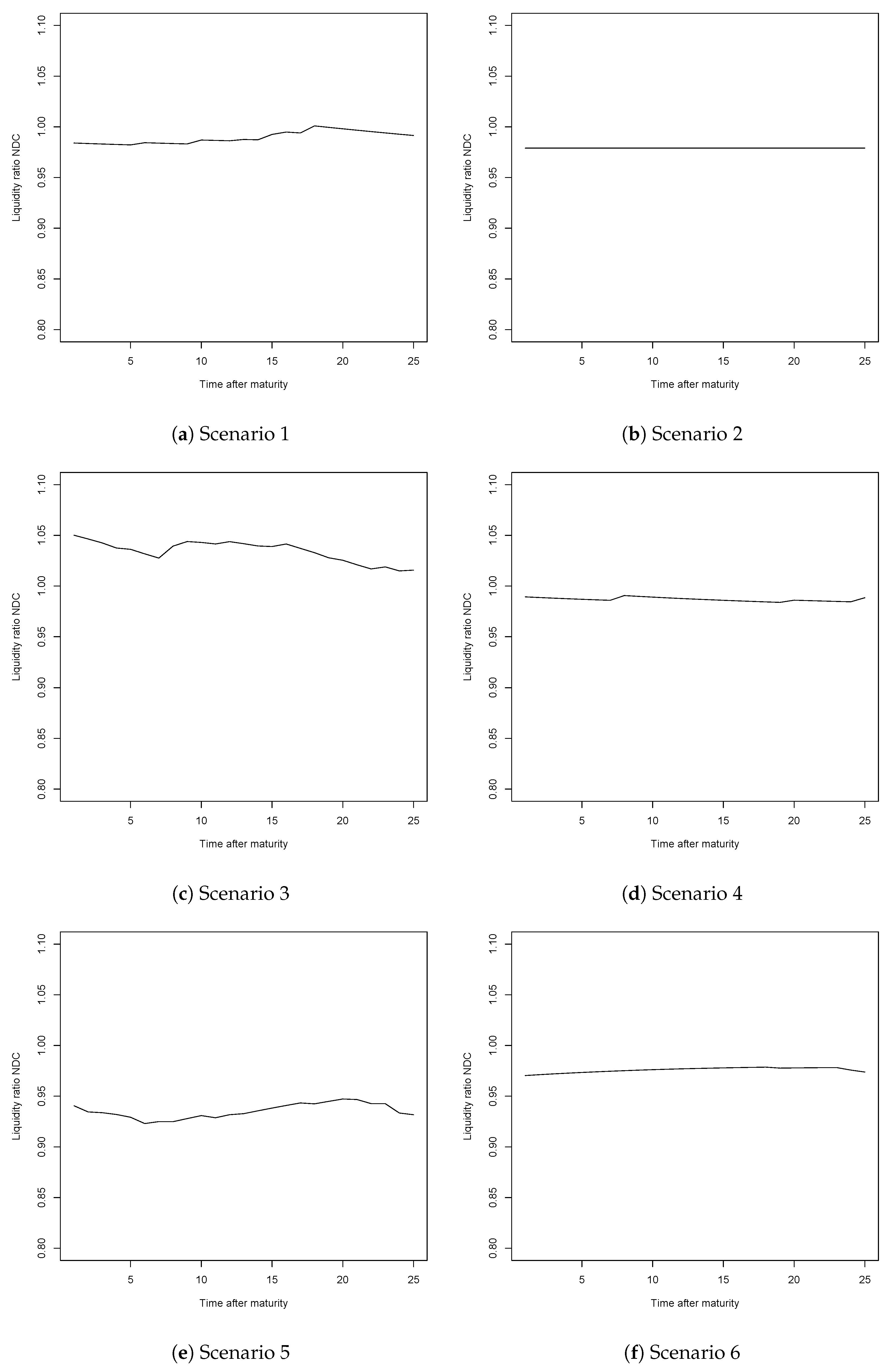
| 12. | The schemes are put in place at time zero, at which only those of entry age are admitted into the system and covered by it. In other words, individuals of all other ages are assumed to stay in the system they previously belonged to and are not covered within the new system. Hence, the first pensions will be paid once this first generation, also referred to as the entry generation reaches retirement. Since the liquidity ratio takes into account the contributions received and the pensions paid, the value of this indicator is only informative once we have individuals of all ages covered by the system, either paying contributions or receiving a pension. Therefore we must wait until the entry generation exits the system and the system thus becomes mature (insuring all active individuals from time zero, thus providing partial pensions for those reaching retirement age that have contributed to the system at least 1 year would lead to the same results since the calculations are done once the system is mature). Since in our case those belonging to class D5 will enter at age 15 and can live up to 100, the system becomes mature (or stable) after 85 years, at which point the liquidity ratio will allow us to get a picture of the financial sustainability of the systems. |
| 13. | Additional details on the used data, model assumptions and results are available from the authors upon request. |
| 14. | The higher retirement age for women might be considered politically incorrect. One could argue that women should retire earlier than 65 to compensate for the lower salaries earned. However, this was not in line with the actuarial fair framework, which considered the higher life expectancy of women and therefore indicated higher retirement ages. A different study is needed to provide a suitable compensation method for the wage inequality between men and women. |
| 15. | The ratios were not exactly equal to one due to the calculation of the contribution rate by using average salaries and not class-specific wages. |
| 16. | For instance, in 2011 the European Court of Justice ruled that discrimination by gender is prohibited in the insurance sector. Hence pricing insurance contracts must be done without considering gender. |
| 17. | The contribution rate was calculated as an average, which took into account the five different entry ages displayed in Table 1. Therefore it was not tailored to one specific entry age. Since in this section we defined five distinct cases, considered individually, with the average individual entering at different ages, while using the contribution rates calculated as explained above, the optimal retirement age was not necessarily 65. Hence we must start by determining the initial optimality. |
| 18. | |
| 19. | Since we imposed the equality , thus assuming a stable economy and demography, the contribution rate calculated here is the same as the one calculated as the ratio between benefits and salaries, as indicated by the PAYG financing method. |

| Category | Descriptive | |
|---|---|---|
| D1 | Superior to Baccalaureate | 21 |
| D2 | Baccalaureate | 18 |
| D3 | CPC (Certificate of professional competence), CPS (Certificate of professional studies) | 17 |
| D4 | National Diploma, CPrS (Certificate of primary studies) | 16 |
| D5 | No diploma | 15 |
| 50 | 41.1304% | 57 | 25.4998% | 64 | 1.8789% | 71 | 37.3178% | |||
| 51 | 39.2355% | 58 | 22.7263% | 65 | - | 72 | 45.0770% | |||
| 52 | 37.2417% | 59 | 19.7822% | 66 | 7.2079% | 73 | 53.6110% | |||
| 53 | 35.1415% | 60 | 16.6518% | 67 | 12.2896% | 74 | 63.0361% | |||
| 54 | 32.9268% | 61 | 13.3174% | 68 | 17.7862% | 75 | 73.4911% | |||
| 55 | 30.5883% | 62 | 9.7592% | 69 | 23.7487% | |||||
| 56 | 28.1163% | 63 | 5.9550% | 70 | 30.2360% |
| v | Scheme | |||
|---|---|---|---|---|
| Scenario 1 | 0.97 | 0.97 | 0.072 | DB |
| Scenario 2 | 0.97 | 0.7 | 260 | DB |
| Scenario 3 | 0.75 | 0.97 | 0.61 | DB |
| Scenario 4 | 0.75 | 0.7 | 2296.12 | DB |
| Scenario 5 | 1.25 | 0.97 | 0.0046 | DB |
| Scenario 6 | 1.25 | 0.7 | 16.25 | DB |
| Scenario 7 | 0.97 | 0.97 | 0.071 | NDC |
| Scenario 8 | 0.97 | 0.7 | 242.89 | NDC |
| Scenario 9 | 0.75 | 0.97 | 0.62 | NDC |
| Scenario 10 | 0.75 | 0.7 | 2205.82 | NDC |
| Scenario 11 | 1.25 | 0.97 | 0.0047 | NDC |
| Scenario 12 | 1.25 | 0.7 | 16.21 | NDC |
| l | Scheme | |||
|---|---|---|---|---|
| Scenario 1 | 0.97 | 0.97 | 4.65 | DB |
| Scenario 2 | 0.97 | 0.7 | 16792.9 | DB |
| Scenario 3 | 0.75 | 0.97 | 39.98 | DB |
| Scenario 4 | 0.75 | 0.7 | 148300.4 | DB |
| Scenario 5 | 1.25 | 0.97 | 0.30 | DB |
| Scenario 6 | 1.25 | 0.7 | 1050.09 | DB |
| Scenario 7 | 0.97 | 0.97 | 4.71 | NDC |
| Scenario 8 | 0.97 | 0.7 | 18750 | NDC |
| Scenario 9 | 0.75 | 0.97 | 39.55 | NDC |
| Scenario 10 | 0.75 | 0.7 | 166666.7 | NDC |
| Scenario 11 | 1.25 | 0.7 | 937.8 | NDC |
| D1 | D2 | D3 | D4 | D5 | |||
|---|---|---|---|---|---|---|---|
| DB | Men | Age | 66 | 64 | 63 | 62 | 60 |
| LE | 24.02 | 25.06 | 25.10 | 25.49 | 25.96 | ||
| Women | Age | 69 | 69 | 68 | 68 | 66 | |
| LE | 24.62 | 24.46 | 25.08 | 24.94 | 26.00 | ||
| NDC | Men | Age | 65 | 64 | 63 | 62 | 61 |
| LE | 24.92 | 25.06 | 25.10 | 25.49 | 25.14 | ||
| Women | Age | 69 | 69 | 68 | 68 | 67 | |
| LE | 24.62 | 24.46 | 25.08 | 24.94 | 25.05 |
| D1 | D2 | D3 | D4 | D5 | |||
|---|---|---|---|---|---|---|---|
| DB | Men | Age | 67 | 66 | 64 | 64 | 62 |
| LE | 24.44 | 24.74 | 25.89 | 25.48 | 26.24 | ||
| Women | Age | 72 | 72 | 71 | 71 | 70 | |
| LE | 24.42 | 24.32 | 25.15 | 25.08 | 25.66 | ||
| NDC | Men | Age | 64 | 63 | 62 | 62 | 61 |
| LE | 27.26 | 27.52 | 27.71 | 27.29 | 27.15 | ||
| Women | Age | 69 | 69 | 69 | 69 | 69 | |
| LE | 27.47 | 27.37 | 27.19 | 27.12 | 26.68 |
| D1 | D2 | D3 | D4 | D5 | |||
|---|---|---|---|---|---|---|---|
| DB | Unisex | Age | 68 | 66 | 65 | 65 | 63 |
| LE | 23.80 | 25.18 | 25.51 | 25.18 | 25.96 | ||
| NDC | Unisex | Age | 67 | 66 | 65 | 65 | 64 |
| LE | 24.73 | 25.18 | 25.51 | 25.18 | 25.08 |
| Anticipate by 1 year | DB | [10.2, 28.0] | [1.2, 17.9] | [14.8, 33.1] | [11.5, 29.5] | [8.4, 26.0] |
| NDC | [8.2, 25.7] | [8.1, 25.7] | [8.1, 25.7] | [8.1, 25.7] | [8.1, 25.6] | |
| Postpone by 1 year | DB | [] | [] | [] | [] | [] |
| NDC | [] | [] | [] | [] | [] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnold, S.; Jijiie, A. Retirement Ages by Socio-Economic Class. Risks 2020, 8, 102. https://doi.org/10.3390/risks8040102
Arnold S, Jijiie A. Retirement Ages by Socio-Economic Class. Risks. 2020; 8(4):102. https://doi.org/10.3390/risks8040102
Chicago/Turabian StyleArnold, Séverine, and Anca Jijiie. 2020. "Retirement Ages by Socio-Economic Class" Risks 8, no. 4: 102. https://doi.org/10.3390/risks8040102
APA StyleArnold, S., & Jijiie, A. (2020). Retirement Ages by Socio-Economic Class. Risks, 8(4), 102. https://doi.org/10.3390/risks8040102






