Financial Bubbles: A Study of Co-Explosivity in the Cryptocurrency Market
Abstract
1. Introduction
2. Methodology
2.1. Testing for Bubbles
2.2. Co-Explosivity
2.3. Probability of Bubble Burst
3. Application
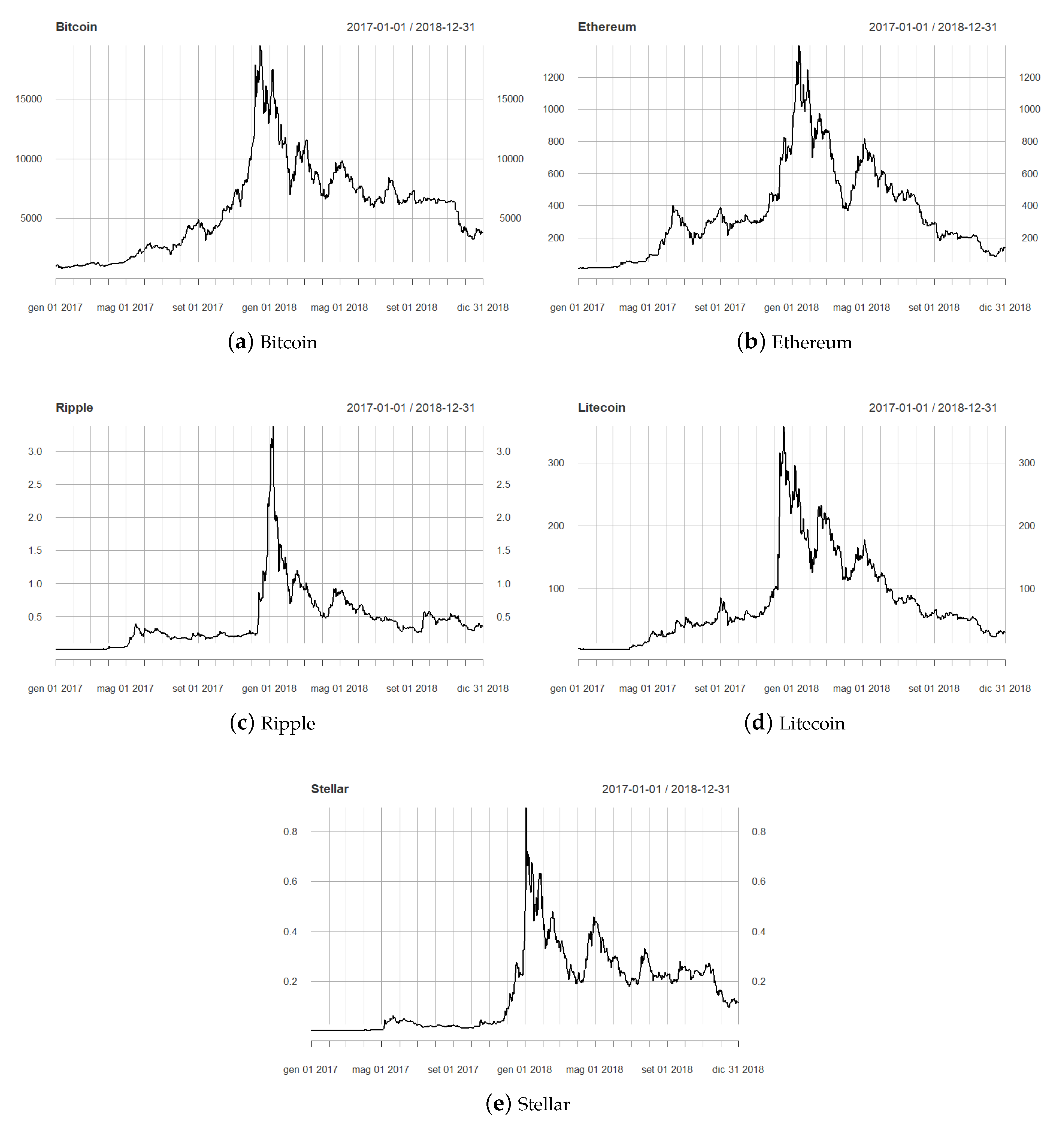
3.1. Data
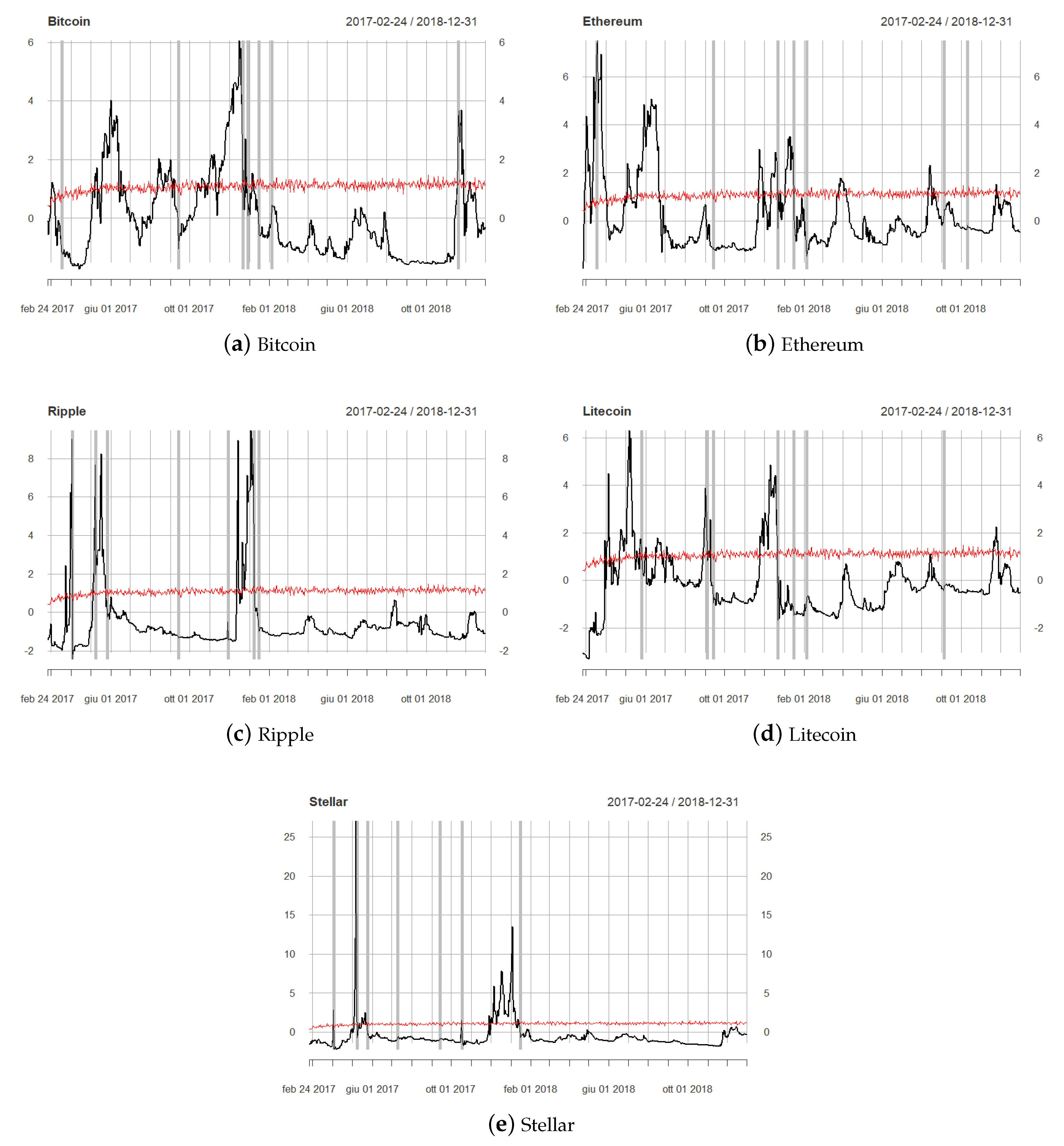
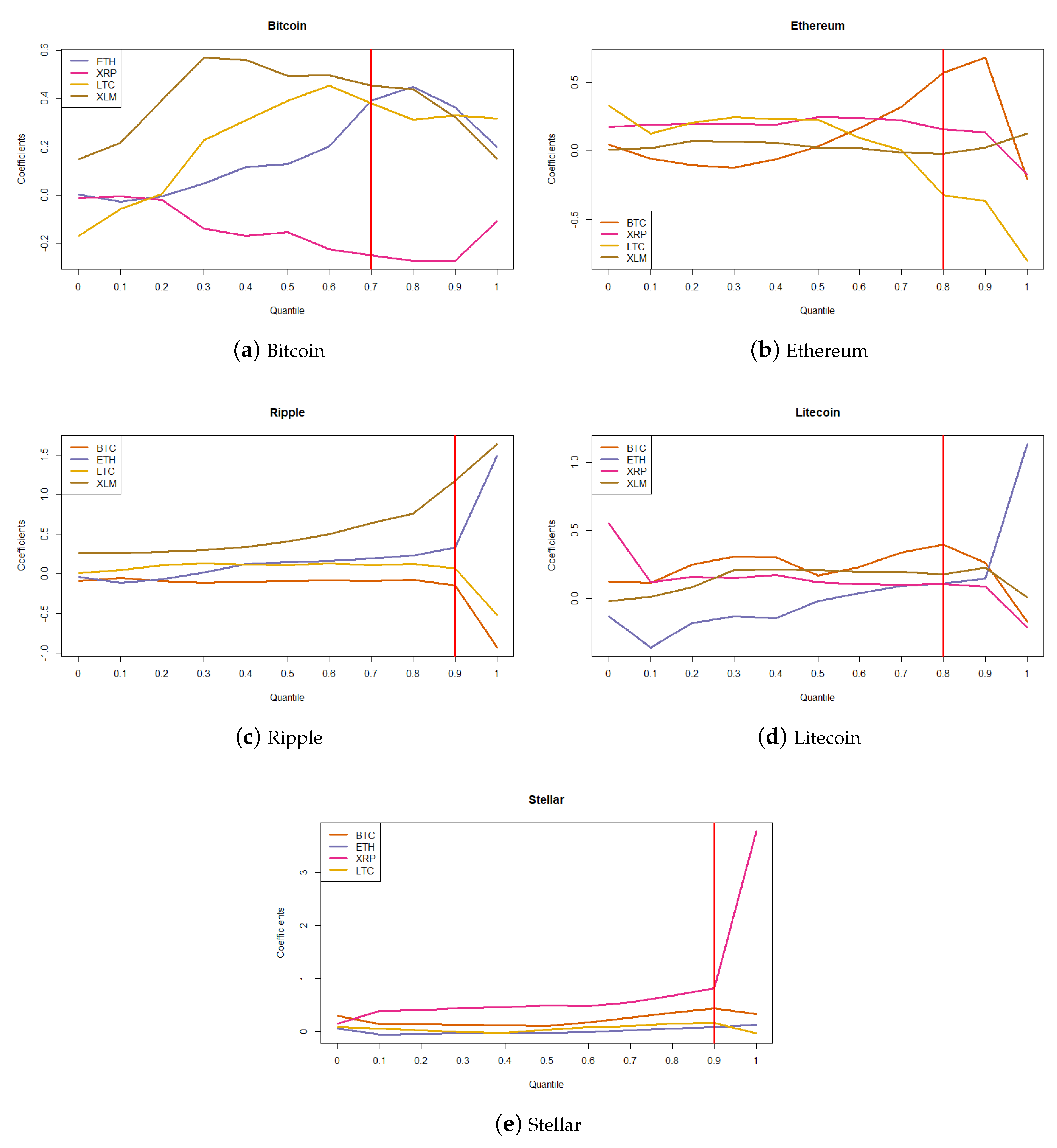
3.2. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Bouri, Elie, Shahzad Jawad Hussain Shahzadb, and David Roubaud. 2019. Co-explosivity in the cryptocurrency market. Finance Research Letters 29: 178–83. [Google Scholar] [CrossRef]
- Brière, Marie, Kim Oosterlinck, and Ariane Szafarz. 2015. Virtual currency, tangible return: Portfolio diversification with bitcoin. Journal of Asset Management 16: 365–73. [Google Scholar] [CrossRef]
- Case, Karl E., and Robert J. Shiller. 2003. Is There a Bubble in the Housing Market? Brookings Papers on Economic Activity 2: 299–362. [Google Scholar] [CrossRef]
- Chen, Ying, Paolo Giudici, Branka Hadji Misheva, and Simon Trimborn. 2020. Lead behaviour in bitcoin markets. Risks 8: 4. [Google Scholar] [CrossRef]
- Cheung, Adrian, Eduardo Roca, and Jen-Je Su. 2015. Crypto-currency bubbles: An application of the Phillips–Shi–Yu (2013) methodology on Mt. Gox bitcoin prices. Applied Economics 47: 2348–58. [Google Scholar] [CrossRef]
- Corbet, Shaen, Andrew Meegan, Charles Larkin, Brian Lucey, and Larisa Yarovaya. 2018a. Exploring the dynamic relationships between cryptocurrencies and other financial assets. Finance Research Letters 165: 28–34. [Google Scholar]
- Corbet, Shaen, Brian Lucey, and Larisa Yarovaya. 2018b. Datestamping the Bitcoin and Ethereum bubbles. Finance Research Letters 26: 81–88. [Google Scholar] [CrossRef]
- Devenow, Andrea, and Ivo Welch. 1996. Rational herding in financial economics. European Economic Review 40: 603–15. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yılmaz. 2014. On the Network Topology of Variance Decompositions: Measuring the Connectedness of Financial Firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef]
- Dreger, Dreger, and Yanqun Zhang. 2013. Is there a Bubble in the Chinese Housing Market? Urban Policy and Research 31: 27–39. [Google Scholar] [CrossRef]
- Eisl, Alexander, Stephan M. Gasser, and Karl Weinmayer. 2015. Caveat Emptor: Does Bitcoin Improve Portfolio Diversification? SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Figà-Talamanca, Gianna, and Marco Patacca. 2019. Disentangling the relationship between Bitcoin and market attention measures. Journal of Industrial and Business Economics. [Google Scholar] [CrossRef]
- Fry, John, and Eng-Tuck Cheah. 2016. Negative bubbles and shocks in cryptocurrency markets. International Review of Financial Analysis 47: 343–52. [Google Scholar] [CrossRef]
- Giudici, Giancarlo, Alistair Milne, and Dmitri Vinogradov. 2019. Cryptocurrencies: Market analysis and perspectives. Journal of Industrial and Business Economics. [Google Scholar] [CrossRef]
- Giudici, Paolo, and Gloria Polinesi. 2019. Crypto price discovery through correlation networks. Annals of Operations Research. [Google Scholar] [CrossRef]
- Giudici, Paolo, and Iman Abu-Hashish. 2019. What determines bitcoin exchange prices? A network VAR approach. Finance Research Letters 28: 309–18. [Google Scholar] [CrossRef]
- Giudici, Paolo, and Paolo Pagnottoni. 2019a. High Frequency Price Change Spillovers in Bitcoin Markets. Risks 7: 111. [Google Scholar] [CrossRef]
- Giudici, Paolo, and Paolo Pagnottoni. 2019b. Vector error correction models to measure connectedness of Bitcoin exchange markets. Applied Stochastic Models in Business and Industry 36: 95–109. [Google Scholar] [CrossRef]
- Hassani, Hossein, Xu Huang, and Emmanuel Sirimal Silva. 2019. Blockchain and Cryptocurrency. In Fusing Big Data, Blockchain and Cryptocurrency. Cham: Palgrave Pivot. [Google Scholar]
- Li, Xin, and Chong Alex Wang. 2017. The technology and economic determinants of cryptocurrency exchange rates: The case of Bitcoin. Decision Support Systems 95: 49–60. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., Yangru Wu, and Jun Yu. 2011. Explosive behavior in the 1990s NASDAQ: When did exuberance escalate asset values? International Economic Review 52: 201–26. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., Shuping Shi, and Jun Yu. 2015. Testing for multiple bubbles: Historical episodes of exuberance and collapse in the S&P 500. International Economic Review 56: 1043–78. [Google Scholar]
- Steenkamp, Daan. 2018. Explosiveness in G11 currencies. Economic Modelling 68: 388–408. [Google Scholar] [CrossRef]
- Trueman, Brett. 1994. Analyst Forecasts and Herding Behavior. The Review of Financial Studies 7: 97–124. [Google Scholar] [CrossRef]
- Yi, Shuyue, Zishuang Xu, and Gang-Jin Wang. 2018. Volatility connectedness in the cryptocurrency market: Is Bitcoin a dominant cryptocurrency? International Review of Financial Analysis 60: 98–114. [Google Scholar] [CrossRef]
| 1. | The BSADF statistic was calculated using the MultipleBubbles R package. The number of lags in the recursive ADF regression was selected through the Bayesian information criteria (BIC). |
| 2. | |
| 3. | Note that the first available value refers to 24 February 2017, that is the end of a 55 day time window, starting from the first observation in the dataset. |

| Period | BTC | ETH | XRP | LTC | XLM | Total |
|---|---|---|---|---|---|---|
| 2017 Q1 | 6 | 31 | 4 | 1 | 0 | 36 |
| 2017 Q2 | 35 | 44 | 22 | 45 | 15 | 161 |
| 2017 Q3 | 24 | 0 | 0 | 13 | 0 | 37 |
| 2017 Q4 | 58 | 18 | 15 | 27 | 33 | 151 |
| 2018 Q1 | 2 | 23 | 8 | 0 | 10 | 43 |
| 2018 Q2 | 0 | 6 | 0 | 0 | 0 | 6 |
| 2018 Q3 | 0 | 8 | 0 | 1 | 0 | 9 |
| 2018 Q4 | 11 | 1 | 0 | 9 | 0 | 21 |
| Total | 136 | 131 | 49 | 96 | 58 | 470 |
| Estimate | Std. Error | Estimate | Std. Error | Estimate | Std. Error | |
|---|---|---|---|---|---|---|
| (Intercept) | −1.111 *** | 0.019 | −0.004 | 0.051 | 1.656 *** | 0.065 |
| ETH | −0.027 *** | 0.011 | 0.130 *** | 0.029 | 0.365 *** | 0.037 |
| XRP | −0.005 | 0.014 | −0.155 *** | 0.037 | −0.272 *** | 0.048 |
| LTC | −0.057 *** | 0.013 | 0.391 *** | 0.035 | 0.331 *** | 0.045 |
| XLM | 0.217 *** | 0.013 | 0.495 *** | 0.034 | 0.323 *** | 0.044 |
| Estimate | Std. Error | Estimate | Std. Error | Estimate | Std. Error | |
|---|---|---|---|---|---|---|
| (Intercept) | −0.674 *** | 0.017 | 0.024 | 1.921 *** | 0.180 | |
| BTC | −0.055 *** | 0.013 | 0.033 * | 0.019 | 0.685 *** | 0.136 |
| XRP | 0.193 *** | 0.013 | 0.248 *** | 0.018 | 0.138 | 0.133 |
| LTC | 0.128 *** | 0.013 | 0.230 *** | 0.018 | −0.369 *** | 0.129 |
| XLM | 0.019 | 0.012 | 0.017 | 0.023 | 0.127 | |
| Estimate | Std. Error | Estimate | Std. Error | Estimate | Std. Error | |
|---|---|---|---|---|---|---|
| (Intercept) | −1.149 *** | 0.036 | −0.472 *** | 0.012 | 0.868 *** | 0.031 |
| BTC | −0.051 * | 0.028 | −0.092 *** | 0.009 | −0.147 *** | 0.024 |
| ETH | −0.115 *** | 0.021 | 0.144 *** | 0.007 | 0.329 *** | 0.018 |
| LTC | 0.048 * | 0.027 | 0.109 *** | 0.009 | 0.068 *** | 0.022 |
| XLM | 0.265 *** | 0.022 | 0.408 *** | 0.007 | 1.173 *** | 0.018 |
| Estimate | Std. Error | Estimate | Std. Error | Estimate | Std. Error | |
|---|---|---|---|---|---|---|
| (Intercept) | −1.198 *** | 0.040 | 0.069 *** | 0.033 | 1.225 *** | 0.084 |
| BTC | 0.116 *** | 0.029 | 0.171 *** | 0.024 | 0.263 *** | 0.062 |
| ETH | −0.358 *** | 0.023 | 0.019 | 0.149 *** | 0.048 | |
| XRP | 0.122 *** | 0.029 | 0.119 *** | 0.024 | 0.062 | |
| XLM | 0.012 | 0.027 | 0.208 *** | 0.022 | 0.228 *** | 0.057 |
| Estimate | Std. Error | Estimate | Std. Error | Estimate | Std. Error | |
|---|---|---|---|---|---|---|
| (Intercept) | −1.006 | 0.018 | −0.403 | 0.030 | 0.777 | 0.034 |
| BTC | 0.143 | 0.013 | 0.111 | 0.023 | 0.434 | 0.026 |
| ETH | −0.056 *** | 0.010 | 0.018 | 0.078 | 0.020 | |
| XRP | 0.390 | 0.011 | 0.500 *** | 0.019 | 0.813 *** | 0.021 |
| LTC | 0.060 *** | 0.013 | 0.035 * | 0.021 | 0.169 *** | 0.024 |
| BTC | ETH | XRP | LTC | XLM | |
|---|---|---|---|---|---|
| BTC | - | 2.320 ** | −1.397 | 2.687 *** | −1.496 |
| ETH | 2.337 ** | - | 1.121 | 0.169 | 2.426 * |
| XRP | −1.437 | 1.113 | - | −1.408 | 3.543 *** |
| LTC | 2.687 *** | 0.162 | −1.308 | - | −1.330 |
| XLM | −1.532 | 2.407 * | 3.543 *** | −1.446 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agosto, A.; Cafferata, A. Financial Bubbles: A Study of Co-Explosivity in the Cryptocurrency Market. Risks 2020, 8, 34. https://doi.org/10.3390/risks8020034
Agosto A, Cafferata A. Financial Bubbles: A Study of Co-Explosivity in the Cryptocurrency Market. Risks. 2020; 8(2):34. https://doi.org/10.3390/risks8020034
Chicago/Turabian StyleAgosto, Arianna, and Alessia Cafferata. 2020. "Financial Bubbles: A Study of Co-Explosivity in the Cryptocurrency Market" Risks 8, no. 2: 34. https://doi.org/10.3390/risks8020034
APA StyleAgosto, A., & Cafferata, A. (2020). Financial Bubbles: A Study of Co-Explosivity in the Cryptocurrency Market. Risks, 8(2), 34. https://doi.org/10.3390/risks8020034





