Abstract
We propose novel nonparametric estimators for stochastic volatility and the volatility of volatility. In doing so, we relax the assumption of a constant volatility of volatility and therefore, we allow the volatility of volatility to vary over time. Our methods are exceedingly simple and far simpler than the existing ones. Using intraday prices for the Standard & Poor’s 500 equity index, the estimates revealed strong evidence that both volatility and the volatility of volatility are stochastic. We also proceeded in a Monte Carlo simulation analysis and found that the estimates were reasonably accurate. Such evidence implies that the stochastic volatility models proposed in the literature with constant volatility of volatility may fail to approximate the discrete-time short rate dynamics.
JEL Classification:
C0; G0
1. Introduction
Financial market volatility is a key factor for many issues in finance, ranging from asset management to risk management (Poon and Granger 2003). In light of this, market participants are preoccupied with both the nature of volatility and its level. Since volatility can be used in investment decisions, derivative pricing and financial market regulation, several approaches have been proposed in the existing literature with regard to its estimation. A key assumption is that that volatility can change over time, thus many changes in volatility can be modeled stochastically. In the existing literature, there is evidence that stochastic volatility models outperform constant volatility models (see Hull and White 1987; Ghysels et al. 1996; Andersen and Lund 1997; among many others). Indeed, there is strong evidence of non-stationarity in the variance (see e.g., Cohen et al. 1972). Stochastic volatility models resolve the shortcoming of the Black and Scholes model that the volatility is constant over time and is unaffected by the changes in the price level of the underlying asset. Although volatility can be estimated by parametric, semi-parametric and nonparametric estimators (see Asai et al. 2006; Maasoumi and McAleer 2008; Asai and McAleer 2011; Caporin and McAleer 2012 for a detailed discussion on this topic), statistical inferences for stochastic volatility models are mainly parametric. Cox et al. (1985) and Heston (1993) offered some indicative examples of parametric estimation.1 However, Alghalith (2012) highlighted some important limitations of these procedures. Few studies have used nonparametric approaches employing integrated volatility. Examples include Vetter (2015), Comte et al. (2010) and Renò (2006). Stochastic volatility stands for one of the main concepts in financial literature used in finance, that is, the endemic time-varying behavior of volatility and the co-dependence observed in markets (see Mandelbrot 1963; Officer 1973; Shephard 2005; among others).
The volatility of volatility is also a separate key risk factor which affects, for example, option returns, beyond volatility itself (Huang et al. 2019). Park (2015) showed that the volatility of volatility implied by options has predictability for tail risk hedging returns. However, the recent literature on the volatility of volatility has mainly used parametric methods. For example, Barndorff-Nielsen and Veraart (2013) considered a non-Gaussian Ornstein–Uhlenbeck process, while Corsi et al. (2008) considered the realized volatility. More recently, Alghalith (2016) considered a stochastic volatility approach. In particular, Alghalith (2016) estimated the means of volatility and its volatility, not the volatility at each time. Furthermore, although the latest asset price models considered the stochastic volatility of the asset price to vary over time, the existing literature still considers the volatility of volatility as constant over time. Additionally, the existing literature does not provide statistical inferences for stochastic volatility models under the assumption of the stochastic volatility of volatility.
In this paper, we propose novel nonparametric estimators for stochastic volatility and the volatility of volatility. The contribution to the existing literature is that, our approach is far simpler than the previous methods (e.g., GARCH type models, Corsi et al. 2008; Alghalith 2016). In addition, we relax the assumption of a constant volatility which allows the volatility of volatility to vary over time, giving a new insight in option pricing. Furthermore, we provided statistical inferences for the stochastic volatility models under the assumption of stochastic volatility of volatility testing if both volatility and the volatility of volatility are stochastic. To this end, we introduced a separate time-varying volatility of volatility model which drives the conditional variance of the variance.
In order to illustrate the usefulness of our approach, we presented an empirical application to the equity market. We focused on the Standard & Poor’s 500 (S&P 500) equity index using intraday (1-min, 5-min and 30-min data) and daily data. Our estimates revealed strong evidence that both volatility and the volatility of volatility are stochastic. Then, we proceeded in a Monte Carlo simulation analysis and found that our estimates are reasonably accurate. This suggests that the stochastic volatility models proposed in the literature with constant volatility of volatility may fail to approximate the discrete-time short rate dynamics. Using predictive regressions, we also showed that both volatility measures are significant predictors of the future market’s volatility expectations and sentiment. By including both measures at the same time, we indicated that the time-varying nature of the volatility of volatility stands as an additional source of risk and such evidence highlights the importance of there being be two different types of risk premia: one for the uncertainty induced by the volatility per se and one induced by the uncertainty of the volatility of volatility. The volatility of volatility is often ignored in most asset price models and can still be associated with deep uncertainty in the market.
This paper is organized as follows: Section 2 details the model specification proposed in this study. Section 3 deals with the estimation technique. Section 4 presents an application with financial data, alone with a Monte Carlo simulation study. Section 5 provides financial implications for volatility and its volatility risk premia. Section 6 concludes by emphasizing the importance of our estimators.
2. Model Specification
We begin by assuming that the asset at time follows the diffusion:
where is the price of the asset at time , is the expected rate of return and is the volatility; is a Brownian motion defined in the probability space , where is the augmentation of filtration which drives equity prices. Models such as the model in (1) are routinely adopted in finance to model equity prices, currency prices or interest rates (see e.g., Heston 1993; Alghalith 2016).
The purpose of this paper is to propose an exact solution for stochastic volatility and its volatility and nonparametric suitable estimators. More specifically, we introduced a separate time-varying volatility of volatility model which drives the conditional variance of the variance. The idea is the following, using Ito’s differentiation rule in (1), we have:
Thus, solving (2) for , we have:
If the volatility is stochastic, it may be given by (see Heston 1993):
where and are constants, is the volatility of volatility (the volatility of the variance ) and is also a Brownian motion which now drives the variance. Note that the drift of only depends on itself and thus, not on the or . Hence, using Ito’s differentiation rule in (4), we have:
Thus, solving (5) for , we have:
Similarly, if the volatility of volatility is stochastic, it may be given by:
where and are constants, is the volatility of volatility (the volatility of the variance ) and is a Brownian motion which in turn drives the volatility of volatility. In the same way as in (4), the drift of the is a function of the . Consequently, again using Ito’s differentiation rule in (7), we have:
Finally, it should be noted that the Brownian components , and in (1), (4) and (7), respectively, can be correlated, that is for all .
3. Estimation Technique
Using (3), the volatility per unit of time is estimated nonparametrically as the ratio (square root) of the squared first difference of the prices and the squared prices, which is given as follows:
where denotes the first difference of the data and is the observed data. Consequently, the annual volatility is given by
where measures the data frequency.
Building on Equation (2), we test whether the volatility is stochastic. In doing so, we estimate the following linear regression equation, while in the case where the true model is non-linear, Taylor expansion can be used to linearize the relationship:
where is the parameter to be estimated and is the error term. If is statistically significantly different from zero, then we assume that the underlying volatility is stochastic and not constant over time affected by the changes of the underlying asset. In particular, considering the following equation, , if volatility is deterministic, then is equal to zero requiring that is also equal to zero. At a discrete time, we can test this hypothesis by (11). In the case when is equal to zero, must be equal to zero too, which in turn suggests that the volatility is deterministic (i.e., cannot change over time).2
Similarly, using (6), the volatility of volatility per unit of time is estimated nonparametrically as the ratio (square root) of the squared first difference of the variance and the variance:
where denotes the first difference of the variance . Furthermore, the annual volatility of volatility is given by
where again measures the frequency of the data.
Finally, we use (4) to test whether the volatility of volatility is stochastic. In doing so, we estimate the following regression equation:
where is the parameter to be estimated and is the error term. In the case where the true model is non-linear, Taylor expansion can be also used to linearize the relationship. In line with the concept of Heston (1993) for stochastic volatility, if is statistically significantly different from zero, then we assume that the volatility of volatility is stochastic, thus it is not constant over time. More specifically, let us assume the following equation, , in order for the volatility of volatility to be deterministic, the would have to be zero requiring that is equal to zero, too. At a discrete time, we can test this hypothesis by (14). In the case when is equal to zero, must be equal to zero too, which in turn suggests that the volatility of volatility is deterministic (i.e., cannot change over time).
4. Application
We used intraday prices for the S&P 500 equity index; the 1-min, 5-min and 30-min data cover the period from 11 August 2016 to 9 November 2016. This sample is strictly restricted by the availability of the intraday data available. We also used daily data for the same index ranging from 31 March 2015 to 31 November 2020. Data was retrieved from the Thomson Reuters database. The S&P 500 is the most common benchmark for the broader US equity markets, while it is one of the most heavily traded and liquid equity indexes. We employed intraday data due to the fact that they reveal important information not easily seen at lower sampling frequencies (e.g., daily data), such as the intraday changes and the market microstructures. Hence, volatility is more accurately estimated by employing high frequency data (see Hansen and Huang 2016; among others). We constructed the corresponding returns of each frequency, as the differences between prices at consecutive time points. Even though each frequency may be just enough to use for our estimators, there is an adequate balance between high and low sampling frequencies. For example, Liu et al. (2015) found that 5 min is an adequate sampling frequency for liquid assets, while 1 min was more appropriate for the diversified set of asset classes. Consequently, our empirical results of volatility and the volatility of volatility were compatible among different intraday frequencies. For our datasets, we applied the data-adjustment (cleaning) procedure suggested by Barndorff-Nielsen et al. (2009).3 Furthermore, we ignored trading days with recorded prices for less than 60% of the operating time’s expected observations and short trading days around major holidays.
We present the empirical results of volatility and the volatility of volatility for the S&P 500 equity index in Table 1, Table 2 and Table 3. An illustrated representation of our estimators is also given in Figure 1, Figure 2, Figure 3 and Figure 4 for each frequency under consideration. We present these figures in an Appendix. As we can see from the figures, there is clear evidence that not only the volatility varies over time, but also its volatility varies over time (mainly when considering lower frequencies i.e., 30-min returns or daily frequency). This also suggests that the stochastic volatility models proposed in the literature with constant volatility of volatility may fail to approximate the discrete-time short rate dynamics. Furthermore, we also see that the volatility of volatility behaves rather differently to the volatility itself. Such results are consistent with the views of Huang et al. (2019). Consistent with a setup of our model which separated volatility from its volatility, the correlation between volatility and its volatility was almost zero for the 1-min data, −0.0228 for the 5-min data and for the 30-min data was equal to −0.0671, while for the daily frequency it was equal to −0.0081. Although both measures have some common peaks, the overall picture is that large increases in volatility are relatively independent of the increases in the volatility of volatility.

Table 1.
Descriptive statistics for volatility and the volatility of volatility of the S&P 500.

Table 2.
Estimation results for the stochastic volatility.

Table 3.
Estimation results for the stochastic volatility of volatility.
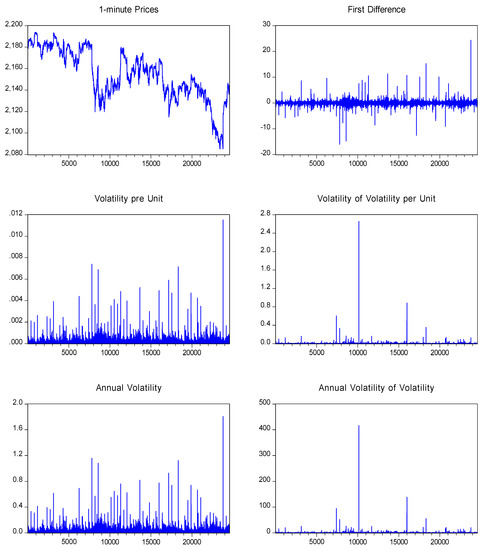
Figure 1.
Plot of the S&P 500 1-min sample.
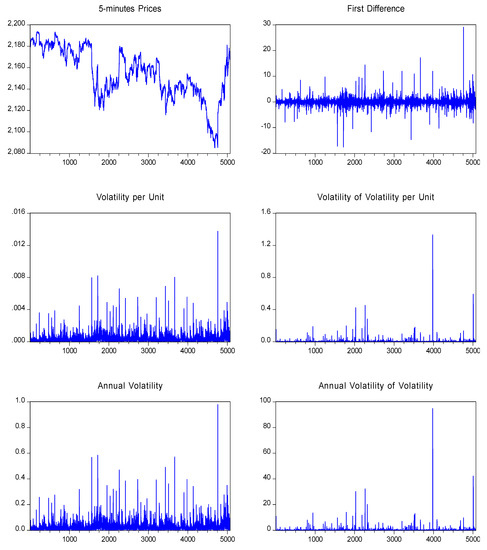
Figure 2.
Plot of the S&P 500 5-min sample.
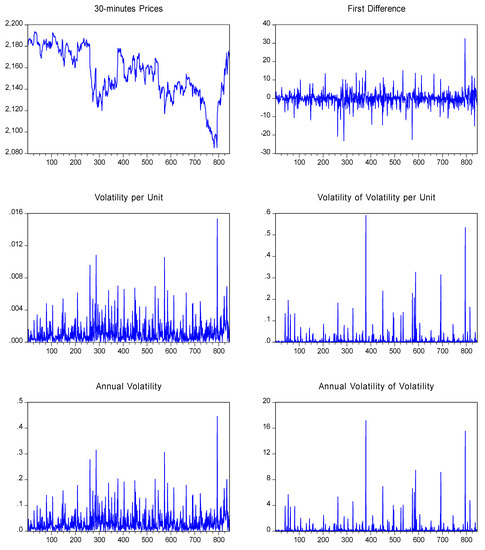
Figure 3.
Plot of the S&P 500 30-min sample.
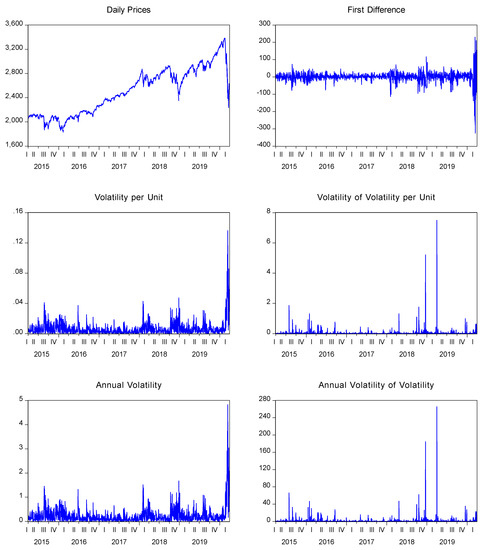
Figure 4.
Plot of the S&P 500 daily sample.
In Table 1, we report the descriptive statistics for the following series: (volatility per unit), (volatility of volatility per unit), (annual volatility), (annual volatility of volatility). Furthermore, we consider three panels: Panel A corresponds to the empirical results using the 1-min returns, Panel B to the empirical results using the 5-min returns, Panel C to the empirical results using the 30-min returns and Panel D to the empirical results using the daily returns. It is worth mentioning that the results are consistent with the Jarque–Bera test, in which the null hypothesis of normality is rejected for both volatility and the volatility of volatility series.
In Table 2, we test if volatility is stochastic via (11) for the null hypothesis . For our study, we applied linear least squares regression and we considered two cases. The first case was based on our real data. The second case was based on a Monte Carlo analysis using 1000 replications with a sample size equal to the number of observations in each sample (24,224, 5042, 841, 1259). We proceeded to a Monte Carlo analysis to check the reliability of the proposed estimators. To this end, we tested them on simulated time series of a diffusion model.4 As for the former case, as expected we rejected the null hypothesis in each sample, which in fact means that volatility is stochastic. As for the latter case, we observed that the standard deviations are very small related to the means and therefore, our regression estimates are reasonably accurate.
In Table 3, we test if the volatility of volatility is stochastic via (14) for the null hypothesis . For our study, we applied linear least squares regression and we considered two cases. The first case was based on our real data. The second case was based on a Monte Carlo analysis using 1000 replications with a sample size equal to the number of observations in each sample (24,224, 5042, 841, 1259). As for the former case, we rejected the null hypothesis in each sample, which in fact means that the volatility of volatility is also stochastic. As for the Monte Carlo simulation analysis, we can see that the standard deviations are very small related to the means and therefore, our regression estimates are reasonably accurate. From a financial point of view, such evidence in the results is consistent with a no-arbitrage asset pricing model which features that volatility and its volatility vary over time. Below we further evaluate this concept using predictive regressions.
5. Financial Implications
To evaluate the implications of the model for volatility and its volatility risks, we studied their predictability of the future market’s volatility expectations. To this end, we used the daily sample used in this study for the S&P 500 index (again from 31 March 2015 to 31 November 2020), along with the Volatility Index () and the Volatility of the Index ( of or ) for the same time period. We focused on daily data frequency due to the lack of availability of intraday data for the and indices. These indices were created by the Chicago Board Options Exchange (CBOE). The index (also called “Fear Gauge” or “Fear Index”) acts as a real-time market index capturing the market’s expectation of 30-day-forward-looking volatility. It is derived from the price inputs of the S&P 500 index options and provides a measure of market risk. As for the index, it can be considered as a measure of the volatility of the capturing the short-term volatility of the S&P 500 indices. It indicates how quickly market sentiment can change.
In particular, we estimate the following regression equations for and indices:
where is the annualized volatility estimated by (10), is the annualized volatility of volatility estimated by (13) and is the error-term ( for the index and for the index).
Table 4 refers to the estimates of (15) and (16) for the and indices, respectively. For this analysis, we applied robust linear least squares and we considered two specifications. The first specification refers to the case when the and indices are expressed in units (Panel A), while in the second specification these indices are expected in logarithmic units (Panel B). We also tested the issue of equality between the coefficients and , i.e., and by Wald tests. The p-values of the tests are given below in brackets.

Table 4.
Estimation results for the stochastic volatility of volatility.
Using predictive regressions, we showed that the and are significant predictors of future market’s volatility expectations and sentiment. Both past volatility and its volatility significantly forecast the future and indices. By including both measures at the same time, we found that the predictive power is positive and shared between volatility and its volatility. However, the impact of the volatility is always higher. Although this result for the volatility per se was expected, the difference in the coefficient estimates between and —as indicated by the Wald tests implemented—can provide new insights in pricing volatility risk premia.5 In particular, the null hypothesis of equality was rejected in all cases. Such evidence shows that the volatility of volatility is a significant additional source of risk which indeed separately can increase financial stress in equity markets. In other words, the time-varying nature of the volatility of volatility stands for an additional source of stress, which in turn implies that there are two different types of risk premia, one for the uncertainty induced by the volatility itself and one induced by the uncertainty of the volatility of volatility. The latter risk factor is often ignored in stochastic volatility models and can still be associated with deep uncertainty in the market.
6. Conclusions
In this paper, we devised new nonparametric estimators for the stochastic volatility and the volatility of volatility. Our method has two main advantages compared to the previous methods in the existing literature. Firstly, they are exceedingly simple, far simpler than the existing methods. Secondly, we relax the assumption of a constant volatility of volatility and thus, we allow the volatility of volatility to vary over time. We also provide statistical inferences for stochastic volatility models under the assumption of stochastic volatility of volatility testing, via simple statistical tests, whether both volatility measures vary over time.
We illustrated the usefulness of our approach giving an empirical example using intraday and daily data for the S&P 500 equity index. Our findings revealed strong evidence that both volatility and the volatility of volatility are stochastic. Then, we proceeded in a Monte Carlo simulation analysis and found that our estimates are reasonably accurate. We also evaluated our estimators by studying their predictability for the future values of the and indices. As we expected, the volatility is a significant predictor of the future market’s volatility expectations, yet surprisingly, we find that the time-varying nature of the volatility of volatility is an additional source of risk. In other words, the volatility of volatility separately increases financial stress in the market. From a financial point of view, both past volatility and its volatility significantly forecast the future and indices, in a no-arbitrage model which features both time-varying volatility factors—as the model employed in this study—are priced by the investors.
Finally, our approach has important implications in identifying volatility risk premia. According to the findings, there are two different types of risk premia, one for the uncertainty induced by the volatility per se and one induced by the uncertainty of the volatility of volatility. The latter is often ignored in most asset price models but can still definitely be associated with deep uncertainty in the market. Future research may compare our estimators with other relevant estimators, either parametric or nonparametric, for stochastic volatility. Finally, another idea for future research would be to expand our estimators in a multivariate framework (see Amendola et al. 2020) or extend them to allow for jumps in the equation driving the observable variable.
Author Contributions
The authors have equal contributions. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alghalith, Moawia. 2012. New methods of estimating volatility and returns: Revisited. Journal of Asset Management 13: 307–9. [Google Scholar] [CrossRef]
- Alghalith, Moawia. 2016. Estimating the Stock/Portfolio Volatility and the Volatility of Volatility: A New Simple Method. Econometric Reviews 35: 257–62. [Google Scholar] [CrossRef]
- Amendola, Alessandra, Manuela Braione, Vincenzo Candila, and Giuseppe Storti. 2020. A Model Confidence Set approach to the combination of multivariate volatility forecasts. International Journal of Forecasting. [Google Scholar] [CrossRef]
- Andersen, Torben G., and Jesper Lund. 1997. Estimating continuous-time stochastic volatility models of the short-term interest rate. Journal of Econometrics 77: 343–77. [Google Scholar] [CrossRef]
- Asai, Manabu, and Michael McAleer. 2011. Alternative asymmetric stochastic volatility models. Econometric Reviews 30: 548–64. [Google Scholar] [CrossRef]
- Asai, Manabu, Michael McAleer, and Jun Yu. 2006. Multivariate stochastic volatility: A review. Econometric Reviews 25: 145–75. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Almut E. D. Veraart. 2013. Stochastic Volatility of Volatility and Variance Risk Premia. Journal of Financial Econometrics 11: 1–46. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., P. Reinhard Hansen, Asger Lunde, and Neil Shephard. 2009. Realized kernels in practice: Trades and quotes. The Econometrics Journal 12: C1–C32. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Marie Hoerova. 2014. The VIX, the variance premium and stock market volatility. Journal of Econometrics 183: 181–92. [Google Scholar] [CrossRef]
- Boukhetala, Kamal. 1996. Modelling and Simulation of a Dispersion Pollutant with Attractive Center. Southampton: Computational Mechanics Publications. Boston: Computational Mechanics Inc. [Google Scholar]
- Caporin, Massimiliano, and Michael McAleer. 2012. Do We Really Need Both BEKK and DCC? A Tale of two Multivariate GARCH Models. Journal of Economic Surveys 26: 736–51. [Google Scholar] [CrossRef]
- Cohen, Jerome B., Fischer Black, and Myron Scholes. 1972. The valuation of option contracts and a test of market efficiency. Journal of Finance 27: 399–418. [Google Scholar] [CrossRef]
- Comte, Fabienne, Valentine Genon-Catalot, and Yves Rozenholc. 2010. Nonparametric estimation for a stochastic volatility model. Finance and Stochastics 14: 49–80. [Google Scholar] [CrossRef][Green Version]
- Corsi, Fulvio, Stefan Mittnik, Christian Pigorsch, and Uta Pigorsch. 2008. The volatility of realized volatility. Econometric Reviews 27: 46–78. [Google Scholar] [CrossRef]
- Cox, John C., Jonathan E. Ingersoll, Jr., and Stephen A. Ross. 1985. A Theory of the Term Structure of Interest Rates. Econometrica 53: 385. [Google Scholar] [CrossRef]
- Cui, Zhenyu, J. Lars Kirkby, and Duy Nguyen. 2017. A general framework for discretely sampled realized variance derivatives in stochastic volatility models with jumps. European Journal of Operational Research 262: 381–400. [Google Scholar] [CrossRef]
- Ghysels, Eric, Andrew C. Harvey, and Eric Renault. 1996. Stochastic volatility. In Handbook of Statistics. Edited by Maddala Gangadharrao. Amsterdam: North-Holland, vol. 14, pp. 119–91. [Google Scholar]
- Hansen, Peter Reinhard, and Zhuo Huang. 2016. Exponential GARCH Modeling With Realized Measures of Volatility. Journal of Business & Economic Statistics 34: 269–87. [Google Scholar] [CrossRef]
- Heston, Steven L. 1993. A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. The Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Huang, Darien, Christian Schlag, Ivan Shaliastovich, and Julian Thimme. 2019. Volatility-of-volatility risk. Journal of Financial and Quantitative Analysis 54: 2423–52. [Google Scholar] [CrossRef]
- Hull, John, and Alan White. 1987. The pricing of options on assets with stochastic volatility. Journal of Finance 42: 281–300. [Google Scholar] [CrossRef]
- Liu, Lily Y., Andrew J. Patton, and Kevin Sheppard. 2015. Does anything beat 5-min RV? A comparison of realized measures across multiple asset classes. Journal of Econometrics 187: 293–311. [Google Scholar] [CrossRef]
- Maasoumi, Esfandiar, and Michael McAleer. 2008. Realized Volatility and Long Memory: An Overview. Econometric Reviews 27: 1–9. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit. 1963. The variation of certain speculative prices. Journal of Business 36: 394–419. [Google Scholar] [CrossRef]
- Mrázek, Milan, Jan Pospíšil, and Tomáš Sobotka. 2016. On calibration of stochastic and fractional stochastic volatility models. European Journal of Operational Research 254: 1036–46. [Google Scholar] [CrossRef]
- Officer, Robert R. 1973. The variability of the market factor of the New York stock exchange. Journal of Business 46: 434–53. [Google Scholar] [CrossRef]
- Park, Yang-Ho. 2015. Volatility-of-volatility and tail risk hedging returns. Journal of Financial Markets 26: 38–63. [Google Scholar] [CrossRef]
- Poon, Ser-Huang, and Clive W. J. Granger. 2003. Forecasting Volatility in Financial Markets: A Review. Journal of Economic Literature 41: 478–539. [Google Scholar] [CrossRef]
- Renò, Roberto. 2006. Nonparametric estimation of stochastic volatility models. Economics Letters 90: 390–95. [Google Scholar] [CrossRef]
- Shephard, Neil. 2005. Stochastic Volatility: Selected Readings. Oxford: Oxford University Press. [Google Scholar]
- Vetter, Mathias. 2015. Estimation of integrated volatility of volatility with applications to goodness-of-fit testing. Bernoulli 21: 2393–418. [Google Scholar] [CrossRef]
- Wong, Hoi Ying, and Yu Wai Lo. 2009. Option pricing with mean reversion and stochastic volatility. European Journal of Operational Research 197: 179–87. [Google Scholar] [CrossRef]
| 1 | Stochastic volatility is an essential component in an asset pricing model, in option pricing. See (Wong and Lo 2009; Mrázek et al. 2016; Cui et al. 2017; among others). |
| 2 | Heston (1993) assumed that the variance follows a square root process, , where σ controls the volatility of volatility. When σ is equal to zero, the volatility is deterministic. Following Heston (1993) and applying Ito’s rule (4), we are able to test whether volatility is stochastic via linear regression equations. We refer to the study implemented by Heston (1993) for more information regarding this issue. |
| 3 | Following Barndorff-Nielsen et al. (2009), (1) we deleted the entries with a timestamp outside the 9:30 a.m.–4 p.m. window when the market is open and (2) we deleted the entries with a bid, ask or a transaction price equal to zero. |
| 4 | For the simulation analysis, we considered a stochastic process of a single random variable based on the S&P 500 index assuming that the variance varies over time (i.e., exhibits serial correlated properties). To this end, we used a stochastic differential equation of the Ito type. The drift and the diffusion parameters are estimated from the original series by the method of maximum pseudo-likelihood (see Boukhetala 1996). |
| 5 | Following Bekaert and Hoerova (2014), the squared index can be decomposed into the variance of equity returns and the variance risk premium. For robustness purposes, in order to isolate the predictive power of past volatility and the volatility on volatility risk premium, we estimated (15) and (16) using the difference between the VIX indices and daily realized variance (estimated as the sum of 5-min intraday returns of the S&P 500) as dependent variables. In this regard, we also used in (15) and (16) the residuals obtained from and their squared specifications as dependent variables. In all cases, the results remain qualitative and quantitatively similar. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).