1. Introduction
The bitcoin is the leading cryptocurrency by capitalisation, with a market share greater than 50% of the total cryptocurrency market, corresponding to 330 billion USD at its historical peak, in December 2017. Recent studies report that the same market capitalisation is concentrated on a limited number of owners. In particular, Credit Swiss in January 2018 provided a study which indicates that 97% of Bitcoins are held by 4% of all Bitcoin addresses. Bloomberg reported similar findings by suggesting that about 40 percent of Bitcoin is held by perhaps 1000 users.
The previous empirical findings suggest that the trading movement by a few bitcoin owners has the potential to cause major disruptions in the price of all cryptocurrencies. An example of this is the transaction that took place on 12 November 2017, when a user moved 25,000 Bitcoins, worth at the time USD159 million, to an exchange. A very important research question is therefore: “to find the bitcoin owners who are most connected in the markets, in terms of trading volumes”.
Unfortunately, the anonymity of bitcoin transactions makes very difficult to find an answer to the previous question. However, although it may be difficult to trace the “physical” identity of the users, it may be possible to understand their “statistical” identity, applying appropriate econometric models to the (very large) database of payments generated by bitcoin trades themselves. This may help to answer a less demanding, but still important research question: “to find groups of bitcoin owners who are most connected in the market, in terms of trading volumes”.
In this study, we classify bitcoin owners according to their observed trading behaviour, in ten classes of increasing average size. We add to this classification the geographical area of the owners, defined (very broadly) by the continent to which they belong. We then apply network econometric models to understand the map of interconnections that exist between the defined owner groups and, in this way, identify the trading groups who lead bitcoin markets, along time.
The econometric research on the dynamics of cryptocurrency markets has mainly been focused on the issue of price discovery and prediction. In this context, many of the stylized facts that are valid for traditional financial time series apply, to some extent, also in the context of these alternative currencies
Elendner et al. (
2017). A large stream of papers consider the dynamics of crypto prices, using VAR models (
Bianchi (
2019);
Catania et al. (
2019);
Bohte and Rossini (
2019);
Giudici and Abu-Hashish (
2019)), VECM models (
Giudici and Pagnottoni (
2019a,
2019b)), similarity networks
Giudici and Polinesi (
2019) and Generalized Autoregressive Conditional Hetheroskedasticity (GARCH) models
Bouoiyour et al. (
2016). The results from the different papers, however, seem far from consistent. In our view, this is mostly due to the nature of the cryptocurrencies. For example, they are much more volatile compared to traditional currencies, their exchange rates cannot be assumed to be independently and identically distributed and their global nature limits researchers’ ability to account for systematic causal factors.
In our opinion, it becomes necessary to move away from traditional price volatility models, and focusing on the identification of the mechanisms that drive trading behaviour, as in our research question. The available literature on trading volume dependency in cryptocurrency markets is very limited. Notable exception to this are the papers by
Tasca et al. (
2018),
Foley et al. (
2019) and
Chen et al. (
2018). In particular,
Tasca et al. (
2018) attempt to identify different clusters within the Bitcoin economy by analyzing the trading patterns and ascribing them to particular business categories. Using network-based methods, the authors have identified three market regimes that have characterized Bitcoin transactions.
Our work intends to extract the network of payment relationship between Bitcoin users, owners, similar to
Tasca et al. (
2018). We extend their work, acquiring evidence on whether trading volumes behaviors of different groups of Bitcoin traders, defined by volume size and geographical region, are interconnected and, therefore, affect each other.
From an econometric viewpoint, we propose an econometric network model which extends Vector Autoregressive models. The extension is based on network models, which improve over pure autoregressive models, as they introduce a contemporaneous contagion component that describes contagion effects between groups of traders.
The validity of the model was demonstrated in recent studies on systemic risk, in which researchers have proposed correlation network models, able to combine the rich structure of financial networks (see, e.g.,
Lorenz et al. (
2009);
Battiston et al. (
2012)) with a more parsimonious approach that can estimate contagion effects from the dependence structure among market prices. The first contributions in this framework are
Billio et al. (
2012) and
Diebold and Yilmaz (
2014), who derive contagion measures based on Granger-causality tests and variance decompositions. More recently,
Ahelegbey et al. (
2016) and
Giudici and Spelta (
2016) have extended this methodology introducing stochastic correlation networks.
While bivariate systemic risk models (such as
Acharya et al. (
2012),
Acharya et al. (
2016) and
Adrian and Brunnermeier (
2015)) explain whether the risk of an institution is affected by a market crisis event or by a set of exogenous risk factors, correlation network models explain whether the same risk depends on contagion effects, in a cross-sectional perspective.
We extend the approach of
Giudici and Spelta (
2016) enriching their graphical Gaussian model with an autoregressive component derived through a VAR model, as in
Ahelegbey et al. (
2016). In contrast with the latter, we employ partial correlations rather than correlations, and we do not follow a Bayesian approach.
We remark that our work is related to some recent papers that explore the cross-country trading in cryptocurrency markets
Makarov and Schoar (
2019), the network dynamics across cryptocurrency markets
Ji et al. (
2019) and the information content of trading volumes in crypto investing
Bianchi (
2019);
Bouri et al. (
2019). We combine the views of the previous paper into a network-based analysis of bitcoin trading patterns across countries and trading groups.
To demonstrate our methodology, we will consider the all world’s bitcoin transactions, independently of the exchange in which they were traded, in the time period 25 February 2012 to 17 July 2017.
Our empirical findings show that transactions activities in bitcoins is dominated by groups of network partici- pants in Europe and in the United States, consistent with the conventional wisdom that posits market interactions, at least nominally, primarily take place in developed economies.
The paper is organized as follows:
Section 2 contains our proposed model;
Section 3 presents the available data;
Section 4 the empirical application of the proposed model to the obtained data;
Section 5 contains some concluding remarks.
2. Proposal
Let
be the traded volume of Bitcoin by a specific group of traders
, at time
. We assume that
is a function of: (a) an autoregressive element that captures the dependence on the past trading volumes of the same group; (b) a cross-sectional element that captures the contemporaneous dependence on the trading volumes of other groups; (c) a stochastic residual. Mathematically, we assume that in the case of the Bitcoin traded volumes, for each volume
i and time
t the following equation holds:
where
p is a time lag (with a maximum value of
),
and
are the coefficients which are to be estimated, and
are residuals, which we assume standard Gaussian and independent.
Equation (
1) models the Bitcoin volume dynamics as a structural VAR, in which the traded volume in each group depends on its
p past values, through the idiosyncratic autoregressive component
and, in addition, it depends on the contemporaneous values of the other groups, through the systemic component
.
Defining
as a
symmetric matrix with null diagonal elements containing the contemporaneous coefficients, the previous model can be expressed in a more compact matrix form, as follows:
where
is a
I-dimensional vector containing the traded volumes of all groups at time
t,
is the same vector, lagged at time
,
is a
matrix that contains the autoregressive coefficients and
is a vector of residuals.
In the following step, we transform the model in (
2) into a reduced form for the purpose of facilitating the estimation process, thus becoming:
with
This reduced form allows the estimation of the vectors of modified autoregressive coefficients , using time series data on the traded volumes contained in the stacked vector .
However, we are not interested in estimating
. In fact, the purpose of this analysis is to disentangle its autoregressive and contemporaneous components, thus separately estimating
and
. In this sense, once
is obtained,
can be derived from (
4).
To estimate
, note that
, so that
. This implies that, for each group
i,
meaning that the off-diagonal elements of
can be obtained regressing each modified residual, derived from the application of (
3), on those of the other groups.
Please note that the regression model in (
5) is based on the transformation derived in Equation (
4), which makes the modified residuals correlated. The direction of such correlation is, however, unknown. In the application of (
5) it is, therefore, not clear which volume residual assumes the form of a response variable, and which one of an explanatory regressor.
To determine the direction of such dependence, we propose to approximate each pair of regression coefficients and , with their partial correlation coefficient, which is undirected.
Mathematically, let
be the correlation matrix between the modified residuals, and let
be its inverse, with elements
. The partial correlation coefficient
between the residuals
and
, conditional on the remaining residuals
), where
, can be obtained as:
It can be shown that:
which means that the absolute value of the partial correlation coefficient between
and
, given all the other residuals, can be obtained as the geometric average between the coefficients
and
defined by equation (
5) setting, respectively,
i rather than
j as response variables. Equation (
7) justifies the replacement of
and
with their corresponding partial correlation coefficient
.
From an economic viewpoint, the partial correlation coefficient expresses how the trading volume of node i is affected by the contemporaneous trading volume of node j (), keeping the other volumes fixed.
An important advantage that derives from the employment of partial correlations lies in the possibility of employing correlation network models based on the conditional independence relationships described by partial correlations.
More precisely, let us assume that the vectors are independently distributed according to a multivariate normal distribution , where represents the correlation matrix (that we assume to be non-singular).
A correlation network model can be represented by an undirected graph
G such that
, with a set of nodes
, and an edge set
that describes the connections between the nodes.
G can be represented by a binary adjacency matrix
E with elements
, each of them providing the information of whether a pair of vertices in
G is (symmetrically) linked between each other (
) or not (
). If the nodes
V of
G are put in correspondence with the random variables
, the edge set
E induces conditional independences on
U via the so-called Markov properties (see e.g.,
Lauritzen (
1996)).
Following up on (
7),
Whittaker (
1990) proved that the following equivalence holds:
where the symbol ⊥ indicates conditional independence.
From a graph theoretic viewpoint, the previous equivalence means that a link between two volume residuals is present if and only if the corresponding partial correlation coefficient is significantly different from zero.
From a financial viewpoint, the previous equivalence implies that, if the partial correlation between two measures is equal to zero, the corresponding volumes residuals are conditionally independent and, therefore, the corresponding groups do not (directly) impact each other.
From a statistical viewpoint, it is also possible to test the null hypotheses that two groups of Bitcoin owners are conditionally independent by controlling whether the corresponding partial correlation coefficient is equal to zero, by means of the statistical test described in
Whittaker (
1990).
However, this poses a problem of multiple testing, and correcting for this problem could results in loss of power (for example using Bonferroni’s inequality). One of the most widely used method for limiting the number of spurious edges—while at the same time obtaining networks that are more interpretable,—is through the use of a regularization approach. One such prominent approach of regularization is the ‘least absolute shrinkage and selection operator (LASSO) which in its essence, allows us to set estimates of exactly zero. More formally, the LASSO limits the sum of absolute partial correlation coefficients which in turn lead to overall shrinkage of estimates and inviolably some become zero. Mathematically, if
represents the sample variance–covariance matrix) LASSO aims to estimate the precision matrix by maximizing the penalized likelihood function (with
being the penalty parameter).
For the purpose of our study, both the significance testing and the graphical LASSO serve as a robustness check for identifying the true network that emerges between Bitcoin owner groups.
3. Data
We consider all data from the Bitcoin blockchain, from 25 February 2012 to 17 July 2017 (1969 days with 1843 observed days), described in detail in
Chen et al. (
2018). Bitcoin blocks are published approximately every 10 min and contain information about the transaction size, the account ID (anonymous), the participating accounts and the timestamp of the transactions.
The previous information is very useful to understand the time dynamics of volume transactions, but it indicates nothing about the nature of the bitcoin owners who generate the trade. Trying to capture some kind of information on bitcoin traders, we consider the website Blockchain.info provides information about the IP address of the relying party that provides a secure access to the originator of each transaction, and extract from it the approximate geographical provenience of the trader who generates the transaction. To avoid a too large approximation error, we decided to group geographical provenience in a few classes, corresponding to six continental groups: Africa (Af), Asia (As), Europe (Eu), North America (N_A), Oceania (Oc) and South America (S_A). More precisely, the continent of the bitcoin trader is identified from the data in Blockchain.info, comparing its IP address with a dataset of IP address from MaxMind Inc. The approximate location of the transaction origin can be tracked by recording the first node relaying it. We remark that this approach works as long as the running node does not use an anonymizing technology.
We thus have a first grouping of bitcoin owners that roughly correspond to their continent of residence. To further characterize them, for each of the six continental groups we associate to each account IDs according the absolute size of the total transaction amount they generate in the considered time period. We then further group the IDs of each continent according to the deciles of their statistical distribution. The first group, which will be labeled 1 after the continent abbreviation, has the smallest transactions, corresponding to the 0–10% percentile class, while the tenth group with the largest transactions is labeled 10, corresponding to 90–100% percentile class. The final result is a classification of bitcoin owners in 60 groups: 10 groups per continent.
With this grouping we will investigate our research hypotheses, and search for the bitcoin owners who mostly impact the market. Specifically we will be able to investigate whether large-size Bitcoin owner affect the trade decisions of the others, or whether a specific continent drives the others, in terms of bitcoin trades, or both.
We remark that, although the Bitcoin is the most liquid and largest cryptocurrency, there is sometimes low liquidity in its transactions. Our data show that there are days without a single transaction in Africa, Asia, Oceania and South America, with frequency of low liquidity varying between and . We can overcome the liquidity problem by accumulating the 10 min data to a daily frequency. In any case, this indicates that a further regional grouping, for example by countries, would lead to lack of data for many of them.
For each of our considered groups, our main variable of interest is the volume of transactions, in any given time point. To normalise such data, we consider the logarithm of the transaction volumes. To avoid computational problems, when no transactions in a group arise within a day, we add 1 Satoshi
1 to each transaction. Given the large numbers under consideration, the bias effect of the correction is negligible.
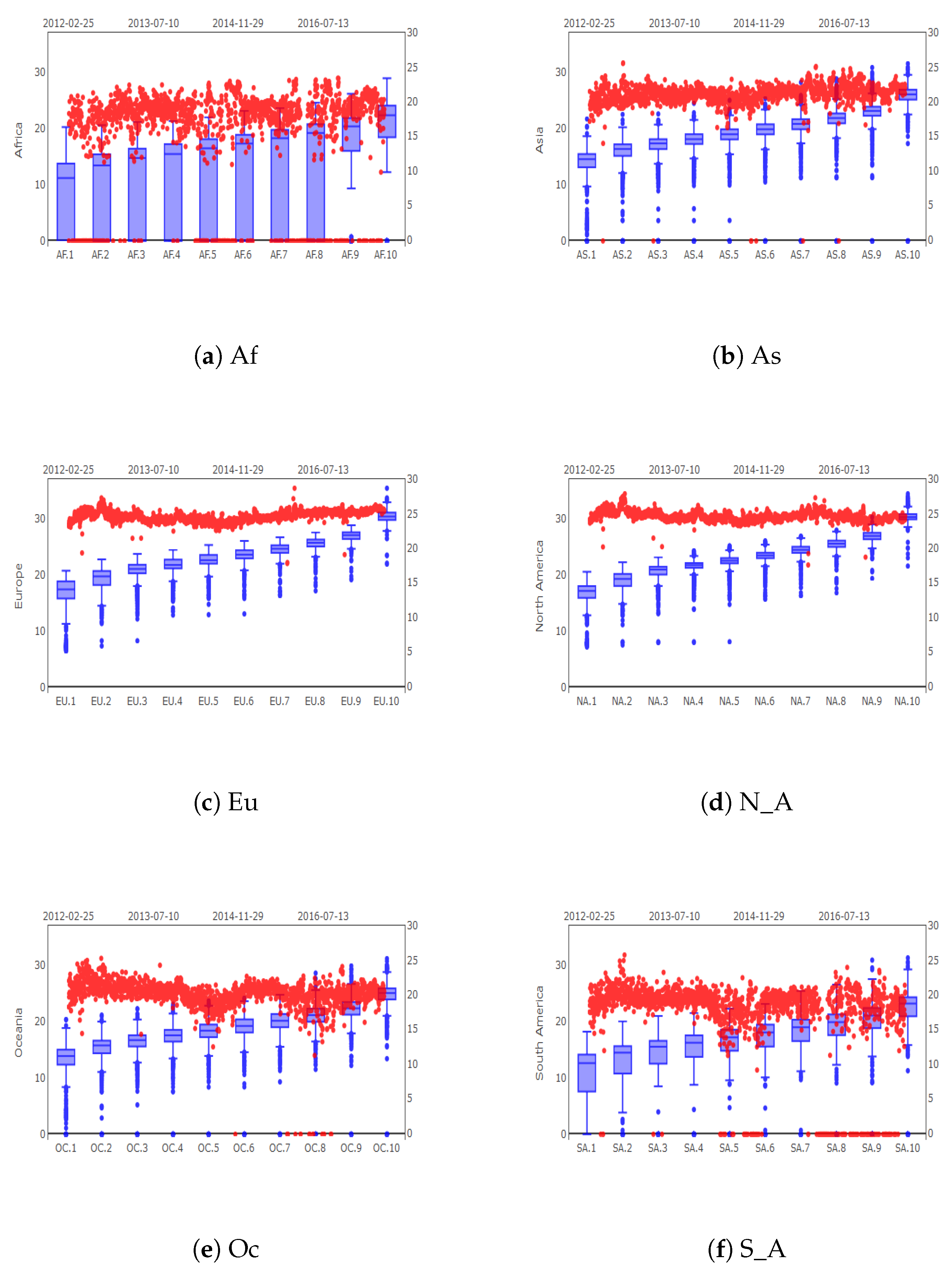
In
Figure 1 we illustrate the daily log accumulated transaction sizes over all 10 groups in each continent. The largest transaction sizes appear in Europe and North America, whose dynamic pattern is quite steady. Asia and Oceania are evidently more volatile then Europe and North America, but less volatile than Africa and South America. The descriptive statistics, reported in
Table 1, provide further evidence to these findings. Note in particular that Asia, Oceania, Africa and South America have a minimum value of zero, indicatinga lack of liquidity in certain time periods.
For deeper insights into the data features of the groups in each continent, the empirical distribution of the log transaction sizes is displayed by means of boxplots in
Figure 1. For each continent, the left plot corresponds to the first group, namely the group 1 with the smallest transactions, and the right one to the group 10 with the largest transactions, respectively.
From
Figure 1, the narrow box width of Europe and North America suggests that these continents are characterised by transaction sizes with low volatility and a few outliers. However for Asia and Oceania the daily transaction sizes are more volatile, and lead to larger center boxes and wider whiskers. South America becomes extreme in the sense of showing even longer whiskers, with transaction sizes varying stronger between groups. Africa follows a very different picture from the other continents: it has the lowest liquidity and a much higher volatility and it shows frequent drops of the transaction volume to 0.
4. Empirical Findings
In this Section secwe present the results from the application of the proposed model. First we evaluate the model in terms of predictive accuracy, to gauge its validity in the present context; second, we interpret the model results in terms of our research hypotheses, aimed at assessing the dependency patterns among the trading behaviour of different bitcoin traders.
We first consider an unregularised network, whose edges are all present, even when the corresponding partial correlation is very low.
By calculating the partial correlations as specified in (
6), we can derive the
matrix and, then, the autoregressive parameters
. We are thus able to disentangle the time-dependent volume of node
i, separately estimating the autoregressive idiosyncratic component and the contemporaneous one, according to Equation (
2).
Table 2 presents the assessment of the predictive performance of our model, to understand if the proposed approach is suitable, from a statistical viewpoint. Specifically, we want to investigate whether the inclusion of the contemporaneous component improves predictive accuracy, with respect to a much simpler pure autoregressive model.
Table 2 contains the results of the predictive assessment.
From
Table 2 note that the proposed model overperforms a pure autoregressive model, as the corresponding root mean squared errors of the one-step ahead predictions are lower in the vast majority of cases. It can be shown that the overall RMSE is equal to about 0.37 for the proposed model, against 0.42 for the autoregressive one, further confirming its superiority.
We now move towards the interpretation of the results that can be drawn from our model and, specifically, from the partial correlations (Equation (
6)). In
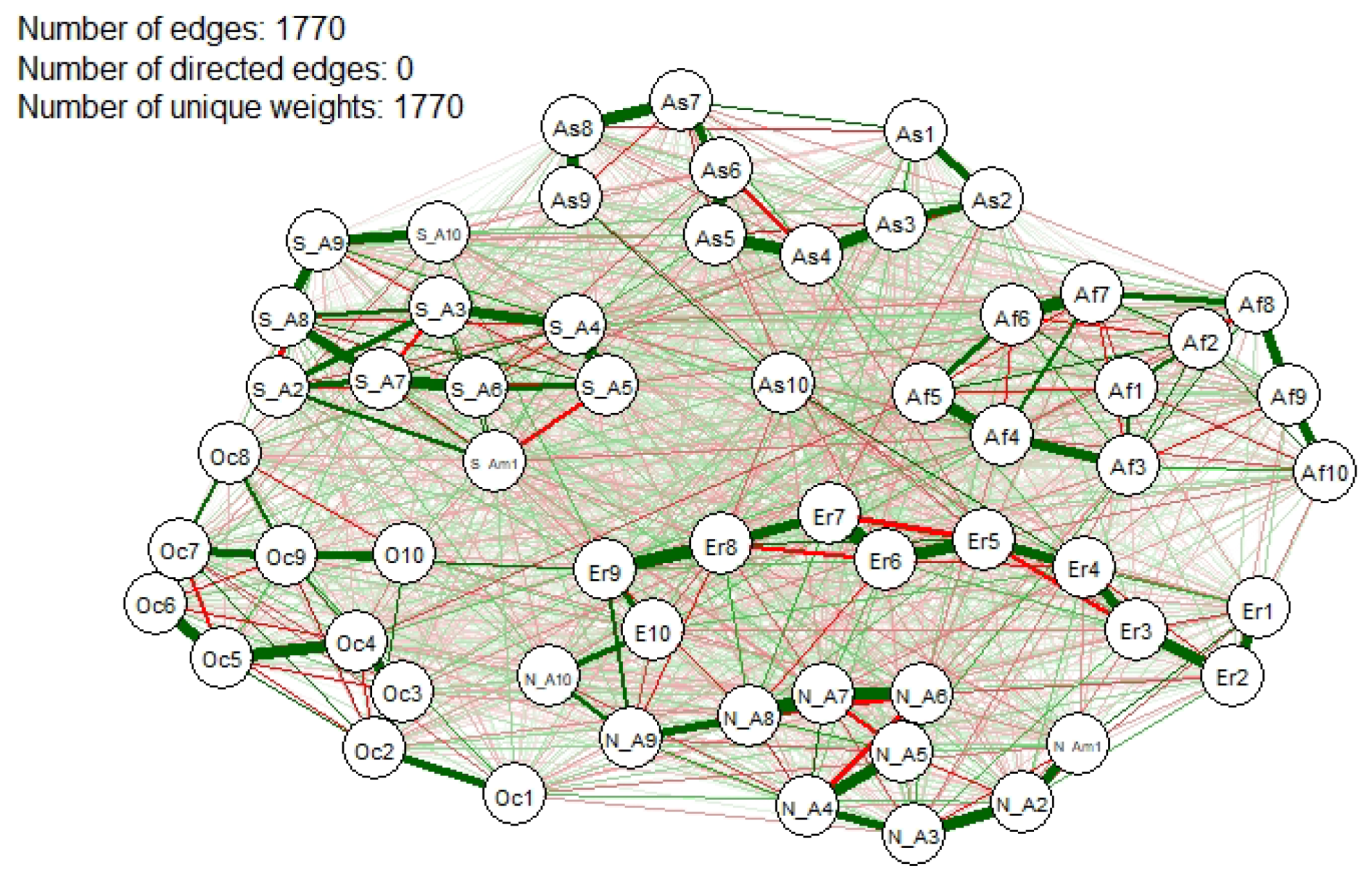
Figure 2, each node represents one of the 60 groups of traders and each present edge indicate that two traders are dependent on each other, in terms of their transactions (conditionally on all the others). Differently, when an edge is missing, the corresponding traders behave independently of each other (conditionally on all the others). Each edge is associated with a weight, which corresponds to a partial correlation coefficient. The size of each edge in
Figure 2 is proportional to such weight. On the other hand, the coloring of an edge between two nodes indicates the sign of the partial correlation coefficient: green highlights a positive partial correlation and red a negative partial correlation.
What we can observe from the network that emerges from
Figure 2 is that there exist many interconnections between Bitcoin groups of users. Precisely, the summary statistics provided in the upper left corner of
Figure 2 indicates that the network contains a total of 1770 non-zero links between groups. Although the graph is difficult to interpret, some clusters can be identified. We can see about five clusters which in most part correspond to the continents, with the exception of Europe and North America which are placed in the same cluster, suggesting that there exist strong dependence between the traders of the two continents. This is something that we expected to see due to the economic and political similarities among the two regions, as well as on their news sharing.
Note also that the groups representing the larger traders in Europe and North America - N_A10, N_A9, Eu10, Eu9 - show stronger positive connections than other groups. This may be explained by the fact that these groups have a comparable size of transactions, which come from a similar set of information, which induce them to behave similarly. If we match this result with that in
Figure 1, which indicates the relatively larger volumes of transactions coming from these groups, we obtain a clear indication that these are the groups which can mostly impact the market. Note also that these exists a strong positive link between Oc10 and Eu9, and not between Oc9 and Eu09. This is consistent with our previous finding: the transaction volumes of Oc10 are more comparable in their size to Eu9, rather than to Eu10 (see
Figure 1) and, therefore, they act similarly.
As mentioned previously, in unregularized correlation networks some edges may present but may not be statistically significant. In the graphical representation, such situations will be visualized as very weak connections in the network. To prevent this and to correctly identify the significant associations between Bitcoin groups, a crucial step is to impose restrictions that will limit (or eliminate) the occurrence of spurious edges. One way to achieve this is by testing the statistical significance of partial correlations.
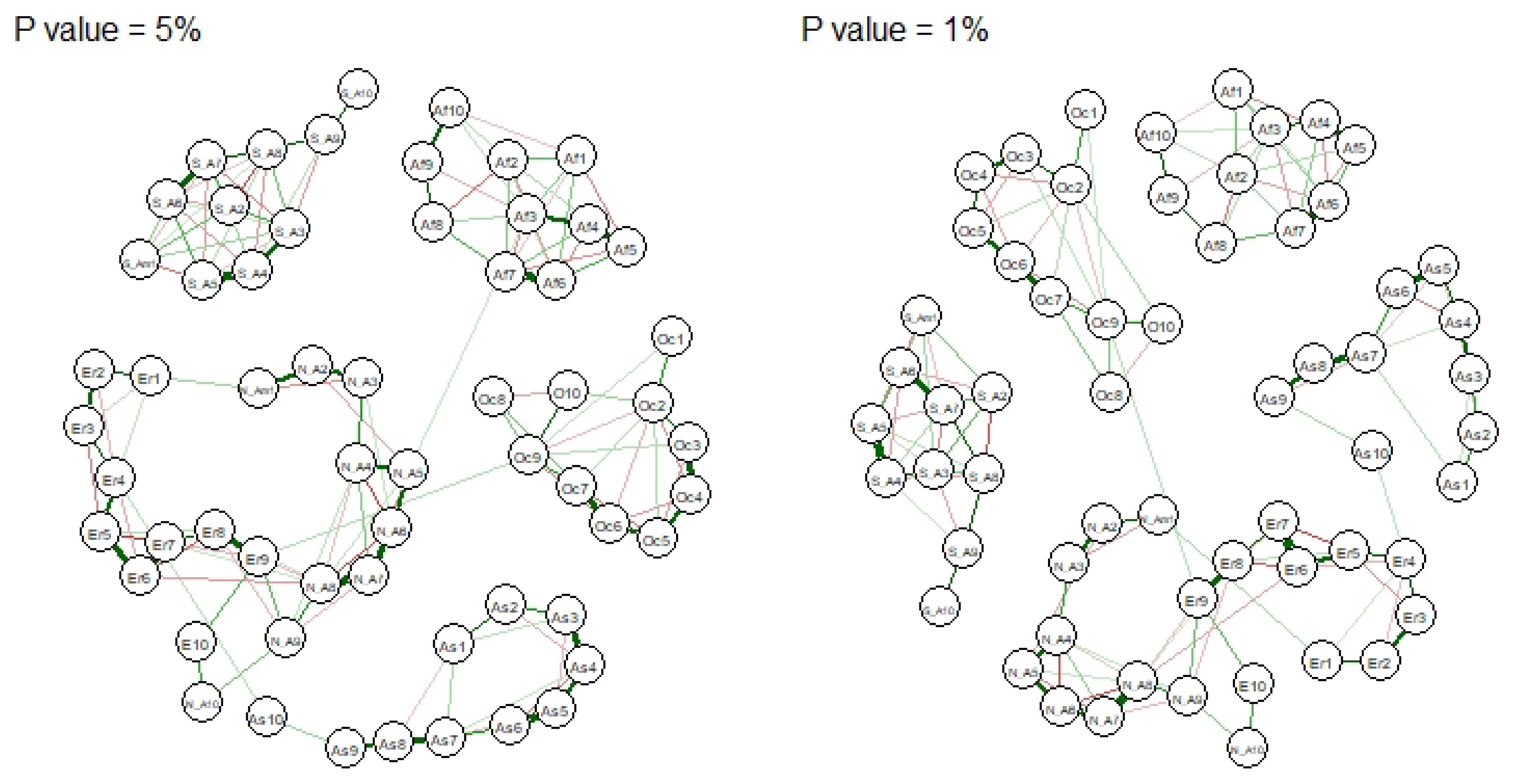
Figure 3 presents the same network containing only links that are found statistically significant at both 5% and 1% level of significance.
Figure 3 shows that the structure of the network does not change significantly if we impose different levels of significance. What we observe from the graphs is that the majority of links that were present in the unregularized network have disappeared, reducing the total number of links from 1770 to 146 and 137, respectively. Interesting, even though a significant portion of the links were removed, the clustering of nodes remains the same as in
Figure 2. Specifically, we see the formation of clusters equivalent to the continents and we also see significant interconnection between traders in Europe and North America. Furthermore, we also see a statistically significant positive correlation Oceania’s top group and Europe’s and between Asia’s top group and Europe’s.
To further confirm our findings, we perform a further robustness check through the application of the graphical LASSO. As discussed previously, LASSO is a very popular method for eliminating spurious links.
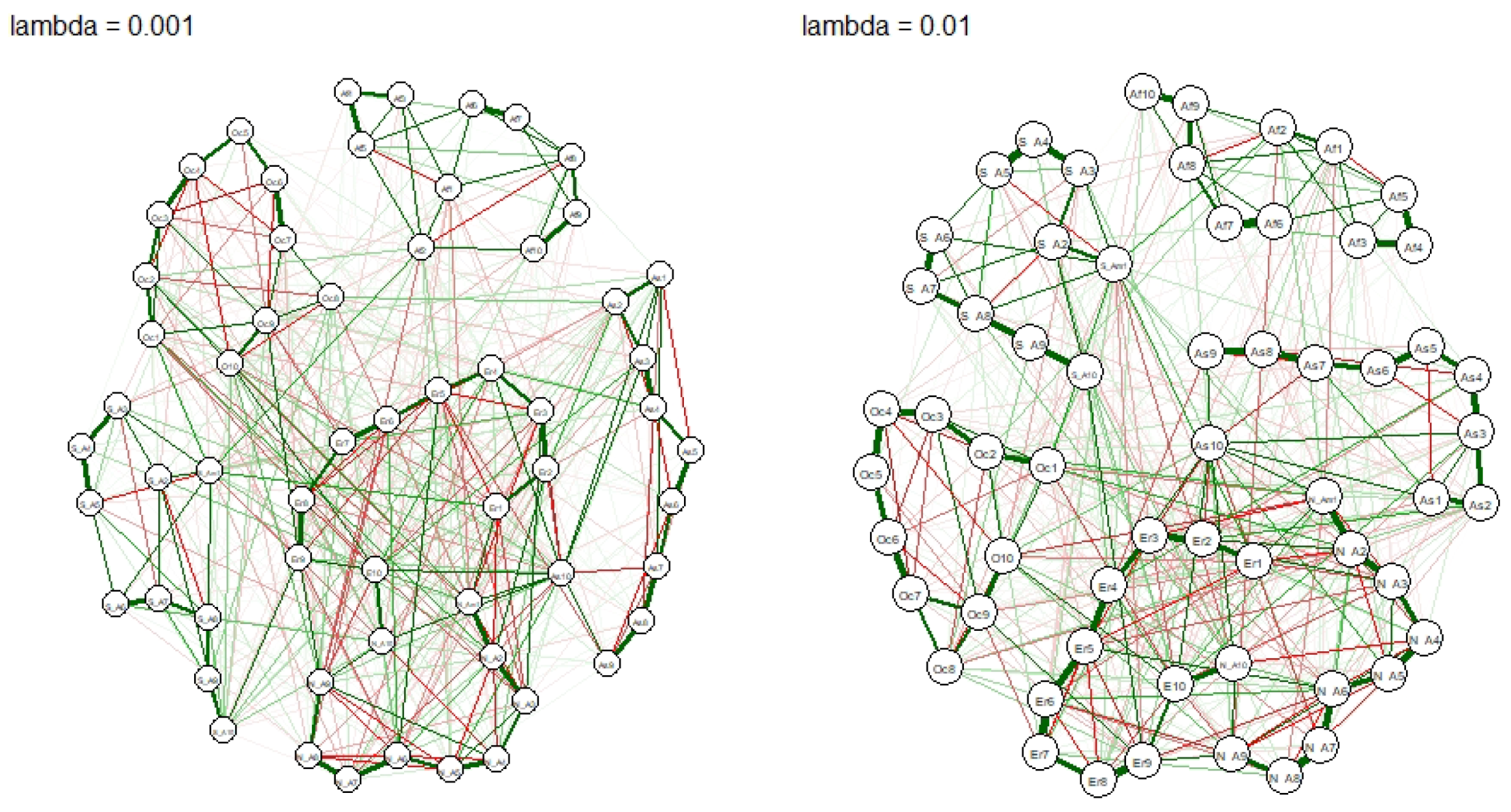
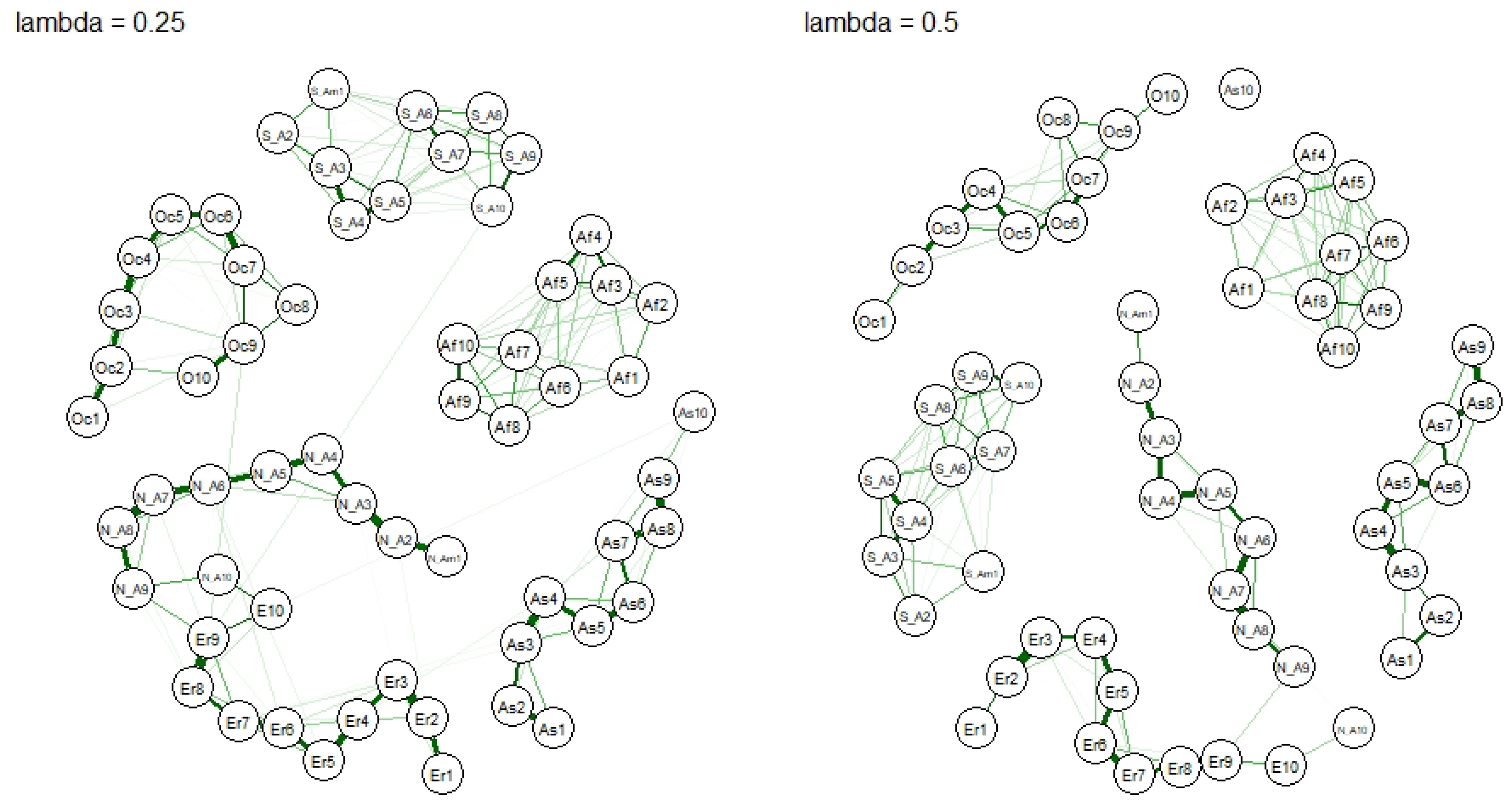
Figure 4 and
Figure 5 represent the networks that emerge by the applying graphical LASSO with different smoothness parameters
. We remark that, unlike the classical LASSO, in the graphical approach the choice of
cannot be done based on cross-validation as it represents a completely unsupervised process. As we are mainly interested in assessing the robustness of the results, we consider four alternative values for
, and see whether what found in
Figure 3 changes.
From
Figure 4 and
Figure 5, the changing
does change the structure of the network, but the underlying clusters remain the same, thus confirming the close interconnection between Europe and North America, as well as those between top traders in Oceania and Europe.
A closer inspection of
Figure 4, reveals frequent linkages between European and North American nodes, which is in line with the previous observations. Positive linkages appear more often inside each continent, compared to negative ones. One the other hand negative and positive edges appear frequently between two continents (see
Table 3). The largest two groups in both continents share strong links with each other, confirming that that they probably share a common information set. Interestingly the largest trader group from Asia, AS10, has multiple positive edges to several groups in Europe and North America. Considering that most bitcoin mining farms are based in Asia, and especially in China, it follows that a large amount of capital is acquired and, therefore, traded, from Asia with the rest of the world. Last, note that the largest volume trading groups from Oceania and South America also share links with each other and with the larger Western-World groups. This observation leads to the conclusion that the large traders around the world are somewhat connected, possibly communicating with each other. On the other hand smaller groups, which have less information, shows less connections around the world.
Figure 5 shows what happens when we increase the penalty level to
. Most edges vanish, but the previously found connections persists. Still the largest trader groups from Europe and North America remain connected, while the edges from Oc9, S_A10 and As10 persist to stay connected with them. The connection goes via the largest groups in Europe, namely Eu9 and Eu10. Other persisting edges exist between the smaller groups from Asia and Europe, yet with small magnitude. Within the continents many edges are not affected by the penalty, hence emphasize the importance of the regional connectedness. Finally, when increasing the penalty parameter to
, most cross-continent edges are ruled out, except for the ones between the largest groups in Europe and North America. The remaining edges only appear within the continents.
To further establish the robustness of the results to the varying value of
,
Table 4 compares some centrality values, averaged over the whole network, under the four considered values of
.
From
Table 4 note that, consistently with our previous findings, by increasing the parameter
the average centrality decreases, according to degree, betweenness and closeness. Regardless of this, our main conclusions remain stable.
To summarise, our empirical findings give an answer to our research proposition: which are the group of traders that mostly affect the bitcoin markets? These groups were found among the top two classes of traders in North America and Europe, strongly and positively connected to each other. These traders are linked to the others, affecting their behaviours. In particular, they are especially linked with the top traders from Oceania and South America. In addition, top traders from Asia, and especially larger ones, are highly linked to the others, likely as a result of their mining activity.
5. Conclusions
In the paper, we proposed a model that explains the dynamics of Bitcoin trading volumes, based on a correlation network VAR process that models the interconnections between different groups of traders.
Our main methodological contribution consists of the introduction of partial correlations and correlation networks into VAR models. This allows describing the correlation patterns between trading volumes and to disentangle the autoregressive component of volumes from its contemporaneous part. The introduction of VAR correlation networks also allows building a volume predictive model that leverages the information contained in the correlation patterns.
Our main financial findings show that trading volumes are highly correlated within geographical regions. Groups of traders with high transaction volumes over all continents covary in the network model, leading to the conclusion this groups share a mutual information set. The results are robust over various penalized network models. This result may have different economical explanations, such as a common behaviour, a common time-zone, similar institutional and legal contexts.
Our results also contribute to the identification of group of bitcoin traders that are the most likely influencers of the market. These are found to high volume traders, especially from North America, Europe, and Asia. These results are in line with the expectation that trading follows the news sharing patterns and the major Bitcoin mining localization patterns.
The proposed model can be very useful for policy makers and regulators. It can be used to predict “regular” trading volumes and, therefore, identify anomalies. Our empirical findings show that the proposed model is able to predict trading volumes with an error that is lower than that of a pure autoregressive model.
Our result suggests that policy makers and regulators, interested in preserving the integrity of bitcoin markets, should also pay particular attention to the transactions coming from large volume traders, and especially of those from America, Europe and Asia, which have the potential to disrupt the market.
The main weakness of this work is related to the available sample. It refers to a specific cryptoasset, the bitcoin; it relates to a specific period of time and is taken directly from blockchain transactions, rather than from market exchanges. These limitations derive from the proprietary nature of the data that was made available to us. However, we believe that our model is rather general, and can be easily extended on a different database. This in particular to deal with transactions that take place on crypto exchanges, more frequent that those taking place on the blockchain, considered here. Further work may concern acquiring data on the electronic identity of the traders, to investigate the reason of “regional” behaviours, as also discussed in
Tasca et al. (
2018) and
Foley et al. (
2019).
From a methodological viewpoint, it may be worth considering extending correlation network models to become time dependent, although this requires acquiring data with a higher frequency. In addition, it may be worth considering an extension of the model that accounts for exogenous factors, such as regulatory interventions, transaction fees, sentiment and media coverage. This may require an event-based analysis, aimed at understanding not only trading patterns, but also what may originate them. To achieve this task our work could be extended with Bayesian network models, following
Giudici et al. (
2003),
Giudici and Bilotta (
2004) and
Cerchiello and Giudici (
2016).