1. Introduction
Predicting claims is a critical challenge for insurers and has significant implications for their managerial, financial and underwriting decisions. Changes in (expected) claims do not only affect the capital of an insurer, but also the capacity to underwrite further business. Insurance companies can increase premium rates and adjust their underwriting policy to balance the effect of unexpected claims (
van der Veer 2019), but this will consequently impact their business opportunities negatively. We are, therefore, investigating machine learning (ML) techniques for claims prediction using an international dataset on export credit insurance claims.
Export credit insurance is a tool for exporters in mitigating risks that arise from exporting to other countries. It covers companies against the risk of non-payment of their buyer due to commercial and political risks. The commercial risks include full or partial default on payments, as well as protracted default or insolvency of private buyers, while political risks, include non-payment of public buyers or due to political events, e.g., government-imposed moratoria on payments, inability to transfer currency, or force majeure (
Berne Union 2019d). Export credit insurance is widely used by exporters to protect their cash flows and receivables. Consequently, it also protects the profits against unwanted volatility due to unsystematic risk. It can also cover lenders involved in the export transaction (usually by granting loans or letters of credit for the buyer) against the default of their credit due to the aforementioned reasons. Often lenders are only willing to grant financing if export credit insurance is provided. Therefore, export credit insurance is regularly a key requirement for the realisation of an export transaction (
Krummaker 2020).
The Export Credit Insurance business is differentiated with respect to the tenure of the credit granted. Short-term (ST) credits are typically up to one year, while medium- and long-term (MLT) credit insurance offers insurance for credit terms up to 15 years. MLT is mainly offered by public Export Credit Agencies (ECAs), even though in recent years the private market has increased its MLT capacities (
Berne Union 2019d). In our study, we focus on MLT insurance provided by ECAs, which is characterised by higher risk than in the ST business. Furthermore, for some, ECAs claims are a rare occurrence. However, as the claims frequency is very low, the severity of potential claims can be high and might also exhibit long-tail properties. In our article we address the challenge of insurers in making reliable and consistent predictions of future claims based on historical claims experiences by conducting a comparative analysis of ML approaches on a long-term dataset of export credit claims.
The aim of this study is to assess the performance of ML techniques in identifying the occurrence of claims in export credit insurance and their potential performance loss when tested under near-realistic forecasting conditions. We were able to access a unique dataset provided by the Berne Union to compare four ML techniques by exposing them to three increasingly challenging prediction tasks. Furthermore, we evaluate their performance against a simple benchmark (BM) technique, as ML approaches are complex and resource-intensive to set up but might not achieve significantly better results for claims prediction and reserving (
England and Verrall 2002).
First, this article contributes to the gap in the literature on export credit insurance and claims. Second, the paper also contribute to the advancement of the literature on claims prediction by providing an evaluation of ML approaches, including a comparison against a simple BM. This, thirdly, also has practical implications for actual claims prediction and reserving for export credit insurers and ECAs.
In the following section, we provide more background to the study before introducing the dataset and a description of ML. After this, we describe the ML techniques used for this study, before discussing the results. The conclusion also includes an outlook for further research.
2. Background
Export credit insurance is offered by private sector insurance companies, public government backed ECAs and some multilateral organisations. Most developed countries, but also many emerging countries and more developing countries, have their own ECA or access to multilateral credit insurers. ECAs are official or quasi-official branches of their governments which offer export credit insurance, guarantees and financing. ECAs are highly regulated in many countries in terms of their product offerings and conditions as they are instruments of governments’ trade and foreign aid. To minimise opportunities for hidden subsidies and state aids, ECAs are regulated by international agreements on several levels. The World Trade Organization (WTO) has an explicit framework for trade policies, and the OECD arrangement imposes further detailed rules on its members. The aim of these regulations is to create a level playing field in the global export environment and coherence between national export credit policies (
OECD 2018). International competition of exporters is supposed to be based on price and quality, and not on the most favourable terms of exporters’ ECAs (
Drysdale 2015). Consequently, ECAs of OECD countries are restricted to offer credit insurance only for risks which are deemed non-marketable, i.e., for which the private insurance market is unwilling to provide cover. ECAs mainly cover transactions with credit payment periods of longer than two years and/or to high-risk countries, as private insurers usually do not cover credit risk with repayment terms of longer than two years and can retreat from covering countries with increasing commercial or political risk. These medium- and long-term business (MLT) are typically capital goods, such as industry or infrastructure projects.
1 A further aspect of OECD ECA regulation is the application of minimum premium rates (MPR) for credit risk.
2 Thus, ECAs have less discretion in setting premiums than private insurers, which limits opportunities for managing underwriting and rates, claims ratios and reserves.
ECAs act as insurers of last resort and are usually reinsured or backed-up by their respective governments. While private insurers are required to maintain certain levels of long-term and short-term solvency, ECAs often just need to break even and not hold technical provisions for the liabilities and potential claims they take on with underwriting export credit insurance (
Moser et al. 2008;
European Commission 2012).
ECAs play an important role in facilitating international trade as they provide critical and significant cover to international trade transactions. In 2018, ca. 13% of global trade was covered by MLT export credit insurance provided by ECAs (Berne Union members,
Berne Union 2019a). Although, ECAs are underwriting mid-and long-term business in non-marketable, riskier countries, claims still might be an exception. Some ECAs might experience claims only irregularly, but if claims occur, they might be significant. Therefore, it is questionable how well previous claims experiences might be suited to predict future claims.
A key challenge for insurers is that, while claims are arising irregularly as a stochastic process of two components, the uncertain number and amount of claims, premiums are not stochastic and they are paid upfront. Although, claims reserving is a critical process in insurance companies, little research has been done on claims in the area of export credit insurance.
van der Veer (
2019) has carried out the only research examining the impact of export credit insurance claims on price and quality of private export credit insurance. With our study, we address this gap in the literature and aim to provide insights into potential advancements of claims prediction methods.
The export credit insurance industry is currently facing a period of higher uncertainty, driven by the global economic and geo-political environment. Claims in 2018 have risen to historically high levels, with total indemnifications of USD 6.4 bn, 17% higher than 2009 during the financial crisis and 75% higher than the annual average for the past decade (
Berne Union 2019b).
This volatile environment makes it challenging for insurers and ECAs to derive reliable predictions of expected claims based on historical data. While, private insurers face increasing financial and regulatory requirements, ECAs have to justify that their use of taxpayers’ money is effective and efficient, and creates the desired economic and social impact. For both, private and public insurers, this means that it is increasingly important to deliver reliable estimates of claims, claims reserves and associated expenses. As ECAs are an instrument of their governments’ economic and international policies, the portfolio and structure of their business and consequently of their claims reflect national industry and (geographical) export structures, thus, are specific to each country. Moreover, some ECAs do not experience claims regularly; in the MLT business particularly, no claim is the norm and (larger) claims are an exception. Predicting claims and estimating claims reserves as accurately as possible thus is key to ECAs management and underwriting decisions, and will help to allocate capital that is provided by the taxpayer more efficiently.
Insurers have been using a range of deterministic and stochastic methods, such as the Chain Ladder or Bornhuetter-Ferguson method, to predict claims and the related claims reserves (
Baudry and Robert 2019). However, developments on regulatory level as well as increasing uncertainty in export credit risks increase the need for the application of more sophisticated methods (
England and Verrall 2002;
Verall et al. 2012). Prior work by
Wüthrich (
2018a,
2018b), as well as
Thesmar et al. (
2019) show that ML approaches have benefits for claims prediction purposes.
3 The algorithms are able to discover patterns in multidimensional datasets or can find new predictors and relationships in the data that have not been used in the traditional methods (
Thesmar et al. 2019).
Wüthrich (
2018a) further argues that ML techniques in claims reserving are flexible and able to work structured, as well as unstructured data.
3. The Berne Union Data
The Berne Union (International Union of Credit and Investment Insurers) is the international trade association of the global export credit and political risk insurance industry. The 85 members are Export Credit Agencies, private insurers of credit and political risk as well as multilateral institutions from 73 countries (
Berne Union 2019a). In 2018, Berne Union members covered 13% of all cross-border merchandise trade, with USD 2.5 trillion covered by credit, and political risk insurers about USD 6bn claims paid (
Berne Union 2019b). From the new MLT business written in 2018, 83% was accounted for by public ECAs (
Berne Union 2019c).
The Berne Union collects comprehensive data on their members’ ST and MLT business twice a year. Their database is unique in that it covers transactional information of 33 of the most relevant ECAs, making it the most extensive collection of structured data on export credit insurance and finance, and the best overall proxy for trade credit in general (
Auboin and Engemann 2014). Its main purpose is to serve as a mechanism for Berne Union members to share their business information amongst themselves; to date, the Berne Union data have been used in only two scientific studies, which analysed the impact of trade credit and trade finance availability on trade (
Auboin and Engemann 2014;
Korinek et al. 2010).
The Berne Union database on MLT ECA business is organised by ECA, destination country, activity (insurance or lending) and half-year, covering the years 2005 to 2018. Each record details the volume of new commitments by type (Sovereign, Other Public, Banks, Corporates and Projects), the volume of claims and recoveries (political, commercial, total), offers, reinsurance, exposure, staff, premium income, administrative costs and cash flow. In light of the aim of this study, it is important to note that the data reflect underwritten but not rejected contracts. Given that ECA transactions undergo a high level of scrutiny before signing, claims are an exception, not the norm.
For the purposes of this study, we focus on combined insurance and lending MLT business, and we enriched the data with ECA and destination summary information to indicate their size, general development, business diversification, and claim history. A detailed list of added attributes, including their rationale, is provided at
Appendix A. All monetary variables were deflated using the 2010 based International Monetary Fund (IMF) Export-Import-Price-Index (XMPI) to obtain constant USD values (
International Monetary Fund et al. 2009).
Table 1 provides descriptive statistics of the 25,396 records available of the ML exercise on exposure, new commitments and claims.
4. Supervised Machine Learning
Supervised ML techniques aim to uncover potential relationships between independent and one or several dependent variables (
Rokach and Maimon 2005), or more often, to simply find a function that allows a good prediction of a target attribute, based on available input attributes (
Varian 2014). The scientific literature on the subject provides a wide range of ML applications, including Naïve Bayesian Classifiers, Bayesian Networks, Logistic Regression, Decision Trees (DT), Conditional Inference Trees, Random Forests (RF), Support Vector Machines, k-Nearest-Neighbour and Neuronal Networks (NN). The Least Absolute Shrinkage and Selection Operator (LASSO) algorithm is used occasionally in economic applications and is alleged to be most familiar to economists (
Mullainathan and Spiess 2017). All these techniques are, in principle, suitable in supporting the prediction of claims as intended by this study.
Amongst other factors, it is the field of application (
Singh et al. 2016), including the dependencies of its inherent variables, data structure, data quality, parameter tuning or the performance measure, that determines whether one algorithm performs better than others. To this date, there is no commonly accepted approach to link a particular problem to the most suitable ML technique to solve it (
Kuhn and Johnson 2013;
Wanke and Barros 2016). It has, therefore, become popular to apply several techniques to the same task and compare their performances (for example,
Fauzan and Murfi 2018;
Lorena et al. 2011;
Mullainathan and Spiess 2017;
Razi and Athappilli 2005;
Singh et al. 2016;
Weerasinghe and Wijegunasekara 2016).
We follow this methodological framework by comparatively investigating DT, RF, NN and PNN to predict claims in export credit insurance. Although, these techniques are well-understood and documented, we will provide brief descriptions and our rationale for employing them in this section. More in-depth explanations can be found in the references of the relevant paragraphs. For descriptions of the techniques not covered here, we refer to the works of
Athey (
2018),
Mullainathan and Spiess (
2017),
Varian (
2014) or
Wanke and Barros (
2016).
Singh et al. (
2016) provide a concise comparison of the advantages and disadvantages of the different techniques, and
Charte et al. (
2019) give an overview on non-standard ML problems.
4.1. Decision Trees
A DT is a recursive partition of a dataset into subsets which, ideally, amongst themselves are most heterogeneous with respect to a given target attribute. The DT model representation begins with a top node covering the entire dataset, characterized by the distribution of the target attribute. A DT algorithm seeks to select from all available input attributes the one attribute which, at an optimal split value, separates the data so that target attribute distributions of the subsets diverge as much as possible from the parent node, and are as pure as possible, meaning that each successor node contains mostly records of the same target attribute value. Options to measure the degree of purity include, but are not limited to, Gini impurity, Gini index, gain ratio and information gain (
Rokach and Maimon 2005).
Let
denote the probability of a target attribute of domain
to be chosen at random. If the record was also labelled randomly according to the target attribute distribution, then the probability of the record being labelled incorrectly is
. If
denotes the cardinality of the target attribute domain, the Gini impurity of target attribute
of a given dataset
is defined as:
In a perfectly pure data (sub)set, the probability of a record of type to be chosen is 1, and its probability to be labelled incorrectly is 0, resulting in a Gini impurity of 0. The less pure the dataset, the larger the Gini impurity measure.
Let
denote the set of
input attributes
,
the domain of input attribute
,
the cardinality of
’s domain, and
the cardinality of subset
of records of
, then the Gini index at split
is defined as:
The optimal split attribute
is the one which results in the maximum Gini gain (the difference between
and
(
Rokach and Maimon 2005), or simply the
which generates the minimum
.
In a DT representation, a split is signified by edges leading from the parent node to child nodes, typically displaying the target attribute distribution of the subsets which they represent. The algorithm continues to split child nodes in the aforementioned manner and stops when predefined criteria are met. Such criteria typically include a maximum number of splits, a minimum Gini gain threshold, or a minimum number of records per node. Nodes that are not further split are called leaves or terminal nodes.
If the DT is to classify new data, the value of the split attribute at each node determines which edge to follow until a terminal node is reached; this node infers the prediction for a given instance (
Varian 2014).
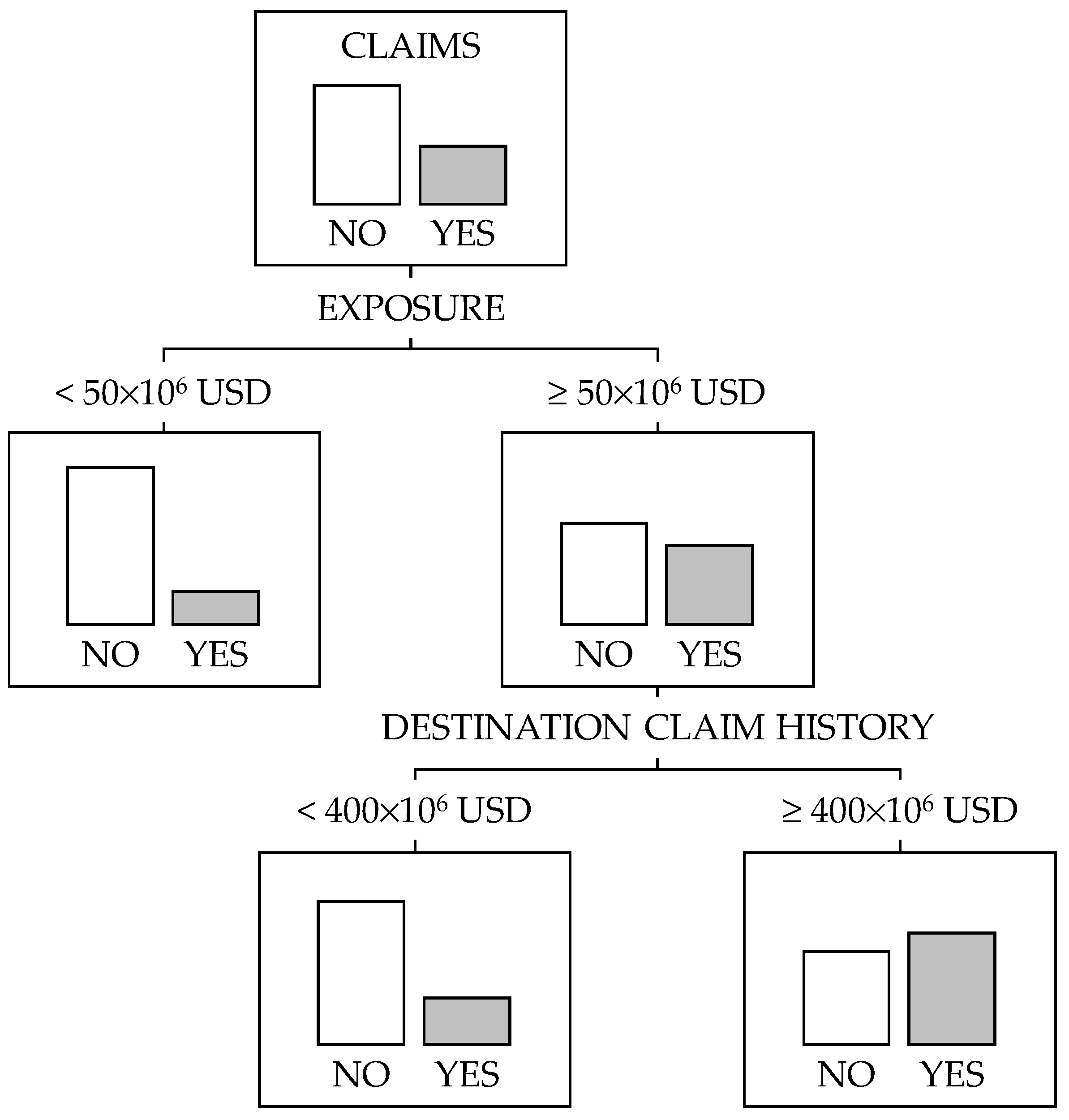
Figure 1 is an indicative example of a DT model representation with a dichotomized target attribute “CLAIMS (NO/YES)”, with its most relevant predictor being “EXPOSURE” at a split point of 50 million USD, and below the ≥50 million USD branch a second predictor of “DESTINATION CLAIM HISTORY” at a split point of 400 million USD.
Finding an optimal DT by brute force is, under normal circumstances, computationally infeasible, because the search space increases exponentially with the number of attributes and their values. However, a range of efficient so-called inducers such as C4.5, CART or CHAID have been developed to find reasonably accurate approximations (
Rokach and Maimon 2005); some are limited to either, discrete or continuous problems, some can process both.
The key advantages of DT are a generally good performance with relatively little computational effort, and the output of intuitive, self-explanatory models (
Singh et al. 2016), which can be communicated well to practitioners. The latter makes DT highly interesting for applied research problems, which is why we include them in this study.
4.2. Random Forests
DT can be sensitive to changes in the training sample, and are also likely to over-fit if training conditions are not carefully controlled (
Singh et al. 2016;
Varian 2014). The general idea behind RF is to train a multitude of DT, based on different bootstrap samples from the training data, and by sampling the input attributes that are available to the algorithm to choose from at each node (
Breiman 2001;
Fang et al. 2016;
Varian 2014). As a result, RF algorithms generate a pre-defined number of DT, which may or may not come to different predictions when presented with new data. The overall prediction returned by an RF is the category chosen by the majority of DT (
Lorena et al. 2011;
Varian 2014), or the average result for continuous problems (
Fang et al. 2016;
Mullainathan and Spiess 2017).
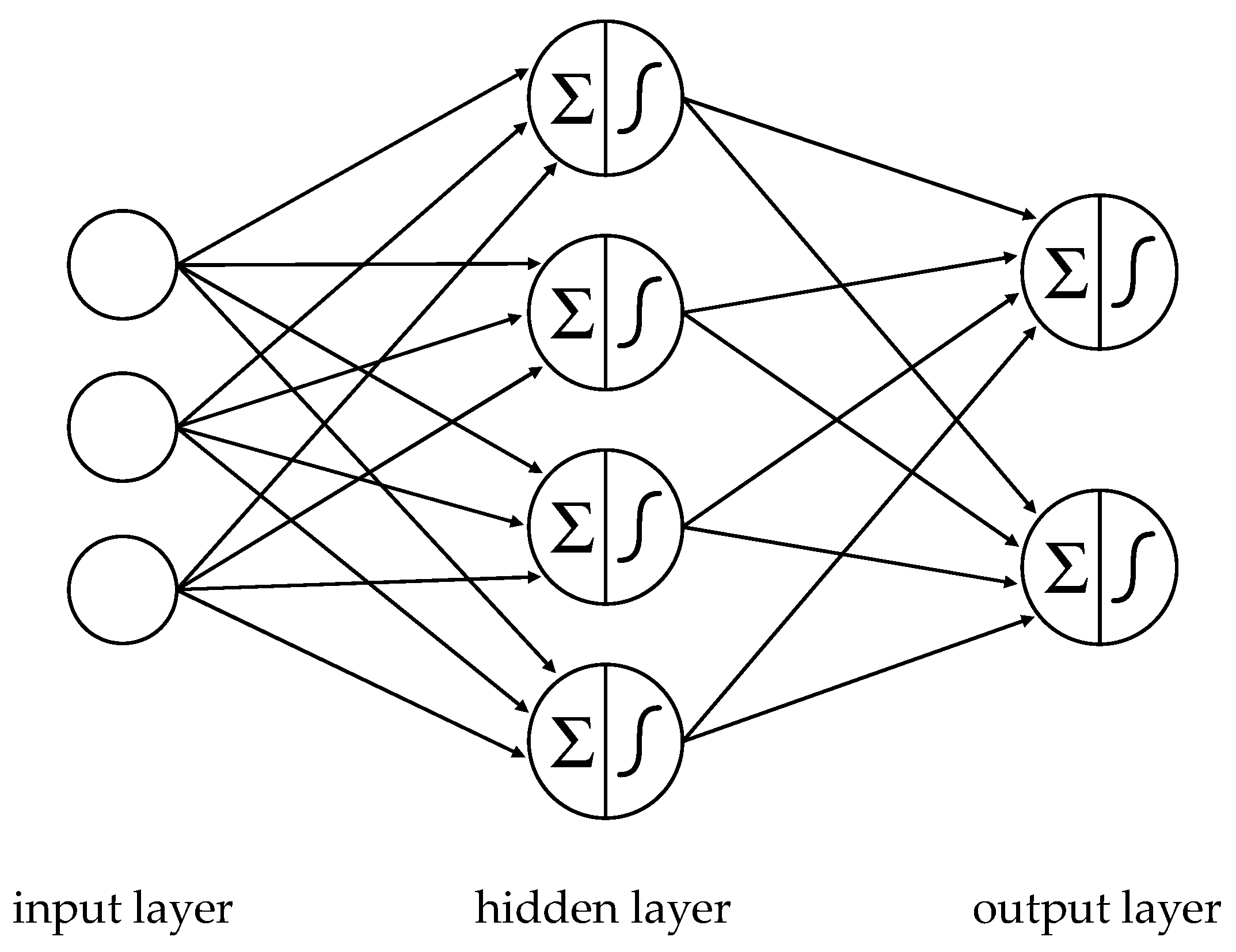
4.3. Neural Networks
NN consist of layers of so-called neurons (
Claveria and Torra 2014). The number of neurons in the input layer equals the number
of input attributes. For a given record, each of the input neurons picks up the value of its associated input attribute
and applies an activation function
to calculate a signal value as output:
. Typically, sigmoid functions such as the hyperbolic tangent
or a logistic function
are used (
LeCun et al. 2015).
is forwarded to the neurons in the subsequent layer. One or several layers, known as hidden layers, collect and aggregate signals from preceding layers, and turn, them into new signals.
Figure 2 is an illustration of an NN with just one hidden layer.
Let
denote the signal that neuron
of layer
receives from neuron
of its preceding layer
,
the weight that
applies to
, and
a bias term, to calculate a weighted sum
,.
’s signal
is generated by applying an activation function
to
:
In classification problems, the number of neurons in the output layer equals the cardinality of the domain of the target attribute. During training, an objective function
measures for each record the (quadratic) error between the output signals
of the output layer, and the actual target value
:
Given that the signals of each layer are functions of the weights, biases and signals of the preceding layers,
is ultimately a function of (averaged) weights and biases from all training records and all layers of the NN. The gradient of
indicates the sensitivity of the objective function to changes in these parameters:
The larger a partial derivative of
, the more the objective function benefits from its manipulation during the descend towards a minimum. Therefore, weights and biases are adjusted simultaneously in proportion of their negative partial derivative in every step of the training. This process is repeated until improvements in the cost function fall below a predefined threshold. When a trained NN is used for prediction, the learned rules are applied to new data, and the resulting output values are used as prediction values (
LeCun et al. 2015).
We include NN in this study because they are thought to be better suited than DT to model complex, nonlinear relationships (
Claveria and Torra 2014;
Razi and Athappilli 2005;
Singh et al. 2016). Although,
Varian (
2014) provides a case to the contrary. Given that it is possible for claims to be the result of nonlinear economic relationships, it is interesting to see whether NN perform better than DT in predicting claims.
4.4. Probabilistic Neural Networks
Specht (
1990) proposed to modify NN by replacing the traditionally implemented sigmoid activation functions with statistically derived exponential functions (
Iounousse et al. 2015). Specht named the class of such algorithms PNN and demonstrated that the introduced modification, under certain, but easy, to meet conditions, makes it possible to asymptotically approach the Bayes optimal decision surface of a classification problem (
Specht 1990). PNN can map any input pattern to any number of classifications, are capable of handling erroneous, sparse or missing data well, and provide probability estimates in conjunction with their classification (
Specht 1990). The feature of explicit probabilities allows for extended analyses, e.g., of classification errors, and provides opportunities to further improve prediction. In addition, PNN are more flexible than NN in handling different types of input variables, and it seems generally valuable to test a variation of NN alongside their original implementation, which is why we include PNN in our set of ML techniques.
5. Methodology
5.1. General Modelling Considerations
All ECAs exist to promote exports, but different national priorities have resulted in various designs and mandates under which they operate (
Stephens and Smallridge 2002). Furthermore, an ECA’s business is significantly impacted by its nation’s economic size and export characteristics-profile. Similarly, the political, judicial and commercial structure and stability of a destination country are important factors of its risk profile. Classic econometric modelling requires such heterogeneity to be accounted for, for example, by introducing ECA or destination dummy variables, to reflect effects that are stable and specific to individual countries, and could, therefore, bias the model if omitted. The DT, RF and PNN techniques, and the NN technique with some limitations, are perfectly capable of recognizing ECA or destination names as input variables. However, in this study we deliberately prevented the ML algorithms from knowing the specific agents of a given transaction. The rationale is that if a certain attribute, such as ECA or destination name, is used during model training (see
Section 5.4 below), the resulting model requires that information to be present for prediction purposes. Otherwise, when attempting to make a prediction for an ECA or destination, not observed during training, the model fails. This can create problems at the training-validation gateway. More importantly, it precludes the model from making predictions for “new” ECAs or destinations. However, these might be the most relevant cases for ML to be employed in export credit insurance claim prediction. To enable our ML models to deal with any agent, whether or not it contributed training data, we exclusively fed generic information such as export volumes, portfolio diversity etc. as inputs (see
Appendix A for used attributes) to reflect different phenotypes of ECAs’ and destinations’ phenotypes. However, this approach bears some risks in introducing unobserved heterogeneity, which should be borne in mind when analysing prediction outcomes.
A second consideration is associated with the nature of the intended prediction. Claims gain most attention when they are exceptional, for example, when an ECA with traditionally low claims gets hit by a large number or sum of claims within a short period of time. Therefore, the identification of patterns preceding singular events of claims was considered as a potential aim of this study. However, during the explorative phase it showed that, across ECAs and destinations, the occurrence of claims is quite diverse. Although, most records in the database report no claims, ECA, destination or annual aggregates often do. There are some ECAs or destinations for which claims are actually rare. However, for some ECAs and destinations claims are a fairly regular feature, and some ECAs and destinations are somewhere in between. Given that this is the first time the Berne Union dataset is extensively analysed with a view towards claims, a decision was made to first explore the overall situation across all agents before focusing on subsets. Consistent with that, the study attempts a more general assessment of the adequacy of different ML techniques to be used in claim prediction.
5.2. Prediction Tasks
Predicting claims can take a variety of shapes. To compare the performance of the different ML techniques, we train models to solve prediction tasks with different degrees of difficulty (see
Appendix A, section “Target attributes”, for implementation details):
“Claims YES/NO”: At the simplest level, the technique is to predict whether or not a given export finance condition will incur claims as a dichotomous yes/no decision.
“Claim ratio class”: Claims can vary significantly in value, so that a yes/no prediction is a great simplification of the problem. Therefore, we also test ability of the techniques to predict the magnitude of claims, expressed as five classes of claims/exposure-ratios.
“Claim ratio”: Ultimately, we also want to evaluate how well ML techniques perform in predicting an actual claim ratio, measured in terms of claims/exposure.
5.3. Technical Implementation of ML Algorithms and Analysis
Today, a range of tools, such as Python, RapidMiner or R, are available to support comfortable implementations of ML workflows. For this study, we use the data analytics platform KNIME. KNIME is a free and open-source software for data retrieval, data blending, modelling, analysis and visualization. It includes a rich collection of ML and data mining components which can be assembled following a modular data pipelining concept (
KNIME 2019). All data preparation, training and testing procedures were entirely designed and set up in KNIME;
Table 2 shows a mapping of the KNIME ML nodes that were selected against the prediction problems. Details on the nodes are available via the KNIME node and workflow search engine (
NodePit 2019).
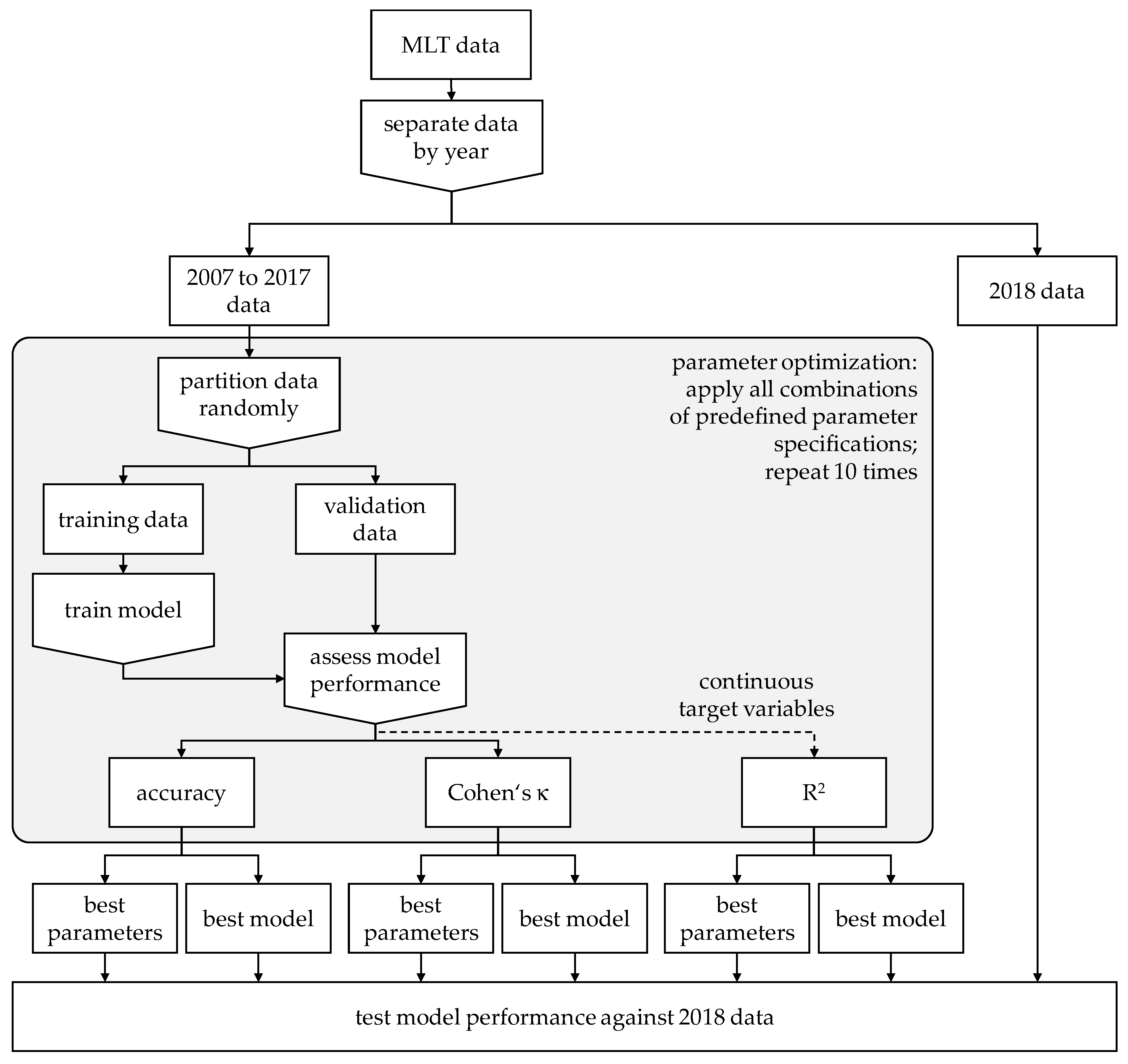
5.4. Training, Validation and Test Data
It is well known that ML algorithms can over-fit, resulting in good in-sample but poor out-of-sample performance. Therefore, it is common to randomly split the data into a training and a validation set (
Kuhn and Johnson 2013;
Mullainathan and Spiess 2017), specify models based on training data and test them against the validation data. The objective function is to minimise deviations between predicted and actual target attribute values in the latter (
Athey 2018). More advanced approaches divide the data into three types of data, including; training data to estimate models; validation data to choose a model, and; test data to assess its performance (
Varian 2014).
Dividing the entire dataset into subsets for training, validation and testing by random sampling is a defence against overfitting. However, it might not be a valid strategy for obtaining reliable prediction models:
Random sampling from the same population might, analogous to the law of large numbers or the Glivenko-Cantelli theorem, result in generally converging conditions in the subsets. A model which reflects the training data well without overfitting may, therefore, also be a good representation of the validation and test sample by sheer principles of statistics.
In a practical setting, an insurer would have no choice but to use historic data to make forecasts about future data. Effectively, this implies a strictly chronological data separation, which is different from random sampling.
To test and counter these concerns, we exclude 2018 data from model development and validation, and only use them as test data later in the process. The records covering the period between 2007 and 2017 are used for training and validation.
Figure 3 depicts the data separation and their use as part of the entire training, validation and testing procedures employed by this study.
5.5. Parameter Optimisation
ML inducers optimise a specific objective function by tuning parameters that can be seen as internal to the algorithm. However, the performance of an algorithm is also affected by a range of parameters that require external intervention. Typical examples are the selection of the objective function itself or stopping criteria. Such parameters can neither be derived from the problem nor otherwise be independently calculated (
Kuhn and Johnson 2013;
Wanke and Barros 2016). External parameter optimisation is, therefore, integral to obtaining a powerful prediction model. Some of the externally determined parameters are specific to an algorithm, but also some more general conditions around data preparation and provision can play a role. Besides algorithm specific parameters, we investigate how the size of the training sample (relative to the validation sample) and the fraction of records with no claims affect model performance:
The relation between the volume of the training and validation data addresses the simple question of whether training with a smaller and validation against a larger sample (which might protect against overfitting), or training with a larger and validation against a smaller sample yields better results.
The rationale for reducing the number of records with no claims is their dominance in the Berne Union dataset (87.5% of the 2007–2017, and 86.2% of the 2018 records register a total of 0 claims paid). This imbalance will cause models to lean towards the prediction of no claims although it might be desirable to identify potential claims with precedence. A prioritized identification of a recessive value can be achieved by partial suppression of the dominant value during training.
An overview of the algorithm-specific and general external parameters, including applied variations, is provided at
Appendix B. We explore all combinations of parameter variations by brute force.
5.6. Model Benchmark
ML techniques require extensive data preparation and can be computationally costly, raising the question of whether they actually perform better than simple heuristics (
see also England and Verrall 2002).
The ML models of this study are generic and can be applied to any ECA and destination country, irrespective of whether or not the ECA has a history of providing cover for the destination. Although, no trivial method offer a fully equivalent capability, moving averages are a simple way for an ECA to predict claims for destinations that it engaged in business with previously. In such cases, an estimator for the claims ratio
of ECA
and destination
in a given year
can be defined as (
denotes the exposure of ECA
to destination
, and
denotes the respective claims;
is the number of preceding years to be considered, also referred to as “window length” of the moving average):
The resulting estimator, or a transformation of it into a binary YES/NO variable or a claim ratio class, can be used as BM to help assess the benefit of instituting a more complex ML technique.
To avoid an arbitrary definition of the moving average’s window length
, for each ECA
and destination
we determine the optimal window length
which minimizes:
The data separation employed during the development of the ML models (see
Section 5.4) is also applied to the BM, i.e., data from 2007 to 2017 are used to identify
, and 2018 data serve to test the BM.
The execution of the BM optimisation yields that the optimal window length is mostly 1, meaning that, on average, the previous year’s claims ratio often best predicts the current year’s claim ratio.
Table 3 provides an overview of the number of times each window length was determined to be optimal.
5.7. Assessment of Model Performance
The obvious measure to assess model performance is accuracy, the proportion of correctly classified records. However, it is useful to additionally consider Cohen’s κ, originally designed to evaluate inter-rater reliability. Cohen’s κ adjusts accuracy
by considering correct predictions that would occur at random,
where
is the proportion of records expected to be correctly classified by chance (
Cohen 1960). A
of 0 means that accuracy is equal to agreement at random, a
of 1 indicates perfect agreement (
Cohen 1960), equating to 100% correct model predictions. A further advantage of this prudent correction is that it penalises false predictions more evenly, irrespective of the predominance of individual values: As mentioned above, 86.2% of the 2018 records register 0 claims. Under these circumstances, a completely naïve model could achieve an accuracy of 0.862 by simply predicting “0 claims” 100% of the time. However, this would equal agreement by chance and result in
, which seems a more suitable evaluation of the worth of the model. For the assessment of continuous target variables, we use R
2.
It is possible for a model to perform well by chance during validation, preceding a much-reduced performance during testing. To account for that possibility, we repeat the parameter optimisation ten times. This approach is different from the more conventionally used cross-validation (
Varian 2014), but should achieve a comparable level of model-validation; it greatly simplifies the implementation of the desired training/validation-sample-size ratio optimisation (see
Section 5.5). The combination of parameters yielding the highest average performance are used to test the models against 2018 data. In addition, we collect the models with the highest performance overall for testing.
All performance measures are also applied to the BM by comparing the BM’s prediction for year
with the actual value of year
. The BM’s window length optimisation (see
Section 5.6) does not involve any type of validation, which is why we apply the performance measures directly to the claims ratio predictions, generated during the optimisation stage. The test performance measures of the BM and the ML techniques are more comparable because, analogous to the ML model optimisation, the BM’s window length optimisation is based on 2007 to 2017 data, with 2018 data reserved for testing.
6. Results
Table 4 shows the validation and test results for both, the “Claims YES/NO” and the “Claim ratio class” task in terms of accuracy. Cohen’s κ results are shown in
Table 5.
Table 6 lists R
2 results, which we used as performance measure for the “Claim ratio” task. The BM performance measure is shown in the rightmost column (identical values are given against the “Best parameters” and “Best model” section per task, as no such distinction exists for the BM). The study observations include:
Amongst the ML techniques, with only two exceptions RF generate the best performance.
The accuracy achieved against the “Claim ratio class” task is not much different from the accuracy of the less challenging “Claims YES/NO” task. However, Cohen’s κ is more reflective of performance differences, indicating that both, validation and test performance, deteriorate as the task becomes more difficult.
None of the investigated ML techniques yield satisfactory results against the “Claim ratio” task; predictions of actual claim ratios turned out to be largely unreliable.
The test performance is lower than validation performance (with only two exeptions), often by just a small margin. Performance losses are more pronounced when measured by Cohen’s κ.
No definitive conclusion can be made on whether validation should serve to identify optimal model parameters, or to actually generate the specific model for prediction (sometimes utilizing the best parameters, sometimes employing the best model yields better test performance; optimal parameters are provided at
Appendix C).
The accuracy of the ML techniques is sometimes better, but generally at similar levels as the BM’s value.
In terms of Cohen’s κ, the BM performs better than any of the ML techniques. The reason is that some ECAs experience uninterrupted sequences of claims with certain destinations. Therefore, the simple rule “claims in
indicate claims in
” employed by the BM (see
Section 5.6) works well against the “Claims YES/NO” task, and also against the “Claim ratio class” task.
Against the “Claim ratio” task, the ML techniques outperform the BM, although at a very low level.
Table 4,
Table 5 and
Table 6 provide a “best performance” comparison, imitating outcomes of an actual insurer’s claim prediction exercise. While, poorly performing models would normally be of little interest to practitioners, we collected all models from the parameter optimisation stage of this study, irrespective of their performance. This allows for more detailed analyses of the results which are provided in the following sections.
6.1. Relationship between Accuracy and Cohen’s κ
A comparison of
Table 4 and
Table 5 indicates that Cohen’s κ accentuates performance differences better than accuracy (parameter optimisation confirmed that Cohen’s κ benefits from reducing the number of records with 0 claims down to 20 to 40% during training; highest accuracies were achieved with 80–100% of records with no claims; see
Appendix C for parameter details). A high Cohen’s κ might be associated with more correctly predicted claims (true positives) at the cost of less true negatives, thereby sacrificing some accuracy. We applied all models from the parameter optimisation stage to the test data, in order to understand the relationship between the two performance measures empirically, logged each model’s accuracy and Cohen’s κ and plotted them against each other.
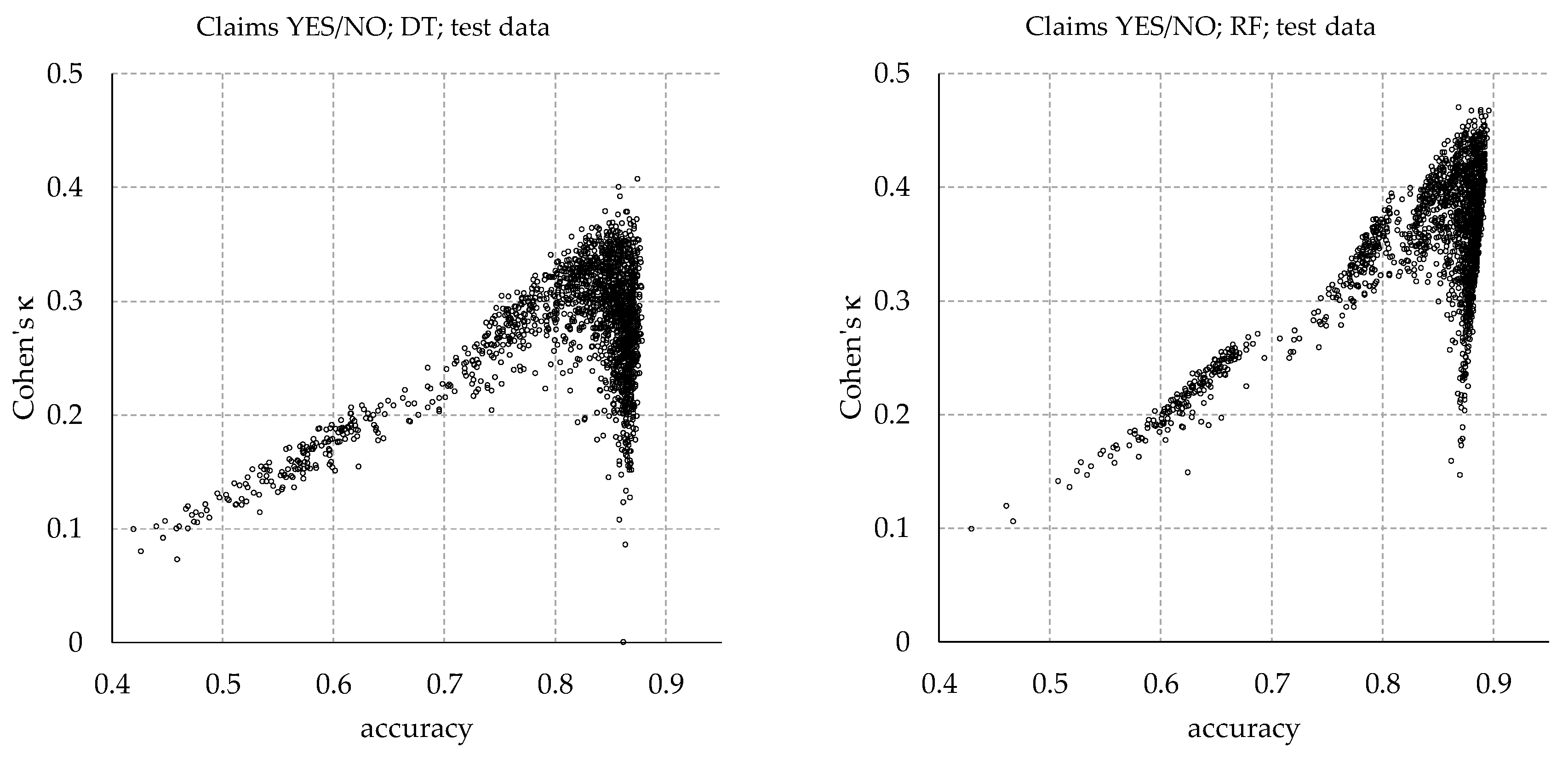
Figure 4 shows scatterplots of accuracy and Cohen’s κ for RF and PNN models:
For the RF models (“Claims YES/NO” task), shown on the left, accuracy and Cohen’s κ increase together, peaking close to (0.89, 0.47). From the peak, there is a sharp drop of Cohen’s κ, accompanied by a moderate reduction of accuracy.
The PNN models (“Claim ratio class” task) on the right also show an initial joint increase of accuracy and Cohen’s κ. Cohen’s κ peaks at a value of 0.22, from which a further increase of accuracy is associated with a marked deterioration of Cohen’s κ.
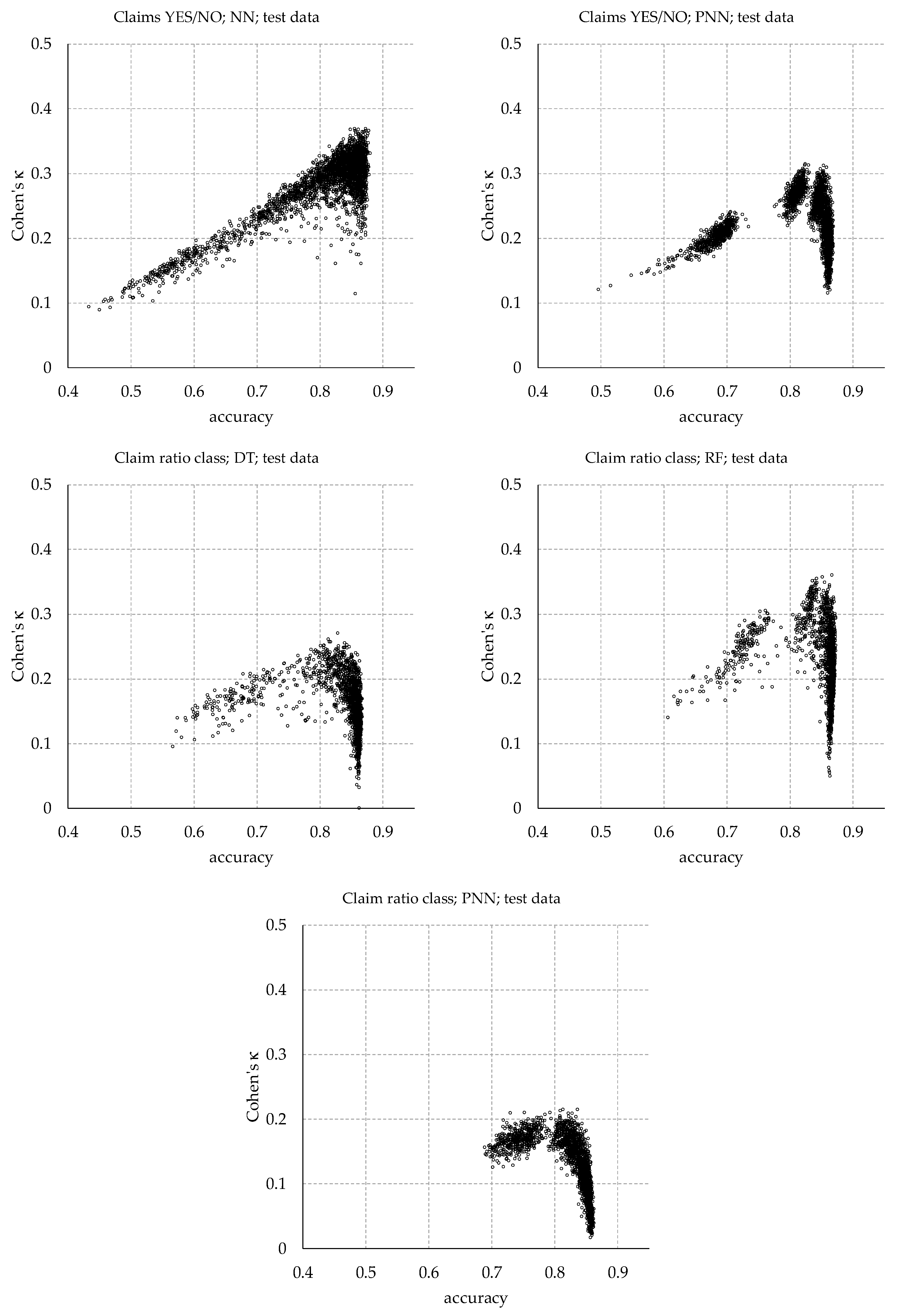
Scatterplots for all investigated ML techniques are provided at
Appendix D, showing that against the “Claims YES/NO” task, DT, RF and NN generated models with high Cohen’s κ while retaining high accuracy at the same time. Against the “Claims ratio class” task, only RF yielded models with both measures being high. In conjunction with its general advantages (see
Section 5.7), Cohen’s κ is assessed to be the more insightful measure for the purposes of this study. However, for other applications, accuracy might be more relevant.
6.2. Comparison of ML Technique Performance
With only two exceptions, RF consistently delivered the best performance (see
Table 4,
Table 5 and
Table 6). We further compared the performance of all models by prediction task and ML technique via Kruskal-Wallis tests; the results are shown in
Table 7.
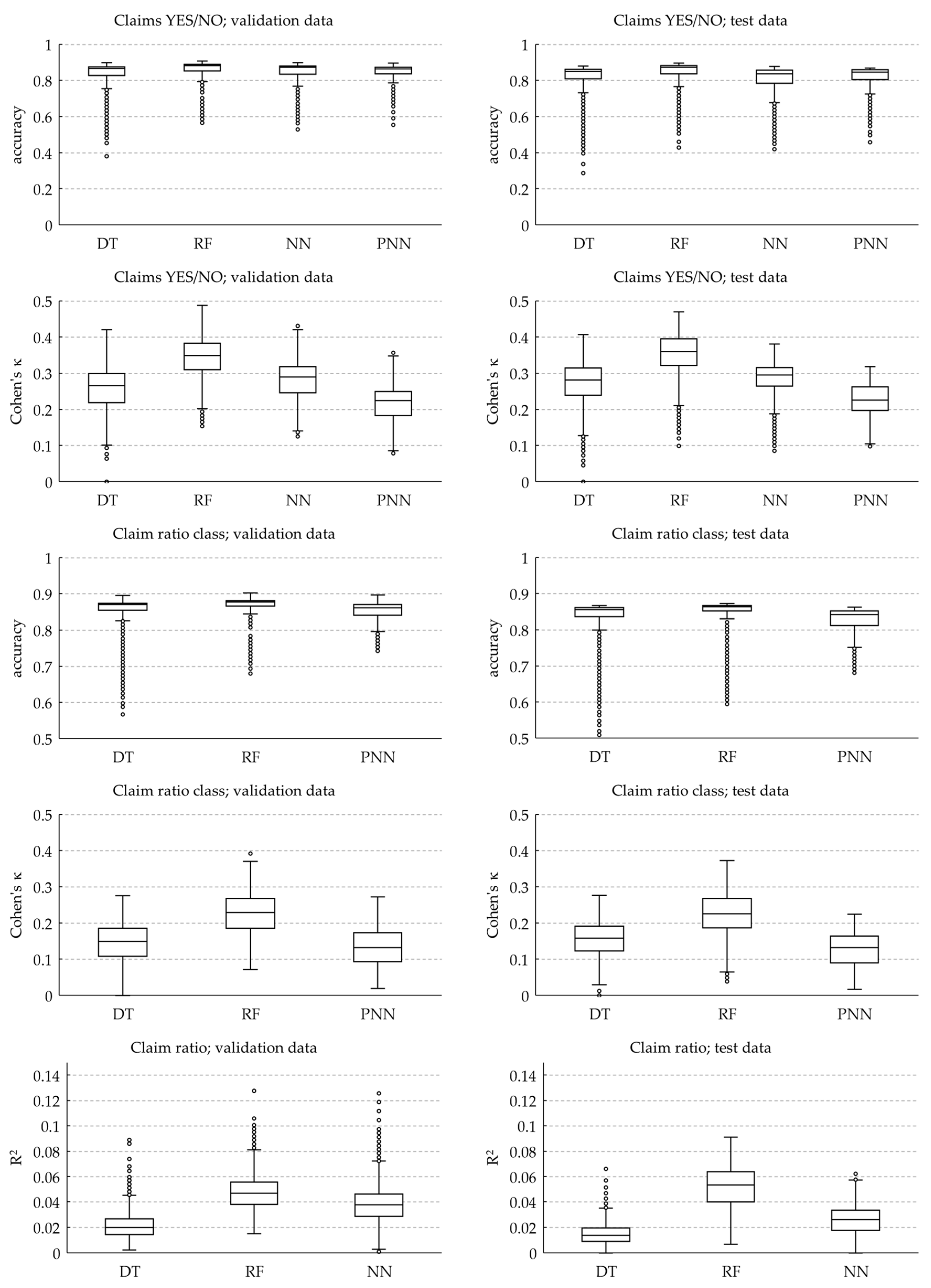
Appendix E provides boxplots to illustrate the performance of all models developed during the parameter optimisation exercise of this study (
Figure A2; the left half of the table shows performance variations measured during validation, mirrored on the right by the corresponding performance of the same models applied to the test data). The tests confirm statistically significant differences between the performances of the techniques. Pairwise Wilcoxon-Mann-Whitney post-hoc tests were all significant with
, corroborating that RF are generally most successful in predicting claims under the conditions of this study (an interesting anomaly is that, against the “Claims YES/NO” task, NN are the worst performer in terms of accuracy, but the second-best performer in terms of Cohen’s κ).
6.3. Validation and Test Performance
Following the methodology outline of the study (see
Section 5), we used the parameters and models that performed best during validation to make predictions for 2018 data, assuming that this approach is most likely to be adopted by practitioners. However, a model that performs well during validation might not be optimal when confronted with new data. In fact, a comparison of corresponding validation and test performance in
Table 4,
Table 5 and
Table 6 shows a performance reduction in all but two cases.
Obviously, for an ML technique to be reliable it is important that its validation performance be a good indicator of its performance when used to make forecasts. To investigate this relationship, we calculated the correlation between validation and corresponding test performance, and estimated linear functions to describe their relationship; results are provided in
Table 8 (standard errors of regression parameters are provided in brackets; all parameters are statistically significant with
):
Against both the “Claims Y/N” and the “Claim ratio class” task, validation and test performance are generally highly correlated. An exception are NN, and also PNN, against the “Claims YES/NO” task, when performance is measured in terms of Cohen’s κ. RF consistently exhibit the highest correlation for all tasks and measures, although sometimes by just a small margin.
Validation-test correlations are much lower against the “Claim ratio” task, but RF, again, achieve the highest value.
In conjunction with a validation-test-correlation close to 1, an intercept close to 0 and a slope close to 1 indicate greatest performance reliability. For Cohen’s κ, which are considered the most insightful performance measure, and R2 this is best achieved by RF.
6.4. Computational Complexity
The four investigated ML techniques exhibited very different properties in terms of run-time and model size. The DT algorithm consistently produced results much quicker than any of the other algorithms, whereas PNN proved to be most time consuming. Depending on the task, the PNN took, on average, up to 675 times as long as the DT to produce and validate one model. RF turned out to be the second quickest technique (between nine to 15 times DT run-time), followed by NN (45 to 50 times DT run-time).
On the other hand, RF models occupied significantly more storage than those produced by of any of the other techniques. To some extent, this is to be expected, given that one RF model consists of many DT (the RF models trained for the purposes of this study consisted of between 50 and 200 DT; see
Appendix B for details of parameter settings). However, PNN models can also be relatively large. This is most certainly driven by their feature to provide probabilities against all possible classifications, rather than just a single classification. However, against the Claims Y/N task, this means three attributes (probability for class “NO”, probability for class “YES”, and prediction) instead of just one (prediction) and does not fully explain the size difference between NN and PNN models. DT and NN models were usually relatively small.
Neither, the run-time of the slowest, nor the model size of the most storage-consuming ML technique are of concern when a single model is being built. However, external parameter optimization, as undertaken as part of this study (see
Section 5.5), can easily result in several thousands of models. In such instances, both, the time consumption of the PNN technique and the model size of the RF technique can easily push a regular office desktop to its limits.
Table 9 provides average run-times (in milliseconds (ms)) to train and validate one model based on 20,000 records for training and 3000 records for validation (64 Bit Windows machine, 2.11 GHz Intel
® Core i7-8650U CPU, 16 GB RAM), and the average size of one model (in kilobyte (kB)) per task and ML technique.
7. Conclusions and Outlook
The purpose of our study was to evaluate ML techniques as a means for the prediction of claims of export credit insurers. ML could be well-suited to provide more accurate claims predictions, as regulatory requirements require for more sophisticated approaches for predicting claims, as well as in calculating claims reserves, and the global environment of international trade might lead to more volatility in actual claims experience. While, insurers have been using deterministic or stochastic methods based on claims development triangles, more complex methods are based on stricter assumptions, which can lead to several issues in their application and interpretation. Insurers welcome automation and appreciate the increased speed of these methods, but it is still common to apply human judgement on the results. However, more advanced models are able provide additional information useful for the decision-making of the insurance company.
Therefore, we conducted a comparative study of four ML techniques and evaluated their ability to accurately predict claims based on a unique dataset of export credit insurance claims over the period of 2005 to 2018. Furthermore, we compared the ML techniques against the performance of a simple heuristic, based on moving averages of claims from destinations that the insurer has done business with previously.
Consistent with previous works (
Fang et al. 2016;
Lorena et al. 2011;
Singh et al. 2016), RF provided the best results by a range of measures. Therefore, it seems advisable to include RF in any further research on the subject. However, RF can predict a target attribute value when provided with new data, but they do not readily reveal the logic underlying that prediction. The strength of traditional econometric approaches is that they help to extract relationships from masses of data by distilling compact equations. These equations can also be applied to new data for purposes of prediction, but more importantly, they can be analysed, in order to understand the relevance and inter-dependencies of the system defining variables. This benefit exists neither for RF nor NN, PNN or many other ML techniques, which is why they have been labelled “black boxes” by some (
Olden and Jackson 2002). It is an interesting question to understand what place a technique that produces good predictions, but does not contribute to a better understanding of a subject, can have in academic research. An exception is the DT technique, because it generates human-readable rules which provide some insight into the most important predictors of the dependent variable. Therefore, we recommend to employ DT alongside with RF as a preparatory or augmenting step.
Several ML techniques have delivered satisfactory results against the “Claims Y/N” and “Claim ratio class” task, but the generally poor performance against the “Claim ratio” task is a serious shortcoming. While, it is unsurprising to find the lowest performance against the most challenging task, it is not obvious why predictions of claim ratios lag behind the two other tasks by such a large margin. A more detailed examination of the actual and predicted data indicates that model quality appears to be significantly hampered by singular events of high claims, suggesting that no model was capable of capturing the conditions preceding their occurrence. However, singular or exceptionally high claims, which were not a focal point of this paper, might be of particularly interesting to ECAs. Therefore, a follow-up study should investigate the prediction of claims of that type. This would require an exploration of the circumstances under which a claim is considered to be exceptional, and probably an addition of external economic data from sources such as OECD or similar.
It can also not be overlooked that the ML models in many respects performed no better, and often worse, than the simple heuristic “claims in
indicate claims in
” as reflected by the BM (see
Section 5.6). Unlike the ML models, the BM is limited to ECAs and destinations with already existing business relations. If such a business relationship does exist, the computationally much less complex BM rule must be seen as superior to the investigated ML techniques. In all other cases, ML might provide an alternative. Looking positively at the performance comparison between the BM and the ML techniques (
Table 4,
Table 5 and
Table 6), it can be stated that ML is capable of predicting the virtue of a non-existing business relationship almost as well as if it would already exist. To help contain the effort of building ML models for practical applications, we provide the optimal model parameters as identified during this study at
Appendix C.
Finally, there are two interesting topics for further research arising from the convergence of ML and traditional techniques employed in insurance economics. The first topic refers to a performance comparison between ML techniques and commonly used approaches such as Chain-Ladder or Bornhuetter-Ferguson methods (
Wüthrich 2018a,
2018b). To allow for a direct and fair comparison, the requirement for ML models to be generic would have to be dropped, and individual claims data over a time period instead of aggregate claims would need to be analysed. In that context it should also be possible to better account for heterogeneity of ECAs and destinations, for example by following the approach proposed by
Wüthrich (
2018b). A second topic might evolve from the question whether classic problem-specific models, for example probability distributions for low-default portfolios (for example,
Kiefer 2009), can or should be merged with ML techniques, and to what extent this could further improve prediction performance.
Author Contributions
Conceptualization, M.B. and S.K.; data curation, M.B.; formal analysis, M.B.; methodology, M.B.; project administration, S.K.; software, M.B.; validation, M.B.; visualization, M.B.; writing—original draft, M.B. and S.K.; writing—review editing, M.B. and S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors thank the Berne Union and Vinco David for the provision of the dataset and particularly Paul Heaney for his support in understanding the specifics of the data. They also thank four anonymous reviewers for their comments and suggestions, which improved the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Data Enrichment
For the ML exercise, the year, the total of new commitments and the total exposure were used directly from the Berne Union database, and augmented with the following variables:
Target attributes (only one used at a time, depending on the prediction task):
A dichotomous claims variable (“Claims YES/NO”: “NO” if the total amount of claims paid equals 0, “YES” otherwise),
Five classes of the claims/exposure ratio (“Claim ratio class”; classes are [0, 0], (0, 0.0033], (0.0033, 0.01], (0.01, 0.05], (0.05, ∞)),
The claims/exposure ratio (“Claim ratio”).
ECA summaries (annual values):
Number of destination countries with exposure,
Number of destination countries with exposure previous year (only used for NN),
Number of destination countries with exposure two years ago (only used for NN),
Number-of-destinations trend (“UP” for three consecutive years of increase, “DOWN” for three consecutive years of decrease, otherwise “AMBIGUOUS”), to indicate whether the ECA appears to generally expand or reduce the number of destinations in their portfolio (not used for NN),
Destination exposure in % of the ECA’s total exposure, to indicate the relevance of the destination for the ECA,
Gini-coefficient of exposure, to indicate the ECA’s exposure diversification across their destinations,
Number of years with claims prior to the current year,
% of years with claims prior to the current year,
Total of new commitments in the current year,
Total of new commitments in the previous year (only used for NN),
Total of new commitments two years ago (only used for NN),
Total of new commitments trend (“UP” for three consecutive years of increase, “DOWN” for three consecutive years of decrease, all other “AMBIGUOUS”), to indicate whether the ECA appears to generally expand or reduce the volume of their commitments (not used for NN).
Destination summaries (annual values):
Number of ECAs with exposure,
Number of ECAs with exposure previous year (only used for NN),
Number of ECAs with exposure two years ago (only used for NN),
Number-of-ECAs trend (“UP” for three consecutive years of increase, “DOWN” for three consecutive years of decrease, all other “AMBIGUOUS”), to indicate whether the destination appears to generally expand or reduce the number of ECAs it is doing business with (not used for NN),
ECA exposure in % of the destination’s total exposure, to indicate the relevance of the ECA for the destination,
Gini-coefficient of exposure, to indicate the destination’s exposure diversification across the ECAs it is doing business with,
Number of years with claims prior to the current year,
% of years with claims prior to the current year,
Running total of claims until prior to the current year,
Total of new commitments in the current year,
Total of new commitments in the previous year (only used for NN),
Total of new commitments two years ago (only used for NN),
Total of new commitments trend (“UP” for three consecutive years of increase, “DOWN” for three consecutive years of decrease, all other “AMBIGUOUS”), to indicate whether the destination appears to generally attract an increasing or decreasing amount of commitments (not used for NN).
Appendix B. Summary of Externally Optimised and Fixed Parameters
Table A1 details algorithm-specific and general externally tested parameters, including their variation boundaries and increments.
Table A1.
Parameter summary.
Table A1.
Parameter summary.
KNIME Node
[ML Technique] | Parameter | Lower Limit | Upper Limit | Increment |
|---|
Decision Tree Learner/
Simple Regression Tree Learner
[DT] | Minimum number of records per node | 30 | 90 | 20 |
| | Quality measure | Gini index (fix) | - | n/a |
| | Pruning method | MDL (fix) | - | n/a |
| | Average split point | Yes (fix) | - | n/a |
| | Binary nominal splits | No (fix) | - | n/a |
Random Forest Learner/
Random Forest Learner (Regression)
[RF] | Number of models | 50 | 200 | 50 |
| | Split criterion | Information gain ratio (fix) | - | n/a |
RProp MLP Learner
[NN] | Number of hidden layers | 1 | 3 | 1 |
| | Number of neurons per layer | 10 | 20 | 5 |
| | Maximum number of iterations | 100 (fix) | - | n/a |
PNN Learner (DDA)
[PNN] | Theta minus | 0.1 | 0.35 | 0.05 |
| | Theta plus | 0.35 | 0.65 | 0.05 |
| General | Training/validation partitioning fraction | 0.1 | 0.9 | 0.1 |
| | Fraction of records with 0 claims | 0.1 | 1 | 0.1 |
Appendix C. Optimal Parameters
Table A2.
Results: Optimal DT Parameters.
Table A2.
Results: Optimal DT Parameters.
| Measure | Task | Outcome | Partitioning Fraction | 0 Claim Fraction | Minimum Number of Records per Node |
|---|
| Accuracy | Claims YES/NO | Best parameters | 0.9 | 1.0 | 30 |
| | | Best model | 0.9 | 1.0 | 30 |
| | Claim ratio class | Best parameters | 0.9 | 0.8 | 30 |
| | | Best model | 0.9 | 0.9 | 70 |
| Cohen’s κ | Claims YES/NO | Best parameters | 0.9 | 0.4 | 50 |
| | | Best model | 0.9 | 0.5 | 30 |
| | Claim ratio class | Best parameters | 0.9 | 0.2 | 30 |
| | | Best model | 0.8 | 0.2 | 50 |
| R2 | Claim ratio | Best parameters | 0.9 | 0.8 | 90 |
| | | Best model | 0.9 | 0.8 | 70 |
Table A3.
Results: Optimal RF Parameters.
Table A3.
Results: Optimal RF Parameters.
| Measure | Task | Outcome | Partitioning Fraction | 0 Claim Fraction | Number of Models |
|---|
| Accuracy | Claims YES/NO | Best parameters | 0.9 | 0.9 | 200 |
| | | Best model | 0.9 | 0.9 | 200 |
| | Claim ratio class | Best parameters | 0.9 | 0.9 | 200 |
| | | Best model | 0.9 | 0.9 | 200 |
| Cohen’s κ | Claims YES/NO | Best parameters | 0.8 | 0.4 | 150 |
| | | Best model | 0.9 | 0.3 | 200 |
| | Claim ratio class | Best parameters | 0.9 | 0.2 | 200 |
| | | Best model | 0.9 | 0.2 | 200 |
| R2 | Claim ratio | Best parameters | 0.9 | 0.6 | 50 |
| | | Best model | 0.9 | 0.8 | 200 |
Table A4.
Results: Optimal NN Parameters.
Table A4.
Results: Optimal NN Parameters.
| Measure | Task | Outcome | Partitioning Fraction | 0 Claim Fraction | Layers | Neurons |
|---|
| Accuracy | Claims YES/NO | Best parameters | 0.8 | 1.0 | 2 | 10 |
| | | Best model | 0.9 | 0.9 | 2 | 10 |
| Cohen’s κ | Claims YES/NO | Best parameters | 0.9 | 0.3 | 3 | 20 |
| | | Best model | 0.9 | 0.4 | 2 | 20 |
| R2 | Claim ratio | Best parameters | 0.9 | 1.0 | 2 | 20 |
| | | Best model | 0.9 | 1.0 | 2 | 20 |
Table A5.
Results: Optimal PNN Parameters.
Table A5.
Results: Optimal PNN Parameters.
| Measure | Task | Outcome | Partitioning Fraction | 0 Claim Fraction | Theta Minus | Theta Plus |
|---|
| Accuracy | Claims YES/NO | Best parameters | 0.9 | 1.0 | 0.30 | 0.65 |
| | | Best model | 0.9 | 1.0 | 0.15 | 0.65 |
| | Claim ratio class | Best parameters | 0.9 | 1.0 | 0.30 | 0.55 |
| | | Best model | 0.9 | 1.0 | 0.15 | 0.65 |
| Cohen’s κ | Claims YES/NO | Best parameters | 0.9 | 0.4 | 0.20 | 0.60 |
| | | Best model | 0.9 | 0.4 | 0.25 | 0.45 |
| | Claim ratio class | Best parameters | 0.9 | 0.2 | 0.30 | 0.40 |
| | | Best model | 0.9 | 0.2 | 0.20 | 0.55 |
Appendix D. Accuracy—Cohen’s κ Scatterplots
Figure A1 shows scatterplots to highlight the relationship between the performance measures “accuracy” and “Cohen’s κ” for all investigated ML techniques and prediction tasks. The data results from applying all models developed during the parameter optimisation exercise to the test data.
Figure A1.
Scatterplots of Accuracy and Cohen’s κ.
Figure A1.
Scatterplots of Accuracy and Cohen’s κ.
Appendix E. Boxplots on ML Technique Performance
The boxplots shown in
Figure A2 illustrate the performance of all models developed during the parameter optimisation exercise of this study. The left side of the table shows performance variations measured during validation, mirrored on the right by the corresponding performance of the same models applied to the test data.
Figure A2.
Boxplots: Comparison of ML techniques’ performance (validation and test data).
Figure A2.
Boxplots: Comparison of ML techniques’ performance (validation and test data).
References
- Abraham, Filip, and Gerda Dewit. 2000. Export Promotion Via Official Export Insurance. Open Economies Review 1: 5–26. [Google Scholar] [CrossRef]
- Athey, Susan. 2018. The impact of machine learning on economics. In The Economics of Artificial Intelligence: An Agenda. Chicago: University of Chicago Press. Available online: https://www.nber.org/chapters/c14009 (accessed on 26 February 2020).
- Auboin, Marc. 2009. Restoring Trade Finance during a Period of Financial Crisis: Stock-Taking of Recent Initiatives. WTO Staff Working Paper ERSD-2009-16. Available online: https://www.wto-ilibrary.org/economic-research-and-trade-policy-analysis/restoring-trade-finance-during-a-period-of-financial-crisis_4de92d90-en (accessed on 16 July 2019).
- Auboin, Marc, and Martina Engemann. 2014. Testing the trade credit and trade link: Evidence from data on export credit insurance. Review of World Economics 150: 715–43. [Google Scholar] [CrossRef]
- Baudry, Maximillien, and Christian Y. Robert. 2019. A machine learning approach for individual claims reserving in insurance. Applied Stochastic Models in Business and Industry 35: 1127–55. [Google Scholar] [CrossRef]
- Berne Union. 2019a. About the Berne Union. Available online: https://www.berneunion.org/Stub/Display/8 (accessed on 29 November 2019).
- Berne Union. 2019b. Press Release 11/04/2019. Available online: http://cdn.berneunion.org/assets/Images/Berne%20Union%20Singapore%20SM%20Press%20Release.pdf (accessed on 29 November 2019).
- Berne Union. 2019c. BU Spring Meeting Newsletter, Berne Union Statistics 2018 YE Commentary. Available online: http://cdn.berneunion.org/assets/Images/3923e9fd-215d-474e-80c9-6d10b984c302.zip (accessed on 29 November 2019).
- Berne Union. 2019d. About Export Credit Insurance. Available online: https://www.berneunion.org/Stub/Display/17 (accessed on 23 December 2019).
- Breiman, Leo. 2001. Random Forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- Charte, David, Francisco Charte, Salvador García, and Francisco Herrera. 2019. A snapshot on nonstandard supervised learning problems: Taxonomy, relationships, problem transformations and algorithm adaptations. Progress in Artificial Intelligence 8: 1–14. [Google Scholar] [CrossRef]
- Claveria, Oscar, and Salvador Torra. 2014. Forecasting tourism demand to Catalonia: Neural networks vs. time series models. Economic Modelling 36: 220–28. [Google Scholar] [CrossRef]
- Cohen, Jacob. 1960. A coefficient of agreement for nominal scales. Educational and Psychological Measurement 20: 37–46. [Google Scholar] [CrossRef]
- Drysdale, David. 2015. Why the OECD Arrangement Works (Even Though It Is Only Soft Law). In The Future of Foreign Trade Support. Edited by Andreas Klasen and Fiona Bannert. Durham: Wiley, pp. 5–7. [Google Scholar]
- Egger, Peter, and Thomas Url. 2006. Public Export Credit Guarantees and Foreign Trade Structure: Evidence from Austria. The World Economy 29: 399–418. [Google Scholar] [CrossRef]
- England, Peter D., and Richard J. Verrall. 2002. Stochastic claims reserving in general insurance. Journal of the Institute of Actuaries 129: 1–76. [Google Scholar] [CrossRef]
- European Commission. 2012. Study on Short-Term Trade Finance and Credit Insurance in the European Union. Prepared by International Financial Consulting Ltd. for the European Commission. Available online: https://op.europa.eu/en/publication-detail/-/publication/a1ae8477-930c-44df-8c41-b38fb9ad94a4/language-en/format-PDF/source-112097066 (accessed on 27 January 2020).
- Fang, Kuangnan, Yefei Jiang, and Malin Song. 2016. Customer profitability forecasting using Big Data analytics: A case study of the insurance industry. Computers & Industrial Engineering 101: 554–64. [Google Scholar] [CrossRef]
- Fauzan, Muhammad A., and Hendri Murfi. 2018. The Accuracy of XGBoost for Insurance Claim Prediction. International Journal of Advances in Soft Computing & Its Applications 10: 159–71. Available online: http://home.ijasca.com/data/documents/11_IJASCA_The-accuracy-of-XGBoost_159-171.pdf (accessed on 27 February 2020).
- Felbermayr, Gabriel J., and Erdal Yalcin. 2013. Export Credit Guarantees and Export Performance: An Empirical Analysis for Germany. The World Economy 36: 967–99. [Google Scholar] [CrossRef]
- International Monetary Fund, International Labour Office, Organisation for Economic Co-Operation and Development, Statistical Office of the European Communities, United Nations, and World Bank. 2009. Export and Import Price Index Manual. Available online: https://www.imf.org/external/np/sta/xipim/pdf/xipim.pdf (accessed on 27 February 2020).
- Iounousse, Jawad, Salah Er-Raki, Ahmed El Motassadeq, and Hassan Chehouani. 2015. Using an unsupervised approach of Probabilistic Neural Network (PNN) for land use classification from multitemporal satellite images. Applied Soft Computing 30: 1–13. [Google Scholar] [CrossRef]
- Kiefer, Nicholas M. 2009. Default estimation for low-default portfolios. Journal of Empirical Finance 16: 164–73. [Google Scholar] [CrossRef]
- KNIME. 2019. End to End Data Science. Available online: https://www.knime.com/ (accessed on 8 December 2019).
- Korinek, Jane, Jean Le Cocguic, and Patricia Sourdin. 2010. The Availability and Cost of Short-Term Trade Finance and Its Impact on Trade OECD Trade Policy Papers No. 98. OECD Trade Policy Papers. Available online: https://www.oecd-ilibrary.org/trade/the-availability-and-cost-of-short-term-trade-finance-and-its-impact-on-trade_5kmdbg733c38-en (accessed on 27 February 2020).
- Krummaker, Simone. 2020. Export Credit Insurance Markets and Demand. In The Handbook of Global Trade Policy. Edited by Andreas Klasen. Chichester: Wiley & Sons, pp. 536–54. [Google Scholar]
- Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. Corrected at 5th Printing. New York, Heidelberg, Dordrecht and London: Springer. Available online: https://link.springer.com/content/pdf/10.1007/978-1-4614-6849-3.pdf (accessed on 26 February 2020).
- LeCun, Yann, Yoshua Bengio, and Geoffrey Hinton. 2015. Deep learning. Nature 521: 436–44. [Google Scholar] [CrossRef] [PubMed]
- Liaw, Andy, and Matthew Wiener. 2002. Classification and regression by random Forest. R News 2: 18–22. [Google Scholar]
- Lorena, Ana C., Luis F. O. Jacintho, Marinez F. Siqueira, Renato de Giovanni, Lúcia G. Lohmann, André C.P.L.F. de Carvalho, and Missae Yamamoto. 2011. Comparing machine learning classifiers in potential distribution modelling. Expert Systems with Applications 38: 5268–75. [Google Scholar] [CrossRef]
- Morel, Fabrice. 2011. Credit Insurance in Support of International Trade: Observations throughout the Crisis. In Trade Finance during the Great Trade Collapse. Edited by Jean-Pierre Chaffour and Mariem Malouche. Washington, DC: World Bank, pp. 337–56. [Google Scholar]
- Moser, Christoph, Thorsten Nestmann, and Michael Wedow. 2008. Political Risk and Export Promotion: Evidence from Germany. The World Economy 31: 781–803. [Google Scholar] [CrossRef]
- Mullainathan, Sendhil, and Jann Spiess. 2017. Machine Learning: An Applied Econometric Approach. Journal of Economic Perspectives 31: 87–106. [Google Scholar] [CrossRef]
- NodePit. 2019. NodePit for KNIME. Available online: https://nodepit.com/nodepit-for-knime (accessed on 8 December 2019).
- OECD. 2018. Arrangement on Officially Supported Export Credits. TAD/PG(2018)1. Available online: http://www.oecd.org/officialdocuments/publicdisplaydocumentpdf/?doclanguage=en&cote=tad/pg(2018)1 (accessed on 15 July 2019).
- Olden, Julien D., and Donald A. Jackson. 2002. Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecological Modelling 154: 135–50. [Google Scholar] [CrossRef]
- Razi, Muhammad A., and Kariakose Athappilli. 2005. A comparative predictive analysis of neural networks (NNs), nonlinear regression and classification and regression tree (CART) models. Expert Systems with Applications 29: 65–74. [Google Scholar] [CrossRef]
- Rokach, Lior, and Oded Maimon. 2005. Top-Down Induction of Decision Trees Classifiers—A Survey. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) 35: 476–87. [Google Scholar] [CrossRef]
- Singh, Amanpreet, Narina Thakur, and Aakanksha Sharme. 2016. A Review of Supervised Machine Learning Algorithms. Paper presented at the 10th INDIACom; 2016 3rd International Conference on Computing for Sustainable Global Development, New Delhi, India, March 16–18; Edited by M. N. Hoda. Piscataway: IEEE, pp. 1310–15. Available online: https://ieeexplore.ieee.org/abstract/document/7724478 (accessed on 26 February 2020).
- Specht, Donald F. 1990. Probabilistic neural networks. Neural Networks 3: 109–18. Available online: https://www.sciencedirect.com/science/article/pii/089360809090049Q (accessed on 26 February 2020). [CrossRef]
- Stephens, Malcolm, and Diana Smallridge. 2002. A Study on the Activities of IFIs in the Area of Export Credit Insurance and Export Finance. INTAL-ITD-STA Occasional Paper 16. Inter-American Development Bank. Available online: https://publications.iadb.org/en/publication/study-activities-ifis-area-export-credit-insurance-and-export-finance (accessed on 26 February 2020).
- Thesmar, David, David Sraer, Lisa Pinheiro, Nick Dadson, Razvan Veliche, and Paul Greenberg. 2019. Combining the Power of Artificial Intelligence with the Richness of Healthcare Claims Data: Opportunities and Challenges. Pharmacoeconomics 37: 745–52. [Google Scholar] [CrossRef] [PubMed]
- van der Veer, Koen J. M. 2015. The Private Export Credit Insurance Effect on Trade. Journal of Risk and Insurance 82: 601–24. [Google Scholar] [CrossRef]
- van der Veer, Koen J. M. 2019. Loss Shocks and the Quantity and Price of Private Export Credit Insurance: Evidence from a Global Insurance Group. Journal of Risk and Insurance 86: 73–102. [Google Scholar] [CrossRef]
- Varian, Hal R. 2014. Big Data: New Tricks for Econometrics. Journal of Economic Perspectives 28: 3–28. [Google Scholar] [CrossRef]
- Verall, Richard J., Ola Hossjer, and Susanna Bjorkwall. 2012. Modelling Claims Run-off with Reversible Jump Markov Chain Monte Carlo Methods. ASTIN Bulletin 42: 35–58. [Google Scholar]
- Wanke, Peter, and Carlos P. Barros. 2016. Efficiency drivers in Brazilian insurance: A two-stage DEA meta frontier-data mining approach. Economic Modelling 53: 8–22. [Google Scholar] [CrossRef]
- Weerasinghe, K. P. M. L. P., and M. C. Wijegunasekara. 2016. A Comparative Study of Data Mining Algorithms in the Prediction of Auto Insurance Claims. European International Journal of Science and Technology 5: 47–54. Available online: https://www.eijst.org.uk/images/frontImages/gallery/Vol._5_No._1/6._47-54.pdf (accessed on 26 February 2020).
- Wüthrich, Mario V. 2018a. Machine learning in individual claims reserving. Scandinavian Actuarial Journal 6: 465–80. [Google Scholar] [CrossRef]
- Wüthrich, Mario V. 2018b. Neural networks applied to chain–ladder reserving. European Actuarial Journal 8: 407–36. [Google Scholar] [CrossRef]
| 1 | Krummaker ( 2020) provides an overview of export credit markets, governance and key forms of export credit insurance. |
| 2 | The MPR is based on several factors, including country risk classification, the time at risk, the buyer risk category and the percentage of risk retention ( OECD 2018). |
| 3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).