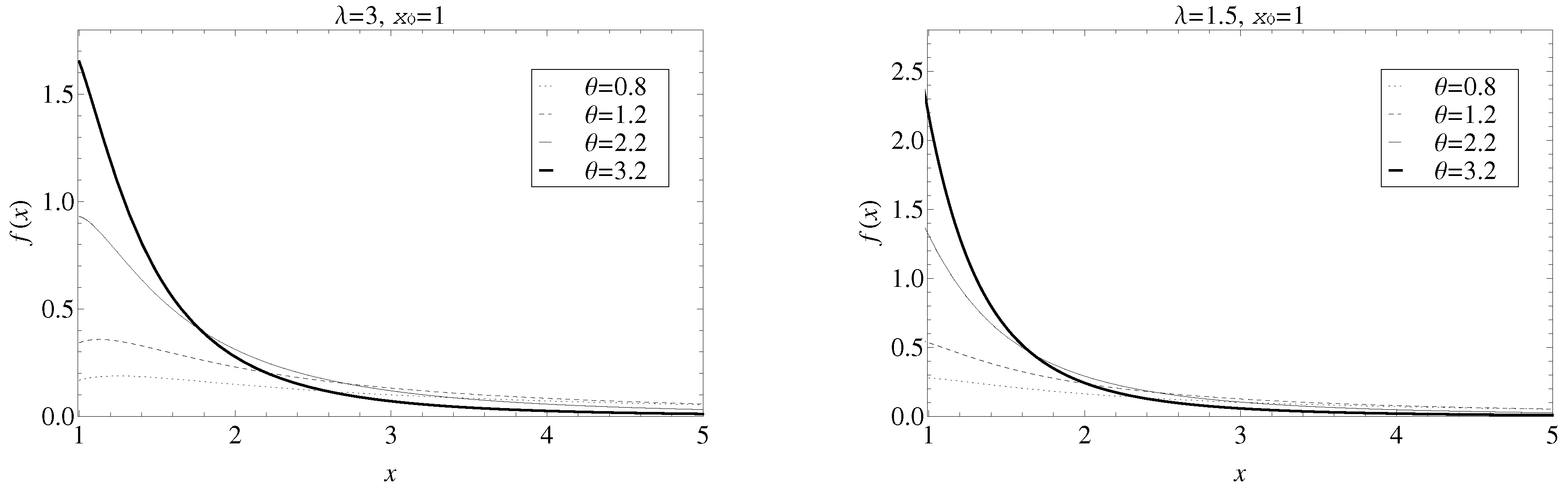1. Introduction
In general insurance, pricing is one of the most complex processes and is no easy task but a long-drawn exercise involving the crucial step of modeling past claim data. For modeling insurance claims data, finding a suitable distribution to unearth the information from the data is a crucial work to help the practitioners to calculate fair premiums. In actuarial statistics and finance, the classical Pareto distribution has been deemed better than other models because it provides a good description of the random behaviour of large claims. Loss data mostly have several characteristics such as unimodality, right skewness, and a thick right tail. To accommodate these features in a single model, many probability models have been proposed in the literature.
Over the last decades, different approaches to derive new classes of probability distributions that could provide more flexibility when modelling large losses has been added to the literature. This includes transformation method, the composition of two or more distributions, compounding of distributions or a finite mixture of distributions among other methodologies. In particular for generalizations of the classical Pareto distribution, the reader is referred to the Stoppa distribution (see
Stoppa 1990), the Pareto positive stable distribution (see
Sarabia and Prieto 2009), the Pareto ArcTan distribution (see
Gómez-Déniz and Calderín-Ojeda 2015) and the generalized Pareto distribution proposed in
Ghitany et al. (
2018). Obviously, adding a parameter to the parent model complicates the parameter estimation.
In this paper, a probabilistic family, the mixture Pareto-loggamma distribution, which belongs to the heavy-tailed class of probabilistic models is introduced. This family is derived by using of an exponential transformation of the generalized Lindley distribution. It is expressed as a convex sum of the classical Pareto and a special case of the loggamma distribution similar to the one presented in
Gómez-Déniz and Calderín-Ojeda (
2014). The former model is obtained as a particular case whereas the latter one is a limiting case. We further present expressions of statistical and actuarial measures such as moments, variance, cumulative distribution function, hazard rate function, VaR, TVaR and limited expected values. For many of these distributional characteristics, closed-form expressions are obtained. Estimation of the parameters of this distribution can be easily calculated by the maximum likelihood method by using the numerical search of the maximum and also by the method of log-moments.
In many instances, composite distributions give a reasonably good fit as compared to classical distributions since the former models have the advantage of accommodating both low magnitude values with a high frequency as well as large magnitude figures with low frequency.
Cooray and Ananda (
2005) introduced a composite lognormal-Pareto distribution with restricted mixing weights.
Scollnik (
2007) improved the composite lognormal-Pareto model by allowing flexible mixing weights.
Bakar et al. (
2015) considered several probabilistic models in place of lognormal and Pareto distribution using the approach discussed in
Scollnik (
2007). Recently,
Calderín-Ojeda and Kwok (
2016) introduced a new class of composite model using mode-matching procedure. They derived composite models using lognormal and Weibull distributions with a Stoppa model, a generalization of the Pareto distribution. As there exists a closed-form expression for the modal value of this new model, in this article, we use the mode-matching procedure to derive new composite models based on this distribution.
The structure of the paper is organized as follows. In
Section 2, we present the genesis of the new distribution, and discuss its relationship with other distributions. Besides, the most relevant distributional properties are studied in the same section. Also, different estimation methods are examined. Finally, composite models based on the proposed distribution are derived. Next, in
Section 3, some results related to insurance are displayed. Numerical applications are displayed in
Section 4 together with the derivation of some income indices. The last section concludes the paper.
2. The Distribution and Its Properties
It can be easily seen that the following expression
with
and
is a genuine probability density function (pdf). Here
are shape parameter and
is scale parameter (see the
Appendix A). Note that the pdf (
1) can be written as a convex sum of the classical Pareto distribution and a special case of the loggamma distribution. The former model is obtained when
and the latter one for
. Observe that the pdf of the loggamma distribution considered in this work is
with
and
. In our model it is assumed that
.
The cumulative distribution function (cdf), survival function (sf) and hazard rate function of a random variable (rv) with pdf (
1) are respectively given, for
, as
Henceforth, a continuous rv
X that follows (
1) will be called as mixture Pareto-loggamma distribution and denoted as
. The shape of the pdf given in (
1) is shown in
Figure 1 for different values of the parameters
and
and a fixed
. It is observable that the larger is the value of
, the thinner is the tail. On the contrary, the thickness of the tail decreases when
drops.
Undoubtedly, the single parameter Pareto distribution is one of the most attractive distributions in statistics; a power-law probability distribution found in a large number of real-world situations inside and outside the field of economics. Furthermore, it is usually used as a basis for Excess of Loss quotations as it gives a pretty good description of the random behavior of large losses. In this sense, many probability distributions can be used for modelling single loss amounts. Then, if the loss is assumed to follow the pdf (
1), we have that
defines the tail behavior of the distribution.
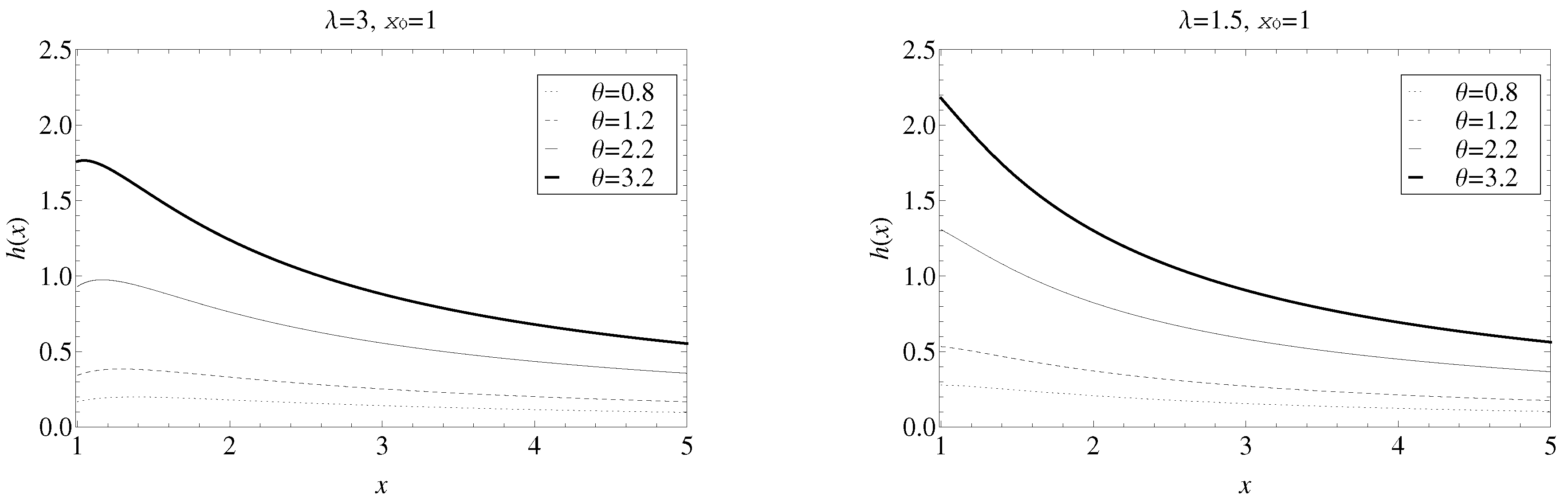
Below, the hazard rate function has been plotted in
Figure 2 for different values of the parameters
and
for fixed
. It is observable that the hazard rate function increases when the parameter
grows and the parameter
declines.
The next result shows the relationship between the and the Generalized Lindley distribution, which is extensively used in lifetime analysis and reliability.
Remark 1. Thedistribution can be also obtained by taking, where Y follows a generalized Lindley distribution with density From this result, it is straightforward to generate random variates from the
distribution by observing that the pdf given in (
5), can be rewritten as
where
,
is the pdf of the exponential distribution with mean
and
is the pdf of the Erlang distribution with shape parameter 2 and rate parameter
. Then, a random variate from the
distribution,
x, can be generated following a modification of the algorithm presented in
Ghitany et al. (
2008) as shown below.
Generate two random numbers and from the standard uniform distribution, .
Generate random variates from the exponential distribution with mean and from the Erlang distribution with shape parameter 2 and rate parameter by using .
If , then set ; otherwise, set .
Generate .
Observe that an analogous algorithm could be implemented by using the fact that (
1) is a convex sum of the densities of Pareto and loggamma distributions.
2.1. Moments and Log-Moments
The
rth raw moment of
is given by
In particular, we have that
Remark 1 can be used to obtain the
rth raw log-moment of the density (
1)
The moment estimator of
and
with known
can be simply derived from (
7).
2.2. Unimodality
The modal value of the
distribution can be found by taking the first derivative of the pdf (
1),
then, by setting (
8) equal to zero and solving for
x, the mode is
. If
, then the mode is at
.
2.3. Stochastic Ordering
Many parametric families of distributions can be ordered by some stochastic orders according to the value of their parameters. A rv
is said to be stochastically smaller
than
if
for all
x. The formal definition of stochastic ordering is
Definition 1. Letandbe continuous random variables with densitiesand, respectively, such thatis non-decreasing over the union of the supports ofand. Thenis said to be smaller thanin the likelihood ratio order.(see Section 1.C of Shaked and Shanthikumar (2007)). Similarly, a rv can be also ordered for stochastic (distribution function), hazard rate and mean excess orders when the following results hold:
- (i)
Stochastic order if for all x.
- (ii)
Hazard rate order if for all x.
- (iii)
Mean excess order
if
for all
x, where
is mean excess function given in expression (
17).
Using Theorem 1.C.1 and Theorem 2.A.1 of
Shaked and Shanthikumar (
2007), the above stochastic orders hold following implications result
This gives rise to Proposition 1.
Proposition 1. Letandbe two rv’s havingdistribution with parameters. Then following results hold
- i.
If,and, then,and.
- ii.
If,and, then,and.
2.4. Integrated Tail Distribution and Equilibrium Hazard Rate
As we have already seen previously, the proposed distribution can be viewed as a mixture of two thick-tailed distributions, the Pareto and loggamma models, thus it can be used to describe events that include heavy-tailed behaviour. In this particular, we define another distribution function called Integrated tail distribution (ITD) (also known as equilibrium distribution)
which often appears in insurance fields (see
Yang 2004). The ITD has many interesting applications, e.g., approximation of the ruin function (see
Yang 2004) or characterisation of the tail of the distribution (see
Su and Tang 2003) just to name a few. Hence, for
distribution bluewith
, ITD is obtained as
The associated equilibrium hazard rate
, for
is given by
Moreover, it can be easily verified that
. Hence by using Theorem 2.1 of
Su and Tang (
2003) we can conclude that
is a heavy-tailed distribution. Heavy-tailed distributions are important in non-life insurance when modeling losses related to motor third-party liability insurance, fire insurance or catastrophe insurance.
2.5. Estimation
Let be an independent and identically distributed (iid) random sample of size n drawn from a population which follows a distribution. Estimate of parameter can easily be obtained, as the support of the distribution is greater than . Therefore for known, we estimate the parameters and by (i) method of log-moments and (ii) maximum likelihood method.
2.5.1. Method of Log-Moments
The first and second log-moments of
distribution obtained by using (
7) are given by
and
. Solving these equations for
and
, we have that these estimates are provided by
2.5.2. Maximum Likelihood Estimation
The log-likelihood function given the iid random sample
of size
n is
and the normal equations obtained by differentiating (
12) with respect to
and
are
The above equations cannot be solved analytically and hence maximum likelihood estimates of
and
can be computed numerically using in-built
-function such as
,
or
. Moreover, in all these functions to initialize the program we use initial values obtained from the method of log-moments. The second partial derivative of log-likelihood function with respect to parameter
and
are
Furthermore,
substituting
, and using Tricomi confluent hypergeometric function
, we get
Hence, the expected Fisher’s information matrix associated to the parameters
and
is given by
with
where
The standard errors of the estimates and can be obtained by inverting the aforementioned matrix and taking the square root of the diagonal entries.
2.6. Composite Models
Composite parametric models are a useful way to describe data that combined loss data of small and moderate size with a high frequency and large observations with a low frequency. They consist of two distributions, the first model is used up to an unknown single threshold value, estimated from the data, and the second distribution beyond this threshold (see
Cooray and Ananda 2005). Another approach to derive composite models is utilizing a mode-matching procedure. In this technique, the two distributions are composed at the common modal value which can be estimated from the claims data. Thus, the composite model uses a truncated version of the first model up to the mode and the rest of the model is based on an appropriate truncation of the second distribution from that modal point onwards. The model after composition is similar in shape to either of the models considered but with a thicker tail. By using this methodology, it is guaranteed that the new density is continuous and smooth. These composite models give a significantly better fit as compared to the standard single models for the same empirical data. Here, we derived composite models of our
distribution with lognormal, Weibull and paralogistic distributions.
2.6.1. Composite Lognormal- Model
Let us consider, for
, the two-parameter lognormal distribution with pdf and cdf respectively given by
with
,
where
is the cdf of the standard normal distribution. Now by taking expressions (
1) and (
2) as the pdf,
, and cdf,
of the
distribution respectively with
and setting equal the modes of lognormal and
distributions we obtain
Note that we must impose the additional constraint
. Now, the unrestricted mixing weight is given by
Then, the pdf of the four-parameter composite lognormal-
distribution is given by
2.6.2. Composite Weibull- Model
Let
be the pdf and cdf of a two-parameter Weibull distribution with
and
. Let us again consider the pdf and cdf of the
distribution given by (
1) and (
2) respectively. By equating the modes of the two distributions, we have that
where the restriction
must be imposed to guarantee that the mode of the Weibull distribution is greater than 0. Now, the pdf of the four-parameter composite Weibull-
distribution is provided by
where the unrestricted mixing weight is given by
2.6.3. Composite Paralogistic- Model
Finally, let us assume that
are the pdf and cdf of the two-parameter paralogistic distribution with
α,
τ > 0, and
. Once again, we consider the pdf and cdf of the
model given by (
1) and (
2). By setting equal the modal values of the two distributions, we have that
where the restriction
is again established to ensure that the mode of the paralogistic distribution is larger than 0. The unrestricted mixing weight is now given by
The pdf of the four-parameter composite paralogistic-
distribution is provided by
3. Insurance Results
In the following, several theoretical results related to insurance for the distribution and related composite models are derived.
3.1. Mean Excess Function
The mean excess function measures the expected payment per claim on a policy with a fixed amount deductible of
x, ignoring the claims with amounts less than or equal to
x. It is defined as
which can also be obtained by inverting the equilibrium hazard rate (
Su and Tang 2003), hence for
the mean excess function for the model with pdf (
1) is given by
3.2. Excess of Loss Reinsurance
Let
X be a rv denoting the individual claim size taking values greater than
d. Let us also assume that
X follows (
1), and the expected cost per claim to the reinsurance layer when the loss in excess of
m subject to a maximum of
l is given by
Now by replacing
and
by expressions (
1) and (
3) and solving the integral, we have that
3.3. Value-at-Risk and Tail Value-at-Risk
In this subsection, we firstly discuss the most widely used risk measure, the Value-at-Risk (VaR). It is defined as the minimum value of the distribution such that the probability of the loss larger than this value does not exceed a given probability. In statistical terms, VaR is a quantile of a random variable and the formal definition is as follows.
Definition 2. Let X be a loss rv with a continuous cdf, and δ be a probability level such that, the Value-at-Risk at probability level δ, denoted by VaRδ(X), is the δ-quantile of X. That is Hence for rv having distribution the Value-at-Risk is given in next Proposition.
Proposition 2. For, the VaRδ(X) of thedistribution iswhereis the negative branch of Lambert-W function. The median of
will be obtained by taking
in VaR
δ(X). As in general, the loss distributions are typically skewed, the VaR is a non-coherent risk measure due to the lack of subadditivity (see
Klugman et al. 2012), for that reason, the Tail Value-at-Risk (TVaR) of
X (see
Acerbi and Tasche 2002) is usually considered as a more informative and more useful risk measure. The TVaR is given by
which is a coherent risk measure. If
X is continuous,
, and then the TVaR is the conditional tail expectation
.
Proposition 3. For, the TVaRδ(X) fordistribution is given bywhere. 3.4. Limited Loss Variable for Composite Models
Finally, in this subsection the kth moment of the limited loss variable for composite models based on the distribution is presented.
Definition 3. The kth incomplete moment transform of a rv X with cdfand pdf, given that, is a rv with pdf given byand cdf given by,.
Definition 4. The limited loss variable is defined as,where u is the maximum benefit paid by the insurance policy.
Proposition 4. The moment of order k of the limited loss variable for the composite models based on thedistribution is given byifandif. Proof. The
kth moment of the limited loss variable can be derived as,
If
,
and we get (
20). Now, if
,
and (
21) is obtained. □
Observe that in expressions (
20) and (
21),
and
denotes the
kth incomplete moment and the cdf of the
kth incomplete moment for lognormal, Weibull or paralogistic distributions (
) and
distribution (
).