Asymptotically Normal Estimators of the Ruin Probability for Lévy Insurance Surplus from Discrete Samples
Abstract
1. Introduction
1.1. Ruin Probability Under Lévy Surplus
1.2. Earlier Works on Estimating Ruin Probability
1.3. Statistical Setting and General Notation
- and and .
- For a matrix , . Moreover, ⊤ stands for the transpose .
- For each , is the zero vector in . Moreover, and are the -zero matrix and identity matrix, respectively.
- For functions f and g, means that there exists a constant such that for all x.
- For , .
- For and , stands for the Laplace transform operator
- For functions ,
- stands for the convolution of f and g:
- and .
- For a -integrable function ,In particular, as for , we write
- for .
- Denote by the tail function of the exponential distribution with mean : for andMoreover, is its density function: .
2. Some Representations for the Ruin Probability
2.1. The Laguerre Expansion of
2.2. Coefficients and
3. Statistical Inference
3.1. Estimating the Lévy Characteristics
- (i)
- There exists some such that .
- (ii)
- For each , .
- (iii)
- For each ,
3.2. Joint Convergence and Asymptotic Normality
4. Main Theorems
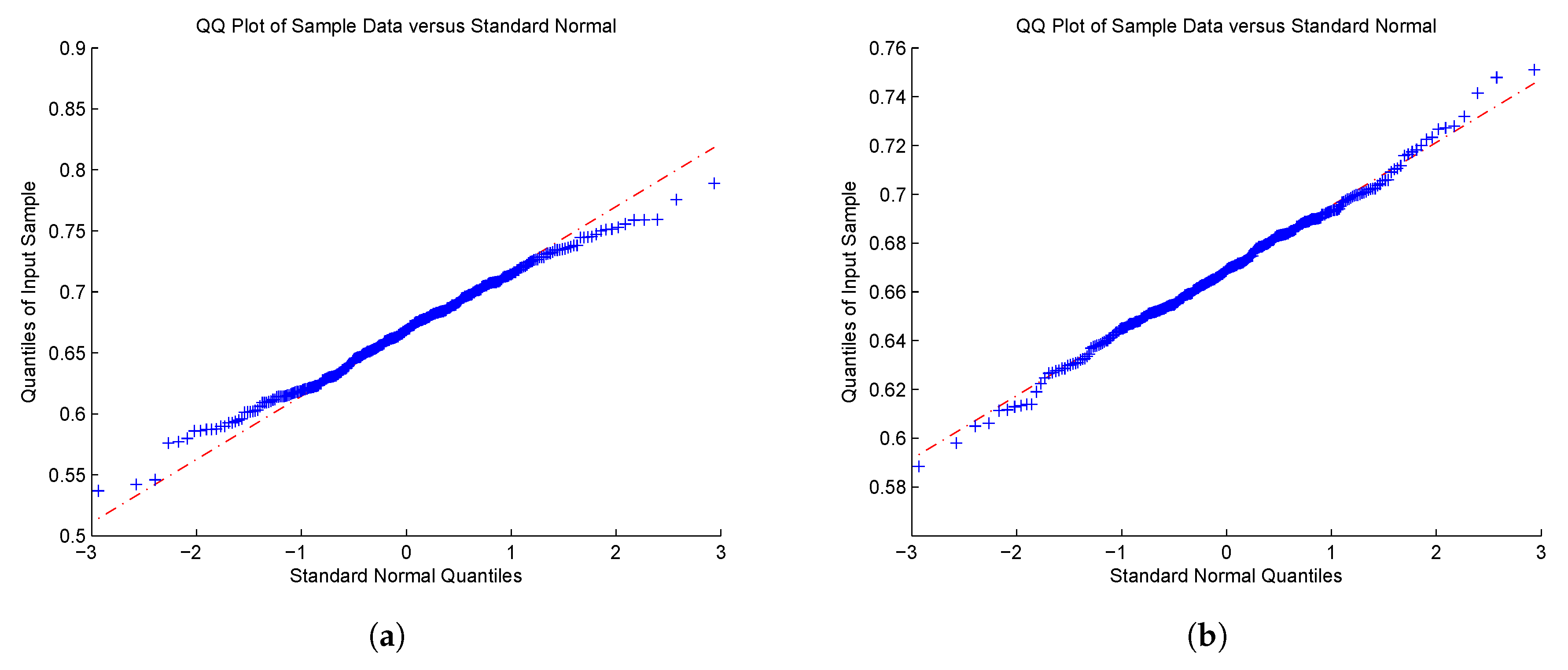
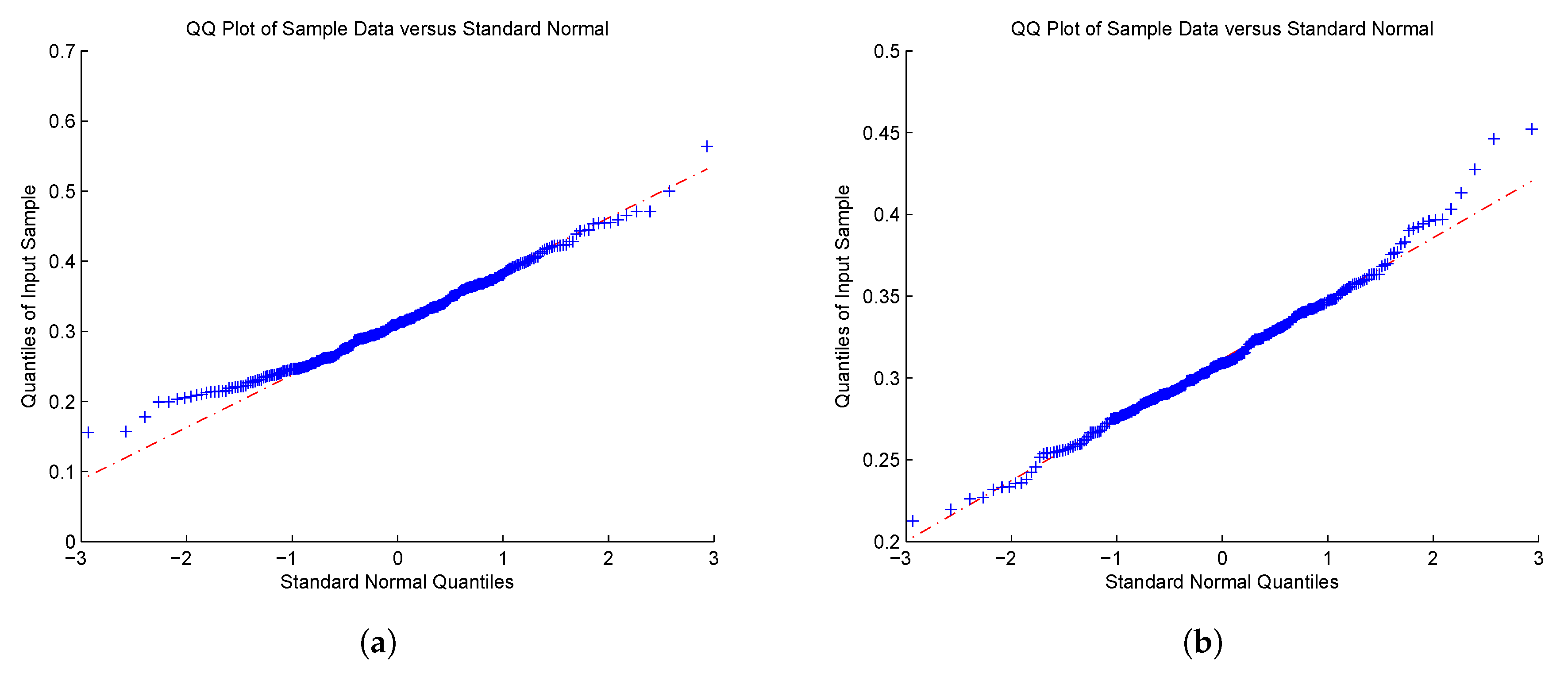
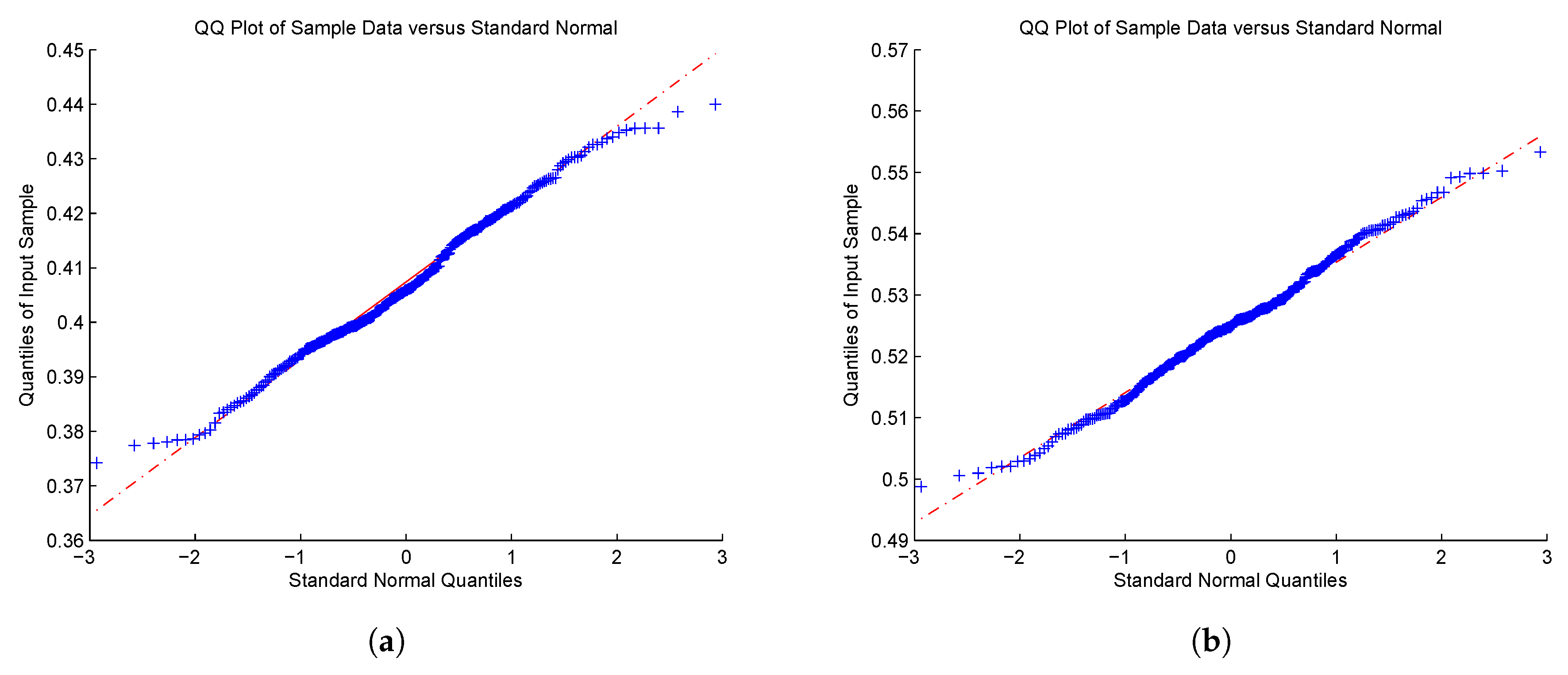
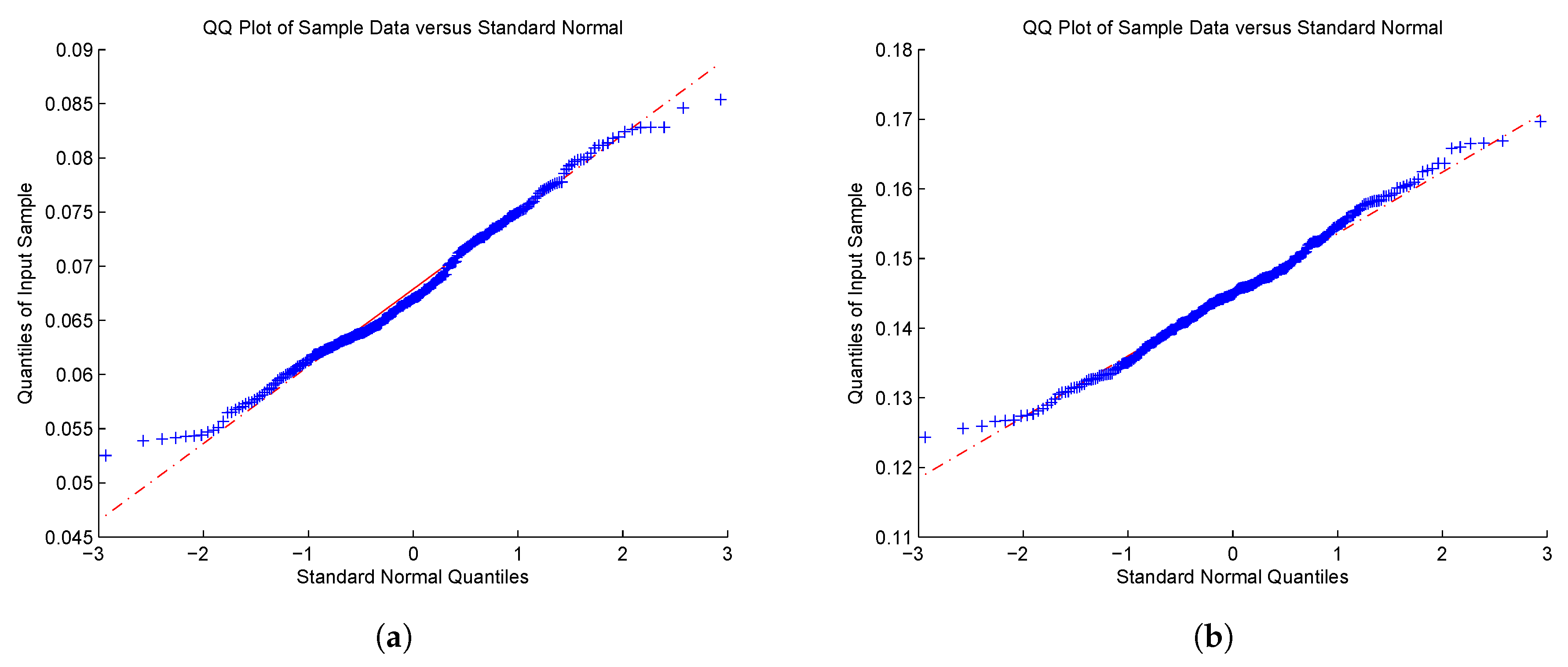
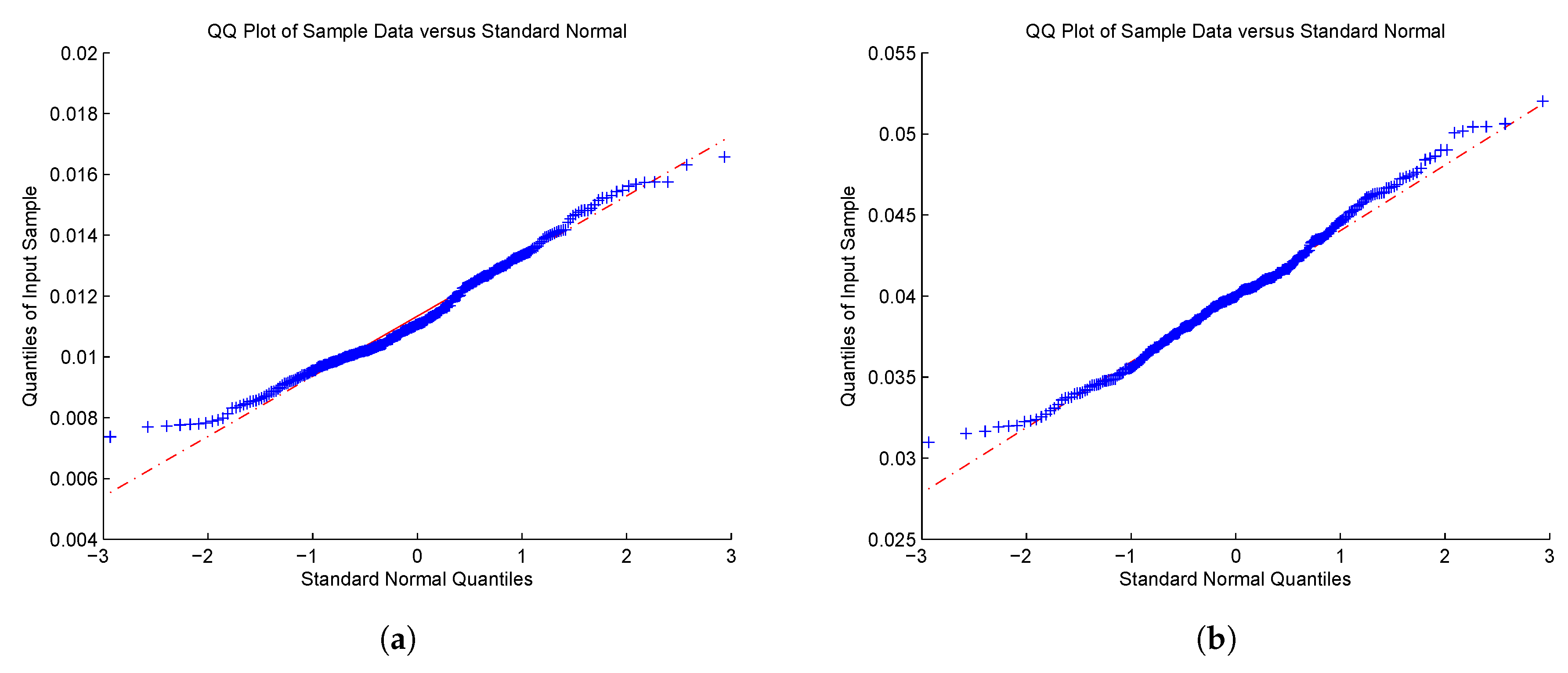
5. Simulations
- (CP)
- Compound Poisson model: forwhere N is a Poisson process with the intensity , and ’s are IID random variables with an exponential distribution with mean ; the Lévy density , and set . In the simulation, we suppose that , and are unknown. In this case, the ruin probability is explicitly known as
- (GS)
- Gamma subordinator model: forwhere L is a gamma process with the Lévy density with , and set . In the simulation, we suppose that and are unknown. In this model, the ruin probability is not explicit, but we can compute it numerically, e.g., via the Fast Fourier Transform; see, e.g., Zhang and Yang (2013).
6. Concluding Remarks
7. Preliminary Lemmas
Author Contributions
Funding
Conflicts of Interest
References
- Biffis, Enrico, and Manuel Morales. 2010. On a generalization of the Gerber-Shiu function to path dependent penalties. Insurance: Mathematics and Economics 46: 92–97. [Google Scholar] [CrossRef]
- Carroll, Raymond J., Arnoud C. M. Van Rooij, and Frits H. Ruymgaart. 1991. Theoretical aspects of ill-posed problems in statistics. Acta Applicandae Mathematica 24: 133–40. [Google Scholar] [CrossRef]
- Chauveau, D. El, A. C. M. Vanrooij, and F. H. Ruymgaart. 1994. Regularized inversion of noisy Laplace transforms. Advances in Applied Mathematics 15: 186–201. [Google Scholar] [CrossRef]
- Feng, Runhuan, and Yasutaka Shimizu. 2013. On a generalization from ruin to default in a Lévy insurance risk model. Methodology and Computing in Applied Probability 15: 773–802. [Google Scholar] [CrossRef]
- Huzak, Miljenko, Mihael Perman, Hrvoje Šikić, and Zoran Vondraček. 2004. Ruin probabilities and decompositions for general perturbed risk processes. The Annals of Applied Probability 14: 1378–97. [Google Scholar]
- Jacod, Jean. 2007. Asymptotic properties of power variations of Lévy processes. ESAIM: Probability and Statistics 11: 173–96. [Google Scholar] [CrossRef]
- Kyprianou, Andreas E. 2014. Fluctuations of Lévy Processes with Applications. Introductory Lectures, 2nd ed.Heidelberg: Springer. [Google Scholar]
- Lundberg, Fillip. 1903. Approximerad Framställning av Sannolikehetsfunktionen. Ph.D. Dissertation, Aterförsäkering av Kollektivrisker, Almqvist & Wiksell, Stockholm, Uppsala. [Google Scholar]
- Mnatsakanov, Robert, L. L. Ruymgaart, and Frits H. Ruymgaart. 2008. Nonparametric estimation of ruin probabilities given a random sample of claims. Mathematical Methods of Statistic 17: 35–43. [Google Scholar] [CrossRef]
- Schoutens, Wim, and Jessica Cariboni. 2009. Lévy Processes in Credit Risk. New York: John Wiley & Sons Ltd. [Google Scholar]
- Shimizu, Yasutaka. 2009. A new aspect of a risk process and its statistical inference. Insurance: Mathematics and Economics 44: 70–77. [Google Scholar] [CrossRef]
- Shimizu, Yasutaka. 2011. Estimation of the expected discounted penalty function for Lévy insurance risks. Mathematical Methods of Statistics 20: 125–49. [Google Scholar] [CrossRef]
- Shimizu, Yasutaka. 2012. Nonparametric estimation of the Gerber-Shiu function for the Wiener-Poisson risk model. Scandinavian Actuarial Journal 2012: 56–69. [Google Scholar] [CrossRef]
- Shimizu, Yasutaka, and Shuji Tanaka. 2018. Dynamic risk measures for stochastic asset processes from ruin theory. Annals of Actuarial Science 12: 249–68. [Google Scholar] [CrossRef]
- Shimizu, Yasutaka, and Zhimin Zhang. 2017. Estimating Gerber-Shiu functions from discretely observed Lévy driven surplus. Insurance: Mathematics and Economics 74: 84–98. [Google Scholar] [CrossRef]
- Trufin, Julien, Hansjoerg Albrecher, and Michel M. Denuit. 2011. Properties of a risk measure derived from ruin theory. The Geneva Risk and Insurance Review 36: 174–88. [Google Scholar] [CrossRef]
- Zhang, Zhimin. 2016. Estimating the Gerber-Shiu function by Fourier-Sinc series expansion. Scandinavian Actuarial Journal 2017: 898–919. [Google Scholar] [CrossRef]
- Zhang, Zhimin, and Wen Su. 2017. A new efficient method for estimating the Gerber-Shiu function in the classical risk model. Scandinavian Actuarial Journal 5: 426–49. [Google Scholar] [CrossRef]
- Zhang, Zhimin, and Hailiang Yang. 2013. Nonparametric estimate of the ruin probability in a pure-jump Lévy risk model. Insurance: Mathematics and Economics 53: 24–35. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, Y.; Zhang, Z. Asymptotically Normal Estimators of the Ruin Probability for Lévy Insurance Surplus from Discrete Samples. Risks 2019, 7, 37. https://doi.org/10.3390/risks7020037
Shimizu Y, Zhang Z. Asymptotically Normal Estimators of the Ruin Probability for Lévy Insurance Surplus from Discrete Samples. Risks. 2019; 7(2):37. https://doi.org/10.3390/risks7020037
Chicago/Turabian StyleShimizu, Yasutaka, and Zhimin Zhang. 2019. "Asymptotically Normal Estimators of the Ruin Probability for Lévy Insurance Surplus from Discrete Samples" Risks 7, no. 2: 37. https://doi.org/10.3390/risks7020037
APA StyleShimizu, Y., & Zhang, Z. (2019). Asymptotically Normal Estimators of the Ruin Probability for Lévy Insurance Surplus from Discrete Samples. Risks, 7(2), 37. https://doi.org/10.3390/risks7020037



