Simple Formulas for Pricing and Hedging European Options in the Finite Moment Log-Stable Model
Abstract
:1. Introduction
2. Lévy-Stable Option Pricing
2.1. Model Definition
2.2. Stable Distributions
- −
- If , then decays exponentially on the positive real axis and has a heavy tail on the negative real axis (that is, decays in );
- −
2.3. Mellin-Barnes Representation of the European Option
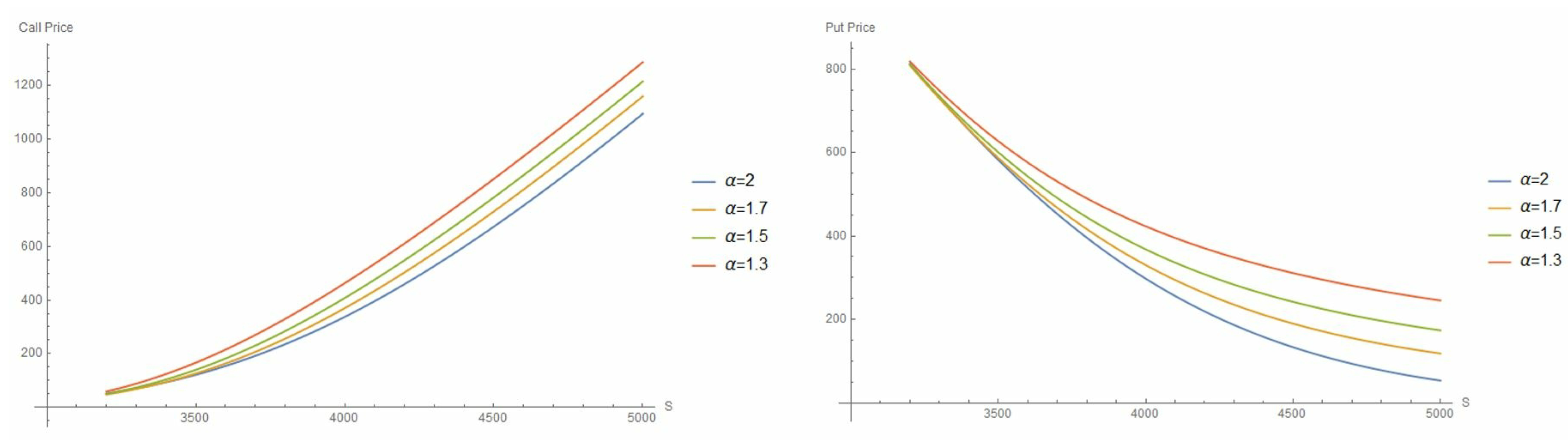
2.4. Pricing Formulas
3. Risk Sensitivities (Greeks)
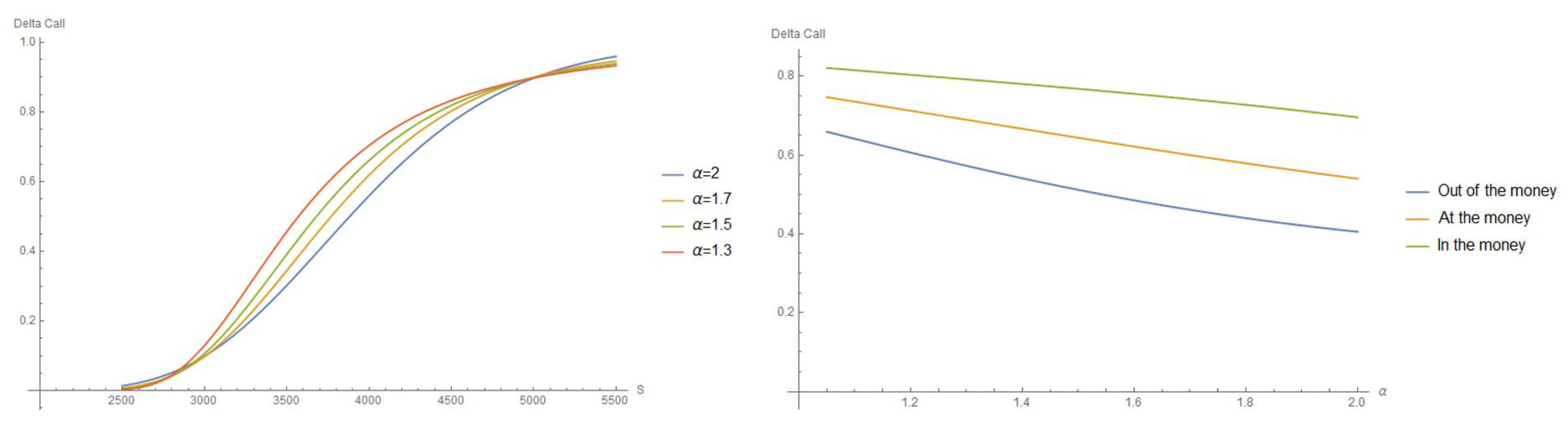
3.1. Delta
- In left figure, we plot the value of in function of the market price, for different cases of ; in all cases, for all S, and admits an inflection in the “out-of-the-money” region (). However, we can observe that in this region, grows faster when decays, and the inflection occurs for smaller market prices.
- In the right figure, we choose 3 different values of S corresponding to the in, at or out-of-the-money situation and we plot the evolution of in function of . We can observe that is in all cases a decreasing function of (as could be expected from the overall factor in (25)) meaning that when becomes smaller, then the options become more sensitive to variations of the underlying price than in the Gaussian () case. This stronger sensitivity can be regarded as a conservative feature of the FMLS model (similar features have also been observed in Robinson (2015)).
3.2. Gamma
3.3. Theta
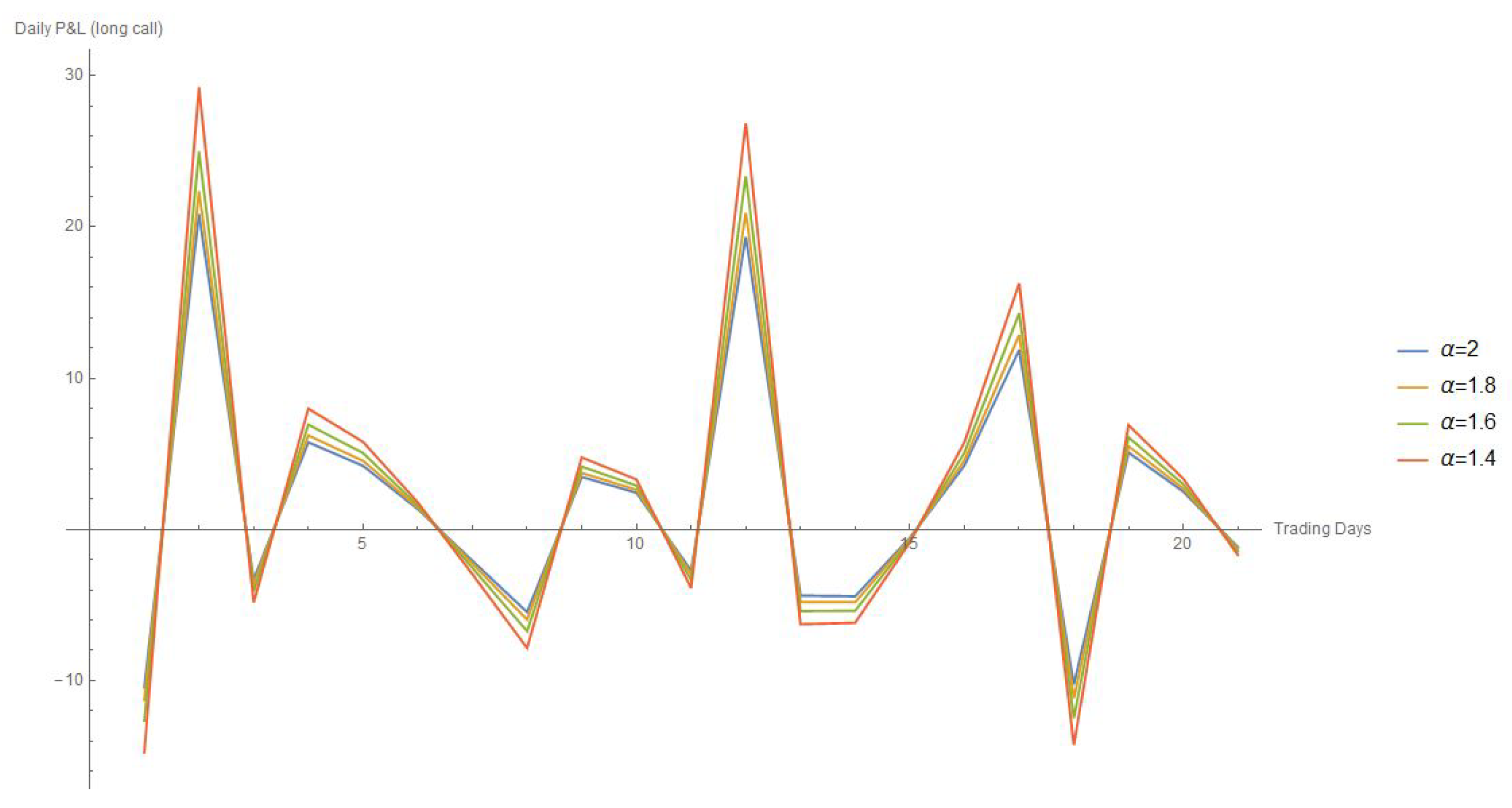
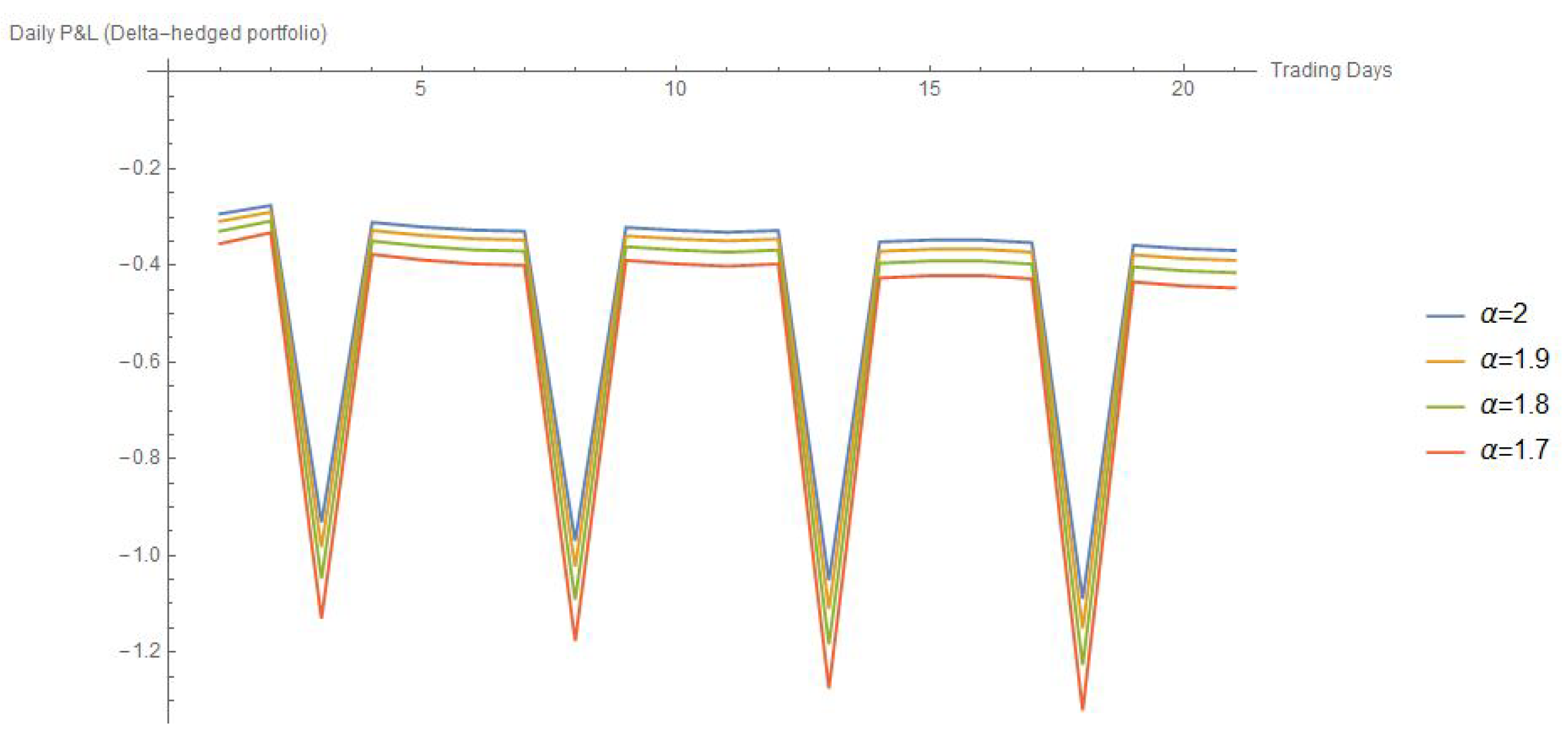
4. Expected P&L
4.1. Long-Call Position
4.2. Delta-Hedged Portfolio
4.3. Gamma-Hedged Portfolio (Synthetic Future)
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abramowitz, Milton, and Irene A. Stegun. 1972. Handbook of Mathematical Functions. Mineola: Dover Publications, USA. [Google Scholar]
- Acharya, Viral V., and Matthew Richardson. 2009. Causes of the financial crisis. Critical Review 21: 195–210. [Google Scholar] [CrossRef]
- Aguilar, Jean-Philippe, Cyril G. Coste, and Jan Korbel. 2017. Non-Gaussian analytic option pricing: A closed formula for the Lévy-stable model. arXiv. [Google Scholar]
- Aguilar, Jean-Philippe, Cyril Coste, and Jan Korbel. 2018. Series representation of the pricing formula for the European option driven by space-time fractional diffusion. Fractional Calculus and Applied Analysis 21: 981–1004. [Google Scholar] [CrossRef]
- Aguilar, Jean-Philippe, and Jan Korbel. 2018. Option pricing models driven by the space-time fractional diffusion: Series representation and applications. Fractal and Fractional 2: 15. [Google Scholar] [CrossRef]
- Bateman, Harry. 1954. Tables of Integral Transforms (vol. I & II). New-York City: McGraw & Hill. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The Pricing of Options and Corporate Liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Brenner, Menachem, and Marti G. Subrahmanyam. 1994. A simple approach to option valuation and hedging in the Black-Scholes Model. Financial Analysts Journal 50: 25–28. [Google Scholar] [CrossRef]
- Calvet, Laurent, and Adlai Fisher. 2008. Multifractal Volatility: Theory, Forecasting, and Pricing. Cambridge: Academic Press. [Google Scholar]
- Carr, Peter, and Liuren Wu. 2003. The Finite Moment Log Stable Process and Option Pricing. The Journal of Finance 58: 753–78. [Google Scholar] [CrossRef]
- Cont, Rama, and Peter Tankov. 2004. Financial Modelling With Jump Processes. New-York City: Chapman & Hall. [Google Scholar]
- Duan, Jin-Chuan, Ivilina Popova, and Peter Ritchken. 2002. Option pricing under regime switching. Quantitative Finance 2: 116–32. [Google Scholar] [CrossRef]
- Flajolet, Philippe, Xavier Gourdon, and Philippe Dumas. 1995. Mellin transform and asymptotics: Harmonic sums. Theoretical Computer Science 144: 3–58. [Google Scholar] [CrossRef]
- Gerber, Hans U., and Elias S. W. Shiu. 1994. Option Pricing by Esscher Transforms. Transactions of the Society of Actuaries 46: 99–191. [Google Scholar]
- Heston, Steven L. 1993. A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. The Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Kleinert, H., and Jan Korbel. 2016. Option pricing beyond Black–Scholes based on double-fractional diffusion. Physica A 449: 200–14. [Google Scholar] [CrossRef]
- Korbel, Jan, and Yuri Luchko. 2016. Modeling of financial processes with a space-time fractional diffusion equation of varying order. Fractional Calculus and Applied Analysis 19: 1414–33. [Google Scholar] [CrossRef]
- Mainardi, Francesco, Yuri Luchko, and Gianni Pagnini. 2001. The fundamental solution of the space-time fractional diffusion equation. Fractional Calculus and Applied Analysis 4: 153–92. [Google Scholar]
- McCulloch, J. Huston. 1996. Financial applications of stable distributions. In Statistical Methods in Finance. Amsterdam: North-Holland, pp. 393–425. [Google Scholar]
- Necula, Ciprian. 2008. Option Pricing in a Fractional Brownian Motion Environment. Advances in Economic and Financial Research. DOFIN Working Paper Series 2; Bucharest, Romania: Bucharest University of Economics, Center for Advanced Research in Finance and Banking—CARFIB. [Google Scholar]
- Podlubny, Igor. 1998. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Amsterdam: Elsevier, vol. 198. [Google Scholar]
- Robinson, Geoffrey K. 2015. Practical computing for finite moment log-stable distributions to model financial risk. Statistic and Computing 25: 1233–46. [Google Scholar] [CrossRef]
- Samorodnitsky, Gennady, and Murad S. Taqqu. 1994. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance. New-York City: Chapman & Hall. [Google Scholar]
- Sun, Lin. 2013. Pricing currency options in the mixed fractional Brownian motion. Physica A 392: 3441–58. [Google Scholar] [CrossRef]
- Zolotarev, Vladimir M. 1986. One-Dimensional Stable Distributions. Providence: American Mathematical Society. [Google Scholar]
- Zhang, Jin E., and Yi Xiang. 2008. The implied volatility smirk. Quantitative Finance 8: 263–84. [Google Scholar] [CrossRef]

| n /m | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 0 | 395.167 | 49.052 | 4.962 | 0.431 | 0.033 | 0.002 | 0.000 |
| 1 | −190.223 | −32.268 | −4.005 | −0.405 | −0.035 | −0.003 | −0.000 |
| 2 | 23.829 | 7.767 | 1.317 | 0.164 | 0.017 | 0.001 | 0.000 |
| 3 | 1.430 | −0.649 | −0.211 | −0.036 | −0.004 | −0.000 | −0.000 |
| 4 | −0.246 | −0.029 | 0.013 | 0.001 | 0.000 | 0.000 | 0.000 |
| 5 | −0.046 | 0.004 | 0.000 | −0.000 | −0.000 | −0.000 | −0.000 |
| 6 | 0.001 | 0.000 | −0.000 | −0.000 | 0.000 | 0.000 | 0.000 |
| 7 | 0.001 | −0.000 | −0.000 | 0.000 | 0.000 | −0.000 | −0.000 |
| 8 | 0.000 | −0.000 | 0.000 | 0.000 | −0.000 | −0.000 | 0.000 |
| Call | 229.914 | 253.790 | 255.866 | 256.024 | 256.035 | 256.035 | 256.035 |
| n /m | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0.613034 | 0.103991 | 0.0129082 | 0.001306 | 0.000113 | 8.8 × |
| 1 | −0.153590 | −0.050059 | −0.008492 | −0.001054 | −0.000107 | −9.3 × |
| 2 | −0.013825 | 0.006271 | 0.002044 | 0.000347 | 0.000043 | 4.4 × |
| 3 | 0.003174 | 0.000376 | −0.000171 | −0.000056 | −9.4 × | −1.2 × |
| 4 | 0.000743 | −0.000065 | −7.6 × | 3.5 × | 1.1 × | 1.9 × |
| 5 | −0.000026 | −0.000012 | 1.1 × | 1.2 × | −5.7 × | −1.9 × |
| 6 | −0.000023 | 3.5 × | 1.7 × | −1.4 × | −1.7 × | 7.7 × |
| 7 | −1.3 × | 2.7 × | −4.1 × | −1.9 × | 1.7 × | 2.0 × |
| Delta | 0.449486 | 0.509990 | 0.516273 | 0.516819 | 0.516861 | 0.516864 |
| Long-Call Position | ||||
|---|---|---|---|---|
| Stability | Total Expected P&L | Time Effect | Spot Price Effect | Gamma Effect |
| = 2 (Black-Scholes) | 36.2548 | −9.6994 | 45.9514 | 0.0027 |
| = 1.8 | 38.6730 | −10.9094 | 49.5790 | 0.0034 |
| = 1.6 | 42.5902 | −12.8088 | 55.3948 | 0.0042 |
| = 1.4 | 48.4861 | −15.6892 | 64.1705 | 0.0049 |
| Long Put Position | ||||
| Stability | Total Expected P&L | Time Effect | Spot Price Effect | Gamma Effect |
| = 2 (Black-Scholes) | −127.1943 | −6.8985 | −120.2986 | 0.0027 |
| = 1.8 | −124.7761 | −8.1085 | −116.6710 | 0.0034 |
| = 1.6 | −120.8589 | −10.0079 | −110.8552 | 0.0042 |
| = 1.4 | −114.9630 | −12.8883 | −102.0795 | 0.0049 |
| Delta-Hedged Portfolio | ||||
| Stability | Total Expected P&L | Time Effect | Spot Price Effect | Gamma Effect |
| = 2 (Black-Scholes) | −9.6966 | −9.6994 | - | 0.0027 |
| = 1.8 | −10.9060 | −10.9094 | - | 0.0034 |
| = 1.6 | −12.8045 | −12.8088 | - | 0.0042 |
| = 1.4 | −15.6843 | −15.6892 | - | 0.0049 |
| Gamma-Hedged Portfolio | ||||
| Stability | Total Expected P&L | Time Effect | Spot Price Effect | Gamma Effect |
| All | 163.449 | −2.8009 | 166.25 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, J.-P.; Korbel, J. Simple Formulas for Pricing and Hedging European Options in the Finite Moment Log-Stable Model. Risks 2019, 7, 36. https://doi.org/10.3390/risks7020036
Aguilar J-P, Korbel J. Simple Formulas for Pricing and Hedging European Options in the Finite Moment Log-Stable Model. Risks. 2019; 7(2):36. https://doi.org/10.3390/risks7020036
Chicago/Turabian StyleAguilar, Jean-Philippe, and Jan Korbel. 2019. "Simple Formulas for Pricing and Hedging European Options in the Finite Moment Log-Stable Model" Risks 7, no. 2: 36. https://doi.org/10.3390/risks7020036
APA StyleAguilar, J.-P., & Korbel, J. (2019). Simple Formulas for Pricing and Hedging European Options in the Finite Moment Log-Stable Model. Risks, 7(2), 36. https://doi.org/10.3390/risks7020036






