Efficient Retirement Portfolios: Using Life Insurance to Meet Income and Bequest Goals in Retirement

Abstract

Life Insurance Retirement Plans (LIRPs) offer tax-deferred cash value accumulation, tax-free withdrawals (if properly structured), and a tax-free death benefit to beneficiaries. Thus, LIRPs share many of the tax advantages of other retirement savings vehicles but with less restrictive limitations on income and contributions. Opinions are mixed about the effectiveness of LIRPs; some financial advisers recommend them enthusiastically, while others are more skeptical. In this paper, we examine the potential of LIRPs to meet both income and bequest needs in retirement. We contrast retirement portfolios that include a LIRP with those that include only investment products with no life insurance. We consider different issue ages, face amounts, and withdrawal patterns. We simulate market scenarios and we demonstrate that portfolios that include LIRPs yield higher legacy potential and smaller income risk than those that exclude it. Thus, we conclude that the inclusion of a LIRP can improve financial outcomes in retirement.

1. Introduction

Retirees face significant financial risk and competing financial objectives. Pfau (2014) summarizes them as lifestyle, longevity, legacy, and liquidity. In retirement, individuals need steady income to fund their day-to-day expenses (lifestyle), they face the risk of outliving their retirement savings (longevity), they may wish to leave a bequest to heirs (legacy), and they must have reserves for healthcare costs or other unforeseen expenses (liquidity). They must construct and manage their portfolios to address both their need for secure lifetime income and wealth accumulation.

In the United States, employer-sponsored retirement plans fall broadly into two categories: Defined Benefit (DB) and Defined Contribution (DC). For both types of plans, employers and employees make contributions to fund future benefits. In a DB plan, the employee’s retirement benefit is calculated on the basis of factors such as age, length of service, final average salary, etc. The retirement benefits may be paid as a life annuity; thus, they offer retirees the prospect of a secure lifetime income. The employer manages the investment fund and assumes all investment and longevity risks. In a DC plan, the participants choose among a set of investment options according to their time horizon and risk tolerance. They contribute to their retirement account and, upon retirement, they must manage their nest egg to fund their retirement. Because of the upside potential of equities markets, DC plans offer the potential for significant wealth accumulation. However, the plan participant bears all of the investment and longevity risk and thus might have insufficient income in retirement or might outlive their savings.

The shift from DB retirement plans, under which retirees can receive guaranteed income for life, toward DC plans is well documented (EBRI 2016). A prudent investor should add longevity-protected vehicles such as life annuities and life insurance to manage longevity risk and to protect against downside market risk.

There is considerable literature on using life annuities to manage income risk (see Chen and Milevsky (2003), Milevsky et al. (2006), and the references contained therein). In a different vein, Bayraktar et al. (2014, 2015) and Bayraktar and Young (2016) used stochastic optimal control to determine strategies to maximize the probability of reaching a bequest goal.

Pfau (2014) considered combinations of investment portfolios, annuities, and life insurance and examined their performance relative to income and legacy wealth. The annuity, along with withdrawals from the investment fund, provided income, and the life insurance provided bequest.

In this paper, we examine the potential of life insurance to meet both income and bequest needs in retirement. In particular, we examine the effectiveness of Life Insurance Retirement Plans (LIRPs) in a retirement portfolio.

LIRPs and Other Retirement Savings Vehicles

In the United States, there are several different mechanisms through which investors can save for retirement while enjoying certain tax advantages. In this section, we will briefly discuss some of these vehicles, including 401(k) and related plans, Individual Retirement Accounts (IRAs), and Roth IRAs, and we will contrast them with LIRPs.

A 401(k) plan is a tax-qualified, employer-sponsored DC plan as defined in subsection 401(k) of the United States Internal Revenue Code. Employees contribute a portion of their paycheck to their 401(k) plan. Often, employers provide a proportional match of the employee’s contribution. Often, employees can choose how to invest their retirement funds from among a menu of investment options offered by the employer. The contributions and investment earnings are tax-deferred; investors do not incur income tax liability until they begin withdrawing funds in retirement, presumably when they are in a lower tax bracket. Nonprofit and governmental employers may offer 403(b) and 457(b) plans, respectively, which share many of the features of 401(k) plans.

An IRA is a self-directed, not an employer-sponsored, retirement savings plan. Contributions to an IRA are tax-deductible, and the investment earnings are tax-deferred. As with a 401(k) plan, individuals only pay taxes when they withdraw the funds at retirement. A Roth IRA is also a self-directed retirement savings plan. Unlike traditional IRAs, contributions are taxable as income; however, the investment earnings and withdrawals are tax-free—not tax-deferred—subject to certain conditions.

The 401(k) plans, IRAs, and Roth IRAs are subject to various income and contribution limits and early withdrawal penalties. A concise overview of traditional and Roth IRAs is given in Spors (2018). We refer the reader to McGill et al. (2010) and Allen et al. (2014) for more detailed information.

Under a LIRP, investors contribute premiums to fund a cash value life insurance policy. Generally speaking, the strategy is to overfund the policy, that is, to pay a large amount of premium for a low face-amount policy. Careful planning is important. If the policy is too overfunded, it will be classified as a Modified Endowment Contract, or MEC, instead of as life insurance for the purposes of taxation. Policyholders can meet their income needs via withdrawals and policy loans. Contributions are not tax-deductible; however, the cash value accumulation is tax-deferred, and withdrawals are tax-free. Moreover, beneficiaries receive a tax-free death benefit upon the death of the policyholder. Thus, a properly structured LIRP (one that is not classified as a MEC) offers tax-deferred cash value accumulation, tax-free withdrawals, and a tax-free death benefit to beneficiaries. In other words, LIRPs share many of the tax advantages of a Roth IRA. More significantly, the limits on income, contributions, and withdrawals are considerably less restrictive than for Roth IRAs (again, subject to MEC limits).

Opinions are mixed about the effectiveness of LIRPs. Ikokwu (2013) enthusiastically recommends LIRPs, describing them as a “turbo charged Roth IRA without the limitations.” McKnight (2012) points out that if a LIRP is properly structured, the cost can be lower than the annual expenses in a typical 401(k). Moreover, LIRPs can insulate investors from rising tax rates, and some insurance companies allow policyholders to access death benefit proceeds to pay for long-term care. Bloink and Byrnes (2011) are more skeptical. They point out that if investors are not savvy, the policy could become classified as a MEC, which would eliminate the tax advantages on policy loans. Moreover, if the policy lapses with outstanding loans, the amount of the loan is taxable. In addition, they point to surrender fees, the cost of insurance, and other charges. They conclude LIRPs offer the greatest benefit and fewer drawbacks for high-net-worth investors who have already maximized other tax-advantaged retirement savings plans.

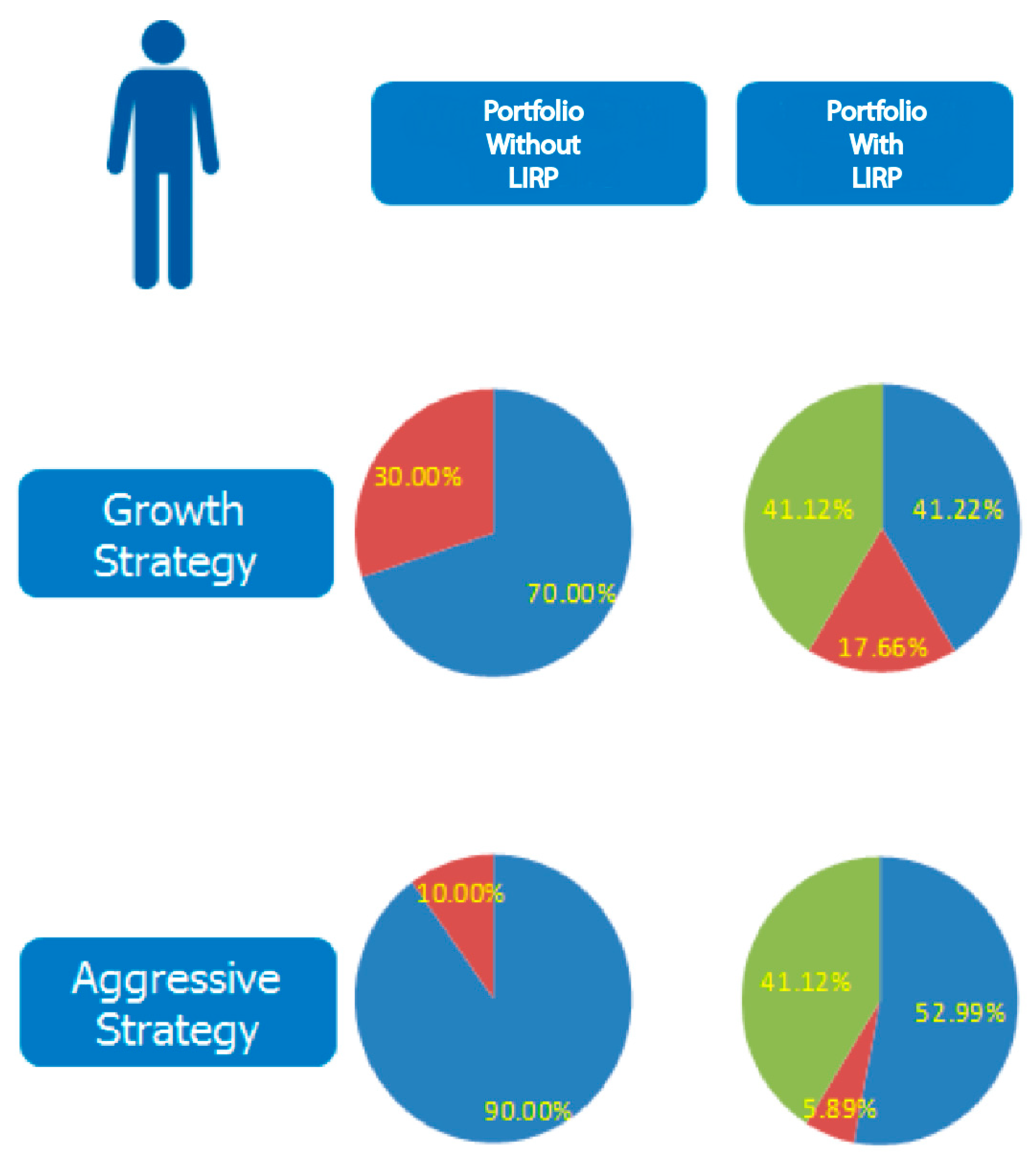
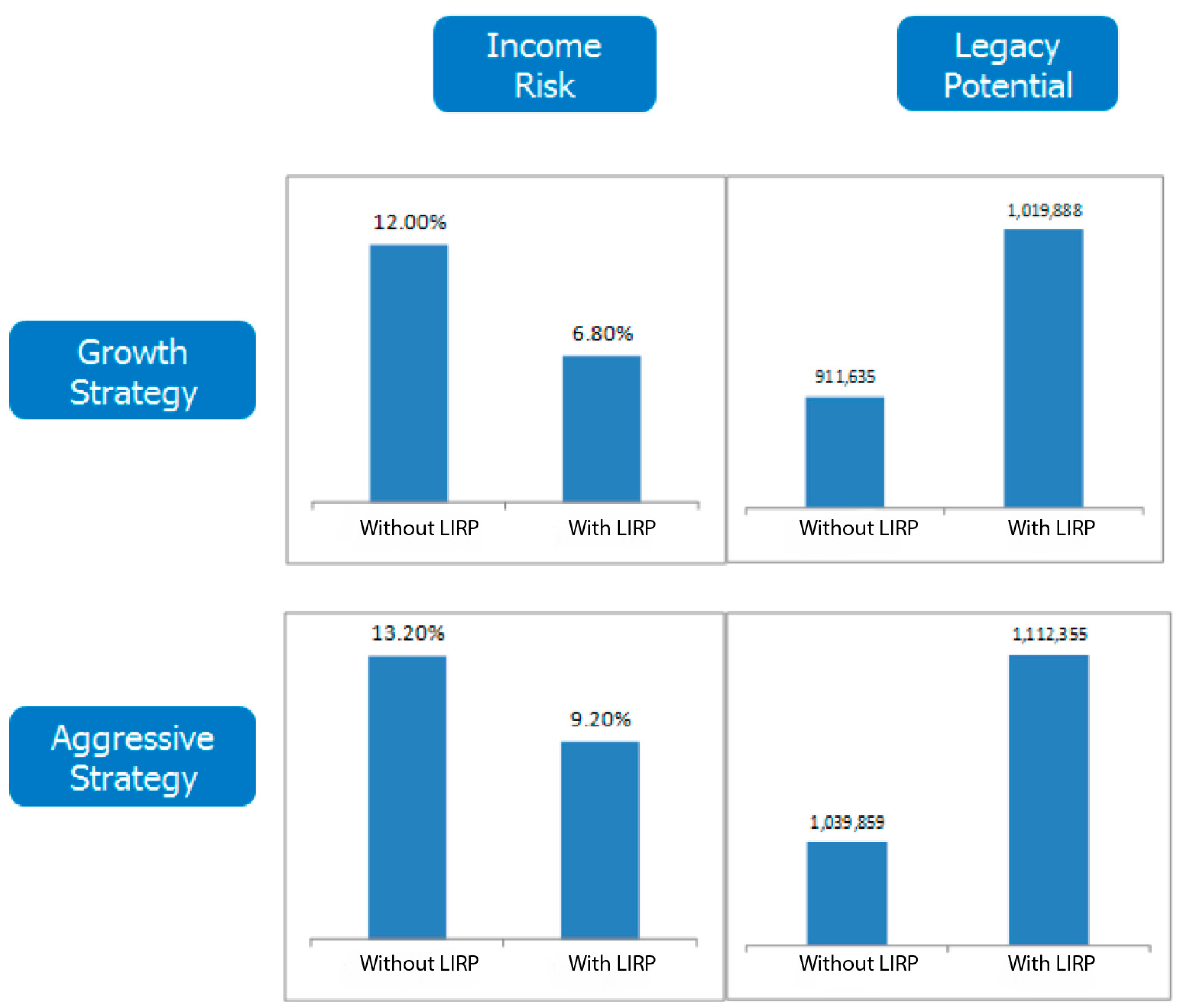
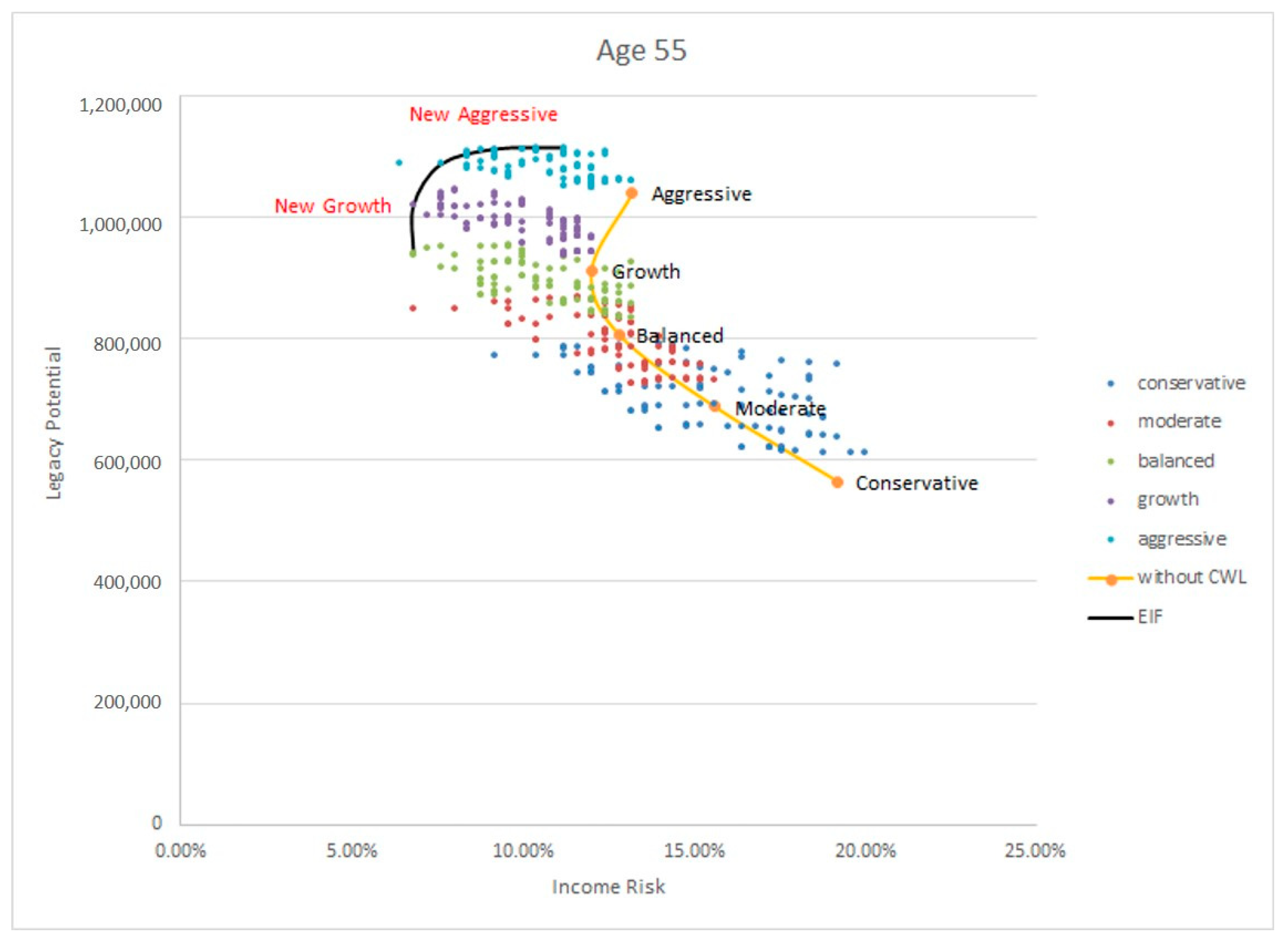
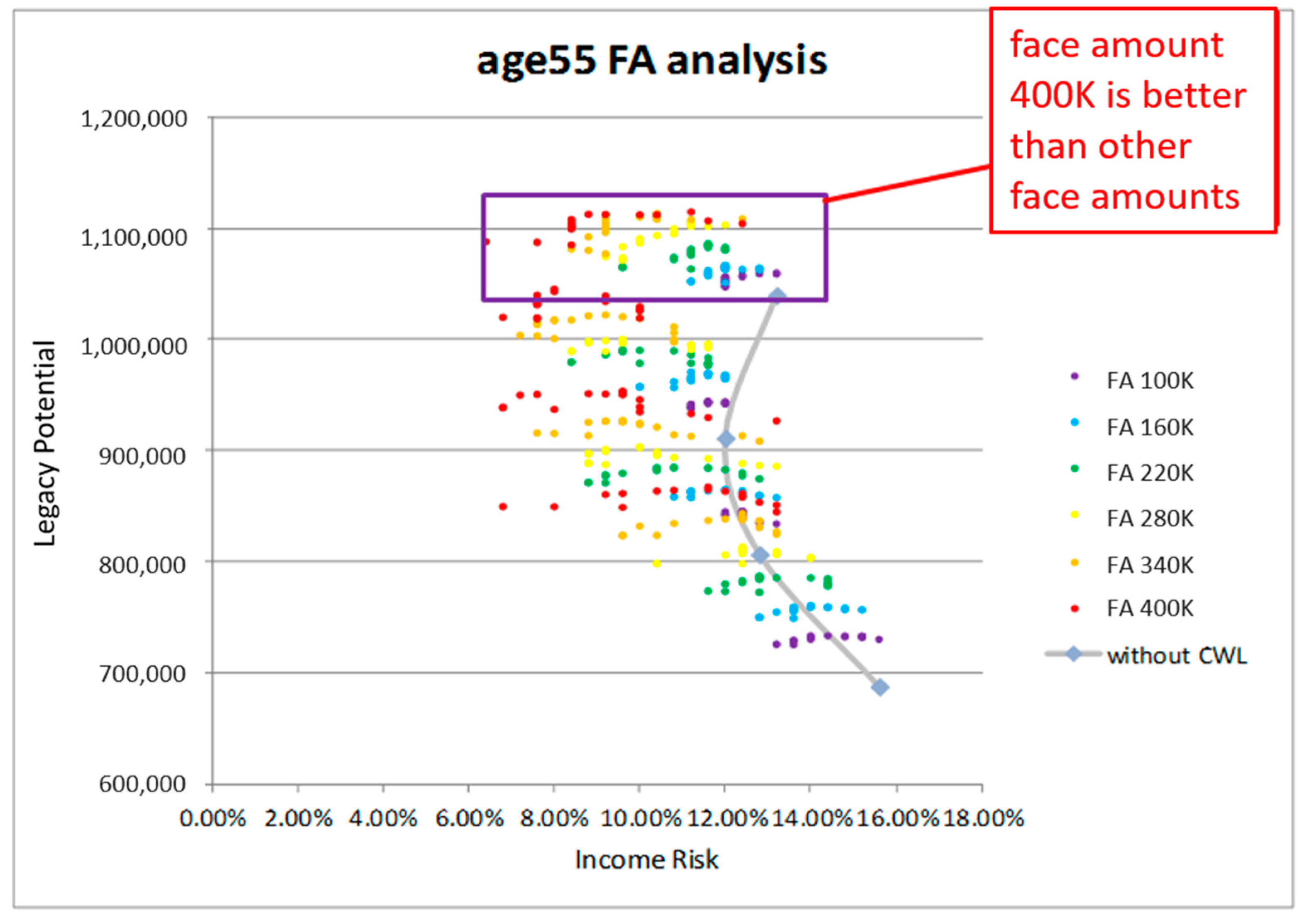
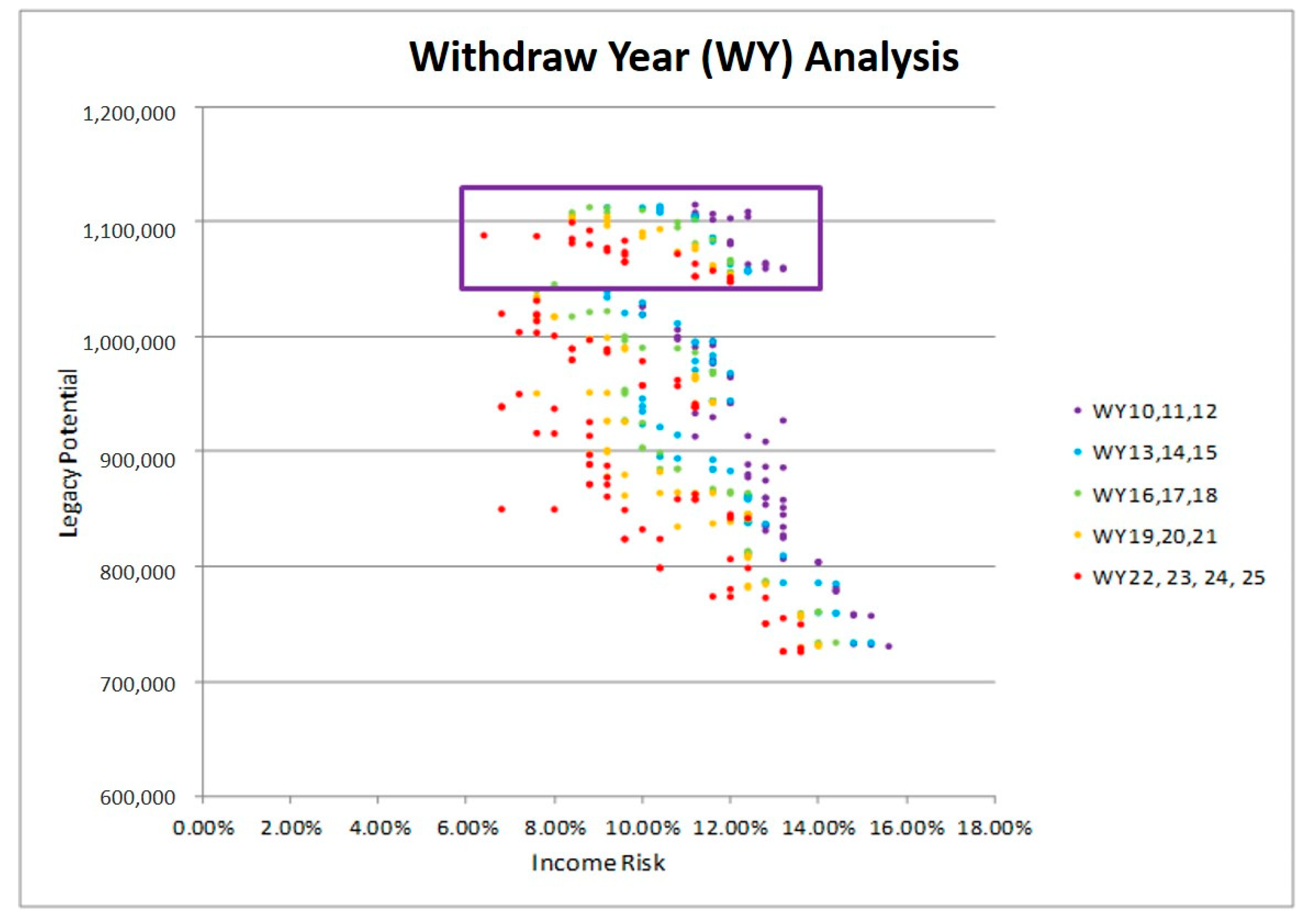
In this paper, we contrast retirement portfolios that include a LIRP with those that include only investment products with no life insurance. In other words, we contrast strategies that include, say, a mutual fund only with those that include both a mutual fund and a LIRP. We consider different issue ages, face amounts, and withdrawal patterns. We simulate market scenarios and, using the Efficient Income Frontier (EIF) of Milevsky (2008) and Pfau (2013), we demonstrate that portfolios that include LIRPs yield higher legacy potential and smaller income risk than those that exclude it. Thus, we conclude that the inclusion of a LIRP can improve financial outcomes in retirement.

2. Methodology and Assumptions

2.1. Overview

Let (x) represent an individual aged x and let T(x) be the future lifetime random variable for (x).

We assume that (x) is endowed with initial wealth E_x. We set E₃₅ = 50K, E₄₅ = 200K, and E₅₅ = 500K, and we assume further that (x) can invest E_x in a mutual fund and purchase life insurance.

We define the following:

• FA = face amount of the life insurance;
• n = number of premium payments;
• E_x = endowment of wealth of (x) at time 0;
• FB = mutual fund balance at age 65;
• α = percentage of accumulated mutual fund balance (FB) to withdraw at age 65. Beyond age 65, the mutual fund withdrawals are increased for inflation;
• m = number of annual withdrawals from the life insurance product.

We fix all of the values except FB a priori and we also fix values for the pre- and postretirement tax rate and the loan interest rate.

We define the premium burden to be the present value of future life insurance premiums divided by E_x.

We perform our calculations using two disjoint models: Our Excel-based market model for the market and mutual fund calculations, and New York Life’s (NYL’s) illustration system for the insurance calculations.

We compute premiums and dividends using the illustration system, with dividends being added to the policy’s cash value. Moreover, we use the illustration system to compute the amount of each annual withdrawal from the life insurance product.

We fix an allocation strategy for the mutual fund and we simulate 250 market outcome scenarios. Please see Section 2.5 for more information about the asset allocation strategies.

In the decumulation phase, we assume that the retiree will follow a systematic withdrawal plan; in other words, they desire an annual income that is a fixed percentage α of their mutual fund balance FB at age 65, increased for inflation thereafter. If they are also using a LIRP, we assume that for the first m years of retirement, they take withdrawals (or loans) from the life insurance product. Thus, they can decrease the amount that they withdraw from the mutual fund, thereby preserving the fund value.

We examine whether the retiree has adequate income and bequest using the metrics described in Section 2.2 below and we compare the performance of the resulting portfolios.

2.2. Mortality Assumption and Measures of Portfolio Performance

We measure the performance of the portfolio using two metrics: Income risk and legacy potential. Income risk measures how often, in 250 scenarios, income sources (both the mutual fund and the income provided by the life insurance product) were depleted before the 75th percentile of T(x). Legacy potential is the sum of the mutual fund value plus the death benefit at the 50th percentile of T(x). Mortality is based on the Society of Actuaries Annuity 2012 Basic Mortality Table with Improvement Scale G2. Thus, for example, according to our mortality table, the 50th percentile of T(35) is 45 and the 75th percentile is 51. For (35), income risk masures how often, in 250 trials, income is depleted before age 86, while legacy potential measures the mutual fund value plus death benefit at age 80.

In the retirement period, retirees are exposed not only to investment risk but also to longevity risk, withdrawal rate risk, inflation risk, and sequence of returns risk. The income risk metric incorporates all of these.

We can visualize portfolio performance by plotting legacy potential versus income risk and then identifying “efficient” portfolios, i.e., portfolios that maximize legacy potential while minimizing income risk. In Section 3, we see that the inclusion of a life insurance product in a retirement portfolio can improve financial outcomes and we identify which face amounts, withdrawal patterns, issue ages, and asset allocation strategies are most efficient.

We describe the life insurance product that we modeled and elaborate on our assumptions below.

2.3. The Insurance Product—Limited Pay Whole Life (LPWL)

In our modeling, we construct the LIRP with NYL’s Custom Whole Life (CWL) product. CWL is a participating (dividend-paying), cash value, limited payment whole life (LPWL) policy. Policyholders can customize the duration of their premium payments. Subject to the limitations of an MEC, the accumulation of the cash value is tax-deferred, the death benefit is tax-free, and policyholders can use partial surrenders and policy loans to supplement their income.

2.4. Issue Ages (X)

We consider policies issued at ages 35, 45, and 55 and assume that retirement occurs at age 65.

2.5. The Portfolio

We consider a portfolio that consists of a mutual fund and possibly a life insurance product for the LIRP. The life insurance product is described in Section 2.3.

For the mutual fund, we examine four different allocations between stocks and bonds.

• Moderate strategy: 30% stocks, 70% bonds
• Balanced strategy: 50% stocks, 50% bonds
• Growth strategy: 70% stocks, 30% bonds
• Aggressive strategy: 90% stocks, 10% bonds

We did initial testing to determine the optimal preretirement asset allocations. We describe the asset allocations that we used in our simulations in

Table 1. Preretirement asset allocation.

Age	Preretirement Asset Allocation
35	Aggressive
45	Age 45–55: Aggressive; Age 55–65: Moderate
55	Balanced

below.

Then, we varied the postretirement asset allocation and examined the portfolio performance with and without the LIRP.

2.6. Simulation of Market Outcomes

We assume that the stock and bond returns are correlated, lognormally distributed random variables. We use the @Risk software package to implement Monte Carlo simulation. We simulate 250 market return scenarios, each of which had a 60-year time frame. Our assumptions are summarized in

Table 2. Market parameters.

	Stock	Bond
Mean Return	7%	3%
Standard Deviation	15%	5.5%
Correlation		20%

below.

2.7. Number of Premium Payments (N)

For policies issued at ages 35 and 45, we assume a 20-year premium payment period. For 55 year olds, we assume a 10-year premium payment period. We compute the premium on the basis of the face amount and the number of years of level premium payments using the illustration software.

2.8. Face Amounts (FA)

For each issue age, we consider six different face amounts. For the 35-year-old case, we look into a range of face amounts from $50,000 to $100,000. For the 45-year-old case, the range of face amount is from $100,000 to $200,000. For the 55-year-old case, the range of face amount is $100,000 to $400,000. We assume lower face amounts for younger individuals because they were endowed with lower initial wealth E_x.

2.9. Number of Withdrawals (M)

As a supplement to mutual funds, the life insurance product allows policyholders to take out a certain amount of money as an income source for their retirement living expenses. We examine withdrawal periods ranging from 10 to 25 years. The money withdrawn will subsequently decrease the accumulated cash value as well as the death benefit. We use the illustration software to compute the withdrawal amount, cash value, loan interest, and death benefit.

3. Results

In this section, we present our numerical results. We first present a case study for illustration, and then, more generally, we contrast numerous portfolios that include a LIRP with those that exclude it. Moreover, we contrast the results for different face amounts, withdrawal patterns, and issue ages. Specifically, we plot legacy potential versus income risk and identify an Efficient Income Frontier (EIF), which consists of portfolios that best maximize legacy potential while minimizing income risk.

3.1. Case Study

Consider a single male aged 55 who has initial wealth of $500,000 to invest in mutual funds. He considers using a LIRP to optimize his retirement portfolio. Upon retirement at age 65, he makes withdrawals according to a systematic withdrawal plan with the initial withdrawal amount equal to 3.5% of the initial mutual fund balance, increased for inflation thereafter.

As we described in Section 2.5, prior to retirement, he invests according to the balanced allocation strategy. In

Table 3. Selected values of income risk for the case study. FA: face amount

Number of Withdrawals	FA = $100,000	FA = $160,000	FA = $220,000
10	20%	20%	20%
11	19%	19%	20%
12	19%	19%	19%

and

Table 4. Selected values of legacy potential for the case study.

Number of Withdrawals	FA = $100,000	FA = $160,000	FA = $220,000
10	$530,067	$560,036	$592,848
11	$531,625	$562,516	$594,654
12	$532,988	$564,898	$596,886

, we show selected values of the income risk and legacy potential, respectively, that result if the investor chooses the face amount and number of withdrawals shown in the header row and column. We assume the balanced asset allocation after retirement as well.

For example, if the investor buys life insurance with 100K face amount and withdraws 10 years of income during retirement, the income risk is 20%, and the legacy potential is $530,067.

Now, we contrast the results for the growth and aggressive asset allocation strategies. In Figure 1, we show the allocation of E_x among stocks (blue), bonds (red), and life insurance premiums (green). For example, for the growth strategy, the premium burden, or present value of future life insurance premiums, is 41% of the initial endowment E_x. The remaining 59% is allocated 70/30 to stocks and bonds.

In Figure 2 we show the values of income risk and legacy potential with and without a LIRP for fixed values of the face amount and number of withdrawals. We see that under both asset allocation strategies, despite the initial outlay of premiums, the inclusion of the LIRP decreases the income risk and increases the legacy potential. The aggressive strategy produces higher legacy potential but also increases income risk compared to the growth strategy.

3.2. The Efficient Income Frontier

In this section, we show several plots of income risk versus legacy potential for portfolios that consist only of a mutual fund, as well as for those that include a LIRP and a mutual fund. As the graphs show, the portfolios that include the LIRP often dominate those that exclude it.

In Figure 3, the issue age is fixed at 55. We first remark that because we wish to maximize legacy potential and minimize income risk, the optimal, or most efficient, portfolios are those in the “northwest” section of the graph. For portfolios that include only a mutual fund, there are only four portfolios corresponding to the four postretirement asset allocation strategies: Moderate, balanced, growth, and aggressive. We connect these four portfolios with the orange curve. We color-code other portfolios according to the postretirement investment strategy: For example, the purple dots represent portfolios which include a LIRP and in which the mutual fund is a growth fund. Each purple dot represents a different face amount or withdrawal strategy. The black curve is the EIF; in other words, it connects some of the most efficient portfolios.

In Figure 4, again, we consider a 55 year old. We color-code the dots on the graph according to the face amount of the life insurance. For example, all of the red dots correspond to portfolios with a $400K life insurance policy but with one of the 16 different income withdrawal patterns and one of the four different postretirement asset allocation strategies within the mutual fund. We see that the highest face amounts occupy the northwest corner of graph; thus, we conclude that higher face amounts produce more efficient portfolios than lower face amounts.

In Figure 5, the issue age is again fixed at 55. This time, we color-code the portfolios according to the number of withdrawals from the life insurance product. Thus, the red dots correspond to portfolios with 22–25 annual withdrawals from the life insurance but with different face amounts for the life insurance and asset allocations within the mutual fund. We see that for a fixed value of the legacy potential, the longest withdrawal patterns (red dots) produce the lowest income risk.

In

Table 5. Insurance parameters that yield the lowest income risk.

Lowest Income Risk	Issue Age	Life Insurance Policy
		Face Amount	Withdrawal Years
	35	100K	12
	45	200K	21
	55	400K	23

, we summarize the combinations of face amount and withdrawal patterns that minimize income risk for issue ages 35, 45, and 55. In

Table 6. Insurance parameters that yield the highest legacy potential.

Largest Legacy Potential	Issue Age	Life Insurance Policy
		Face Amount	Withdrawal Years
	35	100K	10
	45	200K	22
	55	400K	17

, we summarize the combinations of face amount and withdrawal pattern that maximize legacy potential for these issue ages.

Finally, in

Table 7. Issue age comparison.

Issue Age	Initial Asset	Face Amount	Premium Burden	Lowest Income Risk		Largest Legacy Potential
				Without LIRP	With LIRP	Without LIRP	With LIRP
35	50K	100K	67.63%	14.4%	13%	1,144,719	1,208,479
45	200K	200K	44.30%	11.6%	4.8%	1,291,259	1,515,885
55	500K	400K	41.21%	12%	6.8%	1,039,859	1,114,554

, we contrast the results for different issue ages. We see that, in each case, including a LIRP in the portfolio decreases income risk and increases legacy potential. We note that, in our tests, the effect is more pronounced at ages 45 and 55 than at 35.

4. Conclusions and Directions for Future Work

In this paper, we considered different asset allocation strategies, face amounts, and withdrawal strategies and examined the income risk and legacy potential of the various portfolios under simulated pre- and postretirement market outcomes. We demonstrated that portfolios that include a LIRP in addition to mutual funds often outperform portfolios without a LIRP.

There are several avenues for further investigation. First, our metrics of portfolio performance, income risk, and legacy potential, are based on percentiles of the future lifetime random variable T(x). It would be worthwhile to compare the results if we simulated outcomes from T(x) as well as market outcomes. This would allow us to compute the probability of depleting the income source prior to death (or probability of lifetime ruin) and the probability of reaching a bequest goal. These more sophisticated metrics are used in Chen and Milevsky (2003), Milevsky et al. (2006), Young (2004), Bayraktar et al. (2014, 2015), and Bayraktar and Young (2016).

Moreover, beyond the simulation approach that we used here, it would be interesting to investigate this problem via stochastic optimal control. For example, one might try to determine the premium strategy to optimize a value function based on the probability of ruin and the probability of meeting a bequest goal.

We chose to use the LPWL product for our modeling to balance sophistication (dividends, cash value, flexible duration of premium payments) with model tractability. More sophisticated products such as Universal Life (UL), Indexed Universal Life (IUL), and Variable Universal Life (VUL) are more commonly used as investment vehicles than general account whole life products. In future modeling, we would like to examine how portfolios that include, for example, a VUL-based LIRP perform compared to those that exclude a LIRP. We expect that a VUL-based LIRP will improve portfolio performance beyond our results here.